Abstract
Purpose:
Automating and standardizing the contouring of clinical target volumes (CTVs) can reduce inter-physician variability which is one of the largest sources of uncertainty in head and neck radiotherapy. Besides using uniform margin expansions to auto-delineate high-risk CTVs, very little work has been done to provide patient and disease specific high-risk CTVs. The aim of this study is to develop a deep neural network for the auto-delineation of high-risk CTVs.
Methods and Materials:
Fifty-two oropharyngeal cancer patients were selected for this study. All patients were treated at The University of Texas Cancer from January 2006 to August 2010 and had previously contoured gross tumor volume and CTVs. We developed a deep learning algorithm using deep auto-encoders to identify physician contouring patterns at our institution. These models use distance maps information from surrounding anatomical structures and the gross tumor volume as input parameters and conduct voxel-based classification to identify voxels that are part of the high-risk CTV. In addition, we developed a novel probability threshold selection function, based on the Dice Similarity Coefficient (DSC), to improve the generalization of the predicted volumes. The DSC-based function is implemented during an inner cross-validation loop and probability thresholds are selected a priori during model parameter optimization. Volumetric comparison between the predicted and manually contoured volumes was performed to assess our model.
Results:
The predicted volumes had median DSC values of 0.81 (range: 0.62–0.90), median mean surface distance of 2.8 mm (range: 1.6–5.5 mm), and median 95th Hausdorff distance of 7.5 mm (range: 4.7–17.9 mm) when comparing our predicted high-risk CTV volumes with physician manual contours.
Conclusion:
These predicted high-risk CTVs provide close agreement to the ground-truth when compared to current inter-observer variability. The predicted contours could be implemented clinically with only minor or no changes.
Keywords: head and neck cancer, radiotherapy, deep learning, segmentation
Introduction
Manual delineation of clinical target volumes (CTVs) remains a time consuming task in radiation oncology. CTVs are tissue volumes that contain the demonstrable gross tumor volume (GTV) and provide coverage for any suspected microscopic disease and pathways of tumor spread such as regional lymph nodes1. Since radiation dose is prescribed to these volumes and adequate coverage is required to achieve cure, accurate CTV delineation is essential in radiation therapy. While established guidelines are available to delineate site-specific CTVs, these volumes are still subject to high intra- and inter-observer variability for most treatment sites2–6. This variability in delineation and the heterogeneity in clinical practice hinder the ability to systematically assess the quality of the radiation therapy treatment plans and are considered major sources of uncertainty7.
When treating head and neck (H&N) cancer, radiation therapy prevails as the principal non-surgical treatment option. For this site, in particular, the complexity of radiation treatment planning and time required to delineate target and normal tissue volumes are significantly increased8 due to the large number of organs at risk located near H&N tumors. To add to this complexity, H&N treatment plans typically employ several CTVs which are used to deliver different radiation dose levels depending on risk of recurrence for that region (i.e. high-risk, intermediate-risk, and low-risk volumes). In particular, accurate delineation of the high-risk CTV is imperative and failure to provide adequate coverage has the potential to reduce tumor control and to increase the chances of loco-regional recurrence9,10.
While there’s an abundance of work in auto-delineating normal structures using atlas-based registration techniques11–13, little work has been done to auto-delineate H&N CTVs, especially to auto-delineate high-risk target volumes. Machine learning and deep learning normal tissue auto-segmentation approaches have increased in popularity over the past few years. Some improvements in normal tissue segmentation have been observed using these novel techniques; however, there remains a need to investigate these approaches for CTVs auto-delineation. To our knowledge, there are no registration-based approaches to auto-delineate high-risk CTVs. This is not surprising due to the lack of significant features in the computed tomography (CT) images (limited by the coverage of possible microscopic disease) and due to the high variability in GTV geometric shape, location, and sub-site involvement. Although definition of the high-risk CTV is guided by anatomical structures, the high-risk CTV is neither a distinct structure (such as the GTV) nor a specific anatomic structure (such as elective nodal chains). These limitations have hindered the development of auto-delineation algorithms for these volumes.
Our previous work14 has shown that distance metrics can provide sufficient information to automate the delineation of high-risk CTVs and that deep auto-encoders15,16 provide a venue for good generalization even when a few patients are used for training. This is primarily due to the fact that these models were trained on a voxel by voxel basis providing hundreds of thousands of inputs per patient for training. In addition, a preliminary study16 from our group has shown that clustering patients per site and nodal status provides an improvement in prediction performance for oropharyngeal patients.
Automating the CTV delineation process for H&N tumors would offer many clinical advantages. First, it has the potential to reduce variability in target design and clinical practice amongst radiation oncologists. This reduction in variability would provide better data for multi-institutional studies where clinical practices can greatly vary2. Secondly, it would aid in reducing physician contouring time. This would allow physicians to spend more time with patients to provide better quality of care.
In the following study, we propose a novel methodology to auto-delineate high-risk CTVs that overcomes several of the current limitations. Our approach requires only a limited amount of training data and performs well in comparison to manual contours. More specifically:
We propose a deep learning approach where the model is trained on anatomical structure’s distance map’s information to produce patient-specific high-risk CTVs.
We address, for the first time, a non-uniform margin approach to the auto-delineation of high-risk CTVs for H&N patients
We introduce a novel threshold selection function to convert probability maps into binary volumes
We present an evaluation of our methodology and show that our predicted volumes are in close agreement to manually drawn contours.
Methods and Materials
Patient and Image Characteristics
A total of 52 oropharyngeal cancer patients (11 base of tongue node-negative, 15 base of tongue node-positive, 15 tonsil node-negative, and 11 tonsil node-positive) who had undergone curative-intent intensity modulated radiation therapy for H&N squamous cell carcinoma from January 2006 to August 2010 at The University of Texas MD Anderson Cancer Center were selected from an institutional review board–approved protocol. All patients had available simulation CT scans with previously manually contoured GTVs (primary and nodal, where applicable) and high-risk CTVs used for treatment planning. Each CT image of the H&N region of 512×512 with the number of slices varying from 47 to 348 (median: 152). Voxel sizes were 0.976 mm ×0.976 mm ×2.5–3.0 mm. The contours delineated on these images were used in this study.
Stacked Auto-encoders
We chose to use stacked auto-encoders due to their ability to speed up training and to provide an improvement in predictions by initializing weights through unsupervised learning17. During unsupervised learning, only the input data is provided and the auto-encoders learns a general representation of the dataset. Hidden layer neurons were activated using the logistic function. Following this unsupervised learning step, we train the output layer through supervised learning and use cross-validation to fine-tune the network architecture. During the supervised learning step, our algorithm fine-tunes the architecture by updating the network’s weights to match the training set’s inputs to the training set’s known output. Our deep auto-encoders are composed of two hidden layers which are followed by a soft-max layer for binary classification. An illustration of the network’s architecture can be found in Supplementary Materials Figure S1. To provide an improvement in generalization, we implemented L2-norm and sparsity18 (Kullback-Leibler divergence) regularization into the mean squared error cost function (1) used during unsupervised training, while the cross-entropy cost function (2) was used during supervised training and fine-tuning:
| (1) |
| (2) |
where λ is the coefficient for the L2-norm regularization term, β is the coefficient for the sparsity regularization term, tnk is the nkth entry of the target matrix and ynk is the nkth output from the auto-encoder when the input vector is xn. Lastly, scaled conjugate gradient optimization19 was selected for training due to their higher convergence speed and classification performance20,21.
Model features and outcome
Patient’s GTV (primary and nodal for node-positive patients), high-risk CTV, and anatomical structures (mandible, skull, vertebral body, pharyngeal and nasopharyngeal air cavities, left and right parotids, maxillary arch, hyoid, thyroid cartilage, and skin) were manually contoured in Pinnacle treatment planning system (Pinnacle, Phillips Medical Systems). The high-risk CTV and GTV volumes were previously contoured for the purpose of planning the patients’ radiation therapy treatment, and underwent rigorous peer-review by a group of sub-specialized H&N radiation oncologists22, while the selected anatomical structures were contoured specifically for this study. All volumes were converted to 3D binary masks using Matlab 2016b (MathWorks, Natick, MA).
Three dimensional distance maps were calculated from the GTV and anatomical structure’s binary masks as follows: for each voxel, v(x,y,z), in the CT image space, minimum Euclidian distance vectors (r, θ, φ) were calculated for each structure (GTVs and anatomical structures) so that for each v(x,y,z) we would have 12 distance vectors, V(r, θ, φ), (13 if node-positive) and 36 (or 39) distance input features. Signed distances were used to differentiate voxels that were located inside the contoured volume. Along with these features, we extracted each voxel’s corresponding class (0 or 1) based on the high-risk CTV mask providing the following relationship:
| (3) |
To reduce the computational time, we decided to only include voxels within 5 cm of the GTV for training and predicting on new patients. This is a conservative value since all high-risk CTVs used in this study were within 2cm of the GTV. Once models are trained and are used to predict on a test patient, the output on this test patient is a patient-specific probability map of the high-risk CTV. Our preliminary work16 showed that training models by grouping patients per site and nodal status improved overall prediction performance, so this approach was implemented in the following study.
Post-processing and probability threshold selection
Once the probability map for a patient is created, we use a 3D Gaussian filter (σ = 1) to get a smooth probability map. While most machine learning algorithms use a threshold of 0.5 to convert probabilities into binary classes, we chose to optimize this probability threshold selection by including a Dice similarity coefficient23 (DSC) probability threshold selection function during cross-validation in model training. This provided a more useful metric than AUC and classification error due to the imbalance in classes. In addition, we evaluated the performance of the DSC loss function to that of distance metrics such as the mean surface distance (MSD) and the 95th percentile Hausdorff distance (95HD) between the predicted and ground-truth volumes. These metrics were evaluated by converting the probability maps into binary volumes by increasing probabilities from 0 to 1 in 0.005 steps. Three-dimensional and 2D closing and opening algorithms were utilized on the binary images for additional post-processing prior to evaluation. To prevent overfitting our models set, we evaluated the models prediction accuracy, based on DSC, for different training epochs. An epoch is a complete pass through a given dataset, meaning that at the end of each epoch all patients’ data in the trained model is seen at least once by the neural network.
Evaluation
Three-dimensional volume metrics were used to assess the performance of the predicted volumes. In addition to calculating the DSC, MSD, and 95HD between the predicted volumes and the manually contoured high-risk CTVs, we calculated the difference between volumes, the False Negative Dice (FND), the False Positive Dice (FPD)24, and the normalized volumetric difference (VD). The FND and FPD can be used as surrogates for potential near misses and overtreatment, respectively.
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
where TP, FN, and FP stand for true positive, false negative, and false positive, respectively; DNN and G stand for the auto-delineated and ground-truth (manual) contours; and dDNN,G is a vector containing all minimum Euclidian distances from each surface voxel on volume DNN to volume G. In addition, we compared CTV volumes generated using uniform margin expansions (CTV-Uni) to our ground-truth CTVs using these same metrics. An uniform expansion of 0.5 cm from the GTV was selected since it is systematically used by the DAHANCA group25. Lastly, we evaluated the differences in PTV volumes when adding a 0.3 cm margin to the ground-truth (PTV), DNN (PTV-DNN), and uniform margin (PTV-Uni) CTVs.
Cross-Validation
During model training, we utilized nested leave-one-out cross-validation (LOOCV) for parameter tuning using a grid search approach. The parameters optimized during grid search where number of layers, number of node per layer, the L2 weight regularization value at each layer, the sparsity regularization value at each layer, and the sparsity proportion at each layer. In our nested LOOCV methodology (Figure 1), all voxels from the test patient are excluded from training and are not used to predict a volume until parameters are optimized through an internal cross-validation (CV) loop. In this internal LOOCV loop, models are trained leaving out all voxels for the CV patient. Every time a model is trained in the internal LOOCV loop, the model is used to predict the high-risk CTV of the CV patient, and their prediction performance was used to determine optimal parameter selection.
Figure 1.
Block diagram of nested LOOCV. In the inner loop, model parameters are selected by maximizing the score function based on the DSC curves for all patients in the inner loop. The probability threshold value identified for the corresponding model parameters is used after training the final model to convert the predicted probability map into a binary structure on a test patient (outer loop). This final volume is then evaluated using overlap and distance metrics to compare it to the physician manually delineated high-dose CTVs.
Results
Using an Intel Xeon CPU (2.8GHz × 10 cores) and a Tesla K40 GPU, training took on average (± std dev) 2.51 ± 0.85 hours per patient and predicted high-risk CTVs were created with a mean time of 2.75 ± 0.62 seconds. While predictions were almost instantaneous, calculating distance maps for each patient prior to predicting the new volumes took on average 9.0 ± 3.3 minutes. Volume statistics for the manually contoured GTVs and high-risk CTVs, DNN CTV, Uniform CTV, and their respective PTVs, are found in Table 1 and their respective distributions are shown in Figure 2. The mean volume difference between the DNN and ground-truth CTV was 1.0 ± 29.5 cm3 (range: −73.3, 63.9), whereas this difference between the uniform and the ground-truth CTV was 47.7 ± 30.5 cm3 (range: 2.3, 126.6). All CTV volumes generated with uniform margins were found to be smaller than the ground-truth, whereas 50% of DNN predicted volumes were smaller than their corresponding ground-truth volumes. When comparing volume overlap between the ground-truth PTV and PTV-DNN we found a mean DSC of 0.81±0.05 (range: 0.67 – 0.90). The DSC values between the ground-truth PTV and PTV-Uni were significantly reduced (p < 0.0001, Wilcoxon Rank Sum Test) and had a mean of 0.73±0.10 (range: 0.35 – 0.87).
Table 1.
Volume statistics for manually contoured GTVs and high-risk CTVs and predicted CTV1s.
| Min | Median | Max | Mean | Std Dev | |
|---|---|---|---|---|---|
| GTV | 1.0 | 22.4 | 103.9 | 26.8 | 20.7 |
| CTV1 | 14.3 | 101.2 | 255.2 | 102.9 | 58.7 |
| CTV1-DNN | 16.1 | 88.6 | 273.8 | 101.1 | 55.6 |
| CTV1-Uniform | 5.3 | 56.7 | 195.9 | 62.4 | 39.2 |
| PTV1 | 24.2 | 147.0 | 389.5 | 151.1 | 80.5 |
| PTV1-DNN | 29.4 | 127.1 | 423.3 | 145.3 | 77.7 |
| PTV1-Uniform | 11.3 | 87.3 | 267.4 | 93.9 | 53.4 |
Figure 2.
Volume distributions of the gross tumor volume (GTV), ground-truth CTV (CTV1), DNN predicted CTV (CTV-DNN), and the uniform margin expansion CTV (CTV-Uni) volumes. The volume distributions of the CTV1 and CTV1-DNN volumes are similar.
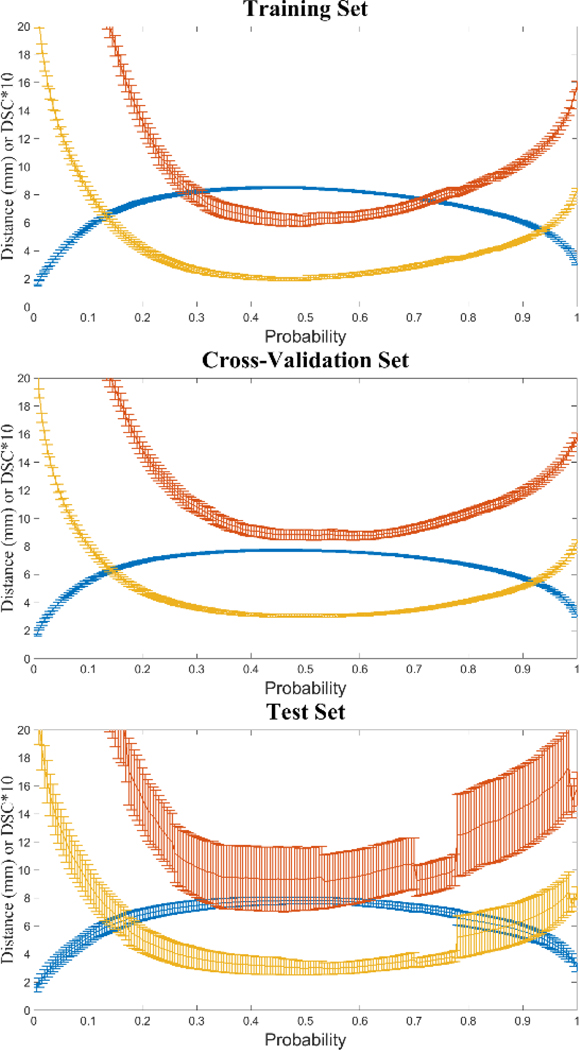
When comparing the DSC threshold selection function to the distance metrics’ performance (Figure 3), we noticed that both functions produced similar results for training, cross-validation and test sets when choosing the maximum DSC and minimum MSD and 95HD scores for probability threshold selection. Since calculation of the DSC requires minimum computational resources we opted to use this metric for probability threshold selection moving forward.
Figure 3.
Comparison of DSC and distance metrics for probability threshold selection. Mean DSC (plus standard error) is depicted in blue, whereas mean 95HD and MSD are in yellow and red, respectively. Note DSC is displayed as DSC×10 for visual comparison.
Evaluation of epochs used for training showed an initial increase in performance which was then followed by a decrease in performance on the cross-validation and test sets when using 500 epochs. This decrease in performance was not observed in the training set hinting that that the models began overfitting somewhere between 250 and 500 epochs (Figure 4).
Figure 4.
Epoch analysis results for training, cross-validation and test sets. Epochs used were 15 (blue), 50 (orange), 150 (yellow), 250 (purple), and 500 (green). Error bars provide standard error from the mean DSC value at each probability threshold.
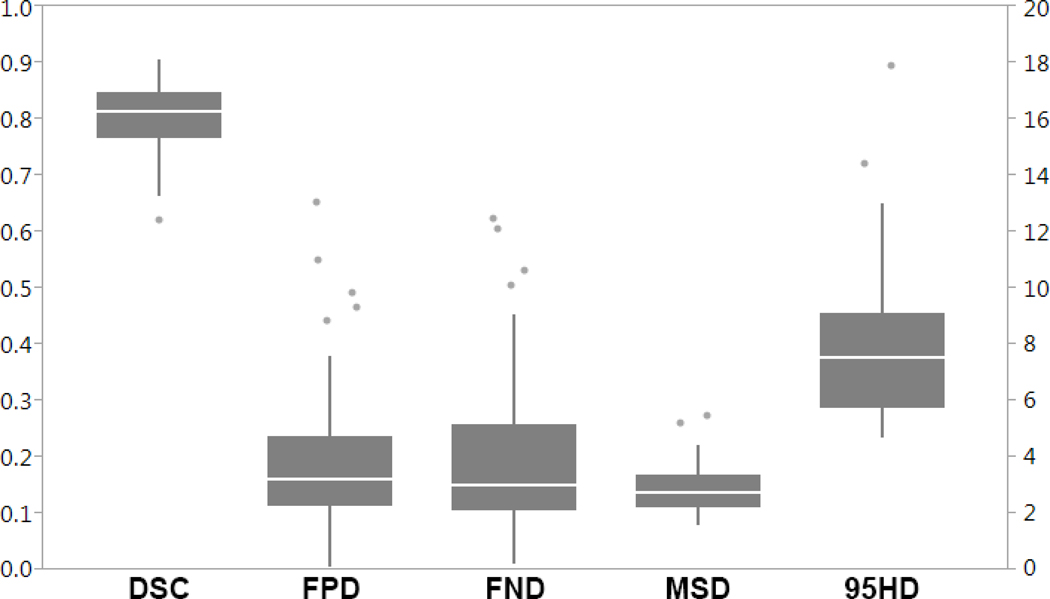
A comprehensive evaluation between the DNN auto-delineated volumes and physician manual contours is shown in supplementary materials Table S1 and Figure 5. Predicted volumes for four patients are illustrated in Figure 6. These volumes show good agreement between these volumes and the physician manual contours. For the 52 patients, the median DSC was 0.814 (range: 0.622–0.904), median MSD was 2.75 mm (range: 1.57–5.47 mm), and the median 95HD was 7.49 mm (range: 4.74–17.85 mm). Overall, the auto-delineated volumes were slightly larger on average (0.034±0.265) with median FPD of 0.199 (range: 0.004–0.652) and the median FND of 0.151 (range: 0.010–0.623). Evaluation of the ground-truth volumes showed large variability of GTV-to-CTV expansions in the cranio-caudal directions, where mean expansions were 10.7 ± 5.1 mm (range: 3.0–26.6 mm) and 9.7 ± 6.2 mm (range: 0.0–30.0 mm) in the cranial and caudal directions, respectively. The variability measured in the cranio-caudal expansion of the ground-truth CTV volumes affected the accuracy of the DNN predicted volumes in these directions showing high FND (under-treatment) and FPD (over-treatment) values for some patients.
Figure 5.
Volumetric comparison between the auto-delineated and manually contoured volumes. The Dice Similarity Coefficient (DSC), False Negative Dice (FND), False Positive Dice (FPD) values are reflected by the left vertical axis, whereas the Mean Surface Distance (MSD) and 95th percentile Hausdorff distance (95HD) values are in millimeters and correspond to the right vertical axis.
Figure 6.
Comparison between predicted CTV1 volumes (Blue) and physician manual contours (Red) for four oropharyngeal patients. The primary and nodal GTVs are included (Green). From left to right, we illustrate a case from each site and nodal status (base of tongue node negative, tonsil node negative, base of tongue node positive, and tonsil node positive).
Inter-disease site and nodal group comparison can be observed in Figure 7. The predicted volumes from patients with nodal disease showed slightly higher overlap agreement, in terms of DSC, to the ground truth than those without nodal disease (median DSC = 0.83 vs 0.77), however this difference was not statistically significant (p = 0.25, Wilcoxon Rank Sum Test). In addition, DSC values for the nodal volumes showed less variability (Table 2).
Figure 7.
Volumetric comparison between predicted and manual volumes per disease site and nodal status. The top panel illustrates the overlap metrics (DSC, FND, and FPD) between the four disease site and nodal status groups (BOT_N+: base of tongue node-positive, BOT_N0: base of tongue node-negative, To_N+: tonsil node-positive, To_N0: tonsil node-negative). The bottom panel provides a comparison between the four disease site and nodal status groups based on the distance metrics.
Table 2.
Volumetric comparison between DNN and ground-truth CTV per tumor site.
| DSC | FPD | FND | MSD (mm) | 95 HD (mm) | ||
|---|---|---|---|---|---|---|
| ToN0 | Min | 0.622 | 0.068 | 0.010 | 1.6 | 4.8 |
| Median | 0.814 | 0.147 | 0.151 | 2.5 | 7.0 | |
| Max | 0.887 | 0.652 | 0.531 | 5.5 | 17.9 | |
| Mean | 0.788 | 0.218 | 0.206 | 2.8 | 7.8 | |
| Std Dev | 0.076 | 0.172 | 0.153 | 1.1 | 3.6 | |
| ToN+ | Min | 0.769 | 0.056 | 0.025 | 1.6 | 4.8 |
| Median | 0.803 | 0.145 | 0.219 | 3.0 | 7.8 | |
| Max | 0.904 | 0.370 | 0.364 | 4.1 | 11.3 | |
| Mean | 0.816 | 0.174 | 0.194 | 3.0 | 8.1 | |
| Std Dev | 0.037 | 0.084 | 0.105 | 0.8 | 2.2 | |
| BOTN0 | Min | 0.664 | 0.004 | 0.050 | 1.9 | 5.0 |
| Median | 0.756 | 0.213 | 0.142 | 3.4 | 8.8 | |
| Max | 0.843 | 0.549 | 0.623 | 5.2 | 14.4 | |
| Mean | 0.755 | 0.234 | 0.257 | 3.5 | 8.8 | |
| Std Dev | 0.059 | 0.195 | 0.210 | 1.0 | 2.8 | |
| BOTN+ | Min | 0.781 | 0.055 | 0.033 | 1.7 | 4.7 |
| Median | 0.838 | 0.149 | 0.122 | 2.7 | 6.6 | |
| Max | 0.887 | 0.338 | 0.262 | 3.1 | 9.5 | |
| Mean | 0.840 | 0.172 | 0.147 | 2.5 | 6.7 | |
| Std Dev | 0.031 | 0.080 | 0.076 | 0.5 | 1.3 | |
Discussion
The use of deep learning in medical image segmentation has become more popular over that past few years. Most efforts have been focused on auto-segmenting normal tissues and very little work has been done to automate the delineation of clinical target volumes. In our approach, we utilized distance maps from normal structures and gross tumor volumes to learn physician patterns in auto-delineating high-risk clinical target volumes. This approach was chosen due to the lack of visible anatomical edges on CT imaging and high variability in GTV location and size. In addition, since our algorithm uses the binary contours to compute the inputs for our model, normal tissue and GTV contours made on any modality (i.e. MRI) could be used to generate automated high-risk CTVs. Furthermore, this approach could be used to train physician- or institution-specific models to automate this process while retaining patterns used for the desired clinical practice. This remains to be evaluated as it is outside the scope of this study.
Our deep learning approach was able to auto-delineate high-risk CTVs with comparable DSC values (mean DSC of 0.81) as those observed for normal tissue auto-segmentation techniques26. In their study, McCarroll et al showed that after clinically implementing a normal tissue auto-segmentation tool the average DSC between the auto-contours and physician-edited volumes was 0.78 for eight H&N normal structures. Overall, our volumes DSC values ranged from 0.62 to 0.90 and the median MSD was found to be 2.75 mm. These results are comparable to what is found in inter- and intra-observational studies for manual delineation of this volumes27,28. When using uniform margin expansions, we found that all auto-generated CTVs were smaller in volume than the ground-truth volumes and that mean difference in volumes between the DNN auto-delineated and ground-truth CTVs was 1.0 ± 29.5 cm3. It was noticed that variability in the cranio-caudal extent of the GTV-to-CTV margin expansion made difficult to assess under- and over-treatment. Upon physician review of all cases with FND and FPD values greater than 0.450, the cranio-caudal extent of the DNN predicted volumes was considered acceptable. The dosimetric effects of using auto-delineated clinical target volumes is difficult to assess without clinical outcomes data. Due to the high overlap between the predicted and ground-truth volumes we expect minimal changes to normal tissue doses. In a preliminary study16, five radiation oncologists visually inspected a subset of the DNN predicted volumes as part of a blinded study. They found 85% of the auto-delineated and 93% of the ground-truth volumes to be acceptable for clinical use with only minor changes.
Very little work has been done to auto-delineate high–dose CTVs. Belshi et al.29 proposed to automate these volumes using a 3D uniform margin expansion from manually contoured GTVs for conformal radiation therapy, however the introduction of intensity modulated radiation therapy allowed for more complex, conformal, and patient-specific RT plans, therefore requiring more accurate target definition to ensure the tumor is not under-treated and to limit dose to surrounding normal tissues. Chao et al30 showed that using a 1 cm uniform margin expansion from the GTV reduced observer variability when auto-delineating high-risk CTVs for two H&N patients, however their study did not provide an overlap comparison of these volumes to the ground-truth volume (volume used for treatment) so the ability of a 1cm uniform margin to reproduce the physicians’ goal was unclear.
Hong et al2. conducted a survey to investigate differences in CTV delineation amongst experienced H&N radiation oncologists and found significant heterogeneity between physician contours and clinical practice. They found that high-risk CTV volumes had a large standard deviation (43 cm3). In our analysis we found that the mean volume difference between predicted and ground-truth volumes was 1.0 cm3, which is just a small fraction of the variability found in the study by Hong et al showing that volume variability could be reduced through auto-delineation. Lastly, their study showed that, even though published guidelines are available to standardize H&N target volume delineation, significant variations between experienced physician contours still exist and that there is an urgent need to standardize this process. A more recent study by Blinde et al28 showed in abstract form that they observed large variability when delineating high-risk CTVs between a group of 20+ radiation oncologists. In their preliminary results they observed volume differences of up to a factor of 8. The lack of standardization in CTV delineation can be problematic for many reasons. The heterogeneity in target design and clinical practice increases variation in clinical information, and reducing this through standardized target volumes could help produce better quality clinical data. Our results are promising since our approach could be implemented in multiple institutions to improve standardization of radiation therapy treatments which could in turn reduce uncertainties in radiation therapy clinical trials.
An inherent product of the auto-delineation of clinical target volumes is the reduction of physician contouring time. This benefit is increased when dealing with H&N tumors as data suggests8 that target delineation in this region is comparatively difficult to contour and has higher inter-observer variability than other anatomical sites. Hong et al2 reported that H&N clinical target volume average contouring time was 102.5 minutes (range 60–210 minutes). While it is unknown how much time was spent delineating CTV1 alone, it is clear that any reduction in contouring time could benefit the treatment planning work-flow. The model presented in this study produces high-risk CTVs with a mean time of 10 minutes, with almost 99% of computational time devoted to preparing the inputs prior to volume prediction. This computationally expensive process could be improved by optimizing the currently used algorithm to compute the inputs using GPUs where voxel-based distance measurements could be calculated in a parallel fashion.
It has been shown that the quality of the radiation therapy treatment plan greatly depends on the delineation accuracy and physician experience31–33. Our institution’s H&N service treats about 400 patients a year and every patient treated undergoes our head and neck planning and development clinic in which the attending physician’s CTV contours are peer-reviewed by the H&N group (22). It is our belief that this peer-review process aids in the reduction of inter-observer variability and provides high quality contours for deep learning approaches. In this regard, the use of automatically delineated CTVs can help physicians bridge this gap in quality assurance when peer review is not available. A CTV auto-delineation tool could be used to provide physicians with contours prior to peer-review sessions where the radiation oncologists would assess the contours’ coverage and make any edits, if necessary, prior to approval of target volumes.
Our approach has a few limitations. First, it relies on manual delineation of normal structures and the gross tumor volume where some inter-observer variability has been reported. Furthermore, image quality and dental artifacts could impact the accuracy of these segmentations, but since the manual segmentations used in this study were reviewed by 2 or more physicians we felt this peer-review process provided better quality normal tissue and target volume segmentations. The time-consuming task of manually delineating the structures used in this study could be overcome by implementing auto-segmentation of these volumes via atlas-based segmentation and PET-based segmentation of normal structures and GTV, respectively, which could aid in the reduction of inter-observer variability. Second, our patient set had high variability in disease presentation. This variability was reduced by training auto-delineation models on patients per disease site and nodal status, but even for patients within each disease site and nodal status groups we noticed that secondary sites of disease (e.g. tonsil tumor invading the soft palate) could translate to poor predictive performance. Using a larger number of patients and clustering these based on disease extent could improve pattern recognition in physician delineation patterns, but this remains to be investigated. Lastly, all volumes used for training our models were collected from a single institution and these might not represent clinical practice at other institutions.
By implementing a DSC-based threshold selection function, our DNN auto-delineation algorithm accurately identified physician patterns to predict clinically acceptable high-risk CTV contours. Our models allowed for the prediction of new volumes within a few minutes and have the potential to greatly reduce physician contouring time. The majority of the predicted high-risk CTVs were in close agreement with the physician manual contours and could be implemented clinically with only minor or no changes.
Supplementary Material
Acknowledgments
Funding sources and financial disclosures: Dr Fuller is supported by the Andrew Sabin Family Foundation; Dr. Fuller is a Sabin Family Foundation Fellow. Dr. Fuller receives funding and salary support from the National Institutes of Health (NIH), including: the National Institute for Dental and Craniofacial Research Award (1R01DE025248–01/R56DE025248–01); a National Science Foundation (NSF), Division of Mathematical Sciences, Joint NIH/NSF Initiative on Quantitative Approaches to Biomedical Big Data (QuBBD) Grant (1R01CA225190–01 and NSF 1557679); the NIH Big Data to Knowledge (BD2K) Program of the National Cancer Institute (NCI) Early Stage Development of Technologies in Biomedical Computing, Informatics, and Big Data Science Award (1R01CA214825–01); NCI Early Phase Clinical Trials in Imaging and Image-Guided Interventions Program (1R01CA218148–01); an NIH/NCI Cancer Center Support Grant (CCSG) Pilot Research Program Award from the UT MD Anderson CCSG Radiation Oncology and Cancer Imaging Program (P30CA016672) and an NIH/NCI Head and Neck Specialized Programs of Research Excellence (SPORE) Developmental Research Program Award (P50 CA097007–10). Dr. Fuller has received direct industry grant support and travel funding from Elekta AB. Drs. Meheissen and Elgohari receive funding from the Egyptian ministry of higher education.
Footnotes
Conflict of interest statement: The authors declare no conflicts of interest.
References
- 1.Commission I, Radiation ON. Prescribing, Recording and Reporting Photon Beam Therapy (Supplement to ICRU Report 50). 1999. [Google Scholar]
- 2.Hong TS, Tome WA, Harari PM. Heterogeneity in head and neck IMRT target design and clinical practice. Radiother Oncol. 2012;103(1):92–98. doi: 10.1016/j.radonc.2012.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Eminowicz G, Mccormack M. Variability of clinical target volume delineation for definitive radiotherapy in cervix cancer. Radiother Oncol. 2015;117(3):542–547. doi: 10.1016/j.radonc.2015.10.007. [DOI] [PubMed] [Google Scholar]
- 4.Li XA, Tai A, Arthur DW, et al. Variability of target and normal structure delineation for breast- cancer radiotherapy: a RTOG multi-institutional and multi- observer study. Int J Radiat Oncol Biol Phys. 2009;73(3):944–951. doi: 10.1016/j.ijrobp.2008.10.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lütgendorf-caucig C, Fotina I, Stock M, Pötter R, Goldner G, Georg D. Feasibility of CBCT-based target and normal structure delineation in prostate cancer radiotherapy : Multi-observer and image multi-modality study. Radiother Oncol. 2011;98:154–161. doi: 10.1016/j.radonc.2010.11.016. [DOI] [PubMed] [Google Scholar]
- 6.Lütgendorf-caucig C, Fotina I, Gallops-Evans E, et al. Multicenter evaluation of different target volume delineation concepts in pediatric Hodgkin’s lymphoma: A case study. Strahlenther Onkol. 2012;188:1025–1030. doi: 10.1007/s00066-012-0182-4. [DOI] [PubMed] [Google Scholar]
- 7.Van Herk M. Errors and Margins in Radiotherapy. 2004;14(1):52–64. doi: 10.1053/j.semradonc.2003.10.003. [DOI] [PubMed] [Google Scholar]
- 8.Multi-Institutional Target Delineation in Oncology. Human – Computer Interaction in Radiotherapy Target Volume Delineation : A Prospective, Multi-institutional Comparison of User Input Devices. 2011;D:794–803. doi: 10.1007/s10278-010-9341-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lee N, Xia P, Fischbein NJ, Akazawa P, Akazawa C, Quivey J. Intensity-Modulated Radiation Therapy for Head-And-Neck Cancer: The UCSF Experience Focusing On Target Volume Delineation. Int J Radiat Oncol Biol Phys. 2003;57(1):49–60. doi: 10.1016/S0360-3016(03)00405-X. [DOI] [PubMed] [Google Scholar]
- 10.Eisbruch A, Foote RL, Sullivan BO, Beitler JJ. Intensity-Modulated Radiation Therapy for Head and Neck Cancer : Emphasis on the Selection and Delineation of the Targets. Semin Radiat Oncol. 2002;12(3):238–249. [DOI] [PubMed] [Google Scholar]
- 11.Sharp G, Fritscher KD, Pekar V, et al. Vision 20 / 20 : Perspectives on automated image segmentation for radiotherapy. Med Phys. 2014;41(5). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yang J, Zhang Y, Zhang L, Dong L. Automatic Segmentation of Parotids from CT Scans Using Multiple Atlases. Med Image Anal Clin A Gd Chall. 2010:323–330. [Google Scholar]
- 13.Han X, Hoogeman MS, Levendag PC, et al. Atlas-based auto-segmentation of head and neck CT images. MICCAI 2008. 2008;(Part II):434–441. doi: 10.1007/978-3-540-85990-1. [DOI] [PubMed] [Google Scholar]
- 14.Cardenas C, Wong A, Mohamed A, et al. Delineating High-Dose Clinical Target Volumes for Head and Neck Tumors Using Machine Learning Algorithms. Med Phys. 2016;43(6):3321–3322. [Google Scholar]
- 15.Cardenas CE, McCarroll R, Court LE, et al. Deep Learning on Clinically-Clustered Patients Improves Auto-delineation of Oropharyngeal High-risk Clinical Target Volumes. Med Phys. 2017;44(7):3052. [Google Scholar]
- 16.Cardenas CE, McCarroll R, Court LE, et al. Deep Learning Algorithm for Auto-Delineation of High-Risk Oropharyngeal Clinical Target Volumes with Built-in Dice Similarity Coefficient Parameter Optimization Function. Med Phys. 2017;44(7):3160–3161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bengio Y, Lamblin P, Popovici D, Larochelle H. Greedy Layer-Wise Training of Deep Networks. Adv Neural Inf Process Syst. 2007;(1):153–160. [Google Scholar]
- 18.Olshausen BA, Fieldt DJ. Sparse Coding with an Overcomplete Basis Set: Strategy Employed by V1? Vis Res. 1997;37(23):3311–3325. [DOI] [PubMed] [Google Scholar]
- 19.Meiller MF. A Scaled Conjugate Gradient Algorithm for Fast Supervised Learning. 1993;6:525–533. [Google Scholar]
- 20.Orozco J, García CAR. Detecting Pathologies from Infant Cry Applying Scaled Conjugate Gradient Neural Networks. 2003;(April):349–354. [Google Scholar]
- 21.Sharma B, Venugopalan PK. Comparison of Neural Network Training Functions for Hematoma Classification in Brain CT Images. 2014;16(1):31–35. [Google Scholar]
- 22.Cardenas CE, Mohamed ASR, Tao R, et al. Prospective Qualitative and Quantitative Analysis of Real-Time Peer Review Quality Assurance Rounds Incorporating Direct Physical Examination for Head and Neck Cancer Radiation Therapy. Radiat Oncol Biol. 2017;98(3):532–540. doi: 10.1016/j.ijrobp.2016.11.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dice LR. Measures of the Amount of Ecologic Association Between Species. Ecology. 1945;26(3):297–302. doi: 10.2307/1932409. [DOI] [Google Scholar]
- 24.Babalola KO, Patenaude B, Aljabar P, et al. An evaluation of four automatic methods of segmenting the subcortical structures in the brain. Neuroimage. 2009;47(4):1435–1447. doi: 10.1016/j.neuroimage.2009.05.029. [DOI] [PubMed] [Google Scholar]
- 25.Hansen CR, Johansen J, Samsøe E, et al. Consequences of introducing geometric GTV to CTV margin expansion in DAHANCA contouring guidelines for head and neck radiotherapy. Radiother Oncol. 2017;(in press). doi: 10.1016/j.radonc.2017.09.019. [DOI] [PubMed] [Google Scholar]
- 26.McCarroll R, Yang J, Cardenas CE, et al. Machine Learning for the Prediction of Physician Edits to Clinical Auto-Contours in the Head-And-Neck. Med Phys. 2017;44(6):3160. [Google Scholar]
- 27.Awan M, Zafereo M, Lewis CM, et al. Interdisciplinary Variation in Segmentation of High-Risk Postoperative Tumor Volumes in the Head and Neck. Radiat Oncol Biol. 87(2):S584–S585. doi: 10.1016/j.ijrobp.2013.06.1551. [DOI] [Google Scholar]
- 28.Belshi R, Pontvert D, Rosenwald J-C, Gaboriaud G. Automatic three-dimensional expansion of structures applied to determination of the clinical target volume in confomal radiotherapy. Radiat Oncol. 1997;37(3):731–736. [DOI] [PubMed] [Google Scholar]
- 29.Chao KSCL Hide SHB, Hen HAC, et al. Reduce in Variation and Improve Efficiency of Target Volume Delineation by a Computer-Assisted System Using a Deformable Image Registration Approach. 2007;68(5):1512–1521. doi: 10.1016/j.ijrobp.2007.04.037. [DOI] [PubMed] [Google Scholar]
- 30.Blinde S, Mohamed ASR, Newbold K, et al. Large Interobserver Variation in the International MR-LINAC Oropharyngeal Carcinoma Delineation Study. Int J Radiat Oncol Biol Phys. 2017;99(2):E639–E640. doi: 10.1016/j.ijrobp.2017.06.2145. [DOI] [Google Scholar]
- 31.Boero IJ, Paravati AJ, Xu B, et al. Importance of Radiation Oncologist Experience Among Patients With Head-and-Neck Cancer Treated With Intensity-Modulated Radiation Therapy. J Clin Oncol. 2016;34(7). doi: 10.1200/JCO.2015.63.9898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Peters LJ, O’Sullivan B, Giralt J, et al. Critical impact of radiotherapy protocol compliance and quality in the treatment of advanced head and neck cancer: Results from TROG 02.02. J Clin Oncol. 2010;28(18):2996–3001. doi: 10.1200/JCO.2009.27.4498. [DOI] [PubMed] [Google Scholar]
- 33.Wuthrick EJ, Zhang Q, Machtay M, et al. Institutional Clinical Trial Accrual Volume and Survival of Patients With Head and Neck Cancer. J Clin Oncol. 2015;33(2):156–164. doi: 10.1200/JCO.2014.56.5218. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.