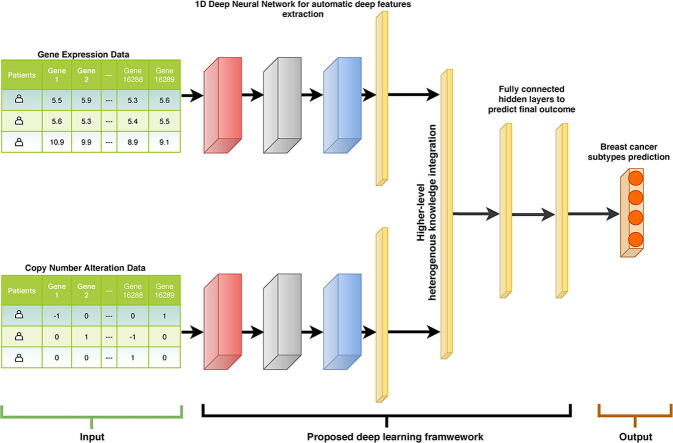
Graphical abstract
Keywords: Deep learning, Omics data, Classification, Data integration, Breast cancer
Abstract
Classification of breast cancer subtypes using multi-omics profiles is a difficult problem since the data sets are high-dimensional and highly correlated. Deep neural network (DNN) learning has demonstrated advantages over traditional methods as it does not require any hand-crafted features, but rather automatically extract features from raw data and efficiently analyze high-dimensional and correlated data. We aim to develop an integrative deep learning framework for classifying molecular subtypes of breast cancer. We collect copy number alteration and gene expression data measured on the same breast cancer patients from the Molecular Taxonomy of Breast Cancer International Consortium. We propose a deep learning model to integrate the omics datasets for predicting their molecular subtypes. The performance of our proposed DNN model is compared with some baseline models. Furthermore, we evaluate the misclassification of the subtypes using the learned deep features and explore their usefulness for clustering the breast cancer patients. We demonstrate that our proposed integrative deep learning model is superior to other deep learning and non-deep learning based models. Particularly, we get the best prediction result among the deep learning-based integration models when we integrate the two data sources using the concatenation layer in the models without sharing the weights. Using the learned deep features, we identify 6 breast cancer subgroups and show that Her2-enriched samples can be classified into more than one tumor subtype. Overall, the integrated model show better performance than those trained on individual data sources.
1. Introduction
Cancer is a disease characterized by the uncontrolled cell growth in an organ, i.e. the site where cells have originated from. Breast cancer begins in the breast tissue and may start in the duct or lobe of the breast. When the “controls” in breast cells are not working properly, they divide continually and result in a lump or tumor. It is a complex, heterogeneous disease at both the cellular level and molecular level with differing prognostic and clinical outcomes. In clinical practice, breast cancer is classified based upon receptor expression. It is known as estrogen-receptor-positive (ER+) if the cancer cells, like normal breast cells, have receptors for the hormone estrogen that they rely on in order to promote their growth. Statistics have shown that approximately 67% of breast cancers test positive for hormone receptors [1]. Testing whether a patient is hormone receptor positive or negative is crucial in clinical diagnosis as the results can help physicians in determining whether the cancer is more likely to respond to hormonal treatments or chemotherapy.
A study done in 2000 has emerged a new genomic paradigm [2] in discovering the intrinsic subtypes of breast cancer. When they looked at the gene expression profiles of breast cancers, they found that the cancers segregated into 5 clusters: luminal A and B, Normal, Basal-like group and the HER-2 enriched. A genome-wide gene expression profiling using microarray data was developed into a PCR-based test with a curated list of 50 genes known as the PAM50 signature. The PAM50 signature measures the expression levels of these 50 genes in tumor samples and classifies breast cancers into one of the four intrinsic subtypes (Luminal A, Luminal B, HER-2 enriched and Basal-like). This classification has shown to be prognostically independent of clinicopathologic factors and can determine the sub-group of patients who are more likely to benefit from adjuvant chemotherapy [3].
Machine learning approaches have been previously applied to identify the molecular subtypes (such as PAM50 subtypes) of breast cancer using microarray-based gene expression profiles [4]. As we know, cancer progression is impelled by the accumulation of somatic genetic mutations, which consist of single nucleotide substitutions, translocations and copy number alterations (CNA) [5]. CNAs are somatic changes in the copy numbers of a DNA sequence that arise during the process of cancer development. This results in changes to the chromosome structure in the form of gain or loss in copies of DNA segments, and has been found to be prevalent in many types of cancer [6]. Genes in the CNA regions, if mutated, can create abnormal proteins and functions which may lead to uncontrollable growth of cancer cells. Therefore, it will be useful to predict the molecular subtypes of breast cancer by integrating both patient-specific CNA profiles and gene expression profiles.
Generally speaking, both of the CNA profile- and gene expression profile-based feature vector for supervised machine learning algorithms includes majority of the genes in the human genome. That is, each sample is represented by almost twenty thousands of genes. Supervised machine learning methods, such as support vector machine (SVM) and random forest (RF), work well to draw a decision boundary between two classes or the decision boundaries among multiple classes, but this becomes challenge when the size of the feature vector is much larger than the number of training samples in many bioinformatics applications. Yeung and Ruzzo used a classical method named as principal component analysis (PCA) for dimension reduction [7]. However, PCA linearly reduces the dimension of the data and fails to capture the non-linear relationship of the data. Recently, deep learning (DL) based models demonstrate advantages to handle high-dimensional data and extract linear and non-linear relationships of the data.
With the improvement of GPU hardware and availability of massive training datasets, Krizhevsky et al. [8] has rekindled the interest in deep learning models such as convolutional neural networks (CNNs) by achieving a significant gain over existing methods in image classification using data sets from the ImageNet challenge. Recently, many advancements and improvements have been made on deep learning. Razavian et al. [9] adapted deep features from CNN to build a pre-trained CNN called OverFeat and achieved remarkable performance improvement by simply applying the model to a variety of visual recognition tasks in which OverFeat was not trained for [10]. Yi et al. developed a Siamese network [11], which includes two subnetworks with two different inputs at the same time. The two subnetworks share the same configuration with the same parameters and weights. The network can learn a unified representation of the inputs from the two subnetworks. Hinton et al. introduced a technique called Dropout as a form of regularization by selecting a random set of activations during training in order to set their weights as zero within each layer [12]. The output is an averaged result of predictions of several other grouped models. Wan et al. proposed DropConnect to generalize the Dropout model [13] and it achieved state-of-the-art performance on the benchmark datasets as compared to Dropout. Another DL architecture is deep belief network (DBN). DBNs can be trained in a layer-by-layer approach and these layers are made of restricted Boltzmann machines (RBMs). Hinton proposed an approach called contrastive divergence to learn the weights of RBM using maximum likelihood method [14].
A deep neural network (DNN) can be pre-trained using a DBN. That is, a DBN network is first trained and the learned weights from this pre-trained DBN are then used to initialize the weights of the DNN. This is useful when the number of training data is small because the random initialization of weights can significantly hamper the performance of the learned model. Since the learned DBN weights are usually close to the optimal values of the best model, this approach not only improves the performance of the model but also minimizes the duration of fine-tuning [15]. Stacked autoencoder is another variant of DL-based approach to produce a good representation of input data. This network can capture the ordered grouping of the input in an unsupervised fashion. Vincent et al. proposed this idea to produce robust representation of the corrupted input data to recover the corresponding input data [16]. This was also referred as feature extraction for the representation of the input data. A DNN can be built to stack an autoencoder on the top of another. They demonstrated that this approach can improve classification performance in many applications.
DNN models have been applied for different bioinformatics domains. Denas and Taylor preprocessed their genomic data as a two-dimensional matrix, where rows are the transcription factor activity profiles of genes and columns are the positions of different genome elements [17]. They applied a deep convolutional neural network (DCNN) model to predict DNA-binding sites. Zeng and Gifford introduced a DNN to predict the DNA methylation level of a single CpG from the corresponding sequence [18], which showed improved performance than all previous models. Leung et al. used mouse RNA-Seq data to build a DNN-based model to predict splicing patterns in individual tissues and achieved the best result among the other available methods such as Bayesian methods [19].
Zhou et al. were the first to propose the DCNN based approach to predict the effects of noncoding-variants from large-scale chromatin-profiling data and achieved state-of-the-art predictive performance [20]. They named their method as the deep learning-based sequence analyzer (DeepSea). Experimental results showed that DeepSea could also precisely predict the consequence of specific SNPs on TF binding. Analyzing gene expression data is very important in discovering tumor-specific biomarkers and clinical diagnosis [21], but high-dimensionality and the noisiness in the gene expression data pose a great challenge to biologists for cancer detection using traditional machine learning methods. Dananee et al. proposed a deep learning based approach which implemented a stacked denoising autoencoder (SADE) to analyze high dimensional gene expression data [22]. This SADE network condensed the high-dimensional gene expression data into a lower dimension and produced a new eloquent illustration of its input. The SADE identified a set of gene regulatory targets, which has the potential to be used in cancer diagnosis. Somatic point mutation based cancer classification (SMCC) is very important in determining the patient-specific cancer conditions so that personalized therapy can be provided. However, existing SMCC methods do not generate satisfactory cancer type or subtype classification results due to the high sparsity and small sample size of the used datasets. Yuan et al. [23] proposed a new DNN based model called DeepGene to overcome these issues. This model first filtered the genes by mutation rate to remove irrelevant genes from their data. It then indexed the genes by their non-zero elements, allowing DeepGene to overcome the data sparsity problem. Finally, the outputs of these two steps were fed into a DNN which performed automatic extraction of features for SMCC. DeepGene achieved 24% better prediction performances than the existing methods. Liang et al. also proposed a model which used DBN for the purpose of clustering cancer patients by integrating multimodal data [24]. They integrated gene expression data and clinical data (e.g. survival time) and fed the output into the DBN model. This model can capture intra- and cross-modality correlations and learn a unified representation of the input. As a result, this model outperformed existing methods in clustering cancer patients.
With the availability of more and more multi-omic data, integration of multiple omic datasets to train a network becomes essential as this technique may incorporate biological knowledge, which may be complimentary in the datasets, into one unified model. For example, Gevaert et al. used a Bayesian network to integrate clinical data and patient-specific gene expression data to predict the prognosis of breast cancer [25]. Van Vliet et al. proposed a new nearest mean classifier to integrate these two types of data to achieve the same goal [26]. A kernel-based method has also been developed to integrate different types of biological data [27]. Kernel-based approach first found the kernel of each of the original datasets represented as matrices via a specified kernel function. Then these kernel matrices were combined into one single kernel matrix by performing a linear sum of these kernel matrices. Finally, SVM was used for classification using the combined kernel matrix. The kernel-based data integration method provided better prediction performances in genomic data analysis than other traditional data integration approaches. Wang et al. used the kernel-based method to integrate three types of biological data: molecular structure, molecular activity, and phenotype data to predict novel drug-disease interactions using SVM [28]. Daemen et al. showed that clinical data and microarray data can be efficiently integrated using the kernel-based method to provide patient-specific therapy [29].
Recently, Eser et al. proposed a new integrative deep learning based framework called FIDDLE (Flexible Integration of Data with Deep Learning) to integrate multiple types of genomic data to predict yeast Transcription Start Site sequencing (TSS-seq) [30]. FIDDLE demonstrated improved prediction performance when its input was the integration of multiple datasets (i.e. RNA-seq and DNA sequence) instead of only one dataset (i.e. RNA-seq or DNA sequence). Dutil et al. [31] used a graph neural network based approach to capture complex spatial context to answer biological questions i.e. prediction of clinical attributes. They have used gene expression data from the Cancer Genome Atlas (TCGA) project [32] to perform their experiments. Ma and Zhang [33] and Jurman et al. [34] introduced DCNN based methods to transform omics data into abstract level in order to get final inferencing output.
Ismailoglu et al. [35] integrated gene expression and protein expression data to classify molecular subtypes of breast cancer. They have 12% improved prediction performance than the model that was trained using only protein data. However, there are no DNN models built for classifying molecular subtypes of breast cancer by integrating both CNA profiles and gene expression profiles. In this paper, we propose to build our CNA profile- and gene expression profile-based classification model for molecular subtypes of breast cancer by using an integrative deep neural network learning approach. The molecular subtypes of breast cancer we aim to predict include the status of estrogen-receptor (ER+ and ER−), which is a binary classification problem, and the status of subtypes (luminal A, luminal B, HER-2 enriched and basal-like), which is a multi-class classification problem.
This paper is organized as follows: Section 2 describes our proposed and baseline DNN architectures, and the datasets that were used during the experiments, then following that 3, 4 present and discuss our experimental findings, and finally Section 5 presents our conclusions.
2. Materials and methods
2.1. Datasets
We used copy number alteration data and gene expression data from METABRIC (Molecular Taxonomy of Breast Cancer International Consortium) project [36]. The group collected around 2000 clinically annotated primary fresh frozen breast cancer specimens along with a portion of normal specimens from different North American and European tumor banks. The primary tumors could be categorically linked to DNA and RNA specimens. The authors performed quality control assessment and excluded the mismatches between DNA and RNA. Paired DNA and RNA profiles were created by collecting tumour samples from 991 female patients, which was called a discovery set (we call it as a training set). A second group of 984 cases was collected in a later stage which included low cellularity tumors, DCIS (Ductal carcinoma in situ), and three benign cases. This group represents a validation set and was used to test reproducibility of the integrative cluster and clinical outcome associations. We use this as an independent test set to evaluate our models.
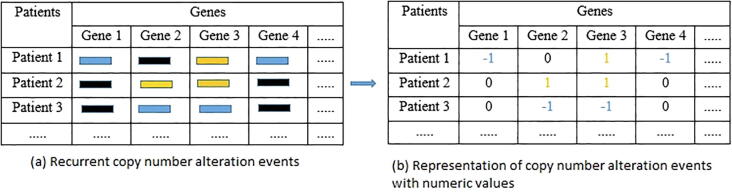
To determine copy number alteration events in each breast cancer patient, we focus on gene-specific CNA events as shown in Fig. 1. We use the set of discrete copy number calls: −1 = copy number loss, 0 = diploid, 1 = copy number gain. For each CNA region in each patient, we retrieve its gene information based on its chromosome positions using the biomaRt R package.
Fig. 1.
Representation of copy number alteration events. Patient-level individual copy number alterations are matched to gene regions in human genome (hg19). (a) Recurrent copy number alteration events. The blue segments are copy number loss, the black segments are copy number diploid and the orange segments are copy number gain. (b) Representation of copy number alteration events with numeric values. “−1” represents copy number loss, “0” represents copy number diploid and “1” represents copy number gain. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Gene expression data was generated from Illumina BeadArrays (i.e. Illumina HT-12 v3 platform). The data was preprocessed (including quantile normalization) using the beadarray R package by Curtis et al. [36]. For our experiment, we focus on the gene expression profiles of the 16,289 genes common in both CNA and gene expression data sets.
For the binary class classification, we take 991 patient samples from the discovery set as our training set and 984 patient samples from the validation set as our test set. In this training set, we have 794 samples for the ER+ class and 197 samples for the ER− class. In the test set, we have 716 samples for the ER+ class and 268 samples for the ER− class. However, for the multi-class classification, we take 935 patient samples from the discovery set as our training set and 842 patient samples from the validation set as our test set since some of the patients in the whole discovery and validation sets have no the tumor subtype information. In this training set, we have 464, 268, 87 and 116 samples for Luminal A, Luminal B, HER-2 enriched and Basal-like classes respectively. Besides, in the test set, we have 255, 224, 153 and 210 samples for Luminal A, Luminal B, HER-2 enriched and Basal-like classes respectively. It should be noted that the separation of training and test sets was done in original study [35], which was based on the samples collected at different periods. The labels of the molecular subtypes of these patients are extracted from the Supplementary Tables 2 and 3 of [36]. The gene expression data and copy number variation data used for the analysis can be accessed from European Genome-phenome Archive [37].
2.2. Deep neural network architectures
2.2.1. Base network architecture
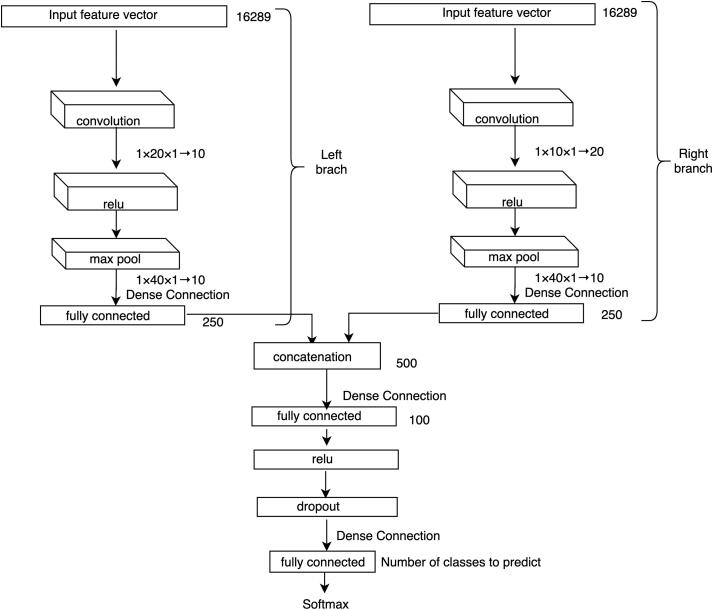
The network architecture of our base DCNN model to predict the molecular subtypes of breast cancer using individual datasets is shown in Fig. 2. Each of our samples is represented by 16,289 genes in both datasets (i.e. CNA and gene expression datasets). We treat each of these genes as a feature of the sample. This means that there are 16,289 features for each of the samples.
Fig. 2.
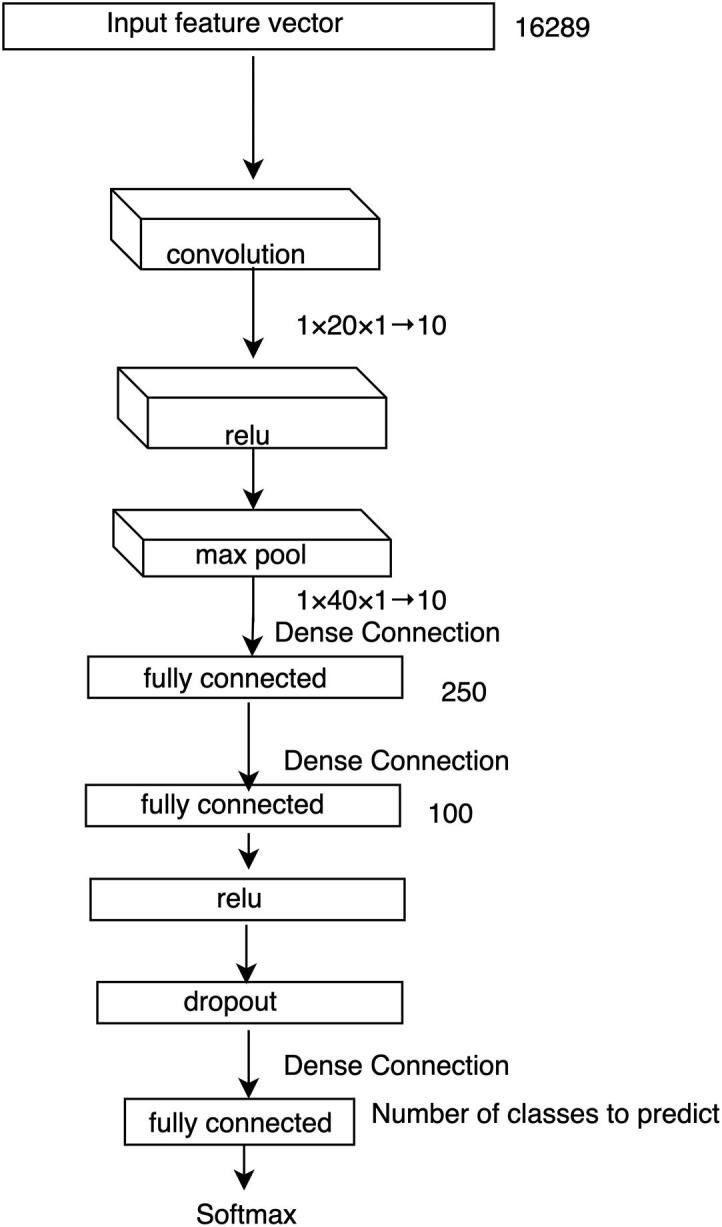
Individual data source-based DCNN architecture. A backpropagation approach is used to train the multi-layer network. The size of input feature vector, the size of the resulted vectors from fully connected layers and the size of different kernels at different layers are listed. Here, represents a kernel of size and the height of all 10 feature maps is 1. We use a stride of size for convolutional layers and for the max pooling layer.
This network takes the single data source (such as CNA or gene expression) of a sample as an input feature vector () which goes directly to a convolutional layer. A filter (also known as kernel), which is an array of numbers (also known as weights), slides over all the positions of . The height of and must be the same and here it is 1 as we are dealing with one-dimensional input vector. The region over which the is currently moving is known as receptive field. An elementwise multiplication is performed between and , which produces a single number to represent . In this way, we can capture the correlation among the neighboring genes of the input data under the weight filter. This process continues until it covers every position of and the resulted vector is termed as activation or feature map. So, if is a -dimenstional vector, then the size of the activation map would be . One can have any number of feature maps by using different s. For our base DCNN model we take 10 convolutional feature () maps and the size of our input feature vector is and the size of the convolutional kernel is . These s represent the local patterns of our input feature vector . This convolutional operation is well known as a robust pattern finder of local features [20], [30], [38]. If this input data has any pattern, it will be captured by this convolutional operation.
The output of our convolutional layer (s) goes to the Relu (Rectified Linear Units) layer. Relu is an activation function, which is useful to model the complex non-linear relationship between the input and output of the model. For our experiment, the input can be either gene-specific CNA profiles or gene expression profiles and the output is the prediction score for a patient assigned to one of the molecular subtypes. Unlike other activation functions (e.g. tanh or sigmoid), Relu implements a simple thresholding function rather than an expensive exponential function. Relu function is expressed as follows:
| (1) |
Here, represents an input into a neuron
We know that a DCNN model with large number of neurons can model any complex relationship between its input and output. However, here we have a small number of training samples for our DCNN model, which can be easily overfitted over the training data. Hence, the Relu layer is followed by a max pooling layer to reduce the size of the input feature vector, which is also known as downsampling. A filter goes over its input and takes the maximum value of the receptive field. Although pooling may cause loss of information, such kind of loss is useful because we will have fewer numbers of parameters to be learned which helps the model overcome the curse of overfitting problem. This layer also helps the model become invariant in terms of translation, rotation and scaling of the input data. Therefore, the pooling layer leads the DCNN model to have better generalization over the test data.
The output of our pooling layers is then input to a fully connected ) layer. This layer has a connection to its previous layer for each of the neurons and the output of this layer is a simple matrix multiplication which is a one-dimensional vector. For our experiment, the size of this vector is . This layer is then followed by another fully connected () layer to get higher level features of our input feature vector . However, since our network trains huge number of parameters using only a few hundreds of training samples, we pass this output to another fully connected layer () via a Relu layer and a Dropout layer. Dropout layer implements a regularization technique to prevent the DCNN model from overfitting. This layer randomly drops different units with its associated connections.
The output of is a vector of size , where and represent the number of classes of estrogen-receptor and tumor subtypes, respectively. takes the high-level features of from the output of and regulates each of the features mostly correlates with a specific class. Each of the values of represents a prediction score for a particular class, which is then converted into a probability score using a softmax classification layer. This layer implements the softmax function using two parameters from the output of : prediction scores () and weights (). So, we can calculate the probability of the -th class using the following formula:
| (2) |
Here, represents an inner product between and .
Finally, we use backpropagation to train our DCNN models.
2.2.2. DNN models for data integration
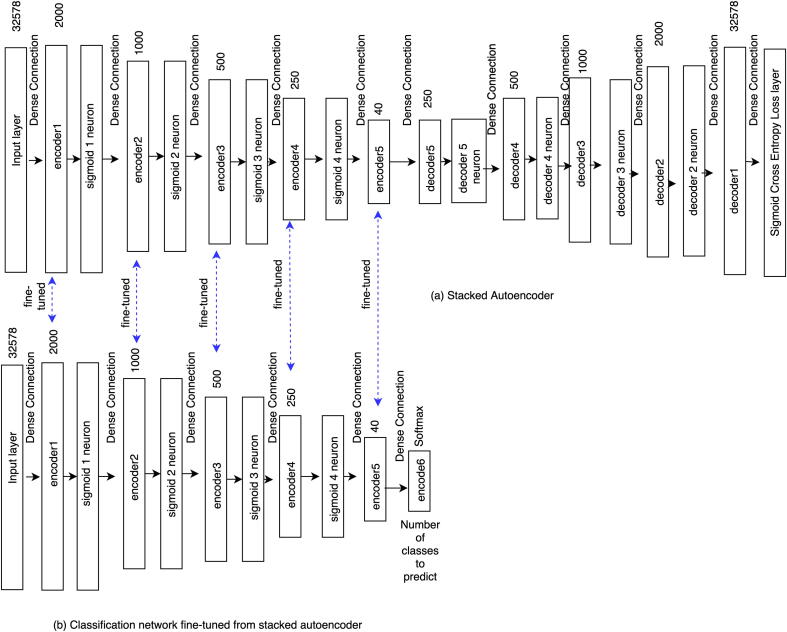
We propose a deep convolutional neural network-based data integration model, which first trains each data source separately, and then the trained deep features are concatenated for the final prediction. This proposed model is called as DCNN_Concat as shown in Fig. 3. We also compare this model with other deep learning-based models. The first model is similar to our proposed DCNN_Concat, but it shares the training weights from each of the two data sources as shown in Fig. 4, which is called as DCNN_Siamese. The second model uses a fully-connected DNN with weights initialized by stacked autoencoder as shown in Fig. 5, which is called as DNN_SE. Below we briefly describe the integration techniques.
Fig. 3.
Concatenation-based data integration for DCNN architecture. The DCNN model is first learned for CNA data (left branch) and gene expression data (right branch), respectively. The high-level features from the two data sources are then concatenated. The DCNN model is further learned based on the concatenated results to make final prediction of the breast cancer subtypes.
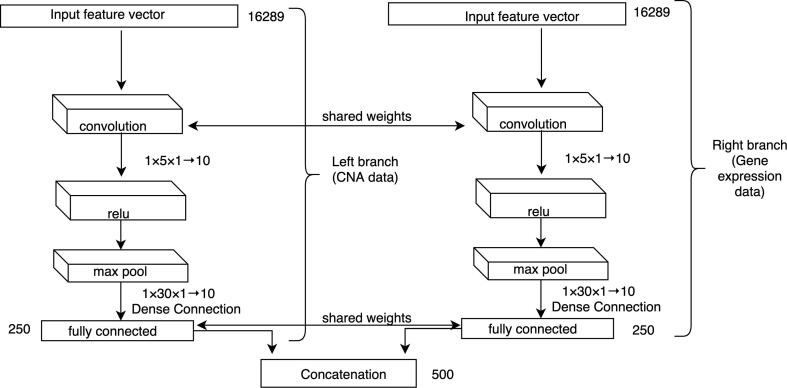
Fig. 4.
Weight sharing-based data integration for DCNN architecture. Weight sharing-based network is similar to the concatenation network except that the two branches for learning models from CNA and gene expression data share the same weights or kernels. To integrate the high-level features from the two data sources, concatenation operation is used in this study, but other operations can be performed.
Fig. 5.
Stacked autoencoder-based data integration for DCNN architecture. (a) Build stacked autoencoder from integrated data; (b) Build classification model fine-tuned from the pre-trained stacked autoencoder in (a).
2.2.2.1. DCNN_Concat model
This method takes two feature vectors as inputs: one from the CNA data and another from the gene expression data. Both of these vectors represent information from the same patient and have the same label.
The outputs of fully connected layers from the left branch () and right branch () represent the DCNN feature vectors of the inputs. To integrate the knowledge of the same patient from these two different sources we use a concatenation layer. This takes the outputs of these two fully connected layers and performs a concatenation operation between them. We call this architecture as DCNN_Concat (Fig. 3).
Suppose, represents the CNA data of patient and represents the gene expression data of and the label (tumor subtype) is the same for both and . Now, goes as an input to the left branch and to the right branch. Then both and go through different layers of left and right branches. So, the outputs of and layers, which are named as and , respectively, are considered as the higher-level representation of and . Both and are -dimensional vectors so the concatenation layer takes and as inputs and produces a -dimensional vector ():
| (3) |
Here, represents the concatenation operation. Then goes through other different layers of the DCNN to provide the final higher-level reasoning from the integrated data. The final output is the predicted probability for a particular class of molecular subtypes of breast cancer.
2.2.2.2. DCNN_Siamese model
Similar to DCNN_Concat (Fig. 3), the weight-sharing network also contains two different branches to take patient-specific CNA data and gene expression data respectively. However, the architecture of this approach involves sharing information (i.e. weight) between layers of the two branches for the two data sources (Fig. 4).
This type of network is termed as Siamese network. Hence, we call this architecture as DCNN_Siamese. This network takes two feature vectors for the two data sources as inputs: CNA data (left branch) and gene expression data (right branch) of the same patient with the same class label. Both convolutional layers of the two branches use the same sized kernel with the same weights. This has been performed in the same way for the fully connected layers of the two branches. However, the Relu and max-pooling layers do not have any weight parameters to learn and they perform only mathematical operations, so they are not involved in weight sharing. This means the model needs to learn fewer parameters which help the model not to be overfitted over the training data. We merge the outputs from and by a concatenation layer. This concatenation and the rest of the architecture of DCNN_Siamese is the same as the architecture of our DCNN_Concat (Fig. 3).
We then pass the combined vector to other different layers of the DCNN to provide the final higher-level reasoning from the integrated data to get the final prediction of a particular class label of molecular subtypes of breast cancer.
2.2.2.3. DNN_SE model
We first train a deep neural network in an unsupervised fashion. This creates a set of feature detector layers without using the labels of the samples. To do this we use a stacked autoencoder (SE) approach.
We concatenate CNA data and gene expression data for each of the samples, which results in a 32,578-dimensional vector as an input to the SE network (Fig. 5(a)).
This architecture includes encoder and decoder two parts. Each of the encoder layers has a corresponding decoder layer. The purpose of learning this network is to reconstruct the raw inputs in the corresponding decoder layers. Each of the encoder and decoder layers is followed by a sigmoid neuron except the last decoder layer. We use sigmoid neuron layer so that small changes in one of the encoder or decoder layers do not make large changes to their outputs since such small changes can sometimes flip the output such as 0 to 1. The output of sigmoid function can be defined as:
| (4) |
Here, represents an input to a neuron. Sigmoid function squashes the real numbers to range between 0 and 1. Therefore, the network becomes non-linear.
We use sigmoid cross entropy loss function (Eq. (5)) to train our SE network in a backpropagation style. This loss function takes the output of a fully connected layer as its input and it uses a sigmoid function to provide a gradient estimation.
| (5) |
Here, is the total number of training inputs, is the label, which is the input itself and is the prediction of the network.
After training the SE, we train another deep neural network (Fig. 5(b)) which contains the same layers as the encoder layers of this SE but has an additional layer on the top to get the final prediction of a particular class label of molecular subtypes of breast cancer. Here, the weights of all layers except the additionally added layer are fine-tuned from the encoder layers of the SE. In this way, the weights of the network are initialized with much more practical values which may lead to better training and classification results. We call this DNN architecture as DNN_SE.
2.2.3. Software and parameters
We build our DNN models using CAFFE [39], which is a C++ based deep learning library. We use all the 16,289 genes common to both data sources as input vectors to each of our DNN models (Fig. 2, Fig. 3, Fig. 4, Fig. 5). To investigate the effects of the selection of different hyperparameter values on the prediction performance of our best DCNN model (DCNN_Concat), we consider different values for two hyperparameters: learning rate (0.1, 0.01, 0.001, 0.0001 and 0.00001) and dropout rate (0.1, 0.3, 0.5, 0.7 and 0.9). We report the parameter values (learning rate 0.001 and dropout rate 0.5) with the best prediction performance.
2.3. Model performance evaluation and traditional baseline models
We use two methods to measure the performance of our DNN classifiers. The first one is overall accuracy, which is the proportion of patients with correctly predicted molecular subtypes. The second one is Receiver Operating Characteristics (ROC) curve, which depicts the pattern of sensitivity (1-FNR) and specificity (1-FPR) of a classifier at several different discrimination thresholds, such as the probability assigning a given sample to a given molecular subtype of breast cancer. Here, FNR means false negative rate and FPR means false positive rate. The quantitative index used to evaluate a classifier based on ROC is the area under the ROC curve (AUC). We use a R function called multiclass.roc [40] to generate multiple ROC curves for computing the multiclass AUC.
The performance of our proposed DNN model (DCNN_Concat) is compared to that of other two state-of-the-art supervised classification models: SVM and RF. We build these models using R packages e1071 for SVM and randomForest for RF. Since we have more than 16,000 genes or features and only approximate 1000 samples in training set, besides using all of the genes, we also select top significant genes to build the baseline SVM and RF models. We calculate the significance of each of the genes using different supervised approaches. For CNA data, we use χ2 test since it is category data while for gene expression data, we perform parametric ANOVA test. The selected top significant genes and all of the 16,289 genes are used to build the traditional baseline models.
RF is suitable for both binary and multiclass classification of microarray data because of the following reasons [41]: RF is suitable when the number of predictors is very large than the number of observations, RF is not sensitive to the enormous number of irrelevant genes while selecting important genes for final prediction, RF includes the relations among predictors and RF does not require extensive fine-tuning as default parameters often lead to the outstanding prediction performances [42]. Besides, Díaz-Uriarte [43] et al. used experimental evaluation of RF with cancer microarray gene expression data and concluded that RF has comparable prediction performance to the SVM based classifiers of omics data. Therefore, in this study, we have chosen SVM and RF as our traditional baseline models.
For SVM models, we use Radial kernel function and optimized the cost parameter of SVM in the range of 1–50 using 10-fold cross-validation on the training data and the optimized parameter value is 1. We have also fine tuned the hyperparameters of our RF models using 10-fold cross-validation: the number of available variables during node splitting in the range of 2–6, maximum number of nodes in a tree in the range of 2–10 and the number of trees in the range of 50, 100, 200, 300, 400, 500, 1000, 2000. The optimized parameter values are: the number of available variables during node splitting is 2, maximum number of nodes in a tree is 6 and the number of trees is 500. We run each model (SVM and RF) with the best found parameter for 10 times and report the mean accuracy and AUC. In addition, we also report the standard deviation (SD) for the accuracies and AUCs from these 10 models.
Furthermore, we implement two other baseline data integration approaches. The first approach is implemented for both SVM and RF. For each specified number of top genes, we first select the genes based on χ2 test for CNA data and ANOVA test for gene expression data. We then concatenate the selected CNA data and gene expression data. Finally, we perform the classification analysis using SVM and RF for the selected gene sets, respectively. This method is called SVM_Concat and RF_Concat, respectively. The second method is a kernel-based SVM integration method (named as BK_SVM_Concat and MK_SVM_Concat for binary class classification and multi-class classification respectively) [28], [29]. For our experiments, we first calculate two kernel matrices for CNA data and gene expression data using the R package called kernlab (default parameter values used). We then take a linear sum of these two kernel matrices and use this integrated kernel matrix to build our kernel-based SVM models.
2.4. Survival analysis
Kaplan-Meier (KM) survival analysis and log-rank test is used to determine survival significance in breast cancer subtypes from Kaplan-Meier survival curves, overall survival (OS), and disease-specific survival (DSS). Cox proportional hazards models are used to calculate hazards ratio (HR), demonstrating differences in survival analysis by pairwise comparison between breast cancer subtypes (P < 0.05). All the analysis is performed using the R package Survcomp.
2.5. Consensus clustering
k-means clustering and consensus clustering are used to determine the optimal number of stable breast cancer subtypes using the R package ConsensusClusterPlus. Cluster robustness is assessed by consensus clustering using agglomerative k-means clustering (100 iterations), with Pearson correlation distance and complete linkage on the 842 breast cancer profiles in the test set using the top 500 deep features trained from the training set. The optimal number of clusters is determined from the consensus distribution function (CDF), which plots the corresponding empirical cumulative distribution, defined over the range [0,1], and from calculation of the proportion increasing in the area under the CDF curve. The number of clusters is decided when any further increasing in cluster number (k) does not lead to a corresponding marked increasing in the CDF area. The breast cancer subtype annotation and heat maps are generated using the R package ComplexHeatmap.
2.6. Data availability
All data sets used in the study are available from the Molecular Taxonomy of Breast Cancer International Consortium (METABRIC): https://ega-archive.org/dacs/EGAC00001000484.
3. Results
3.1. Model performance analysis using the test set
Table 1 presents the accuracies and AUCs of our proposed and baseline DNN models for multi-class (tumor subtypes) classification. It can be seen that the model (Gene_DCNN) using gene expression data can predict the subtypes more accurately than that (CNA_DCNN) using CNA data. The prediction performance of the model “Gene_DCNN” in terms of accuracy is 77.3% and AUC is 0.832, which is significantly better than the model “CNA_DCNN” of accuracy 50.5% and AUC 0.677. Among the DCNN-based integration models, we get the best result when we integrate the two data sources using the concatenation layer without sharing the weights (model: DCNN_Concat). Overall, the proposed DCNN model (DCNN_Concat) has shown better prediction performance than the DCNN models trained on individual data sources (CNA_DCNN and Gene_DCNN) and the baseline DNN-based integration models (DCNN_Siamese and DNN_SE).
Table 1.
The overall accuracies (%) and AUCs of our DCNN models for multi-class classification. CNA_DCNN and Gene_DCNN are based on the architecture of Fig. 2 for CNA data and gene expression data, respectively. DCNN_Concat, DCNN_Siamese and DNN_SE are DNN models based on the network architectures described in Fig. 3, Fig. 4, Fig. 5, respectively.
| Model (all genes) | Datasets | Performance Measurement |
|
|---|---|---|---|
| Accuracy (%) | AUC | ||
| CNA_DCNN | CNA | 50.5 | 0.677 |
| Gene_DCNN | Gene expression | 77.3 | 0.832 |
| DCNN_Concat | CNA and gene expression | 79.2 | 0.850 |
| DCNN_Siamese | CNA and gene expression | 76.7 | 0.838 |
| DNN_SE | CNA and gene expression | 77.3 | 0.838 |
One major advantage of our proposed DNN model than the traditional methods is that the DNN based model can better handle high dimensional data. Unlike SVM and RF, the proposed DCNN_Concat transforms input high-dimensional data into a lower-dimensional size in order to perform final prediction about the input data. Besides, unlike SVM and RF, the proposed DCNN_Concat concatenates transformed CNA and gene expression data. Intuitively, raw features may have little identifiable pattern, especially for complex tumor subtype classification. Therefore, it is important to transform input raw data into abstract level before using these features for the cancer subtypes classification. Furthermore, our DCNN_Concat shows better performance over the baseline DCNN_Siamese because the layers in the two branches for the two data sources in DCNN_Concat model (Fig. 3) learn different weights but those in DCNN_Siamese model (Fig. 4) learn the same weights. This gives us the insight that CNA data and gene expression data need to be treated differently. Furthermore, DCNN_Concat captures the correlation among the neighboring genes in the input vector using convolutional layers while the baseline DNN_SE model (Fig. 5) does not consider this correlation. This may cause the lower performance using DNN_SE over DCNN_Concat.
Performances of our other baseline models (SVM and RF) for the multi-class classification are shown in Table 2 (accuracies) and Table 3 (AUCs). Overall, there are no significant changes in the results of using different number of top selected genes for both SVM and RF models. Similar to our proposed DNN models, SVM and RF also provide better prediction results using gene expression data than CNA data. This may be due to the fact that CNA data is very sparse. Generally speaking, in terms of both accuracy and AUC RF models give better results than SVM models for CNA data while SVM models provide better results than RF models for gene expression data. The integration of the gene expression and CNA data using SVM (SVM_Concat, MK_SVM_Concat) and RF (RF_Concat) has not shown significant improvement of the prediction performance over the individual gene expression data (Table 2, Table 3).
Table 2.
Accuracy of the baseline models and our proposed deep learning model (DCNN_Concat) for multi-class classification. The results are shown for SVM and RF models using individual CNA data (CNA_SVM, CNA_RF) and gene expression data (Gene_SVM, Gene_RF) as well as the integration of both data sources (SVM_Concat, MK_SVM_Concat and RF_Concat). We ran each RF model with the best found parameter values for 10 times and reported the mean accuracy because of the stochastic nature of RF. In addition, we also reported the standard deviation (SD) for the accuracies and AUCs from these RF models. The results for DCNN_Concat using the selected top genes are also shown. The best results for models with different number of top genes selected by χ2 for CNA data and ANOVA for gene expression data are shown in bold color.
| Model (top genes) | Test | Accuracy (Accu: %) based on number of top selected genes |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | |||
| CNA_SVM | χ2 | 41.7 | 43.2 | 41.9 | 42.6 | 42.6 | 43.2 | 43.3 | 42.8 | 43.2 | |
| CNA_RF | χ2 | Accu | 46.6 | 48.1 | 47.5 | 47.9 | 48.5 | 48.5 | 49.0 | 48.9 | 49.9 |
| SD | 0.45 | 0.24 | 0.48 | 0.24 | 0.31 | 0.55 | 0.18 | 0.52 | 0.18 | ||
| Gene _SVM | ANOVA | 72.4 | 75.8 | 75.6 | 75.6 | 76.0 | 75.4 | 75.9 | 75.5 | 75.9 | |
| Gene _RF | ANOVA | Accu | 70.1 | 71.0 | 71.1 | 71.0 | 70.5 | 70.4 | 71.2 | 70.7 | 70.0 |
| SD | 0.34 | 0.45 | 0.61 | 0.78 | 0.23 | 0.8 | 0.82 | 0.45 | 0.37 | ||
| SVM_Concat | 72.0 | 72.7 | 72.4 | 72.3 | 73.4 | 72.8 | 73.1 | 72.9 | 73.1 | ||
| MK_SVM_Concat | 49.1 | 52.1 | 58.1 | 55.7 | 56.1 | 67.1 | 55.8 | 58.3 | 57.8 | ||
| RF_Concat | Accu | 70.2 | 71.4 | 70.4 | 71.2 | 71.0 | 69.3 | 71.0 | 70.2 | 71.3 | |
| SD | 0.4 | 0.14 | 0.43 | 0.18 | 0.61 | 0.57 | 0.12 | 0.88 | 0.47 | ||
| DCNN_Concat | 72.9 | 72.9 | 71.6 | 72.6 | 71.5 | 72.7 | 74.4 | 74.8 | 76.6 | ||
Table 3.
AUC of the baseline models and our proposed deep learning model (DCNN_Concat as shown in Table 1) for multiclass classification. The results are shown for SVM and RF models using individual CNA data (CNA_SVM, CNA_RF) and gene expression data (Gene_SVM, Gene_RF) as well as the integration of both data sources (SVM_Concat, MK_SVM_Concat and RF_Concat). We ran each RF model with the best found parameter for 10 times and reported the mean AUC because of the stochastic nature of RF. In addition, we also reported the standard deviation (SD) for the accuracies and AUCs from these 10 RF models. The results for DCNN_Concat using the selected top genes are also shown. The best results for models with different number of top genes selected by χ2 for CNA data and ANOVA for gene expression data are shown in bold color.
| Model (top genes) | Test | AUC based on top selected genes |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | |||
| CNA_SVM | χ2 | 0.589 | 0.590 | 0.632 | 0.630 | 0.629 | 0.636 | 0.629 | 0.630 | 0.633 | |
| CNA_RF | χ2 | AUC | 0.644 | 0.647 | 0.633 | 0.642 | 0.649 | 0.655 | 0.651 | 0.655 | 0.669 |
| SD | 0.003 | 0.002 | 0.001 | 0.004 | 0.003 | 0.004 | 0.002 | 0.006 | 0.003 | ||
| Gene _SVM | ANOVA | 0.804 | 0.818 | 0.812 | 0.799 | 0.808 | 0.807 | 0.814 | 0.814 | 0.819 | |
| Gene _RF | ANOVA | AUC | 0.805 | 0.810 | 0.805 | 0.802 | 0.809 | 0.802 | 0.803 | 0.79 | 0.801 |
| SD | 0.003 | 0.002 | 0.001 | 0.003 | 0.002 | 0.003 | 0.002 | 0.003 | 0.002 | ||
| SVM_Concat | 0.810 | 0.815 | 0.810 | 0.818 | 0.810 | 0.810 | 0.815 | 0.814 | 0.814 | ||
| MK_SVM_Concat | 0.741 | 0.760 | 0.753 | 0.725 | 0.734 | 0.820 | 0.730 | 0.746 | 0.792 | ||
| RF_Concat | AUC | 0.803 | 0.808 | 0.803 | 0.802 | 0.801 | 0.804 | 0.801 | 0.807 | 0.808 | |
| SD | 0.001 | 0.002 | 0.001 | 0.001 | 0.001 | 0.001 | 0.002 | 0.002 | 0.001 | ||
| DCNN_Concat | 0.810 | 0.817 | 0.815 | 0.817 | 0.821 | 0.811 | 0.829 | 0.834 | 0.852 | ||
Comparison of Table 1 with Table 2, Table 3 shows that when we use only individual data sources to build their DCNN models (CNA_DCNN for CNA data and Gene_DCNN for gene expression data), we get higher accuracy and AUC results than corresponding SVM and RF models (i.e. CNA_SVM and CNA_RF for CNA data and Gene_SVM and Gene_RF for gene expression data). It is also seen that our integrated models (DCNN_Concat, DCNN_Siamese and DNN_SE) outperform the models (CNA_DCNN, Gene_DCNN) built on individual data sources in terms of both accuracy and AUC.
Table 4 shows the best results from Table 1, Table 2, Table 3 and the results of our baseline data integration models using all genes (SVM_ Concat, RF_ Concat, MK_SVM_ Concat, DNN_DBN). It can be easily seen that the integration model DCNN_Concat outperforms all baseline models. This may be due to the fact that the proposed DCNN model consider the correlation among the neighboring genes in the input vectors and the proposed DNN_SE model is less susceptible to the undesirable noisiness in the data.
Table 4.
Performance comparison of multi-class classification. The best results for the models are extracted from our proposed model (Table 1) and the baseline models using top selected genes (Table 2, Table 3) and all genes (SVM_ Concat, RF_ Concat, MK_SVM_ Concat and DNN_DBN). The models with the best results are bolded.
| Model | Accuracy (%) | Model | AUC |
|---|---|---|---|
| DCNN_Concat (all genes) | 79.2 | DCNN_Concat (all genes) | 0.850 |
| DCNN_Concat (top 500 genes) | 76.6 | DCNN_Concat (top 500 genes) | 0.852 |
| Gene_SVM (top 300 genes) | 76.0 | Gene_SVM (top 500 genes) | 0.819 |
| CNA_RF (all genes) | 54.4 | CNA_RF (All genes) | 0.691 |
| Gene_RF(all_genes) | 71.1 | Gene_RF(all_genes) | 0.788 |
| RF_Concat (top 150 genes) | 72.1 | Gene_RF (top 500 genes) | 0.812 |
| SVM_ Concat (all genes) | 69.5 | SVM_ Concat (all genes) | 0.804 |
| MK_SVM_Concat (all genes) | 76.7 | MK_SVM_Concat (all genes) | 0.798 |
| RF_Concat (all genes) | 70.1 | RF_Concat (all genes) | 0.781 |
| DNN_DBN (all genes) | 49.89 | DNN_DBN (all genes) | 0.625 |
The similar procedure for the multi-class classification is applied to binary class classification (the classes of estrogen-receptor) and the results of the accuracies and AUCs of our DCNN, SVM and RF models are shown in Table 5, Table 6, Table 7. Generally speaking, the integration of the CNA and gene expression data using the DCNN and SVM models have greatly improved the prediction performance over individual data sources, but this has not been observed for the RF models (Table 8). Although the proposed DCNN model have better performance than the baseline DNN model (B_DNN_DBN), their performance is slightly worse than those based on integration of the CNA and gene expression data using kernel-based integration model (BK_SVM_Concat) in terms of overall accuracy (Table 6) and the RF models (B_RF_Concat) in terms of both overall accuracy and AUC (Table 6, Table 7).
Table 5.
The overall accuracies (%) and AUCs of our DNN model for binary (B) classification. B_CNA_DCNN and B_Gene_DCNN are based on the architecture of Fig. 2 for CNA data and gene expression data, respectively. B_DCNN_Concat is the DNN model based on the network architecture described in Fig. 3.
| Model (all genes) | Datasets | Performance Measurement |
|
|---|---|---|---|
| Accuracy (%) | AUC | ||
| B_CNA_DCNN | CNA | 62.8 | 0.504 |
| B_Gene_DCNN | Gene expression | 62.9 | 0.502 |
| B_DCNN_Concat | CNA and gene expression | 96.3 | 0.993 |
Table 6.
Accuracy of the baseline models and our deep learning model (B_DCNN_Concat as shown in Table 5) for binary classification. The results are shown for SVM and RF models using individual CNA data (B_SVM_CNA, B_RF_CNA) and gene expression data (B_SVM_GENE, B_RF_GENE) as well as the integration of both data sources (B_SVM_Concat, BK_SVM_Concat and B_RF_Concat). We ran each RF model with the best found parameter for 10 times and reported the mean accuracy because of the stochastic nature of RF. In addition, we also reported the standard deviation (SD) for the accuracies and AUCs from these 10 RF models. The results for B_DCNN_Concat using the selected top genes are also shown. The best results for models with different number of top genes selected by χ2 for CNA data and ANOVA for gene expression data are shown in bold color.
| Classifier (top genes) | Accuracy based on the top selected genes from CNA and gene expression data |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | ||
| B_SVM_CNA | 76.8 | 76.7 | 76.4 | 76.3 | 76.0 | 75.9 | 75.4 | 75.7 | 75.7 | |
| B_RF_CNA | Accu | 81.9 | 82.2 | 82.5 | 81.0 | 82.4 | 81.1 | 81.2 | 82.2 | 82.4 |
| SD | 0.43 | 0.3 | 0.25 | 0.36 | 0.15 | 0.14 | 0.24 | 0.21 | 0.3 | |
| B_SVM_GENE | 73.4 | 74.6 | 73.6 | 74.0 | 73.4 | 74.2 | 73.7 | 73.3 | 73.2 | |
| B_RF_GENE | Accu | 96.1 | 96.3 | 97.0 | 96.5 | 96.6 | 96.3 | 97.0 | 96.8 | 96.6 |
| SD | 0.33 | 0.37 | 0.22 | 0.4 | 0.53 | 0.42 | 0.31 | 0.21 | 0.14 | |
| B_SVM_Concat | 95.7 | 95.5 | 95.2 | 95.2 | 95.3 | 95.2 | 95.1 | 95.4 | 95.4 | |
| BK_SVM_Concat | 97.1 | 96.4 | 97.0 | 97.1 | 97.1 | 97.1 | 96.9 | 96.9 | 97.0 | |
| B_RF_Concat | Accu | 97.0 | 96.0 | 96.8 | 97.3 | 97.2 | 96.8 | 96.3 | 96.6 | 96.8 |
| SD | 0.23 | 0.48 | 0.27 | 0.31 | 0.58 | 0.4 | 0.21 | 0.57 | 0.48 | |
| B_DCNN_Concat | 95.9 | 96.3 | 95.5 | 95.6 | 95.4 | 95.6 | 96.0 | 95.5 | 96.1 | |
Table 7.
AUC of the baseline models and our deep learning model (B_DCNN_Concat as shown in Table 5) for binary classification. The results are shown for SVM and RF models using individual CNA data (B_SVM_CNA, B_RF_CNA) and gene expression data (B_SVM_GENE, B_RF_GENE) as well as the integration of both data sources (B_SVM_Concat, BK_SVM_Concat and B_RF_Concat). We ran each model RF with the best found parameter for 10 times and reported the mean accuracy and AUC because of the stochastic nature of RF. In addition, we also reported the standard deviation (SD) for the accuracies and AUCs from these 10 RF models. The results for B_DCNN_Concat using the selected top genes are also shown. The best results for the models with different number of top genes selected by χ2 for CNA data and ANOVA for gene expression data are shown in bold color.
| Classifier (top genes) | Number of the top selected genes from CNA and gene expression data |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | ||
| B_SVM_CNA | 0.601 | 0.589 | 0.591 | 0.585 | 0.576 | 0.572 | 0.563 | 0.568 | 0.568 | |
| B_RF_CNA | AUC | 0.754 | 0.785 | 0.808 | 0.802 | 0.805 | 0.808 | 0.809 | 0.809 | 0.831 |
| SD | 0.001 | 0.002 | 0.002 | 0.001 | 0.001 | 0.001 | 0.002 | 0.001 | 0.002 | |
| B_SVM_GENE | 0.767 | 0.784 | 0.803 | 0.813 | 0.807 | 0.805 | 0.805 | 0.805 | 0.805 | |
| B_RF_GENE | AUC | 0.991 | 0.992 | 0.993 | 0.992 | 0.992 | 0.992 | 0.991 | 0.993 | 0.994 |
| SD | 0.002 | 0.001 | 0.001 | 0.002 | 0.002 | 0.002 | 0.002 | 0.001 | 0.002 | |
| B_SVM_Concat | 0.940 | 0.936 | 0.931 | 0.930 | 0.932 | 0.929 | 0.927 | 0.932 | 0.932 | |
| BK_SVM_Concat | 0.951 | 0.941 | 0.950 | 0.952 | 0.952 | 0.952 | 0.947 | 0.947 | 0.950 | |
| B_RF_Concat | AUC | 0.992 | 0.991 | 0.992 | 0.993 | 0.992 | 0.991 | 0.993 | 0.994 | 0.991 |
| SD | 0.001 | 0.002 | 0.001 | 0.001 | 0.002 | 0.001 | 0.001 | 0.002 | 0.003 | |
| B_DCNN_Concat | 0.991 | 0.992 | 0.991 | 0.991 | 0.990 | 0.991 | 0.991 | 0.990 | 0.991 | |
Table 8.
Performance comparison of binary classification. The best results for the models are extracted from our proposed models (Table 5) and the baseline models using top selected genes (Table 6, Table 7) and all genes (B_SVM_Concat, B_RF_Concat, BK_SVM_Concat, B_DNN_DBN). The models with the best results are bolded.
| Classifier | Accuracy (%) | Classifier | AUC |
|---|---|---|---|
| B_DCNN_Concat (all genes) | 96.3 | B_DCNN_Concat (all genes) | 0.993 |
| B_DCNN_Concat (top 150 genes) | 96.3 | B_DCNN_Concat (top 150 genes) | 0.992 |
| B_SVM_Concat (top 100 genes) | 95.7 | B_ SVM_Concat (top 100 genes) | 0.940 |
| B_RF_CNA (all genes) | 81.1 | B_RF_CNA (all genes) | 0.818 |
| B_RF_GENE (all genes) | 96.3 | B_RF_GENE (all genes) | 0.991 |
| B_RF_Concat (top 250 genes) | 97.5 | B_RF_Concat (top 450 genes) | 0.995 |
| B_SVM_Concat (all genes) | 90.4 | B_SVM_Concat (all genes) | 0.838 |
| BK_SVM_Concat (all genes) | 96.5 | BK _SVM_Concat (all genes) | 0.952 |
| B_RF_Concat (all genes) | 95.4 | B_RF_Concat (all genes) | 0.991 |
| B_DNN_DBN (all genes) | 86.4 | B_DNN_DBN (all genes) | 0.522 |
Our results from Tables 4 and 8 show that RF model with all genes of the combined gene expression and CNA data has similar performance to our DCNN model for binary class classification. However, the B_RF_Concat with top 250 genes from CAN and gene expression data has achieved best prediction performance in terms of accuracy, but it has worse performance than our DCNN_Concat model for multi-class classification. For SVM model with all genes of the combined gene expression and CNA data, it has worse performance than our DCNN model for both binary and multi-class classifications.
3.2. The DCNN_Concat model reveals Her2-enriched breast cancer as more than one subtype
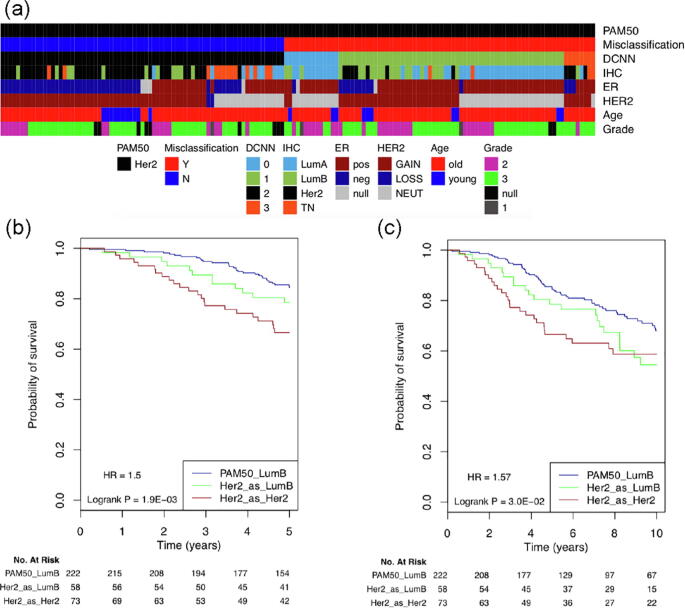
183 out of the 842 breast cancer samples in the test set were misclassified by our DCNN_Concat model during the multi-class classification analysis. 50, 13, 80, and 40 were misclassified in the Lum A, Lum B, Her2-enriched, and basal-like subtypes, respectively. As we can see, the majority (80 out of 153) of the Her2-enriched samples was incorrectly classified and the majority (58 out of 80) of the misclassified Her2-enriched samples were predicted as Lum B by our DCNN_Concat model. Closer examination of the 153 Her2-enriched samples showed that Her2-enriched breast cancer has more than one subtype (Fig. 6a). The correctly predicted Her2-enriched group shows HER2 gene copy number gain and is mainly ER negative while the incorrectly predicted Her2-enriched group contains many cases without HER2 gene copy number gain, and is mainly ER positive. The 58 Her2-enriched samples which were predicted as Lum B samples are mainly ER positive and show a mixture of HER2 gene copy number gain and null.
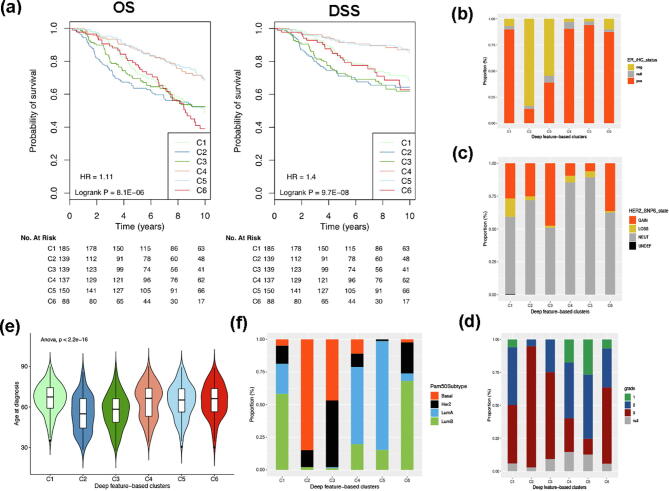
Fig. 6.
Her2-enriched PAM50 subtype annotation and survival analysis. (a) The annotation bars show (from top to bottom): PAM50 mRNA expression subtype, whether a Her2-enriched sampler was misclassified by our DCNN_Concat model, the predicted subtype by our DCNN_ConCat model (0, Lum A; 1, Lum B; 2, Her2-enriched; 3: basal-like), ER/PR/HER2 expression status-defined subtype, ER Immunohistochemistry (IHC) expression status, HER2 copy number state, age (>= 45 as defined as old, <45 as young) and histological grade. Details on color coding of the annotation bars are presented below the bars. (b) 5-year DSS survival analysis. (c) 10-year DSS survival analysis.
We further compared the survival curves for the Lum B PAM50, Her2-enriched PAM50 which were misclassified as Lum B, and Her2-enriched PAM50 which were correctly predicted groups. The three groups showed significantly different 5-year (Fig. 6b) and 10-year (Fig. 6c) DSS. The Lum B group (the dark blue line in Fig. 6b and c) exhibits the best disease-specific survival at both 5 and 10 years while the correctly predicted Her2-enriched group (the dark red line in Fig. 6b and c) showed the worst disease-specific survival at both 5 and 10 years. The misclassified Her2-enriched group (the green line in Fig. 6b and 6c) had a better survival than the latter and a worse survival than the former.
3.3. Deep feature-based k-means and consensus clustering reveal 6 breast cancer subtypes
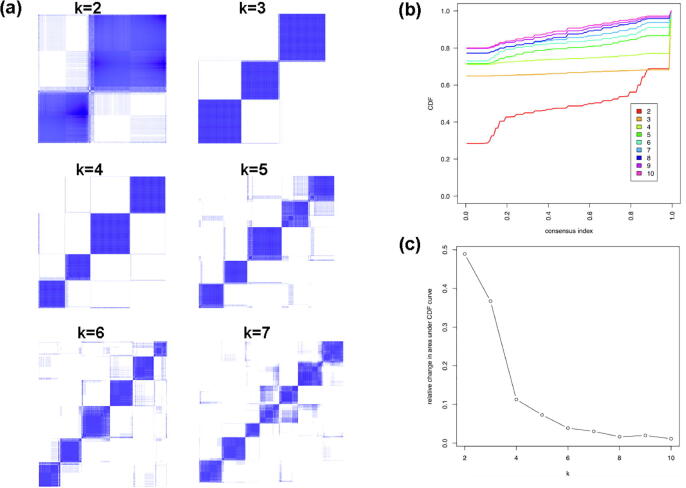
Six breast cancer subtypes were identified from the test set by using the top 500 deep features extracted from the DCNN_Concat model trained on the training set. Sample classification robustness was analyzed by consensus clustering, which involves k-means clustering by resampling (100 iterations) randomly selected tumor profiles. The consensus matrix is a visual representation of the proportion of times in which 2 samples are clustered together across the resampling iterations (Fig. 7a). Groups of samples that frequently cluster with one another are pictorially represented by darker shades of blue. To determine the number of clusters presenting in the data, we examined the area under the curve of the CDF plot (Fig. 7b). The point at which the area under the curve ceases to show marked increases with additional cluster number (k) indicates the ideal number of clusters (Fig. 7c). Therefore, the optimal number of clusters is 6, as defined by the consensus plots consistent with the k-means clustering.
Fig. 7.
Deep feature-based identification of breast cancer subtypes. (a) Consensus clustering displaying the robustness of sample classification using multiple iterations (100) of k-means clustering. (b) The CDF depicting the cumulative distribution from consensus matrices at a given cluster number (k). (c) The optimal cluster number is 6 at the point in which the relative change in area under the CDF plot does not change with increasing k.
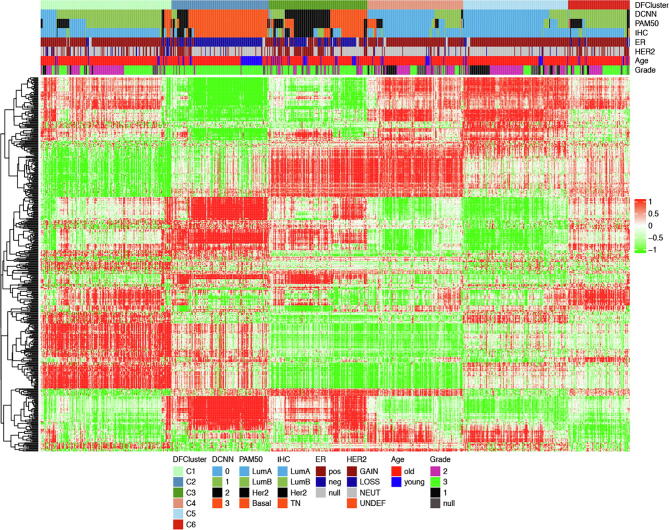
The six breast cancer subtypes correlated with PAM50 subtypes and exhibited distinct associations with other clinical and histological features (Fig. 8, Fig. 9). Of note, deep feature-based clusters 4 and 5 showed high overlapping with the PAM50 Lum A subtype while clusters 1 and 6 showed high overlapping with the PAM50 Lum B subtype. Breast cancer patients in these four clusters are mainly ER-positive. The deep feature-based cluster 2 was composed of basal-like PAM50 subtype, which contained many young, ER-negative and high-grade cases. The remaining deep feature-based cluster 3 was composed of a mixture of basal-like and HER2-enriched PAM50 defined subtypes.
Fig. 8.
Deep feature patterns within the six breast cancer subtypes. The columns are the 842 patients ordered by the deep feature-based six subtypes and the rows are the 500 deep features. The feature clusters were assigned using the hierarchical clustering with complete linkage and Euclidean distance. The top horizontal annotation bars show (from top to bottom): deep feature-based BC subtype, DCNN_Concat predicted subtype, PAM50 mRNA expression subtype, ER/PR/HER2 expression status-defined subtype, ER IHC expression status, HER2 copy number state, age (>= 45 as defined as old, <45 as young) and histological grade. Details on color coding of the annotation bars are presented below the heat map.
Fig. 9.
Deep feature-based 6 breast cancer groups and associated clinical features. (a) Overall survival (OS) and disease-specific survival (DSS) by the deep feature-based cluster; (b) ER IHC status; (c) HER2 gene copy number state; (d) Tumor grade; (e) Age at diagnosis; (f) PAM50 subtype.
The six breast cancer subtypes showed significant OS and DSS differences (Fig. 9a) with p-values 8.1E-06 and 9.7E-08, respectively, which means that the concatenated deep features from both gene expression and copy number alteration data have performed well in predicting the patient’s prognosis. From the KM plot (Fig. 9a), we can see that the patients in clusters 4 and 5, highly concordant with PAM50Lum A subtype, have the best prognosis.
4. Discussion
Breast cancer is typically referred to as a single disease due to the fact that it is originating from the cells in the mammary gland. However, breast cancer is a complex disease with a high degree of inter-tumor heterogeneity, which is known as differences among tumors from different individuals. The heterogeneity in breast cancer has a profound impact on disease progression and therapeutic response, thus making it one of the most important and clinically relevant areas of breast cancer research. During the last few decades, molecular classification of breast cancer based on comprehensive omics data has been extensively explored.
In this paper, we propose a deep learning-based model DCNN_Concat) for multi-class classification and B_DCNN_Concat for binary classification to integrate copy number alteration and gene expression level data measured on the same breast cancer patients to achieve this goal. Our experimental results show that integration of knowledge from these datasets can improve the prediction of the molecular subtypes of breast cancer. The model DCNN_Concat achieves better prediction performance than the models (CNA_DCNN and Gene_DCNN) built using individual data sources.
Comparing with other DNN-based models (DCNN_Siamese, DNN_SE and DNN_DBN) and two traditional machine learning models (SVM and RF), our proposed knowledge integration model achieves improved prediction performance than most of these baseline models. We also observe that the RF models show higher predictive performance for binary classification. This is consistent with previous results that show the RF approach can model high-dimensional and correlated data efficiently. Furthermore, the binary subtypes based on ER status is a well-established breast cancer subtyping system while the multiple subtypes system used for breast cancer subtyping is still debated. Our results showed that the deep learning-based models may have advantages over the traditional models to extract abstract features, which are more useful to classify the more complex tumor subtypes than the raw features used in the traditional models.
The Her2-enriched subtype was defined by overexpression of HER2 gene and multiple HER2-amplicon associated genes. This subtype tends to be clinically HER2-positive defined by a combination of HER2 protein overexpression and HER2 gene amplification. However, the definition of the Her2-enriched subtype is still debated [44]. The tumors classified as Her2-enriched also vary in terms of ER IHC (immunohistochemistry) status, CNAs, and mutation profiles. Furthermore, not all Her2-enriched tumors are clinically HER2-positive, and not all clinically HER2-positive tumors fall into the Her2-enriched subtype [32]. In The Cancer Genome Atlas (TCGA) study [32], the Her2-enriched subtype captured some but not all clinically HER2-positive breast tumors. The TCGA study reported that there existed at least two types of clinically HER2-positive tumours: Her2-enriched/HER2-positive versus luminal/HER2-positive. The Her2-enriched/HER2-positive subtype was associated with high levels of EGF receptor and HER2 protein phosphorylation and a tendency to be ER-negative [32]. Whereas the luminal/HER2-positive subtype had lower level DNA amplification and lower protein-based signaling and tended to be ER-positive/luminal. Therefore, the clinically defined HER2-positive tumors do not represent a separate subtype but a heterogenous group. Our DCNN_Concat model correctly predicted the first group to be HER2-enriched cancers while the second group to be the luminal B subtype. Our DCNN_Concat model reveals Her2-enriched breast cancer as more than one subtype. The correctly classified Her2-enriched samples show HER2 gene copy number gain and are mainly ER-negative while the incorrectly classified Her2-enriched samples tend to be cases without HER2 gene copy number gain and are mainly ER-positive.
5. Conclusions
Collectively, we demonstrate that the proposed integrative DCNN learning framework can efficiently handle multiple high-dimensional omics data sets to improve the prediction of breast cancer subtypes. Although we use only gene expression and CNA data to classify the subtypes of breast cancer in this study, the framework is not restricted to integrate only these two data sources. It can be extended to incorporate many more other data sources, such as methylation data, clinical data, etc. Our proposed deep learning model uses all genes, so the results may be hard to interpret. Sometimes we may be interested in the important genes used for the classification. Hence, our research opens a few future directions which are valuable to be explored. The first one is to develop more efficient deep learning-based data integration approaches, which can handle the correlation among different data sources. Although the DCNN model developed here can handle the correlation among features, but it may not efficiently handle the correlation among different data sources. The second one is to efficiently perform subtyping of the breast cancer. As we closely examined the misclassified samples from our deep learning based classification results, it turned out that many of the misclassified samples may be from different biological groups of the breast cancer. The last one is to develop interpretable deep learning model for the cancer subtype classification. We will investigate these issue in the future in more details.
Conflicts of interest
The authors declare no conflict of interest.
CRediT authorship contribution statement
Md. Mohaiminul Islam: Conceptualization, Formal analysis, Methodology, Software, Validation, Visualization, Writing - original draft. Shujun Huang: Conceptualization, Data curation, Resources, Investigation, Writing - original draft. Rasif Ajwad: Formal analysis, Resources. Chen Chi: Formal analysis, Resources, Software. Yang Wang: Supervision, Funding acquisition, Writing - review & editing. Pingzhao Hu: Conceptualization, Supervision, Methodology, Investigation, Project administration, Resources, Funding acquisition, Writing - review & editing.
Acknowledgments
Acknowledgement
The authors thank the Molecular Taxonomy of Breast Cancer International Consortium (METABRIC) for providing the data sets used in this study.
Funding
This work was supported in part by Canadian Breast Cancer Foundation – Prairies/NWT Region, Natural Sciences and Engineering Research Council of Canada, Manitoba Health Research Council and University of Manitoba. P.H. is the holder of Manitoba Medical Services Foundation (MMSF) Allen Rouse Basic Science Career Development Research Award.
References
- 1.Breast Cancer Information and Awareness. http://www.breastcancer.org. Accessed on 20 January 2017.
- 2.Perou C.M., Sørlie T., Eisen M.B. Molecular portraits of human breast tumours. Nature. 2000;406(6797):747–752. doi: 10.1038/35021093. [DOI] [PubMed] [Google Scholar]
- 3.Parker J.S., Mullins M., Cheang M.C. Supervised risk predictor of breast cancer based on intrinsic subtypes. J Clin Oncol. 2009;27(8):1160–1167. doi: 10.1200/JCO.2008.18.1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Milioli H.H., Vimieiro R., Tishchenko I. Iteratively refining breast cancer intrinsic subtypes in the METABRIC dataset. BioData mining. 2016;9:2. doi: 10.1186/s13040-015-0078-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Futreal P.A., Coin L., Marshall M. A census of human cancer genes. Nat Rev Cancer. 2004;4(3):177–183. doi: 10.1038/nrc1299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Beroukhim R., Getz G., Nghiemphu L. Assessing the significance of chromosomal aberrations in cancer: methodology and application to glioma. Proc Natl Acad Sci. 2007;104(50):20007–20012. doi: 10.1073/pnas.0710052104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Yeung K.Y., Ruzzo W.L. Principal component analysis for clustering gene expression data. Bioinformatics. 2001;17(9):763–774. doi: 10.1093/bioinformatics/17.9.763. [DOI] [PubMed] [Google Scholar]
- 8.Krizhevsky A., Sutskever I., Hinton G.E. Imagenet classification with deep convolutional neural networks. Adv Neural Inf Process Systems. 2012:1097–1105. [Google Scholar]
- 9.Sharif Razavian A., Azizpour H., Sullivan J. Proceedings of the IEEE conference on computer vision and pattern recognition workshops. 2014. CNN features off-the-shelf: an astounding baseline for recognition; pp. 806–813. [Google Scholar]
- 10.Sermanet P, Eigen D, Zhang X, et al. Overfeat: Integrated recognition, localization and detection using convolutional networks. ArXiv e-prints 2013; doi: arXiv:1312.6229.
- 11.Yi D., Lei Z., Liao S., Li S.Z. 22nd international conference on pattern recognition (ICPR) 2014. Deep metric learning for person re-identification; pp. 34–39. [Google Scholar]
- 12.Hinton GE, Srivastava N, Krizhevsky A, et al. Improving neural networks by preventing co-adaptation of feature detectors. ArXiv e-prints 2012; doi: arXiv:1207.0580.
- 13.Wan L., Zeiler M., Zhang S. Proceedings of the 30th international conference on machine learning. 2013. Regularization of neural networks using dropconnect; pp. 1058–1066. [Google Scholar]
- 14.Hinton G.E. Training products of experts by minimizing contrastive divergence. Neural Comput. 2002;14(8):1771–1800. doi: 10.1162/089976602760128018. [DOI] [PubMed] [Google Scholar]
- 15.Larochelle H., Erhan D., Courville A. Proceedings of the 24th international conference on machine learning. 2007. An empirical evaluation of deep architectures on problems with many factors of variation; pp. 473–480. [Google Scholar]
- 16.Vincent P., Larochelle H., Lajoie I. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J Mach Learn Res. 2010;11:3371–3408. [Google Scholar]
- 17.Denas O, Taylor J. Deep modeling of gene expression regulation in an erythropoiesis model. Representation learning, international conference on machine learning workshop 2013.
- 18.Zeng H., Gifford D.K. Discovering DNA motifs and genomic variants associated with DNA methylation. bioRxiv. 2016 doi: 10.1101/073809. [DOI] [Google Scholar]
- 19.Leung M.K., Xiong H.Y., Lee L.J., Frey B.J. Deep learning of the tissue-regulated splicing code. Bioinformatics. 2014;30(12):i121–i129. doi: 10.1093/bioinformatics/btu277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhou J., Troyanskaya O.G. Predicting effects of noncoding variants with deep learning-based sequence model. Nat Methods. 2015;12(10):931–934. doi: 10.1038/nmeth.3547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Maienschein-Cline M., Zhou J., White K.P. Discovering transcription factor regulatory targets using gene expression and binding data. Bioinformatics. 2011;28(2):206–213. doi: 10.1093/bioinformatics/btr628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Danaee P, Ghaeini R, Hendrix DA. A deep learning approach for cancer detection and relevant gene identification. In Pacific symposium on biocomputing. pacific symposium on biocomputing 2016; 22: 219. NIH Public Access. [DOI] [PMC free article] [PubMed]
- 23.Yuan Y., Shi Y., Li C. DeepGene: an advanced cancer type classifier based on deep learning and somatic point mutations. BMC Bioinf. 2016;17(17):476. doi: 10.1186/s12859-016-1334-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Liang M., Li Z., Chen T. Integrative data analysis of multi-platform cancer data with a multimodal deep learning approach. IEEE/ACM Trans Comput Biol Bioinform (TCBB) 2015;12(4):928–937. doi: 10.1109/TCBB.2014.2377729. [DOI] [PubMed] [Google Scholar]
- 25.Gevaert O., Smet F.D., Timmerman D. Predicting the prognosis of breast cancer by integrating clinical and microarray data with Bayesian networks. Bioinformatics. 2006;22(14):e184–e190. doi: 10.1093/bioinformatics/btl230. [DOI] [PubMed] [Google Scholar]
- 26.Van Vliet M.H., Horlings H.M., Van De Vijver M.J. Integration of clinical and gene expression data has a synergetic effect on predicting breast cancer outcome. PLoS ONE. 2012;7(7) doi: 10.1371/journal.pone.0040358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Borgwardt K.M. Handbook of statistical bioinformatics. 2011. Kernel methods in bioinformatics; pp. 317–334. [Google Scholar]
- 28.Wang Y., Chen S., Deng N. Drug repositioning by kernel-based integration of molecular structure, molecular activity, and phenotype data. PLoS ONE. 2013;8(11) doi: 10.1371/journal.pone.0078518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Daemen A., Gevaert O., De Moor B. In 29th annual international conference of the IEEE engineering in medicine and biology society. 2007. Integration of clinical and microarray data with kernel methods; pp. 5411–5415. [DOI] [PubMed] [Google Scholar]
- 30.Eser U, Churchman LS. FIDDLE: An integrative deep learning framework for functional genomic data inference. bioRxiv 2016, doi:10.1101/081380.
- 31.Dutil F, Cohen JP, Weiss M, Derevyanko G, Bengio Y. Towards gene expression convolutions using gene interaction graphs. arXiv preprint 2018, doi:arXiv:1806.06975.
- 32.Network C.G.A. Comprehensive molecular portraits of human breast tumors. Nature. 2012;490(7418):61–70. doi: 10.1038/nature11412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ma S, Zhang Z. OmicsMapNet: Transforming omics data to take advantage of Deep Convolutional Neural Network for discovery. arXiv preprint 2018, doi:arXiv:1804.05283.
- 34.Jurman G, Maggio V, Fioravanti D, Giarratano Y, Landi I, Francescatto M, et al. Convolutional neural networks for structured omics: OmicsCNN and the OmicsConv layer. arXiv preprint 2017, doi:arXiv:1710.05918.
- 35.Ismailoglu F., Cavill R., Smirnov E., Zhou S., Collins P., Peeters R. Heterogeneous domain adaptation for IHC classification of breast cancer subtypes. IEEE/ACM Trans Comput Biol Bioinf. 2018;17(1):347–353. doi: 10.1109/TCBB.2018.2877755. [DOI] [PubMed] [Google Scholar]
- 36.Curtis C., Shah S.P., Chin S.F. The genomic and transcriptomic architecture of 2,000 breast tumours reveals novel subgroups. Nature. 2012;486(7403):346–352. doi: 10.1038/nature10983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.European Genome-phenome Archive. https://www.ebi.ac.uk/ega/studies/EGAS00000000083. Accessed on 14 July 2017.
- 38.Malabat C., Feuerbach F., Ma L., Saveanu C. Quality control of transcription start site selection by nonsense-mediated-mRNA decay. Elife. 2015;4 doi: 10.7554/eLife.06722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Jia Y., Shelhamer E., Donahue J. Proceedings of the 22nd ACM international conference on multimedia. 2014. An open source convolutional architecture for fast feature embedding; pp. 675–678. [Google Scholar]
- 40.Robin X., Turck N., Hainard A. pROC: an open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinf. 2011;12:77. doi: 10.1186/1471-2105-12-77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Statnikov A., Wang L., Aliferis C.F. A comprehensive comparison of random forests and support vector machines for microarray-based cancer classification. BMC Bioinf. 2008;9(1):319. doi: 10.1186/1471-2105-9-319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Breiman L. Random forests. Machine Learn. 2001;45(1):5–32. [Google Scholar]
- 43.Díaz-Uriarte R., De Andres S.A. Gene selection and classification of microarray data using random forest. BMC Bioinf. 2006;7(1):3. doi: 10.1186/1471-2105-7-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Russnes H.G., Lingjærde O.C., Børresen-Dale A.L., Caldas C. Breast cancer molecular stratification: from intrinsic subtypes to integrative clusters. Am J Pathol. 2017;187(10):2152–2162. doi: 10.1016/j.ajpath.2017.04.022. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data sets used in the study are available from the Molecular Taxonomy of Breast Cancer International Consortium (METABRIC): https://ega-archive.org/dacs/EGAC00001000484.