Image-based scaling laws for somatic growth and pulmonary artery morphometry from infancy to adulthood

Abstract

Pulmonary artery (PA) morphometry has been extensively explored in adults, with particular focus on intra-acinar arteries. However, scaling law relationships for length and diameter of extensive preacinar PAs by age have not been previously reported for in vivo human data. To understand preacinar PA growth spanning children to adults, we performed morphometric analyses of all PAs visible in the computed tomography (CT) and magnetic resonance (MR) images from a healthy subject cohort [n = 16; age: 1–51 yr; body surface area (BSA): 0.49–2.01 m²]. Subject-specific anatomic PA models were constructed from CT and MR images, and morphometric information—diameter, length, tortuosity, bifurcation angle, and connectivity—was extracted and sorted into diameter-defined Strahler orders. Validation of Murray’s law, describing optimal scaling exponents of radii for branching vessels, was performed to determine how closely PAs conform to this classical relationship. Using regression analyses of vessel diameters and lengths against orders and patient metrics (BSA, age, height), we found that diameters increased exponentially with order and allometrically with patient metrics. Length increased allometrically with patient metrics, albeit weakly. The average tortuosity index of all vessels was 0.026 ± 0.024, average bifurcation angle was 28.2 ± 15.1°, and average Murray’s law exponent was 2.92 ± 1.07. We report a set of scaling laws for vessel diameter and length, along with other morphometric information. These provide an initial understanding of healthy structural preacinar PA development with age, which can be used for computational modeling studies and comparison with diseased PA anatomy.

NEW & NOTEWORTHY Pulmonary artery (PA) morphometry studies to date have focused primarily on large arteries and intra-acinar arteries in either adults or children, neglecting preacinar arteries in both populations. Our study is the first to quantify in vivo preacinar PA morphometry changes spanning infants to adults. For preacinar arteries > 1 mm in diameter, we identify scaling laws for vessel diameters and lengths with patient metrics of growth and establish a healthy PA morphometry baseline for most preacinar PAs.

INTRODUCTION

The pulmonary vasculature dynamically grows and remodels with age in response to the increasing size and cardiac output of the body. Intra-acinar arteries, which accompany the pulmonary acini and respiratory bronchioles, differ greatly from the preacinar arteries, which are proximal to the acinus, larger, and more adjacent to the heart (20, 23). Morphometric studies of pulmonary arteries (PAs) are critical for understanding PA geometry and hemodynamics with and without pulmonary vascular abnormalities and disease, such as pulmonary arterial hypertension (PAH), pulmonary embolism, and peripheral pulmonary artery stenosis.

Previous studies on PA morphometry date back to the 1970s but fail to capture the changes in preacinar PA morphometry with age in detail. Landmark studies by Haworth and Hislop (20, 22) have shown that the normal pulmonary circulation remodels significantly immediately after birth to compensate for the increase in blood flow as a newborn takes its first breaths of air. This remodeling is characterized by a dynamic change in the number of intra-acinar vessels with age as well as increased muscularization of intra-acinar arteries into the preteen years (20, 23). The average diameter of intra-acinar vessels (following the respiratory bronchiole airways) increases from 26 µm at 5 h after birth to 180 µm at 14 yr (20). It is commonly believed that the growth in size and number of intra-acinar arteries corresponds to increasing cardiac output and vascular demand, somatic growth, and the need to maintain a healthy pulmonary vascular resistance and pressure (20, 52). On the other hand, numerous studies have shown that preacinar vessels remain constant in number, growing only in diameter and length after 19 wk of gestation (16, 22). Studies by Singhal, Horsfield, and Huang and colleagues (25, 27, 46) each used Strahler or diameter-defined Strahler ordering methods to quantify the diameter, length, and connectivity of an entire ex vivo adult human PA tree from the main PA to the preacinar and intra-acinar arteries. Although these studies laid the foundation for our current knowledge of PA morphometry, there remains a need for in vivo human measurements and information on the growth of the entire PA tree with patient metrics—age, body surface area (BSA), and height. These data are particularly crucial for studies of pediatric and congenital heart disease patients with pulmonary abnormalities.

More recent studies have investigated PA morphometry in adult humans and other species with in vivo imaging algorithms, such as volume filling or threshold filtering of a computed tomography (CT) scan (6, 42, 63). However, these studies either solely focused on adult PA morphometry or studied the alveolar arteries (i.e., intra-acinar arteries) and the large PAs (i.e., main, left, and right PAs) while neglecting the intermediate-sized PAs ~50 µm to 10 mm in diameter (4, 5, 18, 25). Related studies of airway morphometry with development have significantly advanced our understanding of the progressive structure, volume, and particle deposition in the trachea and bronchii (3, 31, 33, 43, 53, 62). These advancements use developments in aerosol tracing and CT scans to obtain in vivo measurements of the large and small airways (15, 43, 55, 62). Unfortunately, morphometry of pulmonary artery development has been less obtainable than that of the airways.

Morphometric studies have proven critical for informing computational models of PA hemodynamics to study progression of PA diseases. Mathematical relations (10, 27, 37) derived from morphometric measurements to characterize the radius, length, and branching pattern of the PAs have been used to represent the distal PAs in computational modeling for the pulmonary circulation with and without disease (12, 13, 37, 44, 48, 59–61). These computational models rely heavily on the geometry and structure of the pulmonary tree to estimate hemodynamics (12, 13, 29). However, these computational models, specifically focusing on pediatric populations, relied on simplifying assumptions because of a lack of available data on how PA morphometry changes with age.

To our knowledge, this study presents the first detailed in vivo morphometric study on the growth of preacinar PAs found in medical imaging in a comprehensive cohort of healthy human subjects spanning infancy to adulthood. We expect these data will be of particular value in supporting computational PA modeling studies that rely on morphometric data in health and disease. Our study offers two main contributions: 1) detailed in vivo morphometric measurements of diameters, lengths, tortuosity, bifurcation angles, and connectivity of the healthy PA tree spanning a wide range of ages and stages of somatic growth and 2) regression models for scaling laws of vessel diameter and length with diameter-defined Strahler orders in the PA tree across three patient metrics: BSA, height, and age.

METHODS

Healthy patient cohort selection.

A cohort of 16 subjects with normal PAs were identified from the database of the Stanford Medical Center and the Lucile Packard Children’s Hospital (LPCH) at Stanford under an institutional review board-approved protocol. This cohort of 16 subjects (10 males, 6 females) ranged in age from 15 mo to 51 yr and in BSA from 0.49 to 2.01 m², calculated with the Mosteller formula (34); patient metrics and imaging details of the subject cohort are listed in Table 1. A computed tomography (CT) scan with contrast (5 subjects) or magnetic resonance image (MRI) from each patient was used for morphometric measurements; scans ranged in resolution from 0.04 to 0.2 cm. Adult subjects (>18 yr) were chosen from Tang et al.’s study (49) with healthy control subjects age- and sex-matched to PAH patients. The images and PA trees of these adult subjects were downloaded from the Vascular Model Repository (www.vascularmodel.com) (58). Pediatric subjects (<18 yr) in this cohort were chosen to ensure coverage of pediatric BSA and age ranges and were treated for symptoms affecting the systemic circulation (resulting from aortic coarctation) or mild symptoms of the pulmonary circulation (resulting from bronchiectasis or a history of tuberculosis) but otherwise had healthy PAs, as determined by radiologists at LPCH.

Table 1.

Overview of healthy PA subject characteristics and anatomical PA model details

Age, yr	Sex	BSA, m2	HT, cm	WT, kg	Total No. of Vessel Segments in 3D Model	No. of Vessel Segments used in Analysis*	Minimum Diameter for Analysis, cm	Maximum Diameter for Analysis, cm	Imaging Modality	Image Resolution Axial × Sagittal × Coronal, cm
1	M	0.49	76	11	602	602	0.07	1.09	CT	0.10 × 0.04 × 0.05
2	M	0.51	81	11	1,472	178	0.18	1.38	CT	0.07 × 0.04 × 0.04
5	M	0.71	102	18	613	200	0.18	1.43	CT	0.20 × 0.04 × 0.05
7	M	0.91	125	24	113	113	0.15	1.98	MR	0.05 × 0.05 × 0.10
9	M	1.07	134	31	83	83	0.26	1.46	MR	0.10 × 0.10 × 0.10
11	F	1.20	138	37	1,776	234	0.25	2.08	CT	0.10 × 0.05 × 0.05
11	F	1.35	151	44	1,456	175	0.25	2.01	CT	0.10 × 0.05 × 0.06
15	M	1.68	178	57	112	112	0.21	1.82	MR	0.06 × 0.10 × 0.06
15	M	2.01	162	90	107	107	0.23	2.28	MR	0.08 × 0.08 × 0.10
18	M	1.84	187	66	83	83	0.24	2.71	MR	0.10 × 0.10 × 0.10
21	M	1.76	175	64	155	155	0.24	2.30	MR	0.07 × 0.07 × 0.10
22	F	1.66	168	59	128	128	0.29	2.28	MR	0.07 × 0.07 × 0.10
31	F	1.6	157	59	151	53	0.42	2.47	MR	0.07 × 0.10 × 0.06
35	M	2.00	178	81	265	117	0.42	2.35	MR	0.07 × 0.10 × 0.07
43	F	1.90	165	79	178	76	0.40	2.36	MR	0.07 × 0.10 × 0.07
51	F	1.75	168	66	201	201	0.23	2.13	MR	0.07 × 0.10 × 0.07

CT, computed tomography; F, female; HT, height; M, male; MR, magnetic resonance; PA, pulmonary artery; WT, weight; 3D, 3-dimensional.

^*The number of vessels analyzed was based on a criterion of vessel orders >11.

Construction of three-dimensional PA models.

We used the open-source software package SimVascular (simvascular.org) to create three-dimensional (3D) anatomic reconstructions of the normal PA vasculature from CT or MRI data (54). Six healthy adult (>18 yr) and five pediatric (<18 yr) PA models created from MR images were repurposed from Tang et al. (49) and Yang et al. (59), respectively; these data are also publicly available via the Vascular Model Repository (www.vascularmodel.com) (58). Five pediatric PA models created from CT images were added to this previous healthy PA cohort. All models were created using the standard SimVascular workflow: 1) creation of 3D pathlines for all visible PAs in the CT or MRI data, 2) two-dimensional (2D) segmentation, or outline, of the PA lumen using the cross-sectional views along the pathlines, 3) automated lofting of 2D segmentations into a 3D model, and 4) refinement of the 3D solid PA model into a mesh of finer elements used for detailed analysis of the geometry (54). For each patient, an experienced SimVascular user manually identified all visible PA pathlines, as limited by imaging resolution, from the main PA down to the 9th- to 16th-generation PAs in all lobes of both the right and the left lungs. Manual segmentations as well as a manually verified machine learning-based segmentation algorithm (32) were used to outline the arterial lumen (inner diameter) of vessels consisting of at least 3 pixels in diameter. These segmentations were outlined along pathlines with more segmentations created at regions of bends, area changes, and junctions in the PAs. Segmentations were lofted into a 3D model using the Parasolid library; surface meshes for each model were created with MeshSim (Simmetrix, Troy, NY). Final 3D models of the PA trees are shown in Fig. 1 from the left sagittal view. Although these do not include all preacinar PAs, they represent the majority of vessels found in medical imaging extending down to diameters in the millimeter-sized range. The number of vessels identified for the 3D model ranged from 83 to 1,776 vessels (Table 1). As such, the extensiveness of the PA tree extracted was limited by the resolution and clarity of the medical imaging modality used.

Fig. 1.

Three-dimensional constructed models of the healthy pulmonary artery (PA) tree for all 16 patients in the cohort viewed sequentially in body surface area (BSA) from left to right. A scale for size is shown at bottom right. F, female; M, male, y, year.

Extraction of morphometric information.

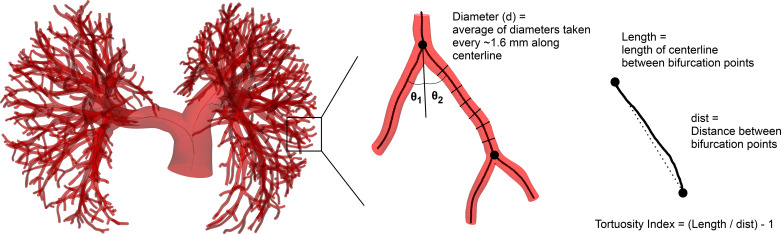
Morphometric information from each PA model was extracted with custom Python software. Centerline extraction methods from the Vascular Modeling Tool Kit (VMTK; vmtk.org) were used to extract all arterial centerlines (2) from the surface mesh of each model and to identify parent and daughter arterial segments at every PA branching point (Fig. 2). For each centerline, vessel segments were identified as vessel regions between adjacent junction regions, defined as the region between the intersection of the maximum inscribed radius of a vessel and the centerline of another vessel and one radius sphere proximal to this intersection (Supplemental Fig. S1a; all Supplemental Material is available at https://doi.org/10.6084/m9.figshare.11862414). For junction regions where more than one daughter vessel splits from the same parent vessel, overlapping junction regions from single combinatorial pairs of bifurcations in the same region are superposed to form one larger junction region (Supplemental Fig. S1b). The length of each vessel segment was then calculated as the length of the centerline between the beginning and end of two adjacent junction regions. The diameter of the vessel was calculated as twice the maximum inscribed sphere radius from the centerline to the model’s exterior surface. These diameter measurements were sampled every ~1.6 mm along the resolved centerline of each vessel segment, not including the junction regions, and averaged. Because of this method of diameter measurement, not all analyzed segments had diameter values > 3 pixel resolutions.

Fig. 2.

Diameter and length measurements from the 3-dimensional pulmonary artery (PA) model were extracted along centerlines of vessels. Multiple diameters were taken along the centerline from a maximally inscribed radius, and lengths were measured along the centerline from subsequent bifurcation points. θ₁ and θ₂ represent the in-plane bifurcation angles of the 2 daughter vessels branching from the parent vessel. Vessel order of the segments in the model was defined with an initial Strahler ordering method, followed by a diameter-defined Strahler order and outlier resorting.

Tortuosity of a vessel is a common indicator of diseased phenotypes or early arterial remodeling (21, 45). Although tortuosity mathematically refers to how twisted a vessel is, it can also be used to refer to curves, angle, twists, and loops of vessels (19), which can be measured by a tortuosity index, sometimes referred to as a distance metric (21). For all PA models in our cohort, we computed the tortuosity index (TI) of each vessel segment, defined as the ratio between the actual segment length and the shortest path between the corresponding adjacent junction regions,

$$\text{TI}=\frac{\text{segment\hspace{0.17em}length}}{\text{line\hspace{0.17em}distance}}-1.$$

We excluded vessel segments where the actual segment length was less than the segment diameter to avoid including TI artifacts from very short segments (9% of all segments from all patients).

In-plane bifurcation angles of every vessel segment branching from a parent vessel were calculated with the VMTK geometry extraction method (41). For junction regions where more than two daughter segments branched from the parent (accounting for 9.8% of all total junction regions in the cohort), the in-plane angles of all daughter segments were calculated with the in-plane orientation of the parent segment immediately before the junction region (Fig. 2).

Murray’s law has been used to determine the optimal branching structure of arterial networks by balancing metabolic demand with the optimal work performed in transporting blood through a vascular network (35, 36). Murray’s law dictates a relation between the parent and daughter radii as

$$r_{\text{p}}^z={\displaystyle {\sum }_i{r}_{\text{d},i}^z},$$

where z is the Murray’s law exponent, i is the index of the daughter vessel, and r_p and r_d are the radii of the parent and daughter vessels, respectively. At each branching point, z was calculated from Murray’s law given the parent and daughter radii.

Diameter-defined Strahler ordering system.

To facilitate comparison with previous morphometric studies of adults, we used the diameter-defined Strahler ordering system to define vessel orders and connectivity (27, 48). Per the diameter-defined Strahler ordering system, vessel segments are defined as vessel sections between branching points; vessel elements are larger units consisting of consecutive vessel segments belonging to the same order (27). In brief, an initial Strahler ordering method was first defined upward from the outlets of the model to the main pulmonary artery (MPA), with all outlet segments initially defined as order 1. If all daughter segments at a junction region were order n, the parent segment proximal to the junction was designated order n+1. If the daughter segments were of different orders, the parent segment was designated an order equal to the largest daughter vessel order. A diameter-defined Strahler ordering method was then used to resort orders based on diameters to capture the heterogeneity of both small and large vessels branching from one parent vessel element. Unlike the PA trees described in Huang et al. (27) and Singhal et al. (46), our PA tree models do not extend down to precapillary levels and only captured <6 distinct orders. Therefore, to match the same ordering system as Huang et al. in which the left and right PA (LPA/RPA) segment was an order 15 segment and the precapillary PA was an order 1 (27), we translated all orders by a constant such that the MPA segment was order 16 and the LPA/RPA segments were order 15, assuming our PA trees captured the larger orders reported in Huang et al. Segments that had outlier diameters within their order, defined as outside 1.5 × interquartile range (IQR), were resorted into adjacent orders until outliers were not present. Specifically, if a segment had an outlying diameter > 1.5 × IQR its order was increased by 1, and vice versa for a diameter < 1.5 × IQR. If a segment with the lowest order in the model had a diameter < 1.5 × IQR, it was removed to avoid creating new orders from outliers; outliers that were removed accounted for an average of 0.58% of all vessel segments in a given PA tree.

The branching of the pulmonary tree was described in a connectivity matrix according to the diameter-defined Strahler ordering method in Huang et al. (27). In the connectivity matrix, rows represent daughter orders and columns represent parent orders, with values corresponding to the average number of elements of the daughter order (row number) branching from the parent order (column number) element. We compared across all patients’ connectivity matrices to determine trends in the branching pattern with age, height, and BSA.

To determine how the definition of the junction region affected the morphometric indexes and connectivity calculated from the diameter-defined Strahler orders, we increased the junction region size by 100% for two sample subjects’ PA trees (9-yr-old male and 21-yr-old male). A 100% increase in the size of the junction region had a significant effect on only the length of order 14 vessel segments. There was no significant difference in the connectivity matrix, diameters, TI values, angles, or Murray’s exponent per order, as determined by a Welch’s t test.

Model selection for diameter and length trends.

For diameter and length regression models, we tested 15 linear and nonlinear least squares regression models that captured changes in diameter and length with patient metrics using the open-source R software package (50). These models were trained with only vessel segments between orders 12 and 16 to ensure that all subjects had similar network extensiveness; the number of vessels used for statistical analysis of morphometric information ranged from 53 to 602 vessels with the smallest diameter of 0.07 cm included in the analysis (Table 1). Models were selected for testing if there was a significant interaction between patient metric and vessel order, with the intent of capturing trends in diameter and length over the physiological ranges of the patient metrics and all vessel orders of the PA tree. Because the morphometric data from the 3D PA models were limited to vessels with >1-mm diameter, we made three main assumptions based on findings of Haworth et al., Hislop et al., and Huang et al. to inform model selection: 1) preacinar vessels remain constant in number and in branching patterns after birth, growing only in diameter and length; 2), max-intra-acinar vessel diameter increases from 50 µm at age 1 to 120 µm at age 14 and is approximately generalizable to all subjects; and 3) pulmonary capillaries maintain a constant diameter of ~0.001 cm, which does not change with age (23, 27, 52).

Based on these assumptions, our generalized models of diameter and length are only applicable to vessel orders corresponding to preacinar vessels and not to smaller vessel orders (intra-acinar vessels), which grow in dimension and number and cannot be captured by the preacinar vessels found in our data set. For comparison to other studies’ preacinar measurements, we used a cutoff of vessel order 5, which corresponds to a diameter of 120 µm reported in Huang et al. (27), to signify the end of preacinar vessels and the start of intra-acinar vessels, assuming that the maximum intra-acinar vessel diameter of 120 µm at age 14 from Haworth’s study (20) also applies to adults. We also assumed that pulmonary capillaries do not change in size with age, using a pulmonary capillary size of 0.001 cm to anchor order 0 vessels for all ages and sizes in our diameter regression model. In addition to these criteria, the regression models tested were informed by allometric scaling studies using power models to capture large increases at small body sizes that level out at larger body sizes (39, 56).

Of the 15 regression models tested for diameter and length, the five top-performing models were selected based on the highest Pearson’s coefficient of determination (R²) and the lowest root mean square error (RMSE); these top-performing models were further evaluated for robustness. A fivefold cross validation was used to evaluate overfitting and generalization from our limited data set with the RMSE from each fold. Furthermore, to determine if the unbalanced data sets due to differences in network extensiveness per subject were biasing the R² values of the regression models, we randomly downsampled each subjects’ data set to match the number of vessels found in the smallest data set from our cohort. To determine if the R² value from the full data set differed significantly from downsampled data sets, we calculated the R² values of 1,000 unique downsampled cohort data sets and performed a t test on the mean value (α = 0.05).

On the basis of these evaluations and prediction of physiological diameters and trends with vessel order, as found in Huang et al. (27) and Singhal et al. (46), Eq. 1 was selected for the diameter regression model where the diameter (cm), D, is a function of vessel order, σ, and patient metric [BSA (m²), height (cm), age (yr)], X, and a, b, and c are model-derived coefficients. Similarly, Eq. 2 was selected for the length (cm), L, regression model based on our model evaluation criteria and ability to scale existing reported length measurements at all vessel orders with patient metrics.

$$D=0.001+a\sigma \exp \left(b\sigma \right)X^c$$ (1)

$$L=a{X}^c$$ (2)

The effect of network size, as measured by the number of segments included in each PA tree, was analyzed for the diameter and length scaling laws (Eqs. 1 and 2) by randomly downsampling and upsampling (with replacement) the vessel segments in each subject to a range of sizes between 40 and 600 vessel segments. For each network size, we refit Eqs. 1 and 2 and calculated the R² values for 1,000 unique data sets from the downsampling and upsampling techniques; we calculated the percent difference between the coefficients and R² values from the original subject data set and the mean of all simulated network sizes with significant coefficient changes determined by a Z test. To determine how variation in diameter due to averaging along the centerline affects the model, we used a normal distribution to randomly increase and decrease the diameters of all vessel segments from 0 to 63%, based on the maximum standard deviation found from averaging diameters along the length of a vessel segment. R² values and coefficients were calculated with Eq. 1 for each percent in diameter perturbation.

Statistics.

All statistics were applied only to orders 12–16 from the PA models since not all PA models captured extensive vessel branching below vessel order 12. Pearson’s coefficient of determination was used to measure the statistical correlation between patient metrics, vessel order, and morphometric indexes—diameter, length, tortuosity, bifurcation angle, and Murray’s exponent, z. P values of <0.05 were considered statistically significant for correlation tests and comparison tests. Welch's t test with a post hoc Holm–Bonferroni correction for multiple comparisons was employed to test for significant differences between the PA connectivity matrix in Huang et al. and the connectivity matrix from each PA model. A one-way ANOVA with a post hoc Tukey honestly significant difference (HSD) test was used to test for significant differences in tortuosity, bifurcation angles, and z across vessel orders. To determine any significant effects of patient metrics (i.e., BSA, age, and height) and vessel order on tortuosity, bifurcation angles, and z, a linear mixed model was used to account for correlations among each subject as a random effect.

RESULTS

Diameter and length models.

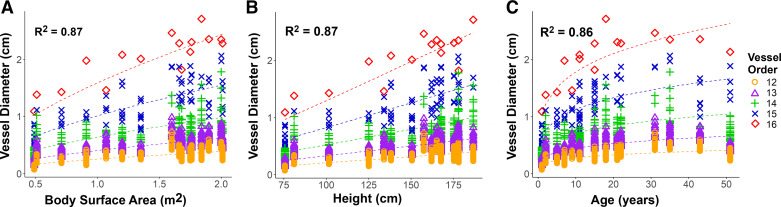
Model coefficients with standard errors and R² values, calculated from Pearson correlation coefficients, for the predicted versus actual diameters in Eq. 1 are listed in Table 2 for BSA, age, and height. These models had strong correlations, R² values of 0.87, 0.87, and 0.86 for BSA, height, and age, respectively, as shown in Fig. 3, with good fits of the predicted versus actual segment diameters with order and BSA, age, and height. Diameter models were not affected by unbalanced data sets, as shown through our downsampling method (P > 0.05). Varying network size resulted in small differences in R² value (<0.1%) and coefficient b (<4%), which was significantly different from coefficient values from the original data set only in larger network sizes. However, coefficient a had larger differences with height (56%), age (30%), and BSA (23%), with significant differences for most network sizes tested; coefficient c also had a moderate difference with varying network size, 11% for BSA, 7% for height, and 3% for age, with significant differences for most network sizes tested as well. Based on the maximum variation in diameters averaged along centerlines, a 63% perturbation in diameter resulted in insignificant differences in the model coefficients and a <12% difference in R² values. Although Eq. 1 was only applied to orders 12–16, we nonetheless observed strong correlations (R² > 0.88 for BSA, R² > 0.88 for height, and R² > 0.87 for age) when we extrapolated Eq. 1 to orders 10 and 11 for the three PA models that extended to the smaller orders. The power exponent for each patient metric (coefficient c in Table 2) varied greatly between patient metrics (c = 0.238 for age, c = 0.617 for BSA, c = 1.05 for height).

Table 2.

Diameter and length regression model coefficients

Model	Equation*	a	a SE	b	b SE	c	c SE	R2**
D vs. BSA, σ	1	1.976e−4	0.087e−4	0.3887	0.0032	0.6172	0.0108	0.87
D vs. HT, σ	1	1.279e−6	0.126e−6	0.3899	0.0031	1.046	0.018	0.87
D vs. age, σ	1	1.203e−4	0.055e−4	0.3927	0.0033	0.2381	0.0043	0.86
L vs. BSA	2	1.070	0.017			0.6444	0.0292	0.19
L vs. HT	2	5.851e−3	1.465e−3			1.084	0.050	0.19
L vs. age	2	0.7088	0.0233			0.2262	0.0114	0.16

BSA, body surface area (m²); D, diameter (cm); HT, height (cm); L, length (cm); SE, standard error of the regression coefficients.

^*Models are based on Eqs. 1 and 2.

^**Coefficient of determination.

Fig. 3.

Diameters of all vessel segments for each patient and vessel order show growth with body surface area (A), height (B), and age (C). Predicted diameters (dashed lines) showed a strong correlation with the actual diameters measured from the 3-dimensional pulmonary artery (PA) models for all patient metrics and orders.

Vessel segment lengths had no correlation with order and a weak correlation with BSA, height, and age. Coefficients of the model from Eq. 2 and standard errors with corresponding R² values are listed in Table 2. We found similar weak correlations for all patient metrics with Eq. 2 (R² = 0.19 for BSA, 0.19 for height, and 0.16 for age). Supplemental Figure S2 illustrates the moderately weak correlation between patient metrics and segment lengths. Distribution of lengths for all segments in each order showed no distinct separation in the lengths between segments for orders 12–14. However, length model correlation coefficients were significantly affected by unbalanced subject data set, with higher R² values in the full data set than the downsampled data sets (P < 0.01 for all patient metrics). Although the length models were less affected by network size compared with diameter, there was a 22% difference in coefficient a with height and an 11% difference in coefficient c with age. All other coefficients and R² values had a difference of <6% when network size was varied, with no significant differences in coefficients for the smallest network size of 40 vessels for all patient metrics.

Morphometric indexes.

Though TI values did not change significantly with BSA, height, or order, there was a weak positive correlation with an increase in age (R² = 0.11). We also found that order 16 segments (mean TI = 0.068 ± 0.036, median = 0.069) had significantly different TI values compared with all other orders, which could reflect the bend of the MPA compared with straighter smaller vessels that bifurcate frequently. Supplemental Figure S3a shows the slight increase in tortuosity with order and the large variability in each order. On average, vessel segments had an average TI of 0.026 ± 0.024 (median = 0.019).

Bifurcation angles did not change significantly with patient metrics. There was large variability in bifurcation angle of all segments in each order, with only a significant difference in bifurcation angles between order 14 and 12 segments. The average bifurcation angle in the entire pulmonary tree was 28.2 ± 15.1°. The average bifurcation angle at the MPA for all patients was 79.6 ± 20.3°. However, there was a more distinguishable downward trend in bifurcation angle between order 12 and order 15 segments that branched from a parent order 15 (Supplemental Fig. S3b). There was a weak correlation (R² = 0.24) between decreases in bifurcation angle with increases in vessel order for segments branching from a parent vessel of order 15. Segments branching from a parent order 15 usually occurred in the upper to middle lobe of the pulmonary arteries where daughter segments consisted of both large and small vessel orders. The average bifurcation angle for daughter vessels with an order 1 less than the parent order was 30°.

Murray’s exponent, z, was weakly correlated with an increase in patient metrics (R² = 0.14 for BSA and height, R² = 0.13 for age) and showed a slight downward trend with increasing vessel order (R² = 0.21; Supplemental Fig. S3c). At smaller vessel orders, which were generally more distal to the tree, z was larger, with average values of 3.15 ± 0.99 (median = 3.03) for order 12 vessels. This value was significantly different from the larger-diameter and more proximal order 13–15 vessels, where z was 2.39 ± 0.95 (median = 2.17) for order 15 vessels. The average z value for all vessel segments was 2.92 ± 1.07.

Comparison with previous morphometric studies.

To validate diameters from our 3D models with previous morphometric studies of the largest PAs, we compared the LPA, RPA, and MPA diameters of patients > 18 yr old in our cohort to measurements from a cohort of 120 adult patients (5). The MPA, LPA, and RPA diameters measured in our adult subjects fell within two standard deviations of the sex-matched average diameter values reported in Burman et al. (5), The diameters predicted using our BSA based model (Eq. 1) and the BSA values in Burman et al. yielded average percent errors of 7.8 ± 5.4% for the MPA, 22.8 ± 11.1% for the LPA, and 13.9 ± 11.1% for the RPA, compared with Burman et al.’s direct measurements. Although diameters from our cohort were similar to Burman et al., major differences can be attributed to different measurement methods. The diameters in Burman et al. were measured with two cross-sectional diameters taken at the same location of the MPA, LPA, and RPA at diastole, whereas diameters measured in our cohort were taken as double the average maximally inscribed radius along the length of the MPA, LPA, and RPA segments, which were not gated at diastole.

We also compared measured diameters from our pediatric 3D models and model-predicted diameters with Boston Children’s Hospital’s Z-score measurements, which are based on echocardiographic measurements of MPA, LPA, and RPA diameters (11, 47). Average Z score of the MPA diameter was −0.37 ± 0.84 for the computed value vs. −0.32 ± 0.37 for the BSA-based prediction vs. −0.63 ± 0.53 for the height (HT)-based prediction vs. −0.37 ± 0.56 for the age-based prediction using an order 16 value. Average Z score of the LPA diameter was 0.90 ± 0.79 for the computed value vs. −0.061 ± 0.39 for the BSA-based prediction vs. −0.27 ± 0.53 for the HT-based prediction vs. −0.34 ± 0.51 for the age-based prediction using an order 15 value. Average Z score of the RPA diameter was 0.26 ± 0.74 for the computed value vs. −0.24 ± 0.40 for the BSA-based prediction vs. −0.44 ± 0.54 for the HT-based prediction vs. −0.52 ± 0.52 for the age-based prediction using an order 15 value. The Z scores of our cohort’s diameters and predictions are within a reasonable range (Z < 1), with variation attributed to the echocardiography imaging techniques used for the Boston Children’s Hospital’s data, which were taken in midsystole.

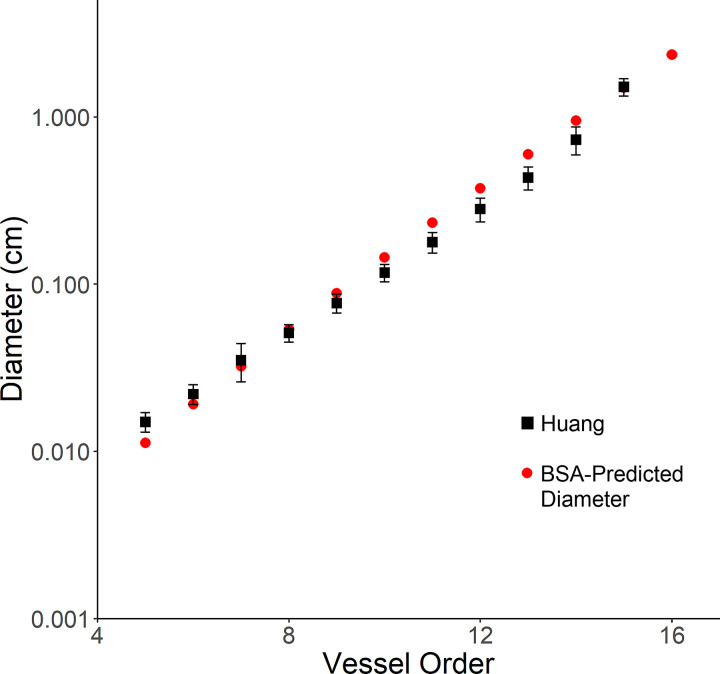
To compare our model’s predicted diameter with the morphometric measurements for the entire PA tree by Huang et al., we extrapolated our diameter BSA-based model (Eq. 1) from order 15 to order 1, using a BSA of 2.2 m² matching specimen no. 1 in Huang et al. (27). Figure 4 shows the comparison of diameters for vessel orders 5–15. Trends in our model’s predicted diameter were similar to the measured diameter in Huang et al., with a <35% error in a majority of the preacinar vessels (orders 5–10) and a minimum error of 0.5% for order 7 vessels. Differences in the diameter could be attributed to generalization of the model, differences in measuring techniques, and the difference between ex vivo and in vivo measurements. Although it is apparent from Huang et al. that there is an increase in length from order 1 to order 15, our segments of orders 12–16 showed no correlation. This finding is consistent with the small changes in length and large standard deviations in orders 12–15 reported in Huang et al. (27). Predicted lengths, using Eq. 2 to scale the original lengths from Huang et al. with BSA, were 26% different from the measured lengths reported in Huang et al. for all vessel orders.

Fig. 4.

Extrapolation of Eq. 1 for prediction of diameter for all vessel orders was compared with the diameter measurements from Huang et al. (27) for an adult man with a body surface area (BSA) of 2.2 m². The predicted diameters from Eq. 1 were similar to Huang et al.’s measurements for all vessel orders, with the lowest standard error of 0.5% at order 7 vessels.

We also compared the average connectivity matrices of each patient with Huang’s original connectivity matrix. Most significant differences in the connectivity matrices came from daughter orders 12 and 13 branching from parent orders 12 and 13. Of the 16 patients, 13 patients had significant differences with Huang’s connectivity matrix for the order 12 coming out of parent order 12s and 8 patients had significant differences for order 13s coming out of parent order 13s. These differences can be attributed to the limited extension of the PA tree for our normal PA cohort that does not account for smaller orders compared with Huang’s PA tree, which extended to precapillary levels. Moreover, since the connectivity matrices did not significantly change with patient metrics, the assumption that the preacinar PA vessels (at least down to order 12) are fully established from birth and do not change in number and branching pattern with somatic growth still holds. The average connectivity matrix from the entire healthy cohort is listed in Supplemental Table S1.

DISCUSSION

To our knowledge, this study presents the first comprehensive analysis of morphometric scaling of the in vivo human pulmonary artery tree from MPA to distal vessels > 1 mm in diameter for pediatric and adult subjects. The diameter and length regression models describe a scaling rule for growth of the PAs from a 1-yr-old infant to a 51-yr-old adult. Diameter models showed that diameter increased exponentially with vessel order and allometrically with BSA, height, and age of subjects > 1 yr; these models predicted diameters similar to previous morphometry studies. Length models showed that length increased allometrically with BSA, height, and age. Additionally, we reported normal tortuosity indexes, bifurcation angles, and Murray’s radius exponent, z, for all healthy subjects. Although changes in patient metrics from children to adults did not significantly affect bifurcation angles, age was weakly correlated with changes to tortuosity and z, and BSA and height were weakly correlated with changes in z. Our analysis of healthy PA morphometry across a wide age range provides a baseline for comparison against diseased pulmonary trees, including those affected by pulmonary arterial hypertension, smoking, and pulmonary stenosis, through all stages of postnatal development. Previously, only Haworth and Hislop have attempted to characterize the development of the pulmonary tree using morphometry but were limited to ex vivo observations in a small number of patients.

The forms of diameter (Eq. 1) and length (Eq. 2) models are similar to previous allometric scaling laws of vessel diameter with body mass (39, 56). Although previous studies report a body mass power exponent of $\frac{1}{4}$ to $\frac{3}{8}$ (38, 39, 56), we found that diameter scaled with BSA to the 0.617 power. Similar to the diameter model, the BSA-based length model had a power exponent of 0.644, which is different from previously reported power exponents of 0.25–0.46 (14, 24) in allometric studies of length. Differences in power exponent could be attributed to previous studies relating theoretical assumptions of metabolic rate with the systemic capillary system as well as measurements of only the large pulmonary artery diameters (i.e., MPA). This could be an indication of differences between the systemic and pulmonary circulation as well as functional differences at smaller generations in the PA tree.

Although there has been a shift toward in vivo morphometric studies with the development of higher-resolution imaging, these studies have mainly focused on adults and large vessels. However, for diseases such as PAH, peripheral pulmonary artery stenosis, and embolism, vascular remodeling and abnormalities occur in both the branch PAs and the distal vasculature. Thus, as imaging techniques improve to resolve the distal vasculature, it is important to characterize healthy distal PA vasculature beyond the lobar and segmental PAs in children and adults. Because tortuosity and branching angles have been hypothesized to be characteristics of disease (1, 7, 19, 21), morphometric analysis of this normal cohort can serve as a control for future studies. The tortuosity index of the normal PA vessels in our cohort was very small, in line with previous theories of optimal blood transport through straight vessels to prevent abnormal pressure gradients and dysfunctional wall properties (19). Moreover, our finding that tortuosity increases slightly with age agrees with previous studies reporting increases in vessel tortuosity with age (9). To fully capture the effects of PA tortuosity with more advanced age, a cohort focusing on elderly patients with image data of the subsegmental PAs is needed.

Our findings on bifurcation angles and z agree well with previous studies of optimal morphometric indexes. The bifurcation angles presented here are similar to Murray’s derived branching angles of 35° for the microcirculation, which optimizes energy at bifurcations without significant power losses (35, 51). Additionally, z values of 3.15 for small order 12 vessels and 2.39 for larger order 15 vessels found in this study agree with previously reported literature values where the ideal z value of 3 was found for small-vessel networks, similar to order 12 vessels, where flow is assumed to be laminar (14, 35, 36) and an ideal z value of 2.33 was found for regions where disturbed flow dominates (26, 30), similar to the flow found in the proximal PAs of order 15. The large variability in z for each vessel order can be attributed to the variance contributed by subject variability and slight increases in z with patient metrics, which may coincide with changes in cardiac output in adults that affect vessel wall properties; more extensive analysis of these changes is needed.

Because of the manual segmentation conducted on all vessels in all models of this normal PA cohort, we have confirmed the anatomy against the image data with high confidence via visual inspection. Other distal morphometric imaging techniques use algorithms, such as volume filling, which make many simplifying assumptions about the branching pattern, angles, and tortuosity of the vessels. Although these techniques are valuable for use in simulations that aim to approximate hemodynamic forces, they should be used cautiously for morphometric studies since some assumptions may not accurately reflect the anatomy. With our manually verified geometric modeling techniques, others can use our 3D models as a check for new imaging and identification techniques. These 3D models can also be easily converted into finite element meshes for computational fluid dynamics simulations to study hemodynamics of branching patterns, pressure losses, and disease progression. All models in this cohort are publicly available on the open-source Vascular Model Repository (www.vascularmodel.com) and are compatible with SimVascular.

Computational modeling studies that have focused on hemodynamics in diseased PAs have used early PA morphometry studies or simplifications thereof (12, 13, 28, 37, 44, 48, 59–61). Because detailed information on the branching patterns, radius, and length of the PAs used in these studies were limited to ex vivo adult single lungs, the geometry of the distal PAs in their patient-specific simulations was oversimplified and may not have accurately reflected the hemodynamics in the distal PA bed. Thus, the diameter and length models for children and adults presented here will be beneficial in informing computational simulations based on patient metrics. Improved models will aid in capturing the dynamic changes that occur in PA hemodynamics with growth and disease, for example, in follow-up studies to Yang et al.’s investigation of pediatric pulmonary hypertension severity (59) or adult patient-specific studies (28). In conjunction with normal morphometric indexes, such as tortuosity, bifurcation angle, and Murray’s exponent, our PA morphometric findings for children and adults can be extended to multifidelity computational simulations of the PA tree to investigate PA remodeling, surgical reconstruction of the PA tree, and disease severity.

The wide age range of patients in this study provides important healthy PA morphometry information for future studies specifically looking at pediatric patients. Because many diseases manifest with somatic growth, age-matched healthy PA geometrics may better capture the changes in PA morphometry due to disease. For example, changes to the PA structure due to a congenital heart defect should be studied in comparison to a toddler or infant normal PA tree with inherent growth of the PAs as the child ages. These methods can also be applied to diseased PA morphometrics, which may be used as risk indicators for disease progression.

Limitations.

This study was based on a normal healthy PA cohort of 16 patients, which likely does not capture the large variation in patient PA morphometry for all ages and body sizes. Future morphometric studies of child and adult preacinar arteries should consider a larger cohort size to reproduce and extend our knowledge of PA morphometry in both the healthy and diseased vasculature with growth for even more extensive trees with automated segmentation techniques. Furthermore, our subject cohort had a disproportionate ratio between male and female subjects, with a majority of male subjects in the pediatric range. Because of this, differences in morphometric indexes due to sex could not be confidently drawn. Future studies with a larger subject cohort using equal proportions of males and females should include comparisons due to sex, which has been shown to have a weak effect on diameters of the large PAs in adults (5, 17, 40).

The CT and MRI data acquired did not have standardized resolutions and were not cardiac gated. Diameters and lengths extracted from models built from the images could have been taken from any period during the diastolic phase and therefore will appear as variability in the data. There are also inherent inconsistencies between CT and MR imaging modalities, with poorer resolution of the distal vessels and small artifacts of elliptical shaped vessels in MRI. Although diameter measurements were averaged along vessel lengths and only the largest vessel orders (vessel orders 12–16) that were present in all subjects’ PA trees were included in the analysis, a morphometric study with a single imaging modality, preferably CT imaging for better resolution for large PA networks, may reduce variation in measurements.

Because of the different image resolutions, with a greater lack in resolution from MR images, there is a consequential difference in the number of arteries and number of generations down the PA tree that were modeled for each patient. Although steps were taken to control for bias from differences in extensiveness of each patient’s tree, a more homogeneous identification of PAs to the same generation in each model could further elucidate changes from children to adults in much smaller arteries.

Areas in the PA tree where a parent vessel segment splits into a densely populated region of many daughter vessels, usually at interlobar regions, are often categorized into one large junction region. This large junction region may encompass a large bend in the middle lobe over multiple centimeters in length. Because bifurcation angle and TI values are extracted from centerlines before and after junction regions, some resolution may be lost within the junction region where angles could be interpreted as more acute and TI values as larger, thus contributing to the variability in angle and tortuosity. Because of the difficulty of discerning distinct small junction regions in areas with many daughter vessels splitting from the same parent vessel, the VMTK method for defining bifurcation angle and tortuosity is sufficient for these end cases.

Previous studies have found large variations in diameters along vessel segments (12), which may affect the results directly related to diameter such as the diameter scaling laws and Murray’s exponent. Although we have limited the variation in diameter by not including the junction regions where much of the uncertainty lies, there may be other variation along the vessel segment that might influence the diameter regression models and Murray’s exponent.

Our analysis of the PAs groups together all lobes and assumes homogeneous morphometry for each lobe. However, it has been shown that PA blood flow distribution is heterogeneous throughout the lungs, with differences in the upper, middle, and lower lobe (8, 10, 57). This would suggest that the morphometry of the PAs would also be different in the different lobes. Although this study presents general morphometric results with age, it does not distinguish between lobes; these differences could be considered in future studies on the morphometry of the PAs.

Conclusions.

We conducted a morphometric study of in vivo healthy PAs for a cohort of children and adults. Diameters and lengths of PAs scaled with vessel order and allometrically with patient metrics, such as BSA, height, and age. Tortuosity index, bifurcation angle, and Murray’s radius exponent, z, had slight trends with vessel orders, but only tortuosity index and z changed with age. BSA and height were weakly correlated with z. Connectivity of the preacinar PAs did not change from children to adults. Our results establish healthy PA morphometric information and scaling relations from children to adults that can be used for comparison with diseased PA vasculature.

GRANTS

This work was supported in part by the Vera Moulton Wall Center for Pulmonary Vascular Disease at Stanford. M. Dong was supported by a National Science Foundation Graduate Research Fellowship under Grant No. DGE-1656518. Additional support was provided by National Library of Medicine Grant R01 LM-013120 to support the Vascular Model Repository.

DISCLOSURES

E. J. Zucker has received consultancy fees from Genentech. None of the other authors has any conflicts of interest, financial or otherwise, to disclose.

AUTHOR CONTRIBUTIONS

M.L.D., W.Y., M.R., A.L.M., and J.A.F. conceived and designed research; M.L.D., W.Y., F.P.C., E.J.Z., and S.K. performed experiments; M.L.D., W.Y., and J.S.T. analyzed data; M.L.D., W.Y., J.S.T., M.R., A.L.M., and J.A.F. interpreted results of experiments; M.L.D. prepared figures; M.L.D. drafted manuscript; M.L.D., W.Y., E.J.Z., A.L.M., and J.A.F. edited and revised manuscript; M.L.D., W.Y., J.S.T., F.P.C., E.J.Z., S.K., M.R., A.L.M., and J.A.F. approved final version of manuscript.