Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2020 Sep 4;11:4415. doi: 10.1038/s41467-020-18111-6

Spin-orbit quantum impurity in a topological magnet

Jia-Xin Yin 1,✉,#, Nana Shumiya 1,#, Yuxiao Jiang 1,#, Huibin Zhou 2,#, Gennevieve Macam 3,#, Hano Omar Mohammad Sura 4,#, Songtian S Zhang 1, Zi-Jia Cheng 1, Zurab Guguchia 1,5, Yangmu Li 6, Qi Wang 7, Maksim Litskevich 1, Ilya Belopolski 1, Xian P Yang 1, Tyler A Cochran 1, Guoqing Chang 1, Qi Zhang 1, Zhi-Quan Huang 3, Feng-Chuan Chuang 3, Hsin Lin 8, Hechang Lei 7, Brian M Andersen 4, Ziqiang Wang 9, Shuang Jia 2, M Zahid Hasan 1,10,✉
PMCID: PMC7474094  PMID: 32887890

Abstract

Quantum states induced by single-atomic impurities are at the frontier of physics and material science. While such states have been reported in high-temperature superconductors and dilute magnetic semiconductors, they are unexplored in topological magnets which can feature spin-orbit tunability. Here we use spin-polarized scanning tunneling microscopy/spectroscopy (STM/S) to study the engineered quantum impurity in a topological magnet Co3Sn2S2. We find that each substituted In impurity introduces a striking localized bound state. Our systematic magnetization-polarized probe reveals that this bound state is spin-down polarized, in lock with a negative orbital magnetization. Moreover, the magnetic bound states of neighboring impurities interact to form quantized orbitals, exhibiting an intriguing spin-orbit splitting, analogous to the splitting of the topological fermion line. Our work collectively demonstrates the strong spin-orbit effect of the single-atomic impurity at the quantum level, suggesting that a nonmagnetic impurity can introduce spin-orbit coupled magnetic resonance in topological magnets.

Subject terms: Magnetic properties and materials, Topological insulators

Single-atomic impurities may induce novel quantum state, but they are unexplored in topological magnets. Here, the authors report spin-down polarized bound states which further interact with neighboring states to form spin-orbit split quantized orbitals in a topological magnet Co3Sn2S2.

Introduction

Understanding the single-atomic impurity state in a quantum material is a fundamental problem with widespread implications in physics and technology1–8. For instance, the Zn impurity state in a high-temperature superconductor uncovers the Cooper pairing symmetry3, the Mn impurity state in a semiconductor elucidates the ferromagnetic coupling4, and the interstitial Fe impurity in a superconductor with topological surface states creates Majorana-like state5. Besides being a local probe of the quantum materials, the impurity state with discrete or (magnetic) bistable quantum levels is valuable for the quantum technology6–8. Most known single-atomic impurity states are, however, either from the spin or orbital channel, limiting their tunability at the quantum level. Recently, spin-orbit coupled kagome magnets have emerged as a new class of quantum materials suitable for microscopic research9–19. In particular, we notice that the In doped Co3Sn2S2 exhibits strongly altered bulk magnetic and transport properties, including reductions of magnetism, suppressions of metallicity, and variations of anomalous Hall conductivity20–22. These effects imply a striking, yet not understood quantum state associated with each nonmagnetic In impurity in this topological magnet. Therefore, a single crystal of Co3Sn2S2 containing a dilute concentration of In impurities is considered a natural and promising quantum material for experiments on atomic impurity state with spin-orbit tunability. Here we report our spin-polarized STM/S study of 1% In doped Co3Sn2S2, which uncovers a spin-orbit quantum impurity state.

Results

Engineered atomic impurity

Co3Sn2S2 has a layered crystal structure and a ferromagnetic ground state (Curie temperature, TC = 170 K) with the c-axis magnetization arising from the Co kagome lattice. Cleaving preferentially breaks its S-Sn bond, which leads to the S and Sn terminated surfaces. Previous STM studies have dominantly observed two surfaces, one with largely vacancy defects and the other with adatom defects11,13,14. Several factors challenge their assignation, as the two surfaces have identical lattice symmetries, their interlayer distance is sub-Å in scale, and STM topographic image convolutes the spatial variation of the integrated local density of states and the geometrical corrugations23. Decisive experimental evidence for surface identification can be found by imaging the symmetry-dictated surface boundary and the layer-selective chemical dopants23–25. In previous work11, we have determined that the vacancy surface is the Sn layer and the adatom surface is the S layer by imaging their surface boundary determined by the crystalline symmetry. We further conclude this assignation by doping the bulk Co3Sn2S2 single crystals with 1% In impurities and imaging the layer-selective In-dopants. The In impurities preferentially replace the Sn atoms according to previous experimental and theoretical studies20,21, as well as our recent systematic single-crystal growth22. Indeed, on the vacancy surface identified11 to be Sn, we observe dilute substitutional atoms with consistent concentration (Fig. 1a), suggesting these impurities to be In atoms.

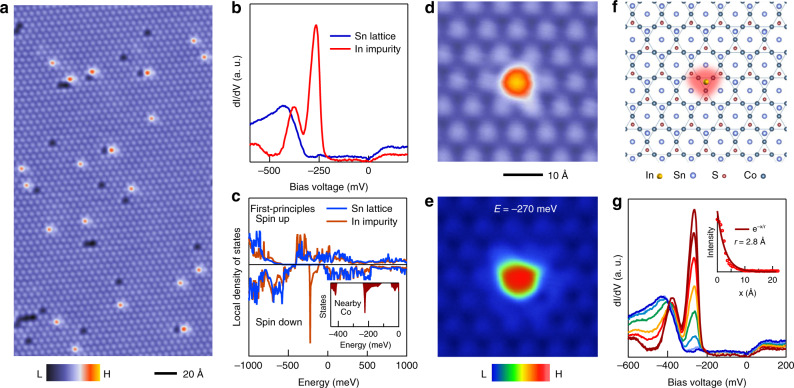
Fig. 1. Engineered atomic impurity state in a topological magnet.

Fig. 1

Open in a new tab

a Atomically-resolved topographic image of Sn layer of 1% In doped Co3Sn2S2. b Differential conductance spectrums taken on the Sn lattice (blue) and at the In impurity (red), respectively. c First-principles calculation13 of the spin-resolved local density of states of the Sn lattice (blue) and an In impurity (red), which shows a magnetic impurity resonance. The inset shows the spin-down states of the Co atom closest to the In impurity. d Topographic image of an isolated impurity. e Corresponding differential conductance map taken at E = −270 meV (resonance energy). f Correlation between the atomic structure and the pattern in the differential conductance map. g Differential conductance spectra taken across the surface with spatial variation from the center of the In impurity (dark red) to far away (blue). The inset shows the exponential fit to the spatial decay of the impurity resonance.

Spatial feature of single impurity resonance

By performing an extensive study on the electronic properties of the In impurities, we find that each impurity repeatedly features a sharp state at the negative energy as shown in Fig. 1b. First-principles calculations show that each In impurity is almost nonmagnetic but introduces a strong resonance (Fig. 1c), similar to the experimental data. The calculations further reveal that the impurity resonance arises from a spin-down state (opposite to the bulk magnetization direction) and resides in the spin-down bandgap. Thus, the magnetic resonance state likely arises from the local impurity perturbation of the spin-polarized band structure. As the low-energy band structure is dominated by Co 3d orbitals, the resonant impurity state of the In atom also implies that there a strong local impact on the Co kagome lattice in real-space. To explore the detailed real-space feature, we probe the local electronic structure for an isolated In impurity, as shown in Fig. 1d. The corresponding dI/dV map at the impurity resonance energy in Fig. 1e shows a localized pattern bound to the impurity site (Fig. 1e). The bound state couples with three nearby Co atoms in the underlying kagome lattice, as illustrated in Fig. 1f. This is consistent with the first-principles calculation that the nearby magnetic Co atoms also feature such resonance state (inset of Fig. 1c), supporting the Co-In coupling (See Supplementary Note 1). Figure 1g shows the representative dI/dV curves measured with increasing distance from the impurity, demonstrating the bound state decaying in intensity without detectable energy dispersion or splitting. An exponential fit to the decay yields a characteristic length scale of 2.8 Å (inset of Fig. 1g). Therefore, these systematic characterizations reveal that the nonmagnetic In impurity couples with the underlying magnetic kagome lattice to introduce a striking localized bound state.

Magnetic nature of single impurity resonance

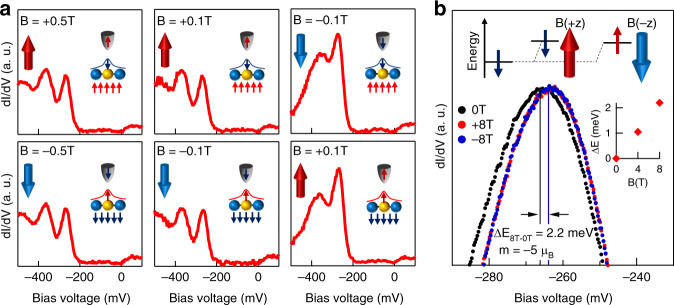
To probe the magnetic nature of the impurity bound state, we perform tunneling experiments with a spin-polarized Ni tip under weak magnetic fields26–29. The bulk crystal has a coercive field BC ~ 0.3 T, and Ni tip is a soft magnet with a BC ≪ 0.1 T that can be easily flipped by reversing the magnetic field29. We measure the tunneling signal of the impurity state while sequentially applying fields along the c-axis of +0.5 T, + 0.1 T, −0.1 T, −0.5 T, −0.1 T, and +0.1 T to systematically flip the magnetization of the tip and sample (Fig. 2a). This sequence allows us to perform spin-polarized measurements of the impurity. The +0.5 T field polarizes both the sample and tip, aligning the spin of the tip and anti-aligning the spin of the impurity state, due to the spin-down nature of the impurity state. A + 0.1 T field does not change the polarization of either the tip or impurity state. Flipping the field to −0.1 T also flips the spin of the tip, leaving the spin of the impurity state unchanged (down). Here, with both tip and impurity state spins aligned down, we observe an intensity increment of the tunneling signal. Next, we further decrease the field to −0.5 T, which flips up the spin of the impurity state with a corresponding reduction of the tunneling signal. Last, by sequentially changing the field to −0.1 T and +0.1 T, we flip the spin of the tip (down) and again observe an increase in the intensity. Our progressive field manipulation strongly supports that impurity state features spin-down polarization tied to the bistable magnetic bulk, consistent with the first-principles calculation.

Fig. 2. Magnetic nature of the impurity bound state.

Fig. 2

Open in a new tab

a Dependence of the impurity state with Ni tip under a weak magnetic field. We apply +0.5 T, + 0.1 T, −0.1 T, −0.5 T, −0.1 T, + 0.1 T fields to systematically flip the magnetization of the tip and sample. The inset schematics illustrate the respective spins of the tip and the impurity state that is anti-aligned with bulk magnetization direction. b Dependence of the impurity state with a strong magnetic field. Under both +8 T and −8T, the peak exhibits a magnetization-polarized Zeeman energy shift of 2.2 meV, which amounts to an effective moment of −5µB. The inset data shows the energy shift for different magnetic field magnitudes. Inset schematic illustrates the magnetization-polarized Zeeman effect. The applied field aligns the spins of the impurity state in the same orientation, hence +z and -z orientation fields lead the energy to shift in the same direction.

To further determine the effective moment of this magnetic polarized state, we probe the state by applying a strong external magnetic field (|B | ≫BC) along the c-axis with a nonmagnetic tip. Under the field, a spin-up/spin-down band hosting an intrinsic magnetic moment of +1/−1 Bohr magneton will exhibit a Zeeman shift to lower/higher energies in a rate of 0.058 meVT−1. Moreover, when the magnetism of the system is polarized with an applied field, the spin-polarized state will always shift to the same energy direction regardless of the relative field orientation11 (top inset schematic in Fig. 2b), which was also experimentally observed for the 8 T and −8T data (Fig. 2b). The positive energy shift indicates the state has a negative magnetic moment, calculated to be −5μB (or a Landé g factor of 10) based on a shift rate of 0.275 meVT−1 (right inset of Fig. 2b). This large value is beyond the spin Zeeman effects (~−1μB) and indicates the additional negatively polarized orbital magnetization. The anomalous Zeeman effect with an unusual moment or g factor has been observed in the electronic bands of kagome magnets9,11,17, which is often linked to the Berry phase physics associated with magnetism and spin-orbit coupling9,11,30,31. Since the In impurity couples with the Co atoms in the kagome lattice, the higher orbital angular momentum of the hybridized In-Co orbital can contribute to the large effective moment. We note that the effective moment of −5μB represents the diamagnetic response induced by the In impurity, and should not be thought as the local magnetic moment of the impurity atom.

Interacting impurity states induced quantized orbitals

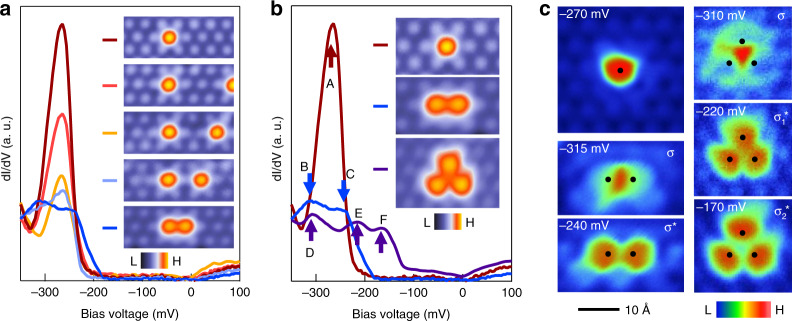
Having characterized magnetic resonance state from the isolated impurity, we further probe the coupled impurity states to understand how they interact with each other through extensive imaging and spectroscopy investigation with a nonmagnetic tip. In Fig. 3a, we present the evolution of the impurity bound state with increasing perturbation strength caused by a second nearby impurity. We find that with decreasing spatial separation, the bound state progressively decreases in intensity and finally splits into two subpeaks. Figure 3b further compares three cases with one isolated impurity, two neighboring impurities, and three neighboring impurities, respectively. We find the quantized number of split impurity states matches with the coupled impurity number, highlighting their atomic-scale quantum-level coupling. Differential conductance maps at these corresponding splitting energies demonstrate their distinct orbital hybridizations (Fig. 3c). For two neighboring impurities, the dI/dV maps show a bonding (σ) and antibonding (σ*) orbital formation4, consistent with the quantum coupling of doubly degenerate states. For three impurities, the dI/dV maps show the formation of one bonding (σ) and two antibonding (σ1*, σ2*) orbitals, an unusual situation in which we discuss below.

Fig. 3. Interacting impurity states induced quantized orbitals.

Fig. 3

Open in a new tab

a Differential conductance spectra taken at the central impurity with perturbations of varying strengths from a second impurity. Inset: respective topographic images for impurity configurations. Note the images are acquired by finding different surface locations. b Local impurity state with coupling to different numbers of impurities. The arrows highlight the quantized splitting with additional interacting impurity numbers. Note the images are acquired by finding different surface locations. c dI/dV maps at the respective bound state energies in (b). dI/dV maps taken at V = −270 mV for a single impurity; −315 mV (bonding state σ) and −240 mV (antibonding state σ) for a double impurity, respectively; −310 mV (bonding state σ), −220 mV (antibonding state σ1*) and −170 mV (antibonding state σ2*) for a triple impurity, respectively. The black dots mark the center of impurities.

Discussion

Geometrically, the three neighboring impurities have C3V symmetry, which would form a doubly degenerate orbital state7 σ* protected by the mirror symmetry. The mirror symmetry operation, however, would transfer spin-up to spin-down. On the other hand, the magnetic resonances induced by different nonmagnetic In impurities are expected to be of the same spin-polarization direction, which is locked by the ferromagnetic ordering of the underlying magnetic Co kagome lattice perturbed by these impurities (See Supplementary Note 2). Therefore, the combination of the same spin-polarization direction of the degenerate impurity states and the atomic spin-orbit coupling naturally breaks the mirror symmetry, leading to the splitting of σ* (see “Methods” for theoretical modeling). Such splitting is analogous to the splitting of the bulk topological nodal line or magnetic Weyl fermion line32,33, which is protected by the crystalline mirror symmetry.

In conclusion, we report the first STM/S studies of the nonmagnetic impurity behavior in a topological magnet. Associated with the atomic nonmagnetic impurities, we find an intense spin-orbit polarized bound state with an unusual magnetic moment and quantized energy splitting under impurity-impurity interaction. The striking spin-orbit quantum states revealed here can advance the understanding of the magnetic and transport behaviors of doped topological magnets, and call for new perspectives on the interplay between magnetism and spin-orbit coupling at the atomic scale. The discrete quantum level of interacting impurities resembles that of a quantum dot, which is critical to nanophotonics and quantum information processing. With the single-atom precision, the atomic quantum dot has a high level of digital fidelity7. The interacting spin-orbit polarized quantum impurity involves multiple degrees of freedom, including charge, spin, and orbital, the quantum control of which in the magnetic bistable platform can provide a useful guideline for the development of spin-orbit entangled quantum technology. Note added in proof: with completion of this work, we became aware of Ref. 29, which reported another kind of impurity resonance in Co3Sn2S2 exhibiting negative magnetism as well.

Methods

STM/S measurement

Single crystals22 of Co3S2-xInxSn2 up to 1.5 mm × 1.5 mm × 0.3 mm were used in this study. Samples were cleaved mechanically in situ at 77 K in ultra-high vacuum conditions, and then immediately inserted into the STM head, already at He4 base at 4.2 K. The magnetic field was applied under zero-field cooling, after which we carefully approached the tip to locate the same atomic-scale area for tunneling spectroscopy11,13. Tunneling conductance spectra were obtained using standard lock-in amplifier techniques with a root mean square oscillation voltage of 0.2 meV–5 meV and a lock-in frequency of 973 Hz. The topographic images were taken with tunneling junction set up: V = −300~−500 mV, I = 100 pA, the conductance maps were taken with tunneling junction set up: V = −100~−500 mV, I = 200 pA, and the tunneling spectra were taken with junction set up: V = −600 mV, I = 300 pA. Commercial STM Ir/Pt tip (nonmagnetic) and STM Ni tip (soft magnet) tips were used in this study. To study the impurity-impurity interaction, we checked the topographic images for over 3000 impurities to obtain the cases in Fig. 3 in the 1% In doped samples.

Evidence for surface identification

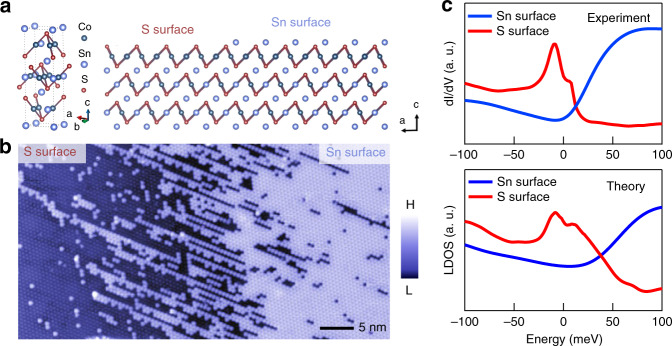
STM studies of Co3Sn2S2 often encounter two kinds of surfaces, one dominated by adatom defects and the other dominated by vacancy defects. Here we discuss our evidence for their assignation11 as S surface and Sn surface, respectively. First, as illustrated in Fig. 4a, based on crystalline symmetry, when S and Sn surfaces meet at a step edge, the Sn surface will be just above the S surface. This experimental evidence is directly provided in Fig. 4b, where we observe the vacancy surface is above the adatom surface. Second, this identification provides a natural explanation for the origin of the surface defects. The Sn vacancy in the S surface and Sn adatom on the S surface are simultaneously created due to incomplete cleaving, as seen in the experiment (Fig. 4b). Third, we show that the first-principles calculation of the surface dependent local density of states matches the experimental data (Fig. 4c). Last, we observe In dopant in the vacancy surface in the main paper, and In is known to substitute the Sn atom both experimentally and theoretically20–22.

Fig. 4. Extended evidence for surface identification in Co3Sn2S2.

Fig. 4

Open in a new tab

a Crystal structure of Co3Sn2S2 (left) and the cleaving surface illustration (right). b Atomically resolved topographic image of the boundary between S surface and Sn surface. The S surface smoothly evolves into the Sn surface with increasing coverage of Sn adatom. c Comparison between spatially averaged surface dependent dI/dV curves with the first-principles calculations.

First-Principles calculations

First-principles calculations were performed in the density functional theory34,35 framework as implemented in the Vienna Ab initio Simulation Package36,37. Generalized gradient approximation in Perdew−Burke−Ernzerhof functional38 was applied to describe electron exchange-correlation interaction with the projector augmented wave potentials39. The supercell consists of a periodically repeating 2 × 2 -slab with a thickness of twice the bulk and a vacuum space of ∼14 Å along the z-direction. The slab is cleaved to reveal the Sn-terminating surface, and one surface Sn atom is replaced with In to simulate dilute doping (~2.3%). The energy cutoff was set at 400 eV and the energies in self-consistent calculations were converged until 10−4 eV. The Brillouin zone was sampled using a 6 × 6 × 1 Monkhorst-Pack40 grid.

Supplementary information

Supplementary Information (611.1KB, pdf)

Acknowledgements

We thank Z. Song, T. Neupert, B. Lian, and H. J. Gao for insightful discussions. Experimental and theoretical work at Princeton University was supported by the Gordon and Betty Moore Foundation (Grant No. GBMF4547 and GBMF9461/Hasan). Sample characterization was supported by the United States Department of Energy (US DOE) under the Basic Energy Sciences programme (Grant No. DOE/BES DE-FG-02-05ER46200). M.Z.H. acknowledges support from Lawrence Berkeley National Laboratory and the Miller Institute of Basic Research in Science at the University of California, Berkeley in the form of a Visiting Miller Professorship. This work benefited from partial lab infra-structure support under NSF-DMR-1507585. M. Z. H. also acknowledges visiting scientist support from IQIMat the California Institute of Technology. The work at Peking University was supported by the National Natural Science Foundation of China No. U1832214, No.11774007, the National Key R&D Program of China (2018YFA0305601), and the strategic Priority Research Program of Chinese Academy of Sciences (XDB28000000). The work at Renmin University was supported by the National Key R&D Program of China (Grants No. 2016YFA0300504 and 2018YFE0202600), the National Natural Science Foundation of China (No. 11774423,11822412), the Fundamental Research Funds for the Central Universities, and the Research Funds of Renmin University of China (RUC) (18XNLG14, 19XNLG17). Work at Boston College was supported by the U.S. Department of Energy, Basic Energy Sciences Grant No. DE-FG02-99ER45747. F.C.C. and H.L. acknowledge support from the National Center for Theoretical Sciences and the Ministry of Science and Technology of Taiwan under Grants No. MOST-107-2628-M-110-001-MY3 and MOST-109-2112-M-001-014-MY3. F.C.C. is also grateful to the National Center for High-Performance Computing for computer time and facilities. B.M.A. and H.O.M.S. acknowledge support from the Independent Research Fund Denmark grant number DFF 8021-00047B.

Author contributions

J-X.Y., N.S., Y.J., and S.S.Z. conducted the scanning tunneling microscopy experiments in consultation with M.Z.H.; H.Z., S.J., Q.W., and H.Lei synthesized and characterized the magnetic and transport properties of samples; G.M., H.O.M.S., G.C., B.M.A., Z-Q.H., F-C.C., H.Lin, and Z.W. carried out the theoretical analysis in consultation with J-X.Y. and M.Z.H.; Z.C., Z.G., Y.L., M.L., I.B., X.Y., Q.Z., and T.A.C. contributed to the calibration of the measurement; J-X.Y., N.S., Y.J., and M.Z.H performed the data analysis and figure development and wrote the paper with contributions from all authors; M.Z.H. supervised the project. All authors discussed the results, interpretation, and conclusion.

Data availability

All relevant data are available from the corresponding authors upon reasonable request.

Competing interests

The authors declare no competing interests.

Footnotes

Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

These authors contributed equally: Jia-Xin Yin, Nana Shumiya, Yuxiao Jiang, Huibin Zhou, Gennevieve Macam, Hano Omar Mohammad Sura.

Contributor Information

Jia-Xin Yin, Email: jiaxiny@princeton.edu.

M. Zahid Hasan, Email: mzhasan@princeton.edu.

Supplementary information

Supplementary information is available for this paper at 10.1038/s41467-020-18111-6.

References

  • 1.Keimer B, Moore JE. The physics of quantum materials. Nat. Phys. 2017;13:1045–1055. doi: 10.1038/nphys4302. [DOI] [Google Scholar]
  • 2.Soumyanarayanan A, Reyren N, Fert A, Panagopoulos C. Emergent phenomena induced by spin–orbit coupling at surfaces and interfaces. Nature. 2016;539:509–517. doi: 10.1038/nature19820. [DOI] [PubMed] [Google Scholar]
  • 3.Pan SH, et al. Imaging the effects of individual zinc impurity atoms on superconductivity in Bi2Sr2Ca(Cu,Zn)2O8+δ. Nature. 2000;403:746–750. doi: 10.1038/35001534. [DOI] [PubMed] [Google Scholar]
  • 4.Kitchen D, Richardella A, Tang J-M, Flatte ME, Yazdani A. Atom-by-atom substitution of Mn in GaAs and visualization of their hole-mediated interactions. Nature. 2006;442:436–439. doi: 10.1038/nature04971. [DOI] [PubMed] [Google Scholar]
  • 5.Yin J-X, et al. Observation of a robust zero-energy bound state in iron-based superconductor Fe(Te,Se) Nat. Phys. 2015;11:543–546. doi: 10.1038/nphys3371. [DOI] [Google Scholar]
  • 6.Fuechsle M, et al. A single-atom transistor. Nat. Nanotechnol. 2012;7:242–246. doi: 10.1038/nnano.2012.21. [DOI] [PubMed] [Google Scholar]
  • 7.Folsch S, et al. Quantum dots with single-atom precision. Nat. Nanotechnol. 2014;9:505–508. doi: 10.1038/nnano.2014.129. [DOI] [PubMed] [Google Scholar]
  • 8.Natterer FD, et al. Reading and writing single-atom magnets. Nature. 2017;543:226–228. doi: 10.1038/nature21371. [DOI] [PubMed] [Google Scholar]
  • 9.Yin J-X, et al. Giant and anisotropic spin–orbit tunability in a strongly correlated kagome magnet. Nature. 2018;562:91–95. doi: 10.1038/s41586-018-0502-7. [DOI] [PubMed] [Google Scholar]
  • 10.Lin Z, et al. Flatbands and emergent ferromagnetic ordering in Fe3Sn2 kagome lattices. Phys. Rev. Lett. 2018;121:096401. doi: 10.1103/PhysRevLett.121.096401. [DOI] [PubMed] [Google Scholar]
  • 11.Yin J-X, et al. Negative flat band magnetism in a spin–orbit-coupled correlated kagome magnet. Nat. Phys. 2019;15:443–448. doi: 10.1038/s41567-019-0426-7. [DOI] [Google Scholar]
  • 12.Li Y, et al. Magnetic-field control of topological electronic response near room temperature in correlated kagome magnets. Phys. Rev. Lett. 2019;123:196604. doi: 10.1103/PhysRevLett.123.196604. [DOI] [PubMed] [Google Scholar]
  • 13.Jiao L, et al. Signatures for half-metallicity and nontrivial surface states in the kagome lattice Weyl semimetal Co3Sn2S2. Phys. Rev. B. 2019;99:245158. doi: 10.1103/PhysRevB.99.245158. [DOI] [Google Scholar]
  • 14.Morali N, et al. Fermi-arc diversity on surface terminations of the magnetic Weyl semimetal Co3Sn2S2. Science. 2019;365:1286–1291. doi: 10.1126/science.aav2334. [DOI] [PubMed] [Google Scholar]
  • 15.Yang H, et al. Scanning tunneling microscopy on cleaved Mn3Sn(0001) surface. Sci. Rep. 2019;9:9677. doi: 10.1038/s41598-019-45958-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Guguchia Z, et al. Tunable anomalous Hall conductivity through volume-wise magnetic competition in a topological kagome magnet. Nat. Commun. 2020;11:559. doi: 10.1038/s41467-020-14325-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Yin J-X, et al. Quantum-limit Chern topological magnetism in TbMn6Sn6. Nature. 2020;58:533–536. doi: 10.1038/s41586-020-2482-7. [DOI] [PubMed] [Google Scholar]
  • 18.Zhang SS, et al. Many-body Resonance in a correlated topological kagome antiferromagnet. Phys. Rev. Lett. 2020;125:046401. doi: 10.1103/PhysRevLett.125.046401. [DOI] [PubMed] [Google Scholar]
  • 19.Yin J-X, et al. Fermion-boson many-body interplay in a frustrated kagome paramagnet. Nat. Commun. 2020;11:4003. doi: 10.1038/s41467-020-17464-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Weihrich R, Anusca I. Half antiperovskites. III crystallographic and electronic structure effects in Sn2-xInxCo3S2. Z. Anorg. Allg. Chem. 2006;632:1531. doi: 10.1002/zaac.200500524. [DOI] [Google Scholar]
  • 21.Corps J, et al. Interplay of metal-atom ordering, Fermi level tuning, and thermoelectric properties in cobalt shandites Co3M2S2 (M = Sn, In) Chem. Mater. 2015;27:3946–3956. doi: 10.1021/acs.chemmater.5b00801. [DOI] [Google Scholar]
  • 22.Zhou H, et al. Enhanced anomalous Hall effect in the magnetic topological semimetal Co3Sn2-xInxS2. Phys. Rev. B. 2020;101:125121. doi: 10.1103/PhysRevB.101.125121. [DOI] [Google Scholar]
  • 23.Li A, et al. Surface terminations and layer-resolved tunneling spectroscopy of the 122 iron pnictide superconductors. Phys. Rev. B. 2019;99:134520. doi: 10.1103/PhysRevB.99.134520. [DOI] [Google Scholar]
  • 24.Guan S-Y, et al. Superconducting topological surface states in the noncentrosymmetric bulk superconductor PbTaSe2. Sci. Adv. 2016;2:e1600894–e1600894. doi: 10.1126/sciadv.1600894. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Aynajian P, et al. Visualizing heavy fermions emerging in a quantum critical Kondo lattice. Nature. 2012;486:201–206. doi: 10.1038/nature11204. [DOI] [PubMed] [Google Scholar]
  • 26.Wiesendanger R. Spin mapping at the nanoscale and atomic scale. Rev. Mod. Phys. 2009;81:1495. doi: 10.1103/RevModPhys.81.1495. [DOI] [Google Scholar]
  • 27.Loth S, Lutz CP, Heinrich AJ. Spin-polarized spin excitation spectroscopy. N. J. Phys. 2010;12:125021. doi: 10.1088/1367-2630/12/12/125021. [DOI] [Google Scholar]
  • 28.Focko Meier, et al. Revealing magnetic interactions from single-Atom magnetization curves. Science. 2008;320:82–86. doi: 10.1126/science.1154415. [DOI] [PubMed] [Google Scholar]
  • 29.Yuqing Xing, et al. Localized spin-orbit polaron in magnetic Weyl semimetal Co3Sn2S2. Preprint at https://arxiv.org/abs/2001.11295 (2020). [DOI] [PMC free article] [PubMed]
  • 30.Yazyev OV. An upside-down magnet. Nat. Phys. 2019;15:424–425. doi: 10.1038/s41567-019-0451-6. [DOI] [Google Scholar]
  • 31.Vanderbilt, David. Berry Phases in Electronic Structure Theory: Electric Polarization, Orbital Magnetization and Topological Insulators. (Cambridge University Press, 2018).
  • 32.Hasan MZ, Xu S-Y, Bian G. Topological insulators, topological superconductors and Weyl fermion semimetals: discoveries, perspectives and outlooks. Phys. Scripta. 2015;164:014001. doi: 10.1088/0031-8949/2015/T164/014001. [DOI] [Google Scholar]
  • 33.Belopolski I, et al. Discovery of topological Weyl fermion lines and drumhead surface states in a room temperature magnet. Science. 2019;365:1278–1281. doi: 10.1126/science.aav2327. [DOI] [PubMed] [Google Scholar]
  • 34.Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys. Rev. 1964;136:B864. doi: 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
  • 35.Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965;140:A1133. doi: 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  • 36.Kresse G, Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B. 1993;47:558. doi: 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  • 37.Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using plane-wave basis set. Phys. Rev. B. 1996;54:11169. doi: 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  • 38.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  • 39.Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 1999;59:1758. doi: 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  • 40.Monkhorst HJ, Pack JD. Special points for Brillouin-zone integrations. Phys. Rev. B. 1976;13:5188–5192. doi: 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information (611.1KB, pdf)

Data Availability Statement

All relevant data are available from the corresponding authors upon reasonable request.

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES