Degree-based topological indices and polynomials of hyaluronic acid-curcumin conjugates

Abstract

Quantitative structure–activity relationship (QSAR) represents quantitative correlation of chemical structural features called as molecular descriptors and pharmacological activity as response endpoints. Topological index is a molecular descriptor extensively used to study QSAR of pharmaceuticals to assess their molecular characteristics by numerical computation. Theoretical assessment of drug like molecules helps to expedite the drug design and discovery process by rationalizing the lead identification, lead optimization and understanding their mechanism of actions. Therefore, in this article, we have computed the general inverse sum indeg index, ${\mathit{ISI}}_{\left(\alpha ,\beta \right)}$ of Hyaluronic acid-curcumin conjugates by using molecular structure analysis and edge partitioning technique. Many standard topological indices are obtained as a special case of ${\mathit{ISI}}_{\left(\alpha ,\beta \right)}$. We also proposed general inverse sum indeg polynomial ${\mathit{ISI}}_{\left(\alpha ,\beta \right)}(G_n,x)$ of Hyaluronic acid-curcumin conjugates from which many well-known polynomials are deduced.

1. Introduction

Drug discovery program encompasses a series of ensuing processes involving target validation, lead identification and lead optimization. Target validation phase involves discovery and analysis of one or numerous targets to ascertain their role in the etiology of a given human ailment (Kwong et al., 2011). In the lead identification step, a plethora of compounds of natural, semisynthetic and synthetic origin are discovered as new pharmacologically active chemical entities, which by sequential modifications may be converted into a clinically useful medicine (Azam et al., 2012, Azam et al., 2009, Wermuth et al., 1998).

However, chemical modification of a biologically active molecule to comply with desirable pharmacokinetic and toxicological properties which are crucial for the clinical usage of the drug is dealt under lead optimization step (Ahmed et al., 2012, Wermuth et al., 1998). In this process, physicochemical properties of the drug molecules are not only considered important for absorption, distribution in the body, metabolism and elimination from the body but equally deemed to influence their toxicity profile (Azam, 2017, Azam et al., 2015). Moreover, as per quantitative structure–activity relationships (QSAR) paradigm, biological activities of drug molecules could be computed as a function of numerous physicochemical parameters capable of evaluating stereo-electronic characteristics.

The foundation of any QSAR model racks exclusively upon numerous molecular descriptors which represent several experimentally or theoretically derived quantitative parameters that characterize distinctive information about a chemical compound. These descriptors are classified into geometric, quantum-chemical, electrostatic, constitutional and topological indices on the basis of type of molecular descriptions that is parameterized (Mauri et al., 2016). Among these, molecular descriptors based on topological indices are known to play vital role in QSAR studies.

Topological indices are simply defined as numerical values associated with chemical constitution, which is used for correlation of chemical structure with numerous characteristics such as chemical reactivity, pharmacological activity and physical properties. They are derived from a topological representation of molecules and can be classified into structure-explicit descriptors such as quantum chemical and structure-implicit descriptors such as hydrophobicity or electronic constants (Estrada et al., 2003). These indices can be easily computed by employing the concepts of molecular topology (MT), a discipline based on the graph theory. In fact, MT has proven to be an excellent tool for fast and precise estimation of many physicochemical as well as biological properties (Galvez et al., 2013, Sporns, 2018). In order to calculate topological indices, fundamentals of MT are employed where chemical compound is converted into a graph considering atoms as vertices and bonds as edges, known as a molecular graph (Gálvez and García-Doménech, 2010). Let $G=\left(V,E\right)$ be a molecular graph with vertex set$V\left(G\right)$ and edge set $E\left(G\right)$. The number of vertices and edges in a graph $G$ can be denote by $\left|V(G)\right|$ and $\left|E(G)\right|$ respectively. The degree of vertex $u\in V\left(G\right)$ is denoted by $d\left(u\right)$ and is the number of vertices that are adjacent to $u$. The edge connecting the vertices $u$ and $v$ is denoted by $e=uv$, where$e\in E\left(G\right).$

The concept of topological index was introduced by Wiener (Wiener, 1947), while working on the boiling points of alkanes. Topological indices are classified into many classes, such as degree-based, distance-based, and counting-based, etc. (Gutman et al., 2018b). Out of these, degree-based topological indices play an important role in theoretical chemistry and pharmacology. Some important degree-based indices are Randić index, Zagreb indices, Harmonic index, Sum connectivity index, and Inverse sum indeg index, etc. (Gutman et al., 2018b). The Zagreb indices are among the oldest topological indices and were introduced by Gutman and Trinajstic in 1972 (Gutman and Trinajstić, 1972); the first and second Zagreb index are defined as $M_1(G)={\sum }_{u\in V\left(G\right)}{\left[d(u)\right]}^2={\sum }_{\mathit{uv}\in E\left(G\right)}\left[d\left(u\right)+d(v)\right]$ and $M_2(G)={\sum }_{\mathit{uv}\in E\left(G\right)}\left[d(u)d(v)\right]$ respectively. There is a vast amount of research on the Zagreb indices and their chemical applications (Todeschini and Consonni, 2000). Another oldest degree-based topological index is Randić index (Randic, 1975), also called as product connectivity index, is one of the most successful molecular descriptors in QSPR and QSAR studies, and suitable for measuring the extent of branching of the carbon-atom skeleton of saturated hydrocarbons. Randić index is defined as:

$$R(G)=\sum _{\mathit{uv}\in E\left(G\right)}\frac{1}{\sqrt{d(u)d(v)}}$$

Mathematical properties of Randić index are well described (Gutman et al., 2018, Li et al., 2006). Motivated by Randić definition of the product connectivity index, the sum-connectivity index was proposed by Zhou and Trinajstić (2009). The sum-connectivity index of the graph G is defined as:

$$\mathit{SCI}(G)=\sum _{\mathit{uv}\in E\left(G\right)}\frac{1}{\sqrt{d\left(u\right)+d(v)}}$$

The Randić index and the sum-connectivity index are highly correlated quantities. For example, the correlation coefficient between the Randić index and the sum-connectivity index of benzenoid hydrocarbons was reported as 0.9992 (Lučić et al., 2009) and 0.9996 for 137 alkane trees (Gutman and Furtula, 2010). The Harmonic index of a graph G is denoted by H(G) and is defined as (Fajtlowicz, 1987):

$$H(G)=\sum _{\mathit{uv}\in E\left(G\right)}\frac{2}{d\left(u\right)+d(v)}$$

It has been found that the Harmonic index correlates well with the Randić index and sum-connectivity index. Ramane et al, showed that in case of benzenoid hydrocarbons the correlation coefficient between harmonic index and Randić index is 1, whereas between the Harmonic index and sum connectivity index is 0.999 (Ramane et al., 2019). Furthermore, Shirdel et al, defined Hyper Zagreb index as (Shirdel et al., 2013):

$$\mathit{HM}(G)=\sum _{\mathit{uv}\in E\left(G\right)}{\left[d\left(u\right)+d(v)\right]}^2$$

Some recent results on the Hyper Zagreb index has been reported (Liu and Tang, 2019). The Redefined third Zagreb index was introduced by Ranjini et al. (2013) and is defined as:

$$\mathit{ReZ}{G}_3(G)=\sum _{\mathit{uv}\in E\left(G\right)}\left[d(u)d(v)\right]\left[d\left(u\right)+d(v)\right]$$

The Geometric-Arithmetic index has been defined by Vukičević and Furtula (2009) as:

$$\mathit{GA}(G)=\sum _{\mathit{uv}\in E\left(G\right)}\frac{2\sqrt{d(u)d(v)}}{d\left(u\right)+d(v)}$$

We refer to the survey article for the various results on the Geometric-Arithmetic index of graphs (Das et al., 2011). A family of 148 degree-based structure descriptors, named Adriatic indices, was put forward and twenty of them were selected as significant predictors of physicochemical properties (Vukičević, 2010, Vukičević and Gašperov, 2010). One of them, the inverse sum indeg index, was singled out as a significant predictor of the total surface area of octane isomers (Vukičević, 2010). The inverse sum indeg is defined as:

$$\mathit{ISI}(G)=\sum _{\mathit{uv}\in E\left(G\right)}\frac{1}{\frac{1}{d(u)}+\frac{1}{d(v)}}=\sum _{\mathit{uv}\in E\left(G\right)}\frac{d(u)d(v)}{d\left(u\right)+d(v)}$$

Recently, Buragohain et al. (2020) proposed the general inverse sum indeg index, denoted by ${\mathit{ISI}}_{\left(\alpha ,\beta \right)}(G)$, and defined as:

$${\mathit{ISI}}_{\left(\alpha ,\beta \right)}(G)=\sum _{\mathit{uv}\in E\left(G\right)}{\left[d(u)d(v)\right]}^{\alpha }{\left[d\left(u\right)+d(v)\right]}^{\beta }$$

where $\alpha$ and $\beta$ are some real numbers. The choice $\alpha =0$ & $\beta =\alpha ,\beta \ne 0,$ corresponds to the general sum-connectivity index (Zhou and Trinajstić, 2010), and defined as

$${\chi }_{\alpha }(G)=\sum _{\mathit{uv}\in E\left(G\right)}{\left[d\left(u\right)+d(v)\right]}^{\alpha }$$

whereas for $\alpha \ne 0$ & $\beta =0,$ the general Randić index $R_{\alpha }$ is obtained as (Bollobás and Erdős, 1998):

$$R_{\alpha }(G)=\sum _{\mathit{uv}\in E\left(G\right)}{\left[d\left(u\right)d(v)\right]}^{\alpha }$$

Some of the degree-based indices of a graph G that can be obtained from the generalized ISI index by only giving specific values to the parameters $\alpha$ and $\beta$ are listed in Table 1.

Table 1.

Degree-based indices of a graph G that can be obtained from the generalized ISI index by assigning specific values to the parameters $\alpha$ and.$\beta$

Topological index	Corresponding ${\mathit{ISI}}_{\left(\alpha ,\beta \right)}(G)$
First Zagreb index,$M_1(G)$	${\mathit{ISI}}_{0,1}(G)$
Second Zagreb index,$M_2(G)$	${\mathit{ISI}}_{1,0}\left(G\right)$
Randić index,$R(G)$	${\mathit{ISI}}_{-\frac{1}{2},0}(G)$
Sum connectivity index,$\mathit{SCI}(G)$	${\mathit{ISI}}_{0,-\frac{1}{2}}(G)$
Harmonic index,$H(G)$	${2ISI}_{0,-1}\left(G\right)$
Hyper Zagreb index,$\mathit{HM}(G)$	${\mathit{ISI}}_{0,2}(G)$
Redefined third Zagreb index,$\mathit{ReZ}{G}_3(G)$	${\mathit{ISI}}_{1,1}(G)$
Geometric Arithmetic index,$\mathit{GA}(G)$	${2ISI}_{\frac{1}{2},-1}(G)$
Inverse sum indeg index,$\mathit{ISI}(G)$	${\mathit{ISI}}_{1,-1}\left(G\right)$
General sum connectivity index,${\chi }_{\alpha }(G)$	${\mathit{ISI}}_{0,\alpha }(G)$
Generalized Randić index,$R_{\alpha }(G)$	${\mathit{ISI}}_{\alpha ,0}(G)$

Numerous graph polynomials have been developed for measuring structural information of molecular graphs. Graph polynomials found applications in chemistry in connection with the molecular orbital theory of unsaturated compounds and also an important source of structural descriptors used in developing structure property models (Balaban and Devillers, 2014, Jäntschi et al., 2009, Shah and Bokhary, 2019). Distance-based and degree-based graph polynomials are useful because they contain a wealth of information about topological indices. Various topological indices can be derived from polynomials by taking their value at some point directly, or by taking integrals or derivatives. For instance, the first derivative of the Hosoya polynomial evaluated at $x=1$ equals to the Wiener index. Similarly, first and second Zagreb index can be derived by differentiating their polynomials at $x=1$ respectively. There are some citable work on Zagreb and other polynomials of special structures (Farooq et al., 2019, Fath-Tabar, 2009, Gao et al., 2016b, Kwun et al., 2018, Liu et al., 2019, Shi et al., 2016, Zheng et al., 2019). Some general graph polynomials (Vetrík, 2019) associated with topological indices are as follows

the general Randić polynomial of a graph G is

$$R_{\alpha }(G,x)=\sum _{\mathit{uv}\in E\left(G\right)}{x}^{{\left[d\left(u\right)d(v)\right]}^{\alpha }}$$

the general sum-connectivity polynomial is

$${\chi }_{\alpha }(G,x)=\sum _{\mathit{uv}\in E\left(G\right)}{x^{\left[d\left(u\right)+d(v)\right]}}^{\alpha }$$

the generalized Zagreb polynomial is

$$M_{\alpha ,\beta }(G,x)=\sum _{\mathit{uv}\in E\left(G\right)}{x}^{{\left(d(u)\right)}^{\alpha }{\left(d(v)\right)}^{\beta }+{\left(d(v)\right)}^{\alpha }{\left(d(u)\right)}^{\beta }}$$

the redefined third Zagreb polynomial is defined as

$${\mathit{ReZG}}_3(G,x)=\sum _{\mathit{uv}\in E\left(G\right)}{x}^{d(u)d(v)\left[d\left(u\right)+d(v)\right]}$$

Motivated by these definitions, we define the generalized inverse sum indeg polynomial of a graph G as

$${\mathit{ISI}}_{\left(\alpha ,\beta \right)}(G,x)=\sum _{\mathit{uv}\in E\left(G\right)}{x}^{{\left[d(u)d(v)\right]}^{\alpha }{\left[d\left(u\right)+d(v)\right]}^{\beta }}$$

where $\alpha$ and $\beta$ are some real numbers (see Table 2).

Table 2.

Relationships between generalized inverse sum indeg polynomial with some other polynomials associated with topological indices.

Polynomials associated with Topological indices	Corresponding ${\mathit{ISI}}_{\left(\alpha ,\beta \right)}(G,x)$
First Zagreb polynomial, $M_1(G,x)$	${\mathit{ISI}}_{0,1}(G,x)$
Second Zagreb polynomial, $M_2(G,x)$	${\mathit{ISI}}_{1,0}\left(G,x\right)$
Hyper Zagreb polynomial, $\mathit{HM}(G,x)$	${\mathit{ISI}}_{0,2}(G,x)$
Redefined third Zagreb polynomial, $\mathit{ReZ}{G}_3(G,x)$	${\mathit{ISI}}_{1,1}(G,x)$
General sum connectivity polynomial, ${\chi }_{\alpha }(G,x)$	${\mathit{ISI}}_{0,\alpha }(G,x)$
Generalized Randić polynomial, $R_{\alpha }(G,x)$	${\mathit{ISI}}_{\alpha ,0}(G,x)$

The computation of degree-based indices and distance-based indices for special molecular drug structures has raised considerable interest among medical and pharmaceutical researchers as it is useful to make up the medicinal and chemical experimental defects. Gao et al. (2016b) have theoretically analyzed and obtained several degree-based topological indices of doxorubicin-loaded micelle consisting of PEG-pAsp block copolymer with chemically conjugated doxorubicin, while many multiplicative topological indices for the same molecular structure have recently been derived (Shao et al., 2020). The forgotten topological index of some important drug structures has been manifested by Gao et al. (2016a). Weiner related indices of hexagonal jagged-rectangle, applied in medical and pharmaceutical engineering were studied by same research group (Gao et al., 2017a). The first multiplicative atom-bond connectivity index of critical drug structures, like alkene, cycloalkenes, dendrimers, benzenoid systems, and phenylenes were analyzed by these researchers (Gao et al., 2017b). Weiner related indices for coronoid and kekulenes structures were reported by Arockiaraj et al. (2018). Very recently, several topological indices of COVID-19 based drugs such as remdesivir, chloroquine, hydroxychloroquine and theaflavin have been investigated (Mondal et al., 2020). In addition, Wang et al. (2020) computed topological indices of hyaluronic acid, which is thoroughly investigated in cancer therapy because of its excellent physical features. Likewise, Zheng et al. (2019) have determined many degree-based topological indices and polynomials for the hyaluronic acid-paclitaxel conjugates, widely used in the therapeutics of cancer.

2. Motivation

Curcumin, also known as diferuloylmethane or 1,7-bis(4-hydroxy-3-methoxyphenyl)-1,6-heptadiene-3,5-dione, is an orange-yellow polyphenolic compound, extracted from the rhizome of Curcuma longa. Since ancient times, it is known to be endowed with remarkable medicinal properties against a range of ailing conditions such as inflammation, cancer, diabetes, neurodegenerative disorders, cardiovascular diseases and asthma (Kocaadam and Şanlier, 2017). It is well tolerated in humans and safety doses of curcumin were noted to be as high as 8 g/day (Cheng, 2001). Unfortunately, poor aqueous-solubility of curcumin leads to inadequate bioavailability in biological systems which is a major obstacle limiting its clinical utility (Kharat and McClements, 2019). To combat the water-insolubility hurdle of this natural phytomedicine, several approaches were adopted which includes the employment of various carriers, such as polymeric micelles, liposomes, emulsion, nanospheres and polymers (Allijn et al., 2016, Zhao et al., 2017, Zhu et al., 2017). In particular, conjugation of curcumin with hyaluronic acid has received appreciable attention in recent times not only for increasing bioavailability but also to target tumor cells and tumor metastases for the treatment of numerous cancer (Saravanakumar et al., 2014, Wang et al., 2018).

Hyaluronic acid (HA) is a nontoxic, nonimmunogenic, biocompatible and biodegradable glycosaminoglycan polymer which is widely distributed in the human body throughout extracellular matrix, articular cartilage, bone marrow and synovial fluids (Fallacara et al., 2018). It is a linear polymer composed of repeating units of β-1,4-D-glucuronic acid and β-1,3-N-acetylglucosamine. The abundance of carboxylic and hydroxyl groups in its structure confer great potential as a drug carrier owing to its unique physicochemical as well as biological properties (Ahmadian et al., 2019). The cluster of differentiation 44 (CD44) protein is regarded as the main receptor of HA (Underhill, 1992), which is activated upon interaction with HA and influence many signaling pathways involved in inflammation, wound healing, morphogenesis and cancer (Swierczewska et al., 2016). Moreover, it is reported to be overexpressed in the tumor microenvironment, and hence, offers great potential for tumor targeting (Luo et al., 2019). In pharmaceutical field, HA is well recognized as visco-supplementation therapy in which it is injected into the knee to enhance the viscosity of the synovial fluids that helps cushion and lubricate the joint (Cameron et al., 2020). It is also used as ophthalmic biomaterial in several kinds of eye surgeries such as retinal detachment repairing, cataract surgery and corneal transplantation (Gupta et al., 2019).

The HA-curcumin conjugate was reported to alleviate the fibrotic functions of myofibroblasts, rationalizing its use in the treatment of joint contracture (Yu et al., 2019). These conjugates have also been reported to increase the aqueous solubility of curcumin to 7.5 mg/ml, which is equivalent of 265 μM of curcumin (Manju and Sreenivasan, 2011). Therefore, conjugates of curcumin with HA is regarded as promising pharmaceutical strategy to improve water solubility, prolong curcumin release at the target site, improve tissue distribution and potentiate therapeutic outcomes (Tripodo et al., 2015). Zheng et al. (2019) computed many degree-based topological indices and polynomials of HA-paclitaxel as paclitaxel is well known drug for its anticancer properties. However, paclitaxel has some side effects such as neurotoxicity, hepatotoxicity, cardiotoxicity etc, demanding innovative approaches to avoid these issues. Ashrafizadeh et al., (2020) demonstrated that curcumin is able to suppress paclitaxel resistance and attenuate its side effects. To the best of our knowledge, there are no degree-based topological results available on the molecular structure of HA-curcumin conjugate in the literature. Thus, due to the enormous pharmaceutical interests of HA-curcumin conjugates, current research seeks to investigate degree-based topological indices and polynomials of the molecular structure of HA-curcumin conjugates. The outcomes of the current findings will enable researchers to have a better understanding of the physicochemical properties and pharmacological characteristics of HA-curcumin conjugates. In addition, these results may provide a theoretical foundation for pharmaceutical engineering. A diagrammatic representation of the motivation behind current study is being illustrated in Fig. 1.

Fig. 1.

An illustration representing motivation of the current study.

3. Main results and proofs

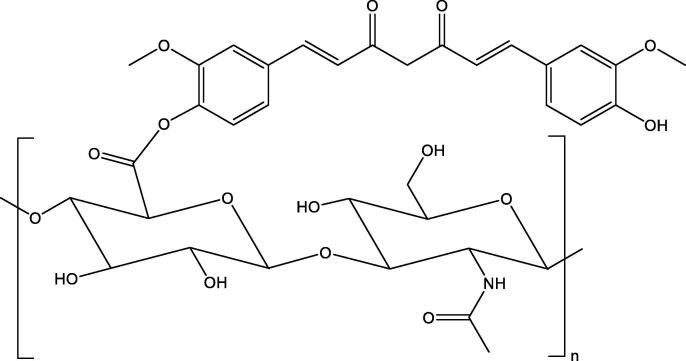
We start this section by computing various degree-based topological indices of HA-curcumin conjugates. The HA-curcumin conjugates structure is shown in Fig. 2.

Fig. 2.

The molecular structure of hyaluronic acid-curcumin conjugates.

The key technique used here is the approach to edge partitioning and vertices degree counting. Let $G_n$ denote the molecular graph of HA-curcumin conjugates in the following discussion with the linear iteration n units. Fig. 3, Fig. 4, Fig. 5 illustrates the molecular graphs of HA-curcumin conjugates for $n=1,2$ and 3 respectively. By the analysis of its molecular structure, we get $\left|V(G_n)\right|=52n+1$ and $\left|E(G_n)\right|=56n$.

Fig. 3.

Corresponding molecular graph of hyaluronic acid-curcumin conjugates $G_1:n=1$.

Fig. 4.

Corresponding molecular graph of hyaluronic acid-curcumin conjugates $G_2:n=2$.

Fig. 5.

Corresponding molecular graph of hyaluronic acid-curcumin conjugates $G_3:n=3$.

The edge sets of $G_n$ is divided into five edge groups, based on the end vertices degrees. So, we write:

$$E\left(G_n\right)=\underset{i=1}{\overset{5}{\cup }}{E}_i\left(G_n\right),where$$

$$E_1\left(G_n\right)=\left\{e=uv\in E\left(G_n\right):d\left(u\right)=1andd\left(v\right)=2\right\}$$

$$E_2\left(G_n\right)=\left\{e=uv\in E\left(G_n\right):d\left(u\right)=1andd\left(v\right)=3\right\}$$

$$E_3\left(G_n\right)=\left\{e=uv\in E\left(G_n\right):d\left(u\right)=2andd\left(v\right)=2\right\}$$

$$E_4\left(G_n\right)=\left\{e=uv\in E\left(G_n\right):d\left(u\right)=3andd\left(v\right)=3\right\}$$

$$E_5\left(G_n\right)=\left\{e=uv\in E\left(G_n\right):d\left(u\right)=2andd\left(v\right)=3\right\}$$

The main results discussed in this section are as follows:

Theorem 1

The general inverse sum indeg index ${\mathit{ISI}}_{\left(\alpha ,\beta \right)}$ of HA- curcumin conjugates is given by,

${\mathit{ISI}}_{\left(\alpha ,\beta \right)}\left(G_n\right)=\left(3n+1\right){\left[2\right]}^{\alpha }{\left[3\right]}^{\beta }+\left(9n\right){\left[3\right]}^{\alpha }{\left[4\right]}^{\beta }+\left(4n+1\right){\left[4\right]}^{\alpha +\beta }+\left(11n-1\right){\left[3\right]}^{2\alpha +\beta }{\left[2\right]}^{\beta }+\left(29n-1\right){\left[6\right]}^{\alpha }{\left[5\right]}^{\beta }.$

Proof

By graph structure analysis and observation, we note that, $\left|E_1\left(G_n\right)\right|=3n+1,$ $\left|E_2\left(G_n\right)\right|=9n,\left|E_3\left(G_n\right)\right|=4n+1,$

$$\left|E_4\left(G_n\right)\right|=11n-1and\left|E_5\left(G_n\right)\right|=29n-1$$

Applying the definition of generalized ${\mathit{ISI}}_{\left(\alpha ,\beta \right)}$ index, we get

$${\mathit{ISI}}_{\left(\alpha ,\beta \right)}\left(G_n\right)=\sum _{\mathit{uv}\in E\left(G_n\right)}{\left[d(u)d(v)\right]}^{\alpha }{\left[d\left(u\right)+d(v)\right]}^{\beta }$$

$${\mathit{ISI}}_{\left(\alpha ,\beta \right)}\left(G_n\right)=\sum _{\mathit{uv}\in E_1\left(G_n\right)}{\left[d\left(u\right)d\left(v\right)\right]}^{\alpha }{\left[d\left(u\right)+d\left(v\right)\right]}^{\beta }+\sum _{\mathit{uv}\in E_2\left(G_n\right)}{\left[d(u)d(v)\right]}^{\alpha }{\left[d\left(u\right)+d(v)\right]}^{\beta }+\sum _{\mathit{uv}\in E_3\left(G_n\right)}{\left[d\left(u\right)d\left(v\right)\right]}^{\alpha }{\left[d\left(u\right)+d\left(v\right)\right]}^{\beta }+\sum _{\mathit{uv}\in E_4\left(G_n\right)}{\left[d\left(u\right)d\left(v\right)\right]}^{\alpha }{\left[d\left(u\right)+d\left(v\right)\right]}^{\beta }+\sum _{\mathit{uv}\in E_5\left(G_n\right)}{\left[d\left(u\right)d\left(v\right)\right]}^{\alpha }{\left[d\left(u\right)+d\left(v\right)\right]}^{\beta }$$

$$=\left|E_1\left(G_n\right)\right|{\left[\left(1\right)\left(2\right)\right]}^{\alpha }{\left[1+2\right]}^{\beta }+\left|E_2\left(G_n\right)\right|{\left[\left(1\right)\left(3\right)\right]}^{\alpha }{\left[1+3\right]}^{\beta }+\left|E_3\left(G_n\right)\right|{\left[\left(2\right)\left(2\right)\right]}^{\alpha }{\left[2+2\right]}^{\beta }+\left|E_4\left(G_n\right)\right|{\left[\left(3\right)\left(3\right)\right]}^{\alpha }{\left[3+3\right]}^{\beta }+\left|E_5\left(G_n\right)\right|{\left[\left(2\right)\left(3\right)\right]}^{\alpha }{\left[2+3\right]}^{\beta }$$

$$=\left(3n+1\right){\left[2\right]}^{\alpha }{\left[3\right]}^{\beta }+\left(9n\right){\left[3\right]}^{\alpha }{\left[4\right]}^{\beta }+\left(4n+1\right){\left[4\right]}^{\alpha }{\left[4\right]}^{\beta }+\left(11n-1\right){\left[9\right]}^{\alpha }{\left[6\right]}^{\beta }+\left(29n-1\right){\left[6\right]}^{\alpha }{\left[5\right]}^{\beta }$$

$$=\left(3n+1\right){\left[2\right]}^{\alpha }{\left[3\right]}^{\beta }+\left(9n\right){\left[3\right]}^{\alpha }{\left[4\right]}^{\beta }+\left(4n+1\right){\left[4\right]}^{\alpha +\beta }+\left(11n-1\right){\left[3\right]}^{2\alpha +\beta }{\left[2\right]}^{\beta }+\left(29n-1\right){\left[6\right]}^{\alpha }{\left[5\right]}^{\beta }$$

Hence the theorem. □

Let us give exact values of the most well-known degree-based indices of HA-curcumin conjugates.

Corollary 1

Let $G_n$ be the molecular graph of HA-curcumin conjugates then,

• i.$M_1\left(G_n\right)=272n-4.$
• ii.$M_2\left(G_n\right)=322n-9.$
• iii.$R\left(G_n\right)=n\left[\frac{3}{\sqrt{2}}+\frac{9}{\sqrt{3}}+\frac{17}{3}+\frac{29}{\sqrt{6}}\right]+\left[\frac{1}{\sqrt{2}}+\frac{1}{6}-\frac{1}{\sqrt{6}}\right].$
• iv.$SCI\left(G_n\right)=n\left[\sqrt{3}+\frac{11}{\sqrt{6}}+\frac{29}{\sqrt{5}}+\frac{13}{2}\right]+\left[\frac{1}{\sqrt{3}}-\frac{1}{\sqrt{5}}-\frac{1}{\sqrt{6}}+\frac{1}{2}\right].$
• v.$H\left(G_n\right)=\frac{1}{30}\left[713n+13\right].$
• vi.$HM\left(G_n\right)=1356n-36.$
• vii.$\mathit{ReZ}{G}_3\left(G_n\right)=1654n-62.$
• viii.$GA\left(G_n\right)=n\left[2\sqrt{2}+\frac{9\sqrt{3}}{2}+\frac{58\sqrt{6}}{5}+15\right]+\left[\frac{2\sqrt{2}}{3}-\frac{2\sqrt{6}}{5}\right].$
• ix.$ISI\left(G_n\right)=\frac{1281}{20}n-\frac{31}{30}.$
• x.${\chi }_{\alpha }\left(G_n\right)=\left(3n+1\right)3^{\alpha }+\left(13n+1\right)4^{\alpha }+\left(29n-1\right)5^{\alpha }+\left(11n-1\right)6^{\alpha }.$
• xi.$R_{\alpha }\left(G_n\right)=\left(3n+1\right)2^{\alpha }+\left(9n\right)3^{\alpha }+\left(4n+1\right)4^{\alpha }+\left(29n-1\right)6^{\alpha }+\left(11n-1\right)9^{\alpha }.$

Proof

From theorem 1, we have

$${\mathit{ISI}}_{\left(\alpha ,\beta \right)}\left(G_n\right)=\left(3n+1\right){\left[2\right]}^{\alpha }{\left[3\right]}^{\beta }+\left(9n\right){\left[3\right]}^{\alpha }{\left[4\right]}^{\beta }+\left(4n+1\right){\left[4\right]}^{\alpha +\beta }+\left(11n-1\right){\left[3\right]}^{2\alpha +\beta }{\left[2\right]}^{\beta }+\left(29n-1\right){\left[6\right]}^{\alpha }{\left[5\right]}^{\beta }.$$ (1)

• i.Put $\alpha =0$ and $\beta =1$ in equation (1), then ${\mathit{ISI}}_{\left(\alpha ,\beta \right)}\left(G_n\right)=M_1\left(G_n\right)$ is the first Zagreb index as $M_1\left(G_n\right)=272n-4$.
• ii.If $\alpha =1$ &$\beta =0,$ then ${\mathit{ISI}}_{\left(\alpha ,\beta \right)}\left(G_n\right)=M_2\left(G_n\right)$ is the second Zagreb index as $M_2\left(G_n\right)=322n-9$.
• iii.If $\alpha =-\frac{1}{2}$ and $\beta =0,$ then ${\mathit{ISI}}_{\left(\alpha ,\beta \right)}\left(G_n\right)=R\left(G_n\right)$ and we obtain Randić index as

$$R\left(G_n\right)=n\left[\frac{3}{\sqrt{2}}+\frac{9}{\sqrt{3}}+\frac{17}{3}+\frac{29}{\sqrt{6}}\right]+\left[\frac{1}{\sqrt{2}}+\frac{1}{6}-\frac{1}{\sqrt{6}}\right].$$

• iv.
  If $\alpha =0$ and $\beta =-\frac{1}{2},$ then ${\mathit{ISI}}_{\left(\alpha ,\beta \right)}\left(G_n\right)=SCI\left(G_n\right)$ and we obtain sum-connectivity index as

  $$SCI\left(G_n\right)=n\left[\sqrt{3}+\frac{11}{\sqrt{6}}+\frac{29}{\sqrt{5}}+\frac{13}{2}\right]+\left[\frac{1}{\sqrt{3}}-\frac{1}{\sqrt{5}}-\frac{1}{\sqrt{6}}+\frac{1}{2}\right].$$
• v.Put $\alpha =0$ and $\beta =-1$ in equation (1) and then multiply this equation by 2, we get harmonic index $H\left(G_n\right)$ as $H\left(G_n\right)=\frac{1}{30}\left[713n+13\right]$.
• vi.If $\alpha =0$ and $\beta =2,$ then we have hyper Zagreb index$HM\left(G_n\right)=1356n-36.$
• vii.If $\alpha =1$ & $\beta =1,$ then we have redefined third Zagreb index,

$$\mathit{ReZ}{G}_3\left(G_n\right)=1654n-62.$$

• viii.Put $\alpha =\frac{1}{2}$ and $\beta =-1$ in equation (1) and then multiply this equation by 2, we get geometric arithmetic index $GA\left(G_n\right)$ as

$$GA\left(G_n\right)=n\left[2\sqrt{2}+\frac{9\sqrt{3}}{2}+\frac{58\sqrt{6}}{5}+15\right]+\left[\frac{2\sqrt{2}}{3}-\frac{2\sqrt{6}}{5}\right].$$

• ix.If $\alpha =1$ & $\beta =-1,$ then we have inverse sum indeg index $ISI\left(G_n\right)=\frac{1281}{20}n-\frac{31}{30}$.
• x.If $\alpha =0$ and $\beta =\alpha ,$ then we have general sum connectivity index as

$${\chi }_{\alpha }\left(G_n\right)=\left(3n+1\right)3^{\alpha }+\left(13n+1\right)4^{\alpha }+\left(29n-1\right)5^{\alpha }+\left(11n-1\right)6^{\alpha }$$

• xi.If $\alpha =\alpha$ and $\beta =0,$ then we have general Randić index as

$$R_{\alpha }\left(G_n\right)=\left(3n+1\right)2^{\alpha }+\left(9n\right)3^{\alpha }+\left(4n+1\right)4^{\alpha }+\left(29n-1\right)6^{\alpha }+\left(11n-1\right)9^{\alpha }\square$$

Using similar fashion, we get the following theorem for general inverse sum indeg polynomial of HA- curcumin conjugates.

Theorem 2

The general inverse sum indeg polynomial ${\mathit{ISI}}_{\left(\alpha ,\beta \right)}(G_n,x)$ of HA- curcumin conjugates is given by,

$${\mathit{ISI}}_{\left(\alpha ,\beta \right)}\left(G_n,x\right)=\left(3n+1\right)x^{{\left[2\right]}^{\alpha }{\left[3\right]}^{\beta }}+\left(9n\right)x^{{\left[3\right]}^{\alpha }{\left[4\right]}^{\beta }}+\left(4n+1\right)x^{{\left[4\right]}^{\alpha +\beta }}+\left(11n-1\right)x^{{\left[3\right]}^{2\alpha +\beta }{\left[2\right]}^{\beta }}+\left(29n-1\right)x^{{\left[6\right]}^{\alpha }{\left[5\right]}^{\beta }}.$$

Proof

Applying the definition of general inverse sum indeg polynomial on HA- curcumin conjugates molecular graph $G_n$, we have

$${\mathit{ISI}}_{\left(\alpha ,\beta \right)}(G,x)=\sum _{\mathit{uv}\in E\left(G\right)}{x}^{{\left[d(u)d(v)\right]}^{\alpha }{\left[d\left(u\right)+d(v)\right]}^{\beta }}$$

$$=\sum _{\mathit{uv}\in E_1\left(G_n\right)}{x}^{{\left[d\left(u\right)d\left(v\right)\right]}^{\alpha }{\left[d\left(u\right)+d\left(v\right)\right]}^{\beta }}+\sum _{\mathit{uv}\in E_2\left(G_n\right)}{x}^{{\left[d(u)d(v)\right]}^{\alpha }{\left[d\left(u\right)+d(v)\right]}^{\beta }}+\sum _{\mathit{uv}\in E_3\left(G_n\right)}{x}^{{\left[d\left(u\right)d\left(v\right)\right]}^{\alpha }{\left[d\left(u\right)+d\left(v\right)\right]}^{\beta }}+\sum _{\mathit{uv}\in E_4\left(G_n\right)}{x}^{{\left[d\left(u\right)d\left(v\right)\right]}^{\alpha }{\left[d\left(u\right)+d\left(v\right)\right]}^{\beta }}+\sum _{\mathit{uv}\in E_5\left(G_n\right)}{x}^{{\left[d\left(u\right)d\left(v\right)\right]}^{\alpha }{\left[d\left(u\right)+d\left(v\right)\right]}^{\beta }}$$

$$=\left|E_1\left(G_n\right)\right|x^{{\left[\left(1\right)\left(2\right)\right]}^{\alpha }{\left[1+2\right]}^{\beta }}+\left|E_2\left(G_n\right)\right|x^{{\left[\left(1\right)\left(3\right)\right]}^{\alpha }{\left[1+3\right]}^{\beta }}+\left|E_3\left(G_n\right)\right|x^{{\left[\left(2\right)\left(2\right)\right]}^{\alpha }{\left[2+2\right]}^{\beta }}+\left|E_4\left(G_n\right)\right|x^{{\left[\left(3\right)\left(3\right)\right]}^{\alpha }{\left[3+3\right]}^{\beta }}+\left|E_5\left(G_n\right)\right|x^{{\left[\left(2\right)\left(3\right)\right]}^{\alpha }{\left[2+3\right]}^{\beta }}$$

$$=\left(3n+1\right)x^{{\left[2\right]}^{\alpha }{\left[3\right]}^{\beta }}+\left(9n\right)x^{{\left[3\right]}^{\alpha }{\left[4\right]}^{\beta }}+\left(4n+1\right)x^{{\left[4\right]}^{\alpha }{\left[4\right]}^{\beta }}+\left(11n-1\right)x^{{\left[9\right]}^{\alpha }{\left[6\right]}^{\beta }}+\left(29n-1\right)x^{{\left[6\right]}^{\alpha }{\left[5\right]}^{\beta }}$$

$$=\left(3n+1\right)x^{{\left[2\right]}^{\alpha }{\left[3\right]}^{\beta }}+\left(9n\right)x^{{\left[3\right]}^{\alpha }{\left[4\right]}^{\beta }}+\left(4n+1\right)x^{{\left[4\right]}^{\alpha +\beta }}+\left(11n-1\right)x^{{\left[3\right]}^{2\alpha +\beta }{\left[2\right]}^{\beta }}+\left(29n-1\right)x^{{\left[6\right]}^{\alpha }{\left[5\right]}^{\beta }}\square$$

Hence the theorem.

Now, we establish the following results by using the theorem 2.

Corollary 2

Let $G_n$ be the molecular graph of HA-curcumin conjugates, then

• (i)$M_1\left(G_n,x\right)=n\left(3x^3+13x^4+29x^5+11x^6\right)+\left(x^3+x^4-x^5-x^6\right).$
• (ii)$M_2\left(G_n,x\right)=n\left(3x^2+9x^3+4x^4+29x^6+11x^9\right)+\left(x^2+x^4-x^6-x^9\right).$
• (iii)$HM\left(G_n,x\right)=n\left(3x^9+13x^{16}+29x^{25}+11x^{36}\right)+\left(x^9+x^{16}-x^{25}-x^{36}\right).$
• (iv)$\mathit{ReZ}{G}_3\left(G_n,x\right)=n\left(3x^6+9x^{12}+4x^{16}+29x^{30}+11x^{54}\right)+\left(x^6+x^{16}-x^{30}-x^{54}\right).$
• (v)${\chi }_{\alpha }\left(G_n,x\right)=n\left(3x^{3^{\alpha }}+13x^{4^{\alpha }}+29x^{5^{\alpha }}+11x^{6^{\alpha }}\right)+\left(x^{3^{\alpha }}+x^{4^{\alpha }}-x^{5^{\alpha }}-x^{6^{\alpha }}\right).$
• (vi)$R_{\alpha }\left(G_n,x\right)=n\left(3x^{2^{\alpha }}+9x^{3^{\alpha }}+4x^{4^{\alpha }}+29x^{6^{\alpha }}+11x^{9^{\alpha }}\right)+\left(x^{2^{\alpha }}+x^{3^{\alpha }}-x^{6^{\alpha }}-x^{9^{\alpha }}\right).$

We illustrate the results obtained in this section by considering the following example

Example 1

Consider the molecular graph $G_2$ of HA-curcumin conjugates shown in Fig. 4. For $G_2$ we have 105 vertices, 112 edges and the edge set has five partitions, based on the degrees of their end vertices with cardinalities $\left|E_1\left(G_2\right)\right|=7,\left|E_2\left(G_2\right)\right|=18,$ $\left|E_3\left(G_2\right)\right|=9,\left|E_4\left(G_2\right)\right|=21and\left|E_5\left(G_2\right)\right|=57$.

Using Theorem 1 we have

$${\mathit{ISI}}_{\left(\alpha ,\beta \right)}\left(G_2\right)=7{\left[2\right]}^{\alpha }{\left[3\right]}^{\beta }+18{\left[3\right]}^{\alpha }{\left[4\right]}^{\beta }+9{\left[4\right]}^{\alpha +\beta }+21{\left[3\right]}^{2\alpha +\beta }{\left[2\right]}^{\beta }+57{\left[6\right]}^{\alpha }{\left[5\right]}^{\beta }.$$

Further using particular values of $\alpha$ and $\beta$ as discussed in Corollary 1, we have

$$\begin{gathered} M_1\left(G_2\right)=540,M_2\left(G_2\right)=635, \\ R\left(G_2\right)=50.1122,SCI\left(G_2\right)=51.6058, \end{gathered}$$

$$\begin{gathered} H\left(G_2\right)=47.9666,HM\left(G_2\right)=2676, \\ ReZ{G}_3\left(G_2\right)=3246,GA\left(G_2\right)=108.0364, \end{gathered}$$

$ISI\left(G_2\right)=127.066,{\chi }_1\left(G_2\right)=540,R_1\left(G_n\right)=635$. Moreover, as we discussed earlier that the degree-based topological polynomials give interesting and valuable information of the graph. For instance, the first Zagreb index $M_1\left(G_2\right)$ and second Zagreb index $M_2\left(G_2\right)$ as computed above can also be obtained by taking the first derivative of $M_1\left(G_2,x\right)$ and $M_2\left(G_2,x\right)$ at $x=1,$ respectively. By Corollary 2, we have $M_1^{\text{'}}\left(G_2,x\right)=2\left(9x^2+52x^3+145x^4+66x^5\right)+\left({3x}^2+4x^3-5x^4-{6x}^5\right)$

which gives $M_1^{\text{'}}\left(G_2,1\right)=540$. Similarly $M_2^{\text{'}}\left(G_2,x\right)=2\left(6x+27x^2+16x^3+174x^5+99x^8\right)+\left(2x+{4x}^3-6x^5-9x^8\right)$ at $x=1$ is 635.

4. Conclusion

In this work, we have calculated some degree-based topological indices of hyaluronic acid-curcumin conjugates such as First Zagreb index, Second Zagreb index, Randić index, Sum connectivity index, Harmonic index, Hyper Zagreb index, Redefined third Zagreb index, Geometric Arithmetic index, Inverse sum indeg index, General sum connectivity index and Generalized Randić index by using general inverse sum indeg index. In addition, some standard polynomials associated with topological indices for hyaluronic acid-curcumin conjugates were also computed. The results obtained in this study can be incorporated in various QSAR models for its applications in the chemical and pharmaceutical science. The computation of other distance-based and counting based topological indices of hyaluronic acid-curcumin conjugates may be another interesting topic for further study.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.