A Stochastic Model of Gene Expression with Polymerase Recruitment and Pause Release

Abstract

Transcriptional bursting is a major source of noise in gene expression. The telegraph model of gene expression, whereby transcription switches between on and off states, is the dominant model for bursting. Recently, it was shown that the telegraph model cannot explain a number of experimental observations from perturbation data. Here, we study an alternative model that is consistent with the data and which explicitly describes RNA polymerase recruitment and polymerase pause release, two steps necessary for messenger RNA (mRNA) production. We derive the exact steady-state distribution of mRNA numbers and an approximate steady-state distribution of protein numbers, which are given by generalized hypergeometric functions. The theory is used to calculate the relative sensitivity of the coefficient of variation of mRNA fluctuations for thousands of genes in mouse fibroblasts. This indicates that the size of fluctuations is mostly sensitive to the rate of burst initiation and the mRNA degradation rate. Furthermore, we show that 1) the time-dependent distribution of mRNA numbers is accurately approximated by a modified telegraph model with a Michaelis-Menten like dependence of the effective transcription rate on RNA polymerase abundance, and 2) the model predicts that if the polymerase recruitment rate is comparable or less than the pause release rate, then upon gene replication, the mean number of RNA per cell remains approximately constant. This gene dosage compensation property has been experimentally observed and cannot be explained by the telegraph model with constant rates.

Significance

The random nature of gene expression is well established experimentally. Mathematical modeling provides a means of understanding the factors leading to the observed stochasticity. There is evidence that the classical two-state model of stochastic messenger RNA (mRNA) dynamics (the telegraph model) cannot describe perturbation experiments, and a new model that includes polymerase dynamics has been proposed. In this article, we present the first detailed study of this model, deriving an exact solution for the mRNA distribution in steady-state conditions and an approximate time-dependent solution and showing that the model can explain gene dosage compensation. As well, we use the theory together with transcriptomic data to deduce which parameters when perturbed lead to a maximal change in the size of mRNA fluctuations.

Introduction

There is widespread evidence that mammalian genes are expressed in bursts: infrequent periods of transcriptional activity that produce a large number of messenger RNA (mRNA) transcripts within a short period of time (1, 2, 3). This is in contrast to constitutive expression in which mRNAs are produced in random, uncorrelated events, with a time-independent probability (4). The size and frequency of transcriptional bursts affect the magnitude of temporal fluctuations in mRNA and the protein content of a cell and thus constitute an important source of intracellular noise (5).

A large number of studies have sought to elucidate the mechanisms leading to bursting by constructing simple stochastic models that can explain the data. The simplest of these models is the telegraph model whereby 1) a gene is in two states, an ON state where mRNA is expressed, and an OFF state where there is no expression, and 2) mRNA degrades in the cytoplasm. These first-order reactions are effective because each encapsulates the effect of a large number of underlying biochemical reactions. The chemical master equation of this model has been solved exactly to obtain the probability distribution of mRNA numbers as a function of time (6). For parameter conditions consistent with bursty expression, the steady-state distribution is well approximated by a negative binomial that fits some of the experimental data (7).

Recent studies have extended the telegraph model in various directions (see (8,9) for a recent review). Mammalian cells have been shown to display complex promoter dynamics during the switch from transcriptionally inactive to active states. Such dynamics cannot be described by a single reaction step whose time is exponentially distributed (2), as assumed by the telegraph model. In (10), this complexity is accounted for by deriving analytical expressions linking the Fano factor of mRNA distributions to the general waiting-time distribution of the time to switch from inactive to active states. In contrast, other works (11, 12, 13) have sought to describe promoter dynamics with transitions between a number of discrete promoter states, only some of which are active; in special cases of such models, the steady-state distribution of mRNA fluctuations can be derived analytically. Moreover, dynamic regulation of eve stripe 2 expression in living Drosophila (14) suggests the occurrence of multiple rates of RNA polymerase II (Pol II) loading, which argues in favor of the multistate model rather than the simpler telegraph model. Another study, based on live cell imaging of the amoeba Dictyostelium, postulates a continuum of transcriptional states (15) rather than discrete states. All these models share a common property with the telegraph model, namely that when a transcript is produced, the gene state is unchanged.

Bartman et al. (16) recently argued that it is unclear how polymerase recruitment and pause release, two well-known steps in mRNA production, map onto the active and inactive states assumed by the telegraph model. This argument also applies to the various multistate variants of the telegraph model. In particular, in these models, one cannot tell whether the initiation of a burst permits polymerase recruitment to occur or whether it permits release from the paused state. In (16), the telegraph model and several possible models of transcription were considered that incorporated bursting (burst initiation and termination steps) together with polymerase recruitment and pause release steps. Using stochastic simulations in conjunction with RNA fluorescence in situ hybridization and Pol II chromatin immunoprecipitation sequencing measurements, they showed that the only model compatible with the data is one in which 1) polymerase recruitment follows after burst initiation, and 2) only one polymerase is permitted to bind each promoter-proximal region at a time, and this bound polymerase has to undergo pause release before a second polymerase can be recruited to a gene copy (in line with the findings in (17,18)). We emphasize that although this model has three effective gene states, it is not a special case of the multistate gene models studied in (11, 12, 13). These models assume that the gene state does not change upon production of mRNA because they model the production of a mature transcript without detailed modeling of the steps between transcriptional initiation and termination. However, the model expounded in (16) models transcription at a finer level of detail, which requires that the production of nascent mRNA results in a change of gene state, a property that is crucial to capture the second property above. Note the number of nascent mRNA molecules, irrespective of their length, is equal to the number of polymerases currently transcribing the gene (19). An interesting recent review discussing the assumptions behind common gene expression models including those with polymerase dynamics can be found in (20).

In this article, we present the first detailed study of the model proposed by Bartman et al. (16). The article is organized as follows. In Model, we introduce the chemical master equation formulation of the model. In Exact Solution, we obtain an exact steady-state solution of this model, and in Sensitivity Analysis, we use the theoretical results and transcriptomic data to investigate the sensitivity of the size of mRNA fluctuations to the five parameters. In Effective Telegraph Model, we show that by mapping the model onto an effective telegraph model, we can obtain an approximate time-dependent solution. In Connection to the Refractory Model, we show that although our model has three effective promoters states, it is not the same as the refractory model of gene expression devised by Naef and co-workers (2). In Protein Dynamics, we show that the protein number distribution can also be obtained in the limit of fast mRNA decay and that this is generally different than that obtained using the conventional three-stage model of gene expression (21). We finish with a discussion of the biological implications of our results in Conclusions.

Results and Discussion

Model

We consider a stochastic transcriptional bursting model (recently introduced in (16) and henceforth referred to as the multiscale model; see Fig. 1 A), whereby a gene fluctuates between three states: two permissive states (D₁₀ and D₁₁) and a nonpermissive state (D₀).

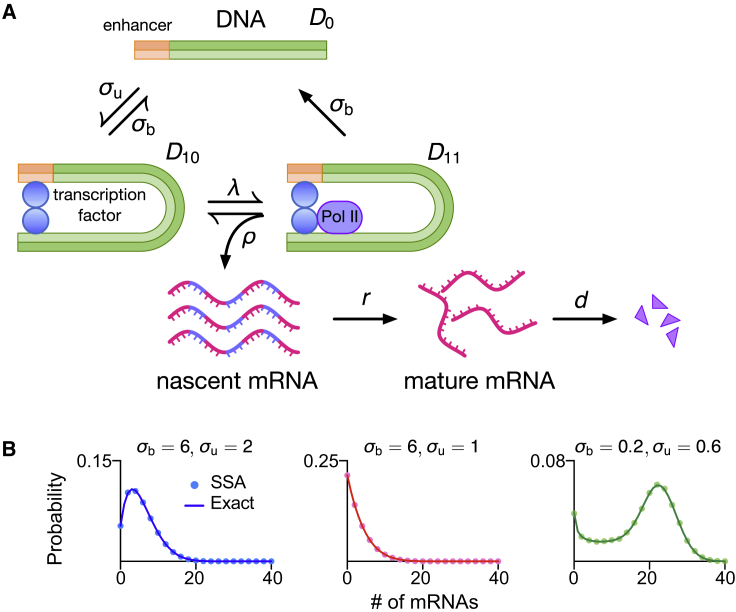
Figure 1.

(A) Schematic of the stochastic multiscale transcriptional bursting model. (B) Analytical distribution for mature mRNA numbers (under the assumption of short-lived nascent mRNA) is given by Eq. 6 and agrees with stochastic simulations using the SSA. The kinetic parameters are ρ = 60, λ = 40, and d = 1; other parameters are indicated in each panel. To see this figure in color, go online.

The transition from D₀ to D₁₀ (burst initiation) is mediated by transcription factor binding with rate constant σ_u, which is reversible with rate constant σ_b (this transition may alternatively represent other processes such as nucleosome remodeling). Subsequently, the binding of Pol II to D₁₀ with rate constant λ (which is proportional to Pol II abundance) leads to D₁₁. This represents a state in which Pol II is paused and models the experimental observation that Pol II pauses downstream of the transcription initiation site preceding productive elongation (18). The polymerase is released from this state with rate constant ρ, leading to two simultaneous processes: 1) because now the polymerase can actively transcribe RNA, it implies the production of nascent mRNA (denoted as N) with rate ρ; and 2) the gene state changes from D₁₁ to D₁₀. This step models the experimental observation that unless the polymerase is unpaused, there is no binding of new Pol II (17,18). In the paused state D₁₁, both the polymerase and the transcription factor can unbind from the gene and lead to the nonpermissive state D₀ (burst termination). Both reversible switches operate at different timescales (hours versus minutes) with max{σ_b, σ_u} ≪ min {ρ, λ}, leading to multiscale transcriptional bursting (16,22). After termination, the nascent mRNA becomes a mature mRNA (denoted by M); this occurs with rate r. Subsequently, the mature mRNA decays with rate constant d. Note that we assume all reactions to be first order, characterized by exponentially distributed waiting times between successive reactions.

In what follows, for simplicity, we assume that the lifetime of nascent mRNA is very short, i.e., r is large, such that the reaction D₁₁ → D₁₀ + N, N → M can be approximated by the single reaction step D₁₁ → D₁₀ + M. In the next section, we derive the steady-state distribution of mature mRNA (simply called mRNA henceforth).

Exact solution

Let P_θ (n, t) (θ = 0, 10, 11) denote the probability of a cell being in state D_θ with n mRNAs at time t (arguments n and t are hereafter omitted for brevity). The dynamics of probability P_θ are described by the set of coupled master equations

$$\begin{array}{l}{\partial }_t{P}_0=\left({\mathbb{E}}^1-1\right)dn{P}_0-{\sigma }_{\text{u}}{P}_0+{\sigma }_{\text{b}}\left(P_{10}+P_{11}\right),\\ {\partial }_t{P}_{10}=\left({\mathbb{E}}^1-1\right)dn{P}_{10}-\left({\sigma }_{\text{b}}+\lambda \right)P_{10}+{\sigma }_{\text{u}}{P}_0+\rho {\mathbb{E}}^{-1}{P}_{11},\\ {\partial }_t{P}_{11}=\left({\mathbb{E}}^1-1\right)dn{P}_{11}-\left(\rho +{\sigma }_{\text{b}}\right)P_{11}+\lambda P_{10},\end{array}$$ (1)

where the step operator ${\mathbb{E}}^i$ acts on a general function g(n) as ${\mathbb{E}}^{i}g\left(n\right)=g\left(n+i\right)$ (23). To solve Eq. 1, we use the generating function method and define $G_{\theta }\left(z\right)=\sum _n{z}^n{P}_{\theta }\left(n\right)$ for θ = 0, 10, 11 so that Eq. 1 can be recast as a set of coupled partial differential equations

$${\partial }_t{G}_0+d\left(z-1\right){\partial }_z{G}_0=-{\sigma }_{\text{u}}{G}_0+{\sigma }_{\text{b}}{G}_{10}+{\sigma }_{\text{b}}{G}_{11},$$ (2a)

$${\partial }_t{G}_{10}+d\left(z-1\right){\partial }_z{G}_{10}=\rho z{G}_{11}-\left({\sigma }_{\text{b}}+\lambda \right)G_{10}+{\sigma }_{\text{u}}{G}_0,$$ (2b)

$${\partial }_t{G}_{11}+d\left(z-1\right){\partial }_z{G}_{11}=-\rho G_{11}-{\sigma }_{\text{b}}{G}_{11}+\lambda G_{10},$$ (2c)

wherein the variable z is dropped for brevity. By setting z = 1 and the time derivatives to zero (considering steady-state conditions), we can deduce that the probability of being in the nonpermissive state D₀ is G₀(1) = σ_b/(σ_u + σ_b) and the probability of being in one of the two permissive states D₁₀ or D₁₁ is G₁₀(1) + G₁₁(1) = σ_u/(σ_u + σ_b).

To solve (2a), (2b), (2c) for G₀(z), G₁₀(z), and G₁₁(z) in steady-state conditions, we set ${\partial }_t{G}_{\theta }=0$, solve G₁₀ from Eq. 2c as a function of G₁₁, and combine the yielded result to solve G₀ from Eq. 2b as a function of G₁₁ so that Eq. 2a consequently becomes a differential equation with G₁₁ being the only variable

$$d^3{u}^2{\partial }_u^3{G}_{11}+\left(3d+{\gamma }_1+{\gamma }_2\right)d^{2}u{\partial }_u^2{G}_{11}+\left[\left(d+{\gamma }_1\right)\left(d+{\gamma }_2\right)-\rho \lambda u\right]d{\partial }_u{G}_{11}-\left(d+{\sigma }_{\text{u}}\right)\rho \lambda G_{11}=0,$$ (3)

with u = z − 1, γ₁ = σ_b + σ_u, and γ₂ = ρ + λ + σ_b. By defining a new variable x = ρλu/d², Eq. 3 can be further simplified to

$$x^2{\partial }_x^3{G}_{11}+\left(1+\frac{{\gamma }_1+d}{d}+\frac{{\gamma }_2+d}{d}\right)x{\partial }_x^2{G}_{11}+\left(\frac{{\gamma }_1+d}{d}\frac{{\gamma }_2+d}{d}-x\right){\partial }_x{G}_{11}-\frac{{\sigma }_{\text{u}}+d}{d}{G}_{11}=0,$$

which is in the canonical form of the differential equation for the generalized hypergeometric function

$$x^2{\partial }_x^{3}f\left(x\right)+\left(1+b_1+b_2\right)x{\partial }_x^{2}f\left(x\right)+\left(b_1{b}_2-x\right){\partial }_{x}f\left(x\right)-a_{1}f\left(x\right)=0,$$

admitting the solution f(x) = C₁F₂(a₁, b₁, b₂, x), with C being an integration constant. Hence, the solution for G₁₁ is in terms of the generalized hypergeometric function

$$G_{11}=C\cdot {}_1{F}_2\left(\frac{{\sigma }_{\text{u}}+d}{d};\frac{{\gamma }_1+d}{d},\frac{{\gamma }_2+d}{d};\frac{\rho \lambda }{d^2}u\right).$$ (4)

On the other hand, summing Eqs. 2a, 2b, and 2c and denoting $G={\sum }_{\theta }{G}_{\theta }$, one can get ${\partial }_{u}G=\rho G_{11}/d$, which together with Eq. 4 leads to

$$G\left(u\right)=C_2\cdot {}_1{F}_2\left(\frac{{\sigma }_{\text{u}}}{d};\frac{{\sigma }_{\text{b}}+{\sigma }_{\text{u}}}{d},\frac{{\sigma }_{\text{b}}+\rho +\lambda }{d};\frac{\rho \lambda }{d^2}u\right).$$

Note that in the last step, we made use of the general relation ${\partial }_z{}_1^{}{F}_2\left(a;b,c;z\right)=\left(a/bc\right){\cdot }_1^{}{F}_2\left(a+1;b+1,c+1;z\right)$. The integration constant C₂ is found to be 1 by using the normalization condition G(0) = 1. Hence, the exact solution for the generating function is

$$G\left(u\right){=}_1^{}{F}_2\left(\frac{{\sigma }_{\text{u}}}{d};\frac{{\gamma }_1}{d},\frac{{\gamma }_2}{d};\frac{\rho \lambda }{d^2}u\right).$$ (5)

Hence, it follows that the marginal probability of finding n mRNAs in a cell is

$$P\left(n\right)=\frac{1}{n!}{\frac{{\text{d}}^{n}G\left(u\right)}{\text{d}{u}^n}|}_{u=-1}=\frac{1}{n!}\left(\frac{\rho \lambda }{d^2}\right)\frac{{\left(\frac{{\sigma }_u}{d}\right)}_n}{{\left(\frac{{\sigma }_b+{\sigma }_u}{d}\right)}_n{\left(\frac{{\sigma }_b+\rho +\lambda }{d}\right)}_n}{}_1^{}{F}_2\left(\frac{{\sigma }_u}{d}+n;\frac{{\sigma }_b+{\sigma }_u}{d}+n,\frac{{\sigma }_{\text{b}}+\rho +\lambda }{d}+n;-\frac{\rho \lambda }{d^2}\right),$$ (6)

where ${(\cdot )}_n$ is the Pochhammer symbol. In Fig. 1 B, we show that distributions obtained from Eq. 6 as well as the corresponding modality (a phenotypic signature (24)) are indistinguishable from distributions produced using the stochastic simulation algorithm (SSA) (25). Note that here, we have solved for the mature mRNA distribution under the assumption that nascent mRNA is short lived. In cases in which this assumption is not physiologically meaningful and one is interested in the nascent mRNA distribution, then the latter is given by Eq. 6 with d replaced by r (the rate at which nascent mRNA changes to mature mRNA because of the termination of transcription).

Special case of bursty transcription

It can be further shown by perturbation theory in Appendix A that when ρ, λ, and σ_b are much greater than the rest of the parameters, the exact solution Eq. 6 reduces to the negative binomial distribution $P\left(n\right)=\text{NB}\left(\left({\sigma }_{\text{u}}/d\right),\left(\rho /\rho +\alpha \right)\right)$ with α = σ_bγ₂/λ. Note the constraint on the parameters leads to a time series with large- and short-lived bursts of transcription (because ρ, λ, and σ_b are large), separated by long silent intervals (because σ_u is small). Such bursty trancription is common in mammalian cells (3).

Relationship to the telegraph model

It can also be shown that that in the limit of large ρ, the exact solution of Eq. 6 reduces to the confluent hypergeometric solution of the telegraph model (see Appendix B). This is equivalent to the steady-state solution of the two-state system $D_0\underset{{\sigma }_{\text{b}}}{\overset{{\sigma }_{\text{u}}}{\rightleftharpoons }}{D}_{10}\stackrel{\lambda }{\to }{D}_{10}+M,M\stackrel{d}{\to }\varnothing$. The reduction to a two-state model results from genes spending a short time in state D₁₁ because of the large value of ρ. The production of an mRNA molecule involves the slow reaction step from D₁₀ to D₁₁ with rate λ followed by a very fast reverse step with rate ρ. Hence, the rate of mRNA production is determined by the reaction rate of the slowest reaction, i.e., it is equal to λ. By similar reasoning, we can deduce that in the limit of large λ, the gene spends a short time in the state D₁₀, and the multiscale model reduces to the two-state telegraph model with a rate of mRNA production equal to ρ.

Sensitivity analysis

The exact solution in Eq. 5 allows us to examine the stochastic properties of the multiscale model over large swathes of parameter space. We investigate the relative sensitivity of the coefficient of variation of mRNA fluctuations, $\text{CV}=\sqrt{\text{Var}\left(n\right)}/\langle n\rangle$, which is typically employed as a measure of the magnitude of transcriptional noise. To this end, we calculate the first two central moments, ($\langle n\rangle$ and $\text{Var}\left(n\right)$), from Eq. 5 using $\langle n\rangle ={{\partial }_{u}G|}_{u=0}$ and $\text{Var}\left(n\right)={{\partial }_u^{2}G|}_{u=0}+\langle n\rangle -{\langle n\rangle }^2$. The mean and CV are then given by

$$\langle n\rangle =\frac{{\sigma }_{\text{u}}\lambda \rho }{d{\gamma }_1{\gamma }_2},$$ (7a)

$${\text{CV}}^2=\frac{1}{\langle n\rangle }+\frac{d}{{\sigma }_{\text{u}}}\cdot \frac{{\gamma }_1}{{\gamma }_1+d}\cdot \frac{{\gamma }_2}{{\gamma }_2+d}.$$ (7b)

Note that because the parameters ρ and λ appear symmetrically in (7a), (7b), for simplicity, we enforce the constraint ρ = λ (we will relax this constraint later). Hence, the relative sensitivity of the quantity $\overline{\text{CV}}={\text{CV}|}_{\rho =\lambda }$, which can serve as a gauge of transcriptional noise, is insightful to study and defined as ${\text{Λ}}_p=\left(p/\overline{\text{CV}}\right)\partial \overline{\text{CV}}/\partial p$ for a model parameter p, meaning that 1% change in p leads to a Λ_p% change in $\overline{\text{CV}}$. The parameter values for the sensitivity analysis were sampled from experimental distributions recently inferred for 3575 genes of CAST allele in mouse fibroblasts (3) using the telegraph model. To obtain values for ρ and λ, we equate the mean of the telegraph model (with ON switching rate σ_b, OFF switching rate σ_u, transcription rate ρ_u, and degradation rate d) ${\langle n\rangle }_{\text{tel}}={\sigma }_{\text{u}}{\rho }_{\text{u}}/{\gamma }_{1}d$ with the mean of the multiscale model (Eq. 7a) under the constraint ρ = λ, giving

$$\rho ={\rho }_{\text{u}}\left(1+\sqrt{1+\frac{{\sigma }_{\text{b}}}{{\rho }_{\text{u}}}}\right).$$ (8)

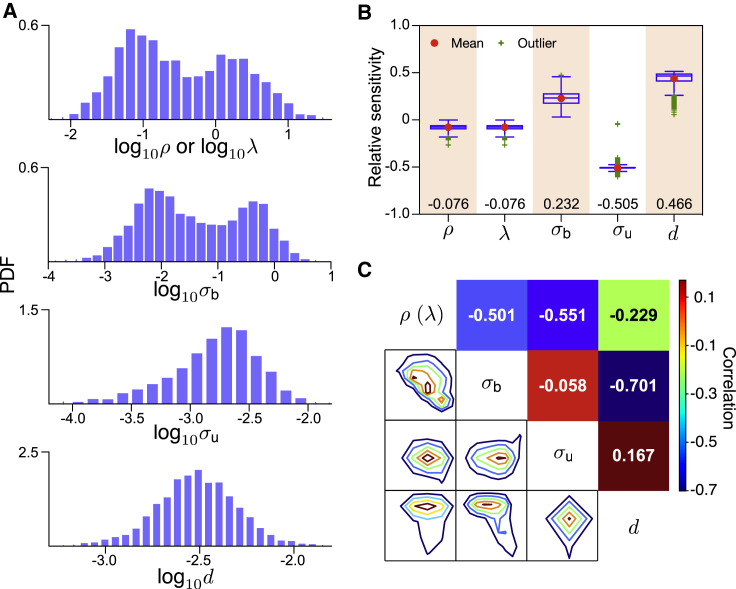
Distributions for each parameter in the data set are presented in Fig. 2 A, and the box plots in Fig. 2 B show the relative sensitivity for each parameter. The parameters in order of most sensitive first are σ_u, d, σ_b, and ρ = λ. This order is the same as obtained by ranking parameters according to the inverse of their mean experimental values (the mean of the distributions in Fig. 2 A), implying that changes to the CV are most easily accomplished by perturbations to the slowest reactions. Given the vectors ${\text{Λ}}_{p_1}$ and ${\text{Λ}}_{p_2}$ for any pair $p_1\ne p_2$ and p₁, p₂ in the set {ρ, λ, σ_b, σ_u, d} where each entry is a different gene, in Fig. 2 C, we calculate the Pearson correlation coefficient between the vectors and the corresponding joint distributions. This shows that (σ_u, σ_b) is the least dependent pairing, and hence, they constitute a quasiorthogonal decomposition of the sensitivity. In other words, a change in the CV due to a change in σ_u is practically uncorrelated with a change in the CV due to a change in σ_b, and hence, these two parameters can be seen as independent “control knobs” to change the CV; this is of interest in synthetic biology, in which an engineering design approach is taken to modify a biological system for improved functionality (26,27). The same set of parameters ranked by sensitivity are obtained, if instead of setting λ = ρ, we consider ρ ≫ λ or λ ≫ ρ, and hence, it appears that our results in this section are robust and invariant with respect to the ratio λ/ρ.

Figure 2.

Relative sensitivity analysis of the coefficient variation $\overline{\text{CV}}$ of mRNA noise over five kinetic parameters for 3575 genes of CAST allele data for mouse fibroblasts. (A) Distributions of the kinetic parameters in the dataset (obtained from (3)); values of ρ or λ are calculated using Eq. 8. (B) Box plots indicate the median (values shown at bottom), the 25% and 75% quantiles, and mean and outliers of relative sensitivity. (C) Joint distributions and Pearson correlation between the relative sensitivity vectors for each pair of parameters suggest that (σ_b, σ_u) and (σ_u, d) are the least-dependent pairs. To see this figure in color, go online.

Effective telegraph model

Earlier, we showed that in the limit of large ρ or large λ, the solution of the multiscale model tends to the solution of the telegraph model. Next, we use the first-passage time method to reduce the multiscale model into an effective telegraph model, without making the aforementioned assumptions. To this end, we consider the transcription motif of the multiscale model, $D_{10}\stackrel{\lambda }{\to }{D}_{11}\stackrel{\rho }{\to }{D}_{10}+M$, whose corresponding master equations for producing newborn mRNA starting from state D₁₀ are

$$\begin{array}{l}{\partial }_t{P}_{10}=-\lambda P_{10},\\ {\partial }_t{P}_{11}=\lambda P_{10}-\rho P_{11},\\ {\partial }_t{P}_{\text{M}}=\rho P_{11},\end{array}$$ (9)

where P₁₀, P₁₁, and P_M represent the probability of staying in states D₁₀, D₁₁, or producing a new mRNA, respectively. We remark that the reaction D₁₁ → D₀ is absent from the motif because of its relatively small reaction rate σ_b compared to ρ and λ. The initial conditions for Eq. 9 are ${P_{10}|}_{t=0}=1$ and ${P_{11}|}_{t=0}={P_{\text{M}}|}_{t=0}=0$. Solving for P_M in Eq. 9, we can calculate the mean first-passage time for mRNA production

$$\langle t_{\text{f}}\rangle ={\int }_0^{\infty }t{P}_f\text{d}t=\frac{\rho +\lambda }{\lambda \rho },$$ (10)

where $P_f={\partial }_t{P}_{\text{M}}$ is the first-passage time distribution (28). Because the effective transcription rate is the inverse of the mean first-passage time, it immediately follows that the effective telegraph model is

$$D_0\underset{{\sigma }_{\text{b}}}{\overset{{\sigma }_{\text{u}}}{\rightleftharpoons }}{D}_{10}{\stackrel{{\rho }_{\text{u}}=\frac{\lambda \rho }{\lambda +\rho }}{\to }}_{10}+M,M\stackrel{d}{\to }\varnothing .$$ (11)

Alternatively, one can obtain this result by equating the means of our model Eq. 7a and of the telegraph model ${\langle n\rangle }_{\text{tel}}={\rho }_{\text{u}}{\sigma }_{\text{u}}/{\gamma }_{1}d$ and solving for the effective production rate ρ_u, giving ${\rho }_{\text{u}}=\lambda \rho /{\gamma }_2\simeq \lambda \rho /\left(\lambda +\rho \right)$ because, typically, ρ, λ ≫ σ_b.

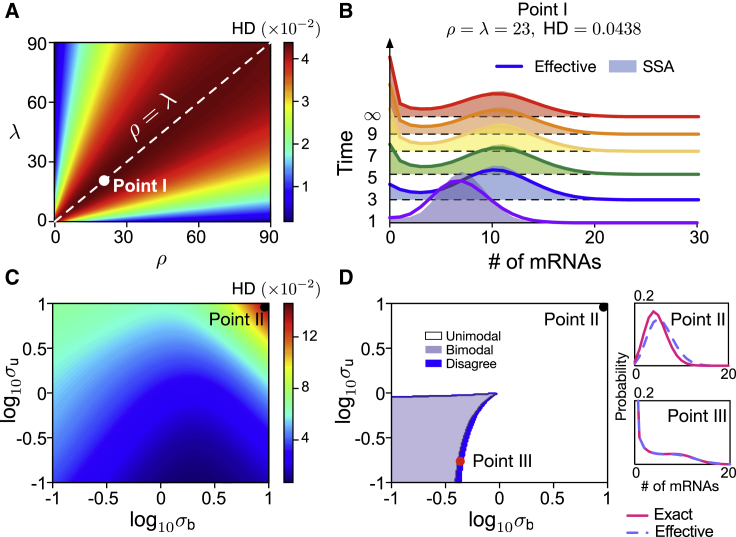
In Fig. 3, we show the high accuracy of the effective telegraph model approximation from Eq. 11. In particular, Fig. 3 A shows a heatmap of the distance between the distributions of mRNA numbers predicted by the effective telegraph model and the multiscale model. As a distance measure, we use the Hellinger distance (HD), a Euclidean distance-based metric normalized to the interval between 0 and 1. The effective telegraph model is naturally a more accurate description to the multiscale model when there is one rate-limiting step (large difference between ρ and λ) rather than when there are two rate-limiting steps (ρ = λ).

Figure 3.

An effective telegraph model (given by reaction scheme (11)) approximates the distribution of mRNA numbers of the multiscale model. (A) Hellinger distance (HD) between steady-state distributions of mRNA numbers for the effective telegraph model and the multiscale model as a function of ρ and λ with σ_u = 0.2, σ_b = 0.1, and d = 1. The discrepancy between the two distributions grows as ρ and λ approach the line ρ = λ. (B) Shown is the time-dependent distributions for Point I in (A) (the point with the largest HD) predicted by the effective model compared to those computed by the SSA for the multiscale model. (C) Heat map of HD between both distributions as a function of σ_b and σ_u with ρ = λ = 23 and d = 1. (D) Stochastic bifurcation diagram for the number of modes of the steady-state distributions predicted by the two models. The small dark blue region is where modality of both models disagree. Insets show distributions corresponding to the points marked in (C and D). To see this figure in color, go online.

Because the time-dependent distribution of the telegraph model is known in closed form (6,29), it follows that by the effective model in Eq. 11 we have an approximation for the time-dependent distribution of the multiscale model too. The accuracy of this approximation is shown in Fig. 3 B, where it is compared to the time-dependent distributions computed using the SSA for the multiscale model. The parameters here correspond to those of Point I in Fig. 3 A (the largest HD). Differences between the distributions of the two models are negligible except near time t = 0. We further investigate how burst initiation and termination rates (σ_u, σ_b) affect the approximation error with a heatmap of HD as a function of σ_u and σ_b (Fig. 3 C) and a stochastic bifurcation diagram for the number of modes of the effective telegraph and multiscale model distributions (Fig. 3 D) at steady state. The point of maximal HD in Fig. 3 C (Point II) displays distributions that are not that different from each other; see upper right inset of Fig. 3 D. The two models display the same number of modes in all regions of parameter space except for a narrow region in which modality detection is challenging because the distributions have a broad plateau; see lower right inset of Fig. 3 D (Point III). This again confirms the high accuracy of the effective telegraph model approximation. The biological implications of the Michaelis-Menten dependence of the transcription rate ρ_u in Eq. 11 on λ and ρ is discussed in Conclusions; in particular, there we argue how this special feature of our model can explain gene dosage compensation observed in experiments.

Connection to the refractory model

Besides the telegraph model, another prevalent stochastic transcriptional model is the refractory model (2) (a three-state model, see Fig. 4 A, left), wherein the burst initiation requires two steps. This model was devised to explain the experimental observation that the distribution of “off” intervals is not exponential but rather has a peak at a nonzero value. To understand the connection between our model and the refractory model, we first exactly solve the refractory model for the steady-state distribution of mRNA numbers.

Figure 4.

Effective telegraph model approximation for the refractory model. (A) Schematics of both models. (B) Hellinger distance between the steady-state distributions of mRNA numbers predicted by both models and a bifurcation diagram of their number of modes (black lines) as a function of σ_u and λ with σ_b = 0.8, ρ_u = 30, and d = 1. (C) Distributions for Points I and II in (B), showing significant disagreement in the height of the zero mode (insets show a zoom at the mode at zero). To see this figure in color, go online.

Given the reaction scheme illustrated in Fig. 4 A, it follows that the temporal evolution of probability P_θ(n) of finding n mRNAs and gene state D_θ (θ = 0, 1, or 2) can be described by the following master equations:

$$\{\begin{array}{l}{\partial }_t{P}_0\left(n\right)=\left({\mathbb{E}}^1-1\right)dn{P}_0\left(n\right)+{\sigma }_{\text{b}}{P}_2\left(n\right)-{\sigma }_{\text{u}}{P}_0\left(n\right),\\ {\partial }_t{P}_1\left(n\right)=\left({\mathbb{E}}^1-1\right)dn{P}_1\left(n\right)+{\sigma }_{\text{u}}{P}_0\left(n\right)-\lambda P_1\left(n\right),\\ {\partial }_t{P}_2\left(n\right)=\left({\mathbb{E}}^1-1\right)dn{P}_2\left(n\right)+\left({\mathbb{E}}^{-1}-1\right){\rho }_{\text{u}}{P}_2\left(n\right)+\lambda P_1\left(n\right)-{\sigma }_{\text{b}}{P}_2\left(n\right).\end{array}$$

The corresponding generating function equations are given by

$${\partial }_t{G}_0+d\left(z-1\right){\partial }_z{G}_0={\sigma }_{\text{b}}{G}_2-{\sigma }_{\text{u}}{G}_0,$$ (12a)

$${\partial }_t{G}_1+d\left(z-1\right){\partial }_z{G}_1={\sigma }_{\text{u}}{G}_0-\lambda G_1,$$ (12b)

$${\partial }_t{G}_2+d\left(z-1\right){\partial }_z{G}_2={\rho }_{\text{u}}\left(z-1\right)G_2+\lambda G_1-{\sigma }_{\text{b}}{G}_2,$$ (12c)

where $G_{\theta }={\sum }_n{z}^n{P}_{\theta }\left(n\right)$. We intend to solve Eqs. 12a, 12b, and 12c at steady state and thus set ${\partial }_t{G}_{\theta }=0$. Then, we solve G₁ as a function of G₂ from Eq. 12c, subsequently substitute it into Eq. 12b, and solve G₀ as a function of G₂. After that, Eq. 12a becomes an ordinary differential equation with G₂ being the only variable to be solved

$$u^2{\partial }_u^3{G}_2+\left(3+\tilde{\lambda }+{\tilde{\sigma }}_{\text{b}}+{\tilde{\sigma }}_{\text{u}}-{\tilde{\rho }}_{\text{u}}u\right)u{\partial }_u^2{G}_2+\left[1+{\tilde{\sigma }}_{\text{b}}+{\tilde{\sigma }}_{\text{u}}+{\tilde{\sigma }}_{\text{b}}{\tilde{\sigma }}_{\text{u}}-{\tilde{\rho }}_{\text{u}}\left(3+{\tilde{\sigma }}_{\text{u}}\right)u+\tilde{\lambda }\left(1+{\tilde{\sigma }}_{\text{b}}+{\tilde{\sigma }}_{\text{u}}-{\tilde{\rho }}_{\text{u}}u\right)\right]{\partial }_u{G}_2-\left(1+\tilde{\lambda }\right)\left(1+{\tilde{\sigma }}_{\text{u}}\right){\tilde{\rho }}_{\text{u}}{G}_2=0,$$ (13)

where ${\tilde{\rho }}_{\text{u}}$, $\tilde{\lambda }$, ${\tilde{\sigma }}_{\text{b}}$, and ${\tilde{\sigma }}_{\text{u}}$ are the kinetic parameters normalized with respect to d and u = z − 1. Eq. 13 is the canonical form of the differential equation for the generalized hypergeometric function ₂F₂, admitting the solution

$$G_2\left(u\right)=C{\cdot }_2^{}{F}_2\left(\tilde{\lambda }+1,{\tilde{\sigma }}_{\text{u}}+1;{\beta }_1-{\beta }_2+1,{\beta }_1+{\beta }_2+1;{\tilde{\rho }}_{\text{u}}u\right),$$ (14)

where C is an integration constant, and β₁ and β₂ denote

$${\beta }_1=\frac{{\tilde{\sigma }}_{\text{u}}+{\tilde{\sigma }}_{\text{b}}+\tilde{\lambda }}{2},{\beta }_2=\frac{1}{2}\sqrt{{\tilde{\lambda }}^2-2\tilde{\lambda }{\tilde{\sigma }}_{\text{b}}+{\tilde{\sigma }}_{\text{b}}^2-2\tilde{\lambda }{\tilde{\sigma }}_{\text{u}}-2{\tilde{\sigma }}_{\text{b}}{\tilde{\sigma }}_{\text{u}}+{\tilde{\sigma }}_{\text{u}}^2}.$$

Summing Eqs. 12a, 12b, and 12c leads to ${\partial }_{u}G={\partial }_u\left({\sum }_{\theta }{G}_{\theta }\right)={\tilde{\rho }}_{\text{u}}{G}_2$, one can obtain G from Eq. 14 in the form of the generalized hypergeometric function

$$G\left(u\right)=C_2{\cdot }_2^{}{F}_2\left(\tilde{\lambda },{\tilde{\sigma }}_{\text{u}};{\beta }_1-{\beta }_2,{\beta }_1+{\beta }_2;{\tilde{\rho }}_{\text{u}}u\right),$$ (15)

and C₂ is found to be 1 by the normalization condition G(0) = 1. Eq. 15 together with $P\left(n\right)=\left(1/n!\right){\left({\text{d}}^{n}G/\text{d}{u}^n\right)|}_{u=-1}$ defines the distribution of mRNA numbers for the refractory model in steady-state conditions. A similar solution is also known for a generalization of the refractory model (11).

The next step is to map the refractory model onto an effective telegraph model by matching the mean mRNA numbers

$${\langle n\rangle }_{\text{ref}}=\frac{\lambda {\sigma }_{\text{u}}{\rho }_{\text{u}}}{d\left(\lambda {\sigma }_{\text{u}}+\lambda {\sigma }_{\text{b}}+{\sigma }_{\text{u}}{\sigma }_{\text{b}}\right)},{\langle n\rangle }_{\text{tel}}=\frac{{\rho }_{\text{u}}{\overline{\sigma }}_{\text{u}}}{d\left({\sigma }_{\text{b}}+{\overline{\sigma }}_{\text{u}}\right)}.,$$

leading to an effective burst initiation rate ${\overline{\sigma }}_{\text{u}}={\sigma }_{\text{u}}\lambda /\left({\sigma }_{\text{u}}+\lambda \right)$ and the corresponding effective model shown in Fig. 4 A (right). Note that whereas the multiscale model is approximately equivalent to an effective telegraph model with a renormalized mRNA production rate, the refractory model’s telegraph approximation leads to a renormalized rate of switching to the active state.

We then compare the steady-state distributions of the refractory model and its effective telegraph model. A heatmap of HD quantifying their distributional difference and a modality diagram (marked as black lines) of the two distributions are illustrated in Fig. 4 B. Both the regions of high HD and Region 2 where only the telegraph model predicts bimodality are significantly large, and Region 1 where both predict bimodality is small. This shows that the refractory model, in general, is not well approximated by the telegraph model, particularly the latter’s probability for low mRNA numbers is not accurate (see Fig. 4 C). Given the telegraph model’s excellent approximation to the multiscale model, it is clear that the multiscale model and refractory model can be distinguished.

Protein dynamics

Finally, for completeness, we extend the multiscale model to provide analytic steady-state distributions of protein numbers. This allows interpretations of single-cell data of protein expression (see, for example, (30)). We consider the network in Fig. 1 A with two additional reactions: 1) a first-order reaction modeling the translation of mRNA to proteins with rate constant k and 2) a first-order reaction modeling the decay of protein with rate constant d_p. It is shown in Appendix C that under the classic short-lived mRNA assumption (d ≫ d_p) (21), the generating function corresponding to the steady-state distribution of protein numbers is given by

$$G\left(v\right){=}_3^{}{F}_2\left(a_1,a_2,a_3;b_1,b_2;bv\right),$$ (16)

with b₁ = (σ_b + σ_u)/d_p, b₂ = (σ_b + λ + ρ)/d_p, the mean translational burst size b = k/d, and the parameters a₁, a₂, and a₃ being solutions of the equations

$$\begin{array}{l}{a}_1{a}_2{a}_3={\sigma }_{\text{u}}\lambda \rho /d_{\text{p}}^3,\\ a_1+a_2+a_3=b_1+b_2,\\ a_1{a}_2+a_1{a}_3+a_2{a}_3=b_1{b}_2+\lambda \rho /d_{\text{p}}^2.\end{array}$$

In the limit of large λ or ρ, we show in Appendix C that Eq. 16 reduces to the Gaussian hypergeometric function (₂F₁), which was reported in (21), for the classical three-stage model of gene expression in the limit of fast mRNA decay.

Conclusions

Here, we performed the first detailed analytical study of a multiscale model of bursty gene expression based on recent experimental data from mammalian cells (16). The conventional telegraph model does not include an independently regulated pause release step and hence cannot differentiate the effects of changing polymerase pause release versus polymerase recruitment rates, whereas the multiscale model studied here can distinguish these effects. Although our model has three effective gene states (one of which regulates pause release), it is not a special case of existing multistate models because in our model, the gene state changes upon production of new nascent mRNAs to model the experimental observation that unless the polymerase is unpaused (and nascent mRNA starts being actively transcribed by this polymerase), there can be no binding of new Pol II. In contrast, current models assume the gene state does not change upon production of mRNA because they model the production of a mature transcript without detailed modeling of the steps between transcriptional initiation and termination.

We have derived simple closed-form expressions for the approximate time evolution of the mRNA numbers and used the theory to understand which reactions contribute mostly to fluctuations. We also showed that 1) this model can be distinguished from the refractory model, another three-gene-state model popular in the literature and 2) a number of previous models in the literature are special cases of our model, valid only in certain parameter regimes. Specifically, the mRNA and protein distributions of the conventional three-stage model of gene expression provide a good approximation to the multiscale bursting model in certain regions of parameter space as shown in Appendices B and C.

The simplicity of the equations for the mean and the variance allow the inference of rate parameters from single-cell data using maximal likelihood methods (31). Potential extensions include 1) the impact of cell cycle effects such as binomial partitioning and variability in the cell cycle duration and 2) introducing a detailed description of polymerase movement along the gene during elongation. The use of the recently developed linear mapping approximation (32) appears to be a promising means to extend the analytical solution of this model to include feedback loops via DNA-protein interactions (33,34).

An important result of the article is that the time-dependent mRNA distribution of the multiscale model with polymerase dynamics and three states can be accurately approximated by the two-state telegraph model, modified with a Michaelis-Menten-like dependence of the effective transcription rate on polymerase abundance. Specifically, by Eq. 11, the transcription rate of a gene locus is ρ_u = λρ/(λ + ρ), where λ is the binding rate of Pol II (see Fig. 1 A), which is proportional to the local number of Pol II molecules at the gene locus with active transcription (35). This equation implies that the transcription rate is proportional to the local number of Pol II molecules if λ is approximately less than ρ, i.e., if the Pol II binding rate is less than or equal to the rate at which Pol II is unpaused. In contrast, if unpausing is the rate-limiting step (ρ ≪ λ), then the transcription rate is practically independent of the local Pol II number.

Now, when the number of gene copies doubles during replication, the local number of Pol II molecules will correspondingly decrease because of increased sharing of Pol II. Hence, if we are in the regime $\lambda \lesssim \rho$, the transcription rate per gene copy decreases; thus, the total transcription rate for a gene per cell postreplication will be consequently slower than twice the total transcription rate prereplication. This implies that the mean number of RNA per cell is not significantly affected by replication; indeed, this “dosage compensation” has been observed experimentally for some genes in mouse embryonic stem cells (36) though a different explanation than above was suggested. In one study (37), it was estimated that for 6 yeast genes (RPB2, RPB3, TAF5, TAF6, TAF12, and KAP104), the formation of the preinitiation complex at the promoter (λ) is approximately equal to the rate at which the RNA polymerase escapes the promoter (ρ); hence, gene dosage compensation via polymerase sharing, as implied by our model, may be common. In contrast, if we are in the regime ρ ≪ λ, the transcription rate per gene copy before and after replication is the same, and hence, the total transcription rate for a gene per cell postreplication will be twice the total transcription rate prereplication. This is also what is predicted by the telegraph model with constant burst initiation and termination rates and observed experimentally for a reporter gene expressed from a strong synthetic promoter (36). Note that because the mean burst size is the mean number of RNAs transcribed when the gene is on, by our reasoning above, it also follows that when $\lambda \lesssim \rho$, the mean burst size is altered upon gene replication. The idea that the number of RNA polymerases is the limiting factor in transcription has been recently hypothesized (38) and has implications for the mitigation of burden imposed by gene circuits in synthetic biology (39). Our model here goes one step further by deriving the explicit relationship between the transcription rate and the number of RNA polymerases. Generally, our model supports the observation that there are differences in transcriptional activity between different stages of the cell cycle (40) that cannot be explained by the conventional telegraph model.

Author Contributions

Z.C. formulated the research question, performed the calculations, produced the figures, and wrote an initial draft of the manuscript. T.F. performed some of the calculations for protein distributions. D.O. supervised the research and edited the manuscript. R.G. formulated the research question, supervised the research, and wrote the manuscript with assistance from the co-authors.

Editor: Alexander Berezhkovskii.

Appendix A: Analytic Distribution For Mrna Numbers When $\rho$, $\lambda$, And ${\sigma }_{\text{b}}$ Are Large

Given the large values of ρ, λ, and σ_b, we implement the following parametrization:

$${\sigma }_{\text{b}}\mapsto {\sigma }_{\text{b}}\delta ,\rho \mapsto \rho \delta ,\lambda \mapsto \lambda \delta ,$$

where δ is a large real number.

By means of the method of characteristics, solving (2a), (2b), (2c) is tantamount to seeking a solution to the ordinary differential equation system

$${\partial }_{s}t=1\Rightarrow t=s$$

$${\partial }_{s}z=d\left(z-1\right)\Rightarrow z-1=r{\text{e}}^{ds}$$

$${\partial }_{s}G=\rho \delta \left(z-1\right)G_{11},$$ (17a)

$${\partial }_s{G}_{10}=\rho \delta z{G}_{11}-{\sigma }_{\text{b}}\delta G_{10}-\lambda \delta G_{10}+{\sigma }_{\text{u}}\left(G-G_{10}-G_{11}\right),$$ (17b)

$${\partial }_s{G}_{11}=-\rho \delta G_{11}-{\sigma }_{\text{b}}\delta G_{11}+\lambda \delta G_{10}.$$ (17c)

Dividing δ on both sides of Eqs. 17a, 17b, and 17c, one obtains a singular system consisting of

$$\{\begin{array}{l}\mathit{ϵ}{\partial }_{s}G=\rho \left(z-1\right)G_{11},\\ \mathit{ϵ}{\partial }_s{G}_{10}=\rho z{G}_{11}-{\sigma }_{\text{b}}{G}_{10}-\lambda G_{10}+\mathit{ϵ}{\sigma }_{\text{u}}\left(G-G_{10}-G_{11}\right),\\ \mathit{ϵ}{\partial }_s{G}_{11}=-\rho G_{11}-{\sigma }_{\text{b}}{G}_{11}+\lambda G_{10},\end{array}$$ (18)

with $ϵ=1/\delta \simeq 0$. Expanding G, G₁₀, and G₁₁ in Eq. 18 as a series in powers of $ϵ$,

$$G=G^{\left(0\right)}+\mathit{ϵ}{G}^{\left(1\right)}+\mathcal{O}\left({\mathit{ϵ}}^2\right),G_{10}=G_{10}^{\left(0\right)}+\mathit{ϵ}{G}_{10}^{\left(1\right)}+\mathcal{O}\left({\mathit{ϵ}}^2\right),G_{11}=G_{11}^{\left(0\right)}+\mathit{ϵ}{G}_{11}^{\left(1\right)}+\mathcal{O}\left({\mathit{ϵ}}^2\right),$$

and matching the orders of $ϵ$, we have

$$\text{Order}\text{of}{\mathrm{ϵ}}^0:\{\begin{array}{lll}\rho \left(z-1\right)G_{11}^{\left(0\right)}=0\hfill & \Rightarrow \hfill & G_{11}^{\left(0\right)}=0\hfill \\ \rho z{G}_{11}^{\left(0\right)}-{\sigma }_{\text{b}}{G}_{10}^{\left(0\right)}-\lambda G_{10}^{\left(0\right)}=0\hfill & \Rightarrow \hfill & G_{10}^{\left(0\right)}=0\hfill \end{array}$$

and

$$\text{Order}\text{of}{\mathrm{ϵ}}^1:\{\begin{array}{lll}{\partial }_s{G}^{\left(0\right)}=\rho \left(z-1\right)G_{11}^{\left(1\right)}\hfill & \hfill & \hfill \\ {\partial }_s{G}_{10}^{\left(0\right)}=\rho z{G}_{11}^{\left(1\right)}-{\sigma }_{\text{b}}{G}_{10}^{\left(1\right)}-\lambda G_{10}^{\left(1\right)}+{\sigma }_{\text{u}}\left(G^{\left(0\right)}-G_{10}^{\left(0\right)}-G_{11}^{\left(0\right)}\right)\hfill & \Rightarrow \hfill & \rho z{G}_{11}^{\left(1\right)}-{\sigma }_{\text{b}}{G}_{10}^{\left(1\right)}-\lambda G_{10}^{\left(1\right)}+{\sigma }_{\text{u}}{G}^{\left(0\right)}=0\hfill \\ {\partial }_s{G}_{11}^{\left(0\right)}=-\rho G_{11}^{\left(1\right)}-{\sigma }_{\text{b}}{G}_{11}^{\left(1\right)}+\lambda G_{10}^{\left(1\right)}\hfill & \Rightarrow \hfill & -\rho G_{11}^{\left(1\right)}-{\sigma }_{\text{b}}{G}_{11}^{\left(1\right)}+\lambda G_{10}^{\left(1\right)}=0.\hfill \end{array}$$

Then, we have

$${\partial }_s{G}^{\left(0\right)}=-\frac{\rho u{\sigma }_{\text{u}}}{\rho u-\alpha }{G}^{\left(0\right)},$$

where α = σ_bγ₂/λ, and u = z − 1 =re^ds. Its solution immediately follows as

$$G^{\left(0\right)}=C\left(r\right){\left(\rho r{\text{e}}^{ds}-\alpha \right)}^{-\frac{{\sigma }_{\text{u}}}{d}},$$ (19)

with C(r) being a function of r to be determined from the initial condition. Suppose that the initial condition for this process is $g\left(u\right)={G^{\left(0\right)}|}_{t=0}$, which is known a priori. For instance, say the initial distribution of n mRNA molecules is P(n) = p_n, then g(u) = ∑_np_n(u + 1)ⁿ. Letting s be equal to 0 (or equivalently t = 0), it follows u = r and g(u) = g(r), and we can establish the following relation

$$g\left(r\right)=C\left(r\right){\left(\rho r-\alpha \right)}^{-\frac{{\sigma }_{\text{u}}}{d}},$$

from which we can solve C(r) as

$$C\left(r\right)=g\left(r\right){\left(\rho r-\alpha \right)}^{\frac{{\sigma }_{\text{u}}}{d}}.$$

Substituting the latter back into Eq. 19 and replacing r = ue^−dt, we can calculate the leading-order solution of G from (Eq. 19) as

$$G\left(u\right)=g\left(u{\text{e}}^{-dt}\right){\left(\frac{\rho u{\text{e}}^{-dt}-\alpha }{\rho u-\alpha }\right)}^{\frac{{\sigma }_{\text{u}}}{d}}.$$ (20)

At steady state, the leading-order solution in (Eq. 20) becomes

$$G\left(z\right)={\left(\frac{\alpha }{\alpha -\rho \left(z-1\right)}\right)}^{\frac{{\sigma }_{\text{u}}}{d}},$$

and the corresponding distribution of mRNA numbers is a negative binomial distribution $\text{NB}\left(\frac{{\sigma }_{\text{u}}}{d},\frac{\rho }{\rho +\alpha }\right)$.

Appendix B: Convergence to Telegraph Model for Large $\rho$

To this end, we parametrize ρ as $\rho \mapsto \rho \delta$, where δ is a large real number. As such, (2a), (2b), (2c) can be recast as

$${\partial }_t{G}_0+d\left(z-1\right){\partial }_z{G}_0=-{\sigma }_{\text{u}}{G}_0+{\sigma }_{\text{b}}{G}_{10}+{\sigma }_{\text{b}}{G}_{11},$$ (21a)

$${\partial }_t{G}_{10}+d\left(z-1\right){\partial }_z{G}_{10}+\left({\sigma }_{\text{b}}+\lambda \right)G_{10}-{\sigma }_{\text{u}}{G}_0=\rho \delta z{G}_{11},$$ (21b)

$${\partial }_t{G}_{11}+d\left(z-1\right){\partial }_z{G}_{11}+{\sigma }_{\text{b}}{G}_{11}-\lambda G_{10}=-\rho \delta G_{11}.$$ (21c)

Dividing both sides of Eqs. 21b and 21c by δ and setting ϵ = δ⁻¹, we have that

$$ϵ\left({\partial }_t{G}_{10}+d\left(z-1\right){\partial }_z{G}_{10}+\left({\sigma }_{\text{b}}+\lambda \right)G_{10}-{\sigma }_{\text{u}}{G}_0\right)=\rho z{G}_{11},$$ (22a)

$$ϵ\left({\partial }_t{G}_{11}+d\left(z-1\right){\partial }_z{G}_{11}+{\sigma }_{\text{b}}{G}_{11}-\lambda G_{10}\right)=-\rho G_{11}.$$ (22b)

Again using the same method as before, we expand G₀, G₁₀, and G₁₁ in Eqs. 21a and (22a), (22b) as a series in powers of $ϵ$, collect the terms for ϵ⁰ and ϵ¹, and obtain

$$\text{Order}\text{of}{\mathrm{ϵ}}^0:\{\begin{array}{l}{\partial }_t{G}_0^{\left(0\right)}+d\left(z-1\right){\partial }_z{G}_0^{\left(0\right)}=-{\sigma }_{\text{u}}{G}_0^{\left(0\right)}+{\sigma }_{\text{b}}{G}_{10}^{\left(0\right)}+{\sigma }_{\text{b}}{G}_{11}^{\left(0\right)},\\ \rho z{G}_{11}^{\left(0\right)}=0,\\ \rho G_{11}^{\left(0\right)}=0,\end{array}$$ (23)

and

$$\text{Order}\text{of}{\mathrm{ϵ}}^1:\{\begin{array}{l}{\partial }_t{G}_{10}^{\left(0\right)}+d\left(z-1\right){\partial }_z{G}_{10}^{\left(0\right)}+\left({\sigma }_{\text{b}}+\lambda \right)G_{10}^{\left(0\right)}-{\sigma }_{\text{u}}{G}_0^{\left(0\right)}=\rho z{G}_{11}^{\left(1\right)},\\ {\partial }_t{G}_{11}^{\left(0\right)}+d\left(z-1\right){\partial }_z{G}_{11}^{\left(0\right)}+{\sigma }_{\text{b}}{G}_{11}^{\left(0\right)}-\lambda G_{10}^{\left(0\right)}=-\rho G_{11}^{\left(1\right)}.\end{array}$$ (24)

From Eq. 23, we can solve that $G_{11}^{\left(0\right)}=0$, with which we can further get $\lambda G_{10}^{\left(0\right)}=\rho G_{11}^{\left(1\right)}$ from Eq. 24. Given both results, Eqs. 23 and 24 can be simplified to

$$\{\begin{array}{l}{\partial }_t{G}_0^{\left(0\right)}+d\left(z-1\right){\partial }_z{G}_0^{\left(0\right)}=-{\sigma }_{\text{u}}{G}_0^{\left(0\right)}+{\sigma }_{\text{b}}{G}_{10}^{\left(0\right)},\\ {\partial }_t{G}_{10}^{\left(0\right)}+d\left(z-1\right){\partial }_z{G}_{10}^{\left(0\right)}=\lambda \left(z-1\right)G_{10}^{\left(0\right)}-{\sigma }_{\text{b}}{G}_{10}^{\left(0\right)}+{\sigma }_{\text{u}}{G}_0^{\left(0\right)},\end{array}$$

which are exactly the generating function equations of the telegraph model (see Eqs. A2 and A3 in (29)), thus showing that the multiscale transcriptional bursting model converges to the telegraph model when ρ → ∞. A similar proof can be constructed to show that the telegraph model is also obtained in the limit λ → ∞.

Appendix C: Analytic Marginal Distribution for Protein Numbers for the Multiscale Model in the Limit of Fast mRNA Decay

To the reaction scheme illustrated in Fig. 1 A, we add two reactions: 1) a first-order reaction modeling the translation of mRNA to proteins with rate constant k and 2) a first-order reaction modeling the decay of protein with rate constant d_p. The following coupled master equations describe the time evolution of the probability P_θ(n, m) of finding n mRNAs, m proteins, and gene state D_θ (θ = 0, 10, 11) in a cell:

$$\{\begin{array}{c}{\partial }_t{P}_0\left(n,m\right)=d\left(n+1\right)P_0\left(n+1,m\right)-dn{P}_0\left(n,m\right)+d_{\text{p}}\left(m+1\right)P_0\left(n,m+1\right)-d_{\text{p}}m{P}_0\left(n,m\right)\\ +kn{P}_0\left(n,m-1\right)-kn{P}_0\left(n,m\right)-{\sigma }_{\text{u}}{P}_0\left(n,m\right)+{\sigma }_{\text{b}}{P}_{10}\left(n,m\right)+{\sigma }_{\text{b}}{P}_{10}\left(n,m\right),\\ {\partial }_t{P}_{10}\left(n,m\right)=d\left(n+1\right)P_{10}\left(n+1,m\right)-dn{P}_{10}\left(n,m\right)+d_{\text{p}}\left(m+1\right)P_{10}\left(n,m+1\right)-d_{\text{p}}m{P}_{10}\left(n,m\right)\\ +kn{P}_{10}\left(n,m-1\right)-kn{P}_{10}\left(n,m\right)+{\sigma }_{\text{u}}{P}_0\left(n,m\right)-\left({\sigma }_{\text{b}}+\lambda \right)P_{10}\left(n,m\right)+\rho P_{11}\left(n-1,m\right),\\ {\partial }_t{P}_{11}\left(n,m\right)=d\left(n+1\right)P_{11}\left(n+1,m\right)-dn{P}_{11}\left(n,m\right)+d_{\text{p}}\left(m+1\right)P_{11}\left(n,m+1\right)-d_{\text{p}}m{P}_{11}\left(n,m\right)\\ +kn{P}_{11}\left(n,m-1\right)-kn{P}_{11}\left(n,m\right)+\lambda P_{10}\left(n,m\right)-\left(\rho +{\sigma }_{\text{b}}\right)P_{11}\left(n,m\right).\end{array}$$ (25)

By defining $G_{\theta }={\sum }_n{\sum }_m{z}_{\text{m}}^n{z}_{\text{p}}^m{P}_{\theta }\left(n,m\right)$, solving Eq. 25 is tantamount to seeking solutions to the set of differential equations

$$\{\begin{array}{l}{\partial }_t{G}_0+\left[d\left(z_{\text{m}}-1\right)-k\left(z_{\text{p}}-1\right)z_{\text{m}}\right]{\partial }_{z_{\text{m}}}{G}_0+d_{\text{p}}\left(z_{\text{p}}-1\right){\partial }_{z_{\text{p}}}{G}_0=-{\sigma }_{\text{u}}{G}_0+{\sigma }_{\text{b}}{G}_{10}+{\sigma }_{\text{b}}{G}_{11},\\ {\partial }_t{G}_{10}+\left[d\left(z_{\text{m}}-1\right)-k\left(z_{\text{p}}-1\right)z_{\text{m}}\right]{\partial }_{z_{\text{m}}}{G}_{10}+d_{\text{p}}\left(z_{\text{p}}-1\right){\partial }_{z_{\text{p}}}{G}_{10}={\sigma }_{\text{u}}{G}_0-\left({\sigma }_{\text{b}}+\lambda \right)G_{10}+\rho z_{\text{m}}{G}_{11},\\ {\partial }_t{G}_{11}+\left[d\left(z_{\text{m}}-1\right)-k\left(z_{\text{p}}-1\right)z_{\text{m}}\right]{\partial }_{z_{\text{m}}}{G}_{11}+d_{\text{p}}\left(z_{\text{p}}-1\right){\partial }_{z_{\text{p}}}{G}_{11}=\lambda G_{10}-\left(\rho +{\sigma }_{\text{b}}\right)G_{11}.\end{array}$$ (26)

By means of the method of characteristics, Eq. 26 is equivalently represented as

$${\partial }_{s}t=1,{\partial }_s{z}_{\text{m}}=d\left(z_{\text{m}}-1\right)-k\left(z_{\text{p}}-1\right)z_{\text{m}},{\partial }_s{z}_{\text{p}}=d_{\text{p}}\left(z_{\text{p}}-1\right),$$

and

$$\{\begin{array}{l}{\partial }_s{G}_0=-{\sigma }_{\text{u}}{G}_0+{\sigma }_{\text{b}}{G}_{10}+{\sigma }_{\text{b}}{G}_{11},\\ {\partial }_s{G}_{10}={\sigma }_{\text{u}}{G}_0-\left({\sigma }_{\text{b}}+\lambda \right)G_{10}+\rho z_{\text{m}}{G}_{11},\\ {\partial }_s{G}_{11}=\lambda G_{10}-\left(\rho +{\sigma }_{\text{b}}\right)G_{11}.\end{array}$$

Assuming that mRNA decays much faster than protein such that ${\partial }_s{z}_{\text{m}}\simeq 0$ ((21a), (21b), (21c)), we get that

$$z_{\text{m}}=\frac{1}{1-bv},\text{and}v=z_{\text{p}}-1,$$ (27)

and b = k/d is the mean translational burst size. Using Eq. 27, we can reduce Eq. 26 to

$$v{\partial }_v{G}_0=-{\tilde{\sigma }}_{\text{u}}{G}_0+{\tilde{\sigma }}_{\text{b}}{G}_{10}+{\tilde{\sigma }}_{\text{b}}{G}_{11},$$ (28a)

$$v{\partial }_v{G}_{10}={\tilde{\sigma }}_{\text{u}}{G}_0-\left({\tilde{\sigma }}_{\text{b}}+\tilde{\lambda }\right)G_{10}+\frac{\tilde{\rho }}{1-bv}{G}_{11},$$ (28b)

$$v{\partial }_v{G}_{11}=\tilde{\lambda }{G}_{10}-\left(\tilde{\rho }+{\tilde{\sigma }}_{\text{b}}\right)G_{11},$$ (28c)

where ${\tilde{\sigma }}_{\text{b}}$, ${\tilde{\sigma }}_{\text{u}}$, $\tilde{\rho }$, and $\tilde{\lambda }$ are kinetic parameters normalized with respect to protein degradation rate d_p. It follows from summing (28a), (28b), (28c) that

$$G_{11}=\frac{\left(1-bv\right){\partial }_{v}G}{\tilde{\rho }b}.$$ (29)

Using the definitions $b_1={\tilde{\sigma }}_{\text{b}}+{\tilde{\sigma }}_{\text{u}}$ and $b_2={\tilde{\sigma }}_{\text{b}}+\tilde{\lambda }+\tilde{\rho }$ and plugging Eq. 29 into Eqs. 28b and 28c, it gives us that

$$\left(1-bv\right)v^2{\partial }_v^{3}G+\left[1+b_1+b_2-bv\left(3+b_1+b_2\right)\right]v{\partial }_v^{2}G+\left\{b_1{b}_2-bv\left[\left(1+b_1\right)\left(1+b_2\right)+\tilde{\lambda }\tilde{\rho }\right]\right\}{\partial }_{v}G-b{\tilde{\sigma }}_{\text{u}}\tilde{\lambda }\tilde{\rho }G=0,$$

which admits a solution

$$G\left(v\right){=}_3^{}{F}_2\left(a_1,a_2,a_3;b_1,b_2;bv\right),$$ (30)

with a₁, a₂, and a₃ being roots of

$$\{\begin{array}{l}{a}_1{a}_2{a}_3={\tilde{\sigma }}_{\text{u}}\tilde{\lambda }\tilde{\rho },\\ a_1+a_2+a_3=b_1+b_2,\\ a_1{a}_2+a_1{a}_3+a_2{a}_3=b_1{b}_2+\tilde{\lambda }\tilde{\rho }.\end{array}$$

Hence, summarizing, Eq. 30 and $P\left(m\right)={(1/m!){\text{d}}^{m}G\left(v\right)/\text{d}{v}^m|}_{v=-1}$ define the steady-state distribution of protein numbers, which is

$$P\left(m\right)=\frac{b^m}{m!}\frac{{\left(a_1\right)}_n{\left(a_2\right)}_n{\left(a_3\right)}_n}{{\left(b_1\right)}_n{\left(b_2\right)}_n}{}_3^{}{F}_2\left(a_1+n,a_2+n,a_3+n;b_1+n,b_2+n;-b\right),$$

given that mRNA is short lived.

Next, we will show the solution Eq. 30 converges to the Gaussian hypergeometric function (₂F₁) for the three-stage gene expression model (21) when ρ is large. To this end, we parameterize $\tilde{\rho }$ in Eqs. 28b and 28c as $\tilde{\rho }\mapsto \tilde{\rho }\delta$, where δ is a large number. Dividing both sides of Eqs. 28b and 28c by δ, we have

$$ϵ\left(v{\partial }_v{G}_{10}-{\tilde{\sigma }}_{\text{u}}{G}_0+\left({\tilde{\sigma }}_{\text{b}}+\tilde{\lambda }\right)G_{10}\right)=\frac{\tilde{\rho }}{1-bv}{G}_{11},$$ (31a)

$$ϵ\left(v{\partial }_v{G}_{11}-\tilde{\lambda }{G}_{10}+{\tilde{\sigma }}_{\text{b}}{G}_{11}\right)=-\tilde{\rho }{G}_{11},$$ (31b)

where $ϵ=1/\delta \simeq 0$. Again similarly, we expand G₀, G₁₀, and G₁₁ in Eqs. 28a and (31a), (31b) as a series in powers of $ϵ$, collect the terms for $ϵ$⁰ and $ϵ$¹, and obtain

$$\text{Order}\text{of}{\mathit{ϵ}}^0:\{\begin{array}{l}v{\partial }_v{G}_0^{\left(0\right)}=-{\tilde{\sigma }}_{\text{u}}{G}_0^{\left(0\right)}+{\tilde{\sigma }}_{\text{b}}{G}_{10}^{\left(0\right)}+{\tilde{\sigma }}_{\text{b}}{G}_{11}^{\left(0\right)},\\ \frac{\tilde{\rho }}{1-bv}{G}_{11}^{\left(0\right)}=0,\\ \tilde{\rho }{G}_{11}^{\left(0\right)}=0,\end{array}$$ (32)

and

$$\text{Order}\text{of}{\mathit{ϵ}}^1:\{\begin{array}{l}v{\partial }_v{G}_{10}^{\left(0\right)}-{\tilde{\sigma }}_{\text{u}}{G}_0^{\left(0\right)}+\left({\tilde{\sigma }}_{\text{b}}+\tilde{\lambda }\right)G_{10}^{\left(0\right)}=\frac{\tilde{\rho }}{1-bv}{G}_{11}^{\left(1\right)},\\ v{\partial }_v{G}_{11}^{\left(0\right)}-\tilde{\lambda }{G}_{10}^{\left(0\right)}+{\tilde{\sigma }}_{\text{b}}{G}_{11}^{\left(0\right)}=-\tilde{\rho }{G}_{11}^{\left(1\right)},\end{array}.$$ (33)

From Eq. 32, we get $G_{11}^{\left(0\right)}=0$, which is used to reduce Eq. 33 and the first equation in Eq. 32 to

$$\{\begin{array}{l}v{\partial }_v{G}_0^{\left(0\right)}=-{\tilde{\sigma }}_{\text{u}}{G}_0^{\left(0\right)}+{\tilde{\sigma }}_{\text{b}}{G}_{10}^{\left(0\right)},\\ v{\partial }_v{G}_{10}^{\left(0\right)}={\tilde{\sigma }}_{\text{u}}{G}_0^{\left(0\right)}-{\tilde{\sigma }}_{\text{b}}{G}_{10}^{\left(0\right)}+\frac{\tilde{\lambda }bv}{1-bv}{G}_{10}^{\left(0\right)}.\end{array}$$ (34)

Note that Eq. 34, which is the leading order of (28a), (28b), (28c), is exactly the same as the generating functions of the three-stage gene expression model reported in (21) (see Eqs. 68–69). By means of similar arguments, one can show the reduction of our model when λ is large.