A study of the nonlinear dynamics of human behavior and its digital hardware implementation

Graphical abstract

Abstract

This paper introduces an intensive discussion for the dynamical model of the love triangle in both integer and fractional-order domains. Three different types of nonlinearities soft, hard, and mixed between soft and hard, are used in this study. MATLAB numerical simulations for the different three categories are presented. Also, a discussion for how the kind of personalities affects the behavior of chaotic attractors is introduced. This paper suggests some explanations for the complex love relationships depending on the impact of memory (IoM) principle. Lyapunov exponents, Kaplan-Yorke dimension, and bifurcation diagrams for three different integer-order cases show a significant dependency on system parameters. Hardware digital realization of the system is done using the Xilinx Artix-7 XC7A100T FPGA kit. Version 14.7 from the Xilinx ISE platform is used in both Verilog simulation and hardware implementation stages. The digital approach of such a system opens the door to predict the love relation after sensing the human personality. Also, this study will help in justifying more human emotions like happiness, panic, and fear accurately. Perhaps shortly, this study may combine with artificial intelligence to demonstrate Human-Computer interaction products.

1. Introduction

Fractional calculus is a mathematical topic that deals with integral and derivative for complex/real orders [1], [2]. It is considered the general form of integer calculus. This topic opens the door for researchers to design and control systems with an additional degree of freedom, which is the derivative order [3]. Applications based on fractional calculus in engineering and physics fields are taking researchers concerns [4] such as information sciences [5], health care [6], oscillators [7], neuron models [8], filters [9], [10] and chaotic systems [11], [12].

Fractional-order operators can be divided into two main types, derivatives and integral operators. Different operators are presented in [13]. Fractional-order differential operators can be obtained using various techniques, Grünwald-Letnikov (GL), Riemann-Liouville and Caputo [14], [15], [16]. In this paper GL method mentioned in [1] is used, this is defined by:

$${}_a{D}_t^{\alpha }x(t)={\displaystyle \underset{h\to 0}{\lim }}[\frac{1}{h^{\alpha }}{\displaystyle \sum _{k=0}^{[\frac{t-a}{h}]}}{w}_k^{(\alpha )}x(t-\mathit{kh})]$$ (1)

while the binomial coefficients $w_k^{(\alpha )}$ are calculated by:

$$w_0^{(\alpha )}=1,w_k^{(\alpha )}=(1-\frac{\alpha +1}{k})w_{k-1}^{(\alpha )},k=1,2,3,\dots \text{.}$$ (2)

A small modification is done to be able to implement the GL operator using FIR form with length L to reach an approximate formula [1]

$${}_{t-L}{D}_t^{\alpha }x(t)=\frac{1}{h^{\alpha }}{\displaystyle \sum _{k=0}^L}{w}_k^{(\alpha )}x(t-\mathit{kh}),$$ (3)

where h and L are the size of step and window respectively.

Fractional-order operator has been implemented based on different approaches. Finite and Infinite Impulse Response filters (FIR, IIR) have been used to implement the fractional-order operator using polynomial functions [17], [18]. Three techniques have been proposed to calculate the fractional-order derivative/integral using power series expansion PSE [19]. Caputo derivative and GL were digitally implemented using different techniques based on Verilog HDL in [20], [21], [22], [23], [24]. In [20], window approach was used in fractional-order GL derivative implementation on FPGA to build a fractional-order chaotic system. A combination between the fixed-window method and a linear equation was used to realize the GL operator in [21]. This system was used to construct a fractional-order PID controller in [23]. In [24], Two algorithms were introduced to implement the fractional-order differentiator and integrator using the quadratic and Piece-Wise Linear PWL approach.

Lorenz firstly described the chaos phenomenon in 1963 [25]; the butterfly attractor was explained, which is considered a simplified model for the atmospheric convection [26]. Many chaotic systems introduced later with full-study to their behaviors. Rössler system was offered in [27], which consists of three fractional-order equations. Different systems were presented sequentially, Chua’s circuit [28], Chen attractor [29], and Liu system [30]. Both conventional chaotic and hyper-chaotic structures are nonlinear systems. However, the difference between them is that the first system has only one positive Lyapunov exponent, where the second one has more than one positive exponents [31]. These systems are employed in describing the dynamics of real natural phenomena [25], [32]. In [33], a modified Vallis temperature fluctuations model was described in detail. Generally, chaotic attractors are irregular and unpredictable; any small deviation in the parameters may lead to a new strange attractor[26]. These features make chaotic systems suitable to be used as a pseudo-random number generators (PRNG) in encryption applications [34].

Human is the miracle that psychologists all over the world try to discover his behaviors, and find a scientific explanation for them. Since the second half of the last century, many researchers applied complicated mathematical equations to model different human feelings [35], [36]. Analysis of panic and how to scape it was done in [37], which helped engineers to reduce the scale of disasters. In this life, happiness is still the main target that humankind is seeking; many authors participated in explaining this sophisticated dynamical process for the sake of achieving this goal [38], [39]. Love is considered one of the fundamental reasons for happiness, and modeling of love emotions takes many concerns at the end of the 90th decade. In 1986, Sternberg defined sides of the love triangle as intimacy, commitment, and passion[40]. Strogatz modeled Romeo and Juliet romance relation using two elementary differential equations [41]. Different exercises were discussed based on Strogatz’s models by Radzicki [36]. The effect of random noise on complex variables was used to model another couple-romantic relationship [42], [43]. In 2007, Wajdi et al. discussed different cases of both integer and fractional-order dynamical models of the love triangle [44].

Chaos generators can be implemented in either analog or digital schemes like Lorenz, Chua and the modified four-order Wei’s systems that were proposed in [45], [46], [47], [48]. In [45], [46], both Chua and the modified Lorenz chaotic systems were implemented using analog current amplifiers, CMOS transistors, current mirrors, and switches. However, Chua circuit based chaotic systems presented in [47] were implemented based on analog circuits using capacitors, resistors, multipliers, and operational amplifiers. In [47], the state variables of the system differential equations were stored in capacitors, where the design is built based on operational amplifiers. The drawbacks of using analog components are the limitations on power supply voltages, inaccuracy of setting the initial conditions, and sensitivity to process variations and temperature. Also, analog circuit implementations need a large on-chip area for the capacitor to store the system state. Moreover, it is difficult to control the initial condition (voltage) of the capacitor. On the other hand, these problems are overcome by the chaotic digital systems, which improve the performance, area, and power. Besides, the state variables are stored in registers where there is no need for large capacitors [20], [49]. In this work, the FPGA design methodology is used to implement the proposed chaos generator.

The objectives of this paper can be summarized into three main points, as illustrated in Fig. 1. The first point is the integer-order representation; it shows the relationship behavior at different parameters, i.e., different human personalities. These effects are found after stimulating the system using different types of nonlinearities. Bifurcation diagrams for integer-order cases are depicted to stand for the chaotic region accurately. Also, Lyapunov exponents are calculated for these models to show the change in the system complexity with the different nonlinearities. The second objective is to propose the fractional-order model of love with an intensive study to the impact of the memory for any individual. This study may help in giving some psychological explanations to these complex relations. Also, it shows the dependency between future human behavior and his experience. Finally, both integer and fractional-order models are digitally realized on a Xilinx FPGA kit.

Fig. 1.

Objectives of the paper.

This paper is organized as follows: theoretical analysis and MATLAB simulations for integer-order different cases of love triangle model are discussed in Section 2. Also, the effect of parameter modifications on human behavior, Lyapunov exponents, and bifurcation diagrams for the different situations are presented. In Section 3, the general fractional-order love triangle model with added three different nonlinearities (soft, hard, and mixed) are addressed. Also, the effect of varying system parameters on attractor conduct. Section 4 proposes the hardware FPGA implementation for different integer and fractional-order cases. The experimental outcomes are displayed in Section 5. The last section concludes this work.

2. Integer-order love models

In this section, the mathematical modeling of some complicated human love behaviors in integer-order form is introduced.

2.1. Model nonlinearities and parameters effect

Human behavior is tough to anticipate, especially when it comes to feelings. However, in [50], Sprott introduced a system of differential equations that model love or hate mechanisms. The model starts with describing the linear relation between two individuals as follows [50]:

$$\frac{{\mathit{dx}}_R}{\mathit{dt}}={\mathit{ax}}_R+{\mathit{bx}}_J,$$ (4)

$$\frac{{\mathit{dx}}_J}{\mathit{dt}}={\mathit{cx}}_R+{\mathit{dx}}_J,$$ (5)

where $x_R$ and $x_J$ represent Romeo’s love for Juliet and vice versa. Also, (a,b) and (c,d) are constants specifying Romeo’s and Juliet’s romantic styles, respectively [50]. These constants values determine the romantic styles of each individual, as suggested and named by Strogatz [26]. The difference between constant values refers to different personalities [39]. These styles were divided into four categories, as follows:

• (1)$(a>0,b>0)$ , the $\mathit{Eagerbeaver}$: where the individual is inspired by his feelings.
• (2)$(a>0,b<0)$ , the $\mathit{Narcissisticnerd}$: where the individual wants more of his feeling but retreats from the other individual feelings.
• (3)$(a<0,b>0)$ , the $\mathit{Cautiouslover}$: where the individual retreats from his feelings. However, the other individual is encouraging him.
• (4)$(a<0,b<0)$ , the Hermit: both individuals retreat from their feelings.

The previous model was elevated in [50] to involve more complicated relations, such as the love triangle shown in Fig. 2(a). This model was originally representing the love triangle between Romeo (R) with Juliet (J) and Guinevere (G) with the assumption that J and G do not know each other’s [50]. The four romantic styles can be applied to the triangle [26]. This model can be represented by both linear and nonlinear differential equations [51], [26]. Following the same steps in [50], the nonlinearities are divided into three main types: soft, hard, and mixed, which leads to three different systems, as discussed below. Fig. 2(b) represents both soft logistic and hard signum functions that used as nonlinearities and defined by:

$$\mathit{nonlinearities}\left\{\begin{array}{cc}u(x)=x(1-|x|),\hfill & \mathrm{soft}\mathrm{logistic}\hfill \\ v(x)=\mathit{sgn}(x).\hfill & \mathrm{hard}\mathrm{signum}\hfill \end{array}\right)$$ (6)

The insertion of these nonlinearities into the love triangle model is very useful and interesting. On the one hand, to discuss the effect of smooth changes of a person’s emotions (logistic function). On the other hand, to study how the abrupt change (signum nonlinearity) in these sentiments affect human behavior (moody personalities). Generally, three numerical solution methods can be used to solve the system integer differential equations, Runge-Kutta fourth-order, mid-point, and Euler techniques [52]. In this work, the Euler method is used to obtain the solution of different cases.

Fig. 2.

(a) Love Triangle between Romeo (R), Juliet (J) and Guinevere (G) (b) Soft and Hard nonlinearities.

General annotations in this section, firstly, all sets of parameters in all simulated cases are representing “cautious lover” Guinevere and Romeo, and “narcissistic nerd” Juliet. Any other case in the above mentioned four categories does not give a chaotic behavior. This identity pushes us to ask an important question; why does the chaos phenomenon appear only in this category? The justification of this question refers to, in both “Eagerbeaver” and “Hermit” cases, the human feeling is stable either love or hate. On the contrary to the other two styles, which includes a flounder in the relationship. This swinging leads to the chaotic behavior that will be discussed. Another important note, for any model, all emotions are stimulated by external circumstances $(x(t)\ne 0)$. Finally, all attractors are simulated at the same time interval. Also, at $t=0$, the color is very dark, and it becomes lighter as time passes. This notation is essential to track the transitions in any phase attractor through the whole paper.

2.1.1. Soft nonlinearity

Soft nonlinearity can be expressed simply using the logistic function. The integer-order system that describes the love triangle between $R,J$, and G can be written as follows:

$$\frac{{\mathit{dx}}_{R_J}}{\mathit{dt}}={\mathit{ax}}_{R_J}+\mathit{bu}(x_J-x_G),$$ (7a)

$$\frac{{\mathit{dx}}_J}{\mathit{dt}}=\mathit{cu}(x_{R_J})+{\mathit{dx}}_J,$$ (7b)

$$\frac{{\mathit{dx}}_{R_g}}{\mathit{dt}}={\mathit{ax}}_{R_g}+\mathit{bu}(x_G-x_J),$$ (7c)

$$\frac{{\mathit{dx}}_G}{\mathit{dt}}=\mathit{eu}(x_{R_g})+{\mathit{fx}}_G\text{.}$$ (7d)

where $x_J$ and $x_G$ represent both Juliet’s and Guinevere’s love for Romeo, respectively. While, $x_{R_j}$ and $x_{R_g}$ represent Romeo’s feelings towards Juliet and Guinevere, respectively. Two more equations are added to the original love model to describe Guinevere’s romantic style between her and Romeo. This style is represented by constants (e, f) while Romeo’s feeling towards Guinevere has the same constants (a,b). The positive sign in all parameters is assigned to a love relationship, while the negative sign is referring to hate. However, different values with the same romantic style indicate different human personalities.

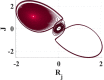
The solution of these equations is found simply using Euler method [52]. The change in system parameters may cause complicated and unpredictable love behavior. This feeling can be translated into a chaotic attractor. Whereas, this change may affect the relation to be smooth and go out of the chaotic range. The case with (a,b) = (−3,4), (c,d) = (−7,2) represents the romantic style “cautious lover” for both R and J, while (e,f) = (2,−1) represents a “narcissistic nerd” for G. Parameters $a,b,d$ and e have a strong effect on the system behavior, and any small change will cause the system to be non-chaotic (stable relationship). However, a minor change in $f,c$ leads to different chaotic behaviors. Table 1 shows the system behavior versus changing the parameter $f,c$ and the step size h with initial values ($x_{R_j},x_J,x_{R_g},x_G$)=(0.1,0,0.1,0). Decreasing value of f from $-1$ to $-2$ leads to refreshment in the relationship which appears as a reduction in the number of attractor lines as shown in Table 1. However, if $f<-2$ the system will be non-chaotic. The variation in the parameter c between $-7$ and $-9$ gives the double ring attractor. At $c=-9$, an exotic diagram generated, and lines smudge one ring while the other one is clear. When $c⩽-9$, the relationship becomes quite without any problems. The last row in the table shows the behavior of the system with a reduction of step size h. In this model with soft nonlinearities, the system gives strange attractors at minimal values for h, approximately zero.

Table 1.

Effect of changing parameters $(f,c)$ and h on system behavior for integer soft nonlinearities.

Effect of f	$f=-1$	$f=-1.5$	$f=-2$
$(a,b)=(-3,4)$, $(c,d)=(-7,2)$, $e=2$
Effect of c	$c=-7$	$c=-8$	$c=-9$
$(a,b)=(-3,4)$, $d=2$, $(e,f)=(2,-1)$
Effect of step h	$h=2^{-10}$	$h=2^{-11}$	$h=2^{-12}$
$(a,b)=(-3,4)$, $(c,d)=(-7,2)$, $(e,f)=(2,-1)$

2.1.2. Hard nonlinearity

In hard non-linearity, a signum function is used instead of the logistic function represented in Eq. (7a), (7b), (7c), (7d). The new form that describes the love triangle will be:

$$\frac{{\mathit{dx}}_{R_J}}{\mathit{dt}}={\mathit{ax}}_{R_J}+\mathit{bv}(x_J-x_G),$$ (8a)

$$\frac{{\mathit{dx}}_J}{\mathit{dt}}=\mathit{cv}(x_{R_J})+{\mathit{dx}}_J,$$ (8b)

$$\frac{{\mathit{dx}}_{R_g}}{\mathit{dt}}={\mathit{ax}}_{R_g}+\mathit{bv}(x_G-x_J),$$ (8c)

$$\frac{{\mathit{dx}}_G}{\mathit{dt}}=\mathit{ev}(x_{R_g})+{\mathit{fx}}_G\text{.}$$ (8d)

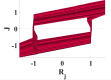
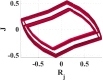
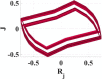
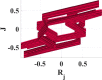
Similar to the soft non-linearity, positive signs for $(a,b,c,d,e$ and f) represent love relationship while negative signs for hate. Euler method is used to solve these differential equations; attractors that describe the relation between $x_{R_j}$ and $x_J$ can be plotted by MATLAB. Table 2 represents the effect of varying a (personal mode) with respect to step size h on the system behavior. In this case, external circumstances stimulate the relationship, i.e., initial values ($x_{R_j},x_J,x_{R_g},x_G$) =(-0.4141,-0.2612,0.4141,0.0486) under condition of constancy other parameters $b,c,d,e$ and f on (10,-5,2,1,-5). From Table 2, if $h>=2^{-3}$, the system will not show chaotic behavior. When h gradually decreased to be close to zero, complex attractors start to appear. As a result of hard nonlinearity used in this model, sharp changes in dynamics are introduced, and it appears with decreasing the value of parameter a. More complicated attractors are illustrated in the last row in Table 2. It shows a wider chaotic range for the parameter a in case $h=2^{-4}$ on the contrary of $h=2^{-3}$ when the parameter a has a smaller range. Decreasing a is to be lower than $-30$ with step size $=2^{-4}$, the model will be stable. A brief conclusion from Table 2 that parameter a is the most sensitive variable and any minor variation in it, causes a new attractor. This phenomenon refers to the direct relationship between Romeo’s feelings - i.e. parameters $(a)$- and both Juliet and Guinevere emotions. As per the assumption that Guinevere and Juliet do not know each other, variations in both Juliet and Guinevere moods slightly affect the relationship on the contrary from Romeo’s sentiments, which can change the whole relationship.

Table 2.

Effect of changing parameters $(a,h)$ on system behavior with integer hard nonlinearities at $b=10,c=-5,d=3,e=1$ and $f=-5$.

	$h=2^{-3}$	$h=2^{-4}$	$h=2^{-5}$
$a=-3$
$a=-5$
$a=-10$
$a=-13$
	$a=-20$	$a=-25$	$a=-30$
$h=2^{-4}$

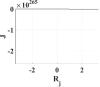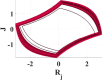2.1.3. Mixed nonlinearity

A mixture of soft and hard nonlinearities is derived. R dynamics are assumed to be soft; on the other hand, J and G dynamics are hard.

$$\frac{{\mathit{dx}}_{R_J}}{\mathit{dt}}={\mathit{ax}}_{R_J}+\mathit{bu}(x_J-x_G),$$ (9a)

$$\frac{{\mathit{dx}}_J}{\mathit{dt}}=\mathit{cv}(x_{R_J})+{\mathit{dx}}_J,$$ (9b)

$$\frac{{\mathit{dx}}_{R_g}}{\mathit{dt}}={\mathit{ax}}_{R_g}+\mathit{bu}(x_G-x_J),$$ (9c)

$$\frac{{\mathit{dx}}_G}{\mathit{dt}}=\mathit{ev}(x_{R_g})+{\mathit{fx}}_G\text{.}$$ (9d)

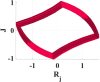
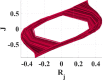
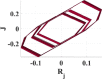
Following the same steps in the two previous integer cases. Using Euler method to solve Eq. (9a), (9b), (9c), (9d) whether the relationship is influenced by initial external motivations ($x_{R_j},x_J,x_{R_g},x_G$) = (−0.241,−0.612,0.241,0.086) with ($b,c,d,e$ and f) = (20,−5,3,0.5,−1). Table 3 illustrates the change of parameter a versus the step size h, and its effect on system attractor between $x_{R_j}$ and $x_J$. The system attractor does not suffer from a massive change if parameter a is larger than $-25$. However, decreasing a to be less than $-25$, the dynamical behavior of the system will depend on the value of step size h. At $h=2^{-4}$, new attractors are generated. However, the system will go out of the chaotic region if parameter $a<=-25$ at $h=2^{-5}$ or $2^{-6}$. The impressive annotation in Table 3 is the refractions in attractor lines. These lines are smoother than in the hard model but still not as smooth as soft nonlinearity.

Table 3.

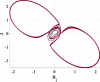
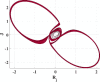
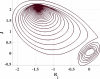
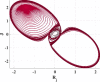
Effect of changing parameters $(a)$ with respect to step size h on the system behavior for integer Mixed nonlinearity at $b=20,c=-5,d=3,e=0.5$ and $f=-1$. Also, effect of changing Window $(L)$ on system behavior for fractional soft nonlinearities at $a=-3,b=4,c=-7,d=2,e=2$ and $f=-1$ with $h=2^{-9}\mathrm{and}h=2^{-10}$.

	$h=2^{-4}$	$h=2^{-5}$	$h=2^{-6}$
$a=-10$
$a=-25$
$a=-30$
	$L=14$	$L=15$	$L=16$
$h=2^{-9}$
	$L=25$	$L=30$	$L=35$
$h=2^{-10}$

2.2. Bifurcation diagram

An interesting fact has been shown in the previous discussion, that Romeo’s parameters have the greatest effect on the chaotic phase attractor, especially parameter a. This fact can be referred to the main concept of the love triangle, which R is considered the focal point that interacts with both J and G. This subsection introduces a full study for the bifurcation diagrams for different love triangle models against system parameters. Fig. 3 illustrates the bifurcation of both soft and hard integer nonlinearities. Fig. 3(a) and (b) show the bifurcation diagrams for Romeo towards Juliet feelings $R_j$ in soft nonlinearities case against parameters c and f. These figures meet the identity represented in Table 1, which is the narrow domain of parameters c and f that give a strange double ring chaotic attractor. The parameter c approximately varies from $-7$ to $-9.7$ to give an erratic action while parameter f can be changed in the space from $-0.9$ to $-2.3$. The remarkable change between Fig. 3(c) and (d) returns to the different values of h from $2^{-3}$ to $2^{-4}$. Bifurcation diagrams affirm the results showed in Table 2 in Section 2. The range of parameter a that generates chaotic attractors is wider when $h=2^{-4}$ than in $h=2^{-3}$.

Fig. 3.

(a) and (b) Bifurcation diagrams for integer soft case while (a) parameter c at $(a,b,d,e,f,h)=(-3,4,2,2,-1,2^{-10})$ (b) parameter f at $(a,b,c,d,e,h)=(-3,4,-7,2,2,2^{-10})$. Figures (c) and (d) for integer hard case for parameter a at $(b,c,d,e,f,h)$ (c) $(10,-5,3,1,-5,2^{-3})$ (d) $(10,-5,3,1,-5,2^{-4})$.

2.3. Maximum Lyapunov exponent

Lyapunov exponent (LE) is considered one of the essential parameters for dynamical system characterization. It is a direct measurement of the divergence rate of the nearby trajectories. Positive LEs indicate the chaotic behavior of the system. Maximal Lyapunov exponent (MLE) can be calculated using different algorithms, such as the Jacobian method or neural networks algorithm [53], [54]. In this study, the LEs calculation process is done using the popular Wolf way [55].

LEs for the integer-order love triangle model with different nonlinearities (soft, hard, and mixed) are numerically found. Fig. 4 shows the Lyapunov exponents for the three different cases. LE coefficients for soft nonlinearity in Fig. 4(a) are equal to ${\lambda }_1=0.39,{\lambda }_2=-0.0007,{\lambda }_3=-2.39,{\lambda }_4=-3$. Since the MLE (0.39) is positive, so the system is chaotic. The Kaplan-Yorke dimension, in this case, can be calculated by:

$$D_{\mathit{KY}}=n+\frac{{\lambda }_1+\dots +{\lambda }_n}{|{\lambda }_{n+1}|}\text{.}$$ (10)

while n is the largest integer number for which ${\lambda }_1+\dots +{\lambda }_n⩾0$. So, in the soft case $D_{\mathit{KY}}=2.16$.

Fig. 4.

Lyapunov exponents for (a) soft integer nonlinearities at $(a,b,c,d,e,f$) = (−3,4,−7,2,2,−1) (b) mixed integer nonlinearities at $(a,b,c,d,e,f$) = (−10,20,−5,3,0.5,−1) (c) and (d) for hard nonlinearities with $(a,b,c,d,e,f$) = (−10,10,−5,3,1,−5) and (−5,10,−5,2,1,−1), respectively. (e) Lyapunov exponents variations with parameter a in integer soft model of the love triangle.

Both mixed and hard nonlinearities have shown a great difference from the soft one because of the Signum function. For mixed case, Lyapunov exponents are ${\lambda }_1=3.01,{\lambda }_2=-1,{\lambda }_3=-10,{\lambda }_4=-10.01$ as illustrated in Fig. 4(b), and the Kaplan-Yorke dimension for the system is $D_{\mathit{KY}}=2.2$. In hard nonlinearity, the effect of changing system parameters on LE components appears in Fig. 4(c) and (d). Exponents in Fig. 4(c) are ${\lambda }_1=3,{\lambda }_2=-5,{\lambda }_3=-10,{\lambda }_4=-10$ at parameters $(a,b,c,d,e,f$) = ($-10,10,-5,3,1,-5$). However, if these parameters are changed to $(-5,10,-5,2,1,-1)$, LEs will be changed to ${\lambda }_1=2,{\lambda }_2=-1,{\lambda }_3=-5,{\lambda }_4=-5$ as depicted in Fig. 4(d). Fig. 4 shows the great dependency between Lyapunov exponents and system parameters $a,c$ and f while the $D_{\mathit{KY}}$ for these cases = $1.6$ and $2.2$, respectively. To follow the change in LEs with parameter variation in the soft nonlinearity model, Fig. 4(e) is established with sweeping on the parameter a between range $[-13,-3]$. It illustrates that when $a<-3$, the system is stable, and it does not have a chaotic behavior. This because all $\lambda$s are negative. At $a=-3$, it gives a positive MLE and the ${\sum }_n^{}{\lambda }_n<0$. This means a dissipative chaotic attractor will be generated.

3. Fractional-order models

Generally, the fractional-order system of four differential equations can be represented by:

$$D^{\alpha }{x}_{R_j}=P(x_{R_j},x_J,x_{R_g},x_G,t),$$ (11a)

$$D^{\beta }{x}_J=Q(x_{R_j},x_J,x_{R_g},x_G,t),$$ (11b)

$$D^{\gamma }{x}_{R_g}=R(x_{R_j},x_J,x_{R_g},x_G,t)\text{.}$$ (11c)

$$D^{\eta }{x}_G=V(x_{R_j},x_J,x_{R_g},x_G,t)\text{.}$$ (11d)

To simulate any system using GL definition, the following equations are usually used [56]:

$$x_{R_j,t_m}=P\left(x_{R_j}\left(t_{m-1}\right),x_J\left(t_{m-1}\right),x_{R_g}\left(t_{m-1}\right),x_G\left(t_{m-1}\right)\right)h^{\alpha }-\sum _{k=1}^n{w}_k^{\left(\alpha \right)}{x}_{R_j}\left(t_{m-k}\right),$$ (12a)

$$x_{J,t_m}=Q\left(x_{R_j}(t_{m-1}),x_J(t_{m-1}),x_{R_g}(t_{m-1}),x_G(t_{m-1})\right)h^{\beta }-{\displaystyle \sum _{k=1}^n}{w}_k^{(\beta )}{x}_J(t_{m-k}),$$ (12b)

$$x_{R_g,t_m}=R\left(x_{R_j}(t_{m-1}),x_J(t_{m-1}),x_{R_g}(t_{m-1}),x_G(t_{m-1})\right)h^{\gamma }-{\displaystyle \sum _{k=1}^n}{w}_k^{(\gamma )}{x}_{R_g}(t_{m-k}),$$ (12c)

$$x_{G,t_m}=V\left(x_{R_j}(t_{m-1}),x_J(t_{m-1}),x_{R_g}(t_{m-1}),x_G(t_{m-1})\right)h^{\eta }-{\displaystyle \sum _{k=1}^n}{w}_k^{(\eta )}{x}_G(t_{m-k})\text{.}$$ (12d)

where n equals to either window size L for GL approximated approach used in calculations or m for the entire state memory.

The different values of the love triangle model parameters, $a,b,c,d,e,f$, window size L and step function h affect on the behavior of the relationship. In this subsection, the impact of memory (IoM) and the effect of previous human experience on the relation are discussed. This impact is described by the fractional-order of an individual $\alpha ,\beta ,\gamma ,\eta$. There is a direct relation between the order value and the IoM, so it increases while the order increases. On the other hand, if the IoM of a human is low, so his/her future influence by experience will be very weak [39]. Also, in this subsection, the system response with different nonlinearities is considered.

3.1. Soft nonlinearity

The GL approximation of the fractional derivative is a common technique used in solving fractional-order differential equations. By applying The GL on the soft nonlinear equations:

$$\frac{d^{\alpha }{x}_{R_J}}{\mathit{dt}}={\mathit{ax}}_{R_J}+\mathit{bu}(x_J-x_G),$$ (13a)

$$\frac{d^{\beta }{x}_J}{\mathit{dt}}=\mathit{cu}(x_{R_J})+{\mathit{dx}}_J,$$ (13b)

$$\frac{d^{\gamma }{x}_{R_g}}{\mathit{dt}}={\mathit{ax}}_{R_g}+\mathit{bu}(x_G-x_J),$$ (13c)

$$\frac{d^{\eta }{x}_G}{\mathit{dt}}=\mathit{eu}(x_{R_g})+{\mathit{fx}}_G\text{.}$$ (13d)

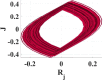
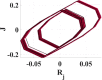
The window function plays a vital role in the output behavior in fractional-order systems, as appeared in Table 3. Window means the limit of the previous human past experience that will be taken into consideration. At certain personalities, changing window function L leads to different chaotic behavior. Table 3 shows that when $L<14$ at step size $h=2^{-9}$, the relation will be stable. At $L=14$, which means the human experience is slightly increased, but still phase attractor is very thin, and it seems to be periodic. Increasing L pushes the system to enter the chaotic region gradually. So, at $h=2^{-9}$, the window size L can be changed in a narrow range. However, at $h=2^{-10}$, the L range that the system can behave in a chaotic manner is wider. When $L=35$, the ordinary double ring is shown. Decreasing the value of L affecting the output phase diagram as shown in Table 3, and it causes the system to go out chaotic region at $L<=25$. Generally, there is a strong link between model parameters step size h and window size L. So, changing the value of h must be followed by modification in L to simulate a chaotic double-ring attractor.

3.2. Hard nonlinearity

Eq. (14a), (14b), (14c), (14d) represents the hard nonlinear love triangle model after the insertion of the Signum function. In this case, the mood of an individual is supposed to be changed suddenly. Solving these equations using the GL method at different fractional-orders leads to several attractor behavior:

$$\frac{d^{\alpha }{x}_{R_J}}{\mathit{dt}}={\mathit{ax}}_{R_J}+\mathit{bv}(x_J-x_G),$$ (14a)

$$\frac{d^{\beta }{x}_J}{\mathit{dt}}=\mathit{cv}(x_{R_J})+{\mathit{dx}}_J,$$ (14b)

$$\frac{d^{\gamma }{x}_{R_g}}{\mathit{dt}}={\mathit{ax}}_{R_g}+\mathit{bv}(x_G-x_J),$$ (14c)

$$\frac{d^{\eta }{x}_G}{\mathit{dt}}=\mathit{ev}(x_{R_g})+{\mathit{fx}}_G\text{.}$$ (14d)

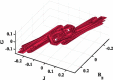
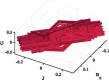
Table 4 displays the results of changing step size h with different Romeo’s personality moods (parameter a). These results are obtained after assuming that both J and $R_g$ dynamics are an integer, while $R_j$ and G have impacted with their past memories dynamics with fractional-order equals $0.8$. The total fractional-order for this system is $3.6$ with parameters $(b,c,d,e$ and f) values = $(2,-3,1,1.5$ and $-1$), respectively. The window function in this case L is chosen to be $=20$ and Initial values for ($x_{R_j},x_J,x_{R_g},x_G$) = (0,0,0.01,0). Depending on these initial values, this case is not stimulated by external events. As illustrated in Table 4, for the same personality (a), decreasing the value of h is translated to less dense in attractor sidelines. Also, the aperture in all figures in Table 4 - which looks like the English character I - is widened with lower values of h. As a result of hard nonlinearity, there is a sudden change in the dynamics of the emotions, which is being translated to fractures in attractor lines. The reason for this case is the fast person’s mood swings, which affect the relationship between lovers. Generally, the phase portrait, in this case, almost has the same shape with increasing a and does not suffer from big changes.

Table 4.

Effect of changing parameters $(a,h)$ on system behavior of fractional hard nonlinearities at $b=1,c=-3,d=1,e=1.5,f=-1$ and window $L=20$. Also, Effect of changing fractional-orders on system behavior of fractional hard nonlinearities, at the condition of constancy of parameters $h=2^{-5},a=-7,b=1,c=-3,d=1,e=1.5,f=-1$ and window $L=30$.

	$h=2^{-5}$	$h=2^{-6}$	$h=2^{-7}$
$a=-7$
$a=-10$
$a=-15$
	$(\alpha ,\beta ,\gamma ,\eta )$= ($0.5,0.9,0.5,0.9$)	$(\alpha ,\beta ,\gamma ,\eta )$= ($0.5,0.6,0.6,0.8$)	$(\alpha ,\beta ,\gamma ,\eta )$= ($0.6,0.2,0.5,0.8$)
$h=2^{-4}$

The identity of the love relationship is influenced by changing the IoM of any person in the triangle has been illustrated in Table 4. This change produces various chaotic conducts between the three parties in the relationship. Three different orders are tested using the same personalities (parameters). Total fractional-orders of these systems = ($2.8,2.5,2.1$), respectively. As shown, the new phase attractor generated by changing fractional-order. The system behaves strangely in small fractional-order values. It means that the chaotic region of the system is wide, and this relationship will suffer from many hurdles and may fail. From a different point of view, this property is considered one of the advantages that can participate in different engineering applications. This chaotic behavior may open the door to use human emotions in multimedia encryption algorithms as a key that changes with the human mood.

3.3. Mixed nonlinearity

In fractional-order mixed model, J and G dynamics are assumed to be hard, while R dynamics are soft.

$$\frac{d^{\alpha }{x}_{R_J}}{\mathit{dt}}={\mathit{ax}}_{R_J}+\mathit{bu}(x_J-x_G),$$ (15a)

$$\frac{d^{\beta }{x}_J}{\mathit{dt}}=\mathit{cv}(x_{R_J})+{\mathit{dx}}_J,$$ (15b)

$$\frac{d^{\gamma }{x}_{R_g}}{\mathit{dt}}={\mathit{ax}}_{R_g}+\mathit{bu}(x_G-x_J),$$ (15c)

$$\frac{d^{\eta }{x}_G}{\mathit{dt}}=\mathit{ev}(x_{R_g})+{\mathit{fx}}_G\text{.}$$ (15d)

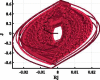
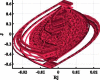
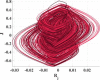
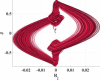
It is considered that both Romeo’s towards Guinevere $R_g$ and J dynamics are integers and equal to 1, but G and Romeo’s towards Juliet $R_j$ feelings are fractional dynamics with orders 0.9 and 0.8, respectively. In Table 5, system response after insertion a mixed non-linearity is shown. Each row represents the effect of changing only one parameter on the system behavior. The first one for Romeo’s personality mood a, range of change in a is quite wide, from $-3$ to $-13$. These variations give an interesting new whirlpool attractor. The second row is for changing Juliet’s parameter c. Big changes in phase diagram shape have happened in a very slight variation in the parameter c. Gradual decreasing of its value from $-2$ to $-3$ transforms the attractor waves from elliptical to vortex one. The next one discusses the distinction in the system behavior by changing step size h. By diminishing values of h, the system is moving towards splitting from the middle until being two identical slits at $a=-13,h=2^{-8}$. Values of parameters $(b,d,e$ and f) are depicted in each simulated case in Table 5. The system is not catalyzed with any types of external factors except $x_{R_g}$. So, initial conditions for ($x_{R_j},x_J,x_{R_g},x_G$) are equal (0,0,0.1,0) and window size $L=30$. Table 5 shows that transitions in the relationship are smoother than the hard signum but still faster than soft nonlinearity. This manner can be seen graphically, by decreasing any parameter value, lines in the phase plane become more condensed in the middle. Only one exception for the case $h=2^{-8}$, the attractor behaves differently, and trajectory becomes less condensed in the middle.

Table 5.

The effect of changing parameters $a,c$ and h on system behavior in fractional-order mixed nonlinearity.

Effect of a	$a=-3$	$a=-5$	$a=-10$	$a=-13$
$b=1$, $(c,d)=(-3,1)$, $(e,f)=(1.5,-1)$
Effect of c	$c=-2$	$c=-2.25$	$c=-2.5$	$c=-3$
$(a,b)=(-10,1)$, $d=1$, $(e,f)=(1.5,-1)$
Effect of step h	$h=2^{-5}$	$h=2^{-6}$	$h=2^{-7}$	$h=2^{-8}$
$(a,b)=(-3,1)$, $(c,d)=(-3,1)$, $(e,f)=(1.5,-1)$

4. Chaotic Generator FPGA Implementation

Chaos generators can be digitally realized using the system differential equations. This work proposes a general technique for realizing the integer and fractional-order chaotic human love behavior in a completely digital manner. Different properties of the proposed design are investigated, such as the effect of the numerical solution, chaotic system parameters change, and the number of registers bits. In this work, the Euler method is used for the integer case of the proposed chaotic generator. Furthermore, fractional-order differential equations can be numerically solved based on GL approximation presented in [20]. Fig. 5(a) describes the general hardware architecture for the proposed chaotic generator. The state variables of the chaotic system are stored in a register, and a combinational logic circuit is used to realize the numerical solution of the system. The combinational circuits are realized using the following blocks:

• •GL modules are used to calculate the summations in the fractional-order differential equation that used the Grünwald-Letnikov approximation method; for example, ${\sum }_{k=1}^n{w}_k^{(\alpha )}{x}_{R_j}(t_{m-k})$ in Eqn. (12a), (12b), (12c), (12d).
• •Multiplexer to select between integer and fractional cases.
• •Romeo and Juliet/Guinevere blocks compute the addition and multiplication in the differential equation, which are the same in both integer and fractional cases.
• •Registers used to store the system state.

Fig. 5.

(a) Main block diagram that used to calculate both integer-order and fractional-order cases with different nonlinearities. (b), (c) General block diagram for human love behavior with soft nonlinearity (d), (e) General block diagram for human love behavior during Hard nonlinearity using signum function.

The integer and fractional-order love triangle models are constructed and implemented using Verilog HDL (see Fig. 5). As depicted in Fig. 5(a), both integer and fractional cases can be implemented with different nonlinearities using the same block diagram. This realization can be done simply using a one-bit signal sel; it controls all multiplexers to choose between integer or fractional calculations. The fractional case can be chosen when $\mathit{sel}=0$ so, the output of GL block and $h^{\alpha ,\beta ,\gamma ,\eta }$ are passing to be the input for Romeo and Juliet/Guinevere blocks. However, if $\mathit{sel}=1$, this indicates the integer case so, the previous state of each register and unit step h will be the input for the blocks. $a,b,c,d,e,f,h$ and $h^{\alpha ,\beta ,\gamma ,\eta }$ are internal fixed registers, which are set with initial conditions. Clk and rst depict the clock and reset, which are used for synchronization.

Fig. 5(b) and (c) illustrate the general inside view for Romeo and Juliet/Guinevere blocks in soft nonlinearities case, while the general HW block diagram for the hard model is depicted in Fig. 5(d) and (e). One output is used for either Romeo or Juliet/Guinevere blocks in addition to six, and five inputs are required for Romeo and Juliet/Guinevere blocks, respectively. Adders, subtracters, multipliers, 2’s complement, multiplexer and, absolute blocks are used to compute the operation in differential equations; for example, the operation in the mixed model ${\mathit{ax}}_{R_J}+b(x_J-x_G)(1-|x_J-x_G|)$ as presented in Eqn. (15a), (15b), (15c), (15d).

To design the mixed nonlinearities block, a combination of Romeo soft block, which is presented in Fig. 5(b) and Juliet/Guinevere hard block in Fig. 5(e). In order to achieve excellent performance for the combinational circuits, different improved methods can be used. The conversion of the constant multiplication to shift operation in which the constant is a power of two is one of these methods. In this case, parameter h is used to be a fraction of two.

Fixed-point operations were generally used in hardware implementations to enhance the performance and hardware resources. A fixed point numbering system format is used in designing the proposed chaotic integer and fractional generators. Registers $R_j,R_g,J$, and G with a 32-bit width are used, 8-bits for the integer part and the remaining 24-bits for the fractional part. After any multiplication operation, the number of bits is doubled, which increases the hardware resources. Truncation of the multiplier’s output is done to decrease the number of bits, and therefore to reduce the area. The truncation is carefully used to ensure the system will not diverge and still in the chaotic range.

The solution based on the Euler method (integer case) uses fewer hardware resources and achieves better performance compared with the solution based on the GL method (fractional). The overall performance of the proposed chaotic generators can be improved using bit-shift and bit-select operations. Also, these operations reduce the hardware resources and power consumption. In which the multiplication operation will be converted to only simple shift operations. This process can be done if one of the multiplier inputs is a power of two.

5. FPGA experimental results

The proposed love models are simulated by the Xilinx ISE simulator and implemented on Nexys 4 (Artix-7 XC7A100T) FPGA. The FPGA implementation results are validated and compared with the simulations done by MATLAB software at the same system parameters. The proposed designs are implemented and verified experimentally. Pmod DA2 12-bit Digital-to-Analog Converter (DAC) is used to display the chaotic system on the oscilloscope, as presented in Fig. 6(a). The DAC provides two channels of conversion, which achieve about 1mV resolution. The data waveforms are displayed on a digital DPO 4104 oscilloscope with four analog channels. Several oscilloscope results for the proposed chaotic integer and fractional generators are presented in Fig. 6.

Fig. 6.

Experimental setup represented in (a). Different cases are tested with parameters (a, b, c, d, e, f ,h) values equal to (b) (−3,4,−7,2,2,−1,$2^{-10}$), (c) (−3,4,−8,2,2,−1,$2^{-10}$) for soft integer nonlinearity. Cases (d) and (e) for integer mixed nonlinearity with parameters = (−10,20,−5,3,0.5,−1,$2^{-6}$) and (−15,20,−5,3,0.5,−1,$2^{-6}$) respectively. Case (f) shows fractional-order mixed attractor with parameters (−3,1,−3,1,1.5,−1,$2^{-6}$).

A report of the utilized resources from Xilinx Artix 7 FPGA for the proposed implementations is given in Table 6. A throughput of 2.322 Gbit/s for integer-order design is delivered, when this value is decreased to be 1.824 Gbit/s in fractional-order design.

Table 6.

FPGA hardware design summary.

Design	No. of Slices (Utilization)	No. of Registers	Maximum Frequency (MHz)	Throughput (Gbit/s)
Integer	140 ($0.88\%$)	152	48.387	2.322
Fractional	707 ($4.46\%$)	2141	38	1.824

6. Conclusion

The love triangle is affected by human personalities and external stimulations, which leads to a chaotic relationship or maybe a quiet one. This effect in the integer-order model of a love triangle was discussed with three different nonlinearities. Maximum Lyapunov exponent in all discussed cases (soft, hard, and mixed) were positive, which admit the chaotic behavior of the systems. Also, bifurcation diagrams of these cases showed the chaotic range accurately. In addition, The effects of human mood changes in the general fractional-order model with different nonlinearities had been displayed. Different insights from this relation were shown in order to understand this complex dynamical behavior. The main observation was, the previous experience of a human and his memory showed a high impact on his behavior. In addition, the effect of Romeo’s parameter and its vital role in the relationship was presented. From a psychological point of view, this was regarding the direct relation between him and both Juliet and Guinevere. A digital realization for both integer and fractional-order models of the love triangle was done using Artix 7 FPGA kit with utilization percentage about $0.88\%$ and $4.46\%$ respectively. Results show that the throughput of integer case equals to 2.322 Gb/s; however, this value is decreased in the fractional case to be 1.824 Gb/s.

Declaration of Competing Interest

None.

Compliance with Ethics Requirements

This article does not contain any studies with human or animal subjects.