Graphical abstract
Keywords: Current–mode, Electronic control, Fractional–order, Frequency filter, Higher–order filter, Reconnection–less reconfiguration
Abstract
The paper discusses a new design of a current–mode reconnection–less reconfigurable fractional–order (FO) low–pass filter of various orders. The filtering structure is based on a 4th–order leap–frog topology using operational transconductance amplifiers as basic building blocks. The resulting order of the filter is given by the setting of current gains (allowing the reconnection–less reconfiguration) alongside with the values of the fractional–order capacitors realized by the RC ladder networks. For this purpose, RC ladder networks of orders 0.3, 0.4, 0.5, 0.6 and 0.7 have been designed. The fractional–order form of the filter contains from one up to four FO capacitors (remaining capacitors (if there are any) are of integer–order) allowing to obtain low–pass functions of order of 3 + α, 2 + α, 1 + α, 2 + α + β, 1 + α + β, α + β, 1 + α + β + γ, α + β + γ and α + β + γ + δ. The proposed filter offers a wide variety of possible order combinations with an increasing degree of freedom as the number of fractional–order capacitors within the structure increases. The proposal is supported by the PSpice simulations of magnitude and phase characteristics, pole frequency adjustment and stability analysis. Moreover, the experimental measurements of the implemented filter were carried out and compared with the simulation results. The possibility of the electronic control of the fractional order is also discussed and presented.
Introduction
In recent years, the matter of the fractional–order (FO) calculus received an increased attention of many scientists due to its possible utilization in various spectrums of industry branches including medicine [1], [2], [3], agriculture [1], [4] and, of course, electrical engineering [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33] giving many new potential applications a chance to arise. In comparison to the integer–order circuits, FO circuits provide an increased degree of freedom, due to the presence of the non–integer–order parameter (α). This can be quite beneficial when it comes to more accurate generation and measurement of biomedical signals, impedance of various organic objects, etc. The electrical engineering field, in particular, covers areas of FO frequency filters [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], oscillators [24], [25], [26], controllers [27], [28] and other circuits [29], [30], [31], [32], [33].
When discussing the FO filters, the slope of the transition between the band–pass and band–stop area is characterized by the relation 20·(n + α), where n is a non–zero integer number and α provides the fractional–order parameter. It is possible to come over two basic design approaches applied to filtering structures in order to obtain fractional–order characteristics. The first approach supposes the usage of a FO capacitor (or inductor) more generally referred to as FOE (Fractional–Order Element). Fractional–order capacitor is a special element with its impedance given as ZC = 1/sαCα, where s is the Laplacian operator (complex number), symbol α represents the fractional order in range of 0 < α < 1 and Cα is a pseudo capacitance with the unit of F·sα–1. Generally speaking, the order of a fractional–order capacitor has its value in between the behavior of a traditional resistor and capacitor [2]. There have been some reports of a fabrication of fractional–order capacitors [34], [35], [36] nonetheless, these elements are expensive and difficult to implement and they are not commercially available. Therefore, they are usually substituted by passive elements (RC ladder networks) [5], [6], [7], [8], [9], [10], [11], [12], [13] or electronic emulators [29], [30], [31] approximating the FO capacitor (or inductor). The other approach involves the approximation of Laplacian operator of fractional–order sα by an integer–order function [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23]. The approximation is applied on the filtering structure as a whole leading to the change of values of standard elements/parameters within the structure (capacitors, resistors, transconductances gm, voltage or current gains A, B).
A FO filter of a low–pass (LP) 1 + α function is used most commonly [11], [14], [15], [16], [17], [21], [22], [23]. Other quite common FO function is a high–pass (HP) 1 + α filter [7], [16], [18], [21], [22], [23]. There are also reports of FO band–pass (BP) [5], [7], [10], [17], [20], [21], [22], [23], band–stop (BS) [7], [21], [22], [23] and all–pass (AP) [8], [19] filtering structures. Some structures suppose the replacement of both capacitors (considering the second–order structure having 2 integer–order capacitors turned into a FO filter) by FO capacitors providing an additional degree of freedom of the order control. Let us mention LP α + β filters [6], [9], [13], LP α + α filter assuming two FO capacitors of identical orders [10] and even LP α + β + γ supposing a FO filter originated from a second–order filter consisting of 3 capacitors [12]. Furthermore, Refs. [15], [17] report FO filters of higher–orders (LP 5 + α) where the higher–order is obtained by a cascade combination of a FO filter of order 1 + α and integer–order filter of order 4 (in this case). Several filters [7], [10], [16], [17], [21], [22], [23] are able to offer more than one type of a FO transfer function. For this purpose, a structure modification is required in case of filter from [16]. Structures in [7], [10] are of either single–input multiple–output (SIMO) or multiple–input single–output (MISO) type requiring switching between different nodes of the structure. Only the filtering structures in [21], [22], [23] offer the ability of the electronic reconnection–less reconfiguration between available functions without any structure modification or switching of nodes needed. Nonetheless, the reconnection–less reconfiguration in case of [22], [23] is solved by the array of electronic switches controlled through a 4–to–16 decoder. Such solution can have rather complex control logic and more importantly does not offer a feature of a fine tuning of the transfer function as the switches are either on or off in comparison to a continuous control when employing a suitable amplifier similarly to [21] and this paper. The feature of the reconnection-less reconfiguration is a beneficial ability of so–called reconnection–less reconfigurable filters [21], [37], [38], [39], [40]. These filters can change the resulting output response by adjusting electronically controllable parameters of various active elements such as transconductance gm in case of an operational transconductance amplifier (OTA) or voltage or current gain A, B in case of a variable gain amplifier (VGA) and adjustable current amplifier (ACA), etc. Thus, no manual modification or switching of inputs/outputs, which are not available for on chip implementation, is required. Table 1 introduces a comparative overview of the above–mentioned FO filters and collates them with the filter proposed in this paper.
Table 1.
Comparative sheet of relevant fractional–order filtering structures.
| Reference number | Type or realization | Type (number) of active element(s) | Type (number) of passive elements | Provided functions | Type of structure | Results | Notes |
|---|---|---|---|---|---|---|---|
| [5] | RC | Opam(3) | R(6), FC(2) | BP α + β | Tow-Thomas | Sim/Meas | – |
| [6] | RC | DVCC(1) | R(1), FC(2) | LP α + β | unspecified | Sim | – |
| [7] | RC | OTA(6) OTA(5) |
FC(2) FC(2) |
LP α + β HP α + β BP α + β BS α + β |
IFLF | Sim | 1 |
| [8] | RC | OTA(2) | FC(1) | AP α | unspecified | Sim | – |
| [9] | RC | DDCC(1) | R(2), FC(2) | LP α + β | unspecified | Sim | – |
| [10] | RC | OTA(3) | FC(2) | LP α + α BP α + α |
unspecified | Sim | – |
| [11] | RC | Opam(3) | R(6), C(1), FC(1) | LP 1 + α | Tow-Thomas | Sim | – |
| [12] | RC | Opam(2) | R(6), FC(3) | LP α + β + γ | unspecified | Sim/Meas | – |
| [13] | RC/ Approx |
Opam(4) Opam(3) |
R(18), C(4) R(6), FC(2) |
LP α + β | unspecified | Sim | 2 |
| [14] | Approx | CFOA(4) | R(10), C(3) | LP 1 + α | FLF | Meas | – |
| [15] | Approx | DDCC(5) | R(7), C(3) | LP 1 + α | IFLF | Sim/Meas | 3 |
| [16] | Approx | CFOA(4) CFOA(4) |
R(9), C(3) (LP) R(8), C(4) (HP) |
LP 1 + α HP 1 + α |
FLF | Sim/Meas | 4,5 |
| [17] | Approx | Opam(10) | R(22), C(7) | LP 5 + α LP 1 + α BP 2(3 + α) |
cannonical | Sim/Meas | 6 |
| [18] | Approx | OTA(3), ACA(3) | C(3) | HP 1 + α | FLF | Sim | – |
| [19] | Approx | OTA(2) | FC(1) | AP α | unspecified | Sim | 7 |
| [20] | Approx | OTA(9) | C(4), trans(11) | BP 2α | IFLF | Sim | – |
| [21] | Approx | OTA(3), ACA(4), CF(2) | C(6) | LP 1 + α HP 1 + α BP 1 + α BS 1 + α |
IFLF | Sim | 8 |
| [22] | Approx | CFOA(8) | R(16), C(3) | LP 1 + α HP 1 + α BP 1 + α BS 1 + α |
FLF | Sim | |
| [23] | Approx | N/A | N/A | LP 1 + α HP 1 + α BP 1 + α BS 1 + α |
FLF | Sim | 9 |
| Fig. 2 | RC | IOGC-CA(1), OTA(4) | C(0–4) FC(0–4) |
LP 3 + α, LP 2 + α, LP 1 + α, LP 2 + α + β, LP 1 + α + β, LP α + β, LP 1 + α + β + γ, LP α + β + γ LP α + β + γ + δ. |
Leap–frog | Sim/Meas | 10 |
List of previously unexplained abbreviations used in this table:
RC – RC ladder network, Opam – operational amplifier, R – resistor, FC – fractional–order capacitor, Sim – simulations, Meas – measurements, DVCC – differential voltage current conveyor, IFLF – inverse follow–the–leader feedback topology, C – (standard integer–order) capacitor, approx. – approximation of Laplacian operator of fractional–order, CFOA – current feedback operational amplifiers, FLF – follow–the–leader feedback topology, DDCC – differential difference current conveyor, CF – current follower, IOGC–CA – individual output gain controlled current amplifier
Notes:
Reference presents two topologies (SIMO and MISO).
Reference introduces two structures (one based on the approximation, the other one on usage of the RC structure).
Paper also presents LP 5 + α created by a cascade combination of 1 + α filter and filter of the 4th–order constructed by DDCC(4), R(4), C(4).
Two different topologies (for LP and HP function).
LP and HP 5 + α filters are also presented created by a cascade combination with a 4th–order filter constructed by CFOA(4), R(9), C(4) for the LP 5 + α and CFOA(4), R(6), C(7) for HP 5 + α.
The number of active/passive elements is specified for LP 5 + α filter (Opam(2), R(10), C(3) for HP 1 + α).
The FO capacitor is approximated by a second–order IFLF topology (OTA(8), C(2)).
The presented topology is fully differential.
The structure is all transistor based.
The structure contains four integer–order capacitors which are gradually replaced by FO capacitors depending on specific FO function.
The first thing, which is necessary to understand from Table 1, is the fact that the proposed filter is based on a different premise than other mentioned filters. Some filters [8], [11], [19], [14], [15], [16], [17], [21], [22], [23] work with one fractional–order parameter while filters in [9], [10], [13], [5], [6], [7] consider two fractional–order parameters. Based on this fact these filters have either one or two (fractional) orders which can be controlled theoretically. These structures, however, do not suggest any other possible modification of the order unless it comes to the design of higher order filters, where a suitable integer–order filter has to be added to the fractional–order filter to provide the desired higher–order function. The proposed filter can offer higher degree of freedom as it operates with a structure of the 4th–order (and can use up to 4 FC as evident from Table 1) and it is up to the user what the resulting order is going to be used by addition or removal of an another block by electronic means. In short, the presented design can offer a higher degree of freedom while choosing a desired order without any needs of the structure modification (physical addition of a next stage in a cascade). Most importantly, with an implementation of a suitable electronically controllable FC emulator, we can choose whether we want the resulting order to be of the integer–order, combination of the integer and fractional order, or a combination of multiple fractional orders (either resulting in integer or fractional order). Based on the above–mentioned fact, the proposed filter can offer nine combinations of functions (and 4 additional functions if considering integer–order functions as well) in comparison to only one function in case of [5], [6], [8], [9], [11], [12], [13], [14], [15], [18], [19], [20]. This useful feature is not available in case of other discussed solutions. Furthermore, the intended function of the proposed filter is supported by experimental measurements, not available in case of [13], [19], [6], [7], [8], [9], [10], [11], [21], [22], [23].
The filtering structure introduced in this paper is designed by the Signal–Flow Graph method (SFG) using a 4th–order leap–frog topology as its foundation. The filter operates in the current mode (CM) and provides LP functions of the first, second, third and fourth order. The 4th–order leap–frog topology is based on OTA elements. The addition of a current amplifier with the ability to control the gain of each output separately to the proposed structure offers the ability of the reconnection–less reconfiguration of the resulting filtering response. The FO characteristics are obtained by the gradual replacement of integer–order capacitors within the structure by their FO counterparts (RC ladder networks). Such modified structure can offer FO functions of LP 3 + α, LP 2 + α, LP 1 + α, LP 2 + α + β, LP 1 + α + β, LP 1 + α + β + γ, LP α + β + γ and LP α + β + γ + δ. The design is supported by PSpice simulations and experimental measurements.
The organization of the paper is as follows: Section ‘Design of an integer–order reconnection–less reconfigurable filter’ introduces the design of the 4th–order leap–frog topology constructed as a reconnection–less reconfigurable LP filter of the first, second, third and fourth order. The simulation and experimental results of this filter are provided in Section ‘Results of the proposed integer–order reconnection–less filter’. The following section describes the modification of the integer–order LP filter from Section ‘Design of an integer–order reconnection–less reconfigurable filter’ into a FO reconnection–less reconfigurable filter. Section ‘Results of the proposed fractional–order reconnection–less filter’ shows the results of the proposed FO filter and offers its stability analysis. Finally, the paper is concluded by Section ‘Conclusion’.
Design of an integer–order reconnection–less reconfigurable filter
The proposed structure was firstly designed in its integer–order form (described in this chapter). Its FO counterpart is described in Section ‘Modification of the proposed integer–order filter in order to obtain a fractional–order reconnection–less reconfigurable filter’.
General structure design
The initial filter design is made through the usage of Signal–Flow Graph method [41] and a 4th–order leap–frog topology. The filter is working in the current mode (has current input and current output). The input current is applied to different circuit nodes via electronically controllable current gains to ensure the presence of the reconnection–less reconfiguration of the transfer function. The proposed (simplified) signal–flow graph of the filtering structure is depicted in Fig. 1.
Fig. 1.
Simplified signal–flow graph of the proposed 4th–order leap–frog topology suitable for the design of a reconnection–less reconfigurable low–pass fractional–order filter.
The transfer function of a signal–flow graph is determined by so–called Mason's gain formula expressed as:
| (1) |
where Pi stands for a gain of i–th forward path and Δ is the determinant of the given graph.
The denominator of the proposed filter, which corresponds with the determinant Δ of the graph in Fig. 1, is calculated as:
| (2) |
then:
| (3) |
The numerator of the transfer function is given as:
| (4) |
From (4), it can be seen that the resulting output response of the filter is controlled by the current gains B1 to B4 and depends on their adjustment. For the 4th–order LP function, current gain B1 is set to 1 and remaining gains are zero, for example. Based on this fact, the numerator turns into gm1gm2gm3gm4B1, other terms of the numerator are canceled. In case of the 1st–order function, current gain B4 is set to 1 and other gains are zero thus, the numerator takes form of s3C1C2C3gm4B4 + s2C2C3gm1gm4B4 + s(C3gm1gm2gm4B4 + C1gm2gm3gm4B4) + gm1gm2gm3gm4B4. Similarly, for the 2nd and 3rd–order function, where the current gain B2 or B3 is set and the remaining gains are zero, the numerator will change accordingly. In order to obtain a specific function, the current gains B are either set to 1 or 0. It is also possible (depending on particular implementation of current amplifiers and their abilities of the control) to set the value higher or lower than 1 although that will shift the function in the matter of gain (the pass band will not have the unity gain). Nonetheless, this feature can be beneficial in case of the fine tuning of the pass–band area of available LP functions if the pass–band is not exactly 0 dB due to innacuracy of filter parameters in real case or if the function does not have its pass band at 0 dB to start with originating from the design itself (which is common for some functions of higher–order filters). The other possibility is to adjust the stop–band area by partial addition of another term (0 < B < 1) as presented in [39], for instance. The resulting functions, based on the setting of curreng gains B in ideal case, are stated in Table 2.
Table 2.
Current gain configuration in regard to the resulting Integer–order transfer function.
| B1 [–] | B2 [–] | B3 [–] | B4 [–] | function |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 4th–order LP |
| 0 | 1 | 0 | 0 | 3rd–order LP |
| 0 | 0 | 1 | 0 | 2nd–order LP |
| 0 | 0 | 0 | 1 | 1st–order LP |
The graph in Fig. 1 can be turned into a circuit scheme (see Fig. 2) considering active elements (described in the following subsection) suitable for the required function fullfilment.
Fig. 2.
Proposed reconnection–less reconfigrable filtering structure based on a 4th–order leap–frog topology used for the design of a reconnection–less reconfigurable low–pass fractional–order filter.
Implemented active elements
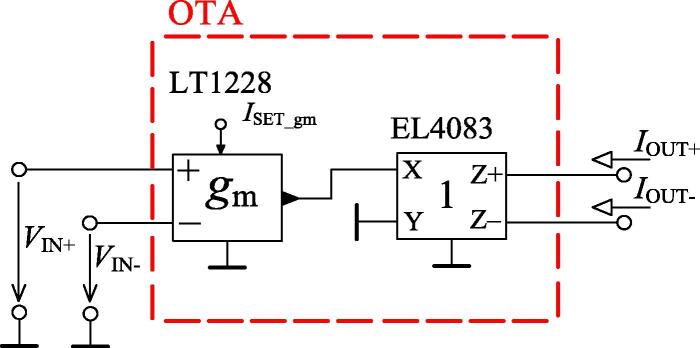
The active elements used in the proposal are four OTAs and one current amplifier with independent gain control of each output separately proposed in [42] (labeled as individual output gain controlled current amplifier (IOGC–CA) throughout the text). The structure also contains four grounded capacitors. The OTA element is represented by the schematic symbol depicted in Fig. 3 a). The relation between the terminal of the OTA is expressed as IOUT± = ±gm(VIN+ − VIN−), where gm is the transonductance of this element. Fig. 3 b) shows a possible (used in case of the measurement results) implementation of this element by a universal current conveyor (UCC) [43], [44] and one resistor R connected to the X terminal. The value of the resistor determines the value of the resulting transcondcuctance by the relation gm = 1/R. This solution does not directly offer the electronic control of the transconductance nonetheless, the OTA elements in the structure (in order to provide the electronic control of transconductances) could be realized by a combination of LT1228 device [45] and EL4083 device [46] as suggested in Fig. 4 (both devices are commercially available), for example. LT1228 device has its transconductance controlled electronically by a DC bias current but it only offers one output. We can obtain two outputs of both polarities by adding EL4083 device at the output of LT1228 device.
Fig. 3.
Operational Transconductance Amplifier (OTA): (a) schematic symbol, (b) its implementation by the UCC.
Fig. 4.
The OTA element with the electronic control of gm and two outputs implemented by LT1282 and EL4083 devices.
The addition of the IOGC–CA to the proposed structure allows the possibility of the reconnection–less reconfiguration of the transfer function. The schematic symbol of the IOGC–CA element can be seen in Fig. 5(a). The original structure of the IOGC–CA from [42] has been modified since the UCC offers two non–inverting and two inverting outputs and thus, the IOGC–CA itself offers the same polarities of its outputs. To ensure that all available functions of the proposed filter have the same polarity (all are non–inverting), all the outputs of the IOGC–CA must have the same polarity. It can be easily solved in case of the (transistor–level) simulations and on–chip implementation of whole circuitry from Fig. 2 when directly designed with this requirement in mind. For the specific implementation using the UCC and EL2082 [47] devices (current gain B is controlled by the DC bias voltage VSET_B), there are two additional OPA860 devices [48] added in series with EL2082 in paths from Z+ outputs of the UCC (B1 and B3 paths as apparent in Fig. 5(b)). OPA860 devices are used to invert the signal polarity of these outputs so all transfer functions have the same polarity. This could be also solved by using a different type of a current amplifier with an opposite output polarity than the EL2082 provides nevertheless, it is quite possible such active element would have a different driving force (current instead of voltage) or even if using voltage as its driving force, the dependence of the current gain on the driving force could be dissimilar. Therefore, the solution utilizing OPA860 devices has been used to make the reconfiguration easier and more transparent. The behavior of the IOGC–CA is given as IOUT = −Bi(IIN), where i = {1, 2, 3, 4} depending on the individual output.
Fig. 5.
Individual output gain controlled current amplifier (IOGC–CA): (a) schematic symbol, (b) its implementation by one UCC and four EL2082 devices (and two OPA860).
Results of the proposed integer–order reconnection–less filter
The appropriate operation of the proposed filter is supported by PSpice simulations alongside with experimental measurements.
Simulation and measurement setup
The simulation results have been carried out by means of transitor–level simulation models based on CMOS 0.18 µm TSMC process. The IOGC–CA elements have been constructued by a current follower and current amplifiers. The transistor–level models of these elemenets were adopted from [49], [50], respectively. The current gain B of the used current amplifier model is controlled by a DC bias current. The OTA element is based on a model available in [51]. The transconductance of this particular model is set via a DC bias current. The supply voltage for all the used simulation models is ±1 V. A practical implementation of the used active elements is done with help of a UCC and EL2082s as decribed in the previous section. The UCC (created in cooperation of Brno University of Technology and ON Semiconductor design center) is implemented in CMOS 0.35 μm IT3T technology. The chip is labeled UCC–N1B_0520 where each chip contains one UCC and a second–generation current conveyor with two outputs (CCII±). The supply voltage of the UCC is ±1.65 V and 5 V for the EL2082. The measurement is performed by a network analyzer Agilent 4395A and voltage–to–current, current–to–voltage converters constructed around OPA860 [48] and OPA861 [52] devices. The block diagram of the measurement setup can be seen in Fig. 6(a). Implemented V–I and I–V converters are based on a simple principle of a suitable connection of a CCII. In case of the V–I (Fig. 6(b)), the input voltage is connected to the voltage input node of the CCII and converted to the output current by means of a resistor R connected to the current input node. The function of the I–V converter (Fig. 6(c)) is as follows, the current from the proposed filter is connected to the current input of the CCII (working as a current follower) and mirrored to the current output node of the CCII. The output current is then transferred to voltage through the resistor R. A voltage buffer (present in the package of OPA860 together with the CCII) connected to the output of the converter provides the impedance separation. In order to eliminate the impact of these converters on obtained measurement results, a careful calibration of the signal path was performed. The actual measuring workspace including the supply voltage and control sources is shown in Fig. 7 (currently measuring order of 3 + 0.5).
Fig. 6.
Measurement setup: (a) block diagram of the measurement, (b) basic principle of the used V–I converter, (c) basic principle of the used I–V converter.
Fig. 7.
Workplace arrangement (measuring order of 3 + 0.5).
Numerical design and results
The numerical design (calculation of individual coefficients of the transfer function in regard to the filter order and chosen approximation) has been made with help of NAF software [53]. Used coefficients stated in (5) are given for the following specifications: Butterworth approximation, the operational angular frequency ω0 = 300,000 rad/s (f0 = 47 kHz), transfer in pass–band KP = −3 dB, the stop–band frequency fs = 470 kHz, transfer in stop–band KS = −80 dB.
| (5) |
These coefficients have been applied onto the denominator (expressed in (3)) of the transfer function. The transconductances gm1 to gm4 can be calculated as:
| (6) |
| (7) |
| (8) |
| (9) |
For selected values of capacitors (C1 = C2 = C3 = C4 = 1 nF), the resulting values of the transconductances (in accordance with coeficients in (5)) are gm1 = 784.4 µS, gm2 = 277.3 µS, gm3 = 190.3 µS and gm4 = 196.1 µS.
The list of available transfer functions for the filter from Fig. 2 is given in Table 3. The setting is now stated for control voltages in comparison to Table II, where VSET_B = 1 V corresponds to current gain B equal to 1.
Table 3.
Control voltage configuration in regard to the resulting Integer–order transfer function.
| VSET_B1 | VSET_B2 | VSET_B3 | VSET_B4 | function |
|---|---|---|---|---|
| 1 V | 0 V | 0 V | 0 V | 4th–order LP |
| 0 V | 1 V | 0 V | 0 V | 3rd–order LP |
| 0 V | 0 V | 1 V | 0 V | 2nd–order LP |
| 0 V | 0 V | 0 V | 1 V | 1st–order LP |
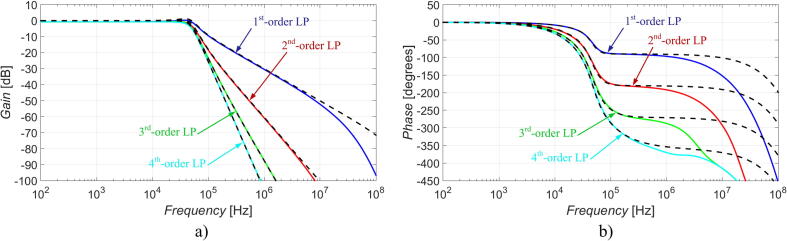
The theoretical (indicated by black dashed lines) and simulation (represented by colored lines) results of the proposed integer–order filter are compared in Fig. 8. Magnitude characterestics of the first, second, third and fourth LP function are depicted in Fig. 8(a) while their phase characteristics are given in Fig. 8(b). Obtained simulation (black dashed lines) and experimental (colored lines) results of the same circuit are shown in Fig. 9. It can be seen that the theoretical and simulation results as well as the simulation and experimental results are in good accordance with each other. Any possible differences are mainly a result of the effect of parasitic characteristics of used simulation models and chips used for the implementation. As we are talking about the influence of the parasitic characteristics which affect the transfer function at higher frequencies, this is mainly caused by the impedance characteristics of the current inputs of used active elements. In the ideal case, the impedance of the current inputs is zero. The actual impedance of the X terminal of the UCC is 0.7 Ω at 10 kHz and it is increasing to 8.7 Ω at 1 MHz and it is already 75 Ω at 10 MHz. The value of the impedance of the current input of the EL2082 device is given (by the datasheet) to be 95 Ω. These values will influence the attenuation in stop–band area at higher frequencies (the function will not continue with given slope of attenuation but rather stay at specific value of attenuation). Around 10 MHz, a slight increase of the transfer function (especially evident in case of the 1st–order function) is a typical parasitic feature of the UCC. The measured results are also affected by the features of used converters and the recognition abilities of the used Analyzer (around −80 dB). The above–mentioned effect of parasitics applies to all presented results. The functions are available based on the setting of current gains B1 to B4 as suggested in Table 2 and the results comfirm the intended reconnection–less reconfiguration of the transfer function.
Fig. 8.
Theoretical and simulation results of the proposed integer–order filter (a) magnitude characteristics, (b) phase characteristics.
Fig. 9.
Simulation and experimental results of the proposed integer–order filter (a) magnitude characteristics, (b) phase characteristics.
Modification of the proposed integer–order filter in order to obtain a fractional–order reconnection–less reconfigurable filter
In order for the proposed integer–order filter to provide FO characteristics, we suppose the filtering structure from Fig. 2 is being understood (and worked with) as two second–order filter sections connected in a cascade [54] which are then considered as integer–order (2nd–order) or fractional–order (either 1 + α or α + β) depending on a specific function. This fact is established due to that a FO filter can be stable only when the order of the filter is less than 2 as stated in [17]. The integer–order capacitors in the filtering structure are gradually replaced by their FO counterparts implemented by RC ladder networks. This gradual exchange can offer functions of LP 3 + α, LP 2 + α, LP 1 + α, LP 2 + α + β, LP 1 + α + β, LP α + β, LP 1 + α + β + γ, LP α + β + γ and LP α + β + γ + δ based on the function which best suits our needs. The presence of multiple FO orders provides an additional degree of freedom since their summation can provide more possible combinations (more obtainable orders from which some can better meet our requirements for the specific slope of the transition between the pass–band and stop–band area or specific phase shift). The FOE elements are substituted by the 5th–order RC structures of the Foster I type [55] depicted in Fig. 10. For the purposes of the proposed filter, four printed circuit boards (presented in Fig. 11) have been constructed to replace integer–order capacitors. Each board contains five RC structures of orders 0.3, 0.4, 0.5, 0.6 and 0.7. The values of the components within the RC structures for the implemented orders are calculated with help of the Oustaloup approximation [56] (using a Matlab script). All the values (calculated for the operational f0 = 50 kHz) are stated in Table 4. This does not directly offer the reconnection–less reconfigurable control of the fractional orders (the integer order can be added to the fractional order by electronic means by current gains B), nevertheless, used RC structures could be replaced by an electronically adjustable emulator introduced in [57] or some other FO emulators in order to ensure the electronic control of the order. This fact will be shown later in the paper in Section ‘Results of the proposed fractional–order reconnection–less filter’.
Fig. 10.
5th–order Foster I type RC topology used to substitute a FO capacitor.
Fig. 11.
Printed circuit boards of the implemented RC structures.
Table 4.
Specification of the part values of the RC structures.
| α [–]/component | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
|---|---|---|---|---|---|
| R0 [Ω] | 149.4 | 57.0 | 50.6 | 29.5 | 17.2 |
| R1 [Ω] | 118.7 | 96.3 | 71.6 | 49.3 | 31.1 |
| R2 [Ω] | 241.3 | 246.1 | 229.5 | 197.8 | 155.9 |
| R3 [Ω] | 465.5 | 590.6 | 685.1 | 734.7 | 720.4 |
| R4 [Ω] | 902.6 | 1431.1 | 2077.6 | 2793.9 | 3444.0 |
| R5 [Ω] | 1960.1 | 4140.7 | 8208.3 | 15643.7 | 29039.1 |
| C1 [nF] | 0.547 | 0.752 | 1.13 | 1.82 | 3.22 |
| C2 [nF] | 2.34 | 2.56 | 3.06 | 3.96 | 5.59 |
| C3 [nF] | 10.58 | 9.29 | 8.92 | 9.27 | 10.54 |
| C4 [nF] | 47.49 | 33.37 | 25.62 | 21.23 | 19.19 |
| C5 [nF] | 190.36 | 100.41 | 56.44 | 33.0 | 19.81 |
Since the values for the RC structure are not standard series values, they are made by a parallel combination of E24 resistors (with tolerance of 5%) and a parallel combination of E12 capacitors (with tolerance of 5–20%).
The denominator of one section of the filter is expressed by (10) if one of the integer–order capacitors is replaced by a FO capacitor and (11) if both capacitors are replaced by their FO counterparts.
| (10) |
| (11) |
All FO filters of higher–order were constructed by a cascade combination of a 1 + α filter with an integer–order structure so far. Our solution is working with whole topology (4th–order in this case) and you can simply decide what is the resulting order of the filter by selecting the setting of current gains B1 to B4.
Results of the proposed fractional–order reconnection–less filter
The simulations and measurements of the FO filter are using the same setup as specified for the simulations and measurement of the integer–order filter (simulations done with CMOS 0.18 µm TSMC models and the experimental measurement with help of the UCCs, EL2082s, network analyzer and convertors). All FO transfer functions are designed to have their f0 being equal approximately to 50 kHz. All simulation results are indicated by black dash lines while colored lines stand for the experimental results except for Fig. 12, Fig. 14, Fig. 16 which compare the theoretical (black dash lines) and simulation (colored lines) results.
Fig. 12.
Theoretical and simulation results of 3 + α, 2 + α and 1 + α orders for a = 0.3 (a) magnitude characteristics, (b) phase characteristics.
Fig. 14.
Theoretical and simulation results of 3 + α, 2 + α and 1 + α orders for a = 0.5 (a) magnitude characteristics, (b) phase characteristics.
Fig. 16.
Theoretical and simulation results of 3 + α, 2 + α and 1 + α orders for a = 0.7 (a) magnitude characteristics, (b) phase characteristics.
Orders of 3 + α, 2 + α and 1 + α
Fig. 12, Fig. 13, Fig. 14, Fig. 15, Fig. 16, Fig. 17 show the results (magnitude and phase characteristics) of the proposed filter when capacitor C4 is replaced by one of the implemented RC structure board. The denominator of the filter with C4 being of fractional order is expressed as:
| (12) |
Fig. 13.
Simulation and experimental results of 3 + α, 2 + α and 1 + α orders for a = 0.3 (a) magnitude characteristics, (b) phase characteristics.
Fig. 15.
Simulation and experimental results of 3 + α, 2 + α and 1 + α orders for a = 0.5 (a) magnitude characteristics, (b) phase characteristics.
Fig. 17.
Simulation and experimental results of 3 + α, 2 + α and 1 + α orders for a = 0.7 (a) magnitude characteristics, (b) phase characteristics.
Such modification offers FO low–pass transfer functions of 3 + α, 2 + α and 1 + α in correlation with the setting of current gains. The first section of the filter (involving OTA1, OTA2 and capacitors C1 and C2) is expressed as a standard 2nd–order filter with its f0 = 50 kHz according to the relation f0 = (1/2π)·((gm1gm2)/(C1C2))1/2. For f0 = 50 kHz and selected values of capacitors C1 = C2 = 4.7 nF, the values of transconductances gm1 and gm2 were calculated to be gm1 = gm2 = 1.477 mS. The second section is using C3 = 4.7 nF and the values of transconductances gm3 and gm4 (stated in Table 5) are calculated in relation to the value of the FO capacitor which is depending on FO parameter α. Figures present the comparison of the theoretical and simulation results and then simulation and experimental results of functions of 3 + α, 2 + α and 1 + α when α is equal to 0.3 in case of Fig. 12, Fig. 13, it is α = 0.5 for Fig. 14, Fig. 15 and α = 0.7 for Fig. 16, Fig. 17. The results show a good correlation with each other. The resulting orders are usually slightly lower than the expected values (about 0.1 less than expected). These differences from the theory are mainly caused by the rounding or calculated values, error caused by the resulting values of parallel combination of resistors/capacitors which do not exactly match the desired values and the tolerance of used parts. Note that this error will be added to each other as more integer–order capacitors are replaced by the implemented RC structures. Nevertheless, this could be easily solved by using higher values of α to better match the required order, if keeping this fact in mind. Other possible solution is the implementation of more accurate RC structures.
Table 5.
Values of transconductances gm3gm4 in relation to the values of alpha.
| α/transconductance | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
|---|---|---|---|---|---|
| gm3 [mS] | 0.610 | 0.757 | 0.933 | 1.139 | 1.375 |
| gm4 [mS] | 3.060 | 2.530 | 2.103 | 1.764 | 1.496 |
Orders of 2 + α + β, 1 + α + β
The proposed filter can offer FO low–pass functions of 2 + α + β, 1 + α + β and α + β by replacing two capacitors (C3 and C4) in the topology by FO capacitors. The denominator for this case is given as:
| (13) |
The first section of the filter is set as in the previous case (C1 = C2 = 4.7 nF, gm1 = gm2 = 1.477 mS). The second section is involving two FO capacitors. Used values of gm3 and gm4 are summarized in Table 6. The value of gm3 is depending on parameter α but the change is minimal (going from 1.45 mS to 1.46 mS for α changing from 0.3 to 0.7). Therefore, transconductance gm3 has been set to 1.46 mS for all used α. Transconductance gm4 is depening on the value of β. Fig. 18 introduces the results of 2 + α + β function for four different combinations of α and β values. The following setting has been used: α = 0.3, β = 0.4, α = 0.5, β = 0.4, α = 0.5, β = 0.6 and α = 0.5, β = 0.7 resulting in orders 2.7, 2.9, 3.1 and 3.3. The characteristics of 1 + α + β functions are provided in Fig. 19. The α and β value combination for this case is α = 0.4, β = 0.3, α = 0.6, β = 0.3, α = 0.4, β = 0.7 and α = 0.7, β = 0.6 (orders 1.7, 1.9, 2.1 and 2.3).
Table 6.
Values of transconductances gm3gm4 in relation to the values of alpha and beta.
| α/transconductance | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
|---|---|---|---|---|---|
| gm3 [mS] | 1.46 | ||||
| β/transconductance | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
| gm4 [mS] | 3.47 | 2.57 | 2.03 | 1.67 | 1.41 |
Fig. 18.
Simulation and experimental results of 2 + α + β, functions for various combinations (a) magnitude characteristics, (b) phase characteristics.
Fig. 19.
Simulation and experimental results of 1 + α + β, functions for various combinations (a) magnitude characteristics, (b) phase characteristics.
Orders of 1 + α + β + γ and α + β + γ
Fractional–order low–pass functions of 1 + α + β + γ and α + β + γ are available if three capacitors (C2, C3, C4) are replaced by the designed RC structures. The denominator takes form of:
| (14) |
The first section of the filter is handled as a 1 + α filter the same way as the second section in case of 3 + α, 2 + α and 1 + α functions. The values of transconductances gm1 and gm2 are then same as the values of gm3 and gm4 in Table 5. The second section is identical to the previous case (gm3 and gm4 are set according to Table 6). The results of the 1 + α + β + γ funtions are shown in Fig. 20 for combinations α = 0.3, β = 0.3, γ = 0.3, α = 0.5, β = 0.4, γ = 0.4, α = 0.5, β = 0.6, γ = 0.6 and α = 0.7, β = 0.7, γ = 0.7 (orders 1.9, 2.3, 2.7 and 3.1). Fig. 21 introduces results of α + β + γ function for α = 0.5, β = 0.3, γ = 0.3, α = 0.3, β = 0.5, γ = 0.7 and α = 0.6, β = 0.6, γ = 0.7.
Fig. 20.
Simulation and experimental results of 1 + α + β + γ, functions for various combinations (a) magnitude characteristics, (b) phase characteristics.
Fig. 21.
Simulation and experimental results of α + β + γ, functions for various combinations (a) magnitude characteristics, (b) phase characteristics.
Orders of α + β + γ + δ
The last possibility with all four FO capacitors suggests both sections of the filter being set according to Table 6 depending on the values of FO orders. The denominator is:
| (15) |
Characteristics of α + β + γ + δ function (for α = 0.3, β = 0.3, γ = 0.5, δ = 0.3, α = 0.3, β = 0.6, γ = 0.5, δ = 0.4, α = 0.7, β = 0.5, γ = 0.6, δ = 0.4, α = 0.7, β = 0.7, γ = 0.6, δ = 0.6) are available in Fig. 22.
Fig. 22.
Simulation and experimental results of α + β + γ + δ, functions for various combinations (a) magnitude characteristics, (b) phase characteristics.
Pole frequency control
Other beneficial ability of the designed filter is the control of the pole frequency which can be adjusted by the change of transconductances gm1 to gm4 as long as the ratio between transconductances given by the FO approximation remains unchanged. This ability has been tested for three different pole frequencies (25 kHz, 50 kHz and 100 kHz) in case of α + β + γ function where α = β = γ = 0.5. The values of transconductances are specified in Table 7. As it can be seen from the graph, the possibility of the pole frequency control while maintaining the desired order of the filter is working as presumed. The limitation of the tunable range of f0 is the range in which used FO approximation stays valid (up to four decades for used 5th–order RC structures). This range can be extended by increasing the order of used RC structures (for the price of increasing circuit complexity).
Table 7.
Values of transconductances used for the pole frequency control.
| f0/transconductance | 25 kHz | 50 kHz | 100 kHz |
|---|---|---|---|
| gm1 [mS] | 0.47 | 0.93 | 1.87 |
| gm2 [mS] | 1.05 | 2.10 | 4.21 |
| gm3 [mS] | 0.73 | 1.46 | 2.91 |
| gm4 [mS] | 1.01 | 2.03 | 4.06 |
Stability analysis
The analysis of the stability of analog circuits, frequency filters, in particular, is an important part of the circuit design. Therefore, it is very important to determinate whether the filter will be stable or not. A general approach to stability analysis of fractional–order circuits by the transformation of the s–plane into a general plane that includes the fractional orders so called W–plane was introduced in [58]. W–plane is defined as s1/m, where m is a positive integer [58]. The unstable and stable regions of the s–plane transform into |θW| < π/2m and into π/2m < |θW| < π/m as suggested in Fig. 24. The region where |θW| > π/m is non–physical. Thus, the system will be stable if all roots in the W–plane lie in the region |θW| > π/2m and unstable if at least one root is in the region |θW| < π/2m. In order to investigate and prove the stability of the proposed fractional–order filter, positions of poles projected into the W–plane of various situations were carried out using a Matlab script based on the mathematical procedure introduced in [59]. Fig. 25, Fig. 26, Fig. 27 depict W–planes for the 3 + α filter, where Fig. 25 shows a situation for α = 0.3, Fig. 26 for α = 0.5 and Fig. 27 for α = 0.7. W–planes in case of the 2 + α + β filter are presented in Fig. 28, Fig. 29 and Fig. 30, respectively for situations α = β = 0.3, α = β = 0.5 and α = β = 0.7. The last three pictures (Fig. 31, Fig. 32 and Fig. 33) offer the W–planes of the 1 + α + β + γ filter for combinations of different fractional–orders (the first combination is α = 0.3, β = 0.5, γ = 0.7, the second one is α = 0.5, β = 0.7, γ = 0.3 and the third one is α = 0.7, β = 0.5, γ = 0.3). It is evident that the filter is stable for all tested cases.
Fig. 24.
W–plane regions [58]
Fig. 25.
Roots in the W–plane for 3 + α filter where α = 0.3.
Fig. 26.
Roots in the W–plane for 3 + α filter where α = 0.5.
Fig. 27.
Roots in the W–plane for 3 + α filter where α = 0.7.
Fig. 28.
Roots in the W–plane for 2 + α + β filter where α = β = 0.3.
Fig. 29.
Roots in the W–plane for 2 + α + β filter where α = β = 0.5.
Fig. 30.
Roots in the W–plane for 2 + α + β filter where α = β = 0.7.
Fig. 31.
Roots in the W–plane for 1 + α + β + γ filter where α = 0.3, β = 0.5, γ = 0.7.
Fig. 32.
Roots in the W–plane for 1 + α + β + γ filter where α = 0.5, β = 0.7, γ = 0.3.
Fig. 33.
Roots in the W–plane for 1 + α + β + γ filter where α = 0.7, β = 0.5, γ = 0.3.
Electronic control of the fractional order
As mentioned before, the proposed filter was implemented with RC networks to substitute the function of fractional–order capacitors due to rather high complexity of the constructed structure, unless it is all designed on one chip, and the complexity of the resulting control necessary for proper function. The electronic control of the fractional order and thus, the reconnection–less reconfiguration of both the integer and fractional order can be achieved by the replacement of the RC ladder structures by electronically adjustable emulators of a fractional–order capacitor/inductor introduced in [57], [29], [30], [31], for example. The other possible solution is to replace the building blocks (OTA + C) of the designed structure i.e. the integrator in this particular case by its fractional–order counterpart. Possible solutions of fractional–order integrators can be found in [60], [61], [62], for instance. For the demonstration of the electronic control of a fractional order, we have decided to adopt the approach described in [60]. The introduced structure is an electronically tunable integrator based on the FLF topology and approximated to function as a fractional–order integrator with order of α. Since the circuit in [60] operates in the voltage mode and the proposed filter requires an current–mode integrator (the input and output of each stage is current), the structure has been redesigned to operate in the current mode. The resulting current–mode integrator used for the aproximation on a fractional–order current–mode integrator is presented in Fig. 34.
Fig. 34.
Current–mode integrator based on FLF topology used for the aproximation of a fractional–order integrator.
The circuit in Fig. 34 is described by the equation:
| (16) |
The general transfer function of a fractional–order (lossless) integrator is given as H(s) = 1/(τs)α. The second–order approximation of sα is described as:
| (17) |
By the substitution of the general transfer function of a fractional–order integrator and the second–order approximation of sα, the transfer function takes form of:
| (18) |
Combining Eqs. (16), (18), the parameters of (16) for desired fractional order can be easily calculated. The values of transconductances and current gains of the FLF topology in Fig. 34, in correspondence with the desired fractional orders (0.3, 0.5 and 0.7) calculated for the center frequency being 100 kHz and C1 = 470 pF, C2 = 4.7 nF, are stated in Table 8.
Table 8.
Values of transconductances and current gains of the structure from Fig. 34 for chosen values of alpha.
| α/parameter | 0.3 | 0.5 | 0.7 |
|---|---|---|---|
| gm1 [µS] | 772.3 | 590.6 | 451.7 |
| gm2 [µS] | 449.4 | 295.3 | 164.1 |
| B1 [–] | 0.4 | 0.2 | 0.09 |
| B2 [–] | 1 | 1 | 1 |
| B3 [–] | 2.5 | 5 | 11.8 |
The function of the designed fractional–order integrator has been tested in case of simulations for functions 3 + α, 2 + α and 1 + α (OTA4 and C4 in Fig. 2 were replaced by the integrator from Fig. 34) for α being equal to 0.3, 0.5 and 0.7 and the results are compared with simulation results of the coresponding solutions with the RC structures (Section ‘Orders of 3+α, 2+α and 1+α’). The values of parameters of the filter (transconductances and current gains of the filter itself not the circuit from Fig. 34) are the same as in Section ‘Orders of 3+α, 2+α and 1+α’. Fig. 35, Fig. 36, Fig. 37 compare the simulation results of the filter when using the RC structure (black dashed lines) with the simulation results of the filter when using the FO integrator (colored lines). The results yeald a good agreement with each other and support the possible employment of the electronic control of the fractional order. There is a slight shift in the frequency for the resutls with the FO integrator increasing the operational frequency as α is getting higher nonetheless, this undesired behavior can be compensated as demostrated in subsection Electronic control of the fractional order.
Fig. 35.
Simulation results of 3 + α, 2 + α and 1 + α orders for the solution with the RC structure and FO integrator when a = 0.3 (a) magnitude characteristics, (b) phase characteristics.
Fig. 36.
Simulation results of 3 + α, 2 + α and 1 + α orders for the solution with the RC structure and FO integrator when a = 0.5 (a) magnitude characteristics, (b) phase characteristics.
Fig. 37.
Simulation results of 3 + α, 2 + α and 1 + α orders for the solution with the RC structure and FO integrator when a = 0.7 (a) magnitude characteristics, (b) phase characteristics.
Conclusion
The proposed structure of a FO reconnection–less reconfigurable filter can offer LP functions of 3 + α, 2 + α, 1 + α, 2 + α + β, 1 + α + β, α + β, 1 + α + β + γ, α + β + γ and α + β + γ + δ (plus 4 additional functions if considering that the filter can provide integer–order functions as well as suggested in chapters describing the design and measurement of the proposed integer-order filter) in dependence on the setting of control gains B1 to B4 and replacement of standard integer–order capacitors by their FO counterparts offering an additional degree of freedom when it comes to the obtainable values of the filter order. The theoretical, simulation and experimental results, which are available for various combinations of orders (see Fig. 12, Fig. 13, Fig. 14, Fig. 15, Fig. 16, Fig. 17, Fig. 18, Fig. 19, Fig. 20, Fig. 21, Fig. 22), confirm the design intentions. The full electronic control of the order can be achieved if the used RC structures are replaced by the electronically controllable FO impedance emulators which is supported by simulation results in Fig. 35, Fig. 36, Fig. 37. The controllability of the pole frequency is supported by the results in Fig. 23 for three settings. The stability analysis of the proposed structure for various orders is shown in Fig. 24, Fig. 25, Fig. 26, Fig. 27, Fig. 28, Fig. 29, Fig. 30, Fig. 31, Fig. 32, Fig. 33. All simulation and experimental results are in good correlation with each other. Considering the lowest and highest value of the RC networks being 0.1 and 0.9, for example, the proposed filter could offer a LP function of the theoretical order range from 0.4 up to 3.6. In other words, it can be fairly simple to choose an order which best fits the situation in relatively wide range of available orders.
Fig. 23.
Demonstration of the f0 adjustability for three different settings for α + β + γ function where α = β = γ = 0.5.
Declaration of Competing Interest
The authors declared that there is no conflict of interest.
Acknowledgements
This article is based upon work from COST Action CA15225, a network supported by COST (European Cooperation in Science and Technology). Research described in this paper was financed by the Ministry of Education, Youth and Sports under grant LTC18022 of INTER-COST program. For the research, infrastructure of the SIX Center was used.
Footnotes
Peer review under responsibility of Cairo University.
References
- 1.Elwakil A.S. Fractional-order circuits and systems: An emerging interdisciplinary research area. IEEE Circuits Syst Mag. 2010;10(4):40–50. [Google Scholar]
- 2.Freeborn T.J. A survey of fractional-order circuitmodels for biology and biomedicine. IEEE J Emerging Sel Top Circuits Syst. 2013;3(3):416–424. [Google Scholar]
- 3.Freeborn T., Maundy B., Elwakil A.S. Extracting the parameters of the double-dispersion Cole bioimpedance model from magnitude response measurements. Med Biol Eng Comput. 2014;52(9):749–758. doi: 10.1007/s11517-014-1175-5. [DOI] [PubMed] [Google Scholar]
- 4.Freeborn T., Maundy M., Elwakil A.S. Cole impedance extractions from the step-response of a current excited fruit. Comput Electron Agric. 2013;98:100–108. [Google Scholar]
- 5.Kubanek D., Freeborn T., Koton J. Fractional-order band-pass filter design using fractional-characteristic specimen functions. Microelectron J. 2019;86:77–86. [Google Scholar]
- 6.Mishra S.K., Gupta M., Upadhyay D.K. Active realization of fractional order Butterworth lowpass filter using DVCC. J King Saud Univ – Eng Sci. 2020;32(2):158–165. [Google Scholar]
- 7.Kaskouta E., Kamilaris T., Sotner R., Jerabek J., Psychalinos C. Proc 41st international conference on telecommunications and signal processing (TSP), 2018, Athens, Greece. 2018. Single-input multiple-output and multiple-input single-output fractional-order filter designs; pp. 356–359. [Google Scholar]
- 8.Kamath D.V., Navya S., Soubhagyaseetha N. Proc. 2nd international conference on inventive communication and computational technologies (ICICCT 2018), 2018, Coimbatore, India. 2018. Fractional order OTA-C current-mode all-pass filter; pp. 383–387. [Google Scholar]
- 9.Mishra S.K., Gupta M., Upadhyay D.K. Proc. 2nd international conference on power, energy and environment: towards smart technology (ICEPE), 2018, Shillong, India. 2018. A low-power compact DDCC based fractional-order filter; pp. 1–6. [Google Scholar]
- 10.Verma R., Pandey N., Pandey R. Electronically tunable fractional order filter. Arab J Sci Eng. 2017;42:3409–3422. [Google Scholar]
- 11.Soni A., Gupta M. Proc 2nd IEEE international conference on power electronics, intelligent control and energy systems (ICPEICES-2018), 2018, Delhi, India. 2018. Design of fractional order butterworth filter using genetic algorithm; pp. 1052–1055. [Google Scholar]
- 12.Hassanein A.M., Soltan A., Said L.A., Madian A.H., Radwan A.G. Proc 2019 novel intelligent and leading emerging sciences conference (NILES), 2019, Giza, Egypt. 2019. Analysis and design of fractional-order low-pass filter with three elements of independent orders; pp. 218–221. [Google Scholar]
- 13.Tutaj A., Piatek P., Bauer W., Baranowski J. Proc 42nd international conference on telecommunications and signal processing (TSP), 2019, Budapest, Hungary. 2019. Approximating fractional filters with analogue active filter structures; pp. 440–444. [Google Scholar]
- 14.Tsirimokou G., Koumousi S., Psychalinos C. Design of fractional-order filters using current feedback operational amplifiers. J Eng Sci Technol Rev. 2016;9(4):77–81. [Google Scholar]
- 15.Khateb F., Kubánek D., Tsirimokou G., Psychalinos C. Fractional-order filters based on low-voltage DDCCs. Microelectr J. 2016;50:50–59. [Google Scholar]
- 16.Verma R., Pandey N., Pandey R. CFOA based low pass and high pass fractional step filter realizations. Int J Electron Commun (AEÜ) 2019;99:161–176. [Google Scholar]
- 17.Maundy B., Elwakil A.S., Freeborn T.J. On the practical realization of higher-order filters with fractional stepping. Signal Process. 2011;91(3):484–491. [Google Scholar]
- 18.Jerabek J., Sotner R., Dvorak J., Langhammer L., Koton J. Proc international conference on applied electronics (AE), 2016, Pilsen, Czech Republic. 2016. Fractional-order high-pass filter with electronically adjustable parameters; pp. 1–6. [Google Scholar]
- 19.Bhat M.V., Bhat S.S.S., Kamath D.V. Proc 3rd international conference on electronics communication and aerospace technology (ICECA 2019), 2019, Coimbatore, India. 2019. Gm-C current mode fractional all pass filter of order α (0 < α < 1) pp. 240–245. [Google Scholar]
- 20.Ahmed O.I., Yassin H.M., Said L.A., Psychalinos C., Radwan A.G. Proc. novel intelligent and leading emerging sciences conference (NILES), 2019, Giza, Egypt. 2019. Tunable fractional-order band-pass filter of order 2α; pp. 76–79. [Google Scholar]
- 21.Langhammer L., Sotner R., Dvorak J., Dostal T. Fully-differential multifunctional electronically configurable fractional-order filter with electronically adjustable parameters. Elektronika Ir Elektrotechnika. 2018;24(5):42–45. [Google Scholar]
- 22.Tsirimokou G., Sotner R., Jerabek J., Koton J., Psychalinos C. Proc 40th international conference on telecommunications and signal processing (TSP), 2017, Barcelona, Spain. 2017. Programmable analog array of fractional-order filters with CFOAs; pp. 706–709. [Google Scholar]
- 23.Bertsias P., Khateb F., Kubanek D., Khanday F.A., Psychalinos C. Capacitorless digitally programmable fractional-order filters. Int J Electron Commun (AEÜ) 2017;78:228–237. [Google Scholar]
- 24.Dar M.R., Kan N.A., Khanday F.A., Tsirimokou G., Psychalinos C. Proc 3rd international conference on electrical, electronics, engineering trends, communication, optimization and sciences (EEECOS 2016), 2016, Tadepalligudem, India, 2016. Design of fractional-order multiphase sinusoidal oscillators; pp. 1–5. [Google Scholar]
- 25.Elwy O., Said L.A., Madian A.H., Radwan A.G. Proc. 30th international conference on microelectronics (ICM), 2018, Sousse, Tunisia. 2018. Fractional-order relaxation oscillators based on Op-Amp and OTRA; pp. 212–215. [Google Scholar]
- 26.Said L.A., Elwy O., Madian A.H., Radwan A.G., Soliman A.M. Stability analysis of fractional-order Colpitts oscillators. Analog Integr Circ Sig Process. 2019;101:267–279. [Google Scholar]
- 27.Soltan A., Xia L., Jackson A., Chester G., Degenaar P. Proc 4th IEEE international conference on applied system innovation (ICASI 2018), 2018, Chiba, Japan. 2018. Fractional order PID system for suppressing epileptic activities; pp. 1–4. [Google Scholar]
- 28.Bauery W., Baranowskiy J., Kapoulea S., Psychalinos C. Proc 24th international conference on methods and models in automation and robotics (MMAR), 2019, Międzyzdroje, Poland. 2019. Digital and analog design of fractional PD controller for a servo system; pp. 472–477. [Google Scholar]
- 29.Kapoulea S., Psychalinos C., Elwakil A.S., Radwan A.G. One-terminal electronically controlled fractional-order capacitor and inductor emulator. Int J Electron Commun (AEÜ) 2019;103:32–45. [Google Scholar]
- 30.Sotner R., Polak L., Jerabek J., Petrzela J. Simple two operational transconductance amplifiers-based electronically controllable bilinear two port for fractional-order synthesis. Electron Lett. 2018;54(20):1164–1166. [Google Scholar]
- 31.Bertsias P., Psychalinos C., Maundy B.J., Elwakil A.S., Radwan A.G. Partial fraction expansion–based realizations of fractional-order differentiators and integrators using active filters. Int J Circuit Theory Appl. 2019;47(4):513–531. [Google Scholar]
- 32.Sotner R., Langhammer L., Jerabek J., Ushakov P.A., Dostal T. Fractional-order phase shifters with constant magnitude frequency responses. Elektronika Ir Elektrotechnika. 2019;25(5):25–30. [Google Scholar]
- 33.Kapoulea S., Tsirimokou G., Psychalinos C., Elwakil A.S. Proc novel intelligent and leading emerging sciences conference (NILES), 2019, Giza, Egypt. 2019. OTA-C implementation of fractional-order lead/lag compensators; pp. 38–41. [Google Scholar]
- 34.Haba T.C., Ablart G., Camps T., Olivie F. Influence of the electrical parameters on the input impedance of a fractal structure realised on silicon. Chaos Solitons Fractals. 2005;24(2):479–490. [Google Scholar]
- 35.Biswas K., Sen S., Dutta P.K. Realization of a constant phase element and its performance study in a differentiator circuit. IEEE Trans Circ Syst—II: Express Briefs. 2006;53(9):802–806. [Google Scholar]
- 36.Krishna M.S., Das S., Biswas K., Goswami B. Fabrication of a fractional order capacitor with desired specifications: a study on process identification and characterization. IEEE Trans Electron Devices. 2011;58(11):4067–4073. [Google Scholar]
- 37.Sotner R., Langhammer L., Domansky O., Petrzela J., Jerabek J., Dostal T. Proc 15th IEEE international conference synthesis, modeling, analysis and simulation methods and applications to circuit design (SMACD 2018), 2018, Prague, Czech Republic. 2018. New reconfigurable universal SISO biquad filter implemented by advanced CMOS active elements; pp. 257–260. [Google Scholar]
- 38.Jerabek J., Sotner R., Polak J., Vrba K., Dostal T. Reconnectionless electronically reconfigurable filter with adjustable gain using voltage differencing current conveyor. Elektronika ir Elektrotechnika. 2016;22(6):39–45. [Google Scholar]
- 39.Langhammer L., Sotner R., Dvorak J., Dostal T. Proc 26th international conference mixed design of integrated circuits and systems (MIXDES2019), 2019, Rzeszow, Poland. 2019. Novel design solution of reconnection-less electronically reconfigurable filter; pp. 1–5. [Google Scholar]
- 40.Sotner R., Petrzela J., Jerabek J., Vrba K., Dostal T. Proc 25th int conf radioelektronika, 2015, Pardubice, Czech Republic. 2015. Solutions of reconnection-less OTA-based biquads with electronical transfer response reconfiguration; pp. 40–45. [Google Scholar]
- 41.Nise N.S. IEEE Press; 1996. Signal-flow graphs. The control handbook. 1566 pages. [Google Scholar]
- 42.Langhammer L., Sotner R., Dvorak J. Proc IEEE 2018 41st international conference on telecommunications and signal processing (TSP2018), 2018, Athens, Greece. 2018. Modification of current follower/amplifier with controllable intrinsic resistance; pp. 70–73. [Google Scholar]
- 43.Sponar R., Vrba K. Measurements and behavioral modelling of modern conveyors. Int J Comput Sci Netw Security. 2006;3A(6):57–63. [Google Scholar]
- 44.UCC-N1B – Universal Current Conveyor (UCC) and Second-Generation Current Conveyor (CCII+/-) (datasheet). Czech Republic: Brno University of Technology; 2010 [accessible on http://www.utko.feec.vutbr.cz/~koton/soubory/UCC_N1B_Rev0.pdf].
- 45.Linear Technology, LT1228 Current feedback amplifier with DC gain control (datasheet) [accessible on http://cds.linear.com/docs/en/datasheet/1228fd.pdf].
- 46.Intersil (Elantec), EL4083 CN Current-mode multiplier (datasheet); 1996 [accessible on www.digchip.com/datasheets/parts/datasheet/235/EL4083CN-pdf.php].
- 47.Intersil (Elantec), EL2082 CN Current-mode multiplier (datasheet); 1996 [accessible on http://pdf.datasheetcatalog.com/datasheet/elantec/EL2082CN.pdf].
- 48.Texas Instruments – OPA860 – Wide Bandwidth Operational Transconductance Amplifier (datasheet) [accessible on http://www.ti.com/lit/ds/symlink/opa860.pdf].
- 49.Jerabek J., Sotner R., Vrba K. Electronically adjustable triple-input single-output filter with voltage differencing transconductance amplifier. Revue Roumaine des Sciences Techniques – Serie ´Electrotechnique et ´Enerǵetique. 2015;59(2):163–172. [Google Scholar]
- 50.Jerabek J., Sotner R., Vrba K. Proc 36th international conference on telecommunications and signal processing (TSP 2013), 2013, Rome, Italy. 2013. General current-mode filtering structure with controllable current active elements; pp. 402–406. [Google Scholar]
- 51.Sotner R., Herencsar N., Jerabek J., Prokop R., Kartci A., Dostaland T. Z-copy controlled-gain voltage differencing current conveyor: advanced possibilities in direct electronic control of first-order filter. Elektronika ir. 2014;20(6):77–83. [Google Scholar]
- 52.Texas Instruments – OPA861 – Wide Bandwidth Operational Transconductance Amplifier (datasheet) [accessible on http://www.ti.com/lit/ds/symlink/opa861.pdf].
- 53.Hajek K., Sedlacek J. Proc of the conference CIBLIS’97, 1997, Leicester, United Kingdom. 1997. NAFID program as powerful tool in filter education area. pp. PK-4 1–10. [Google Scholar]
- 54.Deliyannis T., Sun Y., Fidler J.K. CRC Press; US: 1998. Continuous-time active filter design. [Google Scholar]
- 55.Tsirimokou G. A systematic procedure for deriving RC networks of fractional-order elements emulators using MATLAB. Int J Electron Commun (AEÜ) 2017;78:7–14. [Google Scholar]
- 56.Sugi M., Hirano Y., Miura Y.F., Saito K. Simulation of fractal immitance by analog circuits: an approach to the optimized circuits. IEICE Trans Fundam Electron Commun Comput Sci. 1999;E 82(8):1627–1634. [Google Scholar]
- 57.Dvorak J., Kubanek D., Herencsar N., Kartci A., Bertsias P. Electronically adjustable emulator of the fractional-order capacitor. Elektronika Ir Elektrotechnika. 2019;25(6):28–34. [Google Scholar]
- 58.Radwan A.G., Soliman A.M., Elwakil A.S., Sedeek A. On the stability of linear systems with fractional-order elements. Chaos Solitons Fractals. 2009;40(5):2317–2328. [Google Scholar]
- 59.Petráš I. Stability of fractional-order systems with rational orders: a survey. Fract Calculus Appl Anal. 2009;12(3):269–298. [Google Scholar]
- 60.Dar M.R., Kant N.A., Khanday F.A. Realization of fractional-order double-scroll chaotic system using operational transconductance amplifier (OTA) J Circ Syst Comput. 2018;27(1):1–15. [Google Scholar]
- 61.Dar M.R., Kant N.A., Khanday F.A. Electronic implementation of fractional-order Newton-Leipnik chaotic system with application to communication. J Comput Nonlinear Dyn. 2017;12(5):1–5. [Google Scholar]
- 62.Tsirimokou G., Psychalinos C., Freeborn T.J., Elwakil A.S. Emulation of current excited fractional-order capacitors and inductors using OTA topologies. Microelectron J. 2016;55:70–81. [Google Scholar]