The neural foundations of handedness: insights from a rare case of deafferentation

Abstract

The role of proprioceptive feedback on motor lateralization remains unclear. We asked whether motor lateralization is dependent on proprioceptive feedback by examining a rare case of proprioceptive deafferentation (GL). Motor lateralization is thought to arise from asymmetries in neural organization, particularly at the cortical level. For example, we have previously provided evidence that the left hemisphere mediates optimal motor control that allows execution of smooth and efficient arm trajectories, while the right hemisphere mediates impedance control that can achieve stable and accurate final arm postures. The role of proprioception in both of these processes has previously been demonstrated empirically, bringing into question whether loss of proprioception will disrupt lateralization of motor performance. In this study, we assessed whether the loss of online sensory information produces deficits in integrating specific control contributions from each hemisphere by using a reaching task to examine upper limb kinematics in GL and five age-matched controls. Behavioral findings revealed differential deficits in the control of the left and right hands in GL and performance deficits in each of GL’s hands compared with controls. Computational simulations can explain the behavioral results as a disruption in the integration of postural and trajectory control mechanisms when no somatosensory information is available. This rare case of proprioceptive deafferentation provides insights into developing a more accurate understanding of handedness that emphasizes the role of proprioception in both predictive and feedback control mechanisms.

NEW & NOTEWORTHY The role of proprioceptive feedback on the lateralization of motor control mechanisms is unclear. We examined upper limb kinematics in a rare case of peripheral deafferentation to determine the role of sensory information in integrating motor control mechanisms from each hemisphere. Our empirical findings and computational simulations showed that the loss of somatosensory information results in an impaired integration of control mechanisms, thus providing support for a complementary dominance hypothesis of handedness.

INTRODUCTION

Neural lateralization refers to the asymmetry in neural circuitry between analogous regions of the two sides of the central nervous system. Lateralization is a fundamental organizing feature across a large spectrum of vertebrate nervous systems. However, while lateralization of language, cognitive, emotional, and perceptual processes have been well described (Gazzaniga 2005), the neural foundations of motor lateralization that give rise to handedness in primates remains controversial (Marcori and Okazaki 2020). Here we asked whether motor lateralization is dependent on proprioceptive feedback by examining a rare case of peripheral somatosensory deafferentation.

The paramount role of somatosensory feedback is well established in current models of motor control, evidenced by severe deficits in movement coordination that result from somatosensory deficits (Ghez et al. 1990; Marsden et al. 1984; Sainburg et al. 1993) and by the fact that accuracy of the limb position estimates degrades over time when somatosensation is not available (Medina et al. 2010). To examine the role of somatosensory feedback in lateralization and in differentiating between feedforward and feedback components of motor control, it is necessary to examine behaviors in the complete absence of such feedback, i.e., peripheral deafferentation. GL is an individual with chronic, permanent deafferentation acquired at age 31. While GL has a neurologically intact brain, which suggests the presence of intact motor control networks and intact interhemispheric connections, her somatic sensation of limb posture and movement are absent due to the loss of large fiber afferent projections bilaterally throughout her trunk and her upper and lower extremities. Studies in GL and a few other rare cases of deafferentation have observed profound deficits of intersegmental coordination and of limb stabilization at the end of reaching movements, suggestive of both poor optimal control of trajectory and poor impedance control of stable final postures (Ghez and Sainburg 1995; Gordon et al. 1995; Messier et al. 2003; Sainburg et al. 1993). To our knowledge, differences in control strategies employed by each hand in the absence of peripheral feedback have not been determined until now.

Historically, two competing hypotheses of motor lateralization have been proposed to explain differences in how people move their hands. Global dominance hypotheses propose that the dominant hemisphere is superior in all aspects of motor control while the nondominant hemisphere is inferior in all aspects of motor control (Annett et al. 1979; Liepmann 1908; Volkmann et al. 1998; Ziemann and Hallett 2001). In contrast, complementary dominance hypotheses propose that each hemisphere is specialized for specific aspects of motor control (Fisk and Goodale 1988; Haaland et al. 2004). We have provided evidence that the dominant left hemisphere (in right-handed individuals) is specialized or “tuned” to control dynamic aspects of movement (e.g., movement trajectories) while the nondominant right hemisphere is specialized for stabilization of the limb about desired setpoints (i.e., posture control) during reaching tasks (Mutha et al. 2012; Sainburg 2005; Wang and Sainburg 2007; Yadav and Sainburg 2014a). Although manual interaction with people and things requires movement control and postural stabilization in both hands, the complementary dominance hypothesis explains not only advantages in performance of dynamic movement tasks with the dominant hand and stabilizing tasks with the nondominant hand (Sainburg 2016) but also patterns of sensorimotor deficits after brain injuries, such as stroke (Haaland and Harrington 1989a, 1989b; Schaefer et al. 2009). According to complementary dominance hypotheses, although both hemispheres contribute different aspects of motor control to each arm, it is the contralateral, not ipsilateral, hemisphere that has a greater influence on control of each arm. We previously modeled this combination of hemisphere-specific control as a serial process, with variation in the time that the postural controller is recruited (Scheidt and Ghez 2007; Yadav and Sainburg 2011, 2014b). These models suggest that control of the nondominant left hand shows an early shift from optimizing smooth and efficient trajectories to achieving accurate and stable final postures while the dominant right hand shows a later shift in control. However, these studies were conducted under the assumption that the two complementary (trajectory and postural) controllers received accurate somatosensory information that may be used to integrate/combine the output of each controller.

We hypothesized that motor lateralization is dependent on accurate proprioceptive feedback to combine control mechanisms from each hemisphere regardless of hemispheric dominance. Secondary to this hypothesis, we made predictions regarding the two popular hypotheses on handedness in a condition of complete somatosensory deafferentation. In the global dominance hypothesis, we predicted that if proprioceptive feedback were absent, the dominant hand would perform poorly in all aspects of movement as would the nondominant hand, but there would be no difference between the two hands in terms of the aspects of movement they performed poorly on. In the complementary dominance hypothesis, we predicted that the dominant hand would perform more poorly in producing accurate and stable final postures, while the nondominant hand would perform more poorly in control of trajectory dynamics. To test our hypothesis and accompanying predictions, we compared unilateral movement of each hand in a rare case of human somatosensory deafferentation (GL) as well as in age-matched controls. Here we describe how GL and a group of neurologically intact individuals completed a unilateral reaching task on a virtual reality setup (Fig. 1). Without visual feedback, control participants rely completely on somatosensation while GL has no online peripheral feedback about her movements. We then describe how a hybrid computational model of arm movement and posture control efficiently simulates the behavior of GL and the control participants. We conclude by discussing the implications of deafferentation in developing a more accurate understanding of the neural foundations of handedness.

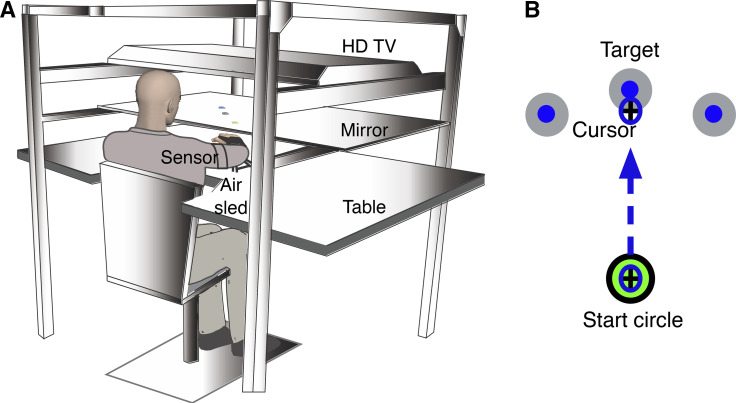
Fig. 1.

Experimental setup. A: an illustration of the KineReach setup showing a participant seated in front of a table with an inverted HD monitor that displayed the task on a mirrorized screen placed at chin level; this screen occluded direct view of the hands. Sensors placed on the hand and upper arm collected data used to compute orientation and location of the wrist, elbow, and shoulder joints. Each hand was supported on an air sled that produced continuous pressurized air to reduce the mechanical effects of friction and gravity. B: schematic of the unilateral reaching task showing movement of a cursor (representing the position of the hand) to the middle target (1 target presented per trial). Participants were asked to move the cursor to the target (appearing in 1 of 3 directions in a pseudorandom manner) within 1 s. The task consisted of 90 trials performed with each of the left and right hands separately. Visual feedback of the cursor was removed upon moving beyond the start circle.

MATERIALS AND METHODS

Participants.

We recruited GL (woman; age: 70 yr), who has been living with large-fiber sensory neuropathy for ~40 yr. Biopsies of GL showed lack of large diameter afferent neurons, resulting in the loss of bilateral proprioception and tactile information from the nose down (Forget and Lamarre 1987, 1995; Gordon et al. 1995). Nerve stimulation studies normally showed a fast and slow peak in the compound action potential; however, the fast peak did not occur in GL, indicating a loss of large diameter sensory fibers (Forget and Lamarre 1987). GL has been confined to a wheelchair since the neuropathy onset at age 31 and performs activities of daily living (e.g., toileting, self-grooming, dressing, eating, showering) without assistance but under constant visual guidance. She has shown no sign of recovery since the presumed viral attack ~40 yr ago (Cole and Paillard 1995; Sarlegna et al. 2010). Before the acquired deafferentation, GL self-reported to have been right-hand dominant. At the time of testing, her laterality quotient was 80%, according to the 10-item version of the Edinburgh Handedness Inventory (Oldfield 1971). We also recruited five neurologically intact age-matched right-hand dominant individuals (4 women; mean age: 67 yr ± 2.91 SD) for comparison purposes. Exclusion criteria for the neurologically intact participants included any current or prior upper extremity motor disorder or stroke and any cognitive disorders that would make it difficult to follow simple instructions. The Edinburgh Handedness Inventory was used to confirm hand dominance in controls, with all five participants having a 100% laterality quotient. We received written informed consent from all participants before study initiation (the consent form and all study procedures were translated word-for-word from English to French for GL by a native French speaker). All study procedures were approved by the Pennsylvania State University’s Institutional Review Board.

Experimental setup.

We used the KineReach virtual reality motion tracking system to implement all tasks (Fig. 1A). Participants were seated on a height-adjustable chair in front of the system, with all arm joints distal to the elbow immobilized using an adjustable brace. Limb position and orientation of each arm were recorded at 116 Hz using two 6-degree-of-freedom magnetic sensors (trakStar; Ascension Technology) placed on the hand and upper arm. We computed 10-degree-of-freedom arm movements from digitized bony landmarks that allowed estimation of the wrist, elbow, and shoulder joints. Each hand was supported on an air sled that produced continuous pressurized air to reduce the mechanical effects of friction and gravity on arm movement. An inverted HD monitor displayed the task on a mirrorized screen placed at chin level, and this projection appeared in the same horizontal plane as the hand. The screen occluded direct view of the hands. A cursor represented the position of the index finger in real-time, a circle (diameter 4 cm) appeared at the beginning of each trial to signify the start position, and another circle (diameter 3.5 cm) appeared 20 cm from the start position to signify the target. A trial lasted 1 s and consisted of a target appearing in one of three locations (90° from start, 35° clockwise from start, 35° counterclockwise from start) in a pseudorandom manner, followed by a reaching movement.

Task.

All participants completed a unilateral reaching task with each of the left and right hands (90 trials per hand i.e., 30 trials per target). Participants were asked to move the cursor from the start circle to the target within 1 s (Fig. 1B). The target remained visible until the end of the trial. Visual feedback of the cursor was removed the moment it moved out of the start position, and visual feedback of the movement trajectory was provided at the end of each trial. Participants were asked to make one rapid movement into the target, without any corrective movements, and to stop in the target. After a 2-s delay, the next target was displayed, and the participants were then provided cursor feedback to allow repositioning into the start position. There was no set time between trials, with a trial beginning only when the cursor returned into the start circle and remained there for 300 ms.

Data analysis.

All kinematic data were processed and analyzed using custom programs designed on IgorPro (version 6.37; WaveMetrics). Movement onset was defined as the first minimum of tangential velocity that was <8% of peak velocity. Movement offset was considered to be at the first minimum of tangential velocity appearing after peak velocity that was <8% of peak velocity. Substantial movements produced after the initial movement were examined and classified as either drift or oscillations depending on the behavior. Error at the end of movement was measured as the distance between target center and cursor position at the end of the trial. Initial direction error was determined to be the angle between two line segments: the line connecting the start circle and the cursor’s position at peak velocity, and the line connecting the target and start circle.

We compared behaviors in each hand of GL to the corresponding hand in the control group (n = 5) on each of the two measures of performance (initial direction error and error at the end of movement) using the Crawford and Howell modified t test (Crawford and Garthwaite 2012; Crawford and Howell 1998), which has been widely used in single case-controls study designs such as ours (Čeko et al. 2013; Cuadra et al. 2019; Lafargue et al. 2003). The modified t test calculates the t statistic using the following equation:

$$t=\frac{x-\overline{x}}{s\sqrt{\left(n+1\right)/n}}$$

where x represents GL’s mean, $\overline{x}$ and s are the mean and SD of the control sample, and $n$ is the size of the control sample. This test is designed to be robust against small control sample sizes, departures from normality, and very severe skew in the data set, which is expected in study designs such as ours (Crawford et al. 2006; Crawford and Garthwaite 2012). We also calculated effect sizes using z_cc, which is an analog of Cohen’s d that is suitable for single case-control study designs since it uses the control sample’s standard deviation instead of the pooled standard deviation and is also insensitive to the size of the control sample (Crawford et al. 2010).

To assess the extent of within-subject differences, i.e., between the left and right hand on each dependent variable, we used the revised standardized difference test (RSDT), which has been shown to be useful in comparing a single case to a small control sample (Crawford et al. 2010; Crawford and Garthwaite 2005). This method uses Bayesian methods to standardize the difference in performance on two tasks in a case (i.e., GL) to that in a control sample, thus allowing us to judge whether significant performance differences between the left and right hand in GL are actually unusual or whether such differences are common even in controls. This also reduces the likelihood of making type I errors (Crawford et al. 2010). We calculated effect sizes for these comparisons using a different z score, z_DCC, which computes the difference between the scores on the two tasks in the case (i.e., GL) by standardizing to the control sample’s means and standard deviations on the two tasks and by determining the correlation between these tasks in the control sample (Crawford et al. 2010).

We used the Singlims_ES.exe and RSDT_ES.exe programs to implement these modified t tests and to calculate effect sizes (Crawford et al. 2010). The family-wise error rate was alpha = 0.05, and we used the Bonferroni correction to set the individual test P threshold for each family (3 comparisons per dependent variable) to 0.0167. Therefore, a comparison was deemed “statistically significant” when the null hypothesis was rejected by a P threshold of 0.0167.

Simulations.

We used a two-segment model of the upper limb to perform forward dynamic simulations of goal-directed reaching movements. The limb was subject to control actions, provided by a trajectory and postural controller (Scheidt and Ghez 2007). Segment lengths and centers of mass were determined using Winter’s equations (Winter 1990). We varied three parameters in this model: 1) joint stiffness, 2) joint damping, and 3) time of switch from trajectory to postural control. For simulating pure forms of control, i.e., when the controller essentially acts alone without input from the other controller as well as typical human movement, we set joint stiffness to 2 Nm/rad. We set joint damping to 0.15 Nm·s·rad⁻¹ to simulate the pure postural controller in GL and 10 Nm·s·rad⁻¹ to simulate typical human movement. Previous studies have provided a range of values for these two parameters (Bennett et al. 1992; Milner and Cloutier 1998; Shadmehr and Mussa-Ivaldi 1994; Yadav and Sainburg 2014b). We chose stiffness and damping values that were within the published range. When simulating GL’s movements, we defined “high” and “low” joint stiffness as 2 Nm/rad and 0.02 Nm/rad, respectively. The corresponding joint damping was set to 0.15 Nm·s·rad⁻¹ and 0.0015 Nm·s·rad⁻¹, respectively. We estimated these stiffness and damping values by fitting a second-order mechanical model to GL’s nondominant hand’s underdamped response to a step change in desired hand position. Joint damping in a deafferented individual is small but nonzero because even when the threshold for stretch reflex cannot be achieved, fractional damping effects that are inherent to muscle mechanical properties are still present (Houk et al. 2002). These stiffness and damping values were consistent with antagonist muscle coactivation in the absence of large-fiber afferent feedback, and included contributions from passive muscle and connective tissue resistance, without reflex-mediated input (Bizzi et al. 1984). The pure trajectory controller was controlled solely by feedforward torques at the elbow and shoulder joints, while the pure postural controller involved a near-instantaneous jump in desired limb posture. The mixing of two controllers required manipulating the switch time parameter. Here, an “early” switch in control was defined as a switch time occurring at 25% of the ideal movement’s duration, thus favoring postural stabilization. A “late” switch in control was defined as a switch time occurring at 70% of the ideal movement duration, favoring online trajectory control over postural stabilization. An assumption was made that peak velocity would be achieved at 50% of the movement trajectory. We switched to postural control at peak velocity (i.e., at 50% of the movement trajectory) or postpeak velocity (i.e., at 70% of the movement trajectory) to simulate typical left- and right-hand behavior, respectively (Sainburg and Schaefer 2004).

RESULTS

Without somatosensory feedback, the dominant right hand drifts and the nondominant left hand oscillates at movement’s end.

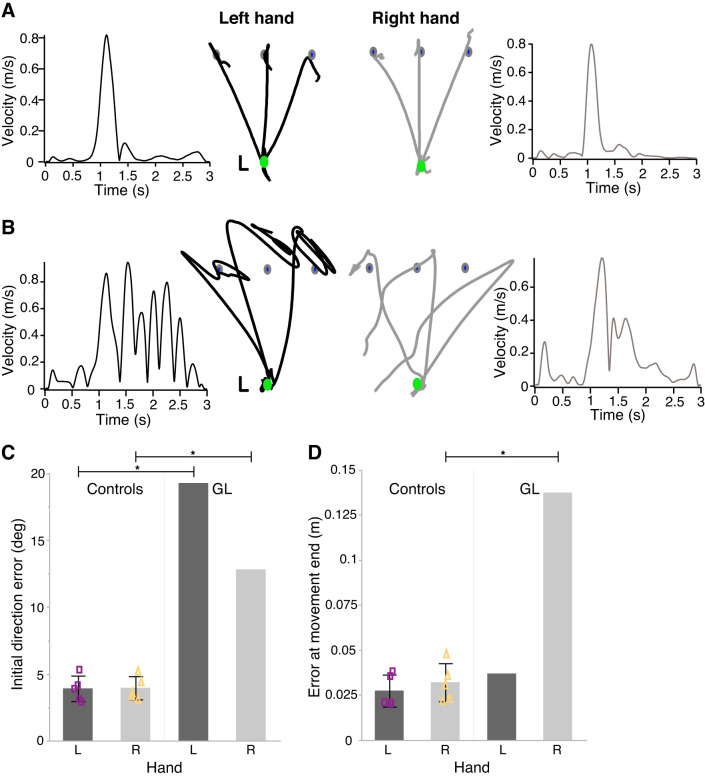
Figure 2 shows representative hand paths and velocity profiles from a control participant (Fig. 2A) and a patient (GL) deprived of limb somatosensory input (Fig. 2B). Control participants made fairly straight and accurate movements toward each target, with few terminal oscillations, regardless of movement direction and hand. By contrast, GL’s movements were substantially curved and showed large errors in both initial direction and at the end of movement. The most striking finding was the substantial differences between the kinematic behavior of the two hands at the end of the initial movement in GL but not in controls. While GL’s left hand was far less accurate in its initial movement direction, movement termination did occur close to the target despite substantial oscillations (note the multiple peaks in her velocity profile in the left-most plot in Fig. 2B). Movements made with GL’s right hand showed somewhat better initial direction accuracy, but they failed to stabilize the hand near the target and instead exhibited substantial terminal drift.

Fig. 2.

Different behaviors exhibited by each hand in the absence of somatosensation. Substantial performance differences between hands are evident in the deafferented patient’s (GL) movements but not in those of neurologically intact control participants. A and B: hand paths and velocity profiles are shown in a representative participant in the control group (A) and in GL (B). Scale bars = 2-cm hand movement. C and D: mean initial direction error (C) and mean error at movement’s end (D) are displayed for each hand of control participants and GL (woman). Error bars in control data represent 1 SD from the mean (n = 5, 4 women). Mean values for each control participant are plotted as purple squares [left hand (L)] or yellow triangles [right hand (R)]. Crawford and Howell modified t test was used: *P < 0.001, statistically significant difference.

Poor accuracy at the end of movement in the dominant hand and poor trajectory control in the nondominant hand of the deafferented patient.

Figure 2, C and D, shows that differences in performance observed between the hands were consistent, regardless of target location, in the deafferented patient. In Fig. 2C, the mean initial direction error in each hand is shown for controls as well as for GL. The plot reveals the striking performance difference between GL’s right- and left-hand paths compared with controls [RSDT: t(4) = 4.92, P = 0.0079, two-tailed; z_DCC = 9.08]; initial direction errors were higher with the nondominant left hand than with the dominant right hand. Additionally, we found marked differences between the left hand of control participants and the left hand of GL [modified t test: t(4) = 14.62, P < 0.001, two-tailed; z_cc = 16.01], as well as between the right hand of controls and the right hand of GL [modified t test: t(4) = 9.35, P < 0.001, two-tailed; z_cc = 10.24]. These results provide evidence of suboptimal control of trajectory in the deafferented patient compared with controls, as well as significantly higher directional errors in left versus right hand in the deafferented patient.

Figure 2D shows the mean error at the end of movement in each hand for control participants and for the deafferented patient. Here again, we found a marked difference between GL’s hands in error at the end of movement compared with controls [RSDT: t(4) = 4.37, P = 0.012, two-tailed; z_DCC = −5.86]. While there were marked differences between the right hand of the deafferented patient and the right hand of controls [modified t test: t(4) = 9.07, P < 0.001, two-tailed; z_cc = 9.94], we observed no statistically significant differences between groups in the left hand with regards to average hand position error at the end of movement [modified t test: t(4) = 0.98, P = 0.4, two-tailed; z_cc = 1.07]. We next used a set of forward dynamic simulations to explore the potential neural basis of these limb-specific performance deficits.

Somatosensory deficits result in two poorly tuned controllers that do not accurately modulate limb stiffness.

We used a torque-activated two-segment model of the arm (Scheidt and Ghez 2007) to simulate reaching trajectories to the middle target in our experiments. In this simulation, two open-loop controllers were simulated: 1) a trajectory controller specified a hand trajectory optimized for straightness and smoothness; and 2) a postural controller specified positional and velocity-dependent impedance about a specified end position. We modeled the control process as a serially engaged, dual control system that initiated movement with the trajectory controller, and terminated movement with the postural controller. We sought to determine the extent to which limb-specific deficits of initial direction accuracy and the presence of terminal oscillations and drift could result from the interaction between three parameters: the time at which the postural controller is recruited, joint stiffness values dependent on the presence or absence of muscle coactivation, and joint damping values dependent on the presence or absence of reflexes.

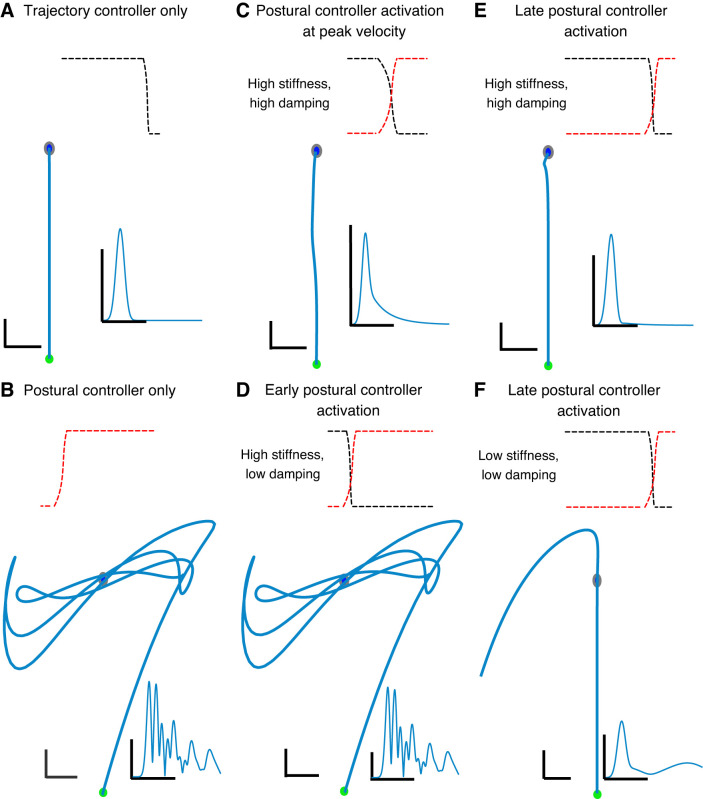
Figure 3 shows simulated right-hand paths and velocity profiles from six simulated conditions. Figure 3A shows a trajectory generated by an ideal, isolated optimal trajectory controller that has perfect knowledge of limb dynamics. Here, feedforward torques drive the hand in a straight trajectory with a bell-shaped velocity profile from perfect start to perfect end. Since there is no postural control, movement and posture are determined solely by the feedforward torque profile at each of the two joints, which are planned before the start of movement. By contrast, Fig. 3B depicts motions that would result from instantiating an isolated postural controller when the desired limb set point (the set of joint angles that determine hand position) jumps from the start location to the goal. Energy from the step change in postural set-point dissipates in the form of oscillations around the desired final position. Large directional errors arise due to the inertial anisotropy of the arm (Gordon et al. 1994) and the absence of an optimal trajectory controller concerned with the accuracy of the initial movement direction. Both of these isolated controllers likely provide unrealistic depictions of human movement, and we expect that a more realistic description of observed behaviors in both GL and in controls may result from a mixing of the two controllers.

Fig. 3.

Serial activation of a dual-controller system describes differences in movement. Simulations of reaching movements show that 2 poorly tuned controllers can predict deafferented patient’s (GL’s) behavior. Hand paths and velocity profiles (insets) are shown for simulations of right arm movements involving pure trajectory control (A), pure postural control in a system with low joint damping (B), activation of the postural controller at peak velocity (C), late activation of postural control in a system with typical joint stiffness and damping values (E), and early (D) and late (F) activation of postural control in a system with joint stiffness and damping values similar to GL’s. Scale bars for trajectories = 2-cm simulated hand movement. Scale bars for velocity profiles represent 0.5 m/s.

Figure 3, C and E, represents systems with joint stiffness and damping values found in typical human joint movement, to simulate typical left- and right-hand behavior, respectively. Movements are generally straight, similar to those of our control participants (see Fig. 2A). Figure 3, D and F, represent systems with joint stiffness and damping values that are representative of a deafferented individual. Figure 3D represents a system with low joint damping (matched to the value estimated by fitting a second-order mechanical model to the frequency and rate of decay of GL’s terminal oscillations) and a transition from trajectory to postural control early in the movement. Under these conditions, the simulated hand path displays large initial direction errors, followed by oscillations around the end point, similar to GL’s left-hand behavior (see Fig. 2B, left hand). Figure 3F represents a system in which the postural controller is activated late in the movement, resulting in nonsignificant amounts of cocontraction at the end point, hence low joint stiffness and much lower joint damping. This results in an initial straight movement to the end point followed by a drift-like movement, similar to GL’s right-hand behavior (see Fig. 2B, right hand).

DISCUSSION

We explored the role that proprioceptive feedback plays in motor lateralization and the neural foundations of handedness by examining unilateral reaching movements performed by GL, a patient with a rare case of chronic, permanent deafferentation. In the absence of concurrent visual feedback, deafferented patients have previously demonstrated deficits in the temporal coordination of sequential control actions (Sainburg et al. 1995) and in the maintenance of stable limb postures (Rothwell et al. 1982; Sanes et al. 1984). We reasoned that patterns of reach kinematics in each arm of a deafferented individual might provide insights into the role of proprioceptive feedback on the hemispheric coordination of limb movements and final stabilized postures. The most intriguing finding was the marked asymmetry in reach performance between GL’s hands. Previous work in deafferented patients observed drift-like behavior at the end of single-limb reaching movements (Rothwell et al. 1982; Sanes et al. 1985; Sarlegna et al. 2006), but the issue of motor lateralization has never before been addressed in deafferentation.

In the absence of concurrent visual feedback of end point motion, the absence of somatosensory feedback resulted in each hand exhibiting seemingly isolated forms of either optimal trajectory control or postural control. We had previously shown, using a serial hybrid computational model of movement, that there were differences in controller switching times between the two hands in neurologically intact individuals, with the nondominant left hand switching from optimizing control of trajectory to achieving stable final postures before reaching peak velocity and the dominant right hand switching after reaching peak velocity (Sainburg and Schaefer 2004; Yadav and Sainburg 2011, 2014b). Therefore, our previous work showed that there is an unequal contribution of each controller to each limb, with the strength of contribution to the ipsilateral limb being substantially lower than that to the contralateral limb. Perturbation to the ipsilateral controller, i.e., removing online peripheral input via deafferentation would, therefore, be expected to make the limb that receives less direct input from that controller be more affected. The computer simulations suggest that the switch to postural control was late and weak in GL’s right hand, resulting in an inability to stabilize at the end point, and instead producing the observed slow drift-like movement toward the last known set point (the start position). In contrast, GL’s left hand switched to postural control very early in movement, resulting in poor online corrections of the trajectory. Therefore, the mixing of two poorly tuned controllers can be used to describe motor behavior in the absence of somatosensory feedback. These results provide further support for a complementary rather than a global dominance hypothesis of handedness since there was a clear difference between hands in the aspects of movement each performed more poorly on than the other.

This serial hybrid computational model of movement fills a gap in the motor control literature by explaining motor control as the coordination of two distinct control strategies interacting through limb dynamics (Scheidt et al. 2011). Current hypotheses of motor control have not succeeded in describing these differences in control between hemispheres. The equilibrium point hypothesis, a popular model of motor control, relies heavily on spinal feedback and specifies limb position via the modulation of a unique motor neuron threshold (Asatryan and Feldman 1965). This hypothesis integrates both optimal trajectory and postural control mechanisms into a single mechanism, thus not allowing for a dissociation of the two forms of control (Sainburg 2015). Optimal feedback control is another model that has gained prominence in describing motor control as a process that involves the use of forward models to estimate limb state, and emphasizing the importance of sensory feedback (Shadmehr 2010; Todorov and Jordan 2002). However, this approach has yet to consider the distinction between optimal trajectory and postural control mechanisms. We do not intend to conduct a lengthy review and analysis of currently available models of motor control; however, we emphasize the current lack of a model to adequately describe laterality in motor control. Our model predicts that the activation of postural feedback mechanisms occurs via the modulation of three parameters: the time at which the postural controller is recruited, joint stiffness, and joint damping. A movement can be initiated in the absence of proprioceptive feedback, but online adjustments cannot be made without accurate estimates of the limb position and velocity.

Although our computational model of lateralized motor control provides an explanation of our empirical findings, we acknowledge that alternative mechanisms may also explain this behavior. Our model cannot, at this time, determine whether the pair of controllers (optimal trajectory and postural control) exists together in both hemispheres (thereby instantiating a superior versus inferior form of one controller in each hemisphere) or whether each hemisphere only instantiates one controller. However, previous work in unilateral stroke patients has indicated the loss of complementary control features; left hemisphere damage produces deficits in trajectory control and right hemisphere damage produces deficits in final position control, thus supporting the localization of each controller to each hemisphere (Mutha et al. 2012; Schaefer et al. 2009). Another important area for future work on this model is to verify the differences in cocontraction levels between the arms predicted by our model, as well as changes in joint stiffness and damping during movement. Previous studies have examined differences in electromyographic activity between deafferented individuals and those with intact sensory afferents (Forget and Lamarre 1987; Rothwell et al. 1982); however, differences in coactivation levels between arms have not been described. We also acknowledge that the conclusions reached in this study were derived from reaching tasks and may not necessarily be valid in other types of motor tasks (for example, see Aoki et al. 2016). Additionally, the results of this study were based on examining reaching in right-handed individuals and we cannot make predictions of behaviors in left-handed individuals. Left-handed individuals exhibit similar patterns of lateralization as right-handed individuals, but to a reduced extent, and there is also a large amount of variability even within their population (Przybyla et al. 2012; Sainburg 2016).

To conclude, this rare case of deafferentation provided us with an opportunity to observe and report differences in motor behavior exhibited by each hand. We used a computational model to associate behavioral differences found in the empirical data with hypothesized differences in control mechanisms between the hemispheres. As reflected by our results, proprioceptive feedback plays a large role in mixing control mechanisms from each hemisphere in the production of human movement. This work provides insights in developing a more accurate understanding of handedness that incorporates the vital role of proprioceptive feedback in controlling arm movement and final posture.

GRANTS

This work was supported by the National Institute of Child Health and Human Development Grant R01-HD-059783 (to R.L.S.) and a National Center for Scientific Research-France International Programmes for Scientific Cooperation (PICS) grant (to F.R.S.).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

R.A.S. and R.L.S. conceived and designed research; S.A.L.J. and F.R.S. performed experiments; S.A.L.J. analyzed data; S.A.L.J., F.R.S., R.A.S., and R.L.S. interpreted results of experiments; S.A.L.J. prepared figures; S.A.L.J. drafted manuscript; S.A.L.J., F.R.S., R.A.S., and R.L.S. edited and revised manuscript; S.A.L.J., F.R.S., R.A.S., and R.L.S. approved final version of manuscript.