Contributions of Elastic Fibers, Collagen, and Extracellular Matrix to the Multiaxial Mechanics of Ligament

Abstract

Elastin is a biopolymer known to provide resilience to extensible biologic tissues through elastic recoil of its highly crosslinked molecular network. Recent studies have demonstrated that elastic fibers in ligament provide significant resistance to tensile and especially shear stress. We hypothesized that the biomechanics of elastic fibers in ligament could be described as transversely isotropic with both fiber and matrix components in a multi-material mixture. Similarly, we hypothesized that material coefficients derived using the experimental tensile response could be used to predict the experimental shear response. Experimental data for uniaxial and transverse tensile testing of control tissues, and those enzymatically digested to disrupt elastin, were used as inputs to a material coefficient optimization algorithm. An additive decomposition of the strain energy was used to model the total stress as the sum of contributions from collagen fibers, elastic fibers, elastic matrix, and ground substance matrix. Matrices were modeled as isotropic Veronda-Westmann hyperelastic materials, whereas fiber families were modeled as piecewise exponential-linear hyperelastic materials. Optimizations provided excellent fits to the tensile experimental data for each treatment case and material model. Given the disparity in magnitude of stresses between longitudinal and transverse/shear tests and agreement between models and experiments, the hypothesized transversely isotropic material of elastin symmetry was supported. In addition, the coefficients derived from uniaxial and transverse tensile experiments provided reasonable predictions of the experimental behavior during shear deformation. The magnitudes of coefficients representing stress, nonlinearity, and stiffness supported the experimental evidence that elastic fibers dominate the low strain tensile and shear response of ligament. These findings demonstrate that the additive decomposition modeling strategy can represent each discrete fiber and matrix constituent and their relative contribution to the material response of the tissue. These experimental data and the validated constitutive model provide essential inputs and a framework to refine existing computational models of ligament and tendon mechanics by explicitly representing the mechanical contributions of elastic fibers.

Graphical Abstract

1. Introduction

Numerous studies have established that the mechanics of ligament and tendon are dominated by fibrillar collagen, but more recently elastin has also emerged as a contributor (Henninger et al., 2013; Henninger et al., 2015). Collagen provides tensile stiffness and strength, whereas the biopolymer elastin, in the form of elastic fibers, provides compliance and supports stress during multiaxial deformation. During tissue deformation, the recoil of elastin occurs via entropy of the disordered network conformation and high numbers of hydrophobic residues in and along the elastin backbone (Muiznieks et al., 2010). In normally developed tissues, alanine and lysine residues within tropoelastin monomers oxidize to form highly stable (iso)desmosine crosslinks (Muramoto et al., 1984; Uitto, 1979). This stability provides elastin with an exceptionally long in vivo half-life of up to 74 years (Shapiro et al., 1991).

In connective tissues such as ligament, tendon, and skin, elastin makes up 4-7% of the tissue dry weight (Baldwin et al., 2013; Gacko, 2000; Henninger et al., 2013; Reddy et al., 2012). Highly extensible tissues such as artery, lung and nuchal ligament have proportionally higher elastin content, often over 50% of their dry weight (Greenwald et al., 1997; Lee et al., 2001; Miskolczi et al., 1997). Genetic mutations in elastin expression in conditions such as cutis laxa (Halper and Kjaer, 2014) and Marfan syndrome (Carta et al., 2009) affect the structural integrity of connective tissues, and significant elastin deficits affect embryo cardiovascular viability in animal models (Hirano et al., 2007). Likewise, acute injury and accumulated oxidative damage to the elastin network can affect the behavior of the tissue given that elastin turnover is extremely slow (Shapiro et al., 1991). It is therefore important to characterize mechanical contribution of elastic fibers in normally developed and pathologic tissues to gauge its contributions to overall tissue function.

The material behavior of ligaments and tendons has often been represented as a composite of a collagen fiber family surrounded by a much softer “ground substance” matrix with transversely isotropic material symmetry (Eleswarapu et al., 2011; Hurschler et al., 1997; Provenzano et al., 2002; Reese et al., 2010; Rumian et al., 2007; Weiss et al., 2002; Wilson et al., 1997). Recent experiments determined the mechanical contributions of elastic fibers by treating porcine medial collateral ligament (MCL) with elastase (Henninger et al., 2013; Henninger et al., 2015), an enzyme that specifically degrades the elastin network (Vered et al., 1985). The data showed that elastic fibers in MCL supported up to 30% of uniaxial tensile stress (~2 MPa, (Henninger et al., 2013)) and up to 60% of transverse tensile and shear stress (~0.02 MPa, (Henninger et al., 2015)). Significant decreases in shear load support after elastase treatment of tendon support the findings in ligament (Fang and Lake, 2016).

The disparity in the magnitude of the resistance provided by elastic fibers in these two different modes of deformation suggests that its contribution to the stress may have transversely isotropic symmetry, with fibrous contributions aligned with the collagen. Multiphoton images of elastin and collagen in ligament and tendon support this assumption (Eekhoff et al., 2017; Henninger et al., 2015). Mechanical data from transverse tensile and shear tests illustrate that lateral binding of collagen fibers and ground substance matrix is quantifiably attributable to elastin (Henninger et al., 2015). This may arise from crosslinking and/or interweaving of the elastic fiber network with the neighboring collagen fibers and ground substance matrix. Given that the stresses in two different loading scenarios are on the same scale, and orders of magnitude smaller than the longitudinal contributions of elastic fibers, an isotropic matrix-like behavior would support the assumption of transversely isotropic material symmetry.

Computational modeling of the mechanics of biomaterials allows us to understand the implications of changes like elastin degradation and genetic insufficiencies on the loading, recoil and failure of fibrous connective tissues. Mechanical experiments provide data upon which to build physiologically motivated models by incorporating the behavior of discrete material constituents. To date, the authors are not aware of any constitutive models explicitly describing the contributions of elastic fibers in ligament or tendon, though two very recent studies modelled elastin and collagen in aortic tissue (Mattson et al., 2018; Rachev and Shazly, 2019).

Therefore, the objective of this study was to develop and test a constitutive model for ligaments and tendons that represented the discrete contributions of elastic fibers to the multiaxial stress-strain response of the tissue. We hypothesized that the total tissue stress could be described by additive contributions from collagen fibers, elastic fibers, elastic matrix, and non-collagenous/non-elastin matrix materials. In addition, we hypothesized that the ligament response to shear deformation along the collagen fibers could be predicted with the model developed using data from longitudinal and transverse tensile tests.

2. Materials and methods

2.1. Experimental Material Characterization

The constitutive model in the present study was optimized with fits to experimental data previously collected by our group. Prior uniaxial tensile tests on control and elastase treated MCL showed that elastin provided a finite contribution to the ligament mechanical response (Henninger et al., 2013). Dogbone shaped specimens were tested in a quasi-static repeated measures protocol up to 10% clamp-to-clamp strain at 1%/sec, then to failure. Elastin supported up to 30% of the tensile stress (~2 MPa, Fig. 1), with no significant changes in tissue strain, modulus, or hysteresis during cyclic or failure loading.

Fig. 1:

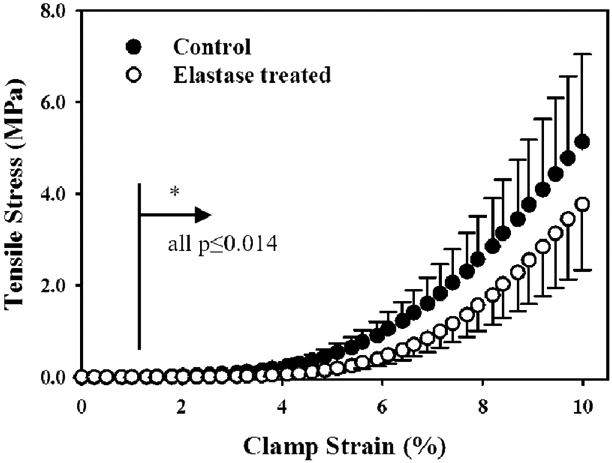
Treatment with elastase to digest elastin significantly decreased the uniaxial tensile stress supported by porcine MCL. Adapted from Figure 4, (Henninger et al., 2013), with permission.

Similarly, strip biaxial tests measured the tensile properties of porcine MCL transverse to the primary collagen fibers in rectangular specimens (Table 1), before and after elastase treatment (Henninger et al., 2015). This same study performed simple shear tests along the primary collagen axis before and after elastase treatment (Table 2). Elastin was again responsible for supporting a significant portion of the stresses, but this time up to 70% of the transverse tensile and simple shear stresses (~0.02 MPa, Fig. 2). In these test configurations the stiffness significantly decreased after elastase treatment, but the hysteresis was unaffected.

Table 1:

Dimensions of experimental specimens used in the transverse tensile optimizations from (Henninger et al., 2015 (Mean±SD)

	N	Height (mm)	Width (mm)	Thickness (mm)	Cross sectional area (mm2)
Elastase Treated	8	9.3±0.7	8.2±1.4	2.0±0.4	19.0±4.5
Control	8	8.5±0.9	7.9±1.0	2.2±0.3	18.6±3.8

Table 2:

Dimensions of experimental specimens used in the shear models from (Henninger et al., 2015) (Mean±SD)

	N	Height (mm)	Width (mm)	Thickness (mm)	Cross sectional area (mm2)
Control	8	8.6±1.0	8.4±1.1	2.3±0.7	19.9±5.9
Elastase Treated	8	8.6±1.2	8.4±1.7	2.7±0.5	23.3±3.9

Fig. 2:

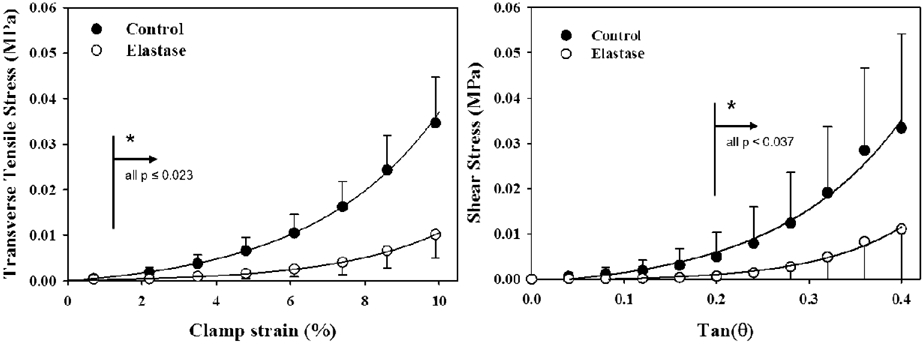
Treatment with elastase to digest elastin significantly decreased the transverse tensile (left) and shear (right) stresses supported by porcine MCL. Adapted from Figure 4, (Henninger et al., 2015), with permission.

2.2. Constitutive Models

To quantify the relative contribution of elastic fibers to the anisotropic and isotropic material behavior of ligament, we assumed an additive decomposition of the hyperelastic strain energy to represent individual contributions of collagen, elastic fibers and the ground substance matrix in ligament. An uncoupled formulation was used to simulate nearly incompressible behavior of ligament. While ligament has been observed to experience high Poisson’s ratios at different scales (Hewitt et al., 2001; Lanir et al., 1988; Reese et al., 2010), no measures of volume loss were available for the experimental data modeled herein. The total strain energy W was assumed to be composed of four discrete deviatoric components (${\tilde{W}}_{ı}$) and a bulk term U(J):

$$W={\tilde{W}}_{cf}+{\tilde{W}}_{ef}+{\tilde{W}}_{em}+{\tilde{W}}_m+\frac{1}{2}K(lnJ{)}^2$$ (1.1)

Here, ${\tilde{W}}_{cf}$ and ${\tilde{W}}_{ef}$ were the contributions of collagen and elastic fibers, respectively, acting along the primary axis of the ligament. The term ${\tilde{W}}_{em}$ was the isotropic contribution of elastic fibers to the matrix, where lateral binding and interweaving of the elastic network could transmit multiaxial forces to other matrix and collagen fiber components. Finally, ${\tilde{W}}_m$ represented the residual response of the remaining matrix molecules that was not considered to be due to either collagen or elastic fibers (i.e., the matrix response after elastase treatment of ligament).

A Veronda-Westmann form of the strain energy (Veronda and Westmann, 1970) was used to represent the matrix terms ${\tilde{W}}_{em}$ and ${\tilde{W}}_m$, as previous research demonstrated that this model accurately described the nonlinear transverse tensile and shear mechanics of ligament (Bonifasi-Lista et al., 2005; Gardiner and Weiss, 2001; Weiss et al., 2002). The strain energy for the matrix was:

$${\tilde{W}}_m,{\tilde{W}}_{em}=C_1\left[e^{(C_2({\tilde{I}}_1-3))}-1\right]-\frac{C_1{C}_2}{2}({\tilde{I}}_2-3).$$ (1.2)

The C₁ coefficient scales the magnitude of the stress response and C₂ scales the degree of nonlinearity. Here, ${\tilde{I}}_1$ and ${\tilde{I}}_2$ are invariants of the deviatoric right Cauchy-Green deformation tensor $\tilde{\mathit{C}}$, which is a function of the deviatoric deformation gradient $\tilde{\mathit{F}}$:

$$\tilde{\mathit{C}}={\tilde{\mathit{F}}}^T\tilde{\mathit{F}},{\tilde{I}}_1=tr(\tilde{\mathit{C}}),{\tilde{I}}_2=\frac{1}{2}\left[tr(\tilde{\mathit{C}}{)}^2-tr({\tilde{\mathit{C}}}^2)\right].$$ (1.3)

The coefficient K represents the bulk modulus of the matrix and J = det(F). To enforce near-incompressibility, K was chosen so that (Weiss et al., 2002):

$$\frac{K}{C_1{C}_2}>1000.$$ (1.4)

The strain energy derivatives of the deviatoric Veronda-Westmann model then followed as:

$${\tilde{W}}_1=C_1{C}_2{e}^{C_2({\tilde{I}}_1-3)},{\tilde{W}}_2=-\frac{C_1{C}_2}{2}.$$ (1.5)

The fiber strain energy contributions ${\tilde{W}}_{cf}$ and ${\tilde{W}}_{ef}$ for collagen and elastin were based on an uncoupled piecewise exponential-linear model previously used to describe the mechanical response of human medial collateral ligament (Quapp and Weiss, 1998; Weiss et al., 2005; Weiss et al., 1996). The fiber model was based on the fiber stretch λ, and a critical stretch λ* that denoted the transition from crimped to fully straightened collagen fibers. The strain energy derivatives described the three experimentally observed phases of collagen fiber deformation (Hansen et al., 2002) as: no contributions when fibers were in compression (λ < 1), a nonlinear toe region as collagen fiber crimp was progressively extinguished (λ < λ*), and a linear response as straightened collagen fibers were directly loaded in tension (λ ≥ λ*). This material represented the fiber-only components of a transversely isotropic material:

$$\begin{gathered} \lambda W_{\lambda }=0,\lambda <1 \\ \lambda W_{\lambda }=C_3(e^{(C_4(\lambda -1))}-1),\lambda <{\lambda }^{\ast } \\ \lambda W_{\lambda }=C_5\lambda +C_6,\lambda \ge {\lambda }^{\ast } \end{gathered}$$ (1.6)

To enforce C⁰ continuity at λ* we defined C₆ as:

$$C_6=C_3\left(e^{(C_4({\lambda }^{\ast }-1))}-1\right)-C_5{\lambda }^{\ast }.$$ (1.7)

2.3. Parameter Optimization

Experimental data from (Henninger et al., 2013; Henninger et al., 2015), including the specimen-specific dimensions (Tables 1, 2), load vs. time and stress vs. stretch curves (Figs. 1, 2) were used in parameter optimization routines to derive the coefficients for each unique material in Eqn 1.1 (Fig. 3). The additive decomposition formulation of the proposed constitutive model was supported by the “solid material mixture” feature of FEBio, a nonlinear finite element solver for biomechanics (febio.org/febio) (Maas et al., 2012). Predictions of shear stresses from optimized tensile material coefficients were performed with “forward” simulations in FEBio.

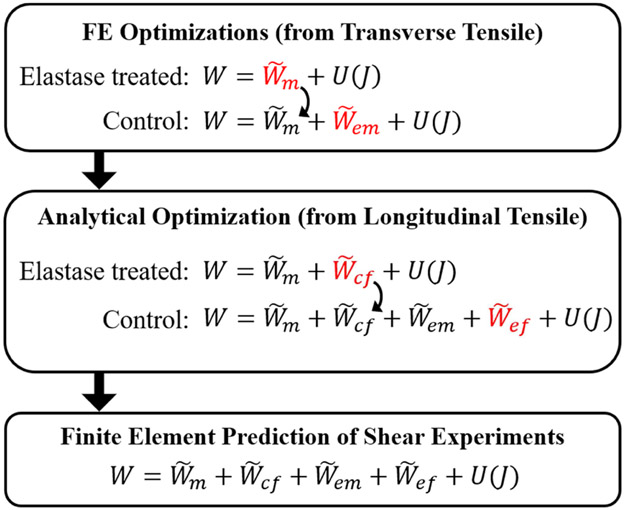
Figure 3:

Flow chart for the parameter optimization sequence of operations. First, coefficients for the matrix terms (${\tilde{W}}_m$, ${\tilde{W}}_{em}$) were determined by material parameter optimization with the elastase-treated and control stress-strain curves from transverse tensile experiments (Henninger et al., 2015), respectively. Next, using these matrix material coefficients, another set of analytical optimizations was used to determine the material coefficients for the fiber terms (${\tilde{W}}_{cf}$, ${\tilde{W}}_{ef}$) by fitting the uniaxial (longitudinal) tensile data (Henninger et al., 2013). Finally, forward FE simulations with the full constitutive model and complete set of material coefficients were used to predict the material response under shear. These predictions were compared to independent experimental data (Henninger et al., 2015). In each step, the model being solved is shown in red.

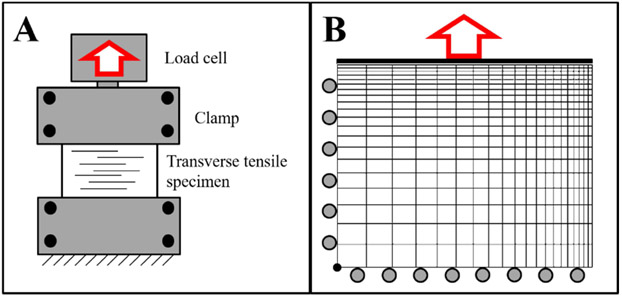
First, data from strip biaxial transverse tensile tests of elastase treated MCL (Henninger et al., 2015) were used to derive the coefficients of the ground substance matrix material. Since the base matrix material response was measured after enzymatic treatment to remove elastin (${\tilde{W}}_{em}={\tilde{W}}_{ef}=0$), and collagen fibers could not contribute to the transverse response (${\tilde{W}}_{cf}=0$), the coefficients of the residual ground substance matrix could be determined ($W={\tilde{W}}_m+U(J)$). Given the inhomogeneous stresses in strip biaxial experiments, optimizations were carried out using the finite element method. A quarter symmetry finite element model was generated in PreView (febio.org/preview) with 20x20x5 hexahedral element mesh, edge biased along the clamped and free surfaces (Fig. 4). The model was assigned a single isotropic Veronda-Westmann material (${\tilde{W}}_m$) and a rigid body was used to apply the displacement uniformly across all nodes on the top surface. For each elastase treated transverse tensile specimen (N=8) the model size and displacement were adjusted to match the experimental conditions. Each model was optimized using the associated experimental force vs. time curve as an input against which to determine the best fit coefficients of the material model using the Levenberg-Marquardt parameter optimization module in FEBio.

Figure 4:

(A) Schematic of the strip biaxial transverse tensile test with collagen fibers oriented transverse to the test axis. (B) Applied boundary conditions for the strip biaxial model with a quarter symmetry edge biased mesh and deformation (red arrow) applied to a rigid body on the top surface.

Next, the coefficients for the isotropic elastic matrix component (${\tilde{W}}_{em}$) were determined by fitting the transverse tensile response of experimental control ligaments. The ${\tilde{W}}_m$ coefficients described one material of a two-material solid mixture ($W={\tilde{W}}_{em}+{\tilde{W}}_m+U(J)$). The solution followed the same optimization strategy described previously, but with unique specimen geometries and force vs. time curves for the control transverse tensile experiments (N=8), as well as the paired matrix coefficients for each corresponding elastase treated specimen. A mesh convergence study determined that densities higher than the 20x20x5 edge biased mesh (Fig. 4) did not result in a change in coefficients of more than 2% for the quarter symmetry model.

After the matrix terms (${\tilde{W}}_{em}$, ${\tilde{W}}_m$) were derived, their average coefficients were used in optimizations to quantify the coefficients of the fiber materials. Given the homogeneous strains in uniaxial tensile tests of elastin in ligament (Henninger et al., 2013), the analytical solution of the stress vs. stretch relationship was optimized using Sigmaplot (Systat Software Inc., San Jose, CA). For each specimen (N=8) the stress vs. stretch response was used for both control and elastase treated repeated measures experiments.

The strain energy derivatives for the fiber terms were discretized into the exponential toe and linear regions of the material response to deformation (Eqn. 1.6). An analytical form of the stress-stretch relationship of the matrix materials to uniaxial extension was required (see Supplementary Material for derivation):

$${\sigma }_{matrix}=6\left[{\tilde{W}}_1\left(\frac{1}{3}{\lambda }^2-\frac{1}{3\lambda }\right)+{\tilde{W}}_{20}\left(\frac{1}{3}\lambda -\frac{1}{3{\lambda }^2}\right)\right].$$ (1.8)

Now in terms of stress vs. stretch, the uniaxial tensile response of ligament was used to solve for the unknown coefficients (C₃, C₄) in the equation:

$${\sigma }_{toe}=C_3\left(e^{(C_4(\lambda -1))}-1\right)+{\sigma }_{matrix}.$$ (1.9)

After the toe region was fit, the linear region was optimized to solve for C₅. Recall that λ* denoted the transition from crimped to straightened collagen fibers, with enforced C⁰ continuity between the toe and linear regions of the fiber response in C₆ (Eqn. 1.7):

$${\sigma }_{\mathit{linear}}={\mathit{C}}_5\lambda +{\mathit{C}}_3({\mathit{e}}^{({\mathit{C}}_4({\lambda }^{\ast }-1))}-1)-{\mathit{C}}_5{\lambda }^{\ast }+{\sigma }_{\mathit{matrix}}$$ (1.10)

Beginning with experimental data for uniaxial tensile tests of elastase treated ligament, and the average coefficients for ${\tilde{W}}_m$, Equations 1.9 and 1.10 allowed the coefficients C_3–5 to be determined for the collagen fibers (${\tilde{W}}_{cf}$). Coefficients for three of the four deviatoric terms in Equation 1.1 were then known (${\tilde{W}}_{cf}$, ${\tilde{W}}_{em}$, ${\tilde{W}}_m$). The final step expanded the optimizations of Equations 1.9 and 1.10 to include two fiber families and two matrix families, and solved for the fiber terms associated with elastic fibers (${\tilde{W}}_{ef}$). The values for λ* used in control and elastase treated optimizations were 1.082±0.000 and 1.079±0.002, respectively. These values were determined by fitting a line to the final 1% clamp stress-strain response and noting the point along the toe region at which the curve deviated from the linear regression.

2.4. Predicting the shear response

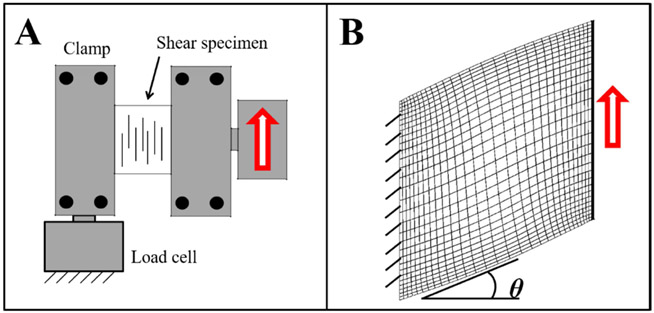
Experimental data from shear testing (Henninger et al., 2015) was used to evaluate the predictive capabilities of the model. A separate finite element model was generated for each of the experimental specimens. Models were created in PreView with 30x30x5 hexahedral element mesh, edge biased along the clamped and free surfaces (Fig. 5). A mesh convergence study determined that densities higher than the 30x30x5 edge biased mesh did not result in a change in coefficients of more than 5%. The models were assigned the hyperelastic constitutive model in Eqn. 1.1, with the average material coefficients for ${\tilde{W}}_m$, ${\tilde{W}}_{em}$, ${\tilde{W}}_{cf}$, ${\tilde{W}}_{ef}$. A uniform vertical displacement was applied to all nodes on one side surface while the opposing side remained stationary. Individual models were analyzed for each control specimen and elastase-treated specimen (N=8 for each group), adjusting the dimensions and displacement to match the experimental conditions (Table 2).

Figure 5:

Shear testing of ligament along the fiber direction. (A) Schematic of the shear test with collagen fibers oriented parallel to the test axis. Red arrow indicates direction of crosshead displacement. (B) Finite element model of one of the test specimens, showing finite element discretization and applied boundary conditions. The shear angle is represented as θ, and where models were run to tan (θ) = 0.2.

As a final check of the model, optimizations were performed to determine the coefficients of the matrix components ${\tilde{W}}_m$, ${\tilde{W}}_{em}$ for shear deformation alone.

2.5. Statistical Methods

Statistical comparisons were undertaken with independent or paired t-tests, as appropriate, given the relationships of the source experimental data. Significance was set at p ≤ 0.05. Root mean square error (RMSE) was calculated to determine the relative fit of optimizations to the input experimental data, and expressed as both a magnitude and percentage of the peak force or stress of the respective experimental data. All data are presented as mean ± standard deviation.

3. Results

3.1. Matrix material coefficients

Finite element models of transverse tensile tests showed excellent agreement between the experimental data and optimized material models (Fig. 6) (RMSE_control = 0.005±0.003 N (0.1% of peak load), RMSE_elastase = 0.002±0.001 N (0.2% of peak load)). The C₁ coefficient, scaling the magnitude of the matrix stress response, was nearly four times greater for the elastin matrix (${\tilde{W}}_{em}$) than the base matrix (${\tilde{W}}_m$)(p = 0.023, Table 3). The C₂ parameter, scaling the nonlinearity of the matrix response, was not significantly different between the materials (p = 0.079), but showed a trend of higher nonlinearity in the base matrix material.

Figure 6:

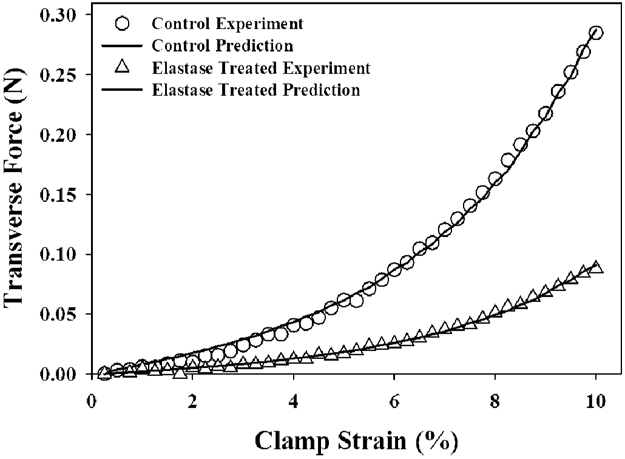
A representative prediction of control and elastase treated transverse tensile experimental data for a pair of ligament specimens.

Table 3:

Transverse tensile coefficients for the matrix materials (mean±SD).

	C1 (MPa)	C2 (no units)
${\tilde{\mathit{W}}}_{\mathit{m}}$	0.0003±0.0003*	39.2±10.1
${\tilde{\mathit{W}}}_{\mathit{em}}$	0.0012±0.0010	30.0±9.4

^*significant difference between ${\tilde{\mathit{W}}}_{\mathit{m}}$ and ${\tilde{\mathit{W}}}_{\mathit{em}}$

3.2. Fiber material coefficients

Curve fits to the analytical equations for uniaxial stress-stretch response for longitudinal tensile tests showed excellent agreement between the experimental data and optimized material models (Fig. 7) (RMSE_control = 0.004±0.006 MPa (0.1% of peak stress), RMSE_elastase = 0.006±0.006 MPa (0.2% of peak stress)).

Figure 7:

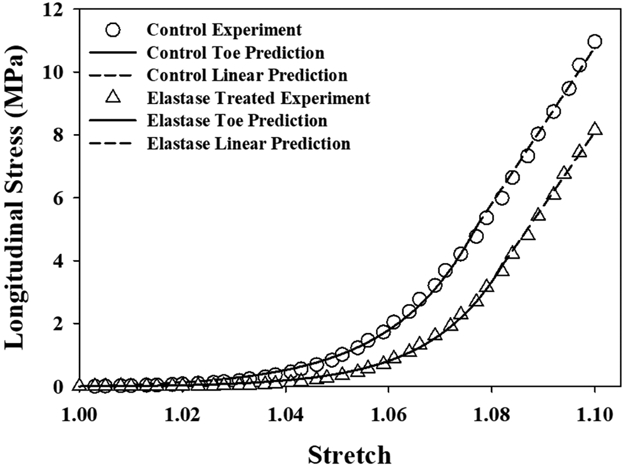
A representative optimization fit of control and elastase treated longitudinal tensile experimental data. Note that the toe and linear regions were fit independently, ensuring C⁰ continuity at λ*.

The C₃ coefficient, scaling the magnitude of the fiber stress response in the toe region, was significantly different between the collagen fibers (${\tilde{W}}_{cf}$) and elastic fibers (${\tilde{W}}_{ef}$) (p ≤ 0.001, Table 4). The elastic fibers supported nearly 4 times the stress as the collagen fibers in the toe region. The C₄ coefficient, scaling the nonlinearity of the fiber stress response in the toe region, was also significantly different between the fiber materials (p ≤ 0.001) where the collagen fibers were more nonlinear than the elastic fibers. The C₅ coefficient, representative of the fiber material stiffness in the linear region, was significantly different between materials (p ≤ 0.001) where collagen fibers were a full order of magnitude stiffer than elastic fibers.

Table 4:

Coefficients for the longitudinal exponential-linear fiber materials (mean±SD).

	C3(MPa)	C4 (no units)	C5 (MPa)
${\tilde{\mathit{W}}}_{\mathit{cf}}$	0.0096±0.0066*	67.0±7.7*	107.8±54.2*
${\tilde{\mathit{W}}}_{\mathit{ef}}$	0.0395±0.0138	43.5±7.3	10.7±3.8

^*significant difference between ${\tilde{\mathit{W}}}_{\mathit{cf}}$ and ${\tilde{\mathit{W}}}_{\mathit{ef}}$.

3.3. Prediction of the shear response

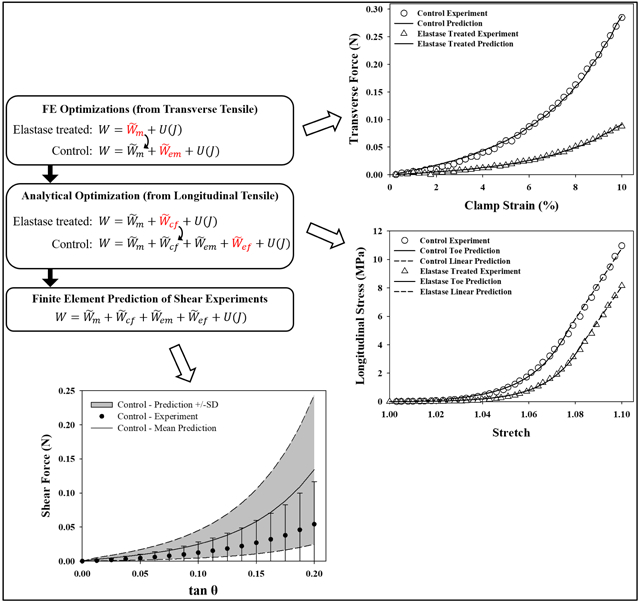
Shear FE model predictions incorporating the average transverse tensile material coefficients showed the characteristic nonlinear response of ligament under shear deformation (Fig. 8, 9) (Bonifasi-Lista et al., 2005; Gardiner and Weiss, 2001; Henninger et al., 2015; Wilson et al., 1997). In every case, the shear FE model predictions (Fig. 8, grey region) overestimated the specimen-specific experimental shear response (Fig. 8, •), resulting in experimental curves that fell within the bottom 1/3 of the model prediction window (RMSE_{trans_coeff_control} = 0.063±0.025 N (115% of peak force), RMSE_{trans_coeff_elastase} = 0.025±0.011 N (269% of peak force)). Inclusion of the collagen and elastic fiber families had a negligible effect on the specimen-specific reaction forces calculated from the model (Fig. 9).

Figure 8:

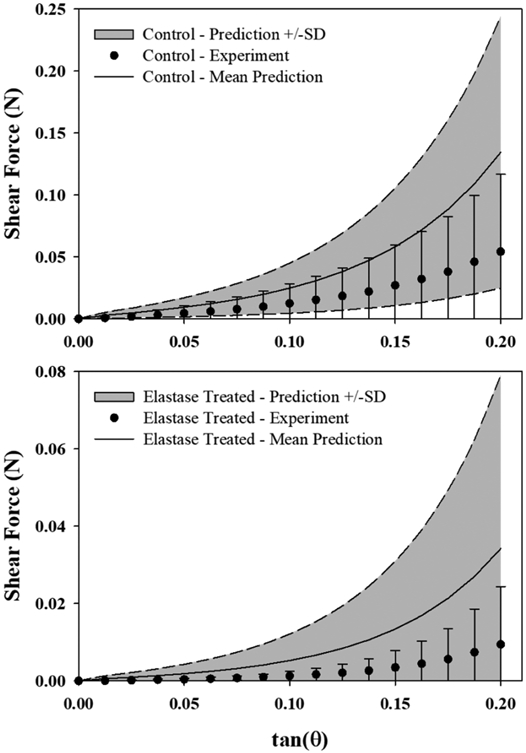
Modeling shear deformation using material coefficients derived from transverse tensile tests (grey) simulated the characteristic nonlinear shear response of ligament, but consistently overestimated the magnitude of the shear reaction forces in specimen-specific control (top) and elastase treated (bottom) experiments (mean±SD). The grey region represents ±1 SD of the mean shear model for N=8 models.

Figure 9:

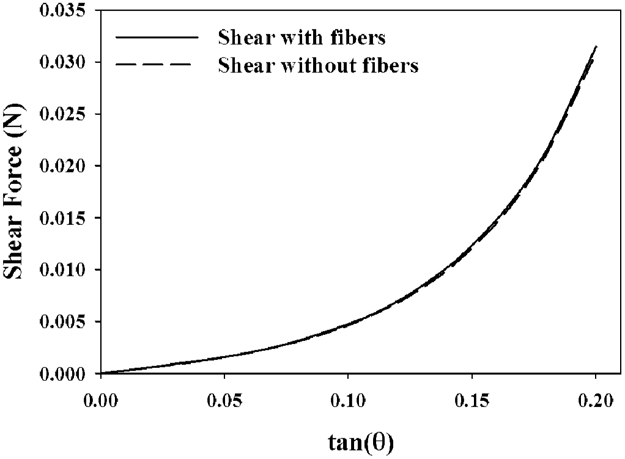
A representative model output showing that inclusion of collagen and elastin fiber terms (${\tilde{W}}_{cf}$, ${\tilde{W}}_{ef}$) had a negligible effect on the predicted reaction forces in shear models.

Optimizations of the shear experiments (Fig. 10) yielded coefficients of similar magnitude and trends as those from transverse tensile optimizations, where C₁ was smaller and C₂ was larger for base matrix materials (Table 5) (RMSE_{shear_coeff_control} = 0.003±0.002 N (1.1% of peak force), RMSE_{shear_coeff_elastase} = 0.001±0.001 N (1.0% of peak force)). In contrast, for shear optimizations no significant differences were detected between the base matrix ${\tilde{W}}_m$ and the elastic matrix ${\tilde{W}}_{em}$ for the C₁ (p=0.181) and C₂ (p=0.204) coefficients. There were also no significant differences in the matrix coefficients between transverse (Table 3) and shear optimizations (Table 5) (p≥0.159).

Figure 10:

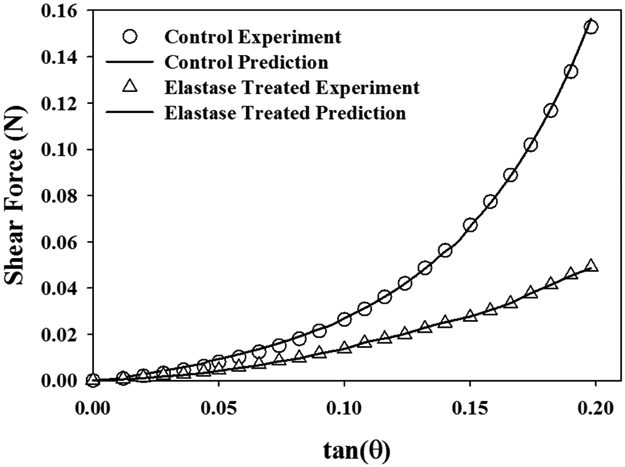
A representative optimization fit of control and elastase treated shear experimental data for a pair of ligament specimens.

Table 5:

Shear coefficients for the matrix materials (mean±SD)

	C1 (MPa)	C2 (no units)
${\tilde{\mathit{W}}}_{\mathit{m}}$	0.0001±0.0002	37.1±27.8
${\tilde{\mathit{W}}}_{\mathit{em}}$	0.0011±0.0018	21.7±12.3

4. Discussion

The purpose of this study was to develop a constitutive model to represent the mechanical role of elastic fibers in ligament, and to validate the descriptive and predictive capability of the tensile model against data from shear deformations. The results of this study support the primary hypothesis that additive contributions of collagen and elastic fiber families and elastic and ground substance matrix materials can represent the material contributions of elastic fibers across three material test configurations. In addition, the model provided a reasonable approximation of data from shear loading experiments. Independently derived model coefficients from the shear experiments did not differ statistically from those of transverse tensile tests, supporting the multiaxial predictive capabilities of the model formulation.

To the best of our knowledge, this is the first validated constitutive model representing the contributions of elastic fibers in the multiaxial loading of ligament. A majority of recent elastin models focus on the mechanics of arteries (Cheng et al., 2013; Horny et al., 2014; Schriefl et al., 2015; Tian et al., 2016; Wang et al., 2016) and heart valve leaflets (Lee et al., 2015; Zhang et al., 2016), while others have studied elastin in the intestinal wall (Sokolis and Sassani, 2013) and pelvic floor (Brieu et al., 2015). Each of these models included some degree of structural motivation, including layer dependent organization of fiber families (Lee et al., 2015; Sokolis and Sassani, 2013; Wang et al., 2016; Zhang et al., 2016) and discrete elastin contributions, often as a function of elastin content (Brieu et al., 2015; Cheng et al., 2013; Wang et al., 2016).

In the present study elastic fibers were shown to behave as a transversely isotropic material, where the ligament was represented as the additive contributions of fiber and matrix materials. Transverse isotropy was motivated by the disparity in elastic stress between longitudinal tensile tests along the primary collagen fibers (~ 2 MPa, (Henninger et al., 2013)) and the off-axis deformations that predominantly loaded the extracellular matrix and isotropic component of elastin (~0.02 MPa, (Henninger et al., 2015)). Elastin is often represented as an isotropic neo-Hookean material (Horny et al., 2014; Sokolis and Sassani, 2013; Tian et al., 2016), which has a nearly linear material response. Herein, the Veronda-Westmann model was able to model the fully nonlinear isotropic behavior of elastic fibers observed during transverse and shear deformation (Figs. 6, 10) (Henninger et al., 2015). As shown in Tables 3 and 5, the elastic matrix (${\tilde{W}}_m$) was fit with a C₁ coefficient that was 4 to 10-fold that of the base matrix (${\tilde{W}}_m$). This measure quantifies the significant contribution elastic fibers play in the mechanical integrity of ligament during deformations where collagen is not the primary load bearing structure, namely transverse and shear deformations and the toe region during uniaxial extension along the collagen fiber direction.

Similar to the present study, Schriefl et al. used selective digestion with elastase to differentiate the primary contributions of elastin from those of collagen in uniaxial tension of aorta tissue (Schriefl et al., 2015). Their data showed that elastin was responsible for the initial stiffness of aorta before collagen crimp engagement, which is the same mechanism by which elastic fibers act on the low-strain longitudinal tensile response of ligament (Henninger et al., 2013). Beyond the toe region, the experimental modulus of the linear region of the ligament stress-strain response was statistically unaffected by elastin digestion (Henninger et al., 2013), with elastin providing a relatively linear contribution to resisting tensile loading of ligament (Fig. 7). This experimental finding was supported by the optimizations, which found that the modulus of the elastic fibers was a full order of magnitude lower than that of the collagen fibers (Table 4). This study is the first to report an effective stiffness of elastin in normally developed ligament.

The choice of a piecewise exponential-linear model for the anisotropic contribution of elastic fibers allowed us to control for the distinctly different behavior of elastic fibers in the toe and linear regions of the uniaxial stress-strain curve when testing along the collagen fiber direction. The isotropic Veronda-Westmann model would have continued to exponentially stiffen the elastic fibers even after collagen crimp was extinguished above λ*. Similarly, the disparity in longitudinal and transverse stresses would have necessitated a scaling factor or penalty parameter in order to represent elastic fibers with a single set of isotropic material coefficients for both loading regimes that differed by orders of magnitude. In its current form, the additive material mixture model provides a physiologically meaningful interpretation of the behavior of elastic fibers where it supports nearly 4 times the stress as the collagen fibers in the toe region and functions more as a linear fiber once collagen crimp is fully extinguished in the linear region of ligament.

Ligament has previously been described as a composite of collagen fibers in an isotropic ground substance matrix (Eleswarapu et al., 2011; Hurschler et al., 1997; Provenzano et al., 2002; Reese et al., 2010; Rumian et al., 2007; Weiss et al., 2002; Wilson et al., 1997). The present study further refines the definition of ground substance to model the influence of elastic fibers as an explicit constituent. As shown in Tables 3 and 5, the impact of the residual base matrix is 4-10 times lower than that of the isotropic elastin (by measure of C₁), which is in turn orders of magnitude softer than the fibrous constituents of collagen and elastic fibers. The resulting base matrix response ${\tilde{W}}_m$ can now be said to encompass the mechanical contributions of the remaining ECM components including fibronectin, laminin and fibrinogen, which serve as ECM organizers, fibrillin and fibulin, which contribute to elastic fiber development and organization, and tenascins and thrombospondin, which are implicated in tissue repair and inflammatory responses (Halper and Kjaer, 2014). These ECM components, and the potential for collagen crosslinking (Eleswarapu et al., 2011; Thornton et al., 2000) and interweaving, are the likely sources of the weak interactions that make up the modest mechanical contributions of the residual base matrix.

The material coefficients were optimized from data collected from longitudinal and transverse tensile experiments, yet in its current multi-material formulation the 4-part model was capable of providing reasonable predictions of the shear response of ligament. It was shown that the fiber components did not significantly contribute to the shear response (Fig. 9), but still the transverse coefficients overestimated the stresses measured in shear experiments (Fig. 8). Note that the shear model was highly sensitive to small changes in C₁ and C₂, therefore use of the average coefficients from transverse tensile tests resulted in RMSE on the order of 100-200% of the peak load in shear experiments. The absolute RMSE in control shear predictions was 2.5x that of elastase treated shear predictions when fit using average transverse tensile coefficients (0.063 N vs. 0.025 N, respectively). This reflects the same 2.5x difference in absolute RMSE between control and elastase specimens in transverse tensile optimizations (0.005 N vs. 0.002 N, respectively). Given that elastase treated shear specimens exhibit very low stress, when RMSE was normalized to peak stress the error appeared as a higher percentage relative to the control data, which had a much higher peak stress and therefore a relatively lower percentage error. For predictive purposes, average coefficients were required since shear and transverse tensile specimens were gathered from different specimens due to size constraints of the porcine ligament. By comparison, optimizations performed directly on the shear specimens yielded unique coefficients with RMSE on the order of 1%. These coefficients were not significantly different than those derived from transverse tensile optimizations.

The current model required that shear strains be restricted to physiologically relevant ranges less than 20% shear strain (tan(θ) = 0.2). Pilot work determined that the exponential Veronda-Westmann model would even more significantly overshoot the soft shear response since no accommodations for shear stiffening effects or interaction terms (Nerurkar et al., 2011; Peng et al., 2013) were factored into the current model. Given that restriction on the model, optimizations of the shear experiments (Table 5) provided coefficients that did not significantly differ from those derived from the transverse strip biaxial experiments (Table 3) when constrained to shear strains less than 20%. This supported that the current multi-material model was capable of predicting the shear response within the measured ranges of experimental variability in the prior studies (Henninger et al., 2013; Henninger et al., 2015).

It is worthwhile to emphasize the assumptions and simplifications associated with the constitutive model that was proposed and used in this research. First, nonlinear hyperelastic material behavior was assumed for each constituent. The experimental test protocol included preconditioning cycles to minimize the transient effects of viscoelasticity in the hydrated ligament, and testing was performed at quasi-static loading rates (~1%/sec). For longitudinal tensile tests (Henninger et al., 2013), cyclic loading was performed below 10% clamp strain in order to avoid the initiation of material failure previously observed to occur near 5-6% tissue strain (Provenzano et al., 2002), where tissue strain is approximately 50% of clamp strain (Bonifasi-Lista et al., 2005). This allowed repeatable material behavior over cycles of loading, and a repeated measures design to the experiment, before and after elastase treatment. Both transverse tensile and shear tests were also performed to 10% clamp strain (Henninger et al., 2015), but the relatively soft material response did not allow repeated measured to be performed since some degree of tissue plasticity was observed after 10% deformation.

Next, the material was modeled as nearly incompressible with uncoupled deviatoric and dilatational strain energy. An incompressible material would be restricted to a Poisson’s ratio of 0.5, but it is known that ligament and tendon undergo significantly more lateral contraction with much higher Poisson’s ratios (up to υ = 3, (Hewitt et al., 2001; Lynch et al., 2003; Screen and Cheng, 2007)) and volume change through water loss (Hannafin and Arnoczky, 1994; Lanir et al., 1988; Wellen et al., 2004). Inclusion of a Poisson’s function (Swedberg et al., 2014) or higher orders of material organization like collagen crimp or helical twist (Reese et al., 2010) could be included to account for this disparity. Poisson’s ratio data were not available from the referenced experiments (Henninger et al., 2013; Henninger et al., 2015), restricting our ability to incorporate and validate that feature in the current model formulation. Provided a complete experimental data set, including Poisson’s ratio, the described methods for decomposing the stress response into a mixture of materials are still applicable. It is expected that the material coefficients would change in response to the internal stress reduction afforded by allowing volume loss in the model.

Our constitutive model also included two highly aligned fiber families and did not account for a distribution of fiber orientations or higher orders of material symmetry. This limits the applicability of the current formulation to only materials or layers of larger biocomposites that exhibit transverse isotropy. Next, we chose to model the experimental response using additive decomposition for 4 discrete fiber and matrix terms. This provided a convenient method to isolate the contributions of given materials that aligned well with experimental conditions. It should be noted that a principle limitation with this strategy is the lack of interaction between the constituents that may be present in the actual material construction and influence material behavior. While our predictions of shear experiments were within reason for the given experimental variability, the optimizations and models were constrained to the low strain shear loading regimen. Prior studies have shown how interaction terms can be used to account for shear stiffening that happens at higher degrees of shear deformation (Nerurkar et al., 2011; Peng et al., 2013). Although the present model could be extended to include such interaction terms, these effects were not a main focus of the current study.

5. Conclusions

This study presented the first experimentally validated constitutive model of elastic fibers in ligament, represented as a transversely isotropic material which acted as both a fiber family oriented along the primary collagen fibers, and as an isotropic matrix providing global resistance to multiaxial deformation. The multi-material model was capable of predicting the shear response of ligament given only coefficients optimized from tensile experiments, refining the ability to describe the multiaxial stress-strain relationships in ligament as a function of collagen, elastic fibers and a base ground substance matrix. This study also utilized the material coefficient optimization algorithms in FEBio, and applied them to a framework of additive decomposition to sequentially incorporate materials as discrete constituents and levels of tissue organization were uncovered. This model, and the techniques described herein, can find application in the study of biocomposite materials as well the role of elastic fibers in normal, pathologic or injured fibrous connective tissues.

Highlights.

• A constitutive model of ligament, including elastic fibers, was developed

• Experimental data were fit to derive material coefficients for fibers and matrix

• Material coefficients from tensile tests predicted the experimental shear response