Deconstructing bias in social preferences reveals groupy and not-groupy behavior

Significance

Group divisions are a continual feature of human history. Using methods from experimental and behavioral economics, this study deconstructs the typical in-group bias in allocation decisions and social preferences by considering bias at the individual level. The results reveal stable individual predilections to engage in group-related discrimination, such that the same individuals who show in-group bias in a political setting also show in-group bias in a highly simplified social context. The findings point to a role for individual “groupiness” in understanding social divisions.

Abstract

Group divisions are a continual feature of human history, with biases toward people’s own groups shown in both experimental and natural settings. Using a within-subject design, this paper deconstructs group biases to find significant and robust individual differences; some individuals consistently respond to group divisions, while others do not. We examined individual behavior in two treatments in which subjects make pairwise decisions that determine own and others’ incomes. In a political treatment, which divided subjects into groups based on their political leanings, political party members showed more in-group bias than Independents who professed the same political opinions. However, this greater bias was also present in a minimal group treatment, showing that stronger group identification was not the driver of higher favoritism in the political setting. Analyzing individual choices across the experiment, we categorize participants as “groupy” or “not groupy,” such that groupy participants have social preferences that change for in-group and out-group recipients, while not-groupy participants’ preferences do not change across group context. Demonstrating further that the group identity of the recipient mattered less to their choices, strongly not-groupy subjects made allocation decisions faster. We conclude that observed in-group biases build on a foundation of heterogeneity in individual groupiness.

The American political landscape is marked by animosity between Republicans and Democrats—an enduring example of group conflict in society. This paper uses this political division to ask whether strength of identification with a group drives in-group bias and whether certain individuals consistently show more bias across different group settings. Participants in an experiment chose allocations of income to themselves and others. Self-declared Democrats and subjects who leaned Democratic (“D-Independents”) were assigned to the “Democrat” group, and self-declared Republicans and subjects who leaned Republican (“R-Independents”) were assigned to the “Republican” group. We compare Democrats with D-Independents and find that party members do show more in-group bias; on average, their choices led to higher income for in-group participants. Yet, these party-member participants also show more in-group bias in a second nonpolitical setting. Hence, identification with the group is not necessarily the driver of in-group bias, and the analysis reveals a set of subjects who consistently shows in-group bias, while another does not.

The study then delves into this finding and analyzes individual responses to group divisions, uncovering significant and robust differences. Some subjects are “strongly not groupy.” They treat in-group, out-group, and control (nongroup) recipients the same way. Other subjects are "strongly groupy," with social preferences that differ between in-group and out-group recipients in both group settings and out-group recipients almost always receive lower levels of income. These distinctions in groupiness can be observed not only in choice behavior but also in speed of decision making, promoting the notion of “(not) groupiness” as an individual tendency.

This paper advances our understanding of identity and economic choices. Identity here describes how individuals categorize themselves in terms of social categories or groups, such as gender, race, ethnicity, nationality, or political party (1, 2). One experimental approach to study the impact of identity on economic behavior employs such societal categories; these groupings affect choices and allocation of income in strategic and nonstrategic settings (such as dictator games, ultimatum games, charitable giving, and redistribution) (3–10). Following the social psychology literature, a second experimental method creates social categories inside the laboratory, using minimal groups where subjects are divided into groups according to aesthetic preferences or random assignment (11–16). Other studies compare two sets of subjects, assigned to either minimal groups or groups with social ties (17).

The present study’s innovation is a within-subject design that employs two group treatments, both a societal group division (where participants were assigned to groups based on a political questionnaire) and a minimal group division (where participants were assigned to groups based on a questionnaire of arbitrary aesthetic preferences). The two group treatments were presented in random order to each participant. Within each treatment, each subject chose income allocations to self and to a recipient in the subject’s own group and chose income allocations to self and to a recipient in the other group, with the full set of within-treatment decisions presented randomly.

This within-subject, two-group treatment randomized design allows several insights into the effect of group divisions on bias in income allocation and social preferences. First, it permits a direct experimental comparison of bias in group settings based on preexisting affiliations vs. minimal groups. A meta-analysis of experimental economic studies indicates that minimal groups induce greater bias (18), a conclusion reached by comparing the relative magnitude of bias in different studies. The present paper pits minimal groups directly against groups based on societal divisions and finds that the political treatment induces significantly higher levels of in-group bias. Second, and relatedly, the design affords a study of individual-level biases in the two group conditions, holding fixed all features of the experiment that could affect choices, such as instructions, the task, the payoff structure (15), the information presented to participants, and experimenter demand effects. Finally, and primarily for our purposes, the within-subject, two-group treatment design allows a deconstruction of population averages through comparisons of different subpopulations across treatments, characterizing individual choices across treatments and relating those choices to demographics and nonchoice behavior.

We first study strength of group identification and in-group biases. We focus on the comparison of Democrats and D-Independents since these subsets are identical in basic demographics and in political positions and differ only in their affiliation with the political party. The comparison of Republicans and R-Independents, which are both small samples,* cannot isolate the effect of group identification since the subsets differ both in affiliation with the political party and in their political positions; the comparison is thus reported only briefly in the text, with full analyses in SI Appendix. We first consider a simple measure constructed from the raw data, labeled “favoritism,” that captures how much more money a subject’s choices give to an in-group recipient than to an out-group recipient. In the political treatment, Democrats show significantly greater favoritism compared with D-Independents. However, Democrats also show significantly greater favoritism than D-Independents in the minimal group treatment; that is, Democrats appear to be more responsive to both group treatments. Furthermore, we cannot reject that the increase in Democrats’ favoritism from minimal group to political group is the same as the increase in D-Independents’ favoritism from minimal group to political group. In sum, the political treatment amplified favoritism equally for Democrats and D-Independents; the difference across treatments in the difference of favoritism of Democrats and D-Independents is zero, indicating that political party affiliation is not key to the political treatment effect per se.

Structural estimation of social preferences (i.e., positing a utility function to model participants’ choices and estimating the utility function parameters) confirms this finding. Subjects on average are inequality averse; that is, they are willing to sacrifice their own incomes to reduce the difference in payoffs between themselves and others. However, relative to D-Independents, Democrats sacrifice less of their own incomes to reduce inequality—in both the political group treatment and in the minimal group treatment—when their counterparts are in the out-group. Paralleling the finding for favoritism, there is no difference across treatments in the difference in estimated parameters between Democrats and D-Independents.

These analyses reveal subpopulations that do and do not consistently exhibit group biases contingent on the identity of recipients. We then unpack this finding and study whether there is consistent (non-)responsiveness to group treatments at the individual level using the full sample, including Republicans and R-Independents. We first consider the raw data measure of favoritism and find a strong correlation at the individual level between favoritism in the political condition and favoritism in the minimal group condition. We then structurally estimate individual social preferences. We identify, within each group treatment, individuals whose social preferences are not contingent on whether the recipient is in their group or not and then further identify individuals whose social preferences are not contingent on the group treatments. Thirty-four percent of subjects satisfy this criterion, and we call them strongly “not groupy.” They do not change their social preference in response to any group aspect of the experiment. On the other side of the spectrum, about 17% are strongly “groupy,” with social preferences contingent on the group identity of recipients in both group treatments. This categorization is also evident in nonchoice behavior. While response time increases when choices are close in utility value (19), the strongly not-groupy participants are faster at deciding between options with similar levels of individual utility (to them). This pattern is consistent with strongly not-groupy subjects ignoring the group identities of the other participants.

Before presenting the methods and analyzing the data, we discuss possible experimenter demand effects. Subjects might think that experimenters are emphasizing groups and act according to what they think experimenters expect. There are several responses to this concern. First, real-world actors create, highlight, and exploit group divisions, and the aim of this experiment—following a long tradition in social psychology—is to see how people behave in such circumstances. Second, if there is a demand effect, there is apparently no common understanding as to what the demand is; many subjects do not differentiate between in-group and out-group, and among those who do, there is heterogeneity in behavior. Finally, if there is a demand effect per se, the within-subject design controls for it when comparing choices in the political and the minimal group treatments.

The paper proceeds as follows. Description of Experiment and Subject Pool explains the experiment in detail. Group Identification vs. Individual Responsiveness in the Raw Data presents the main results in the raw data. Social Preferences and Individual Groupiness: Structural Estimation confirms these results using structural estimation of social preferences and categorizes individuals as groupy or not groupy, showing relations with demographics and response time. The conclusion summarizes the findings and outlines future research. Appendix: Econometric Specifications provides the formulas for the econometric models used in the structural estimation.

Description of Experiment and Subject Pool

In a within-subject design, subjects made 26 allocation decisions in each of five different conditions. Each condition paired the decision maker with a different anonymous recipient who had 1) no group designation or was designated as a member of the 2) minimal group in-group, 3) minimal group out-group, 4) political group in-group, or 5) political group out-group. The allocation task followed refs. 11, 20, and 21 to discern subjects’ “social preferences,” which capture whether and how individuals care about other people’s income, perhaps in relation to one’s own income: individuals could value equality in income levels (i.e., inequality aversion). Individuals could value higher aggregate income regardless of who earns more or who earns less (i.e., total income maximizing). Individuals could prefer that their income is higher than another person’s income (i.e., income dominance).

Specifically, the tasks were to choose one of two rows in 26 different matrices that designated income for the subject and income for the recipient. Let π_i denote the decision maker’s income and π_j denote the recipient’s income within a normalized matrix $\left[\begin{array}{cc}{\pi }_i& {\pi }_j\\ \pi {\prime }_i& \pi {\text{'}}_j\end{array}\right]$ such that i earns as much or more in the top row than the bottom row. Choosing the top row thus exhibits “selfish” preferences. Choosing the bottom row sacrifices one’s own income and exhibits social preferences for 1) “inequality aversion” if ∣π′_i − π′_j∣ < ∣π_i − π_j∣, 2) “maximizing total income” if π′_i + π′_j > π_i + π_j, and/or 3) “dominance seeking” if π′_i − π′_j > π_i − π_j. (SI Appendix, Table S1 provides the set of 26 matrices.)

The pairings were presented as follows. Subjects first participated in the nongroup control (NG) condition (i.e., paired with one other participant who had no group designation for 26 choices). Next, they followed either the minimal group treatment (MG) or the political group treatment (POL), both described in detail below, presented in random order to each subject.^† Within each group treatment, each subject was paired with an in-group participant and with an out-group participant. The in-group allocation choices were labeled YOU-OWN, and the out-group allocation choices were labeled YOU-OTHER. Within each treatment, these 52 decisions were presented randomly. For each matrix presented to each subject, the rows within the matrix, the colors of the rows (blue or green), and which key (left or right) selected which row were also all randomized. (SI Appendix, Fig. S4 shows screenshots.)

In each group treatment, two groups were determined a priori according to answers to survey questions. In the minimal group treatment, subjects viewed pairs of lines of poetry, landscape images, and abstract paintings (by Klee or Kandinsky) and were asked which item in each pair they preferred. (SI Appendix, Figs. S1 and S2 show example screenshots.) The items were matched so that this choice is unrelated to individual characteristics (e.g., a choice between two similar landscape images). Subjects were then divided into two groups according to their answers and matched with one in-group participant and one out-group participant. Subjects were given true information about whether each otherwise anonymous recipient gave similar (for the in-group) or dissimilar (for the out-group) answers to selected questions in a way to keep constant the degree of similarity and difference between all subjects and their respective recipients (SI Appendix has details). We refer to the minimal group pairings as MG YOU-OWN and MG YOU-OTHER, respectively.

The political group treatment began with a political survey. Subjects were first asked their affiliation as Democrat, Republican, Independent, or none of the above. The next question asked subjects to refine their leanings: “strong” or “moderate” for party affiliates, “closer to Democratic” or “closer to Republican” for Independents and none of the above. (SI Appendix, Fig. S3 shows screenshots.) Subjects were then asked related questions, including their opinions on five issues dividing the political spectrum (abortion, gay marriage, tax cuts, immigration laws, Social Security and Medicare vs. small government) (SI Appendix, Table S4 has the wording of the questions). We then placed subjects into two groups according to their responses to the questions on affiliation and political leanings. The Democrat group contained Democrats and closer to Democratic subjects, and the Republican group contained Republicans and closer to Republican subjects. (As noted previously, the Democrats and the D-Independents empirically had identical demographics and political positions, but this was not the case for Republicans and R-Independents [SI Appendix, Tables S4 and S5].) Subjects were then matched with one in-group participant and one out-group participant. We used an algorithm to present subjects with true information about how their own answers matched (and mismatched) the answers of their in-group and out-group recipients, respectively, in a way to keep constant the degree of similarity and difference between all subjects and their respective recipients (SI Appendix). We refer to the pairings as POL YOU-OWN and POL YOU-OTHER.

We conducted the experiment within Duke University’s Human Neuroeconomics Laboratory, which follows no deception protocols. Participants (n = 141) were drawn from the Duke and Durham–Chapel Hill communities^‡ and provided informed consent under a protocol approved by the Institutional Review Board of Duke University. At the start of each experimental session, subjects received the instructions (SI Appendix) and practiced using the computer keys that would indicate their choices. We then presented subjects with the allocation matrices in the control and two group conditions as described above. A postexperiment survey asked demographics (e.g., age, sex, major field of study, hometown, parent information). In addition to the show-up fee of $6, subjects received payment for one choice selected at random from each of the three parts of the experiment—nongroup, minimal group, and political group. Choices were translated into dollars following the laboratory protocol described in the instructions, and subjects earned an average of $15 for a 1-h session. This payment amount was on par with regional compensation rates, consistent with other studies run in the laboratory, and higher than that of nonincentive-compatible studies in other local laboratories.

Group Identification vs. Individual Responsiveness in the Raw Data

All analyses of the data were conducted using Stata Version 16. Data and codes are available at the Inter-University Consortium for Political and Social Research (ICPSR), University of Michigan Depository for Replication Datasets.

Group Identification?

Consider a simple measure of in-group bias, which we call favoritism, defined by the average difference in allocations to in-group and out-group recipients. In each group treatment, each subject faced each allocation matrix twice—once for the YOU-OWN pairing and once for the YOU-OTHER pairing. If a subject consistently chose the same row in each such matrix, there would be no difference in the income earned by that subject’s in-group and out-group recipients, and thus, the subject would have a favoritism score of zero. However, if a subject consistently chose different rows in each matrix for in-group and out-group, yielding more (less) money to the in-group recipient, there would be a positive (negative) favoritism score (with a range of values approximately ±69). We analyzed the distribution of these individual favoritism scores for both the minimal group and the political group across different subsamples of the subject pool and at the individual level.

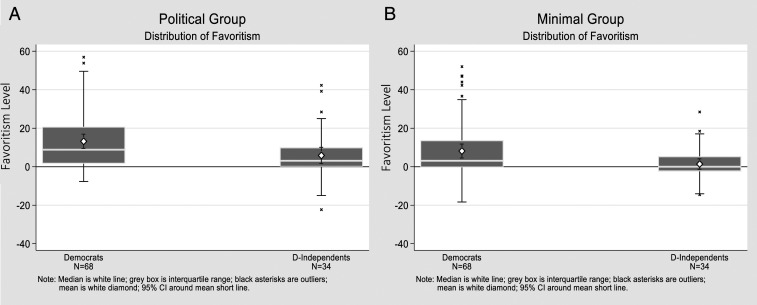
Comparing Democrats and D-Independents in the political group treatment (Fig. 1A), we observe higher favoritism among Democrats (mean, 13.19; SE, 1.89; median, 8.85) than for D-Independents (mean, 5.83; SE, 2.15; median, 3.08). Both means are significantly different from 0 (P = 0.0000 and P = 0.0106, respectively), and the difference, 7.35 (SE, 3.08), is also significantly different from 0 (P = 0.019). By itself, the Democrats’ higher mean favoritism would indicate that greater attachment to the political group relates to greater in-group bias.

Fig. 1.

Distributions of favoritism for Democrats (n = 68) and D-Independents (n = 34). Favoritism is scaled on the y axis, with possible maximums of ±69.23. Shown are box and whisker plots of the medians, interquartile ranges, and outliers. Superimposed are white diamonds for the means and related 95% CI. A contains the distributions for the political condition; B contains the minimal group condition.

However, the results from the minimal group treatment (Fig. 1B) challenge this interpretation. We again observe higher favoritism among Democrats (mean, 8.14; SE, 1.85; significantly different from 0 at 0.01 level; median, 3.08) than for D-Independents (mean, 1.38; SE, 1.39; median, 0). The difference between these minimal groups means, 6.76 (SE, 2.81), is significantly different from 0 (P = 0.018). However, the comparison between the two treatments provides no evidence of differences in favoritism (P = 0.82); Democrats consistently show higher in-group bias than D-Independents, and the political treatment raises both of their favoritism levels equally. Since Democrats have more in-group bias in the minimal group than D-Independents and given that they have the same political positions, the results also suggest that people who are more likely to affiliate with a political party are also more likely to respond to artificial group manipulations.^§

The comparison of Republicans and R-Independents cannot assess the impact of group identification since the subsamples vary not only on affiliation with the political party but also, on three of the five political positions (SI Appendix, Table S5).^¶ These samples are also small and thus, can suffer the problems of weak statistical tests, influence of outliers, and unrepresentative behavior. In the political treatment, the levels of favoritism are not significantly different between Republicans and R-Independents; Republican mean favoritism is 14.11 (SE, 4.38), while R-Independent mean favoritism is 11.69 (SE, 4.16), with a difference of 2.42 (P = 0.69). Nor are minimal group mean favoritism levels significantly different; Republican mean is 3.71 (SE, 3.83), while R-Independent mean is 10.41 (SE, 3.63) with a difference of −6.7 (P = 0.21). The difference in differences across treatments (political vs. minimal group) is significantly different from zero (P = 0.063) due to the R-Independents’ higher favoritism level in the minimal group. However, a replication exercise using a larger dataset from a separate online minimal group study (16) indicates that this R-Independent higher minimal group favoritism is anomalous (SI Appendix, Fig. S13 and Table S14). The replication exercise reproduces the minimal group treatment results for Democrats and D-Independents and shows an identical pattern for Republicans and R-Independents as well as the pooled samples of political party members vs. nonparty members, with party members exhibiting significantly higher minimal group favoritism (SI Appendix, Figs. S12–S14 and Tables S13–S15).

Individual Responsiveness to Group Divisions?

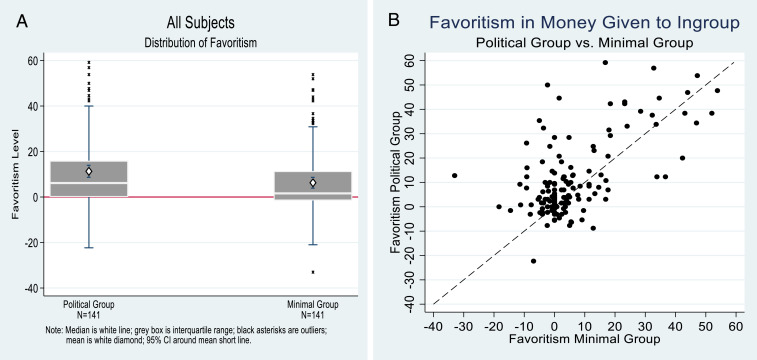
The above analysis raises the question of whether within the entire participant sample, there are individuals who respond more strongly to the group divisions—a tendency we will call individual “groupiness.” Fig. 2A provides the favoritism distributions for all subjects (n = 141) in the political condition (on the left) and in the minimal group condition (on the right). The political group mean is 11.31 (SE, 1.35), and the minimal group mean is 6.28 (SE, 1.22), with a statistically significant difference of 5.03 (SE, 1.82; P = 0.006); these means are larger than the medians due to the presence of individuals with very high levels of favoritism. Are the individuals with the high favoritism levels in the political group condition the same as those with high favoritism levels in the minimal group condition?

Fig. 2.

Favoritism levels for all subjects (n = 141). (A) Favoritism is scaled on the y axis, with possible maximums of ±69.23. Shown are box and whisker plots of the medians, interquartile ranges, and outliers. Superimposed are white diamonds for the means and the related 95% CIs. The political group treatment is on the left, and minimal group treatment is on the right. (B) Individual favoritism levels for each subject in the minimal group treatment (x axis) and the political group treatment (y axis). The dashed line is the 45° line.

The answer is yes. As shown in Fig. 2B, the individuals clustered around (0,0) show no favoritism in the minimal group or the political group treatment: whatever amount they choose to give to an in-group recipient—be it high or low—is the same amount given to an out-group recipient. On the other hand, the participants with allocations higher along the 45° line favor in-group recipients in both the minimal and the political treatment, showing in-group bias regardless of the particular group setting. Overall, there is a strong positive relationship between favoritism in political group and favoritism in the minimal group, with a correlation coefficient of 0.63 and linear regression with R² of 0.4. This finding supports the conclusion that individual responsiveness to group divisions (rather than treatment-specific effects) drives patterns in allocation behavior.

Social Preferences and Individual Groupiness: Structural Estimation

Structural estimation of social preferences, which posits and estimates the parameters of a model for a subject’s choices, confirms the findings of the raw data. First, the social preferences of Democrats show greater in-group bias than the social preferences of D-Independents, in both the minimal group and political group treatments, with a difference in difference of zero. Second, some individuals’ social preferences are contingent on the group identities of recipients; for other individuals, there is no such contingency.

The structural estimation first specifies a model for how subjects decide between the two rows in an income allocation matrix. As discussed above, in choosing a row in the matrix, a subject possibly faces a trade-off between own income and a social objective such as avoiding inequality, maximizing total income, or seeking income dominance. A utility function models these trade-offs by positing the value a person places on own and other’s income. Formally, an individual i’s utility is a function of her income π_i and another person’s income π_j: U_i(π_i, π_j). We adopt the specification of refs. 11, 20, and 21 and let

$$U_i\left({\pi }_i,{\pi }_j\right)\hspace{0.17em}={\beta }_i{\pi }_i+{\rho }_i\left({\pi }_i-{\pi }_j\right)r+{\sigma }_i\left({\pi }_j-{\pi }_i\right)s,$$

where β_i is the weight an individual places on own income, ρ_i is the weight on income difference when π_i ≥ π_j, r is an indicator variable for π_i ≥ π_j, σ_i is the weight on income difference when π_i < π_j, and s is an indicator variable for π_i < π_j. With this specification, i’s disutility from unequal income when i earns more than j (“advantageous inequality”) can be distinct from the disutility when i earns less than j (“disadvantageous inequality”).

Subjects choose one of two rows in each allocation matrix, and the discrete choice data allow the estimation of these utility parameters by the well-known logistic regression model, provided in Appendix: Econometric Specifications. For any subsample of the subject pool, we can estimate the social preferences for any of the five pairings NG, POL YOU-OWN, POL YOU-OTHER, MG YOU-OWN, and MG YOU-OTHER. For the full subject pool, estimating social preferences for MG YOU-OWN and for MG YOU-OTHER, we replicate the findings of ref. 11 for a minimal group treatment; subjects are on average inequality averse, but they suffer less from advantageous inequality and suffer more from disadvantageous inequality vis-à-vis out-group recipients (SI Appendix, Table S19).

Group Identification?

We compare here the social preferences of Democrats and D-Independents toward in-group recipients and out-group recipients in each group treatment.^# For ease of interpretation, we consider the ratios $\rho /\beta$ and $\sigma /\beta$, which are interpreted as the prices a person is willing to pay to reduce advantageous and disadvantageous inequality, respectively, with the estimates presented in Table 1.

Table 1.

Social preferences: Democrats vs. D-Independents

Price of inequality	Democrats n = 68			D-Independents n = 34			Democrats – D-Independents n = 102 Difference in Difference
	In-group	Out-group	Difference	In-group	Out-group	Difference
Political group
$\rho /\beta$	−0.333**	−0.052**	−0.281**	−0.321**	−0.226**	−0.095**	−0.186**
SE	(0.017)	(0.022)	(0.028)	(0.023)	(0.029)	(0.037)	(0.051)
$\sigma /\beta$	0.043	−0.314**	0.356**	−0.117*	−0.292*	0.176*	0.181
SE	(0.044)	(0.058)	(0.073)	(0.062)	(0.087)	(0.106)	(0.135)
Minimal group
$\rho /\beta$	−0.294**	−0.165**	−0.130**	−0.305**	−0.308**	0.0039	−0.134**
SE	(0.018)	(0.021)	(0.027)	(0.025)	(0.025)	(0.035)	(0.050)
$\sigma /\beta$	−0.011	−0.200**	0.189**	−0.155**	−0.143**	−0.013	0.202*
SE	(0.045)	(0.059)	(0.074)	(0.067)	(0.070)	(0.097)	(0.124)
Political group − minimal group
$\rho /\beta$	−0.039	0.113**	−0.151**	−0.016	0.082**	−0.099*	−0.053
SE	(0.024)	(0.030)	(0.039)	(0.034)	(0.038)	(0.051)	(0.071)
$\sigma /\beta$	0.053	−0.114	0.167	0.039	−0.150	0.188	−0.021
SE	(0.063)	(0.083)	(0.104)	(0.091)	(0.111)	(0.144)	(0.183)
Observations = (N × 26 × 4) minus timed-out decisions	7,024	7,024	7,024	3,524	3,524	3,524	10,548

*P < 0.1; **P < 0.05.

We discuss here the ratio $\rho /\beta$; the results for $\sigma /\beta$ are similar. In POL YOU-OWN matches, Democrats reduce their own payoff by 0.33 to avoid an additional 1.00 in advantageous inequality—a much higher price than for POL YOU-OTHER matches (0.05). That is, Democrats are willing to pay 0.28 more per unit to reduce inequality when it is between themselves and a political in-group vs. themselves and a political out-group. This effect of group identity was much smaller for D-Independents (POL YOU-OWN: 0.32; POL YOU-OTHER: 0.23). That is, D-Independents are willing to pay 0.09 more per unit when inequality is between themselves and political in-group vs. themselves and political out-group, an amount only one-third as large as Democrats. In the minimal group treatment, Democrats are again willing to give up more to avoid advantageous inequality with in-group members than to avoid inequality with out-group members, while D-Independents show inequality aversion equally toward in-group and out-group members.

Across in-group and out-group pairings in the minimal and political group treatments, there is no significant difference in the difference of social preference parameters between Democrats and D-Independents (as shown in the bottom-right corner of Table 1). Democrats have consistently more social preference in-group bias, in both the political and the minimal group.

Individual Groupiness?

We next consider social preferences at the individual level. Directly estimating precise individual utility parameters typically requires more decisions than feasible within the laboratory setting.^‖ However, unlike previous economic experiments, our study is within subject and thus, contains multiple choices for each individual in different settings. We can therefore estimate a finite mixture model, also known as a latent class model, which yields utility types each characterized by an estimated set of utility parameters $\left({\beta }_t,{\sigma }_t,{\rho }_t\right)$ and an estimated proportion of the population, p_t, where ∑_t p_t = 1.

The estimation is a generalization of the mixed logit model for the discrete choice data (SI Appendix). We set t = 4 in order to be able to capture the four canonical social preferences described above (selfish, inequality averse, total income maximizing, dominance seeking). The estimation did yield these four types (SI Appendix, Table S38). We emphasize, however, that the estimation process itself is independent of specific types, providing confidence that these estimates reflect the actual types in the population.**

Having estimated the types, we categorize each subject as a type in each condition match {NG, POL YOU-OWN, POL YOU-OTHER, MG YOU-OWN, MG YOU-OTHER}. To do so, based on a subject’s actual choices, we calculate the posterior probabilities, {P₁, P₂, P₃, P₄}, that an individual is of each type in that pairing (see Appendix: Econometric Specifications for formulas). We then categorize each individual i as the type t with highest posterior probability. These categorizations are robust; almost all subjects make decisions that are highly consistent with one and only one type. The median posterior probability of being a single type is higher than 0.99 for every condition match. The mean posterior probabilities are at least 0.93 for selfish, inequality-averse, and dominance-seeking types. Total income-maximizing assignment is only slightly less accurate with lowest mean probability of 0.82^†† (SI Appendix, Table S37).

We next established a set of criteria to ask whether subjects’ social preferences are responsive or nonresponsive to the experimental treatments and matches; these criteria formally define not-groupy and groupy subjects, respectively.

For nonresponsiveness, given the large literature on minimal groups, we start with a criterion specifying that with 90% confidence a subject has the same social preference type for MG YOU-OWN and MG YOU-OTHER pairings.^‡‡ Sixty-one percent of total subjects (86 of 141) satisfy this criterion, showing that response to the minimal group is limited to less than half of subjects. (SI Appendix, Table S45 shows this cross-tabulation.) With our within-subject design, we focus on more stringent criteria, where a subject must have the same social preference type in MG YOU-OWN, MG YOU-OTHER, POL YOU-OWN, and POL YOU-OTHER pairings with 90% confidence. Forty percent of subjects (57 of 141) satisfy this criterion. We call these subjects not groupy since they have the same social preferences no matter the group identity of the recipient. The strongest criterion is that a subject does not change types with 90% confidence across all conditions of the experiment, including the nongroup control. How a subject treats recipients in the nongroup control is especially pertinent since subjects made these decisions prior to any presentation of groups or group assignments. When a subject’s social preferences for MG YOU-OWN, MG YOU-OTHER, POL YOU-OWN, and POL YOU-OTHER recipients are the same as the social preferences for an NG recipient, the subject is treating each recipient in each condition as if the recipient was not a member of a group at all. We call these subjects strongly not groupy since their social preferences do not respond to any group feature of the experiment. Thirty-four percent of the subjects (48 of 141) satisfy this criterion. These subjects are either consistently selfish, inequality averse, total income maximizing, or dominance seeking for all pairings in the experiment.^§§

For responsiveness, the basic criterion for groupy subjects is that with 90% confidence the individual has different social preferences for in-group and out-group recipients within either group treatment; 43% (61 of 141) satisfy this criterion. Strongly groupy subjects are those whose with 90% confidence have different social preferences for in-group and out-group recipients within both group treatments; only 17% (24 of 141) fall into this category.^¶¶

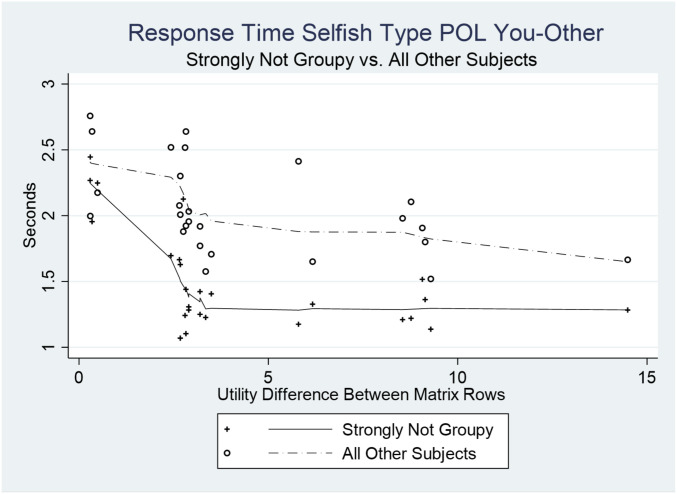
Do these designations relate to participants’ behavior in other dimensions? We compare strongly not-groupy subjects with other subjects in terms of response time and basic demographics. To control for the time to calculate payoffs, we consider the choice to keep as much money for self in POL YOU-OTHER matches. Fig. 3 compares strongly not-groupy subjects with all other subjects. We convert each row in each matrix into a level of utility for selfish types and then order the matrices according to the difference in utility of the rows. When the utility difference is large, both sets of subjects make decisions faster. However, strongly not-groupy subjects choose allocations more quickly on average (1.5 vs. 2.06 s, t = 7.2, P = 0.0000), suggesting that they pay less attention to the YOU-OWN vs. YOU-OTHER labels, which appear above the choice matrices.^##

Fig. 3.

Average response times for selfish types in POL YOU-OTHER for strongly not-groupy subjects (n = 17) and all other subjects (n = 27). For each of 26 matrices, the utility difference between the two rows is measured on the x axis. The average time to make a decision for each matrix is measured on the y axis in seconds. The solid and dashed lines are locally weighted scatterplot smoothing plots. Average response time overall for strongly not-groupy subjects is 1.50 s and for all other subjects is 2.06 s (t = 7.2; P = 0.0000).

We next considered whether not groupiness relates to demographics or political affiliations outside the laboratory (SI Appendix, Tables S47–S49). Race and gender do not relate to the strongly not-groupy categorization, nor does church going or trust of strangers. However, there is evidence that strongly not-groupy subjects are more likely to be politically independent. Forty-eight percent self-declared as politically independent, whereas only 30% of groupy subjects (P = 0.05) and 21% of strongly groupy subjects (P = 0.03) did so. Strongly not-groupy subjects are also significantly more likely than all other subjects to have highly educated fathers (Master’s degree or higher)—69 vs. 48% (P = 0.02)—indicating that family income or education could be at play in general attitudes toward groups.

Discussion and Directions for Future Research

This experiment studies individual behavior in different group settings, building on the experimental tradition in social psychology and on the economics literature on social preferences. Each subject chooses income levels for self and others in a control and two group treatments—minimal group and political group—in both in-group pairings and out-group pairings. Exploiting this within-subject design, the study robustly identifies strongly groupy individuals who show consistent in-group bias and strongly not-groupy individuals who show no bias across the experiment.

The present study shows the stability of individual biased behavior across two group treatments, providing strong evidence of groupiness as an individual property. Further experimental studies could consider psychometric, demographic, and other correlates of individual biased behavior. For example, analysis of a minimal group treatment in a geographically dispersed online experiment indicates that biased social preferences relate to location in deindustrialized counties (16). Experimental research could investigate the extent to which such individual groupiness is stable across different economic contexts, such as public good provision. The results could also inform theoretical research on organizations, such as political parties and firms, and their adoption of different practices and pay schemes. Using tournaments (which compensate groups of workers who outperform other groups) rather than piece rates (which compensate individuals according to their own productivity) could lead to self-selection of more or less groupy people to work for a firm.

This study’s design and results also suggest possible directions for research in other realms with findings of patterns of bias and in-group preferences. In many studies, people’s choices are observed in a single social setting. For example, high schoolers’ preferences for friends of the same race or ethnicity are shown to drive homophily (25), with some consistent differences. White students’ homophily is driven by these preferences, Black and Hispanic students’ homophily is driven by both preferences and different rates of meeting other students, and Asian students fall in an intermediate range. In an example of laboratory experiments of implicit bias, studies show that both police officers and student subjects are more attuned to Black faces after hearing primes relating to crime and violence (26), and participants are more attuned to racial stereotypes in an inattention task after primes of African American names (27). The present study suggests that observing people and subjects in multiple settings could delve into these aggregate patterns and shed light on possible key individual variation. Collecting panel data and conducting within-subject experiments would allow for appropriate measures of individual groupiness for these choices and tasks. Such measures could help better identify the sources of bias and discrimination.

Following the framework of the present study, observing people in several settings could uncover that bias is systematically expressed not only just by some subsets of the population but also, only by some individuals. Groupy individuals would have more affiliative tendencies in general, leading to explicit actions and implicit biases across a wide range of social settings. Importantly, groupiness may cut across other predictors of in-group/out-group biases (e.g., demographics, shared experiences) to influence real-world economic outcomes. Understanding variation in such affiliative tendencies may thus provide insights into how and why people sometimes support in-group members but sometimes harm out-group members—and into institutions that might promote more prosocial behavior overall.

Appendix: Econometric Specifications

Consider a set of individuals S. If all individuals in S have the same preferences $\left(\beta ,\sigma ,\rho \right)$ and if the error term is an extreme value distribution, our structural model has the well-known logit form. For a particular condition match in which each subject in $\mathbf{S}$ faces 26 matrices, we estimate $\left(\beta ,\sigma ,\rho \right)$ by maximizing the following likelihood function, where N_S is the number of people in the set:

$$L\left(\beta ,\sigma ,\rho ;\mathbf{S}\right)={\displaystyle \prod _{i=1}^{N_S}{\displaystyle \prod _{m=1}^{26}{\text{Λ}}_{mi}{\left(\beta ,\sigma ,\rho |{\pi }_i,{\pi }_j\right)}^{b_{mi}}{\left(1-{\text{Λ}}_{mi}\left(\beta ,\sigma ,\rho |{\pi }_i,{\pi }_j\right)\right)}^{1-b_{mi}}}},$$ [1]

where ${\text{Λ}}_{mi}\left(\beta ,\sigma ,\rho \right)\hspace{0.17em}=\hspace{0.17em}\text{exp}\left(U_{mi}^{bot}-U_{mi}^{top}\right)/\left(1+\exp \left(U_{mi}^{bot}-U_{mi}^{top}\right)\right)$ and

$$\left(U_{mi}^{bot}-U_{mi}^{top}|\beta ,\sigma ,\rho \right)=\left(\begin{array}{c}\beta \left({\pi }_{i,m}^{bot}-{\pi }_{i,m}^{top}\right)+\\ \rho \left(\left({\pi }_{i,m}^{bot}-{\pi }_{j,m}^{top}\right)\cdot r^{bot}-\left({\pi }_{i,m}^{bot}-{\pi }_{j,m}^{top}\right)\cdot r^{top}\right)\\ \sigma \left(\left({\pi }_{i,m}^{bot}-{\pi }_{j,m}^{top}\right)\cdot s^{bot}-\left({\pi }_{i,m}^{bot}-{\pi }_{j,m}^{top}\right)\cdot s^{top}\right)\end{array}+\right).$$

SI Appendix, Text and Tables S19–S38 discuss and provide estimations without and with clustering errors by individuals in order to account for within-subject correlation, with substantively similar results.***

For the comparison of estimated utility function parameters, the estimation maximizes the likelihood function for each subset S:

$$\hspace{0.17em}L\left(\mathit{\beta },\mathit{\sigma },\mathit{\rho };\mathbf{S}\right)={\displaystyle \prod _{c=1}^4{\displaystyle \prod _{i=1}^{N_S}{\displaystyle \prod _{m=1}^{26}{\text{Λ}}_{mi}{\left({\beta }_c,v_c,{\rho }_c|{\pi }_i,{\pi }_j\right)}^{b_{mi}}{\left(1-{\text{Λ}}_{mi}\left({\beta }_c,v_c,{\rho }_c|{\pi }_i,{\pi }_j\right)\right)}^{1-b_{mi}}}}},$$ [2]

where $\mathit{\beta },\mathit{\sigma },\mathit{\rho }$ are vectors of the parameters for the four condition matches (POL YOU-OWN, POL YOU-OTHER, MG YOU-OWN, and MG YOU-OTHER) for S_D = Democrats and for S_DI = D-Independents.

The mixed logit model is a generalization of Eq. 1 with t types characterized, respectively, by parameters $\left({\beta }_t,{\sigma }_t,{\rho }_t\right)$ and a proportion of the population p_t, where ∑_tp_t = 1 (SI Appendix). Under the estimated parameters and given the choices i actually made, the probability of making those choices if i is type t is

$${\mathrm{\Gamma }}_t\left(\beta ,\sigma ,\rho \right)={\displaystyle \prod _{k=1}^{26}{\mathrm{\Lambda }}_{\text{tk}}{\left({\beta }_t,{\sigma }_t,{\rho }_t|{\pi }_i,{\pi }_j\right)}^{{\text{d}}_{\text{ki}}}\times \left(1-{\mathrm{\Lambda }}_{\text{tk}}{\left({\beta }_t,{\sigma }_t,{\rho }_t|{\pi }_i,{\pi }_j\right)}^{\left(1-{\text{d}}_{\text{ki}}\right)}\right)}.$$

Using Bayes’ rule with the estimated proportions p_t as priors of being type t, the posterior probability that i is type t is

$$P_t=\frac{p_t{\text{Γ}}_t\left(\beta ,\sigma ,\rho \right)}{{\displaystyle {\sum }_{t=1}^4{\text{Γ}}_t\left(\beta ,\sigma ,\rho \right)}}.$$

Data Availability.

Data and codes are available at the Inter-University Consortium for Political and Social Research, University of Michigan Depository for Replication Datasets, https://openicpsr.org/openicpsr/project/120555/version/V1/view.