Phylogenetic Reconstruction Based on Synteny Block and Gene Adjacencies

Abstract

Gene order can be used as an informative character to reconstruct phylogenetic relationships between species independently from the local information present in gene/protein sequences. PhyChro is a reconstruction method based on chromosomal rearrangements, applicable to a wide range of eukaryotic genomes with different gene contents and levels of synteny conservation. For each synteny breakpoint issued from pairwise genome comparisons, the algorithm defines two disjoint sets of genomes, named partial splits, respectively, supporting the two block adjacencies defining the breakpoint. Considering all partial splits issued from all pairwise comparisons, a distance between two genomes is computed from the number of partial splits separating them. Tree reconstruction is achieved through a bottom-up approach by iteratively grouping sister genomes minimizing genome distances. PhyChro estimates branch lengths based on the number of synteny breakpoints and provides confidence scores for the branches. PhyChro performance is evaluated on two data sets of 13 vertebrates and 21 yeast genomes by using up to 130,000 and 179,000 breakpoints, respectively, a scale of genomic markers that has been out of reach until now. PhyChro reconstructs very accurate tree topologies even at known problematic branching positions. Its robustness has been benchmarked for different synteny block reconstruction methods. On simulated data PhyChro reconstructs phylogenies perfectly in almost all cases, and shows the highest accuracy compared with other existing tools. PhyChro is very fast, reconstructing the vertebrate and yeast phylogenies in <15 min.

Introduction

Today, phylogenies of many species can be reconstructed using sequences from numerous proteins, but, despite the availability of a considerable amount of sequence data, reconstructions are not always accurate and can result in incongruent topologies (Philippe et al. 2011). These limitations are partly due to methodological artifacts such as sequence misalignment (different software give significantly different alignments; Wong et al. 2008), false-orthologous gene assignment (due to horizontal transfer, gene duplication/loss events; Bapteste et al. 2004), and homoplasy inherent to the data. These limitations prompted phylogeneticists to explore different types of signal representing rare genomic changes, such as intron indels, retroposon integrations, changes in organelle gene order, gene duplications, and genetic code variants (Rokas and Holland 2000). Although these genomic changes can be useful to validate some topological uncertainties, they have never been used to reconstruct complete phylogenies at the exception of the coherent mitochondrial phylogeny based on gene composition and gene order of mitochondrial genomes (Sankoff et al. 1992). This result offered, for the first time, a strong validation of the hypothesis that the macrostructure of mitochondrial genomes contains quantitatively meaningful information for phylogenetic reconstruction.

Gene order along nuclear chromosomes follows different evolutionary trends than along mitochondrial genomes (Burger et al. 2003), and it has been observed in several occasions that it comprises useful evolutionary information for phylogenetic reconstruction (Boore 2006; Fertin et al. 2009). Many methods aiming at exploiting this trait as phylogenetic signal have been developed. They all belong to one of the four classical methodological categories, that is, the distance-based methods (Moret, Wang, et al. 2001; Wang et al. 2006; Guyon et al. 2009; Lin et al. 2012; Luo et al. 2012), the maximum parsimony-based methods (Sankoff and Blanchette 1998; Cosner et al. 2000; Moret, Wyman, et al. 2001; Bourque and Pevzner 2002; Tang and Moret 2003; Bergeron et al. 2004; Xu and Moret 2011; Zheng and Sankoff 2011), the maximum likelihood-based methods (Larget et al. 2005; Hu et al. 2011; Lin et al. 2013; Feng et al. 2017), and the quartet-based methods (Liu et al. 2005). Whether they are applied to sequences or gene orders, these methodological categories harbor a variety of intrinsic limitations: computational complexity, sensitivity to short- and long-branch attractions (Felsenstein 1978), and requirement for good evolutionary models (Yang and Rannala 2012). Moreover, gene order-based methods were so far mainly applied to small bacterial or organelle genomes or to highly colinear genomes. The first phylogenetic reconstruction of eukaryotic nuclear genomes harboring different gene contents and different levels of synteny conservation was applied to the very large evolutionary span covered by the super-group of Unikonts and did not assess the performance of the method at known difficult branching positions such as the position of Rodentia relative to Primates and Laurasiatheria (Xu and Moret 2011), or the position of Candida glabrata in Saccharomycetaceae (Lin et al. 2013; Hu et al. 2014). A recent improvement of this method taking into account balanced rearrangements, insertions, deletions, and duplications into an evolutionary model based on the principle of Double Cut and Join was applied to the phylogenetic reconstruction of 20 yeast species. It achieved accurate phylogeny reconstruction although the tree topology showed a couple of disagreements with previously published phylogenies (Feng et al. 2017).

We developed PhyChro with the aim of making the most of the evolutionary information derived from chromosome rearrangements. PhyChro is applied to 13 vertebrate and 21 Saccharomycotina yeast genomes and it reconstructs very accurate tree topologies even at known difficult branching positions.

New Approaches

PhyChro is a method for phylogenetic reconstruction based on synteny block and gene adjacencies. It relies on two important specificities. First, it uses synteny block adjacencies computed for all possible pairwise combinations of species instead of using synteny blocks universally shared by all the species involved in the reconstruction. This pairwise approach has the advantage to efficiently compare genomes with different levels of synteny conservation, without losing the wealth of synteny information that is shared by most closely related genomes. Second, PhyChro achieves tree reconstruction using the idea that for each synteny breakpoint, (a subset of the) genomes can be split into two disjoint groups depending on whether they support one block adjacency defining the breakpoint or the other. Formally, PhyChro relies on partial splits (Semple and Steel 2001; Huson et al. 2004; Huber et al. 2005) (fig. 1), a generalization of the notion of split used in quartet-based methods. By exploiting partial splits associated with all identified breakpoints, PhyChro defines a distance between genome pairs, called partial split distance (PSD), by counting the number of times that two genomes belong to different subsets of a partial split. Note that PSD is a measure defined on a set of n genomes contrary to other previously introduced distance measures based on the comparison of only two genomes at a time. Based on PSD, PhyChro reconstructs tree topologies with a bottom-up approach, by iteratively identifying those sister genomes that minimize the number of times they belong to different subsets of a partial split.

Fig. 1.

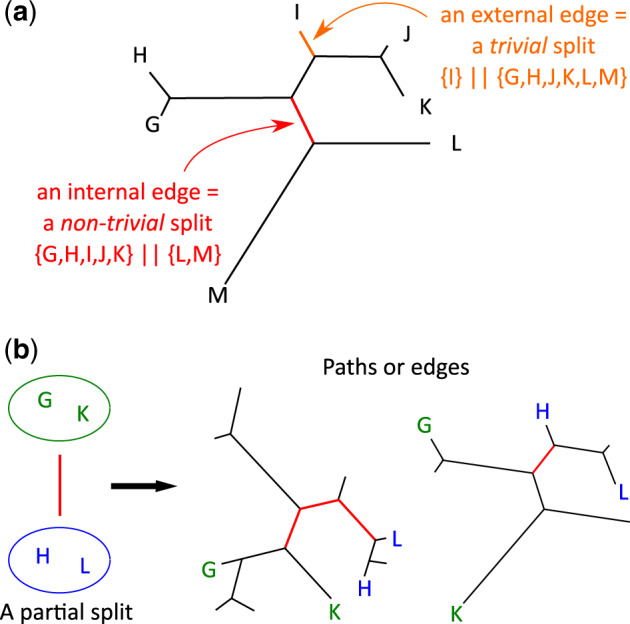
Splits and partial splits. (a) Examples of trivial (orange edge) and nontrivial (red edge) splits. (b) The two sets of genomes $\left\{GK\right\}$ and $\left\{HL\right\}$, forming a partial split, uniquely determine a path (in red, in the left tree) or an edge (in red, in the right tree) that join the smallest subtrees including G, K, and H, L.

Intuitively, sister genomes are pairs of genomes sharing a high number of gene adjacencies at breakpoint positions. One can think of these pairs of genomes as being located close to each other but also as being located further away from all other genomes. Based on these intuitions, PhyChro: 1) focuses on chromosomal rearrangement events supporting internal branches (useful for topology reconstruction) while ignoring all events that occurred on external branches (of no use for topology reconstruction) and 2) minimizes the differences between sister genomes, that is, genomes separated by no internal branch, rather than maximizing their similarity.

Contrary to distance-based methods, each pairwise distance depends on all genomes (as it depends on breakpoints identified through all genome comparisons) and, at each iteration, PhyChro recomputes distances from scratch between all pairs of genomes not yet included in the reconstruction. This iterated updating, affecting all entries of the distance matrix, is original to PhyChro and absent in distance-based methods. The neighbor-joining (NJ) algorithm encodes the somewhat similar idea that pairs of genomes need not only be close to each other but also be distant from all others to be considered first in the reconstruction. This second condition is explicitly handled by the NJ algorithm, whereas PhyChro encodes it directly in its definition of genome distance. In conclusion, PhyChro is an algorithm whose basic data structure is the partial split and whose computational model is a bottom-up iterative reconstruction of the tree based on genome distances. These distances are computed by successive approximations, after the iterative elimination of inconsistencies in the set of partial splits.

PhyChro provides estimations for branch length and branch robustness. Extensive details on the algorithm and on the notions on which it relies are provided in the Materials and Methods section.

Results

Phylogenetic Reconstruction of Yeast and Vertebrate Species

We tested PhyChro on two different sets of species comprising 21 yeast and 13 vertebrate genomes. They harbor very different genome characteristics (in terms of genome size and number and density of genes) as well as very different modes of chromosome evolution (number and rates of rearrangements, proportions of inversions vs. translocations, whole-genome duplication events) (Drillon and Fischer 2011). Previous analyses using the global level of divergence of orthologous proteins revealed that the evolutionary range covered by the Saccharomycotina subphylum exceeds that of vertebrates and is similar to the span covered by the entire phylum of Chordata (Dujon 2006). Moreover, for both clades, the level of synteny conservation is highly variable between subclades with only 50% of genes belonging to synteny blocks between Amniota and fishes, or between yeast species from the Protoploid and CUG clades, whereas >95% of genes are conserved in synteny between Primates or between closely related species within the CUG clade (Drillon and Fischer 2011). Finally, phylogenetic reconstructions in these two groups of species contain some ambiguous branching positions (sometimes controversial in the past), such as the position of Rodentia in the vertebrate tree or the position of Ca. glabrata in the Saccharomycetaceae family of yeast, that we were interested to test with PhyChro. In the following, our reference truth on both yeasts and vertebrates phylogenetic reconstructions is based on consensus trees obtained with large curated phylogenomic data sets (Russo et al. 1996; Romiguier et al. 2013; Pryszcz et al. 2015; Shen et al. 2016; Irisarri et al. 2017).

We applied PhyChro on the sets of synteny blocks reconstructed with SynChro (Drillon et al. 2013, 2014) (see Materials and Methods) that resulted from genome pairwise comparison of the two sets of vertebrate and yeast species. The resulting tree topologies were compared with the reconstructions obtained with existing methods based on protein sequence comparisons, including PhyML, a maximum likelihood-based method, ProtPars, a maximum parsimony-based method, and both Neighbor and FastME, two distance-based methods (Felsenstein 1989; Guindon and Gascuel 2003; Lefort et al. 2015) (see Materials and Methods).

The tree topology reconstructed by PhyChro for the 13 vertebrate species (fig. 2a) is identical to the topology produced by PhyML on 389 families of orthologs (illustrated in supplementary fig. S1, Supplementary Material online). The position of Rodentia is correctly located, closer to Primates than to the Laurasiatheria. By comparison, ProtPars, Neighbor, and FastME do not correctly place Rodentia (supplementary figs. S1 and S2, Supplementary Material online). It should be noticed that PhyChro succeeded in correctly placing the rodent branch in the tree despite the fact that no partial split supports the existence of the branch splitting Primates and Rodentia from the other species. This is due to the fact that PhyChro, contrary to the other methods, does not construct the tree by identifying well-supporting branches; rather, it avoids creating branches that are contradicted. This strategy allows PhyChro to treat difficult cases generated by small branches and characterized by very few rearrangements. In the specific reconstruction of Rodentia positioning, the detection of the short branch preceding their splitting with Primates, is rendered even more difficult by the important evolutionary history of Rodentia that likely erased the traces of the plausibly few ancestral rearrangements of Primates and Rodentia (see long branches in fig. 2a). PhyChro’s corresponding branch length equals zero and its confidence score cS (formally defined in “How to compute branch length and confidence score” of the Supplementary Material online), which assesses the robustness of the branch, is close to 0 (0.03, fig. 2a).

Fig. 2.

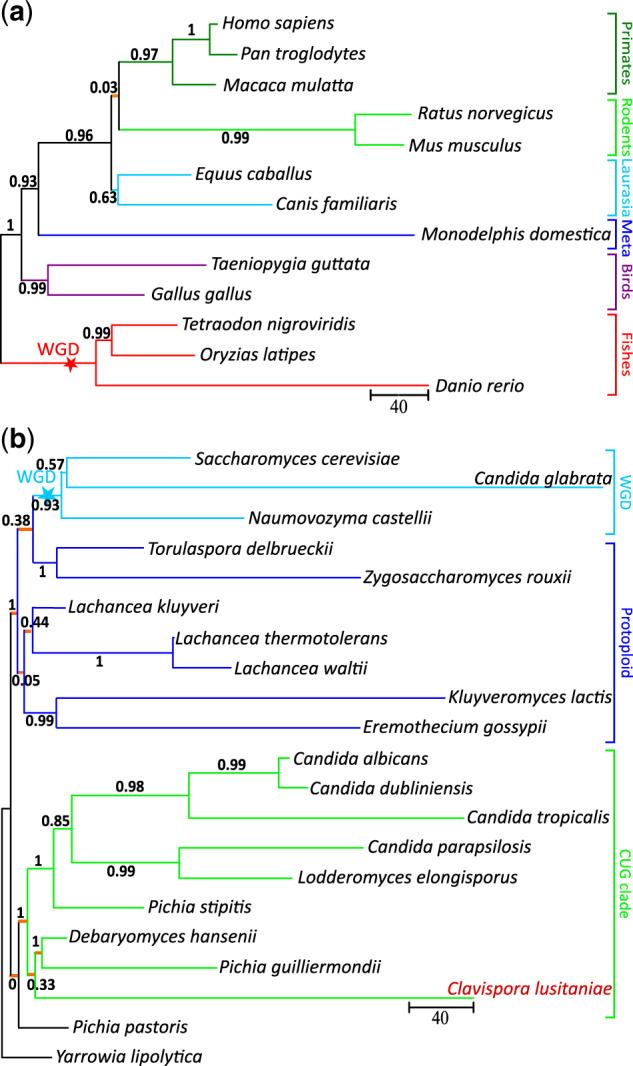
Phylogenies obtained with PhyChro for 13 vertebrate (a) and 21 yeast (b) species. Confidence scores that range between 0 and 1 are indicated on internal branches. Scale bars provide an estimation of the branch lengths, which correspond to the number of breakpoints, indirectly representing a number of rearrangements. For the sake of clarity, internal branches with length smaller than one unit are represented in orange with an arbitrary small, but visible, length. Whole-genome duplication events (WGD) are reported. Clavispora lusitaniae location in the tree is dubious and highlighted in dark orange.

In several ways, the tree topology reconstructed by PhyChro for the 21 yeast species is more accurate than the topologies obtained with either one of the four phylogenetic reconstruction methods, based on protein sequence comparison (fig. 2b and supplementary figs. S1 and S3, Supplementary Material online). The first difference concerns the position of Ca. glabrata relatively to Saccharomyces cerevisiae and Naumovozyma castellii (formerly known as S. castellii). It is known that phylogenies based on protein sequence analysis tend to artefactually place Ca. glabrata outside from N. castellii and S. cerevisiae (Kurtzman and Robnett 2003; Hittinger et al. 2004) due to the short/long-branch attraction problem (supplementary fig. S1, Supplementary Material online). Previous studies based on shared patterns of gene losses and rearrangements showed that in fact, N. castelli is an outgroup to a clade containing S. cerevisiae and Ca. glabrata (Scannell et al. 2006; Gordon et al. 2009). Using the same macroorganizational information, PhyChro correctly recapitulates the phylogeny for these three species, despite the very long-terminal branch length leading to Ca. glabrata present in its tree (fig. 2b). It should be considered that PhyChro reconstruction is automatic, whereas the two previous ancestral gene ordering reconstructions have been manually derived.

In addition, note that PhyML erroneously locates Pichia pastoris as an outgroup, whereas P. pastoris correctly branches at the root of the CUG clade according to PhyChro, Neighbor, FastME, and ProtPars. Note that PhyChro correctly branches P. pastoris in the tree because of >100 compatible adjacencies supporting its proximity to the CUG clade as well as no incompatibilities contradicting it. However, the confidence score of 0 of the corresponding branch is due to the absence of nontrivial split (fig. 1) associated with a breakpoint either supporting or contradicting that branch ($\#\text{Support}(b)+\#\text{Contradict}(b)=0$, see Supplementary Material online).

Neighbor and FastME (run with TaxAdd_OLS) erroneously locates P. stipitis as a sister genome of Debaryomyces hansenii, whereas P. stipitis is correctly positioned by PhyChro, PhyML, FastME (run with NJ, BioNJ, and TaxAdd_BME), and ProtPars. Concerning ProtPars, it erroneously splits the clade containing Kluyveromyces lactis and Eremothecium gossypii, whereas the clade is correctly reconstructed by PhyChro, PhyML, Neighbor, and FastME (fig. 2b and supplementary figs. S1 and S3, Supplementary Material online). In all these instances, PhyChro outperforms the three classical methods based on protein sequence comparison.

The only topological uncertainty that remains corresponds to the position of Clavispora lusitaniae. According to PhyChro, this species branches as a sister genome to the clade containing D. hansenii and P. guillermondii (fig. 2), whereas according to PhyML and ProtPars, Cl. lusitaniae branches at the root of the CUG clade. Moreover Neighbor and FastME (run with TaxAdd_OLS) produce a third topology in this region of the tree (supplementary figs. S1 and S3, Supplementary Material online). The confidence scores of the Cl. lusitaniae branch given by PhyChro, PhyML, and ProtPars show uncertainties (0.33, 0.96, and 0.97, respectively) demonstrating that the topology associated with this branch remains doubtful.

Branch length estimates provided by PhyChro give interesting information notably for subclades where the synteny conservation is still high. For instance, the terminal branch length leading to the yeast Lachancea thermotolerans is computed to be very close to zero (0.33) showing that at most one rearrangement (larger than a six genes inversion) occurred in this genome since its divergence from its last common ancestor with Lachancea waltii, whereas long branches such as the ones leading to Ca. glabrata, Danio rerio, or to Rodentia indicate the accumulation of a large number of chromosomal rearrangements. Note that branch lengths are underestimated for very distant genomes such as Yarrowia lipolytica and P. pastoris (as they are involved in very few partial splits).

Comparison with MLGO, a Gene Order-Based Method for Phylogenetic Reconstruction

Currently, the only large-scale method to reconstruct gene order phylogenies is maximum likelihood for gene order analysis (MLGO) (Lin et al. 2013). The two MLGO trees, issued from the same set of vertebrates and yeasts that we considered, are reported in supplementary figure S4, Supplementary Material online. These trees comprise a number of erroneous splits: we count two erroneous splits for vertebrates and seven for yeasts, contrary to PhyChro that reconstructs correctly both trees as reported above. For vertebrates, the errors are due to the misplacements of Monodelphis domestica and Rodentia. For yeasts, P. pastoris is erroneously located closer to the Protoploid clade than to the CUG clade, L. waltii and the sister genomes Torulaspora delbruechii and Zygosaccharomyces rouxii are erroneously located in the Protoploid clade, and finally, P. stipitis is erroneously located in the CUG clade. As for PhyChro, S. cerevisiae and Ca. glabrata are correctly located.

Robustness of PhyChro

Robustness of PhyChro on Different Definitions of Synteny Blocks

To test the sensitivity of PhyChro to different definitions of synteny block, we generated two sets of synteny blocks by using SynChro (Drillon et al. 2014) and i-ADHoRe 3.0 (Proost et al. 2012) and produced the corresponding trees for vertebrate and yeast species. On vertebrates, PhyChro based on i-ADHoRe synteny blocks gives a tree with an erroneous split corresponding to the misplacement of Rodentia (see supplementary fig. S5a, Supplementary Material online). On yeasts, we count five erroneous splits in the tree reconstruction (supplementary fig. S6a, Supplementary Material online). These discrepancies are explained by the lower proportion of genomes recovered in the synteny blocks generated by i-ADHoRe than by SynChro, as illustrated in supplementary figures S5b and c and S6b and c, Supplementary Material online. A global comparison of block size distributions generated by i-ADHoRe and SynChro over all pairwise comparisons between vertebrate and yeast genomes, is reported in supplementary figure S7, Supplementary Material online. We observe that SynChro allows for small blocks made of only two genes (noted also in Drillon et al. [2014]), whereas i-ADHoRe only allows blocks of at least three genes, and that the number of small blocks (<21 genes) produced by SynChro is systematically larger than for i-ADHoRE. For pairs of genomes that underwent many rearrangements and, in consequence, would have a low-synteny conservation, the small blocks detected by SynChro are expected to play a crucial role. This is visually observable in the matrices of supplementary figures S5b and c and S6b and c, Supplementary Material online, showing higher synteny coverage (lighter blue and darker red colors) for SynChro than for i-ADHoRE for all species pairs. On the other hand, one observes that i-ADHoRE generates a greater number of large blocks ($\ge 21$) than SynChro (supplementary fig. S7, Supplementary Material online). This ensures that for pairs of genomes for which synteny blocks allow for >60% coverage, SynChro and i-ADHoRE show comparable success, as illustrated by the red-colored cells in the matrices of supplementary figures S5b and c and S6b and c, Supplementary Material online. In conclusion, a better synteny coverage reached for all pairs of species allows PhyChro to perform better on SynChro than on i-ADHoRE blocks.

It is also interesting to note that modulating the size of microrearrangements tolerated within synteny blocks with the Δ parameter from SynChro (bigger the Δ, larger the microrearrangements tolerated) has an effect on the number of partial splits contradicting a given topology. For example, PhyChro run with synteny blocks constructed with Δ = 3 (by default, see Materials and Methods) finds 36, 37, and 42 partial splits that contradict the ((Primates, Rodentia), Laurasiatheria), (Primates, (Rodentia, Laurasiatheria)), and ((Primates, Laurasiatheria), Rodent) topologies, respectively. By increasing Δ to 4 (i.e., being more tolerant for larger microrearrangements within synteny blocks), PhyChro finds 24, 37, and 53 contradictory partial splits, respectively. These numbers provide confidence in the ((Primates, Rodentia), Laurasiatheria) topology and, because none of the topologies has zero contradictions, they also show that homoplasy is present. More generally, the number of contradictions is indirectly reflected in the confidence values that PhyChro associates to the branches of its trees. For $\Delta =3,4,5,6$, vertebrate tree topologies are correct and all tree reconstructions exhibit comparable branch confidence (fig. 2a and supplementary fig. S8, Supplementary Material online). For yeast species, $\Delta =3,4$ allow PhyChro to reconstruct correct tree topologies with branch confidence scores increasing with Δ. For $\Delta =5,6$, the trees display 1 and 5 erroneous splits, respectively, showing that increasing the tolerance to microarrangements in synteny blocks gradually increases the number of errors in the reconstruction (see fig. 2b and supplementary fig. S8, Supplementary Material online). In conclusion, by modulating the effect of synteny block constructions with respect to microarrangements and reading the confidence on the branches of PhyChro reconstructions, it clearly appears that microarrangements gather important information for phylogenetic reconstruction.

Robustness of the Algorithm with Respect to Simulated Genomes

In order to test PhyChro on a large set of simulated data representative of yeast and vertebrate genomes, we used computer simulations based on a realistic evolutionary model. We started with hypothetical ancestral genomes characterized by 5,000 genes distributed along eight chromosomes for yeasts and by 18,000 genes distributed on 23 chromosomes for vertebrates. In both cases, we simulated random tree topologies with 21 leaves for yeasts and 13 leaves for vertebrates. The method for the construction of a random tree takes genes as building blocks and goes as follows:

1. It generates a random binary tree by defining the branching nodes uniformly over the time scale, with the exception of the first branching which is put at the root. More precisely, for each branching, it selects a leaf to split. It does it by going recursively from the root to the leaf by passing through internal nodes of the tree, with a half probability of choosing the right or the left subtree at an internal node. Once it selects a leaf to split, it attaches to it two new leaves. This construction is repeated until the number of leaves is equal to the expected number of species (21 species for yeasts and 13 for vertebrates).

2. Based on the tree produced in Step 1, it simulates chromosomal rearrangements along each branch of the tree, following a Poisson distribution, such that the average number of events per branch, from the ancestor (located at the root) to the species (located at the leaves), is ∼500 for yeasts and 1,000 for vertebrates. (We note that these values are comparable to those obtained on actual yeast and vertebrate genomes [Drillon and Fischer 2011] and that a similar simulation was run with an average of 400 events for the Protoploid and WGD yeast genomes in Vakirlis et al. [2016]). Rearrangements were distributed on the tree according to the following proportions: 60% of inversions, 29.79% of reciprocal translocations, 5% of duplications, 5% of deletions, 0.1% of fusions, 0.1% of fissions, and 0.01% of whole-genome duplications (WGD) (Ma et al. 2006; Drillon and Fischer 2011). Following a WGD event, one of the two copies of each duplicated gene was deleted with a probability of 80% (Wolfe and Shields 1997). The number of genes involved in an inversion, duplication, and deletion was chosen following a Poisson distribution (where the parameter of the distribution was set to five genes for inversions and duplications and to one gene for deletions).

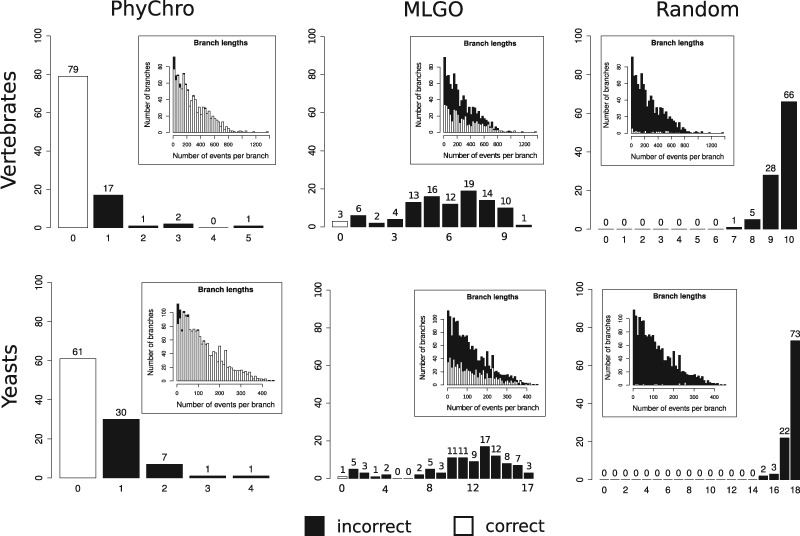
The simulated genomes produced by this approach are consistent with actual yeast and vertebrate genomes in terms of number of genes, number of chromosomes, and number of rearrangements along the branches of the trees. For the analysis, the minimum number of rearrangements per branch was set to 1 or 10 for both yeast and vertebrate trees, and 100 simulations were generated in each case. The distribution of the number of events per branch for yeasts and vertebrates is reported in the inset of figure 3 (first column). Synteny blocks were computed between all pairs of simulated genomes (note that here genes are represented by numerical identifiers, not by actual nucleotide or amino acid sequences) and PhyChro was run on these simulated genomes to compare the predicted topologies with the known (simulated) ones. For determining PhyChro success rate, we counted the number of splits in the trees that were correctly and incorrectly reconstructed by PhyChro. For a minimum number of rearrangements per branch set to 1, the results are reported in figure 3, where one observes that PhyChro is able to reconstruct correct tree topologies without any erroneous split in 79% of the cases for vertebrates and 61% for yeasts, and for the incorrect ones, in most cases (17% for vertebrates and 30% for yeasts), we record just one incorrect split per tree. Over all trees, 97% of the splits are correctly predicted by PhyChro, both for vertebrates and for yeasts, and, most importantly, incorrect splits mainly correspond to very short branches, that is, branches where only very few rearrangement events took place (see inset plot in fig. 3). If we set the number of events in a branch to be at least 10, the number of correct trees for vertebrates increases to 86% and for yeasts to 69%, with 98% and 97% of the splits that are correct over all trees, for vertebrates and yeasts, respectively.

Fig. 3.

PhyChro, MLGO, and random reconstructions tested on simulated trees. Simulated phylogenetic trees describing rearrangement events were generated for vertebrate-like (top) and yeast-like (bottom) genomes and used to check whether PhyChro (left) and MLGO (center) could correctly reconstruct the original phylogeny from the corresponding sets of simulated genomes. The simulated trees have been used also to check to which extent a random assignment of rearrangements (right) on the branches could correctly reconstruct the original phylogeny from the corresponding sets of simulated genomes. The histograms report the number of trees with a fixed number of incorrect splits predicted by the three methods. The inset plots represent the distribution of the number of branches with a fixed length (corresponding to a number of simulated rearrangements that were applied to these branches) in the simulated trees, and describe how many of those branches have been reconstructed correctly (white) or incorrectly (black) by a method.

This analysis helps to evaluate a confidence threshold for scores cS. In fact, 99% of correct splits are obtained with a score $cS\ge 0.2$ for the 100 simulated genomes for yeasts, and with a score $cS\ge 0.6$ for the 100 simulated genomes for vertebrates. This means that in the yeast phylogenetic tree reconstructed by PhyChro, the only weakly supported branch (scoring 0.05) is the one locating E. gossypii and K. lactis within the Protoploid clade, whereas the branch locating Cl. lusitaniae displays a sufficiently strong cS score (0.33) to be trusted (fig. 1b). For vertebrates, as discussed earlier, the position of Rodentia in the tree remains very weakly supported (fig. 1a).

A random shuffling of species in the 100 randomly generated trees is reported in figure 3, where we note a shape of the distribution of errors that has a complementary tendency compared with the one obtained for PhyChro, that is, the vast majority of events associated with a branch is incorrect and the number of erroneous splits corresponds, most of the times, to the number of internal branches (10 for vertebrates and 18 for yeasts). This corresponds to no correct trees obtained for both vertebrates and yeasts; we note that only 1% of the splits are correct for yeasts and only 3% for vertebrates. The same test, based on the same data set of trees (and the same synteny blocks considered by PhyChro and the random tree analyses), has been realized on MLGO (fig. 3). MLGO works much better than the random case but yet is far from PhyChro performance: 3% of trees are correct for vertebrates and 1% for yeasts. Many of the trees that are reconstructed by MLGO have a high number of erroneous splits (57% for yeast and 42% for vertebrates) for both vertebrates and yeasts.

Discussion

PhyChro, a New Strategy of Phylogenetic Reconstruction

An important effort was made in this work to identify how chromosomal breaks coming from chromosomal rearrangements could be used as phylogenetically informative characters to perform phylogenetic reconstructions. PhyChro differs in a fundamental way from the classical reconstruction methods. The first difference comes from the pairwise comparison approach between genomes which allows us to make the most out of the synteny information shared between closely and distantly related genomes at the same time. Another difference comes from the definition of two functions (${\mathrm{f}}_{\text{inc}}$ and ${\mathrm{f}}_{\text{comp}}$, see Materials and Methods) which represent, respectively, the number of times where two genomes are split in two groups of incompatible adjacencies and the number of times where they are grouped together (not split) based on shared adjacencies. The ratio between these two functions is used to identify the least incompatible pairs of species from which sister genomes will be defined. The main originality of PhyChro is that it identifies sister genomes by minimizing the number of incompatible adjacencies rather than by maximizing the number of shared rearrangements. Formally, PhyChro bases its tree reconstruction on the PSD. This distance relies on the notion of partial split that allows to record the number of incompatible adjacencies for pairs of genomes among a set of genomes. Hence, PhyChro does not try to combine internal branches into a tree topology, but rather it reconstructs the topology by iteratively identifying genomes and ancestral genomes that are closely related. It uses a bottom-up approach, similarly to what is done in distance-based methods. Note that PSD is a measure defined on a set of n genomes contrary to other previously introduced notions, measuring genome rearrangements, that are based on the comparison of only pairs of genomes. An example is the well-known breakpoint distance (BD), defined to be the number of breakpoints observable from the comparison between two genomes. The notion was first used in (Nadeau and Taylor 1984), then formally defined for one (Watterson et al. 1982; Sankoff and Blanchette 1997) and multiple (Pevzner and Tesler 2003; Tannier et al. 2009) chromosomes. The direct comparison between PSD and BD is impossible given that for two genomes G, H among n, the distance BD(G, H) depends only on G, H, whereas PSD(G, H) depends on the n genomes. When reconstructing phylogenies, knowledge on the way pairs of genomes split in the tree (recall that the notion of nontrivial split is based on at least four genomes and not on pairs or triplets) is primordial and one can only gather it through comparisons between all genomes involved in the reconstruction. This is why the intrinsic nature of a measure based on n genomes, like PSD, is expected to bring fundamental information for phylogenetic tree reconstruction. It is important to notice that PSD counts only those breakpoints that are supported by at least a quadruplet of genomes, and associated with rearrangements shared by at least two genomes, whereas BD counts all breakpoint events including those associated with rearrangements that are specific to a given genome (occurring on the external branches of a tree).

Thanks to this reconstruction strategy, PhyChro is less affected by “short-branch” attraction, which often leads distance-based methods to put genomes having undergone a lot of rearrangements/mutations higher in the tree than they belong. Another originality of PhyChro is that it provides branch length estimates that reflect the level of chromosome plasticity rather than the rates of punctual mutations, as all classical methods of phylogeny reconstruction do. In addition, PhyChro allows estimation of the robustness of branches in a way that is radically different from the bootstrap methods. The advantage here is that computing confidence scores is very fast as it does not involve additional tree reconstructions.

Phylogenetic Reconstruction Based on Chromosomal Rearrangements

We showed through the analysis of simulated genomes that PhyChro generates very accurate tree topologies by successfully reconstructing known tree topologies. Applications of PhyChro to real biological data sets comprising different types of genomes (yeasts and vertebrates) and covering different evolutionary ranges shows that chromosomal rearrangements are indeed phylogenetically informative and that accurate phylogenies can be reconstructed solely based on these large-scale mutational events. This success demonstrates that the evolutionary signal that derives from chromosome rearrangements comprises at least as much phylogenetic information as the local information present in protein sequences. Moreover, we showed that PhyChro reconstructions are at least as accurate as the best reconstructions deriving from classical methods that use protein sequence comparisons. We also show that at particularly difficult branching positions, such as that of Ca. glabrata relatively to S. cerevisiae and N. castellii, PhyChro outcompetes all other methods of phylogenetic reconstruction.

Another important application of PhyChro was realized (with the same parameters used for vertebrates and yeasts species) on scleractinian corals, the foundation species of the coral-reef ecosystem. Corallimorpharians had been proposed to originate from a complex scleractinian ancestor that lost the ability to calcify in response to increasing ocean acidification, suggesting the possibility for corals to lose and gain the ability to calcify in response to increasing ocean acidification. A phylogenetic analysis based on 1,421 single-copy orthologs combined with PhyChro phylogenetic reconstruction allowed to disprove this hypothesis contributing evidence for the monophyly of scleractinian corals and the rejection of corallimorpharians as descendants of a complex coral ancestor (Wang et al. 2017).

Finally, we investigated to which extent chromosomal rearrangements could be useful to determine the position of species with debated phylogeny in the vertebrate tree. In this respect, we tested PhyChro on an extension of our vertebrate set of species by adding three recently sequenced genomes, the cow, the pig, and the lizard, known to be of difficult positioning. PhyChro tree reconstruction (supplementary fig. S9, Supplementary Material online; compare with fig. 2a) correctly placed Anolis, the lizard, close to the birds; both are known to be members of Diapsida. It also correctly added Bos taurus (cow) and Sus scrofa (pig) to the clade including horse and dog. On the other hand, PhyChro shows a nesting (horse, (dog, (cow, pig))) for the four mammalian species which is in contrast to the position of ((cow, pig),(dog, horse)) (Romiguier et al. 2013; Tarver et al. 2016) and (dog, (horse, (cow, pig))) (Esselstyn et al. 2017). The literature contains an open debate on the positioning of these mammalian species which appear sensitive to the evolutionary information taken into consideration in phylogenetic reconstruction (Foley et al. 2016; Upham et al. 2019). Chromosomal rearrangements might provide further phylogenetic evidence to be used in this kind of studies.

Overall, these results suggest that synteny information should be integrated more broadly in future phylogenetic reconstruction analysis pipelines.

Materials and Methods

The classical notions of synteny blocks, breakpoints, splits, and partial splits are recalled. We introduce the notions of “Partial splits associated with breakpoints” and of “PSD” that are central in PhyChro.

Synteny Blocks

A pairwise genome comparison G/H (or equivalently H/G), between the two genomes G, H, identifies chromosomal segments with conserved orthologous gene order. These segments are called “synteny blocks,” and are also referred to as “blocks.” Without loss of generality, we call B both the occurrences of the synteny block B in G and in H. Different definitions of synteny blocks have been proposed before (Ferretti et al. 1996; Pham and Pevzner 2010; Rödelsperger and Dieterich 2010; Proost et al. 2012; Drillon et al. 2014) and they are based on different conditions on the proximity between orthologs. PhyChro works with blocks B that verify the following five conditions:

• B is described by its pairs of homologous genes in G and H, called “anchors” for B.

• the first and the last genes of B in G (H) have homologs in the corresponding block B in H (G). We say that B in G (H) is delimited by its first and last anchors.

• B is unique, in the sense that duplicated blocks are not explicitly handled and they are defined as independent blocks. For instance, if B is duplicated in G but not in H, the two copies of the block are considered as distinct in G and as overlapping in H.

• B is oriented or signed, and in particular, B can have a different orientation in G and in H. The orientation of B in a genome G may be fixed in some arbitrary way or might depend on conditions that are specific to the definition of a block, such as the order and the orientation of its genes. When impossible to be established, a block orientation is left undetermined and the block is called “unoriented” or “unsigned.” The orientation of a block allows us to differentiate its right and left ends (in order to determine which of its extremities is involved in a breakpoint): the “end” of B corresponds to the “beginning” of −B and reciprocally.

• B, in G or H, can overlap or be included in another block.

A block B is called “telomeric” if it is the first or the last block of a chromosome in G or in H.

Breakpoints

Chromosomal rearrangements generate synteny breakpoints, or analogously, synteny block adjacencies. Given a block B obtained through the comparison G/H, a breakpoint is defined by the pair $[{(B\hspace{0.17em}A)}_G\hspace{0.17em},\hspace{0.17em}{(B\hspace{0.17em}C)}_H]$ of block adjacencies $(B\hspace{0.17em}A)$ in G and $(B\hspace{0.17em}C)$ in H. In I of figure 4, for instance, the right end of block B is contiguous to the left ends of blocks A and C in genomes G and H, respectively. As blocks are oriented, notice that the same breakpoint might correspond to $[{(B\hspace{0.17em}A)}_G,{(-C-B)}_H]$, where −B has −C on its left end instead. Notice also that synteny blocks derived from duplications or chromosome fusions/fissions do not generate pairs of block adjacencies and therefore are not explicitly considered here. Blocks derived from translocations, inversions, and transpositions of DNA segments are the only ones that are informative in our analysis. Each block (except the telomeric ones) should, in theory, lead to two breakpoints (one at each end of the block, see I in fig. 4). However, complex gene order configurations might lead to a reconstruction of synteny blocks that overlap, are included in one another or are unoriented (like for blocks reconstructed by SynChro; Drillon et al. 2014). In the following, we consider as breakpoints only those pairs of regions in G and in H for which preceding and following blocks are unambiguously identified (and ignore the others).

Fig. 4.

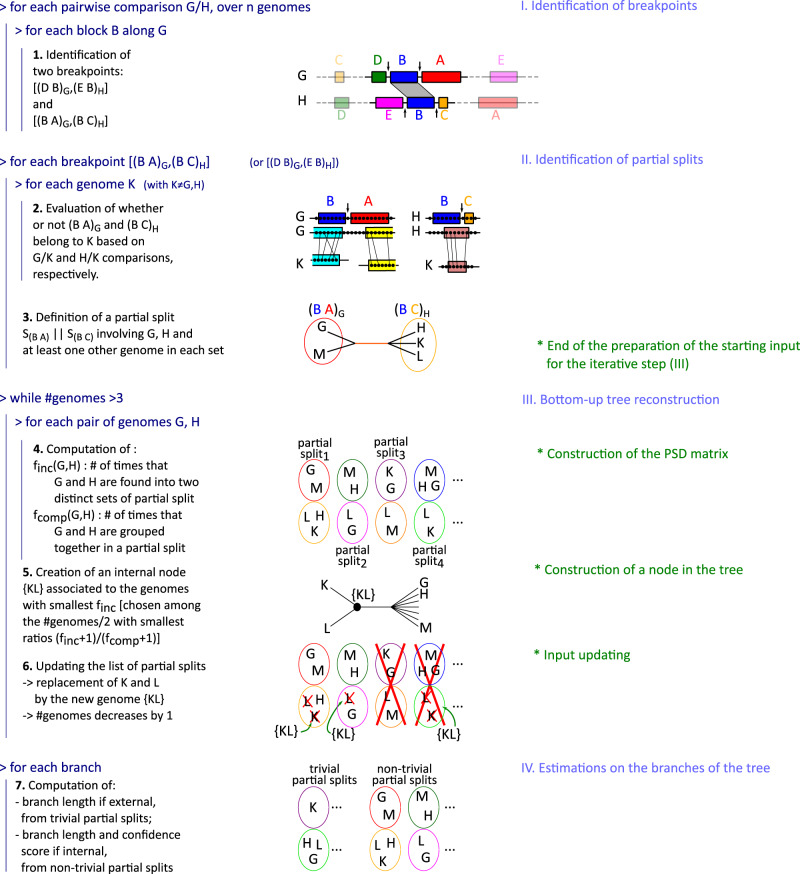
PhyChro algorithm. The four main parts and the seven steps, briefly described here, are detailed in the main text.

Splits

A split is a bipartition of a set of taxa. Figure 1a illustrates an example of a split and of a trivial split, that is, a split induced by an external edge connecting a leaf to the rest of the tree. Splits play an important role in phylogenetic reconstruction (Bandelt and Dress 1992; Huson et al. 2010) as each edge of an unrooted tree is univocally associated with a split. In fact, an edge splits taxa into the two disjoint subsets S₁, S₂ labeling the leaves of the subtrees rooted at the extremities of the edge. We note that the union of S₁, S₂ covers the full set of taxa. In evolutionary terms, we think of genomes in S₁ (or S₂) as having undergone a number of common ancestral rearrangements, specifically the ones that occurred along the edge, that genomes in S₂ (S₁) did not undergo. Strictly speaking, it cannot be established whether these rearrangements took place for S₁ or for S₂ because the tree is not rooted. Hence, ideally, for the reconstruction of a phylogenetic tree, one could hope: 1) to recover rearrangements from genomic data, 2) to define splits of genomes sharing the rearrangements, and 3) to reconstruct the edges of the tree by combining splits identified from the rearrangements.

Partial Splits

For the purpose of tree reconstruction, traces of chromosomal rearrangements may have disappeared in some genomes (due to the accumulation of other rearrangements), and it might become impossible to recover splits. This is why, we shall use a generalization of the concept of split to the one of partial split. This notion was introduced in (Semple and Steel 2001; Huson et al. 2004; Huber et al. 2005). Formally, a partial split is a pair of nonempty disjoint sets of taxa. Intuitively, given an unrooted phylogenetic tree whose leaves are labeled by different taxa and given some path c in the tree, we say that c induces a partial split of the sets of genomes S₁, S₂ if: 1. S₁, S₂ are constituted by some (possibly all) of the taxa associated with the subtrees rooted at the extremes of c; 2. in each S_i, for i = 1, 2, there are at least two taxa that are connected by a shortest path passing through the root of the corresponding subtree (fig. 1b). We note that, by definition, $S_1\cap S_2=\varnothing$ and, also, that $S_1\cup S_2$ does not necessarily correspond to the full set of taxa in the subtrees rooted at the extremes of c. A fortiori, $S_1\cup S_2$ does not necessarily correspond to the full set of taxa in the complete tree, as it is the case for splits. In fact, a split is a partial split where c is an edge, but a partial split induced by an edge need not be a split because of condition (1). As for splits, we think of genomes in S₁ (or S₂) as having undergone a number of common ancestral rearrangements, specifically the ones that occurred along the path c, that genomes in S₂ (S₁) did not undergo.

As for splits, we say that a partial split is “trivial” when one of the two subsets S₁, S₂ is a singleton. Notice that trivial partial splits do not bring information on the topology of the tree (because the set of trivial partial splits is the same for all topologies) and are not used in tree reconstruction. We shall use them to estimate the length of the terminal branches though, that is, branches leading to leaves in the tree.

Testing the Conservation of Block Adjacencies

Given a breakpoint $[{(B\hspace{0.17em}A)}_G,{(B\hspace{0.17em}C)}_H]$ in the comparison G/H, we test for the presence of ${(B\hspace{0.17em}A)}_G$ in a genome K (by definition, ${(B\hspace{0.17em}A)}_G\in G$). The test is similarly stated for ${(B\hspace{0.17em}C)}_H$. The test does not directly search for blocks B and A in K because they might not have direct equivalents in G/K. Instead, it infers the presence of the adjacency ${(B\hspace{0.17em}A)}_G$ in K at the gene level, by testing whether the genes flanking the ${(B\hspace{0.17em}A)}_G$ adjacency in G, that is, the right end of block B and the left end of block A, have syntenic homologs in K. More precisely, the test compares G and K and determines whether there is a synteny block D in K and G such that the following conditions are satisfied (we refer to the notation employed in fig. 5—see also supplementary fig. S10, Supplementary Material online):

Fig. 5.

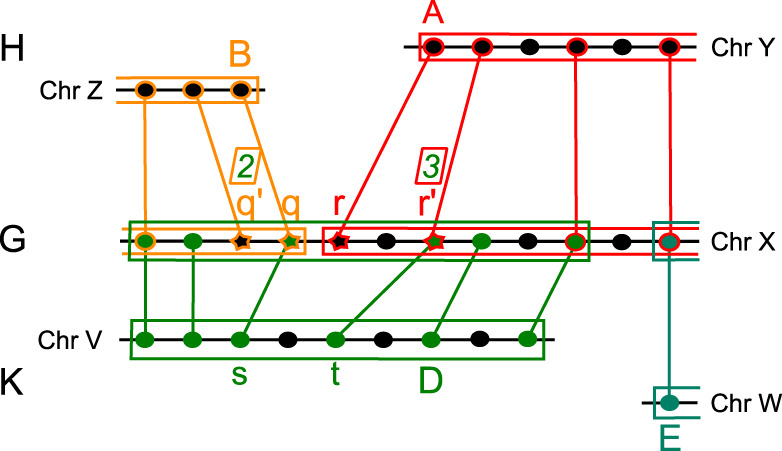
Conservation of the adjacency ${(B\hspace{0.17em}A)}_G$ in the genome K. Genes are indicated as dots or stars. Stars, in G, are used for the two last ($q\prime$ and q) and first (r and $r\prime$) anchors of blocks B and A in the comparison G/H. Red, yellow, and green colors are used to highlight anchors associated with the blocks A, B, and D, obtained in the comparisons G/H, G/H, and G/K, respectively. Genes $q\prime$, q, r, and $r\prime$ belong to the same block D in G/K. The number of anchors of D lying before $q\prime$ (after $r\prime$), and possibly including it, is indicated above $q\prime$ ($r\prime$) within a square. Gene s (t) is the anchor of D whose homolog in G lies in the right (left) most position of B (A). Homology is indicated by links among genes occurring in different genomes: s is homolog of q and t of $r\prime$. Note that, here, the three conditions (i)–(iii) discussed in the text are satisfied and that $K\in {(B\hspace{0.17em}A)}_G$.

1. The two last anchors (or syntenic homologs) $q\prime ,q$ of B and the two first anchors $r,r\prime$ of A, along G, belong to the same synteny block D in G/K;

2. $q\prime ,r\prime$ are preceded and followed along G, respectively, by at least two other anchors in D (possibly including themselves).

3. Let s be the anchor of D in K whose homolog in G lies in the rightmost position of B, and let t be the anchor of D in K whose homolog in G lies in the leftmost position of A. Then, the number of genes between s and t in K and between their homologs in G (see fig. 5) is at most 4.

Conditions (i) and (ii) guarantee block D in G to overlap several anchors of A and B in G, and condition (iii) ensures the genes forming the ${(B\hspace{0.17em}A)}_G$ adjacency in G and K to be in physical proximity. Such proximity is computed for a maximum of four genes between the two anchors s and t in figure 5. All values from 3 to 6 have been tested to choose the best parameter for yeasts and vertebrates (all reconstructions are illustrated in supplementary fig. S11, Supplementary Material online, for vertebrates and in supplementary fig. S12, Supplementary Material online, for yeasts). These three conditions introduce some flexibility in the definition of synteny conservation, without being too permissive. If they are all satisfied, we say that the adjacency belongs to K and write ${(B\hspace{0.17em}A)}_G\in K$. If q and r belong to the same block D in G/K but some of the conditions fail (possibly all), we still say that ${(B\hspace{0.17em}A)}_G\in K$ and consider the relation as “weakly” supported. These weak adjacencies can be due to false ortholog assignments or small inversions. In all other cases, we say that ${(B\hspace{0.17em}A)}_G\cancel{\in }K$.

Partial Splits Assigned to Breakpoints

Given a breakpoint $[{(B\hspace{0.17em}A)}_G,{(B\hspace{0.17em}C)}_H]$, we define a partial split by identifying two sets of genomes, $S_{(BA)}$ and $S_{(BC)}$, where $S_{(BA)}$ comprises genomes sharing the adjacency ${(B\hspace{0.17em}A)}_G$ and $S_{(BC)}$ comprises genomes sharing the adjacency ${(B\hspace{0.17em}C)}_H$. For this, we apply the above adjacency test, checking whether the adjacencies ${(B\hspace{0.17em}A)}_G$ and ${(B\hspace{0.17em}C)}_H$ derived from the G/H comparison are present in a genome K or not, for all $K\ne G,H$. Namely, $K\in S_{(BA)}$ if and only if ${(B\hspace{0.17em}A)}_G\in K$, and $K\in S_{(BC)}$ if and only if ${(B\hspace{0.17em}C)}_H\in K$.

Notice that a genome K that neither contains ${(B\hspace{0.17em}A)}_G$ nor ${(B\hspace{0.17em}C)}_H$ belongs to none of the two sets. In addition, a genome K may contain, at the same time, the two adjacencies defining a given breakpoint. This ambiguous case might occur either for a breakpoint $[{(B\hspace{0.17em}A)}_G,{(B\hspace{0.17em}C)}_H]$ when C follows A in G and A is small enough to make condition (iii) true for ${(BC)}_H$ in K (see supplementary fig. S13a, Supplementary Material online), or for a breakpoint $[{(B\hspace{0.17em}A)}_G,{(B-A)}_H]$ when A is small enough to make ${(BA)}_G\in K$ and ${(B-A)}_H\in K$ (see supplementary fig. S13b, Supplementary Material online).

Intuitively, the coexistence of ${(B\hspace{0.17em}A)}_G\in K$ and ${(B\hspace{0.17em}C)}_H\in K$, for some K, indicates that ${(B\hspace{0.17em}A)}_G$ and ${(B\hspace{0.17em}C)}_H$ are too “similar” to claim that they support a split. Therefore, it is only when the two sets of genomes $S_{(B A)},S_{(B C)}$ are disjoint that we say that they form a “partial split,” denoted $S_{(B A)}\left|\right|S_{(B C)}$, associated with the breakpoint $[{(B\hspace{0.17em}A)}_G,{(B\hspace{0.17em}C)}_H]$ (fig. 1b).

The Partial Split Distance

Given a set of genomes, genome pairwise distances can be computed by considering the set of partial splits associated with all breakpoints issued from all pairwise genome comparisons. For this, we shall define two functions, ${\mathrm{f}}_{\text{inc}}$ and ${\mathrm{f}}_{\text{comp}}$, on the list of nontrivial partial splits.

The first one, ${\mathrm{f}}_{\text{inc}}(G,H)$ (where “inc” stands for incompatible), counts the number of times that genomes G and H belong to different subsets of a partial split (as for partial splits 1 and 2 in III of fig. 4):

$${\mathrm{f}}_{\text{inc}}(G,H)=\left|\right\{S_{(B A)}\left|\right|S_{(B C)} :(G\in S_{(B A)}\wedge H\in S_{(B C)})\vee (G\in S_{(B C)}\wedge H\in S_{(B A)})\left\}\right|$$

The second function, ${\mathrm{f}}_{\text{comp}}(G,H)$ (where “comp” stands for compatible), counts the number of times that genomes G and H are found in the same subset of a partial split, that is, sharing a same adjacency (as for the partial split 4 in III of fig. 4):

$${\mathrm{f}}_{\text{comp}}(G,H)=\left|\right\{S_{(B A)}\left|\right|S_{(B C)} :(G\in S_{(B A)}\wedge H\in S_{(B A)})\vee (G\in S_{(B C)}\wedge H\in S_{(B C)})\left\}\right|$$

The function ${\mathrm{f}}_{\text{inc}}$ represents an “internal” distance between genomes, and we call it PSD. Intuitively, given two genomes, PSD is proportional to the number of rearrangements that occur along the internal branches separating these two genomes in the phylogenetic tree that we want to reconstruct. The number of these rearrangements is estimated with ${\mathrm{f}}_{\text{inc}}$, by using the number of nontrivial splits separating the two genomes. This means that sister genomes, that is, genomes separated by no internal branch, should have a PSD distance equal to zero (independently of the length of their external branches). This property will be used to identify sister genomes and to reconstruct phylogenies bottom-up (see below). In the same way, very close genomes, separated by few and short internal branches, should have a PSD close to zero. However, because ${\mathrm{f}}_{\text{inc}}$ is defined from nontrivial splits, very distant genomes, which do not share many adjacencies with other genomes and, therefore, are not involved in many nontrivial splits, have also a PSD very close to zero with all other genomes. To take into account this fact, we consider ${\mathrm{f}}_{\text{comp}}$ and use the ratio $\mathcal{R}(G,H)=({\mathrm{f}}_{\text{inc}}(G,H)+1)/({\mathrm{f}}_{\text{comp}}(G,H)+1)$ to discriminate among pairs of genomes G, H that have a very small internal distance (${\mathrm{f}}_{\text{inc}}$ close to zero) those that are very closely related (high ${\mathrm{f}}_{\text{comp}}$ value) from those that are very distantly related (${\mathrm{f}}_{\text{comp}}$ close to zero).

Note that, if ${\mathrm{f}}_{\text{inc}}(G,H)\cancel{=}0$ then there exists at least one nontrivial partial split $S_{(B A)}\left|\right|S_{(B C)}$ that separates G from H. This means that there exist genomes K, L such that $(\{G,K\}\subseteq S_{(B A)}\wedge \{H,L\}\subseteq S_{(B C)})\vee (\{G,K\}\subseteq S_{(B C)}\wedge \{H,L\}\subseteq S_{(B A)})$. Ideally, this suggests that in a phylogenetic reconstruction involving genomes $G,H,K,L$, the two genomes G, H should not be considered as sister genomes. In reality, as mentioned earlier, it might be difficult to unravel complete information from breakpoints (due to either convergence or the accumulation of rearrangements) and one might have to treat as sister genomes, those pairs of genomes that display the smallest ${\mathrm{f}}_{\text{inc}}$ value, even if it is different from 0.

The PhyChro Algorithm

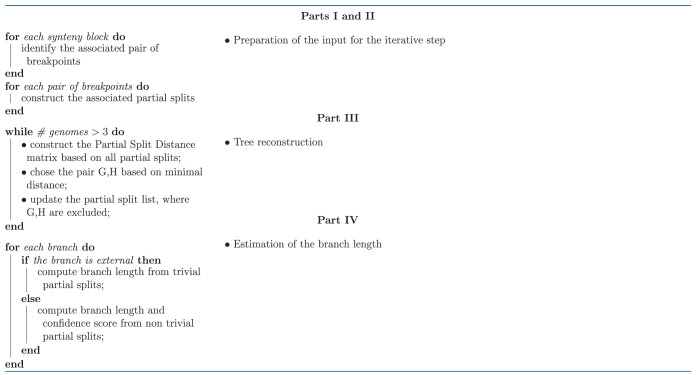
Phylogenetic reconstruction based on partial splits is a more delicate problem than tree reconstruction based on splits (Bandelt and Dress 1992; Semple and Steel 2001; Huson et al. 2004, 2010; Huber et al. 2005). PhyChro comprises four main parts (I, II, III, and IV; see fig. 4 and table 1) divided into seven major steps that are detailed below.

Table 1.

PhyChro Algorithm.

Part I—Identification of Breakpoints

Step 1. For each pairwise comparison G/H between pairs of genomes among n involved in the reconstruction, PhyChro iteratively identifies the breakpoints associated with each synteny block. See I in figure 4.

Part II—Identification of Partial Splits

Step 2. For each breakpoint $[{(B\hspace{0.17em}A)}_G,{(B\hspace{0.17em}C)}_H]$ identified in Step 1 and issued from the comparison G/H and for each genome $K\cancel{=}G,H$, PhyChro determines whether ${(B\hspace{0.17em}A)}_G$ or ${(B\hspace{0.17em}C)}_H$ is present in K (as seen in section “Testing the Conservation of Block Adjacencies”).

Step 3. Based on the results from Step 2, PhyChro defines two sets of genomes, $S{\prime }_{(BA)}$ and $S{\prime }_{(BC)}$, that share one or the other adjacency defining the breakpoint $[{(B\hspace{0.17em}A)}_G,{(B\hspace{0.17em}C)}_H]$. If $S{\prime }_{(BA)}$ and $S{\prime }_{(BC)}$ are not disjoint, then the sets are ignored (as seen in section “Partial Split Assigned to Breakpoints”). These partial splits are associated with ambiguous breakpoints, which are themselves due to small blocks. If $S{\prime }_{(BA)}$ and $S{\prime }_{(BC)}$ are disjoint, then PhyChro removes from the two sets those genomes that support only weakly the adjacency (as seen in section “Testing the Conservation of Block Adjacencies”). Then it checks that both resulting sets $S_{(BA)}$ and $S_{(BC)}$ are not singletons; if so, it adds $S_{(B A)}\left|\right|S_{(B C)}$ to the collection of partial splits. Note that $S_{(B A)}\left|\right|S_{(B C)}$ may be trivial or not.

At the end of the iteration (Steps 2 and 3), PhyChro has identified a collection of partial splits.

Part III—Bottom-Up Tree Reconstruction

Step 4. For each pair of genomes G, H, PhyChro computes their PSD, ${\mathrm{f}}_{\text{inc}}(G,H)$ and ${\mathrm{f}}_{\text{comp}}(G,H)$ (as seen in “The Partial Split Distance”).

Step 5. The creation of an internal node {KL} of the tree relies on the identification of the two sister genomes K and L (among the n genomes) displaying the smallest ${\mathrm{f}}_{\text{inc}}$ value. However, as explained earlier, to avoid considering very distant genomes that could have very small ${\mathrm{f}}_{\text{inc}}$ values, sister genomes are chosen to be the pair displaying the smallest ${\mathrm{f}}_{\text{inc}}$ value among the $n/2$ genome pairs G, H that have the smallest ratio $\mathcal{R}(G,H)$ (III in fig. 4). Notice that the maximum number of possible sister genomes in a tree of n species is $n/2$. If there are multiple identical minimal ${\mathrm{f}}_{\text{inc}}$ values, either they involve different pairs of genomes and they will be treated one after the other in the different and successive iterations, or they involve incompatible pairs of genomes (involving the same genomes; a very unlikely situation that would results into the creation of a node with a low-confidence score—see below) and the choice among them is left arbitrary.

Step 6. Once the internal node {KL} is created, the list of partial splits identified at Step 3, is updated by replacing all occurrences of K and L by the node {KL}. Two types of partial splits $S_{(B A)}\left|\right|S_{(B C)}$ are deleted: 1) partial splits that are discordant with the new node, that is, partial splits where K and L belong to $S_{(B A)}$ and $S_{(B C)}$, respectively (see partial split 3 in III of fig. 4), 2) partial splits characterized by a set of genomes composed by K and L only, because these partial splits would become trivial carrying no useful information for further topology reconstruction (see partial split 4 in III of fig. 4).

The process (Steps 4–6) is iterated on the restricted set of genomes, where K, L are replaced by the ancestral genome {KL}, and on the updated set of partial splits obtained in Step 6: all ${\mathrm{f}}_{\text{inc}}$ and ${\mathrm{f}}_{\text{comp}}$ values are recomputed from the updated list of partial splits, new internal nodes are created, and the list of partial splits is updated again. The iteration is run until only three genomes remain (exactly one unrooted tree topology is then possible).

Part IV—Estimations on the Branches of the Phylogenetic Tree

PhyChro produces an estimation of the branch length and a confidence score of the reconstructed nodes. The branch length is an indicator of the complexity of the chromosomal structures (i.e., of the amount of rearrangements identifiable from the genomes under consideration), and the confidence score indicates how much the reconstruction is supported and/or contradicted by the information contained in the initial nontrivial partial splits.

Step 7. Branch length for internal and terminal branches is estimated by using information contained in nontrivial and trivial partial splits, respectively. Branch length is the sum of a weighted number of partial splits (corresponding to a number of breakpoints, see Supplementary Material online) that support the existence of the branch (fig. 6), and therefore it indirectly represents a number of rearrangements. These values are necessarily an underestimation because most partial splits support the existence of a path in the tree rather than a specific branch, and therefore, are not considered for the calculation of branch lengths. In addition, terminal branches of distant genomes and internal branches between distant clades will be even more underestimated as partial splits supporting this kind of branches are rare.

Fig. 6.

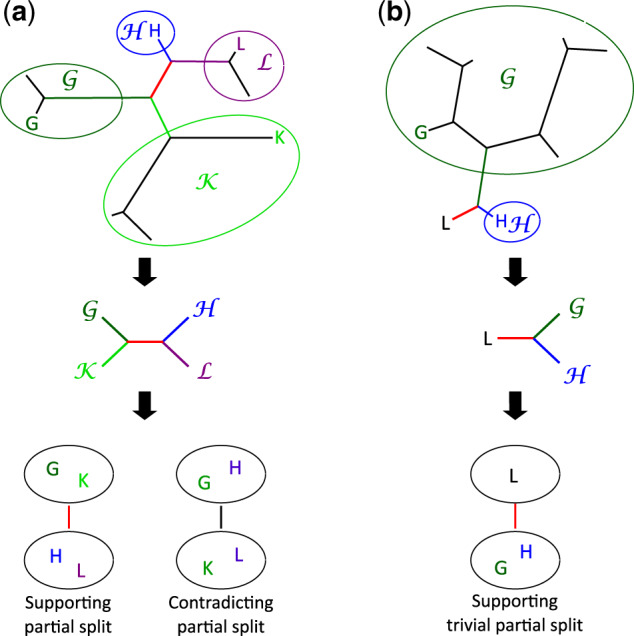
Examples of partial splits supporting or contradicting the existence of a given branch. Given a branch (red edges in the left and right trees), we consider the sets of genomes $\mathcal{H},\mathcal{G},\mathcal{K},\ell$ corresponding to the maximal subtrees associated with the edge by the tree topology. Sets $\mathcal{H},\mathcal{G},\mathcal{K},\ell$ contain genomes $H,G,K,L$, respectively. (a) Each internal branch is characterized by a double pair of genome sets $[(\mathcal{G},\mathcal{K}),(\mathcal{H},\ell )]$, which allows to define the partial splits that support or contradict this branch. (b) Each external branch is characterized by one pair of genome sets $(\mathcal{G},\mathcal{H})$, which allows to define the trivial partial splits that support this branch.

PhyChro also estimates a confidence score for each internal branch by calculating the proportion of nontrivial partial splits that supports its existence over the total number of nontrivial partial splits that either support or contradict it (fig. 6 and see Supplementary Material online). In addition to the confidence score, PhyChro provides the list of all ${\mathrm{f}}_{\text{inc}}$ values computed for genome pairs, which can help to know if a node is trustworthy or not.

Description of Input Data

PhyChro requires as input the list of synteny blocks computed for each pairwise comparison G/H between all pairs of genomes G, H involved in the phylogenetic reconstruction. Anchors must be provided for each pair of synteny blocks issued from a comparison G/H. We recall that synteny blocks handled by PhyChro can overlap and that the same gene can be an anchor for distinct blocks. Duplicated synteny blocks are treated as independent blocks even though their anchors can be shared.

PhyChro accepts synteny blocks that are reconstructed with various tools as long as they are converted into the expected format, described in the README file of the PhyChro package. For the applications to yeast and vertebrate species, synteny blocks were computed with the SynChro software (Drillon et al. 2014), setting the Δ parameter to 3. Δ is a parameter that allows to define synteny blocks by controlling the complexity of internal microrearrangements. Intuitively, high values of Δ are more permissive and allow larger microrearrangements to be tolerated within synteny blocks, whereas smaller values of Δ are more stringent and split synteny blocks at microrearrangement breakpoints. This implies that, for distantly related genomes, increasing the Δ value allows to recover a larger number of synteny blocks. For these genomes, small values of Δ would allow recovering the signal only from small inversions. Notice that when PhyChro reconstructs trees using blocks computed with Δ  =  2, the yeast tree contains three erroneous splits and the vertebrate tree contains 1, whereas both trees are correct when blocks are computed with Δ  =  3 or 4. SynChro automatically reconstructs pairwise synteny blocks that can be directly read by PhyChro, and it can be downloaded at www.lcqb.upmc.fr/CHROnicle/SynChro.html.

To analyze how sensitive is PhyChro to synteny block reconstruction, we constructed a second set of synteny blocks with the program i-ADHoRe 3.0 (Proost et al. 2012). We followed the protocol used in (Drillon et al. 2014) fixing parameters as follows: prob.cutoff = 0.001, gap_size = 15, cluster.gap = 20, q_value = 0.9, and anchor.points = 3. The remaining parameters were set with default values. The i-ADHoRe 3.0 software package is available at bioinformatics.psb.ugent.be/software.

PhyChro was tested on 13 vertebrate species and 21 yeast species. About three more vertebrate species were used to discuss difficult vertebrate positioning and the possible contribution of PhyChro in these analyses. The detailed list is given in the supplementary table S1, Supplementary Material online. The vertebrate genome sequences have been downloaded from NCBI and the yeast species were downloaded from several sites listed in supplementary table S2, Supplementary Material online.

Duplicated Genes, Duplicated Anchors, and Duplicated Blocks

PhyChro does not directly work with genes except while identifying adjacencies found in genomes G, H within a third genome K. By doing it, it considers only genes that are defined as “anchors” (defined in section “Synteny Blocks”—Materials and Methods, point 1). In this respect, PhyChro requires synteny blocks to be provided as input together with the set of their anchor genes.

PhyChro constructed the vertebrate and yeasts phylogenies based on Synchro, a program identifying synteny blocks by reciprocal best hits (RBH) (Drillon et al. 2014). The RBH condition searches for the best bidirectional matching pairs of genes in G and H and creates a one-to-one map. This means that if G has two copies g₁ and g₂ of a gene, the RBH condition does not allow to map both g₁ and g₂ in G to the same gene in H. It is important to notice that this definition does not prevent to have two copies B₁ and B₂ of a block in G that are mapped into the same block in H. This situation is produced in SynChro when the mapping is based on different anchor genes. In conclusion, PhyChro is designed to handle blocks and their duplications.

PhyChro Computational Time

PhyChro time complexity depends on the number of genomes given in input and on the number of rearrangements that took place among these genomes. Phylogenetic reconstructions with PhyChro were tested using one thread on a single machine equipped with an Intel Xeon E5-2670 CPU, running at 2.60 GHz with 132 GB of RAM and a Linux operating system (CentOS release 6.5). PhyChro ran in 13 and 19 min for the 13 vertebrate and 21 yeast species, respectively. A total of 130,485 and 179,649 breakpoints, of 75,675 and 108,935 synteny blocks, and of 17,848 (1,501 different ones) and 20,924 (3,901) partial splits were identified for vertebrate and yeast genomes, respectively. Clearly, the reported time does not include input preparation. This makes a much more expensive step due to homology search between genome pairs and synteny block construction. Note that Synchro used 1,185 and 1,765 min for yeasts and vertebrates, respectively, of which 601 min for yeasts and 1,397 min for vertebrates were used by homology search.

The computational complexity of the PhyChro algorithm is $\mathcal{O}(B\times N)$, where B is the total number of blocks obtained from pairwise comparisons and N is the number of genomes, and where, without loss of generality, we can assume B > N. Indeed, part I (see Materials and Methods, fig. 4, and table 1) runs in $\mathcal{O}(B)$, because for each block in a genome comparison, it finds the corresponding breakpoints; part II runs in $\mathcal{O}(B\times N)$, because it is a nested iteration on the number of breakpoints (which is linear in the number of blocks) and on the number of genomes N; part III runs in $\mathcal{O}(N^2)$, because it is an iteration on all pairs of genomes; and part IV runs in $\mathcal{O}(N^2)$, because the number of splits in a tree of N leaves is linear in N and the computation of the functions p_support and p_contradict for each split (see Supplementary Material online) is also linear in N.

Comparison between Phylogenetic Reconstructions

Given two phylogenetic trees, their comparison is based on all their internal branchings. Formally, we measure the difference between their topologies by counting the number of splits that are not shared. In addition, note that throughout the text, “correct trees” and “correct branching” refer to reconstructions that agree with phylogenies based on a number of characters from fossil records and large curated genomic data sets (Russo et al. 1996; Romiguier et al. 2013; Pryszcz et al. 2015; Shen et al. 2016; Irisarri et al. 2017) providing today a reference framework for the evolutionary history of yeasts and vertebrates.

Comparison with MLGO

PhyChro has been compared with the method of phylogenetic reconstruction MLGO. MLGO’s input is constituted by chromosomes described as sequences of gene identifiers and these latter can be used multiple times, that is, gene duplicates are allowed in MLGO. To prepare the input to MLGO, we used OrthoMCL as suggested in (Lin et al. 2013). Genes have been clustered using OrthoMCL (Li et al. 2003) with 1.5 as inflation value, 30% of similarity cut-off, and a E-value of 10e-5. The same label has been used for genes falling in the same cluster. MLGO analysis was run at geneorder.com/server.php (Lin et al. 2013).

Notice that MLGO cannot directly run on synteny blocks. The lists of genes, one per chromosome, taken as input by MLGO cannot be equipped by an extra structure describing the synteny. This is an obstacle to a direct comparison on PhyChro input. In addition, in contrast with PhyChro, MLGO does not provide an estimation of the branch confidence.

Phylogenetic Reconstructions Based on Protein Sequences

We identified 357 families of syntenic homologs (considered as orthologs) sharing >90% of similarity between the 13 vertebrate species, and 80 families sharing >80% of similarity between the 21 yeast species, using SynChro (Drillon et al. 2014). Orthologous proteins were aligned with MUSCLE (version 3.8.31) (Edgar 2004) and alignments were cleaned with Gblocks (version 0.91 b) (Castresana 2000). Cleaned concatenated alignments were then provided to PhyML 3.0 (which was run with the LG amino acid substitution model) and ProtPars. For Neighbor, we computed the distance matrix using ProtDist and ran it with the neighbor-joining option. ProtPars, Neighbor, and ProtDist are included in the PHYLogeny Inference Package (version 3.67) (Felsenstein 1989) and have been used online at mobyle.pasteur.fr/cgi-bin/portal.py.

FastME 2.0 (accessed online at www.atgc-montpellier.fr/fastme/) (Lefort et al. 2015) was run on both the distance matrix and the concatenated alignments by using the four distance-based algorithms NJ, BioNJ, TaxAdd_OLS, and TaxAdd_BLM to construct the initial tree.

Data Availability

PhyChro is freely available under the BSD license at http://www.lcqb.upmc.fr/phychro2/.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.