Estimating the fraction of unreported infections in epidemics with a known epicenter: An application to COVID-19

Abstract

We develop an analytically tractable method to estimate the fraction of unreported infections in epidemics with a known epicenter and estimate the number of unreported COVID-19 infections in the U.S. during the first half of March 2020. Our method utilizes the covariation in initial reported infections across U.S. regions and the number of travelers to these regions from the epicenter, along with the results of an early randomized testing study in Iceland. Using our estimates of the number of unreported infections, which are substantially larger than the number of reported infections, we also provide estimates for the infection fatality rate using data on reported COVID-19 fatalities from U.S. counties.

1. Introduction

The global pandemic COVID-19 is here in the United States. The number of confirmed cases is rising rapidly, reaching 398,809 as of April 7 with 12,895 reported deaths. The coronavirus outbreak was declared a national emergency on March 1.1 More than half of U.S. states have imposed some levels of lockdown measures.2 In addition to the public health crisis, the country is certainly looking at a deep and possibly long-lasting economic recession, according to Ben Bernanke and Janet Yellen in a recent Financial Times article.3

Given the level of severity of current conditions, a basic yet important question remains to be answered: How many people are actually infected with COVID-19 in the U.S. and what is the true fatality rate? Because of the shortage in testing kits, hospitals and disease control centers were only able to test the subsample of people with severe symptoms or travel history. The number of reported infections, especially early on in the course of the pandemic, is likely much lower than the actual number of infections in the U.S. Indeed, these unreported infections may go unrecognized because they often experience mild or no symptoms (Nishiura et al., 2020a, Andrei, 2020). If not hospitalized or quarantined, they can infect a large proportion of the population. Thus, estimating the number of unreported infections can inform policy-makers about the proper scale of virus control policies (Alvarez et al., 2020, Eichenbaum et al., 2020). These estimates can also help to assess the effectiveness of public health policies such as social distancing in slowing the spread of the epidemic.

Estimating the number of unreported infections may also give a more accurate measure of the infection fatality rate (IFR). The widely reported case fatality rate (CFR), reports the rate of fatalities from reported cases of infection. The infection fatality rate is the proportion of those actually infected who die, not of those reported or confirmed infected. The reported case fatality rate is likely an overestimate of the true infection fatality rate, due to selection bias in testing.

Ideally, a randomized testing experiment will give an unbiased estimate of the IFR. However, given the limited supply of testing kits and surging demand by people with symptoms, randomized testing may be infeasible, especially in the early periods of the outbreak. Therefore, it may be of great value to estimate the fraction of unreported infections with observational data at hand. With that knowledge, policy-makers will be better equipped to assess the proper level and duration of virus control policies.

In this paper we develop an analytically tractable method that utilizes data on travel patterns to identify and estimate the fraction of unreported infections for situations where the epidemic has a known epicenter. Our methodological strategy, described in Section 3, exploits the covariation between the number of initial reported infections in locations away from the epicenter, and the number of travelers from the epicenter to these locations. While we do not see our method as a substitute for the “gold-standard” of well defined randomized/universal testing studies, we believe our method can be useful towards providing estimates of unreported infections when results of randomized testing studies are not available for a given location of interest.

To begin illustrating the idea, consider a time period when the epicenter is the only location with infections, and that the only way another city/country can be infected is through travelers. Also assume, as in Section 3.1, that any infected travelers can only come from the unreported infected population in the epicenter — an assumption we find reasonable (as reported infected individuals would not be allowed to travel), but are able to relax in Section 3.2. Suppose now the hypothetical situation where we know the reporting rate of infections in the epicenter (the fraction of reported infections to the true number of infections), and that we know the number of travelers from the epicenter to another city/country. Assuming travelers resemble the population of the epicenter, we can calculate the expected number of infected (but unreported) travelers entering other cities/countries. Assuming further that we know the rate of transmission of the disease, we can then calculate the expected number of infections these travelers will have generated in these locations. Comparing the expected number of infections that arise from travelers to reported cases of the infection, we can estimate the reporting rate.

What can we do in the realistic case if the reporting rate in the epicenter is unknown? In Section 3.1, we propose the following: suppose we make the assumption that the reporting rate at the epicenter and the previously uninfected city/country are the same (or directly proportional). We can then start with a guess on the unknown rate of reporting at the epicenter, which allows us to calculate the implied reporting rate at the previously uninfected city/country, and check whether these are equal (or satisfy the proportion). If not, we update our guess, and try again. In other words, we can solve for the reporting rate(s) balancing the expected number of infections from travel and the number of infected that are being reported in both locations.

While the above strategy, outlined in Section 3.1, is in principle implementable using only data on travel patterns and reported cases, it is crucially dependent on the assumption that reporting rates are the same across the epicenter and destination locations (or at least proportional). Moreover, its results are very sensitive to knowing the transmission rate of the infection from travelers, as this allows us to project the number of infections in the destination city/country of interest. However, suppose now that we have access to the reporting rate of infections from another destination city/country, e.g. through universal or randomized testing, as has been done in Iceland.4 This allows us to estimate how infectious the travelers from the epicenter are. Assuming that this transmission rate from travelers is the same as the transmission rate at the destination city/country of interest, we can then calculate the expected number of infections we would expect from travel. Intuitively, the ratio between number of travelers to two destination cities/countries from the epicenter should tell us the ratio of total infections between the two cities/countries. Randomized or universal testing at one of the destinations, Iceland in our case, will give us its number of total infections, so total infections at the other destination can be computed. This strategy is laid out in detail in Section 3.2.

We would like to be very upfront that the estimation strategies outlined above are dependent on strong assumptions and reliable data on travel patterns, and that any results are very sensitive to these assumptions. However, our hope is that our approach is clear in terms of its assumptions and its corresponding limitations; we hope that future research can improve upon these limitations. We have attempted to account for some of the limitations. For example, in Section 3.3, we discuss how to correct for the fact that infections are often reported with a delay, as there is a delay to the outset of symptoms that are often a prerequisite for testing for the infection, as well as a delay in laboratory testing. Another important limitation is the assumption that the city/country with randomized test results has the same transmission rate as the city/country of interest. Section 5.4 discusses what may be done to address violations of this assumption.

Our data consists of detailed daily reported infections/deaths for all infected U.S. counties and Iceland collected by Johns Hopkins University of Medicine Coronavirus Resource Center from January 22 to April 13, 2020; international travel data to U.S. in January and February 2020 from I-94 travels data by National Travel and Tourism Office; international travel data to Iceland by Icelandic Tourist Board in January and February 2020.

Our model generates a range of estimates that depend on the traveler data that is incorporated, the date range considered, and assumptions regarding the lags associated with reported case data. We report this range of estimates in Table 3. Across these estimates, we find that 4% to 14% of cases were reported across the U.S. up to March 16, when social distancing measures began to be applied in major metropolitan areas and travel declined significantly (Thompson et al., 2020). This estimate assumes that cases are reported with a lag of 8 days as in Table 3(a); that is, we do not treat reported cases of today as the appropriate measure of true infections today.5 ^, 6 This suggests that for each case reported in late February/early March, between 6 to 24 cases remained unreported (after accounting for an 8 day lag from infection to reporting of a case).

Table 3.

Mean fraction of unreported infections with different cutoffs.

(a) 8 day reporting lag
		$T_0$ date
		Feb 1	Feb 5	Feb 10	Feb 15	Feb 20	Feb 25	Feb 29
$T_1$ date	Mar 9	13.71%	13.75%	13.73%	13.54%	13.35%	13.05%	12.48%
	Mar 10	9.35%	9.38%	9.37%	9.24%	9.11%	8.92%	8.61%
	Mar 11	8.76%	8.79%	8.78%	8.66%	8.55%	8.40%	8.17%
	Mar 12	3.83%	3.85%	3.84%	3.78%	3.72%	3.64%	3.53%
	Mar 13	4.44%	4.46%	4.46%	4.38%	4.31%	4.24%	4.13%
	Mar 14	5.58%	5.61%	5.60%	5.51%	5.43%	5.34%	5.22%
	Mar 15	4.94%	4.97%	4.96%	4.88%	4.81%	4.74%	4.64%
	Mar 16	7.96%	8.00%	7.99%	7.86%	7.76%	7.65%	7.52%
	Mar 17	11.71%	11.78%	11.76%	11.57%	11.43%	11.29%	11.11%
	Mar 18	20.63%	20.74%	20.72%	20.40%	20.17%	19.94%	19.66%
	Mar 19	44.76%	44.93%	44.90%	44.42%	44.07%	43.74%	43.33%
(b) 5 day reporting lag
		$T_0$ date
		Feb 1	Feb 5	Feb 10	Feb 15	Feb 20	Feb 25	Feb 29
$T_1$ date	Mar 6	9.64%	9.65%	9.67%	9.61%	9.53%	9.40%	9.05%
	Mar 7	5.22%	5.23%	5.24%	5.20%	5.16%	5.09%	4.94%
	Mar 8	3.05%	3.05%	3.06%	3.03%	3.01%	2.98%	2.90%
	Mar 9	1.59%	1.59%	1.60%	1.59%	1.58%	1.56%	1.53%
	Mar 10	1.66%	1.66%	1.67%	1.66%	1.65%	1.63%	1.60%
	Mar 11	2.26%	2.26%	2.27%	2.25%	2.24%	2.22%	2.19%
	Mar 12	2.01%	2.02%	2.02%	2.01%	1.99%	1.97%	1.94%
	Mar 13	3.05%	3.06%	3.07%	3.04%	3.02%	2.99%	2.95%
	Mar 14	4.18%	4.19%	4.21%	4.17%	4.14%	4.11%	4.06%
	Mar 15	3.62%	3.63%	3.64%	3.61%	3.59%	3.56%	3.52%
	Mar 16	4.73%	4.74%	4.76%	4.72%	4.69%	4.66%	4.62%
	Mar 17	6.67%	6.68%	6.71%	6.66%	6.62%	6.58%	6.52%
	Mar 18	10.75%	10.77%	10.81%	10.73%	10.67%	10.61%	10.53%
	Mar 19	24.61%	24.63%	24.70%	24.58%	24.48%	24.40%	24.28%

This table displays $\alpha$ value for different dates for both $T_0$ and $T_1$. We vary $T_0$ across the month of February, and $T_1$ across early March. Very early March and February dates for $T_1$ are not available since Iceland confirmed infections only begin February 28. Travel data is assumed uniform across days throughout and is not weighted as $T_0$ or $T_1$ change. We include Italy, Spain, Germany, and the United Kingdom as epicenters as well as China.

How do these estimates compare to other estimates in the literature? A very recent study by Bendavid et al. (2020) tested a representative sample of Santa Clara county residents in early April and reports that 48,000–81,000 people are infected as of April 1, whereas only 956 are reported that day. This leads to their reported ratio of 50–85 of total infections to reported infections. Importantly, this calculation does not account for the lag in reporting infections. Our data allows us to compute a similar statistic for San Francisco County, which we report in Table 2; we obtain this by dividing our estimate of the true infected by the reported infected on that day. For March 13, this yields a ratio of 85, which is at the upper bound of the 50–85 range reported by Bendavid et al. (2020).

Table 2.

Estimated county-level $\alpha$ and infection fatality rates.

County	$\alpha$	$\raisebox{1ex}{$U$}\!\left/ \!\raisebox{-1ex}{$R$}\right.$	National $\alpha =4.27\text{\%}$			County $\alpha$
			U-A	mIFR	cIFR	U-A	mIFR	cIFR
Broward, Fl	3.29%	29.36	349	0.16%	0.26%	453	0.13%	0.20%
Clark, NV	9.84%	9.16	184	0.33%	0.34%	80	0.76%	0.78%
Cook, IL	11.31%	7.84	321	0.21%	0.22%	121	0.55%	0.58%
Dallas, TX	3.56%	27.05	278	0.35%	0.40%	333	0.29%	0.34%
Essex, NJ	0.65%	153.60	834	0.38%	0.28%	5514	0.06%	0.04%
Fulton, GA	2.59%	37.59	290	0.28%	0.52%	478	0.17%	0.31%
Harris, TX	3.28%	29.50	177	0.15%	0.13%	230	0.11%	0.10%
Hillsborough, FL	6.70%	13.93	367	0.11%	0.18%	234	0.17%	0.29%
Honolulu, HI	0.29%	342.85	328	0.02%	$<.01$%	4814	$<.01$%	$<.01$%
Los Angeles, CA	3.20%	30.26	171	0.37%	0.38%	228	0.28%	0.28%
Maricopa, AZ	11.65%	7.59	382	0.33%	0.44%	140	0.89%	1.19%
Miami-Dade, FL	0.13%	776.68	1977	0.04%	0.05%	65714	$<.01$%	$<.01$%
Multnomah, OR	7.08%	13.12	421	0.46%	0.47%	254	0.77%	0.79%
New York City, NY	9.80%	9.21	1144	0.66%	0.78%	499	1.51%	1.79%
Philadelphia, PA	5.10%	18.61	663	0.17%	0.25%	556	0.20%	0.30%
Ramsey, MN	6.58%	14.20	133	0.42%	0.50%	86	0.65%	0.77%
San Diego, CA	18.79%	4.32	371	0.14%	0.20%	84	0.60%	0.89%
San Francisco, CA	3.60%	26.76	85	0.14%	0.20%	101	0.12%	0.17%
Suffolk, MA	10.46%	8.56	97	0.11%	0.12%	40	0.28%	0.29%
Wayne, MI	1.48%	66.63	1193	1.81%	1.93%	3449	0.63%	0.67%
Median	3.60%	26.76	328	0.28%	0.28%	254	0.28%	0.31%

We estimate each counties’ death rate on March 13 using several measures of both the infection fatality rate and estimated infected. $\alpha$ is the estimated fraction of reported infections for each county accounting for an 8-day lag. $\frac{U}{R}=\frac{1-\alpha }{\alpha }$ gives the ratio of unreported to reported infections for that county, again accounting for the fact that observed reported infections have an 8 day lag. U-A gives the under-ascertainment rate on Mar 13 given by the total infected on Mar 13 (accounting for lag) divided by the reported infected on Mar 13. mIFR matches cohorts of infected using a log-normal fatality lag distribution to determine the death rate, and cIFR compares cumulative deaths 15 days later. All of these calculations are based estimating the number of total infected on March 13 by reported infected on March 21st divided by $\alpha$, to account for an 8-day reporting lag. National $\alpha$ is taken from Table 1 Full EU travel. County $\alpha$ uses each county’s individually computed $\alpha$ rather than the nationally computed $\alpha$. $<.01\text{\%}$ indicates positive numbers that round down to 0.00%.

Our estimates of the number of total infections also allow us to estimate the infection fatality rates implied by observed data on fatalities. These calculations are reported in detail in Section 5.5, and reported in Table 2. We estimate a median cumulative infection fatality rate (cIFR) of $0.28-0.31$% across U.S. counties. We note that a representative sample study in Santa Clara County by Bendavid et al. (2020) found an infection fatality rate of $0.12-0.2$%. Our estimates show, however, potentially substantial dispersion of IFR across U.S. counties. Once again, we would like to stress that our estimates are highly dependent on model assumptions, and the data that is used to inform it. We discuss how our results depend on these assumptions in some detail in Section 5 and in Appendix.

In the economic literature, Berger et al. (2020) and Stock (2020) study the importance of unreported cases in the context of the coronavirus pandemic. Our paper contributes to the growing literature in epidemiology on estimating the true number of infections using observational data and structural model assumptions. Notably, Li et al., 2020b, Wu et al., 2020, Flaxman et al., 2020, Liu et al., 2020b, Liu et al., 2020, Nishiura et al., 2020 utilize simulated epidemiological models to estimate the fraction of unreported infections in China and European countries. As Zhao et al. (2020) note, it is often difficult to identify the fraction of unreported alongside the growth of the infection purely by measures of fit. Our paper complements these extant papers: we provide what we believe is a transparent identification argument and a very light computational strategy that allows researchers to assess the sensitivity of model estimates to modeling and data assumptions. That said, our model may miss important components of disease dynamics that these more sophisticated epidemiological models incorporate. These richer models may also allow one to estimate a richer set of model parameters than we have been able to.7 Another related recent paper is Imai et al. (2020), who estimate potential total cases in Wuhan China from the confirmed cases in other countries due to international travel, assuming that all cases outside of China are reported correctly.8 Korolev (2020) discusses non-identification in SEIRD models and proposes estimation strategy conditional on knowing infectious period and incubation period.

Section 2 introduces our model of infection, which describes the early stages of the dynamics of the epidemic. Section 3 presents our two estimation/identification strategies. Section 4 describes the data we are using for estimation. Section 5 lays out the estimation results and our robustness checks.

2. Model

Our model is based on the classic SIR model in epidemiology. We consider the evolution of the virus in both the epicenter $c$ and into target city $i$ over a period of time $T_0\le t\le T_1$. We are considering a relative short period of time in the early stage of the epidemics. Thus, the “recovered” population at the epicenter, which is a small fraction of the population, is assumed not to play a significant role during this period.

2.1. What happens at the epicenter $c$

We denote infected, reported infected, and unreported infected in time $t$ and epicenter $c$ as $I_{c,t},R_{c,t},U_{c,t}$ respectively. In all locations, total infected is given by the sum of reported infected and unreported infected: $I_{.,t}=R_{.,t}+U_{.,t}$.

The epicenter starts with some initial infections $I_{c,0}$. We are considering a short period of time in between $T_0$ and $T_1$, so the number of susceptibles at the epicenter remain relatively constant throughout this period. There are also no infected cases traveling into epicenter. Since we are interested in the cumulative cases, assuming recovery plays no role is not a restrictive assumption. So at time $t$, the total infections at epicenter with transmission rate $\beta$ is given by

$$I_{c,t}=I_{c,0}exp\left(\beta (t-T_0)\right)$$ (1)

It is worth noting that $\beta$ includes spread minus recovery rate, since we do not model a changing number of susceptibles. $\beta$ should be viewed as the net spread of infections over time.

Each time $t$, there is a cohort of travelers $M_{i,t}$ going from epicenter to target city $i$ and potentially bringing the virus to target city.9

2.2. What happens in target city $i$

We denote infected, observed reported infected, and unreported infected in time $t$ and city $i$ as $I_{i,t},R_{i,t},U_{i,t}$ respectively. At period $T_0$, target city $i$ has zero infections, so $I_{i,T_0}=R_{i,T_0}=U_{i,T_0}=0$.

Each time $t\in [T_0,T_1]$, target city receives a cohort $t$ of incoming travelers $M_{i,t}$ from the epicenter. Among these travelers, $I_{i,t}^{inc}$ are infected. Each cohort of incoming infected $I_{i,t}^{inc}$ will transmit the virus in target city with rate $\beta$ for the period of $[t,T_1]$. We assume that the transmission rate at target city is the same as in epicenter, these locally infected people are also infectious. Thus, at period $T_1$, this cohort will infect $I_{i,t}^{inc}exp\left(\beta (T_1-t)\right)$ people in the city $i$. The total new infections at target city at $T_1$ caused by all cohorts of incoming infected travelers will be

$$I_{i,T_1}={\int }_{T_0}^{T_1}{I}_{i,t}^{inc}exp\left(\beta (T_1-t)\right)dt$$ (2)

We define $\alpha$ to be the expected percentage of cases that are reported. $\alpha$ provides a mapping between the expected reported number of cases – which may be small – and the true number of infected spreading in the destination city. Formally, $\alpha$ is defined as:

$$\alpha =\mathbb{E}\left(\frac{R_{i,T_1}}{I_{i,T_1}}|I_{i,T_1}\right)$$ (3)

One can interpret the above equation as the projection of $R_{i,T_1}$ onto $I_{i,T_1}$.10 Expanding Eq. (2) using the definition of $\alpha$:

$$\mathbb{E}\left(R_{i,T_1}|I_{i,T_1}\right)=\alpha I_{i,T_1}=\alpha {\int }_{T_0}^{T_1}{I}_{i,t}^{inc}exp\left(\beta (T_1-t)\right)dt$$ (4)

3. Estimating the reporting rate $\alpha$

The estimation/identification question is: can we recover $\alpha$, the reporting rate, when we only observe reported infections $R_{i,T_1}$ but not $I_{i,t}^{inc}$, the total incoming infected in Eq. (4)? In the following Sections 3.1, 3.2, we provide a complete treatment of how one can recover $\alpha$ under different scenarios of data availability. We consider two sets of data that could potentially be available: (i) data on travel from epicenter to U.S., and (ii) data from a randomized testing implemented outside of U.S. In Section 3.3, we extend our model and estimation strategy to incorporate reporting lags.

3.1. Travel data available but randomized testing data unavailable

When only travel data is available, we must take a stance on how many infected people are leaving the epicenter. We assume that the reported infected are unable to travel, so the spread of the virus is caused by those who are infected but unreported. This allows us to determine how infectious a traveler from the epicenter is (conditional on knowing the parameters of the model.) This is a reasonable assumption especially in the case of COVID-19 because the vast majority of reported infected individuals would be quarantined and not allowed to travel.

Our main assumption in this scenario is:

Assumption 3.1

$$\frac{I_{i,t}^{inc}}{M_{i,t}}=\frac{U_{c,t}}{N_c-R_{c,t}}\text{for any time }t\in [T_0,T_1]\text{, city }i\text{ and epicenter }c$$ (5)

$N_c$ is the population of epicenter. In other words, we are assuming that the fraction of unreported infections among incoming travelers from the epicenter is the same as the fraction of unreported infections among people capable of leaving the epicenter. (We will relax this assumption in Section 3.2.) Let ${\alpha }_c$ be the reporting rate at the epicenter, defined as ${\alpha }_c=\frac{R_{c,t}}{I_{c,t}}$.11 This implies that $U_{c,t}=(1-{\alpha }_c)I_{c,t}=\frac{1-{\alpha }_c}{{\alpha }_c}{R}_{c,t}$. Therefore, Assumption 3.1 becomes:

$$\frac{I_{i,t}^{inc}}{M_{i,t}}=\frac{(1-{\alpha }_c)I_{c,t}}{N_c-R_{c,t}}\forall t\in [T_0,T_1],\text{city }i,\text{epicenter }c$$ (6)

Plugging Eq. (1) in, we get

$$I_{i,t}^{inc}=\frac{(1-{\alpha }_c)I_{c,0}exp\left(\beta (t-T_0)\right)}{N_c-R_{c,t}}{M}_{i,t}\forall t\in [T_0,T_1],\text{city }i,\text{epicenter }c$$ (7)

Plugging back to Eq. (4), we get

$$\mathbb{E}\left(R_{i,T_1}|I_{i,T_1}\right)=\alpha I_{i,T_1}$$ (8)

$$=\alpha {\int }_{T_0}^{T_1}\frac{(1-{\alpha }_c)I_{c,0}exp\left(\beta (t-T_0)\right)}{N_c-R_{c,t}}{M}_{i,t}exp\left(\beta (T_1-t)\right)dt$$ (9)

$$=\alpha (1-{\alpha }_c)I_{c,0}exp\left(\beta (T_1-T_0)\right){\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt$$ (10)

$$=\alpha (1-{\alpha }_c)\frac{R_{c,0}}{{\alpha }_c}exp\left(\beta (T_1-T_0)\right){\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt$$ (11)

$$=\alpha \frac{1-{\alpha }_c}{{\alpha }_c}{R}_{c,0}exp\left(\beta (T_1-T_0)\right){\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt$$ (12)

We assume the reporting rate at the epicenter to be the same as in the target city, i.e. ${\alpha }_c=\alpha$ (this will be relaxed in Section 3.2). Let ${ϵ}_{i,T_1}$ be the error term in prediction, i.e. ${ϵ}_{i,T_1}=R_{i,T_1}-\mathbb{E}\left(R_{i,T_1}|I_{i,T_1}\right)$. Then we have

$$R_{i,T_1}=(1-\alpha )R_{c,0}exp\left(\beta (T_1-T_0)\right){\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}$$ (13)

Regressing $R_{i,T_1}$ on $R_{c,0}{\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt$ will give us a consistent estimate of $(1-\alpha )exp\left(\beta (T_1-T_0)\right)$ since $\mathbb{E}\left({ϵ}_{i,T_1}\right|I_{i,T_1})=0$ by definition of projection.12 ^, 13 Note that even when ${\alpha }_c$ is a known linear function of $\alpha$, we can still obtain consistent estimates of $\alpha$ from Eq. (12) conditional on $\beta$. We can estimate $\beta$ from the growth of reported infections in the epicenter because there is no influx of infected people from other regions. Given that $\beta$ is now determined, we can solve for $\alpha$. However, there is substantial variation in estimation of $\beta$ within the literature, and our estimate of $\alpha$ varies with point estimates of $\beta$ (Liu et al., 2020a, Read et al., 2020, Shen et al., 2020).

3.2. When travel data and a random testing benchmark are available

In this scenario, we will be leveraging the same fact that the number of incoming unreported infections is informed by the travelers from the epicenter. Now we can also allow for selection in traveling. More specifically, if we think that e.g. urban areas are likely to have a higher infection rate than rural areas and travel abroad more,14 then Assumption 3.1 might not hold. Therefore, we introduce a bias correction term $\gamma$ in the relation between the fraction of infected among travelers and the fraction of unreported infected individuals in the general population. This bias correction term $\gamma$ can also account for the fact that a fraction of the unreported infected people might be too sick to travel. Our relaxed assumption in this scenario is:

Assumption 3.2

$$\frac{I_{i,t}^{inc}}{M_{i,t}}=\gamma \frac{U_{c,t}}{N_c-R_{c,t}}\text{for any time }t\in [T_0,T_1]\text{, city }i\text{ and epicenter }c\text{, }\gamma \ne 0$$ (14)

We can further allow for the fact that the reporting rate in epicenter ${\alpha }_c$ can be different from that of region $i$, so $U_{c,t}=(1-{\alpha }_c)I_{c,t}=\frac{1-{\alpha }_c}{{\alpha }_c}{R}_{c,t}$. We can now rewrite Assumption 3.2 as:

$$\frac{I_{i,t}^{inc}}{M_{i,t}}=\gamma \frac{(1-{\alpha }_c)I_{c,t}}{N_c-R_{c,t}}\forall t\in [T_0,T_1],\gamma \ne 0,\text{city }i,\text{epicenter }c$$ (15)

Plugging into Eqs. (1), (4), we get

$$R_{i,T_1}=\alpha \frac{1-{\alpha }_c}{{\alpha }_c}\gamma exp\left(\beta (T_1-T_0)\right)R_{c,0}{\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}$$ (16)

The additional parameters for the bias correction term $\gamma$ and different reporting rate for the epicenter complicate the estimation of $\alpha$ using travel data alone. However, having data from a country that has implemented randomized or complete testing greatly helps overcome this challenge. In our case, we are able to identify $\alpha$ using additional information given by the randomized testing benchmark provided by Iceland. Since the Iceland company deCODE genetics implemented random testing of COVID-19 for a representative sample of the island population,15 we are able to observe the infection rate of a representative sample of Iceland’s population at time $T_1$. Assuming that this is the true infection rate, and multiplying by the population of region $j$ in Iceland will give us the actual number of infections in region $j$ at time $T_1$, which is $I_{j,T_1}$. Thus, for any region $j$ in Iceland we observe $I_{j,T_1}-I_{j,T_0}$, which in turn, equals the infections generated by travelers from the epicenter:

$$I_{j,T_1}-I_{j,T_0}=\frac{1-{\alpha }_c}{{\alpha }_c}\gamma exp\left(\beta (T_1-T_0)\right)R_{c,0}{\int }_{T_0}^{T_1}\frac{M_{j,t}}{N_c-R_{c,t}}dt$$ (17)

If there were repeated observations in countries with randomized testing that allows estimation of the true infection rate, we could allow for an idiosyncratic error term in Eq. (17). However, when there is only one observation with randomized testing, we must treat it as observed without error. Estimating Eq. (17) returns $\frac{1-{\alpha }_C}{{\alpha }_c}\gamma exp\left(\beta (T_1-T_0)\right)R_{c,0}$. Estimating Eq. (16) gives a consistent estimate of $\alpha \frac{1-{\alpha }_c}{{\alpha }_c}\gamma exp\left(\beta (T_1-T_0)\right)R_{c,0}$. Taking the ratio, we have identified $\alpha$.

One intuition for this strategy is the following: the ratio between travel to U.S. and travel to Iceland from the epicenter should tell us the ratio of total infections between U.S. and Iceland. Iceland’s randomized testing gives us its number of total infections, so U.S. total infections can be computed. In other words, we observe the outcome in U.S. with under-reporting, and the unobserved counterfactual outcome with full reporting is given by the benchmark Iceland. An additional advantage of this estimation/identification strategy, as opposed to the previous strategy in Section 3.1, is that now we do not need an estimate of $\beta$ in order to recover $\alpha$. We also allow for the fact that $R_{c,0}$ could be observed with error. Identifying $\alpha$ does not require observing $R_{c,0}$ perfectly because $R_{c,0}$ appears identically in both equations.

We should be clear that for terms with $\beta$ to cancel out, the argument does assume that $\beta$ is the same across Iceland and the U.S. We believe this might be a reasonable assumption for the early periods of the infection when social distancing or other widespread measures had not yet been implemented (in a potentially differential fashion). In the case of heterogeneous transmission rate, we show in Appendix A.2 how to estimate them if we have high quality travel data. We also need the bias term $\gamma$ to be the same for U.S. and Iceland; this means that proportion of (unreported) infected travelers from China to the U.S. and Iceland are the same. More detailed micro-data on travelers may be used to assess the validity of this assumption.

This estimation strategy also works when a complete testing benchmark exists. If the whole population of region $j$ is tested, then we observe $I_{j,T_1}-I_{j,T_0}$ trivially. Eq. (17) still gives consistent estimate of $\frac{1-{\alpha }_c}{{\alpha }_c}\gamma exp\left(\beta (T_1-T_0)\right)R_{c,0}$ and the rest of the argument follows.

Note that if in the model reported infections and unreported infections have different transmission rates, then our strategy would not be able to capture the differential rates. We would need other sources of information to help us pin down these differential rates.

3.3. Incorporating reporting lags

In this section, we show how our model can incorporate a fixed reporting lag in reported infections and derive identification equations. Reporting lags are important, because if people are tested for the virus only after symptoms show up, there will be a lag in reported infections. Another major reason for reporting lag is the lag in testing results. The turnaround time for testing results in U.S. major laboratory companies could be 2 to 3 days (Kaplan and Thomas, 2020).

We denote true infected, true reported infected, and true unreported infected in time $t$ and target city $i$ as $I_{i,t},R_{i,t},U_{i,t}$ respectively. Those for epicenter $c$ as $I_{c,t},R_{c,t},U_{c,t}$. Let $k$ be the lagged report period. At time $t$ city $i$ denote the lagged reported infected $L{R}_{i,t}=R_{i,t-k}$. For epicenter $c$, lagged reported infected is $L{R}_{c,t}=R_{c,t-k}$.

Define reporting rate at city $i$ as $\alpha =\mathbb{E}\left(\frac{R_{i,t-k}}{I_{i,t-k}}|I_{i,t-k}\right)=\mathbb{E}\left(\frac{L{R}_{i,t}}{I_{i,t-k}}|I_{i,t-k}\right)$ and at epicenter $c$ as ${\alpha }_c=\frac{R_{c,t-k}}{I_{c,t-k}}=\frac{L{R}_{c,t}}{I_{c,t-k}}$. This means that we are considering the reporting rate of lagged reported cases as a fraction of the lagged total infections, not the current total infections. We derive an alternative definition of reporting rate as lagged reported cases over current total infections in Appendix A.3.

When travel data are available but randomized testing data unavailable, we still maintain Assumption 3.1. For city $i$ time $T_1$, we estimate $\alpha$ using the following equation.

$$L{R}_{i,T_1}=(1-\alpha )exp\left(\beta (T_1-T_0-k)\right)L{R}_{c,k}{\int }_{T_0}^{T_1-k}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}$$ (18)

where ${ϵ}_{i,T_1}$ is the prediction error defined analogously to Eq. (13). We assume that ${\alpha }_c=\alpha$ as before. $\alpha$ is identified conditional on $\beta$ and $k$.

When both travel data and randomized testing data are available, we maintain Assumption 3.2. In U.S. city $i$ time $T_1$,

$$L{R}_{i,T_1}=\alpha \gamma \frac{1-{\alpha }_c}{{\alpha }_c}exp\left(\beta (T_1-T_0-k)\right)L{R}_{c,k}{\int }_{T_0}^{T_1-k}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}$$ (19)

In Iceland region $j$ time $T_1$, the estimating equation is

$$I_{j,T_1-k}=\gamma \frac{1-{\alpha }_c}{{\alpha }_c}exp\left(\beta (T_1-T_0-k)\right)L{R}_{c,k}{\int }_{T_0}^{T_1-k}\frac{M_{j,t}}{N_c-R_{c,t}}dt$$ (20)

If we know $k$, then we can compute $I_{j,T_1-k}$ from the randomized testing data. Estimating Eq. (20) gives $\gamma \frac{1-{\alpha }_c}{{\alpha }_c}exp(\beta (T_1-T_0-k)L{R}_{c,k}$. Regressing Eq. (19) gives a consistent estimate of $\alpha \gamma \frac{1-{\alpha }_c}{{\alpha }_c}exp\left(\beta (T_1-T_0-k)\right)L{R}_{c,k}$. Taking the ratio, we can identify $\alpha$ if we know $k$. Again here we can also allow for the situation where we do not observe $L{R}_{c,k}$ perfectly. Details of how we derive the estimating equations are in Appendix.

3.4. Identification of $\alpha$, $\beta$, $\gamma$ and ${\alpha }_c$

In this section we recap our identification arguments for both strategies presented above. We summarize which parameters are identified and estimated, and which equations are used to identify them.

3.4.1. No randomized testing available

For simplicity, we will discuss identification of $\alpha$ and $\beta$ under the assumption that ${\alpha }_c=\alpha$. We note that without randomized testing, our model is identified under Assumption 3.1, so $\gamma$ is not present during this specification. The remaining two parameters in Eq. (12) are $\alpha$ and $\beta$. Conditional on knowing $\beta$, $\alpha$ is identified and can be estimated by ordinary least squares estimation.

How do we identify $\beta$ separately from $\alpha$? In the early onset of the pandemic, data on the growth of the virus in the epicenter exclude travelers with the virus entering the epicenter. Applying $R_{c,t}={\alpha }_c{I}_{c,t}$ to Eq. (1), we see that

$$\frac{1}{{\alpha }_c}{R}_{c,t}=\frac{1}{{\alpha }_c}{R}_{c,0}exp\left(\beta (t-T_0)\right)$$ (21)

From this, we can identify $\beta$ by dividing through and taking logarithms.

$$\beta =\frac{1}{t-T_0}log\left(\frac{R_{c,t}}{R_{c,0}}\right)$$ (22)

Data of reported infected in the epicenter identifies $\beta$ separately from $\alpha$. Conditional on an estimate of $\beta$, the only remaining unknown coefficient of Eq. (12) is $(1-\alpha )$. Thus $\alpha$ is identified conditional on $\beta$, and ${\alpha }_c$ is identified by assumption that ${\alpha }_c=\alpha$.

3.4.2. Randomized testing available

When randomized testing is available, the model allows for a more complex relationship between the reporting rates of the epicenter and the destination. We no longer have to assume that ${\alpha }_c=\alpha$; moreover, we introduce an additional parameter $\gamma$. Identification is based on Assumption 3.2. While this specification features more parameters, identification of $\alpha$ requires separately identifying and estimating fewer parameters. The reason for this is the inclusion of additional information from randomized testing. We assume that $\gamma$ and $\beta$ are constant across all countries.

Estimation of Eq. (17) yields $\frac{1-{\alpha }_c}{{\alpha }_c}\gamma exp\left(\beta (T_1-T_0)\right)R_{c,0}$, and estimation of Eq. (16) yields $\alpha \frac{1-{\alpha }_c}{{\alpha }_c}\gamma exp\left(\beta (T_1-T_0)\right)R_{c,0}$. By taking the quotient, $\frac{1-{\alpha }_c}{{\alpha }_c}\gamma exp\left(\beta (T_1-T_0)\right)R_{c,0}$ cancels out, leaving only $\alpha$. Because of this cancellation, with randomized testing, we need not identify $\beta ,\gamma$ or ${\alpha }_c$ to identify $\alpha$.

4. Data

4.1. COVID-19 data

Daily reported infections, recovery, and death data are collected by Johns Hopkins University of Medicine Coronavirus Resource Center from January 22 to April 13, 2020. We use data for all U.S. counties as well as epicenters.

Randomized testing data in Iceland is obtained from the website maintained by the Directorate of Health and the Department of Civil Protection and Emergency Management in Iceland.16 We have daily number of tests conducted by deCODE genetics and daily number of confirmed cases. We use the first half of testing by deCODE which spans March 15–19, 2020. During this round of testing deCODE performed 5490 tests and confirmed 48 cases, which implies an infection rate of .874%.

Testing in Iceland conducted by deCODE genetics featured open invitations for testing among individuals who were not confirmed infected at the time. We believe that the confirmed infected population was very small at the onset of infections into Iceland. As a result, ignoring them from the sample does not contaminate the testing very much.

There is also a risk of selection into testing: people who were in contact with infected individuals are more likely to select into testing than socially isolated individuals. We assume that there is no selection into testing by the more at-risk. Those who are at risk of contracting the virus were not aware of their high risk due to several reasons. The incubation time of the virus was not understood this early into its spread. Another aspect of the virus that was not understood was the high number of asymptomatic but infectious individuals in the population. Under this assumption, we treat open invitations of the unconfirmed as randomized testing.

Moreover, we cannot consider the Iceland data as representative testing because of a sampling issue. The deCODE testing does not attempt to re-weight its sample in order to be representative of the demographics of the population. However, as long as the previous assumption of randomization holds, this does not affect our results.

If the randomization assumption were incorrect, and the deCODE data was biased upwards in the number of infections present in Iceland, this would mean that the infectiousness of travelers from the epicenter was actually lower than what our model predicts. This would mean that reporting rate is higher, and there are fewer total infected in the United States. This would bias our estimates of the infection fatality rate upwards as well.

In Gudbjartsson et al. (2020) more data from Iceland is considered. The paper considers two waves of studies: one set is the open invitation from deCODE testing, and the other is a set of randomized invitations sent out via text-message. This is a much larger set of testing than our data, but uses a later time-frame than our method. Using the entire first wave of deCODE data, they find an infection rate of .8% rather than our .87%. They also consider a second wave of randomly invited individuals which gives a .6% infection rate. However this second sample is restrictive in terms of age, only featuring individuals from ages 20–70, which omits the very young and the elderly, two high-risk groups. This second wave is still vulnerable to the same selection concerns as the deCODE testing data as well.

4.2. Travel data

We obtain monthly data of international arrivals to U.S. by port of entry and country of origin from I-94 Arrivals by National Travel and Tourism Office. We use the number of visitors from China, Italy, Spain, UK, and Germany in January and February 2020 as the measure for incoming travelers to U.S. states. For international arrivals to Iceland, we get the number of visitors from China, Italy, Spain, UK, and Germany in January and February 2020 from the Icelandic Tourist Board. We have not been able to obtain March travel data into either country.

The National Travel and Tourism Office of the United States provides monthly data for entry by port of entry, as well as a separate data set for country of origin. We construct the number of visitors from China, Italy, Spain, Germany, and the UK by scaling the port-of-entry data by the percentage of total visitors that are from these countries. This introduces error, as we cannot observe directly the number of e.g. Chinese travelers into a particular city or state. It is also important to note that we do not observe inter-state travel. While this may not be important for the immediate infections caused by travelers from the epicenter, our projections for the number of infections for $T_1$ that are far removed from $T_0$ will be less accurate due to interstate travel.

To attempt to alleviate this error, we note that The National Travel and Tourism Office of the United States also provides a market profile of travelers from each of the epicenters. This data however appears to be flawed. In particular several major ports such as Portland, Oregon have no recorded travelers from any of our epicenters. This data also only contains travel for $2019$ and the years before, and we have concerns over its stationarity. We report our results using this data in Appendix A.2, but maintain our use of the $2020$ data for our main results.

For Icelandic data, 99% of international travelers arrive through Keflavik airport into Iceland. The data contains a breakdown of arrival by country of origin, broken down by month of arrival. We use January and February arrival data from China, Italy, Spain, UK, and Germany for estimation.

Our travel data for both countries does not control for connecting flights. However the United States data is limited to the top-30 port of entries, many of which are large urban cities for which there will be less connecting flights. Further work that can obtain more precise estimates of entry may be able to control for this. In the case of Iceland: a survey conducted by the Icelandic Tourist Board suggests that 2%–5% of international travelers are aboard connecting flights, suggesting it is less of a problem for this set of data.

4.3. Population data

Estimates of U.S. State and county population data come from the U.S. Census Bureau. Data for the populations of China, Iceland, Italy, Spain, UK, and Germany as of 2020 are obtained from the United Nations Population Division.

5. Empirical application

5.1. Implementation

We now consider estimation of ${\alpha }_{US}$ using randomized sampling in Iceland, as described in Section 3.2. Randomized sampling done by deCODE genetics gives a percentage of the population that has contracted the virus. We estimate Eq. (17) using Randomized Testing to construct $I_{j,T_1-k}$. We do not have city-level travel data into Iceland. 99% of all international travel arrives through a single airport, and while the data provided is accurate, this gives only a single data point for estimation. As a result, $exp\left(\beta (T_1-T_0)\right)\gamma \frac{1-{\alpha }_c}{{\alpha }_c}{R}_{c,0}$ is estimated without error by the ratio of $I_{j,T_1}-I_{j,T_0}$ and ${\int }_{T_0}^{T_1}\frac{M_{j,t}}{N_c-R_{c,t}}dt$.17

For estimation of reporting rates in the U.S., we need several pieces of data: Firstly $M_{j,t}$, and secondly of $I_{j,T_1}-I_{j,T_0}$. We discuss the imputation of these here. We observe only monthly travel data to construct $M_{j,t}$, and to maintain robustness to January travels and infections, we average February and January travel into both the United States and Iceland. We assume that $M_{j,t}$ is uniform over the entire time period such that ${\int }_{Jan1}^{Feb29}{M}_{j,t}$ is equal to the sum of all travel into the city from January and February. Thus the integrand of ${\int }_{T_0}^{T_1}\frac{M_{j,t}}{N_c-R_{c,t}}dt$ varies over time only by confirmed infections in the epicenter. Estimation of $I_{j,T_1}$ is complicated due to randomized testing by Iceland only being conducted at certain dates. To resolve this problem, we scale the Iceland randomized results by the scale of the confirmed cases against March 15. This means that if there were half the confirmed cases in March 5 as in March 15, the total infections would be half of the randomized testing percent times the population of Iceland. This allows for us to consider $T_1$ closer to the onset of the infection than the randomized testing dates. We also remove the number of infected from Wuhan China from our data on confirmed infected in China due to the lock-down restrictions placed on this city. We use the first wave of deCODE testing to determine the percentage of the population that has contracted the disease. This testing took place during Mar 15 through Mar 19. The results show that $.874\text{\%}$ of the population of Iceland have contracted the disease as of Mar $15$.18

We estimate Eq. (19) using multiple data points from U.S. states and counties. We obtain our estimate of $\alpha \gamma \frac{1-{\alpha }_c}{{\alpha }_c}exp\left(\beta (T_1-T_0-k)\right)L{R}_{c,k}$ via OLS without a constant term. One important note is that if the magnitude of measurement error in travel data were high, this problem may be alleviated via instrumental variables strategy using other travel data measured with error.

We then construct our estimate of $\alpha$ by dividing the two estimates. It is important to note that as a result of the division, this method is not reliant on population data from the epicenter of infection. As long as $\gamma$ and $\beta$ are the same between Iceland and the United States we will have identified $\alpha$. It is likely that at the onset of the infection similar preventative measures have been taken in these two countries, meaning that $\beta$ will be reasonably close for each country.

Is China the only epicenter for the United States? While the first confirmed infection in Seattle occurred from a visitor from China, our data on The United States and Iceland occurs later in the global progression of the virus than our Chinese data. By the time these countries were experiencing infections, Italy had also experienced an outbreak. To this end, we also allow for a second epicenter: Italy. Italy is located much closer to Iceland and constitutes a substantial amount of travel to the country. However, to maintain identification, we require that $\alpha$, $\beta$ and $T_0$ be same for both China and Italy, and we observe $L{R}_{c,k}$ for both epicenters with no error. However we find that allowing $T_0$ to vary does not affect our estimates by much. We also consider a broader collection of epicenters of China, Italy, Spain, Germany and the UK. For some collection of epicenters $L$: Our estimation equation for the United States is given below.

$$L{R}_{i,T_1}=\alpha \frac{1-{\alpha }_c}{{\alpha }_c}\gamma exp\left(\beta (T_1-T_0-k)\right)\left(\sum _{\ell \in L}\left[{\int }_{T_0}^{T_1-k}\frac{L{R}_{c,k}^{\ell }{M}_{i,t}^{\ell }}{N_c^{\ell }-R_{c,t}^{\ell }}dt\right]\right)+{ϵ}_{i,T_1}$$ (23)

A similar equation is also estimated with multiple epicenters (China and Italy, also with Spain, Germany, and UK) for Iceland. Our results using multiple epicenters run OLS without a constant using this equation, as well as the corresponding Iceland equation to estimate $\alpha$.

Table 1.

Estimated average fraction of reported infections.

	${\alpha }_{US}$	$\frac{1-{\alpha }_{US}}{{\alpha }_{US}}$
	8 day lag
China and Italy Travel Data
	.0416	23.1
Only Chinese Travel Data
	.0458	20.8
China, Italy, Spain, Germany, UK
	.0427	22.4
	5 day lag
China and Italy Travel Data
	.0161	61.2
Only Chinese Travel Data
	.0169	58.3
China, Italy, Spain, Germany, UK
	.0164	60.1

We report estimated $\alpha$ by OLS without a constant for several specifications of the model. We use $T_0$ as Feb 23 and $T_1$ as March 10,13 for each lag respectively. For the versions including European data, European travel to both Iceland and the United States is considered. King County, WA is omitted from the calculation.

5.2. Results: Illustration

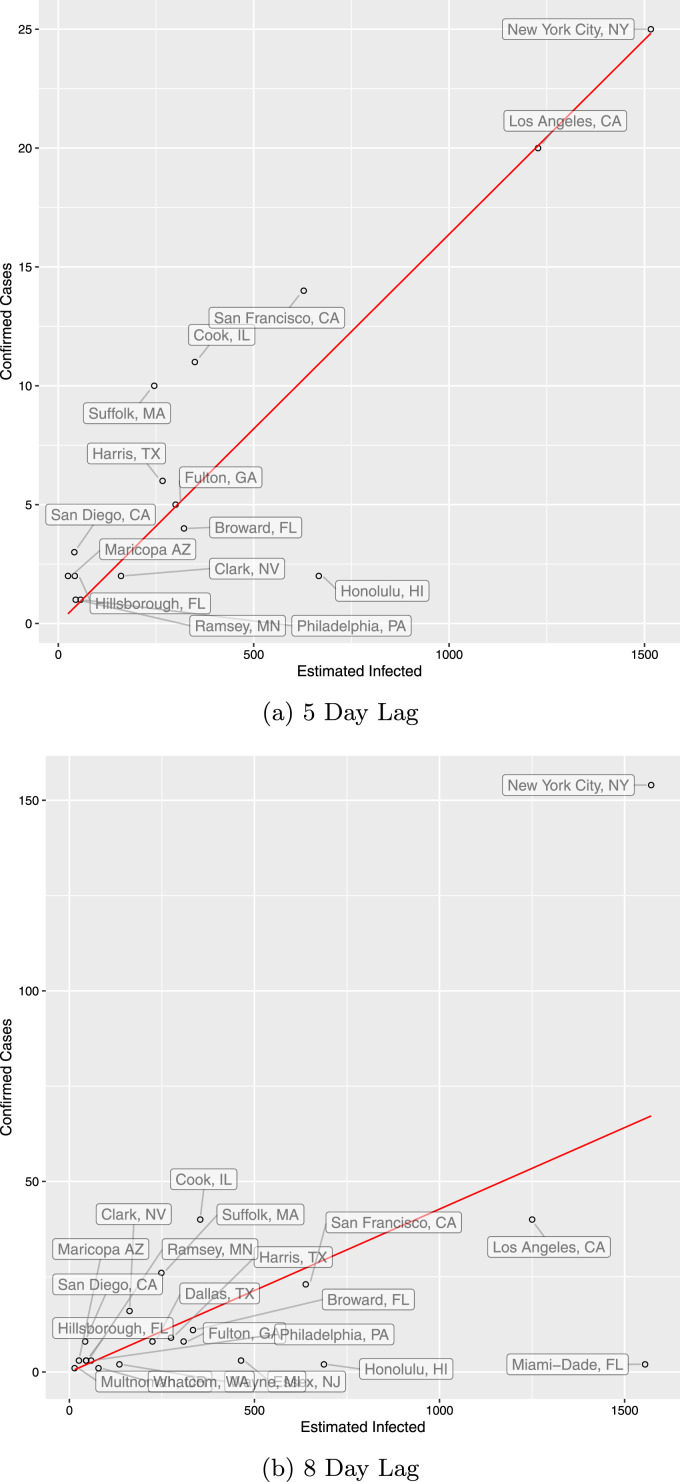
As a first illustration of our approach, we first estimate $\alpha$ using February $23$ as $T_0$ and March 13 as $T_1$ with a lag of 8 days. This is because there were very few infections in January and early February. We check robustness of different time periods in Section 5.3. We choose $T_1$ to include the beginning of the growth of infections in the United States, while still being early into the progression of COVID-19 so travel is still important. Using traveler data from China, Italy, Spain, Germany, and the UK, in Table 1, we estimate $\alpha =0.0427$ (robust s.e. 0.0211). This would mean that for every case confirmed in the United States in early March, there are still $\frac{1-\alpha }{\alpha }=22$ unconfirmed cases (assuming a reporting lag of 8 days). We also consider a $5$ day lag model, the median time for symptoms to appear, but prefer $8$ days, in order to capture the testing lag in addition to symptom onset (Lauer et al., 2020, Kaplan and Thomas, 2020, Li et al., 2020a). For the $5$ day lag, $T_1$ was set to March 10 for comparison. See Fig. 1 for county-level results.

Fig. 1.

Estimated reported infections by county.

This plot shows the ratio of confirmed cases to estimated infected in each county on $T_1=$ March 10 for 5 day lag, and 13 for 8 day lag. $T_0$ is February 23rd. We use the full European entry. Estimated infected are given by the reported on $T_1+Lag$ and divided by $\alpha$.

How does this estimate compare to other estimates in the literature? A very recent study by Bendavid et al. (2020) tests for COVID-19 antibodies in a representative sample of Santa Clara county residents and reports that 48,000–81,000 people are infected as of April 1, whereas only 956 cumulative infected are reported that day. This leads to their reported ratio of 50–85 of total infections to reported infections. Importantly, this calculation does not account for the lag in reporting infections. While we do not have travel data for Santa Clara county, we can compute a similar statistic for San Francisco County: Our estimate of the true infected on March 13, divided by the reported cumulative infected on that day. This yields a ratio of 85, which is at the upper bound of the 50–85 range reported by Bendavid et al. (2020). We report these ratios for the counties in our data set in Table 2.

We note that there is one city present in our data that is a huge outlier. Seattle featured very early infections, and was unable to contain the spread of early infections unlike other cities in the United States. We believe that for King County, $T_0$ may be much earlier than for the other cities. This means that within our time interval, there are substantial amounts of infections caused by residents of the city, not only visitors. As a result, this city has a substantially higher (3700%) amount of confirmed cases per visitor than any other city at the current time so we exclude it. Results from the profile travel data are also provided in Appendix A.2.

Our approach is also sensitive to the travel data magnitudes, which may not be well estimated for the United States due to data limitations. In particular, connecting flights after port of entry may lead to underestimates of international arrivals into smaller cities and counties. We also lack inter-state travel between the United States, which would be important for estimating $\alpha$ later into the spread of the virus.

Have we considered all epicenters of the virus for the United States and Iceland? There were other countries which had seen substantial infections such as South Korea. Their exclusion biases both the estimates from both Iceland as well as the United States, and as long as the magnitudes of travel were even between the two will not bias alpha. If these other epicenters had more travel to the United States relative to Iceland, this would downward bias our estimates of $\alpha$, and vice versa. However, we see little change in our estimates by adding in Spain, Germany and UK. If the travel patterns between the United States and Iceland to and from an omitted set of epicenter countries are not very different, we do not believe their omission will substantially alter our results.

5.3. Results: Range of estimates and robustness checks

Our dates for $T_0$ and $T_1$ are chosen such that they capture the onset of the infection for the United States. As Table 3 shows, our $\alpha$ estimate is reasonably stable along choices of $T_1$, and very stable among choices of $T_0$ all throughout February. We estimate a range of $4\text{\%}-14\text{\%}$ reporting rates when there is a lag of 8 days and a range of $1.5\text{\%}-10\text{\%}$ for the average reporting rate across the U.S. with a reporting lag of 5 days. Using only China as the epicenter, we observe similar patterns in $\alpha$. For early March we note a relatively stable $\alpha$ over $T_1$. For very early choices for $T_1$, our Iceland estimates of confirmed are very small, and this could create very noisy estimates of $\alpha$ (the first case in Iceland was confirmed February 28). As we increase $T_1$, we see an increase in $\alpha$. This may be due to increases in the availability of test kits, which lead to higher reporting rates. However, this result may in part be due to unobserved/unaccounted travel, particularly within the United States, along with the fact that we do not have data on March travel into the U.S. Both of these factors would lead to under-reporting of travel for late March, and cause estimates of $\alpha$ to be upward biased. Moreover, as we progress later into March, social distancing/health policy measures across Iceland and U.S. began to be applied, leading to differential changes in the transmission rate.

Throughout the analysis above, we have excluded King County, Washington which contains Seattle. Table A.2 displays our estimates including this county, which heavily skews the data. We believe this may be due to significant community infections occurring in the county during our time period, as the city was infected much earlier than other cities.

Correct estimation of the reporting lag parameter is essential, as our estimates of $\alpha$ are sensitive to this. We consider our estimates robustness to reporting lags in Table A.3. Our estimates of $\alpha$ appear reasonably robust to a range of lengths of the lag, with an increase as the lag becomes longer.

We note that large lags ($k>10$) pose a problem for estimation in our model. For estimation purposes, we maintain $T_1-k$ to be a constant date as we consider changes in the lag parameter. This means that for large lags, we must consider $T_1$ dates deep into March. However, the further we get into March, the more interstate travel and carrying of infections between cities and states matters, which may lead to overstating $\alpha$.

5.4. Heterogeneity in $\beta$

The above argument is predicated on $\beta$ being constant for both Iceland as well as the United States. However, along with potential differences in normal social interaction patterns leading to virus transmission, Icelandic and the U.S. policies for handling the spread of the virus may have diverged significantly. This means that our assumption of $\beta$ being the same across the U.S. and Iceland may not hold. Evidence from Kucharski et al. (2020) suggests that $\beta$ is very sensitive to changes in policy, leading to this upward bias in $\alpha$.

In Appendix A.4, we attempt to relax that assumption. In our model, $\beta$ cannot be directly estimated from the growth of the infected trajectory due to the majority of infected at the start arriving from travel. The details for our estimation procedure are given in Appendix. A major problem with this approach is that it requires variation in travel over time which we do not measure well. In essence, we use the evolution of the infected in each country over time to learn about how infectious travelers are once they have arrived. With constant daily travel, this variation is poor and makes identification of $\beta$ difficult.

As a coarse estimate, we find that the difference in $\beta$ is about $.06$. The estimate of $\alpha$ resulting from this procedure yields a value of $.007$, suggesting that our estimates using the assumption of same $\beta$ may be upward biased. However, we note our monthly travel data does not allow for variation in travel over time, making it difficult to estimate $\beta$ in a robust manner, so any bias in measuring travel leads to bias in $\alpha$. We thus note that our main estimates of $\alpha$ may be upward biased, suggesting that there may be more total infections than we have estimated. However, better travel data showing adequate variation in time is required for reliable estimation of separate $\beta$s in our model.

5.5. Infection fatality rate

Given our estimated reporting rate over the time period of interest, we can compute the implied infection fatality rate (IFR). Let $D_t$ be the number of deaths observed on day $t$. Let $I_t$ be the number of cumulative total infections on day $t$. Let $p$ be the period from illness onset to death, i.e. the fatality lag. Let $f\left(p\right)$ be the density of $p$ over $[0,P]$ with mean $\overline{p}$.

We consider two alternative definitions of IFR:

• 1.Cumulative Infection Fatality Rate (cIFR): The cIFR at $t$ is the fraction of cumulative deaths adjusted by mean fatality lag and cumulative total infections as of $t$.
• 2.Cohort-matching infection Fatality Rate (mIFR): For each cohort of new infections at time $t$, the mIFR is the ratio of all deaths attributed to cohorts until $t$ and the size of each infected cohort until $t$. This method accounts for a random fatality-lag rather than a fixed interval.

More specifically, we define

$$cIF{R}_t=\frac{\sum _{s=0}^{t+\overline{p}}{D}_s}{I_t}$$ (24)

$$mIF{R}_t=\frac{\sum _{s=0}^t{\int }_0^P{D}_{s+p}f\left(p\right)dp}{\sum _{s=0}^t{I}_s-I_{s-1}}$$ (25)

We follow Linton et al. (2020) when estimating the distribution of the fatality lag and fit a log-normal distribution. $I_{-1}$ is the infected on the day before $T_0$, and may be zero.

We estimate cIFR and mIFR for each U.S. county in our data set, computing death rates at March 13. County-level results are shown in Table 2; we have estimated the cIFR and mIFR using both county-specific $\alpha$ estimates, and the national estimate of 4.27%. We estimate that the median cohort-matching infection fatality rate (mIFR) is 0.28% across U.S. counties, and cIFR of 0.28%.

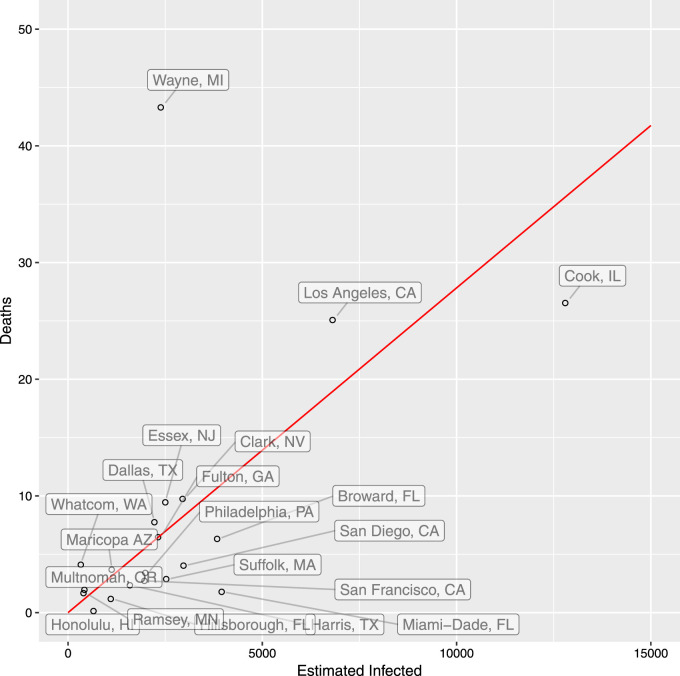
Fig. 2 shows the results for each U.S. county. Wayne MI, where Detroit is located, has low estimated number of infections potentially due to low travel inflow and therefore a high estimated mIFR.

Fig. 2.

Reported deaths per estimated infections by county.

This plot shows the ratio of cohort-matched confirmed deaths to estimated infected in each county on Mar 13th, taking into account an 8 day lag in reporting. We use the full European Entry. We estimate fatality-lag time as a log-normal distribution with mean 14.5 and standard deviation 6.7. Estimated infected are computed for each daily cohort using the National-$\alpha$ of 4.27%. We omit New York City for visual clarity.

How do these estimates compare to estimates of the IFR in the literature? Russell et al. (2020) estimate a comparable definition to cIFR as 1.2%19 with complete testing data on the Diamond Princess cruise ship, using a population that is weighted towards the elderly. Since elderly have a substantially higher case-fatality rate, this suggests the real cIFR may be lower than 1.2%.

Using their estimates of the true infection rate from their representative antibody testing study, Bendavid et al. (2020), compute a cumulative infection fatality rate with projected death accounting for 3 week fatality lag, and obtain an 0.12–0.2% infection fatality rate. Accounting for lags, our cumulative infection fatality rates for San Francisco county are 0.17–0.20%, which lies at the upper bound of their estimates.

Streeck et al. (2020) estimate an IFR of $0.36\text{\%}[0.29\text{\%},0.45\text{\%}]$ with a randomized testing study in a German town. Our estimates of the median mIFR 0.28% and cIFR 0.28% with national reporting rate approximately fall in the 95% CI of their estimates. With county-specific reporting rate, our estimated median mIFR 0.28% and cIFR 0.31% are even closer to their estimates.

While our estimates of the IFR are substantially lower than reported case fatality rates, we note that there is still substantial variation in our estimated IFRs across counties in the early stages of the epidemic. This means that results from a single county, regardless of the quality of the methodology, may not be indicative of the IFR elsewhere. Along with many other factors, the variation in demographic composition, and the variation in the quality and capacity of the health care sector, can lead to drastically different infection fatality rates across the country.

6. Conclusion

In this paper, we lay out an analytically tractable model of early-period disease transmission across a known epicenter and target cities. Using this model, we provide analytical arguments to demonstrate identification of reporting rates in target cities away from the epicenter. Our preferred estimation strategy utilizes variation of travel patterns from epicenter to destination cities and available randomized testing results from elsewhere in the world. The empirical implementation of our model generates a range of estimates for the percentage of infections that have been reported. Using international travel data to the U.S. and randomized testing data from Iceland, for a February to early March window, we estimate an average reporting rate in the U.S. of 4.3%. This estimate leads to an estimated median infection fatality rate of $.28-.31\text{\%}$ across U.S. counties. Our estimates suggest that a large number of infections in the U.S. have not been reported in this early period.

We are not offering or endorsing any policy recommendations based on our estimates. Nor do we suggest that any of our analysis should be taken as a substitute for well designed randomized/universal testing programs, which will provide the most reliable estimates of the true infection rate in the population. However, we believe our method can be useful towards providing estimates of unreported infections when results of randomized testing studies are not available for a given location of interest.

Another aim in this paper has been to obtain tractable analytic results showing how to identify the reporting rate from available data. Our model is a substantially stripped down version of epidemiological models considered by Li et al., 2020b, Wu et al., 2020, Flaxman et al., 2020. These more complex models may allow additional sources of variation in the data to pin down the key parameters of interest. Importantly, we do want to emphasize that our identification and estimation results rely quite sensitively on model assumptions and the (un)availability of high quality data on travel. We hope future research can improve on these important limitations.

Appendix.

A.1. Tables

See Table A.1, Table A.2, Table A.3.

Table A.1.

Summary statistics of fraction of reported infections by county.

Version	Min.	1st Qu.	Median	Mean	3rd Qu.	Max.
China Travel Only	0.001404	0.027434	0.037345	0.060896	0.100897	0.203500
China and Italian Travel	0.001254	0.025142	0.034784	0.055746	0.094906	0.183048
China and EU Travel	0.001286	0.025915	0.036020	0.057454	0.097979	0.187902

Summary statistics reported on the distribution of $\alpha$ for each county in the data. $\alpha$ is estimated for $T_0$ Feb 23, $T_1$ Mar 13, and a lag of eight days. EU travel includes traveler data from Italy, Spain, UK, and Germany.

Table A.2.

Reporting rate ($\alpha$) estimates including king county.

	${\alpha }_{US}$	$\frac{1-{\alpha }_{US}}{{\alpha }_{US}}$
	5 day lag
China and Italy Travel Data
	0.0200	48.9
Only Chinese Travel Data
	0.0211	46.5
China, Italy, Spain, Germany, UK
	0.0204	48.1
	8 day lag
China and Italy Travel Data
	0.0486	19.6
Only Chinese Travel Data
	0.0539	17.6
China, Italy, Spain, Germany, UK
	0.0500	19.0

We report estimated $\alpha$ by OLS without a constant for several specifications of the model. We use $T_0$ as Feb 23rd and $T_1$ as Mar 10,13 for each lag respectively. For the versions including European data, European travel to both Iceland and the United States is considered. King County is included in this data.

Table A.3.

Robustness to Lag.

Lag	$\alpha$
0	0.0055
1	0.0086
2	0.00927
3	0.00984
4	0.0121
5	0.0164
6	0.028
7	0.0284
8	0.0427
9	0.0675
10	0.0699
11	0.113
12	0.194

This table shows estimates of $\alpha$ as the reporting lag period is varied. We use $T_0$ as Feb 23, and $T_1$ as March 5 ＋ Lag days. King County is omitted. We include Italy, Spain, Germany, and the United Kingdom as epicenters as well as China.

A.2. Profile travel data

The United States National Travel and Tourism Office also provides profile travel data for each of our Epicenter Countries. As part of this data, US Port of Entry is listed with population weights for each year. We assume stationarity over time, and estimate travel into the United States from each Epicenter by weighting the total travel data for each country in 2020 by the 2019 port-specific weights. While we believe there may be flaws in this data, with several large ports appearing to have zero travel, we attempt to resolve this by dropping these ports and continuing with ports for which we have data. However dropping these ports may downward-bias our estimates of $\alpha$.

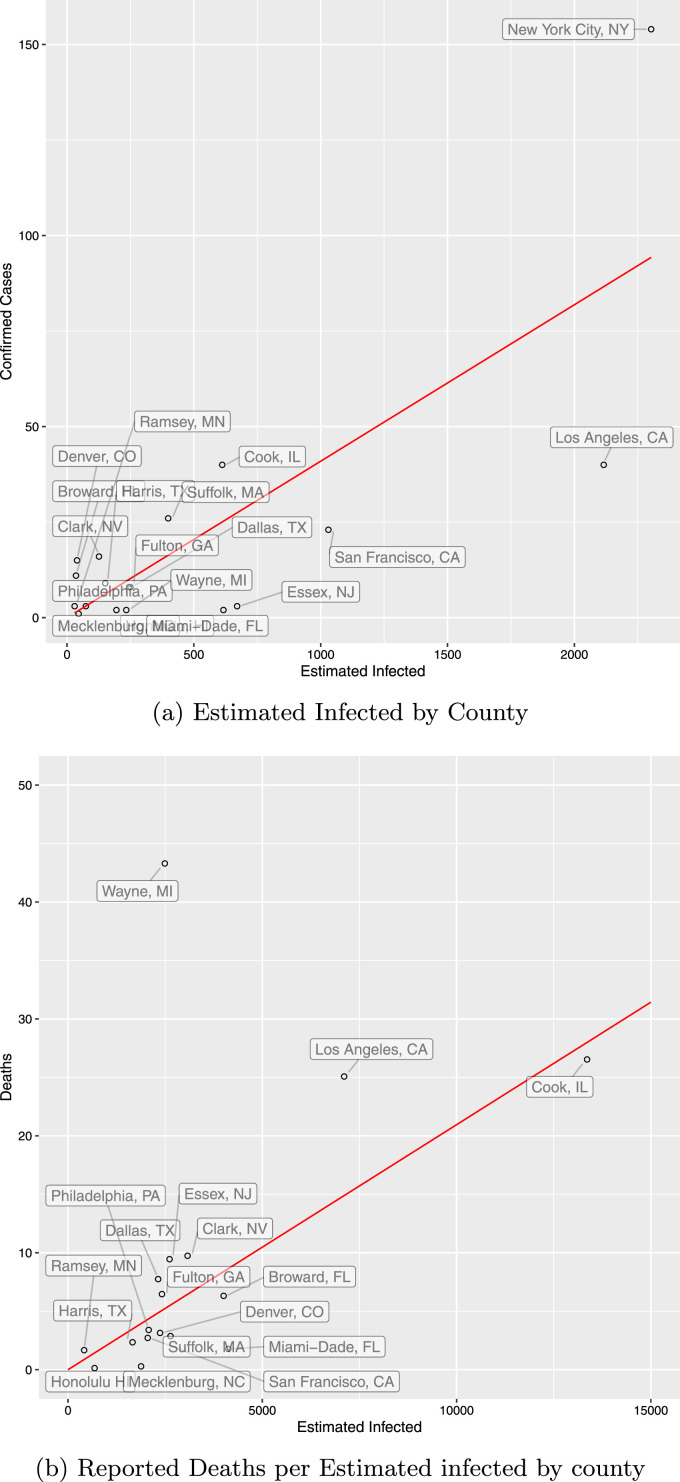
Results below are for the model specification with $T_1$ at Mar 13 and an $8$ day reporting lag. We exclude Seattle WA in all of our estimation below (see Table A.4 and Table A.5).

Our $8$-Day lag results for the Full-European Entry are similar, however results using only the Chinese Data show a severe downward bias from before. This leads to higher total infected predictions, and slightly lower death rates, particularly using the cohort-matching technique. We note that our fit to estimated infected with this data is significantly worse than before (see Fig. A.1).

Fig. A.1.

Estimated infected and deaths using profile travel.

The Estimated infected plot shows the ratio of confirmed cases to estimated infected in each county on $T_1=$ March 13. $T_0$ is February 23rd. We use the full European Entry. Estimated infected are given by the reported on $T_1+Lag$ and divided by $\alpha$. We use an eight-day lag.

The second plot shows the ratio of cohort-matched confirmed deaths to estimated infected in each county on Mar 13th, taking into account an 8 day lag in reporting. We use the full European Entry. We estimate fatality-lag time as a log-normal distribution with mean 14.5 and standard deviation 6.7. Estimated infected are computed for each daily cohort using the National-$\alpha$ of 4.09%. We omit New York City for visual clarity.

Table A.4.

Reporting rate ($\alpha$) using profile travel data.

	${\alpha }_{US}$	$\frac{1-{\alpha }_{US}}{{\alpha }_{US}}$
	5 day lag
China and Italy Travel Data
	0.0108	91.3
Only Chinese Travel Data
	0.0106	93.6
China, Italy, Spain, Germany, UK
	0.0112	88.1
	8 day lag
China and Italy Travel Data
	0.0385	25.0
Only Chinese Travel Data
	0.0330	29.3
China, Italy, Spain, Germany, UK
	0.0409	23.4

We report estimated $\alpha$ by OLS without a constant for several specifications of the model. We use $T_0$ as Feb 23rd and $T_1$ as Mar 10,13 for each lag respectively. For the versions including European data, European travel to both Iceland and the United States is considered. Hamilton OH, Allgeheny, PA; Multnomah, OR; Seminole, FL; Santa Clara, CA; and Baltimore MD counties are all excluded for zero-travel.

Table A.5.

Estimated county-level $\alpha$ and IFR using profile travel data.

County	$\alpha$	$\raisebox{1ex}{$U$}\!\left/ \!\raisebox{-1ex}{$R$}\right.$	National $\alpha =4.09\text{\%}$			County $\alpha$
			U-A	mIFR	cIFR	U-A	mIFR	cIFR
Broward, FL	31.13%	2.21	364	0.16%	0.25%	48	1.20%	1.90%
Clark, NV	12.69%	6.88	192	0.32%	0.32%	62	0.98%	1.01%
Cook, IL	6.54%	14.30	335	0.20%	0.21%	210	0.32%	0.33%
Dallas, TX	3.20%	30.27	290	0.33%	0.39%	371	0.26%	0.30%
Denver, CO	38.02%	1.63	158	0.13%	0.13%	17	1.23%	1.18%
Essex, NJ	0.45%	222.55	871	0.36%	0.27%	7973	0.04%	0.03%
Fulton, GA	3.27%	29.58	302	0.27%	0.50%	378	0.21%	0.40%
Harris, TX	5.97%	15.76	185	0.14%	0.12%	127	0.21%	0.18%
Honolulu HI	1.03%	96.40	342	0.02%	$<.01$%	1364	$<.01$%	$<.01$%
Los Angeles, CA	1.89%	51.89	178	0.35%	0.36%	386	0.16%	0.17%
Mecklenburg, NC	2.18%	44.89	1881	0.02%	$<.01$%	3533	0.01%	$<.01$%
Miami-Dade, FL	0.32%	307.31	2064	0.04%	0.05%	26053	$<.01$%	$<.01$%
New York City, NY	6.69%	13.95	1194	0.63%	0.75%	731	1.03%	1.22%
Philadelphia, PA	4.04%	23.75	692	0.16%	0.24%	701	0.16%	0.24%
Ramsey, MN	10.02%	8.98	138	0.40%	0.48%	57	0.98%	1.18%
San Francisco, CA	2.23%	43.80	89	0.13%	0.19%	164	0.07%	0.11%
Suffolk, MA	6.52%	14.34	101	0.11%	0.11%	64	0.17%	0.18%
Wayne, MI	0.86%	115.87	1246	1.74%	1.85%	5960	0.36%	0.39%
Median	3.66%	26.67	318.5	0.18%	0.24%	374.5	0.21%	0.27%

We estimate each counties’ death rate on March 13 using several measures of both the infection fatality rate and estimated infected. $\alpha$ is the estimated fraction of reported infections for each county accounting for an 8-day lag. $\frac{U}{R}=\frac{1-\alpha }{\alpha }$ gives the ratio of unreported to reported infections for that county, again accounting for the fact that observed reported infections have an 8 day lag. U-A gives the under-ascertainment rate on Mar 13 given by the total infected on Mar 13 (accounting for lag) divided by the reported infected on Mar 13. mIFR matches cohorts of infected using a log-normal fatality lag distribution to determine the death rate, and cIFR compares cumulative deaths 15 days later. All of these calculations are based estimating the number of total infected on March 13 by reported infected on March 21st divided by $\alpha$, to account for an 8-day reporting lag. National $\alpha$ is taken from Table A.4 full EU travel. County $\alpha$ uses each county’s individually computed $\alpha$ rather than the nationally computed $\alpha$. $<.01\text{\%}$ indicates positive numbers that round down to 0.00%.

A.3. Lags

We derive our model incorporating reporting lags in the Appendix and show how we get the estimating equations in Section 3.3.

Recall that we denote true infected, true reported infected, and true unreported infected in time $t$ and target city $i$ as $I_{i,t},R_{i,t},U_{i,t}$ respectively. Those for epicenter $c$ as $I_{c,t},R_{c,t},U_{c,t}$. Let $k$ be the lagged report period. At time $t$ city $i$ denote the lagged reported infected $L{R}_{i,t}=R_{i,t-k}$. For epicenter $c$, the lagged reported infected is $L{R}_{c,t}=R_{c,t-k}$.

Define reporting rate at city $i$ as $\alpha =\mathbb{E}\left(\frac{R_{i,t-k}}{I_{i,t-k}}|I_{i,t-k}\right)=\mathbb{E}\left(\frac{L{R}_{i,t}}{I_{i,t-k}}|I_{i,t-k}\right)$ and at epicenter $c$ as ${\alpha }_c=\frac{R_{c,t-k}}{I_{c,t-k}}=\frac{L{R}_{c,t}}{I_{c,t-k}}$. This means that we are considering the reporting rate of lagged reported cases on the lagged total infection.

We know that in the epicenter $c$, we have the following:

$$I_{c,t}=I_{c,0}exp\left(\beta (t-T_0)\right)$$ (A.1)

$$R_{c,t}={\alpha }_c{I}_{c,t}$$ (A.2)

$$U_{c,t}=(1-{\alpha }_c)I_{c,t}$$ (A.3)

$$=(1-{\alpha }_c)I_{c,0}exp\left(\beta (t-T_0)\right)$$ (A.4)

When only travel data is available, our Assumption 3.1 is

$$\frac{I_{i,t}^{inc}}{M_{i,t}}=\frac{U_{c,t}}{N_c-R_{c,t}}\text{for any time }t\in [T_0,T_1],\text{ region }i\text{ and epicenter }c$$ (A.5)

Applying Eq. (A.4) and solving for $I_{i,t}^{inc}$.

$$I_{i,t}^{inc}=\frac{M_{i,t}}{N_c-R_{c,t}}(1-{\alpha }_c)I_{c,0}exp\left(\beta (t-T_0)\right)$$ (A.6)

In city $i$, at time $T_1$ we observe $L{R}_{i,T_1}$. We have

$$I_{i,T_1-k}={\int }_{T_0}^{T_1-k}{I}_{i,t}^{inc}exp\left(\beta (T_1-k-t)\right)dt$$

$$L{R}_{i,T_1}=\alpha I_{i,T_1-k}+{ϵ}_{i,T_1}=\alpha {\int }_{T_0}^{T_1-k}{I}_{i,t}^{inc}exp\left(\beta (T_1-k-t)\right)dt+{ϵ}_{i,T_1}=\alpha {\int }_{T_0}^{T_1-k}\frac{M_{i,t}}{N_c-R_{c,t}}(1-{\alpha }_c)I_{c,0}exp\left(\beta (t-T_0)\right)exp\left(\beta (T_1-k-t)\right)dt+{ϵ}_{i,T_1}=\alpha (1-{\alpha }_c)I_{c,0}exp\left(\beta (T_1-T_0-k)\right){\int }_{T_0}^{T_1-k}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}=\alpha (1-{\alpha }_c)\frac{R_{c,0}}{{\alpha }_c}exp\left(\beta (T_1-T_0-k)\right){\int }_{T_0}^{T_1-k}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}=\alpha \frac{1-{\alpha }_c}{{\alpha }_c}exp\left(\beta (T_1-T_0-k)\right)L{R}_{c,k}{\int }_{T_0}^{T_1-k}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}$$

For $\alpha ={\alpha }_c$, this equation simplifies to:

$$L{R}_{i,T_1}=(1-\alpha )exp\left(\beta (T_1-T_0-k)\right)L{R}_{c,k}{\int }_{T_0}^{T_1-k}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}$$ (A.7)

When both travel data and randomized testing data are available, we maintain Assumption 3.2:

$$\frac{I_{i,t}^{inc}}{M_{i,t}}=\gamma \frac{U_{c,t}}{N_c-R_{c,t}}\text{for any time }t\in [T_0,T_1]\text{, region }i\text{ and epicenter }c$$ (A.8)

We can write it as

$$I_{i,t}^{inc}=\gamma \frac{M_{i,t}}{N_c-R_{c,t}}(1-{\alpha }_c)I_{c,0}exp\left(\beta (t-T_0)\right)$$ (A.9)

In U.S. city $i$, at time $T_1$ we observe $L{R}_{i,T_1}$. Following the same derivation as above, we have

$$L{R}_{i,T_1}=\alpha \gamma \frac{1-{\alpha }_c}{{\alpha }_c}exp\left(\beta (T_1-T_0-k)\right)L{R}_{c,k}{\int }_{T_0}^{T_1-k}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}$$ (A.10)

A similar derivation shows that for region $j$ in Iceland at time $T_1$, we have

$$I_{j,T_1-k}=\gamma \frac{1-{\alpha }_c}{{\alpha }_c}exp\left(\beta (T_1-T_0-k)\right)L{R}_{c,k}{\int }_{T_0}^{T_1-k}\frac{M_{j,t}}{N_c-R_{c,t}}dt$$ (A.11)

We also consider an alternative definition of reporting rate, which is lagged reported cases as a fraction of current total infections, i.e. ${\tilde{\alpha }}_c=\frac{L{R}_{c,t}}{I_{c,t}}=\frac{R_{c,t-k}}{I_{c,t}}$ and $\tilde{\alpha }=\mathbb{E}\left(\frac{L{R}_{i,t}}{I_{i,t}}|I_{i,t}\right)=\mathbb{E}\left(\frac{R_{i,t-k}}{I_{i,t}}|I_{i,t}\right)$.

In epicenter, we have

$$I_{c,t}=I_{c,0}exp\left(\beta (t-T_0)\right)$$ (A.12)

$$R_{c,t}={\tilde{\alpha }}_c{I}_{c,t+k}$$ (A.13)

$$R_{c,t-k}={\tilde{\alpha }}_c{I}_{c,t}$$ (A.14)

$$R_{c,-k}={\tilde{\alpha }}_c{I}_{c,0}$$ (A.15)

$$U_{c,t}=I_{c,t}-R_{c,t}$$ (A.16)

$$=I_{c,t}-{\tilde{\alpha }}_c{I}_{c,t+k}$$ (A.17)

$$=I_{c,0}exp\left(\beta (t-T_0)\right)-{\tilde{\alpha }}_c{I}_{c,0}exp\left(\beta (t+k-T_0)\right)$$ (A.18)

When only travel data is available, our Assumption 3.1 is

$$\frac{I_{i,t}^{inc}}{M_{i,t}}=\frac{U_{c,t}}{N_c-R_{c,t}}\text{for any time }t\in [T_0,T_1]\text{, region }i\text{ and epicenter }c$$ (A.19)

Then we have

$$I_{i,t}^{inc}=\frac{M_{i,t}}{N_c-R_{c,t}}\left(I_{c,0}exp\left(\beta (t-T_0)\right)-{\tilde{\alpha }}_c{I}_{c,0}exp\left(\beta (t+k-T_0)\right)\right)$$ (A.20)

In target city, at time $T_1$, it is known that $\mathbb{E}\left(L{R}_{i,T_1}|I_{i,T_1}\right)=\tilde{\alpha }{I}_{i,T_1}$. We know

$$I_{i,T_1}={\int }_{T_0}^{T_1}{I}_{i,t}^{inc}exp\left(\beta (T_1-t)\right)dt$$

$$L{R}_{i,T_1}=\tilde{\alpha }{I}_{i,T_1}+{ϵ}_{i,T_1}=\tilde{\alpha }{\int }_{T_0}^{T_1}{I}_{i,t}^{inc}exp\left(\beta (T_1-t)\right)dt+{ϵ}_{i,T_1}=\tilde{\alpha }{\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}\left(I_{c,0}exp\left(\beta (t-T_0)\right)-{\tilde{\alpha }}_c{I}_{c,0}exp\left(\beta (t+k-T_0)\right)\right)exp\left(\beta (T_1-t)\right)dt+{ϵ}_{i,T_1}=\tilde{\alpha }{I}_{c,0}exp\left(\beta (T_1-T_0)\right){\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt-\tilde{\alpha }{\tilde{\alpha }}_c{I}_{c,0}exp\left(\beta (T_1-T_0+k)\right){\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}=\tilde{\alpha }\frac{R_{c,-k}}{{\tilde{\alpha }}_c}exp\left(\beta (T_1-T_0)\right){\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt-\tilde{\alpha }{\tilde{\alpha }}_c\frac{R_{c,-k}}{{\tilde{\alpha }}_c}exp\left(\beta (T_1-T_0+k)\right){\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}=\left(\frac{\tilde{\alpha }}{{\tilde{\alpha }}_c}exp\left(\beta (T_1-T_0)\right)-\tilde{\alpha }exp\left(\beta (T_1-T_0+k)\right)\right)R_{c,-k}{\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}=\tilde{\alpha }\left(\frac{1}{{\tilde{\alpha }}_c}exp\left(\beta (T_1-T_0)\right)-exp\left(\beta (T_1-T_0+k)\right)\right)R_{c,-k}{\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}=\tilde{\alpha }\left(\frac{1}{{\tilde{\alpha }}_c}exp\left(\beta (T_1-T_0)\right)-exp\left(\beta (T_1-T_0+k)\right)\right)L{R}_{c,0}{\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}$$

If $\tilde{\alpha }={\tilde{\alpha }}_c$, then $\alpha$ is identified conditional on $\beta$ and $k$.

When both travel data and randomized testing data are available, we maintain Assumption 3.2:

$$\frac{I_{i,t}^{inc}}{M_{i,t}}=\gamma \frac{U_{c,t}}{N_c-R_{c,t}}\text{for any time }t\in [T_0,T_1]\text{, region }i\text{ and epicenter }c$$ (A.21)

Then we have

$$I_{i,t}^{inc}=\gamma \frac{M_{i,t}}{N_c-R_{c,t}}\left(I_{c,0}exp\left(\beta (t-T_0)\right)-{\tilde{\alpha }}_c{I}_{c,0}exp\left(\beta (t+k-T_0)\right)\right)$$ (A.22)

For U.S. city $i$, we have

$$L{R}_{i,T_1}=\tilde{\alpha }\gamma \left(\frac{1}{{\tilde{\alpha }}_c}exp\left(\beta (T_1-T_0)\right)-exp\left(\beta (T_1-T_0+k)\right)\right)R_{c,-k}{\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}$$ (A.23)

$$=\tilde{\alpha }\gamma \left(\frac{1}{{\tilde{\alpha }}_c}exp\left(\beta (T_1-T_0)\right)-exp\left(\beta (T_1-T_0+k)\right)\right)L{R}_{c,0}{\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt+{ϵ}_{i,T_1}$$ (A.24)

In Iceland region $j$ time $T_1$, we can compute $I_{j,T_1}$. We have

$$I_{j,T_1}={\int }_{T_0}^{T_1}{I}_{j,t}^{inc}exp\left(\beta (T_1-t)\right)dt={\int }_{T_0}^{T_1}\gamma \frac{M_{j,t}}{N_c-R_{c,t}}\left(I_{c,0}exp\left(\beta (t-T_0)\right)-{\tilde{\alpha }}_c{I}_{c,0}exp\left(\beta (t+k-T_0)\right)\right)exp\left(\beta (T_1-t)\right)dt=\gamma \left(exp\left(\beta (T_1-T_0)\right)-{\tilde{\alpha }}_{c}exp\left(\beta (T_1-T_0+k)\right)\right)I_{c,0}{\int }_{T_0}^{T_1}\frac{M_{j,t}}{N_c-R_{c,t}}dt=\gamma \left(exp\left(\beta (T_1-T_0)\right)-{\tilde{\alpha }}_{c}exp\left(\beta (T_1-T_0+k)\right)\right)\frac{R_{c,-k}}{{\tilde{\alpha }}_c}{\int }_{T_0}^{T_1}\frac{M_{j,t}}{N_c-R_{c,t}}dt=\gamma \left(\frac{1}{{\tilde{\alpha }}_c}exp\left(\beta (T_1-T_0)\right)-exp\left(\beta (T_1-T_0+k)\right)\right)R_{c,-k}{\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt=\gamma \left(\frac{1}{{\tilde{\alpha }}_c}exp\left(\beta (T_1-T_0)\right)-exp\left(\beta (T_1-T_0+k)\right)\right)L{R}_{c,0}{\int }_{T_0}^{T_1}\frac{M_{i,t}}{N_c-R_{c,t}}dt$$

Estimating the last equation gives consistent estimate of

$$\gamma \left(\frac{1}{{\tilde{\alpha }}_c}exp\left(\beta (T_1-T_0)\right)-exp\left(\beta (T_1-T_0+k)\right)\right)L{R}_{c,0}$$

and estimating Eq. (A.24) gives

$$\tilde{\alpha }\gamma \left(\frac{1}{{\tilde{\alpha }}_c}exp\left(\beta (T_1-T_0)\right)-exp\left(\beta (T_1-T_0+k)\right)\right)L{R}_{c,0}$$

Taking the ratio, we are left with $\tilde{\alpha }$.

A.4. Heterogeneous transmission rates

In this section, we show how our model can be modified to allow for different transmission rate $\beta$ among target cities and epicenter. Transmission rate of virus could be different across locations due to population density or other reasons (Sajadi et al., 2020). Our identification strategy in Section 3.2 relies on the assumption that transmission rates across Iceland and U.S. are the same. We will relax this assumption in this section. We will be able to capture differential transmission rate through the variation in virus evolution trends across locations, controlling for travel.

Let ${\beta }_c$ be the transmission rate in epicenter, ${\beta }_i$ rate for U.S. city $i$ and ${\beta }_j$ rate for Iceland city $j$. Define ${\tilde{\beta }}_i={\beta }_i-{\beta }_c$ and ${\tilde{\beta }}_j={\beta }_j-{\beta }_c$ as relative transmission rates for U.S. and Iceland. Maintaining Assumption 3.2, for any U.S. city $i$ end period $T_1$ we have

$$R_{i,T_1}=\alpha {\int }_{T_0}^{T_1}{I}_{i,t}^{inc}exp\left({\beta }_i(T_1-t)\right)dt$$ (A.25)

$$I_{i,t}^{inc}=\gamma \frac{(1-{\alpha }_c)I_{c,0}exp\left({\beta }_c(t-T_0)\right)}{N_c-R_{c,t}}{M}_{i,t}$$ (A.26)

Therefore, for U.S. city $i$ we have:

$$R_{i,T_1}=\alpha {\int }_{T_0}^{T_1}\frac{(1-{\alpha }_c)\gamma I_{c,0}exp\left({\beta }_c(t-T_0)\right)}{N_c-R_{c,t}}{M}_{i,t}exp\left({\beta }_i(T_1-t)\right)dt$$ (A.27)

$$=\alpha \frac{1-{\alpha }_c}{{\alpha }_c}{R}_{c,0}\gamma {\int }_{T_0}^{T_1}exp\left({\beta }_c(t-T_0)\right)exp\left({\beta }_i(T_1-t)\right)\frac{M_{i,t}}{N_c-R_{c,t}}dt$$ (A.28)

$$=\alpha \frac{1-{\alpha }_c}{{\alpha }_c}{R}_{c,0}\gamma exp({\beta }_i{T}_1-{\beta }_c{T}_0){\int }_{T_0}^{T_1}exp\left(t({\beta }_c-{\beta }_i)\right)\frac{M_{i,t}}{N_c-R_{c,t}}dt$$ (A.29)

Similarly, for Iceland city $j$ we have:

$$I_{j,T_1}=\frac{1-{\alpha }_c}{{\alpha }_c}{R}_{c,0}\gamma exp({\beta }_j{T}_1-{\beta }_c{T}_0){\int }_{T_0}^{T_1}exp\left(t({\beta }_c-{\beta }_j)\right)\frac{M_{j,t}}{N_c-R_{c,t}}dt$$ (A.30)

Take logs and differencing, we get

$$log{R}_{i,T_1}-log{I}_{j,T_1}=log\alpha +({\beta }_i-{\beta }_j)T_1+log{\int }_{T_0}^{T_1}exp\left(t({\beta }_c-{\beta }_i)\right)\frac{M_{i,t}}{N_c-R_{c,t}}dt-log{\int }_{T_0}^{T_1}exp\left(t({\beta }_c-{\beta }_j)\right)\frac{M_{j,t}}{N_c-R_{c,t}}dt=log\alpha +({\tilde{\beta }}_i-{\tilde{\beta }}_j)T_1+log{\int }_{T_0}^{T_1}exp(-t{\tilde{\beta }}_i)\frac{M_{i,t}}{N_c-R_{c,t}}dt-log{\int }_{T_0}^{T_1}exp(-t{\tilde{\beta }}_j)\frac{M_{j,t}}{N_c-R_{c,t}}dt$$

Assume that we observe $log{R}_{i,t}$ and $log{I}_{j,t}$ with idiosyncratic measurement error ${\eta }_{i,t}$ and ${\eta }_{j,t}$ with $\mathbb{E}\left({\eta }_{.,t}\right)=0$. Denote these observations as $log{\hat{R}}_{i,t}$ and $log{\hat{I}}_{j,t}$. Let $u_{i,j,t}={\eta }_{i,t}-{\eta }_{j,t}$, so $u_{i,j,t}$ is also iid.

$$log{\hat{R}}_{i,T_1}-log{\hat{I}}_{j,T_1}=log{R}_{i,T_1}-log{I}_{j,T_1}+{\eta }_{i,T_1}-{\eta }_{j,T_1}=log{R}_{i,T_1}-log{I}_{j,T_1}+u_{i,j,T_1}=log\alpha +(\widetilde{{\beta }_i}-\widetilde{{\beta }_j})T_1+log{\int }_{T_0}^{T_1}exp(-\widetilde{{\beta }_i}t)\frac{M_{i,t}}{N_c-R_{c,t}}dt-log{\int }_{T_0}^{T_1}exp(-\widetilde{{\beta }_j}t)\frac{M_{j,t}}{N_c-R_{c,t}}dt+u_{i,j,T_1}$$

With a $k$ period lag, we have for U.S. city $i$:

$$L{R}_{i,T_1}=\alpha {\int }_{T_0}^{T_1-k}\frac{(1-{\alpha }_c)\gamma I_{c,0}exp\left({\beta }_c(t-T_0)\right)}{N_c-R_{c,t}}{M}_{i,t}exp\left({\beta }_i(T_1-k-t)\right)dt=\alpha \frac{1-{\alpha }_c}{{\alpha }_c}{R}_{c,0}\gamma {\int }_{T_0}^{T_1-k}exp\left({\beta }_c(t-T_0)\right)exp\left({\beta }_i(T_1-k-t)\right)\frac{M_{i,t}}{N_c-R_{c,t}}dt=\alpha \frac{1-{\alpha }_c}{{\alpha }_c}{R}_{c,0}\gamma exp({\beta }_i(T_1-k)-{\beta }_c{T}_0){\int }_{T_0}^{T_1-k}exp\left(t({\beta }_c-{\beta }_i)\right)\frac{M_{i,t}}{N_c-R_{c,t}}dt$$

Similarly, for Iceland city $j$ we have:

$$I_{j,T_1-k}=\frac{1-{\alpha }_c}{{\alpha }_c}{R}_{c,0}\gamma exp({\beta }_j(T_1-k)-{\beta }_c{T}_0){\int }_{T_0}^{T_1-k}exp\left(t({\beta }_c-{\beta }_j)\right)\frac{M_{j,t}}{N_c-R_{c,t}}dt$$

Take logs and differencing, we get

$$logL{R}_{i,T_1}-log{I}_{j,T_1-k}=log\alpha +({\beta }_i-{\beta }_j)(T_1-k)+log{\int }_{T_0}^{T_1-k}exp\left(t({\beta }_c-{\beta }_i)\right)\frac{M_{i,t}}{N_c-R_{c,t}}dt-log{\int }_{T_0}^{T_1-k}exp\left(t({\beta }_c-{\beta }_j)\right)\frac{M_{j,t}}{N_c-R_{c,t}}dt=log\alpha +({\tilde{\beta }}_i-{\tilde{\beta }}_j)(T_1-k)+log{\int }_{T_0}^{T_1-k}exp(-t{\tilde{\beta }}_i)\frac{M_{i,t}}{N_c-R_{c,t}}dt-log{\int }_{T_0}^{T_1-k}exp(-t{\tilde{\beta }}_j)\frac{M_{j,t}}{N_c-R_{c,t}}dt$$

Taking into account measurement error, we have

$$log{\widehat{LR}}_{i,T_1}-log{\hat{I}}_{j,T_1-k}=log\alpha +(\widetilde{{\beta }_i}-\widetilde{{\beta }_j})(T_1-k)+log{\int }_{T_0}^{T_1-k}exp(-\widetilde{{\beta }_i}t)\frac{M_{i,t}}{N_c-R_{c,t}}dt-log{\int }_{T_0}^{T_1-k}exp(-\widetilde{{\beta }_j}t)\frac{M_{j,t}}{N_c-R_{c,t}}dt+u_{i,j,T_1-k}$$

When we consider multiple epicenters $\ell \in L$, the estimating equation becomes:

$$log{\widehat{LR}}_{i,T_1}-log{\hat{I}}_{j,T_1-k}=log\alpha +(\widetilde{{\beta }_i}-\widetilde{{\beta }_j})(T_1-k)+log{\int }_{T_0}^{T_1-k}\left(\sum _{\ell \in L}\frac{L{R}_{c,k}^{\ell }{M}_{i,t}^{\ell }}{N_c^{\ell }-R_{c,t}^{\ell }}\right)exp(-\widetilde{{\beta }_i}t)dt-log{\int }_{T_0}^{T_1-k}\left(\sum _{\ell \in L}\frac{L{R}_{c,k}^{\ell }{M}_{j,t}^{\ell }}{N_c^{\ell }-R_{c,t}^{\ell }}\right)exp(-\widetilde{{\beta }_j}t)dt+u_{i,j,T_1-k}$$

We parameterize transmission rate as linear in urban population density, and an indicator for social distancing. We can then estimate the equations above with nonlinear least squares pooling different end period $T_1$. We consider European Epicenters as well as China. Because our data only contains constant travel, terms that appear in both ${\beta }_i$ as well as ${\beta }_j$ are very difficult to estimate. In particular, the constant term is very difficult to estimate, and not identified for very large magnitudes. This problem occurs because with constant travel, infected arrivals vary over time only with $R_{c,t}$, which causes very minor changes in arrivals. This makes time-variation of the same cities provide little identification in $\beta$.

To circumvent these issues, we attempted to estimate ${\beta }_j$ separately using differences in infected in Iceland over time, however since travel is still constant for Iceland, the same identification problems were present. We estimate a difference in $\beta$ of $.06$, indicating that in 10 days infections in the United States will double one more time than in Iceland. However, we note that our $\alpha$ estimate is biased downwards because of travel data, and this leads to an upward bias on beta. We consider this to be an upper bound on the difference in $\beta$ between the two countries. With further investigation and better travel data, we believe that this framework can be used to identify the spread of infection with different infection rates.

This strategy is better than naively studying growth rates of infected between countries because it accounts for the origin of the infection: travelers from infected epicenters. While the infection is spreading within the country, it is not isolated, and there are continual arrivals from the epicenter that are also spreading the infection, failing to take into account these arrivals will lead to estimates of the spread of infection being too high in the early stages of the progression of the virus.20