Multi-disciplinary planning in health care: a review

Abstract

Multi-disciplinary planning in health care is an emerging research field that applies to many health care areas with similar underlying planning characteristics. We provide a review of the literature and describe cross-relations between different applications. We identify multiple fields to classify the literature upon. These fields relate to the system characteristics, decision characteristics, and applicability. The relevant papers for each of these fields are discussed, which provides a broad and thorough overview of the present research, and guides readers towards identifying the applicable literature for their research based on the characteristics of their problem. Furthermore, we disclose research gaps and present open challenges for further research.

1. Introduction

Coordinating multi-disciplinary care is becoming increasingly important. As patients get more complex diseases and co-morbidities, the need for coordinated care over multiple departments increases (Mutlu, Benneyan, Terrell, Jordan, & Turkcan, 2015). Treatments are more and more organised as a combination of care from various disciplines or different facilities (Vanberkel, Boucherie, Hans, Hurink, & Litvak, 2009). Furthermore, patients increasingly demand efficient care which is well-organised and suited to their needs. All these trends ask for an integrated approach, in which multiple disciplines together organise and optimise the patients’ care pathways. This review focuses on optimisation and evaluation approaches for multi-disciplinary systems.

We define a multi-disciplinary care system as a care system in which multiple interrelated appointments per patient are scheduled, where health care professionals from various facilities or with different skills are involved.

This review originated from the finding that planning problems in rehabilitation treatment and cancer diagnostics turn out to be quite similar from a mathematical point of view. In rehabilitation treatment, a patient requires appointment series with therapists from multiple disciplines, for example a physiotherapist, a psychologist and a dietician. Furthermore, there might be precedence relations between some of the appointments, for example if physiotherapy training is required after a prosthesis has been made. Since outpatients usually have to travel far to reach the clinic and since they do not want to travel each day of the week, the challenge is to schedule as many appointments as possible on the same day, with minimal waiting time. In cancer diagnostics, patients with a possible tumour arrive to the hospital, and need several diagnostic tests before a diagnosis can be given, such as an intake consultation, imaging, a blood withdrawal, and a biopsy. Some of these tests have precedence relations, but others can take place at any moment. The challenge on how to schedule these appointments, preferably on one day, with as little waiting time as possible, is similar to the challenge in the rehabilitation setting. In Section 2 we show that these so-called cross-relations are not only present for rehabilitation and cancer care, but for many health care settings. Since the underlying systems show similar characteristics, there is ample room for cross-fertilisation between multi-disciplinary environments in health care.

The organisation and optimisation of health care processes got the attention from Operations Management/Operations Research (OM/OR) researchers in the past years. Especially, the situation in which patients require a single appointment within a single discipline is well studied (Ahmadi-Javid, Jalali, & Klassen, 2017). Although there are several good literature reviews on appointment planning in health care (e.g., Ahmadi-Javid et al., 2017; Berg & Denton, 2012; Cayirli & Veral, 2003; Gupta & Denton, 2008), these reviews do not include multi-disciplinary planning. Vanberkel et al. (2009) reviewed the literature and showed that few studies focused on multiple hospital departments. They reviewed literature on both operations research and clinical pathways, from which the first included several works on multi-disciplinary planning. Marynissen and Demeulemeester (2016) reviewed the integrated systems literature, but only included hospital settings. We focus on a broad health care context, which, for example, also includes blood collection sites and nursing homes.

Multi-disciplinary planning is more challenging than single appointment planning, or multi-appointment planning for a single discipline. From a mathematical perspective, there are more constraints that should be simultaneously taken into account, such as precedence relations between appointments of a variety of resources and the availability of resources from various disciplines. Furthermore, through the increasing number of resources, many planning problems encounter a large state space and decision space. Lastly, similar to supply chain management systems, the bullwhip effect is often present in multi-disciplinary systems, since the various involved disciplines do not use the same information. Variability that occurs in early stages of a patient’s care pathway, impacts the possible efficiency in later stages, something that may be relevant when scheduling multi-disciplinary systems.

The multi-disciplinary planning problem in health care consists of the following components:

1. Appointment characteristics: This includes the type of appointments and the resources that are required for each of these appointments. This might also include restrictions on whether patients should be treated by the same doctor or therapist during their care pathway.

2. Resource characteristics: This includes the number of resources, the discipline or skill of each resource, capacity constraints and the (non-)renewable nature of these resources.

3. Care pathway characteristics: This includes the number of patient types, the number and type of appointments required for a certain patient type and the urgency (e.g., emergency) of a patient type. Furthermore, it contains precedence constraints and time constraints that may apply to all or some of the required appointments, and states whether the appointment sequence can be changed during the treatment and if patients can recirculate in some parts of the care pathway.

4. Objective: This includes the model objective, or set of objectives.

5. Planning characteristics: This includes the planning decision, which is either to dimension capacity, to plan capacity, or to allocate capacity to patients. This last setting also includes the decision whether appointment requests are planned immediately at arrival of the patient (online planning), or can be saved up to be scheduled once per time period (offline planning).

6. Environmental characteristics: This includes the (non) punctuality of patients and health care providers, the in- or exclusion of patient no-shows and cancellations, and the admission policy of patient types (e.g., is it allowed to reject patients?).

 

1.1. Focus of the review

The aim of this review is twofold. First, we provide the reader with an overview of multi-disciplinary planning and scheduling literature in the health care context, including the recent developments, which helps to guide further research on multi-disciplinary appointment planning and scheduling. Second, we structure the available literature based on multiple characteristics, such that researchers can easily find literature with similarities to their projects. This facilitates the comparison and cross-fertilisation of approaches, as similar systems are identified.

The focus of this review is on prescriptive techniques which improve and optimise multi-disciplinary appointment systems. Prescriptive techniques include exact and approximate optimisation studies, and evaluation studies, for example using simulation, which are all included in this review. We excluded descriptive and predictive approaches, which include hypothesis testing and forecasting techniques respectively.

Multiple research areas are excluded from this review. First, capacity dimensioning is not included in this review, as decisions for multi-disciplinary planning on this level are similar to these of systems where just single appointments or one discipline are involved. Multi-disciplinary capacity dimensioning involves decision-making over a long planning horizon and is based on highly aggregated information. Therefore, it is not necessary to take multi-disciplinary planning constraints into account, such as constraints on resource availability, precedence constraints and interrelatedness of disciplines and appointments to make capacity dimensioning decisions. More information on capacity planning can be found in Hulshof, Kortbeek, Boucherie, Hans, and Bakker (2012) or in the recent review of Ahmadi-Javid et al. (2017).

Second, we do not consider personnel planning other than for capacity-to-patient assignment decisions, as personnel planning does not have different characteristics for multi-disciplinary systems than for mono-disciplinary systems. More information about personnel planning can be found in Bergh, Beliën, De Bruecker, Demeulemeester, and De Boeck (2013).

Third, at the capacity-to-patient level, we only consider appointment planning systems in which interrelated appointments can be planned separately. An example of a multi-appointment planning system that is not included is Condotta and Shakhlevich (2014), who plan multiple chemotherapy appointments which need to follow a specific cyclic pattern. Note that research considering the planning of chemotherapy drug injections in relation to a consult with the oncologist, and the drugs preparation in the pharmacy, is included in this review, because multiple disciplines (e.g., the pharmacy and the oncologists) are planned simultaneously.

We started our search with the review of Vanberkel et al. (2009), as well as those of Ahmadi-Javid et al. (2017) and Hulshof et al. (2012), as these studies include multi-disciplinary appointment planning research in health care. Furthermore, we searched the databases Web of Knowledge and Scopus for relevant papers, using combinations of relevant keywords, such as appointment planning, scheduling, multi-disciplinary, one-stop-shop, rapid diagnostics, calendar planning, flow shop, open shop, and flexible shop. For any article found, we performed a forward and backward search to find additional manuscripts. We limit the review to papers that are written in English and are published before 1 January 2017. The search procedure resulted in a set of 63 articles, which are all classified in the Orchestra database (www.choir-ut.nl).

As multi-disciplinary scheduling is an emerging research area, standardised terminology is not yet present, and various terms are used in the literature. The Appendix A1 provides a list with all terminology used in this review, together with its definitions.

1.2. Structure of the review

To identify cross-relations, we start this survey with a description of the health care applications in multidisciplinary planning in Section 2. Following Beliën and Forcé (2012) and Cardoen, Demeulemeester, and Beliën (2010), the remainder of this literature review is based on different perspectives to analyse all included articles. In this way, a researcher can query a list of papers according to specific needs and interests. These so-called classification fields are descriptive, and include problem characteristics, solution characteristics, and system

We consider the following classification fields:

1. Decision delineation/hierarchical level (Section 3): reviewing the literature based on various planning decisions, at various hierarchical levels.

2. System characteristics (Section 4): reviewing the literature based on precedence constraints included in the problem context (flow-shop, open-shop, and mixed shop systems).

3. Variability (Section 5): reviewing the literature based on the incorporation of uncertainty and variability.

4. Generality and applicability (Section 6): reviewing the literature based on the scientific impact (benchmarking) and the impact in practice (case studies, implementation).

Each section starts with a short description of the classification field and the distinct areas on which manuscripts are differentiated. Furthermore, the relevant literature in each of these areas is discussed, and a table is provided to categorise manuscripts in this classification field. This review ends with Section 7, which provides a conclusion and open research challenges.

2. Health care applications

A holistic view is essential for optimising the care chain from a patient and provider perspective. In the literature, we see that multi-disciplinary planning is increasingly introduced in health care settings. In Section 2.1 we explore the motivation behind the implementation of multi-disciplinary care, as multi-disciplinary systems are well represented in the medical literature. We identify several application areas and cross-relations in Section 2.2. We conclude with directions for further research in Section 2.3.

2.1. Motivation for organising multi-disciplinary care

There are several reasons for health care systems to introduce multi-disciplinary care in their systems. The first and most heard argument is to provide patient-centred care. Therefore, hospitals focus on improvements in patient satisfaction (Litton et al., 2010) and quality of care. Patient satisfaction is quantitatively measured in terms of access time (Goodridge, Woodhouse, & Barbour, 2013), and waiting and throughput times (Arnaout et al., 2013; Geer et al., 2012; Sorensen et al., 2014). A general pattern is observed that most multi-disciplinary systems in the medical literature are focused towards providing all consultations on a single day. Quality of care is, for example, measured in number of changes in prescriptions or diagnoses, and adverse outcomes (Fleissig, Jenkins, Catt, & Fallowfield, 2006; Geerlings et al., 2016), as more coordination between clinicians is believed to result in fewer mistakes and more first-time-right diagnoses (Fleissig et al., 2006; Geer et al., 2012).

The second reason for health care systems to introduce multi-disciplinary care, is the structure it provides to the system. The implementation of multi-disciplinary care is a means to force coordination between various health care units, and enables to focus on a specific group of patients (Mruşter, Weijters, de Vries, van den Bosch, & Daelemans, 2002).

To facilitate structure in health care settings, easily adoptable tools are preferred. Therefore, researchers should include this requirement in the design of multi-disciplinary planning tools, such as planning software or decision rules. Simple planning solutions are most often the easiest to implement and understand for the health care staff that has to work with the tools. This way, structure and coordination can be provided, together with an increased planning efficiency.

A third reason to introduce multi-disciplinary care, is to facilitate a new clinical practice, which involves clinicians from multiple specialties, such as an intake for ambulatory Huntington’s disease patients (Veenhuizen et al., 2011), or the follow-up for children with neuromuscular diseases (Kortbeek, van der Velde, & Litvak, 2017). Under these circumstances, it is hard to compare the performance of the new system design against practice, as the initial performance does not reflect the performance of the new system. Researchers are, therefore, challenged to show that their design will perform well in practice, compared to other reasonable design options.

2.2. Application areas

Multi-disciplinary systems are present in a variety of health care settings. In this section, we show that multi-disciplinary care knows many applications, and that the organisation of this care, and more specifically the relevant underlying characteristics, show similarities. We found the following application areas:

1. Outpatient and day care clinics

2. Cancer clinics

3. Rehabilitation clinics

4. Emergency patient care

5. Elective patient care

6. Care processes without a patient present

7. Blood collection sites

Outpatient and day care clinics provide non-overnight care for patients. A trend recently introduced in these clinics is to organise care in a patient-centred way. This can facilitate personalised diagnostics and treatment, and increases patient satisfaction. The concept of a flow-shop, where multiple consecutive consultations are offered, is therefore often seen in outpatient and day care clinics, especially for patients with regular checkups, or when patients need an intake or diagnostics (Geerlings et al., 2016; Veenhuizen & Tibben, 2009; Veenhuizen et al., 2011). Geerlings et al. (2016) describes an epilepsy transition outpatient clinic, where staff from multiple disciplines consult patients. Not only single provider consultations, but also consultations with multiple providers at the same time are offered. The clinic operates as a flow-shop, in which all consultations are consecutively scheduled, such that the waiting time for patients is minimised, followed by a diagnostic work-up if needed. Veenhuizen and Tibben (2009) and Veenhuizen et al. (2011) designed an outpatient clinic to facilitate patients with Huntington’s disease with an individual treatment plan. Here, all relevant care providers will see a patient in a predefined order during a visit to the outpatient department. A chemotherapy day care clinic also requires involvement of multiple departments in the treatment of patients. As the planning of the drug preparation by the pharmacy and the drug injection by the nurses should be well-coordinated, an integrated perspective is required in planning the chemotherapy appointments (Lamé, Jouini, & Stal-Le Cardinal, 2016). Other examples of multi-disciplinary outpatient and day care clinics can be found in cancer diagnostics (Geer et al., 2012), neurology (Goodridge et al., 2013), nuclear medicine (Pérez, Ntaimo, Malavé, Bailey, & McCormack, 2013) and ophthalmology (Lin, 2015).

A patient in a cancer clinic needs a diagnosis, personalised treatment plan, and treatment. As many specialties are involved in the diagnostic trajectory of a cancer patient, the treatment opportunities are discussed with a variety of disciplines during a multi-disciplinary meeting. Nowadays, hospitals realise that not only the treatment plan should be developed by a multi-disciplinary team, but also that the patients want to meet this team, and receive all relevant information for their treatment from this team (Litton et al., 2010). Therefore, multi-disciplinary clinics are designed, in which a patient can meet with any relevant clinician for their treatment, as well as with other providers such as psychologists, dieticians, and social workers if needed. The challenge in the organisation of these clinics is that patients only need to consult a subset of clinicians from a multi-disciplinary clinician pool, whereby this subset is known at a very late moment in time and should get a consultation within a small time frame (Leeftink, Vliegen, & Hans, 2017).

In a rehabilitation clinic, patients with various movement disorders are treated. The rehabilitation treatment consists of appointment series with therapists from various disciplines during several weeks or months, coordinated by a rehabilitation physician. Once every several weeks, the physician and all involved therapists discuss the progress and possible adjustments in the treatment. Scheduling the appointments is challenging, as patients prefer to combine several treatments on one day, while they have fixed therapists for every discipline. In the organisation of these treatment pathways challenges are, amongst others, the continuity of the care process, a simultaneous start for all disciplines and a short access time (Braaksma, Kortbeek, Post, & Nollet, 2014).

Emergency patient care considers patients that need (semi-)acute care. To triage and diagnose these patients, they often need multiple tests, which can be performed in various orders, represented by an open-shop or mixed shop system. Multi-disciplinary planning is involved on an online decision level, not only with respect to the timing of the tests, but also to the sequence of the tests (Azadeh, Farahani, Torabzadeh, & Baghersad, 2014).

Elective patient care considers patients that need a planned intervention, such as surgery. Multi-disciplinary planning is done at several levels for this patient population. First, the relation between the outpatient clinics, the operating room, and the wards is relevant. Capacity shortage in one area, may lead to waiting lists or emptiness in other areas. Second, inpatient care services for hospitalised patients require efficient planning when diagnostic tests and treatments are required from multiple departments (Conforti, Guerriero, Guido, Cerinic, & Conforti, 2011). In this case, it is important to minimise a patient’s length of stay, as each occupied bed blocks the access to care for another patient. Finally, multi-disciplinary planning can be approached from an opposite direction. Instead of a patient that has to visit multiple types of providers, a provider has to visit multiple types of patients. For example in patient-to-nurse scheduling at the wards, which can be represented by an open-shop system, time constraints are restricting the possible schedules (Cheng, Ozaku, Kuwahara, Kogure, & Ota, 2008).

In most care processes without a patient present, such as laboratories and sterilisation plants, patients are processed in a fixed activity sequence, where various resources are required for the activities (Leeftink, Boucherie, Hans, Verdaasdonk, Vliegen, & van Diest, 2016a; Rossi, Puppato, & Lanzetta, 2013). Applications from the laboratory, and, on a higher level from the process industry underlying the laboratory process optimisation research, can be used in optimising outpatient clinics. However, the difference between an outpatient clinic and a laboratory is the level of variability on the capacity-to-patient assignment level. Where laboratories are highly automated, and therefore have activities that are well predictable, patient consultations are provided by people. Therefore, laboratories experience less variability in the activity duration.

Blood collection sites are flow-shop type systems with even more variability, as not only variability in activity duration, but also variability in donor arrival has to be taken into account. In line with the laboratory, blood collection from donors requires a fixed series of activities. These activities are often performed by the same staff, but in some countries, such as France, multiple different providers are required since the various activities have to be carried out by certified staff members. In these cases, the design of a blood collection system requires a multi-disciplinary appointment planning approach. As blood donations are often voluntary, high service levels are required to ensure satisfied donors. Therefore, the donor flow through the system needs to be well designed, and matched with the staffing requirements (Alfonso, Xie, Augusto, & Garraud, 2012).

Cross-relations between the various application areas are rarely reported upon. However, five manuscripts are presented in a generic way, without one specific application area mentioned. Villa, Prenestini, and Giusepi (2014) analyse the patient flow through a hospital, which is applicable to the emergency and elective patient flow. Vermeulen et al. (2008) and Vlah, Lukač & Pacheco (2011) consider the scheduling of multiple appointments for multiple patients of various patient types on the same day, a problem which is relevant to the rehabilitation clinics, cancer clinics, and for example ward scheduling. Barz and Rajaram (2015) and Hulshof, Boucherie, Hans, and Hurink (2013) consider an elective patient admission problem with multiple resource requirements and constraints. This is for example applicable to outpatient clinics, cancer clinics, and the planning of the elective patient care chain. Barz and Rajaram (2015) present a case study of a neurosurgery department, to show the applicability of their method, whereas (Hulshof et al., 2013) apply their approach to generated data, representing many different health care settings.

2.3. Conclusions and further research

Multi-disciplinary care systems are present throughout the hospital, from outpatient clinics to laboratories. They are introduced for several reasons, including improved patient centeredness, improved structure and coordination, and to facilitate clinical improvements.

Despite the different application areas, design and optimisation insights can be gained by comparing the underlying planning decisions in these areas. However, crossovers are rarely reported upon, as until now new methods are frequently developed for one specific application area. This offers many opportunities for further research, as a general method that can be applied to several application areas with good performance is of great value to health care professionals.

As an example, insights from the research on the planning of outpatient clinics and cancer clinics with variable resource requirements, such as clinics where patients may need immediate extra tests depending on the results of previous testing Leeftink et al. (2017), are also relevant for treatment planning, for example in a rehabilitation setting. Both application areas can benefit from research into the question on how to deal with an unknown patient pathway and unknown need of resources.

A second example is the question on how to minimise the length of stay for patients. This question is relevant for inpatient care planning, by planning several diagnostic tests and treatments over a couple of days. This question is also relevant for rapid diagnostic trajectories, where cancer patients need to be provided with a diagnosis as fast as possible. Both these areas could therefore benefit from each other, via cross-relations and shared research results.

Most reported application areas are located within a hospital. Multi-disciplinary health care areas outside hospitals are interesting areas for further research. Examples are blood and transplant management, transmural care, home care, and nursing homes. Again, these application areas have similar questions and a similar structure as known multi-disciplinary systems. Blood collection sites for example share commonalities with laboratories and outpatient clinics, and nurses in a home care environment need the same type of planning as nurses in wards.

3. Hierarchical level

Multi-disciplinary planning can be considered at different hierarchical levels:

1. Capacity dimensioning (long-term)

2. Capacity planning (mid-term)

3. Capacity-to-patient assignment (short-term)

Capacity dimensioning involves decision making over a long planning horizon and is based on highly aggregated information. As described in Section 1, capacity dimensioning is not included in this paper, since decisions on this level are similar to mono-disciplinary systems. More information and articles on capacity dimensioning decisions can be found in Hulshof et al. (2012) or in the recent review of Ahmadi-Javid et al. (2017).

Capacity planning specifies the results of capacity dimensioning decisions into a division of the resource capacity to patient groups or time slots (Hans, Herroelen, Leus, & Wullink, 2007). In this way, blueprints for the capacity-to-patient assignment are created in which resources are allocated to different tasks, specialties and patient groups. Patient admission policies and temporary capacity expansions such as using overtime or hiring staff are also part of capacity planning.

Capacity-to-patient assignment involves the appointment planning at the individual patient level (Hulshof et al., 2012). Following the blueprints, a date, time, and resources are allocated to a specific patient.

Note that the decision horizon lengths are not explicitly given for any of the planning levels, since these depend on the specific characteristics of the application. For example, in a one-stop-shop diagnostic setting, horizons will be shorter than in rehabilitation care where treatments take several months.

We found 19 papers on capacity planning, which are described in Section 3.1. Furthermore, we found 49 papers on capacity-to-patient assignment, as described in Section 3.2. Section 3.3 concludes and provides opportunities for further research. Table 1 gives an overview of the papers and categories.

Table 1.

Hierarchical level.

Hierarchical level	Focus	References
Capacity planning	Blueprint schedule	Bikker et al. (2015), Dharmadhikari and Zhang (2011), Lebcir et al. (2017), Leeftink et al. (2016a), Leeftink et al. (2017), Liang et al. (2015), Mutlu et al. (2015), Oh et al. (2014), Oh et al. (2013), Proctor et al. (2007), Qu et al. (2013), Vrugt et al. (2017), Zonderland et al. (2015)
	Patient admission planning	Barz and Rajaram (2015), Conforti et al. (2011), Hulshof et al. (2013), Hulshof et al. (2016), Kortbeek et al. (2017), Romero et al. (2013)
	Temporary capacity changes	Hulshof et al. (2013)
Capacity-to-patient assignment	Offline scheduling	Azadeh et al. (2014), Castro and Petrovic (2012), Cheng et al. (2008), Chern et al. (2008), Chien, Tseng et al. (2008), Chien, Huang et al. (2008), Conforti et al. (2011), Cordier and Riane (2013), Du et al. (2013), Froehle and Magazine (2013), Gartner and Kolisch (2014), Hu et al. (2009), Jerić and Figueira (2012), Leeftink et al. (2016a), Lin (2015), Matta (2009), Matta and Elmaghraby (2010), Pérez et al. (2013), Petrovic et al. (2013), Podgorelec and Kokol (1997), Raschendorfer and Hamacher (2014), Rossi et al. (2013), Saadani et al. (2014), Sadki et al. (2011), Saremi et al. (2015), Schimmelpfeng et al. (2012), Shin et al. (2010), Kortbeek et al. (2017), Vlah et al. (2011), Zhao et al. (2015)
	Online scheduling	Aslani and Zhang (2014), Azadeh et al. (2015), Barz and Rajaram (2015), Braaksma et al. (2014), Cardoen and Demeulemeester (2008), Day et al. (2010), Dharmadhikari and Zhang (2011), Hahn-Goldberg et al. (2014), Kalton et al. (1997), Kapamara et al. (2007), Liang et al. (2015), Matta and Patterson (2007), Oh et al. (2013),Oh et al. (2014), Paulussen et al. (2003), Pérez et al. (2011), Pérez et al. (2013), Vermeulen et al. (2007), Vermeulen et al. (2008), Werker et al. (2009)

3.1. Capacity planning

Capacity planning considers the division of resource capacity to specialties, patient groups or time slots. This can be done by several means:

1. Blueprint schedule

2. Patient admission planning

3. Temporary capacity changes

A blueprint schedule describes the amount of capacity on a day or particular time slots that can be used for specific patient types in the operational planning. It can also be used to plan combination appointments, which are appointments where more than one doctor or therapist should be present. Patient admission planning considers the design of an admission policy that describes how many and which patients should be admitted from the waiting list. Developing guidelines for temporary capacity changes in case of demand peaks and drops is also considered as capacity planning (Hulshof et al., 2012).

Designing a blueprint schedule as a guideline for appointment planning is done with objectives to combine consultations on one day (Dharmadhikari & Zhang, 2011), to minimise waiting time on a day (Liang, Turkcan, Ceyhan, & Stuart, 2015), or to minimise access time or throughput time (Bikker, Kortbeek, van Os, & Boucherie, 2015; Leeftink et al., 2016a). In the blueprint, time slots are assigned to patient types (Bikker et al., 2015; Dharmadhikari & Zhang, 2011; Liang et al., 2015), or to process stages (Leeftink et al., 2016a). Furthermore, the blueprint may prescribe when doctors can best have consultation hours (Bikker et al., 2015; Liang et al., 2015). A blueprint is usually designed based on expected arrival patterns and expected availability of capacity. Robustness to different patient arrival realisations is considered an important characteristic of blueprints (Leeftink et al., 2017). Suitable methods to design blueprints are mathematical programming or heuristics, in combination with robust optimisation or computer simulation to ensure robustness. Also stochastic programming can be used, which takes robustness to several scenarios into account. Dharmadhikari and Zhang (2011) create blueprints for a veteran clinic, where patients have to travel far to see a doctor or dentist and therefore prefer to combine several consultations on a day. In the blueprint, slots are kept open in order to plan such combinations of treatments. Liang et al. (2015) create blueprints for the scheduling of patients who need an appointment with an oncologist followed by chemotherapy treatment. A radiotherapists’ schedule for consultations and scan reviews of different patient types are designed in Bikker et al. (2015), to ensure timely treatment for all patient types. Blueprints that prescribe the order of tasks to be performed in a laboratory setting are designed in Leeftink et al. (2016a).

Used methods include mathematical programming (Bikker et al., 2015; Leeftink et al., 2016a; Liang et al., 2015; Qu, Peng, Kong, & Shi, 2013) and heuristics (Dharmadhikari & Zhang, 2011; Leeftink et al., 2016a), simulation (Bikker et al., 2015; Dharmadhikari & Zhang, 2011; Lebcir, Demir, Ahmad, Vasilakis, & Southern, 2017; Liang et al., 2015; Proctor, Lehaney, Reeves, & Khan, 2015; Vrugt, Boucherie, Smilde, de Jong, & Bessems, 2017), queueing theory (Vrugt et al., 2017) and stochastic programming (Qu et al., 2013).

In some multi-disciplinary systems, patients require one or more combination appointments, that is, a single appointment where more than one doctor or therapist should be present. Examples are group therapy in rehabilitation, where a group of patients is treated by multiple therapists from the same or different disciplines, and multi-disciplinary team meetings, where the diagnosis or treatment is discussed with or without the patient’s presence. For these systems, it is essential to align staff schedules, for example, by means of a blueprint schedule, to ensure that members of a multi-disciplinary team have enough options for combined care or meetings. We found only one article where this problem is addressed: Mutlu et al. (2015) align staff schedules in surgical cancer care, using mathematical programming.

Patient admission planning considers the design of an admission policy. The treatment of skin cancer is considered in Romero et al. (2013), where patients are admitted immediately to either a regular consultation or a one-stop-shop consultation, depending on their medical characteristics and the already booked capacity. Barz and Rajaram (2015) base the admission of elective patients for surgery on expected profit. If (semi-)urgent patients may still arrive after the patient admission decision, it might be worthwhile to take future scenarios into account in admission planning (Hulshof, Mes, Boucherie, & Hans, 2016).

Used methods include mathematical programming (Conforti et al., 2011; Hulshof et al., 2013; Kortbeek et al., 2017), simulation (Romero et al., 2013), queueing theory (Kortbeek et al., 2017) and dynamic programming solved with heuristics (Barz & Rajaram, 2015).

Temporary resource capacity changes are increases or decreases in capacity allocation during a specific time frame, to cope with fluctuations in patient demand (Lovejoy & Li, 2002). Temporary capacity change can improve the balance between access times and resource utilisation (Vermeulen et al., 2009). This topic is not widely studied in health care, but it is important for a good health care planning and control (Hulshof et al., 2012). Especially in the multi-disciplinary case, such a balance is essential to avoid large bullwhip effects in related disciplines. We found one paper studying temporary capacity changes in a multi-disciplinary setting. Hulshof et al. (2013) design allocation policies for resources that divide their time over multiple tasks in the care chain, based on the patient’s waiting list status and access time target. The used method is linear programming (Hulshof et al., 2013).

3.2. Capacity-to-patient assignment

For capacity-to-patient assignment, we distinguish offline planning, where planning requests are saved up and executed once per period, and online or advance planning, where an immediate response is required to each current incoming request. The decision of planning offline or online is a management choice, where trade-offs have to be made between high utilisation (mostly achieved in offline planning) and short response times (mostly achieved in online planning). Online systems are more common in practice, while the offline approach has received more attention in the literature as it is easier to model (Ahmadi-Javid, Jalali, & Klassen, 2017). Applications of both planning methods can be found in all applications of multi-disciplinary care, but online planning is mostly reported in emergency care and cancer diagnostics and treatment, for a quick response is essential (Braaksma, Vrugt, & Boucherie, 2017).

Planning decisions either focus on determining time slots for appointment series that take place on one day, or on determining both days and time slots for appointment series at the same time.

We found 33 papers on offline planning. Most articles focus on scheduling appointments on one day and in particular for outpatient departments (Chern, Chien, & Chen, 2008; Hu, Wu, Zhang, Dai, & Jin, 2009; Lin, 2015; Matta & Patterson, 2007; Matta, 2009; Matta & Elmaghraby, 2010; Podgorelec & Kokol, 1997).

Scheduling series of up to 20 diagnostic and treatment appointments on one day with no specific order is done for an oncology center (Matta, 2009; Matta & Patterson, 2007) and several diagnostic facility outpatient clinics (Chern et al., 2008; Froehle & Magazine, 2013; Hu et al., 2009; Matta & Elmaghraby, 2010), minimising both patient and doctor waiting time. A block appointment system is used in Lin (2015) to schedule treatment appointment series in a specialty clinic, where patients are assigned to arrive at the start of a time block. Scheduling tasks on one day is also done for laboratories (Azadeh et al., 2014; Shin et al., 2010) and sterilisation practices (Rossi et al., 2013).

Scheduling days and time slots for appointments in a several day care path applies specifically to rehabilitation care and inpatient care. Multiple studies schedule rehabilitation appointments on an inpatient and/or outpatient basis (Chien, Huang, & Hu, 2008; Chien, Tseng, & Chen, 2008; Raschendorfer & Hamacher, 2014; Schimmelpfeng, Helber, & Kasper, 2012). Often, a multi-stage model is used to reduce the problem complexity. Schimmelpfeng et al. (2012) formulate a three-stage model where patients are accepted or rejected for the treatment, after which therapists and time slots are determined. Raschendorfer and Hamacher (2014) create treatment schedules on a week level, to be specified later in terms of morning/afternoon appointments and time slots. Scheduling a series of procedures in care chains for inpatients, such as diagnostic activities and surgery, in a several week horizon is done in order to maximise the contribution margin (Gartner & Kolisch, 2014), to minimise the length of stay (Saadani, Bahroun, & Bouras, 2014) or in a day horizon to minimise waiting times and overtime (Jerić & Figueira, 2012; Vlah et al., 2011). Series of examinations for vascular checkups are scheduled in Cordier and Riane (2013), either on one day or on multiple days, for inpatients as well as outpatients. Cheng et al. (2008) schedule various (partially ordered) nurse tasks that have to be performed in a day horizon.

Offline scheduling problems are often NP-hard or NP-complete, which makes them difficult to solve exactly. Therefore, most authors use heuristics and/or decomposition into hierarchical subproblems to solve the problem.

Used methods include mathematical programming (Azadeh et al., 2014; Chern et al., 2008; Chien, Tseng et al., 2008; Cordier & Riane, 2013; Gartner & Kolisch, 2014; Jerić & Figueira, 2012; Lin, 2015; Matta, 2009; Pérez et al., 2013; Raschendorfer & Hamacher, 2014; Saadani et al., 2014; Schimmelpfeng et al., 2012; Vlah et al., 2011), heuristics (Chern et al., 2008; Cordier & Riane, 2013; Hu et al., 2009; Jerić & Figueira, 2012; Lin, 2015; Matta & Elmaghraby, 2010; Podgorelec & Kokol, 1997; Shin et al., 2010; Vlah et al., 2011), simulation (Aslani & Zhang, 2014), genetic algorithms (Azadeh et al., 2014; Chien, Tseng et al., 2008; Chien, Huang, & Hu, 2008; Jerić & Figueira, 2012; Matta, 2009; Podgorelec & Kokol, 1997), local search methods (Cheng et al., 2008), and data mining (Chien, Huang et al., 2008; Aslani & Zhang, 2014).

For online planning, we found 21 papers. Planning appointments on one day applies for example to cancer clinics and emergency departments laboratories. As an example, Kalton et al. (1997) consider the scheduling of appointments where examinations take place in the morning, after which diagnoses and treatment plans are determined in multi-disciplinary team meetings and the outcome is discussed with the patient in the afternoon. Rescheduling is allowed in Vermeulen et al. (2007), where involved departments may change a concept schedule, and in Azadeh et al. (2015) where an arriving patient in a pathology emergency department laboratory is scheduled and other patients are rescheduled, such that the total waiting time of all patients is minimised.

Online planning of appointments on multiple days is done for rehabilitation and cancer treatment. Braaksma et al. (2014) present a methodology to plan appointment series for rehabilitation outpatients. The scheduling of the radiotherapy care pathway is considered in Kapamara et al. (2007) and Werker, Sauré, French, & Shechter (2009), where operating hours of treatment machines and shift hours of machine operators are varied (Kapamara et al., 2007) or different arrival distributions and oncologist productivity are considered (Werker et al., 2009). Hahn-Goldberg et al. (2014) use a template for scheduling chemotherapy patients online, and if the request does not fit in the template, it is updated.

For practical applications of online planning, a short computation time is essential since an immediate response is given to the patient. Therefore, several papers use heuristics for optimisation or simulation for evaluation, in order to obtain a reasonably good solution with a short computation time.

Used methods include mathematical programming (Azadeh et al., 2015; Braaksma et al., 2014), heuristics (Day et al., 2010; Pérez et al., 2011), simulation (Day et al., 2010; Kalton et al., 1997; Kapamara et al., 2007; Pérez et al., 2011; Werker et al., 2009), stochastic programming (Pérez et al., 2013), constraint programing (Hahn-Goldberg et al., 2014), genetic algorithms (Azadeh et al., 2015), and agent-based models (Vermeulen et al., 2007; Vermeulen et al., 2008).

3.3. Conclusions and further research

Mid-term capacity planning in health care has received relatively little attention compared to capacity-to-patient assignment (Ahmadi-Javid et al., 2017), and the same holds in multi-disciplinary care. However, mid-term capacity planning is essential for a good health care system control (Hans et al., 2007).

Three topics in particular are a promising direction for further research. The first is the alignment of staff schedules, for which we only found one paper. However, many applications exist where patients require one or more combination appointments, such as group therapy in rehabilitation, and multi-disciplinary team meetings in diagnostics or treatment planning. For these systems, it is essential to align staff schedules, for example by means of a blueprint schedule, to ensure that members of a multi-disciplinary team have enough options to deliver combined care or to attend joint meetings.

A second direction for further research is temporary capacity changes. Temporary capacity changes are not widely studied in health care, but are important for a good health care planning and control (Hulshof et al., 2012), as they can restore the balance between access times and resource utilisation (Vermeulen et al., 2009). Especially in the multi-disciplinary case, such a balance is essential to avoid large bullwhip effects in related disciplines. Since the problem of when to change capacity and to which extent involves optimisation over time, dynamic programming could be a suitable method for the optimisation of temporary capacity changes. As multi-disciplinary care systems involve complex state descriptions and many possible actions, this should be combined with approximation methods.

The last direction for further research considers online planning in capacity-to-patient assignment. We observe that online planning is frequently studied in a simulation setting, where several scenarios are evaluated. However, only few optimisation studies are known. This would be a promising topic for further research, since many applications exist for online planning. Taking future patient arrivals into account in optimisation can be done by dynamic programming, stochastic programming, or robust optimisation. Using these methods, a combination with approximation methods would be required since the planning of multiple appointments involves many possible actions.

4. Type of system

Precedence relations and time constraints between appointments may be present in multi-disciplinary appointment planning. For example, a patient first has to finish all diagnostic tests, before a consultation with a specialist is planned. We distinguish three different multi-disciplinary systems, based on precedence constraints, since each of these systems faces different optimisation problems:

1. Flow-shop

2. Open-shop

3. Mixed-shop

In a flow-shop system, also referred to as one-stop-shop or carousel, patients undergo a predefined sequence of activities at multiple facilities. Service process divergence is low given the high degree of standardisation that allows for a fixed sequence of appointments. Furthermore, there are strict precedence relations between activities. An example of a flow-shop can be found in a specialty clinic for Huntington’s disease, where multiple symptoms need to be addressed in consultations with several professionals, scheduled in a predefined sequence (Veenhuizen & Tibben, 2009). Also in one-stop-shops for cancer diagnostics, flow-shop systems are often present, as patients follow a predefined trajectory.

In an open-shop system, patients undergo a set of activities which can be scheduled in any order. Service process divergence is high, given the flexibility in the order of activities, such that each patient can get his/her appointments in a different sequence. Open-shop systems contain few or even no precedence constraints. An example of an open-shop can be found in rehabilitation treatment, where patients need an appointment with a physician, physiotherapist, and psychologist, in an arbitrary sequence, as long as these appointments are planned on the same day (Griffiths, Williams, & Wood, 2012) or in the same week (Braaksma et al., 2014).

A mixed-shop system is a combination of a flow-shop and an open-shop system, with an intermediate level of service process divergence and prevalence of precedence relations. A mixed-shop regularly has a fixed sequence of “consultation - examinations - consultation”, but the order in which the examinations take place is variable. An example is a regular diagnostic trajectory, where a patient first has an intake consultation, thereafter has multiple examinations in an arbitrary order, and finishes with another consultation in which the results are discussed (Matta, 2009; Vermeulen et al., 2007).

Figure 1 presents a visualisation of the three system types. In each of these three systems, patients can undergo the complete set of activities, or only a subset of activities that are applicable for them. We call this subcategory a flexible shop. For example in a flexible flow-shop, patients can skip an examination that is not applicable for them, and continue with the next one. This way, patients can undergo a different subset of activities, albeit in the same sequence, as the flow-shop system is still present. In a flexible open-shop, patients can also undergo different subsets of the activities, in any order. These flexible shop systems are especially relevant for personalised health care settings.

Figure 1.

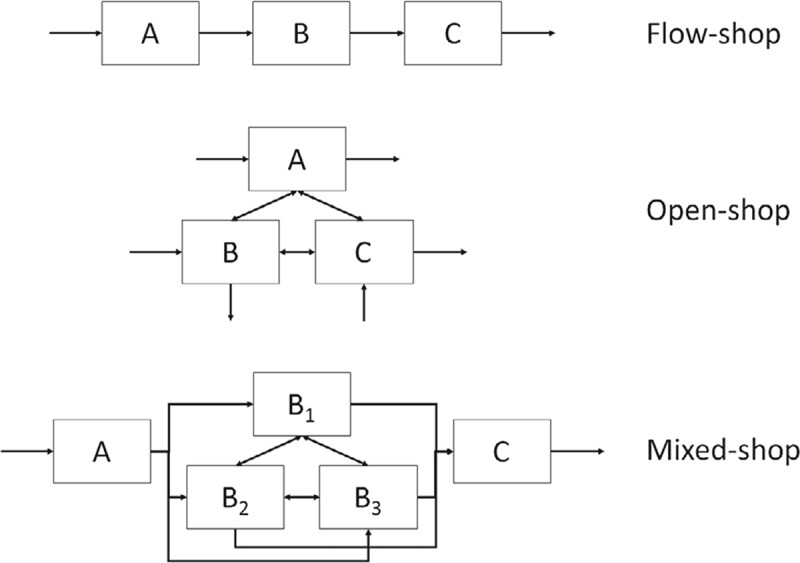
Visualization of a ow-shop, open-shop, and mixed-shop system.

Out of the total of 63 papers found, 36 papers consider a flow-shop system, as described in Section 4.1, 9 papers consider an open-shop system, as described in Section 4.2, and 18 papers consider the mixed-shop system, as described in Section 4.3. Each section gives an overview of the literature, and provides the patient and system measures that are of importance when studying the discussed system. Section 4.4 provides conclusions and opportunities for further research. Table 2 gives an overview of the papers and categories.

Table 2.

Type of system.

Type of system	References
Flow shop	Aslani and Zhang (2014), Azadeh et al. (2015), Barz and Rajaram (2015), Bikker et al. (2015), Braaksma et al. (2014), Cardoen and Demeulemeester (2008), Castro and Petrovic (2012), Day et al. (2010), Du et al. (2013), Gartner and Kolisch (2014), Hulshof et al. (2013), Hulshof et al. (2016), Kalton et al. (1997), Kapamara et al. (2007), Leeftink et al. (2016a), Leeftink et al. (2017), Liang et al. (2015), Lin (2015), Mutlu et al. (2015), Oh et al. (2013), Oh et al. (2014), Pérez et al. (2011), Pérez et al. (2013), Petrovic et al. (2013), Proctor et al. (2007), Romero et al. (2013), Rossi et al. (2013), Sadki et al. (2011), Shin et al. (2010), Venkitasubramanian et al. (2015), Villa et al. (2014), Vlah et al. (2011), Vrugt et al. (2017), Werker et al. (2009), Zhao et al. (2015), Zonderland et al. (2015)
Open shop	Azadeh et al. (2014), Dharmadhikari and Zhang (2011), Hu et al. (2009), Matta (2009), Matta and Elmaghraby (2010), Paulussen et al. (2003), Qu et al. (2013), Vermeulen et al. (2007), Jerić and Figueira (2012)
Mixed-shop	Cheng et al. (2008), Chern et al. (2008), Chien, Tseng et al. (2008), Chien, Huang et al. (2008), Conforti et al. (2011), Cordier and Riane (2013), Froehle and Magazine (2013), Hahn-Goldberg et al. (2014), Kapadia et al. (1985), Lebcir et al. (2017), Matta and Patterson (2007), Podgorelec and Kokol (1997), Raschendorfer and Hamacher (2014), Saadani et al. (2014), Saremi et al. (2015), Schimmelpfeng et al. (2012), Kortbeek et al. (2017), Vermeulen et al. (2008)

4.1. Flow-shop

Flow-shop planning includes the planning of one-stop-shop, rapid diagnostics, and carousel programs, in which predefined care pathways are present. These care pathways most often span a single day, but in specific health care areas, such as for patients with head and neck cancer, rapid diagnostics programs of multiple days are designed (Sorensen et al., 2014).

The large amount of flow-shop papers considers a deterministic variant of the problem on the capacity-to-patient level. Two solution strategies are frequently applied: ILP optimisation evaluated by discrete event simulation, and heuristic approaches.

Patient performance in flow-shop systems is measured by means of the direct waiting time (Azadeh, Baghersad, Farahani, & Zarrin, 2015; Kalton, Singh, August, Parin, & Othman, 1997; Liang et al., 2015; Lin, 2015; Oh, Muriel, Balasubramanian, Atkinson, & Ptaszkiewicz, 2013; Oh, Muriel, & Balasubramanian, 2014), access time (also known as indirect waiting time) (Bikker et al., 2015; Cardoen & Demeulemeester, 2008; Hulshof et al., 2016), and the rejection probability (Alfonso et al., 2012). In single-appointment systems the direct waiting time is measured as the waiting time on the day of the appointment from the planned appointment start until the actual start of the appointment. However, in a multi-appointment setting, the waiting time until the start of the first appointment does not cover all waiting on that day. Therefore, we define direct waiting time as the waiting time spent in the waiting room starting from the scheduled start time of the first appointment until the moment that the patient leaves the hospital. Therefore, it not only includes waiting time caused by a late appointment start, but it also includes the waiting time between two subsequent appointments. Besides direct waiting time, Lin (2015) also include the number of patients in the waiting room in their objective, as a measure of patient satisfaction. As all appointments in a flow-shop are scheduled sequentially, minimising the throughput of a system, as for example studied by Romero et al. (2013), has similar results.

Accessibility, represented by the access time is a second objective in flow-shop systems (Bikker et al., 2015). As many health systems have access time requirements for outpatient and treatment clinics, in order to ensure that patients are seen on time, access time measures become increasingly important.

If allowed for by the system, the rejection probability is included as a performance metric, as a rejection has negative consequences for the patient in terms of quality of care and patient experience. For example blood collection systems may need to reject donors when blood inventory levels are high enough. However, this comes at a cost of losing a donor who could be needed at a later moment in time (Alfonso et al., 2012).

System performance in flow-shop systems, is measured by means of completion times, throughput times, tardiness, the number of patients admitted, utilisation, and overtime (Barz & Rajaram, 2015; Cardoen & Demeulemeester, 2008; Hulshof et al., 2016; Leeftink et al., 2016a; Liang et al., 2015; Rossi et al., 2013; Sadki, Xie, & Chauvin, 2011; Shin et al., 2010). Due to the sequencing relations in a flow-shop system, flexibility in the planning is limited. This influences the timeliness of care. Therefore, time-related objectives, such as completion times, throughput times, and tardiness are a set of frequently studied objectives. These time related objectives are especially relevant in health care settings where patients are not physically present, such as laboratories and sterilisation departments (Leeftink et al., 2016a; Rossi et al., 2013).

When patients are physically present, the number of patients admitted, utilisation, and overtime are relevant measures (Barz & Rajaram, 2015; Cardoen & Demeulemeester, 2008; Liang et al., 2015; Sadki et al., 2011). When a fixed capacity is reserved for such a one-stop-shop, rapid diagnostics, or carousel program, the maximum number of patients to be admitted is restricted (Romero et al., 2013). An important objective in flow-shop planning is therefore to maximise the possible number of patients treated (Braaksma et al., 2014; Hulshof et al., 2013; Vlah et al., 2011).

4.2. Open-shop

Open-shop planning includes the planning of multiple examinations or consultations, in which the order of these appointments is not relevant. Multiple resources are required for the appointments, hence coordination between resources is required. Furthermore, in many situations, patients with various characteristics use the open-shop system, which makes the flexible open-shop system most prevalent both in practice and in the literature. For general information and applications of open-shop systems, refer to Anand and Panneerselvam (2015).

Most open-shop papers consider a flexible variant of the problem on the capacity-to-patient level. The most frequently applied solution strategies are (local search) heuristics.

Patient performance in an open-shop is measured by the number of same day appointments, an equal spread of appointments over the days, and the timeliness of care. Patients who visit a health care institute for multiple appointments with different health care providers, prefer their appointments in the same day (Dharmadhikari & Zhang, 2011). Therefore, the number of same day appointments, is a relevant optimisation criterion. However, in some situations, it is impossible to provide all needed care in one day. In this case, a care pathway of multiple days, with an equal spread of the number of appointments over these days may be more desirable, to level the care load. Where flow-shop planning gives patients more clarity about their care pathway, the benefit of open-shop planning over flow-shop planning is the possible gain in waiting time. Therefore, the timeliness of care is an important objective from a patient perspective for open-shop systems, which is shown in objectives such as access time, throughput time, and direct waiting time (Azadeh et al., 2014; Hu et al., 2009; Jerić & Figueira, 2012; Paulussen, Jennings, Decker, & Heinzl, 2003).

System performance in an open-shop is measured by completion times (Azadeh et al., 2014; Vermeulen et al., 2007) and makespan (Matta, 2009; Matta & Elmaghraby, 2010; Paulussen et al., 2003). By minimising completion times and makespan, hospitals aim to minimise waiting times for the patients, and maximising efficiency for the hospital. These indicators are especially relevant in an open-shop, as the completion time and makespan of a patient is influenced by the sequence of the needed activities (Matta, 2009).

4.3. Mixed-shop

Mixed-shop systems include appointments with precedence constraints, but with some flexibility in the sequence of a subset of all appointments. It can be subdivided in two general situations. First, we have a diagnostic facility, in which each patient first requires an intake consultation, then multiple tests in an undefined order, and finishes with a consultation again in which the diagnosis is explained (Matta, 2009). Second, we have a specialty clinic in which each patient type requires specific treatments to be given in a specific order, together with some general treatment modalities for which the order is irrelevant and which can be scheduled at any free moment during the treatment period (Chien, Tseng et al., 2008).

Most mixed-shop papers focus on the capacity-to-patient level, and behave as a flexible mixed-shop system. Mathematical programming is a frequently applied solution technique, as well as heuristics.

Patient performance is frequently assessed by the direct waiting time (Chien, Tseng et al., 2008; Chien, Huang et al., 2008; Saremi et al., 2015), length of stay (Conforti, Guerriero, Guido, Cerinic, & Conforti, 2011; Cordier & Riane, 2013; Froehle & Magazine, 2013), and levelled care load (Raschendorfer & Hamacher, 2014). A focus on direct waiting times ensures quick access for patients on the day of the appointments. An interesting approach is adopted by Cheng et al. (2008), who assess the timeliness of care by taking both the tardiness and earliness into account. Notably, no authors have evaluated the accessibility in mixed-shop systems from an access time perspective. The patient’s length of stay is minimised in order to reduces all unnecessary delays for the patient (Cordier & Riane, 2013). The length of stay as a performance measure is relevant in one-day diagnostic trajectories (Cordier & Riane, 2013), and inpatient clinics, where hospitalised patients need inpatient care services spread over a few days with night stays (Conforti et al., 2011). In this case, it is important to minimise a patient’s length of stay, as each occupied bed blocks the access to care for other patients. The spread of treatment appointments over multiple days to level the care load for patients is specifically prevalent in mixed-shop systems (Raschendorfer & Hamacher, 2014), in contrast to the objective to plan as many appointments as possible on one day, which is seen in open-shop systems. This is especially relevant in treatment situations that take multiple days, weeks, or even months, such as in rehabilitation care.

System performance in mixed-shop systems is evaluated by the number of patients admitted to the system (Conforti et al., 2011; Raschendorfer & Hamacher, 2014; Kortbeek et al., 2017; Schimmelpfeng et al., 2012; Vermeulen et al., 2008), makespan (Chien, Tseng et al., 2008; Cordier & Riane, 2013; Saadani et al., 2014), and completion times (Matta & Patterson, 2007; Saremi et al., 2015). The number of patients admitted to the system is specifically seen in specialty clinics, such as rehabilitation care (Raschendorfer & Hamacher, 2014; Schimmelpfeng et al., 2012). Minimising the makespan or completion times is frequently studied when analysing outpatient facilities (Chien, Tseng et al., 2008; Matta and Patterson, 2007; Saadani et al., 2014; Saremi et al., 2015). These measures are chosen to optimise the operational efficiency.

4.4. Conclusions and further research

Despite the high prevalence of flow-shop systems in the multi-disciplinary literature, flexible flow-shop systems are not reported upon. As seen in Section 2, the organisation of patient centred clinics and personalised diagnostics and treatment systems is a gap in the literature that deserves considerable research attention in the near future. These systems ask for more flexibility, by only selecting the required steps in a flow-shop system that fit the needs of the patient.

Open-shop planning in health care has not received much attention in the literature so far. It requires high flexibility and coordination of all participating resources, without them being able to fix capacity for specific patient groups. However, the joint optimisation of multiple disciplines rapidly attracts more attention of researchers and of practice, with large improvement possibilities. The implementation of structured pathways, such as flow-shop systems has received much attention in the medical literature. This comes at a cost of reserving capacity for specific patient groups (Leeftink et al., 2016b; Vanberkel, Boucherie, Hans, Hurink, & Litvak, 2012). Therefore, we expect open-shop systems to become of more interest for researchers and practitioners in the near future. As health care systems involve more complex behaviour than those open-shop systems that are polynomial solvable, research in approximation methods and intelligent optimisation techniques is promising (Bai, Zhang, & Zhang, 2016). To ensure implementation, individual resource performance should be analysed as well, to show the individual disciplines the benefits or costs of coordinated care for themselves.

Few papers studied the combination of access time and direct waiting time or throughput time (Bikker et al., 2015; Braaksma et al., 2014; Kortbeek et al., 2017). This offers interesting opportunities for further research. Flow-shop systems, such as the one-stop-shop, are most often designed for specific days of the week, in which the direct waiting time might be low, but access times might take up to a week. On the other hand, open-shop systems might offer direct access to the first activity, but may end up with a long throughput time. It is an open challenge to develop optimisation methods that ensure a good fit between the access times and direct waiting times.

We have seen that in flow-shop systems and mixed-shop systems, the number of patients that gets access to the system is a relevant performance indicator. Access times in mixed-shop systems are especially an interesting area of future research, as no such literature is known at this moment. For flexible shop systems, accessibility as an indicator is more difficult to include. This would create an unfair access policy over different patient types, as it is advantageous to grant short-stay patients access more frequently than long-stay patients.

When a care pathway consists of multiple days, other performance indicators become of interest compared to one-day care pathways. For example an equal spread of the number of appointments over these days is desirable. Until now, this has not been subject of research, and offers opportunities for further research by adapting used methods to use this new objective.

Similar to mono-disciplinary appointment planning, most multi-disciplinary studies consider an objective function with multiple criteria, involving the patient as well as system performance. Most studies sum weighted objectives to derive the final objective value. Other multi-objective optimisation methods, for example with non-linear relations between performance indicators, are still an open challenge in multi-disciplinary appointment planning.

It is well known that hospitals tend to evaluate performance on a local, departmental, level. Therefore, in order to ensure implementation of all three type of systems, not only the entire system’s performance, but also the individual resource performance is of interest. Resource idle time, overtime, and utilisation are thus relevant performance indicators, although not yet considered in the literature. For example, outliers in individual resource performance might indicate that changes in capacity or opening hours are required.

5. Variability and uncertainty

In modelling a planning problem, researchers have to decide whether to take variability into account or not. This decision depends on both the extent to which variability is a characteristic aspect of the planning problem, as well as the model complexity. Variability in multi-disciplinary care exists in various aspects of the system:

1. Patient arrivals

2. Appointment durations

3. Resource capacity

4. Care pathway

For patient arrivals, both the number of arriving patients and their moment of arrival are subject to variation. If patients are assigned a series of appointments, no shows and late arrivals might occur. For walk-in patients, certain time slots might be more popular than others. When scheduling an appointment, the appointment duration per patient or appointment type is often considered fixed. However, in practice these durations can vary to a greater or lesser extent. Resource capacity can vary due to longer term reasons such as sabbaticals or parental leave, or shorter term events such as illness or machine breakdowns. A patient’s care pathway is either known at the moment of arrival (e.g., patients need predetermined appointments for treatment and yearly check-ups), becomes clear during the appointment series (e.g., when a diagnosis is involved) or is modified along the way (e.g., the course of a rehabilitation treatment might depend on the patient’s progress, or a patient might recirculate in some parts of the care pathway).

The extent in which variability and uncertainty are prevalent in the described aspects depends amongst others on the planning decision (see Section 3) and the system type (see Section 4). Information with respect to arrivals and care pathways of individual patients is usually not yet available for long-term and mid-term decision making (Hans, Van Houdenhoven, & Hulshof, 2012). The same holds for information about the (detailed) availability of resource capacity. In order to make decisions, this information has to be forecasted. In short-term decision making, such as capacity-to-patient assignment, more information is available, since (part of) the patients already arrived and staff schedules are made (Hans et al., 2012). All information with respect to arrivals, capacity and care pathways for a time period is gathered in online planning, although information with respect to future arrivals is still uncertain. Therefore, variability in arrivals, care pathways and available capacity are characteristic aspects of problems considering capacity planning and capacity-to-patient assignment in an online setting.

Variability in appointment durations is a characteristic aspect in problems with time constraints or objectives concerning waiting time, idle time or overtime. In these problems, not taking variability into account may influence the robustness of the obtained solution in practical situations.

The system type impacts the incorporation of variable aspects as well. In a flow-shop system, the order of appointments is fixed. However, in an open-shop system, the order of appointments is unknown until the appointments have been scheduled. This allows for (re-)scheduling on the day of the appointments. For example, by deciding upon the order of the appointments according to realised durations of previous appointments and current waiting times.

Researchers can model variability in different ways. A deterministic approach assumes that all information pertaining to the variable factors is known with certainty at the time of the decision making. A stochastic approach considers uncertainty in these variable factors. Adopting the stochastic approach in modelling often significantly increases a model’s complexity, which may result in an “exploding state space” and large computation times. The solving time is often important for practice, especially for capacity-to-patient planning and in particular online planning (Braaksma et al., 2017).

In the next sections, we give an overview of the extent to which the literature takes variability into account in each of the described aspects. Table 3 gives an overview of the papers and categories. Note that, when authors optimise their problem using a deterministic approach, and evaluate their results stochastically, we categorise them as deterministic.

Table 3.

Variability aspects.

Variability aspect	Deterministic approach	Stochastic approach
Patient arrivals	Azadeh et al. (2014), Azadeh et al. (2015), Bikker et al. (2015), Braaksma et al. (2014), Castro and Petrovic (2012), Cheng et al. (2008), Chern et al. (2008), Chien, Huang et al. (2008), Conforti et al. (2011), Cordier and Riane (2013), Du et al. (2013), Froehle and Magazine (2013), Gartner and Kolisch (2014), Hu et al. (2009), Hulshof et al. (2013), Jerić and Figueira (2012), Leeftink et al. (2016a), Leeftink et al. (2017), Lin (2015), Matta (2009), Matta and Elmaghraby (2010), Oh et al. (2013), Oh et al. (2014), Podgorelec and Kokol (1997), Raschendorfer and Hamacher (2014), Romero et al. (2013), Rossi et al. (2013), Saadani et al. (2014), Saremi et al. (2015), Schimmelpfeng et al. (2012), Shin et al. (2010), Vlah et al. (2011), Zhao et al. (2015)	Aslani and Zhang (2014), Barz and Rajaram (2015), Cardoen and Demeulemeester (2008), Chien, Tseng et al. (2008), Day et al. (2010), Dharmadhikari and Zhang (2011), Hahn-Goldberg et al. (2014), Hulshof et al. (2016), Kalton et al. (1997), Kapamara et al. (2007), Kortbeek et al. (2017), Lebcir et al. (2017), Liang et al. (2015), Matta and Patterson (2007), Paulussen et al. (2003), Pérez et al. (2011), Pérez et al. (2013), Petrovic et al. (2013), Proctor et al. (2007), Qu et al. (2013), Sadki et al. (2011), Venkitasubramanian et al. (2015), Vermeulen et al. (2007), Vermeulen et al. (2008), Vrugt et al. (2017), Werker et al. (2009), Zonderland et al. (2015)
Appointment durations	Aslani and Zhang (2014), Azadeh et al. (2014), Azadeh et al. (2015), Barz and Rajaram (2015), Bikker et al. (2015), Braaksma et al. (2014), Castro and Petrovic (2012), Cheng et al. (2008), Chern et al. (2008), Chien, Huang et al. (2008), Chien, Tseng et al. (2008), Conforti et al. (2011), Cordier and Riane (2013), Day et al. (2010), Dharmadhikari and Zhang (2011), Du et al. (2013), Froehle and Magazine (2013), Hahn-Goldberg et al. (2014), Hu et al. (2009), Hulshof et al. (2013), Hulshof et al. (2016), Jerić and Figueira (2012), Kalton et al. (1997), Kortbeek et al. (2017), Leeftink et al. (2017), Lin (2015), Matta (2009), Matta and Elmaghraby (2010), Mutlu et al. (2015), Paulussen et al. (2003), Pérez et al. (2013), Petrovic et al. (2013), Podgorelec and Kokol (1997), Proctor et al. (2007), Raschendorfer and Hamacher (2014), Romero et al. (2013), Rossi et al. (2013), Saadani et al. (2014), Sadki et al. (2011), Saremi et al. (2015), Schimmelpfeng et al. (2012), Shin et al. (2010), Vermeulen et al. (2007), Vermeulen et al. (2008), Vlah et al. (2011), Zhao et al. (2015), Zonderland et al. (2015)	Cardoen and Demeulemeester (2008), Gartner and Kolisch (2014), Kapamara et al. (2007), Leeftink et al. (2016a), Liang et al. (2015), Matta and Patterson (2007), Oh et al. (2013), Oh et al. (2014), Pérez et al. (2011), Qu et al. (2013), Venkitasubramanian et al. (2015), Vrugt et al. (2017), Werker et al. (2009)
Resource capacity	Aslani and Zhang (2014), Azadeh et al. (2014), Azadeh et al. (2015), Barz and Rajaram (2015), Bikker et al. (2015), Braaksma et al. (2014), Cardoen and Demeulemeester (2008), Castro and Petrovic (2012), Cheng et al. (2008), Chern et al. (2008), Chien, Huang et al. (2008), Chien, Tseng et al. (2008), Conforti et al. (2011), Cordier and Riane (2013), Day et al. (2010), Dharmadhikari and Zhang (2011), Du et al. (2013), Froehle and Magazine (2013), Gartner and Kolisch (2014), Hahn-Goldberg et al. (2014), Hu et al. (2009), Hulshof et al. (2013), Hulshof et al. (2016), Jerić and Figueira (2012), Kalton et al. (1997), Kapamara et al. (2007), Kortbeek et al. (2017), Lebcir et al. (2017), Leeftink et al. (2016a), Leeftink et al. (2017), Liang et al. (2015), Lin (2015), Matta and Patterson (2007), Matta (2009), Matta and Elmaghraby (2010), Mutlu et al. (2015), Oh et al. (2013), Oh et al. (2014), Paulussen et al. (2003), Pérez et al. (2011), Pérez et al. (2013), Petrovic et al. (2013), Podgorelec and Kokol (1997), Proctor et al. (2007), Qu et al. (2013), Raschendorfer and Hamacher (2014), Romero et al. (2013), Rossi et al. (2013), Saadani et al. (2014), Sadki et al. (2011), Saremi et al. (2015), Schimmelpfeng et al. (2012), Shin et al. (2010), Venkitasubramanian et al. (2015), Vermeulen et al. (2007), Vermeulen et al. (2008), Vlah et al. (2011), Vrugt et al. (2017), Werker et al. (2009), Zhao et al. (2015), Zonderland et al. (2015)
Care pathway	Aslani and Zhang (2014), Azadeh et al. (2014), Azadeh et al. (2015), Bikker et al. (2015), Braaksma et al. (2014), Castro and Petrovic (2012), Cheng et al. (2008), Chern et al. (2008), Chien, Huang et al. (2008), Chien, Tseng et al. (2008), Conforti et al. (2011), Cordier and Riane (2013), Day et al. (2010), Dharmadhikari and Zhang (2011), Du et al. (2013), Froehle and Magazine (2013), Gartner and Kolisch (2014), Hahn-Goldberg et al. (2014), Hu et al. (2009), Hulshof et al. (2013), Jerić and Figueira (2012), Kalton et al. (1997), Kortbeek et al. (2017), Lebcir et al. (2017), Leeftink et al. (2016a), Liang et al. (2015), Lin (2015), Matta and Patterson (2007), Matta (2009), Matta and Elmaghraby (2010), Mutlu et al. (2015), Oh et al. (2013), Oh et al. (2014), Paulussen et al. (2003), Pérez et al. (2011), Pérez et al. (2013), Petrovic et al. (2013), Podgorelec and Kokol (1997), Proctor et al. (2007), Qu et al. (2013), Raschendorfer and Hamacher (2014), Romero et al. (2013), Rossi et al. (2013), Saadani et al. (2014), Sadki et al. (2011), Saremi et al. (2015), Schimmelpfeng et al. (2012), Shin et al. (2010), Vermeulen et al. (2007), Vermeulen et al. (2008), Vlah et al. (2011), Vrugt et al. (2017), Werker et al. (2009), Zhao et al. (2015), Zonderland et al. (2015)	Barz and Rajaram (2015), Cardoen and Demeulemeester (2008), Hulshof et al. (2016), Kapadia et al. (1985), Kapamara et al. (2007), Leeftink et al. (2017), Venkitasubramanian et al. (2015)

5.1. Patient arrivals

Variability in arrivals is a characteristic aspect of problems in an online setting.

A deterministic approach towards patient arrivals is a relevant approach for offline planning decisions, as all information with respect to arrivals for a time period is gathered before a decision is made. We found 33 papers that model patient arrivals deterministically, which are all on capacity planning or offline planning.

A stochastic approach towards patient arrivals is a relevant approach for online planning decisions, as future arrivals are still unknown. In this case, patient arrivals are often represented by a Poisson distribution.

A second area in which stochastic patient arrivals are considered are capacity planning problems, as patient arrival information is not yet known at this hierarchical level and has to be forecasted. In all papers found, an average of the historic data is used for this. In total, we found 27 papers that model patient arrivals stochastically.

In some cases, the robustness of a capacity planning or offline planning approach is evaluated by simulating the capacity-to-patient assignment in a stochastic environment, under the restrictions provided by the (deterministically determined) capacity planning (Bikker et al., 2015; Romero et al., 2013) or offline planning (Azadeh et al., 2014; Azadeh, Baghersad, Farahani, & Zarrin, 2015; Braaksma et al., 2014; Leeftink et al., 2016a).

5.2. Appointment durations

Variability in appointment durations is a characteristic aspect in problems with time constraints or objectives concerning waiting time, idle time or overtime.

A deterministic approach towards appointment durations is a relevant approach for planning problems where appointment durations have a low variance, such as check-ups, where no patients and staff are directly involved, such as laboratory and sterilisation processes (Rossi et al., 2013), or where variations in appointment durations do not cause significant problems later on the day or in consecutive care stages. We found 46 papers that model appointment durations deterministically.

A stochastic approach towards appointment duration is a relevant approach for problems with time constraints or objectives concerning waiting time, idle time or overtime, and in particular for flow-shop or mixed shop systems with multiple appointments per patient on one day. In these systems, bullwhip effects can occur due to the interrelatedness of appointments, where delays in one step induce enlarged delays in all further downstream steps. This happens for example if all patients have a fixed order of adjacent scheduled appointments and the first appointment of the first patient takes longer than expected. We found 13 papers that include appointment durations stochastically, in most cases by simulation modelling.

From the papers with flow-shop or mixed shop systems where patients have multiple appointments on one day and the objectives concerning waiting time, idle time or overtime apply, only two papers model appointment durations using an empirical distribution (Kalton et al., 1997; Liang et al., 2015). The others model them deterministically (Chern et al., 2008; Chien, Huang et al., 2008; Chien, Tseng et al., 2008; Lin, 2015; Sadki, Xie, & Chauvin, 2011; Saremi et al., 2015).

5.3. Resource capacity

Variations in resource capacity can be due to longer term reasons such as sabbaticals or parental leave, or shorter term events such as illness or machine breakdowns. Especially for multi-disciplinary care, variability in the resource capacity of a discipline can have a large effect on the utilisation of capacity of interrelated disciplines (Samuel, Gonapa, Chaudhary, & Mishra, 2010), especially in flow-shop systems where all appointments have to be rescheduled if the first is cancelled.

A deterministic approach towards resource capacity is a relevant approach for planning problems where enough capacity is available or where resources can easily be replaced. In these cases, if it turns out that there is more or less capacity available than planned, the appointment can still take place and subsequent appointments are not affected. We found 61 papers that model resource capacity deterministically.

A stochastic approach towards available resource capacity is a relevant approach for all problems where capacity is scarce and where there is time between the moment of decision-making and the actual moment to which the decision applies. This holds especially for capacity planning problems, since decisions are made while specific information with respect to resource capacity is not yet known.

We found only two papers in which the total available capacity is modelled stochastically, taking into account longer term capacity variations (Bikker et al., 2015; Hulshof et al., 2013). Bikker et al. (2015) model the absence of doctors due to holidays and illness based on historical data, and these capacity variations influence the access times of patients to a large extent. In Hulshof et al. (2013), the total available resource capacity for a certain period can vary, but is known at the moment that the allocation of the capacity is determined. Capacity fluctuations on shorter term may have a considerable impact on the continuity of care (e.g., when treatments take several weeks or months, during which care professionals can decide to take days off) and on consecutive appointments in a carousel (which all have to be cancelled if there is no capacity available for the first appointment). We have found no papers in multi-disciplinary care that take shorter term capacity variations into account.

5.4. Care pathways

Variations in care pathways are most prevalent in problems where a diagnosis is involved or in long treatments, where the length or intensity of the treatment depends on the patient’s progress.

A deterministic approach towards care pathways is a relevant approach for planning problems with fixed care pathways, as all information on the care pathway is gathered before the decision is made. In literature, care pathways are most often assumed to be known at the moment of arrival: we found 55 papers that model care pathways deterministically.

A stochastic approach towards care pathways is a relevant approach for problems where changes in the care pathway involve a different amount of care or care from different resources on the short term, as this can influence the continuity of care and the capacity utilisation. Incorporating variable care pathways can be beneficial for treatment continuity, for example, to ensure that capacity is not fully booked when treatments are likely to take longer than expected. We found 7 papers that take into account that care pathways are still uncertain at the moment of arrival, namely the length of stay (Barz & Rajaram, 2015; Kapadia, Vineberg, & Rossi, 1985), the required appointments (Cardoen & Demeulemeester, 2008), or the routing of patients to the next care providers (Hulshof et al., 2016; Leeftink et al., 2017; Venkitasubramanian, Roberts, & Joines, 2015).

5.5. Conclusions and further research

Variability in arrivals, care pathways and available capacity are characteristic aspects of problems considering capacity planning and capacity-to-patient assignment in an online setting.

In the literature, variability in care pathways and resource capacity are hardly taken into account, which might cause the resulting planning solutions not to be robust in practice. Especially planning models where care pathways can change during the course of the care pathway would benefit from taking variability into account, in order to ensure continuity of care without delay. As changes in care pathways require quick adaptations of the planning, possible methods include fast approximation algorithms. This offers an interesting direction for further research.

With respect to the resource capacity, short term fluctuations are essential to take into account since they may have a considerable impact on the continuity of the treatment and on consecutive appointments in a flow-shop. Dealing with short-term capacity variability can be done by anticipating for last minute changes in capacity planning or capacity-to-patient assignment, and by rescheduling doctors or therapists when a last minute change occurs. For the latter, fast solution approaches are essential.

Variability in appointment durations has a large impact on problems with time constraints or time-related objectives. These planning problems would therefore benefit from taking variability in appointment durations into account, because otherwise bullwhip effects may occur. However, in literature, appointment durations are often modelled deterministically, which may result in large waiting times and inefficiencies in practice. When variability in appointment durations is taken into account, it is most frequently analysed using a simulation approach (Kapamara et al., 2007; Vrugt et al., 2017; Werker et al., 2009). In contrast, optimisation is not often reported upon. A promising direction for further research would be to use stochastic modelling or robust programming such that care systems can be optimised while taking variability in appointment durations into account.

As approaches for taking variability into account in multi-disciplinary systems might become too computationally involved, researchers can opt for approximations or a deterministic optimisation approach combined with a stochastic evaluation, such as a sensitivity analysis with multiple scenarios.

6. Applicability and generality

For hospital managers and scientists, it is important to know which planning approach is relevant to their situation. Hospital managers want to know if a solution that is proposed in the literature, worked in hospital practice, and whether it will also work in their specific hospital. Scientists want to know under what constraints a solution methodology works, whether the approach is also feasible for other departments, hospitals, or industries with similar characteristics, and whether the performance of that approach is better than other known approaches. To increase the practical applicability, a comparison of the proposed approach with the current hospital practice can be made, using historical data from a hospital. To increase generality in a wide range of health care institutes, not only the specific parameter settings of one hospital, but also a wide range of other possible parameter settings reflecting a wide range of hospitals, can be taken into account (Leeftink & Hans, 2017). To increase scientific relevance, a comparison of the performance of the proposed approach with the performance of relevant approaches in the literature can be made. In order to make a good comparison, numerical experiments based on an extensive dataset need to be provided in the paper (Vanhoucke & Maenhout, 2007). This is also relevant to hospital managers, as they want to implement the best performing solution in their practice.

We first analyse the practice perspective of the approaches in Section 6.1, whereupon the literature is evaluated on a scientific perspective in Section 6.2. Finally, Section 6.3 provides conclusions and opportunities for further research.

6.1. Practical perspective

Table 4 shows the use of datasets by researchers in the multi-disciplinary research field. Note that some papers did not present numerical experiments, and are therefore not included in the table. The majority of researchers use case studies and real-world data to show the applicability of their research to health care practice. This is in line with the findings of Bergh et al. (2013), who observe that real-world data is generally preferred over theoretical data.

Table 4.

Data-sets.

Data source	References
Generated data	Azadeh et al. (2014), Barz and Rajaram (2015), Cordier and Riane (2013), Hulshof et al. (2013), Hulshof et al. (2016), Jerić and Figueira (2012), Matta (2009), Matta and Elmaghraby (2010), Paulussen et al. (2003), Saadani et al. (2014), Saremi et al. (2015), Schimmelpfeng et al. (2012), Shin et al. (2010), Vermeulen et al. (2007), Vlah et al. (2011), Zhao et al. (2015), Zonderland et al. (2015)
Historical data	Aslani and Zhang (2014), Azadeh et al. (2014), Azadeh et al. (2015), Barz and Rajaram (2015), Bikker et al. (2015), Braaksma et al. (2014), Cardoen and Demeulemeester (2008), Cheng et al. (2008), Chern et al. (2008), Chien, Tseng et al. (2008), Chien, Huang et al. (2008), Conforti et al. (2011), Day et al. (2010), Dharmadhikari and Zhang (2011), Du et al. (2013), Gartner and Kolisch (2014), Hu et al. (2009), Kalton et al. (1997), Kapadia et al. (1985), Kapamara et al. (2007), Lebcir et al. (2017), Leeftink et al. (2016a), Leeftink et al. (2017), Liang et al. (2015), Lin (2015), Matta and Patterson (2007), Mutlu et al. (2015), Oh et al. (2013), Oh et al. (2014), Pérez et al. (2011), Petrovic et al. (2013), Podgorelec and Kokol (1997), Proctor et al. (2007), Qu et al. (2013), Romero et al. (2013), Rossi et al. (2013), Sadki et al. (2011), Saremi et al. (2015), Kortbeek et al. (2017), Venkitasubramanian et al. (2015), Vermeulen et al. (2007), Vermeulen et al. (2008), Villa et al. (2014), Vlah et al. (2011), Vrugt et al. (2017), Werker et al. (2009), Zhao et al. (2015)

Most authors consider multi-disciplinary clinic data from a single hospital or a single division within a hospital. This shows a connection of the proposed solution methods with hospital practice. However, this also comes at a risk of optimising an approach towards a single problem setting, and makes it hard for other health care practitioners to evaluate whether the approach will be beneficial to their hospital settings. To show their multi-disciplinary planning approach is suitable for a wide range of health care institutes, Chern et al. (2008) test their approach to data-sets from two hospitals. Next to this work, we found no other papers that include a comparison between multiple hospitals.

Given that the OR literature reports on many promising approaches, with high benefits for practice, the number of papers found in this review that mention implementation in practice is rather low. This is similar to the implementation rate of OR approaches in mono-disciplinary environments (Ahmadi-Javid et al., 2017). Therefore, for multi-disciplinary environments it is even more important that a planning solution is clear, explicit, and easily manageable.

When applying OR approaches in practice, two implementation directions can be chosen. First, interventions can be adopted by the hospital without major changes to existing information systems, such as a new planning rule, staff schedule, or priority system (Leeftink et al., 2016a; Liang et al., 2015). These interventions are often the result of an extensive analysis where the effect of multiple interventions was assessed. Second, planning approaches can be implemented in the existing information systems (Braaksma et al., 2014; Chien, Tseng et al., 2008). However, this type of implementation regularly takes more time and often requires considerable investments from the hospital side. A reason for this is that system changes are bounded by the possibilities of the existing information system(s) and that it requires the (necessary) data to be available. Although the possible impact of interventions that are implemented into existing information systems might be larger, it is harder and more costly to achieve than a successful implementation of simple, hands-on interventions.

Table 4 shows that 28% of the papers in this review use generated data. One-third of them combines the use of generated and real life data, to show both the practical perspective, as well as some theoretical results. The combination of generated data and real life data is used in two ways. First, generated data can be used to show the performance and optimality of a proposed method, whereafter real-life data is used to solve a practical problem (Azadeh et al., 2014; Barz & Rajaram, 2015). Second, generated data can be used to compare the performance of the proposed method with well-known approaches in the literature, where after real-life data is used to solve a practical problem (Saremi et al., 2015).

6.2. Scientific perspective

Multi-disciplinary appointment planning research is relevant in both the OM/OR and the Medical field. Therefore, we assess the scientific perspective in both fields.

6.2.1. Operations Management/Operations Research

For OM/OR researchers, it is relevant to be informed about the technical details of the developed approach, the modelling novelties, and the performance of the approach. Where the first two items are structured in a generic way and well documented in most papers in this review, the documentation on the performance of methods has no generic structure.

First, the performance of a model can be evaluated by showing that an approach provides the optimal solution, or by showing that for smaller instances an optimal solution is derived (e.g., Azadeh et al., 2014; Barz & Rajaram, 2015). This way, researchers show that their approach gives (near-) optimal solutions.

Second, the performance of a model can be compared to the current practice in a partnering hospital (e.g., Azadeh, Baghersad, Farahani, & Zarrin, 2015; Leeftink et al., 2016a). This way, researchers show that their approach results in an improvement for their partnering hospital.

Third, the performance of a model can be compared to the performance of known solution approaches present in the literature. We found 2 papers that compared their solution methodology to already known solution approaches (Saremi et al., 2015; Vlah et al., 2011). A reason for a low comparison rate is the high variation in problem settings of the multi-disciplinary appointment planning problem. In Section 6.1 we saw that many authors perform a case study. Therefore, many authors formulate their problem according to a practical situation which they encountered in the hospital they work with, which creates a high diversity in problem settings. To enable the comparison of approaches, generic multi-disciplinary problem settings should be agreed upon by researchers, which can be extended by authors to create the specific setting of their collaborating health institution. A second reason for a low comparison rate is the lack of benchmarking instances in multi-disciplinary appointment planning. Although some authors mention that their multi-disciplinary planning datasets are available for other users, these are not widely used, which forces researchers to analyse the performance of a solution approach in multi-disciplinary appointment planning with their own dataset. The lack of multi-disciplinary appointment planning benchmarking instances is in line with the lack of benchmarking instances in health care scheduling in general. Only a few benchmark sets are known for health care scheduling problems, such as a patient admission scheduling set (Ceschia & Schaerf, 2011), and a surgery scheduling set (Leeftink & Hans, 2017). Nurse scheduling is an exception, as many nurse scheduling benchmark sets are available, and most authors benchmark their approaches against the existing literature.

The papers that included a comparison with known approaches, perform this comparison in different ways. Saremi et al. (2015) use generated instances to compare their multi agent tabu search approach with a well-known genetic algorithm, although both approaches are implemented in different coding languages. Vlah et al. (2011) first compare their heuristic with an optimal approach to show their approach often derives optimal solutions for small problem instances, and good solutions for real life instance in a reasonable amount of time. Furthermore, they find that their approach results in a lower computation time than the computation time reported upon in another paper covering a similar problem.

6.2.2. Medical

The majority of medical research papers found on multi-disciplinary care systems focuses on (medical) outcomes, the involvement of operations research techniques in the design of these systems is rarely reported upon. Novel approaches that improve the quality of care, quality of work, and the efficiency of processes are of interest to medical researchers. As multi-disciplinary systems are increasingly introduced, an efficient organisation of these systems is of high value.

Multiple multi-disciplinary systems are reported upon in the medical literature. Examples are the implementation of a carousel for Huntington’s disease (Veenhuizen & Tibben, 2009; Veenhuizen et al., 2011), a rapid access clinic for breast cancer (Arnaout et al., 2013), and a multi-disciplinary epilepsy clinic, in which a carousel with consultations with multiple as well as single clinicians are planned (Geerlings et al., 2016).

Although the majority of the multi-disciplinary system papers in the medical literature only focus on outcomes and not on the organisation of care, two exceptions are present (Geer et al., 2012; Leeftink et al., 2016b). Both of these papers, which comment on the implementation of multi-disciplinary systems and highlight the predicted outcomes and impact, have an OR equivalent besides the medical paper (Romero et al., 2013; Leeftink et al., 2016a respectively). This way, results are disseminated both to the OM/OR researchers, and to the medical researchers.

6.3. Conclusions and further research

Planning of multi-disciplinary care is applicable to many health care areas. Therefore, most studies derive their problem formulation from a real-world case, and test their approach in a case study of an existing health care setting.

To increase the practical perspective, and to convince health care managers that an approach is suitable for a wide range of health care institutes, researchers can apply their approach to data-sets from multiple hospitals. Besides comparing multiple hospitals, authors may already be able to show their approach is generic by analysing multiple departments within one hospital. This is especially useful when these departments have different characteristics, such as differences in patient load, throughput time, and capacity.

To create impact with research results in a health care environment, attention should be paid to the dissemination of both the theoretical as well as the practical results (Brandeau, 2016).

7. Conclusions and open challenges

This section presents the conclusions of this review in Section 7.1. Following from the conclusions, several open challenges and research opportunities are identified in Section 7.2.

7.1. Conclusions

This paper provides a review of the literature on multi-disciplinary planning in health care. We evaluated all prescriptive studies on this topic based on several classification fields, including the application area, the decision delineation/hierarchical level, system characteristics, the incorporation of uncertainty, and the theoretical and practical perspective.

Multi-disciplinary systems are more and more observed in the medical context. They are characterised by their low no-show rates, since patients do not intend to risk missing multiple appointments in a row. Most care systems work with pre-scheduled appointments, except for the multi-disciplinary walk-in setting at the emergency department. The involvement of multiple disciplines with often limited availability and time restrictions between appointments make the planning problems complex and highly constrained. Furthermore, often a mix of objectives is considered, since not only the system as a whole should be optimised, but the individual disciplines also require a good performance.

Despite the characteristic aspects of multi-disciplinary planning, it is hard to differentiate multi-disciplinary planning literature from general appointment planning literature without an in-depth literature search, as only few researchers specifically mention the multi-disciplinary nature and its specific characteristics in their work. Therefore, this research aims to give researchers in this field an overview of the available literature in this research area. However, we encourage future researchers to clearly state the characteristics of their work, by including whether they observe a system with multiple interrelated appointments per patient and servers of multiple disciplines or facilities.

Many studies have focused on offline capacity-to-patient assignment, in which all patient demand is known. However, our experience is that we often encounter situations in practice in which patients are scheduled in an online manner, at the moment of arrival. Online planning is frequently studied in simulation settings, where several scenarios are evaluated. However, further research is needed in the optimisation of online planning systems where variability is taken into account.

Most multi-disciplinary appointment planning research has a strong focus on the impact in practice. Many studies include some sort of case study, which may imply collaborating with a health care institute, and the testing of OM/OR approaches in practice. However, not many manuscripts include details about actual implementation in the practical setting. Furthermore, the generality and scientific relevance of the work of most reviewed papers is unclear, as only one case study is evaluated.

To analyse a multi-disciplinary system, the chosen optimisation and evaluation method should be able to deal with a large state and decision space in reasonable time. Therefore, many researchers opt for heuristics and simulation studies. Furthermore, the motivation for organising the care in a multi-disciplinary fashion should be taken into account, as this is a driver for the performance measures to include in the models. When many variable aspects are involved in a planning decision, researchers may consider designing specific planning solutions that can deal with variability, to avoid bullwhip effects.

7.2. Open challenges

Since multi-disciplinary appointment planning is an emerging field in medical practice, and therefore in health care optimisation research, we expect increasing attention for this research field from researchers in the near future. From this review, multiple future research directions can be derived:

1. This review showed cross-relations in optimisation and design questions of different health care applications that were solved in isolation. It is an open challenge to develop general approaches for systems with similar characteristics in multiple medical contexts.

2. Planning problems in multi-disciplinary care systems are often complex and need to be robust against all kinds of variability. It is an open challenge to facilitate in the high need for stochastic optimisation methods that can deal with a large state and decision space in reasonable time.

3. Section 5 showed a lack of robust planning solutions with respect to variability in treatment requirements, resource capacity and appointment durations. It is an open challenge to develop approaches that incorporate multiple of these uncertain variables.

4. Online planning systems, for which many health care applications exist, are most frequently analysed using evaluation methods. It is an open challenge to optimise online systems, where many future scenarios need to be taken into account, for example by means of stochastic programming, dynamic programming or robust optimisation.

5. From a health care perspective, it is an open challenge to evaluate and optimise the alignment of staffing schedules to multi-disciplinary clinic appointment schedules, multi-disciplinary team meetings, and combination appointments in a static and dynamic setting.

6. As health care institutes deliver care from a patient perspective, industry solutions need to be adapted from a system or end-user focus to a patient (product) focus. It is an open challenge to analyse flexible flow-shop systems for systems that focus on patient centeredness, and personalised diagnostics and treatment.

7. Only few researchers analysed open-shop planning, where performance is assessed on the combination of access time and direct waiting time or throughput time. It is an open challenge to combine both time measures in optimisation approaches, as two time scales are involved.

To maximise the chances of actual implementation, researchers should closely collaborate with the multi-disciplinary team and be aware of their motivation for organising care in a multi-disciplinary fashion. This will increase the focus on patient centeredness as well as the development of clear and simple solutions.

In sum, since health care systems are more and more organised in a multi-disciplinary way, and various health care applications share common characteristics and underlying models, cross-relations within different applications can enrich the knowledge on multi-disciplinary care planning solutions. With this review, we encourage researchers to combine the insights and methods from cross-related applications to lift the planning of multi-disciplinary care to a higher level.

Appendix 1.

Terminology

Table A1.

Term used in paper	Other terms used in literature	Explanation
Access time	Indirect waiting time	Time from the request of an appointment series to the start of the first appointment
Activity		Part of a care pathway
Appointment		Scheduled consultation
Appointment duration	Processing time (of an appointment); Service duration	Time that one appointment takes in reality. This might be different from the length of the appointment slot.
Arrival rate		Average number of arrivals per time unit
Batch scheduling		Scheduling a group of jobs which can be served simultaneously
Benchmarking		Comparing performances of different situations
Blocking		Not allowing any patients to enter a full system
Blueprint		Template of the appointment slots in an agenda
Cancellation		Scheduled activity that pre-announced will not take place
Capacity		Maximum amount of patients or time that a resource can serve per time unit
Capacity dimensioning		Hierarchical level of planning decisions that focuses on the long-term and is based on highly aggregated information
Capacity planning		Hierarchical level of planning decisions that focuses on the mid-term and on dividing resource capacity to tasks, specialties or patient groups
Capacity-to-patient assignment		Hierarchical level of planning decisions that focuses on the short-term and on appointment planning at the individual patient level
Care pathway	Patient routing (routing probabilities); Care chain	Sequence of activities that are required for a patient
Carousel	One-stop-shop	Medical term for a (flexible) flow-shop
Case study		Study focused on an existing problem setting
Combination appointment		Appointment where more than one care giver should be present
Consultation		Meeting with a health care professional
Crossover		Use of planning solution designed for one application to a similar care system
Cross-relations		Identification of similar planning problems in different applications
Descriptive techniques		Techniques for hypothesis testing
Discipline		Specialisation
Flexible shop		A shop system in which patients can undergo a subset of the activities
Flow-shop		Job shop system in which the order of activities for every patient is fixed
Idle time		Unproductive time for resources
Long-stay patient		Patients admitted to the hospital who are expected to stay several weeks
Mixed shop		Job shop system in which the order of activities for every patient is partially fixed, and partially not fixed.
Multi-disciplinary care		care in which multiple interrelated appointments per patient are scheduled, where health care professionals from various facilities or with different skills are involved.
No-show		A patient who does not show up for (one of) his/her appointments. The probability of a patient being a no-show is called the no-show rate
Offline planning		Planning where requests are saved up and scheduled once per time period
One-stop-shop		Medical term for a (flexible) flow-shop
Online planning	Advance planning	Planning where requests are scheduled immediately upon arrival
Open-shop		Job shop system in which the order of activities for every patient is not fixed
Outpatient clinic		Part of the hospital designed to treat patients who are not admitted
Overtime		Amount of time worked beyond normal working hours
Punctuality of patient/ doctor		Accuracy of a patient/doctor to start a scheduled activity on time
Precedence constraints		Requirements for the sequence of appointments
Predictive techniques		Forecasting techniques
Prescriptive techniques		Techniques for improvement and optimisation
Resource allocation		Assignment of resources to different tasks, specialties or patient groups
Same day appointments		Multiple appointments that are scheduled on the same day. Not to confuse with an appointment that is scheduled on the same day as the request came in.
Service divergence		The degree of variability in sequences and activities of services.
Short-stay patient		Patients admitted to the hospital who are expected to stay several days
Term used in paper	Other terms used in literature	Explanation
Specialty clinic		Part of the hospital or separate facility that offers all diagnostics and treatment for a certain specialty
Tardiness		Amount of time exceeding a deadline
Throughput time	Turnaround time; Completion time; Makespan; Flow time	Total time that it takes a patient to finish his/her appointment series. This is a summation of the direct waiting time of a patient and the processing times of all appointment slots the patient was scheduled in.
Time slot	Appointment slot	Position in an agenda
Treatment planning		Setting a week, day and/or time slot for treatment appointments
Waiting time	Direct waiting time	Sum of the time from the scheduled start of the appointments in an appointment series to the actual start of these appointments
Walk-in patient		Patient who wants an immediate consultation without a scheduled appointment

Funding Statement

This research is partially funded by the Netherlands Organization for Scientific Research (NWO) [grant number 406-14-128].