Abstract
Since the seminal work of Yarbus, multiple studies have demonstrated the influence of task-set on oculomotor behavior and the current cognitive state. In more recent years, this field of research has expanded by evaluating the costs of abruptly switching between such different tasks. At the same time, the field of classifying oculomotor behavior has been moving toward more advanced, data-driven methods of decoding data. For the current study, we used a large dataset compiled over multiple experiments and implemented separate state-of-the-art machine learning methods for decoding both cognitive state and task-switching. We found that, by extracting a wide range of oculomotor features, we were able to implement robust classifier models for decoding both cognitive state and task-switching. Our decoding performance highlights the feasibility of this approach, even invariant of image statistics. Additionally, we present a feature ranking for both models, indicating the relative magnitude of different oculomotor features for both classifiers. These rankings indicate a separate set of important predictors for decoding each task, respectively. Finally, we discuss the implications of the current approach related to interpreting the decoding results.
Keywords: eye movement, saccades, fixations, machine learning, classification, random forest, logistic regression, features
Introduction
Visual attention is necessary to deal with the enormous amount of information that is presented to our visual system as it filters incoming information to facilitate complex interactions with our environments. A critical part of this filtering process is reserved for the oculomotor system. The goal of this attention-guided system is to focus the fovea on objects of interest by moving our eyes. The decision where to move our eyes is influenced by a range of different factors, including the saliency of the scene in front of us, previous experiences, and the goals and intentions of the observer (Itti & Koch, 2001;Schütz, Braun, & Gegenfurtner, 2011; Van Zoest, Van der Stigchel, & Donk, 2017). It is known, for instance, that the pattern of viewing behavior for identical natural scenes is influenced by the task which has been given to the observer. This was initially demonstrated by Yarbus, who provided convincing evidence that different cognitive tasks produce profound differences in viewing behavior (Yarbus, 1967).
Ever since then, a multitude of work has been conducted regarding the effect of task-set on oculomotor behavior (for a review, see Henderson & Hollingworth, 1998; Vo & Wolfe, 2015). Indeed, Yarbus’ first discoveries have been replicated many times over the years. These studies have shown that oculomotor measures, such as fixations and saccades, may vary as a function of task set. Since then, the field of decoding the underlying cognitive mechanisms behind these task-induced differences has been influenced greatly by advancements in pattern classification. In other fields of research, state-of-the-art machine learning methods for pattern classification have been applied to a wide range of research domains, as well as practical applications (Kotsiantis, Zaharakis, & Pintelas, 2007). Using a more data driven perspective, recent work has shown the application of such models in decoding the underlying cognitive mechanisms behind differences induced by different viewing tasks. Early data-driven approaches at such decoding models were not deemed successful (Greene, Liu, & Wolfe, 2012). However, Borji and Itti found that it was indeed possible to decode the observers’ task by eye-movement features by expanding the search for a better model (Borji and Itti, 2014). Additionally, Henderson and colleagues have reported similar results during photograph, scene, and text viewing by using a naïve Bayes classifier model (Henderson et al., 2013). Similarly, other work has propagated probabilistic models that enable the modeling of time dimensions in eye-tracking data (Haji-Abolhassani, & Clark, 2014; MacInnes, Hunt, Clarke, & Dodd, 2018). Additionally, Tseng, Cameron, Pari, Reynolds, Munoz, and Itti (2013) have shown promising results applying a Support Vector Machine classifier on viewing behavior in an attempt at classifying neurological disorders. Finally, it seems that human observers are also able to classify different trial conditions. In a study by Bahle, Mills, and Dodd (2017), human observers were able to correctly classify conditions above chance when viewing images overlaid with oculomotor metrics (e.g., fixation locations and durations, scan paths) although to a very low degree of proficiency. However, the results here imply that humans themselves may not be able to parse task information from eye movements alone, further emphasizing the importance of machine-learning approaching for decoding cognitive mechanisms.
Previous studies have mostly applied continuous experimental designs to the study of task set. In these studies, observers were instructed to perform individual blocks of trials in which a single instruction was given for each block (or task was manipulated between participants). This design choice raises concerns related to ecological validity. After all, in real-life situations, attention-influenced viewing tasks change continuously and abruptly. It is known that the ability to respond fast and accurately decreases when switching between tasks. For example, a number of studies have shown that introducing a task-switching component in the experimental design results in slower and more error-prone responses (Monsell, 2003). More recent work suggests that abrupt task-switching introduces processing costs, which are represented by altered patterns of viewing behavior compared to conventional continuously continuous experimental designs (Mills, Dalmaijer, Van der Stigchel, & Dodd, 2015). This raises questions about the generalizability of earlier classification models, given that they were applied to data from experimental designs which are notably different from real-life situations.
Another potential shortcoming regarding earlier studies is that the datasets used for pattern classification might not have been large enough to maximize the potential of the models used. The ability of machine learning-based methods to classify patterns is strongly related to the amount of data available for these models. Additionally, technological advancements regarding machine learning algorithms allow for increasingly better models. Therefore modern optimized machine learning methods may provide for better classification models for behavioral viewing data.
Here, we used a large dataset in which observers’ eye movements were recorded as they were presented with a natural scene and were required to either (a) rate the pleasantness of the scene, (b) memorize the scene, or (c) perform a visual search task. To minimize differences between real-life situations, all data used in the current study were composed of experimental designs which contain both task-switching and “normal” continuous components. The main goal of this study was to attempt decoding the observer's task. Additionally, we evaluated the mixed-block subset of the dataset. For these trials, we attempted to decode task-repeat from task-switch trials, also known as task-switching. Both of these models were implemented using a wide range of eye-movement features and modern machine learning techniques. The dataset used is different from earlier work in two distinct ways. First, the dataset here was compiled over multiple experiments, resulting in a significantly larger volume of raw data. Additionally, all data used in the current study consisted of both task-switching and non-task-switching data, maximizing the similarity to real-life scenarios. Finally, both models were evaluated to examine which components of oculomotor behavior (e.g., saccades, fixations) were informative for the decoding performance of the classification models.
Method
Data
The dataset used as input for the models was compiled from several eye-tracking experiments. The setup for these studies were compliant with the guidelines agreed upon by the Declaration of Helsinki. All participants of these studies provided informed consent before participating. In these experiments, 596 observers (see Table 1 for full data description) were instructed to look at computer-generated and real-world images of various natural scenes. The stimuli used in the experiment were 120 real-world images in 1024 by 768 pixels (23.84 × 17.99 visual degrees) in color. There was one single set of images, from which 120 images were sampled for each participant, invariant of conditions. This means that for each participant, the order in which the images were presented was random, in addition to the condition being randomized. Therefore both trial type and block type conditions did not influence luminance biases during the experiments. Each image was unique and contained scene from a variety of scene categories with multiple background and foreground elements. The scenes contained indoor (e.g., bedrooms) and outdoor (e.g., buildings) locations, and none of them contained people. For the search task, participants had to determine whether letter N or Z was present. For data sampling purposes, participants were informed before the experiment that, intentionally, the target was hard to find yet present in each search trial. Because it was important that participants searched for the entire duration of every single trial, the target was present in only five out of 32 to 48 (depending on the experiment) scenes. Afterward, most participants indicated informally that they found at most five to 10 targets. For the memory task, a test display consisting of two side-by-side scenes (each 512 × 384 pixels; 12.05 × 9.05 visual degrees) was presented at the end of each trial. Therefore, during search and rating trials, a single image was used, whereas two images were presented together during memory trials. Test displays contained the same scene as presented during the trial and a slightly modified version of that same scene. It is important to note here that the eye movements during the test phase were ignored, since we were only interested in the eye-movement behavior while the stimulus was presented and not the portion of the trial when a decision was made by the participant. This was true for all conditions. Modifications were either feature substitutions, object substitutions, mirror reversals, or magnitude changes, and were intended to be unpredictable and difficult to detect so as to encourage effortful memorization; modifications were made using Adobe Photoshop 5.0. For each trial, there was a pre-fixation period of 1000 ms. Drift corrections were done after 35 trials. At the start of each trial, a fixation point was shown, after which a question appeared on the screen which determined the trial type: “search for n or z” (search), “which of these two images did you see?” (memory) or “input a numerical value of pleasantness” (rating). The experiments had a total running time of 60 to 85 minutes. The total amount of trials varied slightly per experiment but was between 96 and 144 trials total, of which each trial type was assigned one third of the trials. A visual representation is shown in Figure 1.
Table 1.
Descriptive amounts of trials, fixations and saccades per cognitive trial type and task-switching trials.
| Cognitive state | Task-switching | |||||
|---|---|---|---|---|---|---|
| Search | Memory | Rating | Total | Continuous | Mixed | |
| Participants | 596 | 596 | 538 | 596 | 529 | 212 |
| Trials | 24,427 | 25,572 | 20,212 | 70,211 | 54,100 | 16,204 |
| Fixations | 972,802 | 1,010,340 | 827,493 | 2,810,635 | 2,802,175 | 428,136 |
| Saccades | 956,519 | 994,153 | 813,995 | 2,764,667 | 2,344,991 | 419,676 |
Figure 1.
Visual example representation of search, rating and memory trials during test phase. For all but five trials, there was no actual target present in the search condition to provoke search behavior. Before the start of the experiment, participants were instructed to enter the pleasantness of the image on a seven-point Likert scale. The memory condition represents a mirror reversal modification. Note that although the conditions were randomly sampled from 120 indoor scenes, the current example in this image was not actually among them.
Additionally, some experiments contained both mixed-trial blocks and normal-trial blocks. During normal trial-blocks, an initial instruction was presented at the beginning of each block indicating the task to-be-performed throughout. This was not the case for mixed-trial blocks, in which the type of trial was randomly shuffled within the block itself and task-set was cued at the beginning of each trial. Each scene was viewed for a duration of eight seconds. However, in some conditions a probe was presented after six seconds. Therefore all trials were cut after six seconds. During these different types of trials, an SR Research EyeLink 1000 System eye-tracker (Ottawa, Ontario, Canada) recorded the eye movements of the observers. For a full review of one of the experiments, see Mills et al. (2015).
For simplicity, only event-related data were used for compiling the dataset. These files were automatically generated by the Eyelink and were preferred over raw pupil coordinate data. This event-related data consisted of all measurements related to saccades, fixations and blinks for each trial.
Blinks are known to influence eye-tracking measurements, including the number of saccades. However, earlier analyses of the data found that there weren't any differences in blink rate across conditions. Additionally, blink measurements were prone to data loss and were therefore excluded from the dataset. Since we did not have any theoretical preferences as to which measurements were distinctive for classification, the remaining event-related measurements were selected for further processing. For saccades, the number of saccades, their duration, amplitude and peak velocity were used. For fixations, the number of fixations, their duration and the pupil size were used. Blink measurements were excluded from the dataset, as they were few in number and not consistently spread across the dataset. In summary, a detailed description of the data is shown in Table 1.
Machine learning methods for classification have been around for at least a few decades and have served multiple purposes in a wide range of areas (Weiss & Kulikowski, 1991). Despite recent work, they have not been extensively used with eye-tracking data. What a machine learning classification model does, conceptually, is pattern extraction on a pool of data. In the current study, the classification model was applied to eye-movement data collected from a set of experiments. Therefore, the full data contains different task types and consist of mixed and continuous data. For decoding cognitive state, the full dataset was used (n = 596). Task-switching trials were present only in the mixed data. Therefore a smaller subset of the data was used (n = 212) for decoding task-switching. Consequently, two separate classifier models were built, which were partially overlapping. In both the cognitive state and task-switching models, the first steps are related to cleaning and preparing the data which will serve as input for the model. Subsequently, both classifiers were applied to their respective datasets to assess their ability to decode their respective problems. To maximize the performance of the classifiers, they were tweaked to optimize their fits on the data, using an independent set. Finally, the performance of both models was tested by evaluating the predictions of the model. By doing so, each model was also evaluated to examine which components of viewing behavior were most distinctive for their prediction performance.
Pupil foreshortening error analysis
Before beginning data preprocessing, we did an explorative confound analysis into pupil size confounds. Notable pupil size confounds, such as pupil foreshortening error might influence pupil size measurements and therefore introduce biases in eye-tracking data (Hayes & Petrov, 2016). Since machine learning approaches are sensitive to biases in data, we decided to explore these possible biases in more detail. First, we decided to include an additional analysis into spatial biases in relation to the pupil size. The reason for this is that possible spatial biases in fixation planes could influence pupil size. Therefore, we analyzed the cleaned data for possible biases in the horizontal and vertical planes for both trial type and block type conditions. We analyzed all endpoints of fixations in both the horizontal and vertical planes in the data, given the different trial/block types. Additionally, we ran an additional statistical analysis to analyze possible pupil foreshortening errors. To investigate possible spatial biases given the different trial and block types, we compared the differences between these groups on fixation locations in both the horizontal and vertical plane. The distributions of these locations were found to violate normality assumptions, and therefore required non-parametric testing. For all combinations of comparisons (horizontal/vertical and trial type/block type: 2x2) Kruskall-Wallis analysis of variance was used to determine whether there are differences in the average spatial biases per group. Results for both of these analyses are found in Tables 2 and 3.
Table 2.
Overview of spatial means and standard deviations for trial type conditions. Deviations as a function of condition represent differences in the horizontal/vertical plane. However, these differences were relatively small for trial type conditions.
| Trial type | Search mean (SD) | Memory mean (SD) | Rating mean (SD) | H | p |
|---|---|---|---|---|---|
| Horizontal | 512.38 (278.74) | 519.63 (266.86) | 523.59 (254.21) | 757.229 | <0.001* |
| Vertical | 395.59 (183.04) | 385.68 (163.56) | 391.15 (162.87) | 1357.117 | <0.001* |
*Significant at an alpha level of .01.
Table 3.
Overview of spatial means and standard deviations for block type conditions. Deviations as a function of condition represent differences in the horizontal/vertical plane. As in Table 2, these differences were relatively small for block type conditions.
| Block type | Task-repeat mean (SD) | Task-switch mean (SD) | H | p |
|---|---|---|---|---|
| Horizontal | 518.36 (268.94) | 517.87 (258.89) | 12.28 | <0.001* |
| Vertical | 389.98 (171.89) | 394.97 (161.60) | 298.36 | <0.001* |
*Significant at an alpha level of .01.
Although we found differences in spatial fixation locations as a function of both trial type and block type conditions, these are minor. As shown in Tables 2 and 3, these typically are within a magnitude of a few (4–10) pixels (0.09–0.24 visual degrees). As shown in Table 1, the number of fixations in the total dataset is very large. This prompts the conclusion that the influence of experimental conditions on spatial locations are minimal. Therefore we can relatively safely conclude that there are no major spatial biases present in the data. Additionally, we examined the relationship between pupil spatial locations and pupil size. If there are strong correlations between pupil size and spatial locations, this would indicate the existence of pupil foreshortening errors as a result of spatial biases. To assess these relationships, we used a spearman correlation test as a nonparametric alternative to the standard Pearson correlation. We found minor, but significant correlations between pupil size and fixation location in the horizontal plane (r = −0.026, p < 0.001) and pupil size and fixation location in the vertical plane (r = 0.078, p < 0.001). Again, the magnitude of the found relation between pupil size and spatial location was very minor. Given the fact that the size of the included data set is very large, we conclude that altered pupil sizes as a function of spatial biases are minimal. Therefore we proceeded with the preprocessing our dataset without altering it in respect to possible pupil size confounds.
Pre-processing
Cleaning
Upon initial inspection, most measurements in the data contained outliers. For instance, some saccade amplitudes were extremely high compared to the mean distribution. Machine learning models, like other statistical models, are sensitive to noisy or skewed data. Therefore we aggerated all fixation and saccade measurements over all observers. We then denoted all measurements outside of the 99.5th quantile as outliers, which were subsequently removed. Additionally, all missing values in the dataset were removed. The resulting cleaned dataset, which contained 68330 trials (97% of data), was used for the next step: feature extraction. All data processing, manipulation and analysis was done using the Python programming language (Oliphant, 2007; version 3.7.3), using Pandas (McKinney, 2010; version 0.24) and Numpy (Van Der Walt, Colbert, & Varoquaux, 2011; version 1.16.4).
Feature extraction
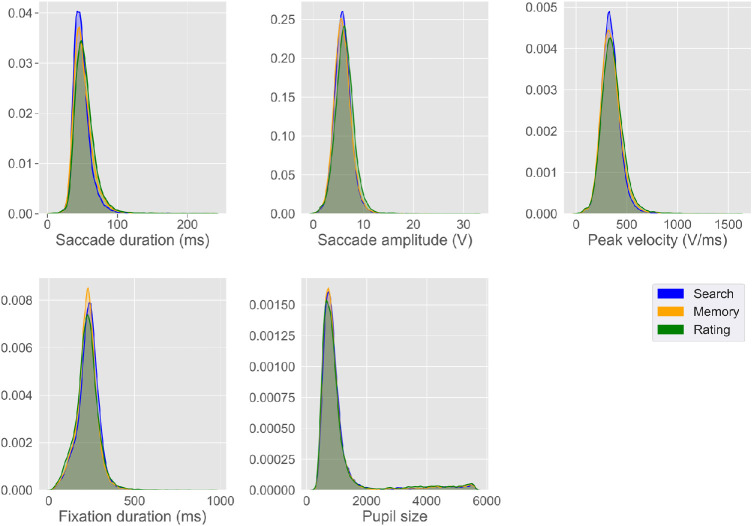
In this step, the cleaned data were transformed into features for the machine learning models. For each trial, the number of saccades, their duration, their amplitude, and their peak velocity were included. Additionally, the number of fixations, their duration, and pupil size were included in the recorded data. A first inspection of these variables showed some differences in distributions, depending on trial type. These differences indicate that these variables may hold information for decoding both trial type and block type. A visual representation of these differences is shown in Figure 2.
Figure 2.
Distributions of the five (excluding saccade and fixation numbers) base features per cognitive trial type. Distribution shapes show some deviations per type of trial.
The number of saccades and fixation were used as standalone features. The other five base measurements (saccade duration, saccade amplitude, saccade peak velocity, fixation duration and fixation pupil size) per trial were then used for computing new variables, or features, used as input for the classification model. As shown in Figure 2, the distributions of these base variables mostly overlap considering the three trial types. Therefore, a wide range of statistical features were computed from these five base variables: range, the tenth percentile, the ninetieth percentile, interquartile range, absolute mean deviation, energy, root mean square, entropy, uniformity, mean, variance, skew, and kurtosis. A more complete description of these features is found in Appendix B. These features were computed using the stats section of scipy (version 1.2.1; Jones, Oliphant, & Peterson, 2016). These features were computed for each trial, resulting in 65 input features per trial. Adding the number of saccades and fixations, this resulted in a total of 67 input features for our classification models. An overview of our preprocessing steps is shown in Figure 3.
Figure 3.

Schematic representation of data pre-processing steps.
Data splitting
It is important to estimate the generalizability of a trained classifier model beyond the input data set. In particular, we had to estimate how well the model was able to correctly predict cognitive tasks on data not seen during training. To this end, the total dataset was split into different parts on an observer level. The data were split into a training set (60% of data) and a test set (40% of data). During exploratory analysis of the data set, it became apparent that class distributions for both the full- and task-switching dataset were not equally distributed. To avoid an overly pessimistic or optimistic performance estimate, the train-test split for both cognitive state and task-switching models was performed in a stratified manner to ensure the training and testing set had the same class proportions. The test dataset is held separate until the final model has been found. Note that this procedure was repeated for both cognitive state and task-switching models.
Model implementation
Model selection
For both cognitive state and task-switching models, a number of classifiers were probed to estimate performance. For predicting trial type, a Random Forest classifier was chosen. The reason for choosing this type of model was twofold. First, the probe into different classifier models suggested that the best performance would be achieved using a Random Forest. This may imply that our features contain complex, non-linear relationships that are needed for predicting trial type. Additionally, earlier work has implicated the suitability of using Random Forest classifiers with eye-tracking based data (Zemblys, Niehorster & Komogortsev, 2018). On the other hand, for the task-switching model, model probing returned approximately equal performance across a range of models. Therefore a logistic regression classifier was chosen. Logistic regression models are straightforward, linear models and are therefore easier to interpret than nonlinear ones. Therefore analyzing which components contributed most to decoding task-switch trials became more straightforward.
Both random Forest and logistic regression classifiers were implemented using the Scikit-learn (version 0.21.2) toolbox, a machine learning library for Python (Pedregosa et al., 2011). It could be expected that a more elaborate model search could lead to better results. However, for each model to be tested it is important to optimize the architecture (hyperparameter tuning), as well as providing a method for selection of the optimal input for the model (feature selection). This process can quickly become very computationally expensive and can lead to optimistic model performances due to implicit overfitting. Therefore we used techniques that significantly reduced computational time, while still pursuing optimal model implementation.
Hyperparameter tuning
All classifier models implement a number of parameters which determine the model architecture. The model parameters—the so-called hyperparameters—that lead to the best performance is strongly dependent on the dataset, and thus requires proper tuning. There are many automated implementations for finding the best hyperparameters of a model. In the current study, a more recently popularized method named Bayesian Optimization was used, since it holds significant advantages over more common approaches, like requiring fewer model evaluations, which reduce computation time costs (Shahriari, Swersky, Wang, Adams & De Freitas, 2015). Bayesian optimization was implemented within a 10-fold cross-validation loop on the training set. Cross-validation enhances hyperparameter tuning by reducing both bias and variance of the hyperparameters (Kohavi, 1995). For this implementation, our training data was split into 10 equal folds using the same stratified procedure as above to account for class imbalance. From these 10 iterations, nine folds were combined into a training set that was the training input for the model. The remaining fold was used to validate the trained model by predicting the trial type. This was done iteratively, resulting in all folds being used to predict on at least once. During the iterations, a different combination of hyperparameters was tested. The result of this training is a set of optimal hyperparameters, cross validated across 10 folds. This procedure was implemented separately for our cognitive state and task-switching models, respectively. An overview of tuned hyperparameters for each model is shown in Appendix A.
Feature selection
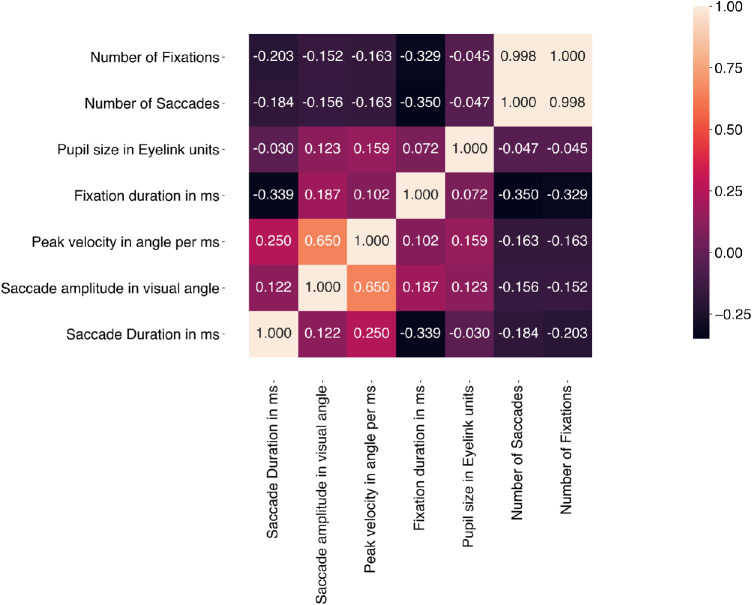
In addition to the architecture of the model, the model performance is also influenced by the input feature. Since we extracted multiple related statistical features for each base feature group, we expected multiple features to be correlated. Indeed, base features had some relationships, as shown below in Figure 4.
Figure 4.
Correlation matrix of base feature measurements.
Typically, some features which are highly interdependent contain no additional discriminative information and can safely be omitted. Furthermore, machine learning models are more susceptible to overfitting when the number of features is large with respect to the size of the dataset. Because we extracted multiple statistical features from the data, collinearity was presumed even more of a problem when expanding from a single base feature to multiple statistical ones. Therefore multiple methods were tried with the purpose of omitting redundant features: Lasso regression, t-SNE, PCA, tree-based feature selection, and recursive feature elimination (RFE). To our surprise however, all methods but RFE actually improved the performance of the model. In terms of the features, this indicates that although features were interdependent, most of them still contained discriminative information. Thus, to estimate the optimal subset of features, RFE was implemented (Blum & Langley, 1997). Identical to hyperparameter tuning, this was also implemented within a 10-fold cross-validation loop on the training set. This was implemented for both cognitive state and task-switching classifier models. The method searches for the optimal subset of features by recursively selecting subsets of features for training and subsequent predicting of the cognitive tasks. Although we used a large number of features that came from the same base distributions, we only found a small number of redundant features. In the case of our cognitive state classifier, an optimal model was found using 62 out of 67 features. For the task-switching model, this was the case for a model with 43 out of 67 features. Given the high number of features, the fact that our RFE model found optimal performance for a relative high number of features further indicates that expanding the feature space was justified given our large dataset. An overview of the full model implementation is shown in Figure 5.
Figure 5.
Schematic representation of model implementation steps.
Model evaluation
In the final step, both the random Forest classifier for cognitive state and the logistic regression for task switching were evaluated. Having optimized both the architecture of the models and the selection of features, the classifier was trained on the training dataset and subsequently applied on the independent test dataset. An additional important step when evaluating classification models is to estimate how much the performance of the model depends on the particular training set. Therefore the classifier was applied onto the same 10-folds as was used for the hyperparameter tuning and feature selection. By using this process, cross-validated average estimates of the classifier's performance could be calculated. A range of metrics can be applied to evaluate the performance of the model's classification prediction on the test set. For the current study, receiver operating characteristic (ROC) metrics were used. ROCs are graphical plots where each point on the curve relates to the number of correctly classified instances and incorrect ones for a certain threshold. These can be used to calculate the area under curve (AUC) for performance estimation.
Feature ranking
To evaluate which components of viewing behavior were important for decoding in both our random Forest/trial type and logistic regression/block type classifiers, we used additional modeling to determine a ranking of feature magnitude in each model.
Random Forest classifier: ranking cognitive state features
While our main model used a wide range of statistical features, these were all calculated based on the five aforementioned base variables (Saccades: duration, peak velocity, amplitude. Fixations: duration and pupil size). Additionally, the number of saccades, as well as the number of fixations, were defined as two additional base features, summing the total to 7. With this in mind, we designed a two-step model to evaluate the magnitude of each feature group within the random Forest classifier model. During feature ranking, we aimed to determine the relative important of the seven base features included. These break down into two groups:
-
1.
the singular values number of saccades and number of fixations,
-
2.
the five variables (saccade duration, saccade amplitude, saccade peak velocity, fixation duration and fixation pupil size) as expressed in thirteen statistics (Appendix B).
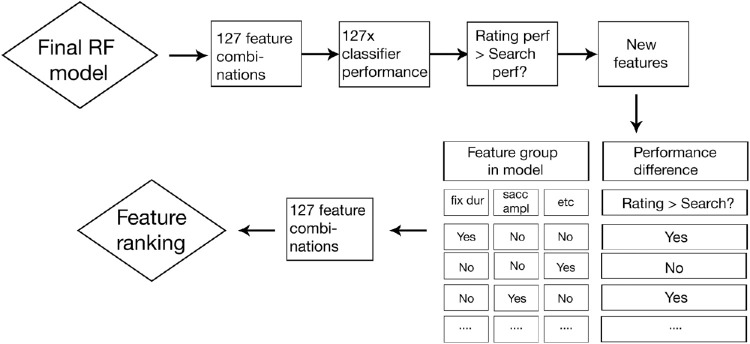
We devised this method to be able to determine, on a group level, the relative importance of each base feature. In our view, other methods for making this inference were not applicable for the current model, since our random Forest model is a tree-based solution. Because there is little need to scale this approach beyond interpretable features, scalability was not a concern. For the first step, using the seven base features groups, we deployed the final model with optimal hyperparameters. Using seven base feature groups, there are 127 unique possible combinations of nonempty feature group sets that can be combined. For each of these unique combinations, our final model was evaluated for performance. This evaluation provided AUC scores for each class over all 127 unique models. We found that depending on the input features, our model's AUC performance was especially close for search and rating trials. This performance difference might provide for a better explanation about the relation between the input features and model's performance between different classes. Therefore, in the second step, we fitted a single decision tree onto our performance metrics to determine a feature ranking. In this model, we used seven binary features which denoted whether a feature group was used in the model. The labels used were also binary; denoting whether the rating AUC for that model was higher than the AUC for search. By fitting a standard decision tree over this data, this model then holds information about the relative magnitude of different feature groups for models which strongly predict for Search trials. An overview of the total feature ranking procedure is shown in Figure 6.
Figure 6.
Schematic representation of the second step in our two-step model for determining the feature ranking for our cognitive state classifier model.
Logistic Regression classifier: ranking task-switching features
Because our logistic regression for task-switching trials was a linear model, it was possible to analyze the magnitude of different features in the classifier more directly than compared with our random Forest classifier. First, we standardized all features by rescaling them into their z-score equivalents, also known as normalization scaling. We then trained our optimal logistic regression on the standardized training set. Logistic regression models assign weights for each feature in the data they are trained on. All the features in the model were calculated from seven base feature groups. By standardizing these features beforehand, averaging the absolute regression weights over each base feature group yields the relative ranking for that feature group. By comparing these base feature groups, we determined the magnitude of each base feature when classifying block type.
Results
For clarity, both the cognitive state- and task-switching classifier models will be discussed separately. Although the technical details of the models differ, evaluating decoding performance was identical for both models (ROC/AUC metrics).
Decoding cognitive state: Random Forest classifier
Our Random Forest classifier was able to decode cognitive state well above chance. However, we found some differences in decoding performance as a function of cognitive state. Because our data included trials of search, memory and rating types, we were able to compute AUC metrics for these three types separately. As shown in Figure 7, all three AUCs were well above chance. The bold lines represent the discriminative ability for each cognitive state in the model, evaluated on the test set. In these cases, the final model is trained on the full training set and tested on the held-out test set. Confidence bands represent the average cross-validation performance of the cognitive states on the training set. For these models, not that they are trained on nine of 10 folds in contrast with the model represented by the solid line, which was trained on all data.
Figure 7.
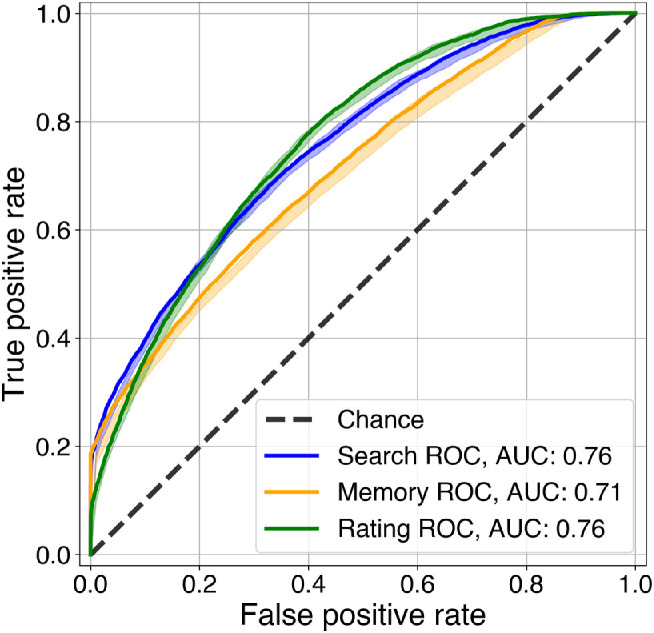
ROC/AUC performance evaluation under false-/true-positive rate for each cognitive state in our final model. Confidence bands represent cross-validation performance estimates. Although this was a single three-way classification model, note that for each trial type, the AUC represents the discriminative ability of the model when distinguishing that trial type from the remaining ones. A random classifier would score an AUCsc of 0.5.
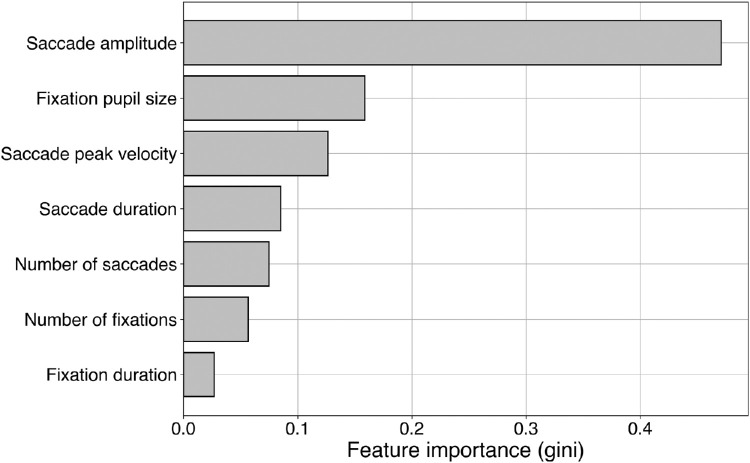
To determine the relative magnitude of each feature when classifying cognitive state, we implemented a two-step model. A decision tree classifier—which was used to determine the feature ranking for our cognitive state classifier—was fit over our data, which held information about which feature groups were important for causing differences in performance for rating and memory trials. Using this decision tree model, the features were ranked to determine the relative magnitude of importance for each feature group. The important features here are defined as the normalized total reduction of the gini criterion brought by that feature. In the context of this article, this gini function represents the amount of information gain when using a feature to split on. In other words: what is the magnitude of importance in relation to the total amount of data when using the current feature to make decisions? The important features are shown in Figure 8, where it is evident that for decoding cognitive state, saccade amplitude was the most important feature in our model. This feature ranking shows that decoding cognitive state is largely dependent on the amplitude of the saccade during the different trial types. However, other features contribute to the model as well. Both the number of saccades and fixations were not among the top features of this model. This suggests that differences in cognitive state are not captured sufficiently by simply counting the saccades and fixations. Additionally, we found pupil size an adequate predictor for cognitive state.
Figure 8.
Feature ranking for the decision tree model. These determine the relative importance of feature groups for models which strongly predicted for Search trials.
Decoding task-switching: Logistic regression classifier
Identical to our cognitive state model, our Logistic regression was able to decode task-switching well above chance (Figure 9). However, the AUC performance of .584 was lower than any of the cognitive state types. In respect to the size of the dataset used, this indicates that task-switching are a more difficult to decode using the current model. Identically to the first model, the bold line represents the discriminative ability of task-switching trials, evaluated on the held-out test set. In these cases, the final model is trained on the full training set and tested on the held-out test set. The small plotted lines represent the performance of the model for each split during cross-validation on the training set.
Figure 9.
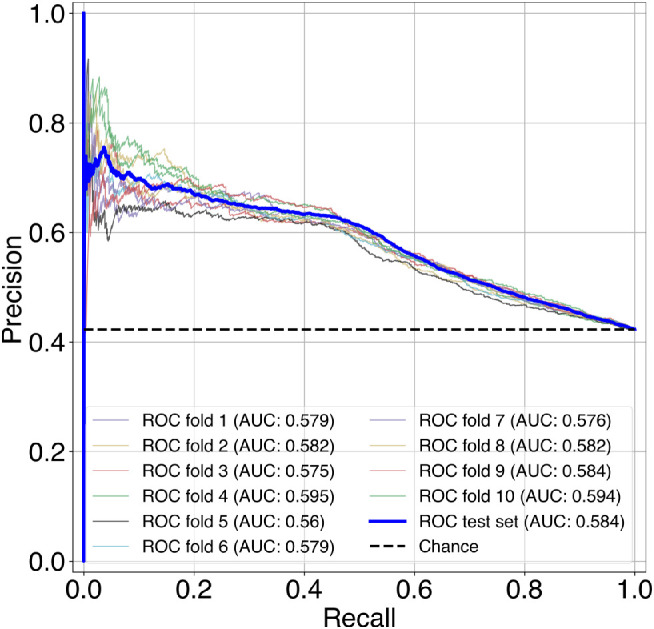
/AUC under precision -recall performance evaluation for task-switching in our final model. Smaller lines represent performance during cross-validation. Here, the AUC represents the discriminative ability of the model when distinguishing task-repeat from task-switch trials. Chance level is represented by the dotted black line.
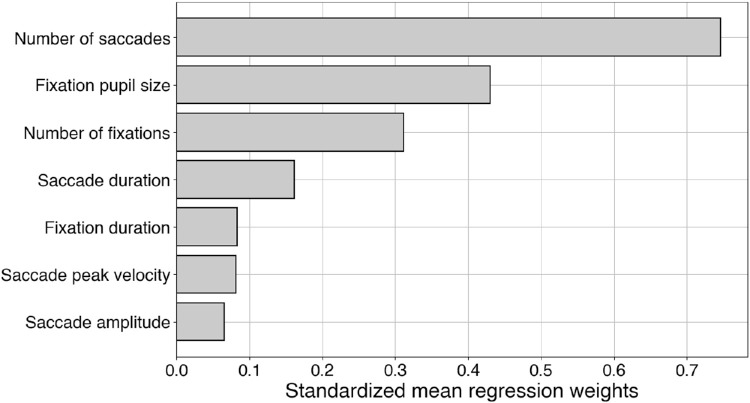
By using the standardized average regression weights over each feature group, we determined the feature ranking for decoding task-switching. The feature ranking is shown in Figure 10. In contrast with our cognitive state feature ranking, simply counting saccades and fixations seems a more fruitful approach for the task-switching model. Here, especially the number of saccades was predictive for task-switching. Even more so than for the cognitive state model, we found pupil size an adequate feature for predicting task-switching.
Figure 10.
Feature ranking for the Logistic regression model. The standardized average regression weights represent the relative magnitude of each feature group in the classifier.
Discussion
The aim of the current study was to decode the task of an observer based on patterns of behavioral viewing data. Additionally, we used the mixed blocks only for decoding task-switching. For both models, we evaluated classification performance and the relative magnitude of different features in the models.
Decoding cognitive state
By using machine learning-based classification and Bayesian hyperparameter optimization techniques, the observer's task could be correctly classified. The first notable observation is that the AUC-metrics for rating (0.76) and search (0.76) trials are similar and that our classifier was therefore able to predict these tasks roughly equally well. Results further showed that saccade and fixation measurements were sufficient for distinguishing cognitive state. A second notable observation is that our model's AUC performance related to memory (0.71) trials was the lowest for all trial types. This finding could have multiple interpretations. First, for memory trials, the patterns of viewing behavior were simply more alike to those patterns elicited by both Rating and Search trials. Largely overlapping distribution could therefore have hindered the discriminative ability of the model. This suggests that participant's viewing behavior during memory trials was still distinctive, but to a lesser degree than the other types of tasks. Regarding experimental design, memory and rating trials both involve fixating on central objects in their respective scenes (Mills et al., 2015). This can provoke viewing behavior that is more similar than comparisons between other cognitive trial types. Another possibility is that the computed features, based on features and saccades, did not fully capture the different viewing patterns for memory trials. A critical point here is that all used features in both models were implemented independent of image statistics. In other words, we did not include information about which objects or scenes were viewed during experimental trials. For memorization-like tasks, what participants fixate might be more indicative of performance than the manner by which they do. Earlier work has found this as well; human classifiers were only able to decode memory-type trials when both the original scenes and eye movements were presented to the participants but not when eye movement metrics were superimposed over a black background (Bahle, Mills, & Dodd, 2017). Additionally, they found an inverse effect for search-type trials; classification performance was reduced when including scene information during presentation. These findings emphasize that certain types of viewing behavior are scene image independent, whereas others require scene information when interpreting them. Finally, memorization tasks might involve more covert attentional processes compared with rating- and search-type tasks, which require more overt attention. Therefore purely gaze information might be less informative for memory-type tasks.
By fitting a classification tree over all 127 models resulting from our 2-step model for feature ranking, we determined the relative magnitude of the base feature groups in our classifier. As shown in Figure 8, saccade amplitude conveys important information for decoding cognitive state. Using classical methods, earlier work has found fluctuations of both saccade amplitude and fixation duration as a function of task induced cognitive state. However, these fluctuations were stronger for saccade amplitude than for fixation duration (Mills, Hollingworth, Van der Stigchel, Hoffman, & Dodd, 2011). For the current study, our feature ranking model determined saccade amplitude as the most important feature for classifying cognitive state. Identically, we found fixation duration to be important, but to a lesser degree than saccade amplitude. This finding indicates that the information in these features is partially overlapping in terms of classifying cognitive state. However, both features should be considered of importance.
Decoding task-switching
By using machine learning-based classification and Bayesian hyperparameter optimization techniques, task switching could be correctly classified (Figure 9). Although our model was able to produce a stable classifier model, decoding task-switching seems a more difficult data-driven problem (0.58 precision/recall AUC vs 0.74 average ROC/AUC). Nonetheless, this result shows the possibility of classifying task-switching with a wide range of statistical behavioral eye-tracking features. One explanation for the discrepancy in performance comes from the change in dataset size. For the task-switching model, we used mixed-block data exclusively. This amounts to 33% of the total data, which drives the point home that classifier algorithms require vast amounts of data from them to optimally utilize existing patterns in data.
By evaluating the standardized regression weights of the task-switching classifier across base feature groups, we were able to determine the feature ranking for classifying task-switching (Figure 10). In earlier work, saccade amplitude was indicated as relevant for predicting task-switching (Mills et al., 2015). For the current study, however, although important, the relative magnitude of this feature in our task-switching model was notably lower than others. In contrast, we found the number of saccades and pupil size to be important features for task-switching trials. Unexpectedly, we also found pupil size to be an important feature. It has been shown multiple times that pupil size may be strongly linked to arousal (Bradley, Miccoli, Escrig, & Lang, 2008). Therefore our feature ranking suggests that task-switching provokes changes in cognitive strain and subsequently modulates arousal. Additionally, switching conditions in between tasks might introduce considerable changes for the participants. Because all tasks required attentional resources, task-switching costs and related pupil size modulations might have been caused by uncertainty in attentional selection (Geng, Blumenfeld, Tyson, & Minzenberg, 2015).
General discussion
In the field of advanced eye-tracking modeling, there have been multiple studies into suitable modeling approaches regarding experimental designs influenced by Yarbus’ initial findings. For example, it was found that a relatively simple classifier model was not able to infer cognitive state based on oculomotor measures and image statistics (Greene, Liu, & Wolfe, 2012). Borji & Itti expanded on this by showing that, using the same feature set, classifying cognitive state was possible at a slightly above chance level by exploring different classifier models and architectures (Borji & Itti, 2014). Additionally, there have been fruitful results in applying classification methods that which explore more complex, time-based models in an attempt to model the sequential nature of viewing behavior (Haji-Abolhassani, & Clark, 2014). This body of work has some important implications compared with the current method. First, a common similarity is that all these classification approaches use some form of image statistics in their modeling. However, it is not always practical to analyze such data. Our approach shows that even independent of statistical image information, classifying separate cognitive states or task-switching costs is still perfectly feasible by using a wide range of statistical features in an attempt to fully capture maximal oculomotor behavior. Therefore oculomotor behavior in itself holds enough information for decoding cognitive constructs. Additionally, our and Haji-Abolhassani and Clark's approaches show that more complex models are likely needed for fully capturing differences in oculomotor behavior as a function of cognitive construct. Although the respectable size of our dataset, the first probed classification models showed marginal performance at first. However, the size of the dataset enabled a more extensive model search (hyperparameter tuning and feature selection) using proper cross-validation methods. These methods resulted in an optimal model that was able to classify cognitive state at a respectable above-chance level. This indicates that in the case of eye-tracking data with different cognitive conditions, extensive model building is recommended. Although our results indicate that more complex modeling is needed for decoding cognitive constructs with oculomotor data alone, this has drawbacks regarding the interpretability of such models. Because we used a high-throughput feature extraction method, we had to design a separate model which was able to determine the relative importance of each base feature, on a group level.
The current study brought forward possible confounds when analyzing pupil size measurements in the data. Pupil sizes as measured by professional eye-trackers are sensitive to possible confounds, such as pupil foreshortening error (PFE) (Hayes & Petrov, 2016). Specifically, for the current study, biases in the spatial locations of fixations were analyzed. We found very minor deviations in spatial locations in both the horizontal and vertical plane as a function of cognitive task or task-switching conditions. Additionally, we found very minor correlations between spatial location and pupil size when analyzing the full data. These results indicate that PFE confounds were not present in experimental data. Furthermore, they validate our discovery of pupil size as an important measurement for distinguishing mental states provoked by cognitive processes in a data-driven modeling approach.
The current study highlights the suitability for analyzing experimental eye-tracking data using machine learning algorithms. Compared to more classical methods of analyzing such data, our approach has certain advantages. First, earlier work has mostly focused on isolated aspects of viewing data in relation to cognitive state. Here, we were able to evaluate classification performance using most event-related eye-tracking measurements which produced a more robust and inclusive classification models for both cognitive-state and task-switching related behavior. Consecutively, this method allowed for more detailed comparisons between feature groups that are most relevant for classifying eye-tracking data. Our approach shows that when using such data, extracting a large number of features, as well as extensive model search may prove fruitful. We found that this approach is perfectly feasible, even invariant of image statistics.
Acknowledgments
Supported by NIH/NEI Grant 1R01EY022974.
Commercial relationships: none.
Corresponding author: T. M. Kootstra.
Email: t.m.kootstra@uu.nl.
Address: Utrecht University, Heidelberglaan 1, Utrecht, 3584 CS, The Netherlands.
Appendix A. Hyperparameter overview
.
| Hyperparameter | Solver | C | Warm start | Maximum iterations | Regularization |
|---|---|---|---|---|---|
| Range | newton-cg, lbfgs, liblinear, sag, saga | 0.0001–10000 | True/false | 1000–5000 | L1, L2 |
| Optimal | lbfgs | 4605 | False | 2604 | L2 |
| Hyperparameter | Minimal sample leaf | Maximal features | Minimal sample split | Criterion | Number of estimators |
| Range | 1–100 | 1–67 | 2–100 | Gini/entropy | 10–800 |
| Optimal | 1 | 1 | 2 | Entropy | 800 |
Appendix B. Used statistical features
.
| Name | Definition |
|---|---|
| Range | Distance between minimal and maximal value |
| The 10th percentile | Value at the tenth percentile of the distribution |
| The 90th percentile | Value at the ninetieth percentile of the distribution |
| Interquartile range | Distance between first and third quartile |
| Absolute mean deviation | Standard deviation |
| Energy | Functions of distances between observations based on Newtonian statistics |
| Root mean square | Square root of the mean square |
| Entropy | Measure of uncertainty within a sample |
| Uniformity | The extent to which a sample conforms to a uniform distribution |
| Mean | Arithmetic mean |
| Variance | Squared standard deviation divided by the sum of squares |
| Skew | Measure of asymmetry compared with gaussian distribution |
| Kurtosis | Measure of asymmetry compared with gaussian distribution |
References
- Bahle B., Mills M., & Dodd M. D. (2017). Human classifier: Observers can deduce task solely from eye movements. Attention, Perception, & Psychophysics, 79(5), 1415–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blum A. L., & Langley P. (1997). Selection of relevant features and examples in machine learning. Artificial Intelligence, 97(1–2), 245–271. [Google Scholar]
- Borji A., & Itti L. (2014). Defending Yarbus: Eye movements reveal observers' task. Journal of Vision, 14(3), 29–29. [DOI] [PubMed] [Google Scholar]
- Bradley M. M., Miccoli L., Escrig M. A., & Lang P. J. (2008). The pupil as a measure of emotional arousal and autonomic activation. Psychophysiology, 45(4), 602–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geng J. J., Blumenfeld Z., Tyson T. L., & Minzenberg M. J. (2015). Pupil diameter reflects uncertainty in attentional selection during visual search. Frontiers in Human Neuroscience, 9, 435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greene M. R., Liu T., & Wolfe J. M. (2012). Reconsidering Yarbus: A failure to predict observers’ task from eye movement patterns. Vision Research, 62, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haji-Abolhassani A., & Clark J. J. (2014). An inverse Yarbus process: Predicting observers’ task from eye movement patterns. Vision Research, 103, 127–142. [DOI] [PubMed] [Google Scholar]
- Hayes T. R., & Petrov A. A. (2016). Mapping and correcting the influence of gaze position on pupil size measurements. Behavior Research Methods, 48(2), 510–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson J. M., & Hollingworth A. (1998). Eye movements during scene viewing: An overview. In: Underwood G, ed. Eye guidance in reading and scene perception (pp. 269–293). Philadelphia: Elsevier Science Ltd. [Google Scholar]
- Henderson J. M., Shinkareva S. V., Wang J., Luke S. G., & Olejarczyk J. (2013). Predicting cognitive state from eye movements. PloS One, 8(5), e64937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itti L., & Koch C. (2001). Computational modelling of visual attention. Nature Reviews Neuroscience, 2(3), 194. [DOI] [PubMed] [Google Scholar]
- Jones E., Oliphant T., & Peterson P. (2001). SciPy: Open source scientific tools for Python.
- Kohavi R. (1995, August). A study of cross-validation and bootstrap for accuracy estimation and model selection. In Ijcai (Vol. 14, No. 2, pp. 1137–1145). [Google Scholar]
- Kotsiantis S. B., Zaharakis I., & Pintelas P. (2007). Supervised machine learning: A review of classification techniques. Emerging Artificial Intelligence Applications in Computer Engineering, 160, 3–24. [Google Scholar]
- MacInnes W. J., Hunt A. R., Clarke A. D., & Dodd M. D. (2018). A generative model of cognitive state from task and eye movements. Cognitive Computation, 10(5), 703–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKinney W. (2010, June). Data structures for statistical computing in python. In Proceedings of the 9th Python in Science Conference (Vol. 445, pp. 51–56). [Google Scholar]
- Mills M., Dalmaijer E.S., Van der Stigchel S., & Dodd M.D. (2015). Effects of task and task-switching on temporal inhibition of return, facilitation of return, and saccadic momentum during scene viewing. Journal of Experimental Psychology: Human Perception and Performance, 41(5), 1300–1314 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mills M., Hollingworth A., Van der Stigchel S., Hoffman L., & Dodd M. D. (2011). Examining the influence of task set on eye movements and fixations. Journal of Vision, 11(8), 17–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monsell S. (2003). Task switching. Trends in Cognitive Sciences, 7(3), 134–140. [DOI] [PubMed] [Google Scholar]
- Oliphant T. E. (2007). Python for scientific computing. Computing in Science & Engineering, 9(3), 10–20. [Google Scholar]
- Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., … Vanderplas J. (2011). Scikit-learn: Machine learning in Python. Journal of Machine Learning Research, 12(Oct), 2825–2830. [Google Scholar]
- Schütz A. C., Braun D. I., & Gegenfurtner K. R. (2011). Eye movements and perception: A selective review. Journal of Vision, 11(5), 9–9. [DOI] [PubMed] [Google Scholar]
- Shahriari B., Swersky K., Wang Z., Adams R. P., & De Freitas N. (2015). Taking the human out of the loop: A review of Bayesian optimization. Proceedings of the IEEE, 104(1), 148–175. [Google Scholar]
- Tseng P. H., Cameron I. G., Pari G., Reynolds J. N., Munoz D. P., & Itti L. (2013). High-throughput classification of clinical populations from natural viewing eye movements. Journal of Neurology, 260(1), 275–284. [DOI] [PubMed] [Google Scholar]
- Van Der Walt S., Colbert S. C., & Varoquaux G. (2011). The NumPy array: a structure for efficient numerical computation. Computing in Science & Engineering, 13(2), 22. [Google Scholar]
- Vo M. L. H., & Wolfe J. M. (2015). The role of memory for visual search in scenes. Annals of the New York Academy of Sciences, 1339(1), 72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss S. M., & Kulikowski C. A. (1991). Computer systems that learn: classification and prediction methods from statistics, neural nets, machine learning, and expert systems. San Mateo, Calif: M. Kaufmann Publishers. [Google Scholar]
- Yarbus A. L. (1967). Eye movements during perception of complex objects. In Eye movements and vision (pp. 171–211). Springer, Boston, MA. [Google Scholar]
- Zemblys R., Niehorster D. C., Komogortsev O., & Holmqvist K. (2018). Using machine learning to detect events in eye-tracking data. Behavior Research Methods, 50(1), 160–181. [DOI] [PubMed] [Google Scholar]
- van Zoest W., Van der Stigchel S., & Donk M. (2017). Conditional control in visual selection. Attention, Perception, & Psychophysics, 79(6), 1555–1572. [DOI] [PubMed] [Google Scholar]