A Bayesian analysis of doubly censored data using a hierarchical Cox model

SUMMARY

Two common statistical problems in pooling survival data from several studies are addressed. The first problem is that the data are doubly censored in that the origin is interval censored and the endpoint event may be right censored. Two approaches to incorporate the uncertainty of interval-censored origins are developed, and then compared with more usual analyses using imputation of a single fixed value for each origin. The second problem is that the data are collected from multiple studies and it is likely that heterogeneity exists among the study populations. A random-effects hierarchical Cox proportional hazards model is therefore used.

The scientific problem motivating this work is a pooled survival analysis of data sets from three studies to examine the effect of GB virus type C (GBV-C) coinfection on survival of HIV-infected individuals. The time of HIV infection is the origin and for each subject this time is unknown, but is known to lie later than the last time at which the subject was known to be HIV negative, and earlier than the first time the subject was known to be HIV positive. The use of an approximate Bayesian approach using the partial likelihood as the likelihood is recommended because it more appropriately incorporates the uncertainty of interval-censored HIV infection times.

1. INTRODUCTION

Infection with GB virus type C (GBV-C) in humans is common, but no association between the virus and any known disease state has been demonstrated [1–3]. Individuals infected with human immunodeficiency virus (HIV) are commonly coinfected with GBV-C, since GBV-C shares the same modes of transmission as HIV. The prevalence of coinfection with GBV-C in HIV-infected individuals ranges from 14 to 43 per cent [4]. Several recent studies of data from an early period in the epidemic, before the availability of effective therapy, suggest that coinfection with GBV-C is associated with prolonged survival among HIV-infected people [5–8]; other studies have concluded that there is no association [9, 10]. A meta-analysis of summary statistics is performed by Zhang et al. [11] which indicates that persistent GBV-C coinfection is associated with prolonged survival when GBV-C is measured 5–6 years after seroconversion. To further investigate this conclusion, which remains controversial [12, 13], individual level data from separate studies are modeled here.

Original data sets from three published studies [6–8] are obtained. These data sets are doubly censored. First, the origin (HIV infection time) Y is interval censored in that it is known to lie in an interval Y ∈ [L, U]. Second, the endpoint (death) time E is possibly right censored. Denote survival time T = E − Y. The dependence of T on covariates and, in particular, on the indicator of GBV-C infection is of interest. In this paper, approaches are developed for the pooled survival analysis of doubly censored data from multiple studies and applied to the pooled data from the three studies.

A random-effects model for the indicator of GBV-C coinfection incorporates the heterogeneity of patient characteristics between the studies. The most popular modeling method in survival analysis, the Cox proportional hazards model [14], avoids making any assumptions about the baseline hazard function λ₀(t). Several authors have considered Cox survival models with random effects [15–19]. Our approach builds on that of Sargent [20] and Gustafson [21] and treats the Cox partial likelihood [22] as the likelihood.

The remainder of this paper is organized as follows. Section 2 gives an introduction to the hierarchical Cox proportional hazards model. Section 3 presents different approaches to incorporating the interval censoring. In Section 4, these approaches are applied to the case study, and the results are summarized and compared. Section 5 concludes with a discussion.

2. HIERARCHICAL COX PROPORTIONAL HAZARDS MODEL

The standard Cox regression represents the relationship between the covariates of interest and the hazard of event at time t through a proportional hazards model:

$$\lambda \left(t;x_i\right)={\lambda }_0(t)\exp \left(x_i\beta \right)$$

where λ(t; x_i) is the hazard function, x_i is a 1 × p covariate vector for individual i, and β is a p × 1 vector of coefficients corresponding to fixed effects.

2.1. The hierarchical model

Suppose there are q covariates to be modeled as random effects in addition to p covariates with fixed effects. For each of the q random covariates, there are r_l levels (e.g. trials, centers, studies), for l =1, … , q, with parameter vector ${\gamma }_l={\left({\gamma }_{l1},\dots ,{\gamma }_{l{r}_l}\right)}^{\text{T}}$ corresponding to the lth random covariate. Let w_il be a scalar indicating the ith subject’s value of the lth random-effect covariate. Let $z_{il}=\left(z_{il1},\dots ,z_{il{r}_l}\right)$, with z_ilj = I_iljw_il, where I_ilj = 1 if subject i falls in the jth level of the lth random covariate, 0 otherwise. Define $\gamma ={\left({\gamma }_1^T,\dots ,{\gamma }_q^{\text{T}}\right)}^{\text{T}}$ and z_i = (z_i1, … , z_iq). Using this notation, the Cox model with random effects, a reparameterized frailty model [20], can be written as λ(t; x_i, z_i) = λ₀(t) exp(x_iβ + z_iγ). Let D denote a right-censored data set, D = {(t_i, δ_i, x_i, z_i) : i = 1, 2, … , n}, where t_i is subject i’s survival time, δ_i is the indicator for censoring, with δ_i = 0 if censored and δ_i = 1 otherwise, and n is the number of observations. Let ${\Re }_{t_i}$ be the set of subjects at risk at time t_i. If there are no ties, the partial likelihood incorporating random effects is given by

$$\mathcal{L}(\beta ,\gamma \mid \mathbf{D})\propto \prod _{i=1}^n{\left[\frac{\exp \left(x_i\beta +z_i\gamma \right)}{{\sum }_{j\in {\Re }_{t_i}}\exp \left(x_j\beta +z_j\gamma \right)}\right]}^{{\delta }_i}$$ (1)

The partial likelihood in (1) serves as the first stage of the hierarchical model and can be treated as a likelihood for computing a posterior density. Kalbfleisch [23] demonstrates that treating the partial likelihood as a likelihood leads to a limiting marginal posterior distribution of the regression parameters, assuming an independent increments gamma process prior distribution for the baseline cumulative hazard and independently a uniform distribution on the regression parameters. This result is shown with a different proof in Sinha et al. [24], which extends the results to situations with time-dependent covariates, time-varying regression parameters, and grouped survival data, and presents a Bayesian justification of a modified partial likelihood for handling ties. See also Chapter 4 of [25]. Chen et al. [26] carry out an in-depth theoretical investigation of Bayesian inference for the Cox regression model and discuss posterior propriety and computation based on Cox’s partial likelihood. Sargent [20] and Gustafson [21] present methods for Bayesian analysis of multivariate survival data using (1).

The level-specific parameters γ_lj are modeled as draws from a distribution g_l with mean μ_l and variance ν_l. Let g denote the joint density for γ, and assume γ_lj’s are independent of each other given μ_l and ν_l, for l = 1, … , q and j = 1, … , r_l. Then

$$g(\gamma \mid \mu ,v)=\prod _{l=1}^q\prod _{j=1}^{r_l}{g}_l\left({\gamma }_{lj}\mid {\mu }_l,v_l\right)$$ (2)

where μ = (μ₁, … , μ_q)^T and ν = (ν₁, … , ν_q)^T.

For the final stage of the hierarchical model, prior distributions need to be specified. A proper prior distribution for the variance component is typically essential for a proper posterior distribution and computational stability. Let f (μ, ν|ω) represent this prior distribution, where ω is the vector of hyperparameters and is taken to be known. Also let β have, independent of γ, a uniform prior distribution.

An approximate posterior distribution for the model parameters is then be assumed to be

$$\pi (\beta ,\gamma ,\mu ,v\mid \mathbf{D},\omega )\propto \mathcal{L}(\beta ,\gamma \mid \mathbf{D})g(\gamma \mid \mu ,v)f(\mu ,v\mid \omega )$$ (3)

where D are right-censored data.

2.2. Estimation of parameters using MCMC methods

The approximate posterior distribution (3) can be estimated with Markov chain Monte Carlo (MCMC) methods. The Metropolis–Hastings algorithm [27, 28] is a general term for a family of MCMC methods that are useful for drawing samples from Bayesian posterior distributions. Let θ denote the set of parameters involved in the hierarchical model. The parameter vector θ is divided into components corresponding to the hierarchy and the single-component Metropolis–Hastings algorithm is used [29].

3. ANALYSIS OF DOUBLY CENSORED DATA

Denote doubly censored data by C = {([l_i, u_i], e_i, δ_i, x_i, z_i) : i = 1, 2, … , n}, where [l_i, u_i] is the interval within which origin y_i falls and e_i is the endpoint time which is possibly right censored. Further, define a function D(·, ·) mapping a doubly censored data set C and a set of origin times y = (y₁, y₂, … , y_n)^T to a right-censored data set; specifically, D(C, y) = {(t_i, δ_i, x_i, z_i) : i = 1, 2, … , n}, where t_i = e_i − y_i. A common approach in medical applications [8, 30, 31] is that midpoints of censoring intervals are used to impute interval-censored origins, ${\widehat{y}}_i=\left(l_i+u_i\right)/2$, and are then used to compute ${\widehat{t}}_i=e_i-{\widehat{y}}_i$ in analysis assuming that they are right-censored data. In this case, $\mathbf{D}(\mathbf{C},\widehat{\mathbf{y}})=\{\left({\widehat{t}}_i,{\delta }_i,x_i,z_i\right):i=1,2,\dots ,n\}$, where $\widehat{\mathbf{y}}={\left({\widehat{y}}_1,{\widehat{y}}_2,\dots ,{\widehat{y}}_n\right)}^{\text{T}}$. Law and Brookmeyer [32] demonstrates that in HIV studies the Kaplan–Meier estimate based on this method is notably biased when origin intervals are longer than two years.

Three alternative methods are proposed below, which can be implemented using MCMC. If the partial likelihood is used as a likelihood in estimating the posterior distribution using MCMC, the assumption has to be made that this is valid under interval censoring of the origin: an assumption which has not been proved, but that seems reasonable given the results in [23, 24, 26].

3.1. MCMC for imputed data (MCMCid) approach

As a potential improvement to using the midpoint of a censoring interval, the MCMCid is proposed here, which samples a value of each interval-censored origin from an estimated distribution of origins. Let G denote the distribution function of origins y. The estimate of G, $\widehat{G}$, can be obtained either parametrically using the maximum likelihood estimation based on a known distribution (e.g. Weibull, log normal) or non-parametrically using Turnbull’s self-consistency algorithm [33]. To perform an analysis for doubly censored survival data using MCMCid, for each subject i, i = 1, … , n, a value of y_i, denoted ${\widehat{y}}_i$, is randomly sampled from $\widehat{G}$, conditional on the interval [l_i, u_i] within which y_i falls. The doubly censored data set C and imputed origins $\widehat{\mathbf{y}}={\left({\widehat{y}}_1,{\widehat{y}}_2,\dots ,{\widehat{y}}_n\right)}^{\text{T}}$ are then mapped to a right-censored data set $\mathbf{D}(\mathbf{C},\widehat{\mathbf{y}})=\left\{\left({\widehat{t}}_i,{\delta }_i,x_i,z_i\right):i=1,2,\dots ,n\right\}$, where ${\widehat{t}}_i=e_i-{\widehat{y}}_i$. The hierarchical Cox proportional hazards model can then be fit to the right-censored data $\mathbf{D}(\mathbf{C},\widehat{\mathbf{y}})$ using MCMC methods.

The MCMCid approach is straightforward to implement and understand, but underestimates the variability of parameter estimates because the uncertainty of imputed origins $\widehat{\mathbf{y}}$ is not incorporated.

3.2. Imputation-embedded MCMC (ieMCMC) approach

The imputation-embedded MCMC (ieMCMC) approach is developed as an alternative. For each MCMC iteration step m, m = 1, … , M (e.g. M = 20 000), origins ${\mathbf{y}}^m={\left(y_1^m,\dots ,y_n^m\right)}^{\text{T}}$ are randomly sampled based on their distribution $\widehat{G}$, conditional on the intervals {[l_i, u_i] : i = 1, 2, … , n} within which they fall. A right-censored data set, $\mathbf{D}\left(\mathbf{C},{\mathbf{y}}^m\right)=\left\{\left(t_i^m,{\delta }_i,x_i,z_i\right):i=1,2,\dots ,n\right\}$, where $t_i^m=e_i-y_i^m$, is generated at each iteration step m. In the ieMCMC approach, the origins y^m vary at each MCMC sampler iteration with a distribution based on $\widehat{G}$, but the estimate $\widehat{G}$ is still fixed. The uncertainty in estimating G by $\widehat{G}$ is therefore not taken into account, although the uncertainty in y^m conditional on $\widehat{G}$ is considered.

3.3. Bayesian partial likelihood (Bayesian-PL) approach

Finally, an approach is proposed with a parametric assumption on origins, which is more complete. Denote h(y|ξ) as the probability density function of the origins, with parameter vector ξ. Let p(ξ|ϖ) represent the prior distribution for ξ, where ϖ is the vector of hyperparameters governing p(·). For a doubly censored data set C = {([l_i, u_i], e_i, δ_i, x_i1, z_i) : i = 1, 2, , … , n}, define $I_{y_i}$ as the indicator function which is equal to 1 if y_i is in [l_i, u_i] and 0 otherwise. The approximate posterior distribution, based on using the partial likelihood as the likelihood, for all model parameters including the interval-censored unknown origins y can be expressed as

$$\begin{gathered} \pi (\beta ,\gamma ,\mu ,v,\xi ,\mathbf{y}\mid \mathbf{C},\omega ,\varpi )\propto \mathcal{L}(\beta ,\gamma \mid \mathbf{D}(\mathbf{C},\mathbf{y}))g(\gamma \mid \mu ,v) \\ \times \left\{\prod _i\frac{h\left(y_i\mid \xi \right)I_{y_i}}{\left[H\left({\mu }_i\mid \xi \right)-H\left(l_i\mid \xi \right)\right]}\right\}f(\mu ,v\mid \omega )p(\xi \mid \varpi ) \end{gathered}$$ (4)

where H(·|ξ) is the cumulative density function of y. At each iteration of the MCMC sampler, the origins y are drawn from their full conditional distribution, given all other model quantities. The resulting analysis provides an updated estimate of the distribution of origins, as well as correctly captures the effect of the uncertainty in origins on the estimation of the parameters of primary interest. Because (4) is an approximation of the posterior distribution, in what follows we refer to this as the Bayesian-PL method.

4. CASE STUDY

The pooled data set consists of doubly censored data sets from three studies [6–8], and each study corresponds to a different population. In studies [6, 7], GBV-C is measured at entry into the study, which is presumed to be late in HIV disease based on the cohorts’ overall CD4+ cell count. In study [8], GBV-C infection is measured at 5–6 years after documented seroconversion to HIV infection. The ‘late’ data set of the Williams study [8] is used, from the Multicenter AIDS Cohort Study (MACS), which has a documented HIV seroconversion window of approximately 6 months on average. In the MACS study, HIV infection is based on the retrospective testing of stored blood samples obtained on a regular basis, and HIV tests are negative before seroconversion and positive after that. In the other two studies, the date of subject’s first-known HIV positive test is used as the right limit of the interval within which seroconversion is assumed to occur, and 1 January 1978 (or date of birth for subjects born after 1 January 1978) is taken to be the left limit of the interval. 1 January 1978 is chosen because an analysis of stored blood samples from a study in San Francisco indicates an extremely low prevalence of HIV infection before this date in a population at risk for HIV [34].

For subjects in all the three studies, the covariate CD4+ cell count is the measurement at the time of the first-known HIV-positive test. The covariate indicating GBV-C infection in [6, 7] is the only GBV-C measurement available for the subjects in these studies. In [8] two GBV-C test results are available, one at 12–18 months after seroconversion and the other at 5–6 years after seroconversion. The measurement 5–6 years after seroconversion is deemed to be most similar to the measurement in the other two studies and the measurement that could best address the question of whether persistent GBV-C infection is associated with prolonged survival. Although the duration of GBV-C infection is not well characterized, GBV-C is shown to persist in approximately 80 per cent of HIV-infected individuals tested at both time points in [8], and acquisition of GBV-C following HIV infection is rare (see [8] and the discussion in Section 5).

The sample sizes of [6–8] are 362, 197, and 138, respectively. A summary of these three studies can be found in [11]. All studies follow subjects through the time period before the advent of highly effective therapy for HIV in 1996.

Fitting the regular Cox model to the three imputed data sets separately, the estimated log hazard ratio of GBV-C coinfection, controlling for baseline log(CD4+ count in cells/mL) and age at HIV infection, is −1.23,−1.62, and −0.97 for [6–8], respectively. For both Xiang and Tillmann studies [6, 7], HIV infection time is heavily interval censored, with a mean interval width of about 10 years. In contrast, HIV infection time in the Williams study [8] has much narrower intervals. The subjects in the Tillmann study are from Germany, and the subjects in the other two studies are from the U.S.A. The differences among the studies could be due to several reasons, including the fact that GBV-C testing is not standardized and each study used a different primer for a qualitative test. A recent study [35] indicates that the sensitivity and specificity of each test vary and that the sensitivity of one particular test depends on GBV-C RNA levels. This motivates the need for an analysis that has the ability to account for the possibly differing effects of GBV-C infection within each population. The primary endpoint for this pooled analysis is the overall survival. All 695 eligible patients are included in the analysis.

Let x_i1, x_i2, and w_i denote log(CD4+ count in cells/mL), age at HIV infection, and GBV-C coinfection status for subject i, respectively. Let I_ij = 1 if subject i is from study j, 0 otherwise, with j = 1, 2, 3 corresponding to the three studies [6–8]. Define z_i = (z_i1, z_i2, z_i3), where z_ij = I_ijw_i. Let β = (β₁, β₂)^T denote the fixed effects of covariates x_i1 and x_i2. Let γ = (γ₁, γ₂, γ₃)^T denote the random effects of covariates z_i = (z_i1, z_i2, z_i3), with constraint γ_j ∼N(μ, σ²), where μ is the population effect of GBV-C infection and σ² the population variance. Specifically, the hazard function for individual i at time t_k is given by

$$\lambda \left(t_k;x_{i1},x_{i2},z_i\right)={\lambda }_0\left(t_k\right)\exp \left(x_{i1}{\beta }_1+x_{i2}{\beta }_2+z_i\gamma \right)$$ (5)

Note that age at HIV infection x_i2 is a known deterministic function of infection time y_i. Fixed effects, rather than random effects, are used for age and CD4+ cell count as the effects from each data set of the three studies are very similar. This is unlike the effect of GBV-C in each study, which shows more variation.

In what follows, approximate posterior density, approximate posterior mean, and corresponding approximate highest posterior density region (HDR) are calculated using the approximation based on the partial likelihood. These will be referred to as posterior density, mean, and HDR for simplicity, without explicitly qualifying that they are approximations.

4.1. Prior distributions

Other than the three studies for which we have individual-level data, there are four additional studies [5, 9, 10, 36] providing only summary statistics (hazard ratio and corresponding 95 per cent confidence interval). A meta-analysis of summary statistics for these four studies is done, similarly to the meta-analysis of all summary statistics in [11]. The estimated combined effect of GBV-C in these four studies is −0.41, with an estimated standard error of 0.42. This result helps to postulate the prior distribution for μ. To be conservative, the standard error is multiplied by 2, so that μ is normally distributed as N[−0.41, (0.42 × 2)²].

A proper prior distribution for σ² is used for the sake of computational stability of the MCMC methods and to generate a proper approximate posterior distribution. A gamma distribution on τ = σ⁻² is used for τ with mean 50 and variance 10 000, denoted as Γ(0.25, 0.005). This distribution is specified by considering what values for the random effects are reasonable. For example, an assumption representing moderate heterogeneity between the studies would be that γ_j (j = 1, 2, 3) vary around μ by ±0.10. Using 0.10 as an estimate of the standard error σ leads to a prior estimate of τ = 100. A prior belief that presents substantial heterogeneity might be that the γ_j vary around μ by ±1.0. Using 1.0 as the prior standard error of γ_j leads to a prior estimate of τ = 1. The prior distribution Γ(0.25, 0.005), with mean 50 and standard error 100, gives reasonable weight to these extremes. A flat prior distribution is used for β.

4.2. Joint posterior distributions

A parametric model for the distribution of y is implemented in the example instead of the non-parametric method. Reasons for this choice include that the non-parametric maximum likelihood estimator $\widehat{G}$ given by Turnbull [133] is only unique up to an equivalence class and also has discrete components. The parametric model gives a smoother distribution for the times of infection, which is thought to more realistically model the reality of the spread of HIV infection. In addition, for the pooled data set, Turnbull’s estimate of the survival function is not very different from the maximum likelihood estimate based on assuming a Weibull distribution (see Figure 1 of a technical report [37]).

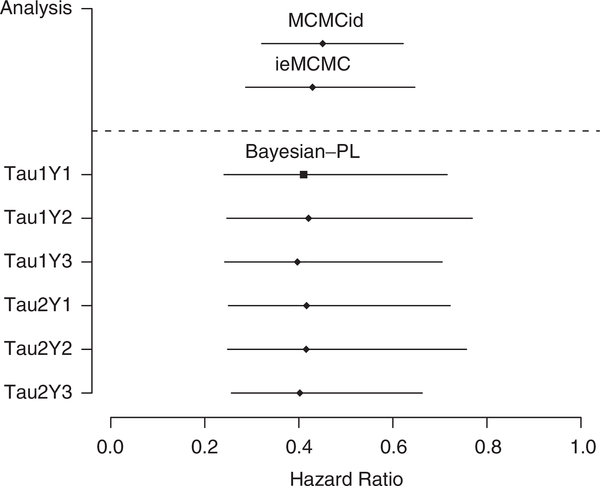
Figure 1.

Estimated hazard ratio and 95 per cent HDR from the MCMCid and ieMCMC approaches (above the dashed line), and from sensitivity analysis with different prior distributions for τ and HIV infection times y using the Bayesian-PL approach (below the dashed line). The primary analysis is Tau1Y1.

4.2.1. MCMCid and ieMCMC approaches

The distribution function G of HIV infection times y is assumed to be a Weibull(α, λ). Conditional on the maximum likelihood estimates $(\widehat{\alpha },\widehat{\lambda })$ and intervals for infection times, infection times $\widehat{\mathbf{y}}$ are randomly sampled. Let C denote the doubly censored data C = {([l_i, u_i], e_i, δ_i, x_i1, z_i) : i = 1, 2, … , n}. Following the prior distributions in Section 4.1, the joint approximate posterior density of all parameters for the MCMCid approach is given by

$$\begin{gathered} \pi (\beta ,\gamma ,\mu ,\tau \mid \mathbf{D}(\mathbf{C},\widehat{\mathbf{y}}))\propto \mathcal{L}(\beta ,\gamma \mid \mathbf{D}(\mathbf{C},\widehat{\mathbf{y}}))\prod _{j=1}^3{\tau }^{1/2}\exp \left[-\frac{{\left({\gamma }_j-\mu \right)}^2\tau }{2}\right] \\ \times \exp \left[-\frac{{\left(\mu -{\mu }_0\right)}^2}{2{\sigma }_0^2}\right]{\tau }^{a_0-1}\exp \left(-\frac{\tau }{b_0}\right) \end{gathered}$$ (6)

where $\mathbf{D}(\mathbf{C},\widehat{\mathbf{y}})=\{\left({\widehat{t}}_i,{\delta }_i,x_{i1},{\widehat{x}}_{i2},z_i\right):i=1,2,\dots ,n\}$, ${\widehat{t}}_i=e_i-{\widehat{y}}_i,{\widehat{x}}_{i2}$ is a function of ${\widehat{y}}_i$, and (a₀, b₀, μ₀, σ₀) = (0.25, 0.005, −0.41, 0.42 × 2).

The joint posterior density of all parameters for the ieMCMC approach is the same as (6), except that $\mathbf{D}(\mathbf{C},\widehat{\mathbf{y}})$ is replaced by D(C, y^m), where $\mathbf{D}\left(\mathbf{C},{\mathbf{y}}^m\right)=\left\{\left(t_i^m,{\delta }_i,x_{i1},x_{i2}^m,z_i\right):i=1,2,\dots ,n\right\}$, $t_i^m=e_i-y_i^m$ and $x_{i2}^m$ is a function of $y_i^m$. In the ieMCMC approach, D(C, y^m) changes at each MCMC iteration m, while $\mathbf{D}(\mathbf{C},\widehat{\mathbf{y}})$ is fixed during the process of the MCMCid approach.

For both MCMCid and ieMCMC approaches, given data and other parameters in the model, the full conditional posterior distribution for τ has a gamma distribution $\pi (\tau \mid \cdot )\propto \mathrm{\Gamma }[a_0+\frac{3}{2},b_0+{\sum }_{j=1}^3{\left({\gamma }_j-\mu \right)}^2/2]$, and the full conditional posterior distribution for μ has a normal distribution $\pi (\mu \mid \cdot )\propto \text{N}\left[\lambda {\mu }_0+(1-\lambda )\overline{\gamma },(1-\lambda ){(3\tau )}^{-1}\right]$, where $\lambda ={(3\tau )}^{-1}/\left[{(3\tau )}^{-1}+{\sigma }_0^2\right]$ and $\overline{\gamma }={\sum }_{j=1}^3{\gamma }_j/3$.

It is straightforward to perform the Gibbs sampling on μ and τ, but there is no direct way to draw from parameters β and γ, and the single-component Metropolis–Hastings algorithm [29] for the sampling of these two parameter components is used.

4.2.2. Bayesian-PL approach

The distribution of y is also assumed to be a Weibull(α, λ), and the prior distributions for α and λ are specified independently as log normal distributions: LogNorm $({\mu }_{\alpha },{\sigma }_{\alpha }^2)$ and LogNorm $\left({\mu }_{\lambda },{\sigma }_{\lambda }^2\right)$, respectively. For y_i ∈ [l_i, u_i], i = 1, … , n, the joint approximate posterior density of all parameters for the Bayesian-PL approach is then given by

$$\begin{gathered} \pi (\beta ,\gamma ,\mu ,\tau ,\alpha ,\lambda ,\mathbf{y}\mid \mathbf{C})\propto \mathcal{L}(\beta ,\gamma \mid \mathbf{D}(\mathbf{C},\mathbf{y}))\prod _{j=1}^3{\tau }^{1/2}\exp \left[-\frac{{\left({\gamma }_j-\mu \right)}^2\tau }{2}\right] \\ \times \exp \left[-\frac{{\left(\mu -{\mu }_0\right)}^2}{2{\sigma }_0^2}\right]{\tau }^{a_0-1}\exp \left(-\frac{\tau }{b_0}\right) \\ \times \prod _{i=1}^n\left\{\alpha {\lambda }^{-\alpha }{y}_i^{\alpha -1}\exp \left[-{\left(\frac{y_i}{\lambda }\right)}^{\alpha }\right]\right\}{\left\{\exp \left[-{\left(\frac{l_i}{\lambda }\right)}^{\alpha }\right]-\exp \left[-{\left(\frac{u_i}{\lambda }\right)}^{\alpha }\right]\right\}}^{-1} \\ \times {\alpha }^{-1}\exp \left[-\frac{{\left(\log (\alpha )-{\mu }_{\alpha }\right)}^2}{2{\sigma }_{\alpha }^2}\right]{\lambda }^{-1}\exp \left[-\frac{{\left(\log (\lambda )-{\mu }_{\lambda }\right)}^2}{2{\sigma }_{\lambda }^2}\right] \end{gathered}$$ (7)

where (μ_α, σ_α, μ_λ, σ_λ) = (1.31, 0.4, 3.51, 0.5).

4.3. Results of primary analysis

All methods are implemented in R [38], using the Metropolis-within-Gibbs algorithm. The posterior full conditional distributions of μ and τ are normal and gamma, respectively, so these parameters were drawn using Gibbs sampling. The approximate posterior full conditional distributions for parameters using the single-component Metropolis–Hastings algorithm [29] in the Bayesian-PL approach are given in the Appendix of the technical report [37]. Code is available from the first author. The WinBUGS software package [39] could not be used easily because of the doubly censored data complicated by an interval-censored covariate. Three independent chains are generated for each of the three approaches (MCMCid, ieMCMC, and Bayesian-PL approach). Each chain consists of 14 000 iterations after a series of 6000 burn-in iterations. The Brooks and Gelman convergence diagnostic [40] indicates that there is no evidence against the convergence of sampler for each parameter in all approaches.

Table I summarizes results from the MCMCid, ieMCMC, and Bayesian-PL approaches based on the hierarchical Cox proportional hazards model. The point estimates from the three approaches are similar for each parameter except for σ. For each parameter estimate, the standard error from the Bayesian-PL approach is, appropriately, the largest among three approaches, while the standard error from the MCMCid approach is the smallest one. Consequently, the 95 per cent HDR from the Bayesian-PL approach is generally wider than the one from the MCMCid or ieMCMC approach; the 95 per cent HDR from the MCMCid approach tends to be the narrowest. The differences are substantial, especially for the parameters of most interest: μ and σ.

Table I.

Comparison of results from different approaches for pooled analysis using the hierarchical Cox proportional hazards model.

	MCMCid*		ieMCMC*		Bayesian-PL†
Parameter	Mean (SE)	95 per cent HDR	Mean (SE)	95 per cent HDR	Mean (SE)	95 per cent HDR
μ	−0.797 (0.174)	(−1.136, −0.475)	−0.846 (0.208)	(−1.248, −0.436)	−0.891 (0.277)	(−1.423, −0.335)
σ	0.327 (0.413)	(0.027, 1.016)	0.425 (0.519)	(0.029, 1.292)	0.727 (0.783)	(0.028, 1.947)
γ1	−0.779 (0.145)	(−1.067, −0.494)	−0.845 (0.158)	(−1.162, −0.544)	−0.998 (0.185)	(−1.360, −0.623)
γ2	−1.073 (0.359)	(−1.812, −0.486)	−1.227 (0.416)	(−2.123, −0.596)	−1.585 (0.476)	(−2.497, −0.775)
γ3	−0.636 (0.274)	(−1.111, −0.039)	−0.623 (0.336)	(−1.190, 0.109)	−0.463 (0.412)	(−1.189, 0.339)
β1	−0.538 (0.086)	(−0.707, −0.371)	−0.569 (0.098)	(−0.756, −0.377)	−0.645 (0.101)	(−0.842, −0.444)
β2	0.013 (0.006)	(0.001, 0.027)	0.017 (0.007)	(0.002, 0.030)	0.008 (0.007)	(−0.006, 0.021)

^*Random imputation for infection times y based on the estimated Weibull $(\widehat{\alpha },\widehat{\lambda })$.

^†Prior distribution for infection times y: Weibull(α, λ), where α ∼ LogNorm(1.31, 0.4) and λ ∼ LogNorm(3.51, 0.5).

Results from all three approaches indicate that GBV-C infection is associated with prolonged survival. From the Bayesian-PL approach, the estimated hazard ratio for GBV-C viremia is $\left(e^{-1.423},e^{-0.335}\right)=e^{-\widehat{\mu }}=e^{-0.891}=0.41$, with 95 per cent probability of falling into the interval (e^−1.423, e^−0.335) = (0.24, 0.72) after adjusting for baseline log(CD4+ count in cells/mL) and age at HIV infection. Baseline log(CD4+ count in cells/mL) is also associated with prolonged survival: estimated hazard ratio $e^{{\widehat{\beta }}_1}=e^{-0.645}=0.52$, with 95 per cent probability of falling into the interval (e^−0.842, e^−0.444) = (0.43, 0.64).

4.4. Results of sensitivity analysis

To examine the behavior of the estimate of μ from the Bayesian-PL approach when the distribution for infection times y is modified, the hierarchical Cox proportional hazards model is fit using different distributions for y. Specifically, we use a flat distribution for y, a single Weibull(α, λ) for y, and a set of three Weibull distributions, one for each of the three studies, Weibull(α_j, λ_j) for y_j, j = 1, 2, 3. The choice of Γ(0.25, 0.005) as the prior for τ is also examined by using Γ(0.001, 0.001). Overall, there are 3 × 2 = 6 scenarios in the sensitivity analyses, with the first one corresponding to the primary analysis (see Table II and Figure 1). The value of $\widehat{\mu }$, the estimate for the logarithm of hazard ratio of GBV-C infection, changes only slightly, as does the standard error and 95 per cent HDR. This analysis suggests that the results are insensitive to the choice of prior distribution.

Table II.

Sensitivity analysis for the Bayesian-PL approach using different prior distributions for τ and y.

Analysis	τ	Infection times y	$\widehat{\mu }$ (SE)	95 per cent HDR
Tau1Y1	Γ(0.25, 0.005)	Weibull(α, λ)	−0.891 (0.277)	(−1.423, −0.335)
Tau1Y2	Γ(0.25, 0.005)	Weibull(αj, λj), j = 1, 2, 3	−0.866 (0.288)	(−1.398, −0.263)
Tau1Y3	Γ(0.25, 0.005)	Flat prior	−0.924 (0.272)	(−1.417, −0.350)
Tau2Y1	Γ(0.001, 0.001)	Weibull(α, λ)	−0.876 (0.271)	(−1.385, −0.326)
Tau2Y2	Γ(0.001, 0.001)	Weibull(αj, λj), j = 1, 2, 3	−0.878 (0.283)	(−1.392, −0.279)
Tau2Y3	Γ(0.001, 0.001)	Flat prior	−0.911 (0.250)	(−1.360, −0.412)

5. DISCUSSION

The imputation-embedded MCMC (ieMCMC) and the Bayesian-PL approaches are developed to deal with doubly censored survival data and compared with an MCMC analysis of a right-censored data set constructed by imputing a single value for each interval-censored origin (MCMCid). The MCMCid approach considerably underestimates the variability of the estimates. The ieMCMC allows for some uncertainty of imputed origins to play a role, but again results in underestimation of the variability of the parameter estimates. In comparison, the Bayesian-PL approach treats unobservable origins y as unknown quantities with a parametric distribution G. Prior distributions are then assigned for the hyperparameters of G. Interval censoring is treated by data augmentation [41] with $\widehat{\mathbf{y}}$ drawn from their posterior predictive distribution. The results from the Bayesian-PL approach more appropriately reflect uncertainty than the MCMCid and ieMCMC approaches. This paper demonstrates the ability of the Bayesian-PL approach to incorporate the uncertainty of imputed origins in doubly censored survival data. Our sensitivity study shows that the results from the Bayesian-PL approach are reasonably insensitive to the specification of the parametric form of G (Figure 1).

Härkänen et al. [42] presented a non-parametric Bayesian intensity model for doubly censored data in the fully Bayesian framework, which treats unobservable origins y as unknown quantities with piece-wise constant hazard functions. Hazard functions are assigned gamma prior distributions. Komárek et al. [43] applied a modified version of this approach to doubly censored dental data to examine the effect of fluoride intake on the time to caries development in children. However, these approaches are complex to implement and computationally demanding.

It should be noted that a formal justification of using the Bayesian-PL approach has not been provided for interval-censored origins and random effects. Given the results in [23, 24, 26] this assumption is not unreasonable, but additional work needs to be done.

In the case study, a completely parametric model could have been used, in which case an estimate of the survival curve would be available. The primary interest in this data analysis is, however, the question of whether or not co-infection with GBV-C is associated with prolonged survival of individuals infected with HIV disease. All three studies and the other studies in the meta-analysis [11] use data before the advent of the highly effective therapy for HIV infection, and so the survival curve itself is not of current interest.

Our analysis examines the association between GBV-C infection late in HIV disease and survival, from the time of HIV seroconversion, of HIV-infected individuals. The data available are not ideal to address the association of persistent GBV-C infection with prolonged survival, but GBV-C infection is typically persistent in that the possibility of GBV-C infection clearance or acquisition of GBV-C infection after HIV infection is small [8, 44]. The results of both [8, 13] indicate that the loss of GBV-C infection late in the disease may be predictive of shorter survival after the loss. Additional testing for GBV-C of stored samples and additional modeling are being planned to examine the joint distribution of survival and GBV-C infection.

In summary, the Bayesian hierarchical Cox model has accommodated random study-specific effects and has therefore incorporated between-study heterogeneity. Through the specification of prior distributions, the prior information relevant to the parameters of interest has been taken into account. The methods for doubly censored survival data developed in this paper have enabled the analysis of these data sets and lead to the conclusion that the hazard of death with GBV-C infection is approximately 40 per cent of that without GBV-C infection, and that the hypothesis of no difference in hazard can be ruled out with high probability. The pooled analysis of the individual subject data therefore augments and supports the meta-analysis result of the summary statistics previously reported in [11]. Biological plausibility for a beneficial mechanism and in vitro evidence in inhibiting HIV replication are provided in [6, 45–49]. However, as in all observational data, the results of our analyses do not provide evidence that GBV-C is causally related to improved survival, and it is possible that GBV-C infection is not the reason that HIV-positive individuals coinfected with GBV-C live longer but, rather, that it serves as a biological marker of a different factor related to HIV disease progression. This warrants further investigation and is a subject of debate in the scientific literature [9, 12, 13, 49, 50].