Genome-wide Modeling of Polygenic Risk Score in Colorectal Cancer Risk

Summary

Accurate colorectal cancer (CRC) risk prediction models are critical for identifying individuals at low and high risk of developing CRC, as they can then be offered targeted screening and interventions to address their risks of developing disease (if they are in a high-risk group) and avoid unnecessary screening and interventions (if they are in a low-risk group). As it is likely that thousands of genetic variants contribute to CRC risk, it is clinically important to investigate whether these genetic variants can be used jointly for CRC risk prediction. In this paper, we derived and compared different approaches to generating predictive polygenic risk scores (PRS) from genome-wide association studies (GWASs) including 55,105 CRC-affected case subjects and 65,079 control subjects of European ancestry. We built the PRS in three ways, using (1) 140 previously identified and validated CRC loci; (2) SNP selection based on linkage disequilibrium (LD) clumping followed by machine-learning approaches; and (3) LDpred, a Bayesian approach for genome-wide risk prediction. We tested the PRS in an independent cohort of 101,987 individuals with 1,699 CRC-affected case subjects. The discriminatory accuracy, calculated by the age- and sex-adjusted area under the receiver operating characteristics curve (AUC), was highest for the LDpred-derived PRS (AUC = 0.654) including nearly 1.2 M genetic variants (the proportion of causal genetic variants for CRC assumed to be 0.003), whereas the PRS of the 140 known variants identified from GWASs had the lowest AUC (AUC = 0.629). Based on the LDpred-derived PRS, we are able to identify 30% of individuals without a family history as having risk for CRC similar to those with a family history of CRC, whereas the PRS based on known GWAS variants identified only top 10% as having a similar relative risk. About 90% of these individuals have no family history and would have been considered average risk under current screening guidelines, but might benefit from earlier screening. The developed PRS offers a way for risk-stratified CRC screening and other targeted interventions.

Introduction

Colorectal cancer (CRC) is a leading cause of cancer death, yet it is among the most preventable cancers in part because CRC screening is effective for both early detection of treatable cancers and for reducing cancer risk by removing pre-cancerous lesions.¹ Despite improvements in screening and treatment, about 50,000 fatal CRC cases occurred in the United States (US) in 2019.² Better treatments have improved survival rates but achieving higher uptake and adherence to CRC screening could more rapidly reduce morbidity and mortality.^2,3 US 5-year relative survival for individuals with advanced stage cancers is below 15%, whereas individuals with cancers detected early have 5-year relative survival approaching 90%.² For those detected with adenomas, survival is essentially 100%. The guidelines for initiating CRC screening are currently based mainly on two risk factors: attained age and family history of CRC.⁴ Use of these criteria results in substantial under- and over-utilization of CRC screening with associated harms, because more than 80% of all CRC cases occur in those without a positive family history in first-degree relatives. It is therefore important to improve risk prediction to inform screening and other prevention strategies. Risk prediction using data from genome-wide association studies (GWASs) has been proposed in Kooperberg et al.⁵ Polygenic risk scores (PRS), such as those based on LDpred,⁶ have shown great promise in improving prediction for complex disease risk. The study from Khera et al.⁷ is part of an emerging corpus considering the plausibility of incorporating genome-wide PRS into disease screening within health care systems.⁸ For coronary artery diseases, the PRS was able to identify 10 times more people at the same or higher risk than the conventionally used monogenic test that identifies about 2 out of 100 individuals with an OR > 3. They showed similar results for other diseases, such as type 2 diabetes or breast cancer. Those at high risk can potentially benefit from targeted interventions, such as lipid-lowering drugs, dietary interventions, or screening.⁷

Models have been developed and evaluated for prediction of CRC risk using known genetic susceptibility variants identified by GWASs.^{9, 10, 11, 12, 13} The area under the receiver operating characteristics curve (AUC) has improved as more susceptibility variants are included with the most recent model that includes 63 known variants and family history yielding AUC = 0.59 for both men and women.⁹ However, we found known variants identified to date explain only about 10% of the heritable fraction of CRC risk.¹⁴ This suggests that substantial improvement in prediction could be achieved by using a genome-wide approach that includes many more single-nucleotide polymorphisms (SNPs) that, individually, may not reach the stringent threshold for genome-wide significance.¹⁵

Machine-learning techniques, such as support vector machines, penalized regression, neural networks, random forests, and the extreme gradient tree boosting approaches, have been applied to GWAS data.^{16, 17, 18, 19, 20} Typically, these approaches require first reducing the number of genetic variants from millions to thousands and then building a risk-prediction model from selected variants with various machine-learning methods. For example, a widely used approach for dimension reduction involves linkage disequilibrium (LD)-based marker pruning or clumping²¹ and applying a p value threshold to association statistics. As some of the familial aggregation of CRC is explained by a polygenic component, such dimension reduction based on p values may discard variants that individually have little predictive power but collectively have substantial predictive power. To account for this possibility, the LDpred method employs a Bayesian framework to jointly model all genetic variants of the genome in building the PRS without a priori dimension reduction.⁶

Using statistical and machine-learning techniques on GWAS data from more than 120,000 CRC-affected case subjects and control subjects of European ancestry, we address the question of whether a PRS that uses variants beyond known CRC risk-associated variants can improve discriminatory accuracy between CRC-affected case subjects and control subjects. We developed PRS using three different approaches, based on: (1) 140 known GWAS variants as the baseline model; (2) SNP selection followed by machine learning; and (3) LDpred. We then evaluated the performance of these scores externally in an independent contemporary community-based cohort of 101,987 study participants, including 72,791 of European ancestry.

Material and Methods

Datasets

Derivation Datasets

To develop an accurate CRC risk prediction model, we used GWAS data on 55,105 case subjects and 65,079 control subjects of European ancestry from large-scale research studies (∼120,000 participants with genotype data on more than 40 million variants), including the Genetics and Epidemiology of CRC Consortium and Colon Cancer Family Registry (GECCO) with 29,864 case subjects and 31,629 control subjects, the CRC Transdisciplinary Study (CORECT) with 19,885 case subjects and 12,043 control subjects, and United Kingdom Biobank (UKB) with 5,356 case subjects and 21,407 control subjects. For more details such as study participant characteristics, genotyping, imputation, quality control, and single-variant association analyses, readers are referred to the Supplemental Material and Methods (Section 3 and Table S1) and Huyghe et al.¹⁴ Briefly, the average age was 62 years (standard deviation [SD] = 11 years). About 52% were men and 11% had a positive family history of CRC in first-degree relatives. Our primary analysis was focused on individuals of European ancestry due to insufficient numbers of CRC cases among other ancestral groups.

Evaluation Dataset

The risk prediction models were externally evaluated in the Genetic Epidemiology Research on Adult Health and Aging (GERA) cohort, an independent contemporary cohort including 101,987 genotyped participants (≥18 years old) nested within the Kaiser Permanente Northern California (KPNC) integrated healthcare delivery system.²² Participants provided a saliva sample and broadly consented to the research use of their DNA and mailed survey data, which was then linked to selected data from electronic health records. Of note, this cohort was not used in any prior discovery of CRC risk variants and, hence, provides the opportunity for an independent evaluation. Details on the genotyping array, quality control, and imputation have been described previously²³ and in the Supplemental Material and Methods (Section 4 and Table S3).

As the model building was limited to case and control subjects of European descent defined by genetic clustering with Europeans from HapMap, we also restricted the primary analysis to the genetically defined European subsets (n = 72,791, 42,520 men and 30,271 women), which included 1,311 CRC cases, 3,949 advanced adenoma cases (AA), 13,472 adenoma cases, and 10,730 individuals with hyperplastic polyps. A personal history of cancer was determined from cancer-registry data and electronic-health-record data. A family history of CRC was ascertained by integrating data from baseline surveys and electronic health records (i.e., diagnosis codes, family history documentation). About 9.6% of participants (n = 7,029) had a positive family history in first-degree relatives. Hyperplastic polyps, AA, and non-AA were identified using Systematized Nomenclature of Medicine (SNOMED) pathology codes and validated using natural language processing.²⁴ We defined an AA as any adenoma with villous histology or which was 10 mm in size or greater. The cohort was unselected for any disease phenotype and GERA participants were not asked to engage in specific medical or screening tests for research purposes. However, given the age distribution of the GERA participants (median age at baseline = 52 years with median follow-up 21 years), 70% of population has undergone screening for CRC as part of their usual care, either by fecal immunochemical testing (FIT, 38%) or endoscopy (sigmoidoscopy or colonoscopy, 58%). All study participants provided written informed consent and the study was approved by the KPNC Institutional Review Board.

Validation Dataset

We further validated the models in an independent study, the Electronic Medical Records and Genomics (eMERGE) (n = 83,717). The details of the study were described elsewhere.²⁵ A brief description of the genotyping array, quality control, and imputation is provided in Supplemental Material and Methods (Section 5). The colorectal cancer case subjects were defined as those who had at least two ICD9/10 codes for CRC. Control subjects had zero ICD9/10 codes for CRC. Participants with a single ICD9/10 code for CRC were excluded from analysis. Adults over age 18 years who had confirmed European ancestry and no missing age were included in the validation dataset, resulting a total of 38,214 participants. The characteristics of these participants are provided in Table S10.

Polygenic Risk Score Derivation

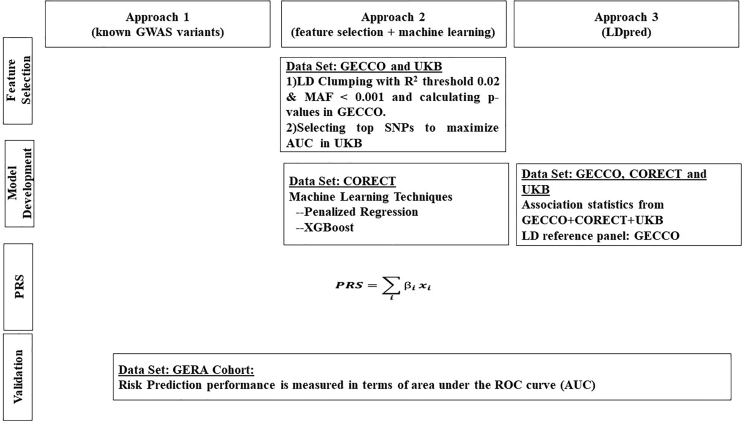
PRS provides a quantitative measure of an individual’s inherited risk based on the cumulative impact of many genetic risk variants. Each variant is scored based on the number of variant alleles an individual carries (e.g., zero, one, or two copies). The individual variant scores are then weighted according to the strength and direction of their association with disease and finally summed to give a single risk score. Imputed variants are scored by expected number of variant alleles (i.e., dosage). We studied three approaches for constructing PRS. Figure 1 depicts the summary of these different PRS derivation strategies. The weights for Approach 1 of known loci are provided in Table S4. As the number of variants for the other two approaches are very large, the weights for these variants are available upon request from the authors.

Figure 1.

Description of Three Approaches to Derive Polygenic Risk Scores (PRS) for Colorectal Cancer

Approach 1: Known GWAS Variants

Using GWAS, we and others have identified 140 SNPs that were independently associated with CRC risk¹⁴ and references therein.^26,27 All but three were present in the GERA dataset. For the three missing SNPs, we selected surrogates based on LD and the p value of univariate association analysis. The surrogates are provided in Table S4.

We calculated the PRS as a weighted sum of risk alleles ${\sum }_i{\stackrel{⌢}{\beta }}_i{x}_i$, where x_i is the expected number of risk alleles and ${\stackrel{⌢}{\beta }}_i$ is the log-odds ratio (OR) estimate of single-variant association from the previously published results that first reported the variants or meta-analysis results of our datasets. The meta-analysis adjusted for age, sex, study, and principal components (PCs) to account for population substructure. For the SNPs discovered in the data from this consortium, we adjusted for the winner’s curse.²⁸ We provided the details of meta-analysis in Section 3.3, Supplemental Material and Methods.

Approach 2: SNP Selection and Machine Learning

In this approach, we first selected a subset of SNPs using LD clumping and p value thresholding and then built risk-prediction models using machine learning. To avoid overfitting, we divided the derivation datasets into two non-overlapping sets, one for SNP selection and the other for model building.

SNP Selection. We used GWAS data from GECCO (29,864 case subjects and 31,629 control subjects) and performed univariate association analysis, adjusting for age, sex, study, and PCs to account for population substructure. To remove highly correlated SNPs, we performed LD-clumping using the LD-driven p value clumping procedure in PLINK v.1.90b (–clump).²⁹ In this process, the algorithm generates clumps around index SNPs with p values less than an a priori defined threshold. Each clump contains all SNPs that are in LD with the index SNP, within 500 kilobases, as determined by pairwise correlation (R²) threshold. The algorithm iteratively cycles through all index SNPs, beginning with the smallest p value, only allowing each index SNP to appear in one clump (non-overlapping). The final output contains the most statistically significant disease-associated SNP for each LD-based clump across the genome. To identify the optimal p value cut-off and LD-R² value, we chose a wide range of p value thresholds, from 5 × 10⁻⁸ to 0.01, and two R² values, 0.02 and 0.2, to select SNPs and calculated the corresponding PRS summing these SNPs weighted by the log-OR estimates, where the log-OR is the log-odds ratio estimate of univariate association analysis using GECCO data. We then used the UKB data (5,356 case subjects and 21,407 control subjects) to evaluate the discriminatory accuracy of these PRS (Figure S1). The AUC reached the maximum when R² = 0.02 and p value = 1 × 10⁻³. At this threshold, we had about 15,000 SNPs. We then explored further the number of SNPs ranging from 1,000 up to 50,000 and calculated the PRS by adding SNPs in the incremental order of p values. The AUC of the PRS peaked when the number of SNPs was at around 10,000 SNPs, which were used for the subsequent model building.

Model Building. Based on these selected SNPs we developed prediction models using machine-learning algorithms, using data from CORECT on 19,885 case subjects and 12,043 control subjects. We used two complementary machine-learning approaches, penalized generalized linear regression³⁰ and XGBoost.³¹ We obtained the optimal values of the tuning parameters using 10-fold cross validation and re-estimated the regression coefficients using the entire CORECT data at the optimal tuning parameter values.

We performed penalized regression including both the known GWAS variants PRS and top SNPs from the SNP-selection step adjusting for age, sex, genotyping phase, and PCs. The confounders and known GWAS variants PRS were not penalized. We calculated the overall PRS by summing the known loci PRS and ${\sum }_{i=1}^N{\stackrel{⌢}{\beta }}_i{x}_i$, where x_i is the i^th selected SNP and ${\stackrel{⌢}{\beta }}_i$ is the corresponding regression coefficient estimate from penalized regression. We performed ridge, lasso and elastic net penalized regression. We used the R package glmnet for the ridge and lasso regression and caret for the elastic net.

XGBoost³¹ is based on gradient boosted decision trees, which, in contrast to penalized regression methods, incorporate complex non-linear interactions into prediction models in a non-additive form. Boosting is a powerful ensemble learning algorithm in which weak classifiers are added sequentially to correct the errors made by existing classifiers toward building a strong classifier. As in the penalized regression, we included both the known loci PRS and top SNPs from the SNP-selection step. The PRS from XGBoost is the classifier that gives the smallest misclassification error in cross-validated datasets. We derived the model using the R package XGBoost, a fast and efficient implementation of the gradient tree boosting method.

Approach 3: LDpred

LDpred⁶ is a Bayesian genetic risk prediction method, developed for genome-wide genetic risk prediction, which takes into account LD among the markers (SNPs). In an infinitesimal model, all markers are assumed to be causal and the marker effects follow a normal distribution, i.e., ${\beta }_i\sim N\left(0,\left(n^2/M\right)\right)$, i = 1, …, M, where M is the total number of markers and h² is the total heritability explained by the markers. In the non-infinitesimal model, only a fraction of the M markers is assumed to be causal. A Gaussian-mixture prior is assumed in which ${\beta }_i\sim N\left(0,\left(n^2/M_{\rho }\right)\right)$ with probability ρ and ${\beta }_i\sim 0$ with probability (1 − ρ). LDpred computes the posterior mean effects of markers, taking into account the LD structure.

We used summary statistics from all GWASs, including GECCO, CORECT, and UKB, and calculated LD using the genotypes from a subset of our samples (29,305 case subjects and 31,727 control subjects) to reduce computational burden; this far exceeded the at least 2,000 individuals as suggested by LDpred. We further restricted the genetic markers to the HapMap3 panel to circumvent the non-convergence issue from training on summary statistics of very large sample sizes. LDPred requires a prior specification of ρ, the fraction of causal variants. Because ρ is generally unknown, we used a range of values for ρ: 1.0, 0.3, 0.1, 0.03, 0.01, 0.005, 0.003, and 0.001, the default values recommended by LDPred. A total of 8 candidate PRS were derived. The analysis was performed using the software LDpred.

Evaluation of Model Performance in an Independent Cohort

We evaluated the discriminatory accuracy of PRS derived from the three approaches described above in the GERA cohort by calculating the AUC.³² Our primary outcome was CRC in European ancestry. We compared CRC case subjects with control subjects who did not have CRC or any precursor lesions, including AA, adenomas, or hyperplastic polyps. As a secondary analysis, we evaluated the AUC for AA, non-AA, and hyperplastic polyps, respectively. As sensitivity analyses, we estimated AUC using control subjects who also had precursor lesions in a sequential manner: that is, for the CRC analysis, control subjects included any precursor lesion; for AA, control subjects included adenoma and hyperplastic polyps; and for adenoma, control subjects included hyperplastic polyps. In addition, we estimated the AUCs stratified on first-degree family history (yes/no), sex (men/women), and other race/ethnicity (Asian, Hispanic, and African American). We adjusted for age (at diagnosis for case subjects and at last observation for control subjects) and sex in all AUC estimations and obtained the 95% confidence intervals by bootstrap resampling. The p values for comparing the AUC estimates between different models or groups were also obtained via bootstrap methods. A total of 500 bootstrap datasets were generated.

We performed the Cox proportional hazards model for CRC and obtained estimates of hazard ratios (HRs) and 95% confidence intervals (CI) by comparing the top percentiles (0.5%, 1%, 5%, 10%, 20%, and 30%) with the remaining percentiles (99.5%, 99%, 95%, 90%, 80%, and 70%) of PRS using Cox proportional hazards regression. Observation time was defined as the earliest of the following times: age at CRC diagnosis, death, or last follow-up. The disease status was 1 if the individual developed CRC and 0 otherwise. As individuals joined GERA at different ages, we treated age at starting membership as left truncated.

We estimated age-dependent disease incidences for CRC and advanced neoplasia (CRC and AA), stratified by the top 5% and bottom 5% of PRS by 1 minus the Kaplan-Meier estimator. For advanced neoplasia, the observation time was defined as the earliest of the following times: age at CRC diagnosis, AA, death, or last follow-up, and the disease status was 1 if the individual developed CRC or AA and 0 otherwise.

To gauge the potential clinical impact of PRS, we calculated the proportion of case subjects and probabilities of developing CRC by age 80, stratified by the deciles of LDpred-derived PRS. In addition, we estimated the proportion of case subjects in the top 10%, 20%, and 30% and the bottom 10%, 20%, and 30% of PRS both alone and together with family history.

We used the R packages survival for the survival analysis and survminer for the plots.

Results

Discriminatory Accuracy of Risk Prediction Models

There were 1,311 CRC case subjects and 53,722 control subjects in the GERA cohort. The AUC estimate for Approach 1 of 140 known GWAS variants was 0.629 with 95% confidence interval (CI): 0.613–0.645 (Table 1). In Approach 2, we selected a total of 10,000 SNPs, based on which we built prediction models using penalized linear regression and XGBoost. Ridge regression produced an AUC estimate of 0.633 (95% CI 0.617–0.648), slightly better than lasso (AUC 0.630, 95% CI 0.601–0.646) and elastic net (AUC 0.629, 95% CI 0.612–0.641). XGBoost had a similar AUC estimate: 0.629 (95% CI 0.614–0.643). Approach 3, LDpred, had the best performance when the fraction of causal variants (ρ) = 0.003, producing an AUC estimate of 0.654 (95% CI 0.639–0.669). This was a substantial improvement (4% increase in AUC) over both Approach 1 (p value = 0.010) and Approach 2 (p value = 0.010 for both ridge regression and XGBoost).

Table 1.

AUC Comparisons of CRC versus Control Subjects for PRS Derived via Three Different Approaches in the Independent GERA Cohort

PRS Derivation Strategy		n Variants	AUC (95% CI)
Approach 1: Known GWAS Variants
Known variants		140	0.629 (0.613–0.645)
Approach 2: SNP Selection and Machine Learning
Ridge		10,000	0.633 (0.617–0.648)
Lasso		10,000	0.629 (0.601–0.646)
Elastic Net		10,000	0.630 (0.612–0.641)
XGBoost		10,000	0.629 (0.614–0.643)
Approach 3: LDpred
LDpred	ρ = 1	1,180,765	0.620 (0.603–0.637)
	ρ = 0.3	1,180,765	0.625 (0.608–0.642)
	ρ = 0.1	1,180,765	0.628 (0.611–0.645)
	ρ = 0.03	1,180,765	0.635 (0.619–0.651)
	ρ = 0.01	1,180,765	0.646 (0.630–0.662)
	ρ = 0.005	1,180,765	0.649 (0.633–0.664)
	ρ = 0.003	1,180,765	0.654 (0.639–0.669)
	ρ = 0.001	1,180,765	0.643 (0.628–0.658)

For LDpred, ρ is the proportion of genetic variants assumed to be causal for CRC.

We further calculated the AUC of the best performing model for each approach stratified by family history and sex (Table S5). All models had statistically significantly greater AUC estimates in individuals with a positive family history than those without (the p values are 0.021, 0.020, and 0.021 for Approaches 1, 2, and 3, respectively) and there is no significant difference in AUC estimates between men and women (p values > 0.05 for all models).

In addition to CRC, we evaluated the performance of the models for advanced neoplasia, as well as CRC precursor lesions separately: AA, adenoma, and hyperplastic polyps in Europeans (Table S5). The AUC estimate of LDpred for the advanced neoplasia was 0.629 (95% CI 0.620–0.637), close to the AUC estimate for AA, as it was mainly driven by the large number of AA compared to CRC case subjects. All models showed some discriminatory accuracy between various precursor lesions compared with control subjects; however, the accuracy was sequentially reduced compared with the model for CRC. Again, LDpred had the best performance among the three approaches. As a sensitivity analysis, we assessed the AUC where the control subjects also included precursor lesions (Table S6). The AUC estimates were all reduced, but the reduction was modest ranging from 0.01 to 0.02, and the AUC still showed a sequential decrease across CRC, AA, adenoma, and hyperplastic polyps.

We estimated the AUC of the PRS among Asians (96 CRC case subjects and 5,758 control subjects), Hispanics (70 CRC case subjects and 5,221 control subjects), and African Americans (56 CRC case subjects and 2,409 control subjects). All models performed more poorly for these demographic groups than for Europeans, whether for CRC, AA, adenoma, or hyperplastic polyps (Table S7). For example, the AUC estimates of LDpred for CRC were 0.601 (95% CI 0.538–0.664), 0.602 (95% CI 0.500–0.624), and 0.543 (95% CI 0.542–0.662) for Asians, Hispanics, and African Americans, respectively, which were considerably poorer than for Europeans.

Association of PRS with Age of Diagnosis of CRC

Focusing on the best model for each approach, we estimated the HR and 95% CI for individuals in the top 30%, 20%, 10%, 5%, 1%, and 0.5% of the PRS compared with the remaining individuals (Table 2). Individuals in the top 1% of LDpred-derived PRS distribution had 2.68-fold increased CRC risk (95% CI 1.82–3.96) compared with the remaining 99% of the individuals. In contrast, the PRS from ridge regression identified only 0.5% of individuals with a similar HR estimate. The estimates for the known GWAS variants were smaller for the same top 0.5%. Furthermore, LDpred identified more than 30% of individuals without a family history of CRC (Table S8) as having about 2.2-fold higher risk of CRC, similar to that of those with a first-degree family history of CRC. In contrast, the ridge regression identified 10%, and the known GWAS variants 5%, of these individuals as being at this level of risk.

Table 2.

Hazard Ratio Estimates (95% Confidence Intervals) of CRC for PRS Derived from Three Different Approaches

	Approach 1		Approach 2		Approach 3
	HR (95% CI)	p Value	HR (95% CI)	p Value	HR (95% CI)	p Value
Top 30% versus remaining	1.92 (1.75–2.23)	<2 × 10−16	1.94 (1.72–2.19)	<2 × 10−16	2.19 (1.94–2.47)	<2 × 10−16
Top 20% versus remaining	1.96 (1.73–2.23)	<2 × 10−16	2.07 (1.82–2.35)	<2 × 10−16	2.42 (2.14–2.74)	<2 × 10−16
Top 10% versus remaining	2.08 (1.82–2.70)	<2 × 10−16	2.26 (1.95–2.63)	<2 × 10−16	2.54 (2.20–2.95)	<2 × 10−16
Top 5% versus remaining	2.13 (1.63–2.69)	<2 × 10−16	2.36 (1.95–2.86)	4.9 × 10−15	2.56 (2.12–3.09)	<2 × 10−16
Top 1% versus remaining	2.15 (1.17–2.90)	8.3 × 10−3	2.34 (1.56–3.51)	3.7 × 10−5	2.68 (1.82–3.96)	6.6 × 10−07
Top 0.5% versus remaining	2.21 (1.16–3.81)	1.0 × 10−2	2.77 (1.64–4.69)	1.5 × 10−3	2.82 (1.66–4.79)	9.7 × 10−04

Approach 1: known GWAS variants; Approach 2: SNP selection and machine learning (ridge regression); Approach 3: LDpred with ρ = 0.003.

Assessing CRC Probabilities for PRS

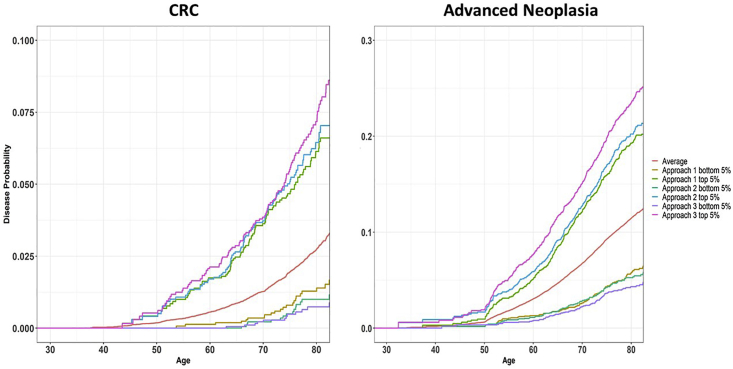
We estimated age-specific probabilities for developing CRC and advanced neoplasia by age 80 by percentile of PRS (Figure 2). Individuals in the top 5% of PRS (high risk) from LDpred had 7.5% (95% CI 5.6%–8.3%) and 23.5% (95% CI 21.3%–25.7%) probabilities of developing CRC and advanced neoplasia, respectively. In contrast, the probabilities for individuals in the bottom 5% of PRS (low risk) were 0.7% (95% CI: 0.1%–1.0%) and 4.3% (95% CI: 3.3%–5.3%), respectively.

Figure 2.

Disease Probabilities for Developing CRC and Advanced Adenoma

Probabilities of developing CRC (left) and advanced neoplasia (right) by age for PRS in the top 5% and bottom 5%, based on models derived from three approaches: known GWAS variants (Approach 1), SNP selection + machine learning with ridge regression (Approach 2), and LDpred with ρ = 0.003 (Approach 3). Average is the overall age-specific CRC (left) and advanced neoplasia (right) probabilities for the GERA.

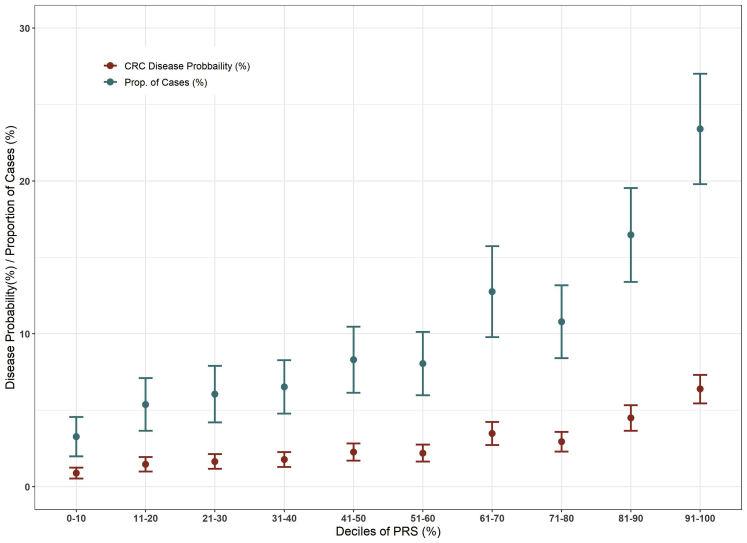
We calculated the proportion of cases stratified by the deciles of LDpred-derived PRS and the corresponding disease probabilities by age 80 (Figure 3). The proportion of cases that fell in the highest decile of PRS was 23.4% (95% CI: 19.8%–27.0%); in contrast, the proportion of cases in the lowest decile was 3.3% (95% CI: 2.0%–4.6%) (Table 3).

Figure 3.

Disease Probabilities and Proportion of Cases (95% CI) Subjects Stratified by the Deciles of LDpred-Derived PRS

Table 3.

Disease Probabilities (%) and Proportion of CRC Case Subjects (%) (95% CI) by Age 80 in High- and Low-Risk Groups

LDPred-Derived PRS			LDPred-Derived PRS + FamilyHx
PRS (%)	Disease Prob (95% CI) (%)	Prop of Cases (95% CI) (%)	PRS or Pos FamHx (%)a	Disease Prob (95% CI) (%)	Prop of Cases (95% CI) (%)
Top 10	6.4 (5.5–7.3)	23.4 (19.8–27.0)	18.0	5.9 (5.2–6.6)	39.3 (38.9–39.8)
20	5.4 (4.8–6.1)	39.7 (32.7–42.8)	26.7	5.3 (4.7–5.8)	51.7 (49.1–54.2)
30	4.6 (4.1–5.1)	50.3 (46.6–55.6)	35.6	4.7 (4.2–5.1)	60.7 (57.5–63.9)
PRS (%)	Disease Prob (95% CI) (%)	Prop of Cases (95% CI) (%)	PRS and Neg FamHx (%)b	Disease Prob (95% CI) (%)	Prop of Cases (95% CI) (%)
Bottom 10	0.9 (0.5–1.2)	3.3 (2.0–4.6)	9.1	0.7 (0.3–0.9)	2.3 (1.9–2.8)
20	1.1 (0.8–1.5)	8.1 (7.5–8.7)	18.4	0.9 (0.7–1.2)	6.1 (5.4–7.1)
30	1.4 (1.0–1.6)	15.3 (14.3–16.5)	27.6	1.0 (0.9–1.2)	10.1 (8.9–12.0)

^aPRS or Pos. FamHx: individuals were in the top x% of PRS or had a positive family history.

^bPRS and negative FamHx: individuals were in the bottom x% and had a negative family history.

We also estimated the disease probabilities stratified by family history of CRC (Figure S2) and advanced neoplasia (Figure S3). There was substantial variation in advanced neoplasia probabilities for top 5% and bottom 5%, even among those with a positive family history. For example, individuals with a positive family history but with LDpred-derived PRS in the low-risk group (bottom 5%) had lower lifetime risk (∼8.0% by age 80) than individuals at average risk but without a family history (∼12%). On the other hand, individuals with a positive family history and a LD-derived PRS in the high-risk group (top 5%) had a lifetime risk of about 35%. In general, compared with the PRS based on known GWAS variants, the LDpred-derived PRS showed a greater separation in disease probabilities between the high-risk and low-risk group and, among high-risk groups, between those with and without a family history.

Taking into account both PRS and family history simultaneously, 18.0% of individuals were either in the top 10% of PRS or had a positive family history in the cohort but constituted 39.3% of case subjects (95% CI 38.9%–39.8%) (Table 3). On the other hand, 9.1% of individuals were in the bottom 10% of PRS and had no positive family history but constituted only 2.3% of case subjects (95% CI 1.9%–2.8%). The proportion of case subjects with a positive family history was 21.0% (95% CI 19.3%–21.4%).

We further validated the LDpred models using eMERGE data. The pattern of AUC estimates for LDPred models were consistent to the results in GERA cohort; however, the AUC estimates were overall weaker. Specifically, LDpred rho = 0.005 had the best AUC 0.629 followed closely by LDpred rho = 0.003 with AUC 0.628, both of which improved substantially compared to the AUC for the known 140 GWAS loci (AUC = 0.591) (Table S11).

Discussion

It is important to be able to identify individuals at high risk of CRC to enable enhanced screening and other interventions, including dietary recommendations, weight loss, and physical activity. Equally pressing is the need to identify individuals at low risk to prevent unnecessary screening and associated complications. As CRC has a sizable heritable fraction³³ and is polygenic in nature with probably thousands of genetic variants contributing to its development,³⁴ utilizing genome-wide data to predict risk holds promise for risk stratification for primary and secondary prevention. Our study comprehensively explores the predictive power for CRC of genome-wide genetic data, using the largest available resources including more than 120,000 CRC case subjects and control subjects of European ancestry with individual-level genetic data for model building and an independent cohort study of more than 100,000 genotyped participants for evaluation. We show that the LDpred approach including 1.2 M variants substantially improves the discriminatory accuracy over an approach that includes only 140 known GWAS variants. In contrast, using a combination of SNP selection and machine learning shows little improvement over the known GWAS variants. To our knowledge, the LDpred-derived PRS has the best performance of any existing CRC genetic-risk-prediction model.

Although the improvement of the AUC from 0.629 to 0.654 may not appear marked (the improvement is 4%), the AUC is an average measurement and it is critical to evaluate the model with other measures to gauge the clinical impact of the model. For example, the LDpred-derived PRS identified the top 30% of the study population as having a relative risk of ∼2.2, which is similar to that associated with having an affected first-degree relative.^14,26 For individuals with an affected first-degree relative, some guidelines recommend initiation of screening with colonoscopy at an earlier age. In contrast, the PRS based on the known GWAS variants identified <5% as having a similar relative risk, demonstrating clearly the substantial improvement of the LDpred-derived PRS. It is important to note that only 10.5% of those individuals who were in the top 30% risk based on LDpred-derived PRS had a family history of CRC, demonstrating that the LDpred-derived PRS can potentially identify a larger fraction of the study population at high risk than family history alone. This means that ∼27% (89.5% × 30%) of the population who are classified as average risk based on current guidelines might benefit from earlier screening. As the PRS is a continuous variable, it allows for tailored recommendation, including a specified age of starting screening,^9,26 rather than simply defining a single high-risk group based on family history that, as we show, is itself heterogeneous.

In Approach 2, if we were to use the same dataset for feature selection and model development, there would be overfitting in the model development, which result in a worse performance in an independent dataset (Supplemental Material and Methods Section 6.1 and Table S9). To mitigate this overfitting, we thus split the data in two sets in the training step. The downside is that there is potential power loss for feature selection due to smaller sample size used in calculating the test statistics compared to the entire dataset as used in Approach 3. Nevertheless, we expect that when the sample size of studies continues to rise, Approach 2 will be further improved. Our observations here are not unique to genome-wide risk prediction for colorectal cancer (see Chatterjee et al.,¹⁵ Abraham et al.,¹⁸ Evans et al.,³⁵ Yang et al.,³⁶ de Vlaming and Groenen,³⁷ and Malo et al.³⁸ for examples).

The LDpred approach, which builds a risk prediction model based on the entire genome, yielded better predictive performance than the approach that initially selected features before applying machine-learning algorithms. It is likely that the derivation dataset that we used for SNP selection is still too small given the large number of features (40M genetic variants) and weak effect sizes. As a result, performing SNP selection may lead to a substantial loss of information that cannot be compensated for, even with machine-learning algorithms like XGBoost. A potential limitation of LDpred is the assumption of additive effects only, whereas machine-learning approaches, such as XGBoost and random forest, can accommodate more complex non-linear effects but are not readily applicable to ultra-high dimensional data. Approaches such as deep learning that can handle ultra-high dimensional data may have potential to further improve the accuracy of prediction.

Including only the known GWAS variants (Approach 1) is simplest computationally. The SNP selection in Approach 2 also reduces computation time substantially. LDpred is the most computationally intensive due to the Monte Carlo Markov Chain (MCMC) procedure. It took ∼4 days for LDpred to compute the regression weights for each parameter setting, using our computing infrastructure, which has a node of 20 cores with 768 GB memory across all cores. Although LDpred is more computationally intensive than the other two PRS approaches, the implementation of the LDpred-derived PRS into electronic health record (EHR) data, once genome-wide array or sequencing data are available, will not be much more difficult. For example, it took ∼6 h to calculate the LDpred-derived PRS for 100,000 individuals in the GERA cohort. As these scores need to be calculated only once (although updates for improved models are likely), they can be calculated upfront and stored as part of individual records like any other measurements (e.g., BMI, serum cholesterol). The more substantial challenge to implementation is perhaps the storage of genotype or sequencing data in a structured data object that is readily available to the EHR. To date, this challenge has not been solved in a standardized way;^39,40 however, the increasing clinical utility of PRS may motivate more rapid adoption of standardized integration of genotype and sequencing information into EHRs, which would serve as a foundation for implementation of a wide array of stratified-medicine tools.

Our study’s large sample size likely is an important factor for the improved performance of the LDpred approach. Further, having access to an independent cohort that has not been included in any previous discoveries is key to provide an unbiased evaluation of the models.

Ideally, CRC would be detected early, allowing easier removal, perhaps even as a precursor lesion with a lower risk of complications and without the need for additional treatment such as radiation or chemotherapy. Previous work has shown that a PRS with fewer than 50 known loci was associated with increased risk of precursor lesions.^41,42 Consistent with these previous reports, we showed here, in our independent cohort, that all three PRS approaches also predicted AA and, to a lesser extent, adenoma and hyperplastic polyps. It is notable that as not all individuals have had endoscopy (colonoscopy or sigmoidoscopy); some control subjects in this study may have precursor lesions. As a result, the actual AUC is likely to be underestimated. Nevertheless, this decline can be expected, as the disease generally progresses from hyperplastic polyps or non-advanced adenomas to AA to CRC, with only a fraction of the precursor lesions giving rise to CRC.

There are several limitations of our PRS. First, they were built using individuals of European descent; hence, the models show substantially lower performance in other ancestral groups. This is not surprising due to the difference in LD across ancestral groups. To address this important issue, dedicated efforts focused on other major racial/ethnic populations (African Americans, Asians, and Hispanic/Latinos) are needed to develop unbiased PRS for these ancestral groups. Second, as CRCs are heterogenous with different molecularly defined subtypes, another limitation of our study is treating CRC as a single entity. However, this problem is not easy to overcome, given the need for large sample sizes and the limited availability of CRC case subjects with detailed molecular characterization. Third, while we validated that the LDpred model with rho = 0.003 performed among the best models in an independent eMERGE study, the model needs to be further evaluated for calibration as our preliminary evaluation shows (Supplemental Material and Methods Section 6.2 and Table S12). Caution must be taken when evaluating the calibration to account for the differences in individual-level characteristics such as screening prevalence and lifestyle risk factors.

An important question remains about how far we can improve the predictive performance using genome-wide genetic data. To this end, we showed that the best normal mixture model for effect-size distribution of our genome-wide data of common variants (allele frequency > 5%) yielded a theoretical maximal AUC of 0.68,³⁴ suggesting that the AUC can be further improved perhaps by using more complex models, larger number of SNPs, larger sample sizes, or some combination of these. We attempted to use all 40M SNPs imputed to the Haplotype Reference Consortium (HRC) when building LDpred models; however, we ran into convergence problems and hence limited the presentation only to SNPs in HapMap. The maximal theoretical AUC of 0.68 does not include rare variants. Based on our HRC imputed data, we estimated that at least half of CRC heritability is due to variants with an allele frequency < 1% (note this does not include high-penetrance variants as these are too rare to be imputed).¹⁴ Accordingly, it can be expected that incorporation of rare variants can further improve the predictive performance of genome-wide genetic prediction models. This is probably not surprising as hundreds of millions of rare variants exist in the genome.

Work from our group^{43, 44, 45} and others⁴⁵ has demonstrated that functional categories of the genome contribute to the heritability of CRC and that most susceptibility loci are in enhancers that vary between tumor and nonmalignant tissue. Thus, including colorectal tissue-specific functional data, such as transcriptomic or epigenomic data, would allow us to narrow down to the variants that are more likely to influence CRC risk. Our future direction is to develop methods that combine different functional annotation scores enriched for heritability, which will be particularly important as we expand prediction to rare variants. Furthermore, we will combine the PRS with other predictive factors, such as age, sex, screening history, high-penetrance genes, environmental/lifestyle risk factors, or biomarkers of early detection, which we expect, based on our previous analysis,⁹ will further substantially improve risk prediction. The modifiable risk factors for the CRC are an important component of risk prediction because the best approach to primary prevention is avoidance or elimination of these risk factors. For secondary prevention, both genetics and modifiable risk factors would be helpful for determining optimal CRC screening timing and frequency.

An aim of precision/stratified medicine is to predict risk of diseases based on an individual’s genetic makeup, which could, in principle, be done at birth. An important consequence of genetic risk prediction is the identification of high-risk individuals who would otherwise not be identified as high risk. Such knowledge could result in changes in healthcare management to mitigate risk with relatively low-cost lifestyle changes or preventive therapies for those at greater risk.⁴⁶ Additionally, genetic risk prediction can identify individuals at low risk who might otherwise be enrolled unnecessarily in more frequent screening or surveillance programs based on age, family history, or history of polyps. The interval between colonoscopies or the modality of screening or surveillance could be informed by PRS. Although the risk of colonoscopic perforation in the setting of cancer screening is not precisely known, estimates from diagnostic (in which there is a clinical suspicion of colorectal pathology) and therapeutic colonoscopies suggest perforations occur about once per 1,000 procedures.^{47, 48, 49} Perforations are life threatening and often require laparotomy, suggesting that non-invasive screening modalities such as FIT are attractive alternatives, particularly in low-risk individuals. These are already used in other countries where population-based endoscopy screening is not available. Of course, in the US, endoscopy is not population-wide either, so the capacity to stratify individuals on screening methods appropriate to their risk should improve uptake, reduce costs, and reduce complications.

We expect that our model will be a useful first step toward prioritizing those at high risk for targeted screening or intervention and to design clinical trials to test prevention strategies in the high-risk group, particularly with the eye toward those below the age of 50 years given the rising rates of early-onset CRC. In the future, it is expected that detailed genome-wide genetic information will become part of electronic medical records of all individuals to calculate an individual PRS and identify those at high or low risk for any disease, perhaps as early as at birth. This information will allow targeted interventions such as lifestyle modifications, chemoprevention, and screening to prevent diseases or diagnose them early. Broad accessibility, dropping genotyping costs, and the need to account for an individual’s risk factor profile to improve screening have provided transformative opportunities in personalized medicine. However, wide-scale adoption of PRS into clinical practice raises key ethical and scientific challenges. For example, as the current PRS has been developed in Europeans given that most GWASs are done in this population, it is substantially more predictive in Europeans compared to other populations, which will widen the health disparity gap. To overcome this major ethical and scientific challenge, it is critical that researchers invest time and effort in developing unbiased PRS across all major US populations. Furthermore, it is important to evaluate the acceptance and effectiveness of genetic testing for risk-stratified interventions among the broader population and health care providers. Cost effectiveness analysis will provide important insights to guide policies related to personalized medicine. In summary, we developed a PRS with substantially higher ability both to predict CRC risk and to identify those at high and low risk than the other two approaches. The proposed CRC PRS offers a way to improve CRC risk prediction, with the potential for translation to optimize clinical decision making.

Declaration of Interests

The authors declare no competing interests.

Published: August 5, 2020

Data and Code Availability

The source data for the findings of this study are available as follows. Genotype data for GECCO and CORECT have been deposited in the database of Genotypes and Phenotypes (dbGaP) under accession numbers phs001078.v1.p1, phs001415.v1.p1, and phs001315.v1.p1. The UK Biobank data are publicly available upon successful application from the UK Biobank. Genotype data of GERA participants who consented to having their data shared with dbGaP are available from dbGaP under accession phs000674.v2.p2. The complete GERA data are available upon successful application to the KP Research Bank. Genotype data of eMERGE participants are available from dbGaP under the accession number phs001616.v1.p1.

The codes used for statistical analysis and generation of tables and figures are publicly available.

Web Resources

• dbGaP, https://www.ncbi.nlm.nih.gov/gap

• Elastic Net, https://cran.r-project.org/web/packages/caret/index.html

• KP Research Bank, https://researchbank.kaiserpermanente.org/

• LDpred, https://bitbucket.org/bjarni_vilhjalmsson/LDpred

• PLINK 1.9, http://www.cog-genomics.org/plink/1.9/

• Ridge and Lasso Regression, https://cran.r-project.org/web/packages/glmnet/index.html

• ROCt, https://www.rdocumentation.org/packages/ROCt/versions/0.9.5

• Survivor, https://www.rdocumentation.org/packages/survival/versions/3.2-3

• Survminer, https://www.rdocumentation.org/packages/survminer/versions/0.4.7

• UK Biobank, https://www.ukbiobank.ac.uk/

• XGBoost, https://www.rdocumentation.org/packages/xgboost/versions/1.1.1.1

Supplemental Data

Table S1

Studies Involved in GWAS Meta-analysis: Characteristics of Studies and Study Participants Contributing to the GWAS Meta-analysis

Table S4

List of CRC 140 Risk Variants: Associations between 140 Risk Variants/Surrogates and Risk of Colorectal Cancer in the Study Population