Accurate deep neural network model to detect cardiac arrhythmia on more than 10,000 individual subject ECG records

Highlights

• •DNN model is proposed to detect arrhythmia.
• •More than 10,000 individual subject ECG records subject records are used.
• •Two different scenarios are employed: (i) reduced rhythms (seven rhythm types) and (ii) merged rhythms (four rhythm types).
• •Achieved 92.24% and 96.13% accuracies for the reduced and merged rhythm classes, respectively.
• •System can aid cardiologists in the accurate detection of arrhythmia accurately.

Abstract

Background and objective

Cardiac arrhythmia, which is an abnormal heart rhythm, is a common clinical problem in cardiology. Detection of arrhythmia on an extended duration electrocardiogram (ECG) is done based on initial algorithmic software screening, with final visual validation by cardiologists. It is a time consuming and subjective process. Therefore, fully automated computer-assisted detection systems with a high degree of accuracy have an essential role in this task. In this study, we proposed an effective deep neural network (DNN) model to detect different rhythm classes from a new ECG database.

Methods

Our DNN model was designed for high performance on all ECG leads. The proposed model, which included both representation learning and sequence learning tasks, showed promising results on all 12-lead inputs. Convolutional layers and sub-sampling layers were used in the representation learning phase. The sequence learning part involved a long short-term memory (LSTM) unit after representation of learning layers.

Results

We performed two different class scenarios, including reduced rhythms (seven rhythm types) and merged rhythms (four rhythm types) according to the records from the database. Our trained DNN model achieved 92.24% and 96.13% accuracies for the reduced and merged rhythm classes, respectively.

Conclusion

Recently, deep learning algorithms have been found to be useful because of their high performance. The main challenge is the scarcity of appropriate training and testing resources because model performance is dependent on the quality and quantity of case samples. In this study, we used a new public arrhythmia database comprising more than 10,000 records. We constructed an efficient DNN model for automated detection of arrhythmia using these records.

1. Introduction

Cardiac arrhythmia, defined as an abnormal heart rhythm, is a common problem in cardiology, and can range from benign to potentially life-threatening rhythm types [1, 2]. Therefore, early detection of arrhythmia is an important clinical task that can save lives. The commonest method to detect cardiac arrhythmia uses the electrocardiogram (ECG), which measures the electrical activity of the heart. The standard 12-lead ECG is recorded over a 10-second interval. In general, ECG records include long durations (i.e., several hours or days) of heart activity samples, as needed for detecting and analyzing arrhythmia [3]. This task can become time-consuming, tedious, subjective, and costly, because it requires the assistance of trained experts [4, 5]. Therefore, enhanced fully automated computer-aided diagnosis systems (CADs) with high accuracy can be feasible and even essential solutions to assist clinical experts during the analysis process [6, 7].

Machine learning-based approaches are frequently utilized to recognize arrhythmia [8], [9], [10], [11], [12]. Pre-processing, feature extraction, and classification tasks are the main steps involved in these approaches [13]. The feature extraction step has a critical role to achieve high classification performance. Researchers choose some clinical features (i.e., P, QRS, T wave amplitude and duration, etc.) and arbitrary features to meet this aim. In the feature extraction phase, useful morphological [14, 15], temporal [14, [16], [17], [18], [19]], frequency-based [20], [21], [22] and/or transform-based [23], [24], [25], [26], [27], [28] features from ECG waveforms are obtained to improve the distinction between samples. The handcrafted feature extraction step requires domain knowledge and increases computational complexity [29, 30]. The requirement for expertise to select optimal features is a challenge [31]. In recent years, deep learning [32, 33] has become a popular subfield of artificial intelligence. The deep learning models usually have an end-to-end structure. This architectural structure enables one to perform feature extraction and classification steps together [34]. It has been effectively used in medical applications such as brain image analysis [35], [36], [37], [38], histopathological images [39], [40], [41], and brain electroencephalogram (EEG) signal analyses [42], [43], [44], [45]. It has also been adopted for the detection of coronavirus (COVID-19) patients [46], [47], [48], [49], [50], [51].

Deep learning has been the preferred mode of ECG classification over the last few years [4, 31, [52], [53], [54], [55], [56], [57], [58], [59], [60], [61]]. One-dimensional convolutional neural networks (1D-CNN) have become popular to classify ECG records because of their one-dimension structure. In 2015, Kiranyaz et. al. [55] proposed a 1D convolutional neural network (1D-CNN) model for patient-specific ECG classification. Acharya et al. [4] developed a nine-layer CNN model to classify five types of heartbeats. They obtained an accuracy of 94.03% from original signals using an augmentation technique. Hannun et al. [56] proposed a CNN model that consists of 33 convolutional layers to classify 12 rhythm categories. They based their work on a large ECG dataset containing 91,232 records from 53,549 patients. Li et al. [57] presented a generic CNN for patient-specific ECG classification. Oh et al. [58] suggested a modified U-net architecture to diagnose beat-wise arrhythmia. Li et al. [59] developed a 31-layer 1D residual CNN model to identify five different types of heartbeats. Li et al. [31] recommended a customized CNN model to classify patient-specific heartbeat using 44 records. Yildirim et al. [60] applied a CNN model for classification of 17 cardiac arrhythmias using long-duration ECG signals. Sharker et al. [61] proposed an end-to-end deep learning model to classify 15 ECG classes.

Another deep learning algorithm for ECG analysis is long short-term memory networks (LSTM), known as sequence learning. LSTM is a practical approach to analyze time-series data [62]. In the last decade, the LSTM algorithm has been employed for arrhythmia detection [[30], [63], [64], [65], [66], [67], [68], [69], [70], [71], [72], [73]]. Yildirim [65] proposed a wavelet sequence-based LSTM model to classify ECG signals. Chang et al. [66] employed a bidirectional LSTM model to classify 12 common heart rhythms on 12-lead ECG signals collected from 38,899 patients. Gao et al. [30] used an LSTM model with focal loss (FL) to classify eight different heartbeats. The combination of the LSTM and CNN model is commonly used in ECG classification. Oh et al. [67] designed a CNN-LSTM model to detect five heartbeats. Warric et al. [68] used a combined deep classifier, CNN and LSTM, in the 2017 PhysioNet/CinC Challenge [69]. Xiong et al. [70] proposed a convolutional recurrent neural network to recognize four different rhythms. Guo et al. [71] developed a deep model, including convolution blocks and a recurrent network, to classify five heartbeat classes. Mousavi et al. [73] applied an alarm system on five types of life-threatening arrhythmia. They used a deep model composed of CNN layers, attention mechanism, and LSTM units.

The performance of deep models tends to improve with more training data [32]. Accessing public databases is a major challenge in medicine, as these records are costly and time-consuming to collect [74]. In addition, legal and ethical issues may arise when collecting data [75]. The most widely used public database for arrhythmia studies is the MIT-BIH Arrhythmia Database [76] collected 40 years ago [77]. This dataset has some limitations, such as imbalanced classes [61]. Therefore, the construction of new large public datasets plays a vital role for studies on arrhythmia. As described herein, we used one of the largest public ECG datasets to detect rhythm classes [78]. The database includes 12-lead ECG signals collected from more than 10,000 individual subjects. We developed a DNN model to classify rhythms from each of 12-lead inputs. We preferred to use the representation and sequence learning structure together because of their salutary performance on both ECG [52, 67, 68, 72] and EEG signals [45]. The novelty of this paper can be summarized as follows: a useful single DNN model has been constructed to detect multiple rhythm classes on 12-lead signals. The experiments are performed on one of the recent largest new ECG datasets, including more than 10,000 subjects. To the best of our knowledge, this is the first deep model study to classify rhythms using this ECG dataset. All of the experiments were performed with inter-patient schema. Additionally, the training and testing subjects were different, so that there is no overlap between the training and the test sets.

2. Materials and methods

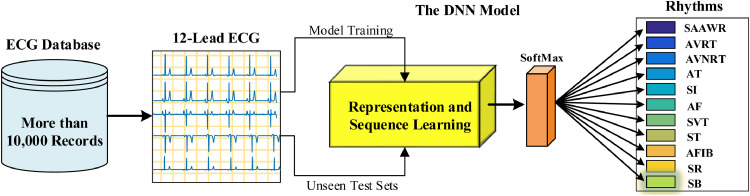
In this paper, we used both representation and sequence learning to detect heart rhythms and conducted the experiments on a large ECG database. The database has been recently published for arrhythmia research and encompasses more than 10,000 individual subject ECG records. In Fig. 1 , a block representation of the materials and methods is given for the study.

Fig. 1.

Block illustration of materials and methods for the study.

2.1. The proposed DNN model

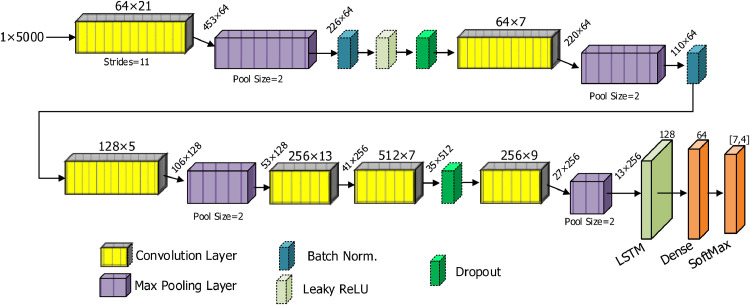
We designed a new DNN model to classify rhythms automatically. In Fig. 2 , a block representation of the proposed DNN model is given. We constructed the proposed deep learning model using different layer combinations. We preferred a one-dimensional convolutional neural network (1D-CNN) due to the one-dimensional structure of ECG signals. One-dimensional-CNN models have an excellent ability to learn distinguishing hierarchical features from the raw inputs when applying a 1D convolution. This procedure is also known as representation learning [45]. The model learns low-level features at beginning layers and high-level features through the consecutive layers hierarchically. After the 1D convolution step, many feature matrices termed feature maps emerge. These maps are sub-sampled by the max-pooling layers to reduce computational cost. A tedious task is to determine the correct parameters, such as the number of filters, kernel size, and strides. We used both our previous experience on the long duration ECG signals [60] and brute force techniques to adjust these parameters. For the number of filters, experiments were made based upon exponents of two, in the range from 16 to 1024. Performance observations were made by selecting values from a smaller search space such as 2, 3, 5, 7, 9 and 13 for kernel sizes. Since the length of the input signal is long, 21 kernels are used in the first layer and 11 strides are used to reduce the computational cost. All of these parameter settings have been adjusted to provide the optimal result by testing for different data partitions. In addition, the parts such as which layers should be used and which parts of the model should be placed are time consuming and difficult processes. These processes can be solved with a satisfactory optimization approach and hardware with high computing power. However, the best opportunity we have is to adjust these parameters with the help of experts by trying many different variations.

Fig. 2.

A block representation of the proposed DNN model for detecting rhythm classes.

In the proposed model, the first convolution layer had 64 filters with 21 kernel size that was applied to the raw input signals using an eleven movement amount (strides). The feature maps obtained from this step were sub-sampled in a max-pooling layer. The proposed model consisted of six different convolution layers and four max-pooling layers. We used two batch normalization layers to normalize the data. Overfitting is an important problem for machine learning tasks during training. Two dropout layers were placed at different positions of the model to avoid the overfitting problem. A Leaky-ReLU layer with 0.1 alpha value was used at the beginning layers. It is a useful function to avoid the dying ReLU problem. All layers mentioned so far were used for representation learning. In the model, a LSTM block was used for sequence learning. Some studies on 1D signals such as EEG and ECG [52, 67, 68, 72] show that the combination of representation and sequence learning can yield a higher performance than by using representation learning alone. According to this information, we used a 128 unit LSTM block at the end of the representation learning layers. In Table 1 , we present our implemented DNN model with detailed layer information.

Table 1.

The layer information of the implemented DNN model.

Layer (Type)	Layer Parameters	Output Shape	Number of Parameters
Conv1D	Filters=64, Size=21, Strides= 11	453 × 64	1408
MaxPooling1D	Pool size=2	226 × 64	0
Batch Norm	-	226 × 64	256
LeakyReLU	Alpha=0.1	226 × 64	0
Dropout	Rate=0.3	226 × 64	0
Conv1D	Filters=64, Size=7, Strides= 1	220 × 64	28736
MaxPooling1D	Pool size=2	110 × 64	0
Batch Norm	-	110 × 64	256
Conv1D	Filters=128, Size=5, Strides= 1	106 × 128	41088
MaxPooling1D	Pool size=2	53 × 128	0
Conv1D	Filters=256, Size=13, Strides= 1	41 × 256	426240
Conv1D	Filters=512, Size=7, Strides= 1	35 × 512	918016
Dropout	Rate=0.3	35 × 512	0
Conv1D	Filters=256, Size=9, Strides= 1	27 × 256	1179904
MaxPooling1D	Pool size=2	13 × 256	0
LSTM	Unit=128, Return Sequences=True	13 × 128	197120
Flatten	-	1664	0
Dense	Unit=64, Activation=ReLU	64	106560
Dense	Unit=[7,4], Activation=Softmax	{7, 4}	260

2.2. The big ECG database

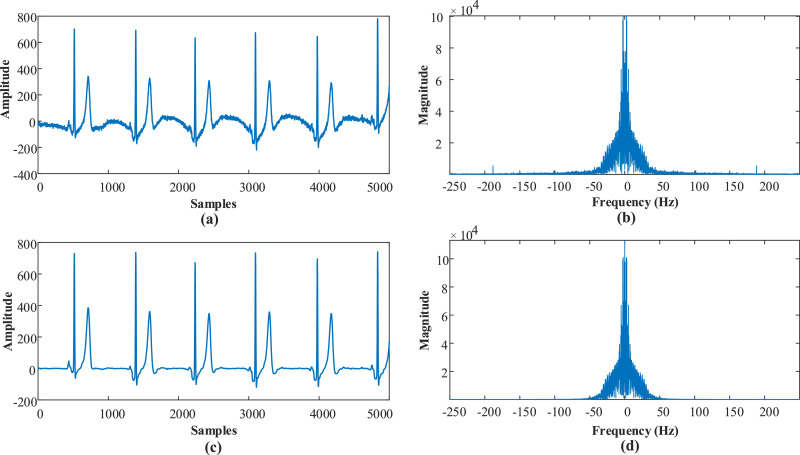
In this work, we used a new large ECG database [78] collected by Chapman University and Shaoxing People's Hospital (Shaoxing Hospital Zhejiang University School of Medicine). The database includes a large number of individual subjects - more than 10,000 - with 12-lead ECG signals sampled at a higher than usual sampling rate of 500 Hz. In this database, there are 11 heart rhythms and 56 types of cardiovascular conditions labelled by professional physicians. The database comprises 10,646 patients, and 12-lead ECGs records were acquired over 10 seconds. The Butterworth low pass filter [79], the local polynomial regression smoother (LOESS) [80], and Non-Local Means (NLM) techniques [81] had been used sequentially to process raw ECG records. Signal components with a frequency above 50 Hz and the effects of baseline wandering were removed using these methods. In Fig. 3 , the pre-process step is shown with a signal sample and frequency spectrums. In this image, it can be seen that after the pre-processing, frequencies above 50 Hz and the baseline wandering effect are removed.

Fig. 3.

An example of the pre-processing step with frequency spectrums, a) raw signal, b) Frequency spectrum of the raw signal, c) Filtered signal, d) Frequency spectrum of the filtered signal.

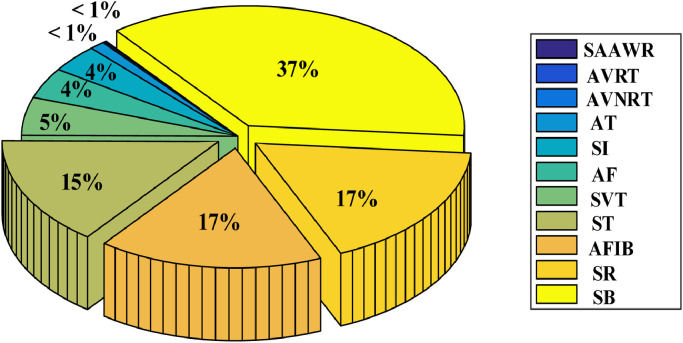
Since some ECG recordings contain only zeros, and some channel values were missing, we used a total of 10,588 topics from this database. Table 2 contains some numerical information about the recordings used, and Fig. 4 depicts a distribution rate graph of rhythm classes across the database.

Table 2.

Some numerical information about the ECG records used.

Rhythms	Number of Samples	Age, Mean ± Std	Number of Females	Number of Males
Atrial Flutter (AF)	438	71.14 ±13.47	182	256
Atrial Fibrillation (AFIB)	1,780	73.35 ±11.13	739	1,041
Atrial Tachycardia (AT)	121	65.21 ±19.30	57	64
Atrioventricular Node Reentrant Tachycardia (AVNRT)	16	57.87 ±17.33	12	4
Atrioventricular Reentrant Tachycardia (AVRT)	8	57.50 ±17.33	3	5
Sinus Irregularity (SI)	397	34.88 ±23.00	175	222
Sinus Atrium to Atrial Wandering Rhythm (SAAWR)	7	51.14 ±31.82	6	1
Sinus Bradycardia (SB)	3,888	58.33 ±13.95	1,408	2,480
Sinus Rhythm (SR)	1,825	54.37 ±16.29	1,024	801
Sinus Tachycardia (ST)	1,564	54.67 ±20.97	769	795
Supraventricular Tachycardia (SVT)	544	55.64 ±18.35	294	250
All	10,588	59.23 ±17.97	4,669	5,919

Fig. 4.

The distribution rate graph of rhythm classes across all records.

3. Experimental results

In this section, we present experimental results to detect rhythm classes on 10-second ECG signals. We used 11 rhythms with two scenarios, namely, with seven and four categories.

3.1. Experimental setups

In this study, two different experiments were performed on the dataset. The first experiment studied seven rhythm classes; the second, four. Also, 12-lead ECG signals from different subjects were used separately for analysis and performance evaluations. We have used an inter-patient scheme during the experiments. Only a single efficient DNN model was used for all experiments. The hyper-parameters of the DNN model were not altered during training. The standard hyper-parameters of the model were set as a learning value of 0.002, and batch size 128. We categorically used the cross-entropy loss function and Adam optimizer to adjust the weights of the model [82]. All experiments were performed on a computer with specifications of Intel Core i7-7700HQ 2.81GHz CPU, 16GB memory, and 8 GB NVIDIA GeForce GTX 1070 graphics card. The DNN model was constructed using the Keras (v 2.3.1) deep learning library [83] and the TensorFlow (v. 1.14.0) framework.

Another important step is preparing training, validation, and test sets for the implementation of the model. There are two standard methods for this task, cross-validation and random splitting. In general, per subject evaluation of the models can provide more reliable results. Each subject in this database has only one unique record. Therefore, the dataset split was done on a per subject basis. The large size of the ECG dataset renders it suitable for random splitting. The dataset was randomly divided into training, validation, and test sets as 80%, 10%, and 10%, respectively. We used the same records for training, validation, and testing for the experiments to compare the performances consistently. We evaluated the performance of the model on the test sets using standard evaluation metrics, such as accuracy, specificity, sensitivity, precision, and F-score. The calculations of these criteria, according to distribution of true positive (TP), true negative (TN), false positive (FP) and false negative (FN) samples, are given as follows:

Accuracy=(TP+TN)/Total (1)

Sensitivity=TN/(FP+TN) (2)

Specificity=TN/(FP+FN) (3)

Precision=TP/(TP+FP) (4)

Recall=TP/(TP+FN) (5)

F-Score=2 × (Precision × Recall)/(Precision+Recall) (6)

3.2. Reduced rhythm classes

In this section, we used the DNN model on seven rhythm classes. Deep models can work efficiently on a large number of samples for each category. Due to the insufficient number of several cases in the initially published dataset, such as 121 atrial tachycardia, 16 atrioventricular node reentrant tachycardia, 8 atrioventricular reentrant tachycardia, and 7 sinus atrium to atrial wandering rhythm, we eliminated these classes during the experiment. In Table 3 , the used dataset includes seven rhythms and is given here with detail.

Table 3.

The numerical information of the reduced class dataset that includes seven rhythms.

Rhythms	Number of Total Samples	Number of Training Samples	Number of Testing Samples	Age, Mean ± Std	Number of Females	Number of Males
AF	438	406	32	71.14 ±13.47	182	256
AFIB	1,780	1,622	158	73.35 ±11.13	739	1,041
SI	397	355	42	34.88 ±23.00	175	222
SB	3,888	3,494	394	58.33 ±13.95	1,408	2,480
SR	1,825	1,632	193	54.37 ±16.29	1,024	801
ST	1,564	1,398	166	54.67 ±20.97	769	795
SVT	544	485	59	55.64 ±18.35	294	250
All	10,436	9,392	1,044	59.16 ±17.94	4,591	5,845

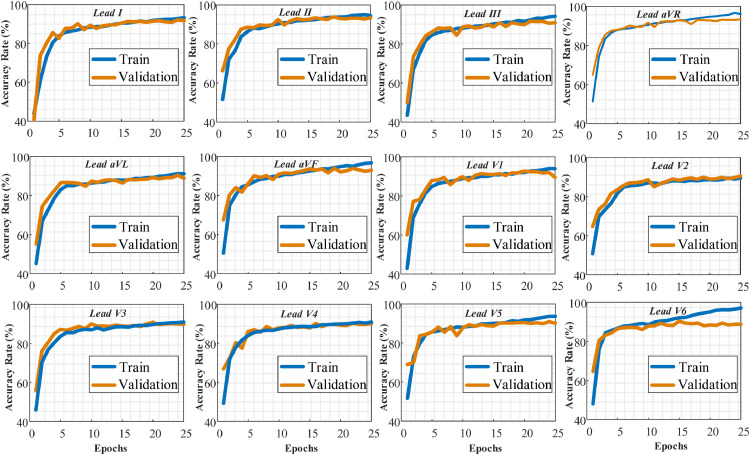
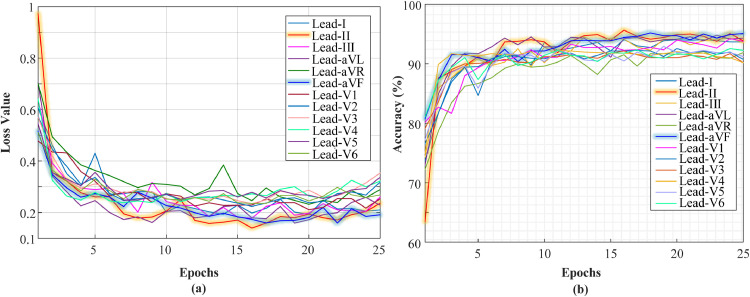
Firstly, we divided the reduced dataset into training, validation, and testing sets as 80%, 10%, and 10%, respectively. It is seen that the data distributions used in this scenario are imbalanced for classes. The data numbers in the AF, SI and SVT classes are lower than the other classes. This problem is mitigated by merging classes in the next scenario. For this reason, the imbalance problem has been attenuated in this scenario. The first process was training the DNN model using both training and validation sets. The DNN model was evaluated on the test sets that were unseen by the model during the training step. According to the training and validation values, the training process is performed for 25 epochs. After 25 epochs, the model tended to encounter an overfitting problem. We did not use the early stop criteria to compare lead performances during the same epochs. The training and validation graphs obtained from the training process are shown in Fig. 5 . We present the performance of each lead separately.

Fig. 5.

The training and validation accuracy values of the proposed model during the training process for each ECG lead signal (Lead-I to Lead-V6) separately.

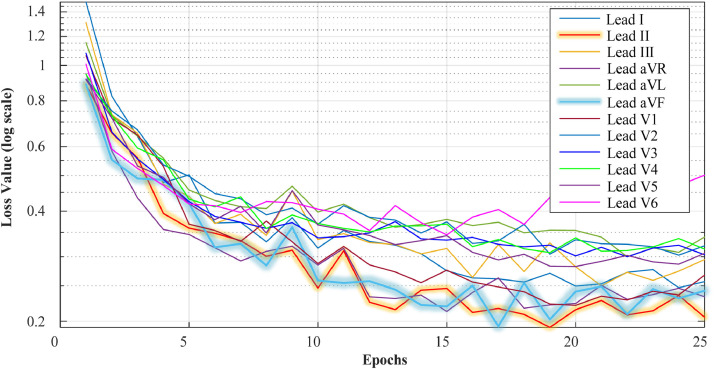
It is evident from these graphs that the DNN model exhibited promising results for all lead ECG signals during training. The best performance was observed on the Lead-II, Lead-aVF, and Lead-V1. The proposed model achieved a lower performance on Lead-aVL, Lead-V5, and Lead-V6. Our model could not start the training process for Lead-V6 inputs with these training records. For this reason, the results for Lead-V6 in this section have been obtained using a different record partition. When the loss values were examined, it was observed that there were no overfitting and underfitting problems during the training of the model. In Fig. 6 , training and validation loss values are presented during 25 epochs for all lead signals.

Fig. 6.

The validation loss values of each lead signal during the training process.

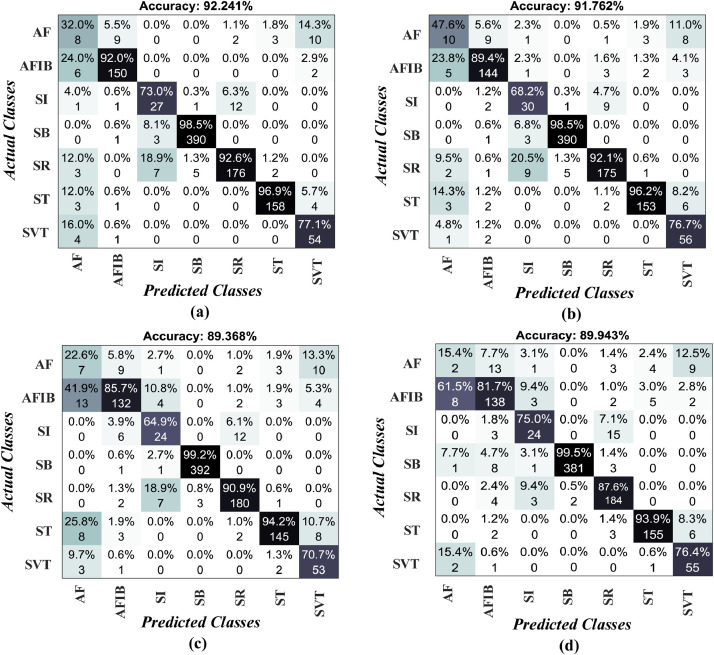
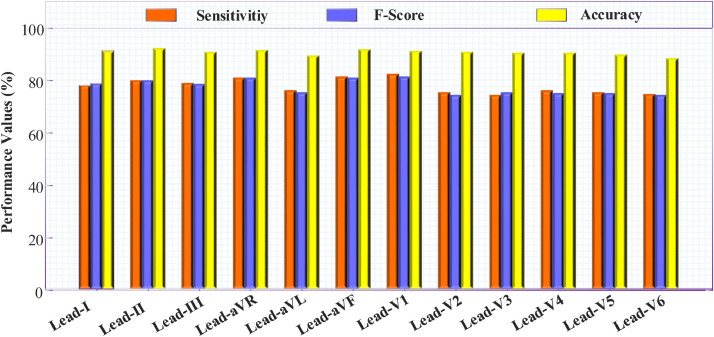
After the training process, the performance of the DNN model was tested on the unseen test sets. Deep learning models use validation samples for adjusting network parameters. Thus, reliable performance measurements could be obtained from the unseen test sets. The trained model was applied to the test records and yielded promising results on unseen data. In Fig. 7 , we showed four confusion matrices obtained during the test process. The confusion matrix has an essential role in the evaluation of the performance of a model. In Fig. 7 (a), it can be seen that the model achieved 92.24% and 91.76% accuracy on Lead-II and Lead-aVF ECG signals. The Lead-aVL and Lead-V5 signals yielded 89.36% and 89.94% accuracies, respectively. In confusion matrices, the model misclassified several rhythm classes. For example, in Fig. 7 (c), 13 actual atrial fibrillation (AFIB) signals were classified as atrial flutter (AF) signals and seven actual sinus rhythm (SR) signals were classified as sinus irregularity (SI) signals. Furthermore, nine original AF signals were labelled as AFIB, and 12 original SI signals are labelled as SR signals. Clinically, the misclassification between AFIB and AF and between SR and SI are not crucial, as the medical management is no different between diagnoses in the respective pairs. According to the confusion matrices, we calculated several performance metrics, including the sensitivity, specificity, precision, F-score, and accuracy, for each lead input. In Table 4 , the performance values of the proposed model on the test set are shown for each lead input. The highest values are marked with bold font in the table. Also, we present some graphical representations for these values, as in Fig 8 .

Fig. 7.

The model test performances on several leads a) Lead-II, b) Lead-aVF, c) Lead-aVL and d) Lead-V5.

Table 4.

Some important performance values obtained using the test sets (highest values marked with bold).

ECG Leads	Overall
	Sensitivity (%)	Specificity (%)	Precision (%)	F-Score (%)	Accuracy (%)
Lead-I	78.17	98.56	80.45	78.83	91.19
Lead-II	80.15	98.72	80.31	80.04	92.24
Lead-III	79.04	98.49	78.53	78.58	90.71
Lead-aVR	80.91	98.60	81.03	80.93	91.57
Lead-aVL	76.07	98.28	75.44	75.53	89.37
Lead-aVF	81.50	98.64	81.25	80.98	91.76
Lead-V1	82.42	98.58	81.22	81.39	91.19
Lead-V2	75.33	98.41	74.90	74.57	90.71
Lead-V3	75.38	98.39	75.05	74.40	90.33
Lead-V4	76.12	98.38	76.92	75.19	90.42
Lead-V5	75.62	98.34	75.63	75.02	89.94
Lead-V6	74.90	98.05	75.76	74.48	88.51

Fig. 8.

A graphic representation for overall sensitivity, f-score, and accuracy values for all leads.

The same test subjects were used for each lead. The highest Sensitivity and F-score values were obtained using Lead-V1 ECG signals with an accuracy of 91.19%. The highest accuracy value was obtained as 92.24% from Lead-II input. According to these values, it can be said that the proposed DNN model yielded promising results on all ECG lead inputs. Only on three lead inputs (Lead-aVL, Lead-V5, and Lead-V6) were accuracy values observed under a 90% rate.

For further performance evaluation, we examined the values of the test results for each rhythm class compared with Lead-II input, so as to ascertain which classes yielded a weak or strong performance by the DNN model. We chose the Lead-II signal for this purpose, due to both its high accuracy values, and the fact that it is commonly used in many ECG analysis studies. In Table 5 , some standard performance measurements of rhythm classes on the test subjects are given.

Table 5.

The performance values for each class using the Lead-II ECG signal on the test subjects.

Classes	Sensitivity (%)	Precision (%)	Specificity (%)	F- Score (%)	Accuracy (%)
AF	25.00	32.00	98.32	28.07	96.07
AFIB	94.93	92.02	98.53	93.45	97.98
SI	64.28	72.97	99.00	68.35	97.60
SB	98.98	98.48	99.07	98.73	99.04
SR	91.19	92.63	98.35	91.90	97.03
ST	95.18	96.93	99.43	96.04	98.75
SVT	91.52	77.14	98.37	83.72	97.98
Overall	80.15	80.31	98.72	80.04	92.24

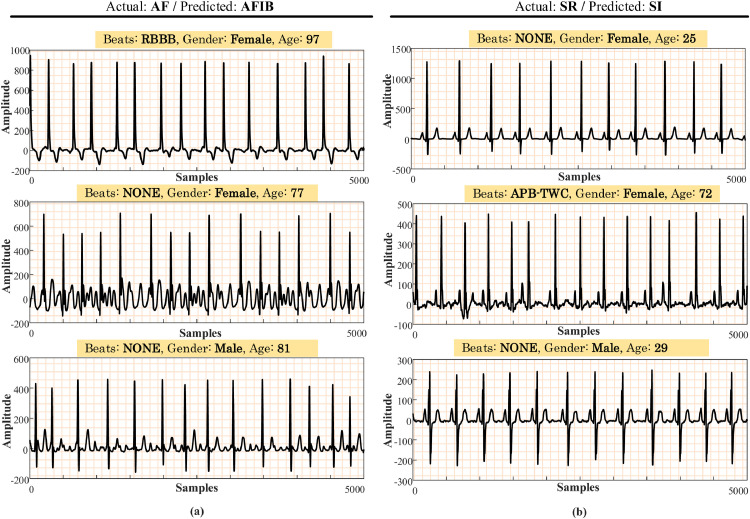
From the above table, performance values on the AF class had the lowest values. The reason for this can be the low number of data in this class. A similar problem was also observed between the SI and SR classes. Accordingly, we present some incorrectly classified signals related to these classes in Fig. 9 . In this figure, some actual and predicted classes are given for the Lead-II signals. On the other hand, the model was able to distinguish sinus bradycardia (SB) signals from other classes, with a 99.04% accuracy performance.

Fig. 9.

Some examples of AF and SR signals that the proposed model incorrectly predicted (Actual: original class, predicted: detected class by the model).

3.3. Merged rhythm classes

In the previous experiments, the DNN model produced some weak class performances due to similarity, e.g. the AF, AFIB, SR, and SI classes yielded low-performance values. Also, in the dataset, several classes had fewer samples, such as AVNRT, AVRT, and SAAWR. To overcome this, we merged 11 rhythms into four classes as AFIB, grouped supraventricular tachycardia (GSVT), SB, and SR, according to the original dataset article [78]. In Table 6 , some brief information is provided concerning the merged classes. In this experiment, we applied the DNN model on these merged rhythm classes.

Table 6.

Some numerical information about merged rhythms.

Merged Rhythms	New Class Name	Number of Total Samples	Number of Training Samples	Number of Testing Samples	Age, Mean ± STD
AF+ AFIB	AFIB	2,218	1,983	235	72.92 ±11.66
SVT+AT+SAAWR+ST+AVNRT+AVRT	GSVT	2,260	2,061	199	55.51 ±20.41
SB	SB	3,888	3,488	400	58.33 ±13.95
SR, SI	SR	2,222	1,997	225	50.89 ±19.18
All		10,588	9,529	1,059	59.23 ±17.97

We divided the merged dataset into training, validation and testing sets as 80%, 10%, and 10%, respectively. The same hyper-parameters from previous experiments were used in this experiment. In Fig. 10 , accuracy and loss graphs for each lead are given during the training step.

Fig. 10.

Validation loss and validation accuracy values for each ECG lead signals, a) loss graphs, and b) accuracy graphs.

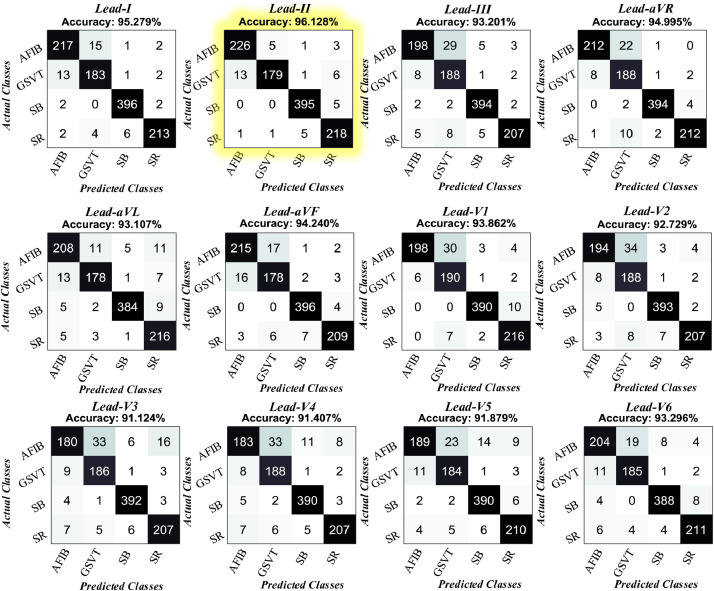
It can be seen from these plots that the best results are obtained from the Lead-II signal. Also, the model showed consistent results with four rhythm classes. There was no overfitting or underfitting problem. Therefore, our proposed model architecture is robust to detect rhythms with two different scenarios. The trained model has been applied to the unseen test records. We present all confusion matrices for each lead signal in Fig. 11 .

Fig. 11.

All confusion matrices for each lead signal obtained from test records.

The results showed that the proposed model generalized the input signals well, with accuracy rates all above 91%. The highest accuracy rates were obtained on Lead-II, Lead-I, and Lead-aVR signals at 96.12%, 95.27%, and 94.99%, respectively. The least accurate classification was observed between AFIB and GSVT classes. For example, according to the Lead-II confusion matrix, 13 of the actual GSVT records were classified as AFIB. Similarly, five of the actual AFIB records were classified as GSVT by the model. This issue can be due to the GSVT category, which comprised six different rhythms (SVT, AT, SAAWR, ST, AVNRT, AVRT). In Table 7 , the performance metrics on the test sets are given in detail.

Table 7.

The DNN model overall performance values on the merged rhythms test set.

ECG Leads	Overall sensitivity (%)	Overall Specificity (%)	Overall Precision (%)	Overall F-Score (%)	Overall Accuracy (%)
Lead-I	94.49	98.44	94.65	94.56	95.28
Lead-II	95.43	98.71	95.78	95.57	96.13
Lead-III	92.30	97.78	92.44	92.21	93.20
Lead-aVR	94.35	98.40	94.21	94.18	95.00
Lead-aVL	92.48	97.76	92.22	92.31	93.11
Lead-aVF	93.20	98.10	93.46	93.32	94.24
Lead-V1	93.30	98.03	93.08	92.98	93.86
Lead-V2	91.81	97.63	91.91	91.67	92.73
Lead-V3	90.01	97.10	89.96	89.76	91.12
Lead-V4	90.46	97.16	90.53	90.27	91.41
Lead-V5	90.93	97.27	91.18	90.92	91.88
Lead-V6	92.63	97.78	92.53	92.56	93.30

The best overall performances were obtained from the Lead-II input with 95.43% sensitivity, 98.71% specificity, 95.78% precision, 95.57% F-score, and 96.13% accuracy. We show the class-based performances for the Lead-II input in Table 8 . The lowest sensitivity performance, which emerged from the GSVT class, was 89.94%.

Table 8.

Class-based performance values for the Lead-II input.

Classes	Sensitivity (%)	Precision (%)	Specificity (%)	F- Score (%)	Accuracy (%)
AFIB	96.17	94.16	98.30	95.15	97.82
GSVT	89.94	96.75	99.30	93.22	97.54
SB	98.75	98.25	98.93	98.50	98.86
SR	96.88	93.96	98.32	95.40	98.01
Overall	95.43	95.78	95.43	95.57	96.13

4. Discussion

Many researchers have attempted to develop an arrhythmia detection system using deep learning architectures. They used different data sources and approaches for this task. We have reported several state-of-the-art studies in Table 9 . Hannun et al. [56] developed a DNN model to detect rhythm classes from raw ECG inputs. Their results show that the DNN can classify ECG signals with high performance. Oh et al. [58] proposed a modified U-net model to detect five different beat class. Their model achieved an accuracy of 97.32% using a total of 83,648 beats from 47 subjects. Li et al. [59] proposed a deep ResNet model to identify five different types of heartbeats. They reported a 99.38% accuracy using 94,013 beats. Acharya et al. [4] obtained an accuracy of 94.03% with a nine-layer CNN model using a total of 109,449 heartbeats. Yildirim et al. [60] proposed a CNN model to classify 17 cardiac rhythms. They reported a 91.33% accuracy rate using 1,000 ECG fragments. Shaker et al. [61] used a generative adversarial network (GAN) and CNN model to classify 15 different ECG classes. They obtained a 98.30% accuracy rate using augmented data with the GAN algorithm. Chang et al. [66] used a sequence-sequence learning task to classify 12 rhythm classes from 38,899 ECG signals. Yildirim [65] reported a 99.39% accuracy rate using a wavelet sequence-based deep bidirectional LSTM (DBLSTM-WS) model. Gao et al. [30] used an LSTM model with FL to detect eight different heartbeats from a total of 93,371 beats.

Table 9.

Comparison of some state-of-the-art study performances to detect arrhythmia.

Study	Num. of Subjects	Num. of Beats/Segments	Input type	Category	Method	Evaluation Scheme	Performance
Acharya et al. [4]	47	109,449	Single lead/ Beat	5 AAMI class	CNN	Intra-Patient	Acc: 94.03%
Xu et al. [5]	22	50,977	Single lead/ Beat	5 AAMI classes	DNN	Inter-Patient	Acc: 93.1%
Gao et al. [30]	-	93,371	Single lead/ Beat	8 Heartbeats	LSTM, FL	Intra-Patient	Acc: 99.26%
Hannun et al. [56]	53,549	91,232	Single lead/ Segment	12 Rhythm	CNN	Inter-Patient	F1: 0.83
Oh et al. [58]	47	83,648	Single lead/ Segment	5 Heartbeats	Modified U-net	Intra-Patient	Acc: 97.32%
Li et al. [59]	47	94,013	2-lead/ Beat	5 AAMI class	Deep ResNet	Intra-Patient	Acc: 99.38%
Yildirim et al. [60]	45	1,000	Single lead/ Segment	17 Rhythm	CNN	Intra-Patient	Acc: 91.33%
Shaker et al. [61]	44	102,098	Single lead/ Beat	15 class	CNN	Intra-Patient	Acc: 98.30%
Yildirim et al. [65]	-	7,326	Single lead/ Beat	5 Heartbeats	DBLSTM-WS	Intra-Patient	Acc: 99.39%
Chang et al. [66]	38,899	65,932	12 lead/ Segment	12 Rhythm	LSTM	Inter-Patient	Acc: 90%
Oh et al. [67]	47	16,499	Single lead/ Segment	5 Heartbeats	CNN-LSTM	Intra-Patient	Acc: 98.1%
Warric et al. [68]	-	8,528	Single lead/ Segment	4 Rhythm	CNN-LSTM	Intra-Patient	F1: 0.82
Xindog et al. [70]	-	12,186	Single lead/ Segment	4 Classes	CNN+RNN	Intra-Patient	F1: 0.82
Oh et al. [72]	170	150,268	Single lead/ Segment	3 Cardiac Disease	CNN-LSTM	Intra-Patient	Acc: 98.51%
Mousavi et al. [73]	-	750	Single lead/ Segment	5 Rhythm	CNN-attention-LSTM	Intra-Patient	Acc: 93.75%
Wu et al. [84]	-	8,528	Single lead/ Segment	4 Classes	Binarized CNN	Intra-Patient	F1: 0.86
Yao et al. [86]	-	6,877	12-lead/ Segment	8 Rhythm	ATI-CNN	Inter-Patient	F1: 0.81
Proposed	10,436	10,436	Single lead/ Segment	7 Rhythm	DNN	Inter-Patient	Acc: 92.24%
	10,588	10,588	Single lead/ Segment	4 Rhythm		Inter-Patient	Acc: 96.13%

Xindog et al. [70] used the 2017 PhysioNet/Computing in Cardiology (CinC) Challenge database to classify four rhythms (sinus, AF, noisy, and other), and they achieved 0.82 F1 scores. Wu et al. [84] used a binarized CNN model on the 2017 CinC database. The authors reached a 0.86 F1 score. Oh et al. [67] constructed an LSTM and CNN combination model to detect five types of heartbeats. They used a total of 16,499 beat signals from 47 subjects, and their model reached a 98.1% accuracy rate. Mousavi et al. [73] proposed a deep learning model to detect true alarms on five types of arrhythmia in the 2015 PhysioNet challenge [85]. Oh et al. [72] performed a CNN and LSTM based deep model to categorize CAD, CHF, and MI cardiac abnormalities. They used a total of 170 patient records and achieved an accuracy of 98.51% to categorize these abnormalities. Yao et al. [86] proposed an attention-based time-incremental CNN (ATI-CNN) model to classify 8 different arrhythmias using 12-lead ECG signals. They achieved an average F1-Score of 81.2% to classify arrhythmias with varied-length inputs.

In this study, we have developed a new DNN model to detect different rhythm types. We used more than 10,000 (10-sec duration ECG records) for this aim. Our model showed 92.24% and 96.13% classification performances on two different class scenarios. When we compare our study with other studies, generally, the prior studies used a limited number of subject records. They also used many beats extracted from the same subjects. This situation can limit the generalizability of models on unseen subjects. In this study, each ECG record was obtained from a unique subject; hence the proposed model generalized well on unseen ECG signals. Hannun et al. [56] constructed a large database that included 53,549 subjects, but this database consists of ECG records with a single lead only. Chang et al. [66] used a large 12-lead ECG database of 38,899 subjects. Their database is not publicly available. We have already obtained highest accuracy using a single lead. Hence, we did not combine the performance of all leads. However, we analyzed all lead signals and according to the results our model performance can be generalizable to 12-lead signals. We intend to explore this further using a new deep learning model in future work. In addition, many of the studies [4, 5, 30, 58, 59, 61, 65, 67] are predicated on the detection of heartbeat signals, unlike in our model, which is based on the 10-second ECG input.

The main advantages of the system presented in this study can be summarized as:

• •Only one DNN model was used to classify different rhythm groups with high performance using all lead signals.
• •We used a public ECG dataset, which is recent, and one of the largest datasets, containing more than 10,000 unique subject data.
• •The experiments were performed using 11 different rhythm categories with 10-sec ECG records.
• •All experimental results were reported with inter-patient schema, and the performance of the model was promising.
• •The model has a good generalization ability to detect ECG arrhythmia for each of 12-lead ECG signals.
• •The model worked on 10-second ECG records and did not require the detection of heartbeats.

The main disadvantage of this work is the requirement for sophisticated hardware due to the nature of the deep models. In future works, we will evaluate these ECG records with multi-task deep learning models. In addition, some features in non-ECG domains were also provided within this database, and we will try to use these features to improve the performance of deep models.

5. Conclusion

In this paper, a new DNN model comprising both representation and sequence learning structures was proposed to detect arrhythmia. Experiments were performed on a new large public ECG database that includes more than 10,000 unique subject records. The DNN model was applied to the 10-s raw 12-lead ECG signals. The proposed DNN model yielded promising results for each lead input. Two different rhythm class scenarios were used for the experiments. The first scenario included seven rhythm classes, for which the model obtained an accuracy of 92.24%. In the second scenario, 11 rhythm classes were merged into four main rhythm classes. The model achieved an accuracy of 96.13% performance on this dataset. According to the obtained results, it can be said that the proposed DNN model has a good generalization ability for subject-wise classes.

Declaration of Competing Interest

The authors declare that there is no conflict of interest.