The effect of the diffusion time and pulse gradient duration ratio on the diffraction pattern and the structural information estimated from q-space diffusion MR: Experiments and simulations

Abstract

q-Space diffusion MRI (QSI) provides a means of obtaining microstructural information about porous materials and neuronal tissues from diffusion data. However, the accuracy of this structural information depends on experimental parameters used to collect the MR data. q-Space diffusion MR performed on clinical scanners is generally collected with relatively long diffusion gradient pulses, in which the gradient pulse duration, δ, is comparable to the diffusion time, Δ. In this study, we used phantoms, consisting of ensembles of microtubes, and mathematical models to assess the effect of the ratio of the diffusion time and the duration of the diffusion pulse gradient, i.e., Δ/δ, on the MR signal attenuation vs. q, and on the measured structural information extracted therefrom. We found that for Δ/δ ~ 1, the diffraction pattern obtained from q-space MR data are shallower than when the short gradient pulse (SGP) approximation is satisfied. For long δ the estimated compartment size is, as expected, smaller than the real size. Interestingly, for Δ/δ ~ 1 the diffraction peaks are shifted to even higher q-values, even when δ is kept constant, giving the impression that the restricted compartments are even smaller than they are. When phantoms composed of microtubes of different diameters are used, it is more difficult to estimate the diameter distribution in this regime. Excellent agreement is found between the experimental results and simulations that explicitly account for the use of long duration gradient pulses. Using such experimental data and this mathematical framework, one can estimate the true compartment dimensions when long and finite gradient pulses are used even when Δ/δ ~ 1.

1. Introduction

Diffusion NMR [1–3] has become an important tool in material and medical sciences since it is capable of providing detailed structural information over a large range of length scales. This technique is currently used to study structural features in sediments [4], polymers [5], porous materials [6], and biological tissues [7]. In these fields the q-space diffusion MR approach was found to be extremely useful for obtaining structural information on the investigated sample [8,9].

q-Space diffusion MR, developed by Callaghan and Cory and Garroway in the early 1990s [8,9], based on Kärger averaged propagator formalism [10], has become a powerful tool for characterizing morphological features of different materials. This method utilizes the attenuated signal of diffusing molecular species to yield structural information regarding the compartments in which the diffusion process is taking place. Under specific controlled experimental conditions, this MR technique can provide an estimation of the displacement distribution of the diffusing molecular species from which structural dimensions and shapes can be inferred [6,8,9,11]. One unique and important feature of the q-space diffusion MR approach is that the extracted structural information can be obtained without the need to invoke a model of the system [8].

The q-space approach, originally used to study porous materials [6,8,11–15], was shown to be a useful tool for studying, inter alia, the dimensions of yeast cells [9], the structural changes induced after cerebral ischemia [16,17], and the size and shape of red blood cells [18–24]. In fact, red blood cells are the only biological tissues in which clear meaningful diffraction patterns that could be related to their structural characteristics were observed [18–24]. Recently, some diffractions were reported for neuronal tissues [25] but their origin is not quite clear. Since it was found that the water signal decay in neuronal tissues, at least at sufficiently high q or b-values, is not mono-exponential [26,27], and considering the fact that white matter (WM) can be regarded as a semi-ordered porous material, the Cohen group suggested studying diffusion in WM using the q-space approach [28,29]. To this end, q-space NMR was extended to imaging [30], for the purpose of obtaining structural information at the micron scale for each pixel in the MR image.

WM tissues are constructed from axon bundles which are surrounded by cell membranes and myelin sheaths that restrict water diffusion across them and therefore water diffusion in WM are known to be anisotropic [31]. Because of these WM characteristics, high b-value q-space diffusion MRI (QSI) was found to be a useful method to investigate WM structure and disorders [30,32–38]. QSI was first used to study structures and pathologies in isolated neuronal tissues using strong magnetic field gradients [30,32–35] and afterwards was extended to study WM disorders on clinical scanners [36–38]. Very recently QSI was extended to CHARMED [39] and AxCaliber [40] which enable one to map axon diameters and neuronal density. Generally, high q-values are needed to achieve such detailed structural information in QSI. However, with clinical scanners, high q-values, i.e., q = (γ/2π)δG, can only be obtained with long diffusion gradients pulses, because of the relatively weak gradients available on clinical MRI scanners. Therefore, the short gradient pulse (SGP) approximation (i.e., δ ~ 0) is not satisfied in these diffusion MRI experiments [36–38]. Under such conditions the compartment sizes extracted from such q-space diffusion experiments are, as expected [41–43], smaller than the real size of the compartment [36–38]. In addition, to be able to extract the dimensions of the compartments in which diffusion takes place, the diffusion distance performed by the diffusing species must be longer or comparable to the compartment dimension, i.e., Δ >> l²/2D (where l is the size of the compartment in which water molecules with diffusion coefficient D are diffusing). Therefore, in many high q diffusion MR experiments performed on clinical scanners, the diffusion time, Δ is on the order of δ (i.e., Δ ~ δ or Δ/δ ~ 1) and the condition generally assumed in q-space analysis, namely, that Δ >> δ, is also not satisfied [36–38].

Recently, efforts have been directed to evaluate the accuracy of the structural information obtained from QSI [35,44]. For such a task, it is useful to use phantoms with micron-scale compartments. Packs of microcapillary tubes seem to be an appropriate phantom to simulate some features of the axonal domain in WM. Avram et al. [44] used phantoms consisting of ensembles of microtubes to test the accuracy of the structural information extracted from q-space diffusion NMR experiments performed under different experimental conditions. Structural information obtained from both the diffraction patterns and from the displacement distribution profiles were compared. It was found that the microtubes’ diameter extracted from the high q-space diffusion MR experiment was exactly that of the actual size of the cylinders only when δ → 0, and Δ >> l²/2D for the 20 μm tubes, i.e., when Δ was higher than 50 ms. In the case of 9 μm tubes, smaller dimensions were estimated even when δ = 3 ms. In these experiments diffractions were observed when Δ was longer than 30 ms. Although the effect of the rotational angle and the length of δ on the extracted compartment size were experimentally evaluated in this study, all experiments in that study satisfied the Δ >> δ condition.

In this study, packs of microcapillary tubes having different diameters were used to study the effect of the diffusion time and gradient duration ratio (i.e., Δ/δ) on the q-space diffusion MR signal decay and on the tubes diameters extracted thereof. We studied the diffusion MR signal decay and the diffraction patterns when the SGP approximation is violated, emphasizing the cases where Δ:δ ratio is nearly 1, i.e., Δ/δ ~ 1. We also describe the effect of the Δ:δ ratio on the signal decay and the observed diffraction pattern for different rotational angles, αs, not described previously. In addition, the signal decay and the structural information extracted therefrom were studied for a mixture of microcapillaries for the first time. The experimental results were then compared with simulations that incorporate the finite duration of the gradient pulse, δ.

2. Materials and methods

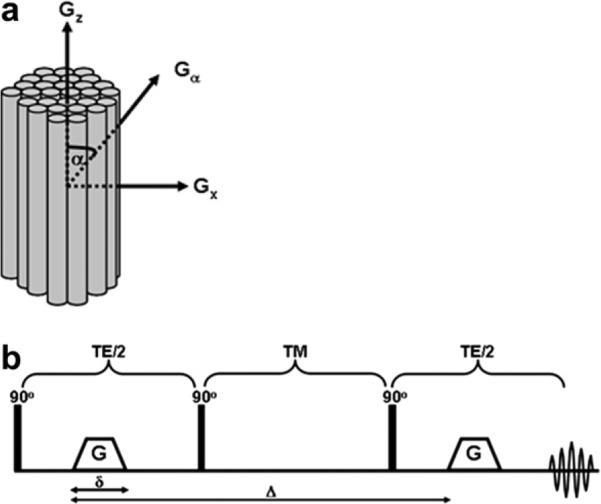
NMR diffusion experiments were performed on packs of 4 cm hollow cylindrical tubes (microcapillaries) having inner diameters (IDs) of 20 ± 1, 15 ± 1, and 10 ± 1 μm (Polymicro Technologies) and mixtures thereof using an 8.4 T NMR spectrometer equipped with a Micro5 gradient system capable of producing pulse gradients of up to 190 G cm⁻¹ in each of the three directions. The microcapillaries were filled with undoped water, packed in a 5 mm NMR tube and aligned along the z-axis in the magnet (Fig. 1a). A pulsed gradient stimulated echo (PGSTE) diffusion sequence [3] (Fig. 1b) was used with different diffusion parameters. Note that according to the manufacturer the accuracy in the IDs of the tubes is ±1 μm.

Fig. 1.

(a) The MR experimental setup used in this study. G_x and G_z are the gradient directions perpendicular and parallel to the main axis of the microtubes, respectively, and α is the rotational angle between the applied diffusion gradient, G_α, and the main axis of the cylinders, i.e., the z-axis. (b) The pulsed-gradient stimulated echo (PGSTE) sequence [3] used for the MR diffusion experiments, where δ is the gradient pulse duration, Δ is the gradient pulses’ separation time, and G is the diffusion gradient strength. TE and TM are the echo time and the mixing time, respectively.

Compartment sizes were extracted from the first minima of the graph of signal decay vs. q (taken as 1.22/q_min) and from full width at half height (1.22× FWHH) of the displacement distribution profile obtained by Fourier transformation of the signal decay vs. q.

2.1. 20 μm ID microtubes

To examine the effect of Δ/δ on the diffusion NMR signal attenuation profile, the diffraction patterns and the structural information extracted therefrom, diffusion was first measured perpendicular to the long axis of the tubes, i.e., α = 90°. In all experiments the maximal q-value, i.e., q_max, was set to 1362 cm⁻¹. In the first set of experiments, where δ = 2 ms, the Δs were set to 15, 30, 50, 100, 200, 500, and 1000 ms. In these experiments TR/TE were 3000/20 ms and G was incremented from 0 to 160 G cm⁻¹ in 32 equal steps.

For δ = 32 ms, Δs of 42, 100, and 300 ms were used, resulting in Δ/δ values of 1.3, 3.1, and 9.4, respectively. TR/TE were 3000/80 ms and G was incremented in 32 equal steps from 0 to 10 G cm⁻¹. For δ = 48 ms, Δs of 60, 100, 200, and 400 ms were used, resulting in Δ/δ of 1.3, 2.1, 4.2, and 8.3, respectively. TR/TE were 3000/112 ms and G was incremented in 32 equal steps, from 0 to 6.67 G cm⁻¹.

The effect of the gradient orientation, α, on the MR results for different Δ/δ values was studied using the following parameters: Δ/δ of 42/32 and 100/32 ms, resulting in Δ/δ of 1.3 and 3.1, respectively, with a G_max of 10 G cm⁻¹. The gradient directions sampled were 90° (perpendicular to the microtubes’ walls), 85°, 80°, 75°, 70°, 60°, and 0° (parallel to the microtubes’ walls). In these cases, again, q_max was 1362 cm⁻¹ and TR and TE were set to 3000 and 80 ms, respectively.

2.2. 10 μm ID microtubes

To examine the effect of the Δ/δ on the MR diffusion data in smaller microcapillaries, i.e., ID = 10 μm, we used a diffusion gradient duration, δ, of 15 ms, with three different pulse gradient separations. The Δ values used were 20, 30, and 45 ms, resulting in Δ/δ of 1.3, 2, and 3, respectively. G was incremented from 0 to 48 G cm⁻¹ in 48 equal steps, resulting in a q_max of 3065 cm⁻¹. In these experiments TR and TE were set to 3000 and 38 ms, respectively.

2.3. Mixture of 15 and 20 μm microcapillaries (1:1)

To assess the effect of different values of Δ/δ on NMR diffusion experiments in a mixture of microcapillaries, we mixed fibers of 15 and 20 μm in about a 1:1 volumetric ratio. For this sample, the following diffusion parameters were used: δ = 32 ms whereas Δ was 42, 100, or 300 ms, to obtain Δ/δ of 1.3, 3.1, or 9.4, respectively. Here, G was incremented from 0 to 16.5 G cm⁻¹ in 32 equal steps, resulting in a q_max of 2246 cm⁻¹. We also examined the diffusion results when all three requirements, i.e., δ → 0, Δ >> δ, and Δ > l²/2D, of the q-space approach, were satisfied. For these experiments, G was incremented from 0 to 160 G cm⁻¹ in 32 equal steps, δ was set to 3.3 ms, and Δ was 42, 100, or 300 ms. In these experiments, TR and TE were set to 3000 and 72 ms, respectively.

In all these diffusion MR experiments the signal-to-noise ratio (SNR) was better than 7000 for the q₀ spectrum.

2.4. Simulations

We employed a matrix product formalism [45] based on the idea of representing a finite-duration gradient pulse as a train of impulses [46]. The discretization was performed according to the scheme proposed in Ref. [47]. The number of impulses (M) representing each of the diffusion sensitizing gradients was determined by rounding the quantity δ (where δ is in ms) to the nearest integer. Hence a train of impulses was constructed, where the separation between two consecutive impulses is approximately 1 ms. The magnitude of each impulse was set to q/M. With this discretization, an approximation to the NMR signal intensity was obtained by computing the matrix product given in Eq. (A4) of Ref. [48].

Our implementation of the matrix product scheme for cylindrical pores followed the description in Ref. [49] although our approach has several differences. Assuming no relaxation at the cylinders’ walls, we started out by computing the β_mn values satisfying the equation $J_m^{\prime }\left({\beta }_{mn}\right)=0$, where J_m(x) is the mth order Bessel function. 100 roots of the derivatives of each Bessel function up to 100-th order were computed using Mathematica. These roots were sorted in ascending order, where each root with a non-zero m value was entered into the resulting array twice. This was necessary because we used a degenerate form of the diffusion propagator, where the eigenfunctions were taken to be proportional to J_m(β_mnr/a)e^imθ, where a is the radius of the cylinder, and r and θ are the polar coordinates in two-dimensional space. In this representation, the index m varies between −∞ and +∞, and the terms corresponding to +m and −m are degenerate. The matrices to be used in the estimation of the signal intensity were computed accordingly. Unlike in [45], the integral of the product of three Bessel functions was computed numerically by combining trapezoidal integration results obtained with 500 and 1000 points using a scheme in Ref. [50] increasing the accuracy of the integration while maintaining its efficiency. Despite the increase in the sizes of the matrices, the degenerate form of the propagator made the implementation simpler. A total of 37 terms were kept in the eigenfunction expansion of the diffusion propagator, although it was found empirically that the results did not change significantly after the 23rd term. The value of the bulk diffusivity was estimated from the first three points of the MR signal attenuation obtained when gradients are applied parallel to the cylinders’ axis, assuming that this corresponds to free diffusion.

It should be noted that the simulations required the IDs of the microtubes as an input. A Levenberg–Marquardt fitting algorithm was used to estimate the tube diameter for each Δ value. An inner diameter was estimated by invoking the narrow pulse approximation. Then the fitting was repeated by taking the finite duration of the diffusion gradients into account. The reported 〈χ²〉 values are computed using the expression $\langle {\chi }^2\rangle =\frac{1}{N}{\sum }_{k=1}^N{(E_k^{\mathrm{sim}}-E_k^{\mathrm{data}})}^2$, where N is the number data points available at that Δ value.

3. Results

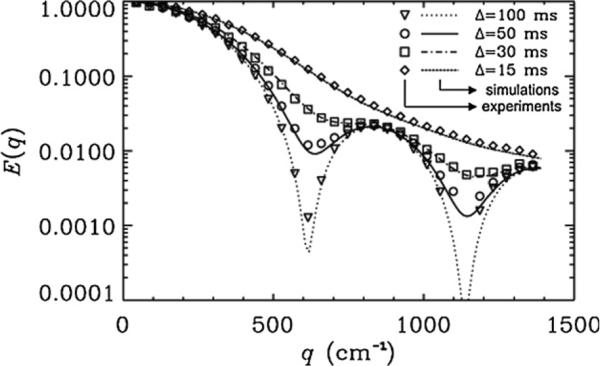
Fig. 2 shows the experimental and simulated signal decay, E(q), for α = 90° (i.e., perpendicular to the long axis of the microcapillaries) as a function of q-values obtained from the PGSTE experiment. Here, we used a pack of 20 μm ID microcapillaries with a short gradient pulse duration, i.e., δ = 2 ms. This figure clearly demonstrates that the diffraction patterns obtained from the q-space diffusion experiments become less pronounced as the diffusion time decreases. Note that there is no difference between the diffraction patterns observed for Δ = 1000 ms (data not shown) or Δ = 100 ms, i.e., when the Δ/δ is 500 or 50, respectively. However, differences are clearly seen when the diffusion time is 50 ms or shorter. Here, shallower diffraction troughs are observed; however, the same structural information is extracted for diffusion times greater than 50 ms, since diffraction minima are observed at the same q-value. These results are expected, since Δ/δ in these experiments is large, δ is short, and the Δ >> δ condition is also fulfilled when Δ is longer than 50 ms. As expected for such an experiment, very good agreement is observed between the experimental signal attenuation and the simulations (χ² < 3.5 × 10⁻⁴).

Fig. 2.

Experimental (symbols) and simulated (lines) MR signal decay as a function of q-values obtained from PGSTE experiments performed on 20 μm microtubes for different Δs when Δ >> δ and when diffusion was measured perpendicular to the main axis of the cylinders, i.e., α = 90°. The pulsed gradient duration, δ, was 2 ms for all diffusion times. The inner diameter used in the simulations was 20 μm. The χ² values which represent the variation of the experimental data from simulations were found to be 2.6 × 10⁻⁴, 1.3 × 10⁻⁴, 2.1 × 10⁻⁴ and 8.5 × 10⁻⁵ for Δs of 100, 50, 30 and 15 ms, respectively.

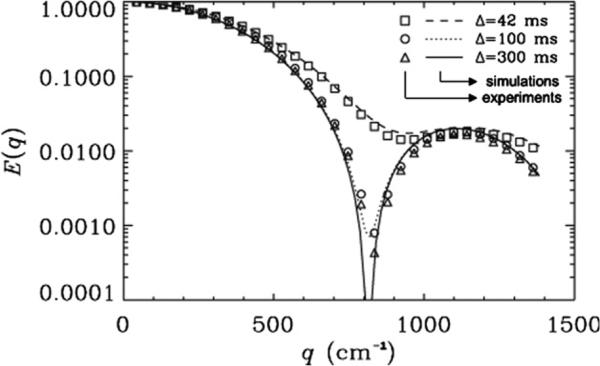
Fig. 3 shows the experimental and simulated signal decays for 20 μm microcapillaries juxtaposed as a function of q for α = 90° when Δ was set to 42, 100, or 300 ms for a δ = 32 ms. For Δ = 42 ms, when Δ/δ = 1.3, diffraction minima appeared at higher q-values and were shallower than the diffraction minima observed for Δs of 100 and 300 ms, when the Δ/δ values were 3.1 and 9.4, respectively. In fact, this figure shows that very similar diffraction minima were obtained for both Δ/δ of 3.1 and 9.4. From these experiments, a value of 14.6 μm is estimated for the 20 μm microcapillaries, which is, as expected, smaller than the actual diameter of the tubes [41–43]. When Δ/δ = 1.3, an even smaller diameter (13.2 μm) is estimated based upon the position of the diffraction minima, and these troughs are significantly shallower. Interestingly, the simulations, which assume a 20 μm ID, show very similar attenuation as obtained from the experimental diffusion MR data (χ² < 7.5 × 10⁻⁵).

Fig. 3.

The effect of the Δ/δ on the MR diffusion signal decay as a function of q for PGSTE experiments collected with a δ of 32 ms on 20 μm cylinders. Δs of 42, 100 and 300 ms were used resulting in Δ/δ values of 1.3, 3.1, and 9.4, respectively. Symbols represent the experimental data, and lines depict the corresponding simulations performed by using an inner diameter of 20 μm. The rotational angle α was 90°. The χ² values which represent the variation of the experimental data from simulations were found to be 6.4 × 10⁻⁶, 7.5 × 10⁻⁵ and 3.7 × 10⁻⁶ for Δs of 42, 100 and 300 ms, respectively.

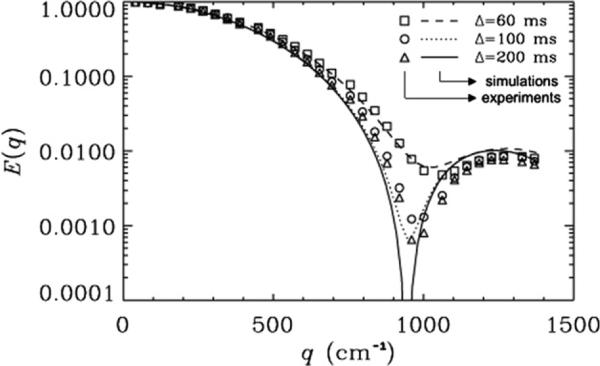
Fig. 4 shows similar data for experiments acquired on 20 μm ID microcapillaries with δ = 48 ms and Δs of 60, 100, or 200 ms, where Δ/δ were 1.3, 2.1, or 4.2, respectively. Under these conditions, we observed that the diffraction minima, as expected [41–43], appear at higher q-values, when compared with Fig. 3, where δ = 32 ms. This is to be expected since when δ is 48 ms the SGP approximation is more strongly violated than when δ is 32 ms. In Fig. 4, again, the same trend as shown in Fig. 3 was obtained. When Δ/δ = 1.3, the diffraction minima were shallower and appeared at higher q-values and hence a smaller ID was extracted (i.e., 12.2 μm) for the 20 μm tubes. For Δ/δ > 2, deeper and more pronounced diffraction troughs were observed, as compared with those observed when Δ/δ = 1.3. Note that the estimated diameter of the microcapillaries for Δ/δ of 2.1, 4.2, and 8.3 (not shown) was the same. The estimated diameter was 12.7 μm, which is larger than that estimated when Δ/δ = 1.3. In this case, again, the simulations, which assume an ID of 20 μm, are in very good agreement with the experimental data (χ² < 7.3 × 10⁻⁵).

Fig. 4.

The effect of the Δ/δ on the MR diffusion signal decay as a function of q for PGSTE experiments collected with a δ of 48 ms on 20 μm cylinders. Δs of 60, 100, and 200 ms were used, resulting in Δ/δ values of 1.3, 2.1, and 4.2, respectively. Symbols represent the experimental data, and lines depict the corresponding simulations. The rotational angle, α, was 90°. The inner diameter used for the simulation was 20 μm. The χ² values which represent the variation of the experimental data from simulations were found to be 4.4 × 10⁻⁵, 7.2 × 10⁻⁵ and 5.1 × 10⁻⁵ for Δs of 60, 100 and 200 ms, respectively.

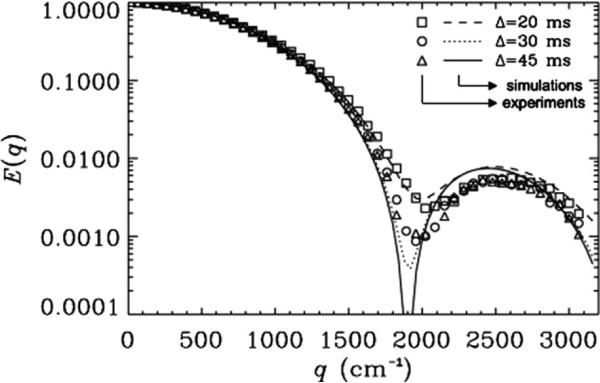
Fig. 5 shows the effect of varying Δ/δ in diffusion NMR experiments performed on 10 μm ID microcapillaries. In these experiments, we found the same behavior as with the 20 μm tubes. For Δ/δ = 1.3 (20/15 ms), very shallow diffraction minima were observed and we estimated an ID = 6.0 μm for the microcapillaries. However, for Δ/δ of 2 or 3 (30/15 or 45/15 ms, respectively) the diffraction minima were more pronounced and a bigger ID of 6.2 μm was estimated in both cases. Note that in this phantom, the simulations are in a good agreement with the experimental signal attenuations for all three examined values of Δ/δ (χ² < 3.8 × 10⁻⁵). From the simulations an ID of 10.4 μm, which is very close to the expected value (10 ± 1 μm), was estimated for Δ/δ of 2 and 3.

Fig. 5.

The effect of the Δ/δ on the MR diffusion signal decay as a function of q for PGSTE experiments collected with a δ of 15 ms on 10 μm cylinders. Δs of 20, 30, and 45 ms were used resulting in Δ/δ values of 1.3, 2 and 3, respectively. Symbols represent the experimental data, and lines depict the corresponding simulations. The rotational angle, α, was 90°. The inner diameter used for the simulation was 10.4 μm. The χ² values which represent the variation of the experimental data from simulations were found to be 3.8 × 10⁻⁵, 2.3 × 10⁻⁵ and 3.6 × 10⁻⁵ for Δs of 20, 30 and 45 ms, respectively.

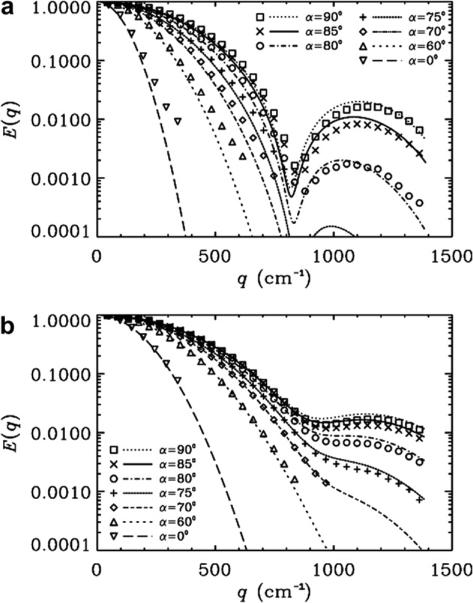
Fig. 6a and b shows the experimental and the simulated signal decays superimposed as a function of the q-values in 20 μm tubes for different rotational angles, α, when δ = 32 ms and Δs were set to 100 and 42 ms, respectively. From Fig. 6a, where the Δ/δ = 3.1, one can observe the high sensitivity of the diffraction patterns to rotational angle, α. Interestingly, as shown in Fig. 6b, when Δ/δ = 1.3, this dependency on α was also observed, but it was less pronounced. In these cases, again, the simulations performed under these experimental conditions are in good agreement with the experimental signal decay profile (χ² < 9.0 × 10⁻⁴), as in the other cases (Figs. 2–5).

Fig. 6.

Normalized signal decay as a function of q-values for different rotational angles, αs, for PGSTE performed on 20 μm microtubes for two different Δ/δ values when δ = 32 ms. (a) Δ = 100 ms, Δ/δ = 3.1. (b) Δ = 42 ms, Δ/δ = 1.3. Symbols represent the experimental data, and lines represent the corresponding simulations obtained by using an inner diameter of 20 μm. The χ² values which represent the variation of the experimental data from simulations were between 5.6 × 10⁻⁵ and 9.0 × 10⁻⁴ for Δ of 100 ms and between 1.5 × 10⁻⁶ and 7.9 × 10⁻⁵ for Δ of 42 ms.

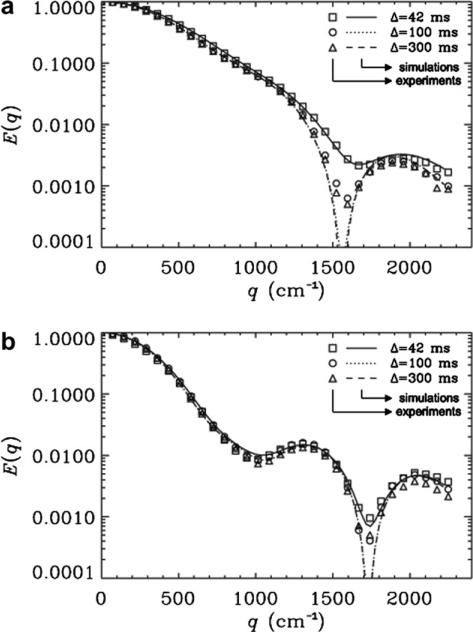
Fig. 7a and b shows the results for a mixture of microtubes with two different inner diameters, i.e., 15:20 μm (1:1, volumetric ratio). Fig. 7a presents the effect of violating the SGP approximation when Δ/δ was 1.3, 3.1, or 9.4. An interesting result was the disappearance of one of the diffraction minima. Clearly, the second diffraction trough was observed for all Δs used when δ = 32 ms but was deeper and more pronounced for Δ/δ of 3.1 or 9.4, as compared with the case when Δ/δ was 1.3. When the same phantom was examined with δ = 3.3 ms and a G_max = 160 G cm⁻¹ (the same q-values as used in Fig. 7a), two diffraction minima were observed for all three Δs used; however, the first diffraction trough was shallower than the second one (Fig. 7b). Interestingly, for both cases (Fig. 7a and b) the simulations agree with the experimental signal decay (χ² < 4.6 × 10⁻⁴). In these cases the simulations were performed by assuming IDs of 20 and 14 μm for the mixture of 20 and 15 μm microcapillaries, respectively.

Fig. 7.

(a) The MR diffusion signal decay as a function of q for PGSTE experiments collected with a δ of 32 ms for a mixture of 15:20 μm (1:1 by volume) cylinders. The results for Δs of 42, 100, and 300 ms with Δ/δ values of 1.3, 3.1 and 9.4 respectively, are shown. Symbols represent the experimental data, and lines depict the corresponding simulations. The χ² values which represent the variation of the experimental data from simulations were 1.9 × 10⁻⁶, 5.4 × 10⁻⁷ and 3.9 × 10⁻⁶ for Δs of 42, 100 and 300 ms, respectively. (b) The effect of the Δ/δ on the MR diffusion signal decay as a function of q for PGSTE experiments collected with a δ of 3.3 ms for a mixture of 15:20 μm (1:1 by volume) cylinders. The χ² values which represent the variation of the experimental data from simulations were 4.6 × 10⁻⁴, 4.7 × 10⁻⁵ and 2.1 × 10⁻⁵ for Δs of 42, 100 and 300 ms, respectively. In these cases the diameter of the 20 μm was taken as 20 μm while the diameter of the 15 μm tubes was taken to be 14.0 μm for the simulations.

Table 1 summarizes the sizes of the compartments extracted from the diffraction patterns (i.e., 1.22/q_min) and the full width at half height (FWHH taken as 1.22× FWHH). Here, we see that there is a good agreement between the two methods as found previously [44].

Table 1.

Compartment sizes extracted from the first minima of the graph of signal decay vs. q (1.22/q_min) and from FWHH (1.22× FWHH) of the displacement distribution profile obtained by Fourier transformation of the signal decay vs. q

Figure	Cylinders diameter (μm)	Δ	δ	Δ/δ	1.22/qmin (μm)	1.22× FWHH (μm)
2	20	50	2	25	19.8	20.0
	20	100	2	50	19.8	20.0
3	20	42	32	1.3	13.2	12.2
	20	100	32	3.1	14.6	13.7
	20	300	32	9.4	14.6	13.8
4	20	60	48	1.3	12.2	12.2
	20	100	48	2.1	12.7	12.7
	20	200	48	4.2	12.7	13.0
5	10	20	15	1.3	6.0	6.3
	10	30	15	2.0	6.2	6.5
	10	45	15	3.0	6.2	6.5
7a	15:20	42	32	1.3	n.d.:7.6	9.8
	15:20	100	32	3.1	n.d.:8.0	10.6
	15:20	300	32	9.4	n.d.:8.0	10.5
7b	15:20	42	3.3	13	7.0:12.0	16.7
	15:20	100	3.3	30	7.0:12.0	16.8
	15:20	300	3.3	91	7.0:12.0	17.0

n.d., not determined. In these cases first diffraction was not observed.

4. Discussion

In this study, microcapillaries with well-defined inner diameters were used as a model to test the microstructural information obtained from the q-space diffusion MR approach, using experimental parameters typical of clinical MRI scanners to collect such data. In clinical scanners q-space data is generally collected when d is nearly equal to Δ, i.e., Δ/δ ~ 1. We found that when experimental conditions of the q-space analysis are fulfilled, i.e., δ ~ 0 and Δ >> l²/2D, the compartment size estimated using the q-space approach is similar to the actual size of the microcapillaries. When microcapillaries of more than 10 μm inner diameter are inspected under these experimental conditions one may predict a priori where the diffraction minima should occur. For much smaller capillaries, even for short δ, the measured size will be significantly smaller than the actual size of the compartment. In such cases one needs to correct for the finite pulse duration used in the MR experiment for extracting the correct compartment size as done in the simulations of the present study.

In this study, we addressed another assumption implicit in the q-space analysis of MR diffusion data, namely that Δ/δ >> 1. Indeed, we found that the value of Δ affects the q-values at which diffraction minima are observed, and hence the compartment size one would infer therefrom. In this study, we used δs of 32 and 48 ms with different Δs in order to measure restricted diffusion using different Δ/δs ranging from 1.3 to 9.4. Importantly, we found that the ratio of Δ to δ (i.e., Δ/δ) does affect the signal decay even when δ is kept constant and consequently the structural information obtained from the q-space diffusion MR experiments. In fact we found that an even smaller compartment size is inferred when δ is kept constant and the ratio of Δ to δ approaches unity. To the best of our knowledge this was not shown previously on micron-scale phantoms. For example, when we used Δ/δ = 1.3, the diameters obtained from the diffraction patterns and from the width of the displacement distributions profile obtained from the Fourier transformation of the signal decay are both smaller than the compartment sizes (Table 1). It was also demonstrated that a Δ/δ of about 2–3 and above yields the same experimental results. This phenomenon was found for both δs of 32 and 48 ms used to study the 20 μm microtube phantoms and for δ = 15 ms used to study the 10 μm microcapillaries. We also found that Δ/δ affects the sensitivity of the signal decay and the diffraction patterns on the rotational angle. For Δ/δ ~ 1, this sensitivity is less apparent. Again, this phenomenon was not reported previously on such microcylinders. Interestingly, all these observations are reproduced by our simulations with high accuracy. In all cases, in our simulations the correct IDs were used in order to simulate the experimental data. This means that despite the shift in the diffraction dip one can, with the aid of simulations which take into account the duration of the gradient pulse δ, extract the true size of the compartment in which the diffusion occurs.

An additional interesting result of the effect of Δ/δ on the signal decay and the diffraction patterns observed for a mixture of 20 and 15 μm microtubes is shown in Fig. 7. Fig. 7b clearly shows that even when all three requirements are fulfilled in this mixture, the first diffraction patterns are less pronounced. However, the situation is even more complex when Δ/δ ~ 1 (Fig. 7a). In this case, there is an additional shift of the diffraction pattern to higher q-values and consequently, even smaller IDs are extracted. In addition, in this case only one diffraction minimum is observed and from the displacement distributions profile only a single value was extracted. In this case, we have not used the procedure recently presented by Kuchel et al. to detect shallow diffractions [51]. Nevertheless, even in these cases, again, our simulations show very good agreement with the experimental data and demonstrate that taking into consideration the finite duration of δ enables one to recover the true compartment size from the q-space diffusion MR data. This can be achieved even if the diffusion data were collected with diffusion MR parameters that violate many assumptions assumed in the q-space approach. Deviation of <1 μm will give very different curves with respect to the experimental one. So once the calibration is done, one can use this approach to extract real sizes with high accuracy. Very recently a special gradient unit capable of producing up to 5000 G cm⁻¹ was designed and used to study q-space diffusion characteristics of a mouse spinal cord. There, very good agreement was found between compartment size obtained from the q-space approach and histology when δ was kept short [35]. Our data show that, at least for the type of samples studied in this paper, one can extract accurate physical sizes with the aid of simulations even when the q-space assumptions are violated and Δ/δ is nearly 1, conditions generally used in clinical MRI scanners when high diffusion weighting is required.

5. Conclusions

We evaluated the effect of varying Δ and δ concentrating on the effect of the Δ:δ ratio and emphasizing the condition of Δ/δ ~ 1. We studied the effect of such conditions on the signal decay, the diffraction patterns, and accuracy of the structural information obtained thereof when q-space diffusion MR is used to study restricted diffusion in micron-size compartments. The experimental results were compared with simulations that take into account the finite duration of δ. When diffusion was measured perpendicular to the compartments’ walls and the conditions δ ~ 0, Δ > l²/2D, and Δ >> δ were fulfilled, the size of the microcapillaries could be obtained accurately using the q-space approach. Under these experimental conditions, clear and prominent diffraction minima were observed. For experiments performed with long δs, smaller diameters were, as expected, obtained. For Δ/δ = 1.3, however, the diffraction pattern minima were shifted to even higher q-values and even smaller inner diameters were estimated from the diffusion data although δ was kept constant. These findings are similar for a mixture of microtubes where the diffraction patterns are even less well defined. Interestingly, for all these cases the simulations were in very good agreement with the experimental data, although the simulations were performed with the actual size of the microtubes. The study clearly demonstrates that for the sizes interrogated in this study (10–20 μm) q-space diffusion MR can be performed under experimental conditions that are typical of conventional clinical MRI scanners and one can still obtain, with the aid of simulations, the correct microstructural information.