Automatic Artifact Detection in Impedance Cardiogram Using Pulse Similarity Index

Abstract

Impedance cardiography (ICG) is a noninvasive technique for evaluation of cardiac hemodynamic parameters such as cardiac output and pre-ejection period. However, the sensitivity of the technique to motion artifact, electrode displacement, and cardiovascular pathologies can severely impact the accuracy of hemodynamic parameter estimates. In this paper, we proposed a new algorithm for the automatic detection and exclusion of corrupted ICG cardiac cycles by defining a pulse similarity index that quantifies the level of pulse corruption and its diversion from a typical-shaped pulse. The index considers different features (activity, structure, shape, and pattern) of the ICG cardiac cycles. The algorithm is compared on sleep data collected from 20 participants against expert identified corrupted cycles. The artifact rejection algorithm achieved a high accuracy of 96% in detection of expert-identified corrupted ICG cycles, including those with normal amplitude as well as out-of-range values, and was robust to different types and levels of artifact. The algorithm shows promise toward applications requiring accurate and reliable automatic measurement of cardiac hemodynamic parameters from prolonged data sets.

I. INTRODUCTION

Impedance cardiography (ICG) is a validated, noninvasive technique for measuring cardiac hemodynamic parameters including stroke volume, cardiac output, left ventricular ejection time, and pre-ejection period [1]. ICG measures impedance to a high frequency, low magnitude current; impedance changes in association with fluctuations in blood volume and flow velocity in the ascending aorta during systole and diastole.

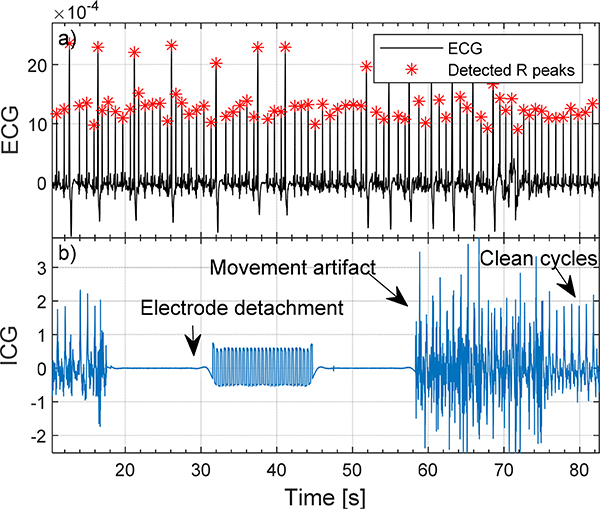
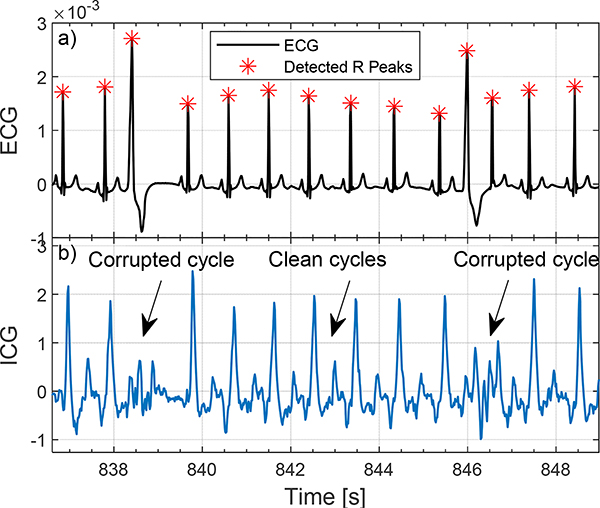
The reliability of hemodynamic parameter measurements depends on the accurate detection of distinct peaks and notches on the ICG signal [1–3]. However, beat-to-beat variation of ICG due to the distorting effect of body movements, muscle contractions, respiration, and different cardiovascular pathologies (see Figs. 1, 2), can impede the detection of these characteristic points, especially during long measurements when it is unreasonable for a participant to remain immobile or during sleep when subject movements are not controlled and electrodes could be easily displaced or lose contact [4]. Researchers have often relied on visual inspection of the signal to identify and discard portions of invalid data from further analysis [5–7]. Visual inspection, however, is time consuming and inefficient when analyzing data collected over extended time periods.

Figure 1.

Examples of electrode detachment and movement artifact on ICG signal.

Figure 2.

Examples of cardiovascular pathologies (here premature ventricular contractions) (PVC) on ICG signal of a 46-year-old female participant.

Although automatic algorithms based on ensemble averaging [8, 9] and digital filtering [10, 11] have been developed, these algorithms are only applicable at moderate levels of noise and artifacts when valid ICG cycles still exist and are recoverable. Other algorithms rely on post-hoc outlier detection from estimated hemodynamic parameters [12, 13], however, parameters that show apparent within-range values could still be invalid if estimated from highly corrupted ICG cycles.

We recently proposed a different approach for artifact rejection based on the detection and exclusion of corrupted ICG cardiac cycles prior to any parameter estimation and evaluation, ideally suited for long datasets with variable noise and artifact levels [14]. The algorithm worked by measuring the ICG signal variations (activity) within each cardiac cycle and was shown to perform well on sleep data. A limitation of the previous work was that it only considered activity and did not consider the shape of the ICG signal over each cardiac cycle, therefore, those corrupted cycles in shape that did not have an out-of-range activity could not be detected.

In the current paper, we addressed this limitation and developed a better automatic algorithm for the detection of corrupted ICG cardiac cycles. A new similarity index is defined as a weighted combination of several indices measuring the activity, structure, shape, and pattern of the ICG signal within each cardiac cycle. Those cycles with lower or higher than normal similarity index were marked as corrupted cycles. The proposed algorithm was found to outperform the previously proposed algorithm with about 10% higher accuracy.

II. Methodology

A. Experimental Design

Twenty healthy adults (10 female) (age 46.2±8.4 years) underwent standard polysomnography (PSG) recordings at the SRI Human Sleep Research Laboratory. Participants slept in temperature-controlled and sound-attenuated bedrooms. The study was reviewed and approved by the SRI International Institutional Review Board, and all participants provided written informed consent.

Electrocardiogram (ECG) signal was collected via a dedicated channel in the PSG system. ECG was recorded in a modified D2 Einthoven configuration via Ag/AgCl Meditrace surface spot electrodes and sampled at 512Hz. ICG dZ/dt signal, representing the rate of change in the impedance waveform on a given beat, was recorded via HIC-4000 Bioelectric impedance cardiography (Bio-Impedance Technology, Inc., Chapel Hill, NC). The dZ/dt output signal was interfaced and acquired within the PSG recording system. ICG was recorded using a 4-lead 8-point connection arrangement: Inner recording electrodes were positioned around the lateral base of the neck and around the lateral thorax, at the level of the xiphisternal junction. Outer electrodes were placed 3 cm above and below each of the recording electrodes. A 4mA AC 100 kHz was transmitted in the outer electrodes and the output voltage recorded by the inner electrodes.

B. Preprocessing

Simultaneously recorded ICG and ECG signals were digitally filtered with a 4th-order Butterworth bandpass filter to remove high frequency noise and artifacts and low-frequency drift. The lower and upper cutoff frequencies were set to 0.5 Hz and 35 Hz, and 0.5 and 25 Hz for ECG and ICG, respectively.

An automatic peak detection algorithm was adopted to detect the ECG R peaks using half of the average R-R interval as the minimum distance criterion between two successive peaks [14, 15]. The average R-R interval was estimated from the ECG power spectral density. ICG cardiac cycles were identified using the ECG R peaks as the reference. Every portion of the ICG signal located between two successive ECG R peaks was marked as an ICG cardiac cycle. ICG cardiac cycles were then interpolated in time to the same length.

ICG signal variations over each cardiac cycle were divided by a normalizing factor F defined as the median of the ICG cycles amplitude, as follows:

$$\mathit{F}={\mathrm{m}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{n}}_{\mathit{i}}\left({\mathrm{m}\mathrm{a}\mathrm{x}}_{\mathit{j}}\left({\mathit{X}}_{\mathit{i}}\left(\mathit{j}\right)\right)-{\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathit{j}}\left({\mathit{X}}_{\mathit{i}}\left(\mathit{j}\right)\right)\right)$$ (1)

where X_i(j) represents the jth sample of ith ICG cycle. Median was calculated over all available ICG cycles for each individual. The ICG cardiac cycle amplitude was defined as the difference between its maximum (Z point) and minimum (X point). This step is crucial to obtain a valid similarity index robust to signal level variations between and within individuals.

C. Artifact Detection Algorithm

Several indices were defined to obtain a reliable measure of signal quality and noise level as follows:

1. Activity Index (AI)

To measure the ICG signal variations over each cardiac cycle, an index was defined as the standard deviation of normalized ICG cycles, as follows [14]:

$$\mathit{A}\mathit{I}=\sqrt{\frac{1}{\mathit{N}}{\sum }_{\mathit{j}=1}^{\mathit{N}}{\left(\mathit{X}\left(\mathit{j}\right)-{\mathit{\mu }}_{\mathit{x}}\right)}^2}$$ (2)

where N is the total number of ICG cycle samples and μ_x is the mean over the samples. Too low values of AI can indicate electrode detachment and too high values can represent movement artifacts and noise [14].

2. Structural Similarity Index (SSI)

To measure the similarity of ICG cardiac cycles to a typical clean ICG waveform, the structural similarity used for evaluation of image qualities [16] was adopted. The SSI was defined for every ICG cardiac cycles versus a template Y as follows:

$$\mathit{S}\mathit{S}\mathit{I}\mathit{M}(\mathit{X},\mathit{Y})=\frac{\left(2{\mathit{\mu }}_{\mathit{x}}{\mathit{\mu }}_{\mathit{y}}+{\mathit{C}}_1\right)\left(2{\mathit{\sigma }}_{\mathit{x}\mathit{y}}+{\mathit{C}}_2\right)}{\left({\mathit{\mu }}_{\mathit{x}}^2+{\mathit{\mu }}_{\mathit{y}}^2+{\mathit{C}}_1\right)\left({\mathit{\sigma }}_{\mathit{x}}^2+{\mathit{\sigma }}_{\mathit{y}}^2+{\mathit{C}}_2\right)}$$ (3)

where μ_x, μ_y, σ_x, σ_y, and σ_xy are the means, standard deviations, and cross-correlation for ICG cardiac cycle X and the template Y. C₁ and C₂ are the regulation constants which were set to 1e-4 and 3e-9, respectively.

The ICG cardiac cycle template Y can be derived by averaging a large number of clean ICG cardiac cycles obtained from different individuals. Here, the template was obtained by averaging 100 clean cycles derived from three subjects not included in the rest of the study.

3. Euclidean Norm Index (ENI)

To measure the distance between the ICG cardiac cycles X and the template Y, the Euclidean norm (L2 norm) was calculated as follows:

$$\mathit{E}\mathit{N}\mathit{I}={\sum }_{\mathit{j}=1}^{\mathit{N}}{\left|\mathit{X}\left(\mathit{j}\right)-\mathit{Y}\left(\mathit{j}\right)\right|}^2$$ (4)

The smaller values of ENI represent closer shape similarity between the ICG cardiac cycle and the template.

4. Cross-Correlation Index (CCI)

To measure the pattern similarities between the ICG cardiac cycles and the template, the cross-correlation at zero delay was derived as follows:

$$\mathit{C}\mathit{C}\mathit{I}=\frac{{\sum }_{\mathit{j}=1}^{\mathit{N}}\left[(\mathit{X}\left(\mathit{j}\right)-{\mathit{\mu }}_{\mathit{x}})\times (\mathit{Y}\left(\mathit{j}\right)-{\mathit{\mu }}_{\mathit{y}})\right]}{\sqrt{{\sum }_{\mathit{j}=1}^{\mathit{N}}{(\mathit{X}\left(\mathit{j}\right)-{\mathit{\mu }}_{\mathit{x}})}^2}\sqrt{{\sum }_{\mathit{j}=1}^{\mathit{N}}{(\mathit{Y}\left(\mathit{j}\right)-{\mathit{\mu }}_{\mathit{y}})}^2}}$$ (5)

In order to obtain a reliable measure of the normalizing factor F in (1), the activity index in (2) was first calculated on unnormalized ICG cycles. Two low sensitivity thresholds, set at 0.02 and 2, were applied to detect and reject those ICG cycles with too low (such as no data segments where the electrodes are detached) or too high (such as sharp spikes due to rapid movements) activity, respectively. This step is required to obtain a reliable estimate of the normalizing factor in cases where majority of the ICG cycles are corrupted. The ICG cycles were then normalized and the defined similarity indices were derived.

The defined similarity indices were then combined to derive a new pulse similarity index (PSI) defined as the weighted summation of the normalized referenced AI, SSI, ENI, and CCI, as follows:

$$\mathit{P}\mathit{S}\mathit{I}={\sum }_{\mathit{k}=1}^4{\mathit{w}}_{\mathit{k}}\times \mathit{f}\left(\mathit{g}\left({\mathit{S}\mathit{I}}_{\mathit{k}}\right)\right)$$ (6)

where SI_k represents any of the four similarity indices defined in (2)-(5), and w_k is its corresponding weight. The operators g(∙) and f(∙) reference and normalize the similarity indices to the same range, as follows:

$$\mathit{f}\left({\mathit{S}\mathit{I}}_{\mathit{k}}\right)=\frac{\mathit{g}\left({\mathit{S}\mathit{I}}_{\mathit{k}}\right)-\mathit{m}\mathit{i}\mathit{n}\left(\mathit{g}\left({\mathit{S}\mathit{I}}_{\mathit{k}}\right)\right)}{\mathrm{m}\mathrm{a}\mathrm{x}\left(\mathit{g}\left({\mathit{S}\mathit{I}}_{\mathit{k}}\right)\right)-\mathit{m}\mathit{i}\mathit{n}\left(\mathit{g}\left({\mathit{S}\mathit{I}}_{\mathit{k}}\right)\right)}$$ (7)

$$\mathit{g}\left({\mathit{S}\mathit{I}}_{\mathit{k}}\right)=|{\mathit{S}\mathit{I}}_{\mathit{k}}-\mathit{R}\mathit{e}\mathit{f}({\mathit{S}\mathit{I}}_{\mathit{k}}\left)\right|$$ (8)

where Ref(SI_k) is a typical value of the similarity index for a clean ICG cycle. Here, it was defined for each individual as the median of the similarity indices obtained on all ICG cardiac cycles recorded over the night.

The weights w_k can be defined based on the importance of the features to be preserved. They can be set to zero if a specific index is not desired to be considered. Here, we set them equally to 0.25.

An outlier detection algorithm was then developed to detect the ICG cycles that appear to be inconsistent with the remainder of cycles based on the defined PSI. Corrupted cycles were defined as those ICG cycles with a PSI of more than four scaled median absolute deviation (MADN) away from the median, as follows:

$$|PSI-\mathrm{m}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{n}(PSI\left)\right|>4\times MADN$$ (9)

Where

$$MADN=1.48\times \mathrm{m}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{n}\left(|PSI-\mathrm{m}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{n}(PSI\left)\right|\right)$$ (10)

where median was computed over all available ICG cycles of each individual.

Data collected from three individuals (not included in the rest of the analysis) that contained different artifact types including movement and electrode displacement were used to design the algorithms and find their parameters.

D. Data Analysis

2000 ICG cardiac cycles (100 per individual) were randomly selected and visually scored by an expert (MdZ), blinded to the algorithm scoring, as either corrupted or clean cycles. Clean cycles were selected as those cycles that followed the general pattern of the ICG signal with B, Z, and X points uncontaminated by artifacts [1]. In order to study the performance of the algorithm at different levels of ICG signal amplitude, the expert-detected corrupted cycles were divided into three groups: below normal, normal, and above normal amplitude. Normal amplitude cycles for each subject were defined as those with an amplitude of > 0.5 or < 2 times of the median amplitude of the clean cycles. Each cycle’s amplitude was defined as the difference between its maximum and minimum values.

In order to evaluate the performance of the algorithm on different artifact types and levels, three categories of artifacts including electrode detachment, low-level movement, and high-level movement were selected by the expert based on the shape of ICG cycles and their pattern variations over time. The accuracy of the artifact rejection algorithm was then analyzed on each artifact category.

True positive (TP), false positive (FP), false negative (FN), and true negative (TN) rates were calculated according to the expert scores. The performance of the algorithm was evaluated in terms of the overall accuracy, overall error, sensitivity, specificity, positive predictive value, and negative predictive value.

All the algorithms were developed in MATLAB R2018a (MathWorks, INC., Natick, MA).

III. Results

A total of 454 out of 2000 ICG cycles were scored by the expert as corrupted cycles among which 420 were correctly detected by the proposed algorithm (TP). The algorithm also detected 41 cycles that were not scored by the expert as corrupted (FP) (see Table I). The proposed algorithm achieved an overall accuracy of 96%, overall error of 4%, sensitivity of 93%, specificity of 97%, positive predictive value of 91%, and negative predictive value of 98%, which shows close agreement with the expert (see Table 2).

TABLE I.

Confusion Table Summarizing the Performance of the Artifact Rejection Algorithms versus Expert

		Expert
	N = 2000	Corrupted cycle	Clean cycle
Proposed Pulse Similarity Index-based Algorithm	Corrupted cycle	420 (TP)	41 (FP)
	Clean cycle	34 (FN)	1505 (TN)
Activity Index-based Algorithm [14]	Corrupted cycle	333 (TP)	149 (FP)
	Clean cycle	121 (FN)	1397 (TN)

TABLE II.

Performance Comparison of the Proposed Pulse Similarity Index-Based Algorithm and a Previous Activity Index-Based Algorithm [14] for Artifact Rejection at Different Levels and Types of Artifacts

Algorithms’ Performance (%)	Proposed Pulse Similarity Index-based Algorithm	Activity Index-based Algorithm [14]
Overall Accuracy	96.25	86.50
Overall Error	03.75	13.50
Sensitivity	92.51	73.35
Specificity	97.35	90.36
Positive predictive value	91.11	69.09
Negative predictive value	97.79	92.03
Accuracy (Below Normal Amplitude)	95.74	90.63
Accuracy (Normal Amplitude)	95.10	74.51
Accuracy (Above Normal Amplitude)	100	100
Accuracy (Low-Level Movement)	93.83	72.84
Accuracy (High-Level Movement)	96.81	94.15
Accuracy (Electrode Detachment)	100	100

Among the expert-selected corrupted ICG cycles, 9% were classified as below-normal, 54% as normal, and 37% as above-normal amplitude. The artifact rejection algorithm detected 96%, 95%, and 100% of the corrupted cycles with amplitudes below normal, normal, and above normal, respectively, which shows its high accuracy at different levels of ICG signal amplitude (see Table 2).

The proposed artifact rejection algorithm detected 100% of the electrode detachment cases, 97% of high-level movement artifacts, and 94% of the-low level movement artifacts which shows its robustness to different types and levels of artifact (see Table 2).

IV. Conclusions

Impedance cardiography is an important noninvasive technique for the evaluation of cardiac hemodynamic parameters such as pre-ejection period in research and clinical applications. However, ICG is sensitive to noise and movement artifact, which can impact accuracy and reliability, particularly during long periods of data collection, such as overnight. Visual inspection of data to identify corrupted portions is highly burdensome and time consuming when considering prolonged datasets and automatic approaches are clearly needed.

In this paper, we developed a new ICG artifact rejection technique to detect the ICG corrupted cycles. The algorithm was applied on sleep data to remove corrupted ICG cycles. It was found to closely match the expert visual inspection and outperform the previously developed artifact detection method by our group [14]. Here, we considered measures in addition to activity, including structural similarity, Euclidean norm, and cross-correlation.

Impedance cardiography is ideally suited to unobtrusively assess cardiovascular hemodynamics during a wide range of procedures, in response to interventions, and in both static and active environments [17]. ICG can also be adapted for portable wearables (e.g. smart clothes) allowing measurements to be made outside the laboratory during daily living for longer periods of time. ICG measurement has a particular application to sleep, allowing the assessment of cardiac function during an ideal prolonged resting state. However, in order for ICG to be more widely used, especially in naturalistic settings, there is a need for more automatized analyses such as proposed here to process potentially noisy signals. Our proposed algorithm performed well in the analysis sleep data corrupted by movement artifacts and electrode displacements. Future work will involve evaluating the performance of the proposed algorithm on a larger number of healthy subjects as well as patients and in other noisy settings such as full-day routine activities.