Abstract
Malacca Strait (MS) has an important role and potential for many countries. It is a major transportation route for oil and commodities across continents. In addition, various activities such as shipping, fishing, aquaculture, oil drilling, and energy are also carried out in MS. Tides strongly affect the MS environment so that it becomes a major parameter in MS management. This paper is the first study, which presents MS tidal hydrodynamics based on a baroclinic and nonhydrostatic approach. Tidal hydrodynamics in MS and the surrounding waters were assessed using tidal forces, temperature, salinity, and density. This study analyzes the amplitude, phase, current ellipses, and semi-major axis of the tides. These variables are obtained from the simulation results of the three-dimensional numerical models of M2 tides and combined tides (M2, S2, N2, K1, and O1) with nonhydrostatic models. Then the results obtained are verified by observation data. Amplitude and phase of the tidal wave in MS originate from two directions, namely the northern part of MS (Andaman Sea) and the South China Sea (SCS). Tides from the north of MS propagate into the MS, while tides from the SCS travel to Singapore Waters (SW) and the south of MS. This causes a complex residual flow in SW and shoaling in the middle of MS. Shoaling in the middle of MS is characterized by a large amplitude and semi-major, as in B. Siapiapi. The results of this analysis show that tidal waves are dominated by semidiurnal types rather than diurnal types. The M2 current ellipse has dominantly anticlockwise rotation along the west of the MS, while along the east of MS, it has generally a clockwise rotation.
Keywords: Oceanography, Computational mathematics, Earth sciences, Environmental science, Geophysics, Three-dimensional model, M2 tides, Semidiurnal tides, Tidal circulation, Singapore Waters, South China Sea
Oceanography, Computational mathematics, Earth Sciences, Environmental science, Geophysics, Three-dimensional model, M2 tides, semidiurnal tides, tidal circulation, Singapore Waters, South China Sea.
1. Introduction
The MS is a vital strait connecting Indonesian waters, the SCS, Andaman Sea and the Indian Ocean. This waters is known as a dense sea crossing because tankers from the Arabian Peninsula to East Asia cross it. The MS also has considerable energy resources and potential derived from tides (Sakmani et al., 2013).
Tides are crucial to study because they control the mainstream circulation and processes in the coastal region. Nodoushan (2018) suggested that physical information such as tides, high waves, and winds are needed to improve the accuracy of forecasting water quality parameters (such as dissolved oxygen, temperature, and salinity). Meanwhile, according to Gholami and Baharlouii (2019), the tidal elevation is needed in determining the extent of coastline expansion or shrinkage in marine ecosystems such as mangroves. Patrick and Strydom (2014), added that tidal current circulation is very important for migration and abundance of larval and juvenile fish in estuarine systems (Embling et al., 2013; Patrick and Strydom, 2014; Abrogueña et al., 2020). In coastal waters, tides and extreme rainfall are the main factors determining the risk of flooding (Xu et al., 2014; Thanh, 2019). Thus, tides are essential to coastal development, energy management, conservation, fishing, port activities, and disaster mitigation planning (Sindhu and Unnikrishnan, 2011; Rose and Bhaskaran, 2017a).
In previous research, the numerical barotropic models (Rizal and Sündermann, 1994; Rizal, 2000) has been performed to MS tide. They show the essential roles of non-linear terms of MS and M2 tides in the MS circulation. Non-linear terms of MS have an essential impact on the hydrodynamic forces. It is equal to the sum of several hydrodynamic forces (eddy viscosity forces, Coriolis, and barotropic gradient). It can affect the results of the amplitude and currents, especially in shallow zones. Non-linear components are present due to the shallow and the sharp gradients of the depth. Non-linear tides are generated from the zone which accumulated with tidal propagation and strengthened in the zone where they are distributed (Rose and Bhaskaran, 2017a,b). According to Rose and Bhaskaran (2017b), in the case of the Head Bay of Bengal, the shallow water tidal modulation and the variation of spring and neap cause amplifying fortnightly tide.
MS tides are from the Indian Ocean in the north and the SCS in the south. Based on the M2 phase, the tides spread from the Indian Ocean to the Andaman Sea and then branched towards Martaban Bay and the rest to the MS (Wyrtki, 1961; Rizal et al., 2012; Sindhu and Unnikrishnan, 2013). M2 amplitude is found to be higher in shallow parts, especially in the southern part of MS. The tides cause the annual flow in the MS towards the Andaman Sea (Wyrtki, 1961). Besides the MS, SW tides were also analyzed using a high-resolution numerical model (Kurniawan et al., 2011; Hasan et al., 2011; Van Maren and Gerritsen, 2012; Xu and Chua, 2016). According to Xu and Chua (2016), the SW circulation and transport are complex. It depends on the change of tides, sea level anomaly, seasonal variation, and local wind.
The motivation of this research is to conduct baroclinic tides simulations in the MS using a three-dimensional numerical model with nonhydrostatic approximation developed by Kämpf (2010). The model has relatively rare to use because of its high effort and time-consuming. However, the model is advanced because it includes non-linear terms of vertical momentum and stratification of seawater. In baroclinic mode, tides correspond to the stratification of water or seawater density. As far as we know, tidal hydrodynamics in MS have never been simulated by considering temperature, salinity, and density, as well as the application of the nonhydrostatic approximation.
This article is composed of the following sections. Research materials and tidal hydrodynamic models are described in Section 2.1 and Section 2.2, respectively. In Section 2.2, the hydrodynamic model consists of two scenarios, namely: M2 tidal and tidal five main components (M2, S2, N2, K1, and O1). Chapter 3.1 explains the results of the M2 tidal simulation analysis consisting of amplitude, phase, ellipse current, semi-major, density changes, current circulation, and residual current. Meanwhile, Section 3.2 describes the results of tidal simulations of five main components consisting of sea level, amplitude, phase, semi-major axis, semi-minor axis, and surface current circulation during spring tide and neap tide.
2. Materials and method
2.1. Hydrography dataset
The bathymetry data of the model domain is obtained from SRTM30 (ftp://topex.ucsd.edu/pub/srtm30_plus/) (Figure 1). SRTM30 is a near-global digital elevation model (DEM) data obtained from the Shuttle Radar Topography Mission by the National Aeronautics and Space Administration (NASA) and the National Geospatial-Intelligence Agency (NGA/NIMA). SRTM30 has a 30 arc-second spatial resolution. The data has good quality and been used in many research. Previously, we used SRTM30 for the wind-driven circulation studies in MS (Haditiar et al., 2016) and Aceh Waters, Indonesia (Setiawan et al., 2018). Also, the sensitivity of open boundary on the Gulf of Thailand circulation (Adliansyah et al., 2016).
Figure 1.
Domain and bathymetry of MS (in meters).
The condition of stratification or density in MS is calculated from the values of temperature, salinity, and pressure based on the EOS80 equation and simplified to σstp or ρ(S, Tw, p) -1000 kg/m3 (UNESCO, 1981; Talley et al., 2011). Temperature and salinity data were obtained from World Ocean Atlas (WOA) (Levitus and Boyer, 1994; Levitus et al., 1994). In-depth, monthly WOA data sets have 24 layers, while quarterly WOA data sets have 33 layers. This data is then interpolated so that it fits the MS grid model. We consider a higher number of layers near the surface layer and a smaller number of layers in the deep sea layer. It is because temperature and salinity tend to vary near the surface layer compared to the layer near the bottom.
The amplitudes and phases of tides (M2, S2, N2, K1, and O1 tides) were prescribed along the open boundaries. The data were obtained from the Indonesian Geospatial Information Agency (GIA) (http://tides.big.go.id/). GIA data is the analyzed data from 128 tidal observation stations in Indonesian waters. Thus, it has good quality as an open boundary and data verification.
We verified the M2 tides model with GIA tides data, observation data (derived from Rizal and Sündermann, 1994), and OSU TOPEX/Poseidon Global Inverse Solution (TPXO7.2) (Egbert et al., 2010). Also, the results of the five major tidal constituents (M2, S2, N2, K1, and O1) were verified with observational data from PUSHIDROSAL (Indonesia Navy) in 2017.
2.2. Numerical model
The model is based on the Navier Stokes equation by involving nonhydrostatic effects and sea level slope. We slightly modified the model Kämpf (2010), so that vertical thickness or vertical resolution can be varied.
We use Cartesian coordinates with the horizontal resolutions of Δx = Δy = 5′ and 14 layers in the vertical directions. Layers consist of 0–5, 5–10, 10–15, 15–20, 20–30, 30–40, 40–50, 50–60, 60–80, 80–100, 100–150, 150–200, 200–250, and over 250 m. The numerical model grid system used is Arakawa C-grid. The advection solution is obtained by the Total-Variation-Diminishing (TVD) scheme with the superbee-limiter. We use time step Δt = 60 s, and it depends on the Courant–Friedrichs–Lewy (CFL) criterion (Δt ≤ (Δx, Δy)/(2gh)0.5). This model applied the density in the equation of motion. While the influence of bottom friction is given according to the Chêzy equation (Rizal and Sündermann, 1994; Rizal, 2000).
In the three-dimensional model, the pressure plane is separated into two parts (P = p + q), where p (lowercase) refers to the field of hydrostatic pressure for disturbance (horizontal) sea level, and q is the effect of pressure due to the influence of sea level slope and contribution of nonhydrostatic pressure (Kämpf, 2010; Rizal et al., 2019, 2020). The hydrostatic pressure field is the first value that should be calculated before the calculation of momentum (Eqs. (2), (3), and (4)), and nonhydrostatic pressure at the sea surface. The hydrostatic pressure p is diagnostically calculated from the hydrostatic equilibrium equation (Eq. 1):
| (1) |
where z is the vertical coordinate, ρ is the actual density, ρo is the surface density, and g is the acceleration of gravity.
According to Kämpf (2010), The equations of motion in x, y, and z direction are as follows (Eqs. (2), (3), and (4)):
| (2) |
| (3) |
| (4) |
The left side of Eqs. (2), (3), and (4) consists of local terms, advection terms, and Coriolis force. Meanwhile, the right side of Eqs. (2), (3), and (4) consists of the total pressure gradient (hydrostatic and nonhydrostatic) and diffusion terms. u, v, and w are velocity components in Cartesian coordinates (x, y, z), with t is time, f is the Coriolis parameter, and ρo is the reference density, AH and AZ are horizontal and vertical turbulence viscosity coefficients, respectively. We used AH based on the previous study i.e., AH = KH = 500 m2/s (Pond and Pickard, 1983; Berloff and Meacham, 1998; Berloff and Mcwilliams, 1999; Nauw et al., 2004; Rizal et al., 2010). Pond and Pickard (1983) have used AH = 4 × 104 m2/s and AZ = 10−4 m2/s. According to Pond and Pickard (1983), a simple rough approach is used to the fact that non-linear terms are about the same size as the turbulent friction terms. Therefore, AH ≈ U L (where U is typical horizontal velocity and L is horizontal length scale). In MS, with U = 0.1 m/s and L = 5’ or about 104 m, we can use AH = 103 m2/s or less. Previously, Rizal et al. (2010) also applied AH and KH = 500 m2/s for hydrostatic currents model of MS (see Table 1).
Table 1.
Notation.
| Symbols | |
|---|---|
| A | M2 tidal amplitude, m |
| AH, AZ | Horizontal and vertical turbulence viscosity coefficients, m2/s |
| Amplitude of tides based on kth constituents, m | |
| c | Free-parameter coefficient for advanced turbulence closure, non-dimensional |
| ε | Epsilon for nonhydrostatic pressure correction, pa |
| f | Coriolis parameter, rad/s |
| ,, | Pressure and difussion terms in the equation of motions, m/s2 |
| fk | Nodal factor for tidal amplitude, non-dimensional |
| g | Acceleration of gravity, m/s |
| h | Water depth, m |
| H | Total water depth (h + η), m |
| i, j, k | Index for indicating the horizontal and vertical coordinates, non-dimensional |
| KH, KZ | Horizontal and vertical turbulence diffusity coefficients, m2/s |
| LN2 | Horizontal length scale, mBrunt-Väisälä frequency, s−2 |
| P | Total pressure, Pa |
| p | Hydrostatic pressure field, Pa |
| q | Initial hydrostatic pressure, PaNonhydrostatic pressure field, Pa |
| qn, | Initial nonhydrostatic pressure, Pa |
| qs, | Nonhydrostatic pressure at the sea surface, Pa |
| S | Salinity, non-dimensional |
| T | The period of M2 tides, s |
| Tk | The period of tidal components, s |
| Tw | Water temperature, oC |
| u,v | Zonal and meridional velocities, m/su-velocity at v-grid, m/s |
| , | The initial of horizontal velocities, m/s |
| , | The first-prediction of horizontal velocities, m/s |
| uf U | Nodal factor for tidal phase, degreeTypical horizontal velocity, m/s |
| V0 | Astronomical argument, degree |
| vres | Residual current, m/sv-velocity at u-grid, m/s |
| w | Vertical velocity, m/s |
| The initial of vertical velocity, m/s | |
| The first-prediction of vertical velocity, m/s | |
| Δq, | Correction for nonhydrostatic pressure, Pa |
| Δt, dt | Time-step for numerical simulation, s |
| Δx, Δy | Spatial resolution in horizontal direction, m |
| Δz | Spatial resolution in vertical direction, m |
| η | Sea level elevation, m |
| ηT/4, ηT/2, η3T/4, ηT | Sea level elevation at M2 tidal period, m |
| ρ | Actual density, kg/m3 |
| ρo | Surface and reference density, kg/m3 |
| φ | M2 tidal phase, degree |
| φk | Phase of tides, degree |
| ϕ | Latitude, degree |
| ω | Free-parameter coefficient for S.O.R. method, non-dimensional |
The continuity equation reads (Eq. 5):
| (5) |
The nonhydrostatic pressure field at the sea surface is indicated by qs = ρogη, where ρo is the constant reference density at the sea surface, η is sea level elevation, H is the total water depth, and < > is the average vertically.
The transport of temperature use the following equation (Eq. 6):
| (6) |
while the transport equation of salinities reads (Eq. 7):
| (7) |
where Tw and S are water temperature and salinity, respectively. The density values are predicted by Tw and S according to EOS80 equation (UNESCO, 1981; Talley et al., 2011).
The viscosity and diffusity coefficients in vertical direction are parameterization by the following equation (Kochergin, 1987; Kämpf, 2010) (Eq. 8):
| (8) |
where KZ is turbulence diffusity coefficient in vertical direction. AZ and KZ values are calculated by an advanced turbulence closure proposed by Kochergin (1987) and Kämpf (2010) (Eq. 8). The equation applied minimum AZ = KZ = 1e−4 m2/s, free parameter (c = 0.15), and Brunt-Väisälä frequency (N2) based on the density stratification.
The nonhydrostatic pressure field q can be solved in two steps, i.e. explicit prediction for the initial pressure and implicit prediction for the pressure correction (). The continuity equation provides a prognostic equation for dynamic surface pressure (Eq. 5). To find the implicit solution of nonhydrostatic pressure (Eq. 5), the continuity results required free divergent condition. Finally, the momentum equations can be solved after the hydrostatic and nonhydrostatic pressure field are known. The flowchart of the research methodology can be seen in Figure 2. Eqs. (9), (10), (11), (12), (13), (14), (15), (16), (17), (18), (19), and (20) show the discretization of the model that has been simplified from Kämpf (2010).
Figure 2.
Flowchart of the research methodology.
The first-prediction of nonhydrostatic pressure:
| (9) |
The first-prediction of nonhydrostatic pressure is indicated by . Meanwhile, the first-prediction of current velocities are marked with , and , respectively. The prediction of velocities has included the effect of advection, diffusion, Coriolis force, hydrostatic and nonhydrostatic pressure without nonhydrostatic pressure correction. Indices i, j, and k indicate x, y, and z-coordinates, respectively. Indices i moves from the surface to the bottom depth, while j and k move in the normal horizontal direction.
The first-prediction of current velocities:
| (10) |
| (11) |
| (12) |
where α= Δt f with f is the Coriolis parameter. The initial current velocities are symbolized by , , and . is the interpolation of u-velocity at a grid v and is the interpolation of v-velocity at a grid u. Current advection terms are symbolized by Adv (u, v, w).
is defined as follows:
| (13) |
| (14) |
| (15) |
where is the pressure and diffusion terms. and are initial hydrostatic and nonhydrostatic pressures, respectively. Diffusion terms are symbolized by Diff (u, v, w). Advection and diffusion terms were solved by the superbee-limiter TVD method. After obtaining the first-prediction of velocities, the nonhydrostatic pressure correction () can be determined by the Successive Over-Relaxation (S.O.R.) method.
S.O.R. method:
| (16) |
where
Successive Over-Relaxation (S.O.R.) method works until the correction of the nonhydrostatic pressure converges to the specified epsilon. Epsilon determines the accuracy of nonhydrostatic pressure. In this study epsilon is ε = 0.01 Pa or equivalent to Δq = ε/gρo = 10−4 cm. Meanwhile, omega is ω = 1.4. Index for S.O.R. defined by r (r = 0, 1, 2, ). If the correction of the nonhydrostatic pressure converges to epsilon, then l = r else l = r + 1.
| (17) |
Finally, the last current velocity (u, v, and w) can be calculated by adding the nonhydrostatic pressure correction.
| (18) |
| (19) |
| (20) |
by continuity equation (Eq. 5) and last current velocity (Eqs. (10), (11), and (12)), the nonhydrostatic pressure at the sea surface layer can be determined ( or qs). Further, the pressure is used to determine tidal elevation by η = qs/(gρo).
2.3. The forcing at the open boundaries
The harmonic equation for open boundaries is given as follows (Eq. 21):
| (21) |
where ɳ is the time series of sea level, Ak is amplitude, and φk is phase lag relative to the Greenwich. The nodal factors for amplitude and phase relative to Greenwich are indicated by fk and uf, respectively. Meanwhile, the astronomical argument is V0, angular velocity is 2π/Tk, where Tk is the period of tidal components, and t is the time.
In the first case, the model was carried out using M2 tides without the correction parameter (V0+uf, fk = 0). Whereas in the second case, we used the five major tidal constituents (M2, S2, N2, K1, and O1 waves) together with the correction parameters. We simulated the first scenario for 40 times the M2 period (T = 12.42 h), and the second scenario for one-month from January 1st, 2017 until January 31st, 2017.
2.4. The analysis of the results
The analysis of the results separately performed using the harmonic analysis (Xu, 2018). However, in the first scenario, the amplitude and phase were analyzed with the following equations (Eqs. (22) and (23)):
| (22) |
| (23) |
where A and φ are the M2 amplitudes and phases, respectively. Meanwhile, ɳT/4, ɳT/2, ɳ3T/4, and ɳT are the sea level during M2 period (T = 12.42 h).
Residual current can be calculated from the following equation (Eq. 24):
| (24) |
where vres is the residual current, H is the total water depth, v is the time-series of velocity during one M2 tide period, and dt is the time-step.
3. Results and discussion
3.1. First scenario (the M2 tides)
Figure 3a shows the amplitude of M2 similar to the observation data, TPX07.2, and BIG tides or GIA, especially in the north and south of MS. However, in the middle of MS consist of T. Tiram, Selangor, and B.Siapiapi, the amplitudes of observations are higher than that of model results. The difference between model amplitude and observation amplitude can reach about 0.25 m. In the other hand, the phases of the M2 model (Figure 3b) are a good agreement with the observations in all stations. The phase increases from Lhokseumawe to Selangor and then decrease to Malacca.
Figure 3.
(a) M2 amplitudes (in 10−2 m) and (b) M2 phases (in degree) of the Malacca Strait Stations were obtained from nonhydrostatic model (black boxes with line), observation from Rizal and Sündermann (1994) (red stars), TPX07.2 (blue stars), and BIG tides or GIA (black stars).
Figures 4a and 4b show the amplitude and phases of M2 tide based on numerical simulation. In the northern part of MS, the tendency for M2 amplitude increases from Lhokseumawe to B. Datoh. The model shows that the highest M2 amplitude is in the central part of MS, namely B. Siapiapi. In general, the central part of MS is narrow (up to 5 × 104 m in width), and located around transition zone (deep in the north and shallow in the south). Therefore, shoaling can occur due to narrowing of the strait and changes in depth in this section.
Figure 4.
(a) The simulation results of M2 amplitude (in 10−2 m) and (b) M2 phase (in degrees).
Around 1.5 oN, M2 amplitude decreases, and it grows again when it approaches the SW. The decrease of amplitude indicates a virtual amphridomic in the MS (Rizal and Sündermann, 1994; Rizal, 2000, 2002). While in the SCS, M2 amplitude increases from north to Peninsular Malaysia (Kuala Rompin), about 3oN. According to Zu et al. (2008), M2 amplitudes are low in SCS and high in the coastal areas of SCS. The highest of M2 amplitude can be seen in the Taiwan Strait, Leizhou Peninsula, northwest of the coast of Kalimantan, around the western, and southern parts of Peninsular Malaysia. The high of amplitudes are possible because there are also shoaling waves around SCS coastal.
Figure 4b shows M2 waves travelling from northwest to the southeast of MS. The time of M2 waves from Lhoksemawe to T. Medang is about 9.1 h. Whereas from the north of MS to T. Medang, the time needed is about 8.25 h (or 120o to 359o). This result is quite similar to the hydrostatic model, which is 8.5 h (Rizal and Sündermann, 1994).
The M2 phase increases from the north of MS to the south of MS. Also, the M2 phase increases from the SCS to the SW. According to phase (Figure 4b), the wave speed in MS and SCS is different. The waves are faster in SCS than in MS because the MS depth relatively shallow compared to SCS. The non-linear interaction of M2 tidal can occur in the shallow depth, and it could generate other constituents such as M4 tides (Rose and Bhaskaran, 2016). However, we do not address that constituent in this paper. The non-linear can also be generated by the variation of bottom friction, coastline, and bathymetry (Rizal, 2000; Rose and Bhaskaran, 2016; Yu et al., 2017).
M2 current ellipses in the surface layer are shown in Figure 5a. Amplitude current ellipses look quite large in the middle and south of MS. In the middle part of MS, the ellipse currents have an anticlockwise direction on the west side and clockwise direction on the east side (Figure 5b). Whereas in the southern part the current ellipse is rectilinear and long. Amplitude current ellipses are decreasing to the north of MS. However, our model shows that the amplitude of ellipses is relatively large compared to barotropic tides results (Rizal, 2000) in the north of MS. It indicates that there is the differences between nonhydrostatic depth-dependent or baroclinic tides and hydrostatic barotropic tides in MS. While in other regions including SCS, amplitudes of current ellipses are relatively small. The current ellipse pattern is quite similar to previous results (Rizal and Sündermann, 1994; Rizal, 2000); there is an anticlockwise ellipse on the west side of MS, especially in the middle.
Figure 5.
(a) Current ellipses of M2 tides, (b) M2 current ellipses and their orientation (red = clockwise and blue = anticlockwise), and (c) Semi-major axis of M2 tides (in 10−2 m/s) at the sea surface.
Figure 5c shows the M2 semi-major axis at the surface layer. The current is quite strong in the central and southern parts of MS. Whereas in the northern part up to 3oN the current is small (0.2–0.4 m/s). In parts of the SCS, the current speed is about 0.1–0.3 m/s. In part of SCS, the maximum current is around Peninsular Malaysia (Kuala Rompin).
Figure 6a shows the transects of M2 semi-major axis in the middle of MS (3 oN). In the middle of MS, the beams of large semi-major axis radiate from the east of the strait (at layer 1 to 4 or 0–20 m) to the west of the strait. The largest semi-major axis can reach more than 1 m/s in this transect. It indicates that the geostrophic adjustment occurs in the middle of MS. According to Kuo (1997), geostrophic adjustment is an adjustment between the pressure gradient, the Coriolis force, and the centrifugal force associated with the current. In a simple two-layer shallow-water model, Fang et al. (2004) found that during geostrophic adjustment, some kinetic energy was converted to potential energy. After the process is finished, in the system, the potential energy increases while the kinetic energy decreases.
Figure 6.
(a) Transects of the M2 semi-major axis (in 10−2 m/s) along middle of MS and (b) north of MS (in 10−2 m/s).
Meanwhile, the transect of north of MS (4.5 oN) is shown in Figure 6b. In this section, the semi-major axis is low compared to the middle of MS. The beams of semi-major axis radiate from the center (~0.3 m/s) to the west and east of strait.
Figures 7a-d show the transect of density in the middle of MS during the M2-tide period at t = T/4, t = T/2, t = 3T/4, and t = T, respectively. T is the period of M2-tide (12.42 h). One can see that there is a small movement of isopycnals due to M2 tides at layer 3–4 (in particular, for densities va1ues of 19.8–20.2) in the middle of MS.
Figure 7.
(a) Transects of the density due to M2 tides along middle of MS at t = T/4, (b) t = T/2, (c) t = 3T/4, and (d) t = T (where T = 12.42 h or M2 period).
Besides semi-major and current ellipses of M2 tides, we also show the sea surface of M2 current. Current velocities at t = T/4, t = T/2, t = 3T/4, and t = T at the surface layer are shown in Figure 8a-d. The surface current are separated in the middle of MS (2.5-3oN). From the middle of MS, current flows to the north and south (t = T/4 and t = T). While at t = T/2 and t = 3T/4, the current flows towards the middle of MS from north and south of MS.
Figure 8.
(a) Sea surface current (arrows) and sea level (contour lines) at t = T/4, (b) t = T/2, (c) t = 3T/4, and (d) t = T (where T = 12.42 h or M2 period).
Residual current velocity is quite small in MS and SCS sections. The residual current in the MS surface layer (Figure 9) is dominantly moving southward to SW. Whereas in the SCS section it leads to Peninsula Malaysia (Kuala Rompin) and also to SW. These residual currents occur due to direction the phase of M2 tide. As a result, the currents in SW are very complex, because the wave from MS and SCS meet in the SW.
Figure 9.
Residual currents of M2-tide at the surface layer (in 10−2 m/s).
Due to complex bathymetry, coastline geometry, seasonal monsoon, seasonal hydrodynamic pressure gradient, tidal changes, and interaction of Indian and Pacific tides (Chen et al., 2005; Kurniawan et al., 2011; Hasan et al., 2011; Van Maren and Gerritsen, 2012; Xu and Chua, 2016), they concluded that the circulation in SW is very complex. Our findings show that M2 superposition from MS and SCS in SW can also support complex circulation.
3.2. Second scenario (The five major tidal constituents)
3.2.1. Sea level elevation
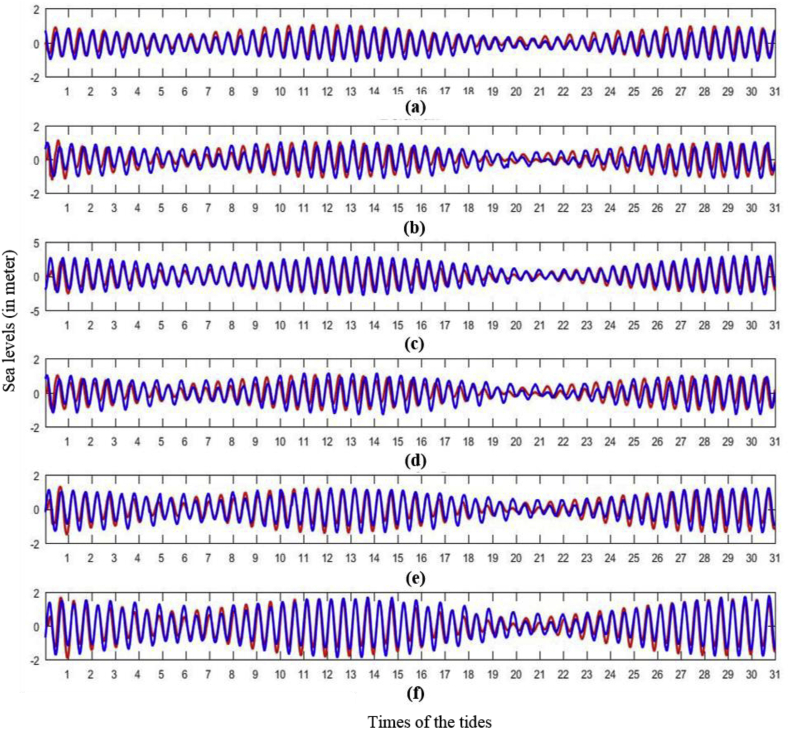
Figures 10a-f show the hourly sea level due to M2, S2, N2, K1, and O1 tides during January 2017 at Lhokseumawe, Belawan, B. Siapiapi, P. Susu, K.Tanjung, and M.S. Asahan, repectively. These stations are located around MS and represent almost part of MS.
Figure 10.
(a) Comparison of sea levels sampled from the nonhydrostatic model (red color) and observation of PUSHIDROSAL (blue) during January 2017 at Lhokseumawe, (b) Belawan, (c) B. Siapiapi, (d) P. Susu, (e) K. Tanjung, and (f) M.S. Asahan (in meters).
In general, the model shows proper verification in all of stations. The sea level due tides in the middle part of MS (B. Siapiapi and M.S. Asahan) is higher than the northern part of MS (Lhokseumawe and Belawan). Therefore, the hydrodynamic due to tides is more active in the middle of MS.
3.2.2. Amplitude and phase of other constituents
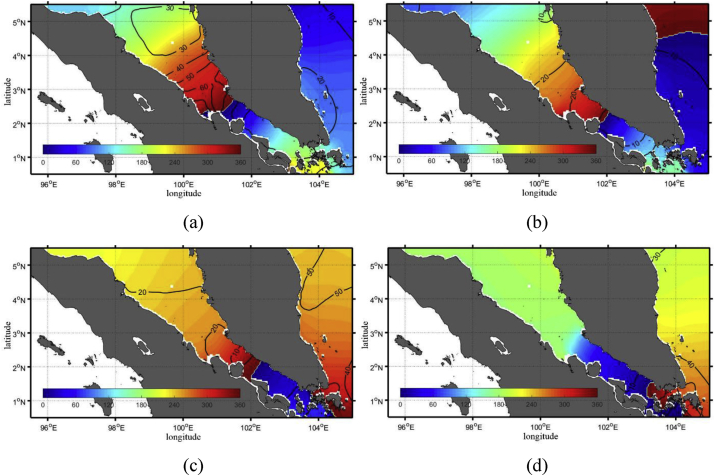
The harmonic analysis methods were used to obtain both the amplitudes and phases of S2, K1, N2, and O1 tides. Figures 11a-d and Table 2 show the amplitudes and phases of tides (S2, K1, N2, and O1 tides, respectively). Meanwhile, the verification is shown in Figures 12a-d, respectively. Despite the composite of tides model are lower resolution than GIA data (model resolution = 5′ × 5′, GIA data resolution = 2.5′ × 2.5′), it can still describe the semidiurnal and diurnal tides quite well.
Figure 11.
(a) Amplitudes and phases of S2, (b) N2, (c) K1, and (d) O1 tides, respectively. Amplitudes (in 10−2 m) are indicated by the contours while phases (in degrees) by the shaded colors. The results were obtained from the five major tidal constituent model.
Table 2.
The results of harmonic analysis from the five major tidal constituents at 6 stations. It shows the Amplitude (Amp), Phase (Phas), and Semi-major axis (Sema) of each constituent.
| M2 | S2 | N2 | K1 | O1 | |
|---|---|---|---|---|---|
| Lhokseumawe | |||||
| Amp (x10−2m) | 58.45 | 30.19 | 18.09 | 12.40 | 5.72 |
| Phas (o) | 94.32 | 124.46 | 81.42 | 221.40 | 177.08 |
| Sema (x10−2 m/s) | 9.59 | 5.16 | 3.79 | 3.67 | 0.88 |
| Belawan | |||||
| Amp (x10−2m) | 54.82 | 31.57 | 17.92 | 22.95 | 8.11 |
| Phas (o) | 185.55 | 219.25 | 180.45 | 247.77 | 195.26 |
| Sema (x10−2 m/s) | 22.48 | 12.72 | 7.31 | 3.24 | 0.80 |
| B. Siapiapi | |||||
| Amp (x10−2m) | 138.66 | 76.99 | 45.11 | 26.49 | 6.76 |
| Phas (o) | 290.03 | 326.39 | 280.75 | 266.01 | 197.31 |
| Sema (x10−2 m/s) | 65.62 | 37.61 | 21.30 | 7.26 | 1.65 |
| P. Susu | |||||
| Amp (x10−2m) | 55.03 | 31.32 | 17.66 | 21.28 | 7.72 |
| Phas (o) | 162.11 | 195.83 | 156.33 | 243.48 | 191.78 |
| Sema (x10−2 m/s) | 26.34 | 14.41 | 8.75 | 4.43 | 0.85 |
| K. Tanjung | |||||
| Amp (x10−2m) | 71.67 | 40.15 | 24.20 | 25.26 | 7.89 |
| Phas (o) | 250.99 | 284.75 | 242.93 | 255.41 | 197.22 |
| Sema (x10−2 m/s) | 45.73 | 25.19 | 14.97 | 4.84 | 0.92 |
| M. S. Asahan | |||||
| Amp (x10−2m) | 98.89 | 54.88 | 32.81 | 25.63 | 7.31 |
| Phas (o) | 272.15 | 307.05 | 263.11 | 259.92 | 197.10 |
| Sema (x10−2 m/s) | 39.59 | 21.90 | 12.91 | 4.17 | 1.30 |
Figure 12.
(a) Amplitudes and phases of S2, (b) N2, (c) K1, and (d) O1 tides, respectively. Amplitudes (in 10−2 m) are indicated by the contours while phases (in degrees) by the shaded colors. The results were obtained from GIA data.
The amplitude of M2, S2, and N2 are highest around the middle of MS. In B. Siapiapi, the amplitude of semidiurnal spring tide (M2 + S2) can reach 2.15 m. The maximum amplitudes of M2, S2, and N2 in B. Siapiapi are 1.39 m, 0.77 m, and 0.45 m, respectively. The minimum amplitudes of M2, S2, and N2 in B. Sapiapi are 0.4 m, 0.3 m, and 0.2 m, respectively.
In the SCS section, the highest tide exists in Kuala Rompin. The maximum amplitudes M2, S2, and N2, around Kuala Rompin, are 0.9 m, 0.3, and 0.3 m, respectively.
These results indicate that the semidiurnal tides in SCS are smaller than those in MS. In addition, M2 tidal waves are more dominant than S2 and N2 tides. The shape of topography causes a high amplitude in the middle of MS.
According to Pugh and Woodworth (2014), when tides propagate from the deep waters into the shallow waters, the reflected and transmitted waves occur. The energy transmitted in unit time by a progressive wave is per unit distance along the wave front (where ρ = density, g = acceleration of gravity, A = amplitude of a Kelvin wave (M2) at the coast, and h = water depth). When tidal wave propagates into the shallower waters, then should be constant. In the case of MS, tidal wave from a depth of 100 m with an amplitude of around 50 cm propagate to the middle of MS, which has 25 m depth. So, amplitude in the middle of MS is around 70 cm.
The funnel-shaped of MS causes amplification of those tidal constituents (shoaling) and it also relatively the same with the tides in the Head Bay of Bengal (Rose and Bhaskaran, 2016, 2017b) and the near-shore waters off Bangladesh (Yu et al., 2017). The geometrical configuration of coastline causes the amplification of semi-diurnal and diurnal constituents (Sindhu and Unnikrishnan, 2013). In Kuala Rompin, the high amplitudes are also possible because there are shoaling waves around SCS coastal.
In MS, S2 amplitude is higher compared to the N2 amplitude. The directions of these waves are relatively similar. The S2 and N2 tides from the north of MS and SCS are directed to the south of MS and SW. The phases rapidly change in the MS compared to those of SCS. The funnel-shape of the MS also plays an essential role in the pattern of phases.
Related to the contour of tidal phase in MS, when M2 tides entering MS, which has a depth of 100 m, the wave speed is with h is water depth (Wright et al., 1999; Pugh and Woodworth, 2014). As a result, the contour lines become denser when the wave moves in the shallower waters. The contours of tidal phase lines are also parallel along MS and perpendicular to the coastlines of Sumatra and Malaysia.
The parallel phase lines are due to MS located at low latitudes (ϕ = 3o). Therefore, amphidromic point is difficult to form in MS. On the other hand, at high latitudes such as the North Sea (ϕ = 54.46o), amphidromic point is relatively easy to form. An analysis of Taylor's problem and virtual amphidromes at low latitudes can be seen in Rizal (2000, 2002).
Diurnal waves (K1 and O1) have different propagation patterns. O1 tides propagate from SCS to the MS, while K1 tides propagate from both the MS and SCS to the south of MS. The previous study also shows that the diurnal waves (K1 and O1) propagate to MS through the Andaman Sea, and it causes the high of amplitude (K1 and O1) at the MS (Sindhu and Unnikrishnan, 2013). The maximum amplitudes of K1 and O1 in MS are found highest in the southern part of MS (about 0.3 m), and in the northern part of MS, the K1 amplitude is still relatively high (0.2 m). When compared with the amplitude of semidiurnal waves (M2, S2, and N2), the effect of diurnal waves is smaller than semidiurnal waves in MS. In Kuala Rompin, the maximum amplitudes of M2, S2, N2, K1, and O1 can reach 0.9, 0.3, 0.2, 0.6, and 0.4 m, respectively. These results reflect that semidiurnal tides are also very dominant in SCS.
The contribution of the diurnal tide in SCS is more significant than the contribution of the diurnal tide in MS and the Andaman Sea. In SW, the diurnal tides (amplitude and phase) are irregular because of the existence of small islands around SW and the shape of the south of MS.
Figure 13 shows the type of tides based on the Formzahl number (F = (K1+O1)/(M2+S2)). In general, the tidal type in MS is mixed-tide prevailing semidiurnal and semidiurnal. The semidiurnal type can also be found in SW, while between parts of SCS and SW, the type become mixed-tide prevailing semidiurnal. It showed that the effect of diurnal tides diminishes on the way to SW and MS.
Figure 13.
The tidal type of MS and part of SCS based on Formzahl number (F= (K1+O1)/(M2+S2)). The colors indicate the tidal types, i.e. semidiurnal (yellow), mixed-tide prevailing semidiurnal (red), and mixed-tide prevailing diurnal (black).
According to Rizal et al. (2012), the semidiurnal tidal type is dominant in the northern boundary of the Malacca Strait, i.e., the Andaman Sea. This tidal type becomes mixed-tide prevailing semidiurnal when it reaches the middle of MS.
3.2.3. Tidal circulation
Figures 14a-d show the sea surface currents and sea level elevation during flood and ebb phase both in spring tides and neap tides, respectively. During spring tides, the tidal current of MS in the middle is divided into two different parts (Figures 14a-b). At the ebb phase, the current moves from the middle to the north of MS and from the middle to the south of MS (Figure 14a). While at the flood phase (Figure 14b), the current from the northern part of MS moves towards to middle of MS, and the current from south of MS moves toward the middle of MS, too. In SW, the current flows towards MS both on flood and ebb phase of spring tides (Figures 14 a-b).
Figure 14.
(a) Sea surface current and sea level elevation during spring tides at ebb phase, (b) spring tides at flood phase, (c) neap tides at ebb phase, and (d) neap tides at flood phase in January 2017.
In the neap tide phase, the currents are shown in Figures 14c-d. At the ebb phase of neap tides (Figure 14c), the direction of the current is similar to that of ebb phase of spring tides (Figure 14a). The magnitude of the current is stronger in spring tides than that of neap tides. Figure 14d (flood phase of neap tides) shows a similar direction of current with that of the flood phase of spring tides (Figure 14b). However, the magnitude of current in spring tides is stronger than that of neap tides.
The complex flow in the middle of MS is caused by differences in tidal types in MS, which are divided into mixed-tide prevailing semidiurnal and semidiurnal. The different types of tides cause the circulation of surface currents to be asymmetrical. The most significant tidal component that affects the current circulation is M2 tide, which has the highest amplitude value, especially in the middle of MS.
Also, the tidal current of MS is stronger (~1 m/s) compared to SW and SCS. The high gradient pressure difference due to sea level and the funnel shape of MS causes a strong current in MS (Haditiar et al., 2019). Strong turbulent currents and energy, according to Yamini et al. (2018), have a relationship with topographic geometry and seabed conditions. In the case of the offshore turbine pile, turbulent currents and energy are strongly associated with variations in pile diameter and variation in the size of bed particles. An addition or reduction of current magnitude can affect the scour pit in the offshore turbine pile (Yamini et al., 2018). Based on Table 2, the contribution of M2 tides, especially in the middle of MS, to current is more significant than other constituents. At B. Siapiapi, the semi-major axis of M2 tides can reach 0.66 m/s or almost the same contribution with other constituents (S2, N2, K1, and O1). While the semi-major axis of K1 tides only reaches 0.07 m/s and other constituents are 0.37 m/s for S2, 0.21 m/s for N2, and 0.01 m/s for O1 tide. It shows that semidiurnal tides dominate in MS tidal circulation.
4. Summary and conclusions
We had successfully carried out numerical simulations of M2 tide and five tidal components (M2, K1, S2, O1, and N2) combined with density and three-dimensional numerical models. We had also shown that tides in MS based on our simulations are generally similar to other investigations and observations. Based on the simulation, M2 amplitude is high in the middle of MS. There are shallowing and narrowing of topography affecting the amplification of the M2 amplitude. M2 waves are from two directions, from north of MS to MS and from SCS to MS. M2 tide from north of MS propagate to the southeast of MS, and M2 waves from SCS propagate to the Kuala Rompin and SW. These waves, wave from north of MS and wave from SCS, can produce a superposition of M2 waves and complex current circulation in SW.
The currents in MS at instantaneous times (t = T/4, t = T/2, t = 3T/4, and t = T) were divided into two directions, i.e., from and to the middle of MS. However, the residual current of MS moves southward to SW. For M2 semi-major current, it shows a high velocity at the narrow and shallow part of MS.
The five tidal components of sea level and currents in time-series in B. Siapiapi station had the highest sea level because of the shallowing and narrowing of the strait. In this station, the ebb and flood currents are branched and heading to the north and south of MS with high velocity (~1 m/s).
The harmonic analysis showed that the semidiurnal waves are dominant in MS. The semidiurnal waves propagate from the north of MS to SW. These findings indicate that besides variations in bathymetry, coastlines, and tidal effects, the superposition of semidiurnal tides can also create complex circulations in SW.
Declarations
Author contribution statement
Y. Haditiar, S. Rizal: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote M. R. Putri: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.
N. Ismail, M. Ikhwan, and Z. A. Muchlisin: Analyzed and interpreted the data; Wrote the paper.
Funding statement
This work was supported by the Ministry of Research, Technology and Higher Education of Indonesia through “Penelitian Dasar” with contract number 72/UN11.2/PP/SP3/2019, and "PMDSU” with contract number 74/UN11.2/PP/SP3/2018.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
We would like to thank Muhammad Nanda and member of Laboratory of Oceanographic Modelling, Universitas Syiah Kuala, Banda Aceh, Indonesia for fruitful discussions. We would like to appreciate and thank the four anonymous reviewers who suggested significant improvements in the paper. This research was conducted at the Laboratory of Ocean Modelling.
References
- Abrogueña J.B.R., Range P., Cruz W., Tentia-Lagumen M.C., Chicharo L. Fish communities and environmental variables during dry season in Pampanga estuary (Philippines) Regional Studies in Marine Science. 2020;34:101053. [Google Scholar]
- Adliansyah, Haditiar, Muhammad Y., Rizal S. 2016 12th International Conference on Mathematics, Statistics, and Their Applications (ICMSA) 2016. Current Simulation in the Gulf of Thailand Due to Wind and Sea Level Elevation. [Google Scholar]
- Berloff P., Meacham S.P. The dynamics of a simple baroclinic model of the wind-driven circulation. J. Phys. Oceanogr. 1998;28(2):361–388. [Google Scholar]
- Berloff P.S., Mcwilliams J.C. Large-scale, low-frequency variability in wind-driven ocean gyres. J. Phys. Oceanogr. 1999;29(8 PART 2):1925–1949. [Google Scholar]
- Chen M., Murali K., Khoo B.-C., Lou J., Kumar K. Circulation modelling in the strait of Singapore. J. Coast Res. 2005;215:960–972. [Google Scholar]
- Egbert G.D., Erofeeva S.Y., Ray R.D. Assimilation of altimetry data for nonlinear shallow-water tides: quarter-diurnal tides of the Northwest European Shelf. Continent. Shelf Res. 2010;30(6):668–679. [Google Scholar]
- Embling C.B., Sharples J., Armstrong E., Palmer M.R., Scott B.E. Fish behaviour in response to tidal variability and internal waves over a shelf sea bank. Prog. Oceanogr. 2013;117:106–117. [Google Scholar]
- Fang J., Wu R., Yi A. Topographic effect on the energetics of geostrophic adjustment. Acta Meteorol. Sin. 2004;19(1):19–30. [Google Scholar]
- Gholami D.M., Baharlouii M. Monitoring long-term mangrove shoreline changes along the northern coasts of the Persian Gulf and the Oman sea. Emerging Science Journal. 2019;3(2):88. [Google Scholar]
- Haditiar Y., Rizal S., Abdullah F. 2016. Current Simulation in the Malacca Strait and Part of South China Sea Due to Wind. 2016 12th International Conference on Mathematics, Statistics, and Their Applications (ICMSA) [Google Scholar]
- Haditiar Y., Putri M.R., Ismail N., Muchlisin Z.A., Rizal S. Numerical simulation of currents and volume transport in the Malacca Strait and part of south China sea. Eng. J. 2019;23(6):129–143. [Google Scholar]
- Hasan G.M.J., van Maren D.S., Cheong H.F. Improving hydrodynamic modeling of an estuary in a mixed tidal regime by grid refining and aligning. Ocean Dynam. 2011;62(3):395–409. [Google Scholar]
- Kämpf J. Springer Verlag; Heidelberg, Germany: 2010. Advanced Ocean Modelling Using Open-Source Software, Using Open-Source Software; pp. 125–144. [Google Scholar]
- Kochergin V.P. Three-dimensional prognostic models. Coast Estuar. Sci. 1987:201–208. [Google Scholar]
- Kuo H.L. A new perspective of geostrophic adjustment. Dynam. Atmos. Oceans. 1997;27(1-4):413–437. [Google Scholar]
- Kurniawan A., Ooi S.K., Hummel S., Gerritsen H. Sensitivity analysis of the tidal representation in Singapore Regional Waters in a data assimilation environment. Ocean Dynam. 2011;61(8):1121–1136. [Google Scholar]
- Levitus S., Boyer T.P. U.S. Dsepartment of Commerce; Washington D.C.: 1994. World Ocean Atlas 1994 Volume 4: Temperature. NOAA Atlas NESDIS 4; pp. 1–117. [Google Scholar]
- Levitus S., Burgett R., Boyer T.P. U.S. Department of Commerce; Washington D.C.: 1994. World Ocean Atlas 1994 Volume 3: Salinity. NOAA Atlas NESDIS 3; pp. 1–99. [Google Scholar]
- Nauw J.J., Dijkstra H.A., Simonnet E. Regimes of low-frequency variability in a three-layer quasi-geostrophic ocean model. J. Mar. Res. 2004;62(5):685–720. [Google Scholar]
- Nodoushan E.J. Monthly forecasting of water quality parameters within bayesian networks: a case study of honolulu, pacific ocean. Civil Engineering Journal. 2018;4(1):188. [Google Scholar]
- Pattrick P., Strydom N. Recruitment of fish larvae and juveniles into two estuarine nursery areas with evidence of ebb tide use. Estuarine. Coastal and Shelf Science. 2014;149:120–132. [Google Scholar]
- Pond S., Pickard G.L. second ed. Pergamon; New York: 1983. Introductory Dynamical Oceanography; p. 329. [Google Scholar]
- Pugh D., Woodworth P. Cambridge University Press; New York: 2014. Sea-Level Science: Understanding Tides, Surges,Tsunamis and Mean Sea-Level Changes; p. 407. [Google Scholar]
- Rizal S., Wafdan R., Haditiar Y., Ramli M., Halfiani V. Numerical study of lee waves characteristics in the ocean. J. Eng. Sci. Technol. 2020;15(2):1056–1078. [Google Scholar]
- Rizal S., Iskandar T., Muhammad, Haditiar Y., Ilhamsyah Y., Setiawan I., Sofyan H. Numerical study of the internal wave behaviour in the vertical ocean slice model. J. Eng. Sci. Technol. 2019;14(5):2836–2846. [Google Scholar]
- Rizal S. The role of non-linear terms in the shallow water equation with the application in three- dimensional tidal model of the Malacca Strait and Taylor’s Problem in low geographical latitude. Continent. Shelf Res. 2000;20:1965–1991. [Google Scholar]
- Rizal S. Taylor's problem—influences on the spatial distribution of real and virtual amphidromes. Continent. Shelf Res. 2002;22:2147–2158. [Google Scholar]
- Rizal S., Sündermann J. On the M2-tide of the Malacca Strait: a numerical investigation. Dtsch. Hydrogr. Z. 1994;46(1):61–80. [Google Scholar]
- Rizal S., Damm P., Wahid M.A., Sundermann J., Ilhamsyah Y., Iskandar T. General circulation in the Malacca Strait and Andaman Sea: a numerical model study. Am. J. Environ. Sci. 2012;8(5):479–488. [Google Scholar]
- Rizal S., Setiawan I., Iskandar T., Ilhamsyah Y., Wahid M.A., Musman M. Currents simulation in the Malacca straits by using three-dimensional numerical model. Sains Malays. 2010;39:519–524. 2010. [Google Scholar]
- Rose L., Bhaskaran P.K. The role of environmental forcing on tidal dynamics along complex near-shore waters off Bangladesh. Ocean. Eng. 2016;116:68–81. [Google Scholar]
- Rose L., Bhaskaran P.K. Tidal propagation and its non-linear characteristics in the head Bay of bengal. Estuar. Coast Shelf Sci. 2017;188:181–198. [Google Scholar]
- Rose L., Bhaskaran P.K. Tidal asymmetry and characteristics of tides at the head of the Bay of Bengal. Q. J. R. Meteorol. Soc. 2017;143(708):2735–2740. [Google Scholar]
- Sakmani A.S., Lam W.-H., Hashim R., Chong H.-Y. Site selection for tidal turbine installation in the Strait of Malacca. Renew. Sustain. Energy Rev. 2013;21:590–602. [Google Scholar]
- Setiawan I., Rizal S., Haditiar Y., Ilhamsyah Y., Purnawan S., Irham M., Yuni S.M. Study of current circulation in the northern waters of Aceh. IOP Conf. Ser. Earth Environ. Sci. 2018;176 [Google Scholar]
- Sindhu B., Unnikrishnan A.S. Return period estimates of extreme sea level along the east coast of India from numerical simulations. Nat. Hazards. 2011;61(3):1007–1028. [Google Scholar]
- Sindhu B., Unnikrishnan A.S. Characteristics of tides in the Bay of bengal. Mar. Geodes. 2013;36(4):377–407. [Google Scholar]
- Talley L.D., Pickard G.L., Emery W.J., Swift J.H. Introduction to descriptive physical oceanography. Descriptive Physical Oceanography. 2011:1–6. [Google Scholar]
- Thanh N.T. Evaluation of multi-precipitation products for multi-time scales and spatial distribution during 2007-2015. Civil Engineering Journal. 2019;5(1):255. [Google Scholar]
- UNESCO The practical salinity scale 1978 and the international equation of state of seawater 1980. Technical Paper Marine Science. 1981;36:25. [Google Scholar]
- Van Maren D.S., Gerritsen H. Residual flow and tidal asymmetry in the Singapore Strait, with implications for resuspension and residual transport of sediment. J. Geophys. Res.: Oceans. 2012;117(4):C04021. [Google Scholar]
- Wright J., Colling A., Park D. second ed. Butterworth-Heinemann; Oxford: 1999. Waves, Tides, and Shallow-Water Processes; p. 227. [Google Scholar]
- Wyrtki K. ume 2. The University of California, Scripps Institutions of Oceanography; La Jolla, California: 1961. Scientific Results of marine Investigations of the South China Sea and the Gulf of Thailand 1959-1961. (Naga Report). [Google Scholar]
- Xu K., Ma C., Lian J., Bin L. Joint probability analysis of extreme precipitation and storm tide in a coastal city under changing environment. PloS One. 2014;9(10) doi: 10.1371/journal.pone.0109341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu M., Chua V.P. A numerical study on circulation and volume transport in Singapore coastal waters. Journal of Hydro-Environment Research. 2016;12:70–90. [Google Scholar]
- Xu Z. A note on interpreting tidal harmonic constants. Ocean Dynam. 2018;68(2):211–222. [Google Scholar]
- Yamini O.A., Mousavi S.H., Kavianpour M.R., Movahedi A. Numerical modeling of sediment scouring phenomenon around the offshore wind turbine pile in marine environment. Environmental Earth Sciences. 2018;77:776. [Google Scholar]
- Yu H., Yu H., Wang L., Kuang L., Wang H., Ding Y., Ito S., Lawen J. Tidal propagation and dissipation in the Taiwan Strait. Continent. Shelf Res. 2017;136:57–73. [Google Scholar]
- Zu T., Gan J., Erofeeva S.Y. Numerical study of the tide and tidal dynamics in the South China Sea. Deep Sea Res. Oceanogr. Res. Pap. 2008;55(2):137–154. [Google Scholar]