Abstract
In recent years, there has been increased interest in the development of adaptive interventions across various domains of health and psychological research. An adaptive intervention is a protocolized sequence of individualized treatments that seeks to address the unique and changing needs of individuals as they progress through an intervention program. The sequential, multiple assignment, randomized trial (SMART) is an experimental study design that can be used to build the empirical basis for the construction of effective adaptive interventions. A SMART involves multiple stages of randomizations; each stage of randomization is designed to address scientific questions concerning the best intervention option to employ at that point in the intervention. Several adaptive interventions are embedded in a SMART by design; many SMARTs are motivated by scientific questions that concern the comparison of these embedded adaptive interventions. Until recently, analysis methods available for the comparison of adaptive interventions were limited to end-of-study outcomes. The current manuscript provides an accessible and comprehensive tutorial to a new methodology for using repeated outcome data from SMART studies to compare adaptive interventions. We discuss how existing methods for comparing adaptive interventions in terms of end-of-study outcome data from a SMART can be extended for use with longitudinal outcome data. We also highlight the scientific utility of using longitudinal data from a SMART to compare adaptive interventions. A SMART study aiming to develop an adaptive intervention to engage alcohol- and cocaine-dependent individuals in treatment is used to demonstrate the application of this new methodology.
Introduction
Abundant heterogeneity is often observed in responses to behavioral interventions. This has led to widespread recognition of the importance of adaptive interventions (AIs), which are protocolized sequences of intervention options (e.g., intervention type, timing, intensity/dosage or delivery modality) intended to address the unique and changing needs of individuals as they progress through an intervention program (Collins, Murphy, & Bierman, 2004; Lavori & Dawson, 2014). This intervention approach plays an important role in various domains of psychology, including clinical (e.g., Connell, Dishion, Yasui, & Kavanagh, 2007), educational (e.g., Connor et al., 2011), organizational (e.g., Eden, 2017) and health psychology (e.g., Nahum-Shani, Hekler, & Spruijt-Metz, 2015). The sequential, multiple assignment, randomized trial (SMART) (Lavori & Dawson, 2000; Murphy, 2005) is an experimental design that was developed to aid in the construction of empirically based AIs. Data from a SMART can be used be answer various types of scientific questions concerning the construction of an AI, including questions about the comparison of AIs.
The uptake of SMART studies is increasing rapidly; these experimental designs have been used to inform the development of AIs in areas such as depression (Gunlicks-Stoessel et al., 2016), weight loss (Naar-King et al., 2016), substance use disorders (McKay et al., 2015), schizophrenia (Shortreed & Moodie, 2012), and attention deficit/hyperactivity disorder (ADHD; Pelham et al., 2016). There has been much progress in the development of methods to analyze data arising from SMARTs (e.g., Ertefaie, Wu, Lynch, & Nahum-Shani, 2015; Nahum-Shani et al., 2012a; Nahum-Shani et al., 2012b; Schulte, Tsiatis, Laber, & Davidian, 2014). Despite this progress, most proposed methods enable investigators to compare AIs based only on outcome data from a single measurement occasion (e.g., end-of-study outcome). This represents a major gap in the science of AIs.
Practical and theoretical interest in AIs rests, in part, on the dynamic nature of people’s experiences and behaviors. For example, AIs for chronic disorders, such as obesity, depression and addiction are often motivated by scientific models highlighting the waxing and waning course of the disorder. These models suggest that a treatment that demonstrates short-term gains (e.g., weight loss) for an individual may not lead to gain in the long-term even if the individual remains on the same treatment over time (Almirall et al., 2014). Even when investigators have focused on a final outcome, this outcome often reflects a dynamic pattern of responses over time. For example, the impact of behavioral parent training on the classroom behavior of children with ADHD reflects dynamic patterns in parent attendance of the training throughout the school year (Pelham et al., 2016); and weight loss outcomes in interventions for obesity are primarily a function of sustained adherence to a reduced-energy diet (Appelhans et al., 2016). The time-varying nature of AIs, whereby new intervention options are introduced over time to address dynamic patterns of response calls for a more nuanced investigation of how the effect of an AI unfolds over time as the individual progresses through the sequence of intervention options.
The current manuscript provides an accessible and comprehensive tutorial to a new methodology for using repeated outcome data from SMART studies to compare AIs. While this tutorial builds on the existing method recently developed and evaluated by Lu and colleagues (Lu et al., 2016), the materials provided here offer several contributions beyond their work. First, this manuscript clearly explains the scientific yield that could be gained by using repeated outcome measurements from SMART studies to compare AIs in the context of psychological research. Second, while many SMART studies are motivated by the notion of ‘delayed effects’ (see Wallace, Moodie, & Stephens, 2016) the current manuscript goes further by defining and quantifying delayed effects using repeated outcome measures arising from a SMART. Third, this manuscript offers clear practical guidelines on using the regression coefficients to estimate various types of contrasts of scientific interest in the context of easy-to-understand piecewise linear models for time. Fourth, to make SMART longitudinal methodology accessible to behavioral scientists, we provide sample code with explicit, step-by-step instructions on how to employ this innovative method, as well as a simulated example dataset (in online supplementary materials) that researchers can use for practice. Fifth, in online supplementary materials, we provide results of simulation studies to evaluate the methodology. These simulation studies go beyond the simulations used in previous research (i.e., in Lu et al., 2016) in that they are based on more realistic scenarios. Finally, to illustrate the method, this manuscript is the first to analyze longitudinal data from ENGAGE, a SMART study aiming to develop an AI to re-engage alcohol- and cocaine-dependent individuals in treatment (McKay, et al., 2015). Since engagement is an important topic in many areas of psychological research (e.g., Bakker et al., 2011; Ladd & Dinella, 2009), this example SMART highlights the utility of this new method to a broad range of researchers in psychology. Below, we begin by discussing the important role of SMART studies in the development of empirically based AIs.
Adaptive Interventions (AIs)
Adaptive interventions, also known as ‘dynamic treatment regimes’ (Lavori & Dawson, 2004; Murphy, 2003), are motivated by empirical evidence that not all individuals benefit equally from the same intervention and that it is often possible to identify early in the course of an intervention those individuals who might not ultimately benefit from their current treatment. Hence, an AI capitalizes on information concerning the individual’s progress in the course of an intervention, such as the individual’s early response status, level of burden, extent of adherence, or a combination of these aspects, to recommend how the intervention options should be altered in order to improve long-term outcomes for greater numbers of individuals (Collins, et al., 2004).
An AI is a multi-stage process that is often protocolized via a sequence of decision rules that specify, for each stage of the AI, how the intervention options should be individualized, namely what type of intervention, dosage/intensity, or delivery mode should be offered at that stage, for whom and under what conditions. Specifically, each stage of an AI begins with a decision point, namely a point in time at which intervention decisions should be made. A decision rule specifies how information about the individual up to that particular decision point can be used to decide which intervention option the individual should be offered.
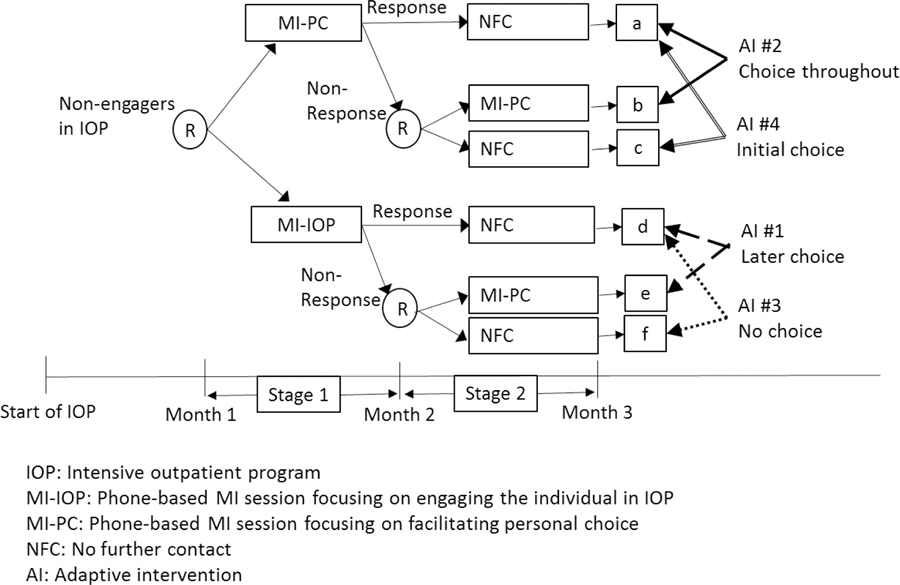
For example, consider the following AI (AI #1; see Table 1) for re-engaging cocaine- and alcohol-dependent individuals in an intensive outpatient treatment program (IOP). As we explain below, this example AI is one of four AIs that are embedded in the ENGAGE SMART study (McKay et al., 2015) and is simplified here for illustrative purposes. IOPs are the most common kind of treatment programs offered to individuals with relatively severe substance-use disorders. These programs typically consist of traditional abstinence-oriented group therapy sessions, based on the principles of Alcoholics Anonymous (AA). While IOPs are generally efficacious, many individuals do not attend the IOP therapy sessions and hence are less likely to benefit from the program (McKay et al., 2015). To re-engage these individuals in treatment, the AI discussed herein begins by offering a phone-based session that uses motivational interviewing (MI) principles to encourage IOP attendance (MI-IOP). Then, at the end of month 2, if the individual continues to show signs of disengagement (i.e., his/her IOP session attendance is below a pre-specified threshold), then s/he is classified as an early non-responder and is offered another phone-based session; but this time, the session uses MI principles to facilitate personal choice (MI-PC), namely to help the individual choose the type of substance abuse treatment s/he would like to use. Otherwise, the individual is classified as an early responder and no further phone contact (NFC) is made with the individual. The following decision rules operationalize this AI:
Table 1:
Decision Rules for Adaptive Interventions (AI) Embedded in ENGAGE
| AI | Stage 1 | Early Response Status | Stage 2 | Cells (Fig. 1) |
|---|---|---|---|---|
| AI #1: Later choice (, ) |
MI-IOP | Response | NFC | d, e |
| Non-response | MI-PC | |||
| AI #2: Choice throughout (, ) |
MI-PC | Response | NFC | a, b |
| Non-response | MI-PC | |||
| AI #3: No-choice (, ) |
MI-IOP | Response | NFC | d, f |
| Non-response | ||||
| AI #4: Initial-choice (, ) |
MI-PC | Response | NFC | a, c |
IOP: Intensive outpatient program
MI-IOP: Phone-based motivational interview (MI) session focusing on engaging the individual in IOP.
MI-PC: Phone-based motivational interview (MI) session facilitating personal choice of treatment.
NFC: No further contact
At the beginning of the re-engagement program
First-stage intervention option = [MI-IOP]
Then, at the end of month 2
IF early response status = non-responder
THEN, second-stage intervention option = [MI-PC]
ELSE, second-stage intervention option = [NFC]
The decision rules above specify that a phone-based session that focuses on engaging the individual in IOP (MI-IOP) should be offered initially to all targeted individuals at the beginning of the re-engagement program (the first decision point). The decision rules also specify how information about the individual’s early response status should be used to individualize the second-stage intervention options, namely to decide who should be offered another phone-based session that focuses on facilitating personal choice (MI-PC) and who should be offered no further telephone contact (NFC) following the month 2 decision point. Note that in this example, response-status is determined based on the participant’s level of treatment engagement at month 2 (i.e., his/her attendance of IOP sessions).
Traditionally, decision rules are informed by clinical experience, empirical evidence, and theory. For example, the AI described above is informed by self-determination theory (Ryan & Deci, 2000) and related empirical evidence (see McKay et al., 2015) suggesting that failure to engage in IOP sessions might be due to barriers (e.g., lack of intrinsic motivation, treatment burden) that can be ameliorated by encouraging the individual to choose the type of treatment that is most suitable for him/her. However, in many cases, there are open scientific questions concerning the selection and individualization of intervention options.
The Sequential, Multiple Assignment, Randomized Trial (SMART)
The SMART (Lavori & Dawson, 2014; Murphy, 2005) is an experimental design that can be used to efficiently obtain data to address scientific questions concerning the development of highly effective AIs. A SMART involves multiple stages of randomizations, such that some or all individuals can be randomized more than once in the course of the study. Each randomization stage in a SMART is designed to obtain data that can be used to answer scientific questions about the intervention options at a particular decision point. These questions may include which intervention option is best at that decision point and how best to individualize intervention options based on individual information available at that decision point. Data from a SMART enables researchers to address these questions while taking into account that at each decision point the intervention options are part of a sequence, rather than stand-alone intervention options.
As an example, consider ENGAGE, a SMART study of cocaine- and alcohol-dependent individuals who enrolled in an IOP, but then failed to engage in the treatment. ENGAGE was motivated by scientific questions concerning the construction of an AI for re-engaging cocaine/alcohol dependent individuals in treatment, including whether and under what conditions facilitating personal choice would improve IOP engagement and substance-abuse outcomes. The following description of the study (see Figure 1) was simplified for didactic purposes (see McKay et al., 2015 for a complete description of the trial). Individuals who failed to engage in the IOP entered the re-engagement program and were randomized with equal probability to two first-stage intervention options: either MI-IOP (phone-based MI session that focuses on encouraging IOP attendance) or MI-PC (phone-based MI session that focuses on fostering personal choice). At the end of month 2, participants who were still not engaged (i.e., those who did not attend treatment sessions consistently in the past two months) were classified as early non-responders and were re-randomized with equal probability to two second-stage intervention options: either MI-PC or NFC (no further contact). Participants who did not show signs of continued disengagement (i.e., responders) were assigned to NFC and were not re-randomized.
Figure 1:
The ENGAGE SMART Study
A wide variety of design options exist for SMART studies. While the issues to be considered in designing a SMART study are beyond the scope of this paper, they are extensively discussed in recent literature (e.g., Almirall et al., 2018; Wallace, Moodie & Stephens, 2016).
Using Data from a SMART to Compare Adaptive Interventions
A prototypical SMART includes several sequences of intervention options that are adaptive by design, namely individualized based on early signs of progress. Consider as an example the ENGAGE SMART study, within which four AIs are embedded (see Figure 1 and Table 1). One of these AIs (i.e., AI #1) was described earlier. AI #1 will be referred to as later choice, as it offers personal choice only during the second stage (to non-responders). Consistent with this AI are individuals who were offered MI-IOP initially, and then MI-PC if they did not respond (subgroup e in Figure 1) and NFC if they responded (subgroup d in Figure 1). The second embedded AI (AI #2) offers second-stage intervention options (for responders and non-responders) that are similar to AI #1, but begins with MI-PC, rather than with MI-IOP. We refer to AI #2 as choice throughout, since personal choice is facilitated initially (to all individuals who enter the re-engagement program), as well as subsequently (to non-responders). Consistent with this AI are individuals who were offered MI-PC initially, and then MI-PC if they did not respond (subgroup b in Figure 1) and NFC if they responded (subgroup a in Figure 1). ENGAGE also includes two other embedded interventions, AI #3 and AI #4, which are actually non-adaptive in that the same second-stage intervention option (NFC) is offered to both early non-responders and early responders. We refer to AI #3, which begins with MI-IOP as no choice, since personal choice is not facilitated at either stage of the intervention. Consistent with AI #3 are individuals, who were offered MI-IOP initially, and then NFC if they did not respond (subgroup f in Figure 1) or if they responded (subgroup d in Figure 1). We refer to AI #4, which begins with MI-PC, as initial choice, since personal choice is facilitated only at the first stage of the intervention. Consistent with AI #4 are individuals who were offered MI-PC initially and then NFC if they did not respond (subgroup c in Figure 1) or if they responded (subgroup a in Figure 1). As noted earlier, both AI #3 and AI #4 are non-adaptive (they involve treating individuals in the same manner regardless of responder status) and are labeled AIs only for simplicity of exposition. In other SMART designs, all four combinations of intervention options may be adaptive.
Many SMART studies are motivated by scientific questions that concern the comparison of embedded AIs (Almirall et al., 2016). An example of such a question is whether the AI that begins with MI-IOP and then offers MI-PC to early non-responders and NFC to responders (i.e., AI #1) produces better results than another AI that offers similar second-stage intervention options but begins with MI-PC instead of MI-IOP (i.e., AI #2). Results could be operationalized in terms of treatment readiness, which refers to an individual’s personal commitment to active change through participation in a treatment program (Simpson & Joe, 1993).
Until recently (Lu et al., 2016), data analytic methods for comparing AIs embedded in a SMART have been limited to end-of-study outcomes, namely outcomes observed at follow-up assessment after treatment has ended (Nahum-Shani, et al., 2012a). For example, these methods enable the use of data from ENGAGE to compare AI #1 and AI #2 in terms of treatment readiness at the end of month 3.
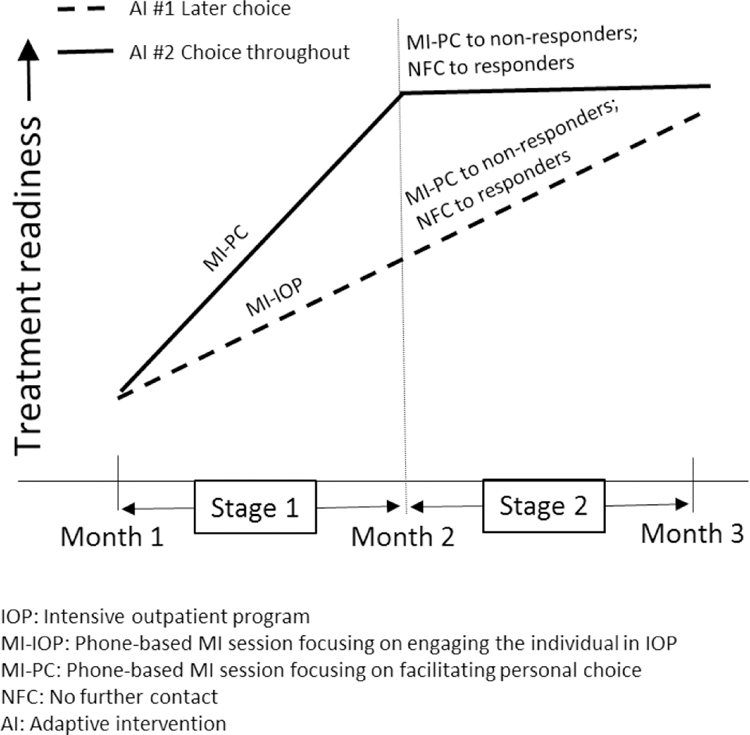
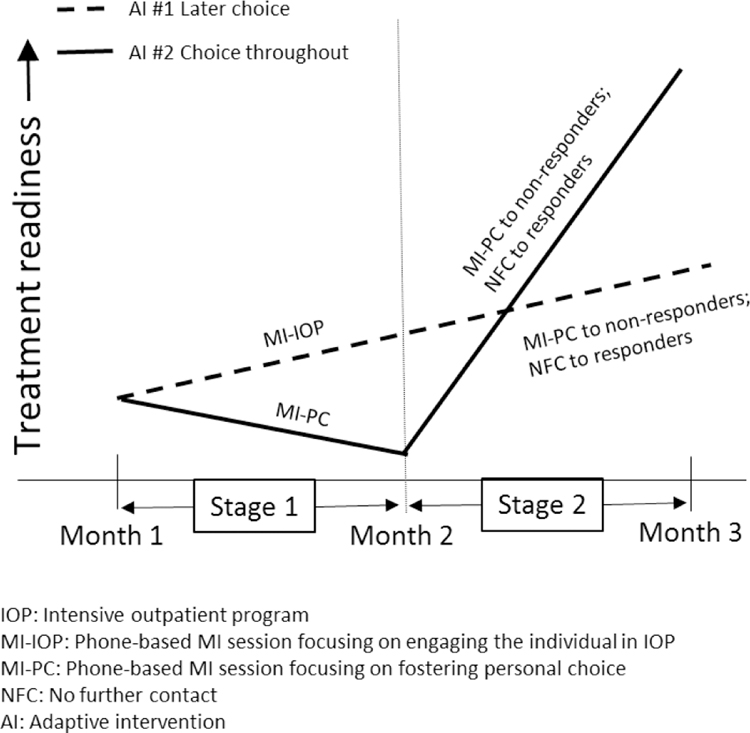
While comparing embedded AIs in terms of end-of-study outcome is highly informative, the course of improvement induced by the sequence of intervention options is also important in selecting and improving an AI. As an example, assume that AI #1 and AI #2 lead to a comparable end-of-study improvement in treatment readiness, but AI #2 leads to faster improvement during the initial stage (see hypothetical illustration in Figure 2a). Alternatively, assume that AI #2 leads to greater end-of-study improvement in treatment readiness compared to AI #1, although it demonstrates slow improvement, or even decline during the initial stage (see hypothetical illustration in Figure 2b). This information would allow clinicians and patients to weight short-term and long-term treatment goals when selecting an AI, rather than focusing on long-term, end-of-study improvement alone.
Figure 2a:
Hypothetical Comparison of Two Adaptive Interventions with Longitudinal Outcome Data
Figure 2b:
Hypothetical Comparison of Two Adaptive Interventions with Longitudinal Outcome Data
Comparing AIs in terms of the process by which outcomes improve over time as the AIs unfold requires the collection of repeated outcome measures in the course of the intervention, ideally before and after each decision point. To illustrate these ideas, we focus on three outcome measurement occasions: (1) immediately before the first-stage randomization; (2) after the first-stage randomization and immediately before the second-stage randomization; and (3) following the second-stage randomization. Suppose that in the ENGAGE study these correspond to treatment readiness measured at months 1, 2 and 3 respectively. Our goal is to discuss how these repeated outcome measures can be used to address scientific questions concerning the process by which the embedded AIs described above increase individuals’ treatment readiness.
Three example scientific questions:
First, does AI #2 lead to greater treatment readiness in the long term (i.e., at the end of month 3) compared to AI #1? Second, does the initial intervention options comprising AI #1 vs. AI #2 impact treatment readiness differently before vs. after these AIs unfold (i.e., before vs. after the second-stage options comprising these AIs are introduced)? Finally, does AI #2 lead to greater treatment readiness averaged over the course of the intervention considering both short-term (by month 2) and long-term (by month 3) gains, compared to AI #1?
While the first scientific question can be addressed by simply using an end-of-study (end of month 3) measure of treatment readiness, the second and third questions require repeated measures of treatment readiness before and after the second-stage interventions are introduced. Standard longitudinal data analysis methods can be used to analyze repeated outcome measures in the context of a standard randomized control trial (RCT) but cannot be used to compare AIs with repeated outcome measures from a prototypical SMART like ENGAGE. As we explain below, standard methods do not accommodate, nor take advantage of the unique features of the SMART and hence would lead to bias and reduced statistical efficiency. Hence, we introduce a data analytic method that can be used with repeated outcome measures from a SMART to obtain a clearer picture of changes in the outcome over time under each AI, to aid in addressing the second and third scientific questions. To ground the discussion, we first provide a brief review of how end-of-study outcomes from a SMART can be used to compare embedded AIs.
Review of Modelling and Estimation With an End-of-Study Outcome
We begin with a review of analytical techniques for comparing AIs embedded in a SMART study in terms of a single, end-of-study outcome. Denote the observed data in the SMART study by , where is a vector of the baseline covariates (e.g., age, gender), and is the end-of-study outcome collected for a particular individual at month 3. is the randomly assigned first-stage intervention option, coded 1 for MI-PC or −1 for MI-IOP. is an indicator for the randomly assigned second-stage intervention options among non-responders, coded 1 for MI-PC or −1 for NFC. Note that throughout we use effect coding (−1/1) rather than dummy coding (1/0) for the assigned intervention options, because by doing so, tests of regression coefficients correspond directly to tests of main effects, which is not generally the case in dummy-coded models with interactions (see Collins, 2018; Myers, Well, & Lorch, 2010).
In this prototypical SMART responders are not re-randomized to second-stage intervention options–they are offered a fixed intervention option (NFC). Hence, the four embedded AIs are coded as (−1, 1) for later choice (start with MI-IOP, then offer MI-PC for non-responders and NFC to responders); (1, 1) for choice throughout (start with MI-PC, then offer MI-PC for non-responders and NFC to responders); (−1, −1) for no choice (start with MI-IOP, then offer NFC to both non-responders and responders); and (1, −1) for initial choice (start with MI-PC, then offer NFC to both non-responders and responders). Special data analytic techniques are required in order to compare embedded AIs in an unbiased and efficient manner because of the unique features of data arising from a prototypical SMART such as ENGAGE.
First, in order to conveniently compare all four embedded AIs simultaneously with regression procedures that are available in standard statistical software, it is necessary to organize the data in a way that indicates which individuals’ data should be used in estimating the outcome for each AI. In particular, because only non-responders received second-stage randomization assignments, the value of for responders is not specified (by design). Hence, it is difficult at first to see how outcome information from responders can be included in a regression of on and . For example, by design, responders to MI-IOP (individuals with ) are never given a level of . Yet, as described above, responders to MI-IOP are consistent with two of the four embedded AIs: the later-choice AI (−1, 1) which is identified with , and the no-choice AI (−1,−1) which is identified with . It stands to reason that the outcome for responders to MI-IOP should be used to estimate the mean outcome under both AIs, but how can this be done with standard statistical software? Nahum-Shani and colleagues (2012a) suggest a way to do this via replication of responders’ data. Specifically, in order to associate a responder’s data with both of the AI’s with which the responder is consistent, each row in the dataset that pertains to a responder is duplicated with the same values for all variables (including ), except for . One of the duplicated rows is assigned , while the other is assigned . To avoid overstating the true sample size when estimating standard errors, an approach similar to generalized estimating equations (GEE) is used when conducting analyses (Liang & Zeger, 1986). This approach accounts for the fact that each pair of rows in the data, corresponding to the two duplicates of a responder, in fact represents only a single individual.
Second, when non-responders are re-randomized to second-stage intervention options, while responders are not re-randomized, outcome information from non-responders is under-represented in the sample mean under a particular embedded AI, by design. In the ENGAGE example, non-responders at month 2 were re-randomized to 2 intervention options (MI-PC or NFC), while all responders were assigned a single intervention (NFC). As a result, for non-responders, the probability of being assigned to a sequence of intervention options that is consistent with a particular embedded AI was 0.25 (because they were randomized twice with probability 0.5 each time), whereas for responders it was 0.5 (because they were randomized only once with probability 0.5). Because there is imbalance in the proportion of responders versus non-responders consistent with any particular AI in the study, and because response status is expected to be associated with the outcome , taking a naïve average of for all individuals consistent with the AI likely leads to bias (Orellana, Rotnitzky, & Robins, 2010; Robins, Orellana, & Rotnitzky, 2008). Importantly, this imbalance, which is known by design, does not refer to how individuals are distributed across the assigned treatments, as is usually the case in the analysis of observational studies (Rosenbaum & Rubin, 1983; Schafer & Kang, 2008). Indeed, in ENGAGE, all individuals (e.g., regardless of baseline severity or history of treatment) are assigned with equal probability to either initial MI-IOP or initial MI-PC; and similarly, all non-responders (e.g., regardless of severity) are assigned with equal probability to either subsequent MI-PC or NFC. One approach to restoring balance is to assign weights that are proportional to the inverse of the probability of treatment assignment. In the case of ENGAGE, responders’ observations are assigned the weight W=2 (the inverse of 0.5), and non-responders’ observations are assigned the weight W=4 (the inverse of 0.25). These weights are often referred to as “known weights” because they are based on known features of the design, namely the probability used to assign the individual to intervention options at each stage (Lu et al., 2016).
Alternatively, these weights can be estimated based on data from the SMART. This has the potential to further improve efficiency of the estimator (i.e., smaller standard errors in the comparison of AIs; Hernan, Brumback, & Robins, 2002; Hirano, Imbens, & Ridder, 2003), as demonstrated in Online Supplement A via simulation studies (https://github.com/dziakj1/SmartTutorialAppendix). In the current setting, this can be employed by conducting two logistic regressions. One regression focuses on estimating the probability of assignment to the first-stage intervention options. This can be done by regressing a dummy-coded indicator for the first-stage intervention options (e.g., define if , and if ) on covariates that are measured prior to the first-stage randomization (e.g., baseline information) and are thought to correlate with the outcomes. A second regression focuses on estimating the probability of assignment to the second-stage intervention options. This can be done by regressing a dummy-coded indicator for the second-stage intervention options (e.g., define if , and if ) among non-responders on covariates measured prior to the second-stage randomization and that are thought to predict the outcome. Such covariates might include both baseline and time-varying information obtained during the first intervention stage. Based on these logistic regressions, for each individual, the probability of assignment for first-stage and second-stage intervention options can be estimated. Multiplying the two estimated probabilities yields the estimated weight for each individual. Table 2 illustrates weighting and replication with simulated data, describing what the data typically look like before and after weighting and replication.
Table 2:
Illustration of Weighting and Replication for End-of-Study Outcome Comparison of Embedded Adaptive Interventions, Using Simulated Data
| Unmodified data layout | ||||||
|---|---|---|---|---|---|---|
| Individual ID | Response Status* | Month | Y | |||
| 1001 | 0 | 3 | 1 | −1 | 24 | |
| 1002 | 1 | 3 | −1 | NA | 26 | |
| 1003 | 0 | 3 | 1 | 1 | 28 | |
| 1004 | 0 | 3 | −1 | −1 | 30 | |
| 1005 | 1 | 3 | −1 | NA | 27 | |
| 1006 | 1 | 3 | 1 | NA | 28 | |
| Weighted and replicated data layout | ||||||
| Individual ID | Response Status | Month | Y | W | ||
| 1001 | 0 | 3 | 1 | −1 | 24 | 4 |
| 1002 | 1 | 3 | −1 | 1 | 26 | 2 |
| 1002 | 1 | 3 | −1 | −1 | 26 | 2 |
| 1003 | 0 | 3 | 1 | 1 | 28 | 4 |
| 1004 | 0 | 3 | −1 | −1 | 30 | 4 |
| 1005 | 1 | 3 | −1 | 1 | 27 | 2 |
| 1005 | 1 | 3 | −1 | −1 | 27 | 2 |
| 1006 | 1 | 3 | 1 | 1 | 28 | 2 |
| 1006 | 1 | 3 | 1 | −1 | 28 | 2 |
Response status is coded such that 0=non-responder; 1=responder
With the data replicated and weighted as described above, a model to compare the four embedded AIs can be fit using standard software (e.g., SAS, R). In our example, we are interested in estimating the mean treatment readiness at the end of month 3 under the four embedded AIs: later choice (−1, 1), choice throughout (1, 1), no choice (−1, −1), and initial choice (1, −1). A straightforward model for this analysis would be
| (1) |
is a vector of the baseline covariates and is a vector of their associated coefficients. For notational convenience and to make the s more easily interpretable, we mean-center the baseline covariates so that the expected value of is zero. As in the primary analysis of conventional randomized trials, only baseline covariates (or covariates that cannot be influenced by treatment) are included in . This means we do not condition on any time-varying covariates in our analyses that could be impacted by , including response status, because doing so would likely lead to bias (Robins, 1997). For each embedded , denotes the expected treatment readiness at the end of month 3 given the covariates and the embedded . We are interested in differences in for different values of . The regression coefficients , , and represent the effects of the first-stage intervention options, second-stage intervention options, and the interaction between them, respectively. Based on this model, is the expected outcome under the later-choice AI, denoted (−1, 1); is the expected outcome under the choice-throughout AI, denoted (1, 1); is the expected outcome under the no-choice AI, denoted (−1, −1); and lastly, is the expected outcome under the initial-choice AI, denoted (1, −1). It follows that is the expected difference between the choice-throughout AI (AI #2) and the later-choice AI (AI #1) in terms of month 3 outcome . Expected differences between other pairs of embedded AIs in terms of month 3 outcome can be obtained in a similar manner. Model (1) can also be extended to investigate whether the difference between the embedded AIs varies depending on the covariates . This can be done by including interactions between , and .
The estimating equations for are given in Appendix A. Estimates of the and their standard errors can be obtained using any standard software that implements GEE with weights (e.g., SAS GENMOD procedure; see example syntax in Nahum-Shani et al., 2012; Appendix B). Nahum-Shani and colleagues (2012a) demonstrate how the weighting and replication approach results in consistent estimators of the population averages for the regression coefficients and provide a detailed justification for the use of a robust (sandwich) standard error estimator. When estimated (rather than known) weights are used in the analysis, a small adjustment to the usual robust standard error estimator is recommended (see Appendix A). In the next section, we discuss how the approach outlined above for comparing AIs in terms of end-of-study outcome data arising from a SMART can be extended for use with longitudinal outcome data.
Using Longitudinal Outcome Data from a SMART to Compare Adaptive Interventions
Suppose now that the investigator is interested in using outcome information from months 1 and 2, in addition to month 3, to compare the four embedded AIs. Specifically, the observed data are now , where is treatment readiness measured at the end of month 1, prior to the initial randomization, and is treatment readiness measured at the end of month 2, after the first-stage randomization and prior to second-stage randomization. As before, is a vector of baseline covariates, is the end-of-study treatment readiness measured at month 3, is the randomly assigned first-stage intervention option, and is the randomly assigned second-stage intervention option. In the following sections we discuss modeling considerations pertaining to using such repeated outcome measures to compare embedded AIs. Note that per convention in randomized longitudinal studies, we assume there is only one primary outcome variable of interest (although the outcome can be a summary of multiple variables; e.g., capturing motivation pertaining to multiple behaviors), whose values are expected to change systematically over time, and this variable is measured with an identical instrument at each of the measurement occasions to ensure outcome comparability (Singer & Willett, 2003).
Modeling Considerations
Model (1) can be extended to include the additional repeated outcome measures described above. However, the longitudinal model ought to accommodate the features of the SMART design, most importantly the temporal ordering of the measurement occasions relative to when the intervention options were offered. Specifically, we consider models that allow for the outcome at each stage to be impacted only by intervention options that were offered prior to that stage. While the outcome at month 3 (i.e.,) can be impacted by both first-stage and second-stage intervention options, the outcome at month can only be impacted by first-stage intervention options, and the outcome at month cannot be impacted by either first-stage or by second-stage intervention options. Lu and colleagues (2016) discussed the bias that could be incurred by failing to properly account for these study design features when using repeated outcome measures from a SMART to compare embedded AIs.
Various longitudinal models can be used to accommodate the features of a SMART, including very flexible models that include a vector of basis functions in time (Lu et al. 2016). For purposes of this tutorial manuscript, we focus on the use of piecewise (segmented) linear regression models because these models are widely used in various domains of psychological research (e.g., Christensen et al., 2006; Kohli et al., 2015; Schilling & Wahl, 2006) and hence are familiar to many psychological scientists. Moreover, as we discuss below, these models can be used to accommodate the features of a SMART in a straightforward manner.
In a piecewise linear regression model, a separate line segment can be fit for different intervals over the course of the study, with the boundary for the time intervals forming a transition point, such as from one intervention stage to another. With respect to the ENGAGE SMART, two intervals of primary interest are used for illustration here: the first stage of the intervention (from month 1 to 2), and the second stage of the intervention (from month 2 to 3), with a transition point between them at month 2. With a piecewise regression model, the linear trend in the outcome during the first stage can be allowed to vary from the linear trend during the second stage and to be impacted by different variables.
The following is a convenient approach for employing a piecewise linear regression model with repeated outcome measures from a SMART like ENGAGE. For simplicity of presentation, we first ignore treatment assignment and briefly review how to fit a single piecewise trajectory.
| (2) |
Here is the outcome measured at month 1, 2, or 3. is an indicator for the number of months spent so far in the first stage by time , and is an indicator for the number of months spent so far in the second stage by time . Hence, for an observation measured at month 1 (pre-intervention), both and are set to 0, as this observation was taken prior to the first and the second stage of the intervention. For an observation measured at month 2, is set to 1 and is set to 0 because this observation was measured 1 month into the first stage and prior to the second stage. For an observation measured at month 3, and are both set to 1 because this observation was measured 1 month into the first stage and 1 month into the second stage. Note that for an observation taken at time always equals , namely the time since the beginning of the study. The separation of time into two variables is done in order to allow the fitted trajectory to shift at the transition point. Because and are each functions of measurement time, they could be written as and ; however, we suppress this here to simplify the notation. represents the expected treatment readiness at month 1, represents the first-stage slope, and represents the second-stage slope. Based on this model, the expected treatment readiness at each measurement occasion can be obtained via a linear combination of the regression coefficients. For example, provides the expected treatment readiness at month 2, and provides the expected treatment readiness at month 3. Additional guidelines for coding time indicators in piecewise linear models for various scenarios can be found in the extant literature (e.g., Flora, 2008; Sterba, 2014).
In order to use measurement occasions at month 1, 2 and 3 to compare the embedded AIs, the indicators for the first-stage and second-stage intervention options can be incorporated into model (2) so that each piecewise slope depends only on intervention options that have been assigned prior to or at that stage. Specifically, at month 1, both and are unassigned. Hence, (the expected outcome at month 1) should not vary depending on or . During the first stage, only is assigned, while is yet to be assigned. Hence, the first-stage slope can be allowed to vary depending on by replacing in model (2) by . Because effect coding was used for , is now the expected monthly change in treatment readiness during the first stage, averaged over all individuals, and represents the effect of the first-stage intervention options on the expected change in treatment readiness during the first stage.
At the second stage, both and have been assigned. Hence, the second-stage slope can be allowed to vary depending on both and by replacing with . is the expected monthly change in treatment readiness during the second stage, averaged over all individuals., , and represent the effects of the first-stage intervention options, second-stage intervention options, and the interaction between them, respectively, on the expected change in treatment readiness during the second stage.
A full piecewise model combining the baseline, first-stage, and second-stage expressions described above, is
| (3) |
Based on model (3), the expected treatment readiness at each measurement occasion can be obtained for each of the four embedded AIs. For example, for individuals consistent with AI #1 (later choice: , ), the expected treatment readiness at month 2 is given by and the expected treatment readiness at month 3 is given by . For individuals consistent with AI #2 (choice throughout: , ), the expected treatment readiness at month 2 is given by , and the expected treatment readiness at month 3 is given by . Table 3 provides the linear combinations that produce the expected outcomes at each measurement occasion for each embedded AI. Notice that if the intervention options at both stages have no effect, model (3) would reduce to model (2).
Table 3:
Expected Outcome for Each Time Point for Each Embedded Adaptive Intervention (AI) Based on the Piecewise Linear Regression Model in (3)
| Embedded AI | Month | Expected Outcome |
|---|---|---|
|
AI #1: Later choice (, ) |
1 | |
| 2 | ||
| 3 | ||
|
AI #2: Choice throughout (, ) |
1 | |
| 2 | ||
| 3 | ||
|
AI #3: No Choice (, ) |
1 | |
| 2 | ||
| 3 | ||
|
AI #4: Initial Choice (, ) |
1 | |
| 2 | ||
| 3 |
Importantly, consistent with existing modeling approaches for comparing AIs with SMART data (e.g., Nahum-Shani et al., 2012; Lei et al., 2012), model (3) is a marginal longitudinal model in that it is a proposal for how the outcome changes over time, on average, had all individuals in the population been offered the AI denoted by (, ); and the primary goal of model (3) is to compare different aspects of these average trajectories between the AIs (see the following section on Estimands). The marginal model is conditional only on baseline covariates ; thus, model (3) does not represent a model for individual-level trajectories, except as characterized by . Model (3) also does not represent a mechanistic model for how the outcomes are generated; for example, we expect response status at the end of first stage to be correlated with subsequent outcomes , yet such associations are not the target of interest in model (3). Further, model (3) makes no distributional assumptions (e.g., normality) about individual-level deviations from the average trajectory, nor assumptions about the marginal variance of such deviations (although note that below we provide an approach to estimating the regression coefficients which permits the analyst to pose a working model for the marginal covariance that often leads to gains in statistical efficiency).
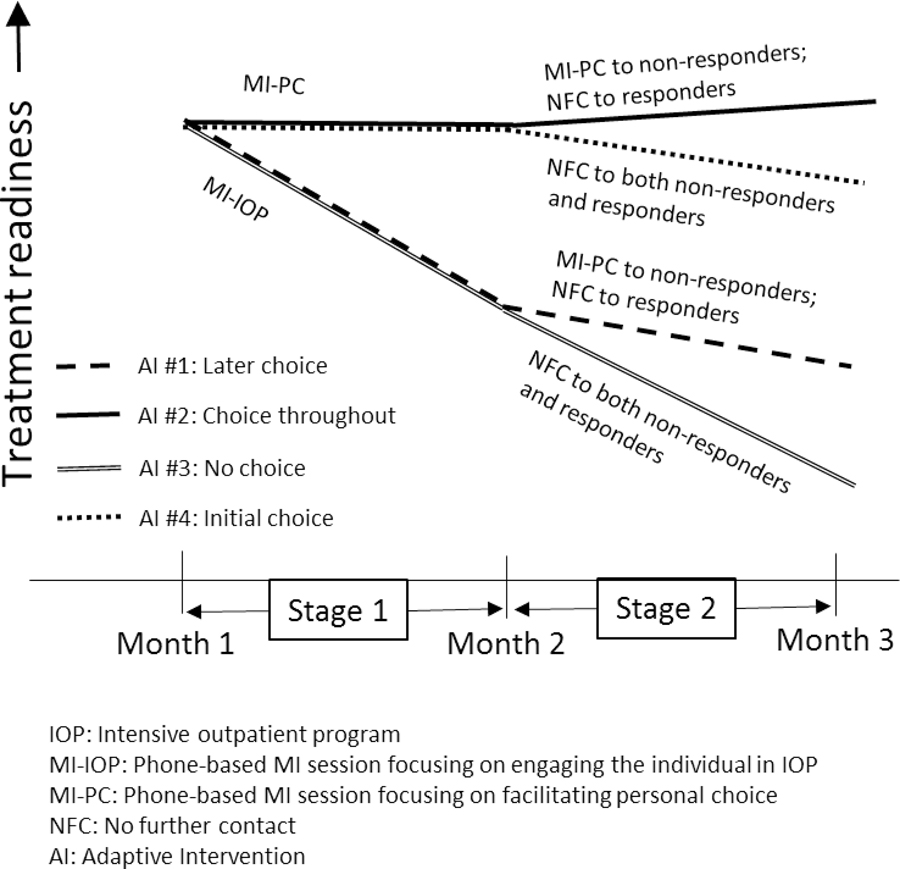
A plot of hypothetical expected outcomes based on model (3) is shown in Figure 3. This plot illustrates how the piecewise linear regression approach employed in model (3) accommodates the key features of longitudinal data arising from a prototypical SMART like ENGAGE. First, all four embedded AIs are expected to produce the same level of treatment readiness at month 1 because no intervention had yet been assigned at that time. Second, during the first stage, embedded AIs that begin with the same initial intervention option share the same slope because second-stage intervention options had not yet been assigned. Specifically, later choice and no choice share the same first-stage slope, as they both begin with MI-IOP. Similarly, choice throughout and initial choice share the same first-stage slope, as they both begin with MI-PC. Third, the trajectory of the outcome variable is allowed to change after introducing the second-stage intervention options. Figure 3 illustrates the transition point in the trajectory of each embedded AI at month 2, the point at which the second stage of the intervention started. At this point, the slope of the trajectory of expected treatment readiness changes from to .
Figure 3:
Hypothetical Expected Outcomes of the Four Embedded Adaptive Interventions in ENGAGE Based on the Piecewise Linear Regression Model in (3)
The modeling assumptions discussed above are motivated by the expectation that randomized groups are balanced on pre-randomization variables (known or unknown), including previous measures of the outcome. As in the analysis of data from any randomized trial, in post-hoc sensitivity analyses, it is useful to check for (im)balance between randomized groups. This can be done, for example, by examining whether the average outcome at month 1 differs between individuals assigned to vs ; or by examining whether, among non-responders, the average outcome at month 2 differs between individuals assigned to vs . As in any randomized trial, imbalances may occur; although much can be done in the design stage to prevent such imbalances. The tools for preventing imbalances are similar to those used in standard randomized trials (Kernan et al., 1999; Therneau, 1993). For example, a useful strategy is to stratify the first-stage randomization based on a baseline measure of the primary outcome (e.g., in our example), and to stratify the second-stage randomization among non-responders based on a measure of the primary outcome at the end of the first stage (e.g., in our example). A second useful strategy is to ensure randomizations are conducted and revealed in “real-time,” as opposed to generating the randomized lists ahead of time (and attempting to keep them locked), which could inadvertently influence pre-randomization outcomes should staff and/or participants have knowledge of subsequent stage treatment assignments. In studies where significant imbalances are suspected or evident, we recommend sensitivity analyses with longitudinal models that relax some or all of the modeling assumptions described above. For example, in sensitivity analyses, one could fit a longitudinal model that allows for all four embedded AIs to have a unique average trajectory in both the first and second stage.
Model (3) requires at least 3 measurement occasions. However, it is in fact a general model that can be employed with more than three measurement occasions. Consider for example a hypothetical scenario in which there are two measurement occasions, instead of one per stage, as follows: . Here, the second-stage randomization occurs at month 3, and there are two measurement occasions during the first stage (at months 2 and 3), and two measurement occasions during the second stage (at months 4 and 5). Model (3) can be employed with such data by coding and in a way that accommodates the ordering of each of the five measurement occasions with respect to the randomization stages in the SMART. Specifically, , which is an indicator for the number of months spent so far in the first stage by time , will be coded 0, 1, 2, 2, and 2, for measurement occasions 1, 2, 3, 4, and 5 respectively; and , which is an indicator for the number of months spent so far in the second stage by time will be coded as 0, 0, 0, 1 and 2 for measurement occasions 1, 2, 3, 4, and 5 respectively. Employing model (3) with this hypothetical data will enable the trajectory of the outcome variable to change at month 3, namely after introducing the second-stage intervention options. Additionally, when a stage involves a longer period of time and more measurements, investigators may consider fitting non-linear trajectories (e.g., a quadratic trajectory by including the square of and/or in the model).
In summary, when specifying a model for the mean trajectory for each AI in a SMART, it is important that the choice of the longitudinal model aimed at comparing embedded AIs accommodates the features of the sequentially randomized trial design. A piecewise-linear model was discussed as one relatively straightforward approach to accommodating these key features. This model can be parametrized in various ways--model (3) presents one approach; another approach is discussed in Appendix C. Unlike when comparing the embedded AIs based on an end-of-study outcome, when using longitudinal data there are various additional ways to operationalize the relative effectiveness between the AIs. Each of these amounts to answering a different scientific question concerning the effect(s) of the AIs. In the next section, we discuss different contrasts of potential scientific interest.
Estimands
This section focuses on various ways to operationalize the effect(s) of the embedded AIs based on longitudinal outcome data from a SMART. As we discuss below, one option is to focus on the final endpoint; however, the longitudinal data affords the scientist the ability to examine various different contrasts of interest. Each of these contrasts can easily be expressed as a linear combination of the regression coefficients in a linear regression model, such as the example piecewise linear regression model introduced earlier. In this section, we list a few of these options. In addition, each of these contrasts can be used to address a different scientific question concerning the relative effect(s) of the AIs on the longitudinal outcome. Investigators will select the estimands that are most appropriate for addressing their scientific questions. Specifically, we consider four types of estimands: time-specific outcomes, stage-specific slopes, area under the curve (AUC), and delayed effects. Continuing to assume a total of three measurement occasions for convenience of presentation (for months 1, 2 and 3), we discuss how these estimands can be used to address the three scientific questions outlined earlier. Throughout the following section, a particular AI is denoted by .
Time-Specific Outcomes.
The simplest option is to compare two or more of the embedded AIs in terms of the mean outcome at a single time point . In our motivating example, because treatment has not yet been offered at time 1 (e.g., month 1), the expected value of the average effect of (, ) on is fixed at zero, so comparisons at time 1 are not of interest (unless a failure of randomization or lack of blinding is suspected). Thus, we focus on comparisons at time 2 and 3.
We begin with . Based on model (3),. Therefore, the difference in expected outcome between any two AIs (, ) and (, ) at time 2 is . For example, denotes the difference in expected readiness at month 2 between the choice-throughout (1, 1) and the later-choice (−1, 1) AIs. As explained earlier, the values of and are irrelevant at time 2 because none of the participants have been offered the second-stage intervention at that time.
Next, we consider . Based on model (3) the difference in expected outcome between AIsAIs (, ) and (, ) at time 3 is . This estimand can be used to address the first question outlined earlier, namely whether the choice-throughout AI (1, 1) leads to greater readiness in the long term (i.e., at the end of month 3) compared to the later-choice AI (−1, 1). For example, if , then choice throughout (1, 1) is better than later choice (−1, 1) in terms of the expected treatment readiness at month 3.
However, as discussed earlier, focusing only on outcomes obtained at a specific measurement occasion to compare embedded AIs reveals only part of the picture concerning the process of change produced by these AIs.
Stage-Specific Slopes.
While the three scientific questions outlined earlier do not directly concern stage-specific slopes, we include this estimand because, as we discuss later, there is a connection between stage-specific slopes and delayed effects. A slope analysis provides an opportunity to compare embedded AIs in terms of rate of change in the outcome of interest. Based on model (3), during the first stage, the expected outcome at time is given by . Recall that is an indicator for the number of months spent so far in the first stage by time . Hence, is the first-stage slope, namely the expected rate of change for every 1 unit (here 1 month) progress in time during the first stage. The expected difference between any two embedded AIs, (, ) and (, ), in terms of first-stage slopes is, therefore,. For example, the difference between the choice-throughout (1, 1) and the later-choice (−1, 1) AIs in terms of the change in treatment readiness over time during the first stage is . Similarly, based on model (3), the expected outcome at time during the second stage is given by . Recall that in this particular example, at the beginning of the second stage (since one month was spent so far in the first stage) and counts the number of months spent so far in the second stage by time . Hence, is the second-stage slope, namely the expected rate of change for every 1 month progress in time during the second stage. It follows that the difference between any two embedded AIs in terms of second-stage slopes is given by . For example, the difference between the choice-throughout (1, 1) and the later-choice (−1, 1) AIs in treatment readiness change over time during the second stage is .
Because we have assumed the intervals between stages have lengths of one unit, the first-stage slope is the same here as the expected change score from time 1 to 2, and the second-stage slope is the same as the expected change score from time 2 to 3. In addition, because the embedded AIs have the same expected outcome at time 1, by design, and because model (3) used a linear trajectory from time 1 to 2, the between-AI contrast of first-stage slopes is also equal to the between-AI contrast of time 2 outcomes. However, the contrast of second-stage slopes is not equal to the contrast of time 3 outcomes, because the time 3 expected outcomes depend on both the expected change from time 1 to 2 and the additional expected change from time 2 to 3.
Area Under the Curve (AUC).
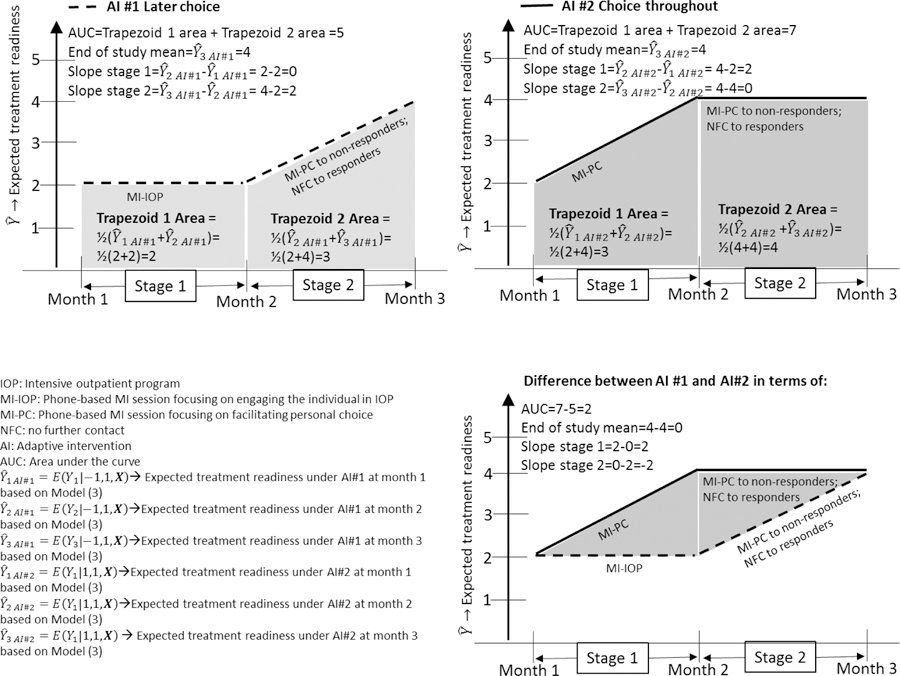
The AUC can be used to address a scientific question such as the third question outlined earlier: Which embedded AI is associated with highest value on the outcome averaged over the course of the intervention? To clarify this, instead of considering times 1, 2, and 3 as separate discrete time values, for now consider time to be continuous, and assume that the expected outcomes on the three time points are connected using a piecewise linear model, as illustrated in Figure 4. In the plot of the expected outcome over time for AI#1 and for AI#2 (Figure 4), the AUC is the total shaded area. The AUC can be used to distinguish AIs associated with higher outcome levels over the duration of the study from AIs with lower levels, even if both may have a similar expected outcome at the end of the study.
Figure 4:
Hypothetical Illustration of Expected Area Under the Curve (AUC) for Embedded AI #1 vs. embedded AI #2 in ENGAGE based on the Piecewise Linear Regression Model (3)
In the case of separate discrete time values (e.g., for month 1, 2, and 3 as in the example above), we define AUC by assuming linear interpolation which reduces to a quantity that can be calculated in a straightforward manner via a linear combination of regression parameters using any software package (see Appendix B). Specifically, because of the piecewise linear assumption the AUC for a particular is equivalent to the sum of the areas of two trapezoids (see Figure 4), one for the first stage: and one for the second stage: . Hence,. The first term, , cancels out in a contrast between two embedded AIs because, as noted earlier, it is assumed the same for all embedded AIs. Therefore, the contrast in AUCs between any two AIs (, ) and (, ) equals . For example, the difference in overall AUC between the choice-throughout (1, 1) and the later-choice (−1, 1) AIs is .
Although AUC is a widely used estimand in research involving repeated outcome measures (e.g., Fekedulegn et al., 2007; Matthews et al., 1990), it is rarely used in randomized trials of behavioral interventions. This may be due to common assumptions of linearity in the outcome trajectory over time. If trajectories are assumed to be linear throughout the course of the study, and treatment groups are assumed to have the same expected value on the outcome variable at baseline, then comparing AUCs is equivalent to comparing final outcomes and therefore provides no new insight. However, when the focus is on comparing AIs, which involve treatment modifications in the course of the program, linearity in the trajectory cannot be assumed. In fact, it is assumed that the trajectory will be deflected at the point in which second-stage treatment is introduced. In this case, comparing AUCs will provide insights that differ from comparing end of study means or slopes (as illustrated in Figure 4).
The AUC can be interpreted as a weighted average of the outcome across all measurement occasions; it gives less weight to the first and last measurement occasions because it is intended to focus on the overall trajectory between the beginning and the end. To clarify, consider the hypothetical comparison of AI #1 and AI #2 in Figure 4. When equal weight is given to each measurement occasion, there is little difference between these two AIs. However, the difference in favor of AI #2 is more apparent when the focus is on approximating the expected value throughout the time interval of interest, in which case values towards the middle are more informative than are values that are exactly at the beginning or end.
Delayed Effect.
Consider the second scientific question outlined earlier: Does the initial intervention options comprising AI #1 (later choice) vs. AI #2 (choice throughout) impact treatment readiness differently before vs. after these AIs unfold? Even if the initial intervention option comprising later choice (MI-IOP) is better than the one comprising choice throughout (MI-PC) by month 2 (i.e., before the second-stage intervention options are introduced), it is possible that later-choice may be no better than choice throughout, or even worse, at month 3 (i.e., after the second-stage intervention options are introduced). This represents a scenario where the effect of the first-stage intervention option within the two AIs is ‘delayed’—it unfolds only after the second-stage interventions are offered. Hence, the difference between the two initial intervention options comprising the AIs (i.e., their effect) varies over time, in particular before and after the second-stage options are introduced. Below we propose a straightforward approach for estimating the delayed effect in the context of two embedded AIs that begin with different initial intervention options. We define a delayed effect in the current setting as the difference between two differences. The first difference is between the two AIs after second-stage options are introduced. The second difference is between the two initial intervention options comprising the AIs before second-stage options are introduced.
The most straightforward way to operationalize a delayed effect is to use time-specific outcomes. In the current setting, the contrast in expected outcomes at month 3 can be used to operationalize the first difference, and the contrast in outcomes at month 2 can be used to operationalize the second difference. Recall that the expected difference between expected outcomes of any two embedded AIs is at month 3, and at month 2. Hence, the delayed effect can be quantified as . In the context of comparing the choice-throughout (1, 1) and later-choice (−1, 1) AIs, a delayed effect is evident in terms of time-specific means if . As can be seen in our earlier discussion of stage-specific slopes, this quantity is equivalent to the difference between these two AIs in terms of second-stage slopes. Notice that this quantity is nonzero for cases in which the first-stage intervention options impact the outcome during the second-stage merely due to the passage of time (i.e., interacts with , namely with the time spent in the second stage) as well as cases in which first-stage intervention options impact the outcome due to positive or negative synergy with the second-stage intervention options (i.e., has a three-way interaction with and ).
An alternative way to quantify delayed effects is via AUCs. Specifically, the first difference can be operationalized as the contrast in second-stage AUCs, and the second difference can be operationalized as the contrast in first-stage AUCs. The difference in second stage AUCs between any two AIs is , and the difference in first-stage AUCs between any two embedded AIs is . Hence, the delayed effect can be quantified as . Thus, in the context of comparing the choice-throughout (1, 1) and later-choice (−1, 1) AIs, a delayed effect in terms of AUCs is evident if . Notice that the delayed effect in terms of time-specific outcomes does not consider .
Estimation
As in an end-of-study analysis, to use existing software to fit a piecewise linear longitudinal model for comparing AIs in a SMART first requires similar procedures such as defining weights and replicated cases. The rationale and procedures for weighting and replicating the repeated outcome measurements are similar to those outlined earlier for the end-of-study analysis. Recall that weights are used because, by design, individuals were not assigned to the embedded AIs with equal probability. Weights are used to correct for this imbalance and to produce unbiased estimates of intervention effects. Replication is needed because responders are consistent with more than one embedded AI. Replication enables an investigator to use outcome information from a single responding individual to help estimate the mean outcome under both of the AIs with which that individual is compatible, and hence to compare all embedded AI simultaneously using standard statistical software procedures. Table 4 shows how SMART data involving repeated outcome measurements can be reformatted as a piecewise coded, weighted, and replicated dataset.
Table 4:
Illustration of Weighting and Replication for Longitudinal Outcome Comparison of Embedded Adaptive Interventions, Using Simulated Data
| Unmodified data layout | |||||||
|---|---|---|---|---|---|---|---|
| Individual ID | Response Status* | Month | A1 | A2 | Y | ||
| 1001 | 0 | 1 | 1 | −1 | 29 | ||
| 1001 | 0 | 2 | 1 | −1 | 22 | ||
| 1001 | 0 | 3 | 1 | −1 | 28 | ||
| 1002 | 1 | 1 | −1 | NA | 30 | ||
| 1002 | 1 | 2 | −1 | NA | 32 | ||
| 1002 | 1 | 3 | −1 | NA | 29 | ||
| Data layout with piecewise indicators | |||||||
| Individual ID | Response Status* | Month | A1 | A2 | Y | S1 | S2 |
| 1001 | 0 | 1 | 1 | −1 | 29 | 0 | 0 |
| 1001 | 0 | 2 | 1 | −1 | 22 | 1 | 0 |
| 1001 | 0 | 3 | 1 | −1 | 28 | 1 | 1 |
| 1002 | 1 | 1 | −1 | NA | 30 | 0 | 0 |
| 1002 | 1 | 2 | −1 | NA | 32 | 1 | 0 |
| 1002 | 1 | 3 | −1 | NA | 29 | 1 | 1 |
| Weighted and replicated data layout with piecewise indicators | |||||||
| Individual ID | Response Status* | Month | A1 | A2 | Y | S1 | S2 |
| 1001 | 0 | 1 | 1 | −1 | 29 | 0 | 0 |
| 1001 | 0 | 2 | 1 | −1 | 22 | 1 | 0 |
| 1001 | 0 | 3 | 1 | −1 | 28 | 1 | 1 |
| 1002 | 1 | 1 | −1 | −1 | 30 | 0 | 0 |
| 1002 | 1 | 1 | −1 | 1 | 30 | 0 | 0 |
| 1002 | 1 | 2 | −1 | −1 | 32 | 1 | 0 |
| 1002 | 1 | 2 | −1 | 1 | 32 | 1 | 0 |
| 1002 | 1 | 3 | −1 | −1 | 29 | 1 | 1 |
| 1002 | 1 | 3 | −1 | 1 | 29 | 1 | 1 |
Response status is coded such that 0=non-responder; 1=responder
An estimation approach very similar to weighted GEE can be used to fit a longitudinal model to the weighted and replicated data (see Lu et al., 2016). This framework allows a working covariance structure to be specified for the outcome across measurement occasions and/or across the embedded AIs, which could lead to improvements in efficiency (see Online Supplement A for a demonstration based on simulated studies). In the implementations described in this tutorial we use a working assumption of a common variance parameter and covariance structure across the AIs and occasions, but this could be extended. Because all the estimands discussed above are linear combinations of the regression coefficients, their estimates and estimates of their standard errors can be easily computed using this approach. Appendix A provides technical details regarding the proposed estimator (see Display [6]), as well as other information concerning the working covariance structure. Appendix B provides a summary and reference to example SAS and R code that takes advantage of existing GEE software (PROC GENMOD in SAS, and geepack in R respectively) to implement the estimator in Appendix A.
Design and Analysis Details for the ENGAGE Study
The example SMART design used for didactic purposes represents a relatively simple version of a SMART study. In practice, SMART studies may differ from this example in various ways. In fact, the actual implementation details of the ENGAGE SMART differed slightly from the simple version described in Figure 1. This section describes some of these differences, along with an explanation of how the analysis model was modified to accommodate them.
In the actual implementation of the ENGAGE SMART, individuals entered an IOP and their engagement with the IOP was monitored. After at least two weeks in the IOP, if their engagement with the IOP was suboptimal, they were randomized to one of the two initial engagement strategies described earlier, namely either MI-IOP or MI-PC, which are represented by the two levels of . In total, 273 such individuals were randomized to MI-PC (n=137) and MI-IOP (n=136). Two months following IOP entry, participants from this group who were classified as non-responders at that point were re-randomized to levels of , namely MI-PC (n=57) and NFC (n=53), as described earlier. Treatment readiness was assessed one, two, three, and six months after the beginning of the IOP and denoted , , and . The treatment readiness variable was measured by asking participants to rate the extent to which they agreed or disagreed, on a 5-point Likert scale ranging from 1 (disagree strongly) to 5 (agree strongly), to eight statements such as, “You plan to stay in this treatment program for a while.” The overall treatment readiness score for each participant was obtained by summing the eight responses, after reverse scoring four of the items; the resulting range was 8–40, with higher scores indicating greater readiness (Institute of Behavioral Research, 2007). In sum, an approximate representative time course would be as follows: is assigned at least two weeks after IOP entry, is assessed one month after IOP entry, was assessed two months after IOP entry, is assigned among non-responders two months after IOP entry, and and were assessed 3 and 6 months following IOP entry, respectively.
The resulting design differs in two ways from the simplified design described in Figure 1. The first main difference is the timing of measurement occasions relative to when the intervention options were offered. We accommodate this by coding of the time variables and as follows: Recall that and are indicators for the number of months spent so far, by time , in the first stage, and in the second stage, respectively. At month 1 (i.e., when ), about half a month had passed since the time of first randomization, and the second-stage randomization had not yet occurred; hence, was set to 0.5, and was set to 0. At month 2 (i.e., when ), about a month and a half had passed since the time of first randomization, and the second-stage randomization had not yet occurred; hence, was set to 1.5, and was set to 0. At month 3 (i.e., when ), the first stage of the SMART was complete (i.e., about a month and a half was spent so far on the first stage) and a month had passed since second-stage randomization; hence, was set to 1.5, and was set to 1. At month 6 (i.e., when ), the first stage of the SMART was complete and four months had passed since second-stage randomization; hence was set to 1.5, and was set to 4. Because the second stage involved a longer period of time and more measurements, it was not considered realistic to assume a linear trajectory. Hence, a quadratic trajectory was specified by including the square of in the model.
The second main difference of the actual study from the simplified description is that is assigned before is assessed, rather than both occurring at the same time. Thus, is not exactly a baseline measure as it would be in many SMART studies. A baseline measure of treatment readiness was obtained at the beginning of IOP, and this could be denoted , but it might not have the same interpretation as the measures of engagement with an ongoing treatment, and is accordingly treated as a covariate rather than a repeated measure. Further, there was no measurement of treatment readiness at the exact time of the first randomization. Including as a repeated measure would have required an assumption of a linear trajectory between and , which was not considered realistic because the assignment of in the middle of this interval could cause a change in trajectory. To account for occurring before , the model was specified in a way that allows to be impacted by A1, unlike in the tutorial model (3). In our analysis we used three baseline covariates: , gender (effect-coded as 1 for male and −1 for female), and the interaction between gender and . Covariates were mean-centered. As before, the set of baseline covariates is denoted by .
Taking these design considerations into account, the analysis model specified for the longitudinal trajectories was as follows:
| (4) |
for .
Notice that the model for the first stage slope in model (4) seems similar to that specified in model (3). However, in model (4) represents the main effect of (i.e., the difference between) the first-stage intervention options on treatment readiness at month 1, whereas in model (3) it represents half the main effect of the first-stage intervention options on treatment readiness at month 2. This is due to the different coding used for the first-stage time variable . Specifically, in model (4) the assumption is that is coded 0.5 for month 1 as opposed to 0, because was assessed half a month after (as opposed to immediately before) was assigned. Hence, unlike model (3), this model allows treatment readiness at month 1 to be impacted by first-stage intervention options. Additionally, the terms , , , and , which were not included in model (3), represent the average curvature of second-stage slope and whether this curvature varies by first-stage intervention options , second-stage intervention options , and the interaction between them , respectively.
There was some missing data due to study dropout (n=53) and missed study assessments (n=61). Because this article is intended as a simple tutorial, we present and report the analyses with complete cases (N=159). However, multiple imputation methods are available for use with SMART study data (Shortreed, et al., 2014). The data were weighted and replicated as described earlier. With this illustrative application, the weights were estimated based on the approach described above. To estimate the weights, three variables (baseline treatment readiness, gender, and age) were used to predict first-stage treatment assignment, and four variables (baseline treatment readiness, treatment readiness at month 1, gender, and age) were used to predict second-stage treatment assignment. An unstructured working correlation structure was applied.
Results: Engage Example
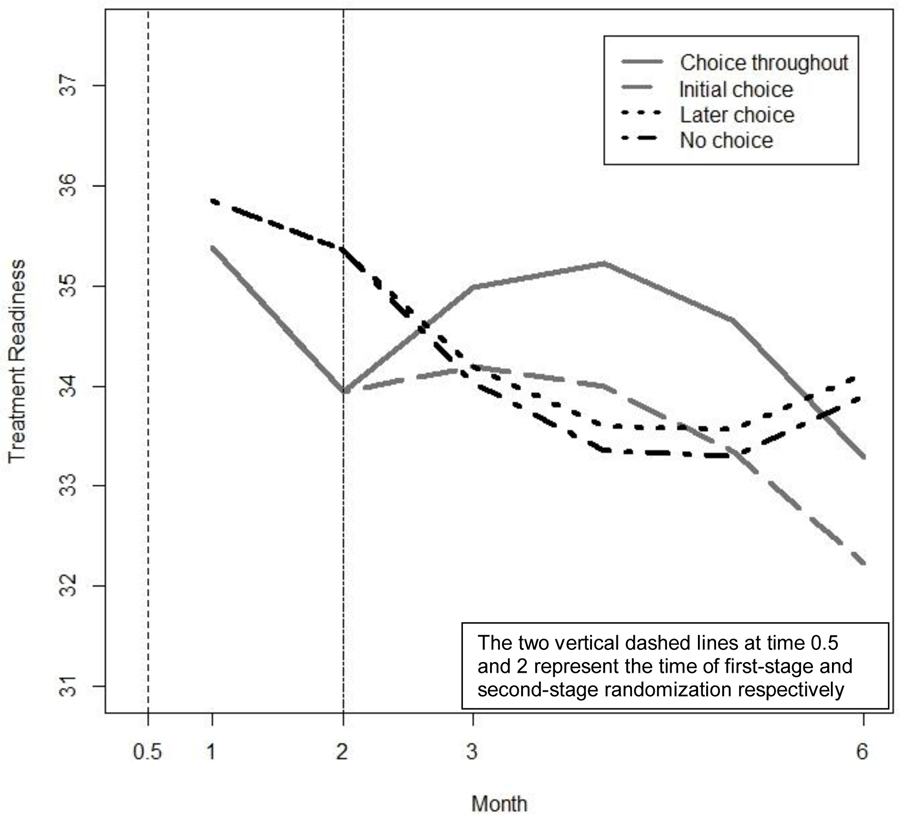
Table 5 presents the estimated regression coefficients for model (4), as well as estimated linear combinations of these coefficients that are of scientific interest; these include the estimated differences between choice throughout (1,1) and later choice (−1, 1) in terms of time-specific outcomes, AUCs, and delayed effects. Figure 5 presents the estimated treatment readiness over time under each of the embedded AIs in ENGAGE (based on model 4).
Table 5:
Results for Model (4) Using Data From ENGAGE (N = 159)
| Parameter | Estimate | SE | 95%CI: Lower Limit |
95%CI: Upper Limit |
|---|---|---|---|---|
| Intercept | 33.11** | 0.50 | 32.13 | 34.08 |
| Month 0 Treatment Readiness (TR0) | 2.57** | 0.31 | 1.97 | 3.18 |
| Gender (Male=1; Female=−1) | 0.93** | 0.35 | 0.25 | 1.62 |
| Gender * TR0 | −0.51ϯ | 0.30 | −1.09 | 0.07 |
| S1 | −0.97** | 0.38 | −1.71 | −0.22 |
| S2 | −0.30 | 0.49 | −1.27 | 0.67 |
| 0.00 | 0.12 | −0.23 | 0.22 | |
| S1×A1 | −0.48* | 0.24 | −0.95 | 0.00 |
| S2×A1 | 1.26** | 0.49 | 0.30 | 2.22 |
| S2×A2 | 0.29 | 0.23 | −0.15 | 0.73 |
| S2×A1×A2 | 0.19 | 0.23 | −0.27 | 0.65 |
| S22×A1 | −0.31** | 0.12 | −0.54 | −0.08 |
| S22×A2 | −0.05 | 0.06 | −0.16 | 0.06 |
| S22×A1×A2 | −0.04 | 0.06 | −0.15 | 0.08 |
| Estimated Means at Month 1 / Month 2 | ||||
| Choice-Throughout | 35.38 / 33.94 | 0.49 / 0.62 | ||
| Later-Choice | 35.85 / 35.36 | 0.48 / 0.65 | ||
| Estimated Means at Month 3 / Month 6 | ||||
| Choice-Throughout | 34.98 / 33.28 | 0.66 / 0.73 | ||
| Later-Choice | 34.19 / 34.12 | 0.71 / 0.77 | ||
| Estimated Differences between Choice Throughout and Later Choice in Terms of Time-Specific Outcomes | ||||
| Month 1 | −0.48* | 0.24 | −0.95 | 0.00 |
| Month 2 | −1.43* | 0.73 | −2.85 | 0.00 |
| Month 3 | 0.79 | 0.80 | −0.78 | 2.35 |
| Month 6 | −0.84 | 0.93 | −2.66 | 0.98 |
| Estimated Area Under the Curve (AUC) at Stage 1 (Months 1– 2); Stage 2 (Months 2–6) | ||||
| Choice-Throughout | 34.66, 141.62 | 0.51, 3.13 | ||
| Later-Choice | 35.61, 133.03 | 0.52, 3.38 | ||
| Estimated Overall AUCs (by month 6) | ||||
| Choice-Throughout | 176.28 | 3.57 | ||
| Later-Choice | 168.64 | 3.37 | ||
| Estimated Differences between Choice Throughout and Later Choice in terms of AUCs | ||||
| Stage 1 | −0.95* | 0.49 | −1.90 | 0.00 |
| Stage 2 (by month 6) | 8.59ϯ | 4.70 | −0.61 | 17.79 |
| Overall (by month 6) | 7.64 | 4.71 | −1.60 | 16.88 |
| Estimated Delayed Effects in Terms of: | ||||
| Time-specific outcomes by month 6 | −0.59 | 0.88 | −2.32 | 1.14 |
| AUC by month 6 | −9.54* | 4.26 | −18.70 | −2.01 |
p≤0.10;
p≤0.05
p≤0.01
CI=95% Confidence Interval
SE=Standard Error
Figure 5:
Estimated Treatment Readiness Over Time Under Each Embedded Adaptive Intervention in ENGAGE (based on Model 4).
The results in Table 5 indicate that the coefficient for (, SE = .38, p ≤ .01), the interaction between and (, SE = .24, p ≤ .05), the interaction between and (, SE = .49, p < .01), and the interaction between and the squared term (, SE = .12, p < .01) are significantly different from zero, whereas the other coefficients are not significantly different from zero. This means that on average, treatment readiness decreases during the first stage (because is negative), MI-PC is associated with significantly lower treatment readiness at month 1 compared to MI-IOP (because is negative), and the second-stage slope as well as its curvature vary significantly by first-stage intervention option (because and are significantly different from zero).
The difference between the choice-throughout (1,1) and later-choice (−1, 1) AIs depends on time, as shown in Table 5. While both AIs produce similar outcomes at month 3 (estimated means 34.98 and 34.19 respectively, difference = .79, SE = .80, ns) and at month 6 (estimated means 33.28 and 34.12 respectively, difference = −.84, SE = .93, ns), the process by which these outcomes unfold over time differs substantially between these two AIs. Specifically, there is evidence of a delayed effect in terms of AUCs (estimate = −9.54, SE = 4.26, p < .05), but not in terms of time-specific outcomes (estimate = −.59, SE = .88, ns).
The nature of this delayed effect is illustrated in Figure 5. During the first stage, choice throughout is associated with lower treatment readiness than later choice, both at month 1 (estimated means: 35.38 and 35.85 respectively, difference = −.48, SE = .24, p ≤ .05) and at month 2 (estimated means: 33.94 and 35.36 respectively, difference = −1.43, SE = .73, p <.05). However, this trend is reversed after the second-stage options are introduced. Then, choice throughout leads to increased treatment readiness, compared to later choice, as evident in higher second-stage AUC (141.62 and 133.03, respectively, difference = 8.59, SE = 4.70, p <.10).
Discussion
This manuscript provides an accessible introduction to a new methodology for using repeated outcome measures from a SMART to compare embedded AIs. We discuss how existing modeling and estimation approaches for comparing AIs in terms of end-of-study outcome data from a SMART can be extended for use with repeated outcome measures that are collected at different stages of the SMART. The proposed analytic approach accommodates the key features of longitudinal data from a prototypical SMART like ENGAGE.
In terms of modeling, the analysis accommodates three key features pertaining to the ordering of the measurement occasions relative to the randomizations in the SMART. First, before the initial randomization, all four embedded AIs are expected to produce the same outcome level since no intervention had yet been assigned at that time. Second, during the first stage, embedded AIs that begin with the same initial intervention are expected to share the same slope because second-stage intervention options had not yet been assigned. Third, the trajectory of the outcome is allowed to change after introducing the second-stage intervention options. We explain how these considerations can be addressed with a piecewise linear regression model.
In terms of estimation, the analysis accommodates three key features of longitudinal data arising from a SMART. First, responders are consistent with more than one embedded AI. Replication is employed to enable the use of outcome data from responders to estimate the mean outcome under two embedded AIs simultaneously. Second, in a prototypical SMART only non-responders are re-randomized. Hence, non-responders are under-represented in the sample mean of an embedded AI. This is dealt with via inverse probability weighting. Finally, since repeated outcome data can be correlated within an individual, the method enables the correlation structure in the longitudinal data to be estimated to enhance efficiency.
We also discuss the scientific yield that can be gained by using repeated outcome measures from a SMART to compare AIs. The illustrative analyses conducted with data from the ENGAGE SMART indicate that simply comparing the choice-throughout and the later-choice AIs in terms of end-of-study outcome would lead to the conclusion that the two perform equally well in terms of preventing a steep deterioration in treatment readiness among cocaine/alcohol dependent patients. However, comparing these two AIs in terms of repeated outcome measures collected before and after each randomization stage reveals that these two AIs differ substantially in terms of how they affect treatment readiness. Specifically, during the first-stage, choice-throughout, which begins with MI-PC, is not as beneficial as later-choice, which begins with MI-IOP. However, when second-stage intervention options are introduced (both of these embedded AIs offer MI-PC for non-responders and NFC to responders), choice throughout leads to increased readiness, which slightly exceeds the gains produced initially by later choice. Overall, while MI-PC (compared to MI-IOP) does not lead to better gains before second-stage intervention options are offered, it appears to build the foundation for the effectiveness of second-stage intervention options. This pattern represents a positive synergy between the first- and second-stage intervention options comprising the AI. However, delayed effects can also capture antagonism, whereby the intervention option that leads to better results initially, ends up being detrimental when followed by a specific second-stage intervention option.
The pattern of delayed effect found in the current example can motivate the development of more dynamic theories that incorporate the element of time in explaining how personal choice affects individuals’ readiness to attend treatment. Moreover, such results highlight the need for additional research aimed at further improving the embedded AIs. For example, the results can motivate future studies to investigate whether the long-term gains produced by facilitating personal choice can be capitalized on and further improved by adding another MI-PC session for individuals who remain non-responding at month 3. While the example SMART we used here for illustration addresses an important problem that is highly relevant across multiple domains of intervention research (i.e., treatment engagement), it is only one of many SMART applications that can benefit from utilizing the proposed methodology. Additional examples of SMART studies with different types of repeated outcome measures can be found in areas such as child mental health (Almirall et al., 2016; Pelham et al., 2016), substance use (Nahum-Shani et al., 2017) and weight loss (Naar-King et al., 2016).
This manuscript suggested a way to operationally define delayed effects in a SMART. While many SMART studies are motivated (often implicitly) by scientific questions concerning the delayed effect of the initial interventions comprising two AIs (Wallace, Moodie, & Stephens, 2016), to our knowledge a systematic operationalization of delayed effects has yet to be provided. Here, we discussed an intuitive operationalization of delayed effects. Specifically, we conceptualize a delayed effect as a difference in two differences: (1) the difference between the two AIs after second-stage options are introduced; and (2) the difference between the two initial intervention options comprising the AIs before second-stage options are introduced. Such an estimand cannot be computed based on end-of-study outcome measurement alone. It requires the repeated measurement of outcomes before and after each decision point in a SMART. It is important to note that consistent with the extant literature on AIs (e.g., Nahum-Shani et al., 2012; Wallace et al., 2016), a delayed effect is conceptualized here as a scenario in which the impact of the initial intervention options differs before vs. after the second-stage options are introduced. However, the definition of a delayed effect can be extended to include scenarios whereby the impact of one AI (after both first-stage and second-stage interventions are introduced) compared to another differs in the short-term compared to the long-term. In this case, a delayed effect can be operationalized as the difference between two differences: (1) the difference between two AIs (after both first- and second-stage options are introduced) in terms of some distal outcome (e.g., treatment readiness at month 6); and (2) the difference between two AIs (after both first- and second-stage options are introduced) in terms of a more proximal outcome (i.e., treatment readiness at month 3). Such an estimand does not require repeated outcome measurements before and after each decision point in a SMART, but rather repeated outcome measurements following the second decision point (i.e., after both first- and second-stage options have been introduced).
The example repeated measures model described in this tutorial article, namely model (3), is only one of various ways to model the mean trajectory for the AIs embedded in a SMART like ENGAGE. Other longitudinal models are also possible, which can accommodate (or approximately accommodate) the features of SMARTs like ENGAGE. For example, as shown in model (4), the marginal mean trajectories need not be linear functions of time (e.g., they could be quadratic, as shown in the analysis of data from ENGAGE). Methods for selecting the best repeated measures model for data from a SMART is one area of future research.
Models (3) and (4) are also design-specific: they are example models that accommodate the key features of SMART studies that are similar to ENGAGE, in which all individuals are randomized to two initial intervention options, and only non-responders are re-randomized at a fixed time point to two second-stage intervention options, so that there are four embedded AIs. Currently, many SMART studies are of this type (Gunlicks-Stoessel et al., 2016; Naar-King et al., 2016; Pelham et al., 2016), but there is great heterogeneity in how SMARTs are designed (Lei, Nahum-Shani, Lynch, Oslin, & Murphy, 2012; Nahum-Shani et al., 2012a). Naturally, different SMART designs might require different repeated measures modeling considerations. For example, a SMART in which responders were also randomized to second-stage intervention options (that differ from those to which non-responders get randomized), resulting in eight embedded AIs, would likely require a model different from model (3). The model might also differ if the timing of the first stage and/or second stage varied. For example, a second-stage intervention might take place over a range of time points depending on when the individual shows signs of early non-response. Lu and colleagues (Lu et al., 2016) describe three SMART design scenarios of increasing complexity and suggest ways to model repeated outcome measurements from such trials.
Limitations and directions for future research
Several other issues warrant further research. First, the repeated outcome measure of interest in the current manuscript was continuous, reflecting treatment readiness. However, researchers might be interested in non-continuous outcomes, such as binary or count measures reflecting the severity of alcohol or cocaine use (e.g., whether the individual experienced a heavy drinking episode, or the number of cocaine use days). The model discussed in the current manuscript can be generalized to binary or count outcomes. The SAS and R procedures discussed in the current manuscript allow the specification of various types of distributions and link functions.
Second, for simplicity of presentation, we focused here on three measurement occasions; however, we also discussed and demonstrated how the models proposed here can be readily extended to incorporate additional measurement occasions within each stage. As in any longitudinal study, careful consideration should be given to the selection of measurement occasions. As noted by Singer and Willett (2003) “there is no single answer to the seemingly simple question about the most sensible metric for time” (page 11). The scientific questions motivating the study should be the primary guide in selecting the timing of measurement occations (Singer & Willett, 2003). In a SMART, at least one measurement occasion per stage is required in order to address scienitific questions concerning delayed effects. Other than that, as noted by Singer and Willett (2003), “more waves are always better, within cost and logical constraints” (p. 10). With more measurement occasions, more complex models can be fitted (e.g., curvilinear). However, when fitting more complex trends, the use of linear combinations of model coefficients to estimate constructs of scientific interest, such as delayed effects, might be less straightforward and require careful consideration. Moreover, when various models can be fitted to the data a question arises concerning model selection. Metrics for evaluating goodness of fit in the context of the weighted and replicated estimation approach have not yet been developed; this is an important direction for future research (Lu et al., 2016).
Third, the proposed approach does not require the time intervals for the measurement occasions to be the same (e.g., one month between measurement occasions), as long as the coding of the time indicators ( and ) are set accordingly. This is demonstrated in the analysis of the ENGAGE study. However, an important assumption made here is that the time intervals between measurment occasions are not person-specific, namely they are the same for all individuals (e.g., all participants were assessed 1 month, 2 months and 3 months folowing study entry). Although longitudinal randomized trials, as well as in longitudinal SMARTs (see Lei et al., 2012) are typically designed such that all individuals have similar time intervals between measurement occasions, extending the current methodology to accommodate different measurement timing for different individuals may be of interest to future research.
Fourth, in the analysis of conventional randomized trials using repeated measures, investigators often use mixed-effect models. Such models are often used because (i) they provide an indirect, yet flexible and intuitive, approach to posing working models for the variance of the repeated measures outcome, and (ii) often there is secondary scientific interest in the variability of, and in predicting, person-specific trends over time (e.g., covariability in the person-level intercepts and slopes, or, related, interest in quantifying the variability in treatment effects) (Bauer, Preacher, & Gil, 2006; Singer, 1998; Singer & Willett, 2003). Similarly, investigators analyzing SMARTs might be interested in examing such variance components when comparing the embedded AIs in terms of a repeated outcome measures. The development of such mixed-effect models for use with data from a prototypical SMART (e.g., ENGAGE) represents an important direction for future research.
Fifth, though we provide the syntax for implementing the estimator in display (6) using existing GEE software in SAS (PROC GENMOD; Appendix B) and R (geepack; Online Supplement), it should be relatively straightforward to develop the syntax to implement the estimator with other existing software packages. In addition, in future work, it may be possible to use existing mixed-effects procedures (e.g., those available in SAS, R or Mplus) to solve the system of equations in (6). Once appropriate methods are developed, such mixed-effect software packages might allow for more flexible working models for the covariance matrix than are permitted by existing GEE software.
In conclusion, the goal of this manuscript is to provide an accessible tutorial for using repeated outcome measurements from SMART studies to compare AIs. An important focus was on highlighting how such longitudinal data affords the scientist the ability to address various types of scientific questions concerning the course of improvement induced by the sequence of intervention options. Various estimands have been provided to aid in addressing these scientific questions by operationalizing the effect(s) (i.e., the difference between the AIs) in terms of slopes, AUC, and delayed effects. For illustrative purposes, we used longitudinal data from a single SMART study (ENGAGE) to demonstrate how these various estimands can be obtained and estimated. This does not imply that an investigator should test all estimands; the appropriate estimand should be selected a priori based on the primary scientific questions motivating the SMART study.
Acknowledgments
This research was supported by awards P01 AA016821, P60 DA05186, K24 DA029062, R01 DA039901, and P50 DA039838 from the National Institutes of Health. The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding institutions as mentioned above.
Appendix A. Technical Details of Estimating Equations
Estimating Equations for End-of-Study Outcome
We first review the analysis involved in comparing the embedded adaptive interventions (AIs) on an end-of-study outcome from data generated by a prototypical SMART, such as ENGAGE. We assume two randomizations: an initial randomization for all participants, and then a second randomization for participants who did not respond to the initial intervention. The first stage is defined as the time between the first and second randomization, and the second stage is the time from the second randomization to end of study. Further, as in the data analysis discussed in this paper, we assume that intervention options at each stage are dichotomous, resulting in a SMART design having four embedded AIs: , , , and . For simplicity, consider model (1) without the term for the baseline covariates ; let denote any one of the four embedded AIs, and let R indicate whether or not the participant was classified as a responder to first-stage intervention options. Thus, the design matrix row for estimating the expected outcome for someone receiving AI is
The four entries represent the intercept, the first-stage intervention option , the second-stage intervention option , and their product term , which may be interpreted as an interaction. Let denote the column vector ; then denotes the mean of under AI according to model (1).
If there are additional baseline covariates , these could be represented by including additional entries of . To accommodate this possibility, the notation would be expanded to in order to allow the values of the covariates to differ among participants receiving the same treatment, and the vector would be expanded to represent all the regression coefficients for the predictors (i.e., to include the coefficients in addition to the four coefficients mentioned above).
Suppose there are N subjects (note that this is the actual number of original subjects, before weighting and replication). Then, one approach to estimating is to solve for β in the following (Nahum-Shani et al., 2012a):
| (5) |
Notice that there are two summations: the first is a sum over participants, and the second is a sum over the four different embedded AIs being considered. is the weight (either known or estimated) assigned to each individual. The indicator has the value one if individual had observed values of (for responders) or of and (for non-responders), which are compatible with an AI ; it has the value zero otherwise. From this notation, one can see why the data must be replicated in order to use standard generalized estimating equation (GEE) software to solve (5). For example, if participant is a non-responder who receives and , then information from participant will be used only once because, for this participant, is equal to 1, whereas , and are equal to zero. However, if participant is a responder to , then information from this participant can be used twice: once for the AI (1, 1) and again for the AI (1,−1). That is, for this participant both and are equal to 1, whereas and are equal to zero.
As described in the paper, the weights are inverse probability of treatment weights. In the case of the ENGAGE study, this can be written as for non-responders and for responders, where and are the zero-one dummy-coded versions of the effect-coded treatment indicators and , and where , and . Because by design and are each set to 0.5, the known weights, as mentioned in the manuscript, are for responders and for non-responders. Inverse probability weights are often used to adjust for confounding in observational studies (Robins, Hernán, & Brumback, 2000; McCaffrey, Ridgeway & Morral, 2004), but here they are being used for a different reason (recall that this is a randomized trial and hence confounding bias generally is not an issue). Specifically, the weights are being used to adjust for the different representation of responders and non-responders in the analysis of the experimental data (Nahum-Shani et al., 2012a; Lu et al, 2016).
Even though the assignment probabilities and are known, there are some statistical advantages to treating them as quantities to be estimated. In this approach, logistic regressions can be used to produce the weights by predicting the intervention assignment probabilities at each stage of the trial using covariates. This has the potential to improve efficiency as explained in the body of the manuscript and demonstrated in Online Supplement A (https://github.com/dziakj1/SmartTutorialAppendix). To accomplish this, the probabilities , where represents the covariates available prior to first-stage randomization, are estimated for the first-stage randomization for all participants. Also, for non-responders (i.e., re-randomized individuals), the probabilities are estimated, where represents the covariates available prior to the second-stage randomization. The covariates included for predicting need not be the same as the covariates used for predicting . It is important to note that only covariates that are known prior to first-stage randomization should be used for predicting , but can additionally be predicted by covariates that are known by the second-stage randomization.
The estimated weight for an individual is then the product of the inverse of that individual’s predicted probability of treatment assignment. Thus, in a study like ENGAGE, the estimated weights would be for non-responders and for responders, similar to the expression for the known weights except for using estimates and instead of known values and .
Estimating Equations for Repeated Outcome Measures
Now suppose that there are measurements of the outcome at multiple time points. Let be the vector of outcomes for the ith participant,. Again, note that N is the actual number of participants (not the total number of rows after replication). In the example used in this tutorial paper, there are three equally spaced measurement outcomes, so .
Let be the design matrix corresponding to the repeated measures model. As above, we assume that intervention options are dichotomous, so that there are four AIs to consider: , , , and . For example, if model (3) is used and no baseline covariates are included in the model, then
The three rows correspond to observation times 1, 2, and 3. The seven columns represent the intercept and the covariates , , , , , and . and represent time since the beginning of the study, separated into stage-one time and stage-two time as described in the paper. As before, if the investigator wishes to include additional baseline covariates in the model, these would be represented by additional columns of , and the notation would be replaced by because the values of the covariates would differ between participants.
Let be the working correlation matrix assumed for the errors at times 1, 2, and 3, as in GEE (Liang & Zeger, 1986). For independence working correlation structure with three measurement times,
For AR-1 (autoregressive of order one) structure with three equally spaced measurement times,
where the correlation coefficient is estimated using the method of moments as in GEE (see Liang & Zeger, 1986). To avoid confusion, note that in this paper, is used for the working correlation matrix in accordance with the conventional notation in the GEE context, is used for the binary variable indicating responder status in accordance with conventional notation in the SMART context, and R is used as the name of the software package (R Core Team, 2015).
A straightforward approach to estimating the unknown parameters in a model such as Model (3) is to solve the following set of estimating equations:
| (6) |
As before, there are two summations: the first is a sum over participants, and the second is a sum over the four different AIs being considered. is the weight (either known or estimated as described earlier) that is assigned to each individual. is coded as one if individual had observed values of (for responders) or of and (for non-responders) compatible with , and as zero otherwise. As before, this notation operationalizes the weighting and replication idea in a single set of equations. Lastly, represents the regression coefficients for the covariates .
Note that the estimating equations in Expression (5) are a special case of the estimating equations in Expression (6). If only a single outcome measurement at the end of the study (or following exposure to both stages of the AIs being compared) is used, then the vector and matrix in Expression (6) would reduce to the scalar and vector in Expression (5), and the correlation matrix , which appears in Expression (6), would be replaced by 1 because a variable has correlation 1 with itself. Therefore, we now only use the more general estimating equations in Expression (6) as we further describe how asymptotic standard error estimates can be computed for estimands of interest.
Covariance of the Estimated Regression Coefficients when Known Weights Are Used
As in GEE (Liang & Zeger, 1986), standard errors for the regression coefficients in (6) can be obtained by using a sandwich estimator. For linear models with continuous outcomes,
is individual i’s contribution to the GEE score function for . The score function (also known as the estimating function) is the vector that is being set to zero in order to solve for the estimated coefficients , so that (6) becomes .
If weights are known by design, the GEE sandwich estimator for is given (see Lu et al, 2016) by , where
and
The formula above assumes known weights. If weights are estimated using covariates, a slightly more complicated formula (leading to narrower confidence intervals) can be used, as described below.
Covariance of the Estimated Regression Coefficients When Estimated Weights are Used
The use of estimated weights may reduce sampling variability in the estimated longitudinal model parameters. Lu and colleagues (2016) show that this can be taken into account in the estimation of the standard errors to produce narrower confidence intervals by using a simple adjustment. They replace with
where is the score function (estimating equations) used in the logistic regression to determine the treatment probabilities. The subtracted quantity is nonnegative definite, so it tends to reduce the values in and therefore in , hence tending to reduce the standard errors.
The score function in logistic regression is the first derivative of the logistic log-likelihood in the logistic regression parameters (see Powers & Xie, 2008, for more technical details on logistic regression estimation). Because there are two treatment assignment stages to be predicted, one way to construct the weights is via two logistic regressions, each including a distinct (but potentially overlapping) set of covariates: covariates for predicting first-stage treatment assignment and covariates for predicting second-stage treatment assignment. To follow the conventions of logistic regression, assume that the treatment assignments here are dummy coded instead of effect coded; for example, define if , and if . The individual contributions to the first-stage logistic regression score functions are , where is the logistic regression fitted value for . Similarly, for non-responders, the individual contributions to the stage-two logistic regression score functions are , where is the logistic regression fitted value for among non-responders. is zero for responders because there is no second treatment assignment to be predicted in their case. The overall score function is the concatenation of with , so that solving solves both and .
Standard Errors of Contrasts of Interest
As described above, can be estimated by , adjusting if necessary when the weights are estimated. The standard errors for the GEE regression coefficients can be computed as as usual. However, it is usually not these coefficients that are of interest to researchers interpreting longitudinal data arising from a SMART. Instead, as argued in this paper, contrasts in outcomes in areas under the curve or in slopes are more practically interpretable. In linear models for normally distributed outcomes, each of these quantities can be estimated as linear combinations of the regression coefficients for some vector of contrast coefficients . The vector of all of the estimands of interest can therefore be written as , where each row of the matrix contains the contrast coefficients for one of the estimands. As usual, the estimates for can be calculated as , their covariance is , and their estimated standard errors are . Many examples of contrast coefficient sets, which could be interesting in various settings, are provided in the sample code (see online supplementary materials).
Appendix B. Summary of R and SAS Code for Estimating Contrasts of Interest
In this appendix, we explain how the methods described in the paper can be implemented using conventional statistical software. It would also be possible to write special software specifically for fitting longitudinal SMART models, but the approach provided here is very practical for SAS and R users. For simplicity, the code provided here only implements the method with rather simple working covariance structures that do not take advantage of possible heterogeneity between individuals over time or across the embedded adaptive interventions (AIs). However, the method can be readily extended to implement more general working covariance structures. In order to illustrate the analyses proposed in this paper, a simulated dataset and analysis code are available as an online supplement. They can be downloaded at https://github.com/dziakj1/SmartTutorialAppendix. SAS code is provided for analyzing the data using a working independence correlation structure. R code is provided for analyzing the data using either independence, AR-1, or unstructured working correlation.
For independence working correlation structure, the process is straightforward. The weighting and replication is performed using DATA steps in SAS, or using analogous code in R. Then a GEE model is fit to the weighted and replicated data, using PROC GENMOD in SAS or the geepack package in the R software environment (R Core Team, 2015; Højsgaard, Halekoh, & Yan, 2005). The coefficients from the GEE model are then used to compute and test the linear contrasts of interest. This is done by using the ESTIMATE statement in PROC GENMOD or by using matrix algebra in the R software environment.
Below, we provide example SAS code and detailed guidelines for implementing the method with a simulated dataset based on the first three measurement occasions of the ENGAGE trial. The simulated dataset, named ‘TutorialDatasetWideFormat’ is provided in the online appendix. For simplicity, the method is employed with an independence working correlation structure.
/* Calculate weights: the variable ‘Weight’ created with the code below includes the value 2 for responders and 4 for non-responders. */ DATA TutorialDatasetWideFormat; SET TutorialDatasetWideFormat; WeightRandomization1 = 2; IF (R = 0) THEN WeightRandomization2 = 2; ELSE WeightRandomization2 = 1; Weight = WeightRandomization1 * WeightRandomization2; RUN; /* Change the original dataset into a long-format data: The original data is in short format, namely there is one line per participant and three variables including the outcome at month 1 (Y1), month 2 (Y2) and month 3 (Y3). This code transforms the original data into a long format data where each participant has three observations for time 1, 2, and 3, similar to the unmodified data layout in Table 4 */ DATA TutorialDatasetLongFormat; SET TutorialDatasetWideFormat; Time = 1; Y = Y1; OUTPUT; Time = 2; Y = Y2; OUTPUT; Time = 3; Y = Y3; OUTPUT; KEEP SubjectID Weight Time A1 R A2 Y; RUN; /* Create the piecewise indicators S1 and S2: S1 is time since the beginning of the study, truncated above at 1; that is, the total amount of time spent so far in Stage 1. S2 is time since the second randomization, truncated below at 0; that is, the total amount of time spent so far in Stage 2. Note: S1 + S2 = Time - 1, that is, time since the beginning of the study. */ DATA TutorialDatasetLongFormat; SET TutorialDatasetLongFormat; IF Time > 2 THEN S1 = 1; ELSE S1 = Time - 1; IF Time > 2 THEN S2 = Time - 2; ELSE S2 = 0; RUN; /* Replication: The code below creates a new dataset, named ‘DataForAnalysis’, in which observations of responders (those with R=0) are replicated, similar to the Weighted and Replicated data layout with piecewise indicators example in Table 4 */ DATA PlusOneReplicates; SET TutorialDatasetLongFormat; /* First create a new dataset ‘PlusOneReplicates’, based on the original long-format dataset*/ WHERE R = 1; /* The new dataset will only include responders (i.e., those with R=1)*/ A2 = +1; /* Set A2 to equal +1 for these observations*/ Wave = Time; /* Make a new copy of Time here, named Wave, because we are going to count replicates as different waves. */ RUN; DATA MinusOneReplicates; SET TutorialDatasetLongFormat; /* Second, create a new dataset ‘MinusOneReplicates’, based on the original long-format dataset*/ WHERE R = 1; /* The new data will only include responders (i.e., those with R=1)*/ A2 = −1; /* Set A2 to equal −1 for these observations*/ Wave = Time + 3; /* Make a new copy of Time here, named Wave, because we are going to count replicates as different waves. */ RUN; DATA RowsNotToReplicate; SET TutorialDatasetLongFormat; /* Third, create a new dataset ‘RowsNotToReplicate’, based on the original long-format dataset*/ WHERE R = 0; /* The new data will only include non-responders (i.e., those with R=0)*/ Wave = Time; /* Make a new copy of Time here, named Wave, because we are going to count replicates as different waves. */ RUN; DATA DataForAnalysis; SET PlusOneReplicates MinusOneReplicates RowsNotToReplicate; /* Finally, combine all three datasets into a new dataset named DataForAnalysis*/ RUN; PROC SORT DATA=DataForAnalysis; /* and sort the new dataset by subject id and Wave*/ BY SubjectID Wave; RUN; /* Perform analysis using Generalized Estimating Equations */ PROC GENMOD DATA=DataForAnalysis; /* Call the GENMOD procedure and specify the working dataset*/ CLASS SubjectID; /* Specify the participant’s identification number (SubjectID) as a categorical variable*/ MODEL Y = S1 S2 S1*A1 S2*A1 S2*A2 S2*A1*A2; /* Specify the model to be estimated, identifying the outcome and the independent variables consistent with Model (3)*/ REPEATED SUBJECT=SubjectID; /* The program will provide robust standard errors for the model parameters when the option REPEATED is included with the participant identification number SUBJECT=SubjectID)*/ WEIGHT Weight; /* Specify the variable that contains the weights in the data*/ /* The series of ESTIMATE statements below specify the comparisons between the adaptive interventions based on the estimated coefficients*/ /* To estimate time-specific means: In the model statement above, we assumed that E(Y) = B0 + B1*S1 + B2*S2 + B3*S1*A1 + B4*S2*A1 + B5*S2*A2 + B6*S2*A1*A2. Hence, At time 1, S1=0 and S2=0, so E(Y) = B0. At time 2, S1=1 and S2=0, so E(Y) = B0 + B1 + B3*A1. At time 3, S1=1 and S2=1, so E(Y) = B0 + B1 + B2 + B3*A1 + B4*A1 + B5*A2 + B6*A1*A2. Substituting the different possible values of A1 and A2 into these equations, we find that the coefficients representing the time-specific means are as given below. Note that the text inside the quotation marks in the Estimate statements below is simply the name or the title the data analyst assigns to each specific estimated linear combination of regression parameters*/ ESTIMATE “Time 1 Mean for Any AI” INTERCEPT 1 S1 0 S2 0 S1*A1 0 S2*A1 0 S2*A2 0 S2*A1*A2 0; ESTIMATE “Time 2 Mean for AI ++ or AI +-” INTERCEPT 1 S1 1 S2 0 S1*A1 +1 S2*A1 0 S2*A2 0 S2*A1*A2 0; ESTIMATE “Time 2 Mean for AI -+ or AI --” INTERCEPT 1 S1 1 S2 0 S1*A1 −1 S2*A1 0 S2*A2 0 S2*A1*A2 0; ESTIMATE “Time 3 Mean for AI ++” INTERCEPT 1 S1 1 S2 1 S1*A1 +1 S2*A1 +1 S2*A2 +1 S2*A1*A2 +1; ESTIMATE “Time 3 Mean for AI +-” INTERCEPT 1 S1 1 S2 1 S1*A1 +1 S2*A1 +1 S2*A2 −1 S2*A1*A2 −1; ESTIMATE “Time 3 Mean for AI -+” INTERCEPT 1 S1 1 S2 1 S1*A1 −1 S2*A1 −1 S2*A2 +1 S2*A1*A2 −1; ESTIMATE “Time 3 Mean for AI --” INTERCEPT 1 S1 1 S2 1 S1*A1 −1 S2*A1 −1 S2*A2 −1 S2*A1*A2 +1; /* To estimate contrasts in time-Specific means: Recall that based on the model above, the difference in expected outcome between any pair of AIs (a1,a2) and (a1’,a2’) is B3*(a1-a1’)at time 2; and B3*(a1-a1’) + B4*(a1-a1’) + B5*(a2-a2’) + B6*(a1a2-a1’a2’) at time 3. Use these terms to specify the corresponding coefficients for each pair of AIs or subtract the corresponding coefficients representing each pair of time-specific means, as follows: */ ESTIMATE “Time 2 Mean AIs starting with + vs. AIs starting with - “ INTERCEPT 0 S1 0 S2 0 S1*A1 +2 S2*A1 0 S2*A2 0 S2*A1*A2 0; ESTIMATE “Time 3 Mean, AI ++ vs. AI +-” INTERCEPT 0 S1 0 S2 0 S1*A1 0 S2*A1 0 S2*A2 +2 S2*A1*A2 +2; ESTIMATE “Time 3 Mean, AI ++ vs. AI -+” INTERCEPT 0 S1 0 S2 0 S1*A1 +2 S2*A1 +2 S2*A2 0 S2*A1*A2 +2; ESTIMATE “Time 3 Mean, AI ++ vs. AI --” INTERCEPT 0 S1 0 S2 0 S1*A1 +2 S2*A1 +2 S2*A2 +2 S2*A1*A2 0; ESTIMATE “Time 3 Mean, AI +- vs. AI -+” INTERCEPT 0 S1 0 S2 0 S1*A1 +2 S2*A1 +2 S2*A2 −2 S2*A1*A2 0; ESTIMATE “Time 3 Mean, AI +- vs. AI --” INTERCEPT 0 S1 0 S2 0 S1*A1 +2 S2*A1 +2 S2*A2 0 S2*A1*A2 −2; ESTIMATE “Time 3 Mean, AI -+ vs. AI --” INTERCEPT 0 S1 0 S2 0 S1*A1 0 S2*A1 0 S2*A2 +2 S2*A1*A2 −2; /* To estimate stage-specific slopes: Recall that based on the model specified above, B1 + B3*A1 is the first-stage slope; and B2 + B4*A1 + B5*A2 + B6*A1*A2 is the second-stage slope. Substituting the different possible values of A1 and A2 into these terms, we find that the coefficients representing the time-specific slopes are as given below.*/ ESTIMATE “Stage 1 Slop for AI ++ or AI +-” INTERCEPT 0 S1 1 S2 0 S1*A1 +1 S2*A1 0 S2*A2 0 S2*A1*A2 0; ESTIMATE “Stage 1 Slope for AI -+ or AI --” INTERCEPT 0 S1 1 S2 0 S1*A1 −1 S2*A1 0 S2*A2 0 S2*A1*A2 0; ESTIMATE “Stage 2 Slope for AI ++” INTERCEPT 0 S1 0 S2 1 S1*A1 0 S2*A1 +1 S2*A2 +1 S2*A1*A2 +1; ESTIMATE “Stage 2 Slope for AI +-” INTERCEPT 0 S1 0 S2 1 S1*A1 0 S2*A1 +1 S2*A2 −1 S2*A1*A2 −1; ESTIMATE “Stage 2 Slope for AI -+” INTERCEPT 0 S1 0 S2 1 S1*A1 0 S2*A1 −1 S2*A2 +1 S2*A1*A2 −1; ESTIMATE “Stage 2 Slope for AI --” INTERCEPT 0 S1 0 S2 1 S1*A1 0 S2*A1 −1 S2*A2 −1 S2*A1*A2 +1; /* To contrast stage-specific slopes: */ Recall that based on the model specified above, the expected difference between any two embedded AIs, (a1, a2) and (a1’, a2’) is B3*(a1-a1’)in terms of first-stage slopes; and B4*(a1-a1’)+B5*(a2-a2’)+B6*(a1a2-a1’a2’) in terms of second-stage slopes. Use these terms to specify the corresponding coefficients for each pair of AIs as follows: */ ESTIMATE “Stage 2 Slope, AI ++ vs. AI +-” INTERCEPT 0 S1 0 S2 0 S1*A1 0 S2*A1 0 S2*A2 +2 S2*A1*A2 +2; ESTIMATE “Stage 2 Slope, AI ++ vs. AI -+” INTERCEPT 0 S1 0 S2 0 S1*A1 0 S2*A1 +2 S2*A2 0 S2*A1*A2 +2; ESTIMATE “Stage 2 Slope, AI ++ vs. AI --” INTERCEPT 0 S1 0 S2 0 S1*A1 0 S2*A1 +2 S2*A2 +2 S2*A1*A2 0; ESTIMATE “Stage 2 Slope, AI +- vs. AI -+” INTERCEPT 0 S1 0 S2 0 S1*A1 0 S2*A1 +2 S2*A2 −2 S2*A1*A2 0; ESTIMATE “Stage 2 Slope, AI +- vs. AI --” INTERCEPT 0 S1 0 S2 0 S1*A1 0 S2*A1 +2 S2*A2 0 S2*A1*A2 −2; ESTIMATE “Stage 2 Slope, AI -+ vs. AI --” INTERCEPT 0 S1 0 S2 0 S1*A1 0 S2*A1 0 S2*A2 +2 S2*A1*A2 −2; /* Note that contrasts in stage 1 slopes are omitted here because in this particular case they the same as contrasts in time 2 means, provided that time 1 means are assumed to be the same. Contrasts in stage 2 slopes must be interpreted with great caution, because the means at the end of stage 1 are *not* necessarily the same, and so a high stage 2 slope could represent a high time-3 mean, a low time-2 mean, or both. */ /* To estimate the area under the curve (AUC): Recall that the AUC between time 1 and time 2 is approximated as the area of a trapezoid with base length 1, left-side height E(Y1), and right-side height E(Y2). The AUC between time 2 and time 3 is approximated as the area of a trapezoid with base 1, left-side height E(Y2), and right-side height E(Y3). Thus, the total area is (E(Y1)+E(Y2))/2 + (E(Y2)+E(Y3))/2 = 0.5*E(Y1) + E(Y2) + 0.5*E(Y3)= 2*B0 + 1.5*B1 + 0.5*B2 + 1.5*B3*A1 + 0.5*B4*A1 + 0.5*B5*A2 + 0.5*B6*A1*A2 Substituting the different possible values of A1 and A2 into this equation, we find that the coefficients representing the AUC for each AI are as given below. */ ESTIMATE “AUC for AI ++” INTERCEPT 2 S1 1.5 S2 0.5 S1*A1 +1.5 S2*A1 +0.5 S2*A2 +0.5 S2*A1*A2 +0.5; ESTIMATE “AUC for AI +-” INTERCEPT 2 S1 1.5 S2 0.5 S1*A1 +1.5 S2*A1 +0.5 S2*A2 −0.5 S2*A1*A2 −0.5; ESTIMATE “AUC for AI -+” INTERCEPT 2 S1 1.5 S2 0.5 S1*A1 −1.5 S2*A1 −0.5 S2*A2 +0.5 S2*A1*A2 −0.5; ESTIMATE “AUC for AI --” INTERCEPT 2 S1 1.5 S2 0.5 S1*A1 −1.5 S2*A1 −0.5 S2*A2 −0.5 S2*A1*A2 +0.5; /* To estimate contrasts in AUCs: Recall that based on the model specified above, the expected difference between any two embedded AIs, denoted as (a1, a2) and (a1’, a2’) is 1.5*B3*(a1-a1’)+0.5*B4*(a1-a1’)+0.5*B5*(a2-a2’)+0.5*b6*(a1a2-a1’a2’). Use this term to specify the corresponding coefficients for each pair of AIs as follows: */ ESTIMATE “AUC AI ++ vs. AI +-” INTERCEPT 0 S1 0 S2 0 S1*A1 0 S2*A1 0 S2*A2 −1 S2*A1*A2 +1; ESTIMATE “AUC, AI ++ vs. AI -+” INTERCEPT 0 S1 0 S2 0 S1*A1 3 S2*A1 1 S2*A2 0 S2*A1*A2 +1; ESTIMATE “AUC AI ++ vs. AI --” INTERCEPT 0 S1 0 S2 0 S1*A1 3 S2*A1 1 S2*A2 +1 S2*A1*A2 0; ESTIMATE “AUC AI +- vs. AI -+” INTERCEPT 0 S1 0 S2 0 S1*A1 3 S2*A1 1 S2*A2 −1 S2*A1*A2 0; ESTIMATE “AUC AI +- vs. AI --” INTERCEPT 0 S1 0 S2 0 S1*A1 3 S2*A1 1 S2*A2 0 S2*A1*A2 −1; ESTIMATE “AUC AI +- vs. AI --” INTERCEPT 0 S1 0 S2 0 S1*A1 3 S2*A1 1 S2*A2 0 S2*A1*A2 −1; /* To obtain estimates for average AUC (=area under curve/time), because our example is two time units (months) long, that is, from time one to time three, simply divide the estimated AUC by two. The p-values for the average AUC contrasts will be the same as the contrasts in AUC above, because they are only rescaled versions of the same quantity. However, the estimates will of course be rescaled. */ /* To estimate delayed effects: Recall that the delayed effect of one AI relative to another is the difference between the contrast of the time-3 means and the contrast of the time-2 means for these AIs. Based on the model specified above, for any two embedded AIs (a1, a2) and (a1’, a2’) that begin with different initial intervention options, this would be: B4*(a1-a1’) + B5*(a2-a2’) + B6(a1a2-a1’a2’). Use this term to specify the corresponding coefficients for each pair of AIs that begin with different initial treatment as follows: ESTIMATE “Delayed Effect AI ++ vs. AI -+” INTERCEPT 0 S1 0 S2 0 S1*A1 0 S2*A1 +2 S2*A2 0 S2*A1*A2 +2; ESTIMATE “Delayed Effect AI ++ vs. AI --” INTERCEPT 0 S1 0 S2 0 S1*A1 0 S2*A1 +2 S2*A2 +2 S2*A1*A2 0; ESTIMATE “Delayed Effect AI +- vs. AI -+” INTERCEPT 0 S1 0 S2 0 S1*A1 0 S2*A1 +2 S2*A2 −2 S2*A1*A2 0; ESTIMATE “Delayed Effect AI +- vs. AI --” INTERCEPT 0 S1 0 S2 0 S1*A1 0 S2*A1 +2 S2*A2 0 S2*A1*A2 −2; /* Note that this is not calculated here for two AIs that begin with the same initial treatment because the delayed effect then simplifies to being the same as the contrast of the time-3 means. RUN;
As noted earlier, this sample SAS code employs the method with an independence working correlation structure. The working AR-1 structure, which is straightforward to use in an ordinary application of GEE, is somewhat more complicated to implement when using a weighted and replicated dataset. For example, for responders, if there are three repeated outcome measurements, there are actually six rows of data per participant. The second three do not occur later in time than the first three; instead, they are replicates as described in the paper. Therefore, an ordinary AR-1 structure with six measurement times would not be reasonable. To avoid this, when implementing the method with conventional software, Lu and colleagues (2016) suggested fitting a block structure like the following:
The upper left block, consisting of the first three rows and columns above, represents the replicates for , and the lower right block represents the replicates for . Observations from non-responders (who are not replicated) are represented by the first block only. Thus the sets of replicates are treated as independent of each other, but AR-1 holds within each set. Because this is not one of the well-known structures available as a default option in GENMOD or geepack, some extra coding is required. One approach, shown in the R code (see online supplement), is to calculate the method of moments estimate for and then provide the estimated correlation matrix as a constant matrix to GENMOD or geepack. If this approach is used, it is important to be very careful with the indexing and sorting of the data, especially if any data are missing, in order to assure that lags between rows always have a consistent meaning (e.g., to ensure that time 3 is not misinterpreted as time 2 for subjects who are missing time 2). For simplicity, in the sample AR-1 code it is assumed that there are no missing data or that multiple imputation has been used to replace any previously missing data.
In addition to AR-1 structure, other correlation assumptions could be used within blocks. For example, an unstructured correlation matrix within blocks would involve the estimation of three correlation parameters:
At first, it might seem as though certain off-diagonal correlations, such as the fourth entry in the first row (the correlation between time 1 responses of two replicates of the same individual) ought to be 1 instead of 0, because they refer to the same observed data. However, this would likely cause computational and interpretational problems. This is because even though the observed values may be necessarily the same for the two replicates, they correspond to different AIs and , and therefore represent deviations from different means and . Thus, the implied residuals have different values even though the observed data is the same. Thus, it is best to consider the two outcomes from the same person as independent given the person’s covariates, as is often done for counterfactuals in causal analysis.
Sample analysis code is also included for creating estimated weights. The probability of assignment to can be predicted from baseline covariates and optionally from . The probability of assignment to can additionally include . Of course, to avoid confounding, later outcomes should not be included as covariates for predicting earlier treatments. Standard errors need to be adjusted when using estimated weights, as described earlier.
Appendix C
An Alternative Way to Express for Model (3)
In this section we demonstrate how model (3) can be presented as a k -group model, where k is the number of embedded AIs being compared-- four in our example. Using indicator coding (i.e., dummy coding), k-1 dummy variables can be constructed. In our example this is (, , ), with set to 1 if the observation is consistent with AI #1 (later choice), and 0 otherwise, set to 1 if the observation is consistent with AI #2 (choice throughout), and 0 otherwise, and D3 set to 1 if the observation is consistent with AI #3 (no choice), and 0 otherwise. AI #4 (initial choice) is not explicitly coded, such that all k – 1 dummy variables are set to 0 for observations consistent with AI #4. This AI functions as the reference category in the analysis. Using these dummy coded variables, model (3) can be written as follows:
Based on this model, the trajectory of treatment readiness can be obtained for each of the four embedded AIs. Specifically, for individuals consistent with AI #1, the first-stage slope is and the second-stage slope is ; for individuals consistent with AI #2, the first-stage slope is and the second-stage slope is ; for individuals consistent with AI #3, the first-stage slope is and the second-stage slope is , and for individuals consistent with AI #4, the first-stage slope is and the second-stage slope is .
In order to make the model interpretable in the context of the experimental design, cross-group constraints can be used on parameters that, by design, should not differ. Specifically, since AI #2 and AI #4 begin with the same initial intervention option, namely MI-PC, these AIs should not differ in terms of first-stage slopes. This can be accommodated by constraining model parameters such that , meaning that and represents the first-stage slope of both AI #2 and AI #4. Similarly, A1 #1 and AI #3 should not differ in terms of first-stage slope since they both begin with MI-IOP. This can be accommodated by constraining model parameters such that , meaning that . We represent the latter combined parameter as , which is the difference in first-stage slopes between AIs beginning with MI-IOP (AI #1 and AI #3) and those beginning with MI-PC (AI #2 and AI #4). With these constraints, the model above can be re-expressed as
Notice that this model includes exactly the same number of parameters as in model (3), specifically six in our example, and has an analogous interpretation as a marginal longitudinal model predicting how the outcome changes over time, on average, had all individuals in the population been offered a particular AI. Based on this model, various estimands of scientific interest can be obtained via linear combinations of the regression coefficients. The same fitted values for the estimands could be obtained using either formulation, but a different set of linear coefficients would be required. Note that if significance tests for main effects of the first-stage , and second-stage intervention options, and the interaction between them, are of scientific interest (this is often the case in SMART studies; see Lei et al., 2012), then the formulation in model (3) may be easier to use because it explicitly contains the effect-coded , and their product term.
Footnotes
Analysis was done using R (copyright 2017 by The R Foundation for Statistical Computing) and SAS (copyright 2013 by SAS Foundation, Inc., Cary, NC, USA) software.
Contributor Information
Inbal Nahum-Shani, Institute of Social Research, University of Michigan.
Daniel Almirall, Institute of Social Research and Department of Statistics, University of Michigan.
Jamie Yap, Institute of Social Research, University of Michigan.
James R. McKay, Department of Psychiatry, University of Pennsylvania and Philadelphia Veterans Affairs Medical Center
Kevin G. Lynch, Department of Psychiatry, University of Pennsylvania
Elizabeth A. Freiheit, Institute of Social Research, University of Michigan
John J. Dziak, The Methodology Center, College of Health and Human Development, Pennsylvania State University
References
- Almirall D, DiStefano C, Chang Y-C, Shire S, Kaiser A, Lu X, … Kasari C (2016). Longitudinal effects of adaptive interventions with a speech-generating device in minimally verbal children with ASD. Journal of Clinical Child & Adolescent Psychology, 45(4), 442–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almirall D, Nahum-Shani I, Sherwood NE, & Murphy SA (2014). Introduction to SMART designs for the development of adaptive interventions: with application to weight loss research. Translational behavioral medicine, 4(3), 260–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almirall D, Nahum-Shani I, Wang L, Kasari C (2018) Experimental Designs for Research on Adaptive Interventions: Singly and Sequentially Randomized Trials In: Collins L, Kugler K (eds) Optimization of Behavioral, Biobehavioral, and Biomedical Interventions. Statistics for Social and Behavioral Sciences. Springer, Cham [Google Scholar]
- Appelhans BM, French SA, Pagoto SL, & Sherwood NE (2016). Managing temptation in obesity treatment: a neurobehavioral model of intervention strategies. Appetite, 96, 268–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakker AB (2011). An evidence-based model of work engagement. Current Directions in Psychological Science, 20(4), 265–269. [Google Scholar]
- Bauer DJ, Preacher KJ, & Gil KM (2006). Conceptualizing and testing random indirect effects and moderated mediation in multilevel models: new procedures and recommendations. Psychological methods, 11(2), 142. [DOI] [PubMed] [Google Scholar]
- Christensen A, Atkins DC, Yi J, Baucom DH, & George WH (2006). Couple and individual adjustment for 2 years following a randomized clinical trial comparing traditional versus integrative behavioral couple therapy. Journal of Consulting and Clinical Psychology, 74(6), 1180. [DOI] [PubMed] [Google Scholar]
- Collins LM (2018). Optimization of Behavioral, Biobehavioral, and Biomedical Interventions: The Multiphase Optimization Strategy (MOST). Springer. [Google Scholar]
- Collins LM, Murphy SA, & Bierman KL (2004). A conceptual framework for adaptive preventive interventions. Prevention Science, 5(3), 185–196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connell AM, Dishion TJ, Yasui M, & Kavanagh K (2007). An adaptive approach to family intervention: Linking engagement in family-centered intervention to reductions in adolescent problem behavior. Journal of Consulting and Clinical Psychology, 75, 568–579. [DOI] [PubMed] [Google Scholar]
- Connor CM, Morrison FJ, Schatschneider C, Toste JR, Lundblom E, Crowe EC, & Fishman B (2011). Effective classroom instruction: Implications of child characteristics by reading instruction interactions on first graders’ word reading achievement. Journal of Research on Educational Effectiveness, 4, 173–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eden D (2017). Field Experiments in Organizations. Annual Review of Organizational Psychology and Organizational Behavior, 4, 91–122. [Google Scholar]
- Ertefaie A, Wu T, Lynch KG, & Nahum-Shani I (2015). Identifying a set that contains the best dynamic treatment regimes. Biostatistics, 17(1):135–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fekedulegn DB, Andrew ME, Burchfiel CM, Violanti JM, Hartley TA, Charles LE, & Miller DB (2007). Area under the curve and other summary indicators of repeated waking cortisol measurements. Psychosomatic Medicine, 69(7), 651–659. [DOI] [PubMed] [Google Scholar]
- Flora DB (2008). Specifying piecewise latent trajectory models for longitudinal data. Structural Equation Modeling, 15, 513–533. [Google Scholar]
- Gunlicks-Stoessel M, Mufson L, Westervelt A, Almirall D, & Murphy S (2016). A pilot SMART for developing an adaptive treatment strategy for adolescent depression. Journal of Clinical Child & Adolescent Psychology, 45(4), 480–494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernan MA, Brumback BA, & Robins JM (2002). Estimating the causal effect of zidovudine on CD4 count with a marginal structural model for repeated measures. Stat Med, 21(12), 1689–1709. [DOI] [PubMed] [Google Scholar]
- Hirano K, Imbens GW, & Ridder G (2003). Efficient estimation of average treatment effects using the estimated propensity score. Econometrica, 71(4), 1161–1189. [Google Scholar]
- Højsgaard S, Halekoh U, & Yan J (2005). The R Package geepack for generalized estimating equations. Journal of Statistical Software, 15, 10.18637/jss.v015.i02. [DOI] [Google Scholar]
- Institute of Behavioral Research (2007). TCU Treatment Needs and Motivation (TCU MOTForm). Fort Worth: Texas Christian University, Institute of Behavioral Research; Available at: ibr.tcu.edu [Google Scholar]
- Kernan WN, Viscoli CM, Makuch RW, Brass LM, & Horwitz RI (1999). Stratified randomization for clinical trials. Journal of Clinical Epidemiology, 52(1), 19–26. [DOI] [PubMed] [Google Scholar]
- Kohli N, Sullivan AL, Sadeh S, & Zopluoglu C (2015). Longitudinal mathematics development of students with learning disabilities and students without disabilities: A comparison of linear, quadratic, and piecewise linear mixed effects models. Journal of School Psychology, 53(2), 105–120. [DOI] [PubMed] [Google Scholar]
- Ladd GW, & Dinella LM (2009). Continuity and change in early school engagement: Predictive of children’s achievement trajectories from first to eighth grade?. Journal of Educational Psychology, 101(1), 190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavori PW, & Dawson R (2000). A design for testing clinical strategies: biased adaptive within‐subject randomization. Journal of the Royal Statistical Society: Series A (Statistics in Society), 163(1), 29–38. [Google Scholar]
- Lavori PW, & Dawson R (2004). Dynamic treatment regimes: practical design considerations. Clinical trials, 1(1), 9–20. [DOI] [PubMed] [Google Scholar]
- Lavori PW, & Dawson R (2014). Introduction to dynamic treatment strategies and sequential multiple assignment randomization. Clinical Trials, 11(4), 393–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavori PW, & Dawson R (2014). Introduction to Dynamic Treatment Strategies and Sequential Multiple Assignment Randomization. Clinical trials, 11(4), 393–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lei H, Nahum-Shani I, Lynch K, Oslin D, & Murphy S (2012). A “SMART” design for building individualized treatment sequences. Annual review of clinical psychology, 8, 21–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang K-Y, & Zeger SL (1986). Longitudinal data analysis using generalized linear models. Biometrika, 73, 13–22. [Google Scholar]
- Lu X, Nahum-Shani I, Kasari C, Lynch K, Oslin D, Pelham W, … Almirall D (2016). Comparing dynamic treatment regimes using repeated-measures outcomes: modeling considerations in SMART studies. Statistics in medicine, 35(10), 1595–1615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews J, Altman DG, Campbell MJ, & Royston P (1990). Analysis of serial measurements in medical research. BMJ, 300(6719), 230–235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCaffrey DF, Ridgeway G, & Morral AR (2004). Propensity score estimation with boosted regression for evaluating causal effects in observational studies. Psychological Methods, 9: 403–425. [DOI] [PubMed] [Google Scholar]
- McKay JR, Drapkin ML, Van Horn DH, Lynch KG, Oslin DW, DePhilippis D, … Cacciola JS (2015). Effect of patient choice in an adaptive sequential randomization trial of treatment for alcohol and cocaine dependence. Journal of consulting and clinical psychology, 83(6), 1021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy SA (2003). Optimal Dynamic Treatment Regimes. Journal of the Royal Statistical Society, Series B (with discussion), 65(2), 331–366. [Google Scholar]
- Murphy SA (2005). An experimental design for the development of adaptive treatment strategies. Statistics in Medicine, 24(10), 1455–1481. [DOI] [PubMed] [Google Scholar]
- Myers JL, Well A, & Lorch RF (2010). Research Design and Statistical Analysis (3rd ed.) New York: Routledge. [Google Scholar]
- Naar-King S, Ellis DA, Idalski Carcone A, Templin T, Jacques-Tiura AJ, Brogan Hartlieb K, … Jen KL (2016). Sequential Multiple Assignment Randomized Trial (SMART) to Construct Weight Loss Interventions for African American Adolescents. J Clin Child Adolesc Psychol, 45(4), 428–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nahum-Shani I, Qian M, Almirall D, Pelham WE, Gnagy B, Fabiano G, … Murphy SA (2012a). Experimental design and primary data analysis for developing adaptive interventions. Psychological Methods, 17(4), 457–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nahum-Shani I, Qian M, Almirall D, Pelham WE, Gnagy B, Fabiano GA, … Murphy SA (2012b). Q-learning: A data analysis method for constructing adaptive interventions. Psychological Methods, 17(4), 478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nahum-Shani I, Hekler E, & Spruijt-Metz D (2015). Building health behavior models to guide the development of just-in-time adaptive interventions: a pragmatic framework. Health Psychology, 34(Supp), 1209–1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orellana L, Rotnitzky A, & Robins JM (2010). Dynamic regime marginal structural mean models for estimation of optimal dynamic treatment regimes, Part I: main content. The International Journal of Biostatistics, 6(2), Article 8. [PubMed] [Google Scholar]
- Pelham WE Jr, Fabiano GA, Waxmonsky JG, Greiner AR, Gnagy EM, Pelham WE III, … Hart K (2016). Treatment sequencing for childhood ADHD: A multiple-randomization study of adaptive medication and behavioral interventions. Journal of Clinical Child & Adolescent Psychology, 45(4), 396–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powers DA, & Xie Y (2008). Statistical methods for categorical data analysis (2nd ed.). Bingley, UK: Emerald Group. [Google Scholar]
- R Core Team (2015). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; Available at http://www.R-project.org/. [Google Scholar]
- Robins JM, Hernán MA, & Brumback B (2000). Marginal structural models and causal inference in epidemiology. Epidemiology, 11, 550–560. [DOI] [PubMed] [Google Scholar]
- Robins J, Orellana L, & Rotnitzky A (2008). Estimation and extrapolation of optimal treatment and testing strategies. Statistics in Medicine, 27(23), 4678–4721. [DOI] [PubMed] [Google Scholar]
- Robins JM (1997). Causal inference from complex longitudinal data In Berkane M (Ed), Latent Variable Modeling and Applications to Causality (pp. 69–117). NY: Springer. [Google Scholar]
- Rosenbaum PR, & Rubin DB (1983). The central role of the propensity score in observational studies for causal effects. Biometrika, 70(1), 41–55. [Google Scholar]
- Ryan RM, & Deci EL (2000). Self-determination theory and the facilitation of intrinsic motivation, social development, and well-being. American Psychologist, 55(1), 68–78. [DOI] [PubMed] [Google Scholar]
- Schafer JL, & Kang J (2008). Average causal effects from nonrandomized studies: a practical guide and simulated example. Psychological methods, 13(4), 279. [DOI] [PubMed] [Google Scholar]
- Schilling OK, & Wahl HW (2006). Modeling late-life adaptation in affective well-being under a severe chronic health condition: The case of age-related macular degeneration. Psychology and Aging, 21(4), 703. [DOI] [PubMed] [Google Scholar]
- Schulte PJ, Tsiatis AA, Laber EB, & Davidian M (2014). Q-and A-learning methods for estimating optimal dynamic treatment regimes. Statistical Science: A Review Journal of the Institute of Mathematical Statistics, 29(4), 640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shortreed SM, Laber E, Scott Stroup T, Pineau J, & Murphy SA (2014). A multiple imputation strategy for sequential multiple assignment randomized trials. Statistics in Medicine, 33(24), 4202–4214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shortreed SM, & Moodie EE (2012). Estimating the optimal dynamic antipsychotic treatment regime: evidence from the sequential multiple‐assignment randomized Clinical Antipsychotic Trials of Intervention and Effectiveness schizophrenia study. Journal of the Royal Statistical Society: Series C (Applied Statistics), 61(4), 577–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson DD, & Joe GW (1993). Motivation as a predictor of early dropout from drug abuse treatment. Psychotherapy: Theory, Research, Practice, Training, 30(2), 357. [Google Scholar]
- Singer JD (1998). Using SAS PROC MIXED to fit multilevel models, hierarchical models, and individual growth models. Journal of Educational and Behavioral Statistics, 23(4), 323–355. [Google Scholar]
- Singer J, & Willett J (2003). Applied longitudinal data analysis. New York: Oxford University Press. [Google Scholar]
- Sterba SK (2014). Fitting nonlinear latent growth curve models with individually-varying time points. Structural Equation Modeling, 21, 630–647. [Google Scholar]
- Therneau TM (1993). How many stratification factors are “too many” to use in a randomization plan?. Contemporary Clinical Trials, 14(2), 98–108. [DOI] [PubMed] [Google Scholar]
- Wallace MP, Moodie EE, & Stephens DA (2016). SMART thinking: a review of recent developments in sequential multiple assignment randomized trials. Current Epidemiology Reports, 3(3), 225–232. [Google Scholar]