A Model for Neural Network Modeling in Neuroscience

Introduction

The ability to see movement is one of the most survival-critical and evolutionarily ancient abilities of animal vision. Yet our perception of motion, like our perception of other visual features, is subject to illusions and biases. For example, when a diagonally striped “barber pole” rotates to the right, its pattern appears to move upward (Guilford, 1929); and reducing the contrast of a moving grating can falsely make it appear to move more slowly (Stone and Thompson, 1992). These perceptual quirks provide invaluable clues to the computations going on in the visual system. After all, computer vision teaches us that there are multiple algorithms that can solve the same visual task. We can use the idiosyncratic errors of human vision to identify those algorithms that most closely replicate our own errors, and therefore are most likely to model the true neural computations.

To probe the biological computations underlying motion perception, Rideaux and Welchman (2020) created a fully transparent, fully interrogable artificial model. “MotionNet” is a convolutional neural network (CNN), comprising layers of interconnected units that have spatially restricted receptive fields and compute weighted sums of their inputs. Unlike the very deep CNNs used in computer vision, with tens or hundreds of layers (Russakovsky et al., 2015; Lindsay, 2020), MotionNet is designed for simplicity and interpretability. It consists of an input layer, a single “hidden” layer of units, and an output layer, and it can be fully trained in 10–15 min (R. Rideaux, personal communication). Despite its simplicity, the model captures an impressive gamut of phenomena when tested against psychophysical and electrophysiological data from the last 5 decades of motion perception research.

MotionNet takes as input short movie clips comprising six image frames (32 × 32 pixel resolution). The main training dataset consists of natural image fragments sliding in random directions at random speeds. The network is trained to output a decision about how fast and in what direction a clip was moving, via 1 of 64 output units, each assigned by the experimenters to indicate 1 of 8 motion directions (4 cardinal, 4 oblique) and 8 velocities.

This implementation means that output layer units are constrained to jointly encode direction and velocity, mimicking neurons in middle temporal (MT) visual cortical area (Maunsell and Van Essen, 1983). These output units are referred to as “MT units.” The similarity of MT unit tuning properties to those of biological neurons is therefore largely dictated by the training objective, whereas units in the hidden layer, equated to primary visual cortex (V1), are unconstrained. Although output (MT) units encoded motion direction and velocity in discrete steps, continuous measures of each were obtained for test movies by fitting a continuous function to the pattern of MT unit activations. Ten instances of the network were trained on each training dataset—a safeguard against the potentially large differences between different randomly initialized instances (Mehrer et al., 2020).

Key findings

Behaviorally, humans are more sensitive to cardinal than oblique motion directions (Green, 1983). Electrophysiology shows this is because of the greater proportion of V1 neurons tuned to cardinal than to oblique motion directions (Salinas et al., 2017). This preference could arise because of the greater prevalence of cardinal orientations in natural images (Switkes et al., 1978) or because a greater proportion of movement occurs in cardinal directions in the natural environment, as a result, for example, of the combined influence of gravity and the ground plane (Bex et al., 2005). “V1 units” in MotionNet trained on sequences of natural images moving in uniformly sampled directions also exhibited a strong cardinal bias (Rideaux and Welchman, 2020; their Fig. 2b). Retraining MotionNet on sequences of 45° rotated natural images instead produced a strong oblique bias (Rideaux and Welchman, 2020; Fig. 2c). Therefore, uneven sensitivities to different motion directions in both MotionNet and biological brains are likely because of the orientation statistics of natural images, rather than the distribution of motion in the natural world. This makes sense, because orientation anisotropies produce visual motion anisotropies, even when real-world motion is uniformly distributed, as we illustrate in Figure 1.

Figure 1.

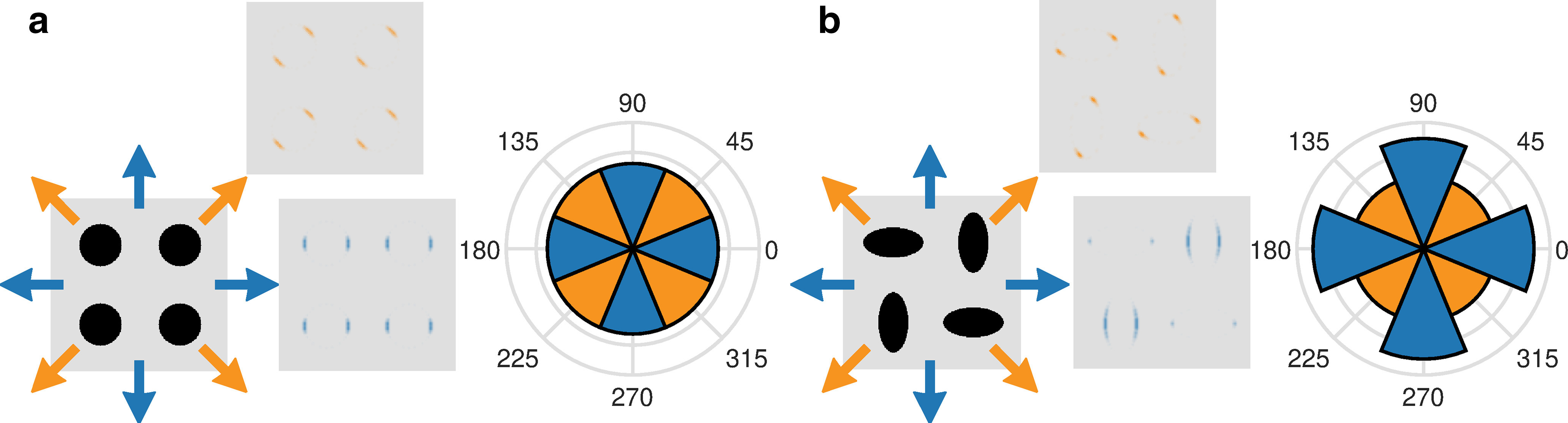
Uniform motion in the environment can produce nonuniform visual motion information. We input different patterns to a simple motion energy algorithm following (Adelson and Bergen, 1985). a, A pattern of circles, containing equal image information at all orientations, is moved by equal amounts along cardinal (blue) or oblique (orange) directions. Motion energy filters detect visual motion information at circle edges perpendicular to the direction of motion (gray squares with filter energy shown in orange and blue for one example oblique and cardinal direction, respectively). The amount of total motion energy produced by the patterns is the same in any motion direction (polar plot). b, A pattern of ellipses, which, like natural images, has more edges at cardinal orientations, produces stronger motion energy when moved in cardinal directions.

Constrained by their training objective, MotionNet MT units are tuned for motion direction: they respond strongly to motion along their assigned direction, and progressively less to motion directions away from assigned. This direction tuning was sharper in units that had been assigned to prefer higher speeds, an interaction not enforced by the training objective. The authors explain this based on the statistics of moving images: two image sequences taken from the same scene but moving in different directions will be more similar when moving at slow speeds, and more dissimilar when moving at high speeds. By reanalyzing published neurophysiological data (Wang and Movshon, 2016), Rideaux and Welchman (2020) indeed found evidence that the relationship between speed and movement direction in natural images is also exploited by MT neurons in macaques. Further analysis of the connections between V1 units and MT units showed that MotionNet MT motion selectivity primarily arose through inhibition, rather than excitation. This is another novel, testable prediction ripe for neurophysiological investigation.

MotionNet replicates and provides computational explanations for several classic motion illusions and (mis)perceptions. For example, MotionNet misperceives upward the motion direction of a rightward rotating “barber pole,” and analyzing MotionNet V1 unit activations shows that this occurs because of the pooling of competing motion signals from the center and the edges of the barber pole.

MotionNet also replicates the tendency of observers to perceive lower-contrast objects as moving at slower speeds (Stone and Thompson, 1992). This has been previously explained by a “slow world prior”: because net motion in the environment is near zero, uncertain motion estimates (e.g., low-contrast signals) are pulled toward slower motion (Weiss et al., 2002; Stocker and Simoncelli, 2006). MotionNet could not have learned this prior, since in its training set all motion velocities are equally likely. Yet the MT offset parameters in MotionNet bias the network toward slower speeds. Why does the network learn this bias? The authors observe that in natural images, spatiotemporal contrast increases with speed: the faster an image moves, the greater the range of objects and surfaces it covers. Retraining MotionNet on datasets in which this speed–contrast relationship was artificially reversed or modulated concomitantly reversed or modulated the bias learned by the network. Conversely, altering the relative frequency of slow-moving and fast-moving image sequences in the training set (artificially creating slow or fast worlds) did not reliably bias MotionNet toward slower or faster speeds.

Does the learned contrast-speed relationship also dominate over a slow world prior in humans? The slow world hypothesis predicts that any uncertainty in motion signals should bias perception toward slower speeds. Rideaux and Welchman (2020) test this prediction in human participants and find that biases occur only for contrast manipulations. Thus, the relationship between speed and spatiotemporal contrast, not a slow world prior, best accounts for motion biases in both MotionNet and humans.

Significance

Extremely deep CNNs have in recent years reached and exceeded human object recognition abilities (Russakovsky et al., 2015; He et al., 2016), and they predict neural activity in high-level visual regions (Yamins and DiCarlo, 2016; Kietzmann et al., 2018; Lindsay, 2020). However, they are sometimes criticized as being “black boxes”—replacing a biological system whose function we do not understand with an artificial system whose function we do not understand—and are only as good as the methods used to interpret them (Funke et al., 2020; Ma and Peters, 2020). In contrast, Rideaux and Welchman (2020) combine a CNN of a tractable size with an array of computational experiments and “in silico electrophysiology” to create a detailed comparison of an artificial system to brain and behavioral data. The article highlights how numerous laboratory techniques are transferable to image-computable neural network models, including the use of synthetic stimuli with precise spatial and motion properties, classification of units by their response profiles, and synaptic weight profiling. It also demonstrates powerful new techniques, such as retraining the system on datasets tailored to test specific hypotheses. This work thus showcases how neural networks can be used as transparent and interrogable models in neuroscience.

One intriguing result is that MotionNet V1 unit tuning more strongly predicts MT unit inhibition rather than excitation. This broadens support for the importance of “proscription” as a computational strategy in vision—neurons signal not only what features are likely present in the input, but, perhaps equally importantly, what features are not likely present. Previously, proscription has been shown to be important for depth perception, with inhibitory binocular neurons suppressing incorrect correspondences between features in the two eyes (Goncalves and Welchman, 2017; Rideaux and Welchman, 2018). Depth from binocular disparity can be thought of as computationally equivalent to motion: depth is derived from differences between two image frames separated in space, while motion is computed from differences between two frames separated in time. Thus, in MotionNet, V1 units signal to MT units which specific motion directions are both likely and unlikely, given the image differences between two frames.

The article by Rideaux and Welchman (2020) also demonstrates how image-computable statistical learning models can help settle debates between conflicting Bayesian theories of perception. For example, although it is plausible that motion anisotropies in biological systems could be learned from uneven environmental motion statistics (Bex et al., 2005), the fact that anisotropies arise even in a model with uniform motion experience suggests that it is more parsimonious to attribute them to the static orientation statistics of natural images (Switkes et al., 1978). Similarly, although MotionNet is capable of learning slow-world/fast-world priors, the effects of priors are overshadowed by a previously underappreciated speed–contrast relationship in natural scenes. By disputing the slow-world prior hypothesis (Weiss et al., 2002; Stocker and Simoncelli, 2006), Rideaux and Welchman (2020) even argue against their own previous work (Welchman et al., 2008).

The authors share data and model code (https://www.repository.cam.ac.uk/handle/1810/300898), providing an excellent opportunity to extend the model, as MotionNet is (necessarily) missing several features of human vision. For instance, MotionNet uniformly samples its inputs, whereas the human visual field has high resolution at the fovea and low resolution in the periphery. Incorporating space-variant resolution (Chessa et al., 2016; Maiello et al., 2020) into MotionNet might help explain illusory motion phenomena in the periphery, such as the curveball illusion (Shapiro et al., 2010). Another challenge is to understand how motion selectivity emerges in biological brains via less strongly supervised learning, without relying on ground-truth motion information or training objectives that impose MT-like motion tunings (Fleming and Storrs, 2019; Storrs and Fleming, 2020).

Finally, although MotionNet qualitatively captures many aspects of motion processing, quantitative fits of the model predictions to behavioral or brain data would likely be low (e.g., MotionNet contrast-dependent biases occur at contrast ranges 10-fold smaller than in human observers). Fitting MotionNet quantitatively to human data is likely possible, for example by introducing noise to the system, and could be considered as an additional validation of the model. The success of the wholly unfitted model in accounting for a wide range of perceptual and physiological phenomena is nevertheless remarkable.