Closed-Loop Theta Stimulation in the Orbitofrontal Cortex Prevents Reward-Based Learning

SUMMARY

Neuronal oscillations in the frontal cortex have been hypothesized to play a role in the organization of high-level cognition. Within the orbitofrontal cortex (OFC), there is a prominent oscillation in the theta frequency (4–8 Hz) during reward-guided behavior, but it is unclear whether this oscillation has causal significance. One methodological challenge is that it is difficult to manipulate theta without affecting other neural signals, such as single-neuron firing rates. A potential solution is to use closed-loop control to record theta in real time and use this signal to control the application of electrical microstimulation to the OFC. Using this method, we show that theta oscillations in the OFC are critically important for reward-guided learning and that they are driven by theta oscillations in the hippocampus (HPC). The ability to disrupt OFC computations via spatially localized and temporally precise stimulation could lead to novel treatment strategies for neuropsychiatric disorders involving OFC dysfunction.

In Brief

Although neuronal oscillations correlate with many high-level cognitive processes, their causal contribution is less clear. Using a novel closed-loop microstimulation protocol, Knudsen and Wallis demonstrate the necessity of theta oscillations in the orbitofrontal cortex for reward-based learning.

INTRODUCTION

The orbitofrontal cortex (OFC) is thought to be important for encoding rewards predicted by environmental cues (Hunt et al., 2018; Klein-Flügge et al., 2013; Rich and Wallis, 2014; Sadacca et al., 2018; Saez et al., 2017), enabling optimal decision-making (Padoa-Schioppa and Assad, 2006; Padoa-Schioppa and Conen, 2017; Rich and Wallis, 2016). A prominent theta oscillation has been observed previously in the OFC when rodents learn the significance of reward-predictive cues (van Wingerden et al., 2010), but the function of this oscillation is unknown. Oscillations may be important for organizing cognitive processes (Canolty et al., 2006, 2010; Loonis et al., 2017; Lundqvist et al., 2018). Such oscillations could facilitate spike timing-dependent plasticity (Buzsáki et al., 2013) and ensure synchronization of neuronal populations responsible for processing different aspects of task-relevant events (van Atteveldt et al., 2014). These processes could be especially important for the process of cognitive control, which involves co-ordination of disparate association areas in the brain (Duncan and Owen, 2000).

Establishing a causal role of a neuronal oscillation is challenging because standard methods for disrupting neural function, such as pharmacological, optogenetic, and electrical manipulations, disrupt not just the oscillation of interest but also the underlying neuronal firing rates. A potential solution to this problem is to use closed-loop control (Jadhav et al., 2012; Siegle and Wilson, 2014), where the theta oscillation is recorded in real time and used to control the application of electrical microstimulation. Here we used closed-loop microstimulation to test the role of OFC theta oscillations in reward-based learning. We trained two monkeys (Macaca mulatta) to perform a learning task that required them to flexibly update their decisions in the face of changing contingencies. We found a strong theta oscillation as animals learned the value of reward-predictive cues and then examined the effect of disruption of this oscillation via closed-loop microstimulation. We employed a similar procedure to disrupt hippocampus (HPC) theta oscillations, targeting this structure because of its prominent theta oscillation (Buzsáki, 2002) and its anatomical connections (Barbas and Blatt, 1995) and functional interactions (Young and Shapiro, 2011) with the OFC.

RESULTS

Two macaques (subjects V and T) performed a task requiring them to learn the values (probability of reward) of three novel pictures and track those values as they changed over the course of a session (Figures 1A and 1B; STAR Methods). Two pictures were presented in 80% of the trials (free choice), and the subject selected one of them. Subjects typically chose the more valuable picture (Figure 1C), choosing optimally in 69% (V, 16 sessions) and 72% (T, 9 sessions) of all trials, demonstrating that they could track the changing reward contingencies. In the remaining 20% of trials (forced choice), a single picture was presented, which ensured that subjects regularly experienced the contingencies associated with all three pictures irrespective of their choices.

Figure 1. Behavioral Task and Performance.

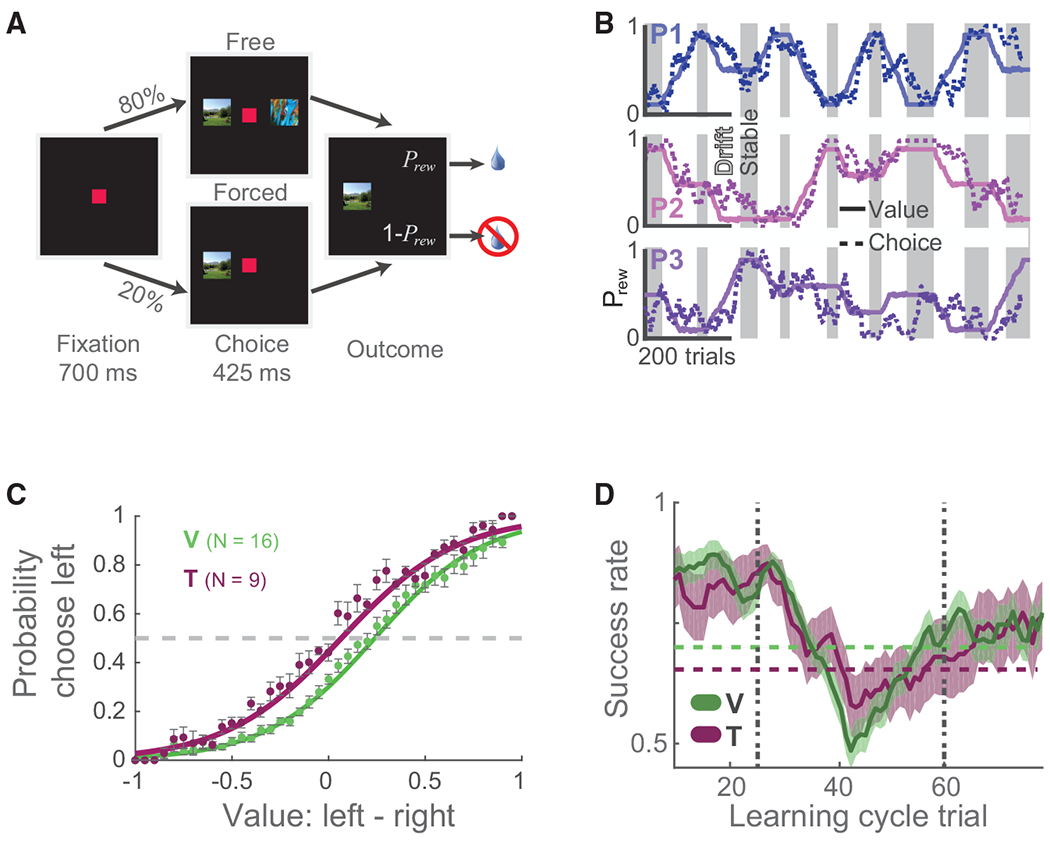
(A) The behavioral task presented either one (forced choice) or two pictures (free choice) that probabilistically predicted reward delivery (P_rew). Subjects indicated their choice by fixating on a picture for 425 ms.

(B) Example session (subject V) illustrating P_rew (solid lines) for each picture (P1…P3) during stable (gray shading) and drift (white) periods and the subject’s likelihood of choosing each picture (dashed lines) across trials.

(C) The probability of each subject choosing the left option as a function of the relative difference in left and right values (subject V, 13,232 trials in 16 baseline sessions; subject T, 5,452 trials in 9 baseline sessions). Each data point is the mean (± SEM) of the value bin. The gray dashed line indicates indifference between the two options. Fits were calculated using a standard logistic fit of behavioral choices to value difference. Both subjects were more likely to choose the left option as its value increased relative to the right option.

(D) Mean behavioral performance (± SEM) across all learning cycles (V, N = 97; T, N = 35). Average performance was smoothed using a 16-trial moving average. Horizontal dashed lines denote learning criteria for each subject. Vertical gray lines denote the onset and offset of drift.

To examine how neuronal activity changed with learning, we binned trials into learning cycles so that we could compare neuronal activity across drift periods of varying lengths (Figure S1). We divided each stable-drift-stable epoch into a uniform 85-trial window consisting of 25 stable trials prior to drift onset (pre-drift), 35 bins of trials during the contingency change (drift), and 25 stable trials following drift (post-drift). We quantified the animal’s performance via a success rate, which was the proportion of trials where they selected the more valuable picture. This measure was required to exceed a criterion level for at least 35 trials before values began to drift. When the reward contingencies first began to change, the success rate began to decrease (Figure 1D). About halfway through the drift period, the subjects realized that the contingencies were changing and modified their choices so that the success rate began to increase, eventually returning to criterion performance levels as the contingencies re-stabilized. Drift periods lasted a mean of 82 ± 1.8 trials for subject V and 62 ± 3.3 for subject T. We quantified learning speed as the number of trials between the cessation of drift and re-establishment of criterion performance. We used this measure because it was less affected by differences in the length and magnitude of the drift period. Subject V reacquired criterion performance within 4.2 ± 0.8 trials, whereas subject T took 8.5. ± 1.4 trials. Drift periods were also characterized by a small increase in response latencies (Wilcoxon rank-sum test, 95% confidence interval [CI] of the median response time during stable versus drift; V: 225–241 ms versus 250–258 ms, z = −11, p = 5 × 10⁻³⁰; T: 215–225 ms versus 233–241 ms, z = −9, p = 2 × 10⁻²⁰).

OFC Theta Oscillations and Reward-Based Learning

We recorded local field potentials (LFPs) from up to 3 multisite electrodes distributed in the OFC (Figures S2 and S3A). During task performance, there was a prominent increase in theta band (4–8 Hz) power relative to other frequencies of the LFP in the OFC (Figure 2A). Cross-trial phase alignment of the theta oscillation occurred at each of the major events in the task (Figure 2B). We quantified the strength of this phase alignment by calculating the mean resultant vector length, R (STAR Methods), which showed that phase alignment was largely confined to the theta frequency (Figures 2C and 2D; Figures S4A and S4B). Furthermore, there was a large increase in the prevalence of theta phase alignment during drift (Figure 2E), particularly during the fixation epoch (Figures S4A–S4E). This increase in phase alignment occurred even as theta power remained constant (Figure S4F).

Figure 2. OFC LFP Oscillations and Learning.

(A) Mean (± SEM) percent change in broadband OFC LFP power during the fixation epoch relative to intertrial interval power. Gray shading indicates the 4- to 8-Hz frequency band used for subsequent analyses.

(B) Theta (4–8 Hz) phase from a representative session (subject T) with trials ranked by reaction time. Symbols denote the times of fixation onset (green triangles), picture onset (red triangles), choice onset (orange circles), and outcome (blue squares).

(C) Time course of cross-trial phase alignment plotted as a function of frequency for a single session from subject V. Phase alignment was most prominent in the theta band.

(D) Cross-trial phase alignment in theta (4–8 Hz), beta (13–30 Hz), and gamma (30–60 Hz) frequencies (subject V).

(E) Mean cross-trial theta phase alignment as a function of learning. Data were taken from the fixation epoch and expressed as the percent increase from baseline values measured during the pre-drift trials. These values are derived from the data in (D) and Figure S4B. Three standard deviations of the bootstrapped shuffled distribution of phase alignments are shown as color-coded lines. For both subjects, cross-trial theta phase alignment increased during drift.

To test the causal significance of the theta oscillation, we used a closed-loop system in which we extracted power and phase information in real time from ongoing activity in the OFC and used this information as a control signal to deliver electrical microstimulation to the OFC at the positive phase of theta (STAR Methods; Figures S3B and S5A). Closed-loop theta stimulation during the fixation epoch severely impaired subjects’ ability to flexibly update choices relative to sham stimulation (Figure 3).

Figure 3. OFC Closed-Loop Theta Stimulation Disrupts Value Learning.

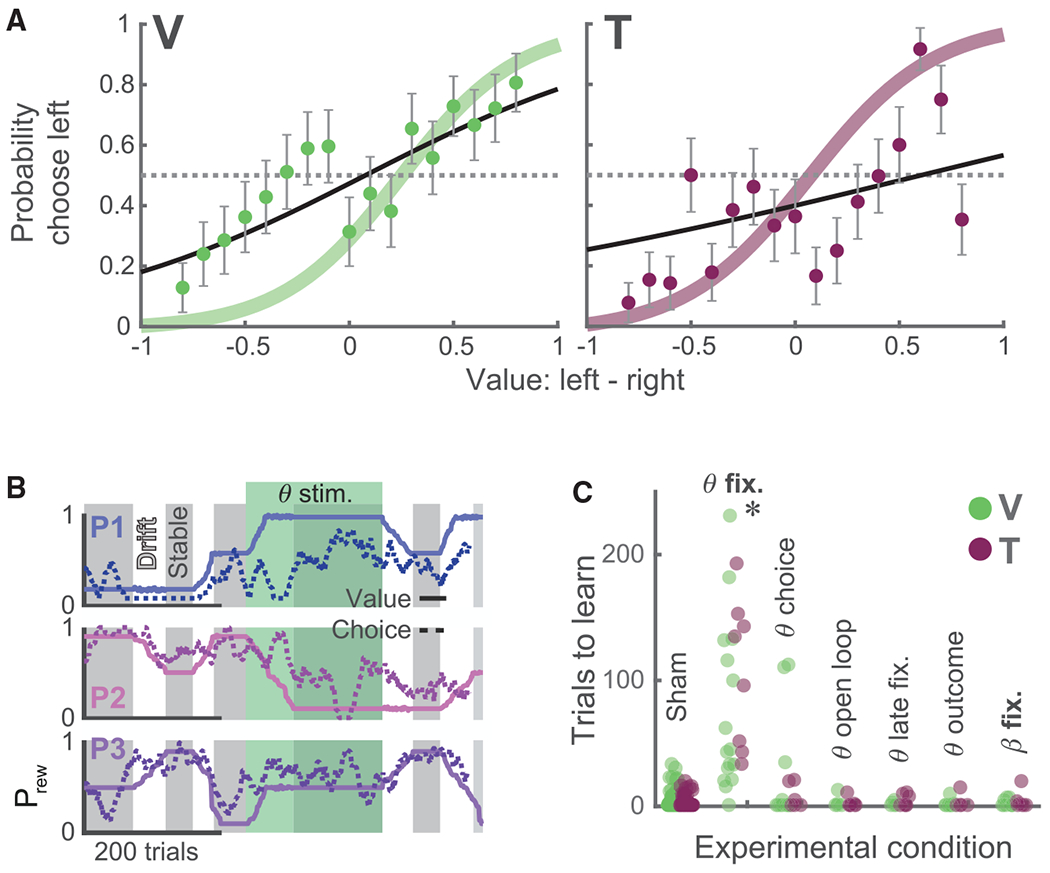
(A) The probability of each subject choosing the left option as a function of the relative difference in left and right values during theta fixation stimulation sessions (subject V, 2,251 trials in 6 sessions; subject T, 1,012 trials in 3 sessions). Convention follows Figure 1C. A colored line denotes mean ± SEM of logistic fit from baseline behavior. Curves are flattened relative to baseline behavior, indicating that subjects’ choices are less well predicted by the relative value of the pictures.

(B) Example session showing the effect of theta stimulation on learning (subject V). Convention follows Figure 1B. A green-shaded region indicates trials where theta-fixation stimulation was delivered.

(C) Number of trials required to reach criterion performance during stimulation. Each point denotes one stimulation block. Only theta stimulation during the fixation epoch significantly impaired learning (*p < 0.0005 in both subjects, rank-sum test, experimental conditions versus sham stimulation, corrected for multiple comparisons).

We performed several control experiments (Figure 3C) to determine whether the behavioral effect was specific to the task epoch, frequency, or learning state. First, theta stimulation during the choice epoch had no effect on learning. We then decoupled theta stimulation from the underlying theta activity by randomly jittering stimulation by 1–300 ms from the controller signal (theta open loop; Figures S5B and S5C) and found no effect on learning. Similarly, restricting closed-loop stimulation to one full cycle beyond the initial cross-trial phase alignment (theta late fixation) had no behavioral effect. Closed-loop theta stimulation during the outcome epoch had no effect. Next we tested the relevance of stimulation frequency by delivering stimulation using extracted beta (13–30 Hz) phase and power as the control signal, which had no effect on learning. The beta oscillation is approximately three times faster than theta, resulting in delivery of more current (Figure S6A). Thus, the behavioral effect of closed-loop theta stimulation is not due to non-specific effects of electrical stimulation.

To understand the mechanism underlying the behavioral effect of closed-loop theta stimulation, we examined the effect it had on neuronal activity. Closed-loop theta stimulation significantly disrupted OFC theta cross-trial phase alignment in both subjects, whereas closed-loop beta stimulation had no effect (Figure 4A; Figure S6B). During closed-loop stimulation experiments, there was also a significant effect of the frequency of stimulation on theta power (Figure 4B; 1-way ANOVA; V: F_741,2 = 80, p = 4 × 10⁻³²; T: F_399,2 = 95, p = 1 × 10⁻³³). Post hoc tests revealed that theta power significantly increased with theta stimulation compared with sham or beta stimulation (p < 0.00001 for both subjects; beta versus sham: V, p = 0.58; T, p = 0.99). To investigate how the increased power in theta interacted with phase alignment during learning, we calculated phase alignment and power and determined the relationship between the two. Figure 4C illustrates this relationship for one example session. During sham stimulation, there was a positive relationship between the two variables; increased theta power was associated with stronger theta cross-trial phase alignment (β_sham = 4.7, p = 0.004). Closed-loop theta stimulation reversed this relationship; increased theta power disrupted theta cross-trial phase alignment (β_θ-stim = —11, p = 0.002). This was consistent across subjects and sessions (Figure 4D); the relationship between power and phase alignment was significantly more negative during theta stimulation relative to sham (paired t test; V: t₂₂₃ = 9.9, p = 2 × 10⁻¹⁹; T: t₁₁₀ = 5.8, p = 6 × 10⁻⁸).

Figure 4. Effect of Stimulation on LFP.

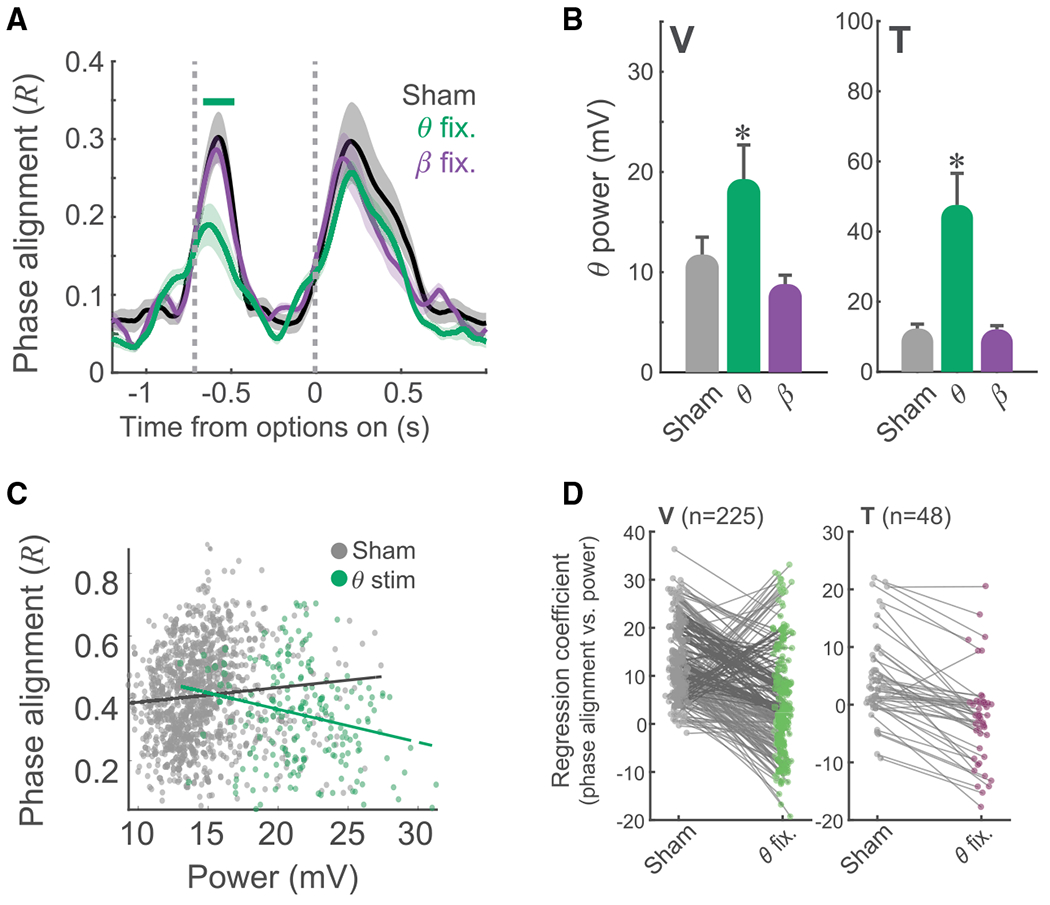
(A) Mean cross-trial theta phase alignment (R) for sham (black), theta (green), and beta (purple) stimulation sessions in subject V. Significant differences were assessed with a sliding 1-way ANOVA evaluated at p < 0.01. A green horizontal line indicates when the cross-trial theta phase alignment was significantly lower during theta stimulation compared with either sham or beta stimulation.

(B) Mean theta power during the fixation epoch as a function of stimulation type.

(C) Single-channel example of the effect of stimulation on the power-phase relationship. Points in gray denote sham trials, and points in green represent stimulation trials. Theta stimulation increased theta power and decreased cross-trial theta phase alignment.

(D) Population data from both subjects, summarizing the phase-power relationship for each OFC electrode. Theta stimulation shifted the power-phase relationship from positive to negative.

Finally, we used data collected from the open-loop experiments to determine which phases of the theta oscillation were most affected by stimulation. For each stimulation pulse, we identified the phase of theta at which the pulse occurred and computed the mean change in theta power evoked by the stimulation pulse (Figure S6C). Stimulation only increased theta power when delivered on the rising cycle of the oscillation. We next examined whether this had any consequences on behavior. We quantified the likelihood of choosing optimally during open-loop stimulation as a function of whether each pulse of stimulation was delivered during the peak or the trough of the oscillation (Figure S7). We performed a two-way ANOVA with factors of valence (peak or trough) and pulse number (1…5). The dependent variable was whether the animal chose the more valuable option. In both subjects, pulses delivered at the positive phase of theta were more disruptive to choice behavior than those delivered at the negative phase.

In summary, adapting behavior to changing reward contingencies was associated with phase alignment of the theta oscillation. Targeting this oscillation with closed-loop microstimulation significantly impaired the ability of animals to adapt their behavior. The effects were mediated by an increase in power to the theta oscillation, particularly during the rising phase of the oscillation.

Single-Neuron Value Encoding in the OFC during Learning

To determine why theta stimulation in the fixation epoch was so disruptive to learning, we examined single-neuron responses. We found that approximately 50% of single neurons fired spikes that were phase locked to theta (Figure 5A; significant Rayleigh’s Z test evaluated at p <0.01; V: 207 of 566 or 37% of neurons; T: 180 of 275 or 65% of neurons). We next examined what information was encoded during the fixation period. To provide single-trial estimates of the subjective value of the pictures, we fit a reinforcement learning (RL) model to choice behavior across the session (STAR Methods; Figure S8). We focused our neuronal analysis on the stable periods, when values were well-learned and maximally divergent. For each neuron, we determined whether it maintained information about the previous trial (the identity and value of the picture and whether it was rewarded) as well as the value of the three pictures (STAR Methods). Many neurons encoded one or more of the values Q_Low … Q_High; V: 308 of 566 or 54% of OFC neurons; T: 103 of 275 or 37% of neurons) independent of the picture with which the value was associated (value-centric model). Figure S9 shows examples of such neurons. Far fewer neurons encoded information about the previous trial (Figure 5B). We also tested an alternate picture-centric model that examined whether neurons encoded specific pictures and their values (Q₁ … Q₃). A similar number of neurons encoded value in both the value-centric and picture-centric models (V, 296 of 566 or 52%; T, 95 of 275 or 35%; χ² comparison between models, p > 0.1 for both subjects). However, the value-centric model explained more variance in neuronal firing rates than the picture-centric model (V: value-centric mean R² = 0.17 ± 0.01, picture-centric mean R² = 0.14 ± 0.01, t₆₀₂ = 2.3, p = 0.01; T: value-centric mean R² = 0.11 ± 0.007, picture-centric mean R² = 0.09 ± 0.01, t₁₉₆ = 1.8, p = 0.04). Consequently, we used the value-centric model in subsequent analyses.

Figure 5. Theta Phase Locking of OFC Value Encoding.

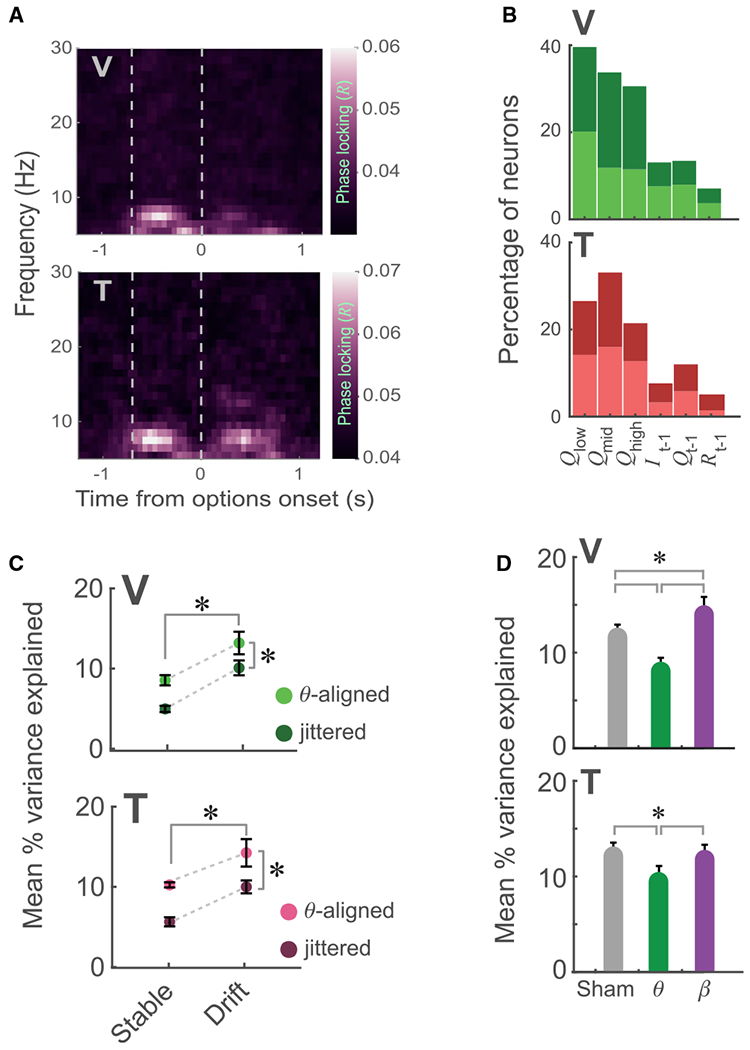
(A) Phase locking of OFC neurons across time and frequency bands. Phase locking was calculated in symmetric 400-ms windows centered on each time point and stepped in increments of 50 ms. Pseudocolor denotes mean resultant vector length (R). Vertical dashed lines indicate the onset of fixation and picture presentation, respectively.

(B) Percentage of OFC neurons whose firing rate was significantly predicted by each parameter of the value-centric model. Darker colors indicate neurons with a positive relationship between value and firing rate, and lighter colors indicate those with a negative relationship. Many neurons maintained information about the current values of the pictures, whereas fewer encoded the events of the previous trial.

(C) Percentage of variance in neuronal firing rates explained by the value-centric model as a function of the stage of learning and whether the firing rates were aligned to the underlying theta oscillation. Asterisks indicate significant main effects (2-way ANOVA, F > 1,000, p < 1 × 10⁻¹⁵ for both subjects).

(D) Mean percent variance explained in firing rate by the value-centric model during sham stimulation, theta closed-loop stimulation, or beta closed-loop stimulation. Asterisks indicate significant differences (1-way ANOVA with post hoc tests, p < 0.005).

To determine whether value encoding was contingent on theta oscillations, for each learning cycle and each neuron, we used the value-centric regression model to predict firing rate in a 100-ms window (±50 ms) centered on the peak positive phase of theta immediately following fixation onset. To account for heterogeneity in individual neurons’ dynamics with respect to value encoding, we repeated this procedure for the following three theta cycles as well as the three cycles immediately preceding fixation onset and determined which cycle contained the maximum value coding for each neuron. We then compared these predictions with a shuffled dataset in which the time of each theta peak in each trial was randomly jittered by ± 100 ms (approximately half a theta cycle, 10 bootstraps). We compared the mean variance explained by the value-centric model for the theta-aligned and jittered firing rates using a 2-way ANOVA with factors of group (theta-aligned versus jittered) and learning (stable versus drift). There was significantly more value information encoded during drift trials, and theta-aligned firing rates contained significantly more value information than jittered firing rates (Figure 5C).

The purpose of the recording probe in the closed-loop stimulation sessions was to record the LFP, but we sometimes serendipitously recorded single neurons. This enabled us to measure the effect of closed-loop stimulation on neuronal firing. For each neuron recorded during either theta stimulation (V, 104 neurons; T, 36 neurons) or beta stimulation (V, 28 neurons; T, 30 neurons), we calculated the number of spikes in a 100-ms window preceding (pre-stimulation) and 100 ms following (post-stimulation) each stimulation pulse (theta) or bout of pulses (beta). We then compared them with a surrogate sham dataset consisting of spikes within ± 100 ms of randomly selected time points during the fixation epoch when stimulation was not applied. A 2-way ANOVA with factors of group (theta, beta, or sham) and time (pre-versus post-stimulation) revealed that, for both subjects, there was no effect of stimulation on the firing rates of OFC neurons (Figure S10; F < 2, p > 0.1 in all cases). As in our main recording experiment, the firing rate of many of the neurons was significantly predicted by the value-centric model (V: 43 of 104 neurons during theta stimulation, 17 of 28 neurons during beta stimulation; T: 14 of 36 neurons during theta stimulation, 17 of 30 neurons during beta stimulation). For each neuron, we determined the maximum amount of value encoding (as determined by the percentage of variance in firing rate explained by the value-centric model) during the drift trials, using the theta-aligned firing rates. In both subjects, closed-loop theta stimulation significantly reduced value encoding, whereas beta stimulation either increased (V) or had no effect (T) on neuronal value encoding (Figure 5D).

In summary, during the fixation epoch, many OFC neurons maintained information in their firing rates about the value of the three pictures. Firing rates and information about value were synchronized to the underlying theta oscillation. Closed-loop theta microstimulation disrupted the theta oscillation and decreased the amount of information about value that was encoded by OFC neurons.

HPC and OFC Synchronize to Support Learning

HPC is a potential source of OFC theta input because the two structures strongly connect (Barbas and Blatt, 1995), and HPC has a prominent theta oscillation (Buzsáki, 2002). To examine whether the two areas interact, we recorded from the OFC and HPC simultaneously and examined theta activity. Similar to the OFC, we found prominent theta phase alignment in HPC LFP (Figure 6A; Figure S11A). We measured the degree to which the theta phase was synchronous between the two regions by calculating the cross-area phase alignment value (PLV; STAR Methods). There was strong theta phase alignment between the OFC and HPC during the fixation and choice epochs (Figure 6B). The time course of HPC-OFC synchrony across the learning cycle (Figure 6C; Figure S11B) closely paralleled the evolution of behavior. Specifically, at the onset of drift, when behavioral performance began to drop, there was a significant reduction in interregional synchrony, particularly during the fixation epoch (Figure 6D). As subjects began to adjust their behavior to the changing contingencies, there was an increase in interregional synchrony that returned to baseline when the contingencies stabilized.

Figure 6. HPC-OFC Interactions Underlying Learning.

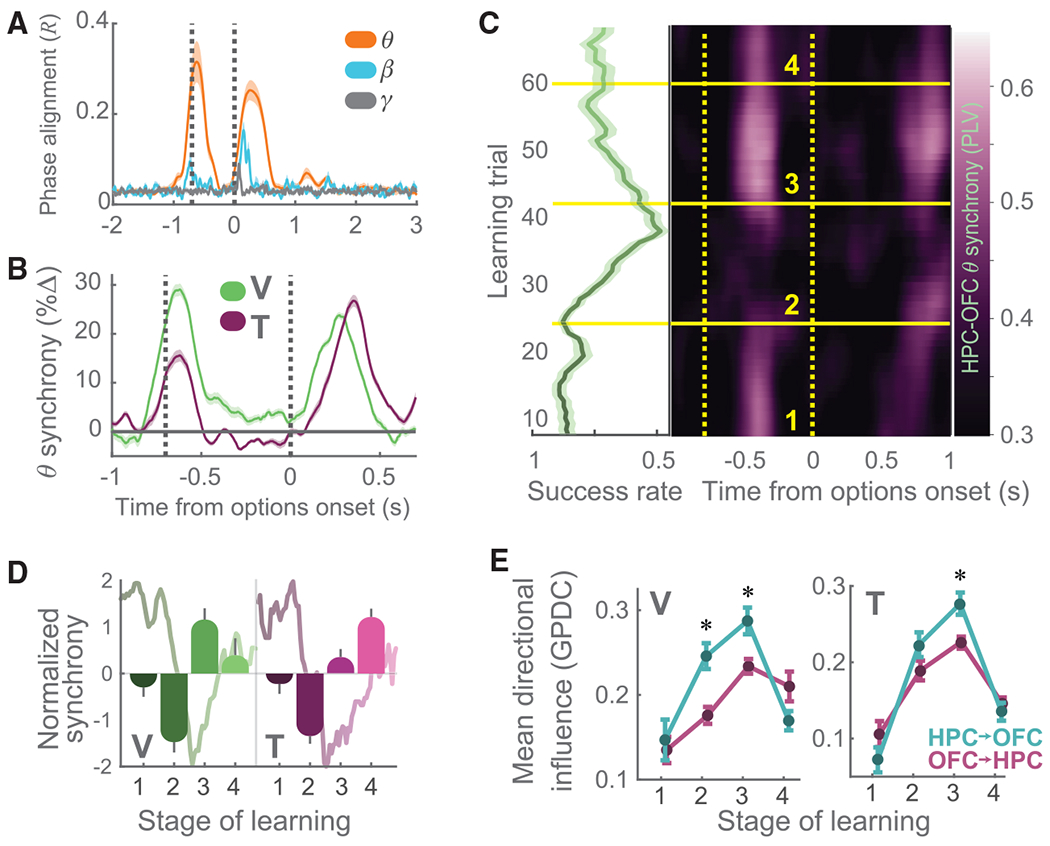
(A) HPC cross-trial theta phase alignment for subject V. Convention follows Figure 2D.

(B) Mean (± SEM) pairwise HPC-OFC theta phase synchrony (V: 1049 channel pairs, green; T: 2,528 channel pairs, red), expressed as percent change from 300 ms before fixation. These data are derived from the data shown in (C) and Figure S11B.

(C) Left: mean learning from Figure 1D plotted in green. Right: HPC-OFC theta phase synchrony during learning (subject V). The pseudocolor scale indicates the amount of cross-area phase alignment, yellow dashed vertical lines denote fixation and picture presentation, and yellow solid horizontal lines segment the learning cycle into four stages.

(D) Mean HPC-OFC theta phase synchrony during fixation across four stages of the learning cycle, with average behavior overlaid. These data are derived from the data shown in (C) and Figure S11B. For both subjects, all comparisons were significant (1-way ANOVA, p < 0.0001, except for subject T, 1 versus 3, p < 0.05).

(E) Mean directional influence as a function of learning stage. HPC→OFC influence is shown in blue and OFC→HPC in pink. Bidirectional influence increased during drift, and HPC→OFC directional influence was greater than OFC→HPC (2-way ANOVA with simple effects; *p < 0.0001 in V, p < 0.05 in T).

To determine the direction of information flow between the OFC and HPC, we examined the relationship between OFC and HPC theta LFP using generalized partial directed coherence (GPDC; Figure 6E; STAR Methods). GPDC measures the direction of influence of one signal on another by computing the degree to which past values of one can predict the future values of another. To examine whether GPDC values differed across the learning cycle, we performed a 2-way ANOVA with factors of directional influence (HPC→OFC or OFC→HPC) and learning (four phases). There was a significant interaction (V: F_23032,3 = 280, p < 1 × 10⁻¹⁵; T: F_29944,3 = 670, p < 1 × 10⁻¹⁵). An analysis of the simple effects showed that there was more influence between the two areas during drift and that it was predominately in the HPC→OFC direction.

This evidence suggests that the HPC provides theta input to the OFC during learning. Therefore, we hypothesized that theta stimulation of the HPC would disrupt learning much like stimulation of the OFC. To test this, we stimulated one region while recording from both. As predicted, HPC closed-loop theta stimulation resulted in behavioral effects that were identical to OFC theta stimulation; it severely impaired our subjects’ ability to learn changing values (Figure 7A). To compare the physiological effects of stimulation on GPDC, we performed a 2-way ANOVA with factors of directional influence (HPC→OFC or OFC→HPC) and stimulation site (OFC or HPC). There was a significant interaction (V: F_618,2 = 9.5, p = 0.0001; T: F_1074,2 = 19, p = 8.7 × 10⁻⁹), which, as a simple effects analysis showed, was because HPC stimulation reduced both OFC→HPC and HPC→OFC influence, whereas OFC stimulation only reduced OFC→HPC (Figure 7B). These results suggest that it is HPC that provides theta input to the OFC to enable value learning.

Figure 7. HPC Stimulation Disrupts Value Learning and Bidirectional OFC-HPC Theta Influence.

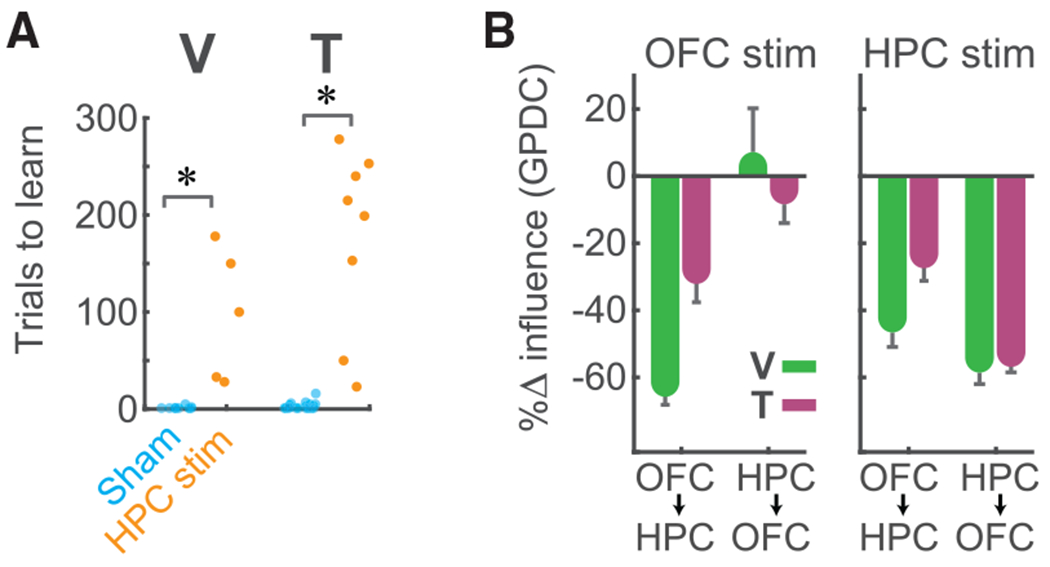
(A) Trials to learn value during HPC stimulation (*p < 1 × 10⁻⁵, rank-sum test).

(B) Percent change (compared with sham stimulation, shown in Figure 6E) in GPDC during OFC or HPC closed-loop theta stimulation. For both subjects, OFC stimulation significantly disrupted OFC→HPC influence but not HPC→OFC, whereas HPC stimulation disrupted influence in both directions.

DISCUSSION

Much of the canonical work of studying the prefrontal cortex during goal-directed behavior focuses on the computations underlying the evolution of choice from evaluation of known options. However, in natural settings, humans and animals need to flexibly control their decisions in response to changes in the environment. An extra glass of wine may be fine when dining with colleagues, but perhaps not when one’s boss is present. Our findings elucidate the neuronal mechanisms that underlie this process. Learning involved marked increases in cross-trial theta phase alignment and theta phase-locking of value-encoding neurons. We used closed-loop microstimulation to demonstrate the causal importance of these mechanisms for choice behavior and showed that OFC theta depends on HPC input.

Functional Significance of OFC Theta Oscillations

Previous studies that have demonstrated the necessity of OFC for reward-based learning have relied on relatively coarse manipulations, such as lesions or inactivations that completely disrupt all neuronal processing, leaving the precise mechanisms by which the manipulation alters behavior unclear. Our closed-loop approach allowed us to disrupt a specific neuronal oscillation without affecting underlying single-neuron firing rates, demonstrating the importance of OFC theta for learning. The OFC connects with cortical areas responsible for processing all sensory modalities (Carmichael and Price, 1995b), as well as most components of the limbic system (Carmichael and Price, 1995a). Phase locking potentially offers one solution by which the OFC can selectively process information from one structure relative to another (Canolty et al., 2010). Synchronizing spikes in both the OFC and HPC to the same theta oscillation increases the likelihood that HPC neurons can cause spike timing-dependent plasticity in the OFC (Buzsáki et al., 2013). This may be a general mechanism by which highly interconnected association cortices are able to prioritize different information sources. Several recent studies have highlighted the feasibility of this mechanism. In rats, single neurons in the medial prefrontal cortex (PFC) have been shown to phase-lock to hippocampal theta (Jones and Wilson, 2005). Increased theta coherence between the medial PFC and HPC has also been observed at the choice point of T mazes during learning (Benchenane et al., 2010) and can predict working memory performance (Hyman et al., 2010). In monkeys, theta phase alignment between the lateral PFC and HPC occurs during learning of sensorimotor associations (Brincat and Miller, 2015). In humans, coupling between theta and gamma oscillations has been found to underpin a variety of cognitive tasks (Canolty et al., 2006). However, these studies are only correlative. In contrast, our results demonstrate the causal importance of theta for reward-based learning.

An additional possibility is that the theta response may be driven by the eye movement to the fixation cue. We think that this is unlikely for several reasons. First, eye movement artifacts are quick events lasting about 20 ms and tend to contaminate the gamma band rather than the theta band (Kovach et al., 2010). In contrast, changes in theta power in our task last approximately 400 ms. Furthermore, changes in theta phase timing occurred when reward contingencies were changing but not when they were stable (Figure 2E), whereas eye movements occurred in every trial. Finally, the results from our analysis of closed-loop stimulation (Figure S7) show that theta phase is a separate event that has explanatory power above and beyond the time of the eye movement. A more likely explanation is that the theta response relates to the neuronal encoding of value that is a feature of OFC neurons. Similar to many neurophysiological studies of the OFC (Hunt et al., 2018; Padoa-Schioppa, 2013; Rich and Wallis, 2014), the most common neuronal tuning we observed related to prediction of rewards. However, there is also a good deal of heterogeneity in response properties, including different types of value coding (Padoa-Schioppa, 2013) and different properties of reward-predictive cues (Sadacca et al., 2018; Strait et al., 2016; Zhou et al., 2019), with little evidence for anatomical organization on the basis of neuronal response properties (Morrison and Salzman, 2009; Rich and Wallis, 2014). Synchronizing neurons with the same tuning property to the same oscillation potentially provides a mechanism to co-ordinate the firing of anatomically interspersed neurons. In support of such a mechanism, our data suggest that firing of OFC neurons encoding reward predictions preferentially occurs at specific phases of the theta oscillation. Closed-loop microstimulation disrupts this synchronization and impairs learning.

An additional question is how a single pulse of microstimulation on a single electrode in the OFC can have such consequential effects on behavior. It is particularly striking because permanent lesions of the OFC do not impair a task similar to the one we used (Rudebeck et al., 2017). However, permanent lesions of the OFC may allow compensatory changes, either via downstream homeostatic regulation of neural activity (Otchy et al., 2015) or in the behavioral strategy the animals adopt to perform the task. There is also precedent for microstimulation having dramatic effects. Previous results, using sensory discrimination tasks, have shown that animals can detect the addition of just a handful of action potentials to a single neuron (Houweling and Brecht, 2008). Because of recurrent excitation, stimulation of a single pyramidal neuron can activate around 2% of neighboring pyramidal neurons and about 30% of neighboring interneurons (Kwan and Dan, 2012). These effects can snowball so that activation of a single pyramidal neuron can be sufficient to cause switches in global brain state, such as between slow-wave and rapid eye movement sleep patterns (Li et al., 2009).

Role of OFC in Reward-Based Learning

Modern accounts of reward-based learning differentiate between two different methods (Daw et al., 2005; Doll et al., 2012). Model-free RL is associated with habits and skills; it relies on trial and error, storing or caching the values of past actions, and inflexibly repeating actions that led to higher values. We have a relatively developed understanding of the neuronal instantiation of model-free RL; it depends on dopamine inputs into the striatum that serve to increase the likelihood of performing rewarded actions (Dolan and Dayan, 2013; Schultz et al., 1997). The second RL method is model-based RL, which is associated with goal-directed actions. It generates predictions via a computationally expensive process that depends on a model of the environment, but it is also able to flexibly respond to environmental changes (Daw et al., 2005). Our understanding of model-based RL is more limited, in part because it requires a model of the behavioral task, and it is unclear how such a model would be implemented at the neuronal level (Behrens et al., 2018).

Recent work has suggested that the OFC might play an important role in using models that represent the structure of a task (Schuck et al., 2016; Wilson et al., 2014). This is similar to the notion of a “cognitive map,” which has long been associated with the HPC (Doré et al., 1998; Eichenbaum et al., 1999; Howard et al., 2014; O’Keefe and Nadel, 1978; Wikenheiser and Schoenbaum, 2016), consisting of a network of associations that specifies how various components of a task relate to one another. However, it is unlikely that the OFC is responsible for building task models because it typically encodes little information about sensorimotor contingencies (Abe and Lee, 2011; Padoa-Schioppa and Assad, 2006; Wallis and Miller, 2003). This contrasts with the HPC, where neurons encode sensorimotor contingencies in addition to spatial and temporal contexts, precisely the kind of information that is essential for building task models (Howard et al., 2014; McKenzie et al., 2014). One possibility is that both the HPC and OFC make critical contributions to model-based RL, with HPC responsible for constructing the cognitive map that instantiates the neuronal representation of the task model and the OFC responsible for using the cognitive map to generate reward predictions that can be used to guide decision-making.

Studies of rodents using sensory preconditioning paradigms have provided support for this separation of OFC and HPC functions (Wikenheiser and Schoenbaum, 2016). Subjects first learn an arbitrary association between two sensory cues; i.e., that cue A predicts the occurrence of cue B. When one of these cues is subsequently paired with a reward, subjects can use their knowledge of the world (that A and B co-occur) to infer that the other cue is also likely to lead to a reward. The retrosplenial cortex is one component of the cortical circuit projecting to the HPC (Aggleton, 2012; Lavenex and Amaral, 2000), and its inactivation leads to specific deficits in learning the association between sensory cues but leaves conditioning to rewards intact (Robinson et al., 2014). In contrast, OFC inactivation impairs the ability to use the A-B association to make inferences about rewards (Jones et al., 2012). Thus, the HPC may be important for constructing associative networks that represent the world, whereas the OFC could use those maps to make better reward predictions that can guide choice behavior.

The interaction of the OFC and HPC therefore reflects the construction of an online representation of value guided by task structure. Our single-neuron data from the OFC is consistent with such a representation, with OFC neurons encoding the current value of the pictures during the fixation epoch. Our task design may have encouraged a strategy whereby the animal explicitly maintained such a representation. The constantly changing reward contingencies could have discouraged reliance on long-term storage of stimulus-reward associations, whereas the small number of pictures could have encouraged the use of working memory processes to retain the picture values. This interpretation is consistent with neuroimaging findings in both humans and monkeys, which have demonstrated the importance of the OFC and HPC when values are not cued by the current sensory environment, such as when choice options are unavailable (Fouragnan et al., 2019) or when estimating the value of a novel choice (Barron et al., 2013).

We note that although HPC stimulation had similar effects on learning as OFC stimulation, it does not mean that the impairment reflects the same underlying function. For example, the cognitive maps constructed of the HPC might be used for a broad range of cognitive processes, whereas, those of the OFC it might be used for a more restricted purpose subserving optimal decision-making. In addition, our HPC stimulation experiment did not include the same battery of controls as our OFC stimulation experiments, and so the effects of HPC stimulation may not be mediated via the theta oscillation. Our results highlight the interaction of the HPC and OFC during reward-guided behavior as a fruitful avenue for future research.

Conclusions

Dysfunction of both the OFC (Fernando and Robbins, 2011) and anterior HPC (Small et al., 2011) has been implicated in a large variety of neuropsychiatric disorders. Many of the symptoms and causes of neuropsychiatric disease can be understood as dysfunctional RL processes, an approach that is central to the nascent field of computational psychiatry (Huys et al., 2016). A better understanding of the patterns of activity in the OFC that underlie model-free and model-based RL could lead to development of treatments based on closed-loop microstimulation, in which microstimulation is only applied when a specific maladaptive pattern of activity is detected. For example, rodent models have shown that electrical microstimulation can be used to reverse the neuronal and behavioral sequelae of addiction (Creed et al., 2015), and optogenetic activation of the OFC can shift behavior away from habitual behavior toward goal-directed behavior (Gremel and Costa, 2013), supporting the notion of using OFC closed-loop microstimulation as a treatment strategy.

STAR★METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources should be directed to the lead contact Eric Knudsen (eric.knudsen@berkeley.edu) and will be fulfilled on request. This study did not generate any new unique reagents.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All procedures were performed in accordance with the National Research Council guidelines and approved by the University of California at Berkeley Animal Care and Use Committee. Subjects were two male rhesus macaques (Macaca mulatta), aged 6 and 8 years, and weighing 9 and 13 kg at the time of recording (subjects V and T, respectively). Subjects sat head-fixed in a primate chair and interacted with the task via eye movements measured with infrared eye monitoring equipment (SR Research, Ottawa, Ontario, CN). Stimulus presentation and behavioral contingencies were controlled using the MonkeyLogic toolbox (Asaad et al., 2013) in the MATLAB (The Mathworks, Natick, MA) environment. Subjects each had a large unilateral recording chamber situated over the frontal cortex with access to the temporal lobe.

METHOD DETAILS

Task Design

Subjects performed a value discrimination learning task in which they were required to learn and choose between pairs of probabilitically-rewarded pictures. A single trial began with the presentation of a small, red fixation cue in the center of the screen which subjects were required to fixate continuously for 700 ms. After the fixation period, we presented one (forced choice, 20% of trials) or two (free choice, 80% of trials) reward-predictive pictures. Three pictures were used within a session and they consisted of natural images sized between 1.5 - 2 degrees of visual angle. Novel pictures were used each day. Subjects could saccade freely between each available option, and the ultimate choice was made by fixating on the preferred picture for 425 ms. Following choice, a 500 ms delay preceded either a reward or no reward. There was a 2000 ms intertrial interval. Initially, each picture was associated with a different probability of reward (P_rew), ranging from 0.1 to 0.9. Stable reward contingencies were selected a priori to ensure that each of the three pictures was discriminable in value, such that one picture rarely earned reward (P_rew < 0.3), one was intermediately rewarded (0.4 < P_rew < 0.6), and the last was highly predictive of reward (P_rew > 0.7).

We quantified the animal’s performance via a success rate, which was the proportion of trials where they selected the more valuable picture. This measure was required to exceed a criterion level for at least 35 trials before values began to drift. Based on training data, we set this criterion at 0.7 for subject V and 0.65 for subject T. Once this criterion was reached, reward probabilities, P_i,t (the probability of reward delivery for ith picture on trial t), drifted toward new stable points according to a bounded random walk, such that P_i,t←P_i,t−1 + N(β, σ), where each step, N, is drawn from a normal distribution of mean μ and standard deviation σ. For all data here, μ = 0.05 and σ = 0.01.

Neurophysiological recording

After initial training, subjects were fitted with head positioners and imaged in a 3T MR scanner. We used these images to generate 3D reconstructions of each subject’s skull and target brain areas (Fedorov et al., 2012; Gray et al., 2007). Both subjects were implanted with custom, radiolucent recording chambers fabricated from polyether ether ketone (PEEK). Each recording session, up to 6 multisite linear electrodes (16-channel V-or K-probes, Plexon, Dallas, TX) were lowered into OFC and/or the anterior portions of HPC. We printed custom designed recording grids on an SLA 3D printer (Form 2, Formlabs, Cambridge MA) to ensure that electrode trajectories targeted the correct brain area (Knudsen et al., 2019). In each region, neurons were sampled randomly rather than prescreened for selective responses. Neuronal signals were digitized using a Plexon OmniPlex system with continuous spike-filtered signals acquired at 40 kHz and local field-filtered signals acquired at 1 kHz.

Neuronal activity was recorded over the course of 25 sessions prior to the stimulation experiments (V: 16 sessions, T: 9 sessions). Our OFC recordings were located within areas 11 and 13 of OFC, as determined from gray-white matter transitions (V: 389 contacts, T: 288). We targeted the CA1 subfield of anterior HPC, since there are strong projections from this region to OFC in the macaque (Barbas and Blatt, 1995) and it has recently been implicated for its role in value learning in rodents relative to other HPC subfields (Jeong et al., 2018). We determined that electrodes were positioned in HPC based on three electrophysiological criteria, which were guided by previous studies of primate hippocampus (Baraduc et al., 2019; Jutras et al., 2013; Skaggs et al., 2007; Wirth et al., 2003). The three criteria were prominent activity in the theta band, the presence of high-frequency events in the LFP (sharp waves), and the presence of complex-spiking neurons, whose overall firing rates were generally sparse (1–2 Hz) but had interspike intervals of < 20 ms (i.e., bursting). For HPC recordings, we sampled from a total of 128 contacts (V: 57 in 7 sessions, T: 71 in 9 sessions). For both OFC and HPC recordings, in order to avoid including spurious results due to volume-conduction within white matter, we only included electrode channels that either recorded LFP in the presence of spiking neurons, or channels that were located between channels where we recorded spiking neurons.

Electrical microstimulation

Single platinum iridium electrodes (100 – 300 kΩ, MicroProbes Inc) were lowered adjacent to at least one multisite probe in the target brain area. Our closed-loop stimulation setup consisted of a neuronal feature extractor and a stimulation trigger (Figure S5). The feature extractor performed online filtering and computations of analytic amplitude and phase from Hilbert-transformed LFP signals, averaged across all recording sites on a given probe. We used a combination of the two signals (analytic power and phase) as the controller signal: a stimulation trigger was sent for every cycle of phase that power exceeded a heuristically defined threshold. We observed the dynamic range of the theta power recorded during the first 200 trials of the session. We then set the trigger level for the closed-loop stimulator at approximately one half of the observed dynamic range. The behavioral task provided the signal to gate the ongoing stimulation trigger from the feature extractor. The feature extractor and behavioral gate both had to be positive (+5 V) to provide the final TTL signal to trigger a PlexStim stimulator (Plexon). There was a mean lag of 64 ± 3 ms from threshold crossing until pulse delivery. We performed pilot experiments to determine the optimum experimental parameters for affecting neural activity and behavior. We stimulated with biphasic, cathodal-leading, 50 μA constant-current pulses. Each pulse lasted 150 ms and was delivered at the peak theta phase. We determined these stimulation parameters via piloting in one subject.

For closed-loop sessions targeting theta, each stimulation trigger corresponded to the delivery of a single current pulse. For those targeting beta, we delivered 3 pulses per trigger at beta frequencies (20 Hz). We adopted this approach due to technical limitations of our closed-loop system. We were constrained to a polling rate of approximately 16 Hz (1/64 ms), so we compensated for this by delivering 3 pulses at beta frequencies (20 Hz) for every peak in beta identified, thus approximating the proportion of beta cycles that would have been decoded given a more optimal closed-loop system. This approach meant that the stimulation was not as tightly aligned to the underlying neuronal oscillation compared to our closed-loop theta stimulation, but we wanted to err on the side of delivering more current than less since this would be a stronger test to rule out non-specific effects of electrical stimulation, such as general increases in cortical excitability.

For open-loop stimulation, we randomly delayed stimulation by 1 to 300 ms from the first triggering of the controller signal on a trial. The stimulation consisted of 5 pulses delivered at 6 Hz. This ensured that we delivered approximately the same number of stimulation pulses during the fixation epoch in both the open- and closed-loop conditions, but the stimulation pulses were uncorrelated with the theta oscillation in the open-loop condition.

Neuronal data preprocessing

Neurons were excluded if their mean firing rate across the course of the session was less than 1 Hz. In addition, to ensure adequate isolation, we excluded neurons where more than 0.2% of interspike intervals were less than 1500 μs. We performed single neuron analyses on 566 neurons in subject V, and 275 in subject T. On average, we recorded 33 well isolated OFC neurons per session. Single neuron activity was transformed into a binary time series at 1 ms resolution, where 1 indicated the presence of a spike, and 0 the absence. Single unit time series were smoothed by a 50 ms boxcar and aligned to the appearance of the reward-predictive pictures. LFP signals were filtered using a finite impulse response (FIR) filter of order 1000 using the FFT-based method of overlap-add (Schafer and Oppenheim, 1989). Signals were notch-filtered at 60 Hz and its harmonics, and then band-pass filtered at theta (4-8 Hz), beta (12-30 Hz), and gamma (30-60 Hz), based on periodograms obtained by band-pass filtering the signal in overlapping windows of 3 Hz. Analytic amplitudes and phases were obtained from Hilbert transforming each pass band.

QUANTIFICATION AND STATISTICAL ANALYSIS

Behavioral modeling and analyses

We modeled behavior using a simple RL model that derived value estimates of each picture based on its reward history (Sutton and Barto, 1998). The model updated the estimated value of pictures after the animal received each outcome (reward or no reward). The learning rule is described by a temporal difference update function:

$$Q_{i,t}\leftarrow Q_{i,t-1}+\alpha (Q_{i,t-1}-R_{t-1})$$

where Q_i,t is the estimate of the value of picture i on trial t, defined as the last estimate (t − 1) plus a prediction error term scaled by α, the learning rate parameter, that weights the contribution of each prediction error to learning. These value estimates were then used to model choice behavior between the currently available pictures < i, j > using the softmax activation function such that:

$$P(choose{Q}_i|Q_i,Q_j)=\frac{e^{\beta Q_i}}{e^{\beta Q_i}+e^{\beta Q_j}}$$

where β is a free parameter that determines the discriminability of value estimates. We fit to subject behavior by iterating the model over α ∈ [0.001, 1] and β ∈ [1, 100] and finding the set of parameters that best described choice behavior (measured via R²). The resultant value estimates from the winning model were then used in subsequent analyses of neuronal data.

Stable periods had fixed reward contingencies that did not change from trial to trial. Drift periods were those where reward contingencies slowly changed from one stable period to the next. Stable and drift periods varied in length, partly due to the speed with which the animal adjusted his behavior to the changing reward contingencies, and partly due to the randomness of the drift process. To correlate neuronal activity with learning across many sessions, we converted the variable-length stable and drift periods into a standardized learning cycle. Pre- and post- drift periods were defined as the 25 trials preceding and following a drift period. We then discretized the drift period into 35 uniformly spaced trial bins, such that each bin contained between 0 and 4 trials depending on the original length of the drift period (Figure S1). For the OFC-HPC theta synchrony data presented in Figures 6 and S11, we broke the learning cycle into four windows: (1) pre-drift, the 25 stable trials before contingencies began to drift, (2) early drift, the first 17 trials of the drift period, (3) late drift, the second 18 trials of the drift period, and (4) post-drift, the 25 stable trials after contingencies stabilized to their new values.

Measuring information encoded by OFC neurons in the fixation epoch

For each neuron, we calculated the average firing rate, FR, during the 500 ms following onset of fixation. We selected this epoch to match the period of high theta power in the LFP. We used the RL model to determine subjects’ estimates of the value of each the three pictures on each trial. We tested two alternate models of how neurons might encode value information during fixation. Specifically, we examined whether values were maintained in a ‘value-centric’ space or a ‘picture-centric’ space. In the value-centric model, we examined whether neurons were encoding the three value estimates, such that on a given trial, t, there were three values: Q_low was the lowest value picture, Q_middle was the middle value picture and Q_high was the highest value picture. In addition, we included parameters that could capture whether neuronal activity encoded events that had happened on the previous trial: I_t-1 was the identity of the chosen picture on the previous trial, Q_t-1 was the value of the previously chosen picture, and R_t-1 was whether it was rewarded. Trial number, t, was included as a nuisance parameter to account for non-specific changes in firing rate across the course of the session. The full regression model was:

$$FR=b_0+b_1{Q}_{low}+b_2{Q}_{middle}+b_3{Q}_{high}+b_4{I}_{t-1}+b_5{Q}_{t-1}+b_6{R}_{t-1}+b_{7}t$$

The picture-centric model examined whether neurons encoded the value of specific pictures, such that on trial, t, there were three values associated with the three pictures, Q₁…Q₃. The full regression model was:

$$FR=b_0+b_1{Q}_1+b_2{Q}_2+b_3{Q}_3+b_4{I}_{t-1}+b_5{Q}_{t-1}+b_6{R}_{t-1}+b_{7}t$$

Analysis of phase alignment, phase synchrony, and directed coherence

To measure cross-trial phase alignment and interregional phase synchrony, we extracted phase information from bandpass-filtered signals using the angle of the Hilbert transform. The strength of phase alignment was determined by calculating the mean resultant vector length, R, across trials, which describes the degree to which a phase is conserved across trials such that for the phase ϕ at time point t at frequency f:

$$R=\frac{1}{\#trials}\left|\sum _{trial=1}^{\#trials}exp(i{\phi }_{trial}(f,t))\right|$$

This analysis was performed separately for each electrode. Average phase alignment, as in Figures 2D and 6A(and Figures S4B and S11A) was calculated across all trials. For learning analyses, we used the standardized learning cycle bins described above to observe how the phase alignment changed across learning using a sliding average of 16 trial bins stepped across each 85 trial bin learning cycle. This same analysis was applied to firing rates to investigate the relationship between theta phase and single neuron firing. For each neuron, we calculated the phases at which spikes occurred, during 400 ms bins (50 ms increments) across the length of the trial. In each bin, we calculated R of the phase distributions.

To measure the strength of interregional synchrony, we calculated a cross-area phase-alignment value, PLV (Brincat and Miller, 2015; Lachaux et al., 1999). PLV is computed similarly to R above, except the exponent term becomes the difference between phase from two electrodes:

$$R=\frac{1}{\#trials}|\sum _{trial=1}^{\#trials}exp(i{\phi }_{trial}(f,t)[{\phi }_{trial,trodei}(f,t)-{\phi }_{trial,trodej}(f,t)])|$$

PLV measures the degree to which the LFP recorded on distinct pairs of electrodes is aligned across trials, independent of signal power or absolute phase. This analysis was carried out for all OFC-HPC pairs (1049 subject V, 2528 subject T). For display purposes only (Figure 6C; Figure S11B), PLV pseudocolor plots were smoothed with a two-dimensional boxcar (3 trials, 100 ms).

To test the influences between OFC and HPC channels, we computed the generalized partial directed coherence (GPDC) between pairs of channels in the two regions (Baccala et al., 2007). This measures the interaction between channels after factoring out autoregressive effects. Pairs of LFP time series were fit to a multivariate autoregressive (MVAR) model:

$$x(t)=\sum _{k=1}^p{A}_{k}x(t-k)+w(t)$$

where x(t) is the LFP time series data vector at time t, A_k is the autoregressive coefficient describing the interactions between the two series at the k^th time lag, p is the maximum lag, and w(t) is the residual error from the model fit. We systematically varied the number of lags used to fit the MVAR model for pairs of HPC and OFC channels, then determined the maximum lag, p, that best described the data by minimizing the least-squares error. This corresponded to ~100 ms, similar to previous work (Brincat and Miller, 2015). Models were fit separately with a 500 ms time window stepped in 100 ms increments across the trial. For analysis of stimulation effects (Figure 7B) model coefficients were calculated from no stimulation and stimulation trials separately. Once computed, model parameters were then transformed into the frequency domain as A_ij for the i^th OFC channel and the j^th HPC channel (or vice versa) such that:

$${\underset{\_}{\overset{}{A}}}_{ij}(f)={\delta }_{ij}-\sum _{k=1}^p{a}_{ij}(k)e^{-j2\pi fk}$$

where f is frequency, and δ_ij = 1 when i = j and 0 otherwise. GPDC, π, for HPC-OFC LFP pair i and j at frequency f was calculated as:

$${\pi }_{ij}(f)=\frac{\frac{1}{{\sigma }_i}{\underset{\_}{\overset{}{A}}}_{ij}(f)}{\sqrt{\sum _{k=1}^N\frac{1}{{\sigma }_k^2}{\underset{\_}{\overset{}{A}}}_{kj}(f){\underset{\_}{\overset{}{A}}}_{kj}^T(f)}}$$

where T is the transpose operation and where scaling by σ, the standard deviation of the residual error from the model fit, serves to mitigate bias introduced by variation in signal amplitude (the generalized part of GPDC). GPDC was computed using-theta filtered LFP data averaged from 4-8 Hz.

Statistics

All statistical tests are described in the corresponding figure legends or the main text. Error bars indicate standard error of the mean unless otherwise specified. All comparisons were two-sided. Post hoc comparisons used Tukey’s Honestly Significant Difference test unless otherwise stated.

DATA AND CODE AVAILABILITY

The datasets and code supporting the current study are available from the lead contact on request.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental Models: Organisms/Strains
Non-human primate (macaca mulatta)	UC Davis	N/A
Software and Algorithms
MATLAB	The Mathworks	https://www.mathworks.com/products/matlab.html
Omniplex	Plexon	http://plexon.com/
Offline Sorter	Plexon	http://plexon.com/
PlexStim	Plexon	http://plexon.com/
Monkey Logic Toolbox for MATLAB	NIH	https://www.brown.edu/Research/monkeylogic/
3D Slicer	BWH	https://www.slicer.org/
Eyelink 1000 frontend	Eyelink	https://www.sr-research.com/eyelink-1000-plus/
Circular Statistics Toolbox for MATLAB	Philip Berens	https://github.com/circstat/circstat-matlab
CubeHelix colormap algorithm	Dave Green	http://www.mrao.cam.ac.uk/~dag/CUBEHELIX/

Highlights.

• Theta activity in macaque OFC correlates with learning values of reward predictive cues

• Disrupting theta with microstimulation impairs learning of new values

• OFC neurons encode value in phase with theta, which is disrupted during stimulation

• Hippocampal stimulation disrupts theta in both regions, leading to learning deficits