Seasonal food webs with migrations: multi-season models reveal indirect species interactions in the Canadian Arctic tundra

Abstract

Models incorporating seasonality are necessary to fully assess the impact of global warming on Arctic communities. Seasonal migrations are a key component of Arctic food webs that still elude current theories predicting a single community equilibrium. We develop a multi-season model of predator–prey dynamics using a hybrid dynamical systems framework applied to a simplified tundra food web (lemming–fox–goose–owl). Hybrid systems models can accommodate multiple equilibria, which is a basic requirement for modelling food webs whose topology changes with season. We demonstrate that our model can generate multi-annual cycling in lemming dynamics, solely from a combined effect of seasonality and state-dependent behaviour. We compare our multi-season model to a static model of the predator–prey community dynamics and study the interactions between species. Interestingly, including seasonality reveals indirect interactions between migrants and residents not captured by the static model. Further, we find that the direction and magnitude of interactions between two species are not necessarily accurate using only summer time-series. Our study demonstrates the need for the development of multi-season models and provides the tools to analyse them. Integrating seasonality in food web modelling is a vital step to improve predictions about the impacts of climate change on ecosystem functioning.

This article is part of the theme issue ‘The changing Arctic Ocean: consequences for biological communities, biogeochemical processes and ecosystem functioning’.

1. Introduction

The Arctic is experiencing larger rises in surface air temperature compared to anywhere else on Earth, a phenomenon known as polar warming amplification [1]. An emergent feature of climate simulations is pronounced seasonality to polar warming amplification: winter warming is occurring four times faster than summer warming due to atmospheric processes such as dynamical feedbacks in energy transport [2–6]. Arctic ecosystems are expected to be profoundly impacted by these aspects of climate change, as biological and chemical processes are structured by seasonal shifts in temperature, snow, ice cover and nutrient availability [7,8]. It is therefore paramount to develop accurate dynamical models based on field data, which capture the seasonality of Arctic community dynamics, in order to make predictions about how warming might impact Arctic ecosystems, including tundra, polar deserts and the Arctic Ocean.

Many empirical studies have assessed the looming threats that face Arctic communities under various climatic regimes [9–11]. Ideally these assessments would involve information about all trophic levels: long-term datasets of multiple population attributes across multiple species [12–15]. In terrestrial ecosystems, Arctic vegetation exhibit various responses to warming in space and time (e.g. through changes in phenology and productivity) as well as species-specific sensitivity to warming [16–18]; in many cases there is an increase in primary production [15]. Warmer temperatures and earlier snowmelt may also impact the phenology of Arctic wildlife, such as the nesting cycle of birds [19] or small rodent population dynamics [20]. Furthermore, trophic mismatch, i.e. a lack of synchrony between the phenology of consumers and their resources, can negatively affect the fitness of Arctic herbivores [21]. When considering the response of ecological communities as a whole, the net effect of climate change may be modified by indirect interactions [22]. But in Arctic communities dominated by vertebrates, herbivore-mediated cascading effects of climate on plants tend to lag behind the direct effects of climate warming, especially when key herbivores are long-distance migrants [23]. It has been suggested that allochthonous subsidies from more productive ecosystems can amplify or dampen the effects of a changing climate on different trophic levels in the Arctic tundra [24,25].

A drawback of many studies on Arctic ecosystems is that data tend to only be available for the growing season, given the unique difficulties of sampling in winter conditions [26]. However, winter is the longest season in the Arctic and a critically important season for these ecosystems [20,27,28]. During winter, active generalist carnivores feed exclusively on resident herbivores, which remain active under snow or ice cover; carnivores may also exploit marine resources, above-snow carrion and cached food. The dynamic behaviour when migrants arrive in the spring depends heavily on the populations of the resident species. Since these populations are in large part determined by winter dynamics, winter may be essential for the overall community dynamics [29]. Despite strong seasonality driving species interactions, very few studies have explicitly modelled multi-seasonal Arctic community dynamics [30,31].

Often the seasonality which is characteristic of some types of communities is not explicitly included in theoretical models, despite the acknowledgement of its importance by ecologists, likely due to the mathematical difficulties in handling large variability [32]. Efforts to incorporate seasonality into models reflects a trend in ecology away from modelling ecological systems with equilibrium dynamics (e.g. mass-balance models) [33]. There has been a growing number of studies using models which can incorporate the seasonality of these communities in a way that reflects the underlying ecology beyond simple time-varying parameters [33–37]. Food web dynamics with migrating species is an example where these more structured models are appropriate because the food web topologies differ among seasons when migrants are present or absent from resident communities at different times of the year. Basic models with migrating species thus require: (i) a dynamical system that can have multiple equilibria, (ii) a set of coupled dynamical equations to capture species interactions for each season, and (iii) a way to switch between seasonal dynamics corresponding to the arrival or departure of migrating species. An appropriate framework to handle systems with both fast (discrete) and slow (continuous) dynamics is a hybrid dynamical system, which also has the capacity to deal with multiple distinct equilibria. The fast dynamics correspond to discrete changes such as migration, a fast-topological change in the food web structure due to the arrival or departure of migrating species. Slow dynamics might correspond better to predator–prey interactions that occur in each season. A hybrid systems framework allows classical, continuous differential equations to be applied to each season without having to resort to discontinuities in dynamical equations via a time-varying parameters approach. Furthermore, hybrid systems can accommodate time-dependent switches such as seasonal changes in predator functional responses [36] in addition to state-dependent behaviours such as a choice of breeding locations by predators in response to prey density.

Our objective is to investigate the relative advantage of using multi-season models to expose essential information about pairwise species interactions compared to non-seasonal models. We build a multi-season dynamical model for predator–prey interactions in a simplified tundra food web (lemmings–foxes–geese–owls). The seasonality in this model is introduced by a switch in dynamics caused by presence/absence of two species: the snow goose (Chen caerulescens atlantica) as a migrant prey and the predatory snowy owl (Bubo scandiaca), which is functionally absent in the winter. Our model is based on a hybrid dynamical systems framework where migration is modelled as fast dynamics and represents a discrete change in the food web topology, thus leading to a system with multiple distinct equilibria. Slow dynamics corresponds to Lotka–Volterra predator–prey interactions for each season. State-dependent behaviour is implemented for the snowy owl which are present in the summer only when the spring brown lemming densities are high. We attempt to include key processes of the underlying dynamics in order to generate representative, long-term time-series for each species over all seasons. We achieve this by constraining the model parameters using summer data on species interactions and population dynamics to generate possible time-series. We show that our model is able to reproduce the multi-annual cycling of lemmings and their amplitudes. We rely on convergent cross mapping [38], which uses time-series to infer causal interaction networks, in order to study direct and indirect interactions between species (i.e. can the population dynamics of a prey be inferred from the predator time-series?). We compare the pairwise species interactions that would be inferred from three modelling scenarios: (i) a static model (no seasonality), (ii) a multi-season model, and (iii) summer snapshots from the multi-season model.

2. Methods

Predator–prey interactions play an important role in the tundra food web of Bylot Island, Nunavut, Canada (73° N, 80° W) and have been parametrized using data from long-term studies of population abundance and diet at this site [39]. In this system, the snow goose (Chen caerulescens atlantica) is a migratory bird species and the dominant herbivore (88% of herbivore biomass on average) during the summer. Two lemming species are present, the brown (Lemmus trimucronatus) and collared (Dicrostonyx groenlandicus) lemming, which constitute 2% and 25% of biomass during years of low and peak abundance, respectively. Both lemming species exhibit synchronous multi-annual cycles, but the amplitude of peaks are far greater in brown than in collared lemmings [15]. The main predator of the snow goose and lemmings are Arctic foxes (Vulpes lagopus). In peak years of brown lemming abundance, snowy owls can also be found on Bylot and represent a significant proportion of carnivore biomass. Although other predators are present in this system [25], these five species were chosen to construct (simplified) food webs in our multi-season model because they are the most abundant and are representative of each key functional group in the system (prey, predator, resident and migrant). The resident food web consists of the Arctic fox and two sympatric lemming species. During summer, migrating snow geese are present and are an important alternative prey for the fox. Depending on the lemming biomass in spring, snowy owls can enter the system as an additional predator on all prey species in addition to the Arctic fox in summer with approximately 85% of their diet coming from both species of lemmings [39].

(a). Data on biomass, diet, consumption and production

We use the same approach as described in Legagneux et al. [39] to conduct fieldwork, compile field data and obtain values for Ecopath model parameters for the period 1993–2009 to extend the dataset to 2010–2018 using more recent field data. Similar diet matrices are used. For both lemming species, we use mean lemming abundance for the months of July and August. Trapping occurred in both mesic and wet habitats. The percentages of wetland and mesic habitats in the study area (15% and 85%, respectively) are taken into account to calculate the overall lemming biomasses [40]. For the snow goose population, the exact same protocols are followed over the period 1993–2018 and provide comparable metrics of snow goose abundance over time [3]. The snowy owl nesting density is calculated over a searching area that varied over time but remained similar since 2007. We consider a constant Arctic fox population over time as the number of reproductive and non-reproductive adults has been found to be stable between seasons using satellite tracking [41]. Furthermore, most juveniles produced during years of high lemming abundance disperse out of the system not long after they are weaned; therefore, they are not significantly adding to the local population (D Berteaux 2020, unpublished satellite tracking data about juvenile dispersal). We use the similar density provided in [39]: 0.08 dry kg km⁻². Lemming density estimates obtained from 1993 to 2003 using snap traps are back-calculated based on new relationships obtained between snap and live trap comparisons [42]. The 2004–2018 dataset is obtained with the same live trapping protocol (see [43] for methodological details).

(b). Translating mass-balance model parameters to a static, predator–prey model

Mass-balance models use the principle that the energy input has to balance the energy output for each species in the model [44]. The Ecopath approach to mass-balancing describes trophic flows within a food web assuming the system is at its stationary point [45–47]. Legagneux et al. [39] use the following master equation, which has been successfully applied to Bylot:

$$\frac{\text{d}{B}_i}{\text{d}t}={\left(\frac{P}{m}\right)}_i{B}_i-\sum _i\left[D{C}_{ij}{\left(\frac{Q}{m}\right)}_j{B}_j\right],$$ 2.1

where B_i is the biomass (in dry kg km⁻²) of species i, (P/m)_i is the production rate (per year) of species i per unit of biomass, DC_ij is the proportion of species i in the diet of predator j, (Q/m)_j is the consumption rate (per year) of predator j per unit biomass. At its stationary point, dB_i/dt is zero and we get a balanced set of inputs and outputs. The Ecopath master equation can be translated into a general Lotka–Volterra model of the form

$$\frac{\text{d}{B}_i}{\text{d}t}=b_i{B}_i+\sum _{i\ne j}{\alpha }_{ij}{B}_i{B}_j,$$ 2.2

where b_i is the intrinsic growth rate of species i and the interaction coefficient between prey species i and predator j is given by

$${\alpha }_{ij}=-{\left(\frac{Q}{m}\right)}_j\frac{D{C}_{ij}}{{\overline{B}}_i},$$ 2.3

where ${\overline{B}}_i$ is the long-term average biomass of species i. The interaction coefficient between species j and i is

$${\alpha }_{ji}=e_{ij}{\alpha }_{ij},$$ 2.4

where e_ij = (P/m)_j/(Q/m)_j is the efficiency in the conversion of biomass for predator j. The long-term average for Lotka–Volterra is equal to its stationary point and can be used to determine the intrinsic growth rates. The static model assumes three prey (brown lemming, collared lemming and snow goose) and two predators (Arctic fox, snowy owl). We use a weighted average diet matrix of peak and low years as well as allometric values of production and consumption rates found in Legagneux et al. [39] to compute intrinsic growth rates and interaction coefficients for the static model. Allometric rather than empirical values are used for the static model to represent a suitable null model with which to compare to a multi-season model.

(c). Using a hybrid dynamical system to model Arctic community dynamics with migration

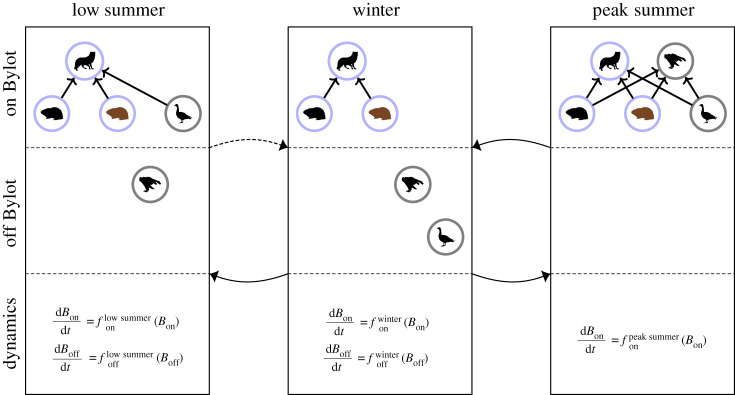
The hybrid system (i.e. automaton) corresponding to our multi-season model (figure 1) derives its structure from the Cartesian product of discrete and continuous-valued states. Our model has three discrete states corresponding to each possible seasonal food web, each represented by a separate box which we denote by winter, low summer and peak summer. A low summer is a summer when owls are absent, and a peak summer is when they are present in the food web. Whether they are present depends probabilistically on the biomass of the brown lemming being above $2.50\hspace{0.17em}{\text{dry kg km}}^{-2}$ which is the average biomass of brown lemmings from the summer data when owls were absent. Winter is taken to occur for 10 months and summer two months (i.e. from mid-June to mid-August) corresponding to the minimum length of the breeding cycle of the snow goose (laying to median end of moult) when Arctic foxes are preying on their eggs and young. The allowable transitions are represented by the arrows connecting the boxes in the automaton in figure 1; winter-to-low summer, low summer-to-winter, winter-to-peak summer and peak summer-to-winter.

Figure 1.

Hybrid automaton describing the multi-season model for a simple high-Arctic tundra food web. The species represented in the seasonal food webs are: brown and collared lemmings, Arctic foxes, snow geese and snowy owls. Their biomasses are labelled by B_on for the biomass on Bylot and B_off for the biomass off Bylot. The resident species are lemmings and foxes. The winter dynamics occurs for 10 months and the summer for two months. Allowed transitions are from winter- to-low summer (and vice versa) and from winter-to-peak summer (and vice versa). Peak summers occur with a probability that depends on the brown lemming density at the end of winter. Lotka–Volterra predator–prey dynamics are used for the species on Bylot and logistic growth is used for species off Bylot. Silhouettes of species are from http://phylopic.org. (Online version in colour.)

For each season, we illustrate the food web on Bylot and off Bylot. In both cases, all species (even the non-interacting species) are assumed to have dynamics. Gilg et al. [30] develops a model for a community of collared lemmings and their predators in eastern Greenland and has both dynamic and non-dynamic predators. Because our goal is to infer causal relationships such as trophic control regimes using time-series, it is essential that we include the dynamics of all predator species. Each discrete component of the model (i.e. ‘season’) is associated with continuous dynamics of five state variables, representing changes in species biomasses from either predator–prey interactions or density-dependent growth. Predator–prey dynamics are assumed to be of Lotka–Volterra type with linear functional responses and intraspecific density dependence for all species (see electronic supplementary material). For the prey, lemmings and snow geese, intraspecific density-dependence is implemented by a carrying capacity. The existence of an upper limit, or carrying capacity, on brown lemming populations may be imposed as it more accurately reflects their observed population dynamics [48]. We assume that the snow goose dynamics also has a carrying capacity for similar reasons [40]. Arctic foxes and snowy owls are self-regulated because of territoriality (D Berteaux & J Clermont 2020; [49]). Intraspecific interaction terms are estimated simultaneously with the model parameters for winter (see §2d and further details in electronic supplementary material). Including intraspecific terms in our model has the added benefit that the dynamics within a season has a stable equilibrium and, as a result, our multi-season model is one with multiple distinct equilibria satisfying the basic requirement of seasonal models. The general form of the dynamics for the biomass of each species, B_i (in units of dry kg km⁻²) in each season is given by

$$\frac{\text{d}{B}_i}{\text{d}t}=b_i^{(q)}{B}_i-{\eta }_i^{(q)}{B}_i^2+\sum _{i\ne j}{\alpha }_{ij}^{(q)}{B}_i{B}_j,$$ 2.5

where i = {brown lemming, collared lemming, Arctic fox, snow goose, snowy owl} labels the species and q = {winter, low summer, peak summer} labels the season. Here, b_i is the intrinsic growth rate (rate of increase for prey and mortality for predators), η_i are the carrying capacity terms for the prey or self-regulation terms for the predators (described above), and α_ij the interaction strength coefficient corresponding to the per capita effect of species j on the growth rate of species i. Geese and owls are assumed to follow logistic growth to their carrying capacity η_i when they are uncoupled from the food web on Bylot.

Choosing the model to be of Lotka–Volterra type with linear, predator–prey functional responses means that we can employ quantities from mass-balance models previously constructed for the system on Bylot [39] to set the parameters in the low and peak summer. Using this information, we can infer parameter values for the winter dynamics of our hybrid system using the method described below.

(d). Unknown parameter guesses for multi-season model

We require a procedure to guess unknown parameter values from equation (2.5) (i.e. $b_i^{(q)}$, ${\eta }_i^{(q)}$, ${\alpha }_{ij}^{(\text{winter})}$) to generate time-series for our multi-season model with which to study species interactions. The difficulty lies in the fact that direct parameter estimates are only available for the summer, but we also require estimates for the winter period as well as estimates for the intrinsic growth rates and intraspecific terms. Summer interaction strengths ${\alpha }_{ij}^{(1)}$ and ${\alpha }_{ij}^{(2)}$ are fixed using data estimates for consumption and production rates as well as diet proportions [39]. They can be found by translating parameters from a mass-balance model following standard approaches to Lotka–Volterra [14,50],

$${\alpha }_{ij}^{(q)}=-{\left(\frac{Q}{m}\right)}_j^{(q)}\frac{D{C}_{ij}^{(q)}}{{\overline{B}}_i^{(q)}},$$ 2.6

where terms have the same interpretations as in §2b; however, the superscript q indicates their value in season q.

To estimate unknown parameters (i.e. $b_i^{(q)}$, ${\eta }_i^{(q)}$, ${\alpha }_{ij}^{(\text{winter})}$) we develop an algorithm to help refine guesses for their values by comparing the multi-season model biomass output, obtained by inserting these guesses into the dynamics of the hybrid system, to the available summer biomass data. We do not constrain the fox dynamics to be constant as observed in the data, instead we allow for fluctuations. Because other resident mammalian predators in this system could actually fluctuate over time, we allowed fox population to fluctuate to account for this process in our system given that we consider foxes to be representative of this functional group. The idea behind this algorithm is to incrementally improve the qualitative aspects of the model output (i.e. reproducing lemming peaks and crashes) by slowly adding more time-points, in this case 3 years at a time up to 26 years which is the entire time-span over which data are available, to make a more informed guess about what the unknown parameters may be. The assumption is that as more data are added in, the ‘difference’ between successive guesses (represented as a vector), {b_i, b_i+1} decreases, where b_i is the parameter set estimated from the time-series over 1993 to 1993 + 3 × i and b_i+1 the set over 1993 to 1993 + 3 × (i + 1). We calculate the difference between successive guesses as

$$\text{difference}=\frac{|{\mathbf{\text{b}}}_{i+1}-{\mathbf{\text{b}}}_i|}{(|{\mathbf{\text{b}}}_{i+1}|+|{\mathbf{\text{b}}}_i|)/2}$$ 2.7

and then take the root-mean-square (RMS) by squaring each of the components, taking the mean of the result, and then taking the square root. Further details are provided in the electronic supplementary material.

(e). Identifying multi-annual cycling in lemming time-series

If the generated time-series shows multi-annual lemming cycling then we expect to see some regular frequencies in the data corresponding to, for example, 3–4 years (year = 1/frequency). If there is no multi-annual cycling, then frequencies tend to exhibit noise. To test for the presence of frequencies we take the Fast Fourier Transform (FFT) of the time-series; the absolute value of the FFT output is how much of each frequency is present in the time-series. To test for multi-annual cycles, we use only the summer points in the time-series which corresponds to how these cycles are identified in data. If multi-annual cycling is present, we expect to see a range of values in the FFT output above the low amplitude noise. The spread of these values will tell us the range of cycling frequencies which are present and the highest peak will tell us the median cycle length. This is similar to the test conducted by Predavec et al. [51] on binary time-series. This test is unbiased, and quite robust, as it does not depend on an arbitrary threshold value in order to define a peak or a low summer.

(f). Inferring species interactions from causal structure

To test the necessity of using multi-season modelling in temporally-forced food webs, we consider the structure of inferred indirect interactions between species using the static model, the multi-season model, and summer snapshots extracted from merging part of the time-series generated from the multi-season model which corresponds to summer. To do this, we examine the inferred causal relationships between species using convergent cross mapping (CCM). CCM has been shown to give information about trophic control regimes (i.e. top-down versus bottom-up control in predator–prey systems) and about interspecific relationships (i.e. interspecific competition; amensalism, commensalism and mutualism) [38]. CCM is designed for testing the presence of these (causal) relationships specifically for ecological time-series, or systems which may be related through nonlinear dynamical equations. If we have two time-series, say N(t) for a prey and P(t) for a predator, CCM measures the extent that the history of N(t), specified as a collection of lags N(t − 1), N(t − 2), etc., can estimate P(t) (and vice versa). Pearson’s correlation coefficient, ρ, is computed between P(t) itself and P(t) predicted from the history of N(t). This estimate must improve (i.e. converge) with longer time-series in order to infer a causal relationship. We know that P(t) causes N(t) if ρ is positive, significant and converges because it means that information about N(t) can be used to learn more about P(t). In other words, P(t) leaves a footprint on N(t). This procedure can be carried out between any two time-series (i.e. between prey, between predators, between a prey and a predator) to infer causal structure. There is also the aspect of bidirectional versus unidirectional relationships. If the cross mapping in both directions converge we say that there is a bidirectional relationship. Otherwise, if one of these relationships is non-significant, then the relationship is unidirectional. Unidirectional relationships may indicate that there is an amensal, commensal or mutual interaction occurring (but which one cannot be determined from the CCM on its own). More details about CCM can be found in the electronic supplementary material. We conduct a CCM between each pair of species using a 500 year time-series generated from our model. First, taking one point per month to capture the seasonality for the static and multi-season model and, second, taking only months corresponding to summer. We compare the causal information between these cases.

3. Results

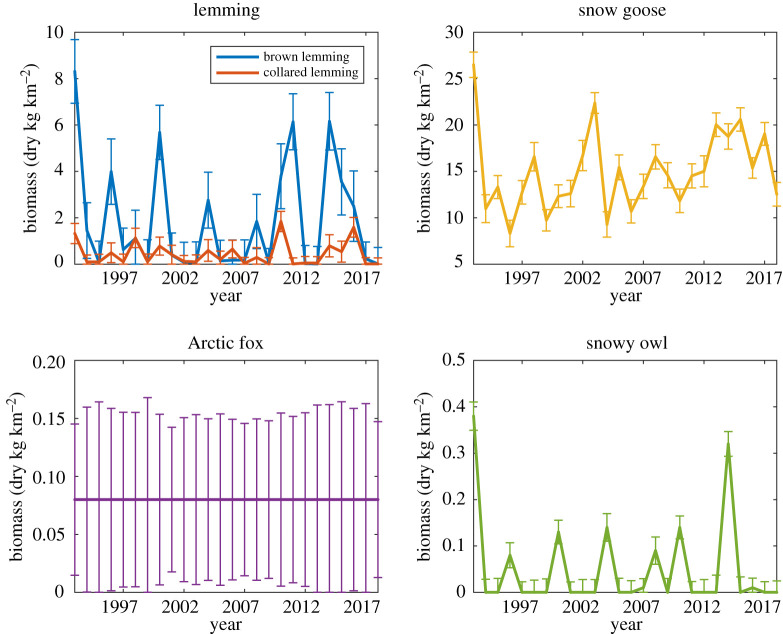
Data from wildlife monitoring on Bylot Island from 1993–2018 show strong, cyclic fluctuations in summer lemming biomass (figure 2). In the brown lemming time-series, there are seven peaks defined as a year of high density which is preceded by a year of increasing density and followed by a year of decreasing density: 1993, 1996, 2000, 2004, 2008, 2011 and 2014. Thus, there are three cycles of 3 years (1993–1996, 2008–2011, 2011–2014) and three cycles of 4 years (1996–2000, 2000–2004, 2004–2008) in the data. On average, the cycle lengths are 3.5 years long. There are 4 years which have biomass peaks greater than 5 dry kg km⁻². Collared lemmings exhibit peaks roughly synchronous with the brown lemmings (in particular, when brown lemming peaks are high) with 4 years between 1–2 dry kg km⁻². Snow geese biomass range from $10-25\hspace{0.17em}{\text{dry kg km}}^{-2}$. The biomass of adult territorial Arctic fox does not fluctuate significantly between years due to the stability of the number of breeding pairs [39] even though foxes reproduce only during peaks; offspring disperse outside the system. Snowy owl peaks almost always coincide with peaks in brown lemmings.

Figure 2.

Summer biomasses for the five species based on data collected on Bylot from 1993 to 2018. Error bars are based on the 95% confidence intervals identified in [39]. (Online version in colour.)

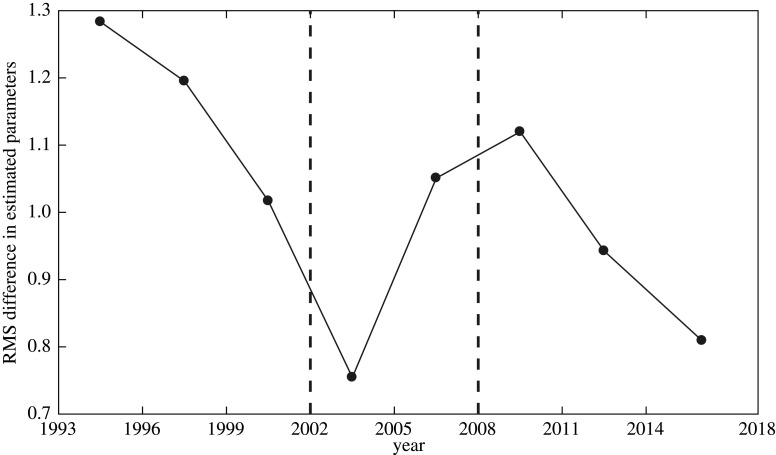
Using these data as a basis to guess unknown parameter values in our multi-season model (specifically, winter model parameters), we find that the root-mean-square (RMS) difference in successive parameter refinements equation (2.7) decreases between 1993–2002 and 2008–2018 but increases between 2002–2008 (figure 3). This suggests parameters may be non-stationary, dividing the data time-series into three segments. This is because as we add in more data, we expect a better refinement of our parameter estimates and thus a decreasing RMS. If the RMS difference becomes larger, it may suggest that the underlying parameters may have changed so we are no longer converging to the parameters describing the dynamics at that time. Thus, from our parameter refinement we find three segments with different parameter values and need to choose between them to generate model time-series. We use the statistics of the brown lemming cycle lengths from the data as this is a key characteristic of the dynamics on Bylot. The first segment between 1993 and 2002 has an average cycle length for the brown lemming density of 3.5 years (one cycle of 3 years and one cycle of 4 years); the second segment from 2002 to 2008 has an average cycle length of 4 years; and the segment from 2008 to 2018 has an average cycle length of 3 years. We therefore believe that choosing the parameter set from the first segment over 1993–2002 is justified in that it more closely represents the overall cyclic dynamics found in the data.

Figure 3.

Computation of root-mean-square (RMS) differences between successive parameter guesses. For example, the point in the middle of 1996 and 1999 represents the RMS difference equation (2.7) between the parameters describing the data from 1993 to 1996 and the parameters describing the data from 1993 to 1999. 2002 is the last year for which the RMS difference is decreasing. In 2005, it is increasing. We take the first parameter segment to be from 1993 to 2002. Afterwards, the RMS difference decreases and, consequently, we define another parameter segment from 2008 to 2018. This suggests that there may be three different parameter regimes in the time-series.

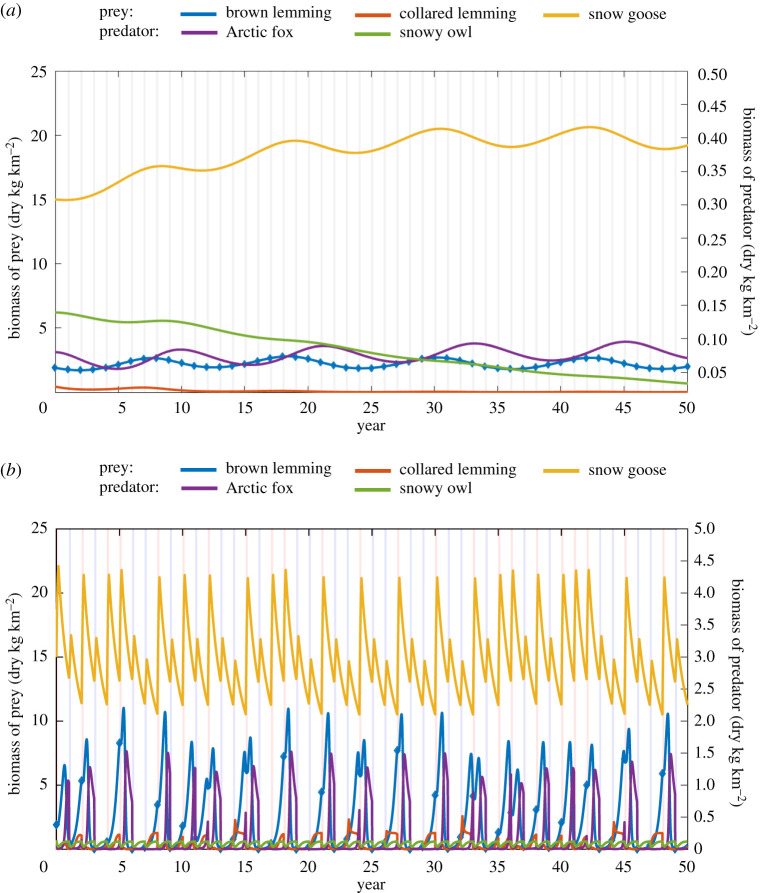
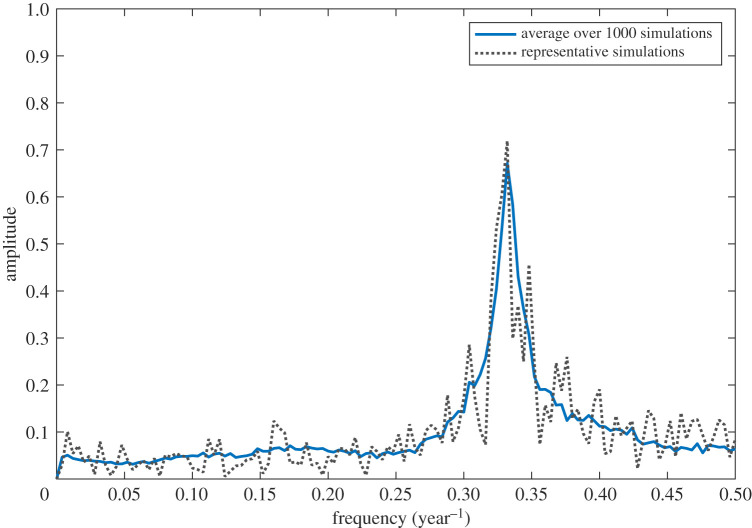
A 50 year time-series simulation is shown in figure 4b. Time-series resulting from the static model does not reproduce at all the dynamics seen in the data (figure 4a). In contrast, the time-series from the multi-season model (figure 4b) shows qualitatively similar behaviour to the data. In particular, we find that brown lemmings have large population fluctuations but with variable amplitudes with peaks of the collared lemming roughly coinciding with brown lemming, but of much smaller amplitude. Also, the fluctuations in snow goose biomass have a similar range than the data. In figure 5, we can see from the power spectrum that there is a peak at a frequency of $0.33\hspace{0.17em}{\text{yr}}^{-1}$ corresponding to a period of approximately 3 years. This peak has a spread which runs between 2.5 and 3.6 years. This is consistent with the cycle lengths observed from the data time-series and the cycling values reported in the literature. This result, in conjunction with the simulated time-series in figure 4b indicates the presence of multi-annual cycling in the brown lemming population.

Figure 4.

(a) Long-time series from the static model. Dark grey bars represent the time periods where summer would be. (b) Long-term time series (50 years) generated using parameters identified for the period 1993–2002. A threshold of $2.50\hspace{0.17em}{\text{dry kg km}}^{-2}$ is used to set the probability that a peak summer occurs. Blue bars represent the period over which a low summer happens and red bars where a peak summer happens. (Online version in colour.)

Figure 5.

Power spectrum averaged over 1000 simulated brown lemming time-series using the densities at the end of winter (diamonds in 4b). Each frequency is associated with a period of time (year=1/frequency). (Online version in colour.)

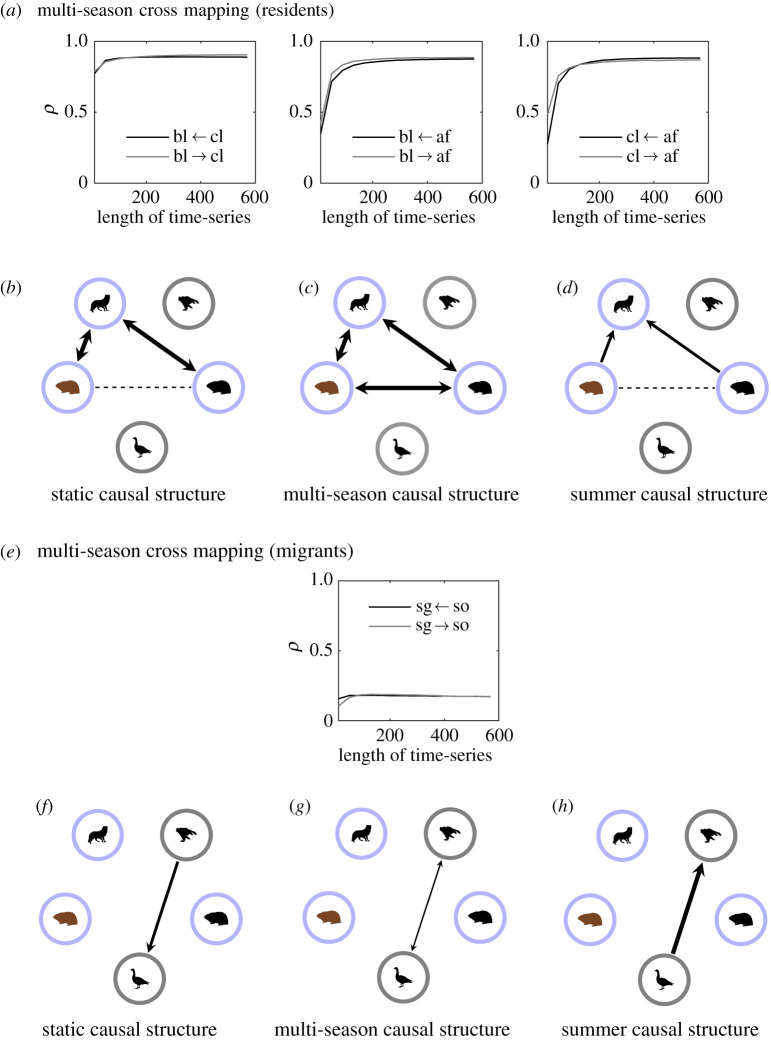
Our multi-season model captures essential season-to-season causal relationships between species: between residents, between migrants, between migrant and resident predator–prey, and intraguild relationships between prey and between predators. This is illustrated in figures 6–8 with cross map plots (Pearson’s correlation coefficient, ρ, versus length of time-series) along with the causal network structures for the three models considered: static, multi-season and summer model. The cross map plots for the static and summer models are shown in electronic supplementary material, figures S3 and S4, respectively.

Figure 6.

(a) Cross maps averaged over 50 simulations for the multi-season model between resident species. Cross maps for the static and summer models can be found in electronic supplementary material, figures S3 and S4, respectively. Only correlation coefficients, ρ, which are significantly different from zero (p < 0.05) are shown (see electronic supplementary material, section 3). A causal relationship is indicated if ρ increases as the length of the time-series increases and if ρ converges to a fixed value. Species 1 ← species 2 means that species 2 causes species 1 if the above criteria are met. Here bl, brown lemming; cl, collared lemming; af, Arctic fox; sg, snow goose and so, snowy owl. If a causal relationship is not present, then ρ can be taken to represent the degree of correlation between the variables. (b–d) Represent the strongest causal direction in the cross map for the three different models. A stippled line in the network indicates a causal relationship could not be determined due to an absence of convergence. The thickness of the lines represent the magnitude of ρ. A thicker line means a larger ρ. (e) Cross map for the multi-season model between migrant species. (f –h) Causal interaction networks between migrant species for the three models considered. (Online version in colour.)

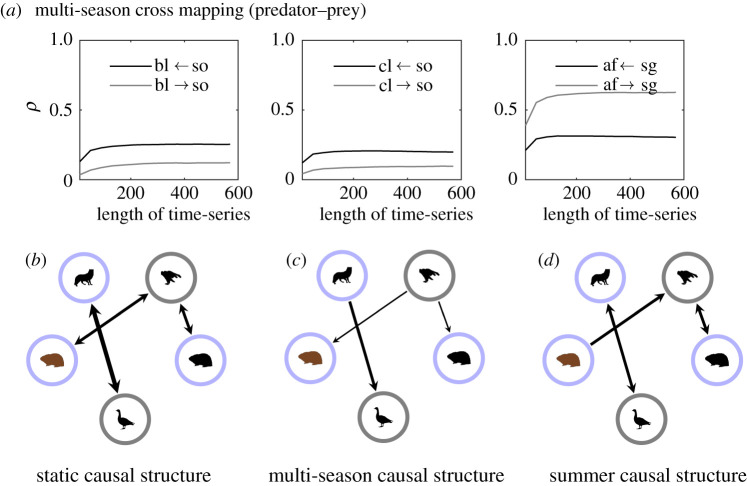
Figure 8.

(a) Cross maps averaged over 50 simulations for the multi-season model between predator–prey species. Cross maps for the static and summer models can be found in electronic supplementary material, figures S3 and S4, respectively. Only correlation coefficients, ρ, which are significantly different from zero (p < 0.05) are shown (see electronic supplementary material, section 3). A causal relationship is indicated if ρ increases as the length of the time-series increases and if ρ converges to a fixed value. Species 1 ← species 2 means that species 2 causes species 1 if the above criteria are met. Here bl, brown lemming; cl, collared lemming; af, Arctic fox; sg, snow goose and so, snowy owl. If a causal relationship is not present, then ρ can be taken to represent the degree of correlation between the variables. (b–d) Represent the strongest causal direction in the cross map for the three different models. The thickness of the lines represent the magnitude of ρ. A thicker line means a larger ρ. (Online version in colour.)

The multi-season cross mapping analysis between residents reveals strong bidirectional relationships between brown and collared lemmings, brown lemmings and arctic foxes, and collared lemmings and Arctic foxes (figure 6c). The predator–prey relationships show both top-down and bottom-up control. In other words, the predator drives population fluctuations of its prey and vice versa. When comparing the multi-season causal structure with the one obtained just looking at the multi-season model time-series over summers (i.e. summer snapshots), we find weaker causal relationships and rather bottom-up control in the brown lemming–arctic fox interaction (figure 6d). In other words, the prey fluctuates and this drives fluctuations in predator populations. Doing the same exercise with the static model (figure 6b) also shows both top-down and bottom-up control similar to the multi-season model but no indirect interaction between the lemming species can be inferred due to a lack of convergence of the cross map likely due to their time-series being strongly correlated. The multi-season cross mapping between migrants (i.e. the snow goose and snowy owl) (figure 6e) shows bidirectional predator–prey relationships (figure 6g) but much weaker ones likely due to the shorter time period over which they interact.

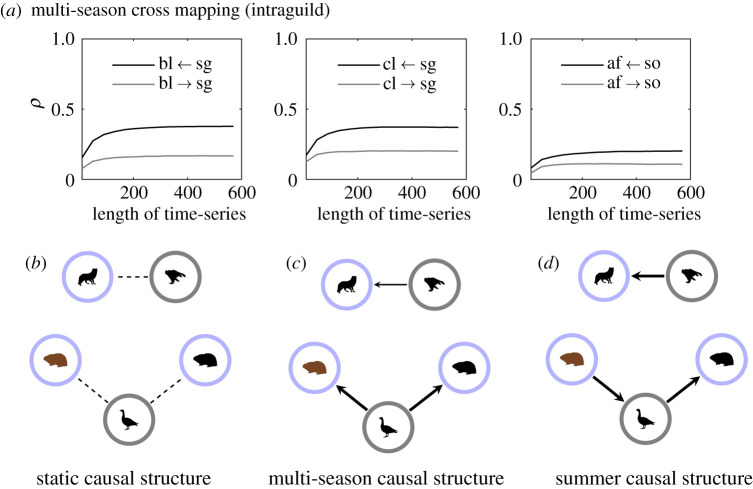
The intraguild multi-season cross mapping reveals that the migrants are causally influencing the residents in their respective guild; that is, the goose influences both lemming species and the snowy owl influences the Arctic fox (figure 7a). Comparing the multi-season causal structure (figure 7c) with the summer one (figure 7d), we see that the direction of strongest causal influence changes between the brown lemming and the snow goose. No indirect interactions can be inferred from the static model (figure 7b) and the cross mapping only reveals that there are correlations, the value of the correlation being indicated by the magnitude of ρ.

Figure 7.

(a) Cross maps averaged over 50 simulations for the multi-season model between resident and migrant predator species and resident and migrant prey species. Cross maps for the static and summer models can be found in electronic supplementary material, figures S3 and S4, respectively. Only correlation coefficients, ρ, which are significantly different from zero (p < 0.05) are shown (see electronic supplementary material, section 3). A causal relationship is indicated if ρ increases as the length of the time-series increases and if ρ converges to a fixed value. Species 1 ← species 2 means that species 2 causes species 1 if the above criteria are met. Here bl, brown lemming; cl, collared lemming; af, Arctic fox; sg, snow goose and so, snowy owl. If a causal relationship is not present, then ρ can be taken to represent the degree of correlation between the variables. (b–d) Represent the strongest causal direction in the cross map for the three different models. A stippled line in the network indicates a causal relationship could not be determined due to an absence of convergence. The thickness of the lines represent the magnitude of ρ. A thicker line means a larger ρ. (Online version in colour.)

Lastly, we consider the multi-season cross mapping between migrant predator and resident prey, and vice versa (figure 8a). We find evidence for top-down control between all pairs; that is, between the Arctic fox and snow goose (relatively strong), and between the snowy owl and lemmings (weak). Looking at the summer causal structure, we find that the relationship between the owl and the brown lemming turns into a bottom-up one (figure 8d). In the static model, both top-down control and bottom-up control is detected (figure 8b).

4. Discussion

Many ecological communities experience strong seasonal variation in their biotic and abiotic environments, particularly at high latitudes. In a strongly seasonal environment like the Arctic, there are very few studies which have modelled, at the food web level, seasonal predator–prey interactions [30,31]. Our study advances existing literature by providing a comprehensive framework (i.e. hybrid dynamical systems) to include migrants as a dynamical part of the community through fast-topological changes in the food web. With our multi-season framework we find two important features. The first is that multi-annual cycles of small rodent populations can be driven by seasonal changes in species interactions and by state-dependent behaviour governing some predator responses to small rodent densities. This result lends support for the model when compared with what is known about the drivers of multi-annual cycles in the literature. Second, and most importantly, our model captures indirect interactions between resident and migrant species in the community which non-seasonal models miss. These interactions may be essential to any model which aims to understand these temporally-forced communities and, especially, the impact of climate change on these communities.

(a). Hybrid dynamical systems capture dynamics of changing food web structure due to migration

We have constructed a multi-season model for a simplified Arctic tundra food web (lemmings–Arctic fox–snow goose–snowy owl) using a hybrid dynamical systems framework where migration is modelled as fast dynamics and predator–prey interactions as slow dynamics. Our model consists of three distinct equilibria, one for each possible seasonal food web: winter, a low lemming summer (snowy owls absent) and a peak lemming summer (owls present). The existence of multiple equilibria is a basic requirement for any model of seasonal food webs and hence represents a coherent way to look at communities that have a fast-topological change in their structure. Furthermore, a hybrid system also allows us to incorporate state-dependent behaviours; for example, in our model presence of snowy owls during summers of peak lemming abundance occurs with a probability that depends on how high the brown lemming biomass is at the end of winter. Being able to incorporate species behaviour into seasonal models is a strength of hybrid models. Gilg et al. [30] built a seasonal model for the collared lemming and its four predators in eastern Greenland: in the summer when lemmings are abundant, there is predation by migratory or partially nomadic species. Tyson & Lutscher [36] also studied predators that switch from being generalists to specialists according to seasonally varying prey densities, such as in the case of the great horned owl and the snowshoe hare. Our study illustrates another way that this state-dependent behaviour is exhibited.

(b). Seasonality and state-dependency as potential drivers of multi-annual lemming cycles

Seasonality and state-dependent behaviour are known to be important for the generation of multi-annual cycles in small rodent populations, such as lemmings. Generating cycles in our model is necessary to make meaningful comparisons of causal interactions between our model and non-seasonal models. The underlying drivers of multi-annual cycling in small rodent populations have been the cause of much debate in the scientific community [48,52]. Of particular importance to rodent cycles in Fennoscandia are seasonality as well as community composition and dynamics of predators and prey [53]. Although it is likely that different processes may come into play for different rodent populations in different geographical locations [54], these two components are common in many studies modelling cycles [30,55–58] including our model. In these models, seasonality is generated by having different parameters in winter and summer or having constantly varying parameters in time, and state-dependent behaviour is incorporated by having a delayed numerical response of predators (typically a 1 year lag) to lemming peaks.

Our model output can reproduce observed behaviours; in particular, the multi-annual cycling of the lemming populations in summer as well as the spread in their amplitudes (i.e. peak versus low densities). We generate seasonal behaviour by assuming there is a topological change in the food web structure in each season and state-dependent behaviour arises from the owl coupling to the summer dynamics (brown lemming–collared lemming–Arctic fox–snow goose) when the density of brown lemmings is high enough at the end of winter. Our approach to including seasonality and state-dependency is likely more appropriate to the type of community seen on Bylot Island and probably the Canadian Arctic in general as opposed to that seen by [58] due to the presence of (often avian) species at specific locations at different times of the year. In Fennoscandia; however, both types of models with seasonality/state-dependency can generate cycles in their respective small rodent populations. Delayed density-dependence has been identified as an important component of small rodent cycles [59]. Here, it may be that seasonality becomes a functional analogue of a delayed response by allowing prey to build up in winter when the impact of predation is lower than in summer thereby generating a time delay, which is known to be destabilizing. This mechanism is somewhat analogous to that found in Barraquand et al. [60] where overcompensating density dependence, together with phase-dependency (e.g. an increasing phase has a different density-dependent structure than a decreasing phase of a population cycle), can explain common vole population cycles in western France. The randomness in the owl coupling expands the potential for multi-annual cycling in the lemming populations. These results suggest that seasonality and state-dependency may be universal determinants of small rodent multi-annual cycles when predation behaviour is the underlying mechanism.

(c). Multi-season models can capture causal information about indirect interactions

Our multi-season model exposes indirect interactions between migrant and resident prey, which static models do not. Indirect interactions require the presence of an intermediary species and unlike direct effects, do not require a physical interaction between two species [61]. They can arise from two general mechanisms: an interaction chain, such as exploitative competition, or an interaction modification, which occurs when one species affects the interaction between two other species. In our static model, the causal signature between intraguild species (e.g. between lemming species, geese and lemmings, foxes and owls) is overshadowed by correlations in their time-series. Due to mediation by a common predator or prey over a part of the year, in our multi-season model we expect to see indirect competition between migrant and resident prey and similarly for predators. Indeed, we find that these types of causal links emerge from our multi-season model; seasonality may expose these causal relationships by disrupting persistent correlations in time-series. In models with multi-seasonality, the mechanism driving the indirect interaction may be that the snow goose ‘modifies’ the interaction between the resident lemming and fox and thus leaves a causal signature on the lemming [62,63]. However, it is not clear from the analysis which mechanism underlies the causal relationship. Furthermore, non-seasonal models appear to be unable to distinguish between resident–migrant, predator–prey relationships and resident predator–prey relationships (i.e. direct interactions). We anticipate that a multi-season perspective should provide a better estimation about real pairwise species interactions.

A further goal for quantifying pairwise species interactions in dynamical models may be to determine the sign as well as magnitude of these indirect interactions to understand phenomena such as trophic cascades. In equilibrium systems, community matrix methods are used to quantify indirect interactions. Extensions of these methods have been developed for smooth non-equilibrium systems [64]. These methods rely on numerically computing the community matrix at each state rather than having a single community matrix defined at the equilibrium. However, our multi-season model is a system which abruptly switches its dynamics between seasons. A given state can thus have more than one possible future depending on the current season. This means that each state can be associated with multiple community matrices which means that these extensions fail. New methods to determine the sign of indirect interactions need to be developed for multi-season models as contemporary methods currently available do not suffice. As a first step to address this challenge, pairwise interactions could be computed on a season-by-season basis. However, there may be discontinuities in the sign and magnitude of the indirect interactions which would require deeper investigation.

Our study demonstrates the need for seasonality in modelling food web dynamics and also the need for collecting data throughout all seasons, not just the growing season. Exclusion of these aspects in food web studies means that important information about trophic interactions and indirect interactions between species in general is lost. In addition to developing multi-season models, new theory needs to be developed to analyse community interactions. This enterprise is even more urgent for Arctic ecosystems which are poised to experience unprecedented changes in community structure and dynamics from a changing climate due to the arrival of new species. We can not assess the impact of climate change on ecosystems, in particular on strongly seasonal systems like the Arctic, without seasonality: seasonal changes in abiotic and biotic processes is fundamental to ecosystem structure and functioning in these systems, which may in some instances amplify and in other instances dampen the effects of climate change. We believe that moving towards an ecology of seasonality, by developing theoretical models which can handle this type of variation and also by spreading data collection over multiple seasons, is crucial to fully assess ecological responses to a changing climate.

Ethics

Field techniques were approved by Université du Québec à Rimouski Animal Care Committee and field research was approved by the Joint Park Management Committee of Sirmilik National Park of Canada.

Data accessibility

Most data are available in the electronic appendices of Legagneux et al. (2012) in Ecology (compiled data used for modelling). More recent raw data for lemming and geese are available online at: [65,66]. Raw data on Arctic foxes and snowy owls are available at: [67,68].

Authors' contributions

C.H. created the model and performed the modelling with significant contributions from F.G. and D.G. G.G., J.B., D.B., D.F. and P.L. collected data. C.H. wrote the manuscript with input from all co-authors.

Competing interests

We have no competing interests.

Funding

F.G. is supported by the National Science and Engineering Research Council of Canada (NSERC) through the Discovery Program (grant no. RGPIN-2017-04266). G.G., J.B., D.B., D.F. and P.L. are supported by the following organizations: Canada Foundation for Innovation, Fond Québécois de la Recherche sur la Nature et les Technologies (FQRNT), International Polar Year Program of Indian and Northern Affairs Canada, National Science and Engineering Research Council of Canada (NSERC, grant no. for D.B. RGPIN-2019-05292), Network of Centre of Excellence of Canada, ArcticNet, Northern Scientific Training Program (Polar Knowledge Canada), Polar Continental Shelf Program, Sentinel North program funded by Canada First Research Excellence Fund, and Environment and Climate Change Canada. D.G. and D.B. are funded through a Canadian Research Chair.