Uses of pathogen detection data to estimate vaccine direct effects in case–control studies

Abstract

The fact that many pathogens can be carried or shed without causing symptoms complicates the interpretation of microbiological data when diagnosing certain infectious disease syndromes. Diagnostic criteria that attribute symptoms to a pathogen which is detectable, whether it is or is not the aetiological agent of disease, may lead to outcome misclassification in epidemiological studies. Case–control studies are commonly undertaken to estimate vaccine effectiveness (VE) and present an opportunity to compare pathogen detection among individuals with and without clinically relevant symptoms. Considering this study context, we present a mathematical framework yielding simple estimators for the direct effects of vaccination on various aspects of host susceptibility. These include protection against acquisition of the pathogen of interest and protection against progression of this pathogen to disease following acquisition. We assess the impact of test sensitivity on these estimators and extend our framework to identify a ‘vaccine probe’ estimator for pathogen-specific aetiological fractions. We also derive biases affecting VE estimates under the test-negative design, a special case enrolling only symptomatic persons. Our results provide strategies for estimating pathogen-specific VE in the absence of a diagnostic gold standard. These approaches can inform the design and analysis of studies addressing numerous pathogens and vaccines.

1. Background

Attribution of infectious disease syndromes to a specific microbiological agent often involves detection of this agent, or its genetic material, among individuals experiencing relevant clinical signs and/or symptoms. However, in certain instances, detection of a pathogenic organism from a symptomatic individual does not provide a specific determination of disease aetiology. Such is the case for pathogens that may be shed or carried in a subclinical state as part of their natural history. For instance, influenza viruses, respiratory syncytial virus, human rhinoviruses and metapneumoviruses, and bacteria such as Streptococcus pneumoniae, Haemophilus influenzae and Staphylococcus aureus may each be found in respiratory tract specimens from individuals experiencing acute symptoms as well as individuals without clinically apparent illness, especially among children [1,2]. Similar circumstances arise with enteric viruses such as rotavirus, norovirus and sapovirus and bacteria such as Shigella and Escherichia coli, which may cause diarrhoea or colonize the gut asymptomatically [3]. Likewise, depending on world region, malaria parasites, arboviruses, Rickettsia and various Gram-negative bacteria may be detectable among individuals experiencing acute febrile illness as well as those without symptoms [4]. Because many or most acquisitions of these pathogens do not progress to disease, only a proportion of symptomatic individuals among whom these pathogens are detectable may in fact be experiencing pathogen-attributable illness [5].

This circumstance creates challenges for studies of the effectiveness of vaccines and other pathogen-specific interventions. Whereas such studies typically aim to assess whether an intervention prevents a well-defined endpoint of disease attributable to the pathogen of interest, the absence of a gold-standard diagnostic tool may lead to misclassification of individuals' outcomes with respect to disease aetiology. Recently, large-scale studies of pneumonia [6] and diarrhoea [7] aetiology among children have employed case–control frameworks, enrolling symptomatic cases and community controls to estimate pathogen-attributable fractions of disease burden. The inferential methods of these studies centre on a comparison of the prevalence of each pathogen among symptomatic cases and asymptomatic controls [8–10]. While similar case–control frameworks may present an opportunity to correct for misclassification when estimating vaccine effectiveness (VE; [11–15]), such approaches have not been routinely incorporated into real-world studies.

Here we introduce strategies for estimation of VE against pathogen-specific endpoints in case–control studies. As estimands, we consider vaccine direct effect parameters that compare counterfactual outcomes for an individual who does or does not receive vaccination, as introduced by Halloran and colleagues in previous work [16]. These effects address the biological reduction in susceptibility conferred by an individual's response to vaccination, including protection against shedding or carriage of the pathogen, protection against progression of the pathogen to disease (conditioned on acquisition) and the cumulative result of these two forms of protection.

2. Study design

2.1. Framework

Consider a case–control study that enrols cases experiencing a clinical syndrome of interest, which may be preventable by vaccination against one of several causative pathogens. Consider that the study enrols controls based on clinical criteria unrelated to the pathogen of interest and to vaccination. Such controls may be asymptomatic persons or those experiencing an ‘alternative’ disease, which does not affect and is not affected by acquisition of the pathogen of interest or vaccination [17]. Assume that all or a proportion of individuals enrolled (including both cases and controls) are tested to determine the presence or the absence of the pathogen of interest.

For the methods described below, we envision a study where there is no a priori basis for determining whether a pathogen, once detected, is the true cause of symptoms for an individual patient. We also present simplifications of the approach for contexts where pathogen detection provides a definitive determination of disease aetiology.

2.2. Examples

Case–control studies involving the detection of enteropathogens from diarrhoea cases and asymptomatic controls [7], or the detection of respiratory viruses and bacteria in the upper respiratory tract of cases with and controls without acute respiratory symptoms [6], present an ideal environment for application of the approaches detailed below. Studies of diarrhoea-causing pathogens are a compelling example because the gastrointestinal tract is the site of both colonization and disease for such organisms. Testing may be performed on stool specimens regardless of the presence of symptoms, and the detection of a pathogen in diarrhoeal stool is not always a clear indication of its aetiological significance [9,18,19]. Similar concerns arise with detection of various pathogens in the bloodstream, urine or respiratory tract among individuals experiencing acute febrile illness in endemic settings [4]. Although these challenges may be mitigated for certain pathogens by the use of quantitative molecular diagnostic tests [5], such testing remains relatively uncommon in clinical practice.

In studies of paediatric pneumonia, inaccessibility of the site of infection (i.e. the lung) presents a unique challenge where the approaches we consider below may offer particular value. The upper respiratory tract (including the oropharynx and nasopharynx) is a readily accessible site for swabbing, but is also the site of colonization or shedding for many pathogens; thus, identification of a pathogen in the upper respiratory tract of a symptomatic individual is not an indication of its aetiological significance. While lower respiratory tract secretions may be desirable because they originate from the site of infection, contamination with organisms from the upper respiratory tract may undermine the benefit of obtaining such specimens [20].

3. Notation and theoretical framework

Here we lay out a formal framework relating observable variables to epidemiological parameters. Define Y_i as an indicator of the case (Y_i = 1) or control (Y_i = 0) status of individual i with respect to the clinical syndrome of interest. With Y_i = 1, the individual experiences disease, while with Y_i = 0, the individual is either asymptomatic or experiencing a control condition unrelated to the pathogen or vaccine being studied. Define X_i as an indicator of the presence (X_i = 1) or the absence (X_i = 0) of the pathogen of interest, and define Z_i as an indicator of the individual's vaccination status as vaccinated (exposed, Z_i = 1) or unvaccinated (unexposed, Z_i = 0; table 1).

Table 1.

Variables or observations.

variable	definition
Yi	indicator of case (Yi = 1) or control (Yi = 0) status, as defined by clinical symptoms, for individual i
Xi	indicator of pathogen presence (Xi = 1) or absence (Xi = 0), for individual i
Zi	indicator of vaccine receipt (Zi = 1) or non-receipt (Zi = 0), for individual i
Di	indicator that a pathogen is detected (Di = 1) or not detected (Di = 0), for individual i

We next consider epidemiological parameters describing the prevalence and natural history of the vaccine-preventable pathogen of interest among cases and controls (table 2). Define the prevalence of the pathogen in the absence of disease and vaccine-derived immunity as π = Pr(X_i = 1|Y_i = 0, Z_i = 0); for simplicity and consistency with prior literature [16], we refer to this state as ‘infection’, recognizing that the terms ‘carriage’ or ‘colonization’ may be preferred when discussing asymptomatic natural history states of certain (e.g. bacterial) pathogens.

Table 2.

Parameters of the model.

parameter	definition	range
π	prevalence of the pathogen of interest among individuals not experiencing disease symptoms potentially related to this pathogen (equal to the expected prevalence among controls)	0–1
θS	prevalence ratio of the pathogen of interest among vaccinated versus unvaccinated control individuals not experiencing disease symptoms potentially related to this pathogen	0–1, for a protective vaccine
ρ	per-acquisition risk for progression of the pathogen of interest to cause disease among unvaccinated individuals	0–1
θP	risk ratio for progression of the pathogen of interest to disease, given acquisition among vaccinated versus unvaccinated individuals	0–1, for a protective vaccine
ω	risk (measured over the same period as ρ) of disease due to all causes other than the pathogen of interest	0–1
v	proportion of individuals in the population who are vaccinated	0–1
λ	rate of acquisition of the pathogen of interest among unvaccinated individuals not currently shedding or carrying this pathogen	greater than 0
γ	rate of clearance of the pathogen of interest among unvaccinated individuals, following acquisition	greater than 0
a	hazard ratio of acquisition of the pathogen of interest among vaccinated versus unvaccinated individuals not currently shedding or carrying this pathogen	0–1, for a protective vaccine
b	hazard ratio of clearance of the pathogen of interest among vaccinated versus unvaccinated individuals, following acquisition	greater than 1, for a protective vaccine
rρ	rate of progression of the pathogen of interest to disease following acquisition by unvaccinated individuals	greater than 0
rω	rate of onset of disease due to all causes other than the pathogen of interest	greater than 0
c	hazard ratio of progression of the pathogen of interest to disease among vaccinated versus unvaccinated individuals, following acquisition	0–1, for a protective vaccine
α0	test sensitivity for detection of the pathogen in an individual experiencing shedding or carriage, without symptoms attributable to the pathogen	0–1
α1	test sensitivity for detection of the pathogen in an individual experiencing symptoms attributable to the pathogen	0–1

Define θ_Sπ as the prevalence of infection with the pathogen of interest among vaccinated persons not experiencing disease, with VE_S = 1 − θ_S indicating the reduction in prevalence attributable to vaccine effects on pathogen acquisition or clearance. Here we consider prevalence comparisons rather than time-to-event comparisons owing to the nature of data available in case–control studies, which would not include longitudinal observations of acquisition and clearance of the pathogen. We address the interpretation of θ_S with respect to vaccine effects on the acquisition and duration of infection in a later section.

Define ρ as the proportion of acquisitions resulting in symptomatic disease in the absence of vaccine-conferred protection or as the proportion of infected individuals experiencing pathogen-attributable symptoms at any time. Define θ_P as the relative risk of progression by the pathogen of interest, given vaccination, so that the vaccine direct effect against progression is VE_P = 1 − θ_P. Last, allow ω to represent the risk (prevalence) of disease attributable to all other causes. We assume here that onset of disease due to causes other than the pathogen of interest is unrelated to either prior vaccination or infection involving the pathogen of interest. This assumption is consistent with the fundamental framework of case–control designs, where a control condition is chosen which is unaffected by the exposure(s) of interest (e.g. vaccination or infection) in order to provide a ‘null’ reference against which the prevalence of this exposure among cases may be compared [21]. Accounting for disease attributable to the pathogen of interest and to all other pathogens, we have

$$\begin{array}{l}Pr(Y_i=1|X_i=1,Z_i=0)=\omega +\rho ,\\ Pr(Y_i=1|X_i=1,Z_i=1)=\omega +\theta \rho ,\\ Pr(Y_i=1|X_i=0,Z_i=0)=Pr(Y_i=1|X_i=0,Z_i=1)=\omega .\end{array}\}$$ 3.1a–c

Note that, in a case–control study, enrolment of individuals with known outcome status Y_i = 1 or Y_i = 0 hinders direct measurement of $Pr(Y_i=y|X_i=x,Z_i=z)$. Thus, we consider estimation frameworks below that do not require prospective observation of the probabilities presented in equation (3.1). As our study considers acute diseases (e.g. pneumonia, severe diarrhoea) that have low point prevalence within whole populations [22], ω + ρ ≈ 1 − (1 − ω)(1 − ρ). We derive ρ and ω with respect to rate parameters in a later section to relate θ_P to the hazard ratio of progression of the pathogen of interest to symptomatic disease, given vaccination, in a competing risks framework.

4. Vaccine direct effect against susceptibility (VE_S)

If an individual's control status is unrelated to risk of shedding the pathogen of interest, the relative risk of detection of the pathogen of interest among controls, given vaccination, provides the most straightforward basis for estimating VE_S,

$$\begin{array}{rl}{\text{RR}}_S& =\frac{\text{Pr}(X_i=1|Y_i=0,Z_i=1)}{\text{Pr}(X_i=1|Y_i=0,Z_i=0)}=\frac{{\theta }_S\pi }{\pi }={\theta }_S\\ & =1-{\text{VE}}_S.\end{array}$$ 4.1

As an alternative, VE_S can be estimated by comparing the odds of vaccination and pathogen detection among controls against the ‘null’ odds of vaccination within the control group, irrespective of pathogen detection [23]. Such an approach may be advantageous under certain design considerations, most notably when pathogen detection data are available only from a subset of all control individuals from whom vaccination data are available (e.g. in the case of expensive or invasive diagnostic procedures [24,25]). Here, the odds ratio (OR) can be expressed as

$${\text{OR}}_S=\frac{[\text{Pr}(Z_i=1,X_i=1|Y_i=0)][\text{Pr}(Z_i=0|Y_i=0)]}{[\text{Pr}(Z_i=0,X_i=1|Y_i=0)][\text{Pr}(Z_i=1|Y_i=0)]}.$$ 4.2

To formalize this intuition, define v as the proportion of individuals receiving vaccination in the population; provided vaccination is independent of control status, we have $Pr(Z_i=1|Y_i=0)=v$. From the assumption that control status is independent of vaccination and shedding of the pathogen of interest

$$\begin{array}{rl}Pr(Z_i=1,X_i=1|Y_i=0)& =Pr(X_i=1|Z_i=1,Y_i=0)Pr(Z_i\\ & =1|Y_i=0)={\theta }_S\pi v\end{array}$$ 4.3a

and

$$\begin{array}{rl}Pr(Z_i=0,X_i=1|Y_i=0)& =Pr(X_i=1|Z_i=0,Y_i=0)Pr(Z_i\\ & =0|Y_i=0)=\pi (1-v).\end{array}$$ 4.3b

Substituting into equation (4.2),

$${\text{OR}}_S=\frac{[{\theta }_S\pi v]\hspace{0.17em}[(1-v)]}{[\pi (1-v)][v]}={\theta }_S=1-{\text{VE}}_S,$$ 4.4

recovering the same effect we would estimate using the risk ratio RR_S.

5. Vaccine direct effect against progression (VE_P)

Here we address the vaccine-attributable reduction in susceptibility to disease, given a pathogen has overcome a host's vaccine-derived protection against acquisition of infection. To estimate this effect, consider first the OR of detection of the pathogen of interest, given symptoms (OR_P). We expect this value to exceed 1 if acquisition of the pathogen increases individuals' risk of experiencing symptoms (i.e. ρ > 0; [8,9]). Among the unvaccinated, the relative odds of pathogen detection given the presence of symptoms is

$${\text{OR}}_P^0=\frac{Pr(X_i=1|Y_i=1,Z_i=0)\text{Pr}(X_i=0|Y_i=0,Z_i=0)}{Pr(X_i=0|Y_i=1,Z_i=0)\text{Pr}(X_i=1|Y_i=0,Z_i=0)},$$ 5.1a

while among the vaccinated,

$${\text{OR}}_P^1=\frac{Pr(X_i=1|Y_i=1,Z_i=1)\text{Pr}(X_i=0|Y_i=0,Z_i=1)}{Pr(X_i=0|Y_i=1,Z_i=1)\text{Pr}(X_i=1|Y_i=0,Z_i=1)}.$$ 5.1b

We may expect that ${\text{OR}}_P^1<{\text{OR}}_P^0$ if vaccination confers protection against progression of the pathogen from infection to disease, thereby attenuating the association between pathogen detection and symptoms among the vaccinated. Of the terms appearing in equation (5.1), we have defined $Pr(X_i=1|Y_i=0,Z_i=1)$ and $Pr(X_i=1|Y_i=0,Z_i=0)$ above in equation (4.1). From the progression parameters ρ, ω and θ_P we may further define the probability of pathogen detection, among cases, as

$$Pr(X_i=1|Y_i=1,Z_i=0)=\frac{\pi (\rho +\omega )}{\pi \rho +\omega }$$ 5.2a

and

$$Pr(X_i=1|Y_i=1,Z_i=1)=\frac{{\theta }_S\pi ({\theta }_P\rho +\omega )}{({\theta }_S\pi {\theta }_P\rho +\omega )}.$$ 5.2b

As the complements of equations (5.2a) and (5.2b), respectively,

$$Pr(X_i=0|Y_i=1,Z_i=0)=\frac{(1-\pi )\omega }{\pi \rho +\omega }$$ 5.2c

and

$$Pr(X_i=0|Y_i=1,Z_i=1)=\frac{(1-{\theta }_S\pi )\omega }{{\theta }_S\pi {\theta }_P\rho +\omega }.$$ 5.2d

Substituting terms from equations (4.1) and (5.2) into equation (5.1), we have

$${\text{OR}}_P^0=\frac{[\pi (\rho +\omega )][(1-\pi )]}{[\omega (1-\pi )][\pi ]}=\frac{\rho +\omega }{\omega }$$ 5.3a

and

$${\text{OR}}_P^1=\frac{[{\theta }_S\pi ({\theta }_P\rho +\omega )][(1-{\theta }_S\pi )]}{[(1-{\theta }_S\pi )\omega ][{\theta }_S\pi ]}=\frac{{\theta }_P\rho +\omega }{\omega }.$$ 5.3b

Here, ${\text{OR}}_P^1<{\text{OR}}_P^0$ for θ_P < 1 and ρ > 0, ω > 0. Rearranging the terms from equation (5.3) reveals $\rho =\omega ({\text{OR}}_P^0-1)$ and ${\theta }_P\rho =\omega ({\text{OR}}_P^1-1).$ Substituting for θ_P

$${\text{VE}}_P=1-{\theta }_P=1-\frac{{\text{OR}}_P^1-1}{{\text{OR}}_P^0-1}.$$ 5.4

Thus, we may estimate the vaccine direct effect against progression of the targeted pathogen to disease by comparing the association of detection of the pathogen with the presence of symptoms, among vaccinated and unvaccinated individuals.

6. Vaccine direct effect against disease (VE_D, including acquisition and progression)

We last consider the cumulative extent of vaccine-conferred protection resulting from prevention of infection, and prevention of progression to disease in the event of breakthrough acquisition (VE_D). From the joint probabilities of pathogen acquisition and progression among the vaccinated and unvaccinated,

$$\begin{array}{rl}{\text{VE}}_D& =1\\ & -\frac{Pr(\text{pathogen -attributable disease}|\text{vaccinated})}{Pr(\text{pathogen - attributable disease}|\text{unvaccinated})}\\ & =1-\frac{{\theta }_S\pi {\theta }_P\rho }{\pi \rho }=1-{\theta }_S{\theta }_P,\end{array}$$ 6.1

which may thus be estimated as

$${\text{VE}}_D=1-{\text{RR}}_S\times \frac{{\text{OR}}_P^1-1}{{\text{OR}}_P^0-1}$$ 6.2a

or

$${\text{VE}}_D=1-{\text{OR}}_S\times \frac{{\text{OR}}_P^1-1}{{\text{OR}}_P^0-1},$$ 6.2b

as defined above.

7. Interpretation of risks and rates

7.1. Pathogen shedding or carriage parameters

Interpretation of pathogen prevalence measures presents a challenge in studies of VE against endpoints such as asymptomatic infection due to the dynamic nature of transmission [16,26,27]. Here we relate θ_S = 1 − VE_S to vaccine direct effects on the rates of pathogen acquisition and clearance.

Define λ and γ as the rates at which unvaccinated individuals acquire and clear the pathogen of interest, respectively. Taking π to indicate the equilibrium prevalence of shedding or colonization, with π > 0, we have λ(1 − π) = γπ and π = λ/(λ + γ). Further defining a and b as the hazard ratios of acquisition and clearance of the pathogen among vaccinated persons relative to unvaccinated persons (table 2), we have aλ(1 − θ_Sπ) = bγθ_Sπ. Substituting for π, we obtain

$${\theta }_S=\frac{a(\lambda +\gamma )}{a\lambda +b\gamma }.$$ 7.1a

If the rate of clearance of the pathogen far exceeds the rate of acquisition (γ ≫ λ), we have

$${\theta }_S\cong \underset{\lambda /\gamma \to 0}{lim}(a(\lambda +\gamma )/(a\lambda +b\gamma ))=a/b.$$ 7.1b

Thus, the prevalence ratio θ_S among controls (as estimated by RR_S or OR_S) may be interpretable as the hazard ratio of acquisition if b = 1 (such that vaccination does not affect time to clearance of the pathogen) or as the inverse of the hazard ratio of clearance if a = 1 (such that vaccination does not affect acquisition of the pathogen).

7.2. Disease progression parameters

We may relate the risk parameters ρ, ω and θ_P to epidemiological rates under a similar intuition. Define r_ρ as the rate of progression of the pathogen of interest to disease, following acquisition by an unvaccinated individual, and define r_ω as the rate of onset of disease due to all other causes. Here we may use a competing risks framework to define ρ and ω as the probability that disease due to each cause precedes disease due to the other cause, or clearance of the pathogen. Defining f(t|r) as the density function for an event with rate r occurring at time t, we have

$$\rho ={\int }_0^{\mathrm{\infty }}\hspace{0.17em}f(t|r_{\rho })(1-F(t|r_{\omega }+\gamma ))\hspace{0.17em}\text{d}t$$ 7.2a

and

$$\omega ={\int }_0^{\mathrm{\infty }}\hspace{0.17em}f(t|r_{\omega })(1-F(t|r_{\rho }+\gamma ))\hspace{0.17em}\text{d}t.$$ 7.2b

Next defining c as the hazard ratio of progression of the pathogen of interest to disease following acquisition (comparing vaccinated with unvaccinated individuals), we have

$${\theta }_P\rho ={\int }_0^{\mathrm{\infty }}\hspace{0.17em}f\hspace{0.17em}(t|c{r}_{\rho })(1-F(t|r_{\omega }+\gamma ))\hspace{0.17em}\text{d}t.$$ 7.2c

Assuming exponentially distributed onset times, we have ρ = r_ρ/(r_ρ + r_ω + γ), ω = r_ω/(r_ρ + r_ω + γ) and θ_Pρ = cr_ρ/(cr_ρ + r_ω + γ), so that

$${\theta }_P=\frac{c(r_{\rho }+r_{\omega }+\gamma )}{c{r}_{\rho }+r_{\omega }+\gamma }.$$ 7.3

If the rate of progression of the pathogen of interest is well below the rate of disease onset due to all other causes (r_ω ≫ r_ρ), or the rate of clearance of the pathogen (γ ≫ r_ρ), we have ${\theta }_P\cong \underset{r_{\rho }/\text{(}{r}_{\omega }+\gamma \text{)}\to 0}{\lim }\text{ (}c\text{(}{r}_{\rho }+r_{\omega }+\gamma \text{)}/\text{)}c{r}_{\rho }+r_{\omega }+\gamma \text{))}=c$. Thus, for diseases that are uncommon, OR_P = θ_P may be interpretable as the hazard ratio of disease progression, following acquisition, for a vaccinated versus unvaccinated individual.

8. Studies with high diagnostic specificity in disease

The framework we introduce above also has value for estimating vaccine-conferred protection against progression to endpoints where the distinction between true disease and subclinical shedding or carriage is unambiguous. For instance, detection of commensal bacteria in ordinarily sterile body fluids such as the bloodstream or cerebrospinal fluid is a defining characteristic of invasive infections involving these organisms. Detection of respiratory viruses in the bloodstream may similarly provide a marker of very severe disease attributable to these pathogens [28–31]. Even when the isolate source is not an indicator of disease aetiology, pathogen abundance may inform the distinction between aetiological and non-aetiological detections [5].

In the event that we may exclude alternative aetiologies among cases in whom the pathogen is detected, the probability of pathogen detection, among cases (equations (5.2a,b)), may be rewritten as

$$Pr(X_i=1|Y_i=1,Z_i=0)=\frac{\pi \rho }{\pi \rho +(1-\pi )\omega }$$ 8.1a

and

$$Pr(X_i=1|Y_i=1,Z_i=1)=\frac{{\theta }_S\pi {\theta }_P\rho }{{\theta }_S\pi {\theta }_P\rho +(1-{\theta }_S\pi )\omega },$$ 8.1b

respectively. Here, we subtract πω(1 − v) and θ_Sπωv from our earlier definitions of $Pr(Y_i=1,Z_i=0)$ and $Pr(Y_i=1,Z_i=1)$, respectively, because episodes of disease not attributable to the pathogen of interest among cases shedding or carrying this pathogen are not observed. Thus,

$${\text{OR}}_P^0=\frac{[\pi \rho ][(1-\pi )]}{[(1-\pi )\omega ][\pi ]}=\frac{\rho }{\omega }$$ 8.2a

and

$${\text{OR}}_P^1=\frac{[{\theta }_S\pi {\theta }_P\rho ][(1-{\theta }_S\pi )]}{[(1-{\theta }_S\pi )\omega ][{\theta }_S\pi ]}=\frac{{\theta }_P\rho }{\omega },$$ 8.2b

so that

$${\text{VE}}_P=1-{\theta }_P=1-\frac{{\text{OR}}_P^1}{{\text{OR}}_P^0}.$$ 8.3

We note from equations (5.4) and (8.3) that estimates of VE_P may be most stable when ${\text{OR}}_P^0\gg 1$ (which may also allow ${\text{OR}}_P^1\gg 1\hspace{0.17em}$ if θ_P is not close to zero). In this regard, the analysis approaches we consider here may be most reliable for pathogens that play an important aetiological role in the disease syndromes under investigation, resulting in high ORs.

The special case of high diagnostic specificity in disease further allows VE_D to be estimated directly by comparing the odds of prior vaccination among symptomatic cases with the pathogen detected versus asymptomatic controls among whom the pathogen is not detected. We show $Pr(Z_i=z|X_i=1,Y_i=0)$ in equation (4.3). Similarly,

$$\begin{array}{rl}Pr(Z_i=1|X_i=1,Y_i=1)& =\frac{Pr(X_i=1,Y_i=1|Z_i=1)\text{Pr}(Z_i=1)}{\text{Pr}(X_i=1,Y_i=1)}\\ & =\frac{{\theta }_S{\theta }_{P}v}{{\theta }_S{\theta }_{P}v+(1-v)}\end{array}$$ 8.4a

and its complement

$$Pr(Z_i=0|X_i=1,Y_i=1)=\frac{1-v}{{\theta }_S{\theta }_{P}v+(1-v)},$$ 8.4b

under the circumstance that the pathogen, if detected in a symptomatic individual, is the true cause of disease. Taken together, the vaccine effect can be expressed as

$$\begin{array}{rl}{\text{VE}}_D=& 1-\frac{Pr(Z_i=1|X_i=1,Y_i=1)Pr(Z_i=0|X_i=0,Y_i=0)}{Pr(Z_i=0|X_i=1,Y_i=1)Pr(Z_i=1|X_i=0,Y_i=0)}\\ & =1-\frac{[{\theta }_S{\theta }_{P}v][(1-\pi )(1-v)]}{[(1-v)][(1-\pi )v]}\\ & =1-{\theta }_S{\theta }_P.\end{array}$$ 8.5

9. Bias under imperfect test sensitivity

For certain conditions, the sensitivity of pathogen detection approaches may differ for individuals experiencing pathogen-attributable disease versus subclinical shedding or colonization. For instance, higher pathogen load among individuals experiencing disease may improve the probability of pathogen detection among true disease cases via certain diagnostic assays [5,32]. Alternatively, for conditions such as pneumonia involving infection at difficult-to-sample anatomical sites, shedding or carriage at the sampled site (e.g. oronasopharynx) may cease before the clearance of the pathogen from the site of infection [33–35].

Take D_i = 1 and D_i = 0 to indicate detection or non-detection of the pathogen of interest (table 1). To account for test sensitivity in the formulations introduced above, we may replace X_i with D_i in our previous equations, so that

$${\text{RR}}_S=\frac{\text{Pr}(D_i=1|Y_i=0,Z_i=1)}{\text{Pr}(D_i=1|Y_i=0,Z_i=0)}$$ 9.1a

and

$${\text{OR}}_S=\frac{[\text{Pr}(Z_i=1,D_i=1|Y_i=0)][\text{Pr}(Z_i=0|Y_i=0)]}{[\text{Pr}(Z_i=0,D_i=1|Y_i=0)][\text{Pr}(Z_i=1|Y_i=0)]}$$ 9.1b

for estimation of VE_S, while

$${\text{OR}}_P^0=\frac{Pr(D_i=1|Y_i=1,Z_i=0)Pr(D_i=0|Y_i=0,Z_i=0)}{Pr(D_i=0|Y_i=1,Z_i=0)Pr(D_i=1|Y_i=0,Z_i=0)}$$ 9.2a

and

$${\text{OR}}_P^1=\frac{Pr(D_i=1|Y_i=1,Z_i=1)\text{Pr}(D_i=0|Y_i=0,Z_i=1)}{Pr(D_i=0|Y_i=1,Z_i=1)\text{Pr}(D_i=1|Y_i=0,Z_i=1)}$$ 9.2b

for estimation of VE_D.

Define α₁ and α₀ as the sensitivity of the detection method—i.e. the probability of detecting the pathogen, given it is present—for individuals who are (α₁) and are not (α₀) experiencing disease attributable to this pathogen. The expected prevalence of pathogen detection among those without symptoms is thus $Pr(D_i=1|Y_i=0)={\alpha }_{0}Pr(X_i=1|Y_i=0)$. Substituting into equation (5.2) reveals no effect on RR_S and OR_S, as α₀ cancels in the numerator and denominator.

Next considering ${\text{OR}}_P^0$, the detection probability among unvaccinated cases is

$$\begin{array}{rl}& Pr(D_i=1|Y_i=1,Z_i=0)\\ & =\frac{Pr(Y_i=1,Z_i=0|X_i=1,D_i=1)Pr(X_i=1,D_i=1)}{\text{Pr}(Y_i=1,Z_i=0)},\end{array}$$ 9.3a

since $Pr(X_i=0,D_i=1)=0$. Among individuals infected with the pathogen of interest, detection and disease may jointly occur with probability α₁ρ for disease due to the pathogen of interest, and with probability α₀ω for disease due to other causes, so that

$$\begin{array}{rl}& Pr(Y_i=1,Z_i=0|X_i=1,D_i=1)Pr(X_i=1,D_i=1)\\ & =\pi ({\alpha }_1\rho +{\alpha }_0\omega )\end{array}$$ 9.3b

and

$$Pr(D_i=1|Y_i=1,Z_i=0)=\frac{\pi ({\alpha }_1\rho +{\alpha }_0\omega )}{\pi \rho +\omega }.$$ 9.3c

The probability of no pathogen detection among those with disease is

$$Pr(D_i=0|Y_i=1,Z_i=0)=\frac{\pi \rho (1-{\alpha }_1)+\omega (1-{\alpha }_0\pi )}{\pi \rho +\omega },$$ 9.3d

which we may obtain from the joint probabilities of disease due to the pathogen of interest and detection failure, πρ(1 − α₁), and disease due to all other causes without pathogen detection, ω(1 − α₀π).

Similarly, among the vaccinated,

$$Pr(D_i=1|Y_i=1,Z_i=1)=\frac{{\theta }_S\pi ({\alpha }_1{\theta }_P\rho +{\alpha }_0\omega )}{{\theta }_S\pi {\theta }_P\rho +\omega }$$ 9.4a

and

$$Pr(D_i=0|Y_i=1,Z_i=1)=\frac{{\theta }_S\pi {\theta }_P\rho (1-{\alpha }_1)+\omega (1-{\alpha }_0{\theta }_S\pi )}{{\theta }_S\pi {\theta }_P\rho +\omega }.$$ 9.4b

Substituting into equation (8.2), we have

$$\begin{array}{rl}{\text{OR}}_P^0& =\frac{[\pi ({\alpha }_1\rho +{\alpha }_0\omega )][1-{\alpha }_0\pi ]}{[\pi \rho (1-{\alpha }_1)+\omega (1-{\alpha }_0\pi )][{\alpha }_0\pi ]}\\ & =\frac{({\alpha }_1\rho +{\alpha }_0\omega )(1-{\alpha }_0\pi )}{{\alpha }_0[\pi \rho (1-{\alpha }_1)+\omega (1-{\alpha }_0\pi )]}\end{array}$$ 9.5a

and

$$\begin{array}{rl}{\text{OR}}_P^1& =\frac{[{\theta }_S\pi ({\alpha }_1{\theta }_P\rho +{\alpha }_0\omega )][1-{\alpha }_0{\theta }_S\pi ]}{[{\theta }_S\pi {\theta }_P\rho (1-{\alpha }_1)+\omega (1-{\alpha }_0{\theta }_S\pi )][{\alpha }_0{\theta }_S\pi ]}\\ & =\frac{({\alpha }_1{\theta }_P\rho +{\alpha }_0\omega )(1-{\alpha }_0{\theta }_S\pi )}{{\alpha }_0[{\theta }_S\pi {\theta }_P\rho (1-{\alpha }_1)+\omega (1-{\alpha }_0{\theta }_S\pi )]}.\end{array}$$ 9.5b

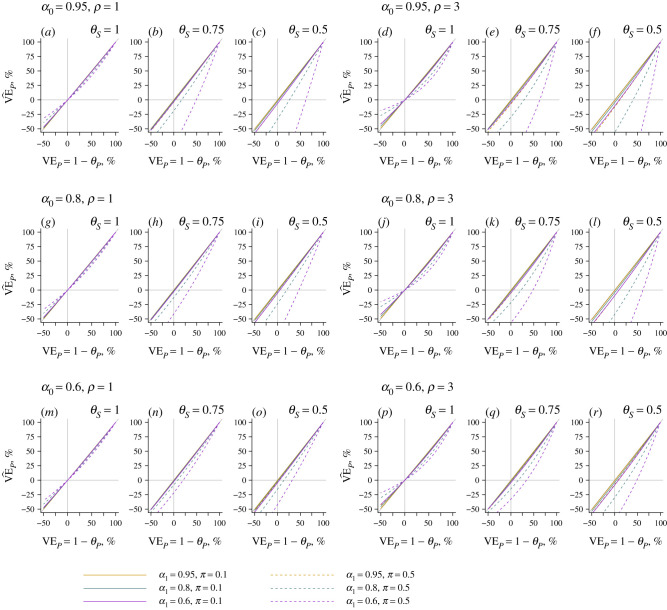
Here, $({\text{OR}}_P^1-1)/({\text{OR}}_P^0-1)={\theta }_P$ if α₁ = 1; otherwise, $({\text{OR}}_P^1-1)/({\text{OR}}_P^0-1)>{\theta }_P$ for 0 < θ_P < 1, over the ranges of all other parameters listed in table 2. Thus, if vaccination confers protection against disease progression, imperfect sensitivity affecting pathogen detection among symptomatic cases is expected to lead to underestimation of the true effect. We illustrate the magnitude of this bias in figure 1 under various parametrizations. Bias increases with higher prevalence of the pathogen among persons without symptoms (π), with higher rates of progression of the pathogen to disease (ρ/ω) and with lower sensitivity for pathogen detection in disease (α₁). Interestingly, bias also worsens as α₀ approaches 1.

Figure 1.

Effect of imperfect test sensitivity on estimates of vaccine-conferred protection against progression of the pathogen to disease. Using the expressions for ${\text{OR}}_P^0$ and ${\text{OR}}_P^1$ in equation (9.5), we plot the estimated effect of vaccination on risk of progression of the pathogen of interest, given acquisition (${\widehat{\text{VE}}}_P=1-({\text{OR}}_P^1-1)/({\text{OR}}_P^0-1)$) under differing conditions of sensitivity of detection of the pathogen when it is or is not the agent of disease (α₁ and α₀ values of 0.95, 0.8 and 0.6). The x-axis indicates the true vaccine effect against progression; departures from the 1 : 1 diagonal (grey) line indicate bias. Solid and dashed lines correspond to estimates assuming 10% and 50% prevalence, respectively, of the pathogen of interest among unvaccinated individuals without symptoms. Within each row, the left three panels assume acquisition of the pathogen doubles individuals' risk of all-cause disease (ρ/ω = 1), while the right three panels assume acquisition of the pathogen results in a fourfold increase in individuals’ risk of all-cause disease (ρ/ω = 3).

The nature and extent of bias further depends upon whether vaccination confers protection against pathogen shedding or carriage (θ_S). With θ_S = 1 (i.e. VE_S = 0), the estimate ${\widehat{\text{VE}}}_P$ converges to the true value when VE_P = 0% or VE_P = 100%, and is sign-unbiased, such that ${\widehat{\text{VE}}}_P>0\text{\%}$ when VE_P > 0%, and ${\widehat{\text{VE}}}_P<0\text{\%}$ when VE_P < 0%. By contrast, the estimate may be sign-biased when vaccination confers protection against shedding (i.e. 0 < θ_S < 1); here ${\widehat{\text{VE}}}_P$ might suggest increased risk of disease progression among vaccinated individuals who acquire the pathogen, when in fact vaccination protects against disease progression. However, this circumstance is expected only under extreme scenarios, where shedding or carriage is very prevalent among asymptomatic individuals, true protection against disease progression is very weak and test sensitivity is very high in the context of subclinical shedding or carriage yet low among those experiencing disease. This latter circumstance is particularly unlikely to be met, as pathogen shedding (and thus likelihood of detection) is often associated with the presence of symptoms [5].

10. Bias under test-negative design approaches

10.1. Protection against disease

The test-negative design (TND) has come into routine use in studies of VE [36]. Studies using this design estimate vaccine direct effects by comparing the odds of prior vaccination among individuals experiencing clinically apparent illness who test positive or negative for a pathogen of interest (${\text{OR}}_D^{\mathrm{TND}}$): in contrast to traditional case–control studies, all subjects experience the clinical syndrome of interest. Case–control studies such as we have considered above may resemble TND studies in that receipt of a test is independent of the likelihood of detecting the pathogen of interest [15,37,38]; however, ‘control’ subjects in TND studies are typically defined as individuals who experience disease without detection of the pathogen of interest. It has been recognized previously that detections of non-aetiological pathogens may influence estimates of VE under TND studies, although the quantitative extent of resulting bias is not well understood [11,13,15]. Here, we derive the mathematical form of this bias using the framework described above.

Studies using the TND aim to estimate the vaccine direct effect against disease attributable to the pathogen of interest according to

$$\begin{array}{rl}{\widehat{\text{VE}}}_D& =1-{\text{OR}}_D^{\mathrm{TND}}\\ & =1-\frac{Pr(Z_i=1|X_i=1,Y_i=1)Pr(Z_i=0|X_i=0,Y_i=1)}{Pr(Z_i=0|X_i=1,Y_i=1)Pr(Z_i=1|X_i=0,Y_i=1)}.\end{array}$$ 10.1

Here we may define

$$\begin{array}{rl}Pr(Z_i=1|X_i=1,Y_i=1)& =\frac{Pr(X_i=1,Y_i=1|Z_i=1)\text{Pr}(Z_i=1)}{Pr(X_i=1,Y_i=1)}\\ & =\frac{{\theta }_S({\theta }_P\rho +\omega )v}{{\theta }_S({\theta }_P\rho +\omega )v+(\rho +\omega )(1-v)}\end{array}$$ 10.2a

and

$$Pr(Z_i=0|X_i=1,Y_i=1)=\frac{(\rho +\omega )(1-v)}{{\theta }_S({\theta }_P\rho +\omega )v+(\rho +\omega )(1-v)}.$$ 10.2b

Similarly, we have

$$Pr(Z_i=1|X_i=0,Y_i=1)=\frac{(1-{\theta }_S\pi )v}{(1-{\theta }_S\pi )v+(1-\pi )(1-v)}$$ 10.3a

and

$$Pr(Z_i=0|X_i=0,Y_i=1)=\frac{(1-\pi )(1-v)}{(1-{\theta }_S\pi )v+(1-\pi )(1-v)}.$$ 10.3b

Substituting equations (10.2) and (10.3) into equation (10.1) to derive ${\text{OR}}_D^{\mathrm{TND}}$,

$$\begin{array}{rl}{\text{OR}}_D^{\mathrm{TND}}& =\frac{[{\theta }_S({\theta }_P\rho +\omega )v][(1-\pi )(1-v)]}{[(\rho +\omega )(1-v)][(1-{\theta }_S\pi )v]}\\ & =\frac{{\theta }_S({\theta }_P\rho +\omega )(1-\pi )}{(\rho +\omega )(1-{\theta }_S\pi )}.\end{array}$$ 10.4

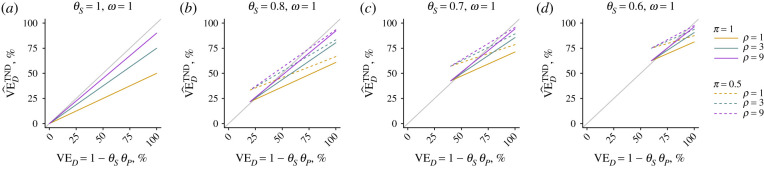
This estimator approaches the true vaccine direct effect against acquisition and progression of the pathogen of interest (VE_D = 1 − θ_Sθ_P) under two conditions. First, if values of π and ω (or the ratio ω/ρ) concurrently approach zero, and, second, if values of θ_S and/or θ_D approach zero (resulting in near-100% protection). We illustrate the quantitative extent of bias under differing conditions in figure 2.

Figure 2.

Bias in estimated protection against disease under the TND. We plot the estimated effect of vaccination on risk of disease attributable to the pathogen of interest generated under the TND (${\widehat{\text{VE}}}_D^{\mathrm{TND}}$), indicating the true vaccine direct effect (VE_D = 1 − θ_Sθ_P) on the x-axis. Departures from the 1 : 1 diagonal (grey) line indicate bias. Solid and dashed lines correspond to estimates assuming 10% and 50% prevalence, respectively, of the pathogen of interest among unvaccinated individuals without symptoms, with differing line colours corresponding to differing values of the relative risk of symptoms given acquisition of the pathogen (ρ/ω).

10.2. Bias in the absence of diagnostic uncertainty

We also identify bias under the TND framework when detection of the pathogen from cases can be assumed to indicate true disease aetiology. Following equation (8.4), in this instance we may express the probability of vaccination among cases as

$$\begin{array}{rl}Pr(Z_i=1|X_i=0,Y_i=1)& =\frac{Pr(X_i=0,Y_i=1|Z_i=1)Pr(Z_i=1)}{Pr(X_i=0,Y_i=1)}\\ & =\frac{(1-{\theta }_S\pi )v}{(1-{\theta }_S\pi )v+(1-\pi )(1-v)}\end{array}$$ 10.5a

and

$$Pr(Z_i=0|X_i=0,Y_i=1)=\frac{(1-\pi )(1-v)}{(1-{\theta }_S\pi )v+(1-\pi )(1-v)}.\hspace{0.17em}$$ 10.5b

Using the expressions for $Pr(Z_i=1|X_i=1,Y_i=1)$ and $Pr(Z_i=0|X_i=1,Y_i=1)$ presented in equation (8.4), we have

$${\text{OR}}_D^{\mathrm{TND}}=\frac{[{\theta }_S{\theta }_{P}v][(1-\pi )(1-v)]}{[(1-v)][(1-{\theta }_S\pi )v]}=\frac{{\theta }_S{\theta }_P(1-\pi )}{1-{\theta }_S\pi },$$ 10.6

which converges to θ_Sθ_P as θ_S, θ_P or π approach zero. Otherwise, this approach will overestimate the magnitude of the true vaccine direct effect (i.e. ${\text{OR}}_D^{\mathrm{TND}}<{\theta }_S{\theta }_P$).

10.3. Protection against infection

Our mathematical framework reveals similar biases affecting estimation of VE_S under TND-like approaches that define cases as asymptomatic individuals among whom the pathogen is detected, and controls as asymptomatic individuals among whom the pathogen is not detected. Although TND studies typically enrol individuals experiencing a clinical syndrome that could be caused by the pathogen of interest, individuals may, in theory, be matched on any clinical status, including the absence of symptoms potentially attributable to the pathogen of interest. Here, investigators would aim to estimate VE against acquisitions that result only in subclinical infection by comparing the odds of prior vaccination among asymptomatic individuals who test positive (cases) or negative (controls) for the pathogen of interest [11,36,38]:

$${\text{OR}}_S^{\mathrm{TND}}=\frac{[\text{Pr}(Z_i=1,X_i=1|Y_i=0)][\text{Pr}(Z_i=0,X_i=0|Y_i=0)]}{[\text{Pr}(Z_i=0,X_i=1|Y_i=0)][\text{Pr}(Z_i=1,X_i=0|Y_i=0)]}.$$ 10.7

We have presented $Pr(Z_i=1,X_i=1|Y_i=0)$ and $Pr(Z_i=0,X_i=1|Y_i=0)$ in equation (4.3). We may similarly derive

$$\begin{array}{rl}Pr(Z_i=1,X_i=0|Y_i=0)& =Pr(X_i=0|Z_i=1,Y_i=0)Pr(Z_i\\ & =1|Y_i=0)=(1-{\theta }_S\pi )v\end{array}$$ 10.8a

and

$$\begin{array}{rl}Pr(Z_i=0,X_i=0|Y_i=0)& =Pr(X_i=0|Z_i=0,Y_i=0)Pr(Z_i\\ & =0|Y_i=0)=(1-\pi )(1-v).\end{array}$$ 10.8b

Substituting into equation (10.7), we have

$${\text{OR}}_S^{\mathrm{TND}}=\frac{[{\theta }_S\pi v][(1-\pi )(1-v)]}{[\pi (1-v)][(1-{\theta }_S\pi )v]}=\frac{{\theta }_S(1-\pi )}{1-{\theta }_S\pi },$$ 10.9

revealing the same form of bias inherent to equation (10.6).

11. Attributable fraction estimation

Data from case–control studies investigating pathogen detection among symptomatic and asymptomatic persons may also be useful for assessing the fraction of cases attributable to the pathogen of interest. Studies addressing the effects of vaccination on non-specific endpoints provide a framework to ‘probe’ the proportion of cases attributable to the vaccine-preventable pathogen [39,40], based on effects against both all-cause and pathogen-specific disease outcomes.

The OR of vaccination among cases and controls, irrespective of pathogen detection, is

$${\text{OR}}_A=\frac{Pr(Z_i=1|Y_i=1)\text{Pr}(Z_i=0|Y_i=0)}{Pr(Z_i=0|Y_i=1)\text{Pr}(Z_i=1|Y_i=0)}.$$ 11.1

As in equation (4.2), we have $Pr(Z_i=1|Y_i=0)=v$ and $Pr(Z_i=0|Y_i=0)=1-v$, while

$$\begin{array}{rl}Pr(Z_i=1|Y_i=1)=& \frac{Pr(Y_i=1|Z_i=1)\text{Pr}(Z_i=1)}{\text{Pr}(Y_i=1)}\\ =& \frac{({\theta }_S\pi {\theta }_P\rho +\omega )v}{({\theta }_S\pi {\theta }_P\rho +\omega )v+(\pi \rho +\omega )(1-v)}\end{array}$$

and

$$Pr(Z_i=0|Y_i=1)=\frac{(\pi \rho +\omega )(1-v)}{({\theta }_S\pi {\theta }_P\rho +\omega )v+(\pi \rho +\omega )(1-v)}.$$ 11.2b

Thus, we may express the effect of vaccination against all-cause disease as

$${\text{OR}}_A=\frac{[({\theta }_S\pi {\theta }_P\rho +\omega )v][1-v]}{[(\pi \rho +\omega )(1-v)][v]}=\frac{{\theta }_S\pi {\theta }_P\rho +\omega }{\pi \rho +\omega }.$$ 11.3

We note that this result equals the risk ratio of disease given vaccination, $Pr(Y_i=1|Z_i=1)/\text{Pr}(Y_i=1|Z_i=0)$.

Rearranging the terms in equation (11.3), we obtain the risk (or rate) ratio of disease attributable to the pathogen of interest, versus other causes, as

$$\frac{\pi \rho }{\omega }=\frac{1-{\text{OR}}_A}{{\text{OR}}_A-{\theta }_S{\theta }_P},$$ 11.4a

where 1 − VE_D (equation (6.1)) may provide an unbiased input for θ_Sθ_P. Thus, the proportion of disease attributable to the pathogen of interest, in the absence of vaccine-derived protection, is

$$\frac{\pi \rho }{\pi \rho +\omega }=\frac{1-{\text{OR}}_A\hspace{0.17em}}{1-{\theta }_S{\theta }_C}.$$ 11.4b

The result is mathematically equivalent to previous formulations of vaccine probe estimators including estimated protection against non-specific and specific endpoints in the numerator and denominator, respectively [22,41].

12. Summary

Microbiological diagnosis of certain infectious diseases may be complicated by the prevalence of putative aetiological pathogens among individuals whose symptoms are due to other causes. Here we present a framework for estimating the direct effects of vaccination on different aspects of individuals' susceptibility through the collection of pathogen detection data in case–control studies. A simple analytic extension provides a ‘vaccine probe’ framework for estimating the proportion of cases attributable to the pathogen of interest.

The approach we have taken also enables assessment of the quantitative extent of bias arising under different scenarios. We identify that pathogen-specific effects of vaccination may be underestimated when a pathogen is detected with low sensitivity among disease cases. Of the disease-specific applications we have described, this circumstance probably has the greatest importance for pneumonia, where pathogens may continue causing disease in the lung after clearance from their commensal niche in the upper respiratory tract. This circumstance would presumably reduce the sensitivity of pathogen detection among disease cases to a greater extent than what is expected among controls.

We also identify that TND studies may produce biased VE estimates either with or without misclassification of symptomatic individuals based on pathogen detection. Notably, we identify that bias in TND studies may result in either over-estimation or under-estimation of true VE, making the interpretation of estimates difficult. Here, we do not consider additional issues that have been found to impact the reliability of estimates from TND studies, including individuals' acquisition of immunity following natural infection and the mode of vaccine action [38,42] (e.g. ‘leaky’ protection conferring partial risk reductions to all individuals, or ‘all-or-none’ protection among a proportion of individuals). Nonetheless, our findings add to a growing list of concerns about the uses of the TND for estimation of VE [11,15,43]. The methods we lay out here provide an opportunity to correct for biases arising in conventional TND studies by enrolling control groups without symptoms potentially attributable to the pathogen of interest.

Case–control studies are commonly undertaken to estimate the direct effects of vaccination. Collecting pathogen detection data from controls, alongside symptomatic cases, presents a simple strategy to correct for misclassification of symptoms not attributable to a detected pathogen. Provided such data are collected, the approaches we describe permit estimation of VE against pathogen-specific endpoints without a diagnostic gold standard.

Data accessibility

Code to replicate the figures is available at https://github.com/joelewnard/ccVE.

Competing interests

I declare I have no competing interests.

Funding

JAL was supported by grant R01AI148127 from the National Institute of Allergy and Infectious Diseases (US National Institutes of Health).