Learning from plant movements triggered by bulliform cells: the biomimetic cellular actuator

Abstract

Within the framework of a biomimetic top-down approach, our study started with the technical question of the development of a hinge-free and compliant actuator inspired by plant movements. One meaningful biological concept generator was the opening and closing movements of the leaf halves of grasses. Functional morphological investigations were carried out on the selected model plant Sesleria nitida. The results formed the basis for further clarifying the functional movement principle with a particular focus on the role of turgor changes in bulliform cells on kinetic amplification. All findings gained from the investigations of the biological model were incorporated into a finite-element analysis, as a prerequisite for the development of a pneumatic cellular actuator. The first prototype consisted of a row of single cells positioned on a plate. The cells were designed in such a way that the entire structure bent when the pneumatic pressure applied to each individual cell was increased. The pneumatic cellular actuator thus has the potential for applications on an architectural scale. It has subsequently been integrated into the midrib of the facade shading system Flectofold in which the bending of its midrib controls the hoisting of its wings.

1. Introduction

Although plants are usually tied to their location, they have developed a variety of movements during the course of biological evolution. In particular, when environmental conditions in their habitat change, various movement mechanisms in the form of rapid responses or longer-term adaptations are of great selective advantage for their survival [1,2]. In contrast with animals, however, plants can move without the actuation and mobility provided by muscles and by conventional hinges, respectively [3]. This makes them particularly interesting for innovative biomimetic actuators.

Plant cells differ from animal cells because of the existence of a stiff cell wall around their cell membrane, which allows plant cells to sustain an internal hydrostatic pressure (= turgor) of approximately 0.5 MPa. The turgor is generated by an osmotic gradient caused by the semipermeable cell membrane, which allows the osmotic flow of water into the cell vacuole, thus placing the cell wall under pressure [4]. In herbaceous plants, such turgor plays a particularly important role in mechanical stability, whereby turgor changes are responsible for plant movements. In general, movements of multicellular plants vary over many orders of magnitude with regard to time scale and tissue size, defined as the smallest macroscopic moving part in a given time period. Slow movements such as reversible swelling and shrinking or irreversible growth are based on hydraulic effects limited by the poroelastic time scale of water diffusion through plant cells and tissues. These movements can be speeded up by mechanical instabilities such as snap-buckling or explosive fracture caused by the sudden release of stored elastic energy [4,5].

The basis for most reversible plant movements are changes in turgor at the cell level causing a microscopic change in the volume of the plant cell. These small changes can aggregate to a macroscopic shape change at the tissue level and finally at the organ level. An impressive example of kinetic amplification, during which a small displacement can lead to a large resulting movement, are the so-called motor cells. Reversible active plant movements are driven by the swelling and shrinking of motor cells attributable to rapid changes of turgor [1].

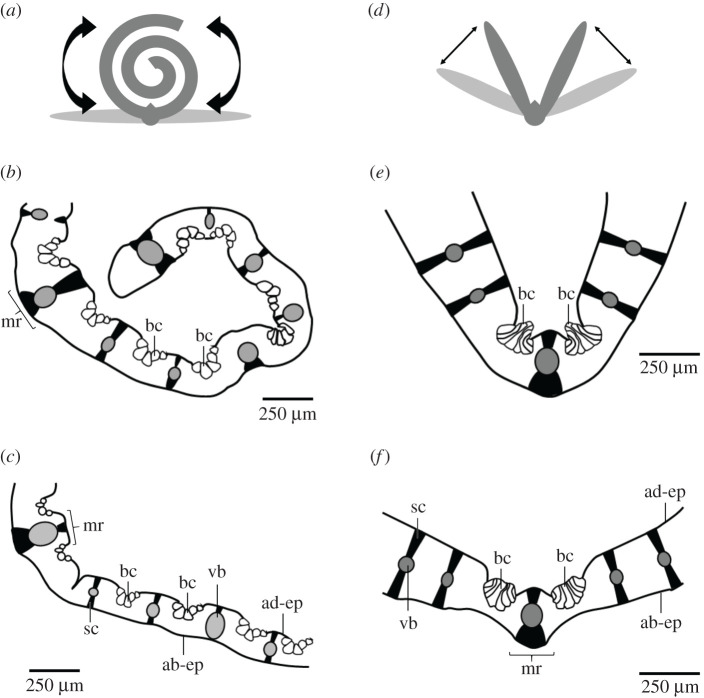
Bulliform cells are huge epidermal cells occurring in fan-shaped groups on the adaxial (= upper) side of leaves of species including the grass families Poaceae, Juncaceae and Cyperaceae. Various functions are attributed to them, such as water storage, participation in young leaf expansion, light entrance to the mesophyll cells and leaf movements of mature leaves. The schematic drawings in figure 1 show different leaf movements depending on the turgor of the bulliform cells and their arrangement along the leaf. If the bulliform cells are distributed along the entire leaf, the leaves roll up under drought stress, thus lowering the turgor pressure of the motor cells. The leaves unroll again as soon as the turgor pressure increases once more as a result of sufficient water availability [6–8]. If the bulliform cells are arranged as two groups to the right and left of the midrib, then the leaf is open in the fully turgescent state, whereas in the case of a water deficit the two halves of the leaf fold together as a result of the low turgor pressures in the motor cells [9]. This corresponds to the current view in the literature that the folding or curling of the leaves at low turgor pressures is a xeromorphic adaptation reducing the transpiration of the leaves and protecting them from dehydration and overheating during drought stress [10].

Figure 1.

Role of bulliform cells in leaf movement. (a–c) Bulliform cells are distributed along the entire leaf. (b) The leaf rolls in, when the turgor pressure in the bulliform cells is low. (c) It unrolls again, when the bulliform cells are turgescent. (d–f) Bulliform cells are concentrated near the midrib. (e) The leaf halves fold, when the turgor pressure in the bulliform cells is low. (f) They unfold again, when the bulliform cells are turgescent. ab-ep, abaxial epidermis (= lower epidermis); ad-ep, adaxial epidermis (= upper epidermis); bc, bulliform cells; mr, midrib; sc, sclerenchyma; vb, vascular bundle.

This article focuses on the hydraulically driven movements of grasses by bulliform cells, which offer the appealing advantages of being suitably distributed, energy efficient and integrative [3]. The pressurized cellular structure of plants is crucial to this functional movement principle and allows the combination of movement and structural rigidity. Thereby, the separation between the movement-inducing actuator and the stability-providing structure inherent to many animal and artificial systems is overcome. These systems combine the positive properties of fluidic actuators, such as high force, high stroke and good energy efficiency, with the benefits of a compliant system including reduced mechanical complexity based on a reduced number of parts and the avoidance of friction hinges [3]. The above-mentioned features make plant movements in general and turgor-dependent kinetic amplification in particular interesting as a valuable source of inspiration fostering the development of adaptive structures combining shape morphing and actuation.

Examples of previously published bioinspired systems based on hydraulically driven movement in plants are pressurized cellular actuators. To date, the greatest potential for the application of fluid-actuated cellular structures inspired by the hydraulic mechanisms of plant cells has been seen in the field of morphing wing applications [11–15] and robotics [3,16]. The systems can be driven by either hydraulics or pneumatics. Sinibaldi et al. [16] have developed a forward osmosis-based actuator with a typical size of 10 mm and a characteristic actuation time of 2–5 min. This plant-inspired actuator, which generates forces above 20 N and consumes power of the order of 1 mW, has potential for application in bioinspired robotic systems. Pagitz et al. [12] introduced a multi-layered module consisting of one layer with pentagonal-shaped cells and an additional layer with hexagonal-shaped cells. By tailoring the pressure differentials between these cell layers, several modules in series enable sophisticated shape changes applicable to adaptive aerofoils or passenger seats [11–13]. The first prototypes of pressurized cellular structures for use in an adaptive aerofoil were built by Gramüller et al. [14] and Vasista & Tong [15]. However, only a few approaches have aimed at developing plant-inspired adaptive actuators for architecture. Poppinga et al. [17] provided a theoretical concept for ‘escaping’ the poroelastic regime of hydraulically driven actuators to attain an architectural scale. These examples show that, in recent years, plant movements have been used as models for technical actuators.

Biomimetics stands for the systematic transfer of functional principles found in natural models into technical applications. Basically, two interdisciplinary approaches between scientists of diverse scientific disciplines can be distinguished. In the bottom-up approach, also called biology push process, a novel technical product is developed based on the findings from basic biological research. The top-down approach, also called technology pull process, starts with a technological challenge of an already existing product that can be solved by biomimetic improvements. The most demanding step in all biomimetic approaches is the abstraction to determine the decisive parameters of the respective function without copying all details of the biological model [18,19]. Although the biological model and the biomimetic product fulfil the same function, they often do not look alike.

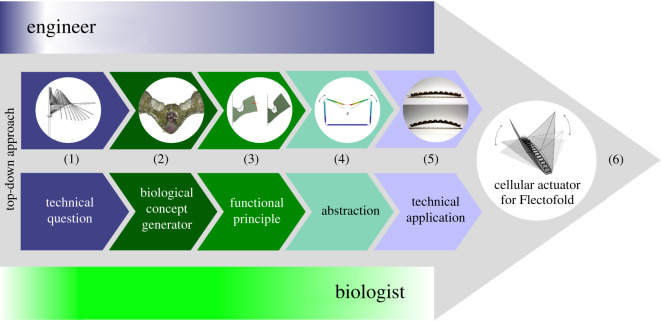
In this publication, we present the development of a pneumatic cellular actuator that can be used to actuate the biomimetic facade shading device Flectofold [20]. We describe the way in which the cellular actuator has been systematically developed by an interdisciplinary team of biologists and engineers using the biomimetic top-down approach [18,19]. For this reason, the publication is structured along the six consecutive steps of the biomimetic approach: (i) consideration of the technical question to be answered by an application-specific actuator, (ii) selection and investigation of a suitable biological model, (iii) identification of the functional movement principle, (iv) abstraction and translation into an engineer-compatible language, (v) feasibility test, and (vi) possible application (see also figure 2).

Figure 2.

The top-down approach (technology pull process) of the biomimetic cellular actuator. (1) Which functional principle of hinge-less plant movement can be transferred to an actuator for compliant architectural structures? (2) Grass leaves with opening and closing movements were investigated with respect to their functional morphology. (3) The kinetic amplification of the leaf halves is based on the interaction of turgor-dependent bulliform cells and strengthening tissues. (4) Finite-element models of the entire pressurized cellular actuator and its individual cells were developed. (5) A prototype of the plant-inspired cellular actuator was built and tested. (6) As a precursor model for the market launch, the actuator was integrated into the facade shading device Flectofold [20]. Shading is generated by a continuous motion of the two shading elements initiated by bending of the midrib in between.

2. Material and methods

2.1. Plant material

Sesleria nitida Ten. (hereafter, S. nitida) belongs to the grass family (Poaceae) and is native to Italy, Sicily and Malta. The plants, which are 20–70 cm high and evergreen, possess linear leaves with entire margins and parallel venation. The leaf samples were obtained via outside cultivation at the Botanic Garden of the University of Freiburg (Germany).

2.2. Anatomical studies of the leaves

Cross-sections of the leaves were obtained at a thickness of 60 µm by means of a cryostat microtome (MEV Cryostat; SLEE Medical GmbH, Mainz, Germany). Before being stained, the samples were bleached in 20% (v/v) sodium hypochlorite. To highlight various tissue types, the sections were stained with 0.3% (w/v) aqueous acridine orange (ACO), a fluorescent dye highlighting lignified tissues in bright yellow. The ACO-stained sections were imaged by using an Olympus BX61 microscope (Olympus, Tokyo, Japan) together with a CP71 camera module. Control staining was performed with hydrochloric acid (10%) and phloroglucinol (3%) in 95% ethanol (PHO), highlighting lignified tissues in red. The PHO-stained sections were imaged by using a Primo Star microscope (Zeiss, Jena, Germany) together with a Axiocam ERc 5S (Zeiss, Jena, Germany) camera module.

2.3. Morphometric analyses of the plant cells

Cell wall diameters (length and width) and cell wall thicknesses of chlorenchyma cells and bulliform cells were measured from microscopic images with the help of software ImageJ (v. 1.52i) [21]. We selected chlorenchyma cells from all regions between the adaxial (= upper) and abaxial (= lower) epidermis.

2.4. Turgor-dependent opening angles of the leaves

To determine the influence of the degree of turgescence of the bulliform cells on the opening angle between the two leaf halves, we measured the opening angles first of 10 fresh samples and, subsequently, of the same 10 samples after having been stored in dry air for 24 h. For the measurement, the transverse plane of each sample was photographed with a camera (Lumix DMC-FZ1000, Panasonic, Kadoma Osaka, Japan). The opening angles were measured from the images with ImageJ software (v. 1.52i) [21]. Each test sample represents the apical 5 cm of a leaf.

2.5. Pre-stress analysis of the leaves

In order to determine the influence of the existence or absence of turgescent bulliform cells on the degree of opening of the two leaf halves, the following manipulation experiment was carried out. A scalpel was used to cut the bulliform cells as completely as possible on one side along the midrib without damaging the surrounding tissue. Intact and damaged leaf samples were imaged by using a binocular microscope (SZX9; Olympus, Tokyo, Japan) equipped with a camera (ColorviewII; Olympus, Tokyo, Japan).

2.6. Statistics

Raw data are provided in electronic supplementary material, S1. Statistical analyses were performed using Gnu R 3.4.0 and R Studio Version 1.2.1335 [22]. Unless otherwise specified, non-parametric data are given as the median and interquartile range (IQR) and parametric data as the mean ± 1 s.d. Data were tested for normal distribution (Shapiro–Wilk test). The paired Wilcoxon rank-sum test was used for significance testing of the data on cell morphometry or opening angles. Levels of significance were p > 0.05: not significant (n.s.); p ≤ 0.05: significant (*); p ≤ 0.01: very significant (**); p ≤ 0.001: highly significant (***).

2.7. Finite-element analysis

A finite-element analysis (FEA) was conducted to improve comprehension of the role of bulliform cells in leaf involution. The geometry derived from the light microscopy images was subsequently reconstructed with the help of computer-aided design software as described in [23]. Based on the image loaded into Rhinoceros^® (v. 5), the outline of the bulliform cells and the leaf cross-section was re-drawn and extruded to achieve the three-dimensional model used in the FEA (ANSYS^® Academic Research, Release 18.2). The cell walls of the bulliform cells were represented by four-node structural shell elements (SHELL181). The average cell wall thickness to be assigned to the shell elements was measured beforehand from the microscopy image by using the image-processing program ImageJ (v. 1.52a) [21]. The mean values of 25 measurements were employed (electronic supplementary material, table S1 in S2). The surrounding tissues were combined into one solid body (a higher order three-dimensional, 10-node element (SOLID187)). The data for Young's modulus of the various materials were approximated with values from the literature. The material behaviour was assumed to be linear-elastic. The cell walls of the bulliform cells were assumed to have Young's modulus of 5 MPa [24] and Poisson's ratio of ν = 0.27 [25]. For the surrounding tissue, Young's modulus was calculated according to a formula by Nilsson et al. [26] by using the cell wall diameter and cell wall thicknesses measured for the chlorenchyma cells.

The aim of this numerical experiment was to examine the capability of the bulliform cells to cause leaf involution by using geometrical, material and pressure parameters as occurring in the natural system. As the microscopic images were taken at a fully turgescent state, the closed state of the leaf was created by applying an external horizontal force of 50 µN. The resulting deformed state served as a basis for the following simulation. All stresses were set to zero and a pressure of 0.07 MPa was applied to the surface of the cell walls of the bulliform cells to imitate increasing turgor, which should lead to a leaf opening. The magnitude of the applied pressure was thereby based on the turgor difference measured for the parenchyma of Caladium bicolor ‘Candyland’ petioles in the fully turgescent state (0.45 ± 0.04 MPa) and under drought stress (0.38 ± 0.08 MPa) [27]. To represent this turgor variation, pressure was applied to the inside of the bulliform cells by hydrostatic fluid elements (HSFLD242), requiring a nonlinear calculation. Like a pressurized fluid, these elements exerted pressure on the inner cell walls.

The angular change was quantified by calculating the centre of rotation from the displacement of the leaf blade ends and the according angular change around this point was determined by trigonometric functions. This was conducted for every time step individually because the centre of rotation shifted slightly with increasing deformation.

2.8. Numerical design process

A numerical design process deriving the cell shape and the thicknesses of compliant hinges was conducted using commercial FEA software (ANSYS^® Mechanical Products Release 17.2). The technical cells were represented by shell elements (SHELL181) and the contained fluid was represented by hydrostatic fluid elements (HSFLD242). The displacement of the hydrostatic fluid elements in the direction of the open sides was restrained, substituting the pouches in the model. The material properties of the glass-fibre-reinforced epoxy composites (GFRP) were assumed to be isotropic (E = 15 GPa; ν = 0.3).

A physical prototype of the cellular actuator was built. For this purpose, a silicone mould representing the pressurizable volume was produced and layers of woven glass fibre prepreg sheets (prepreg details: woven glass fibre fabric pre-impregnated with epoxy resin based on bisphenol A (40 wt%) type ET222 (SAATI S.P.A.); multifilament: E glass (fineness 680d); weave: Twill 2/2; surface weight: 80 g m⁻²) were stacked onto it in a variable number of layers to achieve the defined wall thicknesses. The fibre orientation in the hinges was 0/90°. After the stacking step, the mould was placed into a vacuum bag. With an applied pressure keeping the prepreg sheets together, the epoxy was cured in an oven at 125°C for 2 h. The cells were pressurized by pouches made from heat-weldable airtight thermoplastic polyurethane-coated nylon (area density: 70 g m⁻²) placed inside the technical cells and connected by tubes.

3. Biomimetic top-down approach

3.1. Technical question

The project presented is a typical biomimetic top-down approach starting with a technical question from the field of engineering sciences [18,19]. The main topic was the search for hinge-less kinematics for architectural applications. In collaboration with biologists, the engineers systematically searched for functional principles in living nature. The aim was to find generally valid biomimetic solutions. Functional principles of plant movements are very suitable as a source of inspiration because they function without hinges. The project started with the technical question of the development of a hinge-free and compliant actuator inspired by plant movements (figure 2).

The advantage of compliant systems is based on the reduced mechanical complexity owing to their monolithic construction principle. However, the compliant mechanisms realized so far are actuated by conventional actuators such as electric motor or hydraulic pistons. Since these devices are made up of a large number of parts with sliding elements and thus wear and tear, and since they must be placed close to the element to be actuated, their use contradicts the fundamental idea of a compliant system. Consequently, the next step in the development of complaint systems is the integration of the actuation into the structure of the compliant mechanism itself. Moreover, more distributed actuation reduces stress concentrations in the region where the forces are introduced. A first step in this direction was the actuation by a pneumatic cushion between the midrib of the Flectofold and a stiff backbone. Upon inflation, the cushion causes the bending of the midrib and thus folding of the wings. However, the cushion lies freely and requires the stiffer backbone to act against it. The aim is to create a self-contained system that, like the biological model, elegantly integrates the actuation into the structure.

3.2. Biological concept generator

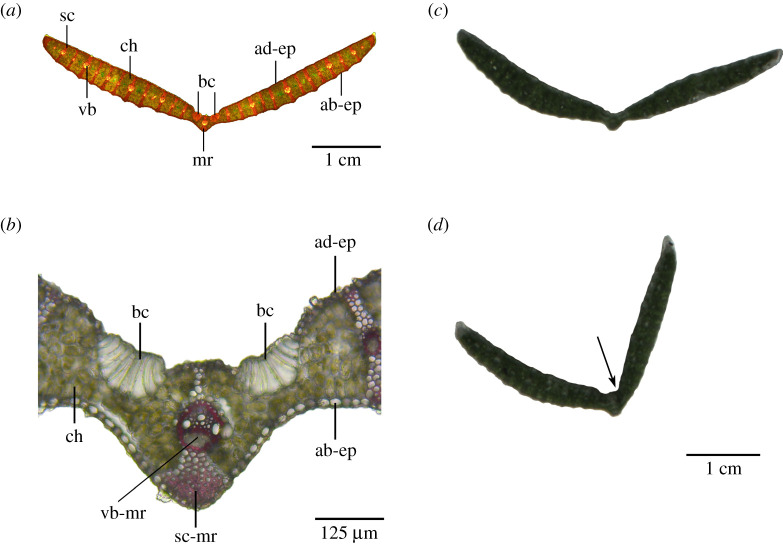
Grass leaves with an opening and closing movement of their leaf halves served as a suitable biological model. Based on the three-dimensional arrangement of tissues with various morphometry and properties, these leaf halves show a pronounced kinetic amplification. Figures 1d–f and 3a,b show the typical structure of a transverse section of the leaf lamina found in the Poaceae family. The V-shaped leaf has a symmetrical structure consisting of a midrib with a midrib vascular bundle (=midvein) and the two lamina halves. According to the parallel venation, which is typical for monocotyledonous plants, further vascular bundles are found at regular intervals along the two lamina halves. The vascular bundles and lignified sclerenchyma strands form a spacer between the adaxial and abaxial epidermis. The uniform mesophyll consists of densely packed chlorenchyma cells. To the right and left of the midrib, on the adaxial side of the S. nitida leaf, turgor-dependent bulliform cells can be found, each forming a group of approximately 10 enlarged epidermal cells. In transverse sections, these bulliform cells are markedly wider and higher than the epidermal cells with gradual transitions in cell dimensions between the individual cells (figure 3a,b). Mechanical damage of bulliform cells results in a clear folding of the respective leaf half (figure 3c,d).

Figure 3.

Leaves of S. nitida. (a) Transverse section of an entire leaf stained with ACO. (b) Detail of the midrib stained with PHO. Unstained leaf segments with (c) intact bulliform cells and (d) mechanically damaged bulliform cells on the right side (arrow). The right half of the leaf lamina can be clearly seen to be tilted inwards after damage to the bulliform cells. ab-ep, abaxial epidermis (= lower epidermis); ad-ep, adaxial epidermis (= upper epidermis); bc, bulliform cells; ch, chlorenchyma; mr, midrib; sc, sclerenchyma; sc-mr, midrib sclerenchyma; vb, vascular bundle; vb-mr, midrib vascular bundle (= midvein).

Electronic supplementary material, table S1 (see electronic supplementary material, S2) presents the morphometric data derived from chlorenchyma cells and bulliform cells. The paired Wilcoxon test revealed that the diameters along the major and minor axis of the chlorenchyma cells (V = 1120.5, p = 3.197 × 10⁻⁶) and the bulliform cells (V = 190, p = 3.815 × 10⁻⁶) differ highly significantly. The opening angle of 10 fresh turgescent leaves and of dried leaves stored in dry air for 24 h is also given in electronic supplementary material, table S1. The paired Wilcoxon test revealed that the opening angle of the fresh samples is very significantly higher than that of the dried leaf samples (V = 55, p = 0.001953).

3.3. Functional principle

The functional principle of the hinge-free folding and unfolding movement of grass leaves served as a suitable biological model for transfer into a technical application. The turgor-dependent bulliform cells on the adaxial side of the leaf are responsible for the movement. The pivot of the movement is located in the midrib area consisting of a midvein, a larger triangular sclerenchyma area on the abaxial side and a thin sclerenchyma strut on the adaxial side (figure 3b). Abutment in the form of the vascular bundles and sclerenchyma arranged as spacers between the adaxial and abaxial epidermis ensures the integrity of the leaf lamina (figure 3a,b).

The pre-stress experiments clearly showed that damage to one of the two groups of bulliform cells markedly reduced the opening angle on the injured side (figure 3c,d). This result supports the hypothesis that the pre-stresses in the folded leaf must be actively counteracted by a high turgor pressure of the bulliform cells to open the leaf. Or in other words, drought stress leads to a decrease in turgor pressure in the bulliform cells and the leaf closes passively as a result of pre-stresses in the surrounding tissues. In both cases, the leaf halves move until a new equilibrium is established. The above-described three-dimensional arrangement of the various tissues and the turgor-dependent swelling and shrinking of the bulliform cells provide evidence that the leaf halves exhibit pronounced kinetic amplification.

For a deeper understanding of the functional principle of the biological model, an FEA of the leaf movements triggered by bulliform cells was performed. Within the scope of this simulation, the focus was placed on three key characteristics: (i) the geometry of the leaf, (ii) the geometry of the bulliform cells in the turgescent and non-turgescent state, and (iii) the opening angles of the two leaf halves in the turgescent and non-turgescent state.

Other aspects were not considered in the FEA. These omissions included the simplification of the model by assuming the surrounding tissues as a single material with uniform linear-elastic material properties calculated from the characteristics of the parenchyma alone and by neglecting the probably stiffer epidermis and vascular bundles. Furthermore, we did not investigate whether the mechanical properties of the tissues changed with the availability of water.

Figure 4 depicts the simulation process from the transfer of the geometry from the original microscopic image of a leaf segment of S. nitida (figure 4a), via a simulation to approximately the closed position created by the pre-stresses in all leaf tissues (figure 4b), to the creation of a drought state in which the turgor in the bulliform cells is reduced as a starting point for a simulation with increasing turgor pressure (figure 4c). In a further simulation step, these bulliform cells were placed under turgor pressure once again (figure 4d).

Figure 4.

Process of finite-element (FE) simulation. (a) The outline of the leaf section and the bulliform cells were directly transferred from a microscopic image. (b) Pre-stresses in the leaf tissues are responsible for the folding of the leaf in the event of a drought-stress-induced volume reduction in the bulliform cells. To reproduce this effect in the numerical model, an external horizontal force is applied to the outer edge of the leaf segment considered here. (c) The geometry in a closed position serves as the starting point for the subsequent FE simulation. (d) An increase in pressure, exclusively in the bulliform cells, causes an increase in the opening angle of the leaf lamina.

The opening angles of fresh (turgescent) leaves were significantly higher than those of dehydrated leaves after a drying period of 24 h (electronic supplementary material, table S1 in S2). As no turgor values were available for the bulliform cells in various turgescent states, value changes of 0.07 MPa measured for petioles of Caladium bicolor ‘Candyland’ with a sufficient water supply and under drought stress were used [27]. Figure 5 shows a calculated and almost linear relationship between the turgor increase in the bulliform cells and angular change resulting in a rotary motion of the leaf lamina with respect to the calculated pivot point. The total opening angle between the two leaf halves increased almost linearly up to 52°. This is in good agreement with the mean change of the opening angle of 54.33 ± 16.03° of fresh and dried samples of S. nitida (electronic supplementary material, S1 and table S1 in S2).

Figure 5.

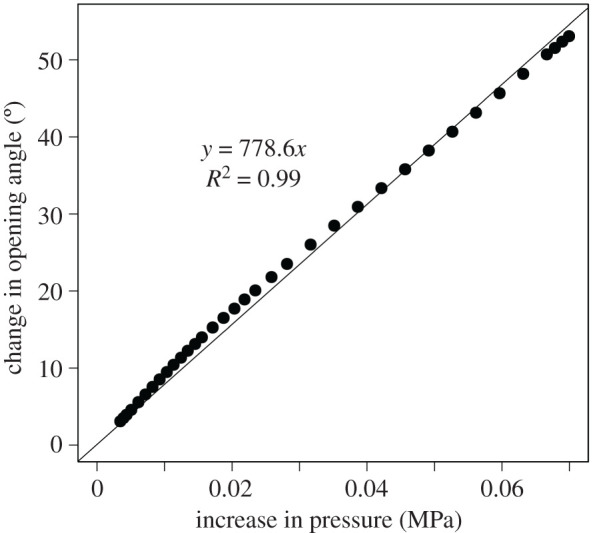
Simulation results for the total opening angle between the two leaf halves depend on the respective increase in turgor pressure inside the bulliform cells. The regression line and the coefficient of determination are presented.

Figure 4d displays the simulation results graphically. The maximum equivalent (von Mises) stress of the bulliform cells is 1.46 MPa. This value can only be interpreted as the stresses added to the cell wall by the pressure increase, because the turgor present in the drought state is not represented in the FEA. It roughly lies in the same range as the calculated Hoop stress ${\sigma }_H=(P\cdot d)/\hspace{0.17em}(2\cdot t)$ of 6.81 MPa for the turgescent state and 5.75 MPa for the dehydrated state, when considering a mean internal diameter of d = 29.67 µm, a cell wall thickness of t = 0.98 µm and a turgor pressure of P_turg = 0.45 MPa and P_dehyd = 0.38 MPa for turgescent and dehydrated cells, respectively [27]. These simulation results show that the bulliform cells can cause the opening and closing motion of the leaves of S. nitida, based on their morphometric data and the literature values of the change of turgor pressure and of the cell wall properties.

3.4. Abstraction

The functional principle worked out on the basis of the literature research, the experiments on the biological model S. nitida (see ch. 3.2) and the corresponding FEA (see ch. 3.3) now had to be abstracted for further technical application. The geometry of the compliant cells needed to be designed so that a pressure change would create the desired motion.

This work focuses on the creation of a bending motion. Bending is created by the differentiated expansion of the upper and lower region of a beam. This is possible in a multi-layered cellular structure in which cells of individual cell rows can be separately pressurized and extended. However, a single cell row set-up is also possible. This offers the advantage of a reduced number of parts and complexity. Such a system requires cells that have an asymmetric geometry and that thus expand more on one side when pressure is applied.

Figure 6 shows the transition from the FE model of the investigated V-shaped leaf segment of S. nitida, with group-wise arranged bulliform cells, to FE models of both a single cell and the technical cellular structure inspired by the biological model. Increasing air pressure inside the cells leads to the outwards tilting of the vertical sidewalls. When accumulated within a row of cells, this tilting of the sidewalls leads to a bending of the overall structure. The compliant hinges allow the cells to attain their original shape when the pressure has decreased once more. This requires a fine balance between the flexibility and stiffness of the compliant cell hinges. They have to be flexible enough to allow reconfiguration but, at the same time, need to provide the necessary structural rigidity of the system in the unpressurized state. The equilibrium position in the pressurized states is defined by the sum of the pressure-induced moments and the moments induced by the hinge stiffness. The individual design of the cells is determined by the specific requirements of the respective application. Driving design parameters are the maximum angular change of the vertical cell walls and the maximum pressure to be applied. These two characteristics rule the cell geometry including the side wall thickness, the hinge geometry and thickness and the material used [14]. The above-mentioned partially counteracting design variables allow the design of cellular structures for a wide range of pressures and scales [13]. The size of the technical cells can span from centimetres to metres, which is several orders of magnitude larger than the biological model. The diameters of plant cells are typically in the micrometres range (electronic supplementary material, table S1 in S2). In order to scale a cellular structure, the internal cell pressure has to be adjusted. To maintain a constant stiffness, the pressure potential of a cell needs to stay the same. As by reducing the cell size the volume reduces, the internal pressure needs to be increased. Thus, the pressure scales inversely proportional to the volume and an individual cell with one-quarter of the reference volume requires a fourfold increase in pressure. This relation is explained in detail by Pagitz & Kappel [13] for a pressurized cellular structure spanning the same distance with a different number of cells. This relation is also reflected in the comparably high internal cell pressure (turgor pressure of approx. 0.45 MPa [27]) of the small plant cells.

Figure 6.

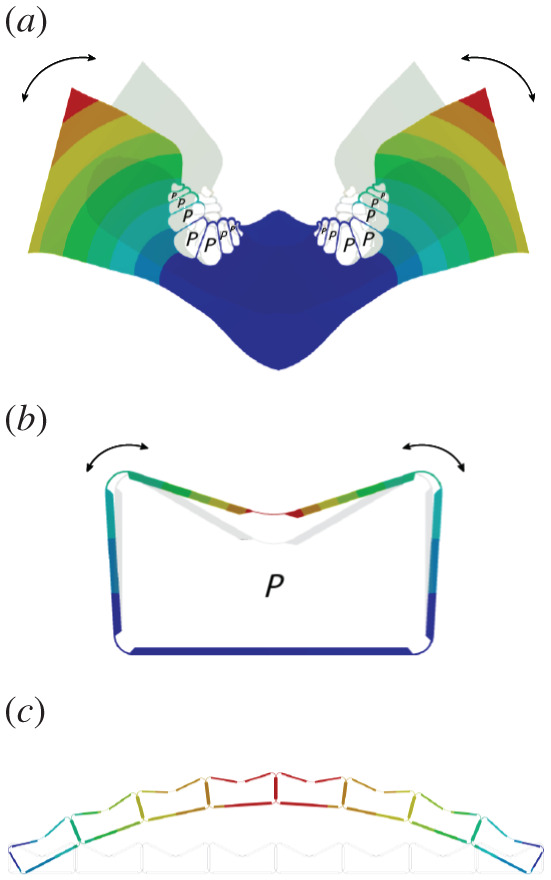
Abstraction process. (a) FE model of a leaf segment of S. nitida with two fan-shaped groups of bulliform cells right and left of the midrib of the biological model. The leaf halves open or close dependent upon the turgor pressure in the bulliform cells. (b) FE model of an individual technical cell. As the air pressure inside the cell increases, the vertical cell walls tilt outwards. (c) If several cells are aligned in a cell row, a bending motion occurs.

The material used has to possess the envisaged flexibility and further combine a low density and high stiffness, in addition to having stable long-term behaviour. This is especially true for large-scale applications and kinetic structures in which the resetting of the original shape can only happen by means of the elastic energy stored in the material. According to Lienhard [28], these criteria are only met by fibre-reinforced plastics (FRPs) and bamboo. Furthermore, FRPs offer the advantage of an adjustable Young's modulus through fibre orientation.

3.5. Technical application

One of the envisaged applications of a compliant cellular actuator is the actuation of compliant systems in the building sector, such as facade shading elements. The Flectofold is a biomimetic compliant kinetic element inspired by the hinge-less motion of the underwater snap-trap of the carnivorous waterwheel plant. The functional principle is based on curved-line folding as a mechanism for kinetic amplification. The bending of a midrib is transformed into a stronger flapping motion of the adjacent surfaces [20]. The dimensions of the cellular actuator were chosen according to the Flectofold prototype size (see fig. 3 in [20]).

The cell design was derived to meet the requirements described below. The maximum height of the cells was limited to 1/10th of the midrib length, namely 42 mm, to allow for a comparably inconspicuous actuation of the system. The cell shape was derived through a parametric design process. By analogy to the outer appearance of a S. nitida leaf section, an inverted pentagonal shape was chosen. This design carries the risk of a snap-through of the upper cell walls if the pressure is too high. On the other hand, cells with an inverted pentagonal shape generate a higher momentum than cells with a pentagonal cell shape at the same pressure applied.

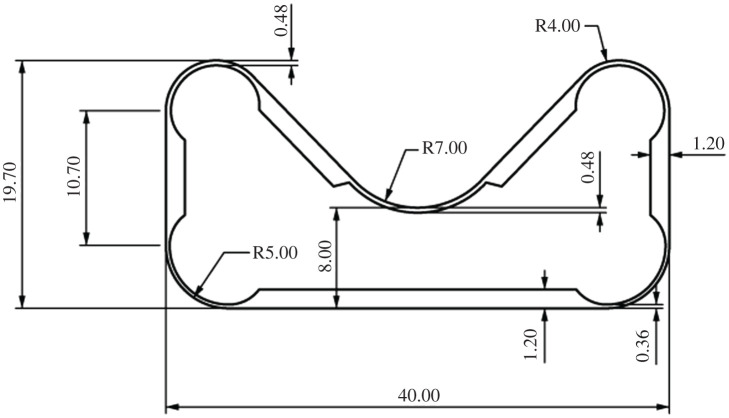
A first approximation of the cell wall thickness and hinge geometry could be calculated analytically according to [14]. However, the available prepreg thicknesses limited producible cell wall thicknesses. In an iterative process, the hinge geometry was defined so that the required angular distortion was achieved and the maximum strength of the material was not exceeded. The straight cell walls were designed so that they were stiff enough not to deform upon pressurization. The dimensions of the produced cells are displayed in figure 7.

Figure 7.

Cell geometry and wall thicknesses for the physical prototype of the biomimetic cellular actuator. All measurements are given in millimetres.

Figure 8 shows the results of the numerical simulation. The sidewall angle α increases with increasing internal cell pressure. The targeted angular deflection of 4.7° (value for actuating the small-scale Flectofold to an angle of 90°) was reached at an internal pressure of 0.02 MPa.

Figure 8.

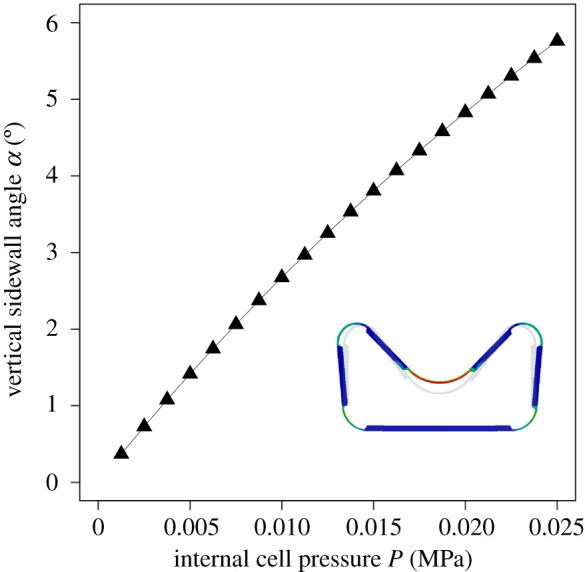
Angular deflection α of the side wall of the technical cell upon increasing internal cell pressure P.

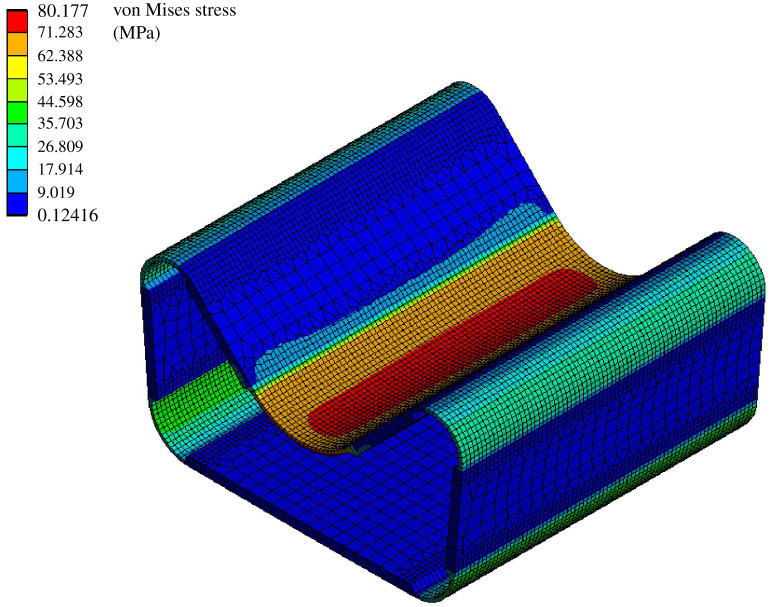
In this configuration, maximum stress occurs in the central hinge of the cell. The maximum attained values of approximately 80 MPa are well below the bending strength of GFRP (figure 9). Even taking into account the cyclic loading and reduced fatigue strength of GFRP, the stress values are sufficiently low. However, if a different structure needs to be actuated, the above-mentioned values may increase in cases when additional energy is required to deform the attached structure. Thus, rechecking might be necessary for each specific application.

Figure 9.

Stresses that occur in the cell wall of an individual technical cell at an internal air pressure of 0.02 MPa. The cell width is 40 mm.

Figure 10 shows the physical prototype of the biomimetic cellular actuator. It is capable of achieving the necessary curvature, as well as exerting additional force and carrying external loads. With an internal pressure of less than 0.4 MPa, a plate attached under the cell row can be bent and an additional mass of 0.5 kg placed on top of the cell row can be lifted simultaneously. This experiment demonstrates the great potential of the cellular actuator.

Figure 10.

Physical prototype of the cellular actuator inspired by the bulliform cells of S. nitida. The structure lifts an external mass of 0.5 kg.

3.6. Cellular actuator for Flectofold

Since cellular systems are supposed to be easier to control and to be more reliable and energy efficient while exhibiting a better strength-to-self-weight ratio [11], they are promising actuators for compliant mechanisms actuated by bending or folding. To illustrate the feasibility of the concept as a bending actuator, the Flectofold [20] was selected as the first application example (figure 11). Compared with the actuation of the Flectofold by a lens-shaped pneumatic cushion, this approach enables a self-contained system that can open and close without the need for an additional supporting substructure. Furthermore, the use of a cellular actuator entails the capacity for a bidirectional actuation and a stiffness variation through the effect of an antagonistic set-up. This would potentially be possible by the comparably small modification of adding a second cell row. Further optimization of the system (cell size, shape and thicknesses) is possible. This is a decisive aspect because the cellular structure has to be adapted to the specific conditions and requirements of each application, such as the scale, internal cell pressure, desired distortion and necessary actuation forces. Further applications in architecture and in other fields of engineering such as robotics, aerospace and automotive developments are possible.

Figure 11.

Physical prototype of the single cell row actuator bending the midrib of the compliant shading system Flectofold.

4. Discussion

A biomimetic cellular actuator was developed within a biomimetic top-down approach through collaboration between scientists from biology and engineering [18,19]. Within the scope of this study, all essential steps could be carried out: (i) from the technical question to (ii) the selection of a biological model, (iii) from the identification of the functional principle to (iv) its translation into a language compatible for both engineers and natural scientists, and (v) from the FEA into (vi) a physical prototype that could be built into the facade shading system Flectfold.

In the reported case, even the technical question regarding the means of developing a hinge-less actuator for compliant structures on an architectural scale inspired by plant movements contained more than one challenge. Hinges are movable connections between two rigid bodies, both in technology and in animals. The disadvantage of articulated hinges is that they are exposed to wear and tear because of friction, making them prone to failure. By contrast, plants do not have conventional hinges. Plant movements have been studied in great detail in recent years and a large number of compliant mechanisms have been found [4,5]. Their transfer to the building sector and their upscaling to the architectural level have also been successfully developed [17]. Well-known examples are the facade shading system Flectofin^® [29] based on the movement of the perch of the bird of paradise flower or the development of the shading system Flectofold inspired by the fast snapping movements of traps of carnivorous plants [20,30].

Grass leaves with opening and closing movements based on the turgor change of bulliform cells have proven to be an excellent model for the development of an actuator. These cells were originally described at the end of the 1800s [31] and are still being investigated today within the framework of basic research by novel methods and from many different aspects [32]. As far as we know, however, they have not as yet been used as models for technical applications in the field of bioinspiration or biomimetics.

The geometry of the bulliform cells varied with respect to the turgor pressure of the bulliform cells. In the turgescent state the bulliform cells had an oval shape and the leaf was open, whereas in the non-turgescent state the bulliform cells were pear-shaped and the leaf was closed (see also fig. 8.1 in [9]). Matschi et al. [32] have been able to show that the cell size of all epidermal cells, including the bulliform cells, decreases significantly through dehydration. In addition, dehydration reduces the volume of abaxial epidermal cells by 41% on average, that of adaxial epidermal cells by 42% and that of bulliform cells by 62%. Matschi et al. [32] have also been able to establish that the shape of dehydrated bulliform cells differs significantly from those in a fully turgescent state (cf. fig. 2 in [32]). Alvarez et al. [7] have documented, for the bulliform cells of Loudetiopsis chrysothrix and Tristachya leiostachya, that their outer periclinal walls are thinner than those of neighbouring epidermal cells. In addition, T. leiostachya also possesses sinuous thin anticlinal walls. These features might support the volume change and thus the shape change upon pressure fluctuations. In analogy to these findings, the results of our simulation for achieving the drought state indicate increasing cell ovalization or cell wall bending to allow deformation of the entire leaf.

The kinetic amplification of the leaf halves is based on the interaction of turgor-dependent bulliform cells as motors and the strengthening tissues in terms of spacers between the abaxial and adaxial epidermis with the pivot point in the area of the midvein. To gain new and deeper insights, we developed a finite-element model. Three key characteristics were identified: the geometry of the leaf, the geometry of the bulliform cells in the turgescent and non-turgescent state and the opening angles of the two halves of the leaf. The hypotheses that bulliform cells play an important role in leaf opening but no specific role in leaf closure were supported by our damage experiments [33].

In the plant kingdom, a huge variety of plant movements have evolved during biological evolution. Each of them is a potential source of ideas for biomimetic actuators on different scales. Movements driven by turgor changes of motor cells or bulliform cells are active, dependent on metabolism, reversible and the direction of the movement is determined by the structure of the moving organ (figure 1). By contrast, movements driven by the release of mechanical instabilities are rapid. Spore liberation of ferns from the annulus cells is the fastest plant movement, is passive and is fully reversible. Energy storage occurs independent of cellular metabolism by evaporation of the annulus cells [34]. This functional principle of transpiration actuation was transferred to a biomimetic microactuator driven by the surface tension of water [35].

The aim of the abstraction step is to determine the decisive parameters that guarantee the desired function of a technical product without copying all of the details of the biological model. These parameters include the cellular structure, the fluid-mediated volume change of motor cells and the reversible movement of the entire component. Abstractions were made regarding the movement (from the folding of the leaf halves to the bending of the cellular actuator), the fluid (from hydraulically driven plant movement to pneumatically driven deformation of single actuator cells), the power (from turgor pressure in the plant cells to pressurized air in the technical cells) and the asymmetric structure (from bulliform cells exclusively on the adaxial leaf side to cells with an asymmetric geometry). Pressurized cellular structures can be driven by both gases and liquids. Gases are suitable for larger cell volumes and low pressures; incompressible liquids are advantageous for small volumes and high pressures. The compressibility of gases causes safety issues in the case of explosive expansion and is responsible for low energy efficiency. This usually limits the application of pneumatics to about 1 MPa. Hydraulic systems can operate at much higher pressures up to 70 MPa, although at the cost of a much higher density and thus a higher weight [13]. In the case reported here, air was chosen as the pressure medium, because the low pressure range was sufficient for the considered application. Based on these insights, finite-element models of the pneumatic cellular actuator and its individual cells were developed, providing a common language understandable by both engineers and natural scientists [18,19].

The above-mentioned FEA is a prerequisite for the development of the physical prototype. As a precursor model for a later market launch, the actuator was integrated into the facade shading elements of the Flectofold [20]. For this reason, the prototype was dimensioned from the beginning in such a way that it could later be used as an actuator for the facade shading system Flectofold. The cellular actuator also has the potential to be built into the middle rib of the shading elements of the Flectofin^® [29], whereby its lamellae would unfold to the side while the midrib bends.

This is the first time that a pressurized cellular structure has been used as an actuator in a complaint system. This means that the pressurization both changes the configuration of the cellular structure itself and bends the adjacent surfaces, which have a motion amplifying folding pattern. This demonstrates its potential use as an actuator in compliant architectural systems beyond the application of pressurized cellular structures discussed previously in the literature.

Interesting aspects for continuing investigations include the airtight sealing of the system, so that a deflection of the system might additionally require the compression of the pressure medium or the use of an incompressible fluid. Further, the addition of a second row of cells might enable the decoupling from pressure and the deflection state. This will allow the stiffness of the system to be increased in any position. In pursuing this idea for the use of the cellular structure as an actuator for planar compliant folding mechanisms, another interesting topic would be the determination of the extent to which the stiffening of the cellular structure contributes to the stiffness of the overall structure.

Data accessibility

Raw data are available in electronic supplementary material, S1. Morphometric data of the biological model are available in electronic supplementary material, S2.

Authors' contributions

All authors were involved in the conceptual design of the study. O.S. selected the biological model. O.S. and M.L. designed the biological experiments, which were carried out by M.L. A.M. performed the finite-element analysis and developed the cellular actuator under the supervision of J.K. A.M. and O.S. wrote the draft and all authors contributed to the final version of the manuscript.

Competing interests

We declare that we have no competing interests.

Funding

We thank the German Research Foundation for funding within the framework of the CRC-Transregio 141 ‘Biological Design and Integrative Structures—Analysis, Simulation and Implementation in Architecture’ and the Ministry of Science, Research and the Arts (Baden-Wuerttemberg, Germany) for funding within BioElast.