THE EVOLUTION OF VARIANCE CONTROL

Abstract

Genetically identical individuals can be phenotypically variable, even in constant environmental conditions. The ubiquity of this phenomenon, known as ‘intra-genotypic variability’ is increasingly evident, and the relevant mechanistic underpinnings are beginning to be understood. In parallel, theory has delineated a number of formal expectations for contexts in which such a feature would be adaptive. Here, we review empirical evidence across biological systems, and theoretical expectations, including nonlinear averaging and bet hedging. We synthesize existing results to illustrate the dependence of selection outcomes both on trait characteristics, features of environmental variability, and species’ demographic context. We conclude by discussing ways to bridge the gap between empirical evidence of intra-genotypic variability, studies demonstrating its genetic component, and evidence that it is adaptive.

Responses to environmental variability

No environment on this planet is stable. Most organisms experience short-term fluctuations (such as seasonal variation, or stochastic fluctuations in temperature, rainfall and resources) as well as longer-term trends (such as those driven by global change). Such environmental variation drives the eco-evolutionary dynamics that contribute to maintaining genetic variation between individuals, and shapes phenotypic change. In turn, the fate of populations is determined in part by whether they harbor sufficient phenotypic variation to adapt to changing environments [1].

Perhaps the most frequently discussed source of phenotypic variation is genetic variation between individuals. Where sufficient genetic variation exists, a shift in the genetic makeup of the population will allow some individuals to persist in new conditions. This process can result in adaptive tracking (see Glossary), where the phenotypic mean of a population tracks a fitness optimum. Alternatively, adaptive phenotypic plasticity may allow populations to keep pace with environmental change, as specific genotypes modulate their phenotype in response to experienced environmental conditions [2]. These two components of population persistence in variable environments have been extensively studied both theoretically and empirically. An alternative strategy has received far less attention: changes in the level of phenotypic variance (rather than the mean) may be a key element in allowing populations to cope with changing environments.

The evolution of intra-genotypic variability, phenotypic variation observed across genetically identical individuals, leads to phenotypic variation even in a constant environment [3] (Box 1). This is in contrast to phenotypic plasticity, in which phenotypic variation is correlated with the environment. A life history strategy that maintains intra-genotypic variability will increase the probability that at least some individuals are well suited to particular environmental conditions [4]. Beyond genetic variation and phenotypic plasticity, intra-genotypic variability can thus be an important third axis by which populations can persist across changing environmental conditions, and is our focus here.

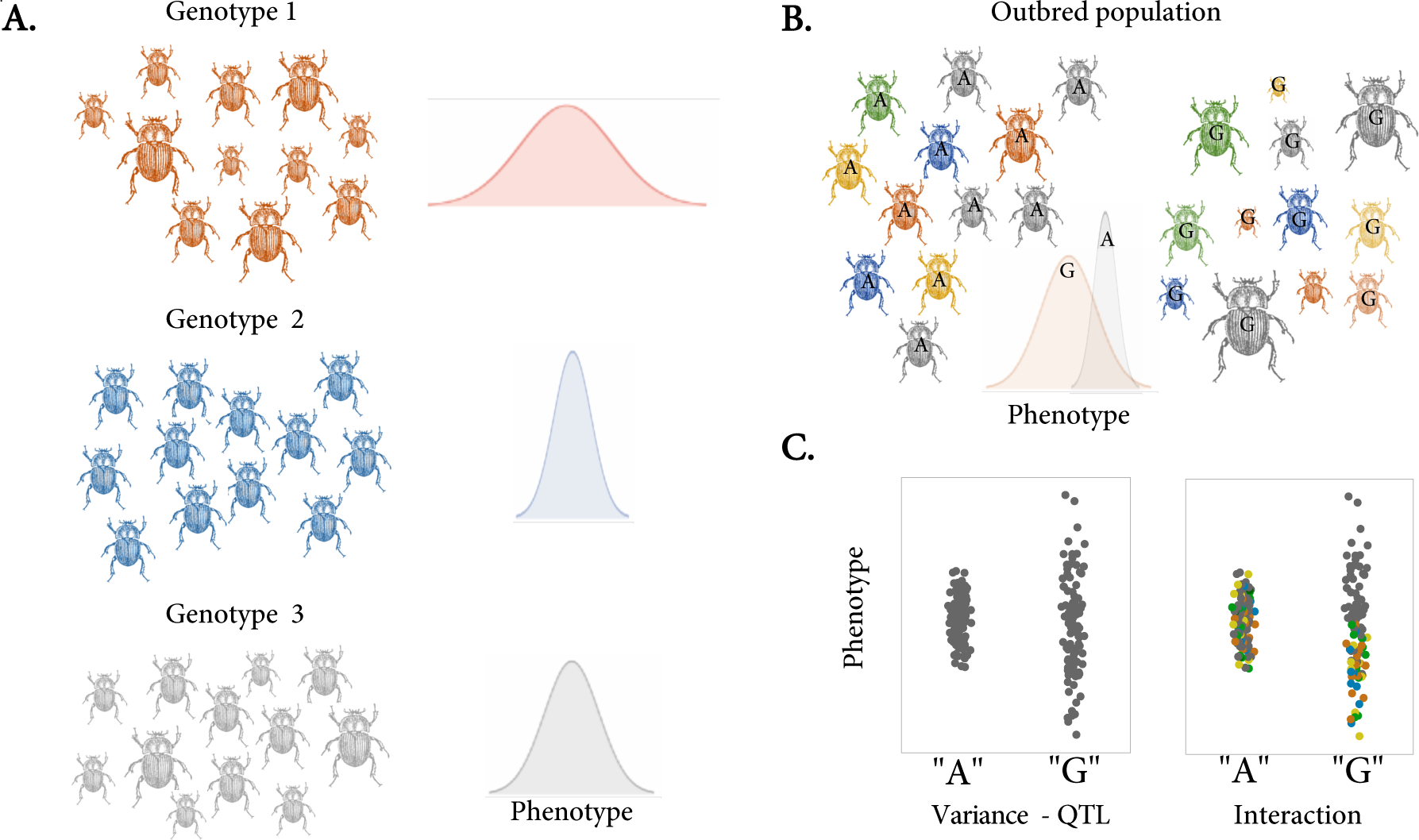
Box 1: Intra-genotypic variability in inbred and outbred populations.

Intra-genotypic variability is often described in the context of genetically identical individuals (e.g., parthenogenic species or isogenic lines). As illustrated in Fig I, panel A, when several isogenic individuals can be reared in the same nominal environment they often display different trait values. Here three genetic backgrounds (different colors) show different degrees of phenotypic variability for size, and the estimated variance across genotypes can be used directly to estimate heritability or map variance-QTLs. However, intra-genotypic variability also contributes to individual variation in outbred populations. Fig I, panel B represents a population of outbred individuals segregated by genotypes at a given locus (e.g., A or G) showing variance heterogeneity for size (the colors represent diverse genetic backgrounds). In both inbred and outbred populations, a given genotypic class is associated with different degrees of phenotypic variability. The key difference is that in an outbred population the observation of variance heterogeneity can either be driven by the presence of a variance controlling allele (e.g., A or G in this figure; the focus of this manuscript) or could result from mean-controlling loci interacting epistatically with another locus, leading to variance heterogeneity across genotypes [95,96]. Please note that an instance for inbred populations is not shown here. Fig I, panel C illustrates this point - on the left, the variance effect is driven by a variance QTL where a polymorphism is directly associated with a difference in variance across these alleles. On the right, the variance effect results from loci interacting epistatically. The phenotype of the “A” harboring individuals has low variance (regardless of the genetic background), while the phenotype of the “G” harboring individuals is a function of the genotype at a different locus (illustrated by the two distributions within the “G” allele). This distinction has important implications for the evolution of variance control and how it is studied. Here, we focus on the evolution of variance control from the perspective of variance controlling alleles, not variance heterogeneity driven by genetic interactions. While such heterogeneity could technically be maintained by epistasis under balancing selection, such cases have yet to be documented.

What is known about intra-genotypic variability?

Although there are surprisingly few studies investigating the contribution of intra-genotypic variability to phenotypic variation between individuals, various lines of evidence indicate that intra-genotypic variability is ubiquitous. Such variance in the variance commonly emerges in artificial breeding programs, as a nuisance to farmers who seek uniformity in their crops or livestock (e.g., observed in birth weight of rabbits (family: Leporidae) [5], mice (Mus musculus) [6] and rainbow trout (Oncorhynchus mykiss) [7]). Moreover, breeders have recently started using intra-genotypic variability as a resilience indicator [8,9]. Intra-genotypic variability has also been commonly observed for a wide range of traits in experimental model systems such as vinegar flies (Drosophila melanogaster), yeast (Saccharomyces cerevisiae) or nematodes (Caenorhabditis elegans) [10–12]. Finally, it has been observed in natural populations of plants (e.g., in seed banks [13,14]), mammals (e.g., in docility behavior in yellow-bellied marmots [Marmota flaviventris] [15]) and birds (in fledgling weight in great tits [Parus major] [16]), to list a few. However, the mechanisms generating intra-genotypic variability are still poorly understood. The phenotypic differences observed among genetically identical individuals are believed to result from both 1) the existence of stochastic micro-environmental variation affecting development (known as “developmental instability” [17]); and 2) the ability of an individual’s genotype to buffer development against these micro-environmental perturbations (and so limiting its effects on phenotype and thus phenotypic variability) [18].

For intra-genotypic variability to be of relevance for evolutionary ecology, it must be under genetic control. There is now ample evidence that this is the case, and heritabilities for intra-genotypic variability for a range of traits are reviewed by Hill & Mulder [19]. Moreover, recently it has become possible to map individual loci that regulate the degree of variability of a trait rather than its mean [20–22]. Such loci have been mapped in a wide range of organisms and for a variety of traits, for example locomotor handedness [12] and bristle numbers [23] in Drosophila, flowering time in Arabidopsis thaliana [24,25], morphological traits in maize (Zea mays) [26], calcium excretion in rats (Rattus norvegicus) [27], litter size in pigs (Sus scrofa) [28] and body mass index in humans [29]. The number of loci associated with variance may be on par with those associated with the mean [24,30] and there seems little overlap between loci affecting the mean of a trait and its variance [12,30] (although [31] provide a counter-example where the mean and variance are under the same genetic control).

When do we expect selection for increased intra-genotypic variability?

Given that intra-genotypic variability is under genetic control, we may expect that it can respond to selection. Results from basic theory allow us to predict selection for intra-genotypic variability and its direction across a range of contexts. If the relationship between traits and fitness is linear, e.g., in plants, the relation between vegetative and reproductive mass (as a measure for fitness) [32,33], there is no selection on the degree of variability (Fig. 1a,e). However, the relationship between traits and fitness is often nonlinear. If the shape of the relationship is convex (accelerating), this means that trait values some magnitude larger than the mean will result in large increases in fitness, while trait values equivalently smaller than the mean will result in relatively small reductions in fitness (Fig. 1b,f). Measures of plant size other than weight can yield such nonlinearities with reproductive output [33], also reported for the relationship between body size and egg number in mites (Sancassania berlesei) [34] and antler size and lifetime breeding success in red deer (Cervus elaphus) [35]. On average, then, if the trait mean is fixed, fitness can nonetheless be increased by increasing trait variance, as a result of ‘Jensen’s inequality’, a mathematical property of nonlinear functions [36,37] (Fig. 2a). The consequences of such nonlinear averaging have been described with respect to species coexistence [38], and may also be important in the evolution of variance control [39]. For example, Mulder et al. [16] found that stabilizing selection acts on variance in fledging weight in great tits due to the sigmoidal curve describing the relationship between fledging weight and recruitment - for such a concave (decelerating) relationship, an increase in the trait value (here, fledgling weight) yields smaller increases in fitness than the symmetrical decline.

Figure 1.

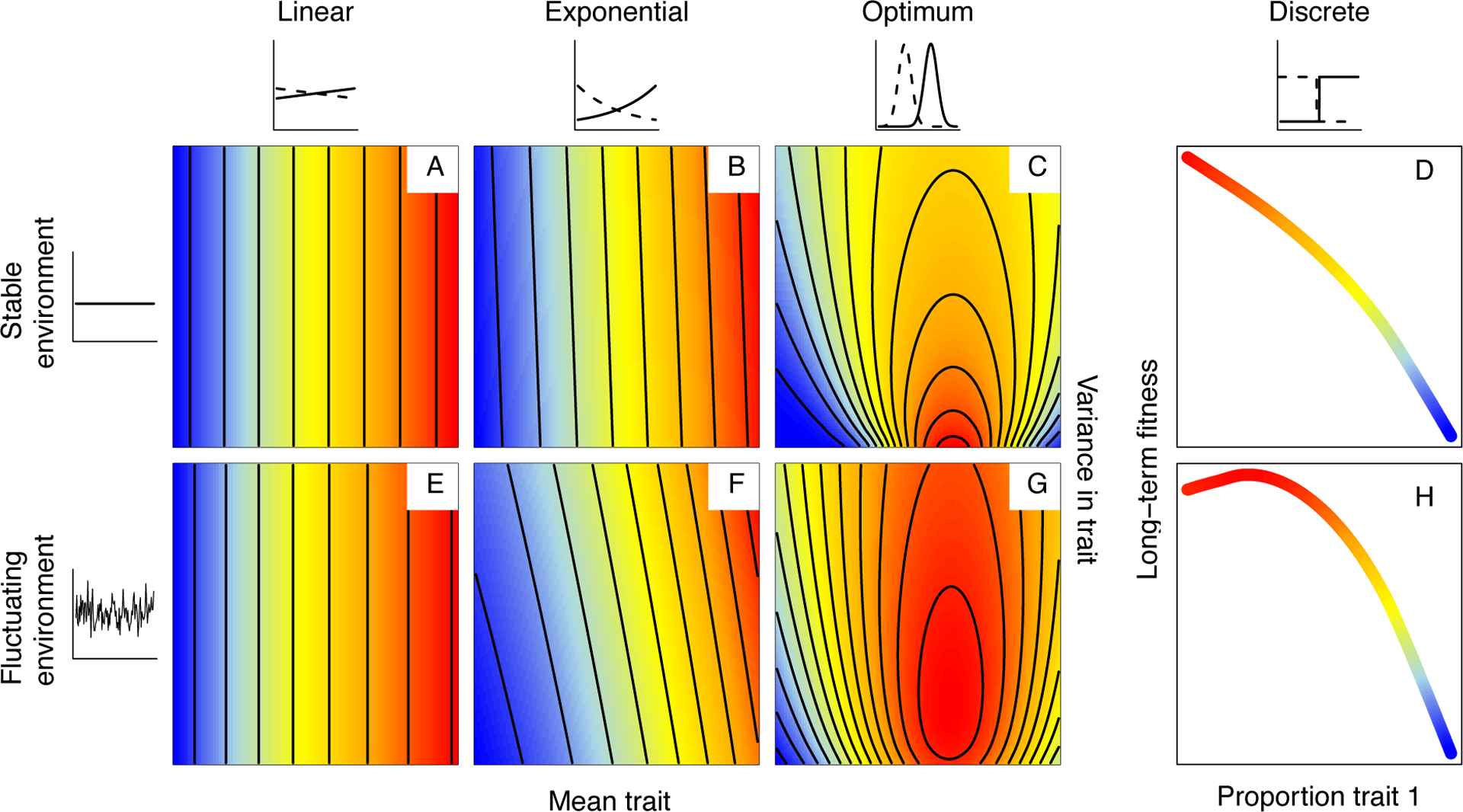
Long-term adaptive landscapes for different combinations of a mean phenotypic trait and variance in that trait to illustrate the conditions that might selection for intra-genotypic variability (Appendix S1–S3 for more information on how these landscapes were obtained). Upper row shows results for a stable environment, bottom row shows results for a fluctuating environment. Different columns show results for different relationships between the phenotypic trait and reproduction, as depicted in the small graphs. The environment modulates the relation between phenotype and fitness, illustrated by the solid and dotted lines. In a-c and e-g fitness landscapes for continuous phenotypic traits are shown. In d,h results for a discrete phenotypic trait are shown. Here, the x-axis shows the proportion of individuals expressing one trait, and is plotted against long-term fitness (y-axis). Red colors indicate higher long-term fitness, blue colors indicate lower values, and values are scaled for each graph separately. Variance has no effect in the case of the linear relation between phenotypic trait and fitness (a,e), while it results in a higher long-term fitness in the case of a convex relation, due to nonlinear averaging (b,f). When there is a phenotypic optimum that changes through time, for either a continuous (g) or discrete (h) trait, a bet hedging strategy results in the highest long-term fitness.

Figure 2.

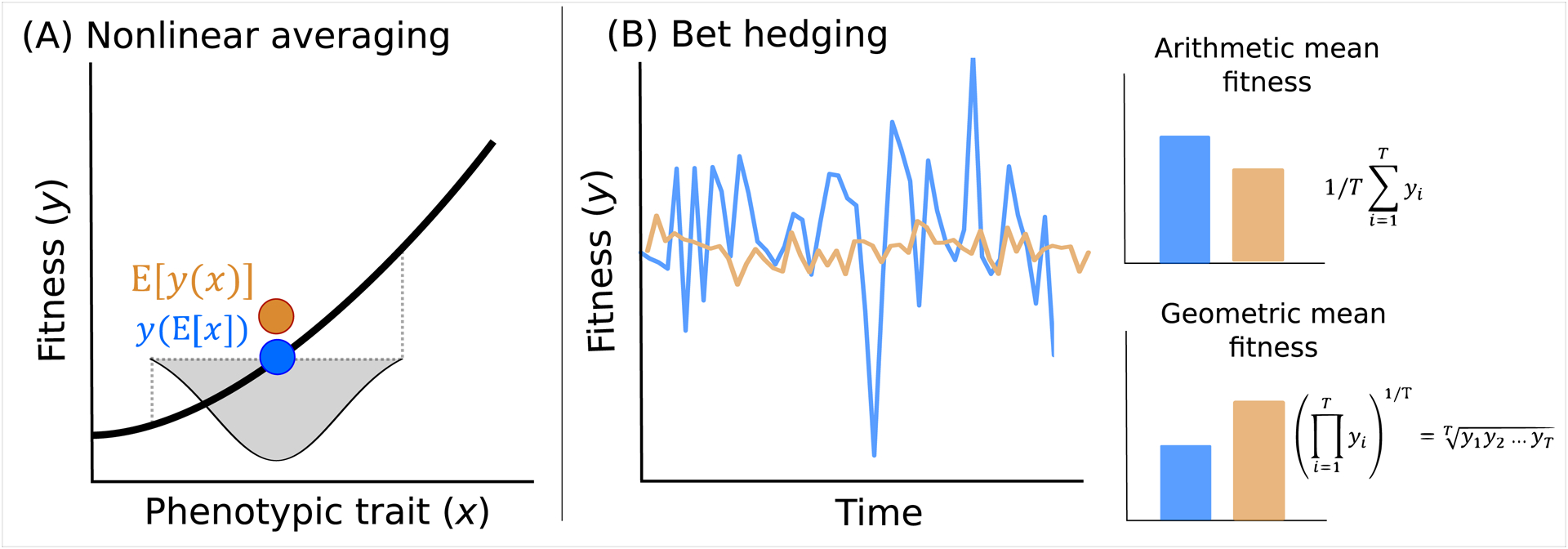
Two conditions that can result in selection favoring intra-genotypic variability: a) nonlinear averaging and b) bet hedging. a) The graph shows fitness (y) as a function of phenotype (x). If the relation is convex, an increase in the variance in x (indicated by the grey shading) results in a higher expected fitness value (E[y(x)]) (orange) than the fitness value of the average phenotype (y(E[x])) (blue), as a result of Jensen’s inequality. b) A bet hedging strategy (orange) reduces variance in fitness across generations compared to a non bet hedging strategy (blue). Despite a decrease in arithmetic mean fitness, bet hedging leads to an increase in geometric mean fitness, and is thus expected to be favored by natural selection.

Moving from constant environments to environments that vary (spatially or temporally), a next core theoretical driver of the evolution of intra-genotypic variability is bet hedging. Bet hedging is formally defined as a strategy that leads to a reduction in fitness variance across generations, thereby increasing geometric mean fitness (long-term fitness), at the cost of arithmetic mean fitness [4] (Fig. 2b). In other words, while year-to-year a bet hedging strategy might produce, on average, fewer offspring, over the long term its fitness will be larger. Germination delays in annual plants provide a classic example of diversified bet hedging, which is our focus here. This in contrast to conservative bet hedging, in which selection favors a single conservative phenotype (these two types of bet hedging may represent two extremes of one continuum, see [40]). A non-bet hedging strategy, where every year all seeds present germinate, leaves itself vulnerable to years of adverse environmental conditions where no or few germinants survive, and thus the population is at risk of extinction. A bet hedging strategy guarantees some seeds will have delayed germination, and thus persist in the seed bank during harsh years. Bet hedging involves a reduction in arithmetic mean fitness, accompanied by a reduction in fitness variance. In order to properly distinguish between bet hedging and nonlinear averaging, the fitness consequences on both the arithmetic mean and the variance of fitness must therefore be considered [41–43].

Research into bet hedging has often focused on traits related to timing, for example, seed germination [14,44,45] or diapause duration [46–51]. For these timing-related examples, the process underpinning bet hedging is often framed as a probability (e.g., probability of germinating). This implicitly defines the core trait underpinning fitness as discrete (e.g., being a seed or a germinant), with variance emerging purely from the binomial variance associated with the probability (implying that variance is maximal for a probability p=0.5, all else being equal). Interestingly, a large majority of both empirical and theoretical studies describing bet hedging in other traits (not related to timing) have also mostly considered discrete traits. Examples include whether or not aphids develop wings [52], left or right handedness in Drosophila [12], investment in spores or vegetative cells in slime molds (Dictyostelium discoideum) [53], stochastic on- and off switching of gene expression in yeast cells [10] as well as an array of theoretical models [54,55]. On consideration, a clear reason emerges for the observation that studies of bet hedging tend to predominantly focus on discrete traits: where the optimal trait value fluctuates unpredictably due to a changing environment and there is no ‘intermediate’ trait value possible, it is beneficial to express both discrete traits every time step [56] (Fig. 1d,h). However, bet hedging has also been observed in continuous traits, including thermal and phototactic preference in Drosophila [57], egg size in gypsy moths (Lymantria dispar) [58] and macrophyte (Scirpus maritimus) offspring size [59]. For continuous traits, theory indicates that bet hedging can be beneficial in traits for which the phenotypic optimum varies between years, provided that the magnitude of environmental fluctuation is sufficiently large [56] (Fig. 1c,g) and being a function of how much the strength of stabilizing selection varies through time [60].

Interaction between environmental fluctuations and lifespan on the evolution of variability

In Figure 1, we describe the range of selection scenarios for intra-genotypic variability depending on both characteristics of the trait: its mapping to fitness, and scope of environmental variation. The broader life history context will also be relevant. This is because fitness emerges from survival and fertility across the life cycle [61], and other life stages will thus define selective pressures on intra-genotypic variability, for example for traits affecting reproduction. Increasing survival probabilities decrease the optimal variance for two relationships between phenotype and reproduction we explored (Fig. 3; see Appendix S4 for more details on the performed simulations). This demonstrates that modifying survival can alter the optimum variance in another, uncorrelated, fitness component (reproduction) that together determine population fitness, and suggests that the more adverse the habitat is to survival, the more important it might be to invest in variable offspring. Furthermore, it implies that intra-genotypic variability, when affecting a trait related to reproduction, may be more adaptive in short-lived species (e.g., annual plants, Drosophila), as also indicated in results from Koons et al. [39]. For short-lived species, individuals are at a higher risk of dying without having reproduced, while for long-lived life cycles (e.g., trees, blue whales), individuals can afford to have one year of zero reproduction, because the yearly fitness is balanced by the high survival [62].

Figure 3.

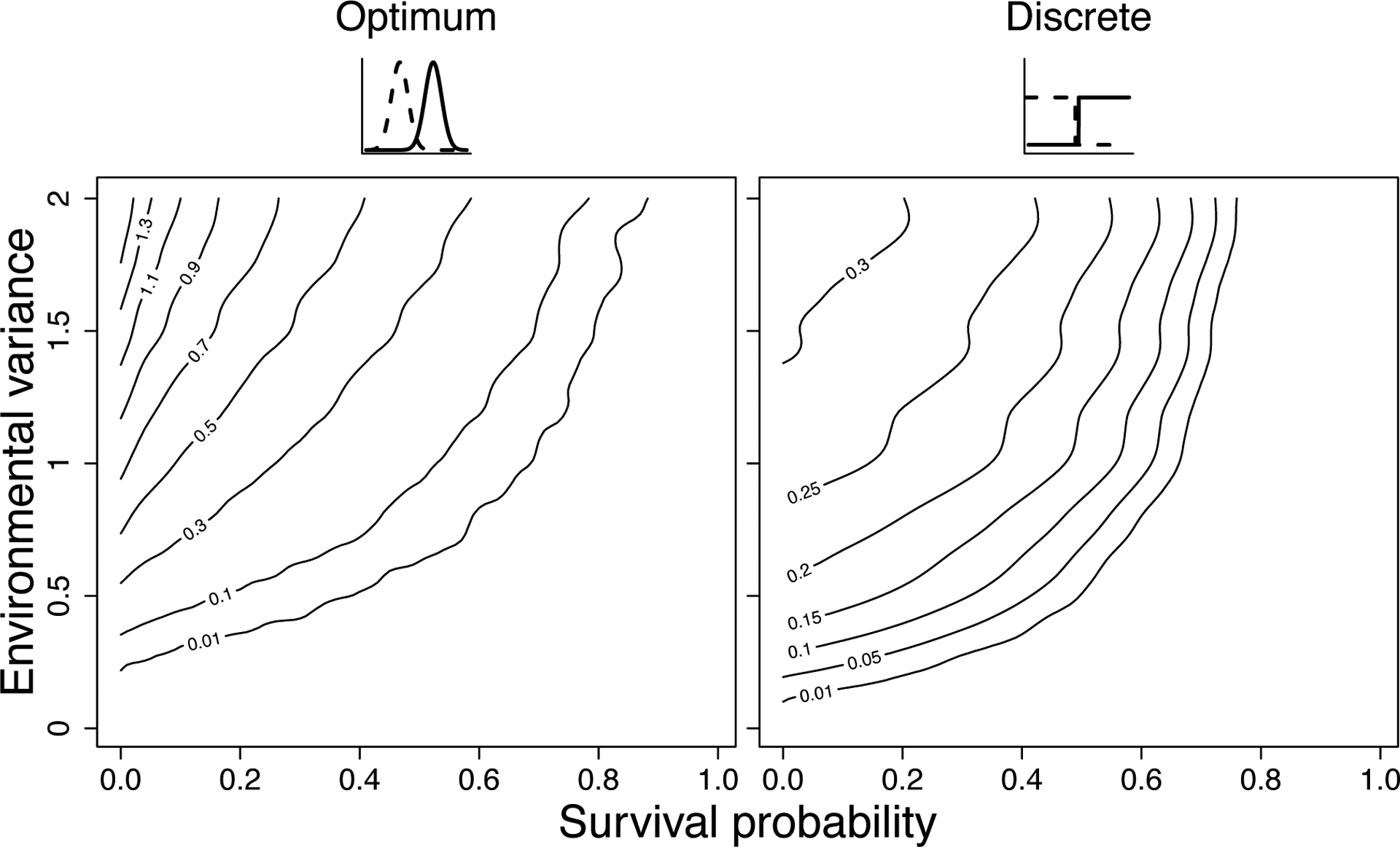
Graphs depict the optimal variance in a phenotypic trait affecting reproduction, as a function of survival probability per time-step (x-axis) and environmental variance (y-axis). Here we vary it between 0 and 2 while in Fig. 1, we set environmental variance at 0 (stable environment) and at 1 (fluctuating environment). We do so to further explore how environmental variance affects the optimal phenotypic variance for two phenotype-reproduction relations, where selection favored intermediate phenotypic variance (left: continuous, Fig. 1g; right: discrete, Fig. 1h). Like in Fig. 1, the environment modulates the relationship between phenotype and fitness, illustrated by the solid and dotted lines (Appendix S4 for more details on these simulations). The graphs show that higher environmental variance favors higher phenotypic variance. For example, when survival probability is set at 0.5, increasing the environmental variance from 0 to 2, increases the optimal phenotypic variance from 0 to 0.4 (left) and from 0 to 0.23 (right). Higher survival probabilities favor lower phenotypic variance. For example, when the environmental variance is set at 1, increasing survival from 0 to 1, decreases the optimal variance from 0.77 to 0 (left), and from 0.28 to 0 (right).

Evolution of intra-genotypic variability in natural populations

An array of demographic models suggests that, at the phenotypic level, non-zero variance is adaptive under commonly encountered environmental conditions and trait-phenotype relations (Figs. 1, 3) [10,16,54,56], but what drives such phenotypic variability? This is largely an open question, and it may, in some cases, reflect non-biological processes such as measurement error or incomplete statistical models [63]. More interestingly, however, it may also be due to stochastic variation in gene expression (‘gene expression noise’) [64]. Work on yeast cells has shown that the average gene expression noise differs between genes, and the degree of variability is suggested to be dependent on the gene function [65]. For instance, essential genes tend to have low stochastic variance in expression [65,66], while genes related to stress and plasma-membrane transporters show elevated noise levels [65,67,68]. Whether increased gene expression noise is adaptive is under debate, with some studies showing selection against variance-increasing alleles [69,70], while others suggest fitness benefits in response to environmental stress [71,72]. Optimal levels of expression noise will depend on the relationship between gene expression and emergent phenotype (both functioning and variance) following the principles linking phenotypic variance to fitness that we outline above. Defining these relationships will help predict for which genes we expect stochastic variation in expression to be beneficial, under which conditions, potentially helping explain why we observe gene expression noise in some genes, but less so in others. For example, for dosage-sensitive genes (in which changing expression levels is harmful), most genes indeed show low expression noise [69]. Whenever the relationship between expression level and performance is convex, we expect variance in gene expression to be beneficial [68]. Further, whenever an unpredictable environment changes the optimal gene expression level, bet hedging might be a beneficial strategy. Such an optimum relation has for instance been observed between lactose operon protein expression and fitness of Escherichia coli, whereby the optimum changes with lactose level [73].

Evidence available to date suggests that heritability for intra-genotypic variability is quite low [7,15,19]. Assuming that estimates are reasonably unbiased, we have three possible explanations for a low heritability of intra-genotypic variability. First, it may be a relatively constrained trait, with little variance. This will be modulated in part by the architecture of the gene networks constraining the degree of gene expression noise, and the degree to which its architecture is sensitive to mutations [74,75]. Second, populations may be close to their fitness optima, such that additional additive genetic variance has been eroded, though this scenario might be unlikely [76]. Evidence on whether populations are close to their optima, is mixed: theoretical predictions on optimal germination and flowering probabilities in plants [14,45,77], have been shown to closely match observations. In contrast, Philippi [78], also focusing on germination probabilities, showed that predicted optimal strategies did not match the observations. An apparent weak selection towards optimal bet hedging strategies in specific cases can be due to: i) selection for bet hedging being of recent origin, simply resulting in insufficient time for optimal strategies to have evolved, or ii) selection on bet hedging being infrequent, implying that bet hedging promoting alleles disappear due to drift or short-term selection against them, despite being beneficial on the long term [79]. Typically, theoretical predictions assume infinite large populations (e.g., Figs. 1,3 or [80]). However, real-world populations consist of individuals that are subject to demographic stochasticity, resulting in genetic drift. Whether a variance-increasing mutation appearing at one time point will get fixed in the population, depends on the population size, in addition to the selective advantage and the experienced environment [79]. Moreover, responses to selection are additionally shaped by genetic (co)variances, which have the potential to create a wide range of evolutionary trajectories towards the optimum (Box 2). Third, there may be standing genetic variation associated with phenotypic variability, but these alleles may appear neutral until particular environmental circumstances occur, and thus their contribution to heritability would be cryptic (Boxes 1 & 2). Research studies on this topic have primarily focused on fitness outcomes across environments that fluctuate, but in a stationary manner (i.e., around a consistent mean) over the long term (Figs. 1, 3) and generally do not allow for context-dependent manifestation of intra-genotypic variability [81,82]. Transient and directional changes in environmental conditions that co-occurred with expression of intra-genotypic variability could help sustain populations across challenging periods [81]. Characterizing these links empirically would require sufficient knowledge of the system to identify the condition-dependence of expression of intra-genotypic variability, as well as its demographic consequences as outlined above.

Box 2: Intra-genotypic variance in a Quantitative Genetic framework.

In a quantitative genetic model, assuming no dominance or epistasis, an individual’s phenotypic deviation from the population mean can be written as the sum of its breeding value (A) and an environmental (residual) effect (E), thus: P = A + E. In the absence of any covariance between A and E, the total phenotypic variance (V_P) can be written as V_P = V_A + V_E, where V_A) is the additive genetic variance and V_E is the environmental variance. Intra-genotypic variability involves a genetic component in the residual variance, where different genotypes can differ in V_E. Different approaches to model this genetic component in the residual variance exist [19], for example according to an additive model [76,97], where the genetic component of the variance is modelled as an additive effect:

$$P=A_{\mathit{\text{mean}}}+\chi \sqrt{V_E+A_{\mathit{\text{variance}}}}$$

Here, χ is a standard normal deviate, distributed as N(0,1), scaled by $\sqrt{V_E+A_{\mathit{\text{variance}}}}.$ Each individual is now characterized by two breeding values: one determining its average phenotype (A_mean), and one determining the variance around this mean (A_variance). The evolutionary response in a population depends on both additive genetic variances V_A-mean and V_A-variance, as well as its covariance (cov_A(mean, variance) (which can be summarized in a so-called G-matrix) (Fig. I). Note that here A_mean and A_variance affect the same phenotypic trait; when affecting different phenotypic traits, nonlinear relations between traits, on a phenotypic level, may emerge [98].

Figs. 1 and 3 (see main text) illustrate the fitness consequences of intra-genotypic variability in a phenotypic trait affecting reproduction, obtained using a demographic model (Appendices S1–3). Combining such adaptive landscapes with a quantification of the underlying genetic variances and covariances (Fig. II) will shed light on an array of interesting research questions on the evolution of variance control (see Outstanding Questions).

Figure I.

Evolutionary trajectories of the mean and variance in a trait. Contour lines depict the fitness landscape, corresponding to Fig. 1g (see main text). For clarity, we only show contour lines here. Green dots indicate the trait combination resulting in the highest fitness. Starting from a population with a low mean trait value and no variance (black dots), trajectories towards the fitness optimum (green dots) are shown, for varying genetic variances and covariances, using the multivariate breeder’s equation [99]. Additive genetic variances for the mean (V_A-mean) and variance (V_A-variance) in phenotypic trait were both set at 0.1, and their covariance (cov_A(mean, variance)) at 0. We then, one by one, varied these variance components, while keeping the rest of the G-matrix constant. We assessed how the phenotypic mean and variance evolve over the course of 200 time steps. Graph on the left shows the effect of varying values for V_A-mean′ middle graph shows the effect of varying V_{A-variance′} and graph on the right the effect of changes in cov_A)(mean,variable). Different colors correspond to the range of values for the variable (see legend). Note that we considered a constant genetic variance-covariance matrix within each scenario, an assumption which might be often violated in natural population [100,101] and/or when environmental conditions change through time [102]

Figure II.

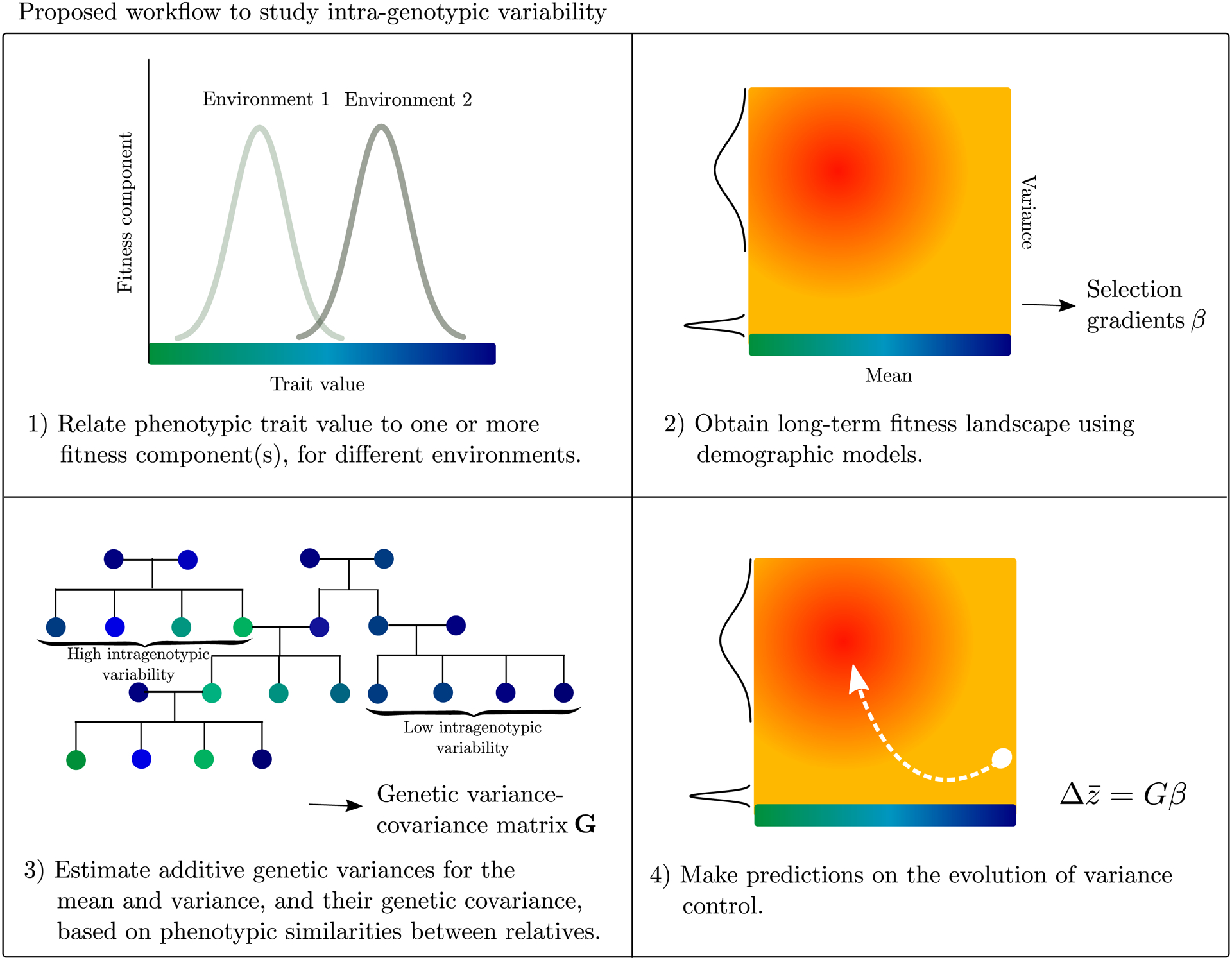
Proposed workflow to study the evolution of intra-genotypic variability, focusing on both the fitness consequences as well as on the genetics underlying the traits. 1–2) By using a demographic model (Appendices S1–3) to define the adaptive landscape, partial selection gradients at a given point in the landscape can be obtained. 3) The additive genetic variance462 covariance matrix (G) can be estimated using linear mixed effects models, based on knowledge on phenotypic similarities between relatives [7,15,16,19]. 4) The evolutionary change in multiple traits ($\Delta \overline{z}$), in this case phenotype mean and variance, can be written as the multivariate breeder’s equation [99], as the product of the genetic variance-covariance matrix (G) and the partial selection gradients for each trait (β).

Going forward

A growing number of studies on intra-genotypic variability are providing heritability estimates and are enriching a catalogue of loci associated with variability [7,15,19,23,24], however few studies have connected the degree of variability to fitness [16]. Observing heritable variation for variability tells us nothing about whether variability is adaptive or not, just that it can evolve. On the other hand, empirical or theoretical studies quantifying fitness gains from variability (for instance through bet hedging) generally lack knowledge of the underlying genetics basis. One notable exception is a recent study by Mulder et al. [16]. Here, the degree of variability in fledgling weight, in a wild great tit population, was related to fitness, showing stabilizing selection on intermediate phenotypic variance. Such studies are needed to understand when we expect intra-genotypic variation to evolve (Box 2).

A key priority is now to use theoretical expectations to guide the experiments that will provide empirical evidence. This remains challenging for a number of reasons. First, some of the best empirical examples have relied on humans, laboratory or domestic animals, making direct application of evolutionary predictions complicated (as these populations may not reflect the outcome of natural selection). Second, inferring the degree to which intra-genotypic variability is adaptive requires quantifying the impacts of a changing environment on (components of) fitness which is intractable unless a life history model can be constructed. This in turn requires measurement of core individual demographic rates (survival, growth, reproduction) as well as measurements of how variation in both the trait and the environment affect these demographic rates. Such information is rarely available (with the notable exception of plants with seed banks [13,14]). Third, evolutionary outcomes will be modulated by the degree to which genetic variation is available for selection to act upon, e.g., both additive genetic variance, and covariances with other traits (Box 2). Estimating genetic variances (e.g., using mixed effects models [83]) already demand large data resources for mean trait values, and the situation only worsens when attempting to do the same for trait variance. Estimating these components (see e.g., [84,85]) requires data on the relatedness between individuals, which generally calls for genetic analyses. Recent advances in genomic technology and the developments of powerful analytical tools are enabling the construction of high quality pedigree on an unprecedented large scale [86,87].

Concluding remarks

Making robust quantitative predictions on the evolution of variance control in natural populations require long-term data on i) temporal changes in one or more environmental variables, ii) individual phenotypes and demographic rates, interacting with the environment, and iii) the relatedness between individuals. Gathering such comprehensive datasets is a considerable undertaking, yet recognizing the unparalleled value of long-term field studies, a growing number of consortiums have risen to the challenge. For example, the Soay sheep (Ovis aries) in Scotland have become a key model to study disease ecology [88], the Amboseli baboon (Papio cynocephalus) project has transformed the field of behavioral ecology [89], other long-term studies in birds [90,91] and in plants [92] promise to be just as valuable. Such studies will provide estimates for key parameters such as the genetic component of phenotypic variance, and its genetic correlation with the mean trait [7,15,16] that are necessary to refine theoretical models and better understand the evolution of variance control (see Outstanding Questions). Model systems in laboratory settings remain an important tool to study the evolution of intra-genotypic variability. They afford the ability to combine genomics tools with quantitative genetics and creative experimental design, using for example experimental evolution under a range of conditions [93,94]. Although the catalog of variance controlling loci (vQTLs) that have been mapped to date remains relatively limited, a population genetics analysis of these loci would shed critical light on the dynamic driving their evolution. Finally, combining the adaptive landscapes with the evolutionary potential of intra-genotypic variability will be essential for making predictions about factors driving its evolution. Future studies applying demographic models, such as the one proposed here, to empirical data, will help to explain the ubiquity of the genetic control of phenotypic variation and to understand its relevance for natural populations facing environmental changes.

OUTSTANDING QUESTIONS.

• How do life history parameters (from reproductive rate to lifespan) impact the adaptive advantage of intra-genotypic variability? In other words, is variance control more likely to evolve in fruit flies than in elephants? And, do we observe smaller coefficients of variation, and thus potentially higher canalization in long living species versus short-living species?

• The relationship between canalization, plasticity and intra-genotypic variability, remains poorly understood. For example, does intra-genotypic variability favor the evolution of phenotypic plasticity and are they genetically correlated?

• What is the genetic correlation between the mean and the variance, either affecting the same phenotypic trait or different phenotypic traits? Are their categories of traits (e.g., life history traits) for which such a correlation is more likely than others?

• What is contribution of cryptic genetic variation to intra-genotypic variability? Is a significant fraction of variance controlling alleles only associated with variance control under certain (e.g., stressful) environments?

• How often do predicted optimal strategies match the observed mean and variance?

• What is the allele frequency spectrum of alleles association with variation in phenotypic variability? And what role does balancing selection play in shaping this spectrum?

HIGHLIGHTS.

• Recent developments in the field of genetics show that the degree of phenotypic variability among genetically identical individuals can be under genetic control and can thus be tuned by natural selection.

• To understand when the degree of intra-genotypic variability for a trait is the outcome of adaptive evolution, it is essential to map the focal trait to patterns of reproduction and survival across the life cycle.

• Here, we evaluate the fitness consequences of phenotypic variance for commonly encountered relationships between traits, fitness, and environmental conditions.

GLOSSARY

Adaptive landscape

(fitness landscape) Visualization of the relation between fitness and one or more phenotypic characters or genes.

Adaptive tracking

Evolutionary change in the average phenotypic trait in a population, where the phenotypic mean tracks a (changing) fitness optimum.

Bet hedging

Selection for increased geometric mean fitness, despite a reduction in arithmetic mean fitness, due to a decrease in the variance in fitness over generations.

Conservative bet hedging

Bet hedging where selection favors a single conservative phenotype, thus reducing fitness variance but without an increase in the phenotypic variance.

Diversified bet hedging

Bet hedging where selection favors phenotypic variance within genotypes.

G-matrix

Additive genetic variance-covariance matrix summarizing inheritance patterns of multiple traits.

Intra-genotypic variability

Phenotypic variation between genetically identical individuals reared in a constant environment, most likely due to differences in an individual’s ability to buffer micro-environmental perturbations, leading to stochastic fluctuations in development.

Jensen’s inequality

Mathematical property of a convex function. The expected value of a convex function (where the 2^nd derivative is positive), is higher than the value at the average x-value, due to nonlinear averaging. In contrast, the expected value of a concave function (2^nd derivative is negative), is lower than the value at the average x-value.

Long-term fitness

The geometric mean population growth rate in a variable environment.

Nonlinear averaging

The expected value of a nonlinear function (E[f(x)]) can differ from the value at the average x-value (f(E[x])). For convex functions, Jensen’s inequality is the result.

Phenotypic plasticity

The ability of an organism to change its phenotype in response to the environment.