Testing the factor structure underlying behavior using joint cognitive models: Impulsivity in delay discounting and Cambridge gambling tasks

Abstract

Neurocognitive tasks are frequently used to assess disordered decision making, and cognitive models of these tasks can quantify performance in terms related to decision makers’ underlying cognitive processes. In many cases, multiple cognitive models purport to describe similar processes, but it is difficult to evaluate whether they measure the same latent traits or processes. In this paper, we develop methods for modeling behavior across multiple tasks by connecting cognitive model parameters to common latent constructs. This approach can be used to assess whether two tasks measure the same dimensions of cognition, or actually improve the estimates of cognitive models when there are overlapping cognitive processes between two related tasks. The approach is then applied to connecting decision data on two behavioral tasks that evaluate clinically-relevant deficits, the delay discounting task and Cambridge gambling task, to determine whether they both measure the same dimension of impulsivity. We find that the discounting rate parameters in the models of each task are not closely related, although substance users exhibit more impulsive behavior on both tasks. Instead, temporal discounting on the delay discounting task as quantified by the model is more closely related to externalizing psychopathology like aggression, while temporal discounting on the Cambridge gambling task is related more to response inhibition failures. The methods we develop thus provide a new way to connect behavior across tasks and grant new insights onto the different dimensions of impulsivity and their relation to substance use.

Introduction

Behavioral tasks are frequently used as a method of assessing patterns of performance that are indicative of different kinds of cognitive deficits. For example, people with deficits in working memory might perform worse on a task that requires them to recall information, or people with impulsive tendencies may find it difficult to wait for rewards that are delayed in time. By analyzing patterns of behavior, we can characterize the dysfunctions in decision-making that predict or result from different mental health or substance use disorders (Bickel & Marsch, 2001; Lejuez et al., 2003; MacKillop et al., 2011; Zois et al., 2014). In turn, we can understand how different traits put individuals at risk for substance use or mental health problems, or design interventions aimed at improving cognitive function to prevent or alleviate these problems (Bickel et al., 2016). Behavioral tasks can therefore grant insight onto traits or characteristics that underlie risky, impulsive, or otherwise disordered decision making both in the laboratory and the real world.

A critical assumption of this approach to assessing decision behavior is that the behavioral tasks used in these approaches provide measures of common underlying traits or characteristics that are related to disordered decision behavior. Naturally, each task is vetted for reliability and some degree of predictive validity before putting into widespread use as assessment tools. Thus, there is typically good evidence to suggest that tasks like delay discounting are reliable, reinforcing the view that they are measuring some stable aspect of choice behavior (Simpson & Vuchinich, 2000). However, there are also multiple tasks that purport to measure the same trait or characteristic using different experimental paradigms. This may be erroneous, as impulsivity is thought to be a multi-dimensional construct with as many as three main factors: impulsive choice, impulsive action, and impulsive personality traits (MacKillop et al., 2016). Impulsive choice is thought to reflect the propensity to make decisions favoring an immediate reward over a larger delayed reward, impulsive action is thought to reflect the (in)ability to inhibit motor responses, and impulsive personality is reflected in self-report measures of individuals’ (in)ability to regulate their own actions.

Within each of these delineations, there are multiple tasks or methods that might serve as valid measures of one or more dimensions of impulsivity. For example, there are a number of self-report and behavioral measures that are designed to measure people’s predispositions toward impulsive decision-making. Understanding the structure of impulsivity and how these different measures are related is key for addressing a number of health outcomes, as impulsivity is strongly implicated in a number of psychiatric disorders, most prominently ‘reinforcer pathologies’ (Bickel et al., 2011) such as substance use disorders (Moeller et al., 2001; Dawe & Loxton, 2004) as well as eating disorders, gambling disorder, and some personality disorders (Petry, 2001; De Wit, 2009). Delay discounting in particular has been proposed as a prime transdiagnostic endophenotype of substance use disorders and other reinforcer pathologies (Bickel et al., 2014, 2012). Obtaining reliable estimates of impulsivity from behavioral tasks has both diagnostic and prognostic value, as it can not only help identify at risk individuals, but also predict response to treatment, and offer the opportunity for effective early prevention and interventions for addiction (Bickel et al., 2011; Conrod et al., 2010; Donohew et al., 2000; Vassileva & Conrod, 2018).

Because of the importance of impulsivity as a determinant of health outcomes, there have been a variety of different paradigms designed to assess different dimensions of impulsive behavior. For example, both the Cambridge gambling task (Rogers et al., 1999) and delayed reward discounting task (Kirby et al., 1999) both aim to measure impulsive behavior, but they use largely different methods to do so. The Cambridge gambling task [CGT] measures impulsivity by gauging decision-makers’ willingness to wait in order to make larger or smaller bets, generally requiring decision makers to wait 5–20 seconds for potential bet values to “tick” up or down until it reaches the bet value they want to wager. The decision maker experiences these delays in real time during the experiment, waiting on each trial in order to enter the bet they want to make as it comes on-screen. Conversely, delay discounting tasks [DDT] such as the Monetary Choice Questionnaire measure impulsivity as a function of binary choices between two alternatives, where one alternative offers a smaller reward sooner / immediately and the other alternative offers a larger reward at a later point in time (Ainslie, 1974, 1975; Kirby et al., 1999). The task paradigm for the CGT lends itself to understanding how people respond to short-term, experienced delays, while the DDT paradigm lends itself better to understanding how they respond to more long-term, described delays. While both situations can be construed as ones where people have to inhibit their impulses to take more immediate payoffs versus greater delayed ones, which falls most naturally under impulsive choice, it is possible that different dimensions of impulsivity are related to behavior on either task.

Computational models of such complex neurocognitive tasks parse performance into underlying neurocognitive latent processes and use the parameters associated with these processes to understand the mechanisms of the specific neurocognitive deficits displayed by different clinical populations (Ahn, Dai, et al., 2016). Research indicates that computational model parameters are more sensitive to dissociating substance-specific and disorder-specific neurocognitive profiles than standard neurobehavioral performance indices (Haines et al., 2018; Vassileva et al., 2013; Ahn, Ramesh, et al., 2016). Similarly, dynamic changes in specific computational parameters of decision-making, such as ambiguity tolerance, have been shown to predict imminent relapse in abstinent opioid-dependent individuals (Konova et al., 2019). This suggests that computational model parameters can serve as novel prognostic and diagnostic state-dependent markers of addiction that could be used for treatment planning.

Based on evidence from other task domains, it seems likely that differences in behavioral paradigms may be substantial enough to evaluate two dimensions or domains of impulsivity. In risky choice, clear delineations have been made between experience-based choice, where risks are learned over time as a person experiences different reward frequencies, and description-based choice, where risks are described in terms of percentages or proportions of the time they will see rewards. The diverging behavior observed in these two paradigms, referred to as the description-experience gap, illustrates that behavior under the two conditions need not line up (Hau et al., 2008; Hertwig & Erev, 2009; Wulff et al., 2018). This appears to result from asymmetries in learning on experience-based tasks, where people tend to learn more quickly when they have under-versus over-predicted a reward (Haines et al., submitted). Given the evidence for this type of gap in risky choice, it seems likely that a similar difference between described (DDT) and experienced (CGT) delays may result in diverging behavior due to participants learning from their experiences of the delays.¹ Of course, it is not necessarily the case that such a gap exists for the CGT and DDT paradigms and how they measure impulsivity, but the diverging patterns of behavior in risky choice should at least raise suspicion about the effects of described versus experienced delays in temporal discounting.

Approach

So how do we test if these two different tasks are measuring the same underlying dimension of impulsivity as measures of impulsive choice? The remaining part of the paper is devoted to answering this question. The first step is to gather data on both tasks from the same participants, so that we can measure whether individual differences in impulsive choice are expressed in observed behavior on both tasks. For this, we utilize data from a large study on impulsivity in lifetime substance dependent (in protracted abstinence) and healthy control participants in Bulgaria (Ahn et al., 2014; Vassileva et al., 2018; Ahn & Vassileva, 2016). This sample includes both “pure” (mono-substance dependent) heroin and amphetamine users as well polysubstance dependent individuals and healthy controls. The majority of substance dependent participants in these studies were in protracted abstinence (i.e., not active users, and were screened prior to participation to ensure they had no substances in their system) but met the lifetime DSM-IV criteria for heroin, amphetamine, or polysubstance dependence. They were also not on methadone maintenance or on any other medication-assisted therapy, unlike most abstinent opiate users in the United States. This participant sample has multiple benefits for the current effort: it both provides a set of participants who are likely to be highly impulsive, increasing the variance on trait impulsivity; and it provides an opportunity to compare the performance of the models we examine in terms of their ability to predict substance use outcomes.

The second step in testing whether the two tasks reflect the same dimension of impulsive choice is to quantify behavior on the tasks in terms of the component cognitive processes. This is done by using cognitive models to describe each participant’s behavior in terms of contributors like attention, memory, reward sensitivity, and those relevant to impulsivity such as temporal discounting (Busemeyer & Stout, 2002). Each parameter in the model corresponds to a particular piece of the cognitive processes underlying task behavior, and improves predictions of related self-report and outcome measures over basic behavioral metrics like choice proportions or mean response times (Fridberg et al., 2010; Romeu et al., 2019). They therefore serve as the most complete and useful descriptors of behavior on cognitive tasks, and their parameters correspond theoretically to individual differences in cognition.

The third step is to construct a model of both tasks by relating parameters of the cognitive models of each task to common underlying factors like impulsivity. This is far from straightforward, as it requires both theoretical and methodological innovations. In terms of theory, a modeler has to make determinations about which parameters should be related to common latent constructs, and therefore how model parameters should relate to one another across tasks. For our present purposes this is made reasonably straightforward, as the most common models of both Cambridge gambling and delay discounting tasks include parameters describing temporal discounting rates that determine how the subjective value of a prospect decreases with delays, but in other cases it may be a case of exploratory factor analysis (using cognitive latent variable model structures like we describe below) and/or model comparison between different latent factor structures. From a practical standpoint, the modeler also requires methods for simultaneously fitting the parameters of both models along with the latent factor values. Using a hierarchical Bayesian approach, Turner et al. (2013) developed a joint modeling approach to simultaneously predict neural and behavioral data from participants performing a single task. These methods connect two sources of data to a common underlying set of parameters, either constraining a single cognitive model using multiple sources of information (Turner et al., 2016) or connecting separate models via latent factor structures (Turner et al., 2017). The benefit of the joint modeling approach is that all sources of data are formally incorporated into the model by specifying an overarching, typically hierarchical structure. As shown in a variety of applications (Turner et al., 2013, 2015, 2016, 2017), modeling the co-variation of each data modality can provide strong constraints on generative models, and these constraints can lead to better predictions about withheld data when the correlation between at least one latent factor is nonzero (Turner, 2015).

Similarly, Vandekerckhove (2014) developed methods for connecting personality inventories to cognitive model parameters, creating a cognitive latent variable model structure that predicts both self-report and response time (and accuracy) data from the same participants simultaneously. As with the joint modeling approach, it allows data from one measure to inform another by linking them to a common underlying factor. In this paper, we develop methods based on the joint modeling and cognitive latent variable modeling approaches that can be used to connect behavior on multiple cognitive tasks to a common set of latent factors.

Finally, we must test the factor structure underlying task performance by comparing different models against one another. Depending on how the models are fit, different metrics will be available for model comparison. Taking advantage of the fully Bayesian approach, we provide a method for arbitrating between different model factor structures using a Savage-Dickey approximation of the Bayes factor (Wagenmakers et al., 2010). This method is particularly useful because it allows us to find support for the hypothesis that the relationship between parameters is zero, indicating that performance on the different tasks is not related to a common underlying factor but to separate ones. In effect, we use the Bayes factor to compare a 1-factor against a 2-factor model, directly yielding a metric describing the support for one model over the other given the data available.

To preview the results, the Bayes factor for all groups (amphetamine, heroin, polysubstance, and controls) favors a multi-dimensional model of impulsivity in delay discounting and Cambridge gambling tasks, suggesting that the different paradigms measure impulsive action and impulsive choice / personality. This is an interesting result in itself, but also serves to illustrate how the joint modeling and cognitive latent variable modeling approaches can be used to make novel inferences about the factor structure underlying different tasks. The remainder of the paper is devoted to the methods for developing and testing these models, with model code provided to assist others in carrying out these types of investigations.

Background methods

Although both tasks are relatively well-established as tools in clinical assessment, it is helpful to examine how each one assesses impulsivity, both in terms of raw behavior and in terms of model parameters. We first cover the basic structure of the delay discounting and Cambridge gambling task, then the most common models of each task, and finally how they can be put together using a joint modeling framework.

It is worth noting that there are several competing models of the delay discounting task. For our purposes, we primarily examine the hyperbolic discounting model (Chung & Herrnstein, 1967; Kirby & Herrnstein, 1995; Mazur, 1987), as it is presently the most widely used model of preference for delayed rewards. However, we repeat many of the analyses presented in this paper by using an alternate attention-based model of delay discounting, the direct difference model (Dai & Busemeyer, 2014), in Appendix A. The main conclusions of the paper do not change depending on which model is used, but the direct difference model tends to fit better for some substance use groups and its parameters are somewhat more closely related to the Cambridge gambling task model parameters.

Tasks

A total of 399 participants took part in a study on impulsivity among substance users in Sofia, Bulgaria. This included 75 “pure” heroin users, 73 “pure” amphetamine uses, 98 polysubstance users, and 153 demographically matched controls, including siblings of heroin and amphetamine users. Lifetime substance dependence was assessed using DSM-IV criteria, and all participants were in protracted abstinence (met the DSM-IV criteria for sustained full remission).

In addition to the Monetary Choice Questionnaire of delay discounting and the Cambridge gambling task described below, all participants also completed 11 psychiatric measures including an IQ assessment using Raven progressive matrices (Raven, 2000), the Fagerström test for nicotine dependence (Heatherton et al., 1991), structured interviews and the screening version of the Psychopathy Checklist (Hart et al., 1995; Hare, 2003), and the Wender Utah rating scale for ADHD (Ward, 1993). They also completed personality measures including the Barratt Impulsiveness Scale (Patton et al., 1995), the UPPS Impulsive Behavior Scale (Whiteside & Lynam, 2001), the Buss-Warren Aggression Questionnaires (Buss & Warren, 2000), the Levenson self-report psychopathy scale (Levenson et al., 1995), and the Sensation-Seeking Scale (Zuckerman et al., 1964). The other behavioral measures they completed included the Iowa Gambling Task (Bechara et al., 1994), the Immediate Memory Task (Dougherty et al., 2002), the Balloon Analogue Risk Task (Lejuez et al., 2002, 2003), the Go/No-go task (Lane et al., 2007), and the Stop Signal task (Dougherty et al., 2005). These are used later on to assess which dimensions of impulsivity are predicted by which model parameters.

Below we describe the main tasks of interest: the MCQ delay discounting task and the Cambridge gambling task. The participants in these tasks were recruited as part of a larger study on impulsivity, and they completed both tasks, allowing us to assess the relation between performance on the DDT and the CGT for each person and for each group to which they belonged. More details on the study and participant recruitment are provided in Ahn et al. (2014) and Ahn & Vassileva (2016).

Delay discounting task.

The delay discounting task was developed for use in behavioral studies of animal populations as a measure of impulse control (Chung & Herrnstein, 1967; Ainslie, 1974). Performance on the delay discounting task has been linked to a number of important health outcomes, including substance dependence (Bickel & Marsch, 2001) and a propensity for taking safety risks (Daugherty & Brase, 2010). Task performance and the parameters of the cognitive model (the hyperbolic discounting model) are frequently used as an indicator of temporal discounting, impulsivity, and a lack of self-control (Ainslie & Haslam, 1992).

The structure of each trial of the delay discounting task features a choice between two options. The first is a smaller reward (e.g., $10 immediately), so-called the “smaller, sooner” (SS) option. The second is a larger reward (e.g., $15) at a longer delay (e.g., 2 weeks), referred to as the “larger, later” (LL) option. This study used the Monetary Choice Questionnaire designed by Kirby & Maraković (1996), which features 27 choices between SS and LL options. Often, impulsivity is quantified as simply the proportion of responses in favor of the SS option, reflecting an overall tendency to select options with shorter delays. However, this can be confounded with choice variability – participants who choose more randomly regress toward 50% SS and LL selections, which may make them appear more or less impulsive relative to other participants in a data set. Therefore, the model we use includes a separate choice variability parameter, which describes how consistently a person chooses an option that they would appear to subjective value higher. The remaining temporal discounting parameter k then quantifies how much options are valued dependent on their delay.

Cambridge gambling task.

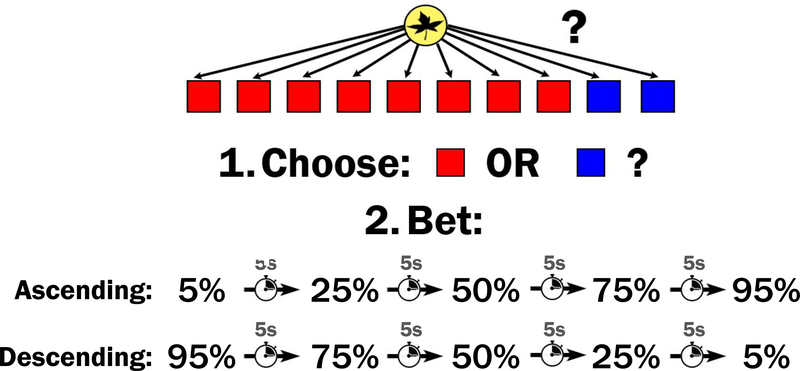
The Cambridge gambling task (Rogers et al., 1999) is a two-stage gambling paradigm where participants decide between colors and then wager a percentage of their accumulated points (exchanged for money at the end of the study) on having made the correct decision. The paradigm is shown in Figure 1. Participants began a session with 100 points. On each trial, they were shown 10 boxes, each of which could be red or blue. They were told that a token was hidden randomly (uniform distribution) in one of the boxes. In the choice stage, the participant responded whether they believe the token was hidden in a red or blue box. ² Once they made their choice, the betting stage of the trial began.

Figure 1.

Diagram of the Cambridge gambling task paradigm

In the betting stage, participants would see a certain number of points appear on the screen, which either increased (ascending condition) or decreased (descending condition) in real time. The number of points would tick up from 5% of their points, to 25, 50, 75, and then 95% of their points in the ascending condition, or down from 95% to 75, 50, 25, and then 5% in the descending condition. The points would tick up or down every 5 seconds. Participants would enter the number of points they wanted to bet by clicking the mouse when it hit the number they were willing to wager.

Naturally, a participant would have to wait longer to make larger bets in the ascending condition and wait longer to make smaller bets in the descending condition. This allows for the propensity to make greater bets to be dissociated from the propensity to stop the ticker earlier (or later). Impulsivity in this paradigm is measured as a function of how long participants are willing to wait for the ticker to go up or down before they terminate the process and make a bet. Participants who are particularly impulsive and unwilling to wait will tend to make small bets in the ascending condition and make large bets in the descending condition. Those who are less impulsive will tend to make bets that are more likely to maximize the number of points they receive, regardless of the delays associated with the bets.

In this way, the Cambridge gambling task measures a number of important cognitive processes aside from impulsivity as well. Participants’ propensity to choose the “correct” (majority) color, their bias toward different choices or bets, and the consistency with which they make particular choices or bets are all factors that will influence the behavioral data. The cognitive model – which we refer to as the Luce choice / bet utility model – quantifies each of these tendencies, allowing us to distill the effect of impulsivity from these other propensities and processes.

Models

Cognitive models for both tasks have been tested against substance use data in previous work. The hyperbolic delay discounting model in particular has been widely used and is predictive of a number of health outcomes related to substance use and gambling (Reynolds, 2006), while the model of the Cambridge gambling task was only recently developed and applied to substance use data (Romeu et al., 2019). Both models are capable of extending our understanding of performance on both tasks by quantifying participant performance in terms of cognitively meaningful parameters, and using these parameters to predict substance use outcomes (better than raw behavioral metrics like choice proportions Busemeyer & Stout, 2002; Romeu et al., 2019).

In this section, we review the structure of each model and then examine what additions are necessary in order to test whether they measure the same or different dimensions of impulsivity. Both models contain a parameter related to temporal discounting, where outcomes that are delayed have a subjectively lower value. Higher values of these parameters lead participants to select options that are closer in time and are therefore linked to impulsivity, so it is only natural to try connecting them to a common latent factor. The joint modeling method we present allows us to do so, as well as permits us to test whether they are measuring the same underlying construct using a nested model comparison with a Bayes factor.

In the following sections we focus on the hyperbolic discounting model of the delay discounting task, but a description of the direct difference model – which fits several of the substance use groups better than the hyperbolic model – is also presented in Appendix A.

Hyperbolic discounting model.

Although early accounts of how rewards are discounted as they are displaced in time followed a constant discounting rate, represented in an exponential discounting function derived from behavioral economic theory (Camerer, 1999), the most common model of discounting behavior instead uses a hyperbolic function (Ainslie & Haslam, 1992; Mazur, 1987), which generally fits human discounting behavior better and accounts for more qualitative patterns such as preference reversals (Kirby & Herrnstein, 1995; Kirby & Maraković, 1995; Dai & Busemeyer, 2014). Certainly, other models could be used to account for behavior on this task, and we test one such model in the Appendix (the direct difference model Dai & Busemeyer, 2014; Cheng & González-Vallejo, 2016). Fortunately, the exact model of discounting behavior seems not to substantially affect the conclusions of the procedure reported here.

The hyperbolic discounting model uses two parameters. The first is a discounting rate k, which describes the rate at which a payoff (x) decreases in subjective value (v(x,t)) as it is displaced in time (t).

$$v(x,t)=\frac{1}{1+k\cdot t}$$ (1)

Higher values of k will result in options that are further away in time being discounted more heavily. Since delay discounting generally features one smaller, sooner option and one larger, later option, a higher k will result in more choices in favor of the smaller, sooner option because the greater impact of the delay in the later option.

The second parameter m determines how likely a person is to choose one option over another given their subjective values v(x₁, t₁) and v(x₂, t₂). The probability of choosing the larger, later option (x₂, t₂; where x₂ > x₁ and t₂ > t₁) is given as

$$Pr(\text{choose}\text{LL})=\frac{1}{1+\exp \left(-m\cdot \left[v\left(x_2,t_2\right)-v\left(x_1,t_1\right)\right]\right)}$$ (2)

Higher values of m will make alternatives appear more distinctive in terms of choice proportions, resulting in a more consistent choice probability. Lower values for m make alternatives appear more similar, driving choice probabilities toward 0.5.

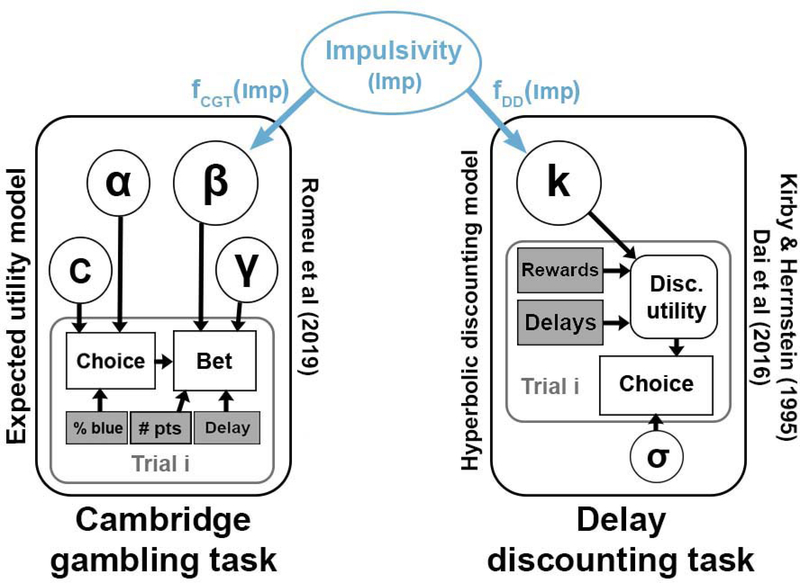
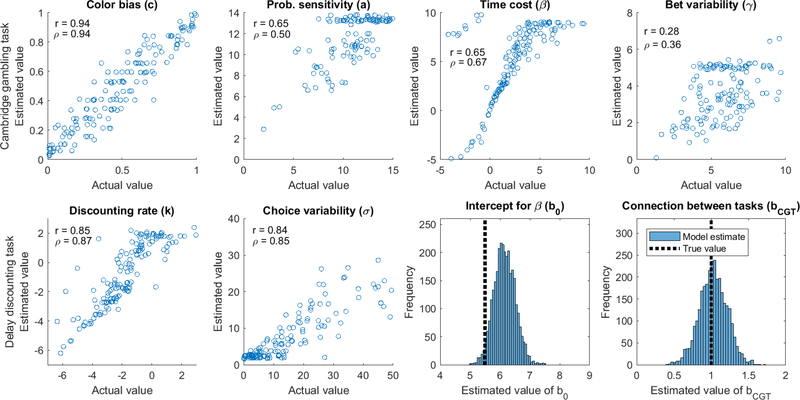
Because the estimates of k tend to be heavily right-skewed, it is typical to estimate log(k) instead of k to have an indicator of impulsivity that is close to normally distributed. Therefore, we use the same natural log transformation of k when estimating its value in all of the models presented here – this is particularly important in the joint model, where the exponential of the underlying impulsivity trait value must be taken to obtain the k values for each individual (Figure 2).

Figure 2.

Diagram of the structure of the joint model.

Luce choice / bet utility model.

The Luce choice / bet utility model for the Cambridge gambling task uses four parameters, reduced by one from the original model presented by Romeu et al. (2019) in order to reduce the likelihood of failing to recover parameters due to correlations among them (in the original model, there was a utility parameter assigned to bet payoffs, but this frequently traded off with the bet variability parameter γ, described below). The first two parameters α and c affect the probability of choosing red or blue as the favored box color. The value of c controls the bias for choosing red or blue. A value greater than .5 indicates a bias toward choosing red, whereas a value less than .5 indicates a bias toward choosing blue. The value of α determines how responsive a decision maker is to shifts in the number of red and blue boxes. Greater values of α will make a person more sensitive to the number of boxes and therefore more likely to select whichever color appears in greater proportion, whereas smaller values of α will make them less sensitive to the proportion of red and blue boxes and therefore more likely to select randomly. Put together, the probability of choosing ‘red’ as the favored box color, Pr(R), is given as a function of the number of red boxes (N_R; a number between 0 and 10) and the parameters α and c:

$$Pr(R)=\frac{c\cdot N_R^{\alpha }}{c\cdot N_R^{\alpha }+(1-c)\cdot {\left(10-N_R\right)}^{\alpha }}$$ (3)

The probability of giving different bet values (either 5%, 25%, 50%, 75%, or 95%) depends on the decision made during the choice stage as well as on the parameters relevant to behavior on the betting component of the CGT. Once a choice is made, the bet is conditioned on that decision. In particular, the probability of the prior choice being correct enters into the probability of making different bets. Formally, the expected utility of making any particular bet (EU(B), where B is a proportion between 0 and 1) is computed as a function of the likelihood of being correct (Pr(C)) and the current number of points (pts).³

$$EU(B)=pts\cdot (Pr(C)\cdot (1+B)+(1-Pr(C))\cdot (1-B))$$ (4)

If a decision maker selected their highest-utility options with no effect of delay, then they would simply stop the counter when it reached the bet (out of B =.05, .25, .5, .75, or .95) that maximized EU(B) regardless of the time it took the ticker to reach that bet value. However, time becomes a factor when waiting imposes a cost that affects the utility of the different bets. This is accounted for by including an additional parameter β that describes the cost associated with waiting one additional unit of time. The amount of time a person has to wait to make a particular bet T_B depends on whether they are in the ascending or descending ticker condition, such that, for B =.05, .25, .5, .75, or .95, respectively:

$$T_B=\{\begin{array}{ll}0,1,2,3,4\hfill & \text{if}\text{ascending}\hfill \\ 4,3,2,1,0\hfill & \text{if}\text{descending}\hfill \end{array}$$ (5)

The adjusted utility of giving a particular bet AU(B,β) is then given by multiplying the cost of each unit of time β by the time associated with the bet T_B:

$$AU(B,\mathrm{\beta })=EU(B)-\mathrm{\beta }\cdot T_B$$ (6)

Finally, these adjusted utilities for the possible bets enter into Luce’s choice rule (Luce, 1959) to map their continuous expected utilities into a probability of making each possible bet b = {b₁,b₂,b₃,b₄,b₅} = {.05, .25, .5, .75, .95}. The consistency with which a decision maker selects the highest-utility bet is determined by the bet variability parameter γ. Higher values of γ correspond to more consistently choosing the highest-utility bet, while lower values of γ lead a person to choose more randomly:

$$Pr\left(B=b_i\right)=\frac{\exp \left(\gamma \cdot AU\left(b_i,\beta \right)\right)}{\sum _{j=1}^5\exp \left(\gamma \cdot AU\left(b_j,\beta \right)\right)}$$ (7)

Note that this is the same Luce choice rule used to determine the probabilities of making different choices (Equation 3). To obtain the joint distribution of choice and bet probabilities – i.e., the likelihood we actually want to estimate – this must be calculated for both “red” and “blue” choices. In total, this yields a probability distribution over the 10 possible selections: Pr(C = red,B = .05), Pr(C = blue,B = .05), Pr(C = red,B = .25), and so on.

This model is shown on the left side of Figure 2. To fit the model in a hierarchical Bayesian way, we assume that each of the individual-level parameters c, α, β, and γ are drawn from a group-level distribution determined by the participant’s substance use classification. The JAGS code for this model is available on the Open Science Framework at osf.io/e46zj/.

Joint model.

The joint model aims to connect elements of the two models to a common latent construct. In this case, both tasks and models purport to measure impulsive choice, a dimension of impulsivity measured through decision tasks like these. Impulsive choice proclivity is measured via the k parameter in the hyperbolic discounting model, and the β parameter in the Luce choice / bet model of the CGT. Joint models are theoretically capable of putting together many different tasks and measures, but as this is the first time it has been applied to modeling behavior across tasks, we have chosen to make the process simple by only connecting the two models. Therefore, the number of new elements needed to construct the joint model is minimal.

One of the innovations here is to add a latent variable on top of the cognitive model parameters that describes a decision maker’s underlying tendency toward impulsive choice. This is shown as the blue region of Figure 2. This Impulsivity (Imp) variable is then mapped onto k and β values through linking functions f_DDT(Imp) and f_CGT(Imp), respectively. In essence, we are constructing a structural equation model where the measurement component of the model consists of an established cognitive model of the task. The advantage of using cognitive models over a simple statistical mapping (usually linear with normal distributions in structural equation modeling) is that the cognitive models are able to better reflect not only performance on the task but the putative generative cognitive processes. This makes the parameters of the model, including the estimated values of impulsivity and the connections between the tasks, more meaningful and more predictive of other outcomes (Busemeyer & Stout, 2002).

To connect the Impulsivity variable to k in the hyperbolic discounting model, we used a simple exponential link function

$$k=f_{DDT}(Imp)=\exp (Imp)$$ (8)

Readers familiar with structural equation modeling will know that one of the parameters of the model will need to be fixed in order to identify them. This is done by fixing the loading of k onto Impulsivity to be 1; there is no free parameter in f_DDT. Conversely, the load of β onto Impulsivity adds two free parameters as part of a linear mapping, including an intercept (giving a difference in mean between log(k) and β) and slope (mapping variance in log(k) or Imp to variance in β).

$$\mathrm{\beta }=f_{CGT}(Imp)=b_0+b_{CGT}\cdot Imp$$ (9)

The remaining parameters inherited from the constituent models are m (DDT) and α, γ, and c (CGT). This essentially completes the joint model. The Impulsivity values for each individual are set hierarchically, so that each person has a different value for Imp but they are constrained by a group-level distribution of impulsivity from their substance use group. The values of b₀ and b_CGT are not set hierarchically but rather fixed within a group, as variation in these parameters across participants would not be distinguishable from variation in Imp values.

Simulation studies

One of the most fundamentally important aspects of testing a cognitive model is to ensure that it can capture true shifts in the parameters underlying behavior (Heathcote et al., 2015). This is difficult to assess using real data, as we do not know the parametric structure of the true generating process. Instead, a modeler can simulate a set of artificial data from a model with a specific set of parameters and then fit the model to that data in order to see if the estimates correspond to the true underlying parameters that were used to create the data in the first place. This model recovery process ensures that the parameter estimates in the model can be meaningful; if model recovery fails and we are unable to estimate parameters of a true underlying cognitive process, then there is nothing we can conclude from the parameter estimates because they do not reflect the generating process. If model recovery is reasonably successful, then at least we can say that it is possible to apply the model to estimate some properties of the data.

This is particularly important to note because the hyperbolic discounting model – a popular account of performance on the delay discounting task – can often be hard to recover using classical methods like maximum likelihood estimation or even non-hierarchical Bayesian methods (Molloy et al, in prep). This problem can be addressed by using a hierarchical Bayesian approach where parameter estimates for individual participants are constrained by a group-level distribution and vice versa (Kruschke, 2014; Shiffrin et al., 2008). The five-parameter version of the Cambridge gambling task (Romeu et al, 2019) suffers from similar issues, but when reduced to four parameters by reducing the power function used for computing utilities to a linear utility and fit in a hierarchical Bayesian way, it is possible to recover as well.

For both models, the simulated data were generated so that they would mimic the properties of the real data to which the model was later applied. To this end, the simulations used 150 participants (approximately the size of a larger substance use group; similar but slightly less precise results can also be obtained for 50- or 100-participant simulations), 27 unique data points per participant for the delay discounting task, and 200 unique data points per participant for the Cambridge gambling task. Participants in the real CGT task varied in terms of the number of points they had accumulated going into each trial, meaning that the bets they could place could differ from trial to trial. To compensate for this, the simulated trials randomly selected from a range of possible point values (from 5 [the minimum] to 200 points) as the starting value for each trial. The rest of the task variables – including payoffs and delays in the DDT, and box proportions and ascending/descending manipulation in the CGT – were set according to their real values in the experiments.

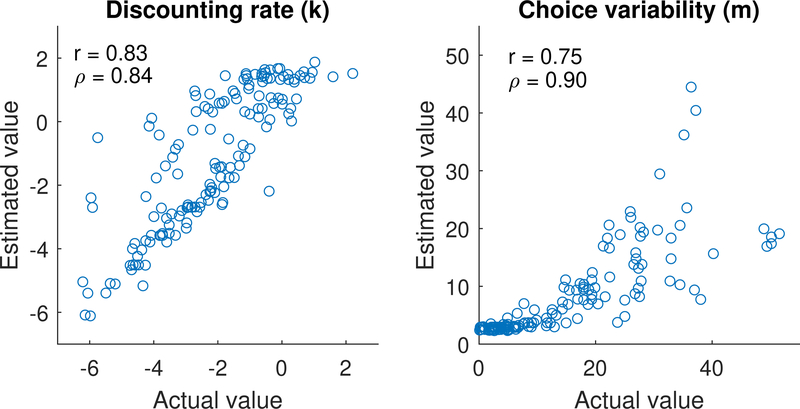
The hyperbolic discounting model used the k, m parameter specification, where k is the discounting rate and m corresponds to the choice variability parameter in a softmax decision rule. Thanks to the hierarchical constraints imposed on the individual-level parameters, it was possible to recover both of these parameters with reasonable precision when the delay discounting task was fit individually. The results of the simulation and recovery are shown in Figure 3. The x-axis displays the true value of each individual’s k or m value, and the y-axis displays the value estimated from the model. The values of k are shown on a log scale, as these values tend to be much closer to log-normally than normally distributed. The linear (r) and rank (ρ) correlations are also displayed as heuristics for assessing how well these parameters were recovered. While the quality was generally good, particularly considering there were only 27 unique data points for each participant, there is potential room for improvement in estimating each parameter. As we show later, the joint model can actually assist in improving the quality of fits like these where data is sparse.

Figure 3.

Parameter recovery for data simulated from the hyperbolic discounting model (DDT) parameters when the task data are fit alone.

We repeated this procedure for the Luce choice / bet utility model of the CGT as well. As before, the ranges of individual-level parameters and the group-level mean(s), along with sample size of n = 150, were set at values that were similar to those we could expect to encounter in real data. This allowed us to assess the fidelity with which we might expect to estimate any true underlying variation in these processes in the real data.

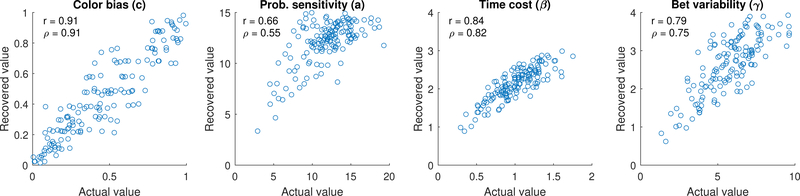
The greater number of parameters in the Luce choice / bet utility model (four) was somewhat balanced out by the greater number of trials per participant, allowing for reasonable parameter recovery. The results are shown in Figure 4. The color bias (c) parameter was the most constrained of these parameters, varying on [0,1] rather than [0,∞) or (−∞,∞) like most of the other parameters, and so it was recovered with high fidelity. Probability sensitivity, time cost, and bet variability were also reasonably well-recovered, although the greater complexity of the task and more subtle influence of each individual variable makes them more difficult to recover when compared to the hyperbolic discounting model and DDT.

Figure 4.

Parameter recovery for data simulated from the Cambridge gambling model when the task is fit alone (i.e., not a joint model with hyperbolic discounting model / delay discounting task).

Finally, we simulated and recovered data from the joint model shown in Figure 2. The value for Imp was set as the log of the value of k in the DDT, so that the linking function f_DD(Imp) was simply an exponential (f_DD(Imp) = exp(Imp)). The value of β in the CGT was a linear function of Imp, set as f_CGT = b₀+b_CGT ·Imp. In order to make the values of β reasonable, we set b₀ = 5.5 and b_CGT = 1 in the simulated data. There was also noise inserted into the resulting β values (which was estimated by the model as well) so that the standard deviation of β in the simulated CGT data was σ_β = 2.

The results of the parameter recovery for the joint model are shown in Figure 5. We were able to recover the b₀ and b_CGT parameters with reasonable accuracy, and actually improved the recovery of the delay discounting model. Both k and m were recovered with greater fidelity in the joint model correlations between true and estimated parameters were .83 and .75 in the non-joint model versus .85 and .84 in the joint model for k and m, respectively. However, the noise introduced into the model by using the value of k to predict β had a mixed effect on the recovery of the CGT model parameters. Because there were substantially fewer data from the DDT (27 trials of binary choice) relative to the CGT (200 trials with both binary choice and a multinomial bet, for 400 data points), the uncertainty in estimates from the DDT translated into uncertainty in some CGT parameter estimates. Because of this, the joint model only seemed to improve estimation of the color bias parameter, while keeping probability sensitivity and time cost relatively similar and decreasing precision of the bet variability estimates. A major benefit of joint modeling is its ability to constrain estimates with multiple sources of data (Turner et al., 2015). The benefit seems to go mainly in the direction of the task with less data, as in previous work (Turner, 2015), thanks to the richer information in the CGT constraining estimates in the DDT.

Figure 5.

Parameter recovery for data simulated from a joint hyperbolic discounting and Cambridge gambling model where k and β are related. Parameters for the joint model that are not included in the individual models are shown at the bottom right.

Overall, it seems that we should be able to identify real differences in the parameter values given the sample sizes in the real data. The joint modeling approach will also allow us to discriminate between 1-factor and 2-factor models by allowing us to estimate the b_CGT factor. If there is no connection between tasks, the value of this slope parameter should turn out to be zero, while it should clearly be estimated as nonzero if there is a true underlying connection between the tasks as in our simulations (see Figure 5). In the next section, we show how these diverging predictions can be leveraged by a Bayes factor analysis that quantifies the evidence for or against the value of b_CGT being zero.

Application to substance users’ data

With the simulations establishing the feasibility of the approach, we can examine the connection between the DDT and CGT in real data. Each model was fit separately to each of the substance use groups: Heroin (red in all plots below), Amphetamine (yellow), polysubstance (purple), and Control (blue). Dividing the participants by group assists in estimation of the models because the group-level parameters from the hierarchical Bayesian model are likely to differ from group to group. It also allows us to evaluate the connection between tasks within each substance use group: it could very well be the case that the tasks are positively (or negatively) associated within groups of substance users but not for controls, for example. Naturally, separating substance use groups also allows us to compare the group-level model parameters to establish any identifiable differences in cognitive processing between different types of substance users.

To examine whether the discounting rates k in the DDT and β in the CGT are related, we compare two different instances of the joint model. The first allows all parameters described in the previous section to vary freely: The group- and individual-level parameters are all fit to the data and b_CGT can take any value. We refer to this as the 1-factor model, since both tasks are connected to the same latent Impulsivity factor. The second model, which is nested within the first, forces b_CGT to be equal to zero, so that there is no connection between the estimates of k and estimates of β. In essence, this forces the two tasks to depend on separate dimensions of impulsivity and is equivalent to fitting the hyperbolic discounting model and Luce choice/bet utility model separately to each participant’s data. This constrained model is therefore referred to as the 2-factor model, as it posits that separate dimensions of impulsivity are responsible for performance on the two tasks.

Estimates

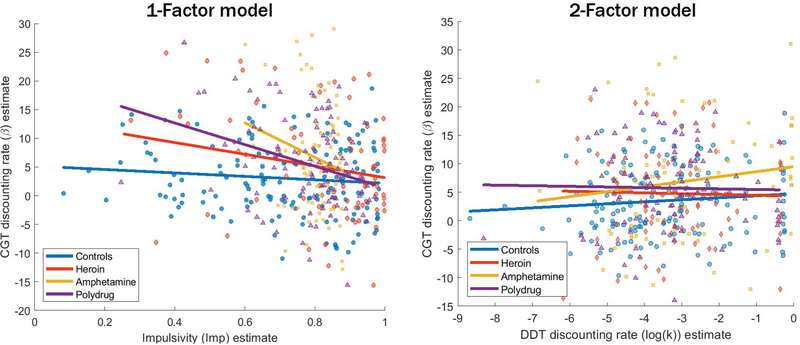
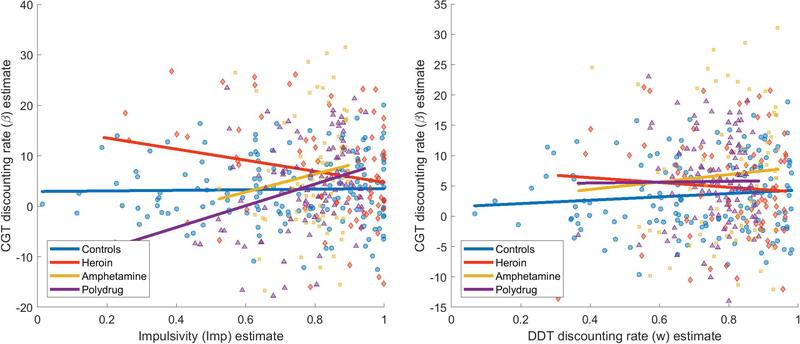
It is helpful to get a first impression by comparing the discounting rates between tasks for each participant. These estimates of log(k) (x-axis) and β (y-axis) for each individual are shown in Figure 6. The corresponding colored lines also show the estimated relationship between the two parameters. These estimates should be positively related if there are overlapping processes in the DDT and CGT (the log transformation is monotonic, preserving order between them), but this does not seem to be the case whether we evaluate them . As shown in the 2-factor model (right), the values of log(k) and β are largely unrelated when they are separately estimated. Nevertheless, we can see that the estimates of both parameters tend to be higher for substance dependent individuals (yellow, purple, red) than they do for the control group (blue).

Figure 6.

Estimates of log(k) (x-axis) and β (y-axis) for each individual, using the joint 1-factor model (left) and separate 2-factor model (right). Each point corresponds to an individual, and the lines show the best estimates of the relationship between the two parameters.

When log(k) and β are fit in a joint 1-factor model where there is a relationship between the two built in (left panel), the model appears to accentuate minor differences in slopes so that there appears to be a slight negative relationship between log(k) and β for all groups. The critical question is whether these are true negative relationships between the parameters or whether these slopes are largely a consequence of noise in the connection b_CGT. This question is addressed formally in the comparison between 1-factor and 2-factor models in the next section, but we can also examine the raw correlations between these parameters. These are shown in Table 1, including both the linear Pearson correlations (r) and rank-based Spearman correlations (ρ). Both measures indicate non-significant relationships between the parameter estimates, suggesting that imposing a linear relationship in the joint model is not what is driving the lack of relationship between the two parameters.

Table 1.

Relationship between estimated values of log(k) and β for each group, based on separate estimates of the CGT and DDT models (2-factor model).

Group	r (linear)	p-value (linear)	ρ (rank)	p-value (rank)
Control	.10	.23	.11	.19
Heroin	−.02	.83	−.04	.74
Amphetamine	.14	.22	.23	.06
Polysubstance	−.02	.83	.02	.87

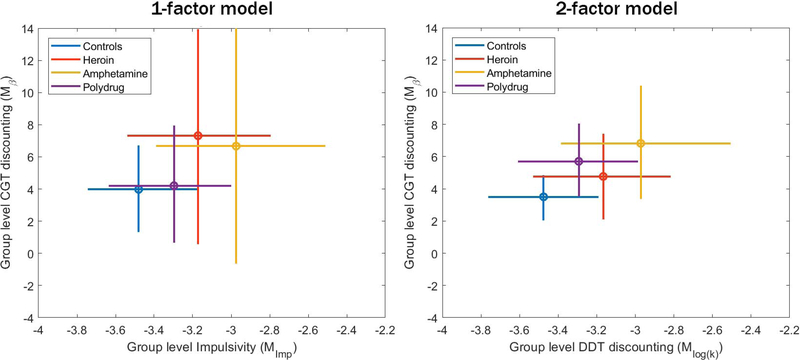
It is also helpful to gain some perspective on the effect of estimating b_CGT by looking at its effect on the precision of the estimates of the group-level parameters. The first thing to note about the group-level estimates, at least in the 2-factor model, is that we can identify differences between the groups in terms of temporal discounting parameter estimates. Amphetamine users seem to be the highest on both log(k) and β, while polysubstance and heroin users also seem to show slightly greater discounting rates in both tasks relative to the controls. This corroborates previous findings suggesting that k (Bickel & Marsch, 2001) and β (Romeu et al., 2019) are both indicators of decision deficits related to substance dependence. It also supports the findings of Ahn & Vassileva (2016), who suggested that delay discounting behavior predicted amphetamine dependence but not heroin dependence, suggesting differences in cognitive mechanisms related to these two different types of substance use.

As we saw in the simulation, jointly modeling two tasks when there is a true underlying relationship between parameters should generally improve the estimates, especially for the task with less information from the data (in this case, the DDT). However, when there is not a true connection between tasks, loading two unrelated parameters onto a common latent factor will simply introduce additional noise into their estimates. As a result, there should be greater precision in parameter estimates when the task parameters are connected, and lower precision when they are not.

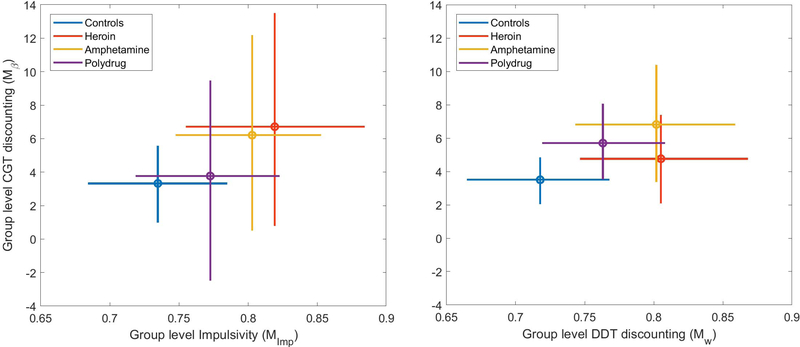
The mean estimates and 95% highest density interval (HDI) ⁴ for the group-level estimates of log(k) (x-axis) and β (y-axis) are shown in Figure 7. Immediately we can see that the precision of the group-level parameter estimates, indicated by the width of the 95% HDIs, is substantially lower in the 1-factor model than in the 2-factor model. This is particularly true for the estimates of β, which show great uncertainty when they are connected to the values of log(k) via the latent Impulsivity factor.

Figure 7.

Mean estimates (circle) and 95% highest-density interval (bars) of group-level means of the log(k) (x-axis) and β (y-axis) for each of the substance use groups. Estimates generated from the joint 1-factor model are shown on the left, and estimates generated from the separate 2-factor model are shown on the right.

This is still not completely decisive evidence that the 2-factor model is superior to the 1-factor model. It is possible, given enough noise in an underlying latent variable, that the joint model could be reflecting true uncertainty about Impulsivity and properly reflecting this uncertainty in corresponding estimates of β and log(k). The factor structure comparison presented next is aimed at formally addressing which model is supported by the data.

Factor structure comparison

The 2-factor model is nested within the 1-factor model, where the differentiating factor is that the 2-factor model removes the connection between the two tasks. In some ways, the 2-factor model can be thought as a nested model where b_CGT = 0. As such, tests based on classical null hypothesis significance testing cannot provide support for the 2-factor model, because they could only reject or fail to reject (not support) the hypothesis that the slope of this relationship is zero. Instead, we use a method of approximating a Bayes factor called the Savage-Dickey density ratio BF₀₁, which can provide support for or against a model that claims a zero value for a parameter (Verdinelli & Wasserman, 1995; Wagenmakers et al., 2010). It does so by comparing the density of the prior distribution at zero against the posterior density at zero. Formally, it computes the ratio

$$B{F}_{01}=\frac{Pr(H=0|D)}{Pr(H=0)}$$ (10)

where H is the parameter / hypothesis under consideration, and D is the set of data being used to inform the model. The value of Pr(H) is the prior, while Pr(H|D) is the posterior.

Data generated from a process with a true value of H ≠ 0 will decrease our belief that a parameter value is zero, resulting in a posterior distribution where Pr(H = 0|D) < Pr(H = 0) and therefore BF₀₁ < 1. Conversely, a data set which increases our belief that a parameter value is zero will result in a posterior distribution where Pr(H = 0|D) < Pr(H = 0) and thus BF₀₁ > 1. In essence, the Bayes factor is quantifying how much our belief that the parameter value (hypothesis) is zero changes in light of the data.

Applied to the problem at hand, we are interested in how much our belief about b_CGT being equal to zero changes in light of the delay discounting and Cambridge gambling task data. An increase in the credibility of b_CGT being zero is evidence for the 2-factor model, whereas a decrease in the credibility of b_CGT being zero is evidence for the 1-factor model.

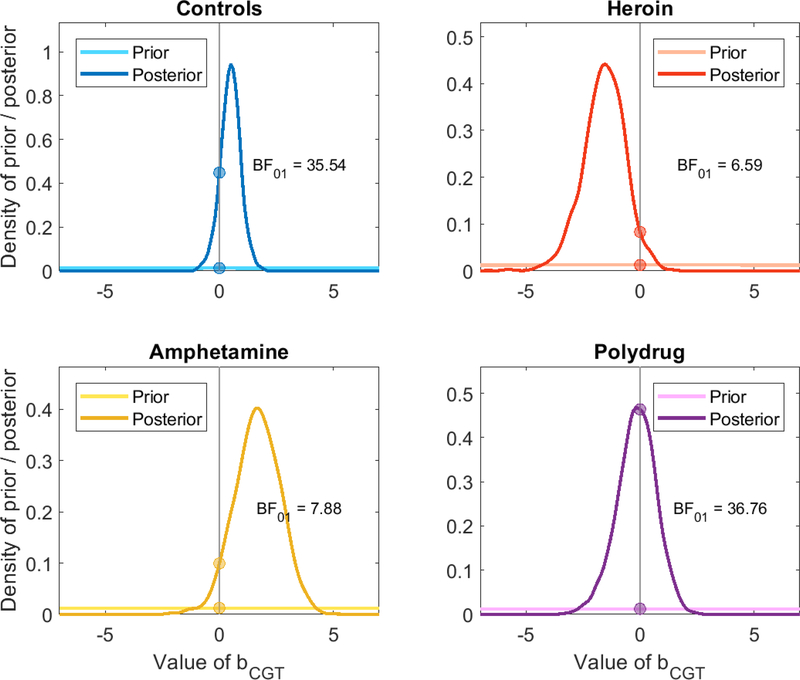
Naturally, the outcome of this test will depend on the prior probability distribution we set for b_CGT. In this application, we have tried to make the prior as reasonable as possible by setting Pr(b_CGT) ~ N(0,10). This allows a reasonable amount of flexibility for the parameter to take many values (improving the potential for model fit) while also providing a suitably high prior probability of Pr(b_CGT = 0) (which will move the Bayes factor toward favoring the 1-factor model). Some readers may disagree over the value of the prior, which will affect the Bayes factor. The prior distribution is shown in Figure 8 for each comparison, which allows a reader to judge for themselves what sorts of priors would still yield the same result. Almost any reasonable set of normally distributed priors with standard deviation greater than 1 for the control / polysubstance groups or greater than 4 for the amphetamine / heroin groups will still yield evidence in favor of b_CGT = 0.

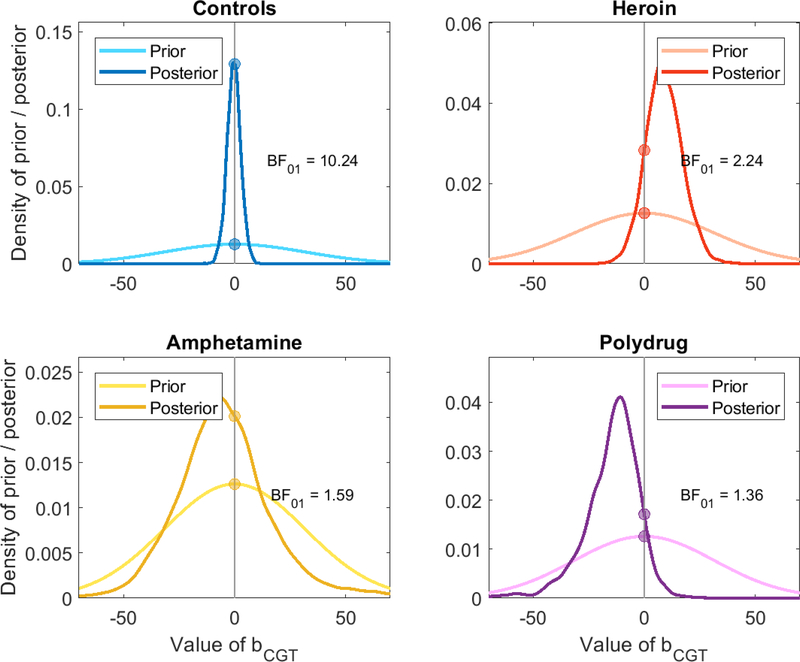
Figure 8.

Diagram of the Savage-Dickey Bayes factor analysis. The posterior likelihood of no relation between the two tasks (darker distributions) is compared to the prior likelihood of no relation between them (lighter distributions) to determine whether the data increased or decreased support for a relationship between parameters of the different tasks.

As shown in Figure 8, the Bayes factors all favor the 2-factor model, with BF₀₁ varying between 6 and 37. For reference, a Bayes factor of 3–10 is typically thought to constitute “moderate” or “substantial” evidence, a Bayes factor of 10–30 constitutes “strong” evidence, and a Bayes factor of 30 or more “very strong” evidence (Jeffreys, 1961; Lee & Wagenmakers, 2014). The evidence therefore favors the 2-factor model across all of the substance use groups at a moderate to strong level.

Of course, the Bayes factors and thus the interpretation of the strength of evidence may change according to the priors. However, the posteriors generally suggest that the evidence can and should favor the 2-factor model. For the control and polysubstance groups, the posterior distributions are centered so close to zero that almost any choice of prior will still result in a Bayes factor favoring the 2-factor model, and the heroin and amphetamine groups (notably, the groups with the smallest number of participants) provide evidence in opposing directions.

Overall, putting together the low correlation between parameters when the models are estimated separately (2-factor; Figure 6), the decrease in precision of parameter estimates when the 1-factor structure is imposed (Figure 7), and the support for the 2-factor model in terms of a Bayes factor under reasonably priors (Figure 8), the evidence overwhelmingly favors a 2-factor structure. This suggests that different dimensions of impulsivity underlie apparent temporal discounting in the CGT and the DDT.

Relation to outcome measures

Given that the analysis indicates that β in the Cambridge gambling task model and log(k) in the delay discounting task model are measuring different dimensions of impulsivity, a natural next question is what differentiates the two dimensions. One way to gain insight into this is to connect each of the temporal discounting parameters to other measures of impulsive tendencies. Table 2 shows the relationship between β from the CGT model, log(k) from the DDT model (or w from the direct difference model, Appendix A), and several other self-report and neurobehavioral measures of impulsivity.

Table 2.

Relationship between model parameters and other measures of impulsivity. Relation to behavioral metrics of performance on IGT and BART were not significant, though they may be connected to model parameters of these tasks if these additional tasks were to be modeled.

Scale	β (CGT)	log(k) (DDT)	1−w (DDT)
Raven IQ	−0.14**	−0.14**	−0.12*
Fagerstrom Nicotine Dependence	0.08	0.14**	0.11**
Psychopathy Checklist: Screening Version	0.06	0.15**	0.12**
Barratt Impulsiveness	0.13**	0.01	0.02
BUSS - Physical Aggression	0.11**	0.11*	0.11**
Wender Utah (ADHD)	0.10**	0.01	0.01
Go/No-go false alarms	0.12*	0.16**	0.14
Go/No-go criterion (c)	−0.10*	−0.12*	−0.08
Immediate Memory discriminability (d)	−0.13*	−0.07	−0.07
Immediate Memory criterion (a)	−0.13**	−0.04	−0.04
Stop Signal inhibition failures	0.11*	−0.05	−0.06

^*p < .05

^**p < .01

In general, the β parameter from the CGT is more closely related to performance on the Barratt Impulsiveness Scale as well as behavioral measures of response inhibition on the Go/No-go task and Stop Signal paradigms. Waiting for the timer to tick over in the Cambridge gambling tasks requires the ability to inhibit making a response until the target bet proportion is reached. A failure to inhibit an early response will naturally result in higher estimates of β. This may naturally be the reason that it is related to inhibition failures in the Stop Signal paradigm as well as the higher rate of responses in the Go/No-go paradigm (resulting in a higher rate of false alarms and hits, and thus a shift in the criterion measure c). This would suggest that it is more closely related to the impulsive action dimension of impulsivity, rather than the impulsive choice dimension normally associated with temporal discounting.

Conversely, the k parameter (and w) are more closely related to measures of externalizing issues like aggression and psychopathy, while both tasks are negatively related to Raven IQ. This lines up closely with the observation of Reynolds et al. (2006), who broke down impulsivity into a response inhibition component – related to performance on Stop Signal (Verbruggen & Logan, 2008) and Go/No-Go tasks – and a more long-term impulsivity that impacts performance on the DDT and BART tasks and self-report measures like the Barratt scale. In terms of the dimensions of impulsivity, these results suggest that the DDT parameter lines up more closely with impulsive choice measures, whereas the CGT parameter lines up with impulsive action or response disinhibition (Hamilton, Mitchell, et al., 2015; Hamilton, Littlefield, et al., 2015; MacKillop et al., 2016). However, the DDT parameter seems to line up somewhat with self-report measures as well, suggesting that it may be related to both impulsive choice and impulsive personality dimensions – or possibly that these two dimensions are more closely related to one another than to impulsive action.

Discussion

Given the differences in task structure, it may not be too surprising that the delay discounting task and Cambridge gambling task actually appear to measure separate dimensions of impulsivity. Much like the diverging results between described and experienced outcomes in risky choice, it may be the case that there is an analogous “description-experience gap” (Hertwig et al., 2018; Hertwig & Erev, 2009; Wulff et al., 2018) in impulsive choice as well. Such a gap would naturally manifest in differences in performance between the delay discounting task, where the delays are not experienced in real time between trials of choices (though of course these decisions may be played out following the experiment), and the Cambridge gambling task, where the delays are experienced on each and every trial before a bet can be made. While the type of analysis developed here is informative, it cannot determine whether these differences reflect a true difference in the tasks measuring different latent constructs, or instead reflect mainly the contribution of learning processes to performance (Haines et al., submitted).

Of course, experience versus description is not the only difference between the tasks. The delay discounting task uses delays that are typically on the order of weeks or months, which is much longer than the 0–25 second time scale implemented for making bets in the Cambridge gambling task. The difference in performance may instead arise because the DDT relies on long-term planning whereas the CGT relies on inhibiting more immediate responses in a similar fashion to Go/No-go and Stop signal tasks (Reynolds et al., 2006). These two tasks may therefore be measuring separate dimensions of impulsivity: the CGT appears to be related to impulsive action, while delay discounting is related to trait-level characteristics like impulsive personality and by definition related to impulsive choice (MacKillop et al., 2016). If delay discounting is indeed a trait-level characteristic (Odum, 2011), this would explain why it tends to be more stable over time (Simpson & Vuchinich, 2000) and its relation to self-report measures of impulsivity (like the BIS or UPPS) that are designed to assess personality.

Impulsivity is best understood as a multidimensional construct that affects many different cognitive processes contributing to substance use outcomes and consisting of both state and trait components (Isles et al., 2018; Vassileva & Conrod, 2018). Having multiple assessment procedures that engage cognitive processes related to long-term planning or response inhibition allows us to uncover their unique and specific contributions to disordered decision making. The observation that they both underlie health outcomes related to psychopathy and substance use disorders (Ahn & Vassileva, 2016) suggest that intervention strategies may need to target multiple avenues leading to substance dependence (Vassileva & Conrod, 2018).

Solving the problem of what creates the diverging factors between CGT and DDT measures of impulsivity is likely to require extensions of empirical paradigms to whittle the difference between tasks down to key factors. For instance, a version of a delay discounting task where the delays before outcomes are actively experienced (early investigations along these lines such as Dai et al., 2018; Xu, 2018) could help eliminate (or confirm) the description-experience gap as a culprit of the 2-factor structure. Likewise, swapping the counter component of the CGT with a deliberate delay selection procedure (where delays are associated with different bets) might bring it closer to a DDT-like procedure. In such a case, delays would be selected in advance rather than relying on response inhibition, and potentially allow the CGT to better measure choice impulsivity instead. If the distinction between impulsive choice and impulsive action splits the DDT and CGT, respectively, we should expect that CGT parameters should be closely related to parameters of other impulsive action models of tasks like Go/No-go (Matzke & Wagenmakers, 2009; Ratcliff et al., 2018) and Stop Signal paradigms (Matzke et al., 2013; van Ravenzwaaij et al., 2012).

On a broader scale, the methods we developed allowed for a more detailed assessment of the factor structure underlying impulsivity and can be applied to a wide range of similar problems given appropriate data. It demonstrated that the joint modeling approach can be applied gainfully to modeling multiple tasks in conjunction with one another, not just to improve the model parameter estimates – although the simulation component of the study showed that this is possible when the tasks are connected – but also to gain insights about the underlying latent factors that cannot be gathered from extant methods. Joint models and cognitive latent variable models like this one improve on simple correlations between cognitive model parameters by eliminating the issue of generated regressor bias, where the estimated cognitive model parameters have sampling variance that is unique from the variance of the regressor in the correlation, leading to under-estimation of the standard error associated with their relationship and thus an inflation of type I errors in conclusions from the resulting correlation coefficients (Pagan, 1984; Vandekerckhove, 2014). As we saw in the simulations, it also permits richer or more numerous data gathered in one task (CGT) to inform the parameter estimates in the other task (DDT), reducing the uncertainty in individual and group level performance resulting from small samples.

In an effort to make this type of method more approachable, we have provided the JAGS code for the hyperbolic, direct difference, Luce choice / bet utility, and joint models at osf.io/e46zj. This approach is closely related to the joint modeling of neural and behavioral data as well as cognitive latent variable models of personality and behavioral data; tutorials on these procedures can be found in Palestro et al. (2018) and Vandekerckhove (2014), respectively. Our hope is that this provides an effective method for factor comparisons using cognitive models as the predictors of behavioral data, allowing for new and interesting inferences about common latent processes that generate decision behavior.

Aside from simply being an illustration of the power of this approach for identifying latent factors, the present work also brings to bear substantive conclusions related to substance use and impulsivity. In line with our previous findings (Ahn et al., 2014; Haines et al., 2018), the current results suggest that computational parameters of neurocognitive tasks of impulsive choice can reliably discriminate between different types of drug users. Future studies should explore the potential of such parameters as novel computational markers for addiction and other forms of psychopathology, which may help refine addiction phenotypes and develop more rigorous models of addiction.

Appendix A: Direct difference model of delay discounting

One concern with connecting the parameters of two separate cognitive models is whether the conclusions of the analysis depend heavily on the models themselves. We tested several variants of the hyperbolic and Luce choice/bet models, arriving on the ones used above primarily because they provided the best mix of recoverability and completeness. However, we also tested an alternative to the hyperbolic discounting model, the direct difference model (Dai & Busemeyer, 2014; Cheng & González-Vallejo, 2016). This model posits that people compare options in the delay discounting task by comparing them on individual attributes. The direct difference model computes the difference between alternatives on a particular attribute – such as delay – and then combines the differences between item attributes into an overall difference in subjective value. This is referred to as an attribute-wise model, which sits in contrast to the hyperbolic discounting model and other alternative-wise models, which compute an overall item value by taking the reward value and discounting its subjective value according to the delay associated with it.

The direct difference model uses three main parameters. The first parameter υ describes the utility (u(x)) associated with different bets (x) as

$$u(x)=x^v$$ (11)

Similarly, the second parameter ν describes the utility (v(t)) associated with different delays (t):

$$v(t)=t^v$$ (12)

Like most utility functions, both of these consist of a power function with a single free parameter (υ or ν), yielding a concave mapping from reward amount or delay to subjective value. Once the values of each attribute are computed for both alternatives, they are contrasted against one another. For two delayed prospects (x₁,t₁) and (x₂,t₂), this yields a utility difference for rewards u(x₁)−u(x₂) and a utility difference for delays v(x₁)−v(x₂). The overall difference in subjective value is computed by putting a relative weight on each attribute. This is done by multiplying a free weight parameter w by the reward utility difference, and its inverse (1−w) by the delay utility difference. For the comparison between a larger later option (x_L,t_L) and a smaller sooner option (x_S,t_S), this gives an overall difference in subjective value d.

$$d=w(x_L^v-x_S^v)-(1-w)(t_L^v-t_S^v)$$ (13)

The direct difference model predicts choice variability as a function of these three parameters as well. We use a random utility implementation of the model, where the difference in subjective value is associated with an accompanying variance, which creates random differences in choice behavior from selection to selection. The square root of this variance (the standard deviation) is given as σ.

$$\sigma =\sqrt{w\cdot {\left(x_L-x_S\right)}^2+(1-w)\cdot {\left(t_L-t_S\right)}^2-d^2}$$ (14)

The probability of selecting the larger later option is a function of d and σ:

$$p_L=\mathrm{\Phi }\left(\frac{d}{\mathrm{\sigma }}\right)$$ (15)

Here, Φ is the cumulative distribution function for a standard normal random variable. The model can then be fit to the data by estimating the choice probabilities as a function of w, υ, and ν. While there isn’t a parameter that directly describes temporal discounting, the w parameter does control the relative weight assigned to reward and delay information. A smaller value of w results in more weight on delay information, and a larger w results in more weight on reward information. A more impulsive participant who discounts rewards heavily should therefore appear to pay more attention to delay information, resulting in a smaller value for w. As a result, we use 1−w as the measure of impulsivity in the direct difference model of the DDT.

Individual Estimates

For the direct difference model, we can repeat the joint (1-factor) and separate (2-factor) modeling analyses. Because w is on a bounded scale of [0,1] and β is on an unbounded scale, we set the transformation from Imp (the latent impulsivity factor) to w as a logistic mapping

$$w=\frac{1}{1+\exp (-Imp)}$$ (16)

This is in place of the exponential mapping used for the hyperbolic discounting parameter k. All other settings were the same for the CGT side of the joint model.

The results of the individual-level estimates for 1−w and β are shown in Figure 9. As before, blue circles are estimates for controls, red diamonds are heroin users, yellow squares are amphetamine users, and purple triangles are estimates for polysubstance users. As shown in the left panel, there are not particularly strong covariances between 1−w and β for any of the substance use groups, reflected in the relatively flat slopes for the lines depicting the average relationship. As with the hyperbolic discounting joint model, the direct difference joint model (left side of Figure 9) accentuated the slopes of the relationships between the two impulsivity parameters, but even these were not particularly strong.

Figure 9.

Individual estimates of w in the direct difference model of the DDT (x-axis) and β in the model of the CGT, along with the strength of relationship between them (color corresponds to lifetime substance use classification). The result when models are fit jointly (1-factor) is shown on the left and fit separately (2-factor) on the right.

Group level estimates

The effects of modeling the DDT and CGT as a 1-factor versus 2-factor model can be observed in the group-level estimates of the w and β parameters as well, shown in Figure 10.

Figure 10.

Group-level mean estimates of w in the direct difference model of the DDT (x-axis) and β in the model of the CGT. The result when models are fit jointly (1-factor) is shown on the left, and fit separately (2-factor) on the right. Error bars correspond to 95% highest density intervals on group-level estimates.

As with the hyperbolic discounting joint model, constraining both w and β using a common Impulsivity factor (1-factor model, left of Figure 10) primarily introduces uncertainty into the posterior of the estimates of β when compared with fitting the models when this relationship is fixed at b_CGT = 0 (2 factor model, right of Figure 10).

Interestingly, the direct difference model seems to be better at capturing differences between substance use groups when it comes to delay discounting behavior: Controls were much lower than substance users in terms of mean estimates of w. However, the direct difference model generally fit worse than the hyperbolic discounting model on this data set. The deviance information criterion [DIC], which indexes the quality of model fit with a penalty for a greater number of parameters (a lower DIC is considered better), was consistently lower for the hyperbolic model: the hyperbolic model fit with DIC values of 1846.4, 726.4, 865.6, and 1180.0 for the control, heroin, amphetamine, and polysubstance groups, respectively; while the direct difference model fit with DIC values of 2212.4, 889.0, 910.7, and 1292.4 for the same respective groups. This leaves a conundrum which will certainly not be answered here, which is whether a model that is better at predicting substance use outcomes but with inferior quality of model fit is preferable to a model that is worse at predicting substance use but has a higher quality of fit. This is certainly an issue that should be addressed in future comparisons between temporal discounting models.

Bayes factor comparison

Finally, we can repeat the comparison between 1-factor and 2-factor models for the direct difference model. As before, we compare the prior likelihood of b_CGT = 0 (before it is updated with the data) against the posterior likelihood of b_CGT = 0 (after it is updated with the data) by computing the ratio from Equation 10. A value greater than 1 indicates evidence in favor of the 2-factor model, while a value less than 1 indicates evidence against it (instead favoring the 1-factor model).

The results of the Bayes factor analysis for the direct difference model are shown in Figure 11. While the evidence in favor of the 2-factor model is not quite as strong as it was with the hyperbolic discounting model – most evidence falls in the “weak” (1–3) to “moderate” strength range (3–10) – the 2-factor model is still favored over the 1-factor model for all substance use groups. It is worth noting that the prior here was somewhat more constrained relative to the posterior; as shown in the Savage-Dickey diagram for the control group (top left), even though the posterior distribution is centered right at zero, the evidence in favor of the 2-factor model is not as strong as in the analysis of the hyperbolic model. This is therefore largely due to the amount of uncertainty in the posterior relative to the prior, rather than particularly strong evidence against a value of b_CGT = 0.

Figure 11.

Diagram of Savage-Dickey Bayes factor for direct difference model, comparing prior (lighter color) against posterior (darker color) distributions on the degree of support for an estimate of zero.

The relation of 1−w to the health outcome measures can be seen in Table 2. Its predictions are generally in line with the log(k) measure from the hyperbolic model, although in general it is a weaker predictor of most outcomes.

Overall, using the direct difference model does not result in substantial changes in the conclusions of the study. It tends to better assess differences between groups, as w discriminates between substance users and non-substance users better than k, but using this model still results in evidence favoring the 2-factor model of impulsivity.

Formal specification of the models

In order to make the models more widely accessible, we have provided the JAGS code for all of the ones listed here – including 1- and 2-factor models as well as hyperbolic and direct difference models – at osf.io/e46zj/. For those who are unable or prefer not to read this code, we outline the content here for the joint model, starting with the ‘highest-order’ impulsivity construct Imp, whose prior is normally distributed (using mean, SD as the parameters of the normal, as opposed to mean, precision as in JAGS):

$$Imp~N(0,10)$$ (17)

The values of log(k) and β for each individual are linear functions of the impulsivity value (plus error), with the coefficient mapping it onto log(k) set to one, to fix the scale of the model and ensure identifiability.

$$\log (k)=Imp+N\left(0,{\zeta }_{DDT}\right)$$

$$\text{β}=b_{CGT}\cdot Imp+N\left(b_0,{\zeta }_{CGT}\right)$$

The priors for each of the other individual-level parameters were set to be uninformative with a different mean for each group, as normal distributions N(0,100) (for probability sensitivity α and bet variability γ in the CGT, and choice variability m in the DDT) or uniform distributions (for the color bias c in the CGT). The prior for b_CGT was also normal, N(0,10), and all precision parameters for group level priors were set to be uninformative as a gamma distribution Gamma(.001,.001) (in shape-rate form). In the direct difference model, the variability parameter σ was set with an exponentially distributed prior Exp(.01) (in rate form). The likelihood of the data was then given as a function of these parameters. For the hyperbolic model, the likelihood of choosing the LL alternative is

$$Pr(LL)=\frac{1}{1+\exp (-m\cdot \left(\frac{x_{LL}}{1+k\cdot t_{LL}}-\frac{x_{ss}}{1+k\cdot t_{SS}}\right))}$$

The Cambridge gambling task had two different data outputs. The first of these was the proportion of times the red boxes (vs blue) were chosen, which is given as a function of the number of red boxes N_R and the free parameters for color bias c and choice variability α.

$$Pr(R)=\frac{c\cdot N_R^{\alpha }}{c\cdot N_R^{\alpha }+(1-c)\cdot {\left(10-N_R\right)}^{\alpha }}$$

The prediction for making a particular bet depended on whether the ticker was ascending or descending as well as whether the initial choice was correct, which is designated as Pr(C) such that Pr(C) = Pr(R)·N_R/10+(1−Pr(R))(10−N_R)/10). Given the time associated with a particular bet T_B, the number of current points the participant had, and the parameters γ and β, the probability of choosing a bet b_i was

$$Pr(B=b_i|C)=\frac{\exp (\gamma \cdot pts\cdot (\mathit{\text{Pr}}(C)\cdot (1+b_i)+(1-Pr(C))\cdot (1-b_i))-\beta \cdot T_{b_i})}{\sum _{j=1}^5\exp =(\gamma \cdot pts\cdot (\mathit{\text{Pr}}(C)\cdot (1+b_j)+(1-Pr(C))\cdot (1-b_j))-\beta \cdot T_{b_j})}$$

Naturally, the bet had to be conditioned on the choice in order to ensure that the sum across all possible combinations of color choice and succeeding bet added up to one. Using these likelihoods and priors, the posterior distribution of each of the parameters was estimated via Markov chain Monte Carlo sampling in JAGS (Plummer et al., 2003), interfacing with MATLAB via matjags (Steyvers, 2011). Typically, the models were run for 4 chains of 4000 samples with 500 burn-in samples and inspected for conversion using the $\widehat{r}$ statistic and visual inspection of the sequences of samples. To compare the posterior against the prior distribution (used for the Savage-Dickey Bayes factor), we passed a standard Gaussian kernel density estimator over the collection of posterior samples and compared the height of this distribution at zero against that of the prior (which was known from the distribution specified in Equation 17. The posterior samples were also used to generate the figures shown here, including Figures 6, 7, 9, and 10.