Numerical evaluation of transcatheter aortic valve performance during heart beating and its post-deployment fluid-structure interaction analysis

Abstract

Transcatheter aortic valve replacement (TAVR) is a minimally invasive procedure that provides an effective alternative to open-heart surgical valve replacement for treating advanced calcific aortic valve disease patients. However, complications, such as valve durability, device migration, paravalvular leakage (PVL), and thrombogenicity may lead to increased overall post-TAVR morbidity and mortality. A series of numerical studies involving a self-expandable TAVR valve were performed to evaluate these complications. Structural studies were performed with finite element (FE) analysis, followed by computational fluid dynamics (CFD) simulations, and fluid-structure interaction (FSI) analysis. The FE analysis was utilized to study the effect of TAVR valve implantation depth on valve anchorage in the Living Heart Human Model, which is capable of simulating beating heart during repeated cardiac cycles. The TAVR deployment cases where no valve migration was observed were then used to calculate the post-deployment thrombogenic potential via CFD simulations. FSI analysis followed to further assess the post-deployment TAVR hemodynamic performance for different implantation depths. The deployed valves PVL, geometric and effective orifice areas, and the leaflets structural and flow stress magnitudes were compared to determine the device optimal landing zone. The combined structural and hemodynamic analysis indicated that with the TAVR valve deployed at an aft ventricle position an optimal performance was achieved in the specific anatomy studied. Given the TAVR’s rapid expansion to younger lower-risk patients, the comprehensive numerical methodology proposed here can potentially be used as a predictive tool for both procedural planning and valve design optimization to minimize the reported complications.

2: Introduction

Calcific aortic valve (CAV) disease is the most common type of valvular aortic stenosis (AS), which causes narrowing of the aortic valve (AV). This disease affects approximately 0.9% of the United States population with 2.8% of people over 75 years of age having moderate to severe AS, ultimately leading to heart failure if untreated [1]. Surgical replacement of the diseased valve has been the gold standard, but for high surgical-risk patients a minimally invasive transcatheter aortic valve replacement (TAVR) is nowadays the standard care [2, 3].

Although TAVR was initially intended solely for high-surgical risk patients, given its promising outcomes the procedure was approved in 2016 for intermediate-surgical risk patients [3, 4] and in 2019 it was further approved for low-surgical risk patients [5]. However, TAVR valve expected durability of 5–10 years [4], valve migration, paravalvular leakage (PVL), and thrombogenicity may lead to increased overall post-TAVR morbidity and mortality- especially given its current rapid expansion to younger low-risk patients. Valve migration occurs due to its improper anchoring into the aortic root – resulting in valve dislocation either in the ascending aorta or in the ventricle [3, 6]. A study of 212 patients receiving CoreValve shows that valve migration occurred in approximately 10% of the patients [6]. According to Geisbüsch et al, incidents of valve dislocation is due to instability of the aortic root caused by heart beating [6]. Suboptimal deployment of a TAVR valve has been shown to increase prosthetic leaflets mechanical stress level with higher level of fatigue damage, which compromises tissue durability [7]. Even after establishing TAVR optimal anchorage in the aortic root, its optimal performance is not confirmed, as some degree PVL could be present. Unlike surgical valve, TAVR valves may not seal the annulus completely, potentially causing PVL which is associated with higher risk of mortality, especially in self-expendable CoreValve [6]. According to a study comparing PVL in self-expandable valves versus balloon-expandable, presence of PVL at pre-discharge from the hospital was higher in patients who received the former (56.7% versus 43.2%) [8]. Blood flow through this PVL gap exposes platelets to elevated shear stress–that may cause thrombosis [3], which could lead to prosthetic leaflet dysfunction or stroke. Current evaluation of PVL and thrombosis is performed via imaging, but limitations exist as conditions are not accurately visualized [7, 9], hence a comprehensive technique is needed to accurately study these complications.

Previous numerical studies that focus on self-expandable TAVR valve complications could be categorized as finite element (FE), computational fluid dynamic (CFD), and Fluid-structure interaction (FSI) analyses. First, FE simulation is used for valve structural analysis and among the three numerical techniques, it is the most popular one. It was widely utilized to study self-expandable TAVR valve optimal implantation depth [10–14], paravalvular gaps [15, 16], and conduction abnormalities [14, 16]. These numerical studies attempted to address these complications but ignored the valve post-deployment performances during heart beating. Simulia Living Heart Human Model (LHHM) is a validated 3D dynamic model of an adult beating heart that includes physiologically realistic structural and electrophysiological properties [3, 17]. The electrical analysis is used to compute the pacing of the heart, which in turn is utilized to derive the myocardium stresses to control the mechanical contraction and relaxation of the ventricular chambers. Therefore, the LHHM capabilities can be used to examine a TAVR valve anchorage during heart beat. Second, computational fluid dynamics (CFD) simulations were mostly utilized to calculate post-TAVR PVL degree [18–20] and thrombogenicity [11]. Lastly, self-expandable TAVR FSI simulations were used to study the valve hemodynamics [4, 12, 21, 22], however clinically relevant parameters such as effective orifice area (EOA) and PVL have not been used widely while evaluating valves performance. Luraghi et al [22] recently considered these parameters in a patient specific FSI model, However, further studies that also take into account the effects of a beating heart on TAVR deployment and performance are needed to gain better understanding of ensuing procedural complications.

This study utilizes all the three numerical methods to evaluate the above-mentioned potential TAVR valve complications. Specifically the goals of this study were (a) to assess TAVR valve deployment during heart-beat to obtain optimal implantation depth via FE analysis; (b) to compare post-deployment TAVR thrombogenic potential for different implantation depths using CFD simulations; and (c) to calculate deployed TAVR valve PVL, geometric and effective orifice areas, prosthetic leaflets mechanical and fluid stress magnitudes- for different implantation depths using FSI simulations.

3: Methods

3.1. FE analysis to evaluate stent anchorage in LHHM

LHHM represents an adult healthy human heart and to study TAVR valve behaviour, a diseased condition was introduced via adding calcifications on the native aortic valves [23]. Coaptation based calcification patterns [23, 24] in the native aortic valve were introduced by assigning characteristic elements sets with homogeneous linear elastic material properties of calcifications (Young modulus, E=12.6 MPa; Poisson ratio, v=0.3) [11]. The LHHM tissue was modeled using Holzapfel-Ogden anisotropic hyperelastic material properties. The three native AVs were modeled using Ogden isotropic hyperelastic material properties, where right coronary (RC), left coronary (LC), and non-coronary (NC) leaflet were assigned unique parameter used previously by our group [11]. A 26 mm self-expandable TAVR valve (Evolut R, Medtronic, Inc., Minneapolis, MN) stent’s implantation process into the LHHM was simulated and parameterized in three implantation depths (aortic, midway, and ventricular). When the implantation depth is defined by the distance between the aortic annulus and intraventricular end of the TAVR stent [25], the aortic, midway, and ventricular positionings are 6 mm, 4 mm, and 2 mm above the annulus, respectively (Fig. 1 A, E, H). The stent has material properties of superelastic nitinol (14 constants user material VUMAT available in Abaqus) [10] and it was crimped by applying a radial boundary condition (BC) on nodes of a cylinder until the stent was crimped into a 14 fr cone-shaped catheter. The catheter’s cone was utilized to open the aortic valve by applying axial BC on the nodes of the catheter. The aortic valves were opened until catheter equipped with crimped stent had enough space to be positioned inside three native aortic leaflets. The stent was then deployed by pulling the catheter axially towards the aorta and allowed to gradually expand. During the crimping procedure, a frictionless contact was defined between the inner side of the cylinder and the outer stent frame and among all the stent’s struts. The catheter cone was only in contact (frictionless) with the ventricularis (ventricular side of the AV leaflets). The LHHM aortic leaflets ventricularis, aortic arch, and left ventricular outflow tract (LVOT) were in frictionless contact with the stent and only a penetration of 5% of the outermost elements layer were allowed. During the simulation, the TAVR valve prosthetic leaflets and cuff were ignored as it was previously shown to have negligible impact on the stent deployment and also inclusion of the prosthetic leaflets and cuff is computationally expensive [26]. A variable mass scaling was employed for stable time increment and to ensure its minimal effect on the model dynamics the ratio between kinetic and internal energy was kept under 5% [11]. The variable mass scaling was set for every 10 increments if the time step size for the stent and LHHM elements go below 1·10⁻⁷ and 2.5·10⁻⁶ respectively. The simulation was run for three cardiac cycles to obtain periodicity and a FE solver Abaqus 6.14 Explicit (Simulia, Dassault Systèmes, Providence, RI) was used to run the simulation. The simulations were run on Stony Brook University’s SeaWulf cluster using four Intel Xeon E5–2690v3 CPUs (12 cores each) and required approximately 40 hours to solve. The stent anchorage was evaluated based on the calculated anchorage contact area and force between the stent frame with the native CAV over time [11, 27].

Figure 1:

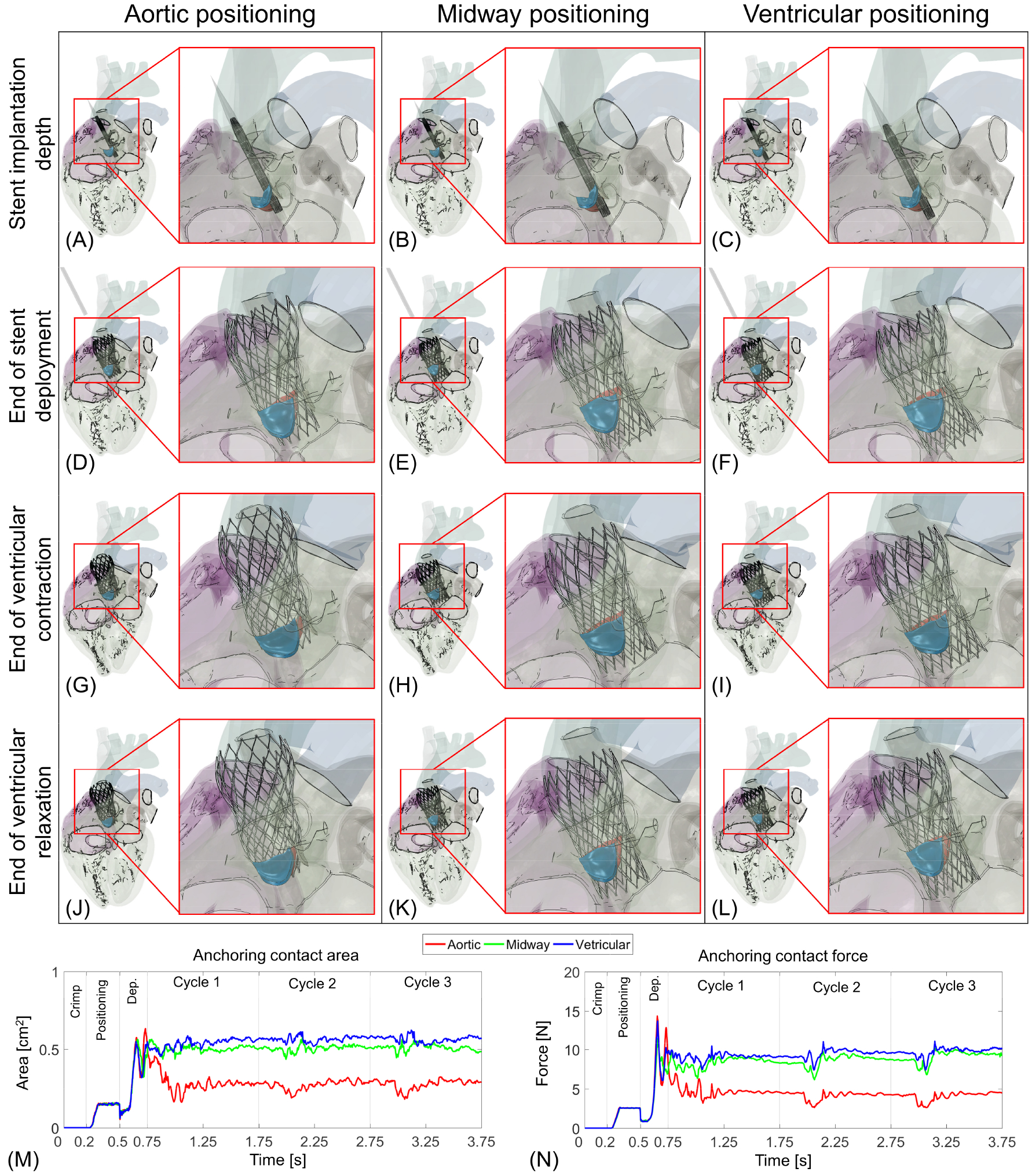
Simulation of Medtronic Evolut R deployment in calcific aortic valve during heart beating and evaluation of the stent anchorage over time. The self-expanding stent was first crimped, positioned (A–C), and deployed for aortic (D), midway (E), and ventricular (F) positionings. Panel G–I and J–L represent stent configuration during ventricular contraction and relaxation at the end of three cardiac cycles, respectively. Panel M and N show the stent anchoring contact area and force magnitudes against the CAVs.

3.2. Deployed TAVR valve and fluid domain geometries

The deployed TAVR valve configuration of the midway and ventricular implantation cases studied were further evaluated by a CFD simulation to calculate their thrombogenic potentials and a FSI analysis to calculate their hemodynamic behaviour. Prior to the flow analysis, the deployed TAVR valve stent equipped with prosthetic leaflets, cuff and LHHM anatomy surrounding the stent were extracted to create the fluid domain. Our previous study [11] describes the detailed steps involved in creating the fluid domain following a TAVR stent expansion. Briefly, the deployed stent displacement fields were calculated in reference to the original (pre-crimped) configurations. A FE analysis (Abaqus 6.14; Explicit dynamics) was then employed where the calculated displacement field was used as a BC on the TAVR valve stent that incorporates the prosthetic leaflets and the cuff. The leaflets and the cuff shared the nodes at the attachment region with the stent and as the pre-crimped stent conforms to the deployed stent configuration, the leaflets and the cuff morphed with it. The prosthetic leaflets and cuff are made of glutaraldehyde-treated porcine pericardium and their properties were obtained from literature [28], which were fitted into Ogden third-degree isotropic hyperelastic material model. The prosthetic leaflets were in frictional contact among each other and with the stent. Second, the LHHM anatomies (aortic arch, aortic root, and native valves) were extracted and smoothed in ANSYS 19.2 SpaceClaim and Fluent Meshing (Ansys, Canonsburg, PA) to obtain a cleaned and merged domain while retaining the anatomical features. The inlets and outlets were extruded to a length of three equivalent diameters to ensure no flow interference with the region of interest.

3.3. CFD analysis to calculate thrombogenic potential

Following the midway and ventricular TAVR implantation in LHHM, the valve’s thrombogenicity was characterized for both configurations by calculating stress accumulation of platelets along their respective flow trajectories via a two-phase fluid flow simulation in ANSYS Fluent 19.2. This approach was extensively utilized previously by our group and detailed description can be found in Bianchi et al. [11] and Marom et al. [29]. Briefly, while calculating the transport equations, Fluent can compute the Lagrangian trajectories of a spherical particles dispersed in the continuous domain through Discrete Phase Models (DPM). During the two-phase flow, the particles represent the platelets and the particle trajectories are predicted by calculating their momentum and drag force. For a given particle path, the stress tensor is calculated, and the stress accumulation (SA) is summation of the instantaneous linear product of stress and the exposure time to it $(SA={\int }_{t_0}^{t_{exp}}\sigma \left(t\right)dt\approx {\sum }_{i=1}^N{\sigma }_i\cdot \Delta t)$; where σ_i is scalar stress value at time step i, extracted from total stress tensor, and Δt is the time step [11, 29, 30]. Around 9,000 particles with a diameter of 3 μm were dispersed in the region close to the wall where the PVL gaps are located (Fig 2 A). The DPM particles were assumed to be neutrally buoyant in the blood. Blood was modeled as a Newtonian fluid with a dynamic viscosity of 0.0035 Pa·s and a density of 1060 kg/m³ [4, 11]. Blood can be assumed Newtonian in the region of aortic root due to the shear rate levels, which are above the non-Newtonian range of less than 100 s⁻¹. The flow was assumed to be laminar [11] and time-dependent pressure waveform BCs were applied at the ventricular and aortic sides [4] and time-dependent flow BCs were imposed at the coronary outlets [11]. The simulations for two implantation depths were run for three successive cycles to achieve periodicity. The calculated SA values were collapsed into a probability density function (PDF) that represents the potential of platelets being activated after flowing past the prosthetic valve domain. Hence, this can be referred as the “thrombogenic footprint” of the prosthetic heart valve. The calculated PDFs for midway and ventricular configurations were used for comparison purposes, where the focus was on two region–the main mode (bulk flow) and the tail region, which represents platelets that are exposed to higher stress accumulation values, hence higher chances of activation. The simulations were run on server machine using two Intel Xeon E7–4870 CPUs required approximately 24 hours to solve.

Figure 2:

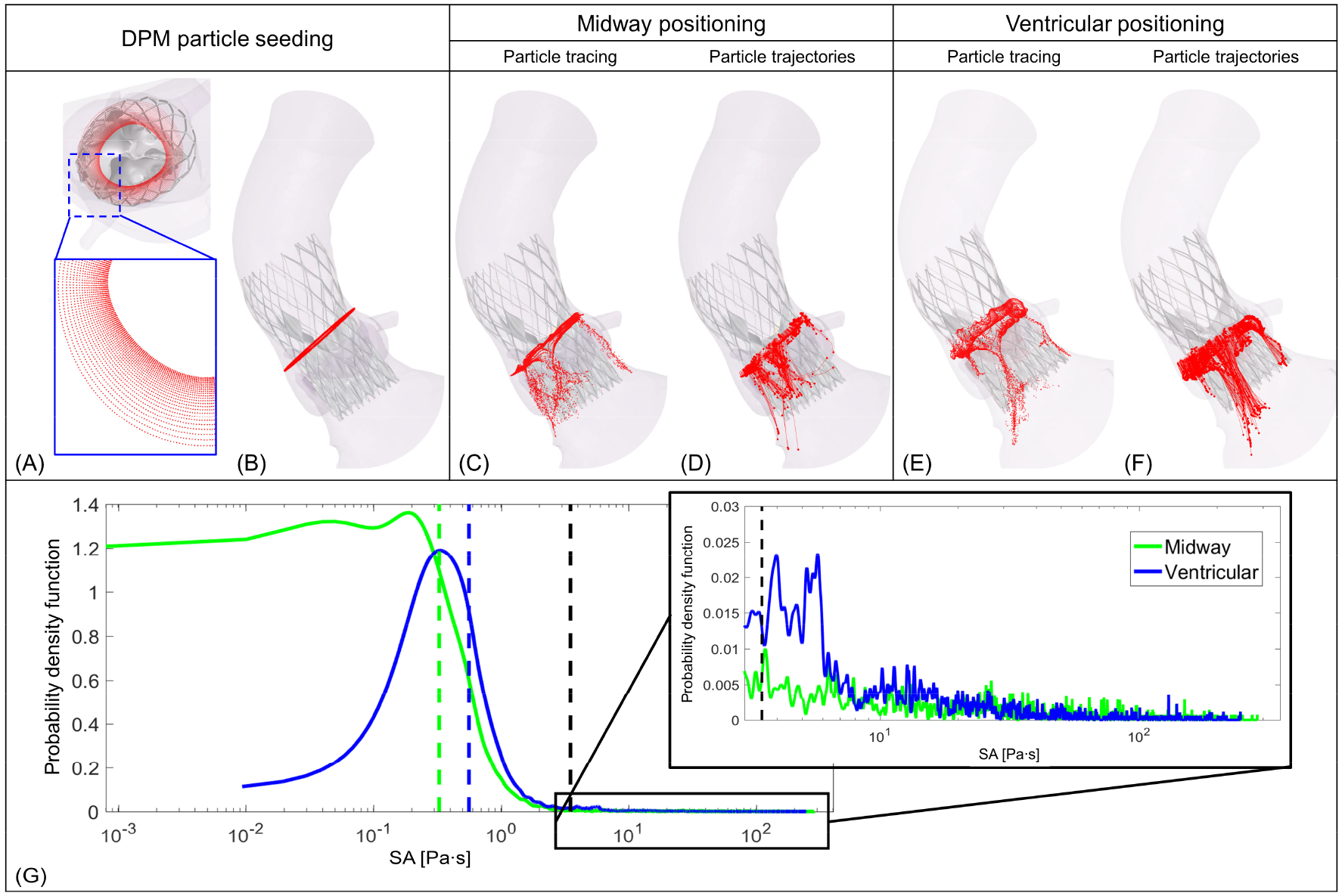
(A) DPM platelet seeding pattern based on our previous study of optimal seeding pattern for TAVR study [11, 28]. (B) Position from where the platelets were released. C and E represent platelet tracing for midway and ventricular positionings, respectively. D and F correspond to the trajectories of the platelets that are exposed to more the 3.5 Pa·s stress for midway and ventricular positionings, respectively. (G) shows PDFs of SA calculated for each configuration; the dashed line represents the median SA for Midway (green) and ventricular (blue) positioning and black dashed line represents the Hellum’s criterion for platelet activation [28].

3.4. FSI simulation to study deployed valve hemodynamics

In this study a partitioned FSI simulation is utilized, where a structural and a flow solver were coupled to model the influence of fluid in structure and vice versa. The calculated forces from the fluid domain cell transfer to the structural domain and solid domain nodal displacement were transferred to the fluid domain. The interface conditions between the two domains are treated as physical boundary and interface location is considered as part of the solution.

Flow solver setup:

A body-fitted sub-grid geometry resolution (SGGR) method was chosen during the FSI fluid solution [31]. The SGGR approach starts with a cartesian grid from which the fluid (aortic arch, native aortic valves, and LVOT) and structural (TAVR valve components) domains are subtracted. This method employed curvilinear mesh at the interface between the structural and fluid solver by taking solid domain surface mesh as the polyhedron cells. The polyhedron cells are then used to intersect or cut the cartesian fluid domain–hence ensuring body-fitted mesh. In this regard, the SGGR is a variation and more advanced version of well-known cut-cell method. The complex polyhedral cells at the interface, coupled with local refinement enable an accurate data transfer between the solvers without requiring intermediate interpolation. During FSI simulation, the fluid cells were automatically meshed and conformed based on the solid domain motion and the moving interface due to structural motion was accounted while solving the fluid equations.

Blood was assumed to be Newtonian with a dynamic viscosity of 0.0035 Pa·s and a density of 1060 kg/m³. Given the transient nature of turbulence in pulsatile valvular flows, an unsteady Reynolds-Averaged Navier-Stokes (RANS) with shear stress transport (SST) was selected. The SST model combines the advantages of k-ϵ and k-ω (former is used in the inner region and latter is used near the wall region to simulate blood flow) and can capture better the turbulent flow in the transition range that characterizes the blood flow past the valve. Time-dependent pressure waveform BCs were applied at the ventricular and aortic side [4] and time-dependent flow BCs were imposed at the coronary outlets [11]. Fluid governing equations were solved using finite volume method in FlowVision 3.10 (Capvidia NV, Leuven, Belgium).

Structural solver setup:

An explicit direct displacement-based FE method was used to calculate prosthetic leaflets motions. Material properties of TAVR leaflets were similar to those in section 3.2. A penalty-based frictionless contact modeling was utilized between the leaflets’ ventricularis (ventricular surfaces). LHHM component (aortic arch, native aortic valve, LVOT), stent, and cuff were modeled as stationary bodies. Abaqus Explicit 6.14 was used a FE solver.

Coupling software:

A 2-way strong explicit coupling was used between these two partitioned solvers and FlowVision Multi-Physics Manager 3.10 (MPM; Capvidia NV, Leuven, Belgium) was used as the coupling solver. MPM coupling software transfer displacement data from Abaqus to FlowVision and force data from FlowVision to Abaqus every 0.5 ms. The FSI analyses were run for three successive cycles to achieve periodicity. The simulations were run on Stony Brook University’s SeaWulf cluster using three Intel Xeon E5–2690v3 CPUs (two for CFD solver and one for FE solver) and required approximately 46 hours to solve.

Fluid and structural analysis from FSI simulation:

FSI simulations of successful TAVR valve deployment were utilized to find optimal TAVR valve implantation depth by evaluating their hemodynamic and structural performances. The valve hemodynamic performance was compared by obtaining flow rate of corresponding implantation configuration. The flow rate was then used to calculate stroke volume, cardiac output (CO), EOA (cm²); $EOA\equiv Q_{RMS}/\left(51.6\sqrt{\Delta p/\rho }\right)$; where Q_RMS is the root mean square of volumetric flow rate (ml/s), Δp is the mean pressure gradient (mmHg), and ρ is blood density (g/cm³) [4]), closing volume, and paravalvular leak volume. The prosthetic leaflets wall shear stress (WSS) nature was evaluated by calculating oscillatory shear index (OSI; $OSI=0.5\left(1-\left|{\int }_0^T{\overrightarrow{\tau }}_{w}dt\right|/{\int }_0^T\left|{\overrightarrow{\tau }}_w\right|dt\right)$; where ${\overrightarrow{\tau }}_w$ is the WSS vector and T represents cardiac cycle period [31]. Prosthetic leaflets structural performance was evaluated by calculating their corresponding geometric orifice areas (GOA; defined as the anatomical area of the valve orifice) [32] and mechanical stresses. Mechanical stress magnitudes were evaluated by calculating their volume-weighted averaged von Mises stress (${\sigma }_V=({\sum }_i^N{\sigma }_{\mathit{\text{Mises}},i}\cdot V_i)/{\sum }_i^N{V}_i$; where, σ_Mises,i and V_i are the von Mises stress and volume of an element i respectively). The fluid stress level were compared by calculating area-weighted wall shear stress (${\tau }_{\mathit{\text{wall}},\mathit{\text{area}}-\mathit{\text{weighted}}}=\left({\sum }_i^N{\tau }_{\mathit{\text{wall}},i}\cdot A_i\right)/{\sum }_i^N{A}_i$; where τ_wall,i and, A_i are the wall shear stress and area of a cell i on the leaflets surface respectively).

3.5. Mesh sensitivity study

The LHHM native aortic valve and its calcifications were meshed using 4-node tetrahedral element. The TAVR valve stent and leaflets were both meshed using 8-node reduced integration hexahedral elements. The cuff was meshed using a combination of 8-node hexahedral and 4-node reduced integration tetrahedron elements respectively. All these are continuum element; hence they contain only the translation degree of freedom. The native AVs, TAVR valve components (stent, prosthetic leaflets, cuff) element sizes were chosen based on our previous studies of TAVR valve implantation in patient-specific anatomies [11, 27]. The fluent CFD computational domain utilized Eulerian grid where polyhedral cells were used to mesh the domain and hexahedral cells were used at the boundary layers. A polyhedral mesh was utilized during the CFD calculation due to its advantages over tetrahedral mesh. Polyhedral mesh can ensure improved mesh quality, and reduce total cell count in comparisons to tetrahedral mesh. Cell size during CFD simulation was chosen based on our previous patient-specific study, where TAVR valve thrombogenicity was calculated [11]. The FSI simulation’s fluid domain in FlowVision utilizes Cartesian grid with local mesh refinement in the aortic root region where the prosthetic valve is located [31]. An extensive grid independent study was conducted for the FSI simulation fluid domain (Fig. 3), where the EOA was used to calculate the optimal cell size.

Figure 3:

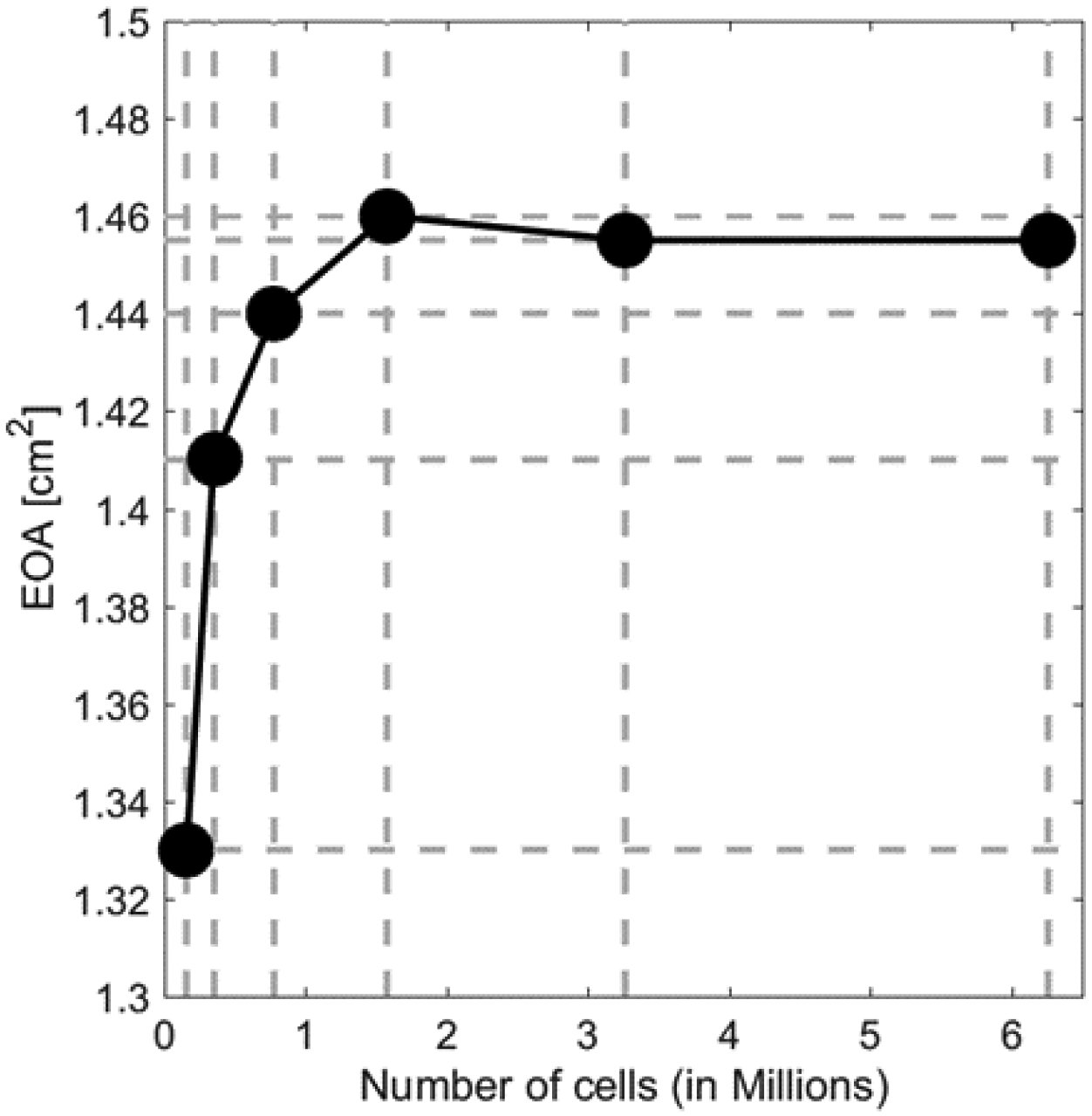
Mesh sensitivity study for FSI simulation demonstrates an optimal total cell number of ~1.6 million.

4: Results

In this section, first, the FE analysis of stent anchorage in LHHM during heart beating is presented. Then, the successfully deployed TAVR valve thrombogenicity is quantified for different implantation depths via incorporating CFD simulations. Lastly, the FSI simulations of deployed TAVR valve are analysed to obtain the optimal implantation depth by comparing the PVL degree, geometric and effective orifice areas, and the prosthetic leaflets mechanical and fluid stress magnitudes.

4.1. Stent optimal implantation depths

The stent’s optimal implantation depths during beating in LHHM were evaluated based on its anchorage with the CAV (Fig. 1 A–L). Figure 1 A–C show a fully crimped stent inside of cone shaped catheter where the stent is positioned more toward the aorta, midway, and ventricle, respectively- before its deployment. Due to the stent’s self-expandable material properties, once the catheter was removed the stent expanded into the aortic root against the disease aortic valve (Fig. 1 D–F). The expanded stent behaviour was observed during LHHM beating for 3 cardiac cycles for these three implantation depths (Fig. 1 G–L). The stent final configurations at the end of complete ventricular contraction and relaxation are shown in Figure 1 G–I and Figure 1 J–L, respectively. The stent configurations right after deployment (Fig 1. D–F) seemed to be similar for the all 3 implantation depths as the stent stayed completely anchored to the CAVs. However, the configurations varied (Fig. 1 G–I) as the beating phase started (>0.75 s; Fig 1 M, N) and the stent migrates toward the aorta when the landing zone was higher – more towards the aorta (Fig. 1 G, J). In addition, for this positioning, once the beating started the stent remained anchored with both the RC and NC leaflets, but did not anchor with the LC leaflet (Fig. 1 G, J).

To evaluate the stent implantation depth further, the stent and the CAV anchoring contact area and force plots over time were computed (Figure 1 M and N). The periodicity behaviour was observed from these two plots over the interval between the 2nd and 3rd cycles. According to the contact area/force plots, from 0 s to 0.2 s interval in which the stent crimping procedure took place, the contact area/force magnitudes are zero since there was no contact between the stent and CAVs. During the positioning phase (Pos; 0.2 s – 0.5 s), the plots show a sharp rise and eventually reach a plateau. This interval depicts the period when the cone-shape catheter containing the crimped stent was in contact with the CAV to open the native valves. The interval from 0.5 s to 0.75 s was the deployment step (abbreviated as Dep in Figure 1 M, N) when the catheter was removed gradually exposing the stent to the CAV. Following the deployment, the largest differences in the contact area/force were observed during beating cycles (0.75 s – 3.75 s), where the ventricular positioning case showed a maximum peak in contact area/force plots. Once the beating starts (after 0.75 s), there was a sharp drop in the contact area/force magnitudes for the case where the stent was deployed more towards the aorta. For this implantation depth, the anchorage contact area/force magnitudes remained the lowest throughout the 3 cardiac beating cycles. The maximum contact area/force magnitudes during beating were 0.59 cm² and 10.26 N, respectively- for the case when stent deployment was more towards the ventricle. Throughout the entire simulation time, the maximum force magnitude was observed right after the full deployment of the stent (Dep; 0.5s – 0.75 s) for all the implantation depths and the values gradually tapered off as the deployed stent becomes stable during heart beating.

4.2. Thrombogenic footprint of the device

DPM platelet representing platelets (Fig. 2A) were injected above the TAVR valve leaflets (Fig. 2B) and the platelets motion for midway (Fig. 2C) and ventricular (Fig. 2E) configurations were determined by the transient flow patterns. The trajectories (Fig. 2 D, F) of the platelets that experience SA (stress accumulation) magnitudes more than 3.5 Pa·s (threshold for platelet activation [29]) are shown for the two configurations. For the midway case (Fig. 2 C, D), the total number of platelets transported with the flow through all the three PVL gaps exhibit similar patterns. However, for the ventricular configuration (Fig. 2 E, F), the number of platelets transported within flow seems to be higher through the PVL gap that resides between RC and LC leaflets suggesting a larger PVL gap.

Statistical distributions of platelet SAs from their Lagrangian trajectories of two TAVR configurations are represented in Figure 2G. For the ventricular positioning, the main mode of the curve (blue) shifted toward the right as compared to the midway positioning SA PDF curve (green). This was apparent from the calculated median SAs 0.328 Pa·s vs 0.56 Pa·s for the midway and the ventricular positioning, respectively (marked as green and blue vertical dashes in Figure 2G). Importantly, zooming in to the SA tail region of the PDFs (detailed view in the inset of Fig. 2G) indicates that the midway positioning platelets experienced overall lower SA magnitudes and ventricular positioning platelets were subjected to overall higher SA. 10.16% and 15.49% of the total DPM platelets seeded in the midway and ventricular positioning, respectively, experienced SAs values exceeding the 3.5 Pa·s threshold for platelet activation (black dashed line in Figure 2G) [30].

4.3. FSI simulation to evaluate TAVR valve hemodynamics

FSI analysis for each successful TAVR implantations were further utilized to study the effect of implantation depths on their corresponding hemodynamic performances. Specifically, differences in flow rates, leaflets geometric and effective orifice area, and lastly the leaflets mechanical and flow stresses magnitudes were compared to determine the optimal valve landing zone. Following the grid independence study (Fig. 3), a total cell count of 1.6 million was utilized for the FSI analysis and all the results presented below were calculated using this total number of cells.

Hemodynamic comparisons:

Figure 4 depicts the flow through the TAVR valves for the midway (Fig. 4 A–D) and ventricular (Fig. 4 E–H) positions throughout the cardiac cycle. Each panel represents the fluid flow streamlines with aortic view of the prosthetic leaflets opening and their time stamp on the cardiac cycle flow rate waveform. Streamlines presented in Figure 4 are coloured by the velocity magnitudes and the colour scale of the velocity was chosen to emphasize the locations of high and low velocity magnitudes. The two post-deployment TAVR valve hemodynamic parameters look similar during systole, however backflow during the diastolic phase accentuated their differences. During peak systole (Fig. 4 B, F), the velocity streamlines show similar flow patterns for the two TAVR valve configurations, where the streamline fields are parallel to the LVOT and the TAVR valve until the flow jet impinged on the aortic arch. Upon jet impingement on the arch, a helical spiral flow pattern in the aortic arch region was observed and the pattern continues up to the outlet region of the ascending aorta. The two hemodynamic configurations during diastole are shown in panels C–D and G–H, where the streamlines with higher velocity magnitudes were observed through the paravalvular gaps. Panels C and G represent the flow right after the valves closure, where the flow had not completely changed direction yet, hence the velocity magnitudes through these PVL gaps were not as high as those during peak diastole (Fig. 4 D, H), where streamlines showed completely backward flow direction. Interestingly, the streamlines through the PVL gap seemed to merge right below the native NC leaflet and this behaviour was observed for both TAVR positions. The change of flow direction occurred when the transvalvular pressure gradient changed from positive to negative and forward and backward flow caused the prosthetic valve to open and close. Lastly, when the prosthetic valves were in their fully closed configuration, there were comparatively more vortices formed in the LVOT region than in the arch region (Fig. 4 C, D, G, H).

Figure 4:

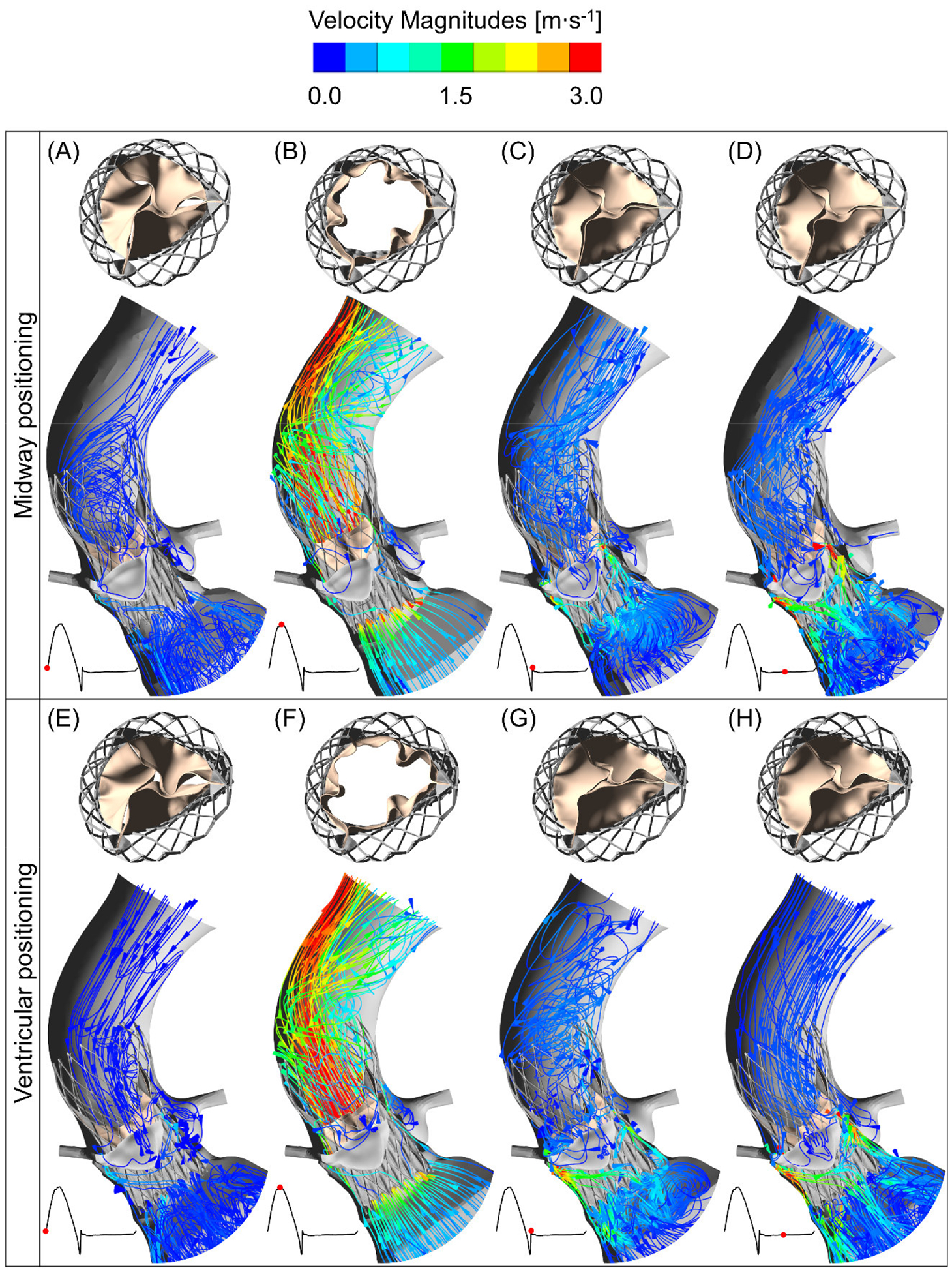
The midway and ventricular positioning flow velocity streamlines at four different instances during cardiac cycle. The top row (A–D) shows the deployed TAVR valve hemodynamics in the midway positioning during a cardiac cycle and top view of the prosthetic leaflet kinematics at their corresponding instances. The TAVR valve ventricular positioning hemodynamics and the top view of the valve opening are shown in the bottom row (E–H).

The flow rates for each case were compared using the same BCs for both TAVR configuration throughout the cardiac cycle. Similar maximum velocity and flowrate magnitudes were observed (35.39 l/min vs 33.17 l/min) for both cases. Highest average velocity during peak systole were 2.88 m/s and 2.87 m/s for the midway and ventricular cases respectively. The flow rates during the third cardiac cycles are plotted over time in Fig. 5A. The flow rate obtained from the ventricular position seemed to reach peak flow rate slightly sooner than the midway case. Since the systolic flowrate for the ventricular case was higher, the stroke volume was higher for this case too (104.14 vs 97.14 ml; Table 1). Calculated EOAs were 1.28 cm² and 1.55 cm² for midway and ventricular positionings correspondingly, which are comparable to a clinical study [33], where the obtained EOA is from the same TAVR valve. According to this post-TAVR clinical study of 71 patients who received 26 mm Evlout R, the EOA was of 1.69 ± 0.4 cm² (mean ± standard deviation) after 30 days. The negative flowrate during diastole was higher in the midway case, resulting from a higher closing volume and PVL degree. The closing volumes were 14.28 ml and 6.87 ml for the midway and ventricular cases, respectively. Total PVL volume was higher for the midway positioning (41.61 ml vs 34.59 ml). Combination of PVL along with closing volume caused a higher total regurgitation [34] for the midway case, hence the lower CO during TAVR deployment in the midway case (2.90 l/min) than in the ventricular case (4.4 l/min).

Figure 5:

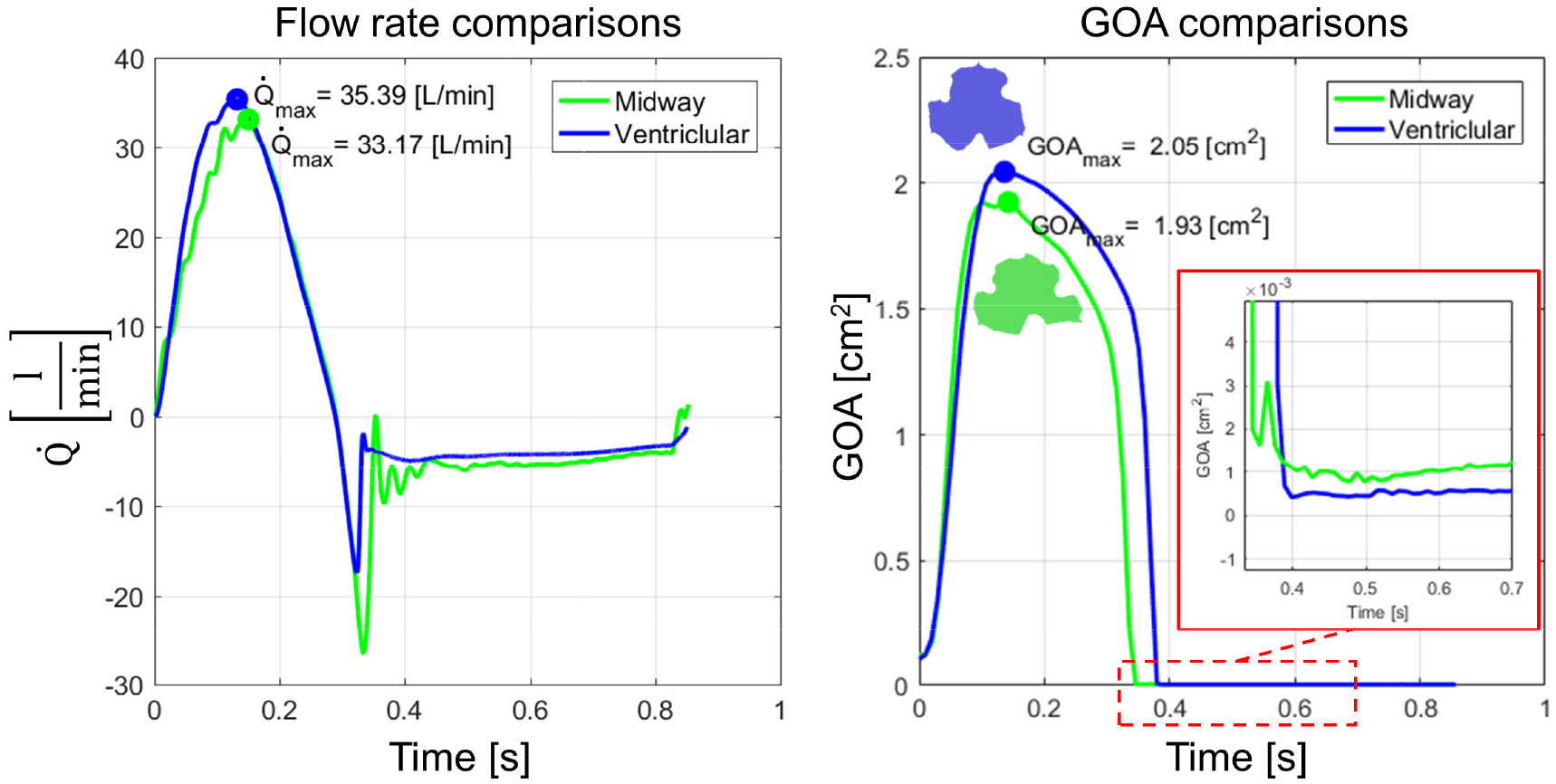
Flow rate and geometric orifice area over a cardiac cycle for two successful TAVR valve implantation. ${\dot{\mathit{\text{Q}}}}_{\mathit{\text{max}}}$ (left) and GOA_max (right) were observed when the valve was expanded more toward the ventricle.

Table 1:

Clinical parameter to further evaluate the successfully implanted TAVR valve hemodynamic performances

Parameters╲Implantation depth	Midway positioning	Ventricular positioning
Stroke vol. [ml]	97.14	104.14
CO [l/min]	2.90	4.40
EOA [cm2]	1.28	1.55
Closing Vol. [ml]	14.28	6.87
PVL [ml]	41.61	34.59

Leaflets kinematics comparisons:

Kinematics of two configurations were compared by plotting their GOAs over time (Fig. 5B). The two GOA curves over time (Fig. 5B) of the two cases show that the valve opening was higher when TAVR was expanded more toward the ventricle. Maximum GOA values for midway and ventricular positionings were 1.93 cm² and 2.05 cm², respectively. Cross section of each valve opening area shows folding in the middle of each prosthetic leaflets resulting in noncircular opening of the valve. In addition, from the cross sectional opening of the valve (Fig. 5, right), it is visible that the prosthetic leaflet located in NC region within a TAVR positioning was buckled more than the other two. Interestingly, looking closely at the GOA during diastole (Fig. 5, right; detailed view) revealed that the GOA for the midway implantation depth shows a wider gap during the valve’s complete closure than the ventricular case.

Mechanical and flow stress comparison:

Calculated stress (WSS and von Mises stress) magnitudes from both fluid and structural domains were utilized to delineate potential differences between two TAVR configurations, which may expose the leaflets to higher stresses. Mechanical stress (σ_V) was compared between the two valves and stress magnitudes over time for three prosthetic leaflets from each case are plotted in Figure 6A. Throughout the cardiac cycle, the leaflets experienced higher stress levels during diastole than during systole. For both cases, prosthetic leaflets located in the RC region experienced higher averaged stresses during the diastole and systole phases. The maximum stress observed in RC leaflets for the midway and ventricular cases were 0.41 MPa and 0.47 MPa, respectively. This maximum stress in the leaflets for both cases was observed during the closing phase of the leaflets. The von Mises stress distribution of the prosthetic leaflets of each TAVR case that experienced the highest stresses over time is shown in Figure 6 B and C for the midway and the ventricular cases, respectively. Both contour plots depict the leaflets in their corresponding full closed configurations. For both cases the maximum stress magnitudes were observed near the middle of each leaflet, in the region where it is attached to the stent and the cuff (Figure 6 B and C). In addition, the leaflets belly and the portion of the intraventricular end also experience high stress levels.

Figure 6:

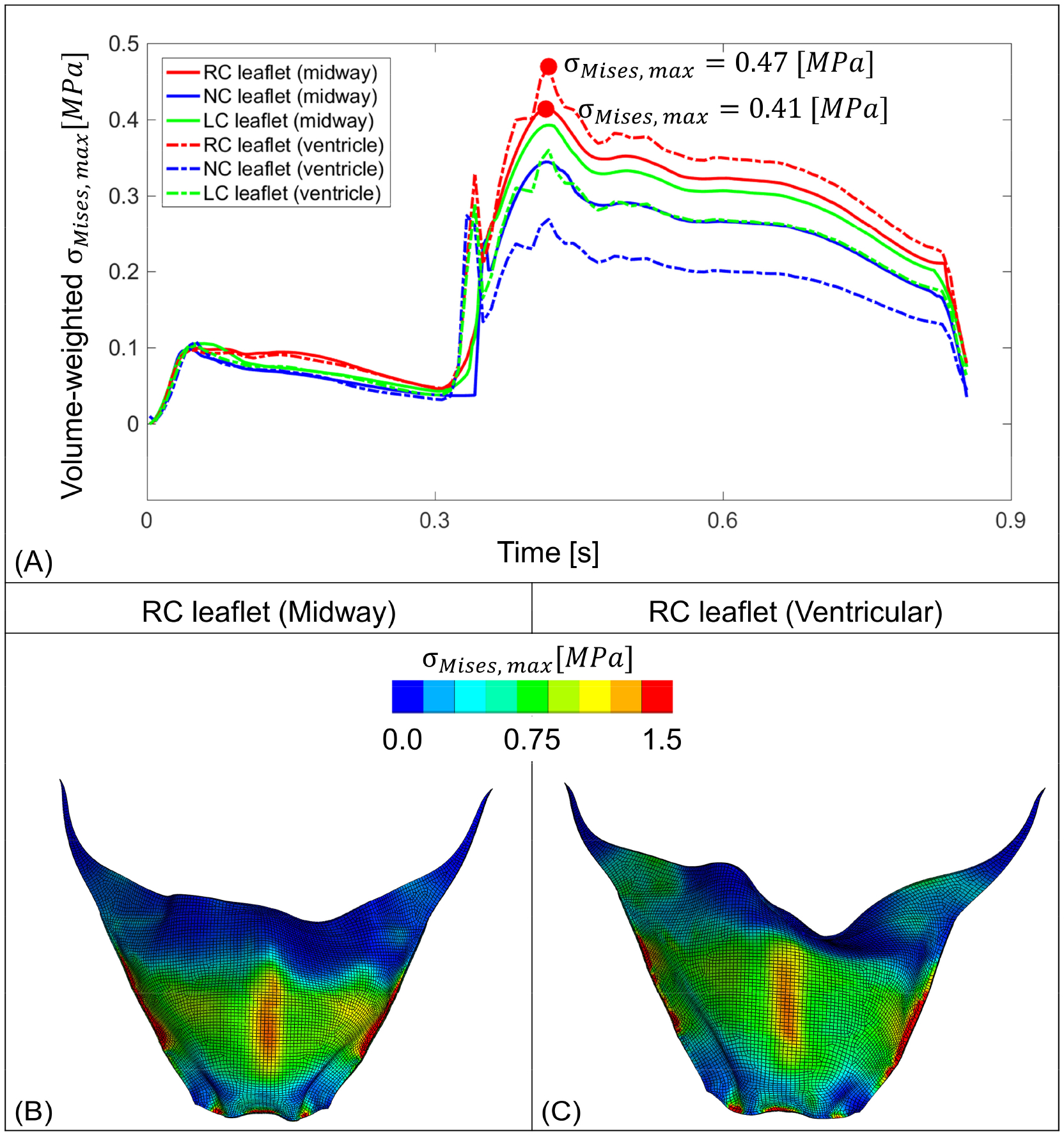
Mechanical stress observed on the prosthetic leaflets. (A) represents volume-weighted stress on the three TAVR valve leaflets throughout a cardiac cycle, where the dot represents the maximum stress value. B and C depict instances where leaflet from each case experienced the highest volume-weighted von Mises stress (red dots on panel A) calculated throughout the cardiac cycle.

Comparison of the area-weighted wall shear stress (τ_wall) for all three TAVR valve leaflets for both cases over time is shown in Figure 7A. The maximum fluid stress magnitudes were observed during systolic phase and the prosthetic leaflets that located at the RC region experienced the highest amount of stress over a cardiac cycle. Leaflets surface contour plots that experienced the highest shear stress for both cases are shown for ventricularis (Fig. 7B, C). The ventricularis was chosen, as during systole it is subjected to unidirectional flow and more prone to experience higher WSS values than those of the recirculating flow on the aortic side [4]. According to the WSS contour plots on the leaflet surface, the belly region toward the bottom of the RC leaflets in midway positioning experienced the highest stress levels. The TAVR valve RC leaflets for the ventricular positioning experiences higher WSS on the left side of the leaflets in addition to bottom of the belly region.

Figure 7:

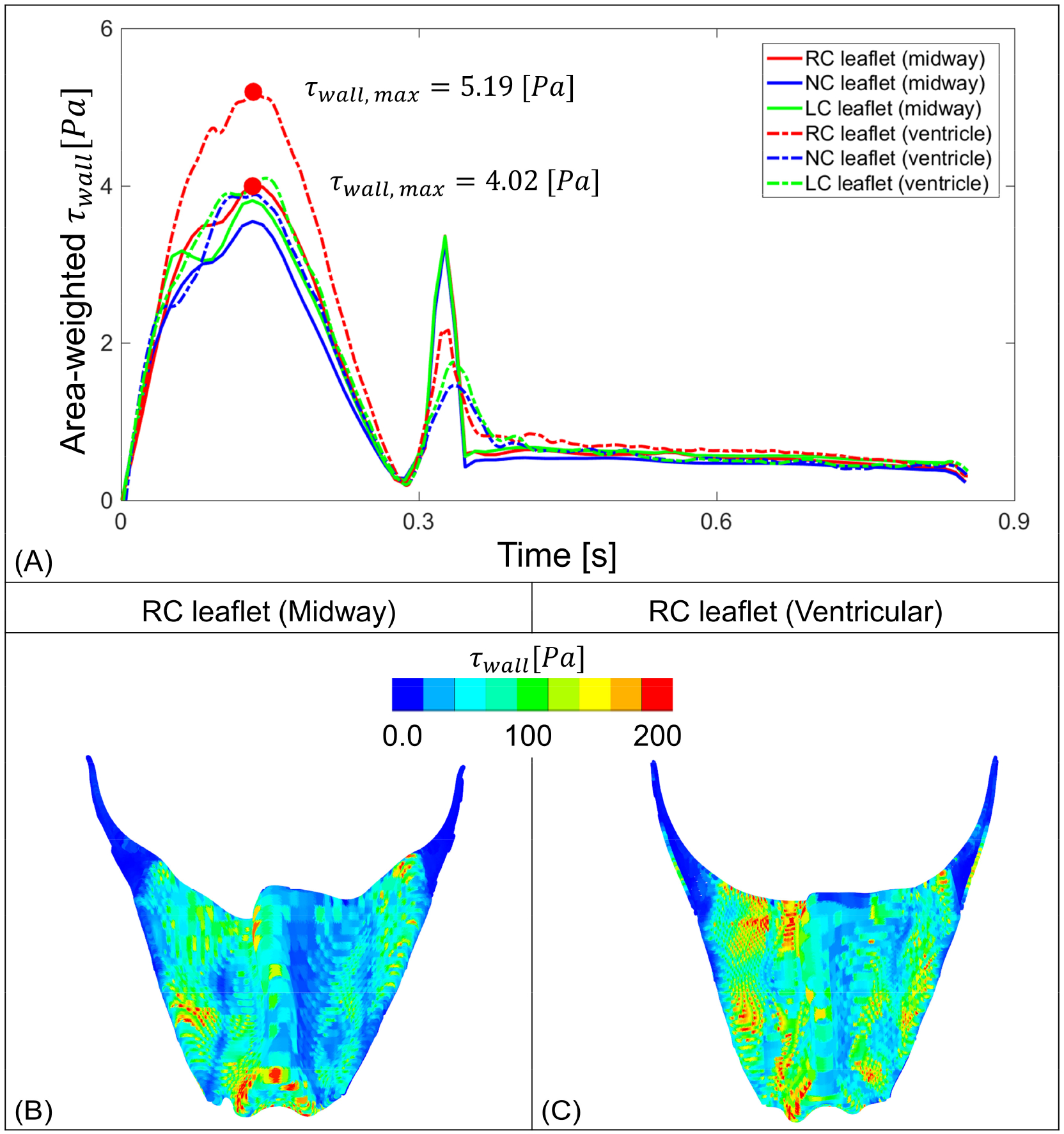
Flow stress observed on the prosthetic leaflets. (A) represent area-weighted stress on the three TAVR valve leaflets throughout a cardiac cycle, where the dot represents the maximum stress value over time. B and C depict instances where leaflet from each case experienced the maximum area-weighted wall stress (red dots on panel A) calculated throughout the cardiac cycle.

The OSI dimensionless parameter was calculated from WSS for all three prosthetic leaflets for both cases throughout the cardiac cycle. The TAVR valve midway positioning OSI for RC, NC, and LC leaflets were 0.0074, 0.1860, and 0.0715, respectively, and the OSI for TAVR valve deployed in the ventricular positioning were 0.0618, 0.0855 and 0.0337 for RC, NC, and LC leaflets, respectively. For both cases, the NC leaflets seemed to have higher OSI. While comparing the six prosthetic leaflets for the two cases, both highest and lowest OSI were observed in the midway case on NC and RC leaflets respectively.

5: Discussion

5.1. TAVR stent deployment during heart beat

Major findings from the FE analysis of TAVR valve implantation simulation in the LHHM showed the importance of considering beating while evaluating a TAVR device performance. Previous FE analyses that simulated the self-expandable TAVR stent and native tissue interaction ran the simulation until the deployment phase (Fig. 1 D, F; 0.5 s – 0.75s) [11, 13–16, 20, 21]. If the simulation is run until this interval, a conclusion is typically drawn that all the deployment configurations were anchored properly to the CAV and the aortic root. Differences of the actual dynamic anchorage became apparent once the beating starts and a drop of the anchorage contact area/force magnitude was observed. Hence, it is important to study the stent-tissue interaction in a dynamic manner by utilizing a beating heart model such as the Simulia LHHM used in this study.

The maximum contact force was observed right after the stent deployment (Fig 1 N; Dep step; 0.5 s – 0.75 s) owing to the impact of the completely crimped stent being released right after the catheter was removed (for this self-deployed TAVR valve). To calculate the stent’s impact on the surrounding tissue it was necessary to completely crimp the stent before its deployment simulation and a similar conclusion was made by Kandail et al [12]. It should be noted that Kandail et al focused on the valve hemodynamics rather than performing a structural analysis. In addition, it is necessary to remove the catheter gradually, otherwise the impact from the stent will be higher and a sharper rise artefact in the contact area/force may be observed. This specific deployment interval is chosen based on our previous patient-specific study where a TAVR stent was deployed [11].

The contact area and force magnitudes plots (Fig. 1 M and N) showed sudden rise and fall of their magnitudes at the interval between 2 s to 2.25 s during the second simulated cycle. Due to the periodic nature of the plots, this pattern also repeated during the third cycle at the interval from 3 s to 3.25 s. These sudden rise and fall could be attributed to the anatomical change after the end of the systolic phase, when the ventricle contracts rapidly, which necessarily contracts the aortic annulus and root. This rapid contraction caused instability in the stent anchorage in the aortic root, hence the change observed in the contact area/force plot. Moreover, these cyclic forces that were applied on the stent, and were ignored in previous studies, can also be related to stent fatigue. Therefore, these calculated forces may be used for future design optimization of TAVR devices.

Under the assumption that the larger anchorage area will ensure better anchorage of the TAVR stent with less likely migration, it can be concluded that the stent implanted in an aft position more toward the ventricular side was the optimal implantation depth for the specific anatomic geometry. In contrast, the stent’s aortic positioning should not be recommended for this anatomy as with this implantation depth the stent migrated toward the aorta and twisted toward the anterior direction once the heart beating starts. This was caused by the stent anchoring with the native RC and NC leaflets and not with the LC leaflets. Not anchoring with LC leaflets forced the stent’s intraventricular end to freely expand more toward the sinotubular junction without any constriction from the LC leaflets. As a result, the distal portion move towards the anterior part of the ascending aorta in order to compensate for this extra proximal expansion of the stent.

5.2. Thrombogenic potential of deployed valve

CFD simulations coupled with DPM were used to quantify and characterize the thrombogenic footprint of two valve configurations. This in silico approach successfully showed that platelets flowing through one configuration are exposed to a riskier stress accumulation range that may lead to their activation. In order to improve thromboresistance of a specific TAVR valve configuration (midway vs ventricular), it is desired to keep the SA range towards to main mode of the PDF (leftward shift of the curve)– meaning fewer platelet trajectories are being exposed to the riskier SA range at the far right PDF range where platelets are likely to be activated. Thrombogenicity comparison between the two configurations indicated that platelets in the ventricular configuration experienced higher overall stress magnitudes than in the midway configuration. While very low percentage platelet population experience a bit higher SA values in the riskier tail region of the distribution in most of the tail, the ventricular position had higher SA values and the main mode of the midway position was significant shifted to the left compared to ventricular indicating that overall the midway position offers lower thrombogenic risk. This appears to result from the smaller PVL gap in midway positioning in comparison to the ventricular.

In addition, during diastole the pressure gradient is higher and pathological backflow through a small gap that elevates the shear stresses. Platelets exposure to elevated shear stresses as a result of this strong regurgitant flow through the gap is a key factor of higher thrombogenicity of a specific device configuration. Although newer generation TAVR devices are designed with reduced PVL degree in mind, the PVL gap along with the increased thrombogenicity through the gaps are still a major drawback that hampers the prospects of TAVR becoming the standard of care to treat CAV disease.

Two-phase CFD simulation coupled with DPM were employed to predict each platelets stress history along their individual trajectories through the PVL gap. Differences between the SAs (Fig. 2G) and their corresponding thrombogenic footprints (the PDF) arise from the two different deployment configurations of the TAVR valve. These configurations thrombogenic footprints can inform clinicians how to improve the procedural planning in order to achieve better clinical outcomes. The numerical techniques used here could also be to optimize a TAVR valve design.

5.3. FSI analysis to compare valve hemodynamics

As shown in the previous section, comparison of the FSI results also demonstrated the PVL in the midway and ventricular positions. TAVR valve hemodynamic comparisons between the two positions showed PVL degree of 34.59 ml and 41.61 ml correspondingly, with both magnitudes in the range of severe paravalvular regurgitation [35]. In this case, a post-balloon dilation is recommended to reduce the paravalvular gap. It should be noted though that according to a clinical study, balloon post-dilation following a TAVR procedure could increase the risk of stroke [36].

Comparing two TAVR implantation depths, higher GOA for the ventricular position was observed. This could be attributed to the less constrained leaflets in this implantation depth. The GOA cross-section clearly indicates that both prosthetic leaflets showed some degree of folding (buckling) in their belly region. This was observed during both the systole and diastole phases. Comparison between the three prosthetic leaflets within a specific TAVR configuration, the leaflets kinematics showed that the RC leaflets for each TAVR case is buckled to a lesser extent than the other two. This could be explained by the different structural stress levels that were observed on the leaflets combined with the pressure loads transferred from the fluid domain onto the RC leaflets that were higher–causing less buckling. In addition, the prosthetic leaflets buckling caused a pin-wheeling effect (Fig. 4), which is an indicator for compromised durability of the prosthetic leaflets [37]. It should be noted that self-expandable TAVR valve leaflets opening was not circular due to the valve’s eccentric opening and this information is usually ignored when the valve performances are being studied and an idealized (circular) configuration is assumed and widely practiced [4, 37, 38].

A more detailed look at the GOA magnitudes during diastole showed that the midway position caused a larger gap area between the leaflets (Fig. 5, right). Such increased gap could enhance the central regurgitation and result in higher closing volume for a TAVR valve implantation in the midway positioning (14.28 ml vs 6.87 ml; table 1). In addition, this flow through the small gap during the closure could generate a jet with a very high velocity during diastole. High central regurgitant flow combined with the PVL gap could cause instability in the flow. Hence during closing a higher negative flow rate and oscillation is observed (Figure 5, left; green curve) in the midway case.

The OSI are calculated in the range of 0 to 0.5 where 0 represents a completely forward flow and 0.5 a case of completely oscillatory flow [31, 39, 40]. High magnitudes of OSI indicate a region with more stagnant flow [40, 41]. Previous study showed that neo sinus created by TAVR valve with flow stagnation could cause thrombosis [42]. Recirculation and flow stagnation regions contribute to thrombus formation by activating platelet as the contact time between blood elements increase [43].

TAVR valve leaflets structural stress magnitudes could provide insight regarding their potential tissue delamination and creeping – providing indications of the durability of each valve device. Mechanical stress comparison (Fig. 6 A) revealed that the prosthetic leaflets in the ventricular configuration (RC, NC, and LC; presented by dashed line) experienced such higher stresses. In addition, a comparison among those three prosthetic leaflets for each case indicated that the RC leaflets experienced the highest averaged stress. According to the surface stress distribution contour plot (Fig. 6 B and C) the top region of the leaflets experienced lower stresses, as these were the coaptation region of the leaflets. Due to coaptation, the leaflets were constrained from extending further and since the belly region was free to stretch but the attachment region in the middle was fixed, higher stress distributions were found. This information could be utilized for designing a TAVR valve. Specifically, an asymmetric prosthetic leaflets design could be adapted as the leaflets that experiences the highest stress could compromised the valve durability. Hence, optimization techniques should be adapted and such techniques were previously proposed by our group [44] and Pott et al [45].

The flow stresses were consistent with the mechanical stresses distribution in terms of the how the stress distribution was influenced by their location on the leaflets. According to the Figure 7, TAVR valve leaflets located in the RC region experienced the highest flow stresses for both implantation depths. The TAVR valve leaflets of the ventricular position experienced the highest averaged WSS over time. This was also confirmed by the WSS contours plot (Figure 7 C), where the RC leaflets in the ventricular position have larger region of high WSS magnitudes. Given that these results are based on FSI analysis, it also enables demonstrating how the WSS is corelated not only with the hemodynamics but also with the leaflet kinematics. This is demonstrated, for example, by the local leaflets buckling where the highest WSS level was observed in the belly of the prosthetic leaflets- likely the result of a rapid recirculation zone formed in the belly region that got enlarged by the buckling. It should be noted that usually a lower GOA (more constrained TAVR valve) results in higher WSS on the leaflets and a lower GOA from midway positioning would have been expected to generate a higher WSS on the leaflet. However, this can be attributed to the higher local velocity gradient observed in the aortic root of the ventricular position (Fig 4F) as compared to the velocity magnitude observed in the aortic root of the midway position (Fig. 4B).

5.4. Limitations

A comprehensive series of numerical studies to predict potential TAVR complications were presented herein. Given the complexity of TAVR structural and hemodynamical phenomena, even the most advanced numerical approaches still entail certain limitations. In the FE analysis studies, most commonly occurring calcification patterns were utilized. Simulation with patient-specific calcification (calcium volume, deposits, and distribution) could provide better or worse anchorage for the stent [11, 27]. During FE analysis, the pre-TAVR balloon valvuloplasty was replaced with a more-idealized cone-shaped cylindrical catheter that opened the calcified leaflets. This simplification was done to reduce the computational complexity and computational cost. Also, the scope of the analysis is to investigate the differences in performances due to different delivery positions, being the pre-dilation a constant parameter across the modeled deployment configurations. In addition, LHHM pacing should be incorporated during the stent positioning and deployment steps as rapid pacing is common during a TAVR procedure. The CFD for the thrombogenicity quantification was calculated for the TAVR components assumed stationary to save computational costs. This assumption is reasonable given that during the diastolic phase that contributes the most to PVL and thrombogenicity, the leaflets are fully closed. Due to this reason, the FSI and CFD models were not compared. In the CFD simulation, a complete valve closure was assumed so that the thrombogenicity was calculated only during PVL flow whereas in FSI model, there were central regurgitation due to presence of small gaps in coaptation region. During thrombogenic potential calculation (CFD simulation), the flow was assumed to be laminar. This assumption was based on our previous study [11], where a rigorous comparison between flow assuming laminar and turbulent flow was conducted, and no significant difference were found. Nevertheless, we are currently incorporating DPM platelet seeding with an FSI simulation of the full cardiac cycle to calculate the thrombogenicity more accurately. The FSI simulation can be further improved by modeling deformable aortic arch, root, and LVOT. The prosthetic leaflets pre-stress due to crimping should be take into consideration during FSI simulation for more accurate mechanical stress calculation. However, it should be noted that the FSI simulations were run for several cardiac cycles and the periodicity was observed prior to the stress analysis. According to Kandail et al [12]¸ multiple cardiac cycles confirm stress to be transferred from cycle to cycle making the residual stress from the initial stage negligible. Lastly, although the EOAs calculated from the FSI simulation (1.28 cm² and 1.55 cm²) were comparable to clinical measurements of the same size TAVR valve (1.69 ± 0.4 cm²) [33], a mean gradient of 31 mmHg was applied as a boundary conditions in the FSI simulation, while in the clinical study a mean gradient of 7.53 ± 2.65 mmHg was observed. It should be noted though that the patient-specific anatomy employed by us in the simulation was not a part of that clinical study. The patient-specific anatomy and unique calcification patterns employed by us are likely the reason for the discrepancy in the mean gradient, additionally because of the different level of the deployed valve eccentricity. Additionally, the clinical study mentioned above [33] utilized transthoracic echocardiographic measurement to calculate the flow, with the mean gradient and EOA calculated using an oversimplified one-dimensional Bernoulli equation, which would likely produce erroneous results. While the flow calculation in our FSI simulation is dependent on the applied pressure gradient (boundary condition), it is based on a three-dimensional Navier-Stokes equations that more accurately represent the flow field.

6: Conclusions

We presented a first of its kind FE analysis of TAVR stent deployment during heart beating using the Simulia Living Heart Human Model (LHHM). This demonstrated that simulating the heart contraction during TAVR deployment is necessary for more accurately evaluating the valve migration. Following the FE analysis, the two successful deployment cases (midway and ventricular) were further studied by implementing two-phase flow CFD and FSI simulations. According to the calculated thrombogenic potential, it was concluded that deploying the TAVR device in the midway position was the optimal implantation approach for this patient specific anatomy. This is further supported by the results of the prosthetic leaflets structural and flow stress magnitudes that were also compared using FSI approach. Certain simplifications were assumed during the simulation such as generic calcification pattern instead of patient-specific one, laminar flow during the CFD simulation, and rigid aortic wall during the FSI simulation. Our future studies with less simplifications will be helpful to achieve better translational clinical value. The results of our extensive quantitative analysis provide better understanding of the complications, and offers a methodology that facilitates minimizing their impact by optimizing the device design and enhance procedural planning for achieving better clinical outcomes.