Estimating brain connectivity with diffusion-weighted MRI: Promise and peril

Abstract

Diffusion-weighted magnetic resonance imaging (dMRI) is a popular tool for noninvasively assessing properties of white matter in the brain. Among other uses, dMRI data can be used to produce estimates of anatomical connectivity on the basis of tractography. However, direct comparisons of anatomical connectivity as estimated through invasive neural tract-tracing experiments and dMRI-derived connectivity have shown only a moderate relationship in nonhuman primate (particularly macaque) studies. Tractography is plagued by known problems associated with resolution, crossing fibers, and curving fibers, among others. These problems lead to deficits in both sensitivity and specificity, which trade off with each other in multiple datasets. Although not yet examined quantitatively, there is reason to believe that some large white matter bundles, those with more topographic organization, may produce more accurate results than others. Moving forward, sophisticated analytical approaches and anatomical constraints may improve tractography accuracy. However, broadly speaking, dMRI-derived estimates of brain connectivity should be approached with caution.

Introduction

Understanding brain connectivity (its “wiring diagram”) is essential for the study and treatment of mental illness. Noninvasive neuroimaging techniques that allow for estimates of connectivity in humans are popular tools for biological psychiatrists. Among these techniques is diffusion magnetic resonance imaging (dMRI), which takes advantage of the differential diffusion of water molecules across tissue types. However, while dMRI can provide essential information about white matter composition, tractography methods for estimating connectivity are prone to error. Here, we review the attempts to validate dMRI-derived connectivity, and provide possible future directions for improvement. Our goal is to communicate the results and meaning of validation studies from the neuroimaging methods community to biological psychiatrists performing dMRI tractography.

How is dMRI tractography implemented?

dMRI is a noninvasive neuroimaging technique that measures the restriction of diffusion of water molecules in tissue(1). Because dMRI provides information about white matter orientation at each voxel, tractography can be used to delineate white matter tracts and track groups of axons through the brain(2). In this review, we are particularly interested in how dMRI data is used to model neuronal projections and estimate structural connectivity, meaning whether and to what extent brain regions connect to one another.

While not the focus of this review, dMRI data can produce multiple informative metrics at each voxel, including fractional anisotropy (FA), apparent diffusion coefficient (ADC), axial diffusivity (AD), and radial diffusivity (RD)(2). FA is the degree of diffusion restriction, thought to reflect white matter integrity. Alterations in FA have been observed when comparing healthy controls to various disease states(3,4), as well as in voxels with crossing fibers(5). ADC is a measure of the magnitude of diffusion of water within a tissue, and can be used in monitoring brain infarctions(6). AD and RD are the diffusion rates along the main and transverse diffusion directions, respectively. The benefits and deficiencies of structural connectivity discussed in this review do not apply to these metrics, which have their own validation literatures.

There are several options for estimating the fiber directions present in each voxel, with the choice of model partially dependent upon how data were collected. The early diffusion tensor model allowed for the estimation of a single orientation in each voxel. While this provided very informative results, it was incapable of discriminating complex fiber arrangements(7). Later models, such as high angular resolution diffusion imaging (HARDI), require the acquisition of more diffusion directions and multiple b-values(8,9). HARDI is capable of estimating multiple fiber directions in each voxel(10,11). Data acquired with a HARDI protocol can be analyzed with various models including Q-ball, persistent angular structure MRI, and diffusion orientation transformation(8,9,12). Additional advances in dMRI acquisition include the b-tensor model, which further improves the estimates of fiber orientation(13,14).

There are two main ways to analyze dMRI tractography(15). In its simplest form, deterministic tractography assumes that the fiber orientation in each voxel is a single, known vector. The tract is generated by selecting a starting location and continuing through adjacent voxels before terminating when it reaches an area where the linear tract ceases to exist. This technique will produce identical results across multiple runs, as the underlying assumptions do not change. Deterministic tractography has the advantage of being computationally simple. However, it is limited in resolving complex fiber patterns, particularly when performed on standard diffusion tensor modeled data. It also does not convey information regarding the strength of the connection(16). Probabilistic tractography utilizes probability distributions based on the uncertainty of the diffusion direction through each voxel. Probabilistic models are run thousands of times, and each run produces slightly different outputs(17). This methodology is less likely to exclude voxels with low FA (which could be caused by crossing, kissing or curving fibers). One downside is that calculations can be computationally intensive. The number of streamlines that pass through each voxel has been used as a surrogate for connection strength, though this is an overly simplistic interpretation that can be influenced by anatomically incorrect reconstructions or complex fiber arrangements(18). Both probabilistic and deterministic tractography can benefit from utilizing models other than the diffusion tensor. One such approach is to model the data using spherical deconvolution, which, unlike the diffusion tensor model, can assign multiple fiber directions to each voxel(19). A benefit of the spherical deconvolution model is that it allows deterministic tractography models to resolve crossing fibers and enhances the accuracy of probabilistic tractography(20).

In addition to identifying the locations and fiber orientations of large white matter bundles (Figure 1A), dMRI tractography can be used to estimate connectivity between gray matter regions (Figure 1B). A region can be used as a seed, then the tracts are followed until structural connectivity with other regions is established. Structural connectivity is commonly treated as being representative of anatomical connectivity. For example, dMRI has been used to examine connectivity of the human striatum(21,22), subthalamic nucleus(23), frontal cortex(24), and cerebellum(25), among other brain regions. It has been used to constrain and/or interrogate the anatomy of functional connectivity(26,27,28,29). Finally, structural connectivity strength has been related to individual differences in cognition and behavior, including in psychiatric disorders(30,31,32,33,34). Clearly, it is important to know exactly how structural connectivity relates to underlying anatomy.

Figure 1:

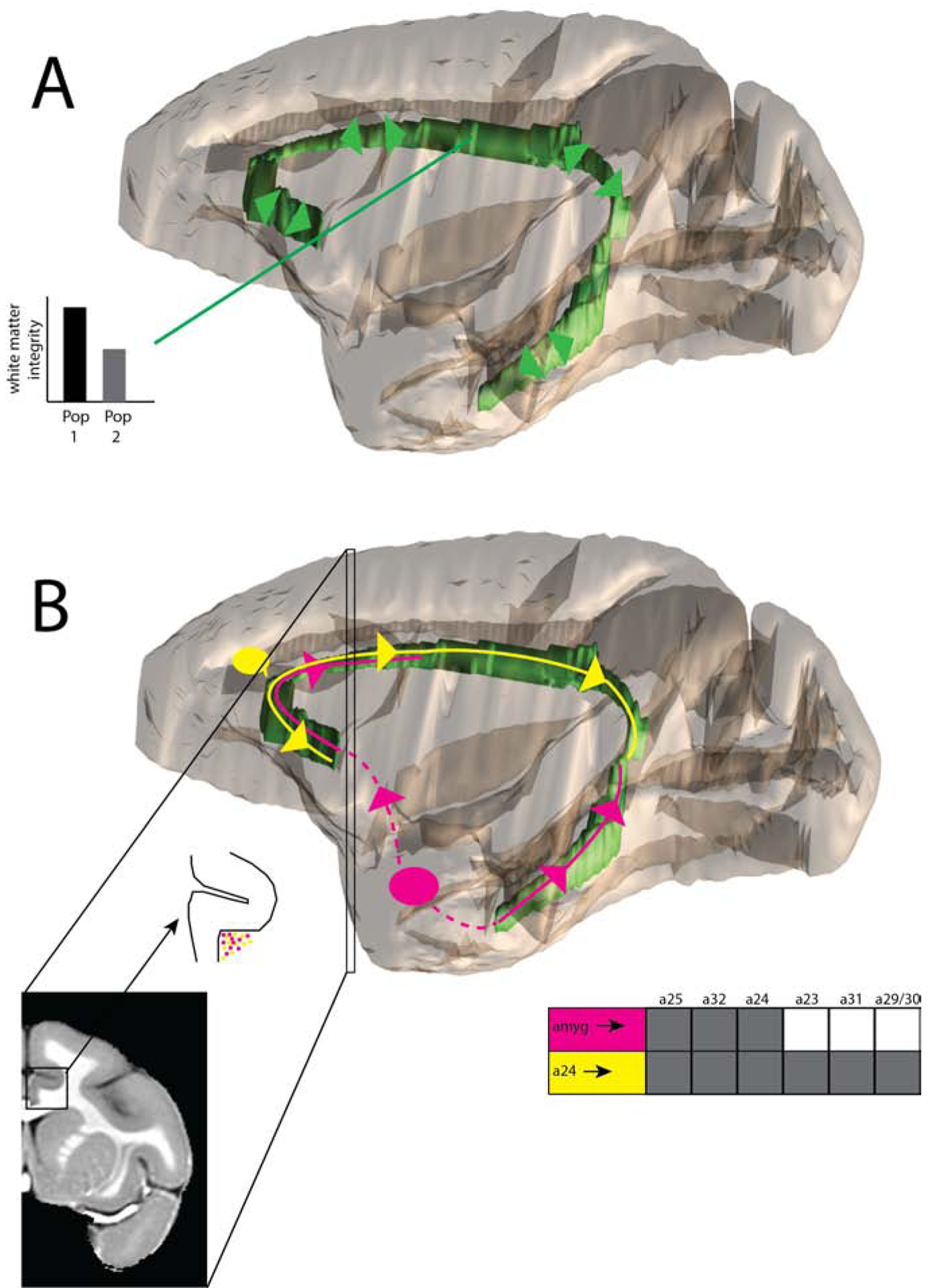
Cartoon illustration of dMRI applications in rhesus macaques, with the cingulum bundle used as an example. A. DMRI can outline the location of a major bundle (cingulum bundle localized in green) as well as the bundle’s major directions (green arrows). This can be used to generate regions-of-interest within the bundle. Metrics, such as fractional anisotropy and apparent diffusion coefficient (discussed in the Introduction), can be compared within these regions-of-interest across populations. B. DMRI is also used to estimate structural connectivity, but this may present challenges. Regions-of-interest are shown in the amygdala (pink) and area 24 (yellow). The true nature of their anterograde projections through the cingulum bundle, as derived from anatomical tract-tracing, are shown as color-matched lines and arrows(88). The amygdala uses the ventral portions of the cingulum bundle (temporal and frontal subgenual), and the rostral portion of the dorsal cingulum bundle. It does not enter the caudal portion of the dorsal cingulum bundle. The resulting anatomical connectivity with anterior cingulate, but not posterior cingulate, is shown as a table, with shaded boxes indicating connectivity(95). By contrast, area 24 uses all of the dorsal cingulum bundle, as well as the frontal subgenual portion of the cingulum bundle. It has anatomical projections to all cingulate regions, as shown by shading in the table(96). It is this anatomical connectivity table that dMRI structural connectivity seeks to re-create, on the basis of streamlines through the white matter. A coronal inset is shown where amygdala and area 24 axons (small colored dots) are both present, and intermixed. A number of challenges are apparent. First, because of overlap with area 24 fibers, it may be challenging to stop amygdala fibers from continuing on to the posterior cingulate cortex. It may also be difficult to correctly identify the points at which fibers from each region join the cingulum bundle. Visualizations created using(97,98).

dMRI faces complex challenges

There are well-established challenges dMRI faces as it attempts to reproduce anatomical connectivity. Perhaps the most obvious is voxel size: an average axon is ~1μm wide, compared to a typical isotropic dMRI voxel of 1.5mm(35). Thus, each voxel can contain millions of axons in various orientations. Another problem with large voxels is partial volume effects, which occur when voxels contain a mixture of tissue types (such as blood vessels and ventricles)(36). Partial volume effects are especially problematic for tracking in the vicinity of ventricles(37), as well as entering the gray matter ribbon.

Voxel sizes cannot currently approach the diameter of a single axon; nevertheless, as spatial resolution improves, we may be able to capture smaller groups of axons. However, it is still necessary to ensure high signal-to-noise ratios (SNR). Unfortunately, dMRI has intrinsically low SNR (relative to other types of MRI). As the b-value (strength of the diffusion gradient applied) increases, the SNR decreases. Moreover, the SNR is proportional to the voxel size at fixed field strength. Because image acquisition is typically performed with isotropic voxels, small changes in the acquisition matrix lead to dramatic reduction in SNR. However, by combining diffusion acquisitions with different resolutions, it is possible to overcome the reduction in SNR(40).

As noted, there are a very large number of axons present in each of these large dMRI voxels. Within the brain, each individual axon can be referred to as a single fiber. When these fibers join together and travel together they form fiber bundles (or tracts). [A fiber bundle/tract, somewhat confusingly, can be either a group of axons with similar geometry originating in many brain regions (e.g., cingulum bundle, corpus callosum), or a subset of labeled axons originating in a particular brain region (e.g., a bundle starting in the prefrontal cortex that crosses the corpus callosum, joins the superior longitudinal fasciculus, and terminates within the parietal lobe)]. While dMRI investigates the microscopic properties of the tissue, tractography is performed at the voxel level, modeling fiber bundles. Current processing pipelines are generally very good at determining the primary diffusion direction of large fiber bundles; however, smaller bundles in proximity to other bundles often have complex patterns(41). Crossing fibers are fibers that cross each other; kissing fibers run in close proximity, but do not cross; bending fibers have a slight curvature. Each of these configurations causes difficulties in analysis determined by how the fiber directions are fit to a model. For example, for a simple diffusion tensor fit, parallel, fanning, bending and crossing fibers are indistinguishable. However, if a fiber orientation density function (fODF) fit is used instead, these fibers start to diverge in their appearance in the modeled data and can be tracked with various algorithms(19). Nevertheless, it is important to remember that fiber tracking recreating the major orientations and locations of most of the white matter bundles is highly accurate and reproducible. Inaccurate tractography often occurs in smaller, deeper bundles and at gray matter/white matter junctions. Hence, problems likely apply more to gray-matter-to-gray-matter tracking (which has to travel through these junctions) than to tractography restricted to white matter(38,39).

Anatomical methods for validation

The methods used for validation of diffusion tractography are mostly drawn from traditional neuroanatomy. None of these techniques is non-invasive, but all provide some form of ground truth against which to measure diffusion tractography studies.

Physical dissections of brain tissue can reveal major white matter bundles(42). These can provide a visual framework from which to validate the results from dMRI studies of where large white matter bundles are located, and what their major orientations are(42,43). However, crucially, dissections are unable to identify axonal start and end points or how fibers enter and exit bundles, and are fundamentally limited in resolution. Thus, they are not well-suited for determining the gray-matter-to-gray-matter anatomical connections that subserve neuronal information processing.

There are various histochemical stains and light imaging methods (such as polarized light imaging) that can be utilized to examine myelinated fibers (and thus fiber directions) in the brain(44,45,46). This method shows whether diffusion directions match the majority of true axonal orientations. However, like dissection methods, it cannot connect fiber orientations with specific gray matter areas, and thus cannot resolve details of anatomical connectivity.

Anatomical tract-tracing can be used as a “ground truth” when assessing the accuracy of diffusion tractography when the latter is estimating gray-matter-to-gray-matter connectivity. It is helped in this regard by the availability of two well characterized datasets, Markov-Kennedy and CoCoMac(47,48). In neural tract-tracer studies, tracer compounds are manually injected into target brain regions. Days to weeks later, the animal is sacrificed. Because this technique requires intracranial surgery, timed sacrifice, and perfusion, it is impossible to implement in humans. Microscopy is performed to locate the cells and axons containing the tracer. Retrograde connectivity strength can be straightforwardly quantified by counting labeled cells within an afferent region. Anterograde connection strength is trickier; labeled axonal boutons can be counted, but this time-intensive process is often unrealistic over large quantities of tissue. Similarly, number of labeled axons in a bundle may also be quantified in some datasets, but the size of the primate brain typically makes this prohibitive (and it can sometimes be difficult to distinguish individual axons). Neural tract-tracing studies provide exquisite detail on the topography and strength of connections from one brain region to another, as well as the sometimes convoluted paths axons take to reach their targets. However, tract-tracing is ill-suited to characterizing, in the span of a single study, the overall composition of a large bundle. This is because the tracer is injected into only one region of the brain, and cannot be moved. Thus, tracer studies are fundamentally not “whole-brain.” Only by combining cases from many injections (as in, 49) can overall composition be estimated, but it will still be limited by the injections available and chosen.

Manganese tracing has been offered as an alternative to the laborious practice of neural tract-tracing(50,51,52,53,54). Manganese can be injected into the live brain, and then visualized on a T1-weighted MRI. For the purposes of connectivity, this means that manganese methods are dependent on the resolution of the MRI. Thus, it is quite coarse. Furthermore, manganese is multi-synaptic, meaning it can cross synapses in a manner that traditional tract-tracers cannot. It can be difficult to distinguish mono vs multi-synaptic effects, along with connection strength, without prior knowledge. Manganese tracing can roughly recapitulate the anatomical connectivity of large networks (such as the cortico-striatal-pallidal network,55). Thus, while it can outline large, strong networks, and has the advantage of being able to do so across multiple synapses, manganese tracing has not replaced traditional tract-tracing in the field, and it will not be our focus here.

We focus on tract-tracing comparisons to diffusion tractography performed in nonhuman primates. The macaque, rather than other nonhuman animal models, has been an essential part of the effort to build a wiring diagram of the brain, because its gross white matter topology is similar to humans’. By contrast, rodents simply do not have well-defined bundles in the same locations as in humans(56,57). There are two sizable databases of anatomical connectivity in macaques. CoCoMac(48,58,59) combines across the vast anatomical literature to estimate connectivity, retrograde and anterograde, between gray matter regions. CoCoMac is a very large database, with many cases per region. One disadvantage, however, is that definitions of connectivity strength may differ considerably across investigators, and this is not fully standardized (the database simply distinguishes among weak, moderate, and strong levels of label). Furthermore, the white matter pathways used to reach each gray matter region are obscure. The Markov-Kennedy(47,60) database was generated in a single laboratory, so the analysis framework (density of cells, cells per region and per brain) is applied identically across cases. They have placed retrograde tracers in 29 cortical regions, and reported connectivity in 91 cortical regions; no subcortical data are available. As with CoCoMac, white matter trajectories remain obscure. Finally, although not a database per se, the definitive text summarizing white matter organization in macaques is Fiber Pathways of the Brain(49). We would refer you to this book for details about axonal trajectories according to region and bundle.

Validating structural connectivity

Herein, we will review the papers comparing anatomical tract-tracing results to tractography, with a focus on the macaque model. We will be explicit about the types of anatomical and dMRI data used. In many cases, the dMRI data were generated quite differently than the typical human dMRI acquisition: notably, many are ex vivo studies with scans lasting several days.

Thomas et al.(61) compared two anatomical cases with ex vivo dMRI from a single macaque brain (using a 7T Bruker BioSpin HARDI MRI; resolution 250μm; acquisition time of 71 hours). One anterograde injection was used from the motor cortex and one from area V4(49). In these cases, fibers of passage and terminating fibers were known. In both gray and white matter, dMRI and anatomical data were segmented into regions; bundles from each method were classified as present in each region or not. Specificity and sensitivity were then evaluated across diffusion models. Specificity is the ability of an algorithm to correctly ignore false tracts, and can be operationalized as true negatives/(true negatives + false positives). Sensitivity is the ability for a tractography algorithm to properly identify a true tract, and can be operationalized as true positives/(true positives+false negatives). Specificity and sensitivity varied considerably according to the specific diffusion model applied; however, accuracy overall was quite low. To demonstrate this, the authors combined sensitivity and specificity into one metric, the Youden index(62): specificity + sensitivity - 1. A Youden index of 1 represents perfect specificity and sensitivity. In this study, Youden index values ranged from 0.04 to 0.59. Unfortunately, the optimal diffusion models were different for the two anatomical cases, meaning that a diffusion model that produced a high Youden index for one region often produced a low one for the other. This severely limits one’s ability to find a widely applicable, accurate diffusion model. In addition, an increase in sensitivity was accompanied by a decrease in specificity, meaning that capturing more true tracts came at the cost of including more false tracts. The authors conclude pessimistically that “there is an inherent limitation in determining long-range axonal projections based on voxel-averaged estimates of local fiber orientation.”

Another study(63) ceompared th CoCoMac and Markov-Kennedy databases with dMRI data drawn from 10 macaque brains (3T Siemens Trio Tim, resolution 1.1 mm; 86 minutes). Q-sampling imaging was used to fit multiple fibers to each voxel, and deterministic fiber tracking was used. Cortical gray matter was segmented into 39 regions(64,65), and whole-brain connectivity matrices were generated (with empty cells for unsampled anatomical data). These matrices were then correlated with each other. Correlation coefficients between structural and anatomical connectivity strengths were significant, but weak (r=0.25–0.31).

In Reveley et al.(66), ex vivo datasets (7T Bruker MRI; 250μm resolution; ~3 days) from 2 macaques were compared with myelin-stained sections (within-subject) and a tracer injection (between-subjects). The investigators were interested in the transition points between white matter and cortical gray matter. The myelin stains demonstrated that the boundary had many different fiber orientations present: for example, local U-fibers running parallel to the boundary were intermixed with outgoing projections. With the tract-tracer injection case (in the intraparietal sulcus), fibers could be seen exiting the injection site, crossing the white matter boundary, and entering the deep white matter. The dMRI data were unable to capture this pattern. When seeding inside the gray matter, only 24% of brain regions managed to generate long-range projections deep into the white matter, with the rest caught in local fiber systems. Expanding the seeds to capture some of the white/gray matter boundary did lead to more projections to the deep white matter, but at the expense of accuracy. Although there were problems with both gyral and sulcal seeds, the challenges associated with superficial white matter were more pronounced in sulci.

Donahue et al.(67) compared anatomical connectivity from Markov-Kennedy(47) with scans from ex vivo macaque and vervet brains (4.7T Bruker MRI; macaque brain scanned at 0.43mm resolution for 27 hours; vervet brain scanned twice, 0.5mm resolution, for 20 hours and 68.5 hours). A number of different analysis strategies were used: area-based vs vertex-based (for the injection site), crossed with seeding in the white matter vs surface. Seeding in the white matter enhanced the gyral bias described above(66). Importantly, the anatomical and dMRI datasets were “reasonably” correlated, with correlation coefficients of 0.55–0.60. This study successfully employed fractional scaling (number of streamlines/labeled cells in an area was normalized by total number of streamlines/labeled cells in the brain) and symmetrization (averaging connection strength from region A to B with B to A); without these, the correlation coefficient was 0.48. In addition, accuracy decreased with distance between regions.

Focusing exclusively on connectivity within the cortical visual system, Azadbakht et al. used two fixed macaque brains to acquire ex-vivo dMRI data(68) (rhesus macaque brain imaged for 64 hours at 0.8mm resolution; crab-eating macaque imaged for 27 hours at 0.43mm resolution; 4.7T Bruker MRI). Anatomical data were drawn from a landmark synthesis of visual system connectivity(69,70), in which reports from many prior studies were combined to determine whether two brain regions were connected (but without regard to strength of connectivity). Accuracy (true positives plus true negatives divided by the sum of true positives, true negatives, false positives, and false negatives) was 77% in one dataset and 70% in the other, indicating that similar tractography results can be attained with different acquisition methods. These numbers may have been helped by the relatively close distance between regions under investigation, which are mostly in the caudal cerebral cortex. False positives were mostly short-range projections, while false negatives were weighted toward longer pathways. Imposing FA thresholds reduced accuracy (perhaps due to partial volume effects), and distance corrections did not dramatically alter accuracy (likely because of a sensitivity/specificity tradeoff). The authors followed up on the most consistent “false” connections by comparing with the more recent Markov-Kennedy database. Among those that had been tested in Markov-Kennedy, 8 out of 9 “false positives” were found to have anatomical connectivity. This might suggest that the tractography more accurately matches anatomical connectivity than is suggested by comparison to(69). However, 8 of 10 tested “false negatives” were also absent in the Markov-Kennedy database, suggesting that the majority of false negatives, were, in fact, errors. Ultimately, this study shows the use of tract-tracing data as the “ground truth” comparator is limited by the particulars of a given dataset. Potentially, one way to mitigate this problem is with quantitative assessments of anatomical connectivity (as in the Markov-Kennedy database); a weak connection may have been missed by early anatomical work, when tract-tracers were less sensitive. Connections also vary considerably in their strength, and this feature of the brain will ultimately be important to capture.

Schilling et al.(71) developed challenge datasets to determine whether any particular tractography algorithm could accurately replicate anatomical connectivity. For the macaque dataset, both the anatomical and dMRI data were the same as used in Thomas et al.(61). An ex vivo squirrel monkey dataset was also generated (50 hours at 9.4T; 300μm resolution). The squirrel monkey anatomical connectivity was generated from an injection of tract-tracer into the primary motor cortex. Uniquely, these occurred within the same brain, allowing for within-subject comparison. There were ultimately 176 submissions generated by 9 research groups. Like Thomas et al.(61), Schilling et al(71) conclude that sensitivity and specificity trade off in the submissions. The median Youden index values were notably low: 0.21 and 0.30 for the macaque and squirrel monkey datasets, respectively (the highest were 0.56 and 0.58). Intriguingly, the squirrel monkey dMRI tractography slightly outperformed the macaque, perhaps because of reduced cortical folding or the within-subject design.

Shen at al. (79) examined cortical tractography results from ten macaques imaged in vivo (7T Siemens Magnetom, 1.0mm resolution), and systematically manipulated parameters in the probabilistic tractography model. Resulting connectivity matrices were compared to the Markov-Kennedy and CoCoMac databases. When compared with the Markov-Kennedy database, “default” tractography settings yielded a very high sensitivity (0.99), but very low specificity (0.01), consistent with many of the other studies described here. Precision (true positives divided by the sum of true and false positives), however, was significantly above chance (0.79), and seemed to depend upon analysis parameters used. The two parameters with the biggest impact were the curvature threshold and the discarding of “weak” connections. The curvature threshold restricts how much a streamline is permitted to change angles along its path, and the optimal one was below 0.6. “Weak” connections were defined as streamlines that fail to meet a minimum criterion(80). After determining the “optimal” tractography parameters for each subject, a correlation coefficient (r) (between the tractography estimates of connectivity network edge weights and those from the Markov-Kennedy database) of 0.71 was achieved. This suggests that subject or tract -specific optimization may dramatically improve accuracy.

Although not as comparable to human dMRI because of dramatic differences in gross brain anatomy, mice have also been used for structural connectivity validation. In a comparison of anatomical tract-tracing results from the Allen Brain Atlas database(72,73,74) and dMRI tractography, DICE coefficients (overlap between labeled tracer and tractography) were in the 0.4–0.5 range(75). These improved somewhat with the addition of anatomical constraints. Chen et al.(76) found dramatic variation in tractography performance across number of regions used (coarseness of the atlas) and streamline length, with optimal performance with coarser parcellations and longer connectivities. They also agreed with the conclusions of(61): specificity comes at the cost of sensitivity, and vice versa.

The above studies, which ask how individual brain regions use each bundle, stand in contrast to more promising studies in which the location and major fiber directions of the largest white matter bundles of the brain are identified by tractography. The difference between these approaches is analogous to the difference between knowing where in the country and in what direction (north/south vs east/west) a highway runs, versus knowing which entry and exit points a particular vehicle used on its journey. For example, in a recent challenge to identify 25 major fiber bundles (as segmented by an expert radiologist)(77,78), the majority of the processing pipelines were able to reconstruct portions of all but the smallest of fiber bundles with some specificity. Despite challenges with the finer details of tracking each bundle, the match between the anatomical bundle boundaries and the dMRI ones was very high, indicating tractography is an excellent tool for estimating the locations and fiber orientation(s) of large bundles.

In summary, validation studies consistently show a moderate relationship between structural and anatomical connectivity, though careful manipulation of the tractography parameters can increase the correlation between diffusion data and anatomical data, particularly in gray-matter-to-gray-matter connectivity studies. Moreover, sensitivity and specificity consistently trade off, such that an increase in sensitivity comes at the expense of specificity, and vice versa. By contrast, dMRI is quite good at replicating the locations and fiber orientations of major white matter bundles. Decreased accuracy appears to come in smaller and deeper brain structures, gray/white matter junctions, as well as longer distances, which helps to explain the challenges associated with gray-matter-to-gray-matter connectivity.

Case studies

Although it has not yet been examined quantitatively, it seems likely that connections running through some white matter bundles are easier to recreate. Here, we will consider the very different challenges posed by two bundles: the anterior limb of the internal capsule (ALIC) and the cingulum bundle.

The ALIC carries fibers running between the prefrontal cortex and the thalamus, subthalamic nucleus, and brainstem. Tract-tracing has revealed a distinct topography prefrontal fibers use in the ALIC(83,84). For example, fibers from dorsal prefrontal regions run dorsal in the ALIC to those from ventral prefrontal regions. These relationships are generally maintained in tractography studies on macaques and humans. There are some challenges associated with reconstructing tracts through the ALIC (for example, ventromedial prefrontal cortex fibers get “stuck” as they attempt to traverse fascicles through the anterior commissure), but they can be corrected to reproduce the underlying biology.

The cingulum bundle runs rostral-caudally through the frontal, parietal, and temporal lobes(85,86,87) (Figure 1). In contrast to the topographically organized ALIC, it has only minimal organization. Tract-tracing shows that fibers traveling through the cingulum bundle segregate mainly in the rostral-caudal dimension, but not in the medial-lateral or dorsal-ventral(88). Thus, fibers from different brain regions are largely intermixed in the cingulum bundle. These projections are very different: they start and/or end in different brain regions. However, since each voxel contains fibers from multiple regions, dMRI streamlines may not exit the cingulum bundle at the appropriate location. Instead, multiple seed regions (with distinct anatomical connectivity) may enter the cingulum bundle, and the streamlines may either fail to exit the bundle, or else exit falsely at places where other regions are exiting. Thus, we anticipate that anatomical connectivity through the cingulum bundle is particularly difficult to replicate with dMRI. Indeed, on visual inspection, Donahue et al.(67) identified the cingulum bundle as the source of many obvious false positives in their study. The cingulum bundle also highlights the differences between identifying a bundle and its major diffusion directions (which, for the cingulum bundle, is relatively straightforward using tractography) versus identifying gray-matterto-gray-matter connectivity patterns.

Paths forward

The validation studies described above have a few obvious weaknesses. First, with one exception (in the squirrel monkey,71), studies were in different cohorts of subjects. That is, some animals were used for anatomical tract-tracing, while others were used for dMRI. This brings up problems associated with primarily with registration (of the injection site/seed, of the brain regions, of the tracts and connections), but also with individual differences in anatomical connectivity. Second, two landmark studies (71,61) rely upon the same anatomical dataset, which uses just two cases. Other studies(63,67) took advantage of larger anatomical datasets. However, these did not include subcortical connectivity. While tractography in subcortical structures is likely to be much more difficult due to their small size and SNR problems, it will be important to assess these areas moving forward. Finally, it is not yet clear whether certain bundles are easier to track connections through than others, as proposed above.

It is also clear that improved dMRI data collection and analyses do enhance the accuracy of structural connectivity. On the data collection side, increasing b-values, improving resolution, and combining acquisitions with different resolutions to enhance SNR(40) may enhance quality. It is not exactly clear how to translate the impressive resolutions in the validation studies described here to human. The macaque brain is ~6% the volume of the human brain (e.g., 89), but axons are roughly the same size (e.g., 90). Achieving better resolutions will probably help, but it is not obvious where the goalpost should be. On the data analysis side, the fractional scaling and symmetrization employed by Dohanue et al.(67), the anatomical constraints imposed by Aydogan et al.(75), and the individualized curve thresholds and discarding of weak connections by Shen et al.(79) appear promising. Additionally, a well-known problem with tractography is the difficulty of tracking longer range connections, largely due to the propagation of uncertainty as the tract increases in length (82). Distance correction can be applied, which increases the number of true positive connections reconstructed, but also increases the number of false positives (68). Further studies have shown this may not improve the accuracy of tractography (79), so this approach must be utilized with caution. Finally, studies on the individual anatomical constraints needed for each white matter bundle will ideally go hand-in-hand with novel anatomical tract-tracing studies, focused on the particular problems with each bundle.

Clinical Applications

Despite the limitations of diffusion neuroimaging, it has been used effectively in multiple clinical settings. For example, for surgical resection planning, numerous studies have shown that diffusion imaging can assist in removal of brain tumors in close proximity to white matter bundles such as the pyramidal tracts(91). Diffusion tractography is also effective at determining deep brain stimulation electrode placement in multiple disease states, including treatment-resistant depression(92), movement disorders(93), and chronic pain(94). It should also be reiterated, that while dMRI may not fully recapitulate anatomical connections, it remains the best non-invasive method to study white matter organization in the human brain in vivo.

Conclusion

Here, we have reviewed the validation of dMRI-derived structural connectivity. We conclude that, while there is consistently a significant, positive relationship between anatomical connectivity and structural connectivity, it is definitely not strong enough for dMRI tractography to act as a stand in for gray-matter-to-gray-matter anatomical connectivity. Nevertheless, moving forward, advancements in dMRI tractography (on both the data acquisition and analysis sides), along with the imposition of anatomical constraints, may improve this scenario. Other usages of dMRI, including localization of large white matter bundles and identification of differences in white matter integrity between populations, are unaffected by this critique. As investigators analyze their structural connectivity data, we encourage tailored approaches, with an eye toward ensuring that streamlines are following biologically plausible pathways.