Abstract
Clinical adoption of mechanical circulatory support for shock is rapidly expanding. Achieving optimal therapeutic benefit requires metrics of state to guide titration and weaning of support. Using the transvalvular positioning of a percutaneous ventricular assist device (pVAD), device:-heart interactions are leveraged to determine cardiac output (CO) and systemic vascular resistance (SVR) near-continuously without disrupting therapeutic function. An automated algorithm rapidly alternates between device support levels to dynamically modulate physiological response. Employing a two-element lumped parameter model of the vasculature, SVR and CO are quantified directly from measurements obtained by the pVAD without external calibration or invasive catheters. The approach was validated in an acute porcine model across a range of cardiac (CO = 3–10.6 L/min) and vascular (SVR = 501–1897 dyn s/cm5) states. Cardiac output calculations closely correlated (r = 0.82) to measurements obtained by the pulmonary artery catheter-based thermodilution method with a mean bias of 0.109 L/min and limits of agreement from − 1.67 to 1.89 L/min. SVR was also closely correlated (r = 0.86) to traditional catheter-based measurements with a mean bias of 62.1 dyn s/cm5 and limits of agreement from − 260 to 384 dyn s/cm5. Use of diagnostics integrated into therapeutic device function enables the potential for optimizing support to improve outcomes for cardiogenic shock.
Keywords: Cardiogenic shock, Mechanical circulatory support, Ventricular assist device
INTRODUCTION
Clinical use of mechanical circulatory support (MCS) devices to support patients with cardiovascular disease is increasing exponetially.14 New devices offer physiological advantages over medical therapy and aortic counter-pulsation to more fully maintain systemic perfusion and homeostasis.1 At present, there are limited prospective clinical trials evaluating the efficacy of newer support devices and none employing protocolized hemodynamic management and device operation in critically ill patients.19,21,25 Concurrently, there is expanding evidence that ready access to metrics of cardiac and vascular state –such as cardiac output, systemic vascular resistance and left ventricular end diastolic pressure—to guide therapy is associated with improved outcomes in patients with cardiogenic shock.6,18 The advent of new support technologies presents an opportunity to reexamine current approaches. Leveraging interactions between the heart and new devices, it may be possible to obtain valuable metrics of cardiovascular state to guide titration of support to patient hemodynamics.
Pulmonary artery catheters (PACs) are widely deployed by clinicians to gain insight into cardiac and vascular state.11 Cardiac output (CO) is estimated by differences in heat or oxygen flow across the catheter, and left ventricular end diastolic pressure can be inferred from pulmonary capillary wedge pressure. A fixed systemic vascular resistance (SVR) is computed as a single lumped parameter for the entire vasculature and assuming purely linear mechanics. While these data are of value, wedge pressure, for example, cannot be tracked continuously and is only an inferred measure of LV pressure. Moreover, PACs are an additional vascular catheter, and placement of this device is not without complication.17 These limitations and the inability to identify improved outcomes in all but cardiac shock has led to a precipitous decline in PAC use.13 Yet, the desire to have hemodynamic metrics at the bedside has remained a persistent need with the use of advanced MCS devices.28
To provide quantitative guidance, we and other groups proposed using MCS devices themselves as a means to assess cardiovascular state to tailor maintenance and weaning.3,7,24 Percutaneous ventricular assist devices (pVADs) already residing in the left heart and arterial vasculature are particularly suited to achieve the dual function of therapeutic support modality and diagnostic device capable of realizing continuous real-time and direct measures of state. The ventriculo-aortic positioning of pVADs presents an opportunity for direct assessment of individual and coupled vascular and ventricular function. Such continuous, direct, and instantaneous metrics of state and temporal trends can guide titration of MCS devices and confirm the addition of adjunctive pharmacotherapy. With this information we may now see the improved clinical outcomes not realized in clinical trials performed to date.27
Using a paradigmatic transvalvular intraventricular pVAD (Impella CP, Abiomed, Danvers, MA), we have previously shown how intrinsic device signals can be related to clinically relevant cardiac parameters, such as the left ventricular end diastolic pressure, without need for additional intervention.3 Furthermore, we demonstrated how coupling between a pVAD and the vasculature is similar to ventricular-vascular coupling and can be leveraged to determine cardiovascular state.4 Though effective at demonstrating the applicability of device-arterial coupling, the prior method necessitated significant changes in support for several minutes, limiting frequency of measurements, and required user-selected data segments for analysis in the setting of background physiological noise, limiting its clinical application.
Here, we leverage device-arterial coupling to determine accurate measures of cardiac output and vascular resistance to provide the clinician with real-time metrics of function to guide support. We employ a novel, impulse-like square wave pVAD speed pulse in which switching between states was induced automatically and consistently without interrupting MCS. This approach was implemented using a prototype pVAD controller for prospective validation in a series of animal studies to prior to clinical deployment and evaluation.
METHODS AND MATERIALS
Mechanical Circulatory Support Device and Control
The Impella CP, a percutaneous catheter mounted MCS device, is used as our paradigmatic pVAD. The Impella is deployed via the femoral or axillary artery and advanced such that the pump inlet resides within the left ventricle and the outlet in the ascending aorta by crossing the aortic valve.32 The device moves blood from the left ventricle to the aorta at a fixed rotational speed set by the controller across the entire cardiac cycle.23 The flow rate is dependent on the Impella’s rotational speed and the pressure head across the device. The controller measures and records motor current, real motor speed, and aortic pressure, while also estimating the blood flow rate that the Impella is providing. The aortic pressure measurement by the Impella is recorded via an optical pressure transducer located directly proximal to the aortic valve near the pump flow outlet.32
During normal Impella operation, the controller is set to a particular performance-level (P-level) and remains fixed until changed by the operator. Each P-level corresponds to a specific rotational speed of the motor ranging from P-1 (23,000 RPM) to P-8 (44,000 RPM). Consequently, the amount of power, or motor current, used by the device changes in the face of variable load from the heart throughout the cardiac cycle in order to maintain this fixed rotational speed. In this study, a modified controller is used to generate a novel impulse-like square wave pVAD speed pulse. When triggered, the controller drops the rotational speed to the lowest operational rotational speed setting (23,000 RPM, P-1) for two seconds and then returns the speed back to the previous operational speed (Fig. 1a). It takes the pump approximately 200 ms to respond to the rapid decrease and increase in speed. The two second duration is the minimum time for applicable Impella flow estimation.
FIGURE 1.
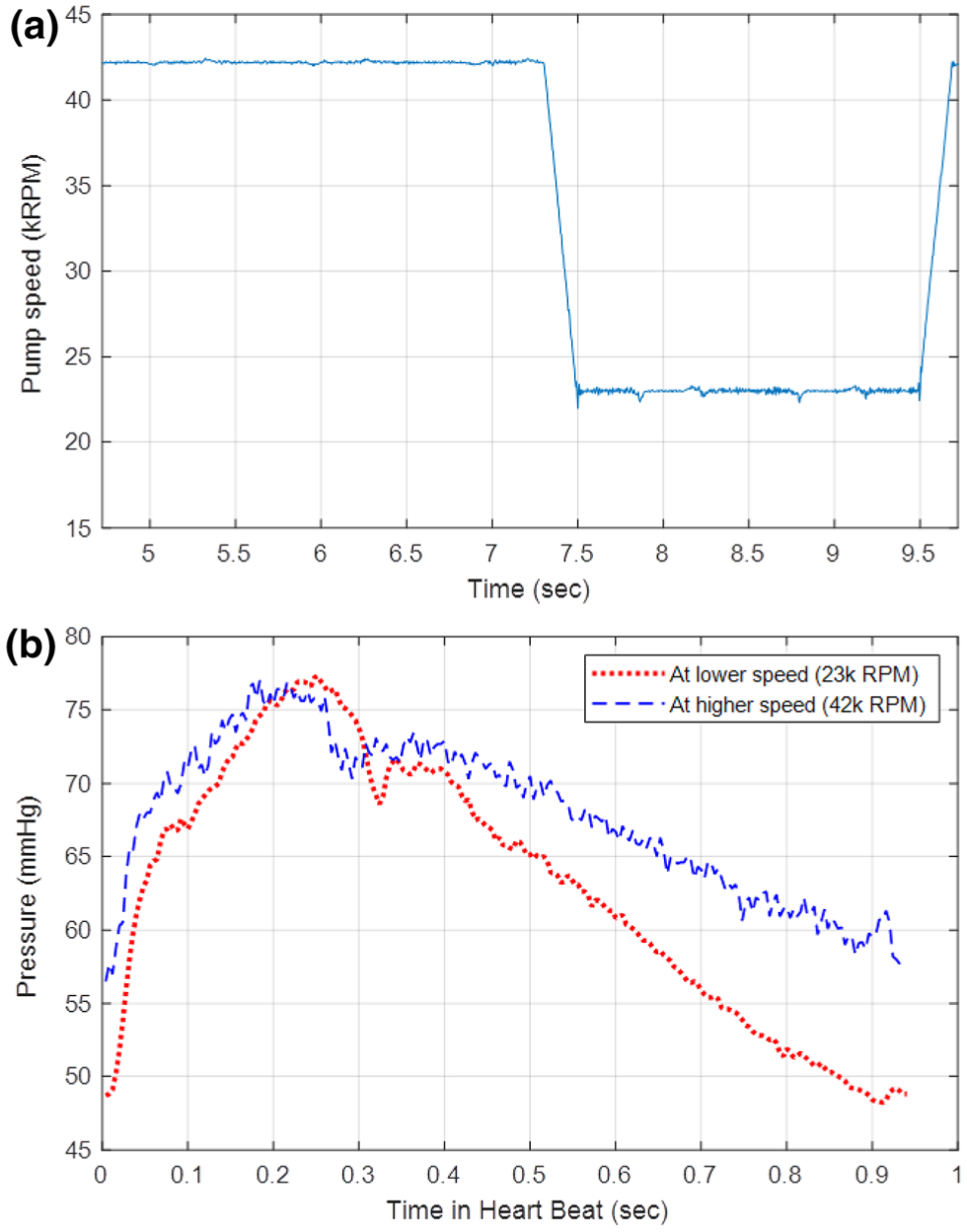
Representative data segment from animal study. (a) Change in rotational speed corresponding to the speed pulse. The rotational speed drops to the lowest operational setting in order to induce an impulse-like input to the vasculature. (b) Aortic pressure as measured from the Impella placement signal has a change in pressure that corresponds to the rapid speed change. With lower Impella speed there is lower mean arterial pressure but higher pulse pressure.
Model to Evaluate Device-Arterial Coupling
The cardiovascular system can be modeled using electrical circuit analogs such as resistors, capacitors, inductors, and current or voltage sources.2 In its simplest form, the cardiovascular system can be modeled as a current source with a parallel resistor and capacitor, a configuration that is conceptually familiar to most clinicians (Fig. 2).30 Using this model, cardiac output from the heart flows into an arterial system represented by the parallel systemic vascular resistance and compliance with a resultant pressure wave form. In the setting of the Impella, the device acts as an additional parallel current source with the native heart such that the governing differential equation for this circuit is as follows:
| (1) |
where P is the aortic pressure waveform that is measured, R is the systemic vascular resistance, C is the systemic vascular compliance, ih is the flow generated by the heart, and ip is the flow produced by the Impella.
FIGURE 2.
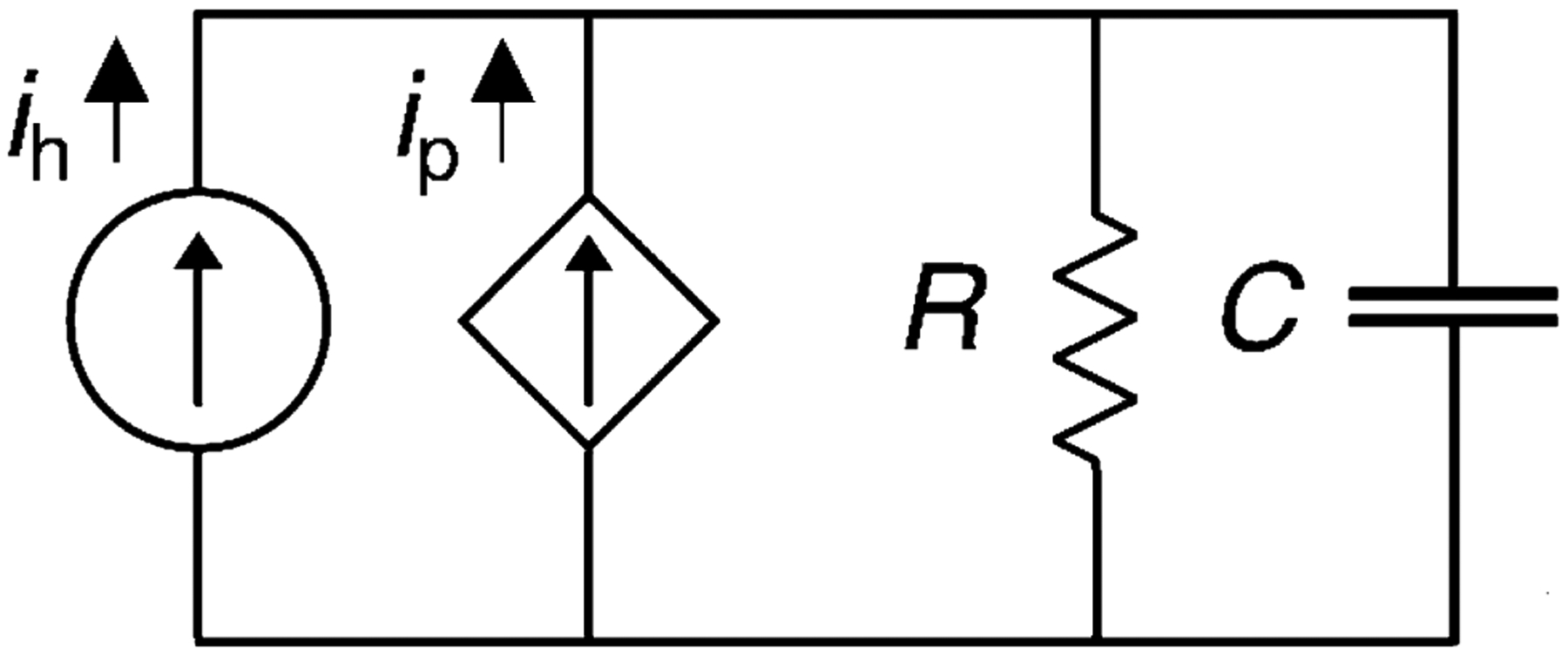
Lumped parameter model of cardiovascular system with pVAD support. A two element lumped parameter modeling of the cardiovascular system representing perfusion of the vascular system as current sources representing the cardiac and Impella derived components.
With the appropriate systemic vascular resistance and compliance, the flow generated by the heart can be estimated with the prior equation. However, values for systemic vascular resistance and compliance can vary substantially even in normal physiology.16 While several complex methods have been developed to estimate vascular characteristics, they often rely on specific conditions, require external calibration, and have questionable accuracy and usability.10,31 Here, we present a method that uses the controllable function of the Impella and the unique flow conditions that are present during its deployment. During diastole, there is no native cardiac flow and all flow into the vasculature is from the Impella, which is known from the controller, and relatively constant, steady, and fully developed.32 With this assumption, the prior differential equation can be simplified to the following:
| (2) |
where P0 is the effective initial pressure for the diastolic exponential decay and the remaining terms remain the same during diastole (ipR). Notably the pressure measured in the waveform at the beginning of the diastolic decay would not be P0.
To determine R, the square wave speed pulse from the Impella (Fig. 1a) is used to generate a change in the aortic pressure waveform within a sequential set of cardiac cycles (1–2 s). During a speed pulse, a decrease in Impella rotational speed decreases pump flow rates, which results in a decrease in mean arterial pressure. This decrease in pump flow also increases cardiac preload to increase stroke volume, which manifests as increased pulse pressure (Fig. 1b). This response within each speed pulse is the basis to solve (Eq. 2) for the systemic vascular resistance. When considering these two levels of Impella support, (Eq. 2) at baseline and during the speed pulse at the beginning of the diastolic decay (t = 0) can be rewritten as follows:
| (3.1) |
| (3.2) |
where the equations above retain the same variables as previously described.
With these two aortic pressure waveforms from the square wave speed pulse, a linear system of equations (Eqs. (3.1) and (3.2) can be solved for R, with the assumption that R remains relatively constant. However, notably, P0 is impacted by the presence of the Impella and is different at the two states. During normal physiology, the initial diastolic pressure value, as marked by the dicrotic notch, is related to the magnitude of decay. The dicrotic notch corresponds directly with the incisura, and thus aortic valve closure, in this pressure tracing since it is measured by the Impella in the proximal aorta near the heart. In the setting of pVAD support, the initial diastolic decay pressure value (P0) is altered by the constant Impella flow as well as the change in cardiac preload impacting stroke volume.26 As a result, the impacts on P0 from simply changing pump speed are not readily apparent.
If P0 is considered the hypothetical decay value that is a result of cardiac ejection, P0 will be directly proportional to local changes in preload for a given vascular state. This is because stroke volume is directly and linearly related to preload for local changes as described by the Frank-Starling relationship. It can be assumed that the volume removed from the ventricle to decrease preload by the Impella will scale linearly with the Impella flow rate; in other words, higher Impella flow rates lead to lower preload. Impella flow rate is proportional to its motor rotational speed. As a result, it can be assumed that P0 is inversely proportional to the Impella motor speed as follows:
| (4.1) |
where the motor rotational speed (ω) relationship to P0 is valid during local changes in preload that remain on the linear portion of the Frank–Starling relationship without changes in vascular state. When considering a base and pulse state with short duration change in level of Impella support, this can be rewritten as follows:
| (4.2) |
Where the product of P0 at the baseline speed (P0,base) and the baseline rotational speed (ωbase) is equivalent to the product of P0 at the pulse speed (P0,pulse) and the pulse rotational speed (ωpulse).
Equations (3.1) and (3.2) can then be combined with Eq. (4.2) to yield the following equation to calculate a systemic vascular resistance, R:
| (5) |
where the equation above retains the same variables as previously described.
Alternatively, R can be determined by calculating the slope of the aortic pressure curve at the baseline and pulse speeds. Differentiating Eq. (1) and substituting for the exponential at the baseline speed and the pulse speed during diastole (i.e., ih = 0) yields:
| (6.1) |
| (6.2) |
where and are slopes that can be measured from the diastolic pressure waveforms at the base speed and the pulse speed, respectively. In a similar form as Eq. (5), R can be determined from Eqs. (6.1) and (6.2) as follows:
| (7) |
where the equation above retains the same variables as previously described.
Therefore, R can be determined by measuring the changes in aortic pressure created by changes in flow, with values that are scaled by their respective Impella speeds (Eq. 5) or by the pressure decay slope at their counterpart speed (Eq. 7). Equation 5 remains the preferred method of estimation because the time derivative is estimated using the local slope of the pressure. The local slope changes through the decay and is highly susceptible to noise in the pressure signal. However, limitations in Impella controller sampling rate make it difficult to capture the start of diastolic decay at high heart rates, which is needed for (Eq. 5). In this study, Eq. (5) was used if the subject’s heart rate was low (lower than 85 beats per minute) or from Eq. 7 if the result from (Eq. 5) was out of physiological range (for example, negative R).
The systemic vascular compliance, C, can be derived by rewriting Eq. (1) as:
| (8) |
where the equation above retains the same variables as previously described. During diastole, ih is zero and C can be calculated from the pressure (P) and the pump flow (ip), which are known by the pump controller and the previously calculated R.
The total cardiac flow (ih + ip), equivalent to the total cardiac output, is then determined by measuring the arterial pressure and then applying Eq. (1) with the calculated R and C values. A 10-s arterial pressure measurement corresponding to the duration of a 10-s reference thermodilution cardiac output measurement is used to allow direct comparison between the modalities.
For clarity throughout this article, R is used to denote the systemic vascular resistance determined by the algorithm. The acronym SVR is reserved to denote the systemic vascular resistance calculated by current clinical practice using the following equation:
| (9) |
where the mean arterial pressure (MAP), central venous pressure (CVP), and the cardiac output obtained by the thermodilution method (TCO) are clinically measured to estimate systemic vascular resistance. The total cardiac output determined by the algorithm and TCO is made up of the individual flow components corresponding to native heart component, ih, and the component produced by the Impella, ip. All calculations were performed using custom scripts and built-in functions in MATLAB (MathWorks, Natick, MA)
Animal Models
We investigated a novel implementation of device-arterial coupling to determine cardiac output using the Impella as a paradigmatic device. Experimental procedures were conducted on 12 young adult castrated male Yorkshire swine (70–80 kg) in accordance with NIH and AAALAC guidelines (CBSET, Lexington MA). Animals were continuously monitored via oxygen saturation, core body temperature, and electrocardiography while being maintained under general anesthesia with inhaled isoflurane following sedation with an intramuscular injection of Telazol (6 mg/kg) and endotracheal intubation.
Vascular access was obtained at both femoral arteries and one femoral vein. Invasive blood pressure transducers were used to record femoral arterial and venous pressures. The Impella was introduced via the left femoral artery over a wire and advanced into appropriate positioning within the left ventricle. A pulmonary artery catheter was introduced in the right femoral vein and advanced into the pulmonary artery for intermittent thermodilution cardiac output measurement. Positioning of the catheters was confirmed using fluoroscopy. The Impella was maintained at maximum support speed commonly used clinically (44,000 RPM, P8) with continuous measurement of motor speed, motor current, and aortic pressure.
Following measurements obtained at the physiological baseline, animals underwent various pharmacological and physiological interventions to induce changes in cardiac and vascular state. Pharmacological interventions consisted of bolus infusions of epinephrine, norepinephrine, phenylephrine, and esmolol to induce transient changes in native cardiac output and vascular impedance. Cardiac output measurements were obtained at baseline states and following completion of vasoactive medication injections. Depressed cardiac function was induced via either balloon occlusion of the left anterior descending artery or through the injection of microbeads directly into the left anterior descending artery to produce vascular occlusion and myocardial ischemia. Occlusion was titrated such that cardiac output dropped by at least 1 L/min from baseline via thermodilution. Across all animals and conditions, multiple independent speed pulses (n = 75) were completed using the prototype controller with corresponding separate thermodilution validations for cardiac output estimation.
Statistical Analysis
Correlation and Bland–Altman plots were used to confirm validity of estimation by comparing measured and calculated cardiac output using ± 2 standard deviation confidence intervals.29 Statistical comparison of the algorithm calculated cardiac output and vascular resistance with the thermodilution measured cardiac output and traditional systemic vascular resistance was performed for the cumulative data. Values are expressed as means ± range for a 95% confidence interval. Correlation coefficients and the slope and intercept of the linear regression were calculated for comparisons of cardiac output and vascular resistance. Measurements of bias, precision, and percentage error were calculated. All statistical analysis was conducted using MATLAB and the Statistics and Machine Learning Toolbox from MATLAB.
RESULTS
We assessed a novel method to define systemic vascular resistance and cardiac output directly, continuously, and without interrupting cardiac support. Where past attempts have used ramp tests over minutes that require the patient tolerate prolonged reductions and increased support,4 we now gain greater insight using short two second pVAD speed reductions. Measurements were obtained at baseline states and as acute interventions changed cardiovascular state in a controlled fashion. The pVAD pump speeds were modulated between two extremes for the two second duration (Fig. 1a) to obtain measurable differences in the aortic pressure (Fig. 1b). For validation cardiac output was measured by the thermodilution method immediately after square-wave pump speed variation.
Algorithm determined CO was measured using aortic pressure waveforms during the duration of the thermodilution measurement. The total data includes 274 distinct measurements from 12 animal studies with reference measurements ranging from 3 to 10.6 L/min. Data from two animals (Fig. 3) show the temporal trends in the measurement that is representative of all cases. Algorithmic and TCO measurements from all animals are closely correlated (r = 0.82, p < 0.0001) and illustrated on a Bland–Altman diagram (Fig. 4) with a mean bias of 0.109 ± 0.106 L/min and limits of agreement from − 1.67 ± 0.183 to 1.89 ± 0.183 L/min or − 30.7 ± 3.08 to 29.3 ± 3.08% (Table 1) across a wide range of physiological states. Correlation analysis between TCO and algorithm determined CO showed close correlation with close agreement in linearity with minimal offset (Table 1). Notably, the spread and divergence between TCO and algorithm increase at higher cardiac outputs (Fig. 4b), corresponding with well-described decreased reliability of TCO measurement at high flows9,12,15 Overall, the algorithm estimates showed greater precision than previously reported thermodilution, consistent with clinical TCO experience requiring multiple measurements (3 to 5) to arrive at sufficient data quality (Table 1).
FIGURE 3.
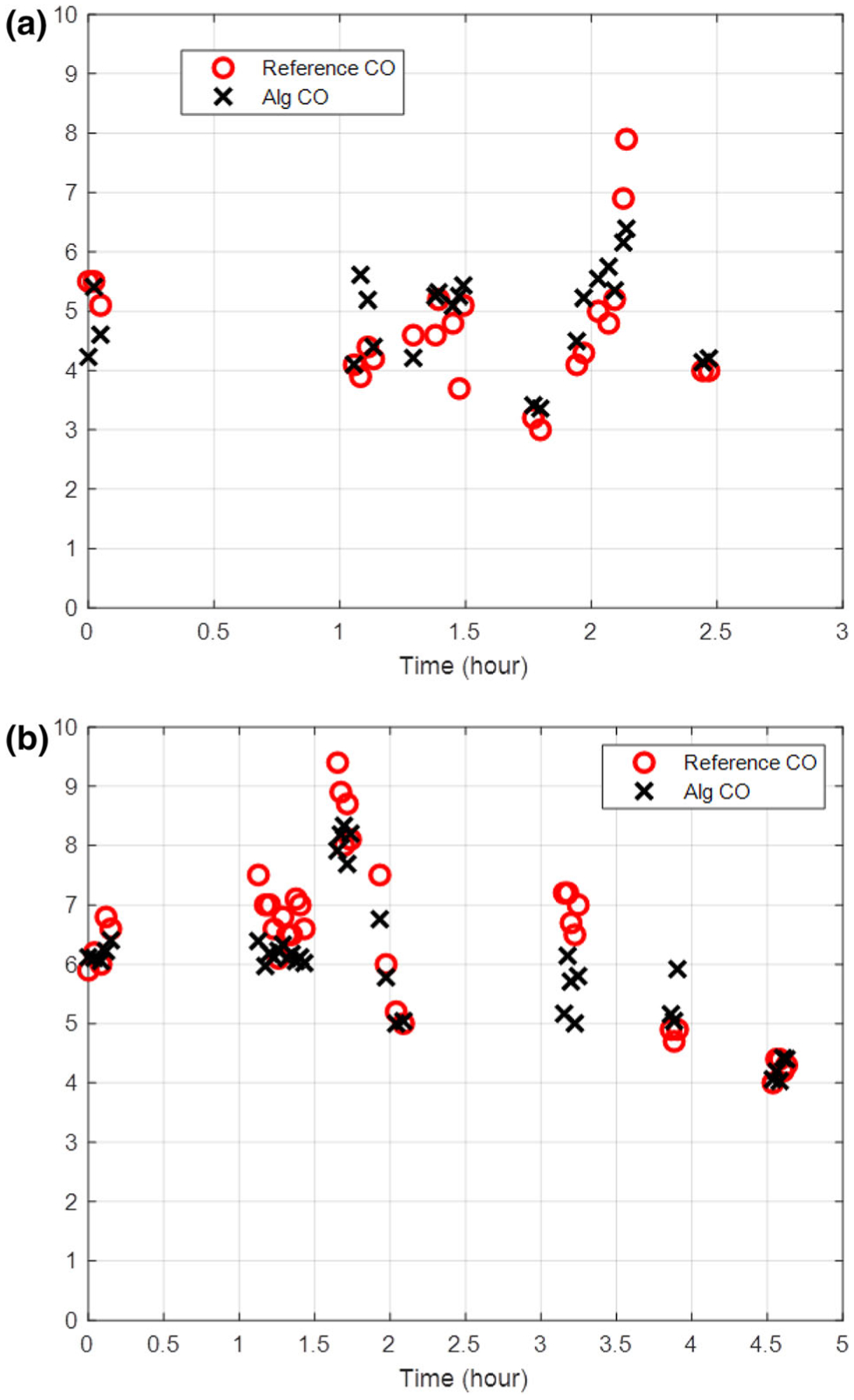
Comparison of thermodilution reference cardiac output (CO) measurements with pulse algorithm calculated CO during the duration of animal models. Cardiac output as measured by thermodilution and pulsed wave algorithm in two representative animals are shown in (a) and (b).
FIGURE 4.
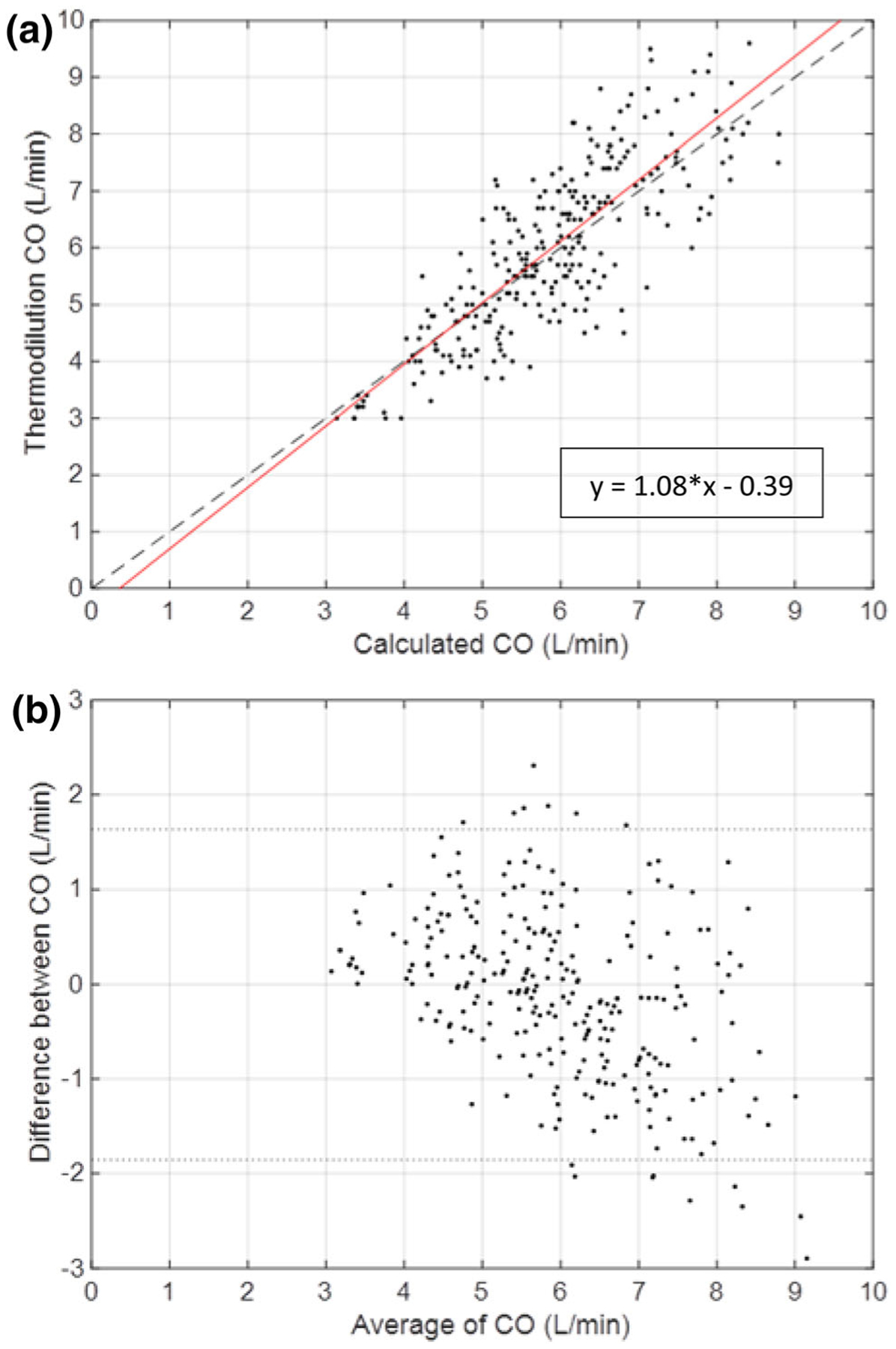
Correlation (a) and Bland–Altman (b) plot of thermodilution CO and algorithm determined CO. Data from 12 animals with an Impella pVAD are shown at varying baseline and cardiac intervention states. (a) Correlation plot comparing CO determined by single thermodilution measurement and algorithm estimated CO. Least squares regression line shown in red. (b) Bland–Altman plot for all cases indicated with standard confidence intervals using ± 2 standard deviations of the difference between the thermodilution measured CO and algorithm estimated CO.
TABLE 1.
Statistical analysis of algorithm determined cardiac output (ih + ip) and systemic vasculature resistance (R) compared against the thermodilution measured cardiac output (TCO) and systemic vasculature resistance (SVR).
| Cardiac output (L/min) | Systemic vascular resistance (dynes-s/cm5) | |
|---|---|---|
| Reference mean (low-high) | 6.0 (3–10.6) | 1054 (501–1897) |
| Bias (mean) | − 0.11 | − 62 |
| Precision (standard deviation) | 0.89 | 161 |
| Limits of agreement (95% confidence interval) | 1.75 | 315 |
| Percentage error | 29.1% | 29.9% |
| Correlation plot (slope) | 1.08 | 1.04 |
| Correlation plot (offset) | − 0.39 | 18.8 |
| Correlation coefficient (r) | 0.82 | 0.86 |
The algorithm-determined resistance, R, was also compared with the SVR calculated from invasive pressure measurements and the TCO values obtained from 66 distinct measurements obtained from five animal studies (Fig. 5). The two measures of vascular resistance demonstrated close correlation (r = 0.86, p < 0.0001) with a mean bias of 62.1 ± 39.9 dy s/cm5 and limits of agreement from − 260 ± 69.2 to 384 ± 69.2 dyn s/cm5. There was linear agreement across a wide range of physiological states (501 to 1897 dyn s/cm5) representing values seen in the cardiogenic shock patient population (Table 1). Notably major deviations between the methods were due to underestimation of R when compared to SVR.
FIGURE 5.
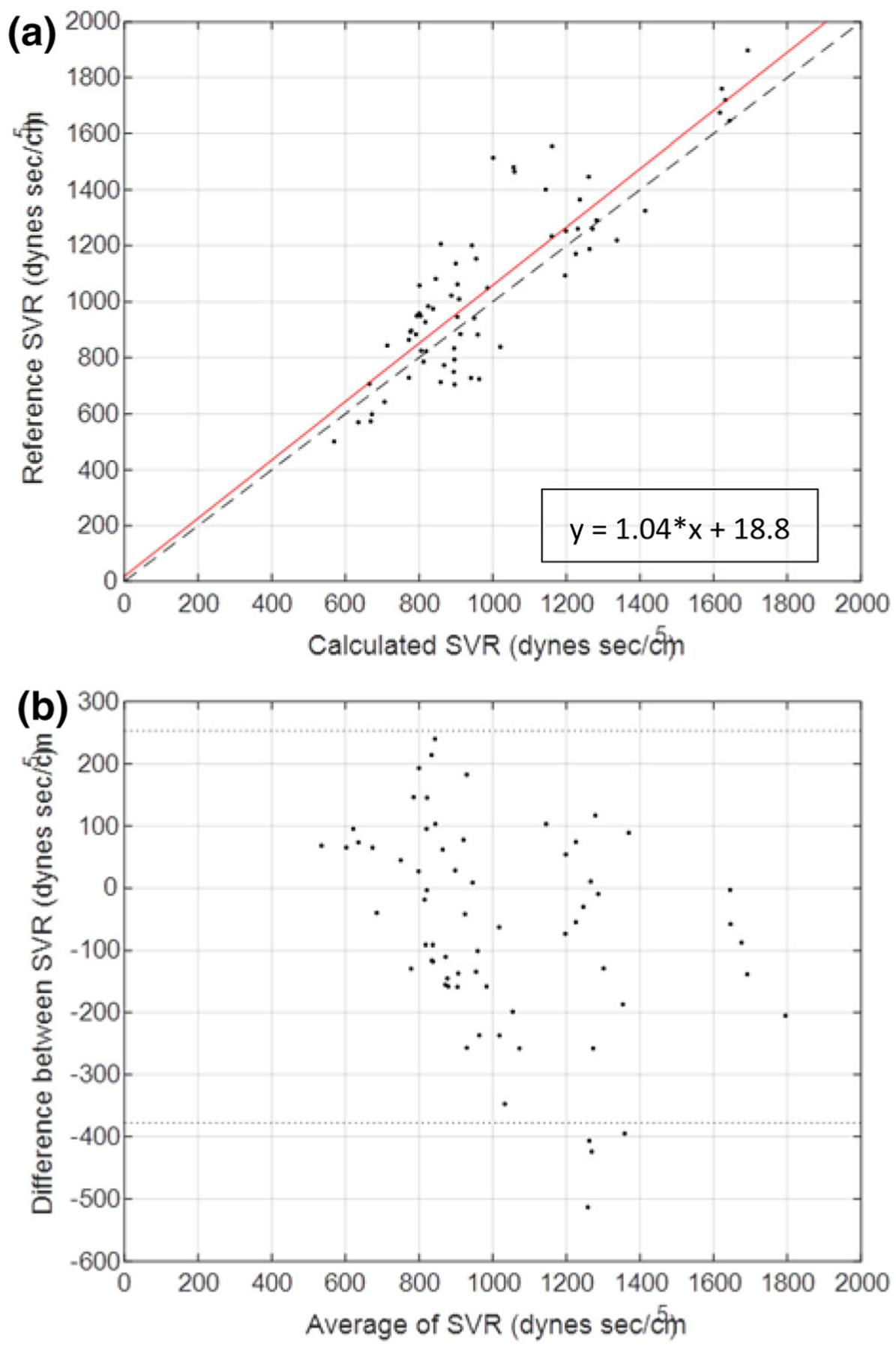
Correlation (a) and Bland–Altman (b) plot of thermodilution-based SVR and algorithm-determined SVR. Data from 5 animals with an Impella pVAD are shown at varying baseline and cardiac intervention states. (a) Correlation plot comparing SVR determined by Eq. 9 and algorithm determined vascular resistance. Least squares regression line shown in red. (b) Bland–Altman plot from the 5 animals indicated with standard confidence intervals using ± 2 standard deviations of the difference between SVR and algorithm determined vascular resistance.
DISCUSSION
Cardiogenic shock remains a highly morbid condition despite rapidly increasing adoption of advanced MCS to restore systemic perfusion. While the introduction of new therapeutic devices provides clinicians with expanded options to maintain critically ill patients, the clinician continues to lack definitive metrics to guide the initiation, titration, and weaning of support. Without adequate metrics, the patient may receive inadequate support resulting in persistent shock, cardiac injury and ongoing organ dysfunction, and ultimately death despite the use of advanced devices. This knowledge gap is evidence in the current trial data which have yet to demonstrate improved patient outcomes using MCS devices in cardiogenic shock.28 The development and clinical implementation of diagnostics to guide the clinician in the optimal management of MCS is urgently needed to improve clinical outcomes and realize the benefit of advancing technology.
At present though clinicians rely on intermittently obtained metrics of cardiac function. The pulmonary artery catheter is the primary clinical means of determining cardiac output and vascular resistance relying on linear ohmic relationships of flow and resistance. Left ventricular filling pressures are inferred from the capillary wedge pressure despite known limitations of the fidelity of this measurement.22 Even thermodilution-based measurements of cardiac output are highly variable and require averaging of repeated measurements for clinical decision making. Furthermore, there is variability even between clinically accepted measurement techniques. Estimated Fick cardiac output is another widely used clinical measure of cardiac output reliant on oxygen saturation and has been found to have wide limits of agreement with thermodilution (− 50.1 to 49.4%).20
In this paper, we present a method to automatically and consistently determine cardiac output and vascular resistance in near real time and in a more direct manner that can be integrated with device function without therapeutic interference. We leverage dynamic heart-device interactions created by intentional perturbations in the support provided by the device to induce controlled changes in aortic pressure. Using the differences in aortic pressure during diastole at the two support levels and after modeling the vascular system as a two-element lumped parameter model, we can determine total cardiac output from flow waveforms estimated using calculated vascular resistance and capacitance. The resulting cardiac output is in close agreement with thermodilution measurements of cardiac output with superior limits of agreement when compared with prior studies studying thermodilution versus estimated Fick cardiac output measurement (− 30.7 to 20.3% vs. − 50.1 to 49.4%20). This result suggests that this approach can uniquely provide clinically meaningful estimations of cardiac output automatically and near continuously without additional devices or intervention. Of note, our approach provides cardiac output measurements with a calculated percentage error of 29.1% compared to TCO measurements which is similar what other investigators have reported for continuous pulmonary artery thermodilution and calibrated pulse contour analysis methods, 26.7 and 29.3%, respectively, currently used in clinical practice.5 These findings further confirm the clinical applicability and value of the reported methodology for determining cardiac output.
The ideal MCS device would use these metrics to direct operation to the level required to optimize the balance of myocardial oxygen consumption and systemic perfusion demands. In this way, potential for cardiac recovery can be optimized while maintaining end-organ viability. This scenario is profoundly different from the present reality of clinician-controlled mechanical support titrated to intermittently obtained diagnostics of uncertain value. Diagnostics integrated within a support device provide for more precise care guidance and the potential for automated and self-titrating support to preset targets. This capability mirrors the advances made with mechanical ventilators which began as open-loop fixed volume or pressure gas delivery that forced air into the lungs of patients with respiratory failure. Today these machines provide volume, pressure and gas content based on continuous metrics of pulmonary function derived from device-lung interactions. We envision a similar evolution of mechanical circulatory support in which integrated diagnostics provide real-time information on the state of the cardiac and vascular systems allowing for titration of support to physiological state. These integrated metrics may prove to be of particular importance in guiding the clinician on the challenge of weaning mechanical support. Integrated measures of left ventricular filling pressures and the contribution of the heart to total cardiac output will aid the clinician in determining a patient’s readiness for weaning while also providing near-instantaneous feedback on the patient response to reductions in support.
The work presented here, when coupled with prior work detailing a novel method to continuously estimate left ventricular end diastolic pressure,3 lay the foundation for a truly automated mechanical circulatory support device capable of titrating support to the physiological state of the patient. Forward flow through the heart can be theoretically titrated to optimize filling pressures of the left ventricle in an effort to improve cardiac function and decrease cardiac work while simultaneously meeting total perfusion targets. We posit that part of the lack of evidence to date for improved outcomes with MCS derives from the lack of adequate diagnostics to guide therapy. Current evidence suggests that improved access to metrics of cardiovascular state improves outcomes for critically ill patients requiring mechanical support.6,18 By leveraging the interconnected relationship between device flow and cardiac pulsatility to obtain diagnostic metrics while simultaneously providing mechanical support, our approach reduces the barrier to obtaining vital information require to guide therapy. We anticipate that improved titration will better ensure adequate support is obtained and thereby achieve the therapeutic promise of MCS devices.
Study Limitations and Future Work
The underlying assumption of the method is that the changes in aortic pressure that follow support pulsing primarily arise from changes in Impella support and forward cardiac flow without any confounding physiologic alteration. It is assumed that cardiac behavior remains in the linear regime and that patients on support will not be volume limited over the range of flow changes from pulse variation. The assumption that the majority of the measured pressure in the diastolic decay is due to forward flow is partially supported by of the positioning of the aortic pressure sensor close to the heart and the measured pressure closer resembling systolic pressure augmentation8 (Fig. 1b). However, there would still be an effect of pressure reflection waves on the diastolic decay portion and may be a source of increased variability and biases. Diastolic augmentation from reflection waves would increase the measured pressure leading to underestimation of decay rates and thus systemic vascular resistance. This could be a cause of the bias in lower values of calculated R (Fig. 5). The presence of larger deviations between SVR and R through the midrange of systemic vascular resistances (Fig. 5a) could be due to the balance of high resistances leading to earlier systolic augmentation and lower resistances have reduced amplitude of reflection. Addressing the impact of reflection waves can improve the reliability of this approach as well as potentially provide additional insights into the state of the vasculature. However, the results of our current approach already improve upon existing clinical measures for cardiac output while introducing additional capability of automation and semi-continuous measurement.
In addition to the underlying assumptions on the pressure waveform itself, multiple factors can induce temporal variability in systemic pressures. These include respiratory driven changes in venous return and changes in vascular impedance. In response, we average pressures at different Impella speeds reducing transient effects of the respiratory cycle and assume that changes in vascular impedance are minimized with the use of shorter duration step-wise speed variations over two seconds. Moreover, as calculations are limited solely to diastole, variations in Impella flow prediction and aortic pressure seen in systole due to native cardiac contribution to flow are limited.4 We further appreciate that like all hemodynamic monitors, irregular heart rhythms may pose a challenge as beat-to-beat variability in stroke volume, such as with atrial fibrillation or with frequent premature ventricular contractions, might induce changes in the aortic pressure waveform.
Future work will focus on clinical application of the method to validate its effects in patients with cardiogenic shock. Longer term work will focus on development of automated methods to integrate control of support with device diagnostics to create a self-controlled device. Application of these metrics to titrate support create new opportunities to expand use of mechanical support and to determine if improved feedback and use of timely metrics may improve patient outcomes.
REFERENCES
- 1.Burkhoff D, Sayer G, Doshi D, and Uriel N. Hemodynamics of mechanical circulatory support. J. Am. Coll. Cardiol 66:2663–2674, 2015. [DOI] [PubMed] [Google Scholar]
- 2.Casas B, et al. Bridging the gap between measurements and modelling: a cardiovascular functional avatar. Sci Rep 2017. 10.1038/s41598-017-06339-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chang BY, Keller SP, Bhavsar SS, Josephy N, and Edelman ER. Mechanical circulatory support device-heart hysteretic interaction can predict left ventricular end diastolic pressure. Sci. Transl. Med 10:eaao2980, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chang BY, Keller SP, and Edelman ER. Leveraging device-arterial coupling to determine cardiac and vascular state. IEEE Trans. Biomed. Eng 66:2800–2808, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cho YJ, Koo CH, Kim TK, Hong DM, and Jeon Y. Comparison of cardiac output measures by transpulmonary thermodilution, pulse contour analysis, and pulmonary artery thermodilution during off-pump coronary artery bypass surgery: a subgroup analysis of the cardiovascular anaesthesia registry at a single tertiary centre. J. Clin. Monit. Comput 30:771–782, 2016. [DOI] [PubMed] [Google Scholar]
- 6.Cooper LB, et al. Hemodynamic predictors of heart failure morbidity and mortality: fluid or flow? J. Card. Fail 22:182–189, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dandel M, and Hetzer R. Myocardial recovery during mechanical circulatory support: weaning and explantation criteria. Hear. Lung Vessel 7:280–288, 2015. [PMC free article] [PubMed] [Google Scholar]
- 8.Denardo SJ, Nandyala R, Freeman GL, Pierce GL, and Nichols WW. Pulse wave analysis of the aortic pressure waveform in severe left ventricular systolic dysfunction. Circ. Hear. Fail 3:149–156, 2010. [DOI] [PubMed] [Google Scholar]
- 9.Dhingra VK, Fenwick JC, Walley KR, Chittock DR, and Ronco JJ. Lack of agreement between thermodilution and Fick cardiac output in critically ill patients. Chest 122:990–997, 2002. [DOI] [PubMed] [Google Scholar]
- 10.Francis SE Continuous estimation of cardiac output and arterial resistance from arterial blood pressure using a third-order Windkessel model. 89, 2007. [Google Scholar]
- 11.Gidwani UK, and Goel S. The pulmonary artery catheter in 2015: the Swan and the Phoenix. Cardiol. Rev 24:1–13, 2016. [DOI] [PubMed] [Google Scholar]
- 12.Heerdt PM, Blessios GA, Beach ML, and Hogue CW. Flow dependency of error in thermodilution measurement of cardiac output during acute tricuspid regurgitation. J. Cardiothorac. Vasc. Anesth 15:183–187, 2001. [DOI] [PubMed] [Google Scholar]
- 13.Ikuta K, et al. National Trends in Use and Outcomes of Pulmonary Artery Catheters Among Medicare Beneficiaries, 1999–2013. JAMA Cardiol. 2:908–913, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Khera R, et al. Trends in the use of percutaneous ventricular assist devices: analysis of National Inpatient Sample data, 2007 through 2012. JAMA Intern. Med 175:941–950, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kubo SH, Burchenal JEB, and Cody RJ. Comparison of direct fick and thermodilution cardiac output techniques at high flow rates. Am. J. Cardiol 59:384–386, 1987. [DOI] [PubMed] [Google Scholar]
- 16.Laskey WK, Parker HG, Ferrari VA, Kussmaul WG, and Noordergraaf A. Estimation of total systemic arterial compliance in humans. J. Appl. Physiol 69:112–119, 1990. [DOI] [PubMed] [Google Scholar]
- 17.Marik PE Obituary: pulmonary artery catheter 1970 to 2013. Ann. Intensive Care 3:38, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nalluri N, et al. Temporal trends in utilization of right-sided heart catheterization among percutaneous ventricular assist device recipients in acute myocardial infarction complicated by cardiogenic shock. Am. J. Cardiol 122:2014–2017, 2018. [DOI] [PubMed] [Google Scholar]
- 19.O’Neill WW, and Ohman EM. Impella support for acute myocardial infarction complicated by cardiogenic shock: matched-pair IABP-SHOCK II trial 30-day mortality analysis’. Circulation 140:e557–e558, 2019. [DOI] [PubMed] [Google Scholar]
- 20.Opotowsky AR, et al. Thermodilution vs estimated Fick cardiac output measurement in clinical practice: an analysis of mortality from the Veterans Affairs Clinical Assessment, Reporting, and Tracking (VA CART) program and Vanderbilt University. JAMA Cardiol. 2:1090–1099, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ouweneel DM, et al. Percutaneous mechanical circulatory support versus intra-aortic balloon pump in cardiogenic shock after acute myocardial infarction. J. Am. Coll. Cardiol 69:278–287, 2017. [DOI] [PubMed] [Google Scholar]
- 22.Parviainen I, Jakob SM, Suistomaa M, Takala J, and Scandinavian Society of Anaesthesiology and Intensive Care Medicine (SSAI). Practical sources of error in measuring pulmonary artery occlusion pressure: a study in participants of a special intensivist training program of The Scandinavian Society of Anaesthesiology and Intensive Care Medicine (SSAI). Acta Anaesthesiol. Scand 50:600–603, 2006. [DOI] [PubMed] [Google Scholar]
- 23.Pirbodaghi T, Weber A, Carrel T, and Vandenberghe S. Effect of pulsatility on the mathematical modeling of rotary blood pumps. Artif. Organs 35:825–832, 2011. [DOI] [PubMed] [Google Scholar]
- 24.Rihal CS, et al. 2015 SCAI/ACC/HFSA/STS clinical expert consensus statement on the use of percutaneous mechanical circulatory support devices in cardiovascular care. J. Am. Coll. Cardiol 65:e7–e26, 2015. [DOI] [PubMed] [Google Scholar]
- 25.Schrage B, et al. Impella support for acute myocardial infarction complicated by cardiogenic shock. Circulation 139:1249–1258, 2019. [DOI] [PubMed] [Google Scholar]
- 26.Stolin ski, J., Rosenbaum C, Flameng W, and Meyns B. The heart-pump interaction: effects of a microaxial blood pump. Int. J. Artif. Organs 25:1082–1088, 2002. [DOI] [PubMed] [Google Scholar]
- 27.Tayara W, et al. Improved survival after acute myocardial infarction complicated by cardiogenic shock with circulatory support and transplantation: comparing aggressive intervention with conservative treatment. J. Hear. Lung Transplant 25:504–509, 2006. [DOI] [PubMed] [Google Scholar]
- 28.Thiele H, et al. Intraaortic balloon support for myocardial infarction with cardiogenic shock (IABP-SHOCK II trial). N. Engl. J. Med 367:1287–1296, 2012. [DOI] [PubMed] [Google Scholar]
- 29.Watson PF, and Petrie A. Method agreement analysis: a review of correct methodology. Theriogenology 73:1167–1179, 2010. [DOI] [PubMed] [Google Scholar]
- 30.Westerhof N, Elzinga G, and Sipkema P. An artificial arterial system for pumping hearts. J. Appl. Physiol 31:776–781, 1971. [DOI] [PubMed] [Google Scholar]
- 31.Westerhof N, Lankhaar JW, and Westerhof BE. The arterial windkessel. Med. Biol. Eng. Comput 47:131–141, 2009. [DOI] [PubMed] [Google Scholar]
- 32.Abiomed Impella CP ® instructions for use & clinical reference Manual., 2011. [Google Scholar]


