How hydrogel inclusions modulate the local mechanical response in early and fully formed post-infarcted myocardium

Abstract

Expansion of myocardium after myocardial infarction (MI) has long been identified as the primary mechanism that progresses adverse left ventricular (LV) remodeling towards heart failure and death. Direct injection of hydrogels into the myocardium to mechanically constrain the infarct has demonstrated promise in limiting its remodeling and expansion. Despite early successes, there remain open questions in the determination of optimal hydrogel therapies, key application characteristics for which include injected polymer volume, stiffness, and spatial placement. Addressing these questions is complicated by the substantial variations in infarct type and extent, as well as limited understanding of the underlying mechanisms. Herein, we present an investigation on how hydrogel inclusions affect the effective stiffness and strain fields in myocardium using full three-dimensional (3D) finite element simulations of early and late post-MI time points. We based our analysis on triaxial mechanical and structural measurements from cuboidal specimens of LV post-infarcted myocardium, 0 and 4 weeks post-MI, injected with a dual-crosslinking hyaluronic acid-based hydrogel. Simulations included multiple deformation modes that spanned the anticipated physiological range in order to assess the effects of variations in inclusion size, location, and modulus on tissue-level myocardial mechanics. We observed significant local stiffening in the hydrogel-injected specimens that was highly dependent on the volume and mechanical properties of the injected hydrogel. Simulations revealed that the primary effect of the injections under physiological loading was a reduction in myocardial strain. This result suggests that hydrogel injections reduce infarct expansion by limiting the peak strains over the cardiac cycle. Overall, our study indicated that modulation of the effective tissue stiffness and corresponding strain reduction are governed by the volume and stiffness of the hydrogel, but relatively insensitive to precise placement. These findings provide important insight into mechanisms for ameliorating post-MI remodeling, as well as guidance for the future design of post-MI therapies.

Graphical Abstract

1. Introduction

Heart failure is one of the most widespread causes of death worldwide [1]. A major heart disease is the detrimental remodeling of the left ventricle (LV) after myocardial infarction (MI). Specifically, expansion of infarct has been identified as the sustaining factor that progresses post-MI remodeling [2–5], causing elevations in heart wall stress accompanied by a cascade of complex remodeling events [6–8]. As such, mitigation of infarct expansion, in part driven by a reduction of ventricular wall stress, has been a critical target of therapeutic interventions for MI. One method taken has been implantation of acellular polymeric biomaterials directly into the infarct region of the LV wall [9–11]. Results have demonstrated an improved maintenance of cardiac function post-infarction. Approaches have encompassed a wide range of materials, including hyaluronic acid and alginate polymers of varying stiffnesses and degradation characteristics [11–15], and have offered the possibility for developing minimally invasive surgical procedures.

Nevertheless, challenges remain in the full clinical realization of this exciting intervention. Many important aspects, such as the stiffness, volume, and placement (at both a single point and collectively) of the injected biomaterial can all influence the efficacy injectionbased therapies. It is obviously not feasible to use preclinical animal experimentation alone to evaluate all of these interrelated parameters. In-silico approaches can be leveraged to make these therapeutic applications a clinical reality. One of the unique advantages of computational modeling of cardiac function is its ability to estimate quantities that cannot be measured directly, such as ventricular wall stress. This is especially important, as there is a continued lack of understanding of the underlying mechanisms behind how polymeric inclusion reduces infarct expansion.

Use of computational modeling to assess injection therapies is not new [10, 16–18]. Extant studies, while informative, remain limited in accuracy and detail, occasionally excluding discrete injection volumes altogether [9, 13, 19] and using simplistic myocardium models that may not address how the hydrogel interacts with the surrounding tissue. Such considerations are critical, as myocardium is known to possess a hierarchical structure that produces multifaceted three-dimensional (3D) mechanical behavior [20]. This suggests that the interactions of injected biomaterials and the heart wall are similarly multifaceted and require further investigation with more sophisticated modeling efforts. Given the complexity of normal myocardial structure, let alone remodeled post-infarct myocardium, it is understandable that more advanced studies have yet to be undertaken.

As a step towards addressing these challenges, we have recently applied a novel numerical-experimental methodology [21] to develop a more realistic constitutive model for passive ventricular myocardium by integrating 3D optimal loading paths, spatially varying material orientations, and inverse modeling techniques. Our findings indicated previously unreported coupling behaviors deriving from the shearing of myofibers and extracellular collagen fibers in normal myocardium. Accurately modeling the myocardium mechanical behavior in the expanded kinematic space necessitated extension of a well-known constitutive model first proposed by Holzapfel and Ogden [22] with additional coupling-based terms. The modified model accurately reproduced all optimal loading paths, exhibited improved predictive capabilities, and implicated the need to investigate myocardial behavior under non-physiological conditions [20].

In the present study, we utilized a comprehensive in-silico approach, based on novel 3D experimental studies [20, 21] of hydrogel-injected post-infarct ventricular myocardium, to gain insight into the tissue-scale impact of hydrogel inclusions on post-infarcted myocardium. Focusing on changes in local effective stiffness and the stress and strain fields surrounding the inclusion, we quantify how polymeric injections modulate the myocardial mechanical environment and subsequent remodeling. In particular, we explore variations in the following key hydrogel injection characteristics: (i) placement, (ii) volume, and (iii) mechanical properties. These parameters are evaluated using myocardial properties acquired from two different time points post-MI, short-term (0 weeks) and long-term (4 weeks), in order to identify key metrics in the design of MI injection therapy.

2. Materials and Methods

2.1. Overall approach

We used the methods developed in Avaz et al. [21] and Li et al. [20] to first perform novel experimental studies on hydrogel-injected 1 × 1 × 1-cm cuboidal specimens of myocardium. 0 and 4 weeks post-MI time points were used to represent the immediate post-infarct and remodeled states, respectively. Results of these studies were then incorporated into forward simulations to perform parametric studies of how various hydrogel characteristics modulate the local mechanical responses of myocardium, as well as the effective response of the cuboidal volume. This was done for both applied and fundamental reasons. First, although a variety of different patterns and distributions of injectable hydrogels have been evaluated in both clinical and modeling studies within the literature, selection of delivered material volume, location of injection, and hydrogel mechanical properties are still done largely empirically. Second, we seek to gain insight on how a local polymeric inclusion affects the local responses of early- and later-stage post-MI myocardium. Given the unknowns of how inclusions can affect local mechanical behaviors in nonlinear, anisotropic, structurally complex biological tissues such as myocardium, such approaches are clearly necessary to put injection therapies on a stronger, engineering-based footing. Details of the methodologies are presented in the following.

2.2. Experimental methods

2.2.1. Dual-crosslinking injectable hydrogel

A hyaluronic acid (HA)-based hydrogel was developed that can be delivered into myocardium by percutaneous injection and undergoes dual-crosslinking (DC). Physical crosslinking via guest-host interaction retains the gels at the injection site. The in-vivo Michael-addition reaction subsequently increases the hydrogel modulus post-injection. These hydrogels have been synthesized from HA modified with admantane and thiols (Ad-HA-SH) or β-cyclodextrin and methacrylates (CD-MeHA), dissolved in phosphate buffered saline at 4.5 wt% and mixed in equimolar ratios at pH 5 [14]. DC hydrogels exhibit compressive moduli of 25.0–41.4 kPa [14, 23] and have been evaluated in ovine posterolateral infarcts. Animals subjected to post-MI hydrogel injection exhibited reduced LV remodeling, maintained heart wall thickness, and improved ejection fraction relative to untreated MI after 8 weeks.

2.2.2. Mechanical characterization of injected myocardium

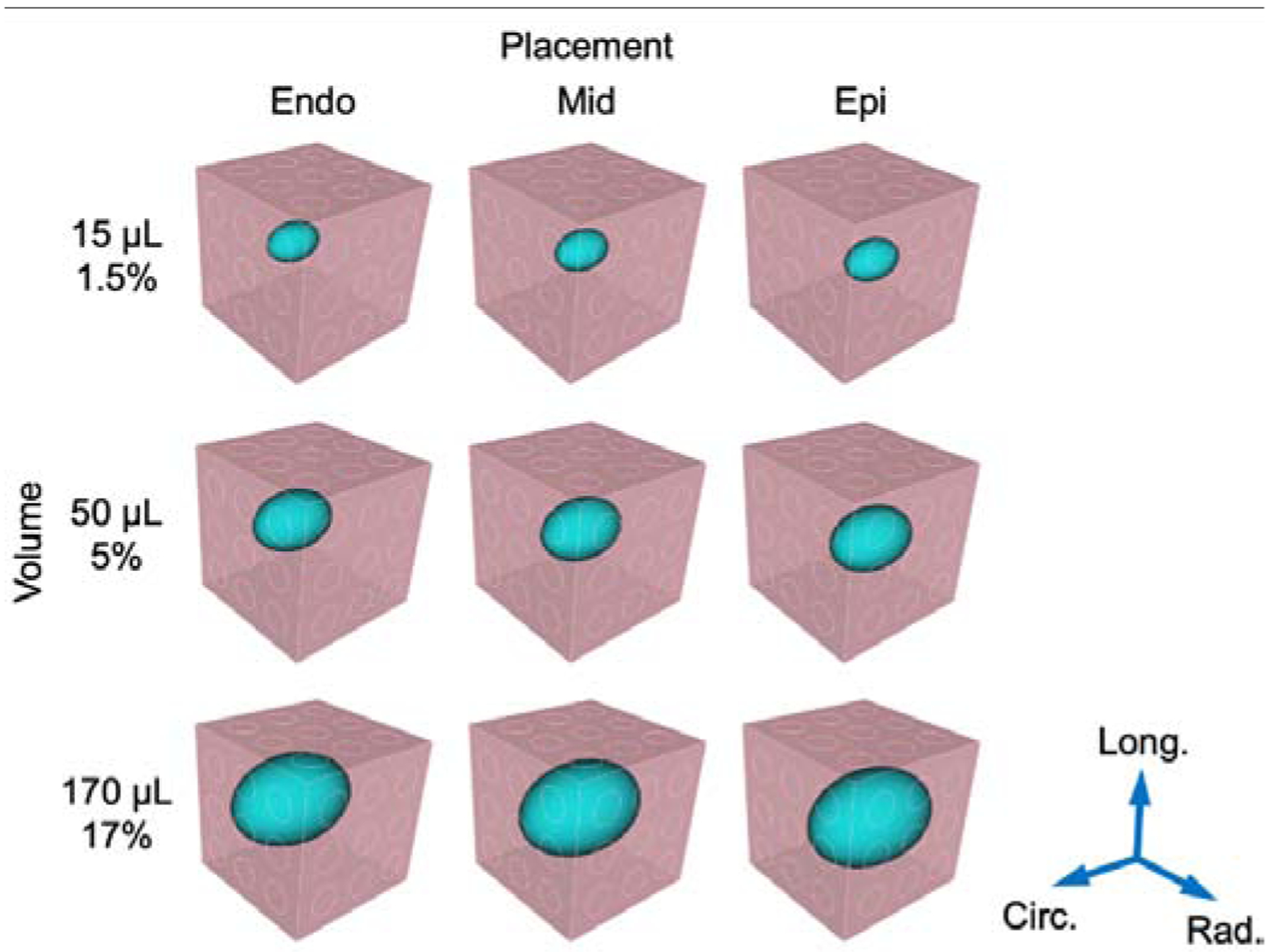
Sections of noninfarcted LV myocardium were obtained from a cohort of adult Dorset sheep (n=6) through methods previously described [20, 21]. Each sample spanned the full LV wall thickness, with edges of the specimens aligned with the longitudinal, circumferential, and radial directions of the LV (Fig. 3 in [20]). Animals in this study were used in compliance with the National Institute of Health’s guidelines for care of laboratory animals, with approval by the Institutional Animal Care and Use Committee at the University of Pennsylvania (805038) and the University of Texas at Austin (AUP-2017–00204). Immediately post-harvest, 100-μL injections of either cardioplegic solution (Plegisol) as a control or DC hydrogel were administered, with the injection site at the approximate cuboid center. The myocardium samples were subsequently incubated immersed in cardioplegic solution with 20 mM 2,3-butanedione monoxime for 24 hours at 37 °C and 5% CO₂ to allow for hydrogel crosslinking. After crosslinking had completed, the sections were trimmed to 1 × 1 × 1-cm cuboids for mechanical testing, where the full 3D triaxial response was measured with optimally selected deformation protocols (Fig. 1) [20, 21]. Each protocol was applied as a cyclic deformation with a 30-second cycle time to minimize preconditioning effects. Strain ranges measured in mechanical testing are described in [20], with κ ≈ 0.4 in all shears and λ ≈ 1.2 and 0.85 in tension and compression, respectively.

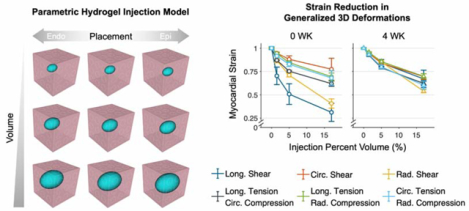
Fig. 3: Model geometries used in the simulation study.

Injection (blue) placement was varied along the radial direction at endocardial (endo), midwall (mid), and epicardial (epi) locations within the myocardium cuboid (pink). Injection volume ranged 1.5%–17% of the total region volume. A separate FE mesh was constructed for each combination of the hydrogel characteristics.

Fig. 1: Optimal 3D deformation modes.

Triaxial testing protocols consisting of simple shear and tension-compression modes, as used in previous studies [20]. Abbreviations: long., longitudinal; circ., circumferential; rad., radial.

2.2.3. Structural characterization of injected myocardium

As in previous work, myocardium specimen fiber structure was quantified using diffusion tensor imaging (DTI) [20, 24–28]. Each scan produced a 400-μm isotropic voxel array containing spatially varying 3D vectors describing the local fiber-sheet-normal orientations within the tissue. The fiber structure was generated by dividing the radial direction into 20–25 levels, each of which contained a set of three mutually orthogonal vectors representing the fiber, sheet, and normal directions. As in our previous studies, it was assumed that the fiber structure did not vary within the circumferential-longitudinal plane, which was found to have a negligible effect on subsequent mechanical simulations [20]. For each transmural level, averaged 3D orientation vectors were computed per plane (Fig. 2) in order to summarize the injected specimen fiber structure.

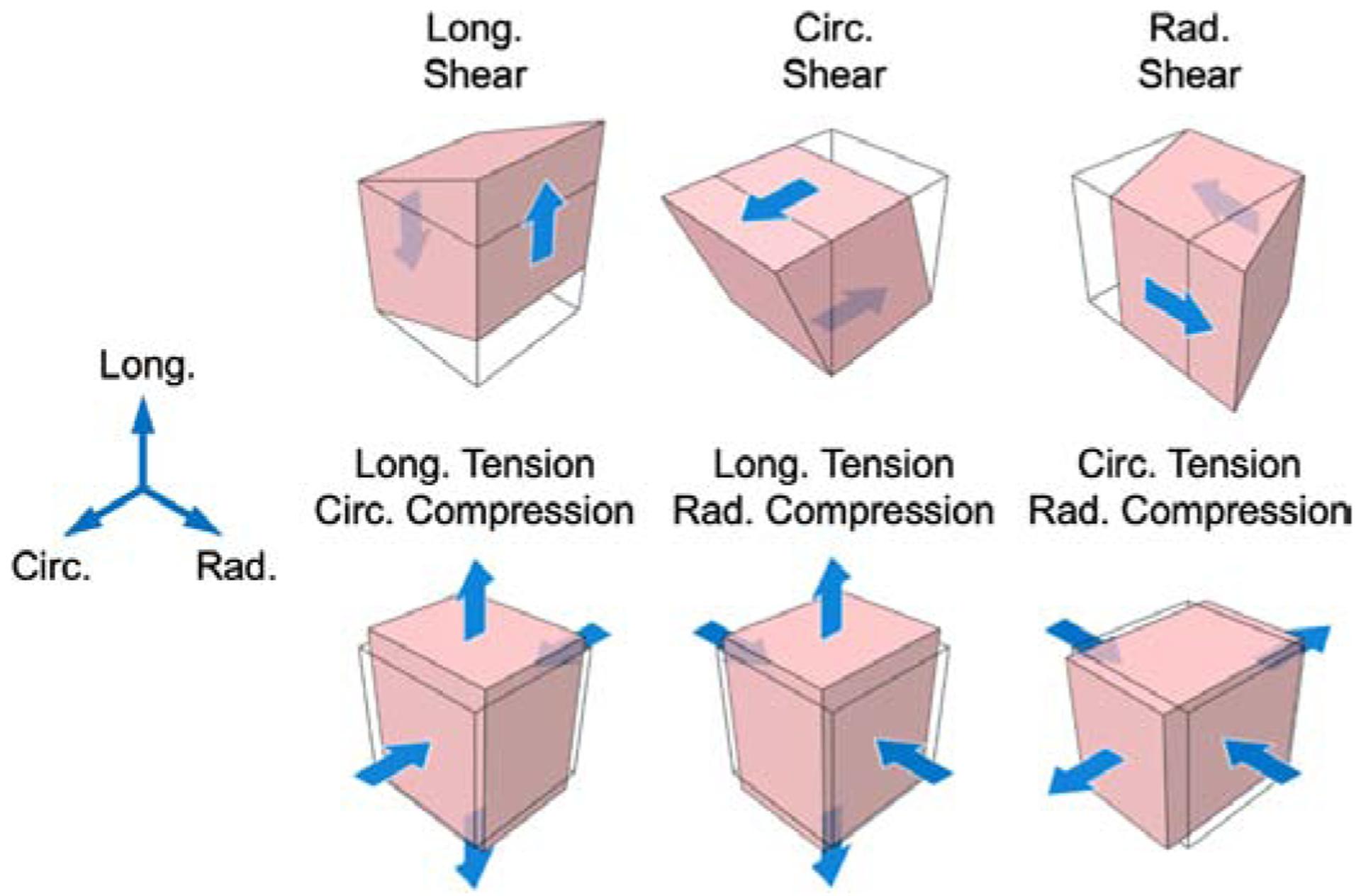
Fig. 2: Finite element model development pipeline.

Fiber orientations from DTI assigned onto myocardium mesh (pink). Hydrogel geometry segmented from DTI and idealized to prolate spheroid to yield the final FE model.

2.2.4. Analysis of injected myocardium tissue-level mechanics

From the triaxial testing experiments, we computed a maximum effective tangent modulus M (experimentally measured) for each deformation mode directly from the mechanical response data. M was obtained from the slope of the relevant component(s) of the first Piola-Kirchhoff stress tensor P as a function of the corresponding component(s) of the deformation gradient tensor F, for simple shear and tension-compression modes at maximum deformation.

2.3. Simulations of myocardial mechanical responses to injection

2.3.1. Finite element model formulation

As in our past investigations [20, 21], we employed finite element (FE) volume meshes of linear tetrahedra (~0.6–0.7-mm edge length, approximately 14–15 elements per cuboid edge) to model the triaxial deformations and compute stresses in the injected myocardium. Myocardium elements were assigned material orientations according to an interpolation of the vectors of the DTI voxels within a local neighborhood around each element centroid.

2.3.2. Variation of hydrogel injection characteristics

Our aim herein was to assess the impact of hydrogel inclusion characteristics within a representative volume. We confined our attention to a 1-cc tissue volume in order to better isolate the localized effects of injection in the context of well defined, generalized deformation modes. Additionally, this was done to match the length scale of the experimental and simulation studies, where the 1-cc tissue volume allowed for tractable experiments to be performed, approximated realistic LV myocardium tissue-level behavior, and was local enough to study the effects of a single injection.

The geometry of the hydrogel injection was initially determined through segmentation of the corresponding B₀ image from the DTI in Simpleware ScanIP (Synopsys). The morphology of these injections was fairly ellipsoidal, with increased length in the circumferential direction. Thus, inclusions in the FE simulations were idealized as prolate spheroids embedded within the myocardium volume, 50% longer in the circumferential direction than in the longitudinal and radial directions (Fig. 2). We assumed the myocardium and hydrogel were perfectly bonded with a no-slip boundary.

Three inclusion placements and volumes were assessed, yielding a total of nine combinations. Since the location of the injection was varied as part of the in-silico study, we only utilized the shape of the injection and allowed the location to vary along the radial direction, centered in the circumferential-longitudinal plane. Placements were defined based on proximity to the endocardium, midwall, and epicardium, in order to encompass the entire treatment placement range. Next, selected volumes encompassed small (1.5% cube volume), intermediate (5% volume), and large (17% volume) inclusions, roughly corresponding to injections of 15, 50, and 170 μL (Fig. 3). Additionally, simulations of myocardium without hydrogel elements were performed to represent the control group. Finally, a range of hydrogel moduli from 0.1–100 kPa was assigned to the injection elements to assess the sensitivity of the effective tissue mechanics to hydrogel mechanical properties (Table 1). Injection results were compared against simulations of myocardium without hydrogel, for which multiple meshes were employed to evaluate the consistency of the finite element approach.

Table 1:

Characteristics considered in the hydrogel injection finite element model used for the in-silico sensitivity study.

Characteristic
Injection volume	15, 50, 170 μL
Injection placement	Endo, Mid, Epi
Hydrogel stiffness	0.1–100 kPa
Post-MI myocardial properties	0 weeks [20], 4 weeks [21]

2.3.3. Myocardial constitutive models

To represent the passive response of the myocardium, we utilized hyperelastic incompressible orthotropic material models [20, 21]. In particular, we used the constitutive form ψ_myo (Eq. 1), based on the extension of the form proposed by Holzapfel and Ogden [20, 22],

$${\psi }_{myo}=\frac{a}{2b}\left\{\mathrm{e}\mathrm{x}\mathrm{p}\left[b\left(I_1-3\right)-1\right]\right\}+\sum _{i=f,s}\frac{a_i}{2b_i}\left\{\mathrm{e}\mathrm{x}\mathrm{p}\left[b_i{\left(I_{4i}-1\right)}^2\right]-1\right\}+\sum _{i,j=f,s,n}\frac{a_{ij}}{2b_{ij}}\left[\mathrm{e}\mathrm{x}\mathrm{p}\left(b_{ij}{I}_{8ij}^2\right)-1\right],$$ (1)

where I₁, I_4i, and I_8ij are invariants of the right Cauchy-Green tensor C, and {a,…,b_ij} are the twelve constitutive parameters. Parameter values were scaled down from a representative parameter set from healthy myocardium (Equation 11 and S4 in Table 3 of [20]), which was determined using previous mechanical tests in the same full 3D kinematic space (Table 2). Specifically, we computed the reduction in total strain energy of the myocardium triaxial response relative to that of noninfarcted myocardium over all deformation modes (see Subsection 3.1), and applied the reduction coefficient to each parameter of the model. This was assumed to be a reasonable approximation for the myocardium at the early post-MI time point (0 WK), as the myocardium was no longer fully viable, but scar tissue had not yet begun to form.

Table 3:

Description of quantities of interest.

Quantity	Description
M	Maximum effective tangent modulus (experimentally measured)
m	Maximum tangent modulus (simulated)
$\widehat{m}$	Normalized maximum tangent modulus (simulated)
E1	Maximum principal Green-Lagrange strain
${\widehat{E}}_1$	Normalized maximum principal Green-Lagrange strain
ε1	Maximum principal logarithmic strain

Table 2:

Parameters of ψ_myo (Eq. 1) used in FE simulations. Values were uniformly scaled down according to the ratio of total strain energy between post-MI myocardium and healthy myocardium [20].

a (kPa)	b	af (kPa)	bf	as (kPa)	bs	afs (kPa)	bfs	afn (kPa)	bfn	asn (kPa)	bsn
0.00046	5.41	1.29	1.35	0.215	0.0378	0.160	0.00477	0.743	29.9	0.238	0.508

To predict the effects of hydrogel injection in long-term post-MI myocardium (4 WK), corresponding to administering injections after scar tissue has formed in the infarct region, we calibrated the mechanical properties of the myocardium elements in the model to the structural-mechanical dataset of post-infarcted myocardium (Equation 11 and Table 2 in [21]). For both time points, we simulated the same optimal deformation modes as in the triaxial experiments, maintaining the existing fiber structure and hydrogel geometry and modulus (Table 1). In each combination of inclusion placement and volume, the hydrogel was modeled using a Neo-Hookean form with a modulus of 25.0 kPa [23]. Simulations were performed using custom scripts in MATLAB (MathWorks, MA, USA) and ABAQUS (Dassault Systèmes, RI, USA).

2.3.4. Analysis of simulation results

Maximum tangent modulus.

To evaluate effective tissue-level stiffening as predicted by the finite element simulations, we used the same fixed-displacement approach as in the experiments and reproduced the strain ranges described above. Deformations were prescribed as Dirichlet boundary conditions to node subsets on each face to emulate the pad array of the triaxial attachments. Maximum tangent modulus m (simulated) was determined using the reaction forces computed on the mesh boundaries in all deformation modes for each of the parametric simulations (Fig. 4a).

Fig. 4: Representative finite element simulations of simple shear and tension-compression.

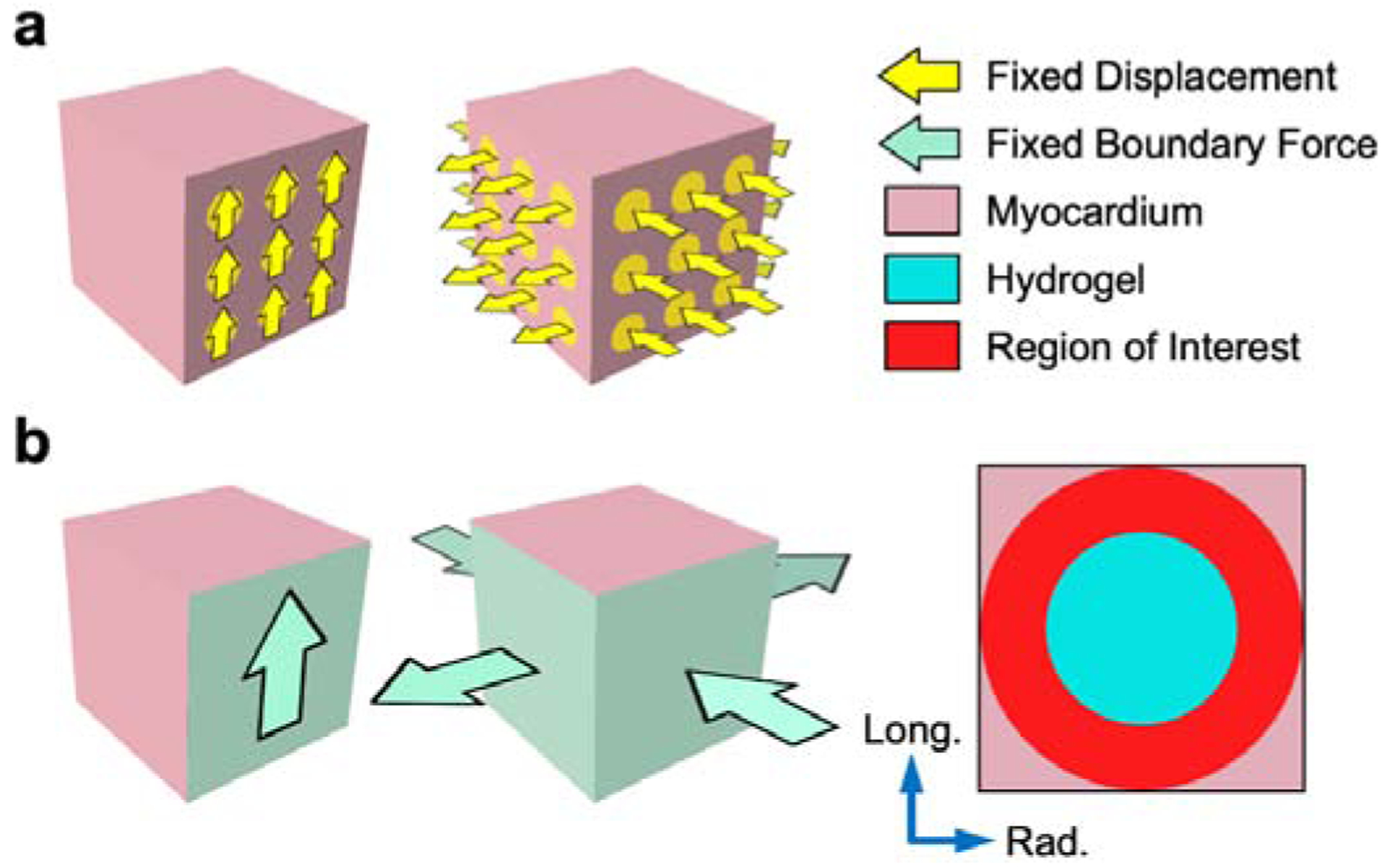
(a) Fixed displacement applied to experimental attachments (yellow). Maximum tangent modulus m computed from tangent slope of stress-stretch curve at maximum deformation. (b) Fixed boundary force applied to cuboid faces (green). Region of interest (red) in myocardium elements (pink) surrounding the injection (blue), over which maximum principal strain E₁ was evaluated for the fixed boundary force simulations.

Maximum principal strain.

Another remaining question in the understanding of hydrogel injection mechanics is to determine the effect of inclusions in the context of in-vivo loading conditions. We extended our simulation approach to include a fixed boundary force, stressbased design to approximate this in-vivo state and quantify the local myocardial strain fields in generalized 3D deformations. The optimal triaxial loading paths (Fig. 1) were represented as fixed forces applied to the entire cuboid boundary rather than the experimental attachments (Fig. 4b), with separate magnitudes for simple shear modes (50 N) and tension-compression modes (200 N in both directions), in order to achieve final strains comparable to the experimental testing.

At maximum deformation, the Green-Lagrange strain tensor E was calculated for all myocardium elements within a spherical region of interest centered in the cube domain, excluding both distal myocardium elements and hydrogel elements (Fig. 4b). A volume-averaged strain tensor E¯ was obtained by averaging each corresponding component of E across all elements in the region of interest and used to determine the maximum principal strain for the myocardium in each deformation mode. The maximum principal strain in each deformation mode E₁ was evaluated (i) for all placement-volume combinations at both post-MI time points, and (ii) as a function of hydrogel modulus for the mid-placed inclusion of 17% cuboid volume.

2.4. Statistical methods

Maximum effective tangent modulus M was computed from the experimental data and was presented as median and interquartile range. We used a nonparametric Mann-Whitney test to compare group averages, and p-values ≤ 0.05 were considered statistically significant.

Simulations varied by injection placement in the transmural direction, injection volume, hydrogel stiffness, and post-MI myocardium material parameters. We simulated the myocardium without hydrogel inclusion to emulate the control response, using n = 3 meshes with identical fiber orientation mappings and material properties. To assess maximum tangent modulus m and maximum principal strain E₁ as a function of injection volume, group averages of all transmural placements (endo, mid, epi) were computed at each volume (0%, 1.5%, 5%, and 17%), n = 3 for each group. Evaluating changes in maximum principal strain as a function of hydrogel stiffness was performed using only the 17% injection volume with a mid placement. These computations were done separately for both post-MI time points (0 WK and 4 WK).

Group-averaged m and E₁ were displayed as mean ± standard error of the mean (SEM). In the cases of maximum tangent modulus and maximum principal strain, we used a two sample t-test to compare group averages, and p-values ≤ 0.05 were considered statistically significant. All statistical analysis was performed using MATLAB.

3. Results

3.1. Experimental findings

The triaxial mechanical responses of the control and hydrogel-injected myocardium specimens were compared to those of noninfarcted [20] and long-term post-MI [21] tissues. The overall nonlinear shape of the stress-stretch curves observed in previous studies was preserved in the triaxial testing data for the injected specimen group, indicating that MI and the presence of hydrogel did not alter the general passive behavior profile. The post-MI myocardium exhibited some level of softening relative to noninfarcted myocardium, which can be seen in simple shear modes (27% change over all shears), but was comparable to the noninfarcted data in tension-compression (Fig. 5a). In contrast, the long-term post-MI myocardium had a substantially stiffer response than both the noninfarcted and post-MI tissues, consistent with the fact that long-term post-MI myocardium is comprised largely of collagenous scar tissue (Fig. 5a). The maximum stress reached in hydrogel-injected specimens was greater than the control in all deformations (on average, ~10% in simple shear and 68% in tension-compression) (Fig. 5b). The finite element simulations of hydrogel injection using myocardial properties at the short-term (0 WK) and long-term (4 WK) post-MI time points showed similar effects compared to simulated controls (Fig. 5c,d).

Fig. 5: Triaxial mechanical data and simulations.

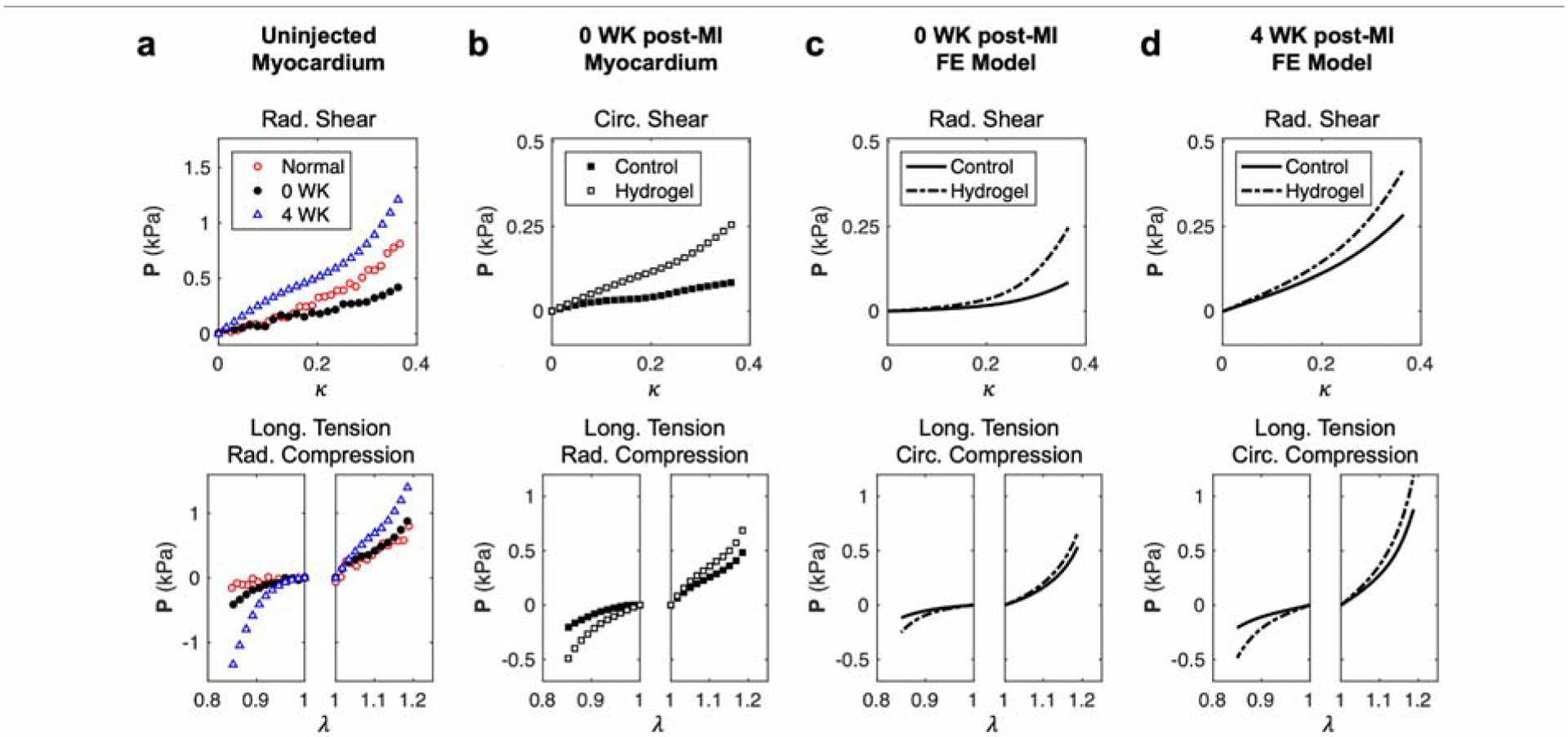
(a) Representative stress-stretch responses in simple shear and tension-compression for noninfarcted (red), 0 WK post-MI (black), and 4 WK post-MI (blue) myocardium without hydrogel injections. (b) Representative stress-stretch responses for 0 WK post-MI myocardium without (black) and with hydrogel injections (white). Representative fixed displacement finite element simulations of hydrogel injections with (c) 0 WK post-MI (orange) and (d) 4 WK post-MI (cyan) myocardial properties.

The moduli of tension-compression modes were also consistently higher than those of simple shear modes. We observed significant yet nonuniform stiffening in the mechanical response of hydrogel-injected tissues compared to control tissues. This effect was predominantly found in the tension-compression modes, with less observable effects in simple shear, although only some of the tension-compression modes exhibited a statistically significant increase in M, specifically in radial compression modes (Fig. 6). Despite the general trend of M increase resulting from hydrogel injection, in some cases, there was an apparent decrease in the moduli of injected tissues in simple shear.

Fig. 6: Comparison of maximum effective tangent modulus.

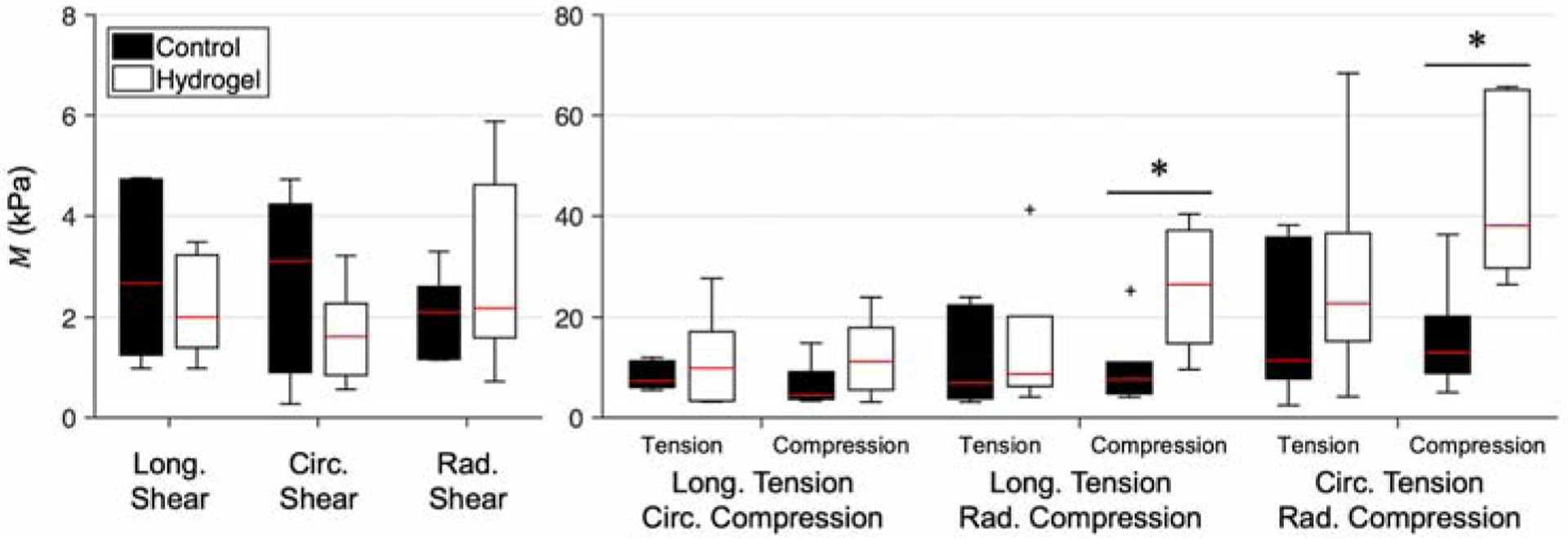
M derived from experimental mechanical testing data of control (black) and hydrogel-injected (white) myocardium, for each triaxial deformation mode. Quantities are grouped by deformation mode and shown in terms of median (red line) and interquartile range. *p ≤ 0.05 (n=6).

The transmurally varying 3D fiber structure maps obtained from DTI showed that the average fiber direction decreased from the endo- to epicardial sides of the specimens by roughly 100–120°. Using the B₀ image, we were able to clearly distinguish the shape of the crosslinked hydrogel within the tissue samples, whereas in control tissues the cardioplegic solution had washed out by 24 hours. Consistent with histological evidence of previous works, the injected gel was completely bonded to the surrounding myocardium, similar to typical foreign body reactions [29]. General structural characteristics of the injected tissue consisted of local distortion in the fiber direction parallel to the injection boundary, and myofibers along the injection boundary had a stretched appearance. Beyond 3–5 mm away from the periphery of the hydrogel injection, the myofiber structure was not significantly perturbed.

3.2. Simulation results

3.2.1. Sensitivity to injection volume and placement

Maximum tangent modulus.

Similar to the mechanical testing outcomes, the FE simulations achieved the same overall stiffening, also dependent on the direction of deformation. m was found to be sensitive to both injection placement and injection volume, though to varying degrees. Grouping the transmural placements by injection volume revealed that the group-averaged m increased as injection volume increased. Comparing the 0 WK and 4 WK post-MI myocardium mechanical properties, we observed the long-term post-MI tissue to have a greater baseline (uninjected) stiffness in nearly all deformation modes. Although m at short-term post-MI exhibited a more nonlinear response to increasing injection volume, it showed a more linear increase at long-term post-MI.

We evaluated the proportional increase of maximum tangent modulus $\left(\widehat{m}\right)$ by normalizing to the mean m of the uninjected myocardium simulations. This revealed that the presence of hydrogel injection had similar relative effects for both the short- and long-term time points at intermediate volumes, only exhibiting more noticeable differences with increases between ~1.5 to 22% for the largest volume (Fig. 7). As also seen in the experimental analysis, $\widehat{m}$ was most altered in the compression direction of tension-compression modes. For injection volumes smaller than 5% cube volume, variation of injection placement did not dramatically alter $\widehat{m}$, shown by the low standard error at small volumes (Fig. 7). For the largest injection volume (17%), there was greater sensitivity to injection placement in all deformations, especially the tension-compression modes, as can be seen in the large standard error (Fig. 7). In some shear modes, high-volume injections led to dramatic differences in $\widehat{m}$ (Fig. 7); however, the softening observed in some experiments (Fig. 6) was not reproduced by the simulations.

Fig. 7: Normalized maximum tangent modulus as a function of injection volume.

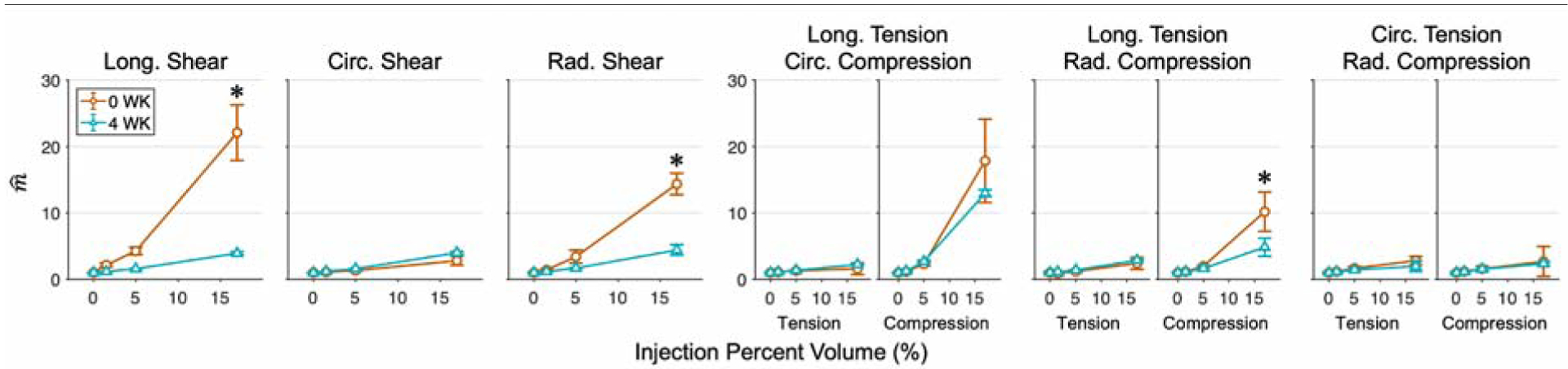
$\widehat{m}$ derived from finite element simulations of injected myocardium with hydrogels of increasing volume for the 0 WK (orange) and 4 WK (cyan) post-MI time points. Quantities normalized to the mean m of uninjected myocardium simulations and averaged across multiple meshes for control (0%) and across all placements for each injection volume, displayed as Mean ± SEM. Significant differences between the 17% injection of the 0 WK and 4 WK time points indicated with *p ≤ 0.05.

Maximum principal strain.

The long-term post-MI tissue exhibited substantially lower baseline strains compared to the short-term time point for a given fixed boundary force. The maximum principal strain E₁ decreased with increasing injection volume in a mildly nonlinear manner, with decreases tapering off for larger volumes. As discussed above, injection volume was found to have a greater influence on E₁ than placement. This decrease was observed in all deformation modes considered in this study, with significant reductions beyond 5% volume (Fig. 8).

Fig. 8: Maximum principal strain as a function of injection volume.

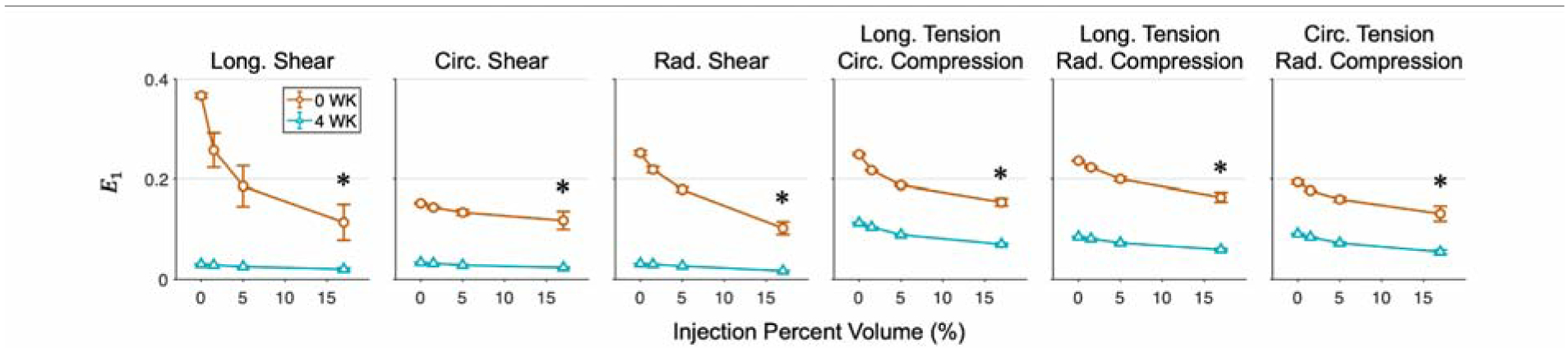
Maximum principal strain derived from finite element simulations of injected myocardium with hydrogels of varying placement and volume for the 0 WK (orange) and 4 WK (cyan) post-MI time points. Quantities are averaged across multiple meshes for control (0%) and across all placements for each injection volume, displayed as Mean ± SEM. Significant differences between the 17% injection of the 0 WK and 4 WK time points indicated with *p ≤ 0.05.

Normalizing the maximum principal strain to the mean strain of the uninjected myocardium simulations $\left({\widehat{E}}_1\right)$ demonstrated that the relative effect of hydrogel placement and size was somewhat sensitive to the choice of model, and was moderately dependent on the deformation type, with strain reductions ranging more widely (~23–69%) for the 0 WK model and more narrowly (~31–40%) for the 4 WK model (Fig. 9).

Fig. 9: Normalized maximum principal strain as a function of injection volume.

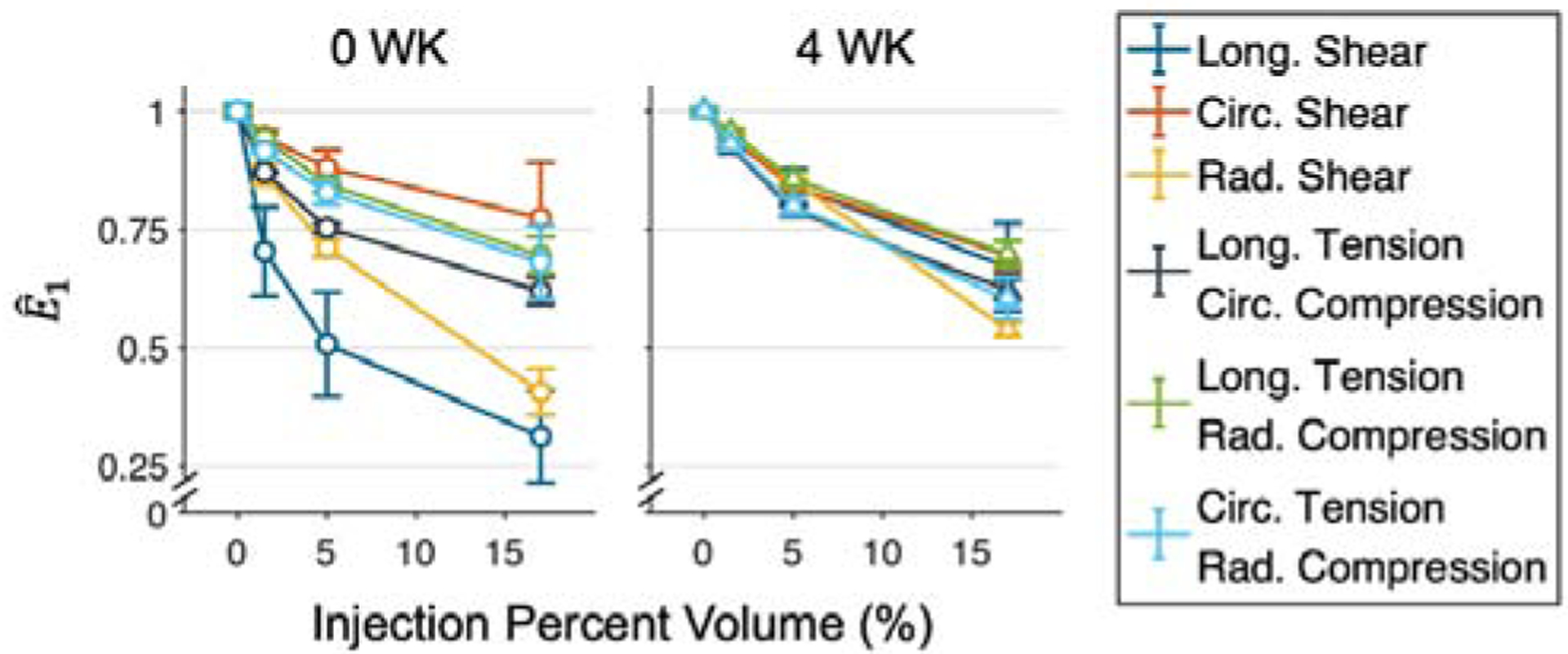
Quantities are normalized to the mean E₁ of uninjected myocardium simulations. Reductions of 23–69% are observed for the 0 WK time point, and 31–40% for the 4 WK time point.

3.2.2. Sensitivity of myocardial strain to injection mechanical properties

Maximum principal strain was also evaluated as a function of injection modulus for the mid-placed, largest injection volume (17%) at both time points. Increasing injection modulus at this placement-volume combination was found to decrease myocardial strain at a decreasing rate, with a range of 29–76% decrease for 0 WK and 33–53% decrease for 4 WK, depending on deformation mode, for the stiffest hydrogel. For all deformation modes, the trend resembled an exponential decay, tapering off beyond 25–50 kPa (Fig. 10).

Fig. 10: Maximum principal strain as a function of injection stiffness.

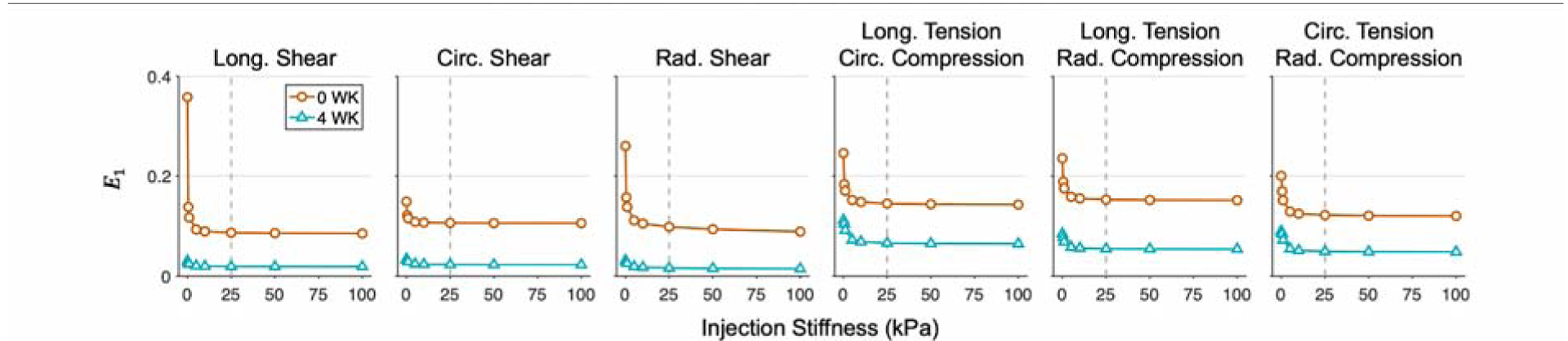
E₁ of the 0 WK and 4 WK post-MI time points undergoing optimal deformations modes with increasing hydrogel modulus. The largest injection volume (17%) at mid placement is evaluated. Further increases in modulus have a minimal effect beyond stiffness values indicated by the dotted gray lines.

4. Discussion

Using an in-silico platform based on full 3D kinematics and mechanical-structural data, we have evaluated the tissue-level impacts of DC hydrogel inclusions and predict their sensitivity to parameters such as inclusion location and size, hydrogel stiffness, and myocardial mechanical properties. The information obtained in this study demonstrates that hydrogel injection increases the passive stiffness of myocardium. However, the injection does not simply stiffen the tissue in a bulk sense, but produces complex local mechanical effects, necessitating the present methods. Interestingly, the primary effect of the injections under physiological loading is reduction in myocardial strain. This result suggests that hydrogel injections reduce infarct expansion by limiting the peak strains over the cardiac cycle, possibly below some trigger level. The findings discussed in the following offer supporting evidence for the efficacy of the hydrogel injection approach to limit post-MI LV remodeling via regional strain reductions.

4.1. Heterogeneous effects of hydrogel injection

There was a high degree of variation in maximum effective tangent modulus, potentially due in part to interspecimen variability in passive mechanical properties (and possibly fiber structure), which may have also contributed to apparent decreases in the median value of M for injected tissue if some uninjected specimens exhibited a particularly high baseline M. Other work has suggested that injection leads to an increase in passive stiffness upwards of 300 times that of normal myocardium and 50 times infarcted myocardium; however, we do not observe such increases with the hydrogel and volume used in this study. Additionally, in light of the fact that injection position demonstrated a mild influence on the resulting tissue stiffness at the 100-μL volume range used in triaxial testing (between the intermediate-and large-sized inclusions in the study), there is potential that the hydrogel location after crosslinking contributed to this complex profile of mechanical effects, as there were undoubtedly differences in the final injection shape from one specimen to another. Still, the relative lack of sensitivity of the inclusion’s mechanical effects to its precise position suggests that precise placement of the injections is not critical. This result has important practical implications in the clinic, where precise injection placement is understandably difficult but shown here to be non-critical.

4.2. Injection volume has a greater influence on effective properties

The outcomes of our simulation study reveal that m and E₁ are both sensitive to the parameters considered in this investigation, although less so to the location of the injection. The finding is intuitive in that the greater volume of hydrogel that is delivered, the greater effect it is capable of producing. Similar sensitivity studies have also demonstrated the same effect of decreased myocardial stress and strain with increasing injection volume in the myocardium [17]. This effect is highlighted when examining two-dimensional (2D) cross sections of the maximum principal logarithmic (Hencky) strain ε₁ with increasing inclusion volume and stiffness. In the simulations of uninjected myocardium, variations in the myocardial strain profile are likely due to the heterogeneous fiber structure of the specimens. With the introduction of the smallest-volume hydrogel inclusion, significant alterations to the strain profile are immediately apparent, where the maximum principal strain is consistently reduced up to ~5 mm beyond the hydrogel-myocardium interface. Further increases in hydrogel volume continue to drive down the local strain, even up to the boundary of the specimen (Fig. 11).

Fig. 11: Cross-sectional view of maximum principal strain with increasing injection volume.

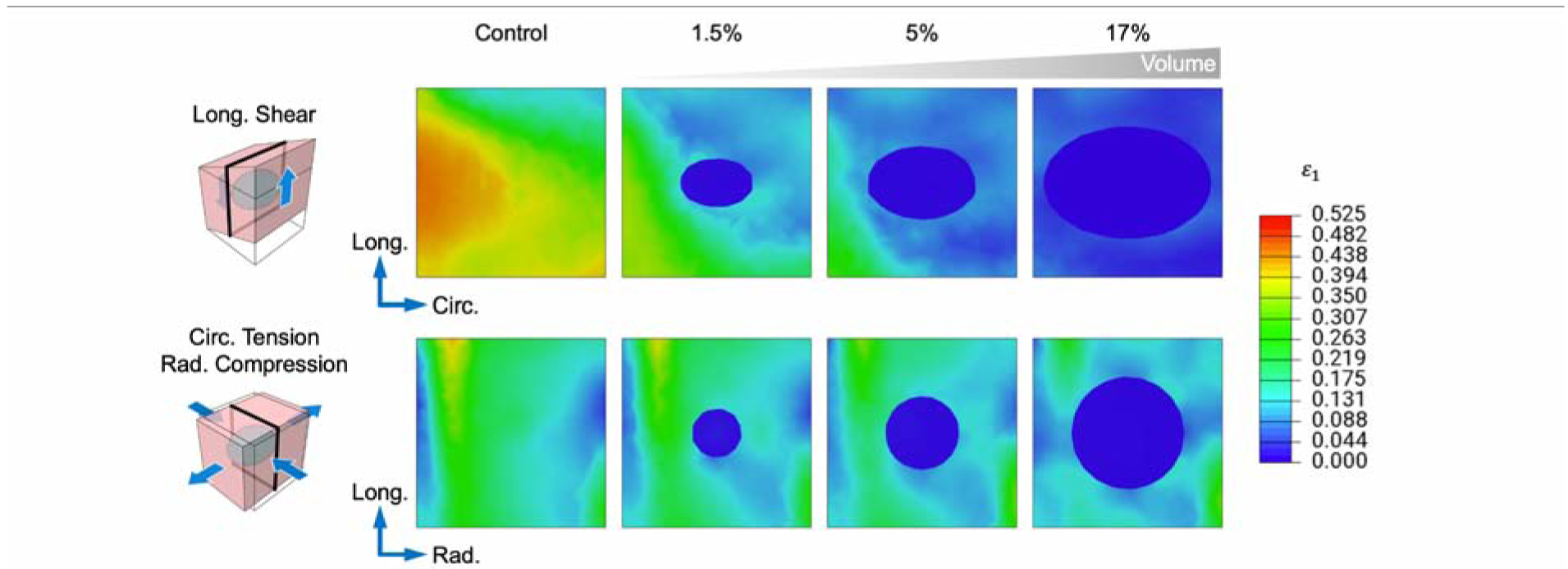
Localized strain reductions surrounding the inclusion as volume is increased. Hydrogel modulus = 25.0 kPa. For clarity, a single representative shear and tension-compression mode pair for the 0 WK time point is shown. Cross sections indicated by black outline.

Increasing hydrogel mechanical properties also has diminishing returns in terms of inducing strain reduction within the myocardium. Hydrogel inclusions with the lowest stiffness (0.1–0.5 kPa) experience similar strain levels to the uninjected myocardium. The most rapid reductions in myocardial strain occur for injection moduli between 1–25 kPa, and strain within the hydrogel inclusion becomes significantly less than the surrounding tissue. Beyond 25 kPa, dramatically higher hydrogel stiffnesses would be required to achieve further reductions (Fig. 12). The approximate stiffness at which the benefit tapers off is similar to that found in other investigations [17]. Thus, the range of hydrogel moduli studied in the literature seems to be appropriate to act as a local strain reduction.

Fig. 12: Cross-sectional view of maximum principal strain with increasing injection stiffness.

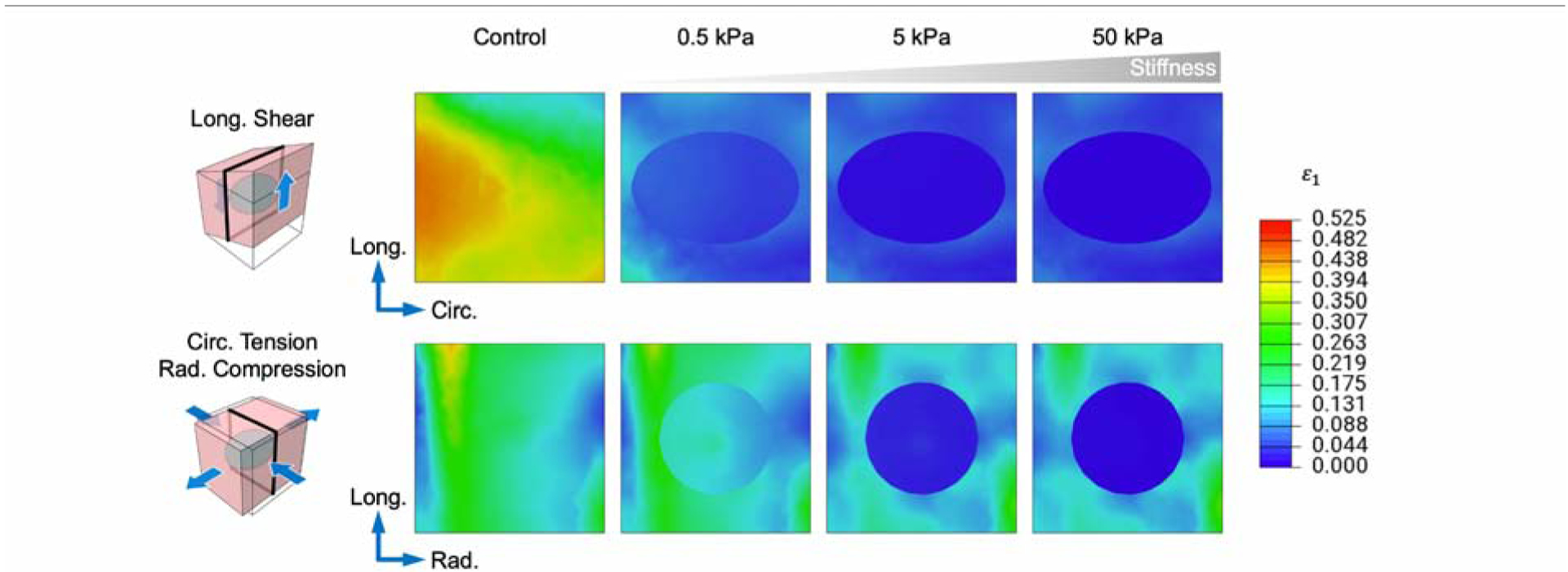
Localized strain reductions surrounding the inclusion as hydrogel modulus is increased. Inclusion volume = 17%. For clarity, a single representative shear and tension-compression mode pair for the 0 WK time point is shown. Cross sections indicated by black outline.

It must be noted that m and E₁ are related measures, since both are a consequence of an increase in overall stiffness. However, it is unclear in this work whether these changes would lead to a decrease in the myocardial wall stress, as some simulations contained step changes in stress and strain at the interfaces. However, since the soft tissue and biomaterials are relatively soft and compliant, and the inclusion has a smooth geometry, these factors will lead to relatively smooth stress and strain fields on the whole. The lower sensitivity to transmural placement could suggest that the orientation of the hydrogel injection is instead driven more by the local fiber direction or the direction of deformation, rather than independently chosen, as done in this study. When injected into the midwall, the final DC hydrogel morphology was typically correlated to the preexisting local myofiber orientation [13, 14], with the long axis of central cross-sections of the injection roughly aligned with the mean fiber direction in the center of the specimen. Examining the structural measurements, it is evident that the hydrogel injection induced some degree of fracturing between myofiber planes, as has been discussed in other works. Further work is needed to determine the relationships among the pre-injection 3D fiber structure, hydrogel shape, and resulting anisotropy of stiffening.

4.3. Implications for the optimization of hydrogel injection therapy

Simulations using both the short- and long-term post-MI constitutive models showed similar relative increases in m and decreases in E₁. Even though most previous works have focused on the effect of injections on wall stress, comparisons between maximum tangent modulus as an indication of stress and maximum principal strain could underscore the advantage of using strain reduction as a metric (as opposed to stress or maximum tangent modulus) due to its uniform qualitative effect across all deformation modes. This approach is also in contrast with previous organ-level studies, which, while obtaining important initial insights, can only determine injection effects in a limited manner. That is, in these previous simulations, the loading paths were restricted to those that were estimated to occur in a single estimated state, and were more limited in fidelity (i.e. did not use realistic time varying material properties, local fiber structures, etc.). On the other hand, our use of varied 3D loading paths allowed us to more fully investigate how the injection interacts with the local myocardium. This is important as it is unknown what the patient specific deformation patterns within the infarcted myocardium are, so that exploration of all in-vivo potential loading paths is required.

In addition to the more practical findings of the effects found in this study, perhaps the most interesting long-term finding is that modulation of the effective tissue stiffness with hydrogel inclusions results in localized reductions in myocardial strain. As tissue growth and remodeling is well known to be driven by local strains in response to changes in local stress [30–33], it can be speculated that the ability for the hydrogels to substantially modulate the local myocardial tissue strains is the local macroscopic driver for the reduction in subsequent post-MI remodeling [34]. It should be noted that these findings held regardless of the deformation mode and time post-MI, though their relative ranges and magnitudes varied with these properties. Further studies are required to put this initial observation on more solid footing to guide the optimal application of hydrogels for treatment of MI. For example, the strain reduction effect should be optimized such that it would not compromise diastolic filling (or systolic function) while arresting maladaptive remodeling. Moreover, other catheter-deliverable gels (such alginate and extracellular matrix) have shown a good safety profile but limitations in clinical efficacy. It is hoped that this phenomenon can ultimately be harnessed in cardiac simulations to develop efficacious patient-specific hydrogel injection therapies.

4.4. Limitations

Due to the nature of the triaxial testing approach, we were unable to repeat the experimental analysis on the same specimens pre- and post-hydrogel injection. As a consequence, M was subject to interspecimen variability. Despite this, when considered alongside the simulation predictions, the population-averaged properties would still likely be consistent if the analysis were conducted in a pre- and post-injection manner.

While the approach of matching the experimental and simulation studies to the 1-cm length scale was suitable for the goal of our study, selection of this length scale limited linking of findings to the organ-level response, as well as the maximum injection volume that can be studied with this platform, as the largest volume that can be placed is close to the lower bound of organ-level work. Although the injection volumes used in this investigation are smaller than those used in similar literature (~0.3–5 mL), the smaller volume was chosen in order to fully contain the injection volume within the specimen.

The loading conditions considered in this work are based on optimally selected 3D deformation modes. While these results must still be contextualized in actual post-MI mechanics, the fact that myocardial strain reductions were consistently observed across generalized deformation types strongly suggests that this behavior would also be present in-vivo, where complex loading conditions prevail. These studies are currently underway using in-vivo organ-level strain measurements for cardiac cycles pre- and post-MI.

We also note that residual stresses resulting from hydrogel injection are not accounted for. While these considerations have been incorporated in some simulation studies, they remain to be widely adopted in the modeling of these therapies, as alterations in the pre- and post-injection stress and strain distributions throughout the myocardium relate profoundly to remodeling mechanisms that drive post-MI remodeling. To account for fiber distortions in the finite element simulation, we generated a “non-distorted” fiber structure map and a full-detail “distorted” map, which were interpolated into separate FE models. Incorporating fiber distortions in simulations was not found to have a significant effect on the resulting mechanical properties of the injected tissue. Based on these results, we determined that a single 3D orientation vector for each transmural level was adequate to describe the fiber structure of the myocardium specimens. Deeper knowledge of the microstructural changes that occur directly from the expansion of the hydrogel within the myocardium is needed to develop more detailed models; however, we suspect that accounting for the pre-stress of the injected tissue will have a minimal effect on the key findings of this study.

5. Summary and implications

The driver for the present study was to gain mechanistic insights into how hydrogel injections mechanically interact with the surrounding myocardium. To do this, we utilized our fully 3D kinematic simulation/experimental soft tissue mechanics approach, which included realistic 3D fiber structures and high fidelity material models that utilized actual post-MI and 4 weeks post-MI parameters.

The primary effect of hydrogel injection was to reduce the average strain levels in the vicinity of the injection in all injection scenarios. The effective modulus of the injected biomaterial affected the level of strain reduction in relation to the local tissue stiffness, which implies that the biomaterial modulus should be calibrated to the time post-MI to obtain the best results (for example, too soft a modulus would produce an insufficient effect later post-infarct (e.g. at 4 weeks)). The fact that transmural placement of hydrogel had a limited effect is an important finding for clinical applications, as it suggests that high precision depth placement is not required for efficacy. However, absolute volume used had a very substantial one. These latter findings will help inform clinical application, as we have identified a lower bound of volume of the injection that is effective.

The fact that the substantial myocardial strain reduction was consistent across all deformation types strongly suggests that this behavior is also present in-vivo, providing support that local strain reduction could be a major mechanism behind the ability of hydrogel inclusions to reduce post-MI myocardial remodeling. The implications of the present study suggest that properly tuned injection physical characteristics, such as volume and modulus, should be tailored to the specific infarct state (mainly as a function of time post-MI) to allow the present therapies to have the greatest effects. Our study showed that this modulation of effective tissue stiffness is also governed by the volume and properties of the hydrogel, which can ultimately be harnessed in cardiac simulations to develop optimal, patient-specific hydrogel injection therapies.

Statement of Significance.

Although limiting myocardial remodeling after myocardial infarction (MI) has been achieved via implantation of hydrogels into the heart wall, systematic improvement is hampered by a lack of understanding of the local mechanical events resulting from these inclusions. In the present study, we apply a finite element approach to simulate the tissue-scale impact of hydrogel inclusions on the local stress and strain fields of the myocardium, evaluating their sensitivity to injection location, volume, and mechanical properties. Our study indicates that hydrogel inclusions result in localized strain reductions, governed by the injection volume and stiffness, which may serve as a mechanism for the prevention of post-MI remodeling. This mechanism can ultimately be harnessed to develop optimal hydrogel injection therapies.