Slice Profile Effects on Quantitative Analysis of Hyperpolarized Pyruvate

Abstract

Magnetic resonance imaging of hyperpolarized pyruvate provides a new imaging biomarker for cancer metabolism, based on the dynamic in vivo conversion of hyperpolarized pyruvate to lactate. Methods for quantification of signal evolution need to be robust and reproducible across a range of experimental conditions. Pharmacokinetic analysis of dynamic spectroscopic imaging data from hyperpolarized pyruvate and its metabolites generally assumes that signal arises from ideal rectangular slice excitation profiles. In this study, we examined whether this assumption could lead to bias in kinetic analysis of hyperpolarized pyruvate and if so, whether such a bias can be corrected.

A Bloch-McConnell simulator was used to generate synthetic data using a known set of “ground truth” pharmacokinetic parameter values. Signal evolution was then analyzed using analysis software that either assumed a uniform slice profile, or incorporated information about the slice profile into the analysis. To correct for slice profile effects, the expected slice profile was subdivided into multiple sub-slices in order to account for variable excitation angles along the slice dimension. An ensemble of sub-slices was then used to fit the measured signal evolution. A mismatch between slice profiles used for data acquisition and those assumed during kinetic analysis was identified as a source of quantification bias. Results indicate that imperfect slice profiles preferentially increase detected lactate signal, leading to an overestimation of the apparent metabolic exchange rate.

The slice profile correction algorithm was tested in simulation, in phantom measurements, and applied to data acquired from a patient with prostate cancer. The results demonstrated that slice profile induced biases can be minimized by accounting for the slice profile during pharmacokinetic analysis. This algorithm can be used to correct data from either single or multi-slice acquisitions.

Graphical Abstract

Using simulation and phantom studies, we show that slice selective excitation can bias metabolic rate quantification using hyperpolarized pyruvate. By accounting for the slice profile during pharmacokinetic analysis (slice corrected fitting) such bias can be eliminated. The improved fitting of the slice corrected pharmacokinetic analysis was validated in simulation, phantom, and patient prostate cancer studies.

Introduction

Dissolution dynamic nuclear polarization (DNP) allows for the magnetic resonance signal of select compounds to be increased by many orders of magnitude (1). While transient, the hyperpolarized (HP) signal can be used to perform real-time spectroscopic imaging in vivo. The most commonly used HP agent to date is [1-¹³C]-pyruvate (2,3). Detection of the conversion of HP pyruvate to HP lactate shows tremendous potential as an imaging biomarker for cancer presence, stage, and response to therapy (4–9).

In order to be effectively utilized as a biomarker, measurements of the conversion of HP pyruvate into lactate must be robustly quantifiable. One approach to quantification of the HP pyruvate to lactate conversion rate is by fitting a parameterized pharmacokinetic model to the measured data (10,11), following a process that is very similar to the quantification methods used for dynamic contrast-enhanced (DCE) MRI (12). Quantitative HP MRI, similar to DCE-MRI, requires careful consideration of confounding factors such as the B₁ homogeneity and accuracy, receive coil sensitivity, and the slice profile (13–15).

Since the thermal polarization of [1-¹³C]-pyruvate is low, steady-state signal is negligible compared to the HP signal (1). All detectable signal is assumed to be generated by the DNP process and is non-renewable once in the MRI scanner. Therefore, excitation of the HP signal permanently reduces the longitudinal magnetization that is available for future excitations. Due to practical limitations in slice selective excitation (13,16), there will always be some deviations of the slice profile away from the ideal slice shape that is often assumed. Repeated excitation, like those commonly used for studies of HP agents, could exacerbate these imperfections, allowing for magnetization along the slice profile direction that evolves over time and could significantly deviate from the assumed ideal slab excitation. The slice profile has been shown to impact quantitative results for DCE MRI (17), T₁ measurement (18,19), and steady-state HP gas imaging (16). It is likely that the time-varying slice profile associated with HP metabolic agents will also affect metabolic quantification. Therefore, studies are needed to understand how slice selective excitation could affect quantitative analysis of HP pyruvate.

A potential complication imparted on metabolic rate quantification by a non-uniform slice profile is that the excitation angle, and thus excitation losses that deplete the HP signal pool, will be variable along the slice direction (20,21). However, it is generally assumed in pharmacokinetic modeling and that the measured signal is the result of excitation using an ideal rectangular shape (10,22–24) that imparts uniform excitation losses within the slice. This variable excitation angle along the slice direction can be accounted for during pharmacokinetic analysis if the signal distribution along the slice is relatively uniform and the slice profile is known (16,19,25–27). In order to achieve this, a previously described pharmacokinetic analysis technique that subdivides the slice profile into a series of uniform sub-slices (19,26) was adapted to account for multi-slice packages and was evaluated for pharmacokinetic analysis of HP signal. In this work, we assess this slice profile correction technique using simulation, phantom, and in vivo data and demonstrate that this approach can reduce bias and improve the accuracy of metabolic rate constants derived from pharmacokinetic analysis of hyperpolarized pyruvate.

Methods

Simulation Architecture and Pharmacokinetic Model

The MATLAB (MathWorks, Natick, MA) based simulation architecture used in this work (28,29) combined the classic Bloch-McConnell equations with a multi-compartment model of tissue perfusion (10). This simulation architecture was expanded to allow for spatial dependencies along the slice select dimension. This platform divides isochromats into spatially co-registered perfused volume compartments that are linked by a pharmacokinetic model which governs the evolution of the longitudinal magnetization (M_z). The complex signal amplitude is calculated as the summation of the transverse magnetization (M_xy) for all chemical pools and physical compartments that are weighted by their relative volume.

A pharmacokinetic model with two spatial compartments (intravascular, extravascular) and two chemical pools (HP pyruvate, HP lactate) was used for simulation and analysis of signal evolution. In order to determine the measured apparent metabolic conversion rate, signal intensity curves resulting from simulation were fit to the same pharmacokinetic model that drove the simulation environment. Signal in the vascular compartment was assumed to be dominated by an arterial input function (AIF). The extravascular compartment represents a well-mixed combination of intracellular space, where conversion of hyperpolarized pyruvate to lactate occurs, in rapid equilibrium with extracellular space (10). In this model, extravascular HP signal evolution follows:

$$\left[\begin{array}{c}{M}_{\mathrm{P},\mathrm{ev},n}\\ M_{\mathrm{L},\mathrm{ev},n}\end{array}\right]=e^{\mathit{A}\cdot \mathrm{TR}}\left[\begin{array}{c}\cos \left({\theta }_{\mathrm{P},(\mathrm{n}-1)}\right)\cdot M_{\mathrm{P},\mathrm{ev},\left(n-1\right)}\\ \cos \left({\theta }_{\mathrm{L},(\mathrm{n}-1)}\right)\cdot M_{\mathrm{L},\mathrm{ev},\left(n-1\right)}\end{array}\right]+\frac{k_{\mathrm{ve}}}{v_{\mathrm{e}}}{\int }_{\left(n-1\right)\cdot \mathrm{TR}}^{n\cdot \mathrm{TR}}{e}^{\mathit{A}\left[n\cdot \mathrm{TR}-\tau \right]}\left[\begin{array}{c}{\mathrm{AIF}}_{\mathrm{P}}\left(\tau \right)\\ {\mathrm{AIF}}_{\mathrm{L}}\left(\tau \right)\end{array}\right]d\tau$$ [1]

where,

$$\mathit{A}=\left[\begin{array}{cc}-\frac{1}{T_{1,\mathrm{P}}}-k_{\mathrm{p}\mathrm{l}}-\frac{k_{\mathrm{v}\mathrm{e}}}{v_{\mathrm{e}}}& k_{\mathrm{l}\mathrm{p}}\\ k_{\mathrm{p}\mathrm{l}}& -\frac{1}{T_{1,\mathrm{L}}}-k_{\mathrm{l}\mathrm{p}}\end{array}\right]$$

Here M_P,ev,n is the total extravascular pyruvate magnetization just before the n^th excitation, θ_P is the excitation angle for pyruvate, AIF_P is the arterial input function for HP pyruvate, and T_1,P is the spin-lattice relaxation time for pyruvate. Similar terms for lactate are denoted with the subscript L. Perfusion terms k_ve and v_e reflect the vascular exchange rate and extravascular volume fraction, respectively. Chemical exchange terms k_pl and k_lp represent the forward and reverse apparent rates for conversion of HP pyruvate to lactate. This approach models excitation losses as a discrete event (30). The total signal observed after the n^th excitation is a weighted combination of signals arising from vascular and extravascular spaces:

$$\left[\begin{array}{c}{S}_{\mathrm{P},n}\\ S_{\mathrm{L},n}\end{array}\right]=\left[\begin{array}{c}\sin \left({\mathrm{\theta }}_{\mathrm{P},\mathrm{n}}\right)\\ \sin \left({\mathrm{\theta }}_{\mathrm{L},\mathrm{n}}\right)\end{array}\right]\cdot \{(1-v_e)\left[\begin{array}{c}{\mathrm{AIF}}_{\mathrm{P}}(n\cdot TR)\\ {\mathrm{AIF}}_{\mathrm{L}}\left(n\cdot TR\right)\end{array}\right]+v_e[\begin{array}{c}{M}_{\mathrm{P},\mathrm{ev},n}\\ M_{\mathrm{L},\mathrm{ev},n}\end{array}\left]\right\}$$ [2]

Slice Profile Correction Method

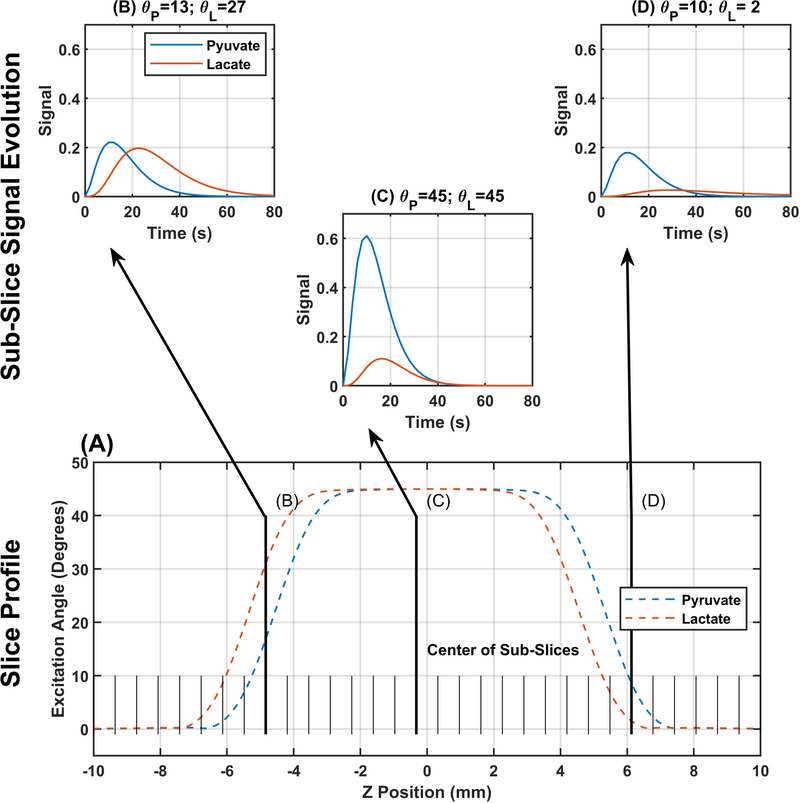
In order to account for the distribution of excitation angles along the slice profile, that profile can be subdivided into a set of sub-slices(19,26), as illustrated in Figure 1. We used the Bloch-McConnell simulator to calculate the slice profile for all of the excitation strategies used in this work. The expected slice profile for each metabolite was used to determine the excitation angle for each sub-slice (Figure 1A). Each sub-slice had independent signal evolution described by Equations 1–2 with excitation angles determined by the location of that sub-slice (Figure 1 B–D). The signal from the overall slice was calculated as the sum of signals from all sub-slices. A similar process was implemented for multi-slice acquisitions (supplemental information).

Figure 1.

Illustration of the slice profile correction method. The lower portion of the figure shows representative slice profiles for pyruvate and lactate resulting from a 45° sinc pulse centered between pyruvate and lactate (177.15 ppm). Information about the slice profile is incorporated by subdividing the slice profile into a number of sub-slices (32 in this illustration) that are analyzed individually then summed together to yield a single curve for signal evolution across the slice. The top portion shows three expected signal evolution curves from sub-slices taken along the slice profile.

Phantom Scanning Hardware

All phantom imaging and dynamic spectroscopy was performed on a 7-T/30-cm Biospec System (Bruker Biospin Corp., Billerica, MA) using B-GA12SHP gradient and a dual-tuned ¹H/¹³C volume coil (40-mm ID, Bruker Biospin MRI). 4 mL of 80 mM HP [1-¹³C]-Pyruvate was generated using a HyperSense dissolution DNP system (Oxford Instruments, Abingdon, UK). A phantom chamber that was machined from Ultem resin stock with a rectangular cavity that was 1×1×10 cm (31) was used for slice profile and T₁ measurements. The phantom was fitted with a 1 m polyethylene catheter (3.175 mm diameter; Coilhose Pneumatics, East Brunswick, NJ) for remote injection into the cavity when located at the isocenter of the magnet.

Slice Profile Measurements

To demonstrate that the simulation architecture faithfully reproduces dynamic magnetization slice profiles, simulations were performed to match measurements carried out using proton and HP pyruvate phantoms at 7T. Slice profiles were measured using a 1D gradient echo sequence with slice select and readout along the $\widehat{z}$-direction. A 3 cm slice was excited with a single broadband 90° excitation for proton scanning. For HP pyruvate, slice profile evolution over 60 repetitions was carried out with excitation angles of 20° or 60° with a 2 cm slice thickness centered on pyruvate’s resonance frequency. Both proton and carbon scans used a repetition time of one second, a three-lobed 3 kHz sinc pulse, a 5.8 cm field of view, and a 128 point readout over a 5 kHz bandwidth. Slice profile measurements were simulated, assuming noise-free conditions and sequence parameters that were otherwise identical to those used for scanning. A few degree downward slope in the sled holding the phantom resulted in a slight slope in the slice profile measurement that was corrected by linear fitting.

Simulations of Dynamic Slice Profile Evolution in Perfused Tissue

To assess the accuracy of slice-localized dynamic spectroscopy in vivo, we simulated acquisitions with ten evenly spaced excitation angles ranging from 1° to 90° and ten evenly spaced repetition times from 1 to 10 seconds over a 3 minute scan duration using the perfused Bloch-McConnell framework, assuming a uniform slab of perfused tissue. The chemical shift for pyruvate and lactate were set to 171.6 and 183.2 ppm respectively, with T₁ times of 43 and 33 seconds. $T_2^{*}$ was assumed to be 20 ms for both pyruvate and lactate, consistent with our prior observations in vivo. Vascular extravasation (k_ve) was assumed to occur at a rate of 0.0066 s⁻¹, volume fractions of the vascular (1 − v_e) and extravascular space (v_e) were assumed to be 0.0372 and 0.9628, respectively. These perfusion values represent the average prostate cancer values reported in literature (32–48) and simulations were also performed at the higher and lower ends of these ranges (k_ve [0.0045 – 0.0219], and ve [0.9015 − 0.9915]) which only had minor impacts on the measured k_pl errors (data not shown). The AIF was modeled as a gamma variate (49) following: $b_{\mathrm{P}}(t)=c*{(t-t_{inj})}^{\alpha -1}{\mathrm{e}\mathrm{x}\mathrm{p}(}^{\raisebox{1ex}{$-(t-t_{inj})$}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.}),t_{inj}=0,\alpha =2.8,\beta =4.5$, where c is an arbitrary amplitude scaling constant. The pyruvate to lactate exchange rate, k_pl, was assumed to be 0.1 s⁻¹ and reverse exchange was assumed to be negligible (22). These values were derived to match previous animal studies (28). A slice-selective pulse-acquire spectroscopic measurement was simulated for a 1 cm slice excited by a 5-lobed, broadband 5 kHz Blackman filtered sinc pulse centered in between resonance frequencies for pyruvate and lactate (177.15 ppm), with 2048 readout points over a bandwidth of 5 kHz, and 90 repetitions over a three minute period. The resulting noise-free dynamic spectral peaks were integrated over their full-width at half-height to derive dynamic signal curves for pyruvate and lactate. Finally, the signal curves were fit by the conventional pharmacokinetic model assuming uniform excitation across the slice profile, or using the slice correction method (30). A least-squares method was used to fit simulated data to the pharmacokinetic model and determine amplitude scale factor for the vascular input function and the apparent rate of conversion from HP pyruvate to HP lactate (k_pl). All other parameters were assumed to be known as the values used during simulation. The fitted k_pl values were compared to the k_pl value used for simulation to characterize error imposed by measurements involving non-ideal (28) slice profiles. In order to determine k_pl accuracy independent of a slice profile, non-slice-selective simulations were performed using identical sequence and digital phantom parameters but with no slice select gradient.

Validation of Slice Profile Corrections: T₁ Measurement

To evaluate the effect of the slice correction method on quantitative analysis of signal evolution for HP pyruvate in a reproducible phantom system, we examined its effect on quantification of the spin-lattice relaxation time constant. Like k_pl analyses, T₁ measurements for HP agents also require dynamic sampling and correction for losses due to signal excitation. HP pyruvate was prepared and injected into the slice profile phantom as described above. Serial pulse-acquire measurements were made on HP pyruvate over a 1 cm slice excited by an 8.4 kHz, 3-lobed broadband sinc pulse centered on pyruvate, with 2048 readout points sampled over a 5 kHz bandwidth, TR = 8s, and 32 repetitions. In order to demonstrate the effects of slice selective measurements using different excitation angles, this acquisition was repeated with fresh HP pyruvate and excitation angles of 10°, 20°, 30°, and 40°. The T₁ of pyruvate was estimated by fitting the observed signal to a model of exponential signal decay that includes spin-lattice and excitation losses. Excitations were modeled using either idealized uniform excitation or by including and accounting for slice profile effects. In order to determine the reference value for T₁ of pyruvate without bias due to slice profile, similar serial pulse acquire measurements were performed in triplicate but without slice selective excitations, and using a nonselective 1° excitation to reduce the impact of B₁ miscalibration. Matching simulations were performed using identical sequence and curve fitting methods, and the reference T₁ value determined from the latter measurements and analyses.

Slice Profile Corrections: Patient Measurements

Data acquired from a patient with prostate cancer was used to compare the multi-slice corrected fitting algorithm to conventional fitting in a clinical setting. Images were acquired on a GE 3T MR system (MR750, GE Healthcare, Waukesha, WI) (50 mT/m maximum gradient strength, 200 mT/m/ms maximum slew-rate), using a ¹³C “clamshell” transmitter and receiving with a dual-tuned ¹H/¹³C endorectal coil. Dissolution DNP was performed using a 5T SPINLab (GE Healthcare, Waukesha, WI) with 15 mM (EPA) AH111501 that was filtered out prior to injection. 0.42 mL/kg of 250 mM hyperpolarized [1-¹³C]pyruvate (MilliporeSigma Isotec, Miamisburg, OH) was administered at 5 mL/s and followed by 20mL saline flush.

Dynamic ¹³C imaging was carried out using a broad-band EPI sequence (50). The 12.8 cm field-of-view (FOV) was encoded over a 16×16 image matrix using a single shot readout, with 14 interleaved, 8mm thick slices covering the prostate. Metabolites were excited with a spectral-spatial RF pulse that only excited a single metabolite using a variable excitation angle strategy shown in Supplemental Figure 2 M. Due to the use of spectral spatial excitation, metabolite image pairs were acquired every 2s with 1s separating each pyruvate and lactate image.

A voxel-wise fit was performed on the 61 imaging voxels that had a total lactate SNR greater than 50. The fit parameters included: the AIF scale factor, the conversion rate of pyruvate to lactate (k_pl), the vascular extravasation rate (k_ve), and the extravascular volume fraction (v_e). A global AIF was determined by fitting the 128 voxels with the highest pyruvate SNR for the pharmacokinetic parameters t_inj, α, β, k_ve, v_e, k_pl, and AIF_scale. The average AIF parameters from these voxels were an injection time (t_inj = 2.9s) and gamma variate shape terms (α = 1.25, β = 5). These values were then used as a global AIF for fitting the 61 high lactate SNR voxels. Each voxel was fit using either conventional pharmacokinetic analysis assuming ideal rectangular slice profiles or the multi-slice correction method. During pharmacokinetic analysis, since the patient data was acquired at 3T, the assumed T₁ values for fitting were adjusted to 30s and 25s for pyruvate and lactate respectively (51). The resulting k_pl values and the root mean square (RMS) differences between the fits were compared using a paired t-test to test for significant differences between the two fitting approaches.

Results

Simulated Slice Profile Validation

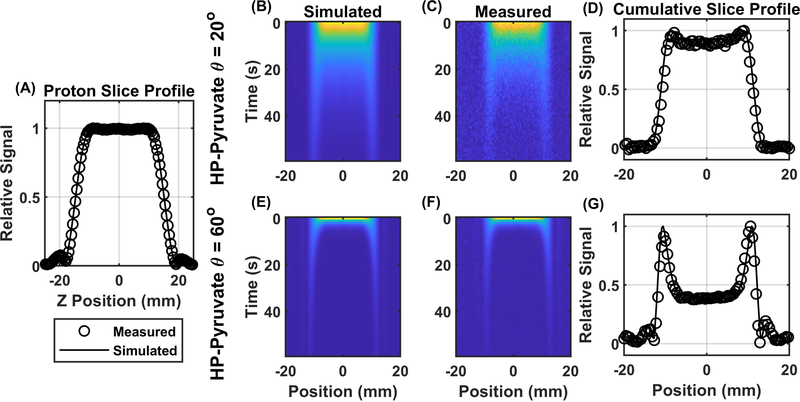
Simulated excitation profiles for proton and HP pyruvate show good qualitative agreement with measured slice profiles, as illustrated in Figure 2. Due to the reduced excitation angle along the penumbra, or transition region, of the slice, signal from that region was preserved longer than in the center of the slice. This effect was demonstrated both in simulation and in measurement, with good qualitative agreement seen for the cumulative slice profiles that were summed over time (Figure 2 D, G). This effect was enhanced at higher excitation angles as demonstrated by comparing the 20° excitation profile (Figure 2 B–D) to the 60° profiles (Figure 2 E–G). For a 60° excitation, the signal in the penumbra of the cumulative slice profile can more than double the signal from the center of the slice.

Figure 2.

Measured and simulated slice profiles from a 3-lobe sinc pulse. Good qualitative agreement between the measured and simulated slice profile for a single slice 90° excitation 30 mm slice through water is seen in Panel A. Simulated (panel B), and measured (panel C) slice profiles from HP pyruvate with a 20 mm slice, 20° excitation angle and 1 second repetition time again show good qualitative agreement and persistent signal from the penumbra of the slice. The measured and simulated cumulative slice profiles are overlaid in panel D. the excess signal in the penumbra of the slice is enhanced with an 60° excitation angle (Panels B -D).

Slice Profile Effects on Metabolic Rate Quantification

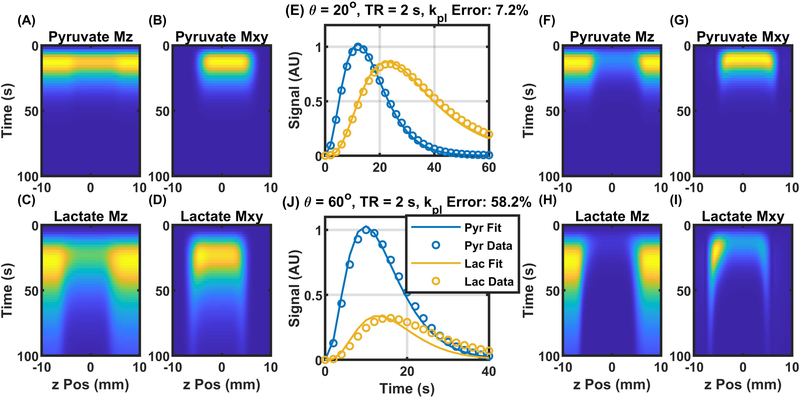
To explore how HP slice profiles could impact metabolic rate quantification, magnetization evolution from two slice selective serial pulse acquire sequences were simulated and fit with pharmacokinetic analyses that assume an ideal rectangular slice profile.

When the excitation angle was low, the pyruvate slice profile was relatively uniform as seen in Figure 3 A, B. The lactate signal, by contrast, had signal from the penumbra of the slice persisting longer than signal from the center of the slice, as seen in Figure 3 C, D. Additionally, there was a slight asymmetry in the lactate slice with increased signal on the upfield edge of the slice, most prominently observed on the left in Figures 3 D, I, due to chemical shift displacement in the slice direction. Both of these slice effects result in increased lactate signal that is not accounted for in the conventional pharmacokinetic analysis and results in k_pl overestimation of 7.2% (Figure 3 E). Even with the overestimated k_pl values, the fit does not perfectly match the simulated data, seen as a separation between the detected signal and the fit curves in Figure 3 E. Both the slice asymmetry and increased signal from the penumbra were enhanced when the excitation angle is increased to 60°, as illustrated in Figure 3 F–I. These effects also lead to an increased lactate signal resulting in a more severe k_pl overestimation of 58.2% and a lower quality fit (Figure 3 J).

Figure 3.

Magnetization evolution and fitting results for two slice selective sequences. A slight increase in the lactate signal is seen at the edge of the slice profile is apparent in the simulated magnetization evolution for 20° excitation and a 2 second repetition time (Panels A-D). The excess signal results in a minor fitting error using the relative signal evolution(Panel E). Panels F-I show the magnetization evolution for an excitation angle of 60° and the relative signal curves and fit results are shown in panel J where the slice penumbra and slice offset effects are enhanced leading to an even larger fit error.

The sources of the increased signal on the edge of the slice were due to the reduced excitation angle in the penumbra of the slice. Since the magnetization at the edge was not being excited and consequently consumed as much as at the center of the slice, the longitudinal magnetization at the edge is preserved longer. Therefore, the penumbra of the slice contributed ever-larger portions of the detected signal from slice selective excitation as serial excitations preferentially attenuate the available magnetization in the center of the slice. This effect was reduced for pyruvate, as compared to lactate, due to the rapid loss of pyruvate signal from chemical conversion and washout. The asymmetry in the slice profile was a result of broadband excitation used for this set of simulations. Broadband excitation, as opposed to the spatial spectral excitation used in the prostate studies, inevitably results in some spatial offset between the slice profiles of each spectral band. This resulted in a region of the lactate slice that does not overlap with the pyruvate slice. This region had a larger pool of HP pyruvate magnetization to convert into HP lactate as that region of the HP pyruvate pool is not losing longitudinal magnetization to excitation. That, in turn, resulted in a higher than expected HP lactate signal along one edge of the slice. When reverse conversion (k_lp) is negligible, this slice asymmetry only affects the HP lactate signal. Both the slice penumbra and offset combine to preferentially increase the detected HP lactate signal and lead to the overestimation in k_pl as seen in Figure 3 E and J.

Slice Profile Metabolic Rate Quantification Errors Corrected for a Range of Sequence Parameters

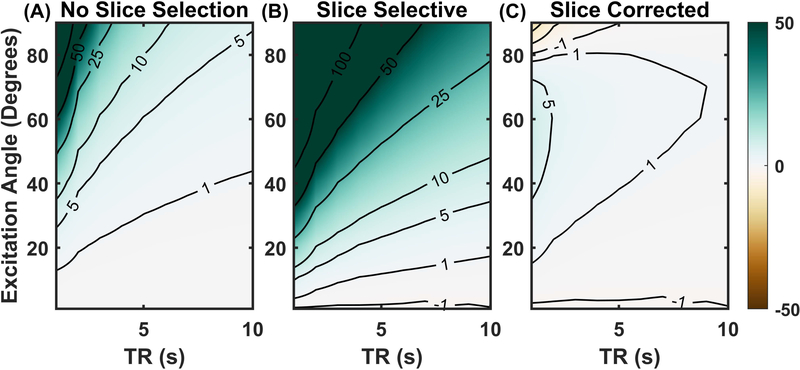
To explore how slice profile errors could affect metabolic rate quantification across a range of acquisition parameters, sequences were simulated with a range of excitation angles and repetition times. The resulting signal curves were fit using both the conventional and slice corrected methods. The estimated HP pyruvate to lactate conversion rate (k_pl) was then compared to the value used in simulation to determine quantitative accuracy.

For non-slice-selective excitations, the quantitative accuracy was quite robust across a wide range of experimental conditions (Figure 4 A). Many combinations of excitation angles and repetition times resulted in estimation errors of less than 1%, with most having errors less than 10%. Some excitation angles and repetition times did result in k_pl overestimation, primarily for large excitation angles with short repetition times. Rapid, large-angle excitations quickly expunged the HP signal and did not allow for sufficient lactate signal to develop. Even under noise-free conditions, the reduced lactate signal from such large excitation angles results in inaccurate fitting of k_pl.

Figure 4.

Percent error in measured pyruvate to lactate exchange rate (k_pl) with out and with slice profile correction: The percent errors in k_pl as a function of repetition time and excitation angle for non-slice-selective excitation are relatively low (Panel A). Errors in k_pl using a naïve pharmacokinetic analysis of slice selective excitation are much more sever (Panel B). Panel C shows the k_pl errors of slice selective excitation but using the slice correction method of pharmacokinetic analysis which nearly eliminates all errors in k_pl.

When slice selective excitation was used but not accounted for in analysis, k_pl tends to be overestimated, as shown in Figure 4 B. Few combinations of excitation angle and repetition times result in errors of less than 5% and almost none less than 1%. Again, the bias imparted by excitation was most severe when the excitation angle is large and the repetition time is short. The results of refitting the simulation data using the slice correction method are shown in Figure 4 C. Figure 4 C and Figure 4 A show similarly high k_pl accuracy, suggesting that the slice correction method virtually eliminates the bias imposed by slice selective excitation. The main difference between the slice corrected fitting and the non-selective excitation was that k_pl errors are reduced at higher excitation angles for the slice correction method. This was likely due to the excess lactate signal from the slice penumbra that was not present in non-slice-selective data. While this excess signal resulted in overestimation of k_pl for conventional fitting, when properly accounted for using the slice correction technique, the preserved signal actually improved fitting accuracy.

Slice Profile Correction Validation by T₁ Measurement of Hyperpolarized Pyruvate

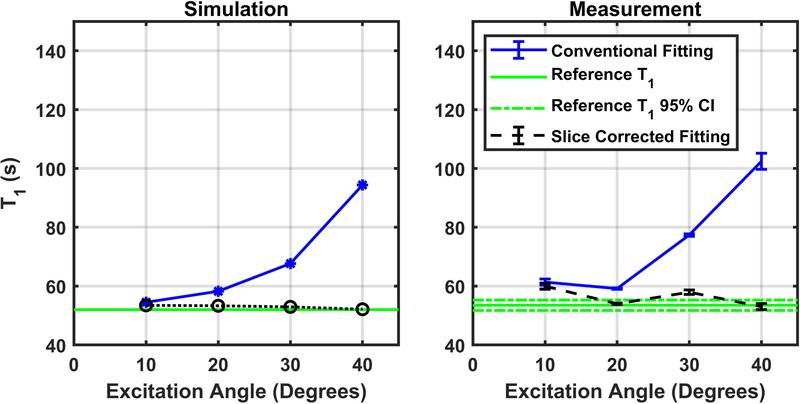
To confirm that the correction method will correct for slice profile effects in quantitative and reproducible phantom measurements, we carried out a series of simulations and T₁ measurements using several excitation angles. The T₁ relaxation time constant for HP pyruvate was measured to be 53.5 ± 0.9 seconds using non-slice-selective excitations with an excitation angle of 1°, and this value was assumed as the unbiased reference T₁ value for pyruvate in solution at 7T for comparison with subsequent analyses. When conventional fitting was used with slice-selective measurements, the residual signal in the penumbra of the slice was not properly accounted for, and the observed T₁ value increases rapidly with the nominal excitation angle (Figure 5). When the slice correction method was used, the measured T₁ values were found to be much closer to the reference value. This effect was observed in noise-free simulation and confirmed in phantom measurements. There were, however, larger errors in the measured T₁ values as compared to the simulated results. This is likely caused by experimental conditions that were not fully simulated, such as inaccuracies in the excitation angle, residual turbulence from the injection, or the impact of noise. Overall, Figure 5 serves as a validation that an imperfect slice profile can induce quantitative errors in the analysis of dynamic HP measurements, and that these errors can be reduced by using the evaluated slice profile correction method.

Figure 5.

Pyruvate T₁ simulation and measurement. Simulation results show that fitted T₁ relaxation time increase as a function of excitation angle using either conventional naïve fitting (blue line) while they remain constant when the slice correction technique (black line) is used. The green line is the assumed T₁ of pyruvate of 53.5 seconds. Measured results with phantom and sequences parameters matched to those used for simulation in panel A show a similar trend (Panel B).

Improved Pharmacokinetic Analysis of Prostate Cancer Patient Data with Slice Profile Correction

Figure 6 shows representative images acquired from a patient with prostate cancer. Figure 6 A shows the pyruvate image over the corresponding T2-weighted image. The pyruvate signal is strongest closest to the coil, with modest pyruvate signal seen in the prostate gland. The lactate image seen in Figure 6 B, shows significant lactate signal in the left posterior portion of the gland as well as some additional signal in the right posterior portion of the gland. The fitting results seen in Figure 6 C and D show two regions of elevated k_pl corresponding to the areas of elevated lactate signal in the prostate gland. Notably, with slice profile corrections, Figure 6D, shows overall lower k_pl values compared to the conventional fitting, which is consistent with our other observations (Figure 4; Supplemental Table 1). The RMS of the fit residual is much lower for the slice corrected fitting as seen in Figure 6 E vs F demonstrating improved fitting agreement with the measured signal for the multi-slice corrected method.

Figure 6.

Representative fitting results from a prostate cancer patient: Normalized area under the curve (AUC) for pyruvate and lactate signals signal in a central slice over the corresponding T₂ weighted image (Panels A and B) show two regions of lactate production in the prostate. k_pl maps derived using either conventional pharmacokinetic analysis, panel C, or the multi-slice correction method, panel D show regions of high k_pl in areas with increased lactate production. The root mean square error of the pharmacokinetic analysis for the k_pl maps are seen in panels C and D respectively are shown in panels E and D where a marked decrease in the RMS error is seen when the slice profile correction is used. Panel G shows representative pharmacokinetic analysis results for a single voxel (black outlined in panel A). The pyruvate signal and fits are in blue with lactate in red. The measured signal is marked with an o while the resulting fit curves for the conventional and multi-slice correction methods are dashed and solid lines respectively. Box plots showing the decrease in k_pl and the root mean square error for all 61 analyzed voxels are respectively displayed in panels H and I.

A representative voxel signal curve and fit results are seen in Figure 6 G. Both conventional and slice corrected fitting approaches show agreement with the data at the early time points. However, the later time points show a dramatic increase in signal. This increase in signal is not well captured by the conventional fitting curve but is much better modeled by the slice corrected fitting method. This increase of signal is likely from the additional signal in the penumbra of the slice that is being excited at increasing excitation angles due to the variable excitation strategy. It should be noted that since spectral spatial excitations were used for this study there would be no spatial offset between the pyruvate and lactate slices. Therefore, the slice asymmetry seen in figure # S & I would not be a source of the increased signal towards the end of the acquisition. This increased signal is likely due exclusively to the effect of the slice penumbra.

There was a significant (p<0.001) pairwise reduction in the measured k_pl when correcting for the slice profile, as seen in Figure 6 H, with a mean reduction of 17%. This is consistent with the simulation results suggesting that the slice profile effects would lead to an overestimation of k_pl (Figure 4; Supplemental Table 1). Additionally, there is a significant (p<0.001) pairwise reduction in the RMS of the fit residual for all the voxels analyzed, as seen in Figure 6 I. The overall reduction in RMS error of 33% demonstrates improved agreement between the fitting results and the measured signal when corrections for the profiles of the multi-slice package are used.

Discussion

The spatial, temporal, and spectral metabolic information that evolves after administration of HP pyruvate spans five dimensions (52). Slice selective and spectral-spatial excitations reduce the dimensionality of the encoding space in order to more efficiently utilize the finite signal pool afforded by dynamic nuclear polarization. The transient nature of HP signal results in unique interactions between the acquisition strategy and signal evolution (16). This work shows that imperfections in the excitation profile are compounded for HP signals, leading to a potential bias in metabolic rate quantification. This bias can be minimized if the slice profile is properly accounted for during pharmacokinetic analysis.

Due to practical limitations in slice selective excitation, the excitation angle profile along the slice direction will always deviate from the ideal rectangular function (20). These deviations are generally most pronounced in the penumbra of the slice (16). The reduced excitation angles in the penumbra preserves the HP signal longer than in the center of the slice resulting in increased signal from the edge of the slice at later time points. The additional signal from the edge of the slice was demonstrated experimentally and in simulation (Figure 2). This additional signal will not be properly accounted for with conventional metabolic rate quantification (10,22–24) which assumes an ideal rectangular excitation profile, leading to an overestimation of the apparent exchange rate for conversion of HP pyruvate to lactate (Figure 2, 3, 4, 6, and Supplemental Table 1). Aside from signal arising from the slice penumbra, the slice displacement offset inherent to broadband excitation of multiple chemical species also serves as a source of bias. In the region where the slices are not overlapping, the HP lactate pool is being fed by a larger pool of HP pyruvate that is not attenuated by excitations, resulting in larger than expected lactate signal on that side of the slice (Figure 3). Importantly, this slice offset would not impact the spatial spectral excitations used in figure 6, highlighting an advantage afforded by longer, spectrally selective pulses.

The severity of both the slice penumbra as well as the slice offset bias increases with increasing excitation angle and shorter repetition times. This is because both excitation angle and repetition time determine how quickly the HP signal pool is attenuated due to excitation losses. Therefore, sequences that use large excitation angles will need to control for the slice profile more than the acquisitions that utilize smaller excitation angles. The increased impact of the slice penumbra effects with increasing excitation angle is highlighted by the patient data employing variable excitation strategies. The later time points where the excitation angle was high showed a marked increase in signal (Figure 6 G and Supplemental Figure 2 O–Q). Additionally, when multi-slice acquisitions are used, there is the potential for slice cross-talk between adjacent slices that can also complicate metabolic quantification (Supplemental Figure 2). This slice cross-talk could be reduced by employing a slice gap such that the slice penumbras do not overlap. A non-zero slice gap however, would result in reduced organ coverage which is not ideal for prostate cancer staging and is not recommended for conventional MRI of prostate cancer(53).

The choice of excitation pulse shape should offer an opportunity to reduce these errors by designing pulses with smaller transition bands or less of a broadband slice offset. However, such pulse designs will likely require higher power or longer pulses that have their own set of tradeoffs. The spectral-spatial pulses used for the patient studies did not have any slice offset but did have longer pulse durations and broader penumbras compared to traditional slice selective pulses. Additional simulation and phantom studies could clarify how the effects, of the slice penumbra, spectral slice offset (if present), and slice cross-talk combine to bias signal evolution. This highlights the need for further study of well-optimized excitation pulses that properly balance the temporal, spatial and spectral constraints of hyperpolarized imaging and minimize any quantification bias.

Another possible strategy to mitigate these effects is to modify the slice profile of individual RF pulses. The pulse profiles can be individually designed to account for RF and T1 losses (54), or the slice profile can be dynamically scaled to reduce signal from the penumbra (13,16). While these approaches cannot completely compensate for perfusion and chemical conversion, they may provide some alleviation of slice profile effects.

Slice profile imperfections resulted in a bias towards additional HP lactate signal when excitation losses are the dominant mechanism for loss of HP lactate signal. The effect is not as pronounced for HP pyruvate, which is also affected by vascular exchange and chemical conversion. In this work, we have assumed that conversion of HP lactate back to HP pyruvate is negligible (22), and that HP lactate does not rapidly washout (7,55–57). Both assumptions are consistent with prior observations in cancer (10,22,57). However, the effects of slice profile on quantification will have to be explored for biological systems where these assumptions may not hold such as tissue with more rapid washout of HP lactate (58). It is also likely that the extent to which the slice profile biases signal evolution will depend on tissue parameters such as the metabolic exchange rate k_pl or the rate of vascular washout k_ve which will also need to be investigated. Since the amount of bias imposed by the slice profile will depend on tissue and sequence parameters, other changes in tissue or differences in sequences could manifest as an increased or decreased k_pl measurement even if there was no change in the underlying metabolic conversion rate. This erroneous variability could limit the clinical utility of quantitative metabolic rate constants determined from hyperpolarized MRI data.

Fortunately, the bias imposed by slice selective excitation can be corrected. The slice correction method evaluated in this work incorporates an ensemble of excitation angles along the slice profile to more realistically model signal evolution. The technique requires an estimation of the slice profile, which can be measured or calculated from the excitation pulse shape. Simulation results suggest that the slice correction method can compensate for the slice penumbra, slice offset bias, and cross-talk between adjacent slices. The approach presented can also be readily extended to include other metabolites (e.g. alanine and bicarbonate).

The lack of available phantom systems that can accurately recapitulate delivery and activity of HP pyruvate in a biological system limits our ability to confirm some of our results in phantom studies. Additionally, biologic models lack a known ground truth and the controllability and repeatability necessary to investigate quantitative imaging accuracy. Therefore, simulation studies were used to test quantitative accuracy of pharmacokinetic analyses by comparing estimated apparent exchange rates against those that were assumed during simulation.

These simulation results were only partially validated in phantoms, by evaluating bias in T₁ quantification. These results showed that T₁ measurements are also sensitive to bias due to the slice penumbra (18,19) and measurements of T₁ for HP pyruvate using slice selective excitation showed strong agreement with simulation. Additionally, bias in T₁ measurements were nearly eliminated using the slice correction method, and the residual errors were likely due to other experimental limitations such as noise or slight errors in the excitation calibration.

A limitation of using clinical data to validate quantification accuracy is that the ground truth k_pl is not known and therefore a simple determination of k_pl accuracy can’t be performed. Despite this, evidence of slice profile effects were observed in the presented clinical data. This data shows the increase in pyruvate and lactate signal at later time points due to variable excitation as predicted by the slice profile modeling (compare Figure 6 G vs Supplemental Figure 2 O–Q). Additionally, the fitting results show that the slice correction method results in a significant decrease in k_pl, which also agrees simulation results (compare Figure 6 H vs Supplemental Table 1). Finally, the slice corrected fitting shows better agreement with the measured signal curves as seen in the significant reduction in the fit residual, again indicating the validity of slice profile corrections (compare Figure 6 I vs Supplemental Table 1).

This work assumes that there is a uniform distribution of HP signal along the slice direction. This assumption should be valid for thin slices. However, if large slab excitations are performed this assumption may not remain valid. The effects of slice profile errors on non-uniform distributions of HP signal will need to be explored and the slice profile correction method investigated in this work may not be valid if there is a large amount of heterogeneity in signal distribution along the slice dimension. Spin diffusion across the slice profile was also assumed to be negligible in this work. The strong agreement seen between the simulated and measure HP pyruvate slice profiles in Figure 2 shows that such a simplification is likely valid for these dynamic sequences. More advanced simulation architectures that allow for spins to exchange between adjacent isochromats would be useful to explore any diffusion effects.

Successful metabolic quantification using hyperpolarized pyruvate is a complicated task in which many interacting confounds must be accounted for. In order to focus on slice profile effects in isolation, simulation studies assumed no noise and did not account for the effect of potential errors in other modeling parameters. We have previously explored the effects of noise and errors in modeling parameters on metabolic rate quantification for hyperpolarized pyruvate (59). Errors introduced by modest mis-estimation (~20%) of k_ve and v_b are similar in magnitude to the bias introduced by analysis of uncorrected slice profiles that is correctible and consistent across a range of model parameter values (data not shown).

This work demonstrates that the unique behavior of HP agents combined with non-ideal slice profiles can impart bias in the quantitative analysis of signal evolution. If not properly accounted for, these biased signals can result in biased measurement of k_pl, a quantitative imaging biomarker for tumor metabolism. Using simulation, phantom, and patient studies, this work demonstrates that a slice profile correction method that accounts for variations in the slice profile can effectively eliminate such bias.

Abbreviations

AIF

Arterial Input Function

AUC

Area Under the Curve

DCE

Dynamic Contrast-Enhanced

DNP

Dynamic Nuclear Polarization

FOV

Field-Of-View

HP

Hyperpolarized

RMS

Root Mean Square