Deciphering the protein motion of S1 subunit in SARS-CoV-2 spike glycoprotein through integrated computational methods

Abstract

The novel severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is a major worldwide public health emergency that has infected over 8 million people. Spike glycoprotein, especially the partially open state of S1 subunit, in SARS-CoV-2 is considered vital for its infection with human host cell. However, the mechanism elucidating the transition from the closed state to the partially open state still remains unclear. In this study, we applied a series of computational methods, including Markov state model, transition path theory and random forest to analyze the S1 motion. Our results showed a promising complete conformational movement of the receptor-binding domain, from buried, partially open, to detached states. We also estimated the transition probability among these states. Based on the asymmetry in both the dynamics behavior and the accumulated alpha carbon (Cα) importance, we further suggested a relation among chains in the trimer spike protein, which leads to a deeper understanding on protein motions of the S1 subunit.

Communicated by Ramaswamy H. Sarma

Introduction

As of June 18 2020, there has been over 8 million confirmed cases and over 440,000 cases of death of the newly discovered coronavirus, named as SARS-CoV-2, according to the World Health Organization (WHO). The number of confirmed cases is still growing with the speed of over a hundred thousand per day. SARS-CoV-2 is related to bats-derived coronaviruses and the SARS-CoV reported in the Guangdong province of China in 2002, and identified as a new member of betacoronavirus (Lu et al., 2020; Wu et al., 2020). Due to its fast spread through human contacts, the WHO declared it as a Public Health Emergency of International Concern (PHEIC).

SARS-CoV-2 is known to infect human through the interaction between its spike (S) protein and human host receptors (Cavanagh, 1995; Lu et al., 2015; Wang et al., 2016). The S protein is a trimer (chain A, B and C) and each chain is formed by S1 and S2 subunits that are related with host receptors binding and membranes fusion, respectively (Li, 2015, 2016; Walls et al., 2020). The S1 subunit consists of an N-terminal domain (NTD), receptor-binding domain (RBD) and two subdomains (SD1 and SD2) (Wrapp et al., 2020). It is reported that RBD undergoes a conformational change from stable closed state to dynamically-less-favorable partially open state in chain A (Bosch et al., 2003; Li, 2016). In the closed state, the determinants of receptor binding are buried and inaccessible to receptors. But in the partially open state, they are exposed and expected to be necessary for the interaction with host cells (Gui et al., 2017; Pallesen et al., 2017). In the cases of SARS-CoV-2 and SARS-CoV, S glycoprotein is found to inherently sample the closed and open states. This behavior is suggested to exist in the most pathogenic coronaviruses (Shang et al., 2018; Walls et al., 2020). While the partially open state plays an important role in human cell infection, little study is done to illustrate this protein motion at residue level.

Molecular dynamics (MD) simulations can provide atomic scale information and are widely used in sampling protein movement and structure landscape (Prinz et al., 2011). Two kinds of trajectories of SARS-CoV-2 S protein initiating from the closed state (PDB ID 6VXX) and partially open state (PDB ID 6VYB) are available from D E Shaw Research (D. E. Shaw Research, 2020). However, the timescale (10 microseconds) is still relatively trivial compared with the timescale of biological processes in the real world. To gain more information from the result of MD simulation, Markov state model (MSM) is applied to obtain long-time kinetic information given time-limited simulation trajectories (Adelman et al., 2016; Suárez et al., 2016). One advantage of MSM is that it can divide a large number of protein structures from simulation into subspaces based on the extracted kinetic information. The differences among those spaces can be calculated and used for comparison.

Machine learning techniques have achieved great accomplishments in chemistry and biology including material discovery (Raccuglia et al., 2016), structure representation (Faber et al., 2015) and computation acceleration (Botu & Ramprasad, 2015). The great contributions from machine learning mainly come from its ability to deal with large scale data and its accurate and explainable models (Jing et al., 2018; Kotsiantis et al., 2007), which provide an opportunity to decipher protein dynamics. In this study, tree-based machine learning models were used to identify important residues. Specifically, random forest model was applied as a classification model to classify different structures and calculate the contribution of each residue and structure importance for the closed-open transition process.

The transition from the closed state to the partially open state of S1 subunits of SARS-CoV-2 S protein is investigated in this research through Markov state model, transition path theory and random forest. Our analyses provided the closed-open transition probability, showed a complete transition path from the closed to the open state, and identified a relationship between the motion of chain A and two other chains.

Methods

Analysis of simulation trajectories

The root-mean-square deviation (RMSD) is used to measure the overall conformational change of each frame with regard to a reference structure in a MD simulation trajectory. For a molecular structure represented by Cartesian coordinate vector r_i ($i=1\mathrm{ }\text{to}\mathrm{ }N$) of N atoms, the RMSD is calculated as following:

$$\text{RMSD}=\sqrt{\frac{\sum _{i=1}^N{(r_i^0-U{r}_i)}^2}{N}}$$ (1)

where $r_i^0$ represents the Cartesian coordinate vector of the $i^{\text{th}}$ atom in the reference structure. The transformation matrix U is defined as the best fit alignment between the protein structures along trajectories with respect to the reference structure.

The root-mean-square fluctuation (RMSF) is used to measure the fluctuation of each atom in each frame with regard to a reference structure in a MD simulation trajectory.

$${\text{RMSF}}_i=\sqrt{\frac{1}{T}\sum _{j=1}^T{(v_i^j-\overline{v_i})}^2}$$ (2)

where T is the total frames and r_i is the average position of atom i in the given trajectory.

Feature processing

Distances between pairs of backbone Cα were chosen as features to represent the protein configuration. The distances between each Cα and all other Cαs were calculated. A protein contact map is formed by combining the pairwised Cα distances. Each element in the contact map is normally transformed into 1 if that value is below a threshold or 0 otherwise (Doerr et al., 2017). However, this feature preprocessing technique risks to ignore potentially useful spacial information forcing a boolean value on the features. Therefore, inspired by ReLU activation function (Nair & Hinton, 2010) in neural network, whose equation is shown below, we proposed a revised feature transformation method by transforming each feature value into 0 if that feature is above a threshold and keep it the same value otherwise. Compared with reference feature transformation rule, our proposed technique can still build a protein contact map while can differentiate local features with the least local information loss.

$$f(z)=\max (0,z)$$ (3)

Random forest model

Random forest is a machine learning technique that can be used for classification (Liaw & Wiener, 2002; Wang, Shen, et al., 2019). A random forest is composed of several decision trees (Utgoff, 1989), which are trained based on given training data. The final classification output of a random forest model is a collection of classes predicted by each decision tree model. The random forest algorithm carried out in this study is implemented in scikit-learn (Pedregosa et al., 2011) program package version 0.20.1. The number of decision trees used was 50. One advantage of random forest model over decision tree model is that employing multiple decision tree models mitigates the overfitting problem suffered by single decision tree model.

Feature importance

In a random forest model, a quantitative evaluation of the importance for each feature used for training is calculated through training process. This feature importance is calculated using Gini impurity:

$$\text{Gini}\mathrm{ }\text{impurity}=\sum _{i=1}^C-f_i(1-f_i)$$ (4)

where f_i is the frequency of a label at a node of being picked to split the data set and C is the total number of unique labels. A random forest model is a collection of several decision tree models. The importance of node i in decision tree is calculated as:

$$n_i=w_i{C}_i-\sum _1^m{w}_{m\left(i\right)}{C}_{m\left(i\right)}$$ (5)

where w_i is the weighted number of samples reading node i, C_i is the impurity value of node i and m is the number of child nodes. The feature importance of feature i is calculated as

$$f_i=\frac{\sum _1^s{n}_j}{\sum _{\mathrm{k}\in \text{all}\mathrm{ }\text{nodes}}{n}_k}$$ (6)

where s is the number of times of node j split on feature i. Feature importance within a decision tree is further normalized by:

$$\text{norm }{f}_i=\frac{f_i}{\sum _{j\in \text{all}\mathrm{ }\text{features}}{f}_j}$$ (7)

The feature importance in random forest is the averaged importance of feature i in all decision tree models:

$$F_i=\frac{\sum _{j\in \text{all}\mathrm{ }\text{decision}\mathrm{ }\text{trees}}\text{norm }{f}_j}{N}$$ (8)

where norm f_i is the normalized feature importance of one single decision tree and N is the number of decision trees (Breiman, 2001).

Feature importance of all pairwise Cα distances were calculated using the above methods. The feature importance of an amino acid is the summation of importance of features that are related with that amino acid. The relative accumulated feature importance of each amino acid shows the distinguishability and contribution of that amino acid among all amino acids in differentiating states.

Markov state model

Markov state model (MSM) is used to construct long-timescale dynamics behavior (Wang, Zhou, et al., 2019). MiniBatch k-means clustering was used to classify each simulation frame to microstates. Macrostates were clustered based on the Perron-cluster cluster analysis (PCCA) (Deuflhard & Weber, 2005). Macrostates are considered as equilibrium or steady states. Transition matrix and transition probability were calculated to quantitatively show the transition dynamics among macrostates. A specific time interval, referred to as lag time, needs to be determined to construct transition matrix. The value of the lag time, as well as the number of macrostates, is selected based on the result of estimated relaxation timescale (Bowman et al., 2009). MSMBuilder (Harrigan et al., 2017) version 3.8.0 was employed to build Markov state models in this study.

Transition path theory

Transition path theory (TPT) (Metzner et al., 2009; Noé et al., 2009) is used to calculate the probability of transitioning from one state to another within the framework of a MSM. In the current study, macrostates 2 and 8 were chosen as closed and open states, respectively. All other states are treated as intermediate states. Possible transition pathways from the closed to the open state were explored. The committor probability $q_i^{+}$ is defined as the probability from state i to reach the target state rather than initial state. Based on definition, $q_i^{+}=0$ for all microstates in initial state and $q_i^{+}=1$ for all microstates in target state. The committor probability for all other microstates are calculated by the following equation:

$$-q_i^{+}+\sum _{k\in I}{T}_{ik}{q}_k^{+}=-\sum _{k\in \text{target}\mathrm{ }\text{state}}{T}_{ik}$$ (9)

where T_ik is the transition probability from state i to state k. Sequentially, the effective flux is calculated as:

$$f_{ij}={\pi }_i{q}_i^{-}{T}_{ij}{q}_j^{+}$$ (10)

where π_i is the equilibrium probability of state i in the normalized transition matrix $T$, and $q_i^{-}$ is the backward-committor probability calculated as $q_i^{-}=1-q_i^{+}.$ However, backward flux f_ji should also be considered and subtracted when calculating net flux. Therefore, the net flux $f_{ij}^{+}=\max (0,f_{ij}-f_{ji}).$ Total flux can then be calculated as:

$$F=\sum _{i\mathrm{\hspace{0.17em}}\in \mathrm{\hspace{0.17em}}\text{initial}\mathrm{\hspace{0.17em}}\text{state}\mathrm{ }}\sum _{j\mathrm{\hspace{0.17em}}\notin \mathrm{\hspace{0.17em}}\text{initial}\mathrm{\hspace{0.17em}}\text{state}\mathrm{ }}{\pi }_i{T}_{ij}{q}_j^{+}$$ (11)

The flux from initial state to target state can be decomposed to individual pathways p_i. Dijkstra algorithm is implemented in MSMBuilder for pathway decomposition. A set of pathways p_i can be generated along f_i, which provides a relative probability by:

$$p_i=\frac{f_i}{\sum _j{f}_j}$$ (12)

Results

Simulation trajectory analysis shows dynamical activity

Two 10 microseconds simulation trajectories of the trimeric SARS-CoV-2 S glycoprotein were treated as reference and backbone Cα of the trimer were chosen and extracted as representative features of structures.

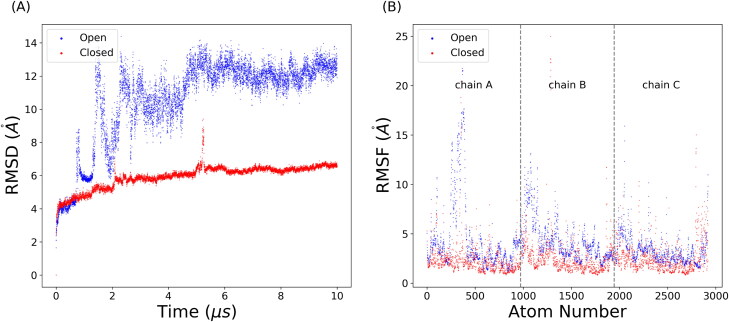
To probe the dynamical stability of two structures, the time evolution of the RMSD were plotted in Figure 1(A). All RMSD values were calculated with reference to the first frame of each trajectory. The average RMSD values in two states are $5.9\AA$ and $10.6\AA ,$ respectively. The plot suggested that the closed state is relatively stable while the partially open state is dynamically active and undergoes significant conformational changes after 1 microsecond. However, the simulation of open state after 6 microseconds suggested a convergence in the RMSD value and a relatively stable structure, which corresponds to the detached S1 subunit from S2 fusion machinery.

Figure 1.

Simulations of SARS-CoV-2 S glycoprotein. (A) RMSDs of the trajectories in the closed (red) and open (blue) states. (B) RMSFs of simulation trajectories in the closed (red) and open (blue) states. The protein is divided into three chains separated by grey dashed lines. Atom number was counted from 0.

RMSF results were plotted in Figure 1(B). The asymmetry in protein motion was noticed by comparing the individual dynamics behavior among three chains. Corresponding to the RMSD results in chain A, the RMSF results showed a similar high-degree conformational change in the RBD domain. However, the detachment in chain A, chain B, and C showed different movements that both NTD and RBD in chain B are more dynamically active than those in chain C, while in closed state the chains B and C displayed similar dynamics.

Markov state model and transition path theory elucidates the closed-open transition

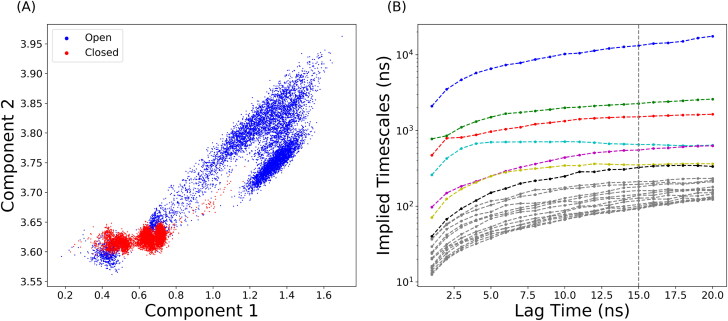
Simulation trajectories were projected onto a two-dimensional (2D) plot in RMSD of Cα atoms with reference to the closed and open state structures, respectively (Figure 2(A)). To apply MSM analysis, MiniBatch k-means clustering was applied to divide the simulation sampling space into 300 microstates based on the reduced-dimension plot, shown in Figure S1. The estimated relaxation timescale was plotted in Figure 2(B). The trend of implied relaxation timescale showed that the estimated timescale was converged after 15 ns, which was chosen as the lag time for MSM.

Figure 2.

Distribution of SARS-CoV-2 S glycoprotein simulations. (A) 2D protein conformation space using RMSD values with references both closed and partially open states. (B) Implied relaxation timescale of top 20 variables based on the data coordinates in the reduced map regarding with the different lag times as interval.

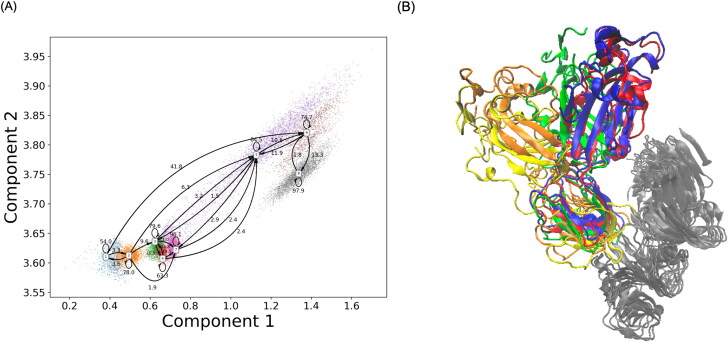
The number of macrostates were determined based on the band gap in estimated relaxation timescale plot. Total of 8 macrostates were chosen to divide simulations into kinetically separate macrospaces. PCCA was applied to map microstates onto macrostates based on the eigenfunction structure of transition probability matrix. The resulting macrostates with transition probability are shown in Figure 3(A). Closed state and open state were equally divided into 4 macrostates, as states 2, 3, 4, 7 belonging to the closed state and states 1, 5, 6, 8 belonging to the open state. The closed state is stable with 95.5% probability to stay within closed macrostates. Macrostate 2 was found important due to its high probability of 9.9% to transfer from itself to open macrostates. The average transition probability from closed macrostates to open macrostates is 4.5%.

Figure 3.

Markov state model based on the simulation. (A) Macrostates and estimated transition probabilities among them. (B) Representative structures of macrostate 2 (blue), 3 (red), 5 (green), 6 (orange) and 8 (yellow).

Macrostate 2 was selected as the representative closed states based on the similarity with its corresponding crystal structure. However, it is not reasonable to apply this rule when choosing the representative macrostate of open states since the open states undergo a dramatic conformational change. Instead, it should be chosen based on the transition probability. There is a probability of 97.9% in macrostate 8 to stay within itself and therefore was selected. Transition path theory was applied to calculate possible transition pathways connecting these two states. Total of 2,317 pathways were generated and divided as 51 distinct channels floating from state 2 to state 8. The probability of each channel was calculated based on net flux from initial state to the target state. Overall, the probability of top 5 channels was listed in the Table 1, with the contribution from the top 10 channels accounting for 88.7% of total population. The most probable path was state 2 → state 3 → state 5 → state 6 → state 8, and the corresponding representative structures were plotted in Figure 3(B) to show a series of transition processes.

Table 1.

The probability of top 5 channels.

Channels	Probability
2,3,5,6,8	23.7%
2,3,4,7,5,6,8	15.8%
2,5,6,8	11.0%
2,3,7,5,6,8	9.6%
2,3,4,7,8	8.0%
Top 10 channels	88.7%

Random forest identifies important residues and structures

To better understand the shift between closed and open states in S1 subunit, the pairwised Cα distances of S1 were extracted as features representing the character of protein configurations. There are 540 residues on each chain, residue ID from 27 to 676, and total of $1,620*1,619/2=1,311,390$ Cα distances were collected as features. Before further analysis, features were transformed into contact map with our proposed feature transformation technique described in the Methods section. Considering the non-bonded chemical interactions length, we pick $10.0\AA$ as threshold for feature transformation.

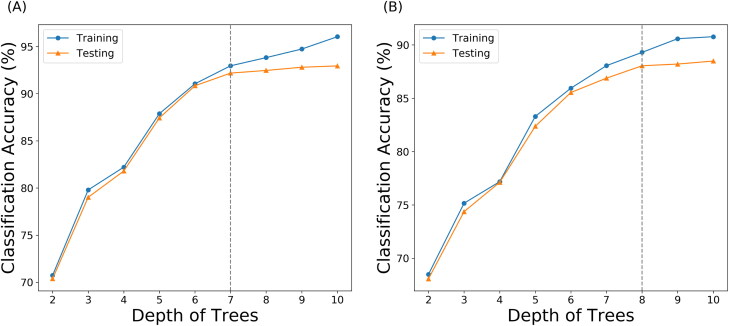
Supervised machine learning model was applied to extract the key residues that are vital during allosteric process and study the structural differences among macrostates. For each simulation trajectory, frames were saved for every 1.2 nanoseconds (ns), resulting in 8,334 frames. Therefore, 16,668 samples with 1,311,390 features were extracted from the trajectories. Each sample was labeled based on the above macrostate result. Full dataset was further split into training set (70%) and testing set (30%). After the preparation of data, random forest model was applied to distinguish the intrinsic conformational differences among macrostates. Training scores and testing scores were plotted in Figure 4(A). 7 was chosen for the depth with corresponding testing accuracy of 92.18%, which indicated that the random forest model was able to catch the conformational characteristics of each macrostate only using pair-wised Cα distances. To further investigate the relationship between chain A and two other chains, the original Cα distances related with chain A were excluded and applied to another random forest model. Training and testing results are shown in Figure 4(B). The top 500 features accounted for 74.8% percent of the overall feature importance, shown in Figure S2. The testing accuracy with reduced features reached 88.04% at depth 8.

Figure 4.

Random forest classification model using pair-wised Cα distances in S1 subunit. (A) Classification accuracy using different depths of trees. Depth 7 (shown in grey dashed line) was chosen with 92.18% accuracy. (B) Classification accuracy regarding different depths of trees using pair-wised Cα distances within chain B and C. Depth 8 (shown in grey dashed line) was chosen with 88.04% accuracy.

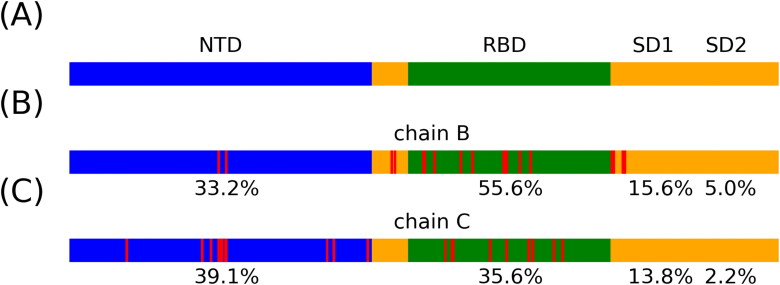
The top five important Cα distances were listed in Table 2. In order to identify key residues along the transition from the closed to the partially open state, the feature importance of each Cα distance was added and accumulated to the two related residues. S1 subunit structure was plotted in Figure 5(A) as reference. Top 20 important residues on chain B and C, with corresponding structure and accumulated structure importance under each figure, were plotted in Figure 5(B, C). Full results of residue importance on chain B and C are shown in Figure S3.

Table 2.

Top 5 Cα distances.

Cα distances	Importance
Chain C Phe 342, Chain C Asp 442	0.86%
Chain C Ala 419, Chain C Tyr 423	0.83%
Chain B Thr 323, Chain B Thr 333	0.76%
Chain C Cys 136, Chain C Gly 142	0.71%
Chain B Leu 390, Chain B Gly 545	0.60%

Figure 5.

S1 protein structure and accumulated feature importance. (A) Residue sequence with tertiary structure in S1 subunit, referenced to the released structure in the prefusion conformation (Wrapp et al., 2020). NTD (blue), N-terminal domain; RBD (green), receptor-binding domain; SD1 and SD2 (orange), subdomains. The sequence starts with residue Ace 26 to Thr 676. (B-C) The position of top 20 important residues are shown in red color. Accumulated tertiary structure importance in chain B and chain C are shown in numbers, respectively.

Discussion

The significance of the partially open state of receptor-binding domain in SARS-CoV-2 for interacting with the host cell receptor has been extensively studied (Walls et al., 2019; Yuan et al., 2017). Specifically, the opening of S1 subunit, thus exposing RBD, is necessary for engaging with ACE2 and following cleavage of $S_2^{\prime }$ site (Kirchdoerfer et al., 2018). While the RBD exhibits inherently flexibility enabling itself recognized by the receptor (Kirchdoerfer et al., 2016), the motion of this closed to open state shift still needs in-depth study.

It is reported that the SARS-CoV-2 S trimer shows a C3 symmetry at closed state and asymmetry with chain A at open state (Wrapp et al., 2020). Through the RMSF result, we noticed the asymmetry in dynamics at both closed and open states. The S1 subunit in chain B and the S2 subunit in chain C are more dynamically active than their corresponding structures in the closed state. The S1 domain in chain B is also more flexible than that in chain C in the open state. Above results implies the asymmetrical biological functions among the three chains.

Two random forest models were applied with different input features. The first model reached high accuracy in predicting macrostates based on all pair-wised Cα distances on S1 subunit. The second model with reduced features that does not include the motion of chain A also had comparable prediction accuracy. This indicates that chain B and C contain information of the closed-open transition in chain A. Combined with the finding of asymmetric dynamics in RMSF result, we hypothesized that there is a correlation between the chain A and two other chains. The correlation among chains may come from the chain B and C’s contribution to the protein motion in chain A. This could also originate from the protein-protein interaction along the opening movement of chain A. Further investigation of this mutual influence is warranted for a detailed clarification. Moreover, in order to understand the important structures on the tertiary level, the importance of Cα distances was accumulated to residues on S1 domain structure and we numerically identified key structures as RBD in chain B, NTD in chain C, RBD in chain B and NTD in chain B in descending order.

The result of Markov state model showed a great difference in the probability of macrostates to transition within themselves with macrostate 2 (closed state) of 78.0% and macrostate 1 (open state) of 54.0%. This result implies that S1 subunit is more likely to stay in closed state, which agrees with the experimental finding that the closed state is more dynamically stable than the partially open state (Wrapp et al., 2020). Moreover, a possible dynamically stable state followed by the partially open state of the RBD was found and could be important in the closed-open transition. Specifically, macrostate 8 (open state) exhibited a high probability (97.9%) to stay within itself, where the RBD is detached from the S2 fusion machinery. Transition path theory further provided potential channels from macrostate 2 to 8 with the most probable channel (2-3-5-6-8) of 23.7% probability. This channel is considered important in representing the transient shifting and can be treated as the typical protein movement.

Conclusion

The spike protein is essential for SARS-CoV-2 as it destabilizes the trimer structure, causing the detachment of S1 subunit and exposing the RBD domain to host cell membrane. In this study, we used publicly available simulation trajectories of spike protein and studied the asymmetric dynamics nature of the trimer structure. Markov state model was applied to divide the conformational space into 8 macrostates. The representative structures of each macrostate in the most probable channel are shown to present a clear route from the closed state to the partially open state. Transition matrix was calculated to determine the probability of the 8 macrostates with maximum of the summed probability of 9.9% from the macrostate 2 (closed state) to open macrostates. In order to represent the protein motions, the pairwised Cα distances from the amino acid residues located on the S1 subunit were extracted from each frame of simulations. Random forest models were applied to identify the key residues for the structural changes between macrostates based on these Cα distances. The little difference between prediction accuracy results from two random forest models, where one includes the movement of chain A and the other does not, implied a correlation between chain A and two other chains. Yet, whether this correlation originates from the mutual influence among chains or the intrinsic asymmetry in biological functions needs further investigation. Overall, our study quantitatively analyzed the S1 subunit with important Cα distances and residues, which contributes to the research on the states transitions in S protein.

Glossary

Abbreviations

Cα

alpha carbon

MSM

Markov state model

NTD

N-terminal domain

PCCA

Perron-cluster cluster analysis

PHEIC

Public Health Emergency of International Concern

RBD

receptor-binding domain

RMSD

root-mean-square deviation

RMSF

root-mean-square fluctuation

SARS-CoV-2

Severe Acute Respiratory Syndrome Coronavirus 2

SD

subdomain

S protein

spike protein

TPT

Transition path theory

WHO

World Heath Organization

Funding Statement

Research reported in this paper was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award No. R15GM122013.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

The data that support the findings of this study are available at https://www.deshawresearch.com/downloads/download_trajectory_sarscov2.cgi/.