Abstract
The SIQR model is exploited to analyze the outbreak of COVID-19 in Japan where the number of the daily confirmed new cases is explicitly treated as an observable. It is assumed that the society consists of four compartments; susceptible individuals (S), infected individuals at large (I), quarantined patients (Q) and recovered individuals (R), and the time evolution of the pandemic is described by a set of ordinary differential equations. It is shown that the quarantine rate can be determined from the time dependence of the daily confirmed new cases, from which the number of infected individuals can be estimated. The infection rate and quarantine rate are determined for the period from mid-February to mid-April in Japan and transmission characteristics of the initial stages of the outbreak in Japan are analyzed in connection with the policies employed by the government. The effectiveness of different measures is discussed for controlling the outbreak and it is shown that identifying patients through PCR (Polymerase Chain Reaction) testing and isolating them in a quarantine is more effective than lockdown measures aimed at inhibiting social interactions of the general population. An effective reproduction number for infected individuals at large is introduced which is appropriate to epidemics controlled by quarantine measures.
Keywords: Covid-19, SIQR model, Quarantined patients, Estimation of the number of infected individuals at large, Controlling the outbreak, Effectiveness of the quarantine measure, Effective reproduction number
1. Introduction
The pandemic COVID-19 due to the novel coronavirus (SARS-CoV-2) is still expanding throughout the world 9 months after the first outbreak in November 2019 in China (WHO Coronavirus disease pandemic, Situation report). Compared to other viral outbreaks such as Influenza, for which the SIR model is applied, COVID-19 has the following characteristics (WHO Coronavirus dosesase Situation Report 73; Lauer et al., 2020): (1) A long incubation period; (2) Prevalence of asymptomatic transmission; (3) Detection of infection by PCR (Polymerase Chain Reaction) tests. The biggest challenge in modeling the COVID-19 outbreak is that a large number of patients are hidden in the general population as they continuously infect others, and that the only observable metric, on which we can base estimates, is the number of daily new cases confirmed positive by PCR tests.
Traditionally, the dynamics of infectious diseases have been understood by the deterministic compartmental models described by differential equations such as the SIR model (Kermack and McKendrick, 1927) and the SEIR model (Anderson and May 1982; Chowell et al., 2007) or by the stochastic model described by a renewal integral equation (Fraser et al., 2004). In the SEIR model, the population consists of susceptible individuals (S), exposed individuals (E), infectious individuals (I) and removed individuals (R). The SIR model does not include the compartment of exposed individuals. In these compartmental models, quarantine is considered to be an efficient way for medical treatment of patients and one of the removal processes. The average removal time is usually treated as the unit of time, and thus the quarantine rate is included only in the unit of time and in the reproduction number. The SIR-X model proposed by Maier and Brockmann (Maier and Brockmann, 2020) includes the quarantine process in the analysis of the early state of the outbreak in China.
In the renewal model, the number of infected individuals at a given time is assumed to be determined by a convolution of a time-dependent transmission coefficient and the number of infected individuals at earlier times with the reproduction number as a multiplier, and the quarantine process is hidden in the reproduction number.
There are several attempts to understand the nature of the outbreak of COVID-19 on the basis of the SEIR model (Arinoa and Portet, 2020; Maier and Brockmann, 2020) and the renewal model (Nishiura et al., 2020). Apparently few attempts have treated quarantined patients as a compartment and the quarantine rate as a controllable parameter, although it plays an essential role in the measures against the COVID-19. At this moment in the middle of outbreak of COVID-19, it is important to establish a universal, predictable and simple model for the outbreak which can be understood by citizens and policy makers.
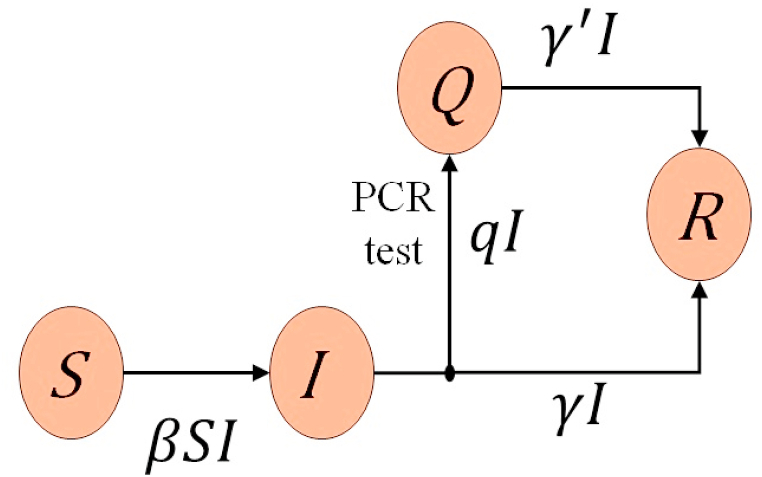
In this paper, keeping the characteristics of the COVID-19 explained above in mind, I exploit the SIQR model (Hethcote et al., 2002; Jumpen et al., 2009) with four compartments; susceptible individuals (S), infected individuals (I call them infecteds for the sake of simplicity) at large (I), quarantined patients (Q) and recovered individuals (R), and describe the transmission process by a system of ordinary differential equations where the quarantine rate of infecteds is introduced as a key parameter. In the present SIQR model, the quarantine process is treated as a measure controlled by policy and the number of the daily confirmed new cases is focused upon as an essetial observable. I also consider the quarantined patients not only as individuals to be treated in the hospital but also as key players in combating the spread of the virus. Fig. 1 shows the flow diagram of the SIQR model.
Fig. 1.
Flow diagram of the SIQR model. If the quarantine process is included in the recovery process, the SIQR model is reduced to the SIR model.
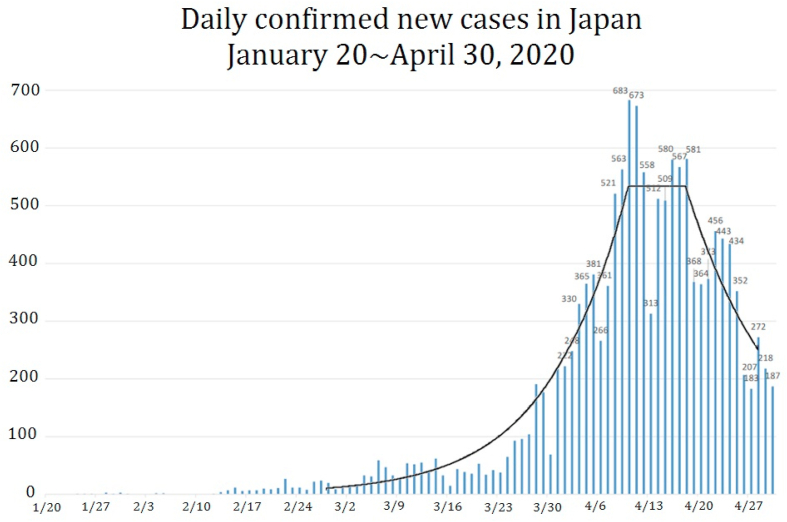
In §2, I explain the SIQR model and parameters to be used. I show in §3 that the number of infecteds at large can be estimated from the daily confirmed new cases. In §4, I analyze the time dependence of the daily confirmed new cases reported in Japan till the end of April which is shown in Fig. 2. This period saw a rapid rise in daily confirmed new cases, and is also notable for a succession of policy milestones, one being the planned Olympiad postponed by IOC on March 24th, and the other being the prime minister announcing on April 5th that a state of emergency, asking 80% reduction of social contact, would be formally declared two days later on the 7th.
Fig. 2.
The daily confirmed new cases in Japan till the end of April. The solid curve represents fitting by four piecewise exponential functions with parameters and periods given in Table 1. Data are from Ministry of Health, Labor and Welfare, Japan (Ministry of Health, Labour, & Welfare, 2020).
In §5, I compare the time dependence of daily confirmed new cases if different measures would have been taken at the beginning of April in Japan. I also compare various policies characterized by a combination of differing degrees of testing/quarantine and societal lockdown and show that the quarantine measure is more efficient than the lockdown measure to control the outbreak. Discussion is given in §6, where an effective reproduction number appropriate to COVID-19 is introduced.
2. SIQR model
The dynamics of the SIQR model (Hethcote et al., 2002) are described by the following set of ordinary differential equations:
| (1) |
| (2) |
| (3) |
| (4) |
where t is the time, and S, I, Q and R are the stock of susceptible population, infecteds at large, quarantined patients and recovered (and died) patients, respectively. Here, I assumed that the net rate at which infections spread is in proportion to the number of encounters between susceptibles and infecteds at large, , where β is a transmission coefficient. The parameter represents a per capita rate of quarantine of the new patients immediately after they get infected. For COVID-19, can be set to zero since the incubation period is long. Infecteds at large, regardless of wheter they are symptomatic or asymptomatic, are quarantined at a per capita rate q and become non-infectious to the population. Quarantined patients recover at a per capita rate (where is the average time it takes for recovery) and infecteds at large become non-infectious at a per capita rate γ (where is the average time that an infected patient at large is capable of infecting others). It is apparent that Eq. (1) (4) guarantee the conservation of population .
If we assume and regard as the recovered compartment, Eq. (1) (4) are identical to those of the SIR model with removal rate of infecteds . Since the value of q depends strongly on government policies and the only observable is the number of quarantined patients on each day, the SIQR model which treats the quarantine process explicitly is superior to the SIR and SEIR models in the analysis of the outbreak of COVID-19.
In the following discussion, I concentrate on the number of infecteds in the early stage of the outbreak where is satisfied so that I can assume . Then the basic equations of the SIQR model become
| (5) |
| (6) |
where the rate of change of the number of infecteds at large
| (7) |
determines the short-term behavior of the number of infecteds.
The parameter β determines the initial growth of infecteds and is determined by the cumulative effect of the virulence of the virus and social factors. The longer latent period and shorter infectious periods reduces the number of infectious patients in the infecteds at a given time which in turn makes β effectively smaller. Similarly, the shorter incubation period and the higher onset probability increases the number of quarantined individuals which makes the quarantine rate q larger.
The parameters are dependent on the lifestyle of each community and measures taken by governments. For example, availability of a vaccine, implementation of social distancing or lockdown measures will all decrease β, while widespread PCR testing to isolate patients will increase q. Although the recovery rate for quarantined patients will be increased when a new drug for SARS-CoV-2 is developed, it would not increase γ since a patient is unlikely to seek treatment unless they are first identified.
It should be noted that the characteristics of the outbreak of the COVID-19 can be understood by effective values of three parameters β, q and γ.
It is usual to take the inverse of the removal rate () or the recovery rate () as the unit of time, and the dimensionless time and the reproduction number are used in the analysis. However, these parameters are policy dependent and cannot be considered as an intrinsic time unit of the problem. In order to present results in the style that citizens and policy makers can easily understand, I take one day as the unit of time in this paper.
Although an exact solution to Eq. (1) (4) can be obtained by introducing a scaled time when parameters do not depend on time (Harko et al., 2014), the solution is impractical for the purpose of analyzing the outbreak and predicting the outcome of various measures.
The SIQR model has been applied to estimate the infection trajectory of COVID-19 in Italy (Pedersen & Meneghini, 2020), India (Tiwari, 2020a; 2020b) and Sweden (Krasnochub & Polishchuk, 2020).
3. Estimation of the number of infecteds at large
The term in Eqs. (5), (6) is the number of daily confirmed new cases and thus the number of infecteds is given by
| (8) |
Note that individuals isolating themselves without taking PCR test are considered as infecteds at large and are not included in the quarantne class. Equation (8) indicates that if λ can be determined from the time dependence of the daily confirmed new cases, β from the initial increase of infecteds and infectious period of asymptomatic patients, then the number of infected at large can be obtained from the daily confirmed new cases.
In the data reported in Japan (Ministry of Health, Labour, & Welfare, 2020), the daily confirmed new cases are apparently a constant around in the period from 11th to 19 th of April 2020 as shown in Fig. 2. If this is the case, λ must be negligibly small in this period, and thus
| (9) |
As will be seen later, and in this period when (or 33 days of the latent plus infectious periods) is used, I find
| (10) |
This means that there were about 5300 infecteds in Japan at the beginning of April. This number increases to 8030 if (17 days for the recovering time) is used.
4. Time evolution of outbreak
The solution to Eq. (5) can be readily written as . Therefore, in the time period when the parameters do not depend on time, the solution to Eqs. (5), (6) is given by:
| (11) |
| (12) |
Equation (11) indicates that the number of infecteds at large is determined by λ and its initial condition. The parameter λ depends on measures that the government employs. Therefore, we can fit the data by piecewise exponential functions and assess the measures from the time dependence of the number of infecteds at large.
In order to find the relation of to the number of daily confirmed new cases , I assume that patients tested positive are quarantined either in a hospital or at home, and are no more infectious to the population. The daily confirmed new cases is proportional to the number of infecteds who have an onset of symptoms. Since the latter is given by a convolution of the incubation period distribution function and the number of infecteds , can be expressed as
| (13) |
The incubation period distribution is a well behaved function with a single peak (Backer et al., 2020; He et al., 2020). Then, the integral can be evaluated by the saddle-point method of integration and I find
| (14) |
where τ is a characteristic time representing the peak position of and .
In fact, the number of daily confirmed new cases of many countries seem to be represented by piecewise exponential functions (WHO Coronavirus Disease, dashboard 2020).
I analyze the daily confirmed new cases from March 1st to April 29th in Japan by fitting it with four piecewise exponential functions, where I neglected the effect of the transition periods. The solid curve in Fig. 2 shows a piecewise fitting with λ listed in Table 1 in the period.
Table 1.
Parameter λ used for fitting in Fig. 2 and estimated values of other parameters. Numbers in ( ) are estimated from other data and numbers in [] are inherited from the previous period. γ is fixed in the entire period.
| Period | 3/14/2 | 4/24/11 | 4.114/19 | 4.19 4/29 |
|---|---|---|---|---|
| (14 days earlier) | (2/163/19) | (3/19 (3/28) | (3/284/5) | (4/54/15) |
| λ | 0.096 | 0.090 | 0.0 | |
| 0.126 | [0.126] | [0.126] | 0.051 | |
| q | (0) | 0.006 | 0.096 | [0.096] |
| γ | (0.03) | (0.03) | (0.03) | (0.03) |
From the λ value determined by the fitting, other parameters can be estimated. I assume that parameters do not change unless effective measures are introduced. First I set in the entire period assuming that the recovery time of infected at large is 33 days. Here I took a longer period among widely distributed observations (Backer et al., 2020; He et al., 2020; Housen et al., 2020). Next, I set in the first period since virtually no infecteds were quarantined in this period. The estimated values for and q are listed in Table 1.
Several comments are in order: (1) the basic reproduction number is estimated to be for the first two periods and becomes 0.4 after April 5th passing the period where . (2) The reduction of after April 5th is about % which may be attributed to the emergency declaration by the government on April 7th. Apparently the effect is seen two days earlier since the government announced it on April 5th in advance. (3) The effectiveness of PCR test and quarantine, that is the probability of a patient being qurantined when symptoms appear, is rather low around 25 50% due to the strict conditions set by the Japanese government for PCR tests (such as a mandatory 4 day waiting period before a symptomatic patient is allowed a test). Since onset rate the probability of getting PCR test, the onset probability is estimated to be 20 40%. These values are within the wide range 20 95% of estimations by other researchers (Heneghan et al., 2020).
5. Comparison of possible measures
In this section, I compare how the number of daily confirmed new cases would have reduced if Japanese government had taken different measures.
A measure can be characterized by two parameters x and y, which define an effective decay constant as
| (15) |
where and must be satisfied. For the purposes of this paper, I will treat social distancing and lockdown measures as part of the same effort to reduce social contact, whose cumulative effectiveness is represented by x, with representing no change to social behavior, and representing the most extreme form of societal lockdown.
Parameter y denotes the enhancement factor of quarantine rate. Since is supposed to be negative when the number of infecteds is declining, the smaller and the larger y are, the decay rate becomes larger. Note that the four-day waiting period before PCR testing imposed in Japan has made q as small as , and thus y can be made as large as by lifting the requirment for PCR testing if the medical care system is working.
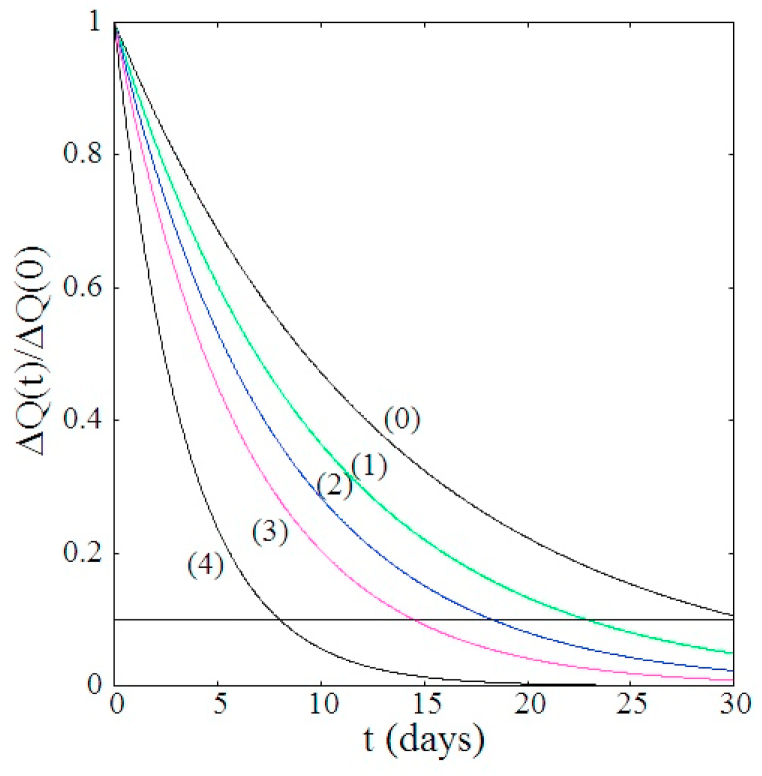
From the values of in the third and fourth periods in Table 1, the reduction rate of social contact is estimated to be 60% after the emergency declaration. Therefore, I compare, relative to the third period of Table 1 (, , and ), hypothetical measures of (1) 80% reduction of outings that the government requested and at the same level of the PCR test (, ) and (2) 100% reduction of outings, that is the strictest form of lockdown, and at the same level of the PCR test (, ). I also estimate the reduction rate for (3) 50% reduction of outings and doubled quarantine rate by introducing an expanded policy for PCR testing (, ) and (4) quadrupled quarantine rate without any restriction on social interactions (, ).
Fig. 3 compares the reduction rate of the daily confirmed new cases for different measures, had they been taken from April 5th. Fig. 3 shows clearly that partial or strict lockdowns are less effective than increase of the quarantine rate. Countries like Korea, Vietnam and Taiwan which took strong lockdown and quarantine measures have apparently succeeded in controlling the first wave outbreak of COVID-19 (WHO Coronavirus Disease dashboard (Korea); WHO Coronavirus Disease dashboard (Korea), WHO Coronavirus Disease dashboard (Viet Nam); COVID-19 dashboard JHU (2020)).
Fig. 3.
Comparison of reduction rate of the daily confirmed new cases for four different hypothetical measures, relative to the third period of Table 1, if it was taken on April 5th (). Observed decay given in the fourth period is also shown by curve (0). If γ is set to a larger value, the effect in decay rate due to the enhanced quarantine rate becomes somewhat moderate. The horizontal line represents .
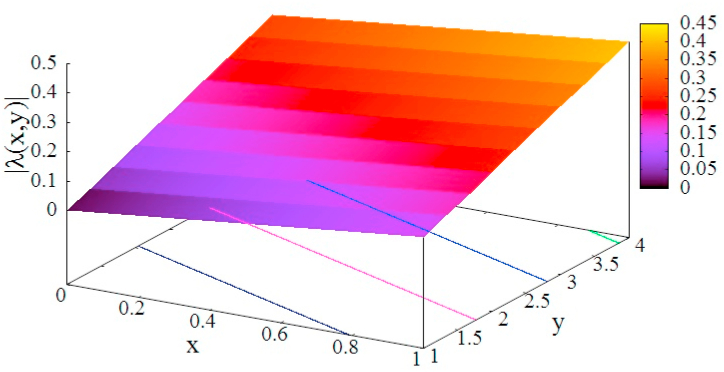
In order to see the effectiveness of measures characterized by parameters x and y, the effective decay rate is plotted as a function of x and y in Fig. 4.
Fig. 4.
Dependence of the effective decay rate on parameters x and y which represent the strength of lockdown and the enhancement factor of the quarantine rate, respectively. The values for , q and γ are taken from the third period of Table 1.
The decay constant Eq. (15) shows that y has more leverage than x in making () a large negative value. Therefore, we see that increasing the quarantine rate is a more effective measure than any forms of societal lockdown. Although this figure depends on the value assumed for the parameters, effectiveness of the quarantine does not change (Odagaki, 2020; Sjödin et al., 2020).
6. Discussion
The pandemic COVID-19 has unusual nature such as infectious asymptomatic patients and a long incubation period in comparison to known epidemics (WHO coronavirus disease pandemic, situation report). In the typical epidemics, all infected individuals become infectious after a latent period and show onset of symptoms after an incubation period. Therefore the number of infecteds at large can be estimated from the number of symptomatic patients. We cannot do the same for COVID-19, however, because of the prevalence of asymptomatic patients in the general population. Short of testing the entire population in a single day, the only visible metric we have for the purpose of estimating the total number of infecteds is the number of daily confirmed new cases . Therefore, what we need is to construct a physical model for the pandemic in which is treated explicitly and can be related to the number of infecteds at large .
In order to determine parameters of the model, I fitted the data of the daily confirmed new cases reported in Japan. Using the time dependence of the parameters, I analyzed the characteristics of the outbreak in Japan from mid-February to mid-April. Because of the advance notice of the declaration of the national emergency expected on April 7th, the effect is seen apparently from April 5th. After April 5th, the partial lockdown appears to have resulted in 60% reduction of the social contacts, which is 20% less than the value 80% that the government requested. Has the government introduced other measures as well at the same time, the reduction of infecteds would have been much faster. In particular, the four-day waiting period required for symptomatic patients before they were allowed a PCR test has made the situation much worse. If the waiting period was halved, the quarantine rate would have been doubled. The curves (3) and (4) in Fig. 3 clearly show the effect of efficiency of quarantine measure based on the PCR test. The Japanese government could have taken much better and stronger measures.
It should be mentioned that the growth or decay rate of infecteds is deteremined by λ in Eq. (7) and there is arbitrariness in deteremining β, q and γ from λ. In this paper, I focused upon formulating the best measure for citizens which can be achieved by small γ and small β. Therefore, I set the longest incubation period 15 days (Backer et al., 2020) and the longest infectious period 18 days (He et al., 2020), which make . If these periods are shorter, γ becomes larger and the effect of quarantine measure shown in §5 is somewhat reduced, though the effectiveness of the quarantine measure in controlling the outbreak is not altered as shown in the rigorous treatment of the SIQR model (Odagaki, 2020).
In order to check the consistency of the present analysis in Japan, I verified that the daily confirmed new cases in Japan up until the first two weeks of May are on the curve (0) in Fig. 3.
The basic equation can be modified so as to include the memory effect in the infection process and the quarantine process. To this end, the first two terms in the middle part on the right-hand side of Eq. (5) can be written as
| (16) |
where denotes the time dependence of the transmission coefficient and represents the rate of quarantine of infecteds at time t who got infected at time ,
Although the present model is based on the same compartmental approach as the SIR and SEIR models, it proposes a novel concept in that the quarantine is an effective measure in combatting the spread of the COVID-19 (Sjödin et al., 2020). According to the SIR model apparently employed by the Japanese government, the quarantine was considered as a part of treatment and the last two terms in Eq. (2) are considered together for effective treatments in a hospital. Therefore, many doctors in Japan were strongly against increasing the number of PCR tests, fearing the collapse of the medical care system and false positives in PCR tests leading to placing healthy individuals in quarantine. The policy on quarantine set by the Japanese government was not appropriate to COVID-19.
Since the early stages of civilized history, the quaratine process was considered an effective method for reducing the spread of infection. Therefore, the term in Eq. (5) is considered the number of infecteds newly added in the population, that is is the number of infecteds removed from the population. It is apparent that increasing the quarantine rate is more effective in making negative than lockdown measure, since the former can reduce by several times of q while the latter can contribute at most .
For COVID-19, we should go back to this tradition with contemporary method in identifying pre-symptomatic and asymptomatic patients by PCR tests. In this sense, an effective reproduction number relevant to COVID-19 should be defined by
| (17) |
which represents the rate of change of the number of infecteds at large. The effective reproduction number in Japan in each period shown in Table 1 is 4.2, 4.0, 1 and , where indicates that the number of infecteds in the population is steady. When the epidemic is expanding, becomes larger than 1. On the other hand if becomes less than 1, the epidemic is declining. When , the convergence of the epidemic is achieved by the recovery of patients. The measure which makes must be introduced by each government suitable to the country to accelerate the convergence.
Declaration of competing interest
The author declares no competing interests.
Acknowledgments
I would like to thank Drs. M. Matsushita, M. Sano, Y. Yamazaki and R. Fujie for valuable discussion. My deepest appreciation goes to my family who helped me in preparation of this manuscript.
Handling editor: Dr. J Wu
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
References
- Anderson R.M., May R.M. Science. 1982;215:1053–1060. doi: 10.1126/science.7063839. [DOI] [PubMed] [Google Scholar]
- Arinoa J., Portet S. Infectious Disease Modelling. 2020;5:309–315. doi: 10.1016/j.idm.2020.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Backer J.A., Klinkenberg D., Wallinga J. Euro Surveillance. 2020;25:2000062. doi: 10.2807/1560-7917.ES.2020.25.5.2000062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chowell G., Nishiura H., Bettencourt L.M.A. Journal of The Royal Society Interface. 2007;4:155–166. doi: 10.1098/rsif.2006.0161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- COVID-19, Dashboard, JHU . by the center for systems science and engineering (CSSE) at Johns Hopkins University (JHU); 2020. https://coronavirus.jhu.edu/map.html [Google Scholar]
- Fraser C., Riley S., Anderson R.M., Ferguson N.M. Proc. Natl. Acad. Sci. 2004;101:6146–6151. doi: 10.1073/pnas.0307506101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harko T., Francisco F.S.N., Mak M.K. Applied Mathematics and Computation. 2014;236:184–194. [Google Scholar]
- He X., Lau E.H.Y., Wu P. Natura Med. 2020;26:672–675. doi: 10.1038/s41591-020-0869-5. [DOI] [PubMed] [Google Scholar]
- Heneghan C., Brassey J., Jefferson T. The centre for evidence-based medicine. 2020. https://www.cebm.net/covid-19/covid-19-what-proportion-are-asymptomatic/ April 6.
- Hethcote H., Zhien M., Shengbing L. Mathematical Biosciences. 2002;180:141–160. doi: 10.1016/s0025-5564(02)00111-6. [DOI] [PubMed] [Google Scholar]
- Housen T., Parry A.E., Sheel M. The conversation. https://theconversation.com/how-long-are-you-infectious-when-you-have-coronavirus-135295 April 13, 2020 6.20am. AEST.
- Jumpen W., Wiwatanapataphee B., Wu Y.H., Tang I.M. International Journal of Pure and Applied Mathematics. 2009;52:247–265. [Google Scholar]
- Kermack W.O., McKendrick A.G. Proc. Roy. Soc. A. 1927;115:700–721. [Google Scholar]
- Krasnochub A., Polishchuk V. 2020. [DOI]
- Lauer S.A., Grantz K.H., Bi Q., Jones F.K., Zheng Q., Meredith H.R., Azman A.S., Reich N.G., Lessler J. Annals of Internal Medicine. 2020;172:577–583. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maier B.F., Brockmann D. Science. 2020 doi: 10.1126/science.abb4557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiura H., Linton N.M., Akhmetzhanov A.R. The Internet Journal of Infectious Diseases. 2020;93:284–286. doi: 10.1016/j.ijid.2020.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ministry of Health . 2020. Labour and Welfare, Japan.https://www.mhlw.go.jp/content/10906000/000626140.pdf COVID-19 cases reported on Apr. 29, 2020 (Japanese) [Google Scholar]
- Odagaki T. https://arxiv.org/abs/2007.12846
- Pedersen M.G., Meneghini M. [DOI]
- Sjödin H., Wilder-Smith A., Osman S., Farooq Z., Rocklöv J. COVID-19) outbreak in Italy. Euro Surveillance. 2020;25:2000280. doi: 10.2807/1560-7917.ES.2020.25.13.2000280. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiwari A. 2020a. [DOI]
- Tiwari A. 2020b. [DOI]
- WHO Coronavirus disease (COVID-19) pandemic, Situation report. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/
- WHO coronavirus disease (COVID-19) dashboard. https://covid19.who.int/
- WHO Coronavirus Disease COVID-19) dashboard (Korea) https://covid19.who.int/region/wpro/country/kr
- WHO Coronavirus Disease COVID-19) dashboard (Viet Nam) https://covid19.who.int/region/wpro/country/vn
- WHO coronavirus disease 2019 (COVID-19)Situation report-73. https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200402-sitrep-73-covid-19.pdf?sfvrsn=5ae25bc7