Abstract
Separating facial pose and expression within images requires a camera model for 3D-to-2D mapping. The weak perspective (WP) camera has been the most popular choice; it is the default, if not the only option, in state-of-the-art facial analysis methods and software. WP camera is justified by the supposition that its errors are negligible when the subjects are relatively far from the camera, yet this claim has never been tested despite nearly 20 years of research. This paper critically examines the suitability of WP camera for separating facial pose and expression. First, we theoretically show that WP causes pose-expression ambiguity, as it leads to estimation of spurious expressions. Next, we experimentally quantify the magnitude of spurious expressions. Finally, we test whether spurious expressions have detrimental effects on a common facial analysis application, namely Action Unit (AU) detection. Contrary to conventional wisdom, we find that severe pose-expression ambiguity exists even when subjects are not close to the camera, leading to large false positive rates in AU detection. We also demonstrate that the magnitude and characteristics of spurious expressions depend on the point distribution model used to model the expressions. Our results suggest that common assumptions about WP need to be revisited in facial expression modeling, and that facial analysis software should encourage and facilitate the use of the true camera model whenever possible.
1. Introduction
Facial expression analysis is one of the most studied problems in computer vision, motivated by numerous applications in industry, clinical research, entertainment, and marketing. Variations in head pose create a significant challenge for facial expression analysis [30], as expressions look significantly different from different angles. Disentangling facial expression from pose is important for improving expression recognition accuracy, as well as from an explainable AI standpoint, as one cannot reliably interpret the decisions of a facial behavior analysis system if the expression coefficients are confounded by head movements.
The dominant approach for disentangling pose and expressions within 2D images is to project facial shape to the 3D space, where it can be decomposed into rigid (rotation, translation) and non-rigid factors (expressions) (Section 2.1). This process necessitates a camera model responsible for the 2D-3D projection. The weak perspective (WP) camera (i.e., scaled orthographic camera) is the de facto standard model, used in almost all state-of-the-art approaches (Section 1.1). The conventional wisdom is that WP camera is appropriate when subjects are not close to the camera (Section 1.1); however, to our knowledge, no study investigated this claim in 20 years of research. Such an investigation is particularly urgent now, as advances in mobile technologies and online communication lead to a surge in facial videos recorded using cameras with large field-of-view (FOV) from close distances, and WP camera’s approximation errors increase under those circumstances [19].
In this paper, we theoretically and experimentally investigate the suitability of WP camera for separating facial pose and expressions. Specifically, we show that WP camera leads to spurious expression estimation, thereby introducing pose-expression ambiguity. This paper has four contributions. First, we theoretically prove the existence of spurious expressions under WP camera. Second, we experimentally quantify the magnitude of spurious expressions across a large set of camera configurations, including different FOVs and face sizes (Fig. 1) that are representative of a range of modern cameras and common uses (e.g., photography, webcam/smartphone recordings). Third, we show that the magnitude of spurious expressions varies substantially with the point distribution model (PDM) used to model facial expressions. Last, we show that errors in pose-expression separation have significant practical implications, as they lead to false positives in Action Unit (AU) detection [30].
Figure 1.
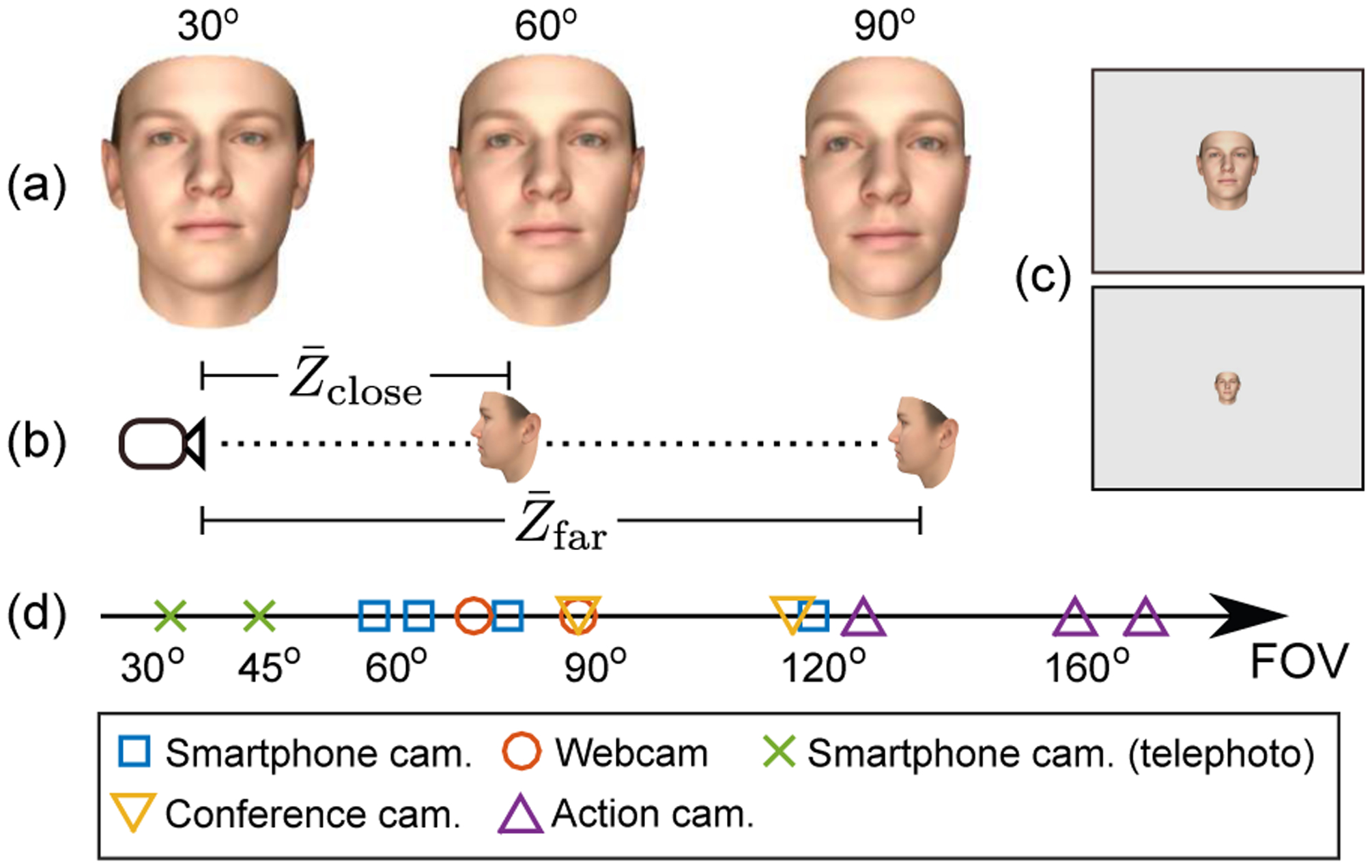
(a) The three FOVs used in this paper; the perspective effect increases with FOV. (b) Two subject-to-camera distances for each FOV. () was (8.5m, 3.5m), (3.9m, 1.6m) and (2.3m, 0.9m) for 30°, 60° and 90° FOV, respectively. (c) Illustration of head size relative to image size with (top) and with (bottom); the head size was approximately the same, independently of FOV, for either distance. (d) The FOV of several cameras; the sources for these data are in [3, 6, 5, 4, 1, 2, 7]
Our analyses yield the following conclusions, which are important for both users of current 3D facial analysis software and for researchers developing novel methods.
Facial pose and expression cannot be separated with existing methods even when WP errors are small, as errors are exacerbated in the optimization process. This finding contradicts the conventional wisdom, which suggests that pose and expression can be separated with WP if the subject is far from the camera.
The PDM used to model expressions can significantly contribute to the exacerbation of WP camera’s approximation errors. Future research is necessary to design PDMs and optimization procedures that allow for facial pose and expression separability.
WP camera makes large approximation errors and should be abandoned for cameras that have high FOV (60°+) especially when the face is relatively close to the camera, as often happens with personal videos or in online communication.
The results of our paper call for reconsideration of the use of WP camera (Section 5). The paper’s main results can be reproduced with the code on https://github.com/sariyanidi/WP_pose-expression-separation.
1.1. Related work
Since the seminal study of Tomasi and Kanade [31], the orthographic projection, which is a special case of WP projection [19], has been very popular in computer vision. WP is a simplistic camera model as it cannot represent the perspective effect [19]; that is, parts of objects do not appear relatively smaller or larger depending on their distance from the camera. While WP is clearly not a realistic camera model, the conventional wisdom is that it is appropriate for facial analysis, because WP approximation errors are inconsequential if subjects are far enough from the camera since the within-face depth variation is generally much smaller than the subject-to-camera distance [13, 17, 26, 9, 35]. WP camera has been broadly used in facial analysis [15, 27, 28, 42, 33, 17, 39, 36, 32, 37, 26, 9, 29, 35, 21, 22, 41, 16] as it facilitates the projection of 2D facial shape to 3D space by removing the non-linearity of perspective projection. More specifically, WP camera is used to separate facial pose and expression [13, 9, 27, 42, 17, 26, 35, 41] or, more generally, to disentangle rigid and non-rigid motions [38, 40, 34, 14]. Notably, no study has tested the main assumption of the WP camera in the context of facial expressions, and it is unclear whether the approximation errors of WP are indeed small enough to allow for facial pose-expression separation. Revisiting this assumption is particularly timely as novel studies continue to use WP camera [41, 10, 11, 22, 16]. Moreover, there is recent increased interest in 3D shape and texture estimation from 2D images, with recently proposed 3D morphable models [25, 18] and publicly available software [10, 20, 8], all using the WP camera.
2. Pose-expression separation
Studies that separate pose and expression within 2D image(s) typically map the face onto the 3D space, as 3D facial shape can be expressed as a combination of pose and expression (Section 2.1). Thus, one can separate facial pose and expression by accurately estimating the pose and expression coefficients in this combination. Most methods use the facial model that is reviewed in Section 2.1. We then review in Section 2.2 the use of this model to estimate pose and expression coefficients from 2D images. These reviews allow us to theoretically demonstrate that pose-expression ambiguity is inherent in WP camera (Section 3).
2.1. Modeling pose and expression
Let be a set of N 3D points (i.e., ) that represent a facial shape that is neutral and frontal w.r.t. camera. Moreover, let be a set of N points from the same person but with a possible expression and pose variation. Then, the latter can be plausibly generated as
| (1) |
where R is a 3 × 3 rotation matrix (we ignore translation for simplicity) and ΔXi := (ΔXi, ΔYi, ΔZi)T represents the facial expression variation in ith point. Typically, the expression variation is modeled with a linear model. That is, , where is a prelearnt expression basis matrix (referred to also as expression PDM) with M components, and e is the set of coefficients that explains the expression in the given facial shape.
The facial model used in most methods that decouple pose and expression [41, 12, 21, 26, 34] is essentially the same as (1); the main difference is the way in which neutral face is modeled. Neutral face is generally assumed to be unknown and estimated with an identity PDM [41, 12].Since the aim of our study is to analyze pose-expression separability, we will assume that the neutral face is known and thus avoid possible errors in its estimation.
2.1.1. 2D-3D mapping
With the formulation in (1), the problem of pose and expression separation is essentially equivalent to the accurate estimation of the rotation matrix R and expression coefficients e. The estimation of R and e from 2D images requires a proper mapping defined between the 2D and 3D points.
Suppose that the images are captured with a CCD camera. Then the 2D image points, xi, are accurately computed with a perspective projection [19] matrix P defined as1
| (2) |
where (cx, cy) is the principal point and αx and αy are the focal length of the camera in the horizontal and vertical direction, respectively. To obtain the image point xi corresponding to Xi, we first compute the homogeneous image coordinates define as , where t := (tx, ty, tz) is the 3D location of the camera. The image point xi can finally be obtained by dehomogenizing, i.e.
| (3) |
For analytical clarity, hereafter we assume that tx = ty = 0.
2.1.2. Mapping via weak perspective camera
A major challenge to separating pose and expression is that the camera model (i.e., P) is generally not known. Moreover, the dehomogenizing in the perspective transformation adds a non-linearity that complicates the estimation of unknown variables. Therefore, most studies use the WP projection (Section 1.1), which is a simple model but generally considered to be reasonable when the camera-to-object distance is large compared to within-object depth variation. The image point corresponding to the 3D point Xi under a WP camera model can be computed as [19]
| (4) |
where W(σ) is the WP projection matrix defined as
| (5) |
and c = (cx, cy)T. The parameters σx and σy in (5) are the horizontal and vertical scale factors, respectively. The practical role of those factors is to make the face appear bigger or smaller depending on its proximity to the camera; the WP model cannot otherwise adjust the face size as it does not have the perspective effect.
2.2. Estimating pose and expression coefficients
We can now formulate the problem of estimating pose and expression coefficients under WP camera. We assume that we know the neutral face (i.e. the points {}) to facilitate the interpretation of experimental outcomes, as in this case R and e remain as the only unknowns.
Suppose that we are given a set of 3D points corresponding to a neutral and frontal face of a person, and a set of 2D image points representing the facial shape of the same person, , with a possible pose (i.e., rotation) and expression variation. Let be the zero-mean image points defined as . Then, the rotation and expression coefficients can be estimated by minimizing the error function JB defined as
| (6) |
w.r.t. variables σ, R and e which respectively correspond to WP scale parameter, rotation matrix and expression coefficients2. (The term c in (4) can be eliminated when we operate on zero-mean image points [31].) R is subject to the implicit constraint R ∈ SO(3). The operation [⋅]i outputs a 3-vector that represents the expression variation in the ith point; that is, [Be]i contains the three values of the vector Be corresponding to positions 3i−2, 3i−1 and 3i. The minimization of error function (6) is often carried out with the Gauss-Newton method [13, 28, 12, 11].
3. Ambiguity in pose-expression separation
If the image points represent a facial shape with neutral expression, then the expression coefficients e estimated by minimizing (6) should ideally be 0. As we theoretically demonstrate below, this is not the case; instead, the use of WP camera leads to inherent ambiguity.
If a facial shape has a neutral expression, then ΔXi = 0 for i = 1, …, N and (1) can be rewritten as
| (7) |
Since we assume that there is no expression, let us for now assume that the expression PDM is the null matrix, i.e., B = 0. Then, the function (6) simplifies to
| (8) |
Note that this can be interpreted as the 3D-to-2D mapping error of the WP camera for parameters R and σ, since () represents the difference between the correct 2D projection of the point Xi and the 2D projection of the same point under the WP camera [see (4) for ΔXi = 0]. The minimal 3D-to-2D mapping error (in terms of ℓ2) is encoded in the residual vector
| (9) |
where and are column vectors and . and are block-diagonal matrices with N matrices on their diagonals, and . R* and σ* are minimizers of (8). We now list this paper’s main theoretical result.
Theorem 3.1. Suppose we have 3D facial points with a neutral expression, , and 2D image points corresponding to those 3D points but with a rotation. Let R* and σ* minimize J0(R, σ), r be defined as in (9), and be a matrix such that rank . Then,
| (10) |
Moreover, this inequality holds strictly (i.e., without equality) if , in which case ∣∣e*∣∣>0 where e* is the minimizer of JB(R, e, σ) w.r.t. variable e.
For the proof, refer to Supplementary Appendix A. The assumption rank is a mild one, because PDMs are typically obtained with principal component analysis, which yields skinny and full column-rank matrices, and also because and are full (row) rank. Moreover, as we argue in Supplementary Appendix B, is not a practically likely event. The theorem states that the error in (6) will be smaller than the error in (8) even when there is no expression (i.e., a neutral face), since the error between the correct 2D projection of the point Xi and the 2D projection of the same point under the WP camera will be reduced by employing spurious expression coefficients in (6). Thus, this theorem formally demonstrates that spurious expressions will be generated (i.e., e ≠ 0) if . Next, we empirically investigate whether those spurious expressions are sufficiently large to be harmful in practice.
4. Experimental Analysis
We now experimentally show that the WP camera creates facial pose-expression ambiguity. Our experiments are coherent with our theoretical analysis in Section 3; that is, we use sequences that contain a neutral (i.e., expressionless) face and demonstrate that the use of WP camera leads to spurious expression detection.
Our experimental analysis is threefold. Section 4.3 quantifies the 3D-to-2D mapping errors of the WP camera w.r.t. pose. Section 4.4 quantifies spurious expressions and also investigates the effect of the facial expression PDM (i.e., B) choice. Section 4.5 shows that spurious expression coefficients lead to false positives in AU estimation.
4.1. Dataset
We conduct our analysis on synthesized data to ensure that the facial sequences that we use contain no expression variations, and to know the exact facial pose (i.e., ground truth) and 3D locations of facial points. We experiment with three fields of view, 30°, 60°and 90°, and two face sizes (relative to image) per FOV, namely large and small (Fig. 1b, c).
We synthesize facial sequences using the Basel’09 model [24]. We generate 100 facial identities by randomly choosing 100 different identity coefficients from the Basel model (Fig. 2a). We use the widely used set of N = 68 facial landmarks, known also as iBUG-68 points (see Fig. 2b). Throughout experiments, we study the effect of (out-ofplane) pose variation, namely rotation along the yaw and pitch axes. To this end, for each synthesized identity we generate two sequences, each containing a face rotated from −45° to 45° along one of the two afore-listed axes (see Fig. 3). Thus, our experiments involve 200 sequences per FOV and distance, and since we have three FOVs and two distances, a total of 1200 sequences.
Figure 2.
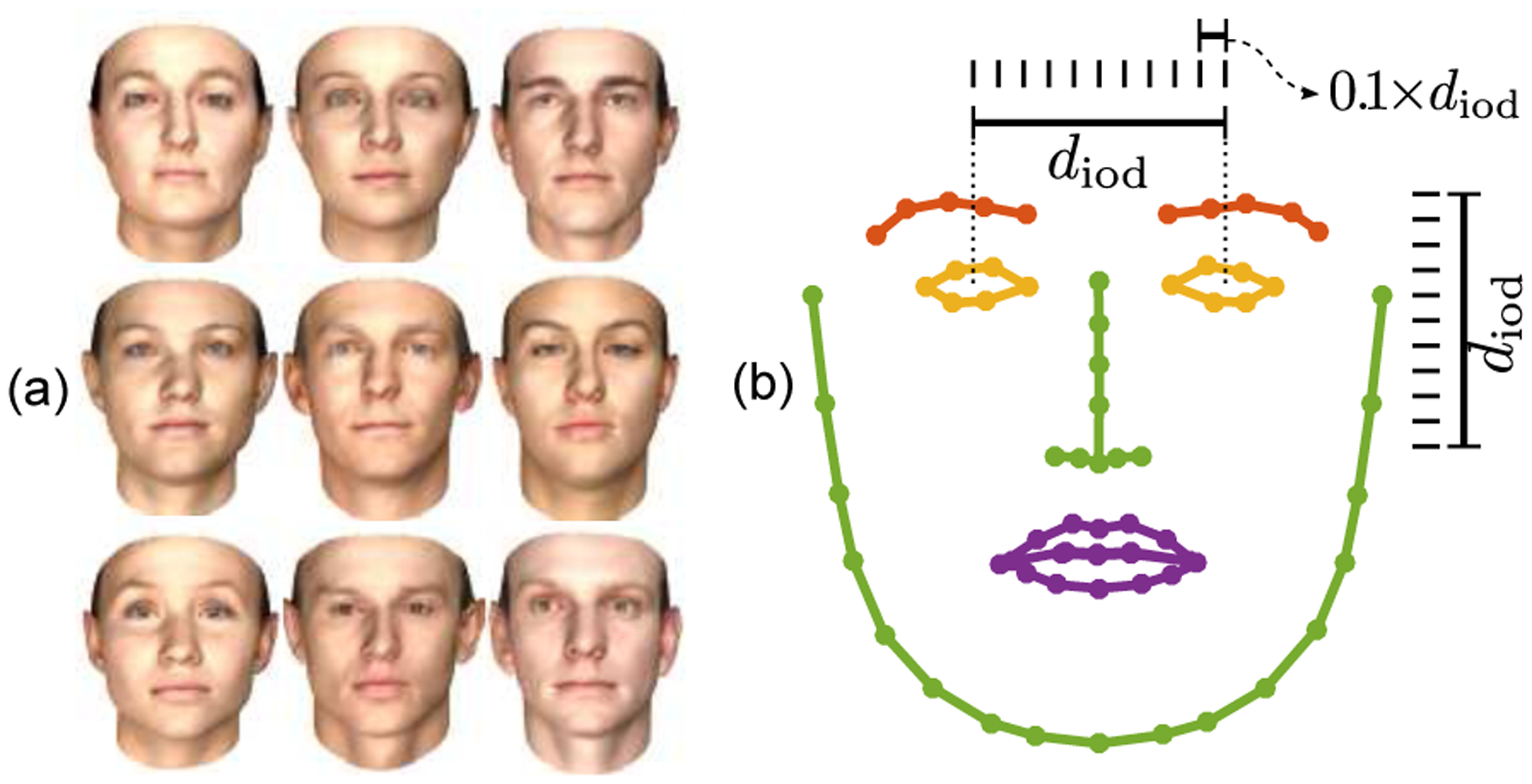
(a) Examples of the generated facial identities that were used in the experiments. We use only facial shape but here we show also facial texture to enhance interpretation. (b) The 68-point facial shape model (iBUG-68) that is used for the experiments, and the illustration of the interocular distance diod. Note that even a spurious expression of 0.1diod magnitude is large enough to create the impression, say, of a blink or a raised eyebrow.
Figure 3.

The rotation range; (a) yaw rotation, (b) pitch rotation.
4.2. Optimization
In all experiments, we use the Gauss-Newton optimization algorithm to minimize (6) and (8), as this algorithm has been used by previous studies (Section 2.2). To initialize the estimated rotation matrix for (6), we use the rotation matrix obtained by minimizing the simpler function (8).
4.3. Analysis of 3D-to-2D mapping errors
We now experimentally analyze how the 3D-2D mapping error of the WP camera varies with head rotation.
Metric.
The mapping error for the ith facial point of kth sequence is , where σ* and R* are obtained by minimizing J0 (Section 3). We report the average mapping error for all the N = 68 landmark points (eoverall) and also the average for landmarks related to brows (ebrow), eyes (eeyes) and mouth (emouth). Let Ieyes be a set that contains the landmark indices corresponding to the eyes (i.e., the yellow points in Fig. 2b). Then, average mapping error for the eye landmarks, eeyes, is computed by averaging both over the sequences and over the landmarks in Ieyes as
| (11) |
where we divide to the interocular distance of the 3D face, , to better interpret the error (Fig. 2b). The errors eoverall, ebrows and emouth are computed similarly by replacing the set Ieyes accordingly (Ioverall is {1, …, N}).
Results.
Fig. 4 shows the average errors eoverall, ebrow, eeyes and emouth against rotation amount; each panel shows the error for a unique FOV and subject-to-camera distance combination. The symbols θ and ϕ denote rotation around yaw and pitch axes, respectively. As expected, the mapping errors increase with FOV when the face size is constant (Fig. 1c). Errors are also higher when the subject is closer to the camera. Since faces are approximately symmetric w.r.t. the vertical line, the rotation around the the yaw axis (Fig. 3a) generates a nearly symmetric error pattern (Fig. 4a). The average error varies for each facial feature. Eyebrows generate consistently the highest error for yaw rotations, followed by eyes and mouth. For pitch rotations, the ranking of features in terms of errors depends on the rotation amount. The error for a FOV of 60° can get close to 0.1diod, which is a magnitude quite noticeable to the eye; for example, it is large enough to create an impression of a raised/lowered brow or a blink (Fig. 2b).
Figure 4.
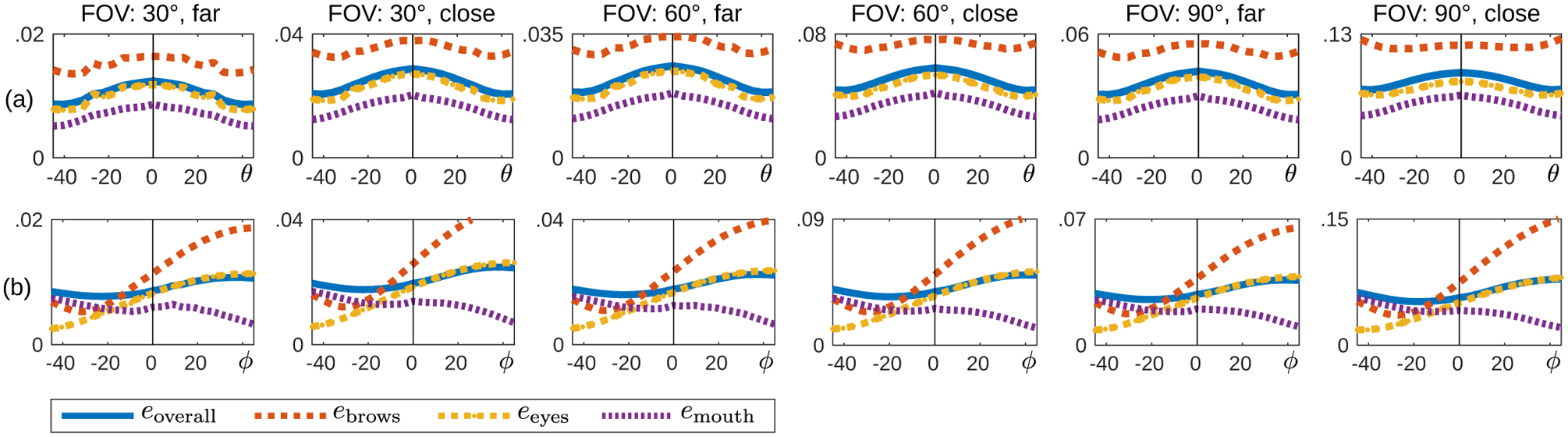
3D-to-2D mapping errors vs. rotation amount for various FOVs (30°, 60°, 90°) and subject-to-camera distances (close, far; Fig. 1). (a) yaw rotation; (b) pitch rotation. The y axis shows error rate relative to interocular distance (Fig. 2); e.g., 0.01 means 0.01diod. Note that errors increase with FOV; the range of y axis is scaled separately for each subplot to enhance interpretation.
4.4. Analysis of spurious expression coefficients
We now analyze the magnitude of spurious expressions, whose existence is suggested by Theorem 3.1. Importantly, we show how spurious expressions vary with the choice of facial expression PDM, B, as well as facial pose, FOV and subject-to-camera distance.
Metrics.
We measure the magnitude of spurious expressions via the l2 norm of the estimated expressions in the kth sequence, . Since our sequences contain no expression variation (Section 4.1), a non-zero will always indicate spurious expressions. Similarly to Section 4.3, we report results separately for eyes, brows and mouth. The average magnitude of spurious expression for eyes is denoted with yeyes and computed by averaging over the K sequences as
| (12) |
where and are defined as in Section 4.3. Here we consider only the spurious expression magnitude along the x and y axes: The operator parses the two values that correspond to the expression variation ignoring the z axis; that is contains the values of the vector corresponding to the positions 3i−2, 3i−1. This allows us to compare the magnitude of spurious expressions yeyes with the 3D-to-2D mapping errors eeyes, when there is no rotation. The average magnitude of spurious expressions for all points, yoverall, and for other facial features, ybrows, ymouth, are computed similarly.
Facial expression PDMs.
We use two PDMs which, to our knowledge, are the only publicly available PDMs to model expressions alone: (i) Basel’17: The expression PDM of the Basel’17 model [18]; and (ii) ITWMM: The expression PDM of the in-the-wild method by Zhu et al. [41], used also by a morphable model in-the-wild study [12]. We omitted PDMs which do not model expressions alone (e.g. OpenFace PDMs [10], Surrey PDM [20]).
Results.
When we use an expression PDM, estimated 2D points improve significantly (e.g. compare Fig. 5b, c with Fig. 5a) as predicted by Theorem 3.1. However, this causes spurious expressions (Fig. 6) and therefore harms pose-expression separation, as we elaborate in this section.
Figure 5.
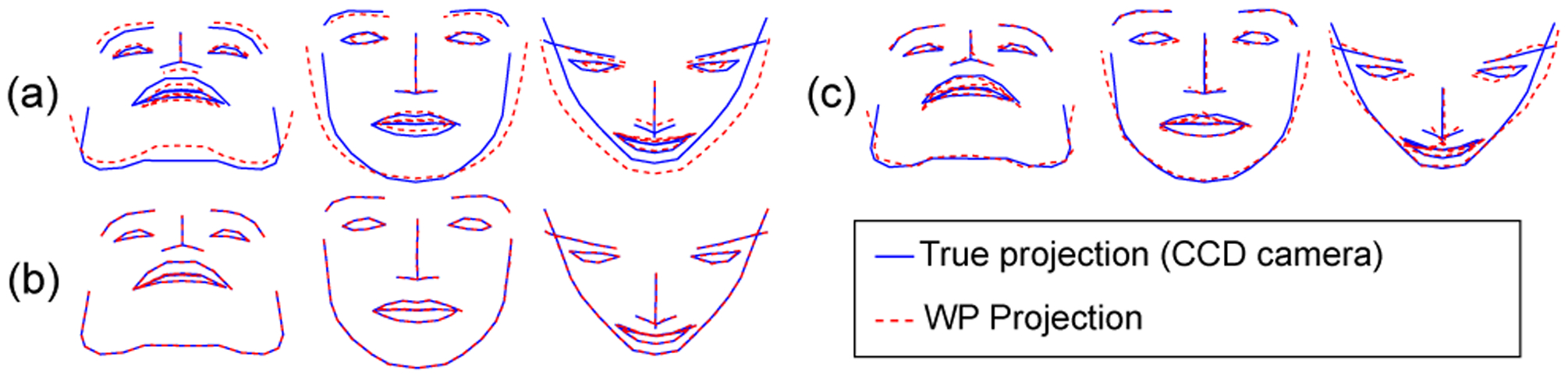
Projection of facial points according to the correct perspective projection (CCD camera model) and according to the WP projection for a camera with FOV of 90° and close subject-to-camera distance and for −45°, 0° and 45° pitch rotation. The WP projection is carried out with (a) no expression PDM, i.e. B=0, (b) with the Basel’17 PDM and (c) with the ITWMM PDM.
Figure 6.

The spurious expressions obtained by minimizing JB where the B used is the (a) Basel’17 PDM and (b) the ITWMM PDM. Each red arrow depicts the effect of the spurious expression Be* on the corresponding landmark.
Fig. 7 quantifies the magnitude of spurious expressions for different PDMs as well as FOVs and subject-to-camera distances. As predicted by Theorem 3.1 and the argument that follows it, there are always spurious expressions. The magnitude of spurious expressions increases with FOV and is also higher when the subject is close to the camera. However, Fig. 7 uncovers an important result that is not obvious: Facial parts that have small 3D-to-2D mapping errors can have high spurious expressions and vice versa. For example, mapping errors for the mouth (Fig. 4a) are lower compared to other features, and yet spurious expressions for the mouth are larger than those of other features for the ITWMM PDM (Fig. 7a). Another novel result is that the magnitude of spurious expressions is generally larger than the mapping errors. These observations are explained by the fact that e is not the only variable when minimizing (6), and that the optimal R and σ determined by the optimization algorithm depend on whether B is 0 or not. The differences in the values of R and σ cause additional landmark movement, which is compensated by the algorithm via additional activation of e coefficients. Another important result of Fig. 7 is that the magnitude of spurious expressions, and the facial features that have the highest spurious expressions, depend on the PDM used. For example, the ITWMM PDM makes larger errors for the mouth region, whereas the Basel’17 PDM makes comparable errors across all features.
Figure 7.
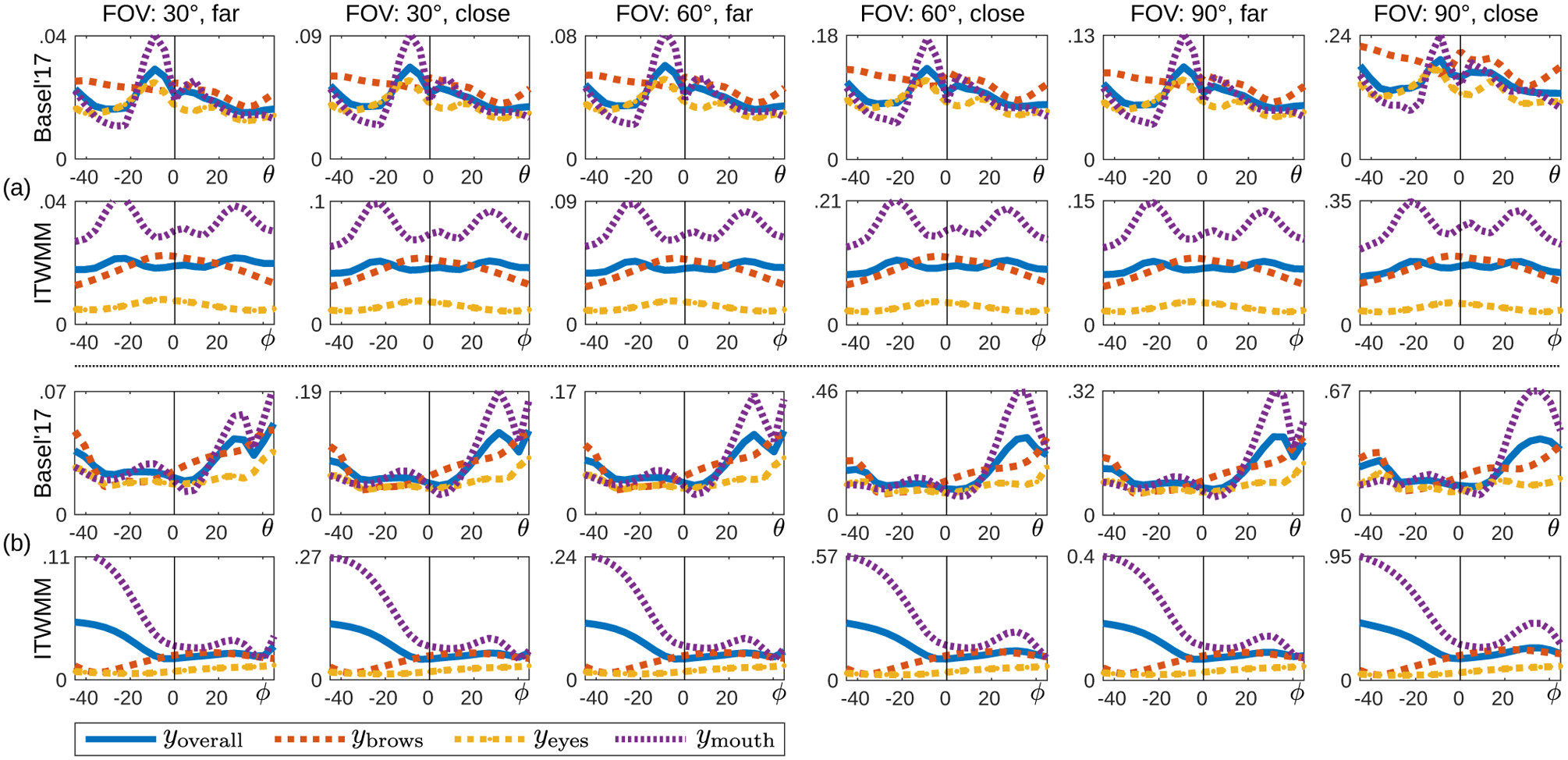
The magnitude of spurious expressions against the rotation amount, shown separately for the Basel’17 PDM and the ITWMM PDM, and for various FOVs (30°, 60°, 90°) and subject-to-camera distances (close, far; see Fig. 1). (a) Yaw rotation; (b) pitch rotation. The y axis shows error rate relative to interocular distance diod (Fig. 2). Note that spurious expressions increase with FOV; the range of y axis is scaled separately for each subplot to enhance interpretation.
4.5. Analysis of spurious Action Units
While we have demonstrated the presence of spurious expressions, the question of whether they have significant practical implications for automated facial expression analysis systems remains. In this section, we show that spurious expressions can indeed be damaging, and lead to false positives in the application of AU detection. To this end, we train AU detectors that take as input the expression coefficients e* and output the predicted AU. We use an SVM classifier and avoid more sophisticated classifiers (e.g., deep learning) as our purpose is not to maximize AU detection accuracy but to analyze the possible false positives that may be caused by spurious expression coefficients e*.
Training AU detectors.
To train AU detectors, we use the 327 videos from MMI dataset [23] that contain temporal phase annotation. We train 8 detectors for 8 AUs, namely AU1, AU2, AU4, AU45 AU12, AU17, AU25 and AU26. To train them, we compute the e* coefficients by minimizing (6). Since the MMI dataset is 2D, it does not have the neutral 3D facial shape needed in (6). To estimate we use the first frame of each MMI video; this contains a neutral expression and therefore we can use the Basel’09 model to estimate the 3D shape of the person from this frame. We train each AU detector with differential features; that is, we subtract the expression coefficients of the first (i.e. neutral) frame from the frame that contains the AU. As negative samples, we used the frames with other AUs and frames without AUs (i.e., neutral frames other than the first frame). We validated each AU detector with a 5-fold cross-validation via F1 score (Table 1). The false positive rate (FPR) of any AU was not higher than 0.02 (Table 1), highlighting the feasibility of the experiment; i.e., we can reliably assert that false positives in the test set will be mostly due to spurious expressions. The Basel’17 PDM achieved the highest F1 score for most AUs [23].
Table 1.
AU detection results in terms of F1 score, true positive rate (TPR) and false positive rate (FPR) on MMI dataset reported separately for the Basel’17 PDM and the ITWMM PDM.
| AU1 | AU2 | AU4 | AU45 | AU12 | AU17 | AU25 | AU26 | ||
|---|---|---|---|---|---|---|---|---|---|
| Basel’17 | F1 | 0.66 | 0.64 | 0.47 | 0.70 | 0.43 | 0.48 | 0.80 | 0.45 |
| TPR | 0.58 | 0.63 | 0.41 | 0.58 | 0.31 | 0.36 | 0.72 | 0.36 | |
| FPR | 0.01 | 0.01 | 0.02 | 0.01 | 0.01 | 0.02 | 0.02 | 0.02 | |
| ITWMM | F1 | 0.62 | 0.42 | 0.4 | 0.68 | 0.34 | 0.36 | 0.8 | 0.08 |
| TPR | 0.49 | 0.31 | 0.28 | 0.56 | 0.24 | 0.24 | 0.71 | 0.05 | |
| FPR | 0.00 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.01 | |
Test sequences.
Our testing sequences are strictly the 1200 synthesized sequences (Section 4.1) that have no expression variation, as our purpose is to analyze how an AU detector behaves when it is fed spurious coefficients. Therefore, an AU detector that yields a positive output to any frame in our test sequences will be yielding a false positive.
Metrics.
We measure the false positive rate (FPR) for each AU. For brevity, we report average FPR over all AUs. We have Nseq=600 sequences with yaw rotation (Section 4.1). The average FPR over the 8 AUs under θ degrees yaw rotation is denoted with FPRθ, which is defined as
| (13) |
where is the number of false positives for AUi under θ degrees yaw rotation and IAU is the set of the 8 AUs that we use. The average FPR for AUs under pitch rotation of ϕ degrees, FPRϕ, is defined similarly.
Results.
Fig. 8 shows the FPRs in AU detection on synthesized sequences (Section 4.1). As expected from the results of previous sections, FPRs increase with FOV and are higher when the subject is closer to the camera. Never-theless, FPRs are non-zero even when the FOV is as small as 30° and the subject is as far from the camera as shown in Fig. 1c (bottom), for pitch or yaw rotations of 25° or higher. For FOV of 60°, some false positive AUs exist even when there is a rotation only slightly higher than 0°. In sum, the standard approach to facial pose and expression separation leads to an unacceptable number of false positives.
Figure 8.
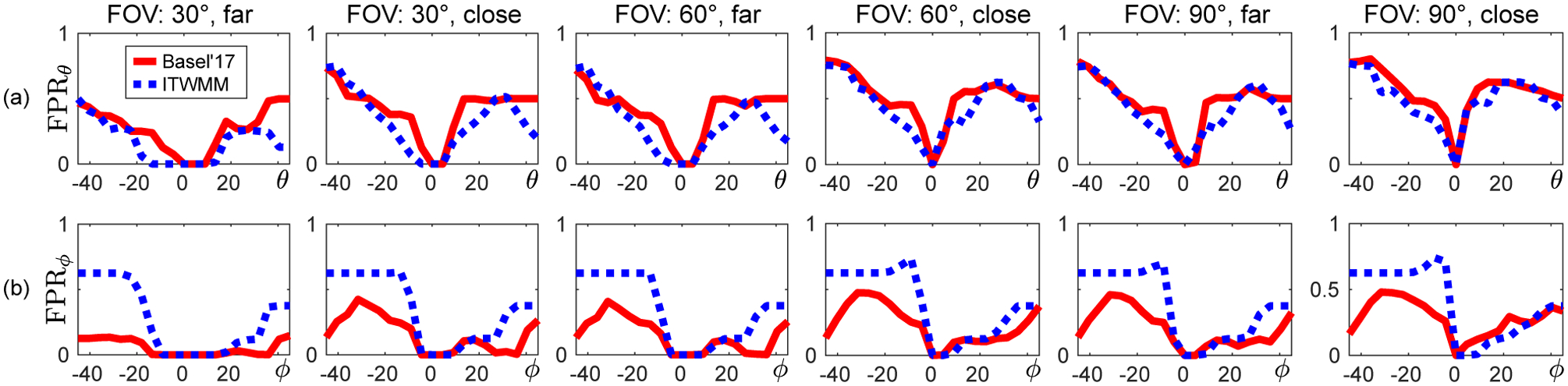
The AU false positive rates (FPRs) against the rotation amount for various various FOVs (30°, 60°, 90°) and subject-to-camera distances (close, far; see Fig. 1). (a) Yaw rotation; (b) pitch rotation.
Results with original ITWMM software.
To verify this section’s findings, we repeated experiments using the original ITWMM [12] source code (with WP camera), which, to our knowledge, is the only publicly available 2D-based 3D facial shape estimation method that contains a separate PDM for expressions only and uses Gauss-Newton optimization. The results similarly indicated a severe pose sensitivity, and there were false positive AUs across all FOVs even when the face was far from the camera (Supplementary Appendix C). This experiment ensures that our findings are not artifacts of our own implementation, further emphasizing the significance of spurious facial expressions induced by the WP camera model.
Results with perspective camera.
To verify that the false positive AUs stem from the WP camera, and are not due to changing data characteristics between the training and testing sets (MMI vs. synthesized images), we re-run this section’s experiments by replacing the WP model in (6) with the true camera model—the perspective transformation according to (2). There were no false positives of AUs for any FOV or subject-to-camera distance in this case, which is not surprising as we use noiseless 3D and 2D points.
5. Discussion
For nearly two decades, the WP camera has been a common component in virtually all methods that separate facial pose and expression. While it continues to be the default camera model in very recent studies published in top-tier conferences and journals, the suitability of WP camera for this task has never been thoroughly and systematically investigated (Section 1.1). Our study takes a first step in critically evaluating this issue, with two important findings.
First, pose and expression cannot be separated reliably even when WP camera errors are indeed small. This is a particularly striking finding as it contradicts the conventional wisdom that WP camera is usable when the face is not close to the camera (Section 1.1). The ambiguity in these circumstances is caused by the interactions between the estimated rotation and expression coefficients: The optimization algorithm can find a solution that explains the 2D points well, but with incorrect pose and expression parameters (Section 4.4). Moreover, our results highlight that the PDM used to model expressions has a significant impact on the amount and characteristics of errors (i.e., spurious expressions). These observations naturally beg the question (and future research direction): Can one find design criteria for PDMs that minimize spurious expressions? As an extreme example of a badly designed PDM, one can imagine an “expression” PDM that contains components resembling rotation. In such a case, clearly one cannot guarantee to correctly estimate pose and expression by minimizing (6), even when no camera approximation errors exist.
Second, our experiments that quantify the approximation errors of WP camera in terms of interocular distance diod show that it is particularly unreliable for modeling facial expressions recorded from close distance cameras with large FOV, such as smartphones or web-cams (Fig. 1). Given the surge in videos of this kind of late, novel methods and software likely need to re-consider the use of WP camera. While use of the WP camera model may be justified for applications that use images with completely unknown sources, in many applications, it is used with no theoretical or practical reasons. For example, in most clinical applications or personal social/entertainment/artistic applications, the camera that is used is known. One can use the images’ metadata or the camera’s technical specifications (i.e., FOV and image width/height), or add a simple camera calibration step, to estimate the true perspective projection, thereby obviating the need for WP camera. Facial expression analysis software should warn users about the limitations of the default WP camera and instead encourage the use of the true projection matrix, especially if the camera has large FOV and/or the size of the face is small relative to the image.
6. Conclusion
We revisited a problem studied for more than 20 years, namely separating facial pose and expression within 2D images, and showed that the use of the WP camera model is a barrier to achieving reliable results. We theoretically showed that WP camera generates spurious expressions. Our systematic experiments demonstrated that, contrary to conventional wisdom, pose-expression ambiguity exists even when subjects are far from the camera (i.e., when WP camera’s errors are small). We also showed that spurious expressions led to false positives in facial AU detection. We discussed the implications of our findings and suggested future research directions to address the issues caused by WP camera. Of note, WP camera is used in many computer vision applications (Section 1.1), suggesting that the findings of this study may have implications beyond facial analysis.
Supplementary Material
Acknowledgment
The work of E. Sariyanidi, C. J. Zampella, R. T. Schultz and B. Tunc is partially funded by the NIMH of the US under grant R01MH118327 and by the Eagles Autism Foundation. The work of R. T. Schultz is partially funded also by the McMorris Family Foundation.
References
- [1].Conference Room Camera Comparison. https://cdn2.hubspot.net/hubfs/2799205/Conferenc%20Room%20Camera%20Comparison.pdf?t=1510772566947. Accessed: 2010-09-1.
- [2].GoPro cameras. https://gopro.com/help/articles/question_answer/hero7-field-of-view-fov-information. Accessed: 2010-09-1.
- [3].iPhone Cameras. https://developer.apple.com/library/archive/documentation/DeviceInformation/Reference/iOSDeviceCompatibility/Cameras/Cameras.html. Accessed: 2010-09-1.
- [4].Logitech B910 HD Webcam. https://www.logitech.com/assets/64666/2/b910datasheet.pdf. Accessed: 2010-09-1.
- [5].Logitech C930e 1080p HD Webcam . https://www.logitech.com/en-us/product/c930e-webcam. Accessed: 2010-09-1.
- [6].Samsung Galaxy S10e, S10 & S10+. https://www.samsung.com/global/galaxy/galaxy-s10/specs/. Accessed: 2010-09-1.
- [7].YI 4K Specs. https://www.yitechnology.com/yi-4k-action-camera-specs. Accessed: 2010-09-1.
- [8].Joan Alabort-i Medina Epameinondas Antonakos, Booth James, Snape Patrick, and Zafeiriou Stefanos. Menpo: A comprehensive platform for parametric image alignment and visual deformable models In Proc. ACM Int’l Conf. on Multimedia, pages 679–682. ACM, 2014. [Google Scholar]
- [9].Tadas Baltrušaitis Peter Robinson, and Morency Louis-Philippe. 3d constrained local model for rigid and non-rigid facial tracking In 2012 IEEE Conference on Computer Vision and Pattern Recognition, pages 2610–2617. IEEE, 2012. [Google Scholar]
- [10].Baltrusaitis Tadas, Zadeh Amir, Lim Yao Chong, and Louis-Morency Philippe. Openface 2.0: Facial behavior analysis toolkit. In Proc. Int’l Conf. on Automatic Face & Gesture Recognition, pages 59–66, 2018. [Google Scholar]
- [11].Bas Anil, Huber Patrik, William AP Smith Muhammad Awais, and Kittler Josef. 3d morphable models as spatial transformer networks. In Proc. Int’l Conf. on Computer Vision, pages 904–912, 2017. [Google Scholar]
- [12].Booth James, Roussos Anastasios, Ververas Evangelos, Antonakos Epameinondas, Ploumpis Stylianos, Panagakis Yannis, and Zafeiriou Stefanos. 3d reconstruction of inthe-wild faces in images and videos. IEEE Trans. on Pattern Analysis and Machine Intelligence, 40(11):2638–2652, 2018. [DOI] [PubMed] [Google Scholar]
- [13].Brand Matthew and Bhotika Rahul. Flexible flow for 3d non-rigid tracking and shape recovery. In Proc. IEEE Conf. Computer Vision and Pattern Recognition, volume 1, pages I–I, 2001. [Google Scholar]
- [14].Bregler Christoph, Hertzmann Aaron, and Biermann Henning. Recovering non-rigid 3d shape from image streams. In cvpr, volume 2, page 2690 Citeseer, 2000. [Google Scholar]
- [15].Fernando De la Torre, Jordi Vitria, Petia Radeva, and Javier Melenchon. Eigenfiltering for flexible eigentracking (efe). In Proc. Int’l Conf. Pattern Recognition, volume 3, pages 1106–1109, 2000. [Google Scholar]
- [16].Deng Jiankang, Roussos Anastasios, Chrysos Grigorios, Ververas Evangelos, Kotsia Irene, Shen Jie, and Zafeiriou Stefanos. The menpo benchmark for multi-pose 2d and 3d facial landmark localisation and tracking. International Journal of Computer Vision, 127(6–7):599–624, 2019. [Google Scholar]
- [17].Dornaika Fadi and Davoine Franck. Simultaneous facial action tracking and expression recognition in the presence of head motion. Int’l J. computer vision, 76(3):257–281, 2008. [Google Scholar]
- [18].Gerig Thomas, Andreas Morel-Forster Clemens Blumer, Egger Bernhard, Luthi Marcel, Sandro Schönborn, and Thomas Vetter. Morphable face models-an open framework. In Proc. Int’l Conf. on Automatic Face & Gesture Recognition, pages 75–82, 2018. [Google Scholar]
- [19].Hartley Richard and Zisserman Andrew. Multiple view geometry in computer vision. Cambridge university press, 2003. [Google Scholar]
- [20].Huber Patrik, Hu Guosheng, Tena Rafael, Mortazavian Pouria, Koppen P, Christmas William J, Ratsch Matthias, and Kittler Josef. A multiresolution 3d morphable face model and fitting framework. In Proc. Int’l Joint Conf. on Computer Vision, Imaging and Computer Graphics Theory and Applications, 2016. [Google Scholar]
- [21].Jourabloo Amin and Liu Xiaoming. Pose-invariant 3d face alignment. In Proceedings of the IEEE International Conference on Computer Vision, pages 3694–3702, 2015. [Google Scholar]
- [22].Liu Feng, Zeng Dan, Li Jing, and Zhao Qi-jun. On 3d face reconstruction via cascaded regression in shape space. Frontiers of Information Technology & Electronic Engineering, 18(12):1978–1990, 2017. [Google Scholar]
- [23].Pantic Maja, Valstar Michel, Rademaker Ron, and Maat Ludo. Web-based database for facial expression analysis. In Proc. Int’l Conf. on Multimedia and Expo, pages 5–pp, 2005. [Google Scholar]
- [24].Paysan Pascal, Knothe Reinhard, Amberg Brian, Romdhani Sami, and Vetter Thomas. A 3d face model for pose and illumination invariant face recognition. In Proc. Int’l Conf. on Advanced Video and Signal Based Surveillance, pages 296–301, 2009. [Google Scholar]
- [25].Ploumpis Stylianos, Wang Haoyang, Pears Nick, William AP Smith, and Stefanos Zafeiriou. Combining 3d morphable models: A large scale face-and-head model. In Proc. IEEE Conf. Computer Vision and Pattern Recognition, pages 10934–10943, 2019. [Google Scholar]
- [26].Raducanu Bogdan and Dornaika Fadi. Dynamic facial expression recognition using laplacian eigenmaps-based manifold learning. In Proc. IEEE Int’l Conf. on Robotics and Automation, pages 156–161, 2010. [Google Scholar]
- [27].Romdhani Sami, Canterakis Nikolaos, and Vetter T. Selective vs. global recovery of rigid and non-rigid motion. Technical report, CS Dept, 2003.
- [28].Romdhani Sami and Vetter Thomas. Efficient, robust and accurate fitting of a 3d morphable model. In Proc. Int’l Conf. Computer Vision, volume 3, pages 59–66, 2003. [Google Scholar]
- [29].Sangineto Enver. Pose and expression independent facial landmark localization using dense-surf and the hausdorff distance. IEEE Trans. on Pattern Analysis and Machine Intelligence, 35(3):624–638, 2012. [DOI] [PubMed] [Google Scholar]
- [30].Sariyanidi E, Gunes H, and Cavallaro A. Automatic analysis of facial affect: A survey of registration, representation and recognition. IEEE Trans. on Pattern Analysis and Machine Intelligence, 37(6):1113–1133, 2015. [DOI] [PubMed] [Google Scholar]
- [31].Tomasi Carlo and Kanade Takeo. Shape and motion from image streams under orthography: a factorization method. Int’l J. computer vision, 9(2):137–154, 1992. [Google Scholar]
- [32].Tong Yan, Chen Jixu, and Ji Qiang. A unified probabilistic framework for spontaneous facial action modeling and understanding. IEEE Trans. on Pattern Analysis and Machine Intelligence, 32(2):258–273, 2008. [DOI] [PubMed] [Google Scholar]
- [33].Tong Yan, Liao Wenhui, Xue Zheng, and Ji Qiang. A unified probabilistic framework for facial activity modeling and understanding In 2007 IEEE Conference on Computer Vision and Pattern Recognition, pages 1–8. IEEE, 2007. [Google Scholar]
- [34].Torresani Lorenzo, Hertzmann Aaron, and Bregler Chris. Nonrigid structure-from-motion: Estimating shape and motion with hierarchical priors. IEEE transactions on pattern analysis and machine intelligence, 30(5):878–892, 2008. [DOI] [PubMed] [Google Scholar]
- [35].Unzueta Luis, Pimenta Waldir, Goenetxea Jon, Lúıs Paulo Santos, and Fadi Dornaika. Efficient generic face model fitting to images and videos. Image and Vision Computing, 32(5):321–334, 2014. [Google Scholar]
- [36].Wang Te-Hsun and Lien Jenn-Jier James. Facial expression recognition system based on rigid and non-rigid motion separation and 3d pose estimation. Pattern Recognition, 42(5):962–977, 2009. [Google Scholar]
- [37].Wang Xiaoyan, Huang Xiangsheng, Cai Huiwen, Wang Xin, et al. A head pose and facial actions tracking method based on effecient online appearance models. WSEAS Transactions on Information Science and Applications, 7(7):901–911, 2010. [Google Scholar]
- [38].Xiao Jing, Chai Jinxiang, and Kanade Takeo. A closed-form solution to non-rigid shape and motion recovery. Int’l J. computer vision, 67(2):233–246, 2006. [Google Scholar]
- [39].Zhang Yongmian, Ji Qiang, Zhu Zhiwei, and Yi Beifang. Dynamic facial expression analysis and synthesis with mpeg-4 facial animation parameters. IEEE Trans. on Circuits and Systems for Video Technology, 18(10):1383–1396, 2008. [Google Scholar]
- [40].Zhou Xiaowei, Zhu Menglong, Leonardos Spyridon, and Daniilidis Kostas. Sparse representation for 3d shape estimation: A convex relaxation approach. IEEE Trans. on Pattern Analysis and Machine Intelligence, 39(8):1648–1661, 2016. [DOI] [PubMed] [Google Scholar]
- [41].Zhu Xiangyu, Liu Xiaoming, Lei Zhen, and Stan Z Li. Face alignment in full pose range: A 3d total solution. IEEE Trans. on Pattern Analysis and Machine Intelligence, 41(1):78–92, 2017. [DOI] [PubMed] [Google Scholar]
- [42].Zhu Zhiwei and Ji Qiang. Robust real-time face pose and facial expression recovery. In Proc. IEEE Conf. Computer Vision and Pattern Recognition, volume 1, pages 681–688, 2006. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


