Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2020 Sep 11.
Published in final edited form as: Phys Med Biol. 2019 May 8;64(10):10LT01. doi: 10.1088/1361-6560/ab1ba0

Compton PET: a layered structure PET detector with high performance

Peng Peng 1, Martin S Judenhofer 1, Simon R Cherry 1
PMCID: PMC7485538  NIHMSID: NIHMS1625363  PMID: 31013481

Abstract

In most high-resolution PET detector designs, there is an inherent trade-off between spatial resolution and detector efficiency. We have developed and tested a new geometry for the detector module which avoids this trade-off. The module uses a layered structure, in which four crystal slabs are stacked in the depth direction and optically separated by enhanced specular reflector (ESR) film. The scintillation light within each layer is measured by 16 SiPMs located on the four sides of the crystal. Analog signals from all SiPMs (4×16) on the four sides of the crystal are digitized individually using a 64-channel TOFPET-2 module. The four-sided readout method reduces the problem of light trapping resulting from total internal reflection when reading out the end(s) of traditional scintillation crystal arrays, thus increasing the light collection efficiency. In this work, we demonstrate the readout of a complete layered detector with 4 layers. The high light collection efficiency results in a FWHM energy resolution of 10.3%, and a FWHM timing resolution of 348 ps. The distribution of scintillation light detected by the SiPMs was used to decode the interaction position of each gamma ray using a trained neural network. A FWHM spatial resolution of 1.1 ± 0.1 mm was achieved. This design allows the detection efficiency of the module to be increased by adding additional crystal slabs along the depth direction. Since the position, energy, and timing are measured for each layer independently, increasing the system sensitivity by adding more layers will not affect the spatial/energy/timing resolution. Furthermore, the layered structure allows partial recovery of position information for events that undergo Compton scatter within the detector.

Keywords: PET, scintillation crystal, side readout, SiPM, machine learning

1. Introduction

Despite the tremendous improvement of the performance of PET systems since their introduction in the 1970s, further improvements are still possible with the advent of new technologies and ideas (Berg and Cherry, 2018; Jones and Townsend, 2017). One of the problems in high performance PET scanner design is that there are trade-offs between the important features of the scanner (Lewellen, 2010). The trade-off between spatial resolution and system sensitivity is caused by the increasing parallax error as thicker crystals are used for a given ring diameter (Godinez et al., 2012). The trade-off between spatial resolution and energy/timing resolution is caused by the decreasing light collection efficiency for crystal arrays as the aspect ratio decreases (Cherry et al., 1995; Levin, 2002). The first trade-off can be mitigated by using depth of interaction (DOI) enabled detectors (Moses, 2001). However, the extraction of DOI information often comes at the expense of using more photodetectors (Yang et al., 2016; Inadama et al., 2016), or more complicated system designs (Ito et al., 2011). Moreover, the reduction of crystal cross sectional area (needed for better spatial resolution) will degrade the crystal identification accuracy due to inter crystal scatter, which counteracts the gain of spatial resolution for pixelated array using smaller pitch crystals (Shao et al., 1996; Miyaoka and Lewellen, 2000; Ota et al., 2017). For the trade-off between spatial resolution and energy/timing resolution, the design for high spatial resolution PET systems usually sacrifice energy/timing resolution to achieve high spatial resolution (Lewellen, 2010; Cherry et al., 1997). The poor energy resolution is acceptable for small animal studies, since the low scatter fraction from the object enables the use of a wide energy window. Furthermore, currently achievable timing resolution of ~200 ps is not sufficient to be helpful in small animal studies, therefore timing resolution is not prioritized. However, for human brain imaging, the scatter fraction is higher (Wienhard et al., 2002; Kolb et al., 2012; Watanabe et al., 2017; Tao et al., 2018), and a narrow energy window is required to reconstruct high contrast images. The combination of a narrow energy window and poor energy resolution will reject many true events, thus degrading system sensitivity. Also, the size of the human brain is large enough to achieve an effective SNR gain with a timing resolution of ~200–400 ps (Conti, 2011).

Detectors with monolithic crystals have been used to achieve high spatial and energy/timing resolution at the same time. However, monolithic detectors require a complicated calibration process and the resolution performance degrades with increasing crystal thickness(Seifert et al., 2013; Vinke et al., 2010; Pierce et al., 2018), thus the same trade-off between spatial resolution and sensitivity exists for these designs as well.

In this study, we experimentally study a layered structure detector module (McCallum et al., 2005; Moehrs et al., 2006; Li and Furenlid, 2016; Li et al., 2018; Peng et al., 2019) that addresses these trade-offs. The detector consists of a stack of slabs of LYSO scintillator that are read out from the sides by silicon photomultiplier (SiPM) arrays. This geometry results in high light collection efficiency. Furthermore, since each layer is read out individually, additional layers can be added to improve efficiency with no degradation in other performance parameters, and positioning ambiguity due to Compton scatter between layers can be partially resolved. Building on earlier simulations (Peng et al., 2019), we constructed a complete multi-layer detector and evaluated its performance.

2. Material and methods

2.1. Experimental Setup

The Compton PET detector (Figure 1) consisted of 4 LYSO slabs (Crystal Photonics Inc., Sanford, FL) and 4 SiPM arrays (4×4 SensL ArrayJ-30035–16P). Each slab had a dimension of 13.34×13.34×2.76 mm3, and the 4 slabs were stacked along the depth direction with a pitch of 3.36 mm. ESR (Vikuiti™, 3M, St. Paul, MN) films were glued between the crystal slabs, thus the energy deposited by the gamma rays in each layer could be measured separately. The SiPM array was a 4×4 array with 3.36 mm pitch thus matching the crystal layer pitch. Optical grease (BC-630) was used between the crystals and the SiPMs.

Figure 1.

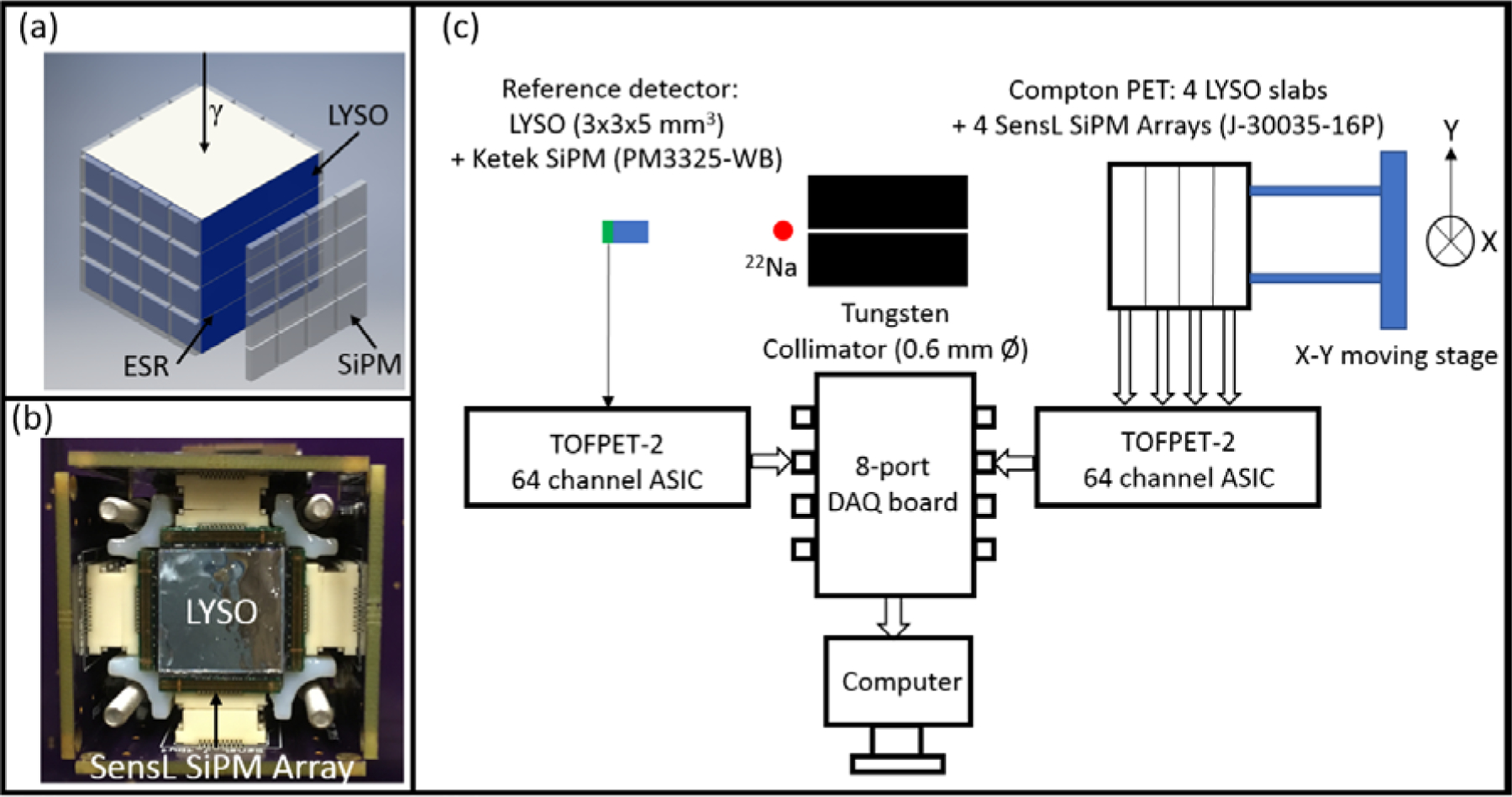
Figure 1.

Open in a new tab

(a): schematic drawing of the Compton PET detector module, (b): photograph of the Compton PET detector module viewed from the front (entrance) side, (c): Schematic for the coincidence setup.

A coincidence setup with combined electronic and physical (tungsten) collimation was used for the measurements (Figure 1c). The test detector was the Compton PET detector, the reference detector was a KETEK PM3325-WB SiPM coupled with a 3×3×5 mm3 LYSO crystal. The tungsten collimator (7 cm in thickness) was placed between the 22Na source (4.7 MBq) and the Compton PET module and provided a collimated gamma ray beam with ~0.6 mm diameter for the Compton PET module. The PET module was attached to a 2D moving stage and was moved automatically along the X and Y directions. The signals from the Compton PET module and the reference detector were measured by two TOFPET-2 64 channel ASICs from PETsys (Oeiras, Portugal). All experiments were performed in a temperature controlled, light tight box. The temperature was set to T = 21.0 ± 0.5 °C, and the SiPM bias voltage was set 4.00 V over breakdown.

2.2. Energy resolution and linearity

The sum of signals from all SiPMs was used to determine the energy deposited by the incident gamma ray in the detector module. Due to the non-linearity of the SiPM response(Roncali and Cherry, 2011), calibration was needed to obtain the correct 511 keV photopeak position and energy resolution (Peng et al., 2018). The following radiation sources were used for the energy calibration: 57Co (122 keV), 133Ba (356 keV), 22Na (511 keV, 1275 keV), 137Cs (662 keV), 54Mn (835 keV).

Because of variable absorption and scattering of scintillation light inside the crystal, the central ADC (analog to digital converter) value for the 511 keV photopeak varies slightly for different incident gamma ray positions. The collimated gamma ray beam shown in Figure 1c was used to irradiate the detector at 169 different positions (13×13 grid of 1 mm pitch) to collect ~20,000 events at each location (60 mins). The photopeak position was determined from a Gaussian fit of the 511 keV peak in the energy spectrum for each incident position. The average ADC value for the photopeak was calculated and used to calibrate the 169 energy histograms. The energy histograms using the corrected data from all 169 irradiation positions was then used to estimate the FWHM energy resolution for the detector.

2.3. Position decoding and spatial resolution

A machine learning method (Bishop, 2006) was used to decode the gamma ray interaction position inside the detector as shown in Figure 2. Since different gamma ray interaction positions generate different scintillation light distribution patterns on the SiPMs surrounding the crystal slabs, a neural network was trained to learn the relationships between the interaction positions and the scintillation light distributions. Afterwards, the trained neural network can be used to determine the gamma ray interaction position based on the scintillation light detected by the SiPMs. We used a convolutional neural network provided by the Neural Network Toolbox in MATLAB R2017a (MathWorks, 2019) in this study. The structure of the neural network was relatively simple, with only one convolutional layer. More details on the structure of the neural network can be found in our previous simulation study (Peng et al., 2019).

Figure 2.

Figure 2.

Open in a new tab

Position decoding using machine learning: (a) 511 keV gamma rays interacting with the Compton PET module at three example positions. (b) The light distributions on the 16×4 array of SiPMs (four 4×4 arrays) corresponding to the three positions in (a). (c) A neural network was trained to determine the gamma ray interaction position from the scintillation light distribution on the SiPMs. (d) In the training set, the gamma beam irradiates the crystal perpendicularly in a 13×13 grid with 1 mm pitch. (e) In the completely independent testing set, the gamma rays irradiate three regions of the crystal: center, edge, and corner. For each region, the center of the beam was scanned across a 13×13 grid with a 0.25 mm pitch. Thus, the test data sampled locations for which no training data was available.

To train the neural network, the 0.6 mm wide collimated gamma ray beam was used to irradiate the Compton PET module perpendicularly at 169 different positions (13×13 grid with 1 mm pitch, shown in Figure 2d). For each position, ~3500 events were acquired within the 420–600 keV energy window. The test data was collected in three different regions of the detector: center, edge, and corner (Figure 2e). In each region, the collimated beam was moved in 0.25 mm steps, and the central location of the 0.6 mm diameter beam was used as the ground truth interaction position. An interpolation method (see Supplementary file for details) was used for predicting the interaction position using the neural network, in which the probabilities of a test event being classified in each of the 169 training positions were used as weights in a center-of-mass calculation to estimate the interaction position. The histogram of the difference between the ground truth and the estimated interaction position was obtained, fit with a Gaussian function, and the FWHM of the fit used as a measure of the spatial resolution.

Since there were four layers in the detector module, events were divided into different groups according to the number of layers in which scintillation light was collected. In the results, only events interacting in one layer or two layers were analyzed, because less than one percent of the events yielded signals across three or four layers. For the one-layer events, only the 16 SiPMs surrounding this layer received photons, the measured ADC values from these 16 channels were used as the input layer for the position decoding neural network. For the two-layer events, three strategies were studied to determine which of the two layers was better, in terms of spatial resolution, for position decoding: (1) the layer closer to the radiation source, (2) the layer further from the radiation source, (3) the layer with maximal deposited energy. Since it was found that the strategy (3) gave the best result for spatial resolution, this layer was used to provide both the DOI information and the 16 ADC values for the neural network for position decoding. Strategy (3) likely provides the highest spatial resolution as it gives the best signal-to-noise ratio signals for positioning, while positioning errors for low-angle forward scatter are still quite small. In the next section, for two-layer events, we only show spatial resolution results using the third strategy.

2.4. Timing resolution

The timing resolution for the new module was evaluated using the histogram of the timing difference between the Compton PET module and the reference detector (Figure 1c). For the Compton PET module, each of the 64 SiPMs generated its own timing signal in the TOFPET-2 system. The timing of the Compton PET module was determined as the weighted average of all the recorded timing signals, in which, the weights were the ADC values from the corresponding channels. Since the TOFPET-2 system used a leading edge discriminator to determine the timing information (Di Francesco et al., 2016), a time walk correction was needed for each SiPM. After the correction, the timing resolution of the module was evaluated for each of the 169 gamma ray incident locations (Figure 2d) and for the entire detector.

3. Results

3.1. Energy resolution and linearity

As shown in Figure 3(a), gamma ray sources with six different energies (122, 356, 511, 662, 835, 1275 keV) were used to calibrate the energy response of the Compton PET module. The non-proportionality of LYSO crystal light yield was accounted for in the 122, 356, 511 keV data points, which had 88%, 97%, 99% of the light yield per MeV relative to that of a 662 keV gamma ray (Chewpraditkul et al., 2009; Dorenbos et al., 1995). A two-step procedure was used to take into account the non-zero offset of the DAQ system and the saturation effect of the SiPM. In the first step, the two data points with gamma ray energies of 122 keV and 356 keV were used to do a linear extrapolation to find the non-zero offset value of the DAQ system. Only the two lowest energy points were used in the first step to avoid the effect of SiPM saturation effect. In the second step, the SiPM saturation effect was fitted by an exponential function (Peng et al., 2018) as follows:

ADCraw=ADCoffset+ADCmax⋅[1−exp(−ADCcalADCmax)] (1)

Figure 3.

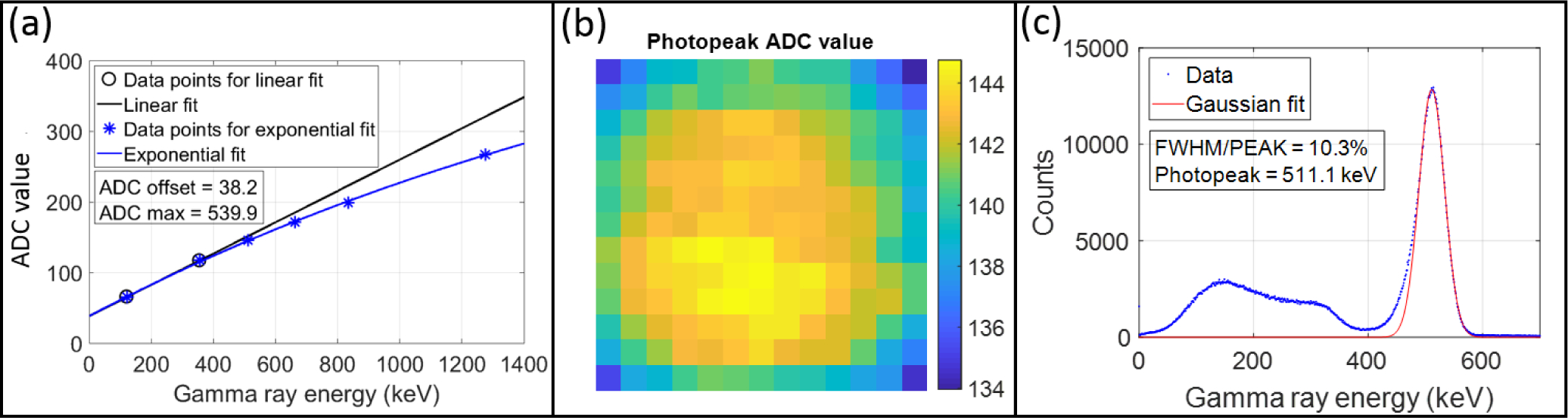
Figure 3.

Open in a new tab

(a) ADC value vs. gamma ray energy for the Compton PET module. (b) 511 keV photopeak ADC values for pencil beam irradiating the detector at the 169 positions. (c) Energy histograms for events from all beam positions after both nonlinear calibration and interaction position calibration.

In Equation (1), ADCoffset used the offset value calculated in the first step, ADCraw is the measured ADC value corresponding to the photopeak, ADCmax is the maximum ADC value the SiPM can output, ADCcal = b · Ey is the relationship between the output ADC value and the gamma ray energy that would be observed for a photodetector with a linear response, where b is a scaling factor. Only two parameters, b and ADCmax, need to be determined from the fitting. After the fitting, the calibrated energy can be calculated from:

ADCcal=−ADCmax⋅ln(1−ADCraw−ADCoffsetADCmax) (2)

To study the effect of gamma ray interaction position on the energy response of the system, we used collimated 511 keV gamma rays to irradiate the Compton PET module at 169 positions as shown in Figure 2(d). The central ADC value for the 511 keV photopeaks is shown in Figure 3(b), the photopeak values are lower near the edges and corners due to fact that the scintillation light is more concentrated on just a few SiPMs, which causes more saturation on those SiPMs. To remove the interaction position dependence of the energy histograms, we normalized the summed ADC values to align the photopeak to the same value for different gamma ray irradiation positions. After calibrating the pulse amplitudes for the SiPM nonlinearity and interaction position, all events from the 169 irradiation positions were used to generate the energy histogram shown in Figure 3(c). The FWHM energy resolution for the 511 keV photopeak was 10.3%. The excellent energy resolution is the result of increasing light collection efficiency by mitigating the total internal refection problem (Peng et al., 2019).

3.2. Position decoding and spatial resolution

To characterize the spatial resolution of the detector module, we plotted the histogram of the difference between the predicted and true gamma ray interaction positions. The predicted positions were the output of the neural network, the true positions were the known central locations of the pencil beam (Figure 2e). Figure 4a shows the 169 beam positions for the “center” testing region. Figure 4b and 4c show the position difference histograms for 1-layer and 2-layer events. After fitting the points in the histograms with Gaussian function, the FWHM spatial resolution along x and y directions were calculated.

Figure 4.

Figure 4.

Open in a new tab

(a) indicates the central positions for the gamma ray pencil beam interactions; (b) and (c) show histograms of the difference between the predicted and true interaction positions for 1-layer and 2-layer events, respectively for the center region.

The histogram for the 2-layer events (Figure 4c) shows wider tails than the histogram for the 1-layer events (Figure 4b) due to the wrong choice of the first interaction point for some of the Compton scattered events. To fully recover the sequence of interactions, both the energies deposited at the two interaction points and the scattering angle have to be determined (Compton, 1923). However, for obliquely incident gamma rays, there are cases for forward scatter and backward scatter that give the same interaction positions and energies, and ambiguity exists for determining the first interaction point without knowing the gamma ray incidence direction. Moreover, the limited spatial and energy resolution, and the possibility of having more than one Compton scatter, make it complicated to determine the interaction sequence unambiguously. In this paper, we only use the energy information to choose the layer for the position decoding. The three strategies introduced in Section 2.3 were studied, and the strategy using the layer with maximal deposited energy gave the best result. The wide tails in Figure 4c indicate that this method is not perfect, and further studies are needed to improve the position decoding for the 2-layer events. However, these are a fairly small fraction of the detected events (Table 1).

Table 1.

The FWHM spatial resolution for all three testing regions (center, corner and edge) corresponding to Figure 2e.

1-layer events 2-layer events
Testing area Percentage FWHM x_res (mm) FWHM y_res (mm) percentage FWHM x_res (mm) FWHM y_res (mm)
Center 86.3% 0.93 0.90 13.7% 1.49 1.49
Edge 92.8% 1.09 0.93 7.2% 1.36 1.07
Corner 95.2% 1.14 1.18 4.8% 1.28 1.31
Open in a new tab

The FWHM spatial resolution for the three different testing regions (Figure 2e) are shown in Table 1. It is important to emphasize that testing included source positions not used in the training dataset. For all three regions, the majority of the events are 1-layer events. The percentage of 2-layer events is lower in the corner and edge regions, because Compton scattered photons have a high chance of escaping the detector. Taking the average for all regions (one center, four corners, four edges), and using the percentage as the weighting factor, the average FWHM resolution for this detector is 1.1 ± 0.1 mm.

3.3. Timing resolution

To obtain the most accurate timing information, a time walk correction was applied to each of the 64 SiPMs. As shown in Figure 5a, the time difference between the Compton PET module and reference detector depends on the ADC value. We firstly found the central value for the time difference for each ADC value with Gaussian fitting (red points in Figure 5a), then fitted the relationship between the time difference and ADC value with an empirical equation (Eq. 3), in which only the points with ADC value > 5 (blue circles in Figure 5a) were used for fitting. In Eq. 3, a, b, c, and d are fitting parameters.

Figure 5.

Figure 5.

Open in a new tab

(a) Time walk correction for one SiPM. (b) Timing resolution for all 169 gamma ray incident positions. (c) Timing resolution for the entire detector module combining the events from all gamma ray incident positions.

Tdiff=a⋅exp(b⋅ADC)+c⋅exp(d⋅ADC) (3)

Since each SiPM gave one timing signal, a weighted average method was used to evaluate the timing resolution of the new module, in which the weighting factor was the ADC value of the SiPM. The timing resolution of the system was defined as the FWHM value of the fitted Gaussian curve for the time difference histogram (Figure 5c). We evaluated the timing resolution of the detector in two different ways: Figure 5b shows the timing resolution for all 169 gamma ray incident positions (Figure 2d), which has a range of 268 – 414 ps, the corner and edge regions have better timing performance than the central region; Figure 5c shows the timing resolution for the entire detector, which is 348 ps.

4. Discussion

We have tested a layered PET detector module with both high spatial resolution (1.1 mm), high energy resolution (10.3%), and high timing resolution (348 ps). The high spatial resolution was accomplished by using machine learning to decode the gamma ray interaction location for each layer. Here, a cross entropy loss function was used, however, it is possible other loss functions could give better performance. Further studies for optimizing the structure of the neural network will be conducted in the future. The good energy/timing resolution comes from the high light collection efficiency of this geometry. For sub millimeter spatial resolution detectors, this new approach using four-sided readout has advantages over modules using pixelated arrays or monolithic crystals (Marcinkowski et al., 2016; Kuang et al., 2018), since the energy, timing and interaction location for each layer are measured independently, the number of layers, and thus the system sensitivity, can be increased independently without affecting the performance of the system. Because of the layer structure, the detector has an intrinsic DOI resolution of 3.36 mm. Moreover, this design has the potential to reduce the cost of a PET scanner because the cost for using crystal slabs is lower than using pixelated arrays with small cross section crystal elements. A similar approach, using optical barriers introduced within the crystal slabs to control the light distribution, is being studied by Li et al (Li and Furenlid, 2016; Li et al., 2018) and could improve spatial resolution even further.

At first glance, a criticism of this geometry is that it requires more photodetectors and will lead to large dead-spaces between detector modules, thus reducing sensitivity in a scanner geometry. However, this is not necessarily the case when the module has a relatively large cross-sectional area compared to its depth, as explained in (Peng et al., 2019). The fractional volume taken up by reflector in sub-mm scintillator arrays can easily add up to 2–3 mm in a 25–30 mm wide detector, which is similar to space needed to accommodate SiPMs on the detector sides. Since the position decoding is based on the pattern of the scintillation light distribution, it may also be possible to use sparsely populated photodetectors to decode the position, further reducing the number of photodetectors.

A further challenge is that to use the method developed here, all 64 SiPMs need to be recorded individually. However, ASICs are now available to read out high-density SiPM arrays and with further integration of the electronics between SiPMs, ASICs, and FPGAs, the cost and density of electronics needed should not be limiting. Indeed, commercial PET systems using SiPM arrays with individual readouts have been developed.

It also would be interesting to evaluate the performance with lower light scintillation materials such as bismuth germinate (BGO). Since the number of layers, and thus the system sensitivity, can be increased without degrading performance, it may be possible to build an efficient detector for gamma rays with very high energy (several MeV), which can be used for prompt gamma detection for proton range determination in proton beam therapy (Knopf and Lomax, 2013).

5. Conclusion

In this paper, we studied the feasibility and benefits of constructing a PET detector module with crystal slabs and using machine learning for position decoding. We demonstrated that the new detector module achieved high spatial/energy/timing resolution and high sensitivity at the same time, and provides DOI information as well. The design is a good fit for the requirements for high performance human brain PET imaging (Nordberg et al., 2010; Loane and Politis, 2011; Chen, 2007).

Supplementary Material

Supplementary material

Acknowledgments

The authors would like to thank members of the MIPET group at UC Davis for helpful discussions. This work was funded by NIH R01 EB019439.

References

  1. Berg E and Cherry SR 2018. Innovations in Instrumentation for Positron Emission Tomography Semin. Nucl. Med 48 311–31 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bishop CM 2006. Pattern Recognition and Machine Learning (Information Science and Statistics) (New York: Springer; ) [Google Scholar]
  3. Chen W 2007. Clinical applications of PET in brain tumors J. Nucl. Med 48 1468–81 [DOI] [PubMed] [Google Scholar]
  4. Cherry SR, Shao Y, Silverman RW, Meadors K, Siegel S, Chatziioannou A, Young JW, Jones WF, Moyers JC, Newport D, Boutefnouchet A, Farquhar TH, Andreaco M, Paulus MJ, Binkley DM, Nutt R and Phelps ME 1997. MicroPET: A high resolution PET scanner for imaging small animals IEEE Tran. Nucl. Sci 44 1161–6 [Google Scholar]
  5. Cherry SR, Shao YP, Tornai MP, Siegel S, Ricci AR and Phelps ME 1995. Collection of scintillation light from small BGO crystals IEEE Tran. Nucl. Sci 42 1058–63 [Google Scholar]
  6. Chewpraditkul W, Swiderski L, Moszynski M, Szczesniak T, Syntfeld-Kazuch A, Wanarak C and Limsuwan P 2009. Scintillation Properties of LuAG:Ce, YAG:Ce and LYSO:Ce Crystals for Gamma-Ray Detection IEEE Tran. Nucl. Sci 56 3800–5 [Google Scholar]
  7. Compton AH 1923. A quantum theory of the scattering of x-rays by light elements Phys. Rev 21 0483–502 [Google Scholar]
  8. Conti M 2011. Focus on time-of-flight PET: the benefits of improved time resolution Eur. J. Nucl. Med. Mol. Imaging 38 1147–57 [DOI] [PubMed] [Google Scholar]
  9. Di Francesco A, Bugalho R, Oliveira L, Pacher L, Rivetti A, Rolo M, Silva J, Silva R and Varela J 2016. TOFPET2: a high-performance ASIC for time and amplitude measurements of SiPM signals in time-of-flight applications J. Instrum 11 [Google Scholar]
  10. Dorenbos P, deHaas JTM and vanEijk CWE 1995. Non-proportionality in the scintillation response and the energy resolution obtainable with scintillation crystals IEEE Trans. Nucl. Sci 42 2190–202 [Google Scholar]
  11. Godinez F, Chaudhari A, Yang Y, Farrell R and Badawi R 2012. Characterization of a high-resolution hybrid DOI detector for a dedicated breast PET/CT scanner Phys. Med. Biol 57 3435–49 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Inadama N, Hirano Y, Nishikido F, Murayama H and Yamaya T 2016. Development of a DOI PET Detector Having the Structure of the X’tal Cube Extended in One Direction IEEE Trans. Nucl. Sci 63 2509–16 [Google Scholar]
  13. Ito M, Hong SJ and Lee JS 2011. Positron Emission Tomography (PET) Detectors with Depth-of-Interaction (DOI) Capability Biomed. Eng. Lett 1 70–81 [Google Scholar]
  14. Jones T and Townsend D 2017. History and future technical innovation in positron emission tomography J Med Imaging 4 011013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Knopf A and Lomax A 2013. In vivo proton range verification: a review Phys. Med. Biol 58 R131. [DOI] [PubMed] [Google Scholar]
  16. Kolb A, Wehrl H, Hofmann M, Judenhofer M, Eriksson L, Ladebeck R, Lichy M, Byars L, Michel C, Schlemmer H, Schmand M, Claussen C, Sossi V and Pichler B 2012. Technical performance evaluation of a human brain PET/MRI system Eur Radiol 22 1776–88 [DOI] [PubMed] [Google Scholar]
  17. Kuang Z, Sang Z, Wang X, Fu X, Ren N, Zhang X, Zheng Y, Yang Q, Hu Z, Du J, Liang D, Liu X, Zheng H and Yang Y 2018. Development of depth encoding small animal PET detectors using dual-ended readout of pixelated scintillator arrays with SiPMs Med. Phys 45 613–21 [DOI] [PubMed] [Google Scholar]
  18. Levin CS 2002. Design of a high-resolution and high-sensitivity scintillation crystal array for PET with nearly complete light collection IEEE Tran. Nucl. Sci 49 2236–43 [Google Scholar]
  19. Lewellen T 2010. The Challenge of Detector Designs for PET AJR Am J Roentgenol 195 301–9 [DOI] [PubMed] [Google Scholar]
  20. Li X and Furenlid LR 2016. An analysis of side readouts of monolithic scintillation crystals Proc. of SPIE 9969 996908 [Google Scholar]
  21. Li X, Ruiz-Gonzalez M and Furenlid LR 2018. An edge-readout, multilayer detector for positron emission tomography Med. Phys 45 2425–38 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Loane C and Politis M 2011. Positron emission tomography neuroimaging in Parkinson’s disease Am. J. Transl. Res 3 323–41 [PMC free article] [PubMed] [Google Scholar]
  23. Marcinkowski R, Mollet P, Van Holen R and Vandenberghe S 2016. Sub-millimetre DOI detector based on monolithic LYSO and digital SiPM for a dedicated small-animal PET system Phys. Med. Biol 61 2196–212 [DOI] [PubMed] [Google Scholar]
  24. MathWorks 2019. MATLAB Deep Learning Toolbox. https://www.mathworks.com/products/deep-learning.html
  25. McCallum S, Clowes P and Welch A 2005. A four-layer attenuation compensated PET detector based on APD arrays without discrete crystal elements Phys. Med. Biol 50 4187–207 [DOI] [PubMed] [Google Scholar]
  26. Miyaoka RS and Lewellen TK 2000. Effect of Detector Scatter on the Decoding Accuracy of a DOI Detector Module IEEE Tran. Nucl. Sci 47 1614–9 [Google Scholar]
  27. Moehrs S, Del Guerra A, Herbert DJ and Mandelkern MA 2006. A detector head design for small-animal PET with silicon photomultipliers (SiPM) Phys. Med. Biol 51 1113–27 [DOI] [PubMed] [Google Scholar]
  28. Moses W 2001. Trends in PET imaging Nucl. Instrum. Methods Phys. Res. Sec. A 471 209–14 [Google Scholar]
  29. Nordberg A, Rinne J, Kadir A and Langstrom B 2010. The use of PET in Alzheimer disease Nat. Rev. Neurol 6 78–87 [DOI] [PubMed] [Google Scholar]
  30. Ota R, Omura T, Yamada R, Miwa T and Watanabe M 2017. Evaluation of a Sub-Millimeter Resolution PET Detector With a 1.2 mm Pitch TSV-MPPC Array One-to-One Coupled to LFS Scintillator Crystals and Inter-Crystal Scatter Studies With Individual Signal Readout IEEE Tran. on Rad. and Plas. Med. Sci 1 15–22 [Google Scholar]
  31. Peng P, Judenhofer M, Jones A and Cherry S 2019. Compton PET: a simulation study for a PET module with novel geometry and machine learning for position decoding Biomed. Phys. Eng. Express 5 015018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Peng P, Liu CC, Du JW, Bai XW and Cherry SR 2018. Improving Edge Crystal Identification in Flood Histograms Using Triangular Shape Crystals Biomed. Phys. Eng. Express 4 025031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Pierce LA, Pedemonte S, DeWitt D, MacDonald L, Hunter WCJ, Van Leemput K and Miyaoka R 2018. Characterization of highly multiplexed monolithic PET / gamma camera detector modules Phys. Med. Biol 63 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Roncali E and Cherry SR 2011. Application of Silicon Photomultipliers to Positron Emission Tomography Ann. Biomed. Eng 39 1358–77 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Seifert S, van der Lei G, van Dam HT and Schaart DR 2013. First characterization of a digital SiPM based time-of-flight PET detector with 1 mm spatial resolution Phys. Med. Biol 58 3061–74 [DOI] [PubMed] [Google Scholar]
  36. Shao YP, Cherry SR, Siegel S and Silverman RW 1996. A Study of Inter-Crystal Scatter in Small Scintillator Arrays Designed for High Resolution PET Imaging IEEE Tran. Nucl. Sci 43 1938–44 [Google Scholar]
  37. Tao W, Chen G, Weng F, Zan Y, Zhao Z, Peng Q, Xu J and Huang Q 2018. Simulation study of a high-performance brain PET system with dodecahedral geometry Med. Phys 45 3297–304 [DOI] [PubMed] [Google Scholar]
  38. Vinke R, Dam H T v, Seifert S, Beekman FJ, Löhner H, Schaart DR and Dendooven P 2010. Thick monolithic scintillation crystals for TOF-PET with depth-of-interaction measurement IEEE NSS/MIC 1981–4 [Google Scholar]
  39. Watanabe M, Saito A, Isobe T, Ote K, Yamada R, Moriya T and Omura T 2017. Performance evaluation of a high-resolution brain PET scanner using four-layer MPPC DOI detectors Phys. Med. Biol 62 7148–66 [DOI] [PubMed] [Google Scholar]
  40. Wienhard K, Schmand M, Casey M, Baker K, Bao J, Eriksson L, Jones W, Knoess C, Lenox M, Lercher M, Luk P, Michel C, Reed J, Richerzhagen N, Treffert J, Vollmar S, Young J, Heiss W and Nutt R 2002. The ECAT HRRT: Performance and first clinical application of the new high resolution research tomograph IEEE Tran. Nucl. Sci 49 104–10 [Google Scholar]
  41. Yang Y, Bec J, Zhou J, Zhang M, Judenhofer M, Bai X, Di K, Wu Y, Rodriguez M, Dokhale P, Shah K, Farrell R, Qi J and Cherry S 2016. A Prototype High-Resolution Small-Animal PET Scanner Dedicated to Mouse Brain Imaging J. Nucl. Med 57 1130–5 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary material
NIHMS1625363-supplement-Supplementary_material.pdf (136.1KB, pdf)

RESOURCES