Mechanism of Color and Photoacidity Tuning for the Protonated Green Fluorescent Protein Chromophore

Abstract

The neutral or A state of the green fluorescent protein (GFP) chromophore is a remarkable example of a photoacid naturally embedded in the protein environment and accounts for the large Stokes shift of GFP in response to near UV excitation. Its color tuning mechanism has been largely overlooked, as it is less preferred for imaging applications than the redder anionic or B state. Past studies, based on site-directed mutagenesis or solvatochromism of the isolated chromophore, have concluded that its color tuning range is much narrower than its anionic counterpart. However, as we performed extensive investigation on more GFP mutants, we found that the color of the neutral chromophore can be more sensitive to protein electrostatics than can the anionic counterpart. Electronic Stark spectroscopy reveals a fundamentally different electrostatic color tuning mechanism for the neutral state of the chromophore that demands a three-form model as compared to that of the anionic state, which requires only two forms (J. Am. Chem. Soc. 2019, 141, 15250–15265). Specifically, an underlying zwitterionic charge-transfer state is required to explain its sensitivity to electrostatics. As the Stokes shift is tightly linked to excited-state proton transfer (ESPT) of the protonated chromophore, we infer design principles of the GFP chromophore as a photoacid through the color tuning mechanisms of both protonation states. The three-form model could also be applied to similar biological and nonbiological dyes and complements the failure of the two-form model for donor–acceptor systems with localized ground-state electronic distributions.

Graphical Abstract

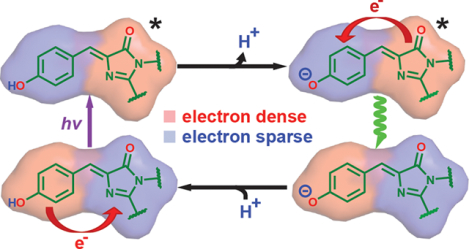
1. INTRODUCTION

The jellyfish Aequorea victoria green fluorescent protein (avGFP) exhibits two visible absorption bands: a major band (A) at 395 nm and a minor band (B) at 475 nm.¹ The A and B bands correspond to the protonated neutral and the deprotonated anionic chromophores, respectively (Figure 1). The hallmark of the neutral state is its large Stokes shift (~5600 cm⁻¹), which is attributed to its ability to generate the deprotonated intermediate (I) state via excited-state proton transfer (ESPT) upon photoexcitation (Figure 1). The chromophore’s photoacidity and the associated proton transfer process(es) have prompted many subsequent studies. Within those studies, GFP serves either as a unique model system with a well-defined hydrogen-bonding network that accepts a proton following photoexcitation^3–7 or as a naturally occurring photoacid from which inspiration is drawn for designing small-molecule analogues.^8–10 Because of phototoxicity from nearultraviolet irradiation, the lower cross section, and incompatibility with the standard fluorescein filter sets for practical applications,¹¹ much less attention has been paid to the A state as compared to the B state, and the latter is the main optimization target for imaging.¹² The Stark tuning rate (electronic redistribution upon excitation) is a critical quantity for understanding both the color tuning behavior^13,14 and the photoacidity¹⁵ of the neutral chromophore in response to environmental mutations; however, there has been only limited investigation of the Stark tuning rate for the neutral chromophore.¹⁶

Figure 1.

Canonical ESPT scheme for avGFP with spectroscopically characterized protonation states (A, B, and I states) and their structures (with T203 shown in red). The wavelengths associated with the excitation and emission (straight and curved vertical arrows, respectively) are measured at room temperature,^1,2 except for the absorption maximum of the I state, which can only be identified as a small band at low temperature.^1,17 Ground-state processes, including proton transfer (GSPT) and environmental reorganization, are required to reach an equilibrium among the states. The A* emission (shown with a dashed curved arrow) is largely suppressed at steady state due to efficient ESPT.² T203 is not the only residue that undergoes structural change following ESPT; see Figure 4 in ref 18.

Previously, we have elucidated how the photophysical and electro-optical properties of the anionic B-state GFP chromophore are modulated by its environment through electrostatics.¹³ We applied the Marcus–Hush theory, which is based on electronic coupling between the intuitive resonance structures with explicit consideration of vibronic coupling to the bond length alternation (BLA) mode, to explain the strong and monotonic correlations among properties including electronic excitation energy, Stokes shift, and Stark tuning rate. We then identified the relative energetics of the resonance forms, or the driving force, to be the dominant factor that is tuned by environmental electrostatics. The additivity of the driving force from combinations of mutations allowed us to demonstrate the predictive power of the model and infer design principles for the anionic state. In this study, we continue this effort but instead focus on the neutral state of the chromophore. We find that the Stark tuning rates for the A state, which are obtained via electronic Stark spectroscopy,¹⁹ can sometimes exceed those of the B state, and protonation completely alters the qualitative trend between the absorption maximum and the Stark tuning rate previously documented for the B state. The simple resonance picture, which worked well for the anionic chromophore, breaks down, but, as shown in the following, inclusion of a third form is sufficient to quantitively capture the new correlation while inheriting the minimalistic spirit of the Marcus–Hush model. Combined with our understanding of the anionic chromophore,¹³ we can track the electron flow within the chromophore before and after ESPT and reveal design principles for the excited state pK_a, or pK_a*, in the protein environment. In the subsequent discussion, to clarify the term “states” in different contexts, “states” are reserved for electronic states (e.g., S₀ and S₁) and protonation states (e.g., A and B states) that can be experimentally observed and are energy eigenstates (adiabatic states), while “(resonance) forms” refer to resonance structures, which are convenient diabatic states for chemical intuition and whose linear combinations can well approximate the electronic eigenstates S₀ and S₁. As these forms are thought to be consistent in different environments,¹³ they provide an ideal set of bases for understanding modulation of electronic distribution caused by environmental effects.

2. RESULTS AND DISCUSSION

2.1. Mutant and Variant Design.

In this work, we take advantage of a subset of GFP mutants from our B-state color-tuning work¹³ that also populate the A state at nondenaturing pH’s (Tables 1 and S1; see Figure 2 for the critical residues in the protein environment). The mutations involving R96 and noncanonical amino acids were enabled by the semisynthetic reconstitution strategy of split GFP as described previously,^13,20 in combination with amber suppression. Because T203, H148, and R96 in the GFP environment can stabilize the anionic chromophore via hydrogen bonding, any mutations at these positions that remove the hydrogen bond(s) disfavor chromophore deprotonation, which can also be achieved by negatively supercharging the β-barrel (supercharged −30, where surface residues are extensively replaced with negatively charged amino acids).^13,21 The model chromophore 4-hydroxybenzylidene-1,2-dimethylimidazolinone (HBDI) in ethanol was also examined to complement the protein study.

Table 1.

GFP Mutation Sites Chosen for This Study to Sample the A State in a Wide Range of Protein Environments^a

mutation sites	amino acids
	Environmental Mutants
R96	R, M
T203	T, V, H, F, Y, 4-F1F, F5F, 4-NH2F, 3-OCH3Y
	Chromophore Variants
S65	S, T

^aNoncanonical amino acids are abbreviated as follows: 4-fluorophenylalanine is 4-F₁F, 2,3,4,5,6-pentafluorophenylalanine is F₅F, 3-methoxytyrosine is 3-OCH₃Y (3-OMeY), and 4-aminophenylalanine is 4-NH₂F (see also Table S1).

Figure 2.

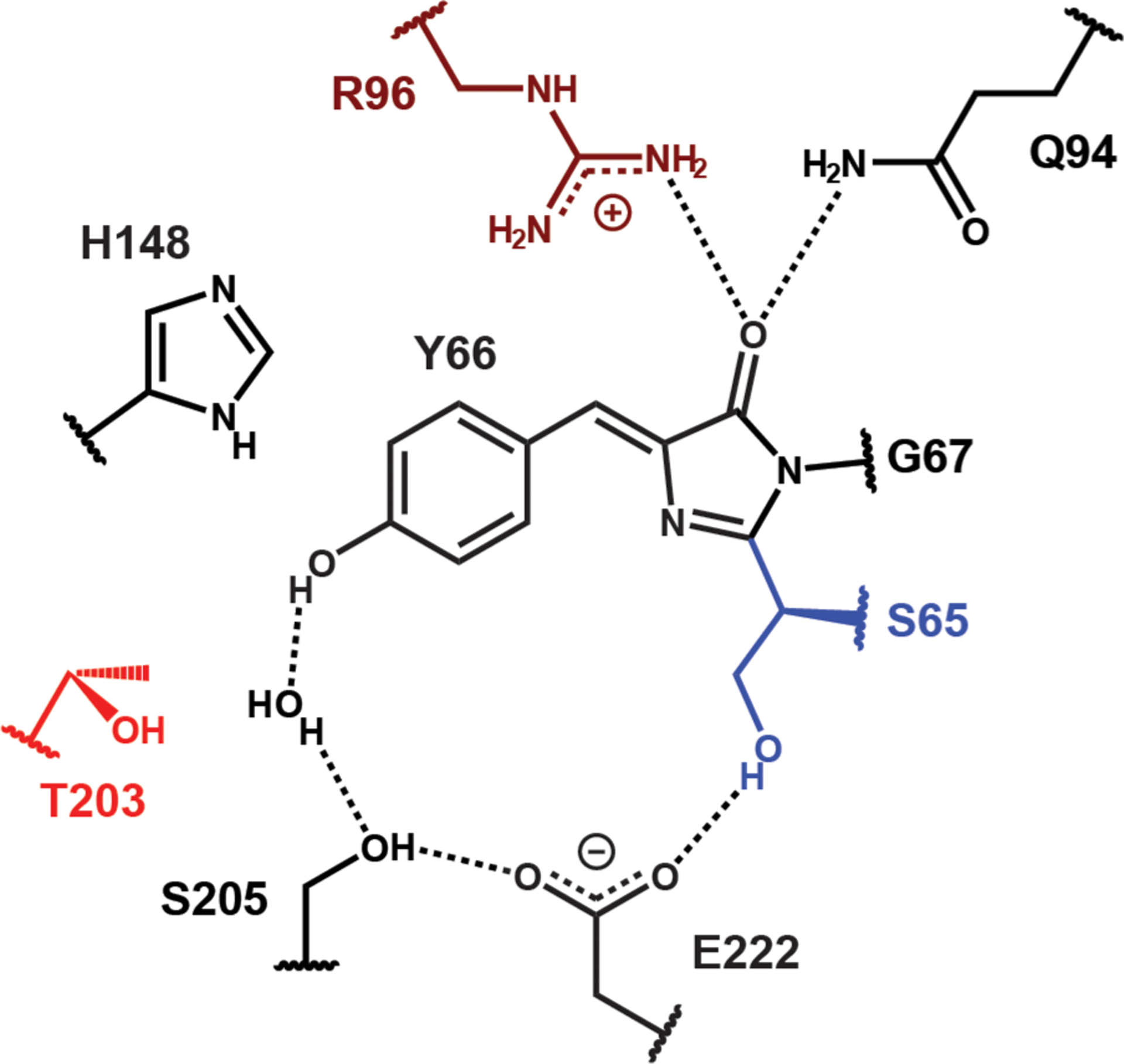
Surrounding residues of the GFP chromophore in the protonated state (A state) for avGFP, whose residue 65 is a serine.¹⁸ The ESPT chain is explicitly shown here. The colored residues represent those mutated in this work. Note that E222 mutants cannot be used for investigating the A state as the mutation suppresses chromophore protonation.¹³

2.2. 77 K Absorption Spectra and Color Tuning.

We first focus on the absorption spectra at 77 K and the color tuning behavior of A states. Even though the A bands are rather featureless at room temperature, a clear vibronic progression can be seen at 77 K (Figure 3A–C). Substructure can be resolved by taking the second derivative of the absorption, and the results resemble those from B states,¹³ where the energy spacing (1320 ± 60 cm⁻¹) between the presumed 0–0, 0–1, and 0–2 electronic transitions agrees well with the vibrational frequency assigned to the BLA mode (Figures 3D and S2; see also Figure S23 in ref 13; an exception is the 610 cm⁻¹ spacing for neutral HBDI in ethanol; see Figure S2). Because the vibronic peaks are rather broad, the assignment to the BLA mode is not definitive and could be mixed with other normal modes with similar frequencies. On the basis of the relative intensity of these vibronic peaks, we can assert that the Huang–Rhys factors for the A states consistently fall between 1 and 2, showing spectral features similar to those of the anionic HBDI model chromophores in water/glycerol.¹³

Figure 3.

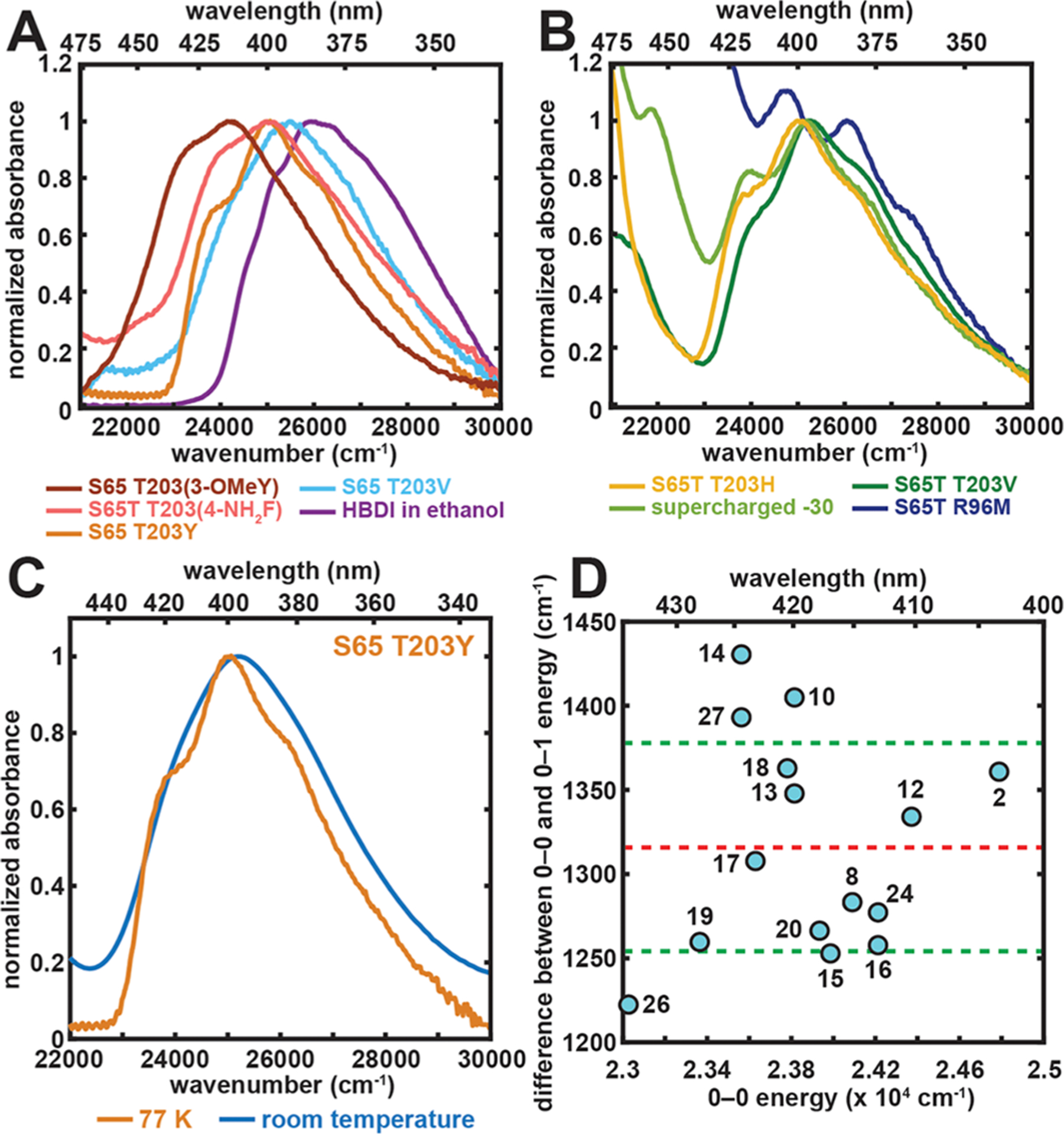
Spectral properties and color tuning of the A state. (A and B) Representative 77 K absorption spectra of GFP mutants and the model chromophore HBDI in ethanol. The spectra are all normalized at their A-state peak maxima. The absorption maximum, later used in Figure 4, corresponds to the wavenumber at which the largest absorbance is observed for each mutant and the model chromophore, except for the R96M mutant, for which spectral deconvolution is done through Stark spectroscopy to extract the A-state absorption maximum (Figure S1). For GFP mutants, the samples of S65 T203(3-OMeY) and S65T T203(4-NH₂F) were at pH 5.0 and 8.0, respectively. The rest were prepared at pH 10.0. Panel B includes constructs that contain the longer wavelength B band, corresponding to the anionic chromophore, in the spectral region of interest.¹³ (C) Representative room-temperature and 77 K absorption spectra for the A state of S65 T203Y. (D) Difference between the 0–0 and 0–1 energy plotted against 0–0 electronic excitation energy for GFP mutants obtained from a second derivative analysis (Figure S2). The x–y coordinates and the numerical labels for the species are listed in Table S2. The values are within a quite narrow range with an average of 1320 ± 60 cm⁻¹. The red and green dashed lines represent the mean value and ±1 σ, respectively.

The qualitative trend of A state color tuning follows that of the B state (Table S3): any mutation that eliminates the positive charge of R96^22–24 results in a blue-shift (see also ref 25), while mutating T203 to an aromatic residue that π−π stacks with the chromophore’s phenol moiety red-shifts the absorption maximum. This suggests that the same direction of electron flow from phenol(ate) to imidazolinone during excitation can be assigned to both protonation states.^13,26 Within the π−π stacking series, as we modulate the π-system’s electron density at position 203 from electron-deficient to electron-rich by using electron-withdrawing and -donating groups, respectively, a clear red-shift is observed. The corresponding color tuning range is appreciably larger for the A state than for the B state (1550 cm⁻¹ vs 650 cm⁻¹, respectively, Table S3).¹³ In contrast, for neutral and anionic HBDI in various organic solvents, the color tuning range is much smaller for the former as compared to the latter (962 cm⁻¹ vs 2755 cm⁻¹, respectively).²⁷ As such, we see a drastic change in color tuning behaviors for the chromophore in its two protonation states, which hints at a fundamental difference in the magnitude of charge redistribution upon excitation between the A and B states. Consequently, we measured the Stark tuning rates using electronic Stark spectroscopy to uncover the A-state color tuning mechanism.

2.3. Stark Tuning Rate and Color Tuning Mechanism.

Stark spectra of the A states are dominated by the second derivative of their corresponding absorption spectra (Figure S1 and Table S4), which indicates a significant contribution from the linear Stark effect characterized by a Stark tuning rate fΔμ19 (where f is the local field factor, which is necessary due to the larger field experienced by the chromophore as compared to the externally applied field based on the unavoidable polarization effect of the chromophore environment; see section S6 in ref 13). The largest Stark tuning rate for the A states (24 D) from various mutants is twice as large as the B-state counterpart (12 D),¹³ suggesting the A-state excitation is strongly associated with charge-transfer character, and its electronic excitation energy can be more sensitive to electrostatic color tuning. The large Stark tuning rates fΔμ of the A state for some protein mutants may seem surprising at first. However, the calculated Stark tuning rates Δμ as large as 10 D have been suggested by Filippi et al. when accounting for nearby residues in GFP using quantum mechanics/molecular mechanics (QM/MM) methods,²⁸ in good agreement with our experimental results because/ is likely to be close to 2 (see section S6 in ref 13). As gas-phase calculations yield Stark tuning rates between 2 and 2.5 D,^28,29 the protein environment is indeed a crucial factor that increases the Stark tuning rate.

From the prior investigation conducted by Drobizhev et al.¹⁴ and us,¹³ it is informative to plot the absorption maximum against the Stark tuning rate for the A state to reveal how electron delocalization within the neutral chromophore is modulated by electrostatics (Figure 4A). Here, we follow our previous B-state study and plot the S65 and S65T mutants together to illustrate that the presence or absence of the methyl group does not modify the intrinsic response of the π system to the protein environment (Figure 4A and B).^23,30 It can be readily seen that the A-state correlation plot indicates larger Stark tuning rates for redder species as compared to the B-state counterpart (Figure 4B).¹³

Figure 4.

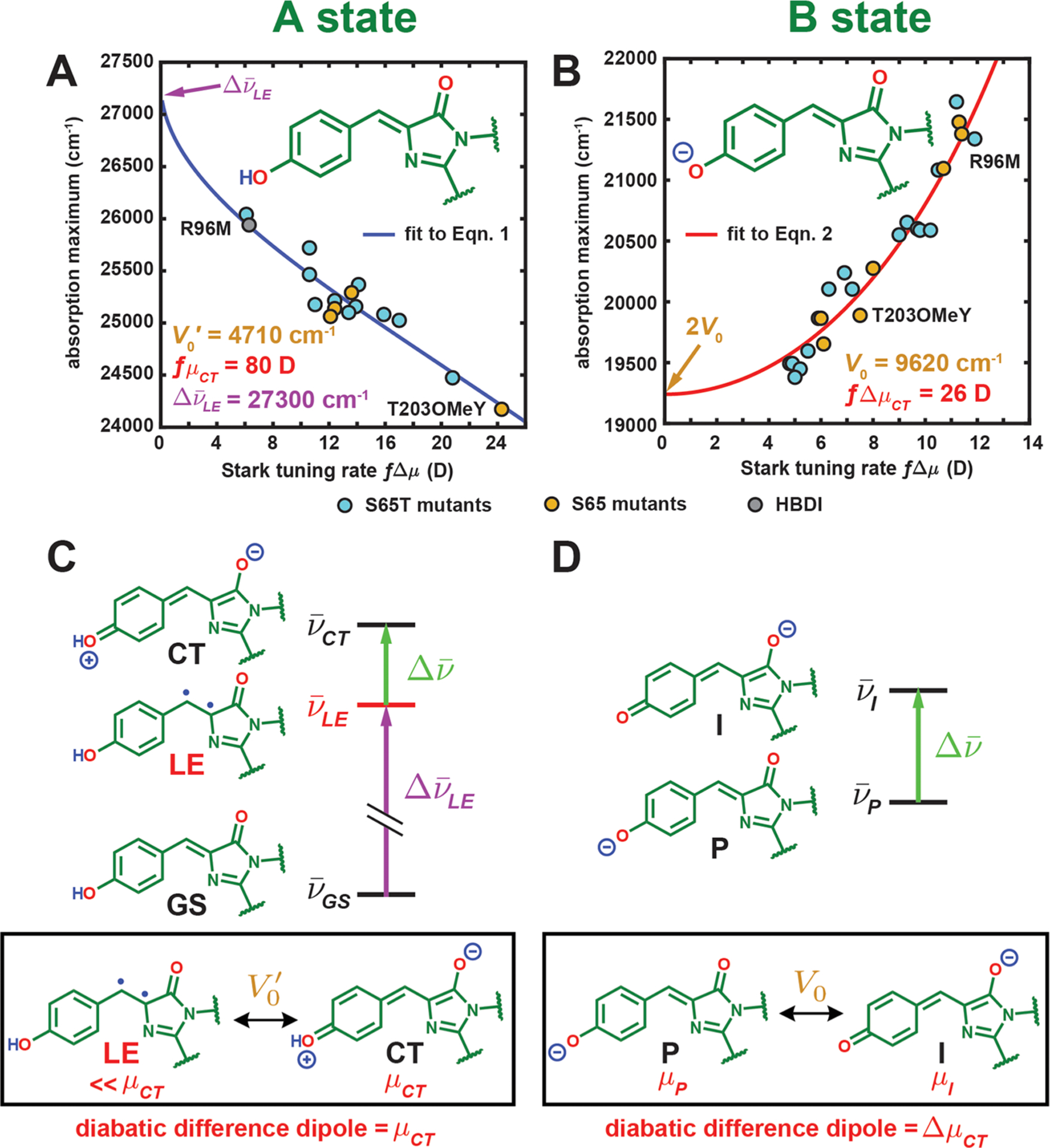
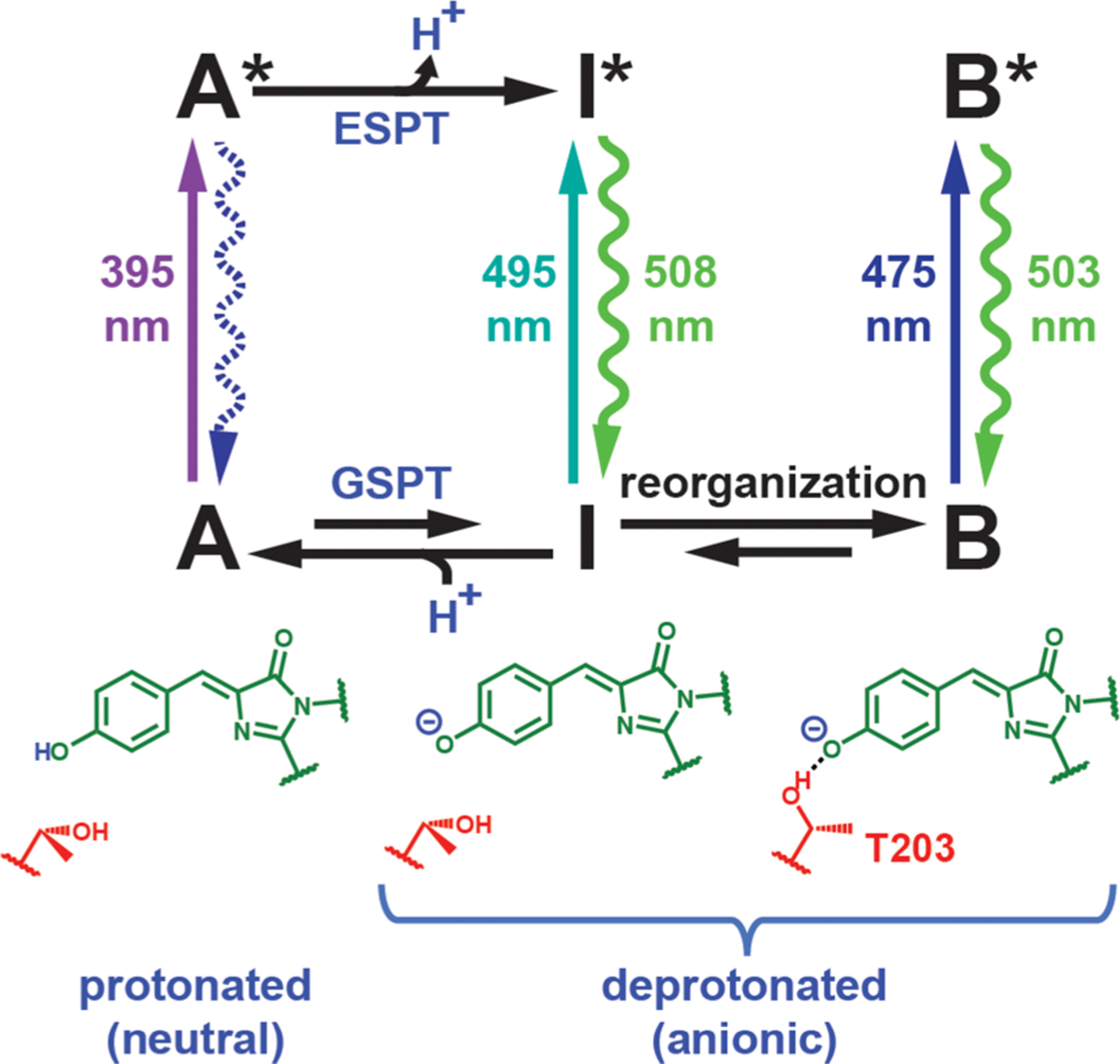
Correlation between the absorption maximum and Stark tuning rate for GFP mutants and HBDI in the (A) A and (B) B states at 77 K, respectively. Panel B is reproduced from Figure 9 in ref 13 including only the S65T and S65 mutants’ data. The curves for panels A and B come from fitting all data (S65T for the latter) to eqs 1 and 2, respectively. See Figure S3 for an identical figure reproduced with numerical labels to identify the species. (C) The three-form model for the A state and (D) the two-form model for the B state. The two diabatic forms with substantial mixing are shown in the black box below each model with the corresponding electronic coupling and diabatic difference dipole. For both models, only $\Delta \overline{v}$ is assumed to be tunable by the environment among all parameters. Note that the LE form has a nontrivial dipole moment, but it is much smaller than μ_CT (5 D²⁹ vs 40 D for the CT form if f = 2), so we can approximately assign μ_CT to the dipole moment of the CT form. The diradicaloid structure illustrated for the LE form should not be treated as exact, but rather it is meant to represent the locally excited and nonzwitterionic nature of this third form (see section 2.3 for further discussion).

To understand this trend, as a first approximation it might seem reasonable to treat the A-state chromophore as an anionic chromophore experiencing the electric field exerted by the proton and assume that the naïve picture of a two-form resonance (P and I forms, Figure 4D), that is, interaction between two distinct resonance forms, still holds. In this picture, the proton biases the driving force $\Delta \overline{v}$ through electrostatics by strongly stabilizing the P form (now ground-state, GS, form after proton attachment) over the I form (now charge-transfer (CT) form, Figure 4C). The direct logical consequence is that the data points of the A-state absorption maximum versus Stark tuning rate (Figure 4A) should simply fall on the corresponding correlation line obtained from the B state in Figure 4B, contrary to what is observed for the A state. This is not at all surprising because the phenol oxygen is in fact covalently linked to the proton.

On the basis of Olsen’s multiconfigurational calculation on a series of modified neutral GFP chromophores,³¹ there exists a third form close in energy with the CT form (Figure 4C). This form is locally excited (LE) and mixes with the CT form to yield two adiabatic states, the lower of which is the S₁ state. Because of the large energy gap between the CT and GS forms caused by proton stabilization, the latter stays mostly intact upon coupling and becomes the S₀ state. We can accordingly set up a minimal three-form model, in which the GS and LE forms are neutral with their relative energies largely unaltered across different environments, while the CT form’s energy is strongly affected by the environment due to its dipolar nature (Figure 4C). In the context of Figure 4C, the energy gap between LE and GS ($\Delta {\overline{v}}_{\text{LE}}\equiv {\overline{v}}_{\text{LE}}-{\overline{v}}_{\text{GS}}$) is assumed to be constant, while that between the CT and LE ($\Delta \overline{v}\equiv {\overline{v}}_{\text{CT}}-{\overline{v}}_{\text{LE}}$) is the only tunable parameter by electrostatics from the environment. We expect the latter to be positive because the charge-separated CT state should be higher in energy than the neutral LE state, which we will verify later. An electronic coupling V₀′ is required to account for the mixing between LE and CT, and the notation is primed to distinguish it from the electronic coupling V₀ between the P and I forms of the B state (Figure 4D). For simplicity, we neglect the coupling between GS and the other two forms due to the large energy differences. To calculate the Stark tuning rate associated with the excitation, we also assign a large dipole moment ${\overrightarrow{\mu }}_{\text{CT}}$ with a magnitude of $\left(\equiv \left|{\overrightarrow{\mu }}_{\text{CT}}\right|\right)$ for the CT form relative to the other two forms, which possess similar yet relatively negligible electronic dipoles (vide infra). Therefore, only four essential parameters, $\Delta \overline{v}$, $\Delta {\overline{v}}_{\text{LE}}$, V₀′, and μ_CT, are required, and only $\Delta \overline{v}$ is influenced by the environment. Again, to avoid potential confusion, we refer to diabatic states as “forms” and the adiabatic states as “states”.

As we will elaborate later, the S₁ state for the chromophore in vacuo or in solvents is almost exclusively LE-like, and thus inferring the nature of LE form is possible from excited-state calculations. The LE form has been proposed as a diradicaloid structure at the methine bridge according to Olsen’s computational study.³¹ It has likewise been introduced in the context of retinal and other polyene chromophores as the 2A_g state (as opposed to the 1B_u state with a dominant charge-transfer character).^32–40 While for the neutral all-trans polyene, the diradicaloid state is indeed lower in energy than the charge-separated state, the former tends to have a small oscillator strength when excited from the ground state (1A_g for all-trans polyenes) due to the unfavorable parity.³⁷ The assignment of the diradicaloid behavior seems to be in contradiction to the large extinction coefficients for the protonated GFP chromophore observed from experiments and calculations,^{28,29,41–43} where the S₀−S₁ transition is consistently designated to be of π−π* character. Some of these studies offer results for us to re-examine the exact nature of the LE form.

First, consistent with our model, there is nearly no net charge transfer across the neutral GFP chromophore in vacuo upon excitation,^28,29,41 so the corresponding LE form does not have a strong CT character and its name is thereby justified. In other words, the GS and LE forms share similar dipole moments (~5 D²⁹). Our model is flexible enough to accommodate these nontrivial dipole moments through a constant offset in dipole moments for all three forms (and three resulting states after mixing), because our observable is the difference dipole moment (i.e., Stark tuning rate) between S₀ and S₁ states. The same flexibility also analogously applies to a constant energy shift in all energy levels as we only measure the difference energy (i.e., electronic excitation energy) between S₀ and S₁. Moreover, the calculated difference electron density between S₀ and S₁ states suggests localized π electron redistribution at the rings and/or the methine bridge,^41,43 which is still “locally excited” but slightly more delocalized than the diradicaloid structure would imply. Given that the GFP chromophore is two rings connected by a short methine bridge, whose symmetry is grossly different from C_2h for long all-trans polyenes, it is conceivable that the LE form is essentially excited at the rings (excitonic state) with a large oscillator strength, which is more similar to the heterodimeric special pair of the bacterial reaction centers⁴⁴ (section S5) and other donor–acceptor systems with short bridge(s).^45,46 This assignment with localized excitation at the rings and/or bridge rather than just at the bridge for the LE form is consistent with a large π−π* character, a high oscillator strength, and still retains its small dipole moment. However, because the corresponding resonance form is not exactly known, we will still illustrate the LE form with a diradicaloid structure in the figures to represent its locally excited and nonzwitterionic nature with this caveat in mind. As Olsen’s calculation is largely inspired by the allylic model³¹ that could imply localized radicals, the diradicaloid structure may actually represent a subset of neutral valence bond structures that allow for radical delocalization within the rings and the conundrum could likely be resolved as such. Because we aim to present a physically reasonable model that captures the global charge distribution (i.e., dipolar or not) rather than the exact wave function for each electronic state of the chromophore, this ambiguity is not relevant to our subsequent analysis.

By including the LE form as a third form, this model already qualitatively predicts the opposite trend from that inferred from the two-form Marcus–Hush theory that was used to describe the deprotonated B state as in ref 13: if the environment stabilizes the CT form and brings it closer in energy to the LE form, the LE form mixes more strongly with the CT form and leads to a decrease in electronic excitation energy and a larger dipolar character for S₁ (Figure 5). The quantitative correlation of the Stark tuning rate fΔμ and absorption maximum $\Delta {\overline{v}}_{\text{abs}}$ can be deduced as (section S4):

$${\overline{v}}_{\text{abs}}=\Delta {\overline{v}}_{\text{LE}}-V_0{}^{\prime }\frac{2\frac{f\Delta \mu }{f{\mu }_{\text{CT}}}}{\sqrt{1-{\left(2\frac{f\Delta \mu }{f{\mu }_{\text{CT}}}-1\right)}^2}}$$ (1)

The vibronic shift between 0–0 electronic excitation energy and absorption maximum (0–1 transition) is absorbed by the $\Delta {\overline{v}}_{\text{LE}}$, so the use of either observable for $\Delta {\overline{v}}_{\text{abs}}$ would not affect the parameters in the second term on the right of eq 1 because the shift is roughly constant (Figures 3D and S2). The absorption maximum is chosen to facilitate comparison between 77 K and room-temperature spectra, for which the vibronic features are poorly resolved (Figure 3C). Using this equation, we obtain an excellent fit to the data in Figure 4A, and we can thus determine $\Delta {\overline{v}}_{\text{LE}}$, V₀′, and fμ_CT to be 27 300 ± 100 cm⁻¹, 4710 ± 50 cm⁻¹, and 80 ± 4 D, respectively. For reference, the corresponding correlation for the anionic chromophore derived from the two-form model (Figure 4D) is

$${\overline{v}}_{\text{abs}}=\frac{2V_0}{\sqrt{1-{\left(\frac{f\Delta \mu }{f\Delta {\mu }_{\text{CT}}}\right)}^2}}$$ (2)

which is exactly eq 2 in ref 13 and to which the data in Figure 4B are fit.

Figure 5.

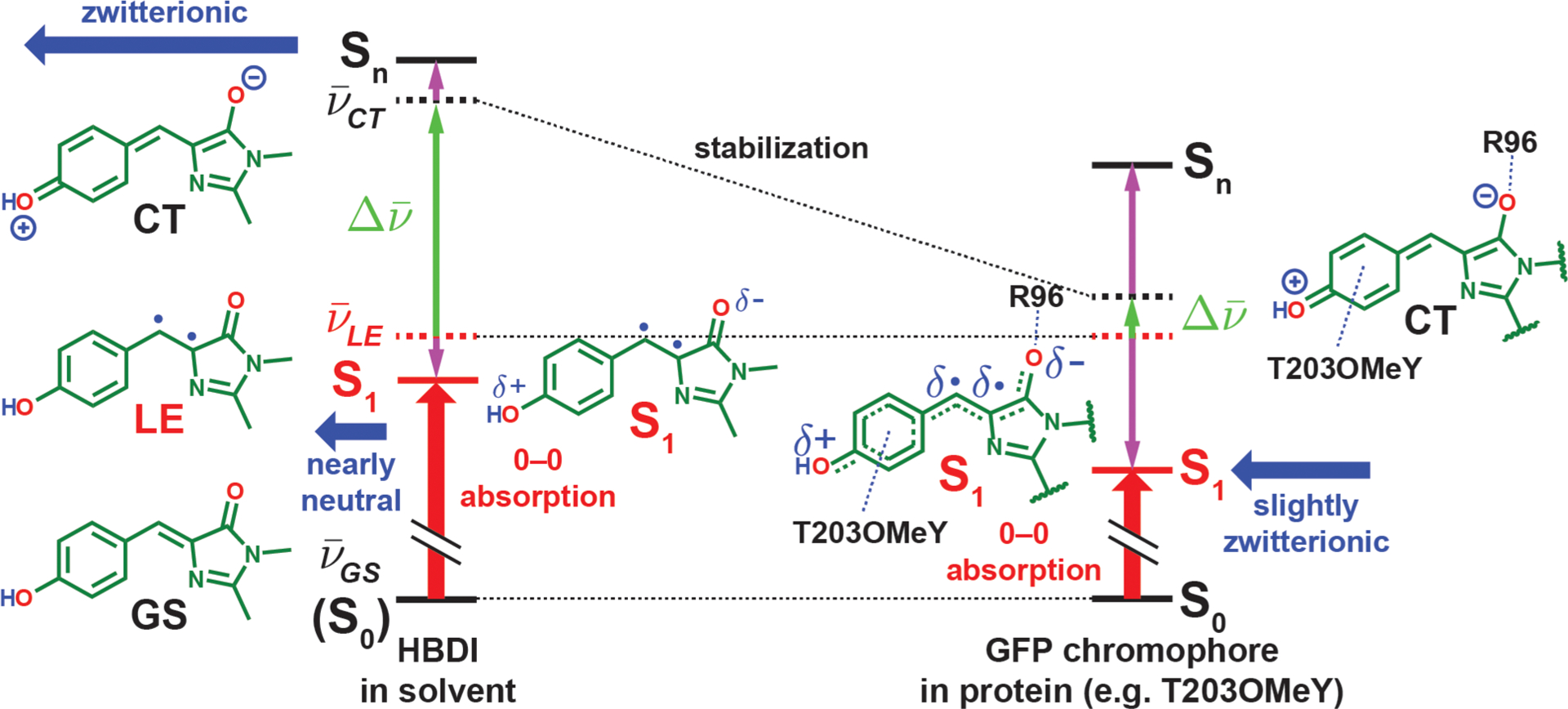
Electrostatic color tuning mechanism of the protonated GFP chromophore, HBDI in solvent, and the covalently linked chromophore in proteins, illustrated qualitatively in different environments (energies not drawn to scale). The energy levels of the diabatic forms and adiabatic states (electronic eigenstates) are represented with dashed and solid lines, respectively. Because the GS form stays intact upon mixing and becomes the S₀ state (denoted with parentheses on the left), we represent its energy levels with solid lines. The energy changes before and after mixing are shown with vertical purple arrows. The dipole moments of the CT form and the resulting S₁ states are depicted with horizontal blue thick arrows, while the 0–0 electronic excitation energy is shown as a vertical red thick arrow in each scenario. The protein environment is more capable of stabilizing the zwitterionic CT form with R96 and the residue at position T203 than solvents, thereby bringing the CT form closer in energy to the LE form and leading to stronger mixing, which subsequently lowers the S₁ energy and imparts stronger charger-transfer character to the S₁ state and thus a larger Stark tuning rate. The resulting CT character of the S₁ state ranges from 7–31% for the mutants we sampled (Table S4). The diradicaloid character for the LE form and the S₁ state should not be taken literally (see section 2.3 for further discussion).

From eq 1, $\Delta {\overline{v}}_{\text{LE}}$, corresponding to 366 nm, is the predicted bluest possible absorption maximum through electrostatic color tuning of the neutral chromophore. The bluest absorption maximum among our protein mutants is 384 nm (from R96M); however, studies of neutral HBDI absorption in various solvents from Tolbert and colleagues show a tight range of absorption maxima between 360 and 373 nm,²⁷ which is comparable with our prediction. V₀′ is about one-half of V₀ between the P and I forms of the B state (9620 cm⁻¹, Figure 4B), while fμ_CT is roughly 3 times as large as the intrinsic dipole moment difference fΔμ_CT between the P and I forms of the B state (26 D).¹³ If f is approximately 2 as suggested by comparing previous experiments from us and Drobizhev et al. (see section S6 in ref 13), Δμ_CT corresponds to two opposite elementary charges with a separation distance of 8.3 Å for the CT form, which closely matches the actual 0–0 distance of the chromophore (8.7 Å). This suggests that the CT form is indeed fully charge-separated, as opposed to the smaller Δμ_CT from the B state, which is due to strong electron delocalization (section S9 in ref 13). The corresponding $\Delta \overline{v}$ for each environment is also estimated via eq S5 (Table S4) and shows that the CT form is always higher in energy than is the LE form, which justifies our aforementioned claim.

It is interesting that the solvatochromism of the neutral HBDI never recapitulates the color range observed from the protein mutants, unlike the anionic counterpart.²⁷ Because the absorption maxima in solvents are all close to $\Delta {\overline{v}}_{\text{LE}}$, our model suggests that solvents are much less effective at stabilizing the dipolar CT form than is the GFP environment. This results in a consistently large energy gap $\Delta \overline{v}$ between CT and LE in the solvents (>2V₀′), which leads to minimal CT and LE mixing, so no appreciable solvatochromic shift is observed (Figure 5, left). This is not surprising because the organization of solvent molecules maximally stabilizes the GS form and is unable to simultaneously solvate the CT form with a significantly larger dipole moment. On the other hand, the GFP environments are preorganized and can better stabilize the CT form via R96 and electron-donating residues at the 203 position, which brings the CT form close to the LE form and leads to substantial mixing that results in a much wider range of absorption maxima (Figure 5, right). This reconciliation suggests that one should be cautious when extrapolating the color tuning behavior from solvatochromic studies on the absorption of dyes to proteins.

While the neutral HBDI has a weak solvatochromism for absorption, if the CT form is indeed present and closely coupled to the LE form, the ability for polar solvents to reorganize and stabilize the CT form should impart HBDI with strong solvatochromism for emission (solvatofluorochromism). This is in fact not that easy to test, because HBDI in solutions are fraught with side photoreactions such as photoisomerization and, to a much lesser extent, ESPT.⁸ However, for neutral HBDI analogues that suppress these side reactions, solvatofluorochromism ranges as wide as 95 nm (~3700 cm⁻¹) have been observed.^47–49 In contrast, absorption and emission maxima for GFP mutants that allow for significant A* emission by disrupting the ESPT chain (e.g., S205V,⁵⁰ T203V/S205A,⁵¹ and deGFPs⁵²) are all fairly close to 400 and 460 nm, respectively, which could be due to the limited sampling of protein environments and/or the relatively poor ability for protein environments to reorganize as compared to simple solvents.

As discussed in detail in ref 13, the color tuning of the B state is achieved by modulating the driving force between the P and I forms (Figure 4D), while we now see that color tuning of the A state is done through changing the relative energies between the CT and LE forms (Figure 4C). Given the same direction of the difference dipoles ${\overrightarrow{\mu }}_{\text{CT}}$ and $\Delta {\overrightarrow{\mu }}_{\text{CT}}$ between the corresponding underlying diabatic states for the A and B states, respectively, we can explain why both states show the same qualitative color tuning trends in various protein environments (Figure 4C and D), as noted in section 2.2. However, due to the dissimilar mechanisms between a two- and three-form model for B and A states, while the B state shows the reddest possible absorption maximum (2V₀) for electrostatic color tuning, the A state possesses the bluest possible absorption maximum ($\Delta {\overline{v}}_{\text{LE}}$) instead (Figure 4A and B). Therefore, as opposed to the common belief generalized from solvent studies, we conclude that the A state’s color can be more easily tunable in the protein environment than can the B state, as was illustrated previously by the π−π stacking series in section 2.2. A correlation plot between the A and B state maxima from protein mutants can also attest this trend (Figure S4), in which the only violations can be found when comparing T203 and T203Y mutants. The T203Y mutation is a frequently invoked example for demonstrating the insensitivity of the A-state color to environmental changes, a common notion derived from solvatochromic studies,²⁷ because T203Y red-shifts the B state by 1400 cm⁻¹ while leaving the A state relatively unaffected (red-shift by 375 cm⁻¹).⁵³ However, there is an important rotameric difference in T203 when interacting with the neutral and anionic chromophores (Figure 1). Specifically, while there is a drastic change in the environment from hydrogen bonding to π−π stacking for the B-state chromophore when T203 is replaced with tyrosine, the corresponding environmental change for the A-state chromophore is much less significant because the hydrogen bond is no longer present to begin with (as in the T203V mutant). Therefore, the situations are not entirely comparable, and we cannot conclude the lack of color tunability for the A state on the basis of this example. In other words, inferring the intrinsic color tunability between the two protonation states from color shifts is only valid when both states are embedded in the same exact environments (Figure S5). Of course, this is also not possible in solvents as solvent molecules reorganize to accommodate different protonation states.

From our explanations of A and B state color tuning, we can now discern the (de)stabilizing characteristics of specific interactions to link structure to energetics. Specifically, because T203 stabilizes the P form and destabilizes the CT form, while R96 prefers both I and CT forms, we can conclude that hydrogen bonds tend to stabilize anions but destabilize cations;⁵⁴ in contrast, π−π stacking on the phenol(ate) moiety selectively destabilizes the P form over the I form and stabilizes the CT form, which shows a tendency of the π system to interact more favorably with cations. This observation casts doubt on the early assertion that the redder color for yellow fluorescent protein from wild-type GFP through the mutation of T203Y is achieved by the polarizability of the π system,^55,56 because a polarizable electronic system should be able to accommodate both cations and anions via redistribution of its electrons accordingly. Instead, it is the electron-rich nature of the π system that results in the overall stabilization of cations, which rationalizes the prevalence of cation–π over anion–π interactions in protein structures,^57,58 also partially due to the lack of naturally occurring amino acids bearing electron-deficient aromatic side chains such as F₅F.⁵⁹ It is also satisfying to see that we are able to treat these interactions on an equal footing through models of electrostatic color tuning demonstrated in Figure 4A and B.^60–62

2.4. Photoacidity.

The color tuning behaviors and Stark tuning rates of neutral and anionic chromophores have profound implications on the photoacidity of the A state chromophore. According to the Förster cycle,⁶³ the difference in pK_a between the excited and ground states of the protonated chromophore (∆pK_a = pK_a* − pK_a) can be readily estimated from the Stokes shift after ESPT from A state excitation, if we assume the entropy change is the same for ground- and excited-state protonation of the corresponding anionic species (I and I*, Figure 6). Therefore, any color tuning of the deprotonated and protonated states caused by the environment directly determines how the environment modulates ΔpK_a. In other words, both electron redistribution during excitation and emission before and after ESPT, respectively, can be driving forces for promoting excited-state deprotonation.¹⁵ Because we know from section 2.2 that the excitation of both protonation states leads to an electron flow from the phenol(ate) to the imidazolinone moiety, electron redistribution upon excitation of both states works in the same direction to aid the photoacidity (Figure 6). Specifically, inferred from the electron flows, the excited-state protonated chromophore (A*) is a stronger acid than the ground-state counterpart (A), and the excited-state deprotonated chromophore (I*) is a weaker base than the ground-state counterpart (I). Note that we approximate the emission of the I* state as the reverse of its absorption process, because the anionic chromophore is known to exhibit a small Stokes shift.¹³ On the basis of the measured magnitudes of Stark tuning rates, the intramolecular electron flow for the protonated state in the redder mutants (e.g., T203OMeY) is nearly the only contributor to the photoacidity due to its much larger Stark tuning rate than the I-state counterpart, while for bluer mutants such as R96M, electron flow for the I state is dominant (Figure 4A and B). Because the protein environment is more capable of red-shifting the color of the protonated than is the deprotonated chromophore (section 2.3), the Stokes shift is decreased and the ΔpK_a becomes less negative for redder mutants. Consequently, to render the protonated GFP chromophore a better photoacid, one should follow the same strategy as blue-shifting the chromophore, by designing hydrogen-bonding groups that interact with the phenol oxygen or attaching electron-withdrawing groups to the phenol moiety, the latter of which echoes Fang and Solntsev’s recent work on ESPT of GFP model chromophores.¹⁰ However, the ground-state pK_a itself is not correlated with color when modulated by electrostatics as we previously argued (see sections S7 and S8 in ref 13). Specifically, as the chromophore deprotonation involves a net charge loss, while color tuning only relates to the electronic redistribution across the chromophore with an intact overall charge, the pK_a and the color of the chromophore are governed by electrostatic potentials and projected electric fields (gradients of potentials) exerted by the environment, respectively. These two electrostatic quantities are not necessarily correlated with each other. However, because ΔpK_a entails the difference in energetics of the two deprotonation processes, the net charge changes associated with them are balanced out, and the resulting response to the environment can be understood simply through color tuning, as the Förster cycle indicates. Also note that, in addition to the strong photoacidity, the chromophore has to be somewhat buried and interacts with a terminal proton acceptor through a well-positioned hydrogen-bond network for ESPT to occur in proteins.

Figure 6.

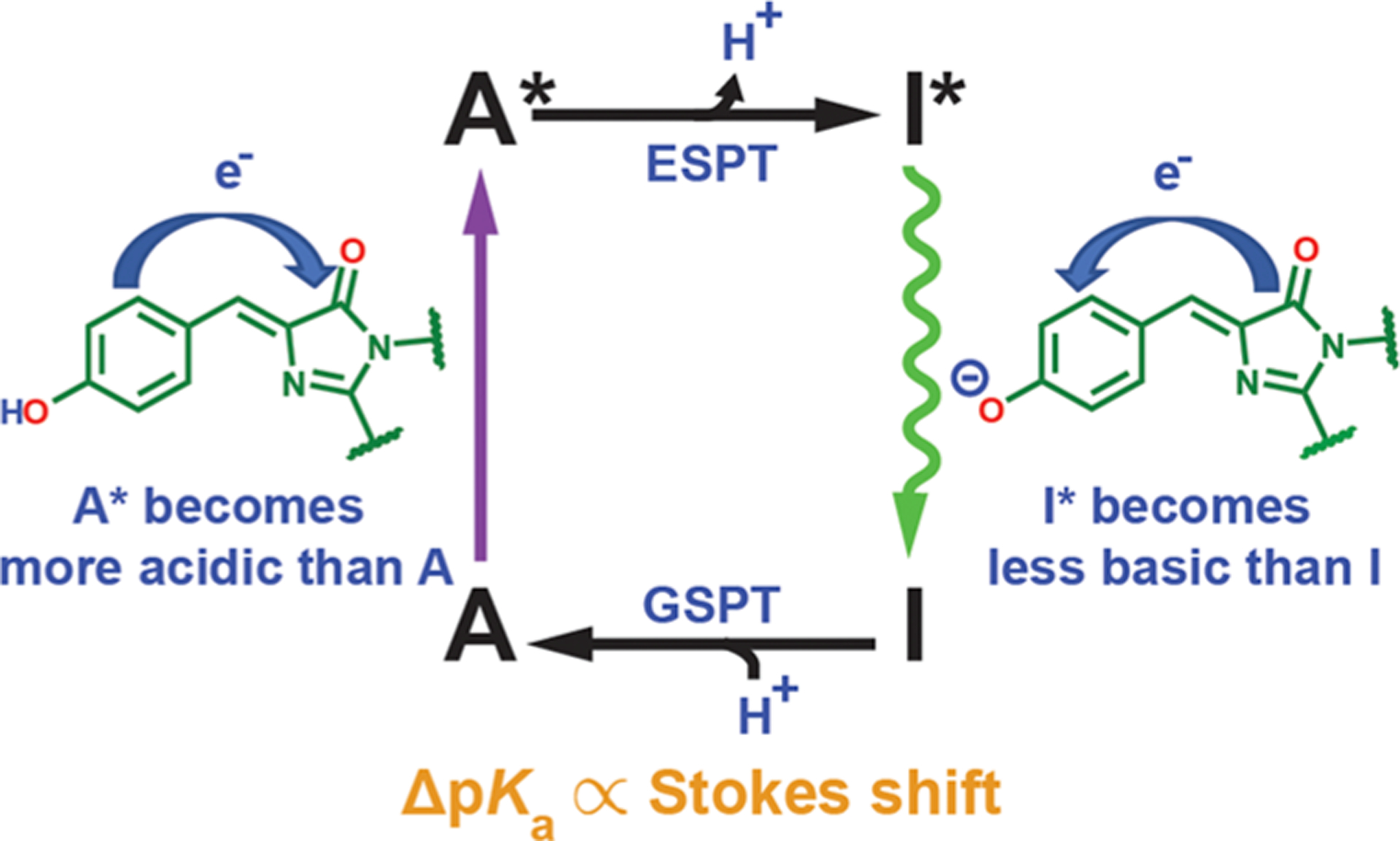
Scheme for proton and electron flow in the Förster cycle of GFP in the A state (Figure 1). Electron redistribution serves as a driving force for ESPT and photoacidity.

3. CONCLUSIONS

Through extensive mutational studies and electronic Stark spectroscopy, we have elucidated the electrostatic color tuning behavior of the protonated GFP chromophore using a simple three-form model, which is surprisingly different from yet not much more sophisticated than the two-form model for the deprotonated chromophore. In particular, after the anionic chromophore is protonated, while the electron flow direction from phenol(ate) to imidazolinone upon excitation is retained, the ease of color tuning in response to environmental electrostatics is drastically changed due to the difference in relative energetics of the diabatic forms. This difference not only allows us to better understand the solvatochromism of the GFP model chromophores, but also offers a strategy for increasing the GFP chromophore’s photoacidity through electrostatic modulation. This work showcases the correlation plot between Stark tuning rates and absorption energies as a powerful tool for characterizing excited-state electronic structures and the underlying color tuning mechanisms for dyes, and also the electrostatic role of the environment in which they are embedded.

The three-form model is not only limited to the protonated GFP chromophore but can likely be also applied to donor–acceptor dyes with strongly asymmetric characters and narrow solvatochromic ranges for absorption,^64–68 which would be two contradictory properties if the two-form model were invoked^69,70 In those cases, the corresponding CT forms are energetically penalized and comparable in energy with the rather unexpected LE form. Because of the moderate electronic couplings between the donor and acceptor moieties, electrons are effectively delocalized in the excited state for such dyes, as opposed to systems with weaker couplings such that thermally activated excited-state electron transfer can occur instead.^71,72 Intriguingly, these dyes also tend to exhibit strong solvato- fluorochromism as expected from the model. As another notable biological example, heterodimeric special pairs of bacterial photosynthetic reaction centers, in which one of the bacteriochlorophylls has been replaced with bacteriopheophytin,⁴⁴ also obey the same color tuning mechanism (section S5). It could be informative to re-examine the validity of the two- form model with donor–acceptor systems with relatively localized ground-state electronic distributions.