Data Augmentation Based on Substituting Regional MRIs Volume Scores

Abstract

Due to difficulties in collecting sufficient training data, recent advances in neural-network-based methods have not been fully explored in the analysis of brain Magnetic Resonance Imaging (MRI). A possible solution to the limited-data issue is to augment the training set with synthetically generated data. In this paper, we propose a data augmentation strategy based on regional feature substitution. We demonstrate the advantages of this strategy with respect to training a simple neural-network-based classifier in predicting when individual youth transition from no-to-low to medium-to-heavy alcohol drinkers solely based on their volumetric MRI measurements. Based on 20-fold cross-validation, we generate more than one million synthetic samples from less than 500 subjects for each training run. The classifier achieves an accuracy of 74.1% in correctly distinguishing non-drinkers from drinkers at baseline and a 43.2% weighted accuracy in predicting the transition over a three year period (5-group classification task). Both accuracy scores are significantly better than training the classifier on the original dataset.

1. Introduction

In neuroimaging studies, structural Magnetic Resonance Imaging (MRI) is often used to examine the influence of neuropsychological diseases and disorders on brain structures [1-3]. These neuroscience studies frequently first extract morphometric measurements associated with regions-of-interest (ROI) from the brain MRI of each subject. Then statistical group analysis aims to identify disease-specific biomarkers by comparing these measurements between healthy and diseased subjects [4,5]. An alternative group analysis is to first train a classifier to accurately differentiate healthy subjects from diseased ones based on the measurements [6-8]. Then the subset of measurements highly influencing the classification outcome are identified as disease-specific imaging biomarkers.

The most advanced classification frameworks nowadays are arguably based on neural networks [7,8]. Despite their successful use in the computer vision community, it is well-known that the training of neural networks on medical imaging data suffers from the “high-dimension low-sample-size” problem [9]; that is, the number of subjects in each group is significantly lower than the dimension of measurements rendering the network easily overfitted. One way of alleviating this issue is to perform data augmentation, i.e., generating synthetic training data using information only from the existing training set, thereby reducing overfitting during training.

While affine transformations (including translation, flipping, and rotation) are commonly used for creating synthetic 3D MR images from existing ones [10], these operations are not meaningful for ROI-based measurements. Another commonly used augmentation strategy is based on adding Gaussian noise to the training data [10]. However, the noise level has to be manually chosen, which is not an intuitive procedure. For non-image data augmentation, approaches based on feature-space warping [11] have been proposed. These approaches aim to create synthetic data by warping the measurements of existing samples. For example, the Synthetic Minority Over-Sampling Technique (SMOTE) [12] computes the weighted average of measurements of two existing training subjects. Instead of synthesizing all measurements of a subject, we propose here a regional-feature-substitution strategy to incorporate the assumption commonly used in many neuroimaging studies [13] that brain morphometric measurements are only locally dependent and the fact that many neurological disorders only affect local brain regions [14]. Specifically, to create a new training sample, we substitute regional ROI measurements of an existing sample by those from another sample of the same cohort. We do so by arranging the ROI measurements as a matrix and substituting within sub-matrices, which we call “kernel” matrices. The kernel is constructed in compliance with the cortical parcellation of the brain to ensure that the warping only affects nearby brain regions.

In this study, we tested the augmentation strategy on the National Consortium on Alcohol and Neurodevelopment in Adolescence (NCANDA) dataset [15], which consists of longitudinal structural MRI scans of 505 subjects. The subjects were categorized into 5 groups according to their drinking behavior in the 4-year study period. We built a neural-network classifier to predict the group label based on the longitudinal measures of ROI cortical thickness. We show that by performing augmentation within each group separately to produce a well-balanced augmented dataset, our neural-network achieved a significant improvement on classification accuracy. Finally, we identify ROIs that highly influence the decision of the classifier through a visualization technique named layer-wise relevance propagation (LPR) [16].

2. Data Augmentation via Local Feature Warping

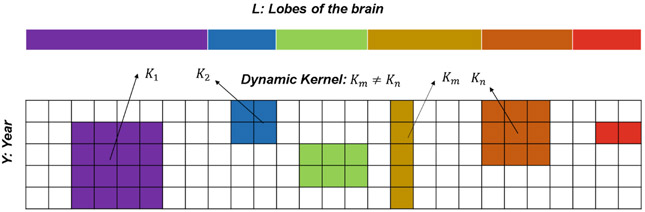
Suppose we have structural MRI images from S subjects that can be categorized into C groups. We further assume that morphometric measurements (e.g., gray-matter thickness) associated with V brain regions-of-interest (ROI) can be derived from each MRI image. We generalize the scenario to a longitudinal design, where these measurements are repeatedly measured T times, such that the measurements of each subject form a T × V matrix. Now, the V brain regions can be grouped into L major lobes, which we encode in the T × V matrix by arranging the columns so that neighboring ones are associated with ROIs belonging to the same lobe (see Fig. 1)

Fig. 1.

Exemplar dynamic kernels within a toy measurement matrix. Columns are ordered such that ROIs of the same lobe (indicated by color) are adjacent. The location of a kernel is confined within a specific lobe.

To augment the training set, our approach is to “substitute” selective entries in the measurement matrices across subjects. To achieve this, we construct lobe-specific kernel matrices $K_l\in {\mathbb{R}}^{{\alpha }_l\times {\beta }_l}$, where l ∈ {1, 2, ⋯ , L} indicates the lobe and (α_l, β_l) indicates the size of the kernel. For instance, in the example of Fig. 1, α₁ = 4, β₁ = 4 for K₁, and α₂ = 2, β₂ = 2 for K₂. We then create a new synthetic subject by first randomly selecting a kernel and substituting the measurements inside the kernel of an existing subject by the ones from a different randomly-chosen subject in the same group (Fig. 2). As suggested by Fig. 1, the location of a kernel is confined within its specific lobe, so that the warping does not affect measurements of distant regions that are unlikely to correlate. Note that instead of using the weighted average strategy as in SMOTE that would generate unseen (thereby potentially unrealistic) measurements, our substitution strategy always uses existing measurements to synthesize new subjects.

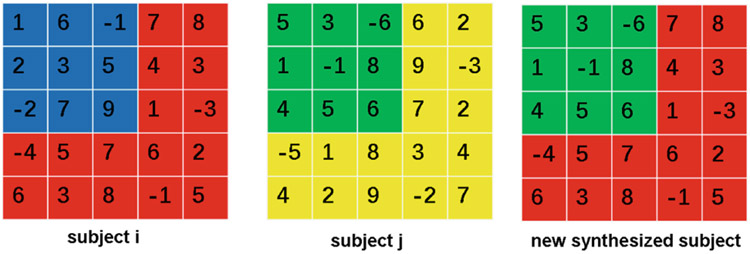
Fig. 2.

Measurements of subject i within the kernel (blue) are substituted by the ones of subject j (green) to yield the measurements a new synthetic subject.

Now let S_c denote the number of subjects in the c^th group and V_l the number of ROIs in the l^th lobe. Given the sizes {α_l, β_l} of the L kernels, the maximum number of subjects N that can be generated for a group is the product of the number of subject pairs (i.e., (S_c − 1) · S_c) and the number of possible kernel matrices in all lobess:

$$N≔\sum _{c=1}^C{S}_c(S_c-1)\sum _{l=1}^L(T-{\alpha }_l+1)(V_l-{\beta }_l+1)$$ (1)

3. Experimental Setup

3.1. Dataset

The experiments were based on data from the NCANDA study [15] comprised of 4-visit longitudinal data of 505 adolescents (S = 505, ages 12–22, 250 boys/255 girls; the data release NCANDA_PUBLIC_Y3_STRUCTURAL_V01 is made public according to the NCANDA Data Distribution agreement¹). Each subject had T1-weighted MRI scans (T = 4) that were acquired annually. They were categorized into 5 groups according to the specific year the subject transitioned from a no-to-low to medium-to-heavy alcohol drinker [15]. As shown in our previous studies [17], initiation of binge drinking alters normal development of brain morphometric patterns, so we hypothesize that subjects from different groups can be classified based on their brain morphometric measurements. In doing so, we have S₁ = 265 subjects who met the no-to-low drinking criteria of the NCANDA study [15] at baseline and throughout the study, S₂ = 49 subjects who met the criteria for the first 3 visits but transitioned to exceed-criteria drinkers at visit 4, S₃ = 56 transitioned at visit 3, S₄ = 58 transitioned at visit 2, S₅ = 77 subjects who remained exceeds-criteria drinkers throughout the study. Structural MRIs were processed using the publicly available NCANDA pipeline [17]. FreeSurfer (V 5.3.0) was applied to the skull-stripped MR images yielding the measurements of average thickness associated with 34 bilateral cortical ROIs (V = 34). Then confounders including age, sex, race and supratentorial volume were removed from the raw thickness measurements by general linear model analysis [14], which resulted in a 4 × 34 residual score matrix for each subject. Based on these score matrices, our goal was to apply data augmentation to train a classifier that could accurately predict the group label of each subject.

3.2. Data Augmentation for Classification

We tested whether the proposed data augmentation strategy could boost classification accuracy in two scenarios: 5-group classification and binary classification between Group 1 and 5 (subjects remained non-heavy or heavy drinking through the 4-year study period) as these two groups were most distinguishable with respect to their drinking history across the 5 groups. For either scenario, the accuracy of classifiers in correctly labelling individuals was derived based on a 20-fold cross validation. The training data was enriched with the synthetic samples produced by our augmentation strategy, and the normalized classification accuracy (i.e., the accuracy of correctly labeling samples while accounting for differences in sample size among groups) was measured on the testing fold. Next, we detail the setup of kernel matrices used in our augmentation strategy and describe the up-sampling strategy as a benchmark approach in our experiments.

Kernel Setup.

Kernels were constructed with respect to the lobe parcellation of the brain. Adopting the Freesurfer parcellation, the brain was segmented into 6 major lobes: temporal lobe (9 ROIs), frontal lobe (11 ROIs), occipital lobe (4 ROIs), parietal lobe (5 ROIs), cingulate (4 ROIs) and insula. Given these dimensions, we set up kernel sizes ({α_l, β_l}) such that the resulting augmented training set was as balanced as possible for the 5-group and binary classification (Table 1). Based on Eq. 1 and our kernel settings, the maximum number of synthetic samples generated from the training folds was 1,655,888, which was the sum of

$$\begin{gathered} N_1=260\ast (1+1+1+1+1+1)\ast 259=404040, \\ {N}_2=44\ast (36+44+16+20+16+4)\ast 43=257312, \\ {N}_3=51\ast (24+44+16+20+16+4)\ast 50=316200, \\ {N}_4=53\ast (20+44+16+20+16+4)\ast 52=330720, \\ {N}_5=72\ast (8+18+12+15+12+3)\ast 71=347616. \end{gathered}$$ (2)

Similarly, the maximum size of augmentation for the binary classification task was N = 344160 + 276060 = 620220.

Table 1.

Kernel dimension setup of 5-group (upper) and binary (lower) classification

Group	Temporal	Frontal	Occipital	Parietal	Cingulate	Insula
1	(4,9)	(4,11)	(4,4)	(4,5)	(4,4)	(4,1)
2	(1,1)	(1,1)	(1,1)	(1,1)	(1,1)	(1,1)
3	(1,4)	(1,1)	(1,1)	(1,1)	(1,1)	(1,1)
4	(1,5)	(1,1)	(1,1)	(1,1)	(1,1)	(1,1)
5	(1,8)	(2,6)	(2,1)	(2,1)	(2,1)	(2,1)
Group	Temporal	Frontal	Occipital	Parietal	Cingulate	Insula
1	(4,9)	(4,11)	(4,4)	(4,5)	(4,4)	(4,1)
2	(4,9)	(4,11)	(4,4)	(4,5)	(4,4)	(4,1)

To relate the accuracy of classification with the size of the augmented training set, we also performed classification on subsets of the augmented dataset with different sizes (500, 2.5k, 50k, 250k, 500k). For each setting, the subset was randomly selected from the maximumly augmented training set while keeping the size of each group balanced.

Up-sampling.

We also measured the classification accuracy when training was performed on balanced datasets generated by up-sampling (sample with replacement). Specifically, the raw training set was up-sampled to 2500 for 5-group and 430 for binary classification. Note that the size of these up-sampled datasets was determined to create a balanced training set rather than to perform data augmentation; Extensive up-sampling will only produce repeated training samples, so it does not improve the accuracy of the classifier.

3.3. Classifiers

The above data augmentation was independent of the choice of the classifier. Here, we tested the data-augmentation strategies on three different approaches: a simple, fully connected neural network called SmallNet as well as Random Forest (RF) and Supporting Vector Machine (SVM), two approaches that have been shown to be able to work reasonably on small training datasets. SmallNet only contained 3 hidden layers with each layer having 50 neurons. The activation function of each hidden layers was Relu, and the final output was the softmax functional for a general multi-group classification. To train our SmallNet classifier, the Kaiming’s method [18] was used and initialized with a batch size of 128. Learning strategy of SmallNet was SGD with momentum of 0.1. All experiments were ran for 10 epochs at 0.0001 learning rate. During training, batch normalization and early stopping method were used for lowering the impact of overfitting. Note, we used SmallNet for simplification to illustrate the power of our augmentation strategy, and more sophisticated network structures might produce more accurate results. Our implementation of RF consisted of 100 decision trees. Each decision tree had the depth of up to 5, and the feature number for each split was 10. The weighted accuracy was obtained by averaging 100 training sessions. SVM was setup with a relaxation coefficient of 2.0, a maximum number of iterations of 5000, and an average of 50 out of 5000 cross-training. After 100 cross-training, the average was taken as the final results.

4. Results

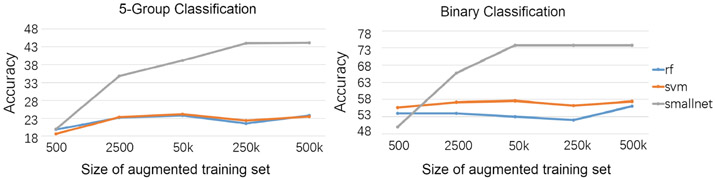
Here we analyze the accuracy of the 3 classifiers trained with and without data augmentation. We can see from Table 2 that all 3 classifiers performed poorly on the raw datasets for both 5-group and binary classification. When trained on the up-sampled dataset, the accuracy of RF and SVM slightly improved in the 5-group classification setting to approximately 28% (randomly labeling samples would produce an accuracy of 20%). However, these two methods showed little further improvement when the training set was augmented by the proposed strategy. On the other hand, even though SmallNet was often less accurate than RF and SVM on small training sets, it achieved significantly more accurate 5-group and binary classification results when trained on the augmented set. These results support the fact that RF and SVM are suitable for small to moderate datasets, so extensive data augmentation provides little merit. On the other hand, the implementation of neural networks requires a large-scale training dataset. In our specific application, training SmallNet benefited from the proposed data augmentation strategy resulting in the most accurate prediction for both classification settings. The above claims are further supported by Fig. 3. As the size of the augmented set increased, the accuracy of RF and SVM only increased marginally, whereas SmallNet showed a significant improvement. The performance of SmallNet converged approximately at 250k training samples for 5-group and 50k for the binary classification task.

Table 2.

Accuracy of 5-group and binary classification produced by random forest (RF), support vector machine (SVM) and SmallNet on different training sets.

Task	Training set	Size	RF	SVM	SmallNet
5-group classification	Raw data	405	19.9%	23.3%	19.2%
	Up-sampling	2500	27.5%	28.7%	23.1%
	Augmentation	1.6M	27.9%	29.3%	44.1%
Binary classification	Raw data	405	54.7%	57.7%	53.7%
	Up-sampling	430	55.6%	58.1%	56.1%
	Augmentation	600K	55.5%	58.2%	73.8%

Fig. 3.

Accuracy of RF, SVM and SmallNet based on different sizes of training dataset.

Visualization via LRP.

As mentioned, another critical goal of most neuroimaging studies is to identify critical ROI biomarkers associated with specific cohorts, so we analyzed the subset of measurements that highly impacted the classification decision based on the Layer-wise relevance propagation (LRP) technique [16]. Given a feature matrix and a classifier, the aim of LRP is to assign each entry of the measurement matrix a relevance score such that negative scores contain evidence against the presence of a class, while positive scores contain evidence for the presence of a class. These pixel-wise relevance scores can be visualized as an image called heatmap. Here we focused the analysis on the binary classification as it highlighted the difference between normal adolescents (Group 1) and youth that had already initiated medium-to-heavy drinking at baseline (Group 5). Figure 4-left shows the heatmaps (relevance scores) associated with the input matrix. Yellow blocks in the upper figure correspond to the matrix entries that strongly indicate the presence of Group 1, whereas the yellow blocks below correspond to Group 5. The general agreement between the two heatmaps suggests that the binary classification was mainly based on several key measurements (in yellow). To relate those measurements to specific brain regions, these scores were averaged in the longitudinal dimension and then averaged between the two groups. The resulting 34-D vector was then color-coded on the cortical surface (Fig. 4 right). Yellow regions correspond to ROIs that contributed more to the prediction. We can see that brain regions in the temporal lobe (specifically superior temporal, fusiform, and inferior temporal regions) are more salient than others. The impact of alcoholism that leads to significant volume deficits in cortical gray/white matter in the temporal lobe has been frequently suggested in the alcohol literature [19].

Fig. 4.

Heat-map of relevance scores on the binary classification task

5. Conclusion

While data augmentation has been shown to be effective in increasing the performance of many image-based classifiers, our proposed augmentation strategy designed for ROI-measurements not only provided us sufficient data for training simple neural networks, but also showed a significant improvement on prediction results when applied to the NCANDA dataset. We showed that progression of drinking behaviors could be differentiated based on longitudinal brain morphometric measurements. Furthermore, by applying the LRP method, we were able to derive the relevance scores for the input measurement matrix, from which we could interpret and visualize the importance of ROIs in the decision process of the classifier.

In this work, however, we only explored kernel construction with respect to the spatial properties of the brain. We will further consider temporal correlation of the longitudinal measurements in constructing kernels. Moreover, we aim to extend the usage of our augmentation strategy in the context of image-based classification by applying regional warping to either raw images or intermediate features. This could potentially complement current image augmentation strategies based on global affine/deformable transformation.