Experience-Dependent Development of Dendritic Arbors in Mouse Visual Cortex

Abstract

The dendritic arbor of neurons constrains the pool of available synaptic partners and influences the electrical integration of synaptic currents. Despite these critical functions, our knowledge of the dendritic structure of cortical neurons during early postnatal development and how these dendritic structures are modified by visual experience is incomplete. Here, we present a large-scale dataset of 849 3D reconstructions of the basal arbor of pyramidal neurons collected across early postnatal development in visual cortex of mice of either sex. We found that the basal arbor grew substantially between postnatal day 7 (P7) and P30, undergoing a 45% increase in total length. However, the gross number of primary neurites and dendritic segments was largely determined by P7. Growth from P7 to P30 occurred primarily through extension of dendritic segments. Surprisingly, comparisons of dark-reared and typically reared mice revealed that a net gain of only 15% arbor length could be attributed to visual experience; most growth was independent of experience. To examine molecular contributions, we characterized the role of the activity-regulated small GTPase Rem2 in both arbor development and the maintenance of established basal arbors. We showed that Rem2 is an experience-dependent negative regulator of dendritic segment number during the visual critical period. Acute deletion of Rem2 reduced directionality of dendritic arbors. The data presented here establish a highly detailed, quantitative analysis of basal arbor development that we believe has high utility both in understanding circuit development as well as providing a framework for computationalists wishing to generate anatomically accurate neuronal models.

SIGNIFICANCE STATEMENT Dendrites are the sites of the synaptic connections among neurons. Despite their importance for neural circuit function, only a little is known about the postnatal development of dendritic arbors of cortical pyramidal neurons and the influence of experience. Here we show that the number of primary basal dendritic arbors is already established before eye opening, and that these arbors primarily grow through lengthening of dendritic segments and not through addition of dendritic segments. Surprisingly, visual experience has a modest net impact on overall arbor length (15%). Experiments in KO animals revealed that the gene Rem2 is positive regulator of dendritic length and a negative regulator of dendritic segments.

Introduction

Dendritic architecture plays a fundamental role in the functional capacity of neurons (Mainen and Sejnowski, 1996; Schiller et al., 2000; Krichmar et al., 2002; Bramham and Wells, 2007; Hausselt et al., 2007; Johnston and Narayanan, 2008; Branco and Hausser, 2010; Behabadi et al., 2012; Kulkarni and Firestein, 2012; Lavzin et al., 2012; Ferrante et al., 2013; Hay et al., 2013; Major et al., 2013; S. L. Smith et al., 2013; Cochran et al., 2014; Grienberger et al., 2015; Kastellakis et al., 2015; Kostadinov and Sanes, 2015; Stuart and Spruston, 2015; Koren et al., 2017). Dendrites provide the real estate for housing synaptic contacts and, in concert with intrinsic membrane properties, dictate how incoming current will flow from these contacts to the soma. Despite the importance of dendritic architecture, much remains to be understood about how dendrites develop in mammalian sensory areas and the roles of genetic programs and sensory experience in this process. While many developmental studies have illuminated the details of cell migration (Zipurksy, 2001; Nadarajah et al., 2003; Marin et al., 2010; Wamsley and Fishell, 2017), differentiation (Molyneaux et al., 2007; Seung and Sumbul, 2014; Moore and Livesey, 2015), and dendritic spine formation (Valverde, 1971; Majewska and Sur, 2003; Konur and Yuste, 2004; Bosch et al., 2014; Elston and Fujita, 2014; Moyer and Zuo, 2018), a high-resolution examination of the postnatal maturation of dendritic branches in a mammalian model system is lacking.

Existing reports suggest that the basal arbor of pyramidal neurons in visual cortex increases in length early in postnatal development and may reach a steady length beginning at postnatal day 30 (P30), at which time the arbor is largely resistant to changes in visual experience (Chen et al., 2011b). However, these works have focused on very early postnatal development (Miller, 1981) or sampled only a few later ages (Juraska, 1982). More recent work has focused on post-critical period plasticity (Lee et al., 2008; Chen et al., 2011a; Chen and Nedivi, 2013), and dendrite development and plasticity in juvenile mice are relatively unexplored. Reports in other vertebrate species, such as Xenopus laevis, suggest that visual experience plays an important part in proper development of dendritic arbors of optic tectum neurons and many molecular regulators have already been identified (Cline, 1991; Nedivi et al., 1998; Wu and Cline, 1998; Wu et al., 1999; Zou and Cline, 1999; Sin et al., 2002; Van Aelst and Cline, 2004; Bestman and Cline, 2008; Van Keuren-Jensen and Cline, 2008; Ghiretti et al., 2014). However, numerous outstanding questions remain to be answered in mammalian systems: What are the processes by which dendritic arbors adopt their adult configuration? Is maturation regulated by experience? Which molecular mechanisms underlie these processes?

We performed a detailed analysis of dendritic architecture in layer 2/3 of mouse visual cortex beginning before eye opening (P7) and continuing through the height of the critical period (P30) (Gordon and Stryker, 1996). Our analyses reveal that the length of the pyramidal cell basal arbor undergoes significant outgrowth between P16 and P21, and that this growth is composed primarily of increases in the length of dendritic segments but not increases in the number of segments. That is, the net number of dendritic branches is relatively established by P7. Furthermore, we found that this increase in segment length is mediated by both experience-dependent and experience-independent processes. We also establish Rem2, a small GTPase previously implicated in dendritic complexity in vitro and in X. laevis optic tectum (Ghiretti et al., 2014; Parent et al., 2017), as an experience-dependent negative regulator of dendritic complexity in mammalian visual cortex. This work demonstrates that Rem2 cell-autonomously regulates the arrangement of the basal dendrites: neurons in which Rem2 has been deleted are less likely to exhibit significant directionality, clustering of branches in one region with reference to the soma, and sometimes exhibit abnormal directionality. Our results establish a unified dataset of early postnatal pyramidal neuron dendritic development in the mammalian cortex and expand our understanding of how dendritic arbors are established and maintained in an experience-rich environment.

Materials and Methods

Experimental design and statistical analyses

For all Golgi-Cox experiments, those using Rem2^+/+and Rem2^−/−, 3-12 neurons (average 10 or 11 neurons) from 2-4 mice of either sex, were sampled from primary visual cortex for each genotype, age, and rearing condition (for additional information, see Table 1 and figure legends). We did not consider sex as a variable. For acute Rem2 KO experiments using sparse viral transduction and related controls, all cells that were able to be reconstructed (1-11 cells per animal) were reconstructed from 4 to 6 mice of either sex per genotype and time point. Because of poor TdTomato reporter expression, an insufficient number of cells were able to be reconstructed at 3 days post injection (dpi) (1-4 cells per animal, 1 or 2 animals), and these data were not included. Exact animal and cell number for each condition appear in each figure caption.

Table 1.

Animal information for Golgi-Cox experiments

Mouse	Condition	Age	Sex	Genotype	Weight (g)	Brain weight (g)	Cell number
RI-0099	TR	P7	F	KO	7.5	0.26	12
RI-0100	TR	P7	F	WT	7.6	0.27	12
RI-0204	TR	P7	M	KO	5.7	0.19	10
RI-0206	TR	P7	M	WT	6.9	0.23	12
RI-0022	TR	P12	F	WT	7.1	0.31	8
RI-0023	TR	P12	F	KO	6.5	0.45	11
RI-0077	TR	P12	F	WT	6.5	0.31	12
RI-0078	TR	P12	M	KO	5.9	0.30	12
RI-0090	TR	P12	F	WT	7.7	0.37	12
RI-0094	TR	P12	F	KO	7.5	0.42	12
RI-0175	TR	P12	M	WT	7.9	0.23	12
RI-0178	TR	P12	F	KO	7.6	0.34	12
RI-0053	TR	P16	F	KO	10.3	0.35	11
RI-0058	TR	P16	F	WT	9.8	0.38	10
RI-0271	TR	P16	M	KO	9.1	0.48	12
RI-0272	TR	P16	M	WT	10.3	0.48	5
RI-0719	TR	P16	M	KO	11.1	0.25	12
RI-0721	TR	P16	M	WT	11.9	0.18	12
RI-0727	TR	P16	M	WT	8.1	0.34	12
RI-0728	TR	P16	M	KO	7.6	0.29	12
RI-0135	DR	P16	F	KO	11.2	0.26	12
RI-0136	DR	P16	F	WT	11.4	0.53	11
RI-0137	DR	P16	M	WT	11.3	0.25	12
RI-0139	DR	P16	M	KO	11.9	0.46	9
RI-0142	DR	P16	F	KO	6.1	0.42	12
RI-0145	DR	P16	M	WT	6.9	0.28	12
RI-0147	DR	P16	M	KO	7.2	0.35	12
RI-0148	DR	P16	F	KO	7.0	0.37	12
RI-0150	DR	P16	F	WT	6.3	0.24	11
RI-0153	DR	P16	M	KO	5.6	0.39	11
RI-0082	TR	P21	F	KO	11.4	0.31	12
RI-0085	TR	P21	F	WT	14.7	0.31	11
RI-0095	TR	P21	F	KO	11.8	0.33	10
RI-0096	TR	P21	M	WT	11.7	0.28	11
RI-0157	TR	P21	M	KO	11.6	0.36	9
RI-0159	TR	P21	M	WT	11.1	0.35	11
RI-0407	DR	P21	M	KO	11.8	0.52	10
RI-0408	DR	P21	M	WT	11.6	0.42	10
RI-1112	DR	P21	F	WT	14.4	0.44	10
RI-1117	DR	P21	M	KO	15.2	0.40	6
RI-1121	DR	P21	F	WT	15.7	0.39	3
RI-1471	DR	P21	F	KO	12.8	---	12
RI-1473	DR	P21	F	KO	11.0	0.33	10
RI-1477	DR	P21	M	WT	13.4	0.46	11
RI-0037	TR	P30	F	KO	13.7	0.42	6
RI-0038	TR	P30	F	WT	16.4	0.59	3
RI-0070	TR	P30	F	KO	12.5	0.35	10
RI-0074	TR	P30	F	WT	15.2	0.36	11
RI-0274	TR	P30	F	KO	15.3	0.36	10
RI-0277	TR	P30	F	WT	15.0	0.49	12
RI-1452	TR	P30	F	KO	15.0	---	12
RI-1453	TR	P30	F	WT	16.3	0.5	12
RI-0400	DR	P30	F	WT	---	---	11
RI-0405	DR	P30	F	KO	---	---	10
RI-1101	DR	P30	F	WT	16.8	0.30	10
RI-1102	DR	P30	F	WT	14.9	0.52	12
RI-1111	DR	P30	M	WT	16.8	0.30	12
RI-1475	DR	P30	M	KO	---	---	11
RI-1476	DR	P30	M	KO	---	---	11

All statistics were performed in R using individual pyramidal cell values as the experimental unit. Because distributions of values for virtually all measures were skewed, a log transform was applied before testing for Golgi-Cox experiments. Single genotype analyses over time were analyzed using one-way ANOVA followed by post hoc Tukey tests. Genotype × time or condition analyses were performed using two-way ANOVA followed by post hoc Tukey tests. Sholl data were analyzed using one-way ANOVA followed by Scheffé test. Pairwise comparisons were analyzed using a Welch's t test for Golgi-Cox studies and the Wilcoxon Rank-Sum test for acute Rem2 KO experiments, with Bonferroni correction applied when performing multiple comparisons for both types of experiments. Significant correlations were determined by Pearson's R. In all relevant figures, large point indicates mean (see Figs. 3–7, yellow; Figs. 8, 9, blue); error bars indicate SD. Small points indicate per-cell values. In boxplots (see Figs. 4E, and 8E), pink dot indicates mean, pink error bars indicate SE, white line indicates median, box indicates 25th and 75th quartiles, gray error bars indicate the range, and small yellow dots indicate outliers.

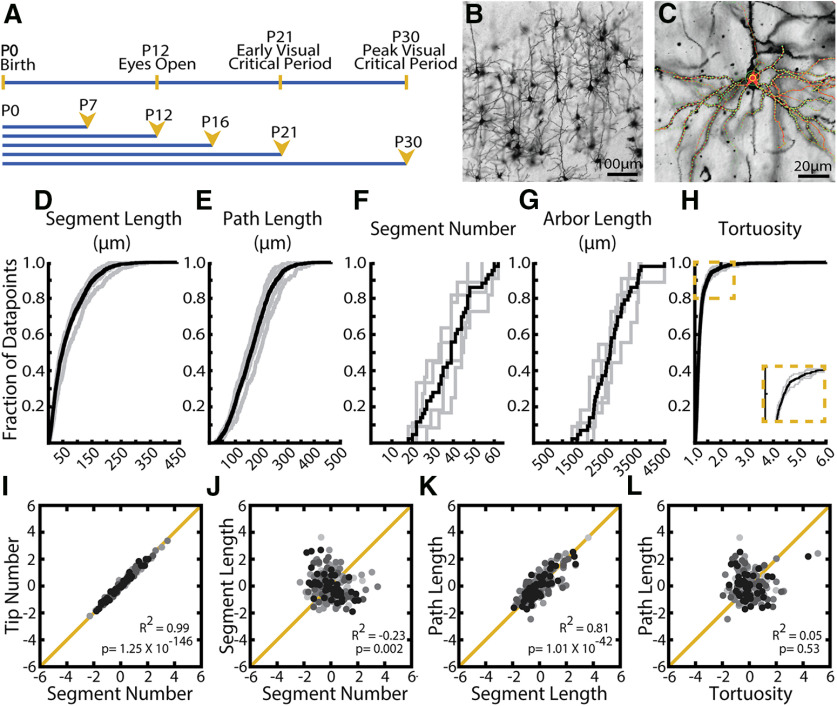
Figure 3.

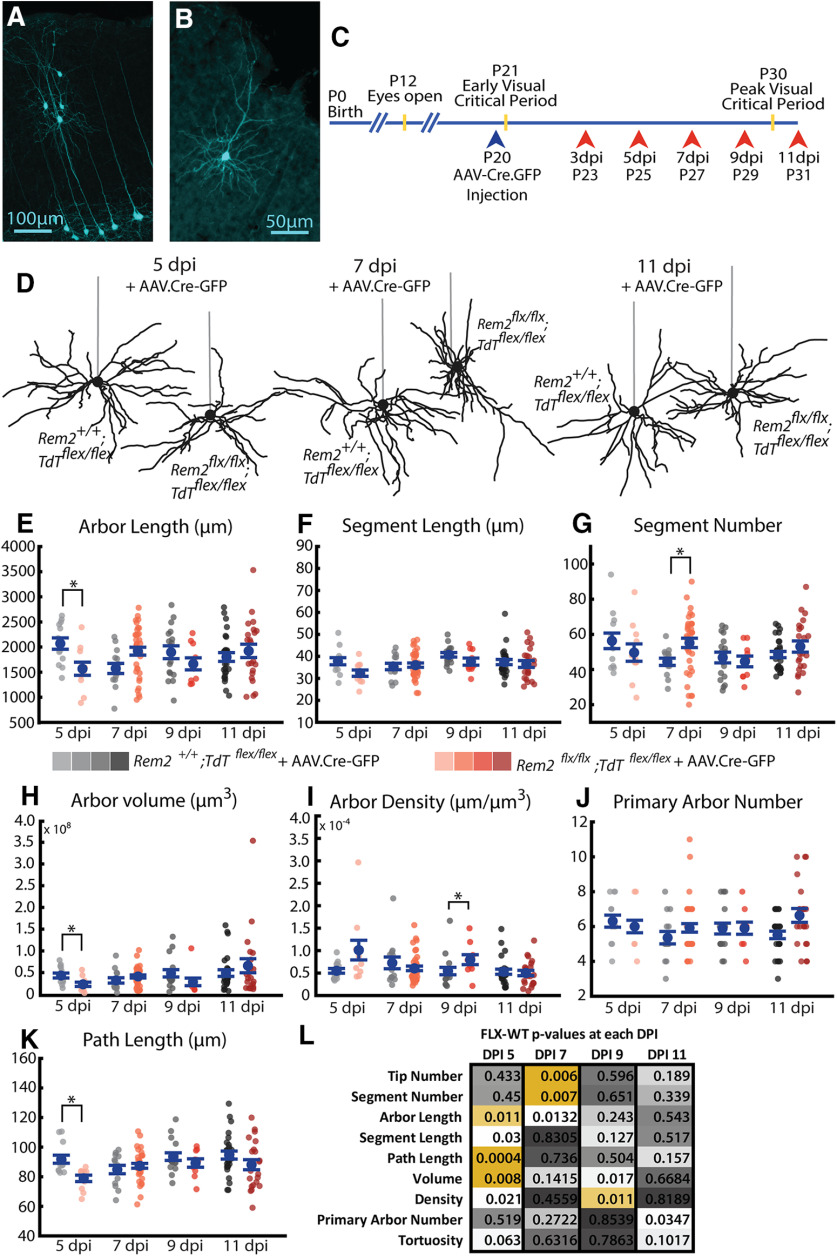
Distributions of observed values for arbor parameters suggest distinct regulatory mechanisms. A, Timelines of visual development in the mouse (top) and morphologic sampling across development (bottom). Ages sampled indicated by postnatal day (P#) and yellow arrowheads. B, Example field of Golgi-stained cortical pyramidal neurons demonstrating dark fill of neurites and ability to differentiate cell types. C, Example 3D tracing of basal dendrites of L2/3 pyramidal neuron in visual cortex. Green circles represent experimenter-placed nodes. Red lines indicate edges connecting nodes. Some traced branches are not in-plane. D–H, Cumulative distributions of (D) segment length, (E) path length (F), segment number (G), arbor length, and (H) tortuosity. Gray lines indicate all observations from individual WT mice at age P30. Black lines indicate the complete population of all observations across animals at P30. I-L, Correlations between listed parameters for entire population of all neurons across all ages. R² values and p values are listed for each comparison. Neurons sampled at different ages are indicated by different colors, with light grays representing young animals and black representing older animals. No noticeable clustering by age was observed.

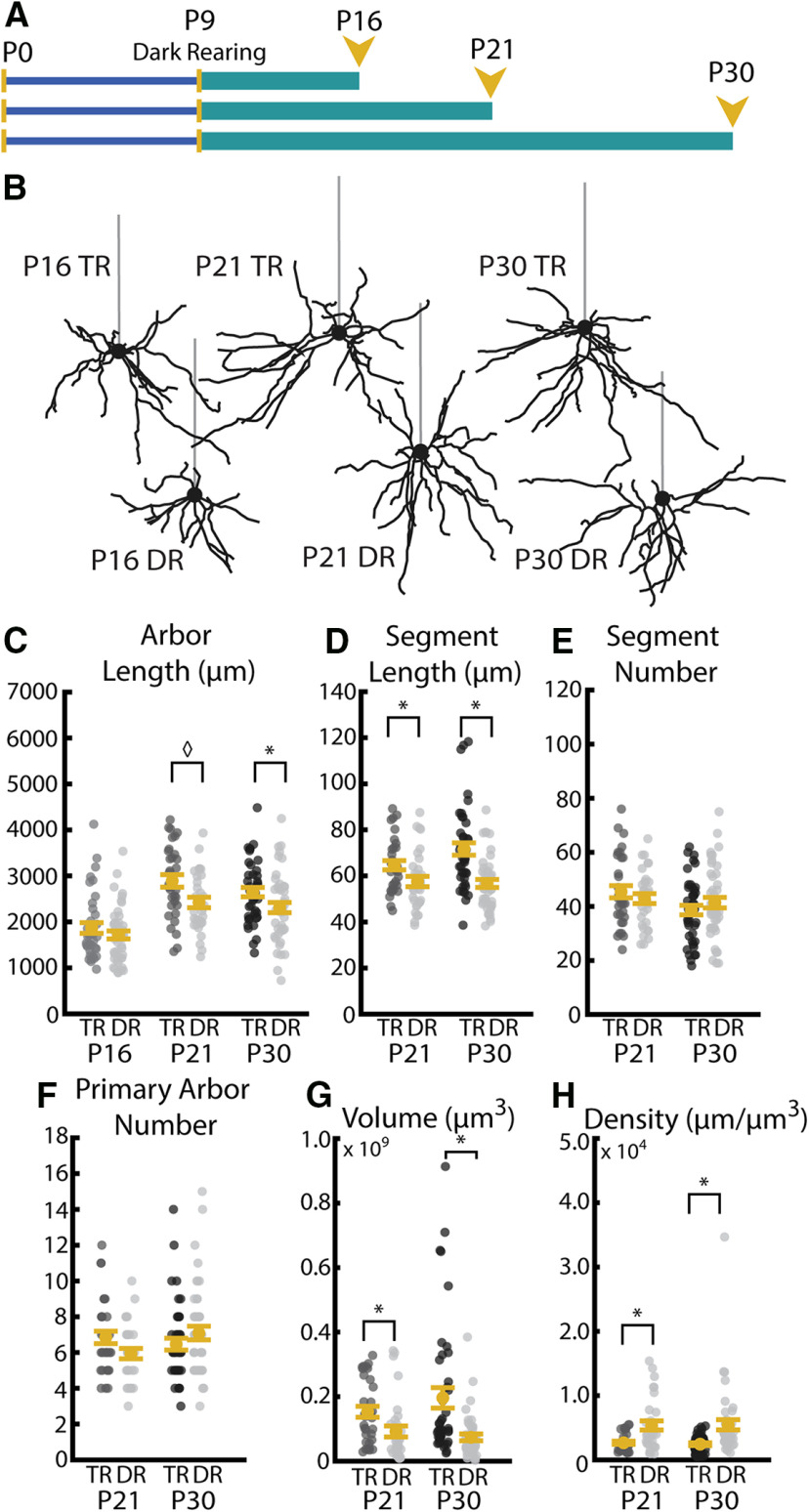
Figure 7.

Visual experience during the critical period promotes increases in segment length leading to typical arbor development. A, Timeline of DR experiments. All mice were DR starting at P9 and DR (indicated by teal bar) continued until death at P16, P21, or P30. B, Example reconstructions of TR (12 h light/12 h dark) and DR (24 h dark) neurons at P16, P21, and P30. Straight gray lines diagram the unreconstructed apical dendrite to indicate the orientation of cells. C, Total arbor length with (TR) and without (DR) visual experience at P16, P21, and P30. D, Segment length at P21 in neurons sampled from mice with and without visual experience at ages P21 and P30. E, Segment number at P21 and P30 in neurons sampled from mice with and without visual experience. F, Primary arbor number sampled at P21 and P30 with and without visual experience. G, Arbor volume sampled at P21 and P30 with and without visual experience. H, Arbor density sampled at P21 and P30 with and without visual experience. Error bars indicate mean ± SEM. Yellow dots indicate means. Gray dots indicate single neurons. For all measurements: P16 TR: N = 38 cells, 4 mice; P16 DR: N = 46 cells, 4 mice; P21 TR: N = 33 cells, 3 mice; P21 DR: N = 32 cells, 4 mice; P30 TR: N = 43 cells, 4 mice; P30 DR: N = 45 cells, 4 mice *p < 0.016; ◊p = 0.017; Welch's t test, Bonferroni-corrected α = 0.016.

Figure 8.

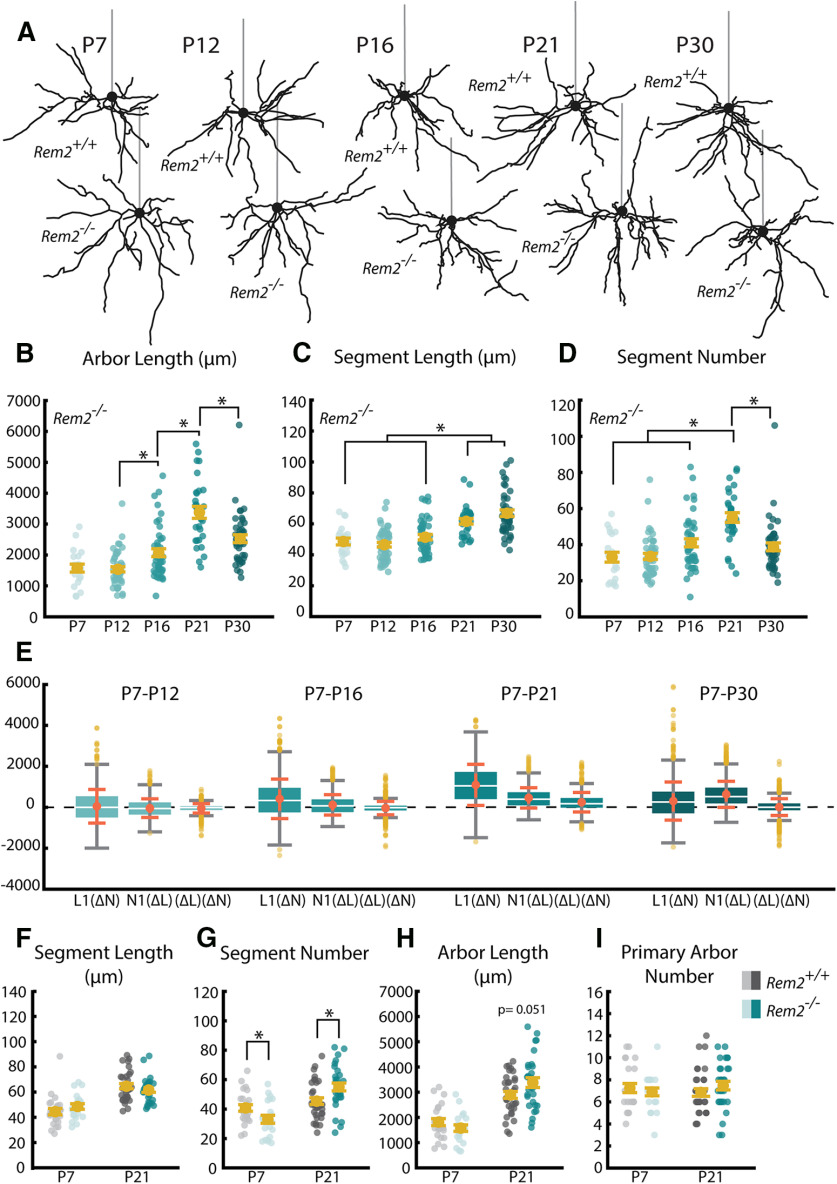
Rem2 regulates the development of basal dendritic arbors. A, Example reconstructions of TR (12 h light/12 h dark) WT (Rem2^+/+) and Rem2 KO (Rem2^−/−) neurons at ages P7, P12, P16, P21, and P30. Straight gray lines diagram the unreconstructed apical dendrite to indicate the orientation of cells. B, Total arbor length of the basal arbor in Rem2^−/− neurons at P7, P12, P16, P21, and P30. C, Average length of dendritic segments of Rem2^−/− neurons sampled at P7, P12, P16, P21, and P30. D, Segment number of Rem2^−/− neurons sampled at P7, P12, P16, P21, and P30. E, Number of dendritic primary arbors of basal dendrites across development. Yellow dots indicate flyers. F, Average segment length at ages P7 and P21 sampled from Rem2^+/+ and Rem2^−/− neurons. G, Segment number at ages P7 and P21 sampled from Rem2^+/+ and Rem2^−/− neurons. H, Total arbor length at ages P7 and P21 from Rem2^+/+ and Rem2^−/− neurons. I, Primary arbor number at ages P7 and P21 from Rem2^+/+ and Rem2^−/− neurons. Error bars indicate mean ± SEM. Yellow dots indicate mean. Teal dots (Rem2^−/−) and gray dots (Rem2^+/+) indicate single neurons. For all Rem2^−/− measurements: P7 TR: N = 21 cells, 2 mice; P12 TR: N = 47 cells, 4 mice; P16 TR: N = 44 cells, 4 mice; P21 TR: N = 30 cells, 3 mice; P30 TR: N = 43 cells, 4 mice. For all Rem2^+/+ measurements: P7 TR: N = 24 cells, 2 mice; P21 TR: N = 33 cells, 3 mice. B–D, *p < 0.05 (one-way ANOVA with post hoc Tukey test). F–I, *p < 0.025 (Welch's t test, Bonferroni-corrected α = 0.025).

Figure 9.

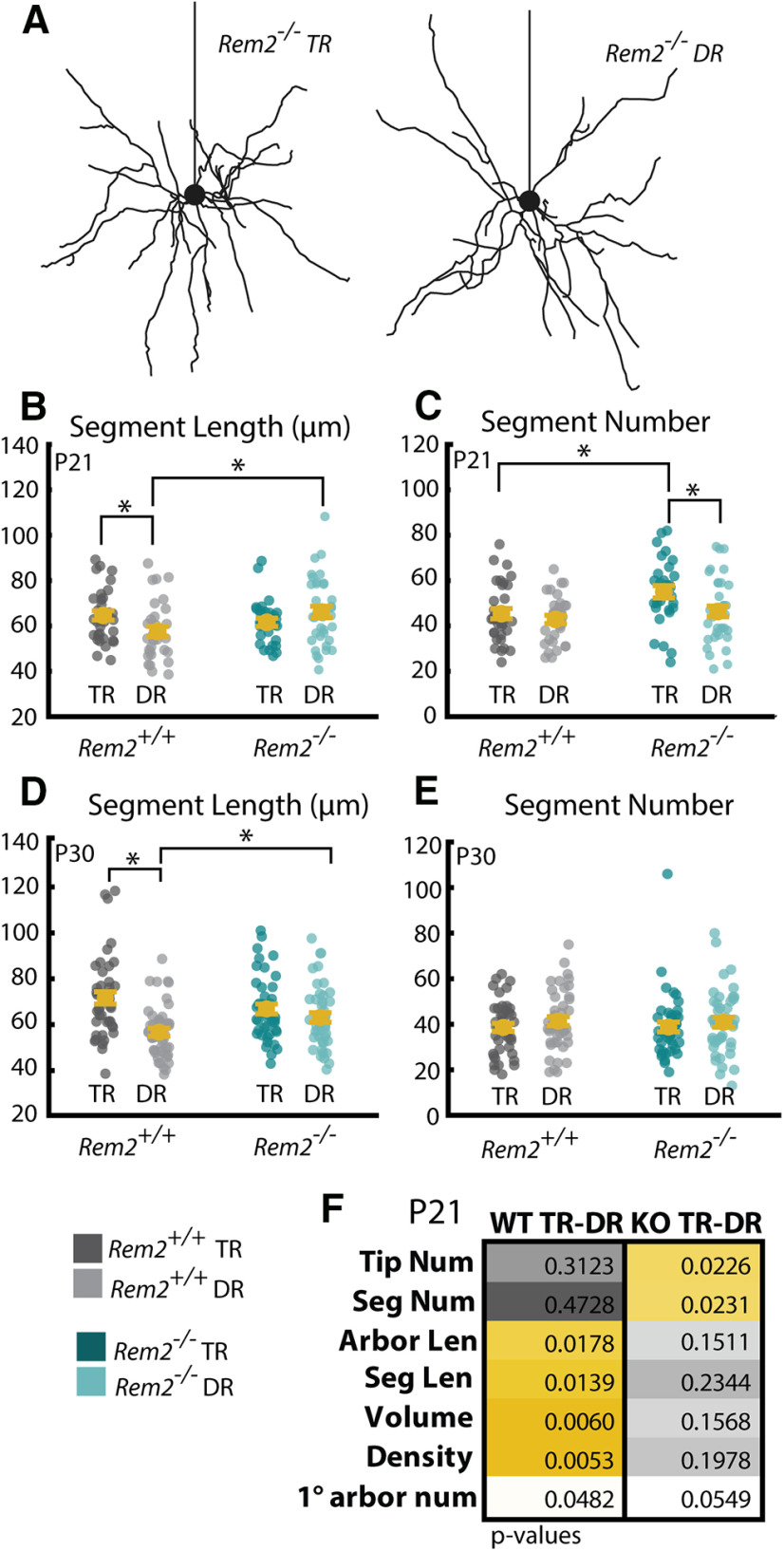
Rem2 regulates segment number in an experience-dependent manner. A, Example Rem2^−/− neurons with (left) and without (right) visual experience. B, Average segment length of Rem2^+/+ and Rem2^−/− neurons exposed either to TR conditions or DR from before eye opening and sampled at P21. C, Number of dendritic segments of Rem2^+/+ and Rem2^−/− neurons exposed to either TR conditions or DR from before eye opening sampled at P21. D, Average segment length of Rem2^+/+ and Rem2^−/− neurons exposed either to TR conditions or DR from before eye opening and sampled at P30. E, Number of dendritic segments of Rem2^+/+ and Rem2^−/− neurons exposed to either TR conditions or DR from before eye opening sampled at P30. F, Summary of p values from all comparisons when Rem2^+/+ and Rem2^−/− are exposed to DR from before eye opening until P21. Yellow boxes represent significant results after multiple comparisons correction. Error bars indicate mean ± SEM. Yellow dots indicate means. Teal dots (Rem2^−/−) and gray dots (Rem2^+/+) indicate single neurons. For all Rem2^−/− measurements: P7 TR: N = 21 cells, 2 mice; P12 TR: N = 47 cells, 4 mice; P16 TR: N = 44 cells, 4 mice; P21 TR: N = 30 cells, 3 mice; P30 TR: N = 43 cells, 4 mice; P21 DR: N = 36 cells, 4 mice. For all Rem2^+/+ measurements: P7 TR: N = 24 cells, 2 mice; P21 TR: N = 33 cells, 3 mice; P21 DR: N = 32 cells, 4 mice. *p < 0.05 (two-way ANOVA with post hoc Tukey test). Table 4 provides the means ± SEM and p values for post hoc Tukey tests relating to this figure.

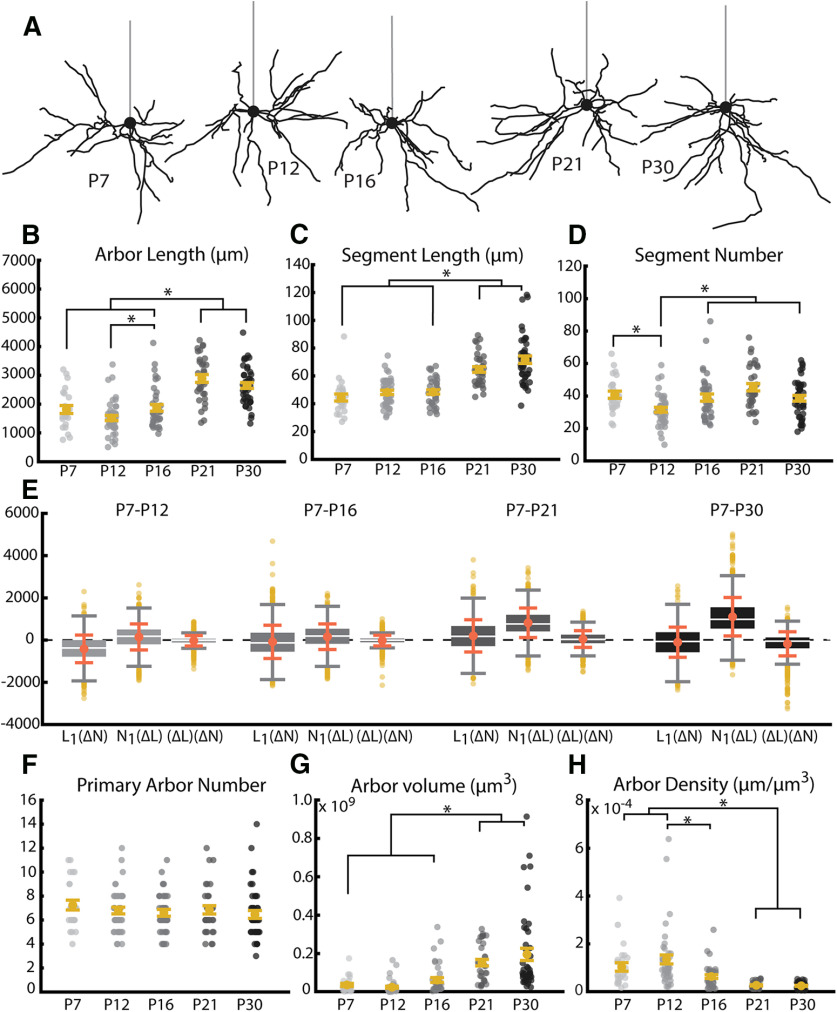
Figure 4.

Length and volume of WT arbors undergo significant growth near the opening of the visual critical period coincident with an increase in the length of dendritic branches. A, Example reconstructions of basal arbors from L2/3 WT visual cortex neurons at the five ages sampled. Straight gray lines diagram the unreconstructed apical dendrite to indicate the orientation of cells. B, Total arbor length of the basal arbor across development. Light to dark gray dots indicate individual neurons. C, Segment length of basal dendrites across development. Segment length for each neuron is an average of all path lengths sampled from that cell. Light to dark gray dots indicate individual neurons. D, Segment number of basal dendrites across development. Light to dark gray dots indicate individual neurons. E, Analysis of relative contribution of changes in segment number (L₁(ΔN)), segment length (N₁(ΔL)), or the combination of these factors ((ΔL)(ΔN)). Boxes represent 25th-75th percentile of the data. White line indicates median. Coral dot and error bars indicate mean ± SE. F, Number of dendritic trees (number of primary neurites) of basal dendrites across development. Yellow dots indicate flyers. G, Three-dimensional volume of convex hull fit to nodes composing basal arbor across development. H, Density of the basal arbor across development. Calculated as microns of dendritic material per cubic micron of arbor volume. Error bars indicate mean ± SEM. Yellow dots indicate the mean. Gray dots indicate single neurons. For all measurements: P7: N = 24 cells, 2 mice; P12: N = 43 cells, 4 mice; P16: N = 38 cells, 4 mice; P21: N = 33 cells, 3 mice; P30: N = 43 cells, 4 mice. *p < 0.05 (one-way ANOVA with post hoc Tukey test).

Golgi-Cox labeling and tissue preparation

We collected brains from typically-reared (TR) and dark-reared (DR) littermate mice of two genotypes, WT (Rem2^+/+) and Rem2 KO (Rem2^−/−), for our Golgi-Cox experiments. TR WT and Rem2^−/− littermate mice of either sex were housed in a 12 h light/12 h dark cycle from birth until the specified age (P7, P12, P16, P21, P30). DR mice (both WT and Rem2^−/− littermates) were placed in a light-tight box beginning at P9 until termination of the experiment (P16, P21, or P30). At the specified age, mice were anesthetized with ketamine/xylazine cocktail (ketamine 100 mg/kg, xylazine 10 mg/kg) and transcardially perfused with 0.9% saline in ddH₂O. DR mice were anesthetized in the dark and then shielded from light until after perfusion using a mask constructed of several layers of light blocking tape (Thor Labs) to cover the eyes. Immediately following perfusion, brains were weighed and submerged in Golgi-Cox solution (FD NeuroTechnologies). Throughout all steps involving Golgi-Cox, brains were protected from light. Golgi-Cox solution was changed 24 h after initial immersion, and brains continued to be stored in Golgi-Cox solution for 7 d. After 7 d, brains were transferred to Solution C (FD NeuroTechnologies) for at least 2 d. Coronal sections were cut at 150 µm using a cryostat and immediately mounted on slides coated with 2% porcine gelatin. Histology was conducted according to the protocol supplied by FD NeuroTechnologies RapidGolgi Stain Kit. Briefly, slides were washed with ddH₂O, developed using FD Neurotechnologies Solutions D and E, rinsed in ddH₂O, dehydrated with a graded series of ethanols, and cleared using xylenes. Slides were then coverslipped using Permount (Thermo Fisher Scientific).

TdTomato reporter tissue preparation

TR Rem2^+/+;TdT^flex/flex and Rem2^flx/flx;TdT^flex/flex mice of either sex were housed in 12 h light/12 h dark cycle from birth until the specified ages and dpi (5 dpi/P25, 7 dpi/P27, 10 dpi/P30) (for more detailed information, see Table 2 and figure legends). Mice (both Rem2^+/+;TdT^flex/flex and Rem2^flx/flx;TdT^flex/flex) were injected with AAV.GFP-Cre at P20 (see detailed method below) to activate reporter expression and, in Rem2^flx/flx;TdT^flex/flex mice, manipulate Rem2 expression. At the specified age, mice were anesthetized with ketamine/xylazine cocktail (ketamine 100 mg/kg, xylazine 10 mg/kg) and transcardially perfused with 0.1 m PBS followed by 10% formalin in PBS. Immediately following perfusion, brains were extracted and transferred to 10% formalin for 24 h at 4°C. Brains were then transferred to 30% sucrose in PBS for at least 2 d before sectioning in the coronal plane at 200 µm on a freezing microtome. Sections were immediately mounted on SuperFrost Plus (Thermo Fisher Scientific) slides, allowed to dry until adhered to slides, covered with Fluoromount G (Diagnostic BioSystems), and left to dry overnight. Slides were sealed with clear nail polish (Electron Microscopy Sciences). During all steps, the brains and brain sections were shielded from light whenever possible. Neurons were visualized using the genetically encoded TdTomato fluorophore, and no additional staining of any kind was performed.

Table 2.

Animal information for acute Rem2 KO experiments

Mouse	dpi	Sex	Genotype	Virus	Weight at injection (g)
SR-RFLXTdT-065	3	F	FLX	AAV-GFP Cre	10.1
SR-RFLXTdT-067	3	F	WT	AAV-GFP Cre	8.6
RFLXTdT-297	3	M	WT	AAV-GFP Cre	8.5
RFLXTdT-276	5	F	FLX	AAV-GFP Cre	7.6
RFLXTdT-278	5	M	WT	AAV-GFP Cre	8.5
SR-RFLXTdT-025	5	M	WT	AAV-GFP Cre	7.1
SR-RFLXTdT-044	5	M	WT	AAV-GFP Cre	8.9
SR-RFLXTdT-047	5	F	FLX	AAV-GFP Cre	8.7
SR-RFLXTdT-130	5	M	WT	AAV-GFP Cre	9.6
SR-RFLXTdT-131	5	M	FLX	AAV-GFP Cre	8.9
SR-RFLXTdT-170	5	M	FLX	AAV-GFP Cre	10.5
SR-RFLXTdT-172	5	M	WT	AAV-GFP Cre	9.9
RFLXTdT-269	7	F	FLX	AAV-GFP Cre	11.7
RFLXTdT-270	7	F	WT	AAV-GFP Cre	9.2
RFLXTdT-271	7	F	FLX	AAV-GFP Cre	10.2
RFLXTdT-277	7	F	FLX	AAV-GFP Cre	9
RFLXTdT-279	7	M	WT	AAV-GFP Cre	9.7
SR-RFLXTdT-027	7	M	FLX	AAV-GFP Cre	5.1
SR-RFLXTdT-054	7	M	FLX	AAV-GFP Cre	10.2
SR-RFLXTdT-056	7	M	WT	AAV-GFP Cre	10.9
SR-RFLXTdT-133	7	F	FLX	AAV-GFP Cre	9.8
SR-RFLXTdT-135	7	F	WT	AAV-GFP Cre	9.1
SR-RFLXTdT-321	7	M	FLX	AAV-GFP Cre	10.9
SR-RFLXTdT-323	7	M	WT	AAV-GFP Cre	10
SR-RFLXTdT-036	9	F	FLX	AAV-GFP Cre	9.6
SR-RFLXTdT-039	9	M	WT	AAV-GFP Cre	9.6
SR-RFLXTdT-040	9	M	WT	AAV-GFP Cre	10.9
SR-RFLXTdT-051	9	M	WT	AAV-GFP Cre	10.6
SR-RFLXTdT-052	9	M	FLX	AAV-GFP Cre	10.5
SR-RFLXTdT-111	9	M	FLX	AAV-GFP Cre	9.5
SR-RFLXTdT-115	9	M	WT	AAV-GFP Cre	8.9
SR-RFLXTdT-136	9	F	WT	AAV-GFP Cre	7.9
RFLXTdT-131	11	M	FLX	AAV-GFP Cre	8.9
RFLXTdT-132	11	M	WT	AAV-GFP Cre	8.4
RFLXTdT-137	11	F	WT	AAV-GFP Cre	6.5
RFLXTdT-151	12	M	FLX	AAV-GFP Cre	8
RFLXTdT-154	12	F	WT	AAV-GFP Cre	7.8
RFLXTdT-156	12	F	WT	AAV-GFP Cre	7.8
RFLXTdT-255	11	M	FLX	AAV-GFP Cre	8.8
RFLXTdT-256	11	F	WT	AAV-GFP Cre	9.4

Virus injections

The AAV-GFP-Cre (AAV1.hSyn.HI.eGFP-Cre.WPRE.SV40; AV-1-PV1848) construct was obtained from the Vector Core facility at the University of Pennsylvania. Mice age P20 were anesthetized with a cocktail of ketamine (100 mg/kg) and xylazine (10 mg/kg), mounted on a stereotaxic frame, shaved, and the head was scrubbed using alternating washes of betadine and 70% ETOH. A single midline incision was performed, and underlying tissues scraped to expose the skull. Primary visual cortex was targeted by using the mouse brain atlas after adjusting for the λ-bregma distance for age. In our hands, coordinates were ∼3.5 mm lateral from the midline and 1.2 mm anterior to λ. A small 1-2 mm in diameter hole was drilled in the skull and a glass micropipette delivered 50 nL adeno-associated virus (AAV, diluted 1:250 in 0.9% sterile bacteriostatic saline) 150 μm below the dural surface. The incision was sutured, and triple antibiotic ointment was applied topically. Mice recovered on a heating pad and were returned to the animal facility until use.

Neuron selection and imaging

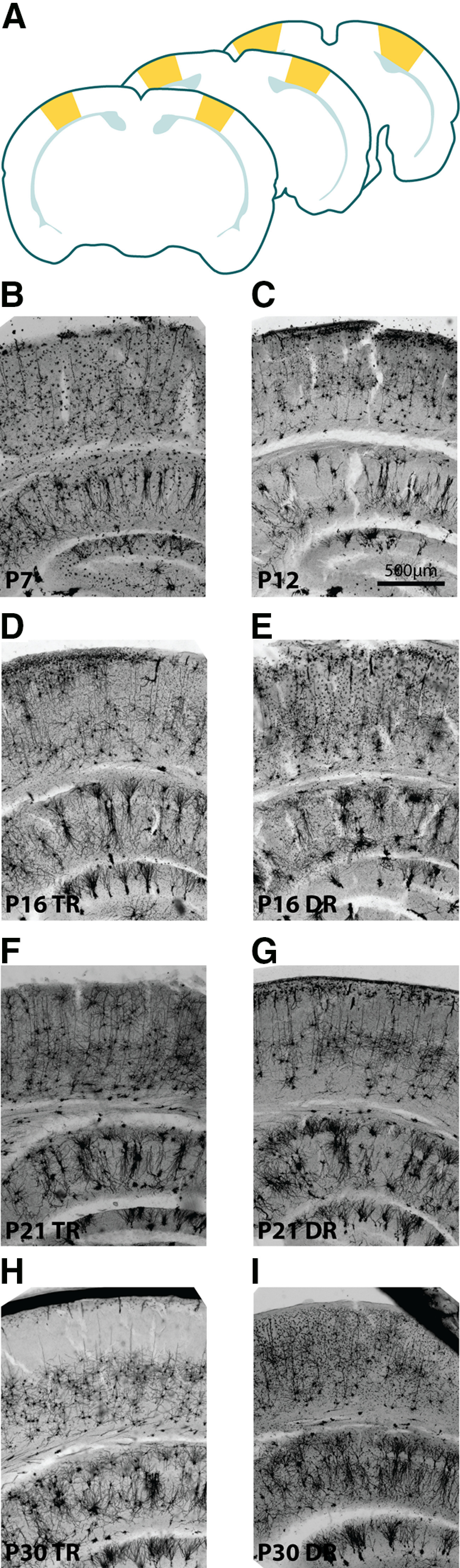
Primary visual cortex was identified using landmarks, primarily the morphology of the hippocampus and corpus callosum, as depicted in the coronal Allen Reference Atlas (http://mouse.brain-map.org/static/atlas) and as indicated in Figure 2A. Pyramidal neurons were selected from layer 2/3 of primary visual cortex for reconstruction and analysis. Pyramidal neurons were identified by characteristic soma shape and the presence of a distinct apical dendrite oriented toward the cortical surface. Neurons selected for reconstruction met several criteria: the entire basal arbor was present in one tissue section, there was not extensive overlap with arbors of neighboring cells, Golgi staining or fluorescent fill was dense and complete in all processes, dendritic branches were not broken or truncated, artifact in the surrounding neuropil was minimal and allowed for unambiguous reconstruction. If it was not possible to differentiate branches of the target cell's arbor from that of neighboring cells using separation in the z axis or morphologic characteristics, such as large differences in dendrite diameter, the cell was excluded from reconstruction. Gross differences in cortical layers or thickness were not observed among any conditions (see Fig. 2B-I).

Figure 2.

Identification and gross morphology of primary visual cortex. A, Diagram adapted from the Allen Mouse Brain Reference Atlas showing the anterior-most plane of primary visual cortex (V1, front), the approximate middle of the anterior-posterior extent of V1 (middle), and the posterior-most plane of V1 able to be reliable used for reconstruction (back). Yellow shape represents V1. Light teal represents the corpus callosum. B, View of part of the P7 primary visual cortex at 4× magnification C, View of part of the P12 primary visual cortex at 4× magnification. Scale bar applies to all images. D, E, View of part of the P16 visual cortex from TR (D) and DR (E) mice at 4× magnification. F, G, View of part of the P21 visual cortex from TR (F) and DR (G) mice at 4× magnification. H, I, View of part of the P30 visual cortex from TR (H) and DR (I) mice at 4× magnification.

A z stack of images with a 2 µm step was captured of the entire basal arbor of each neuron using a 20× air objective. All Golgi-stained neurons were imaged using an AxioObserver microscope (Carl Zeiss) under bright-field illumination. Neurons expressing the TdTomato reporter construct were imaged using either a Nikon Eclipse Ti3 microscope or an 880 LSM (Carl Zeiss). For determining the mediolateral orientation of TdTomato-expressing neurons, additional low-magnification images were captured with a 4× or 10× air objective using either an 880 LSM (Carl Zeiss) or a BZX-700 microscope (Keyence).

Reconstruction of neurons

All neurons were reconstructed using Knossos, a free annotation program developed by the Max Planck Institute for Medical Research (https://knossos.app/). Images were prepared for reconstruction by unstacking each z stack and converting to 8 bit tif files using a custom Fiji macro to be compatible with Knossos. Images were then converted to a Knossos-compatible format (called “cubing”) using Python code distributed by the creators of Knossos.

Neurons were reconstructed by manually placing sequential nodes in the center of the width of each dendritic branch along the entire basal arbor. Neurons were reconstructed in 3 dimensions by scanning through the depth of the z stack and placing nodes where each segment of dendrite was in focus. Care was taken to conform to the curvature of dendritic branches by increasing node density in highly tortuous regions. All dendritic primary arbors were connected to a central, spherical node at the soma that was sized to match the diameter at the widest point of the soma (used as calculation of soma size as approximated as a sphere).

Analysis of reconstructions

Neuronal morphology was analyzed using a suite of custom Python code created for this project. The analysis code relies on identities and 3D coordinates of each node and associated auto-generated edges to calculate a variety of parameters about whole dendritic arbors as well as individual primary arbors. Detailed explanations of each analysis are found in Table 3. All code is available on the Van Hooser Lab GitHub repository (http://github.com/VH-Lab/) in the SRNeuronAnalysis project folder (for more detailed analysis for complex measures, see below). Additional measures not used in this publication are described in detail in the README included in the Python project for these analyses.

Table 3.

Arbor analyses^a

Parameter	Units	Function name	Description
Segment length	µm (real)	segment_length	Length of each segment between branch points
Segment number	NA (int)	segment_number	Number of segments between branch points
Arbor length	µm (real)	arbor_length	∑(segment lengths)
Tip number	NA (int)	tip_number	Number of terminal dendritic branches
Path length	µm (real)	path_length	Length from soma to tip of dendrite
Tortuosity	NA (real)	tortuosity	$\frac{PathLength}{Euclidiandistance}$
Soma diameter	µm (real)	soma_size	Diameter of sphere fit to soma at widest point
Primary arbor number	NA (int)	primary_arbor_number	Number of neurites emerging directly from soma
Arbor volume	µm3 (int)	volume	3D volume of convex hull fit to all arbor nodes
Arbor density	µm/ µm3 (real)	density	$\frac{ArborLength}{Volume}$
Arbor directionality and orientation	NA (real)	directionality	${\theta }_r=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}(X,Y)r=\sqrt{X^2+Y^2}$
(X, Z) directionality and orientation	NA (real)	xz_directionality	Same as directionality using (X, Z) coordinates
Radial Sholl	NA (real)	radial_sholl	Number of paths within angle θ from the apical dendrite around the arbor in 30° step
Sholl analysis	NA (real)	sholl	Number of segments X distance from soma (20 μm increments reported, customizable)
Relative contribution	NA (real)	relative_contribution	ΔA = ΔL(NT1) + ΔN(LT1) + (ΔL)(ΔN) Where A = arbor length, N = segment number, L = mean segment length, and T1= P7

^aList of each parameter name, unit of measure, function name in custom analysis package, and plain language description of measurement.

Arbor length changes over time (ΔA) because of changes in the number of branches (ΔN), changes in the length of existing branches (ΔL), and the combined contribution of these factors (see Figs. 4E, and 8E). We computed the fractional contribution of each of these components between each pair of neurons in each group (e.g., all P7 neurons compared with all P12 neurons, and so on) as below, where N₁ and L₁ indicate the initial time point and N₂ and L₂ indicate a subsequent time point (e.g., to measure developmental change from P7 to P12, P7 is the initial state and P12 is state 2) as follows:

A value of 0 for any measure indicates no change in arbor length results from that measure. Positive values indicate that changes in a given measure contributed to increased arbor length were as negative values indicate that changes in a given measure lead to decreased total arbor length.

To calculate basal arbor orientation and directionality, neuronal reconstructions were rotated to align the axis of the apical dendrite to 0°. Because neurons were reconstructed from both hemispheres, some reconstructions were reflected across the y axis so that the lateral side of each arbor was at 90° and the medial side at 270°. The tip node of each path was used to create vector between the path tip and the soma node with length of 1 unit and the angle (a) between each path vector (path) and the apical vector (apical) was used for calculation of the mean vector of path angles. The degree of orientation or directionality is indicated by the length of the mean vector (r), which ranges from 0 to 1. The vectorized arbors were also used to calculate Radial Sholl and Apical Cone Measures (Table 3).

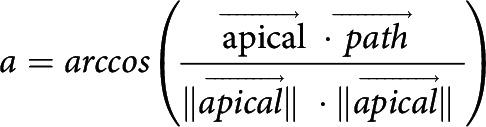Significant orientation and directionality were determined by calculating the Raleigh z statistic and comparing this value to the critical value for significant directionality for each arbor where n is the number of paths and r is the mean vector.

Results

Quantification of arbors

In order to quantify the development of basal dendritic arbors in mouse visual cortex, we developed a reconstruction and analysis pipeline consisting of freely available reconstruction software (Knossos, Max Planck Institute, Heidelberg) and a library of custom analyses written in Python. Figure 1 describes the majority of the analyses as performed on an example cell (Fig. 1A). Our analyses can best be grouped into arbor-centric (Fig. 1B-E,H) and tissue-centric (Fig. 1F,G,I) measures. Arbor-centric measures focus on characterizing each arbor in terms of its size (Fig. 1C), number of components (Fig. 1D,E), and measurements of individual components (Fig. 1B,H). In contrast, tissue-centric measures characterize how the arbor is arranged with respect to the entire tissue, such as the volume the arbor occupies in the cortex (Fig. 1G) or how the dendrites are arranged in the space around the soma (Fig. 1F). Both types of measures consider the arbor as 3D when relevant, such as when calculating length-based parameters.

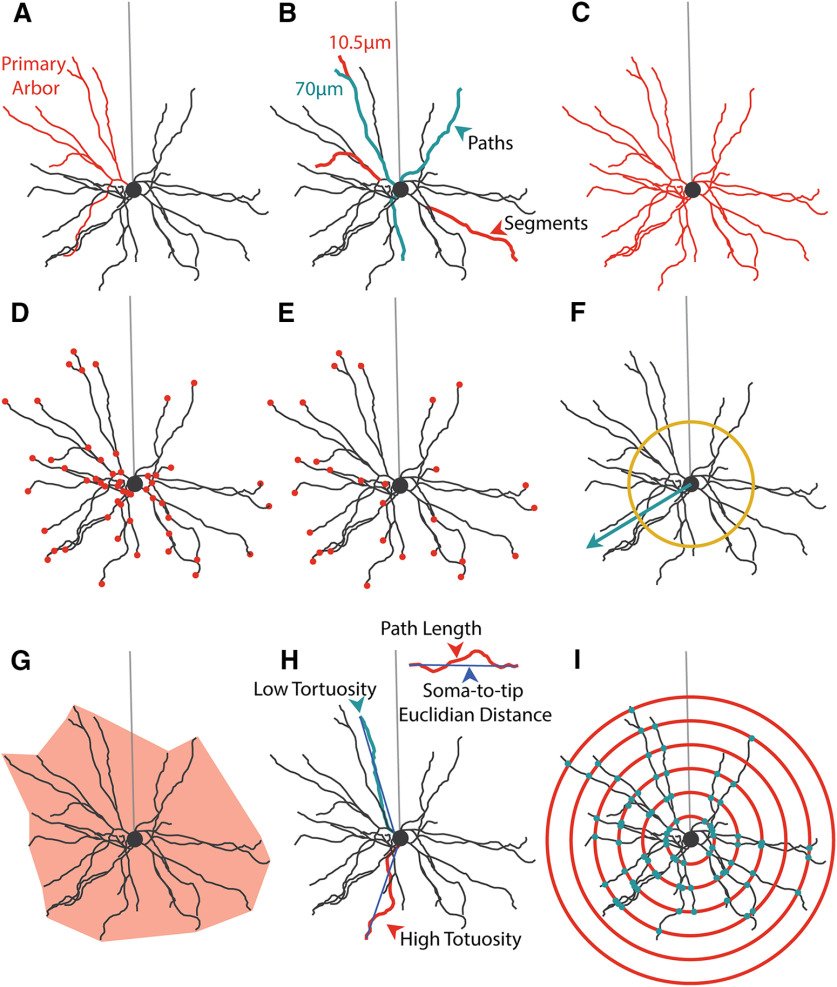
Figure 1.

Analysis of basal dendrite morphology. A, Example hand-reconstructed L2/3 WT pyramidal neuron sampled from mouse primary visual cortex. Coral represents one primary arbor. Light gray represents position of unreconstructed apical dendrite. Soma is diagrammed as a circle. B, Segment (coral) and path (teal) diagram. Segments are the smallest span of dendrite between two branch points. Paths are the length of dendrite that connects branch tips to somas. Paths are composed of one or more segments. C, Total arbor length diagram. Total arbor length is the summed length of all segments, measuring the total length of the arbor in microns. D, Segment number diagram. Each dot (coral) indicates one branch point in the arbor. E, Tip number diagram. Each dot (coral) indicates the terminal tip of a path. This is equivalent to the number of paths. F, Arbor polarity diagram. Arbor polarity is calculated in several ways, including analysis of dendritic material (number and length of segments and paths) on each side of the soma and in terms of absolute arbor directionality calculated as mean vector length (teal arrow) and tested using the Raleigh test. Mean vectors with length greater than yellow ring indicate significant directionality of the arbor. G, Arbor volume diagram. Arbor volume is the 3D volume of a least-size polygon fitted to all points in the basal arbor (light coral). Arbor density is the total arbor length divided by the arbor volume. H, Tortuosity diagram. Tortuosity is the path length for an individual path divided by the soma-to-tip Euclidian distance. I, Sholl analysis diagram. Sholl analysis counts the number of segments (teal dots) at several evenly spaced distances from the soma (coral circles) to measure the relationship between distance from the soma and arbor complexity.

Measures also differ in whether the unit of dendritic length is the dendritic segment or the dendritic path. Dendritic segments (Fig. 1B) are the smallest units of dendritic material and are defined as the length of dendrite spanning two branch points, between the edge of the soma and a first branch point, or between a branch point and a tip. Dendritic paths (Fig. 1B), in contrast, are the summed length of dendrite between the edge of the soma and the branch tip (Fig. 1E). A dendritic path can be conceptualized as the distance a synaptic current originating at the branch tip (Fig. 1E) would have to travel to reach the soma. Given this definition, dendritic paths are typically an assembly of several dendritic segments, except in the case of an unbranched segment which is considered to be a dendritic segment, path, and primary arbor. Primary arbors (Fig. 1A) are the largest subassembly of the arbor and are defined as a primary neurite emerging from the soma and all subsequent dendritic segments arising from that primary neurite.

Setup and initial characterization

Previous studies have quantified dendritic arbor development in mouse primary visual cortex using very sparse sampling during development or have analyzed dendritic arbors at times that are well past the relevant epochs of circuit plasticity, such as the extensively characterized critical period for ocular dominance plasticity (Miller, 1981; Juraska, 1982). We set out to densely sample arbor development in primary visual cortex (Fig. 2A) by assessing arbor complexity approximately every 5 postnatal days (Fig. 3A) starting before eye opening (postnatal day 7 [P7]), at eye opening (P12), and during the first few days of visual experience (P16). We also made measurements near the opening of the critical period (P21) and during the peak of the critical period (P30). To visualize neurons, we performed Golgi-Cox histology and identified L2/3 pyramidal neurons based on canonical morphologic features of pyramidal neurons, including a triangular cell body and apical dendrite oriented toward the pial surface (Fig. 2B–I). All reconstructed neurons had complete basal dendritic arbors and were located in primary visual cortex (Fig. 3B). We then made manual reconstructions using Knossos (Max Planck Institute for Medical Research, Heidelberg) and analyzed them as described above (Fig. 1; Table 3).

In order to establish organizing principles of dendritic arbors, we performed analyses on the entire population of reconstructed neurons at a given age, in this case P30, both between animals (individuals animals are gray lines) and pooled across animals (black lines). We found that observed values of each measure show a unique amount of variability in terms of both total variation (Fig. 3D-H, black lines) and between-animal variation (Fig. 3D-H, gray lines). For example, we found a wide range of dendritic segment counts across the population as well as between animals (Fig. 3F). Conversely, we found that the length of these dendritic segments and paths is relatively less variable both on the whole and across animals (Fig. 3D,E). This suggests that, although the number of segments is quite variable, their length is fairly constant, which may suggest distinct regulatory mechanisms of these two characteristics. As might be expected, the length of whole arbors (Fig. 3G, sum of length of segments) is intermediately variable compared with the number and length of paths (Fig. 3D-F). Interestingly, some measures of arbor complexity, such as tortuosity (Figs. 1H, 3H), are extremely invariant both within and between animals. This may indicate strict maintenance of a set value either through precise regulation at the molecular level or unknown biophysical constraints that tightly restrict path tortuosity.

We observe that several neuron-centric parameters are highly correlated. As expected, the number of branch tips is almost directly proportional to the number of dendritic segments (Fig. 3I; R² = 0.99, p = 1.25 × 10⁻¹⁴⁶, α = 0.05), which led us to focus only on segment number for the remainder of this article. Similarly, the length of dendritic paths is very closely related to the length of segments (Fig. 3K; R² = 0.81, p = 1.01 × 10⁻⁴², α = 0.05). While these relationships may be expected, we also found novel correlations between measures. For example, we found that segment number is negatively correlated with segment length (Fig. 3J; R² = −0.23, p = 0.002, α = 0.05), suggesting that arbor length overall may have a set point and the architecture of the arbor develops to fit this loosely predetermined total length. Interestingly, we at times found no relationship between quantities that on first consideration may seem likely to be coregulated, such as the length of paths and their tortuosity (Fig. 3L; R² = 0.05, p = 0.53, α = 0.05). Together, these results suggest that some arbor parameters may be coregulated, while others may be regulated by isolated processes.

Development of WT arbors in TR conditions

In WT cells, the total length of the basal arbor tends to increase over time with some additional nuanced dynamics (Fig. 4A). Early in development, between P7 and P16, arbor length is relatively stable, with the exception of a small, but significant, increase in arbor length between P12 and P16 (Fig. 4B; p = 0.03, df = 4, α = 0.05). However, there is a large increase in total arbor length between P16 and P21 (p = 4 × 10⁻⁷, df = 4, α = 0.05), resulting in P21 arbors that are significantly larger than arbors at any of the three earlier time points (Fig. 4B; P7-P21 p < 1 × 10⁻⁵, P12-P21 p < 1 × 10⁻⁷, P16-P21 p = 4 × 10⁻⁷, df = 4, α = 0.05). When we observed arbors at P30, we saw no change from arbors at P21 (Fig. 4B; P7-P30 p < 2.24 × 10⁻⁵, P12-P30 p < 1 × 10⁻⁷, P16-P30 p = 9.4 × 10⁻⁶, P21-P30 p = 0.84, df = 4, α = 0.05), suggesting that total arbor length may have stabilized. This is supported by previous work indicating that arbors are stable from P30-P60 in rodent visual cortex (Miller, 1981; Juraska, 1982).

When considering how this increase in total arbor length could arise, three possible sources of new arbor are immediately evident: existing segments increase in length, new segments are added, or a combination of these two factors accounts for the added length. To differentiate among these possibilities, we quantified each factor. Similar to the total length of the arbor, we found that the mean length of individual segments undergoes a sharp increase between P16 and P21, resulting in an increase in the average segment lengths at P21 compared with all earlier time points (Fig. 4C; P7-P21 p < 1 × 10⁻⁷, P12-P21 p = 1 × 10⁻⁷, P16-P21 p = 4 × 10⁻⁷, df = 4, α = 0.05). No further increase is seen between P21 and P30, as was also observed with total arbor length (Fig. 4C; P7-P30 p < 1 × 10⁻⁷, P12-P30 p < 1 × 10⁻⁷, P16-P30 p < 1 × 10⁻⁷, P21-P30 p = 0.36, df = 4, α = 0.05).

However, a different pattern of developmental change emerged when we instead considered the number of segments that compose the arbor. During pre-critical period development, we observed small, dynamic changes in segment number characterized by an early reduction in mean segment number between P7 and P12 (p = 0.006, df = 4, α = 0.05) followed by an increase in mean segment number from P12 to P16 (Fig. 4D; p = 0.02, df = 4, α = 0.05). Segment number during the critical period (P21-P30) is similar to that observed at P7 or P16 and differs significantly only from P12 (Fig. 4D; P7-P21 p = 0.73, P12-P21 p = 4.6 × 10⁻⁶, P16-P21 p = 0.17, P7-P30 p = 0.91, P12-P30 p = 0.02, P16-P30 p = 0.99, df = 4, α = 0.05), highlighting the lack of a distinct transition point that we observed in both total arbor length and segment length. While there was a noticeable numerical decrease in mean segment number between P21 and P30, this difference did not reach the criterion for statistical significance (P21-P30 p = 0.13, df = 4, α = 0.05). Interestingly, the number of primary arbors did not change during postnatal development (Fig. 4F; P7-P12 p = 0.90, P7-P16 p = 0.72, P12-P16 p= 0.99, P7-P21 p = 0.93, P12-P21 p = 0.99, P16-P21 p = 0.99, P7-P30 p = 0.39, P12-P30 p = 0.83, P16-P30 p = 0.98, P21-P30 p = 0.84, df = 4, α = 0.05), which suggests that arbor-centric development occurs primarily through regulation of segments as opposed to the addition or removal of primary arbors.

To better understand whether the outgrowth of existing segments (Fig. 4C) or the addition of new segments (Fig. 4D) contributes more to arbor development, we computed the relative contribution of these factors (Fig. 4E), as well as their interaction, to the observed changes in total arbor length (Fig. 4B) between each pair of neurons at each age compared with our youngest age, P7 (Table 3). We found that changes in segment number impact the small change in arbor length most in the P7-P12 comparison, but that changes in segment length predominated at each subsequent age (Fig. 4E). This effect is most clearly demonstrated at the later time points we investigated (P7-P21 and P7-P30), at which point changes in segment number account for effectively no change in arbor length (Fig. 4E). Our results strongly suggest that overall arbor length arises predominantly through changes in the length of dendritic segments, with changes in segment number being a minor component primarily influencing early development.

In addition to developing characteristics within the arbor of a single cell, it is worth considering whether the “footprint” of the arbor within the larger tissue changes over time. To quantify this, we investigated both the volume that the arbor occupies within the tissue as well as the density of the arbor within that area. The volume, or 3D spread, of the arbor relates to the area over which the arbor can search for synaptic partners, whereas the density is related to the likelihood of a synapse occurring at any given point in that space.

As arbors grow and change, the “footprint” they occupy in the larger tissue may also be altered, impacting the availability of synaptic partners and the likelihood that a given axon will encounter the arbor if passing through a region of cortex. When we considered arbor volume (Fig. 4G), we observed that this feature corresponds to arbor length extremely well. Arbor volume undergoes a sharp transition between P16 and P21 (P7-P12 p = 0.52, P7-P16 p = 0.59, P12-P16 p = 0.005, P16-P21 p = 4 × 10⁻⁶, df = 4, α = 0.05) that is maintained through P30 (Fig. 4G; P7-P21 p < 1 × 10⁻⁷, P12-P21 p < 1 × 10⁻⁷, P16-P21 p = 4 × 10⁻⁶, P7-P30 p < 1 × 10⁻⁷, P12-P30 p < 1 × 10⁻⁷, P16-P30 p < 1 × 10⁻⁷, P21-P30 p = 0.96, df = 4, α = 0.05). Also notable is the remarkable increase in variability over development. In contrast, arbor density decreased over development (Fig. 4H; P7-P12 p = 0.84, P7-P16 p = 0.26, P12-P16 p = 0.005, P7-P21 p < 1 × 10⁻⁷, P12-P21 p < 1 × 10⁻⁷, P16-P21 p = 6.8 × 10⁻⁶, P7-P30 p < 1 × 10⁻⁷, P12-P30 p < 1 × 10⁻⁷, P16-P30 p < 1 × 10⁻⁷, P21-P30 p = 0.39, df = 4, α = 0.05), with the most striking decrease occurring at P21, similar to the timing of arbor volume development (Fig. 4G). This indicates that, although both arbor length and arbor volume are increasing, the 3D spread of the arbor outpaced the increase in arbor length, leading to decreased arbor density. Interestingly, the variability of arbor density starkly decreased throughout development, complementary to the variability increase seen in arbor volume (Fig. 4G,H). This indicates that mature arbors vary greatly in volume, perhaps indicating cell type-specific arbor volumes, but maintain very similar density across cells.

Basal arbors show distinct coronal and tangential orientation and directionality

The relative placement of dendritic paths in space dictates the ability of presynaptic partners to encounter postsynaptic cells. To this end, tiling of sensory tissues by dendritic processes is a fundamental organizing principle of sensory circuits, such as in the mammalian retina. Several known molecular regulators, such as DSCAMs (Fuerst et al., 2008, 2009; Zhang et al., 2012, 2015) and Semaphorins (Sun et al., 2013), contribute to the establishment of proper arbor shape, self-avoidance, and mosaic spacing in the mammalian retina. Although tiling has been hypothesized to be present in higher-order sensory areas, such as the visual cortex, a direct measurement of dendritic orientation or directionality has not been made in rodent systems and few molecular regulators have been identified (Zhang et al., 2012). Thus, we became interested in calculating basal arbor orientation and directionality and turned to circular statistics (Batschelet, 1981) commonly used to assess direction selectivity in visually responsive neurons. In short, cells were aligned along the axis of their apical dendrite and a mean vector angle and length was computed from the angular orientation of each normalized path vector. Normalized vector length (Fig. 5C) is expressed as a value ranging from 0 to 1, in which 0 indicates no directionality (or orientation) and 1 would indicate a perfectly directional (or oriented) arbor. This analysis is schematized for a directional (left) and nondirectional (right) cell in Figure 5A, in which the mean vector, also called direction vector, is indicated by a teal line and the Raleigh z test criterion is indicated by the yellow circle. This mean vector can be described in terms of both length (Fig. 5C) and angle (Fig. 5D), with the angle indicating the mean angle of all vectors with regard to the apical dendrite. An orientation vector (Fig. 5E) was also calculated for each arbor, high values of which would indicate symmetric clustering of paths on either side of the soma, for example, a high density of paths at both 90° and 270°. We calculated basal arbor directionality and orientation in two viewpoints: a coronal viewpoint (Fig. 5A–I) as would be achieved using a standard coronal sectioning technique and a tangential viewpoint (Fig. 6A–D) as would be achieved by looking down onto the cortical surface. We computed directionality in neurons sampled from WT mice between 23 and 30 d of age (P23–P30).

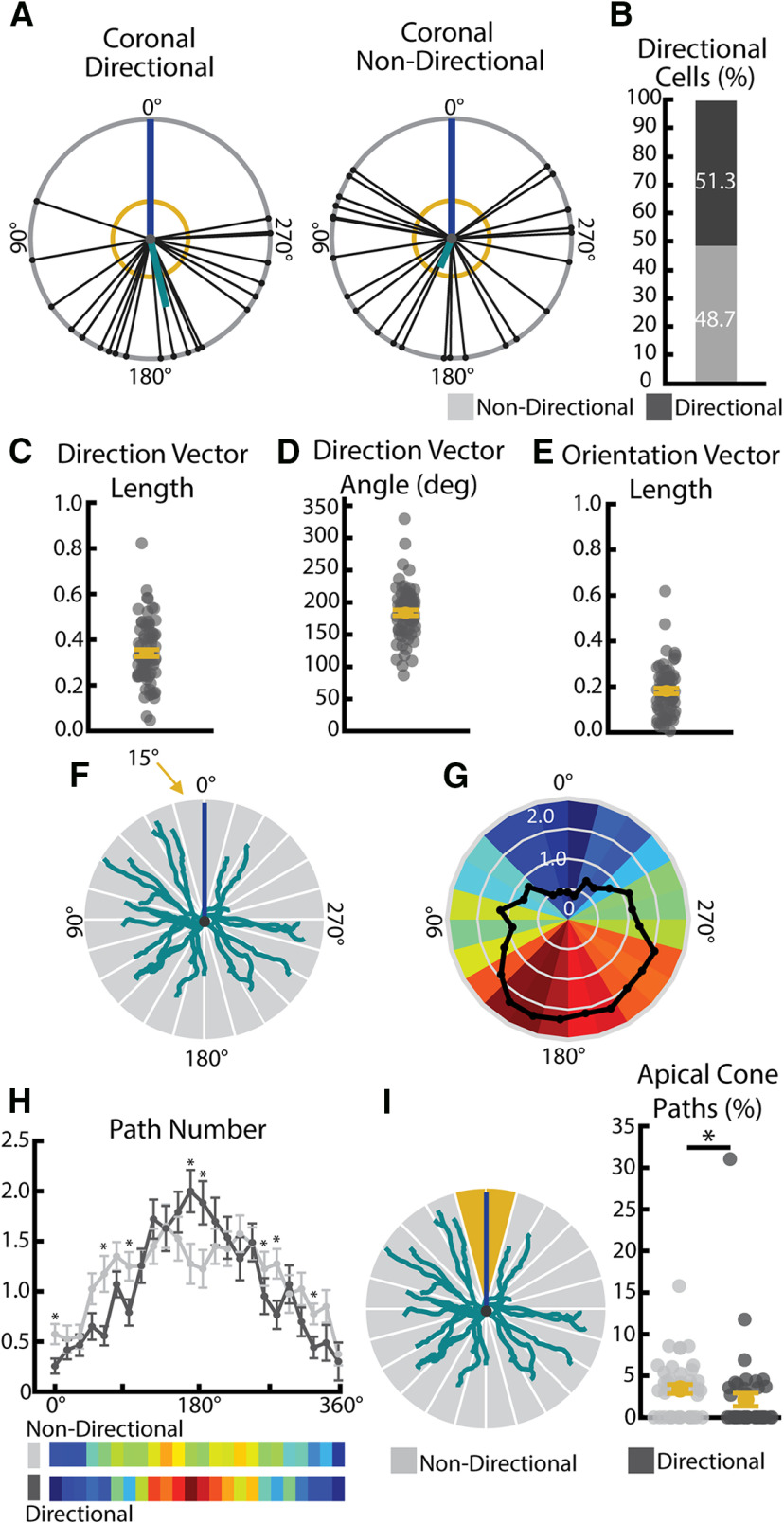
Figure 5.

Basal arbors show significant directionality in path location. A, Example directional (left) and nondirectional (right) basal arbors sampled from WT mice in the coronal viewpoint. Each arbor is schematized as soma (center dot) and soma-to-tip vectors (lines with dots at tip) arranged on a unit circle with apical dendrite diagrammed as a blue line. Thick teal line indicates the mean directional vector. Yellow circle represents length of mean directional vector required to declare the arbor directional by the Raleigh test. B, Pie chart showing portion of total WT population that are categorized as direction and nondirectional using the Raleigh test. C, Length of the coronal normalized directional vector calculated from all basal paths. Larger values indicate greater directionality. D, Angle of coronal directional vector calculated from all basal paths. E, Length of the coronal normalized orientation vector calculated from all basal paths. Larger values indicated greater orientation. F, Diagram of radial Sholl measure. Number of paths falling into each 15° increment (gray wedges) is calculated for each cell. Teal represents basal arbor. Blue represents apical dendrite position. G, Heat map indicating number of paths in each 15° bin for each cell (colorful wedges) from many (warm colors) to few (cool colors) and the mean (black line). H, Radial Sholl quantification in 15° bins (top) and represented as heat maps of mean bin values (bottom) for significantly directional (dark gray) and nondirectional (light gray) WT arbors. *p < 0.05 (Scheffé test). Error bars indicate mean ± SEM. I, Diagram of apical cone measurement (left). The number of paths falling in the 30° span around the apical dendrite (“apical cone,” yellow wedges) is calculated for each cell. Number of paths in the apical cone (right) in significantly directional (dark gray) and nondirectional (light gray) arbors. *p < 0.05 (Wilcoxon rank sum test). Error bars indicate mean ± SEM. Yellow dots indicate the mean.

Figure 6.

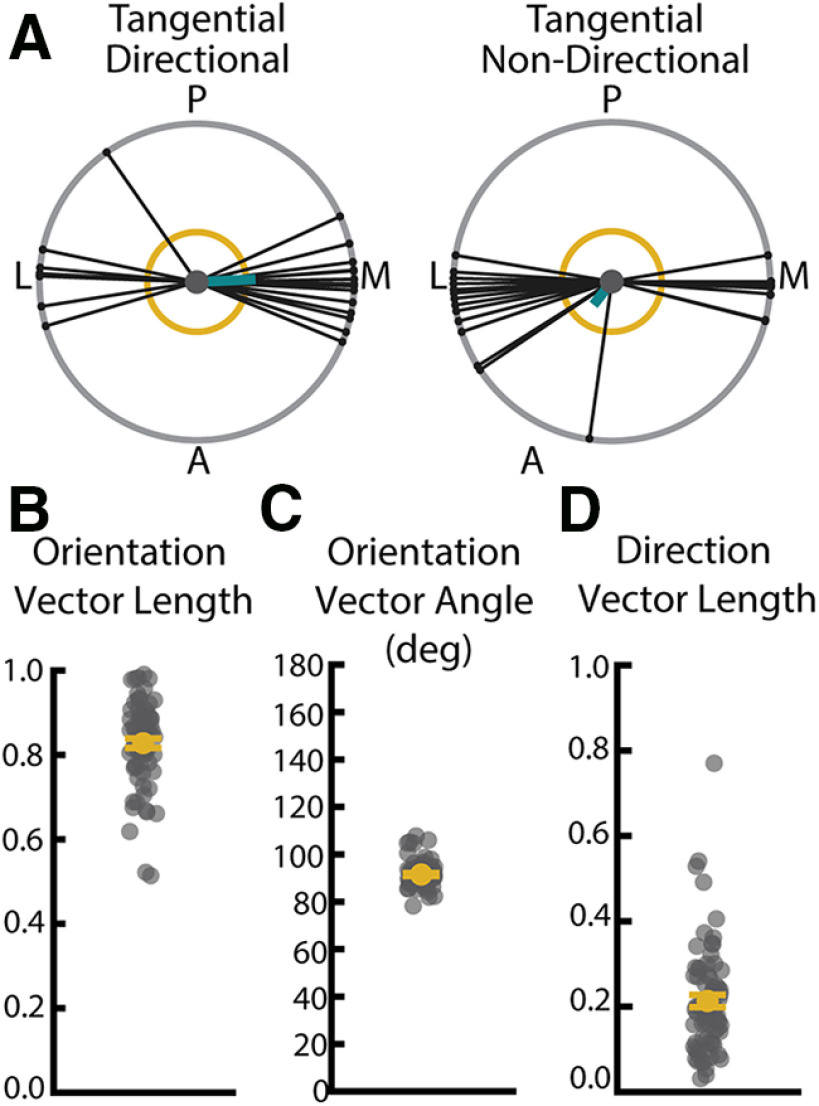
WT neurons have oriented arbors in the tangential plane. A, Example directional (left) and nondirectional (right) basal arbors sampled from WT mice in the tangential viewpoint. Each arbor is schematized as soma (center dot) and soma-to-tip vectors (lines with dots at tip) arranged on a unit circle. Thick teal line indicates the mean direction vector. Yellow circle represents length of mean direction vector required to declare the arbor directional by the Raleigh test. Posterior (P), anterior (A), medial (M), and lateral (L) are indicated around the diagrams. B, Length of the tangential normalized orientation vector calculated from all basal paths. Larger values indicate greater degree of orientation. C, Angle of tangential orientation vector calculated from all basal paths. D, Length of the tangential normalized direction vector calculated from all basal paths. Larger values indicated greater directionality. Error bars are mean ± SEM. Yellow dots indicate the mean and gray dots indicate single neurons.

In the coronal plane, we found that slightly >50% of neurons have significantly directional arbors as determined by Raleigh z test (Fig. 5B). The directional vector of these arbors tends to be at 180°, or directly opposite the apical dendrite (Fig. 5D). In order to gain a more nuanced view of path location, we performed additional analyses in which the 360° around the soma were divided into 15° bins and the number of paths falling into each bin was calculated (analysis schematized in Fig. 5F) for each neuron. When the number of paths was averaged across the population, we observe an enrichment of paths near 180° and a paucity of paths falling near the apical dendrite (Fig. 5G). When we compared directional and nondirectional cells as determined by the Raleigh z test, we found a widening of the distribution of paths such that nondirectional cells have an increase in the number of paths falling in the ∼0–90° and 270–360° regions as well as a decrease in the number of paths within the region adjacent to 180° (Fig. 5H;0–15° p = 0.0121, 15–30° p = 0.5150,30–45° p = 0.5956, 45–60° p = 0.0684, 60–75° p = 0.0026, 75–90° p = 0.1418, 90–105° p = 0.0198, 105-120° p = 0.9806, 120–135° p = 0.3069, 135–150° p = 0.9440, 150–165° p = 0.3753, 165–180° p = 0.0147, 180–195° p = 0.0249, 195–210° p = 0.4082, 210–225° p = 0.6876, 225–240° p = 0.3821, 240–255° p = 0.9578, 255–270° p = 0.2760, 270–285° p = 0.0148, 285–300° p = 0.0121, 300–315° p = 0.1329, 315–330°p = 0.0288, 330–345° p = 0.1381, 345–360° p = 0.7468, Scheffé test, α = 0.05). We also found that nondirectional cells show a small, but significant, increase in the number of paths falling within the region directly adjacent to the apical dendrite, which we have termed the “apical cone” (Fig. 5I; p = 0.006, Wilcoxon, α = 0.05). Despite these small differences, basal arbors of all cells showed a strong tendency to avoid the “apical cone.” When we considered tangential directionality and orientation, we observed that that only 10%-20% of arbors exhibit directionality (Fig. 6D), but that 100% of the arbors sampled demonstrated robust orientation along the mediolateral axis (Fig. 6B,C). However, we are unable to distinguish whether this principle applies to all L2/3 pyramidal neurons or only our target population, which consists entirely of cells whose whole basal arbors fit intorelatively thin (150 µm) histologic sections. Further studies will be required to establish how this finding may generalize to larger L2/3 neurons that may have distinct arbor shapes from those observed here.

Development of WT arbors in the absence of visual experience

We were interested in understanding how visual experience might impact dendritic development in the mammalian visual cortex because previous work has found visual experience to be an important regulator of dendritic maturation in other species (Sin et al., 2002; Van Aelst and Cline, 2004; Bestman and Cline, 2008; Chiu et al., 2008; Van Keuren-Jensen and Cline, 2008; Shen et al., 2009; Bestman et al., 2015; Faulkner et al., 2015; He et al., 2016). To address this question, we used DR to eliminate visual experience and sampled complexity at three time points corresponding to early visual experience (P16), the opening of the critical period (P21), and the peak of the visual critical period (P30) (Fig. 7A), at which point we have evidence that the arbor size and architecture are relatively stable (Fig. 5B). We observed no change in total arbor length between cells from TR and DR mice at the earliest time point (P16, p = 0.283, df = 79.118, Bonferroni-corrected α = 0.016), but we did observe that arbors from DR mice were smaller than those from TR mice at both P21 and P30 (Fig. 7C), an effect that was only marginally significant at P21 (p = 0.01765, df = 62.9, Bonferroni-corrected α = 0.016) but reached significant at the P30 time point (p = 0.01611, df = 79.8, Bonferroni-corrected α = 0.016). Interestingly, we found that arbors sampled from DR mice have a greater total length at P21 and P30 than arbors from P16 mice (both TR and DR, compare Fig. 5C), indicating that some arbor growth occurs, even in the absence of visual experience. This suggests that arbor growth in typically developing animals is likely mediated by both experience-dependent and experience-independent mechanisms (Fig. 7C), possibly including activity- or experience-dependent negative regulators to limit outgrowth when visual experience is present (Ghiretti et al., 2014). However, our findings establish that the majority of postnatal arbor branching occurs independently of visual experience in the mouse visual cortex, with only a net gain of ∼15% additional arbor length added with experience, which is in sharp contrast to previous findings that sensory input strongly promotes both dendrite branching and length in X. laevis tadpoles (Sin et al., 2002). While we expect that nuanced dynamics of segment outgrowth and retraction or pruning occur when visual experience is present, future studies using longitudinal approaches to monitor dendritic plasticity will be needed to elucidate this process.

The differences in dendritic arbor lengths with and without experience could arise from three general sources: a decrease in the number of segments, a decrease in the length of segments, or a combination of both. We observed no change in the number of segments (Fig. 7E; P16 TR-DR: p = 0.4203, df = 76.9; P21 TR-DR: p = 0.472, df = 62.539; P30 TR-DR: p = 0.3515, df = 86.0; Bonferroni-corrected α = 0.016) but found that arbors sampled from TR animals exhibited significantly longer dendritic segments at both P21 and P30 (Fig. 7D; P16 TR-DR: p = 0.6026, df = 82.0; P21 TR-DR: p = 0.01425, df = 60.4; P30 TR-DR: p = 5.5 × 10⁻⁵, df = 82.025; Bonferroni-corrected α = 0.016) compared with DR animals, indicating that visual experience is required to properly establish the length, but not number, of dendritic segments in WT mice.

Interestingly, we also observed marked changes in the “footprint” of each cell in the tissue. As expected given a decrease in arbor length, cells from DR mice exhibited a decrease in arbor volume relative to those from animals with typical visual experience (Fig. 7G; P16 TR-DR: p = 0.2511, df = 81.22; P21 TR-DR: p = 0.0061, df = 61.1; P30 TR-DR: p = 3.5 × 10⁻⁶; Bonferroni-corrected α = 0.016). We observe a complementary increase in density (Fig. 7H; P16 TR-DR: p = 0.2496, df = 81.9; P21 TR-DR: p = 0.005619, df = 58.1; P30 TR-DR: p = 1.3 × 10⁻⁷; Bonferroni-corrected α = 0.016) in DR cells, indicating that arbor length and volume do not necessarily scale to maintain arbor density. One possible outcome is that this basal architecture could decrease the variety of synaptic partners that a cell is able to access but maximize the likelihood of a partner axon in the region contacting a dendrite probabilistically. Stated differently, in the case the cortex receives visual input, arbors expand in both length and volume but decrease in density. While little is known about the possible functional impact of these changes, one might hypothesize that such an architecture may give greater access to diverse synaptic partners but with a lower chance of stochastically encountering any given partner.

Rem2 contributes to arbor development through regulation of segment number

The findings presented here suggest that proper development of dendritic arbors progresses through interaction of experience-dependent and experience-independent mechanisms. Furthermore, our findings show that parameters of arbor complexity do not necessarily follow a single pattern of change or even demonstrate correlated changes, but instead may be regulated independently such that some values increase, whereas others decrease or undergo no significant alteration over time at all. For example, when basal arbors grow from P7 to P30, they do not haphazardly increase length and add segments, but appear instead to specifically increase segment length as opposed to forming new branches. While observations such as these do not amount to direct evidence that segment number and length are governed by distinct regulatory programs at the molecular level, it does seem likely that these decoupled parameters would require some distinct regulatory mechanisms to orchestrate such discrete patterns of development. We were therefore interested to investigate whether a known regulator of dendritic complexity influences one of these defined characteristics of dendritic architecture (e.g., arbor length, segment number, tortuosity). We chose to investigate the small-Ras like GTPase Rem2, a known activity-dependent negative regulator of dendritic complexity identified both in vitro in dissociated cortical culture and in vivo in the X. laevis optic tectum (Ghiretti et al., 2014; Parent et al., 2017). To this end, we used Rem2 KO littermates of our previously discussed WT mice to investigate the role of Rem2 in regulating the development of dendritic complexity.

To better understand how loss of Rem2 might impact the dendritic arbor of L2/3 pyramidal neurons in visual cortex, we described how development of the arbor progresses over time within our sample of Rem2^−/− mice with regard to each of our key measures of dendritic complexity (Fig. 8A-D). In Rem2^−/− mice, we observe a decrease in arbor length (Fig. 8B; P7–P12 p = 0.99, P7–P16 p = 0.31, P12–P16 p = 0.001, P7–P21 p < 1 × 10⁻⁷, P12–P21 p < 1 × 10⁻⁷, P16–P21 p < 1 × 10⁻⁷, P7–P30 p = 2.7 × 10⁻⁶, P12–P30 p < 1 × 10⁻⁷, P16–P30 p = 0.024, P21-P30 p = 0.007; df = 4, α = 0.05) and segment number (Fig. 8D; P7-P12 p = 0.99, P7–P16 p = 0.09, P12–P16 p = 0.06, P7–P21 p =5 × 10⁻⁷, P12–P21 p < 1 × 10⁻⁷, P16–P21 p = 7.3 × 10⁻⁴, P7–P30 p = 0.25, P12-P30 p = 0.22, P16–P30 p = 0.98, P21–P30 p = 1 × 10⁻⁴; df = 4, α = 0.05) between P21 and P30 that is absent in WT animals. We also calculated the relative contribution of segment addition, segment elongation, and the combination of these changes. In contrast to WT neurons (Fig. 4E) in which elongation of segments is the primary contributor to arbor length increases, segment number plays a more central role in the arbor development of Rem2^−/− neurons (Fig. 8E-H). This is especially noticeable at the later time points, P21 and P30, which lacked the predominance of length-based changes characteristic of WT arbors (compare Fig. 4E with 8E). From these data, we conclude that typical Rem2 signaling acts to regulate the number of dendritic segments added and removed throughout early development and that deletion of Rem2 results in a developmental trajectory dominated by changes in segment number as opposed to segment length (compared Fig. 4E with 8E).

Rem2 bidirectionally regulates segment number in distinct developmental epochs

After finding that Rem2 loss may result in a different sequence of developmental events in basal arbors (Fig. 8B-E), we were interested to directly compare how each metric of basal arbor morphology of Rem2^−/− cells differs from WT arbors at different ages. We found significant changes only during the early postnatal period (P7) and during the early visual critical period (P21), but not at other time points. Time points with no significant changes in any of the analyzed measures (P12, P16, and P30) have not been included in Figure 6. As suggested by our developmental results, we observed that Rem2^−/− cells show changes in the number of dendritic segments (Fig. 8G; P7 WT-KO: p = 0.02, df =35.2; P21 WT-KO: p = 0.01, df = 59.6; Bonferroni-corrected α = 0.025), but not their length (Fig. 8F; P7 WT-KO: p = 0.15, df = 42.9; P21 WT-KO: p = 0.29, df = 60.9; Bonferroni-corrected α = 0.025), in a developmentally regulated fashion. Early in development (P7), we observed a significant decrease in the number of dendritic segments in Rem2^−/− cells (Fig. 8G) that is absent at P12. In contrast, we observed an increase in the number of dendritic segments by our early critical period time point (P21, Fig. 8G). We were interested to see whether this dysregulation of segment number resulted in a change in the total length of the arbor or represented instead a rearrangement of a set arbor length (Fig. 8H). While we observed a numerical increase in the mean arbor length of Rem2^−/− cells at P21, this narrowly misses our criterion for statistical significance (Fig. 8H; p = 0.06, df = 58.9; Bonferroni-corrected α = 0.025), suggesting hat Rem2 primarily regulates the formation of segments as opposed to the amount of dendritic material composing the arbor. We also did not observe a significant change in the number of dendritic primary arbors at either P7 or P21 (Fig. 8I; P7 WT-KO: p = 0.59, df = 42.5; P21 WT-KO: p = 0.33, df = 57.0; Bonferroni-corrected α = 0.025), suggesting that segments are, respectively, absent or added to existing primary arbors.

Rem2 is an experience-dependent negative regulator of segment number

Rem2 function has previously been shown to be regulated by neuronal activity and sensory experience (Ghiretti et al., 2013, 2014; Kenny et al., 2017; Moore et al., 2018). Therefore, we investigated whether visual experience was required for Rem2-dependent regulation of segment number. To test this, we dark-reared Rem2^+/+ and Rem2^−/− mice from before eye opening until P21 and assessed segment number. We found that Rem2^−/− cells reconstructed from DR mice failed to increase segment number (Fig. 9C) compared with either Rem2^+/+ group (TR and DR) and had significantly fewer dendritic segments than Rem2^−/− arbors from mice that had visual experience (Fig. 9C; see Table 4 for means ± SEM and p values, df = 1, α = 0.05). These results indicate that one function of Rem2 is to oppose visual experience-dependent segment addition/branching during the visual critical period. Interestingly, Rem2^−/− neurons lack an experience-dependent enhancement of segment length, and Rem2^−/− neurons from both DR and TR animals exhibit lengths that resemble Rem2^+/+ neurons from TR animals (Fig. 9B,D; see Table 4 for means ± SEM and p values, df = 1, α = 0.05). These data indicate that Rem2 may normally act to oppose the growth of segment length in the absence of visual experience. Adding to the evidence that Rem2 mediates both segment number and length, Rem2^−/− cells show a nearly complementary set of DR-associated changes to those observed in Rem2^+/+ cells at P21 (Fig. 9F; see Table 4 for means ± SEM and p values, df = 1, α = 0.05) such that Rem2^−/− cells show changes mostly restricted to parameters of number, whereas Rem2^+/+ cells show changes in mostly parameters of length. Interestingly, overall path length is similar in DR and TR mice, with neither Rem2^+/+ nor Rem2^−/− cells showing a change regardless of rearing regimen (main effect of rearing condition: p = 0.10 557, df = 1, two-way ANOVA, α = 0.05).

Table 4.

Means and p values for Figure 9A^a

	Mean ± SEM				Post hoc Tukey test, p value
	WT TR	WT DR	KO TR	KO DR	WT TR-WT DR	KO TR-KO DR	WT TR-KO TR	WT DR - KO DR
P21 segment number	45.4 ± 2.3	42.9 ± 1.8	55.0 ± 2.7	46.3 ± 2.4	0.392	0.018*	0.008*	0.255
P21 segment length	64.6 ± 2.0	57.5 ± 2.2	61.6 ± 1.8	66.1 ± 2.5	0.022*	0.161	0.271	0.014*
P30 segment number	38.6 ± 1.8	41.4 ± 1.9	38.8 ± 2.2	40.9 ± 2.2	0.299	0.494	0.953	0.872
P30 segment length	71.7 ± 2.7	56.7 ± 1.7	66.8 ± 2.1	63.1 ± 2.1	0.000009*	0.218	0.165	0.020*

^ap values for additional P21 comparisons can be found in Figure 9F.

*Significant comparison.

Acute, sparse deletion of Rem2 during the visual critical period alters arbor directionality

Our results indicate that Rem2 primarily contributes to arbor development and plasticity through establishing the number of segments in the dendritic arbor with modest impact on the length of segments or the total length of dendritic material composing the arbor. However, our Rem2^−/− mice are constitutive null for Rem2, which eliminates our ability to manipulate Rem2 expression with any spatial or temporal control. Additionally, because of the constitutive nature of our Rem2^−/− mouse model, we are unable to determine whether the observed changes are cell-autonomous or may originate from network-level changes in Rem2^−/− cortices. To overcome these limitations, we crossed Rem2 conditional KO mice (Rem2^flx/flx) to Ai9.TdTomato (Tdt^flex/flex) reporter mice that express the fluorophore TdTomato when Cre recombinase is present. We performed small, dilute injections of an AAV-expressing GFP-tagged Cre recombinase into the visual cortex of Rem2^+/+;Tdt^flex/flex and Rem2^flx/flx;Tdt^flex/flex at P20 (Fig. 10A-C), enabling us to visualize sparse populations of neurons (Fig. 10A) and reconstruct whole arbors from just the TdTomato reporter fill (Fig. 10B). We reconstructed arbors approximately every 2 d starting at 3 dpi and continuing until the peak of the critical period (11 dpi, P31; Fig. 10C).

Figure 10.

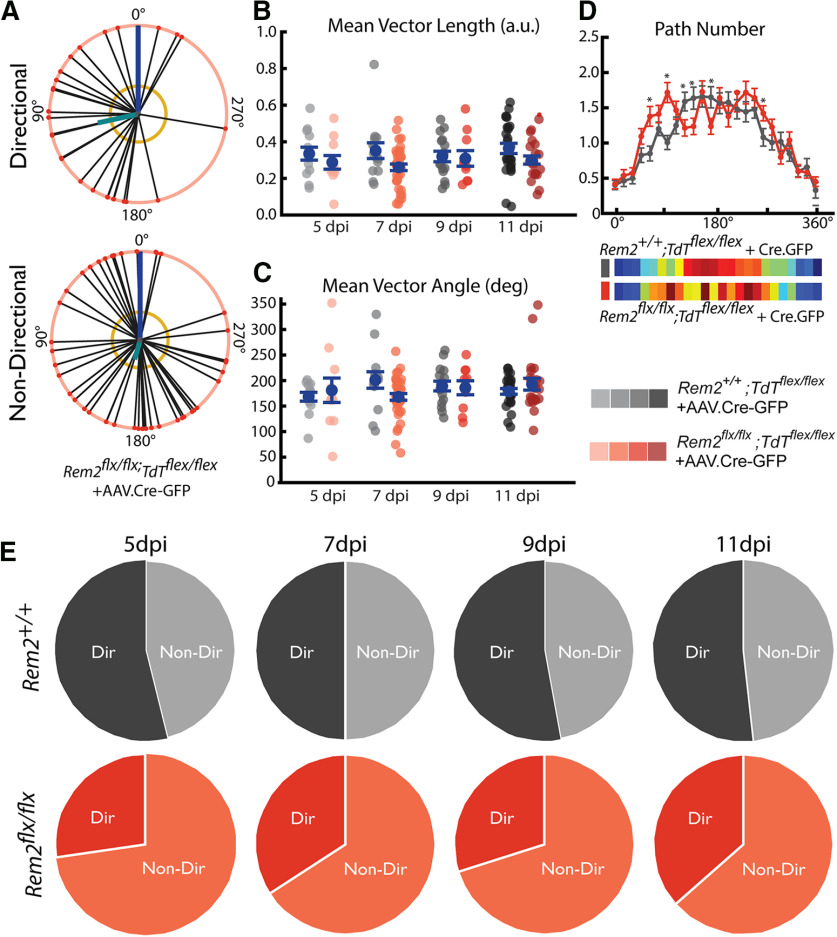
Acute deletion of Rem2 results in many transient changes in basal arbor architecture. A, Example sparse population of WT neurons infected with AAV.Cre-GFP in primary visual cortex expressing Ai9.TdTomato reporter (pseudocolored cyan). B, Example single WT neuron expressing Ai9.TdTomato reporter (pseudocolored cyan). Entire dendritic arbor is visible and amenable to reconstruction. C, Timeline for AAV.Cre-GFP injection (blue arrowhead) and morphologic sample collection schedule (coral arrowheads). D, Example L2/3 pyramidal neurons in the primary visual cortex of Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP mice sampled 5, 7, or 11 dpi. Straight gray lines diagram the unreconstructed apical dendrite to indicate the orientation of cells. E, Length of the complete basal arbor of Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons sampled at 5, 7, 9, and 11 dpi. F, Average segment length of neurons from Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP mice sampled at 5, 7, 9, and 11 dpi. G, Segment number of neurons from Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP mice sampled at 5, 7, 9, and 11 dpi. H, Volume of the complete basal arbor of Rem2^+/+;Tdt^flex/flex and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons sampled at 5, 7, 9, and 11 dpi. I, Density of the complete basal arbor of Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons sampled at 5, 7, 9, and 11 dpi. J, Number of basal dendritic primary arbors of Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons sampled at 5, 7, 9, and 11 dpi. K, Average path length of neurons from Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP mice sampled at 5, 7, 9, and 11 dpi. L, Summary of p values from all comparisons between Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons at each of the sampled dpi time points with significant results shown in yellow. Arbor characteristics impacted by Rem2 deletion are not conserved across ages/time points. Error bars indicate mean ± SEM. Blue dots indicate means. Gray/coral dots indicate single neurons. For all Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP measurements: 5 dpi: N = 11 cells, 4 mice; 7 dpi: N = 38 cells, 7 mice; 9 dpi: N = 10 cells, 4 mice; 11 dpi: N = 22 cells, 4 mice. For all Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP measurements: 5 dpi: N = 13 cells, 5 mice; 7 dpi: N = 14 cells, 5 mice; 9 dpi: N = 17 cells, 4 mice; 11 dpi: N = 27 cells, 6 mice. *p < 0.0125 (Wilcoxon rank-sum test, Bonferroni-corrected α = 0.0125).

Qualitative observation of Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP arbors at all dpi reveals dendrites that are often extensively self-overlapping and have unusual distributions around the soma (Fig. 10D). Quantification of these arbors revealed complex, varied remodeling of arbors following acute Rem2 deletion (summarized in Fig. 10L; Wilcoxon, Bonferroni-corrected α = 0.0125) that occur as early as 5 d after Rem2 KO (5 dpi) and are transient on a timescale of days. The total arbor length of Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP cells is significantly decreased compared with Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP cells at 5 dpi and increased at 7 dpi, with no significant change at 9 dpi or 11 dpi (Fig. 10E; statistical comparisons in Fig. 10L; Wilcoxon, Bonferroni-corrected α = 0.0125). In contrast to previous results with constitutive Rem2 KO, we observed compromised age-dependent arbor stability that is present across both measures of segment length and number in the context of visual experience that are highly dependent on the duration of Rem2 loss or, perhaps, animal age (Fig. 10L). We found that segment number is increased compared with Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP cells at 7 dpi in Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP (Fig. 10G; statistical comparisons in Fig. 10L; Wilcoxon, Bonferroni-corrected α = 0.0125) but that only segment length is decreased at 5 dpi without a significant change in segment number (Fig. 10F; statistical comparisons in Fig. 10L; Wilcoxon, Bonferroni-corrected α = 0.0125). We also observed increased arbor density (Fig. 10I; statistical comparisons in Fig. 10L; Wilcoxon, Bonferroni-corrected α = 0.0125) at 9 dpi with only limited changes in any arbor-centric parameters (Fig. 10J; statistical comparisons in Fig. 10L; Wilcoxon, Bonferroni-corrected α = 0.0125), indicating that this tissue-centric change arises from perhaps many subtle changes in underlying arbor architecture. From these results, we conclude that acute Rem2 deletion in individual cells during the critical period leads to altered arbor stability arising from transient, bidirectional changes in several parameters of arbor complexity.

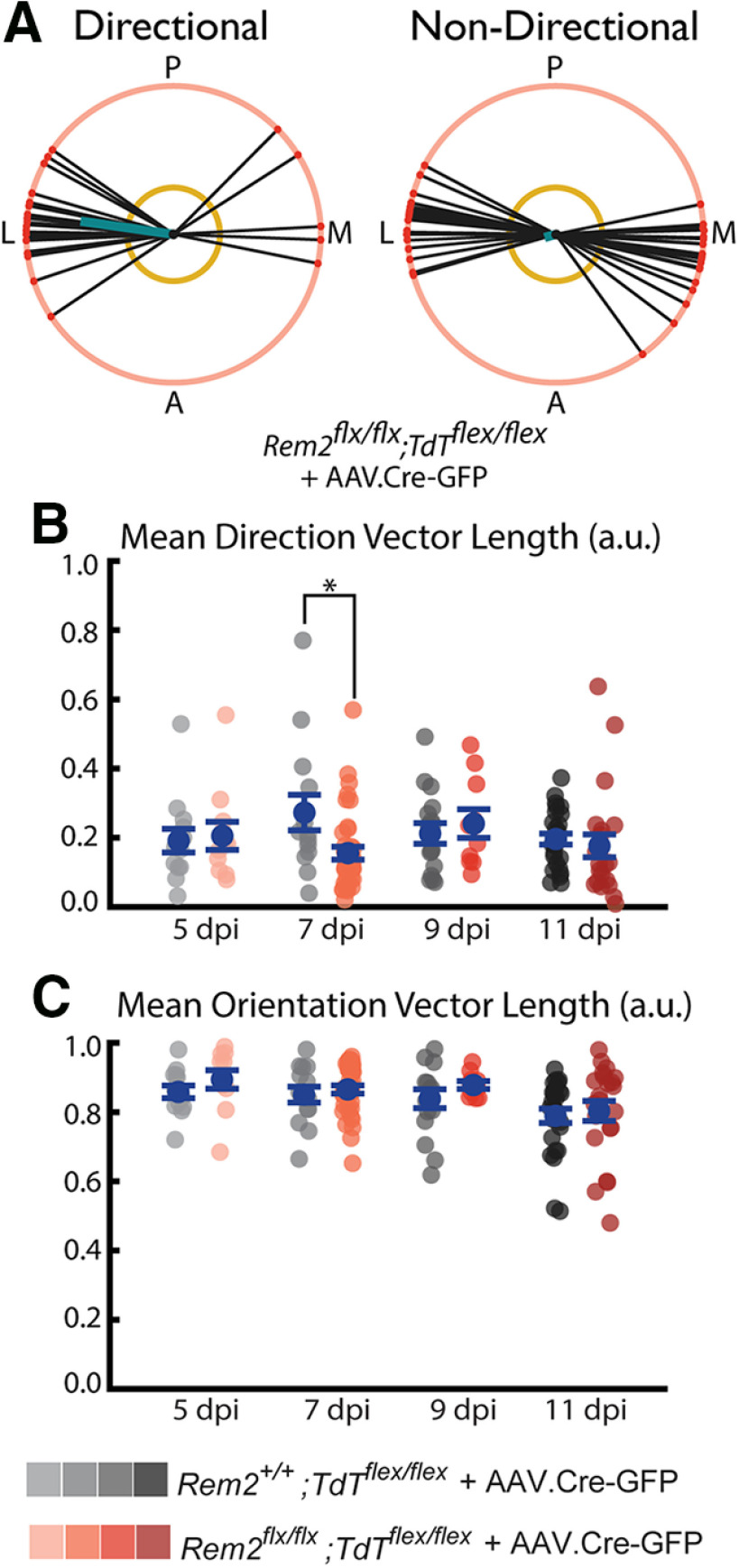
Upon our initial observations of Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons, we noticed that several of the neurons exhibited highly irregular basal dendrite orientation and directionality (Fig. 11A). For example, some neurons had the majority of paths directed to either the medial or lateral side of the soma (Fig. 11A, top), instead of originating from the basal surface of the soma, as is most typical in WT arbors (Fig. 5). Thus, we became interested in comparing the degree to which Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP express directionality and whether the directionality of these cells is similar to WT neurons.

Figure 11.

Rem2 promotes basal dendrite coronal polarity. A, Example directional (top) and nondirectional (bottom) basal arbors sampled from Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP mice in the coronal viewpoint. Each arbor is schematized as soma (middle dot) and soma-to-tip vectors (lines with dots at tip) arranged on a unit circle with apical dendrite diagrammed as blue line. Thick teal line indicates the mean directional vector. Yellow circle represents length of mean directional vector required to declare the arbor directional by the Raleigh test. B, Length of the mean vector computed for Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons sampled at 5, 7, 9, and 11 dpi. C, Angle of the mean vector computed for Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons sampled at 5, 7, 9, and 11 dpi. D, Number of paths per radial bin (radial Sholl) for Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons pooled across all ages (top) and heat map of the same data (bottom). *p < 0.05 (one-way ANOVA followed by Scheffé test). E, Fraction of neurons meeting the Raleigh test criterion for significant directionality of the basal arbor is noticeably decreased (∼20% decrease) in Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons at all sampled ages. Error bars indicate mean ± SEM. Blue dots indicate means. Gray/coral dots indicate single neurons. For all Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP measurements: 5 dpi: N = 11 cells, 4 mice; 7 dpi: N = 38 cells, 7 mice; 9 dpi: N = 10 cells, 4 mice; 11 dpi: N = 22 cells, 4 mice. For all Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP measurements: 5 dpi: N = 13 cells, 5 mice; 7 dpi: N = 14 cells, 5 mice; 9 dpi: N = 17 cells, 4 mice; 11 dpi: N = 27 cells, 6 mice. *p < 0.0125 (Wilcoxon rank-sum test, Bonferroni-corrected α = 0.0125).

While we saw no significant difference in either the length of the mean vector (Fig. 11B; 5 dpi WT-FLX p = 0.4244, 7 dpi WT-FLX p = 0.06138, 9 dpi p = 0.8971, 11 dpi p = 0.0718; Wilcoxon, Bonferroni-corrected α = 0.0125) or the angle of this vector (Fig. 11C; 5 dpi WT-FLX p = 1, 7 dpi WT-FLX p = 0.02139, 9 dpi p = 0.9382, 11 dpi p = 0.683; Wilcoxon, Bonferroni-corrected α = 0.0125) when we considered coronal directionality, we did observe a marked change in the number of neurons reaching the Raleigh criterion for significant directionality (Fig. 11E). In Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP neurons, ∼50% of the reconstructed cells achieved significant directionality consistently across the observed time points (see also Fig. 5). In contrast, only ∼25%-35% of Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons met this criterion, indicating that Rem2 would normally function to promote a more isotropic distribution of basal dendrites in the coronal plane (see also Fig. 11D; 0-15° p= 0.8793, 15-30° p = 0.5305, 30-45° p = 0.5292, 45-60° p = 0.0.0684, 60-75° p = 0.0035, 75-90° p = 0.1886, 90-105° p = 9 × 10⁻⁵, 105-120° p = 0.2216, 120-135° p = 0.0339, 135-150° p = 0.0388, 150-165° p = 0.7605, 165-180° p = 0.0272, 180-195° p = 0.7158, 195-210° p = 0.3481, 210-225° p = 0.5947, 225-240° p = 0.2083, 240-255° p = 0.3916, 255-270° p = 0.0379, 270-285° p = 0.1646, 285-300° p = 0.1792, 300-315° p = 0.2449, 315-330° p = 0.9581, 330-345° p = 0.5955, 345-360° p = 0.3526; Scheffé test, α = 0.05). When we instead considered tangential directionality (Fig. 12), a different pattern of results emerges. We observe little significant Rem2-dependent regulation of tangential directionality and orientation. However, the 7 dpi time point shows that Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons have decreased tangential directional vector length compared with their WT littermates (Fig. 12B). Together with our findings concerning coronal polarity, these results identify a new role for Rem2 in regulation of dendritic architecture and identify a cell-autonomous molecular regulator of this little-studied component of dendritic complexity (Elston and Rosa, 1998).

Figure 12.

Rem2 promotes basal dendrite tangential directionality. A, Example polar (left) and nonpolar (right) basal arbors sampled Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP mice in the tangential viewpoint. Each arbor is schematized as soma (center dot) and soma-to-tip vectors (lines with dots at tip) arranged on a unit circle. Thick teal line indicates the mean direction vector. Yellow circle represents length of mean direction vector required to declare the arbor directional by the Raleigh test. Posterior (P), anterior (A), medial (M), and lateral (L) are indicated around the diagrams. B, Length of the mean direction vector computed for Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons sampled at 5, 7, 9, and 11 dpi. C, Length of the mean orientation vector computed for Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP and Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP neurons sampled at 5, 7, 9, and 11 dpi. Error bars indicate mean ± SEM. Blue dots indicate means. Gray/coral dots indicate single neurons. For all Rem2^flx/flx;Tdt^flex/flex + AAV.Cre-GFP measurements: 05 dpi, N = 11 cells, 4 mice; 07 dpi, N = 38 cells, 7 mice; 09 dpi, N = 10 cells, 4 mice; 11 dpi, N = 22 cells, 4 mice. For all Rem2^+/+;Tdt^flex/flex + AAV.Cre-GFP measurements: 05 dpi, N = 13 cells, 5 mice; 07 dpi, N = 14 cells, 5 mice; 09 dpi, N = 17 cells, 4 mice; 11 dpi, N = 27 cells, 6 mice. *p < 0.05 (Wilcoxon rank-sum test).

These experiments reveal that Rem2 is required for the continued, active maintenance of the basal arbor during a time that previous results, including our own, would suggest arbors have reached stable maturity. Strikingly, notable changes occur in as little as 5 d after Cre injection and subsequent Rem2 deletion, highlighting the rapidity with which remodeling occurs in arbors that had previously developed normally. Following from this idea, our results challenge the notion that a dendritic arbor undergoing no observable net change is devoid of regulation; in contrast, it may instead be the case that an equilibrium of regulatory forces maintains the arbor and that removal of one regulator, such as Rem2, can disrupt the structure of an outwardly stable arbor.

Discussion

Dendrite morphogenesis is a complex developmental process subject to precise molecular regulation. Neurons must find their proper location in the tissue (Nadarajah et al., 2003; Ayala et al., 2007; Marin et al., 2010; Lefebvre et al., 2015; Ohtaka-Maruyama and Okado, 2015; Hoshiba et al., 2016), polarize neurites into dendrites and axons (Namba et al., 2015; Takano et al., 2015), and elaborate their dendritic arbor in adherence to the structure of their local circuitry (Scott and Luo, 2001; Gao, 2007; Parrish et al., 2007; Jan and Jan, 2010; Koleske, 2013; Santiago and Bashaw, 2014; Lefebvre et al., 2015). Proper patterning of dendrites, for example, being the appropriate size and shape to tile functionally relevant spaces, is a key component to the development of neural circuits (Z. D. Smith, 1981; Jhaveri and Morest, 1982; Scott and Luo, 2001; Gao, 2007; Parrish et al., 2007; Jan and Jan, 2010; Koleske, 2013; Santiago and Bashaw, 2014; Lefebvre et al., 2015; Richards and Van Hooser, 2018). Conversely, the dendritic arbor is shaped by ongoing circuit activity both in early prenatal and postnatal spontaneous activity as well as through sensory input in later postnatal development. Many regulators of this process have been identified across a variety of species, although many of the details remain to be uncovered.

This study establishes a cohesive, detailed description of postnatal dendritic arbor development in mouse visual cortex with and without the influence of sensory experience. We established that proper dendritic development is a carefully orchestrated process involving both experience-dependent and experience-independent components. Our results suggest that the gross structure of basal dendritic arbors arises independently of sensory experience, but that sensory experience is required to achieve full dendritic segment length. Additionally, we characterize basal arbor directionality and orientation and show that basal dendrites tend to avoid the area surrounding the apical dendritic arbor.

Furthermore, we establish that Rem2 is an age- and experience-dependent regulator of this process, primarily impacting segment number as opposed to segment length. However, acute loss of Rem2 reveals a complex role for Rem2 in actively regulating many parameters of the basal arbor including both dendrite length and number parameters. Finally, we show that Rem2 promotes basal dendrite directionality with Rem2 deletion resulting in an ∼20% decrease in significantly directional basal arbors.

Dendritic growth in the visual cortex

Before these results, works describing the maturation of basal arbors in rodent visual cortex were limited by the lack of digital 3D reconstruction pipelines available at the time they were produced (Miller, 1981; Juraska, 1982). These works were unable to differentiate between possible alternative growth programs of dendritic arbors. We found that arbor length increases primarily through the outgrowth of existing dendritic segments as opposed to the addition of new segments or more primary arbors. Consistent with previous works (Miller, 1981; Hoshiba et al., 2016), we found that the number of primary arbors is established very early in development, before postnatal day 7, and is stable throughout the time period we investigated.

One of the most surprising conclusions of this work is the relatively small influence of visual experience on the total dendritic length of the basal arbor, especially compared with other circuits, such as X. laevis optic tectum (Sin et al., 2002). We found that visual experience only slightly promotes increased segment length, with no significant impact on the number of dendritic segments. Visual experience also reshapes the spatial extent of arbors, leading to an increase in arbor volume and decrease in arbor density. However, our results demonstrate that the vast majority of normal arbor growth occurs independently from visual experience: at P21 and P30, only about an additional 15% of the total arbor length is attributable to the presence of experience (P21, WT DR arbor length is 83% of WT TR; P30 WT DR arbor length is 87% of WT TR). One possible explanation for these modest experience-dependent changes is the relatively impoverished visual environment of the laboratory. Many studies show that environmental enrichment can enhance dendritic complexity and spine density in visual cortex of rodents (Diamond et al., 1964, 1966; Volkmar and Greenough, 1972; Turner and Greenough, 1985; Sirevaag and Greenough, 1987; Markham and Greenough, 2004), suggesting that laboratory mice may be somewhat deprived in standard housing conditions. Interestingly, one study suggests that multimodal engagement is required for enrichment-dependent hypertrophy of visual cortex (Ferchmin and Bennett, 1975), which may explain the limited impact of manipulating one modality of experience as in our experiments. Longitudinal in vivo imaging methods or environmental enrichment may be able to uncover subtle or enrichment-dependent changes that were not revealed here.

Rem2 and arbor development

Our results add to prior studies in culture (Ghiretti and Paradis, 2011; Ghiretti et al., 2013) and X. laevis (Ghiretti et al., 2014) that showed that Rem2 negatively regulates dendritic complexity by revealing two key roles of Rem2 in regulating the basal arbor. First, we conclude that Rem2 acts to promote segment length growth in the presence of visual experience: when Rem2 was present, we saw increased segment length in neurons sampled from TR mice compared with DR mice, and this increase was absent in Rem2^−/− arbors, with both TR and DR segments having similar length to those of TR WT mice. Second, Rem2 functions to restrict the number of dendritic segments in response to visual experience: when Rem2 was deleted, there was an increase in the number of dendritic segments that was not observed in WT mice. We hypothesize that visual experience promotes a complex growth program for basal dendritic arbor maturation, but that specific negative regulators, such as Rem2, sculpt the developmental process into a length-dominated growth program. Rem2 may detect activity through its strong inhibitory interactions on CaMKII (Royer et al., 2018). CaMKII has been implicated in synapse pruning (Mower et al., 2011), ocular dominance plasticity (Taha et al., 2002), Hebbian forms of synaptic plasticity (Kirkwood et al., 1997), and maturation of dendritic arbors (Wu and Cline, 1998; Zou and Cline, 1999; Puram et al., 2011; Flynn et al., 2012; Ghiretti et al., 2013).

Sparse, acute knockdown of Rem2 yielded a more variable phenotype with respect to the increase in segment number that was observed in constitutive KO animals. Future experiments using time-lapse imaging in vivo may help to clarify these results. The strong effects observed in the constitutive KOs could reflect changes in the initial circuitry and/or the impact of removing Rem2 from all neurons in the circuit, including those presynaptic and postsynaptic to the neurons studied. Nevertheless, the constitutive KO experiments reveal that there are separate pathways by which visual experience and development impact circuit growth by changes in dendritic segment length and changes in dendritic segment number.

Implications for models

These results offer a number of useful constraints for those building models of cortical development and the influence of experience. Basal arbor tortuosity hardly varies across animals or development and takes values close to 1 (median: 1.23; interquartile range: 0.09), so a “ball-and-stick” model of basal dendritic architecture is an excellent approximation. The number of primary neurites is determined very early (by P7) and is not dependent on visual experience, and the approximate number of dendritic branches is also determined early. Basal arbors do grow with age and experience (42% increase in arbor length from P16 to P30) but grow only a little bit more with visual experience (15%) than without visual experience. These observations indicate that models that leave out an experience-dependent component of increases in basal dendritic length would not be missing too much, and models could instead focus on experience-dependent contributions of active channels and dynamic synapses over relatively fixed dendritic lengths.

Future directions

What links synapses, neural activity, and the shapes of dendritic arbors? Work from the Cline laboratory among others has established numerous molecular regulators of dendritic outgrowth (Sin et al., 2002; Bestman and Cline, 2008; Chiu et al., 2008; Van Keuren-Jensen and Cline, 2008; Shen et al., 2009; Bestman et al., 2015; Faulkner et al., 2015; Pratt et al., 2016; Thompson and Cline, 2016; Truszkowski et al., 2016), including many pathways directly connected with activity-dependent mechanisms promoting dendrite outgrowth (Cline, 1991; Wu and Cline, 1998; Sin et al., 2002; Ghiretti et al., 2014; Ghiretti and Paradis, 2014; He et al., 2016; Pratt et al., 2016). The canonical model of this process, the synaptotrophic hypothesis, suggests that dendrites grow toward areas that have active inputs and are stabilized by the presence of maturing synaptic contacts (Cline and Haas, 2008). Deletion of Rem2 causes an increase in arbor size (Ghiretti et al., 2013, 2014; Moore et al., 2013; present study), a loss of synapses (Paradis et al., 2001; Ghiretti and Paradis, 2011; Moore et al., 2018), and increases in intrinsic excitability (Moore et al., 2018), implying that Rem2 is a key component at the nexus of the biochemical pathways that mediate all of these processes. Future studies will be needed to dissect the interactions of Rem2 with the proteins that directly mediate growth, channel insertion, and synapse formation.