Significance
The brain exhibits a tremendous amount of heterogeneity, and to make sense of this seemingly random system neuroscientists have explored various ideas to organize it into distinct areas, each performing certain computations. One such idea is the timescale at which neural response fluctuates. Here, we developed a comprehensive method to estimate multiple timescales in neural response and link these timescales to processing of task-relevant signals and behavioral adjustments. We found multiple types of timescales that increase across cortical areas in parallel while being independent of each other and of selectivity to task-relevant signals. Our results suggest that there are multiple independent mechanisms underlying generations of neural dynamics on different timescales.
Keywords: neural heterogeneity, reward integration, prefrontal cortex
Abstract
A long-lasting challenge in neuroscience has been to find a set of principles that could be used to organize the brain into distinct areas with specific functions. Recent studies have proposed the orderly progression in the time constants of neural dynamics as an organizational principle of cortical computations. However, relationships between these timescales and their dependence on response properties of individual neurons are unknown, making it impossible to determine how mechanisms underlying such a computational principle are related to other aspects of neural processing. Here, we developed a comprehensive method to simultaneously estimate multiple timescales in neuronal dynamics and integration of task-relevant signals along with selectivity to those signals. By applying our method to neural and behavioral data during a dynamic decision-making task, we found that most neurons exhibited multiple timescales in their response, which consistently increased from parietal to prefrontal and cingulate cortex. While predicting rates of behavioral adjustments, these timescales were not correlated across individual neurons in any cortical area, resulting in independent parallel hierarchies of timescales. Additionally, none of these timescales depended on selectivity to task-relevant signals. Our results not only suggest the existence of multiple canonical mechanisms for increasing timescales of neural dynamics across cortex but also point to additional mechanisms that allow decorrelation of these timescales to enable more flexibility.
Despite the tremendous heterogeneity in terms of cell types, connectivity patterns, and neural response across the brain, neuroscientists have long entertained various ideas about parsimonious organizational principles that could be used to parcellate mammalian brains into distinct areas with specific functions (1–6). For example, regularities in cyto- and myeloarchitecture have been successfully used for anatomical parcellation of cortex (4, 5). This and other anatomical regularities have also inspired the idea of a canonical microcircuit (7), a unit dedicated to a specific computation in the brain. Consequently, computational neuroscientists have explored how heterogeneity in such a circuit contributes to multiple brain computations (8–11).
Functionally, although neurons in different cortical areas display a vast range of response properties, activity of individual cortical neurons commonly displays specific temporal correlations. This raises the possibility that timescales of neural activity might reflect an important organizational principle of cortical computations. For example, dynamic properties of neurons in the primary sensory cortical areas might be tuned for rapidly changing sensory stimuli and moment-to-moment fluctuations in their ongoing activity might show shorter intrinsic timescales than those of neurons in the association cortex. Indeed, recent studies have demonstrated that the intrinsic timescales of ongoing neural activity across the brain follow the anatomical hierarchy determined by tract-tracing studies (12–15). Whereas the exact role of these intrinsic timescales is currently unknown, time constants of modulations by reward, presumably contributing to reward memory, also increase in tandem with intrinsic timescales across cortical areas (15, 16), pointing to specialization of brain areas for integration of reward information on specific timescales.
These parallel hierarchies of timescales in intrinsic fluctuations and reward memory, however, were estimated previously with different methods. Intrinsic timescales were estimated using the decay rate of autocorrelation in neural response across the population of neurons in a given area (15), whereas reward-memory timescales were obtained using activity profiles of individual neurons across multiple trials (16). Therefore, it is unclear whether the presumed relationship between intrinsic and reward-memory timescales holds at the level of individual neurons. If these timescales are correlated across individual neurons, it would suggest that mechanisms involved in intrinsic fluctuations might also contribute to the persistence of task-relevant signals. By contrast, the absence of such a relationship among individual neurons could indicate that multiple mechanisms underlie the generations of these timescales. Therefore, exploring the relationship between intrinsic and reward-memory timescales at the level of individual neurons could address the specificity of computations in a canonical microcircuit. Moreover, such neural dynamics could be linked to timescales of adjustments in behavioral response in order to provide an insight into how neural dynamics contribute to behavioral adjustments.
Finally, it is also unknown whether the observed behaviorally relevant hierarchy of reward-memory timescales (16) depends on the selectivity of individual neurons to external or task-relevant signals. For example, long reward-memory timescales might also require strong reward selectivity. If so, heterogeneity in response selectivity might decorrelate reward-memory timescales from intrinsic timescales across different neurons, even if they were generated via a single mechanism in a canonical microcircuit. Interestingly, a few recent studies have demonstrated that intrinsic timescales during the fixation period––presumably before strong task-relevant signals emerge in the cortical activity––can predict encoding of task-relevant signals later in the trial for some cortical areas (17–22). By contrast, independence of timescales and response selectivity could indicate that reward-memory and intrinsic timescales might be generated via separate mechanisms. This would challenge the idea that the hierarchies of timescales occur due to similar processing of information by canonical microcircuits across the brain (23, 24) and instead points to the importance of the heterogeneity of local circuits (9). Nonetheless, understanding the relationships between timescales of neural dynamics and response selectivity would enable us to determine how mechanisms underlying the generation of those timescales are related to other aspects of neural processing.
Here, we developed a general and robust method to simultaneously estimate four distinct timescales from the activity of individual neurons along with their selectivity to task-relevant signals. This was done to ensure that dynamics associated with these timescales and selectivity to task-relevant signals capture unique variability in neural response. By doing so, we aimed to address the following questions. 1) Is there any relationship between intrinsic timescales and behaviorally relevant timescales within individual neurons? 2) Do these timescales depend on the selectivity of individual neurons to task-relevant signals? 3) Does any of these timescales predict behavioral flexibility? We applied our method to single-cell recordings in four cortical areas shown to be involved in decision making and reward processing.
Results
Reinforcement Learning during a Matching-Pennies Task.
We analyzed the activity of 866 single neurons in four cortical areas (lateral intraparietal cortex, LIP; dorsomedial prefrontal cortex, dmPFC; dorsolateral prefrontal cortex, dlPFC; and anterior cingulate cortex, ACC) commonly implicated in decision making and reinforcement learning (25, 26) from six monkeys performing the same competitive game of matching pennies (Fig. 1). On each trial of this task, monkeys chose one of two color targets by shifting their gaze while the computer made its choice by simulating a competitive opponent that tried to predict monkeys’ upcoming choice based on previous choices and reward outcomes (16). The animal received a reward if its choice matched that of the computer (see Methods for more details). Animals adjusted their choices during this task according to their choice and reward outcomes over multiple trials (27). This feature makes the game of matching pennies unique for addressing our questions as it allows us to estimate timescales of such integrations at neural as well as behavioral levels.
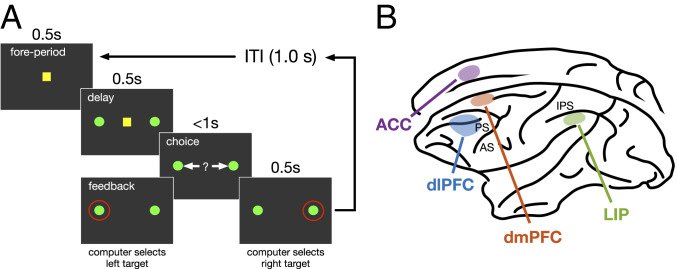
Fig. 1.
Experimental paradigm and recording sites. (A) Each trial of the oculomotor free-choice task starts with a fixation point followed by presentation pf two identical targets. The animal could select between the two targets by making a saccade as soon as the fixation point disappeared. The animal was rewarded with a drop of juice if it selected the same target as the computer opponent. (B) Recording sites in four cortical areas.
Presence of Multiple Timescales in Neural Response.
Based on previous studies, we assumed that neural response at any time point in a trial could depend on activity during earlier epochs in the same trial and similar epochs in the preceding trials, as well as on reward outcome (reward vs. no reward) and choice (left vs. right) on the preceding trials (Fig. 2 A–C). This resulted in a general method for estimating timescales while capturing heterogeneity in neural response.
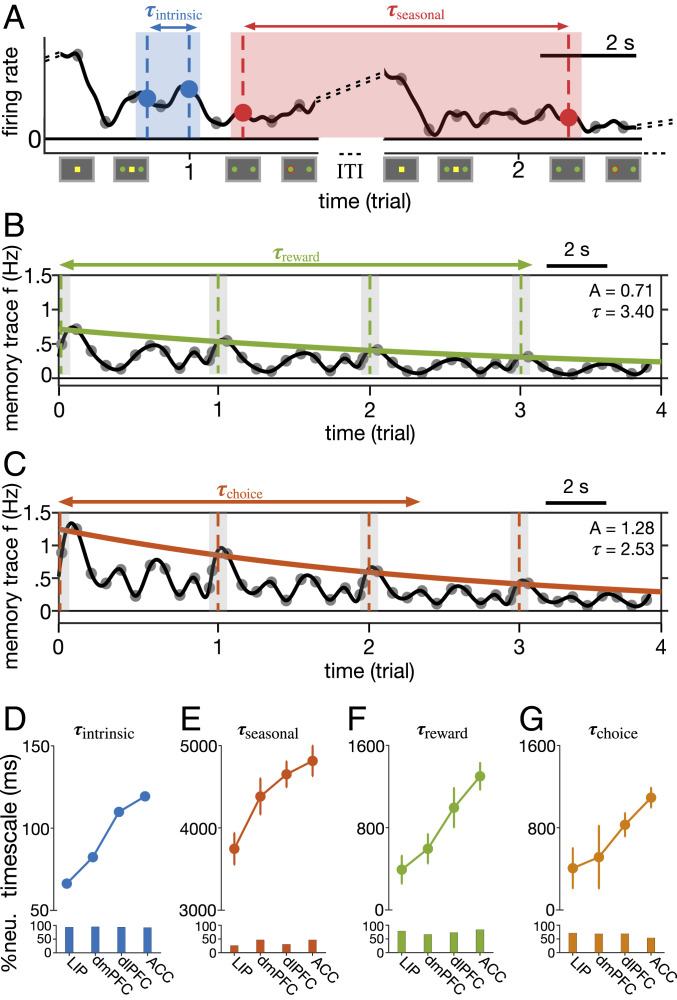
Fig. 2.
Multiple hierarchies of timescales of neural fluctuations and integration of task-relevant signals across cortex. (A–C) Simultaneous estimation of four types of timescales in neural response, illustrated for activity of an example ACC neuron. Activity in a given time epoch is related to response during previous epochs in the same trial (intrinsic timescale: ; A), response during the same epoch in the preceding trials (seasonal timescale: ; A), reward outcome on previous trials (reward-memory timescale: ; B), and monkeys’ choice (left vs. right) in the preceding trials (choice-memory timescale: ; C). (D–G) Hierarchies of the four types of timescales across the cortex. Plots show the median of intrinsic (D), seasonal (E), reward-memory (F), and choice-memory (G) timescales in four cortical areas estimated using the best model for fitting response of each neuron. Error bars indicate SEM. Only neurons that showed significant timescales are included in each panel. Bar graphs show the fraction of neurons with a significant timescale in each area.
The first type of dependence—activity from epochs in the same trial—was captured by an autoregressive (AR) component that predicts spikes in a given 50-ms time bin based on spikes in the preceding eight time bins (Fig. 2A). In addition, because of the structured nature of the task with specific time epochs, we hypothesized that neural response on a given epoch could be influenced by the activity in the same epoch in the previous trials, and thus we included a second AR component to estimate a “seasonal” timescale for each neuron. In order to estimate timescales associated with the intrinsic and seasonal AR components, we then solved a fifth-order difference equation separately for coefficients obtained from each AR component (see Methods for more details). Intrinsic timescales based on this method closely match timescales based on autocorrelation (discussed below).
The third and fourth types of dependence were captured by two exponential memory-trace components (filters) to describe fluctuations of each neuron’s response around its average activity profile in a given time bin based on reward feedback and choice on the previous trials, respectively. The corresponding exponential coefficients were then used to estimate a single timescale of “reward memory” (Fig. 2B) and “choice memory” (Fig. 2C) for each neuron (16). Finally, we also included multiple exogenous terms to capture selectivity to reward outcome and choice in the current trial, and their interactions. We used all possible combinations of the two AR and two memory-trace components as well as the presence or absence of exogenous terms (task-relevant signals) to generate models (SI Appendix, Table S1).
Considering the complexity of our method, we first tested whether it could identify the correct model by fitting data generated with one model using all of the 32 models (Model Recovery). We found that our method could identify the correct model most of the time despite the large number of models considered (SI Appendix, Fig. S1). Moreover, we also tested how reliably our method can identify the best model for each neuron by computing the coefficient of determination (R-squared) for best models and comparing them with those of the second-best models as well as models that only include exogenous terms and thus no timescales.
We found that the best model for each neuron, which often involved about three types of timescales (SI Appendix, Fig. S2), captured larger variances of neural activity than the second-best model and the model that did not include any timescales (SI Appendix, Fig. S3). These results show that dynamics associated with these timescales indeed capture unique variability in neural response beyond what is predicted by task-relevant signals. Interestingly, the best model for most neurons (∼99.5%) in all four cortical areas included an intrinsic AR component (Fig. 2 D, Inset), illustrating the importance of intrinsic fluctuations in explaining neural variability across cortex. Together, these results demonstrate the robustness of our method in estimating multiple timescales related to dynamics of neural response.
Parallel but Independent Hierarchies of Timescales.
After validating our estimation method and fitting procedure, we used all 32 models to fit individual neurons’ response to identify the best model for each neuron based on cross-validation and to simultaneously estimate selectivity to task-relevant signals as well as intrinsic, seasonal, choice-memory, and reward-memory timescales. We observed hierarchies for all of the estimated timescales across the four cortical areas, from the LIP and the dmPFC to the dlPFC and the ACC.
The median value of intrinsic timescales increased from ∼70 ms in LIP to ∼125 ms in ACC, with the dmPFC and dlPFC exhibiting intermediate values (Fig. 2D). These intrinsic timescales, however, were smaller than those reported in Murray et al. (15), which could be due to using the decay on autocorrelations between spikes during the fixation period in that study. To test this possibility, we applied the autocorrelation method and our method to neural response during the fixation period only and found the median intrinsic timescales to be significantly larger for the activity during this epoch compared with the entire trial (SI Appendix, Fig. S4 A and B). Nonetheless, by applying our method to neural response during the fixation period, we observed a range of intrinsic timescales similar to those reported based on autocorrelation.
Similar to intrinsic timescales, our seasonal timescales also increased from LIP to ACC (Fig. 2E). However, seasonal timescales were one to two orders of magnitude larger than intrinsic timescales and significantly smaller fractions of neurons exhibited these timescales. Similarly, reward- and choice-memory timescales increased from parietal to prefrontal to cingulate cortex; these timescales assumed values between intrinsic and seasonal timescales (Fig. 2 F and G). Overall, we found that LIP and ACC consistently exhibited the shortest and longest timescales, whereas the two prefrontal areas showed intermediate values. Therefore, our method extended previous findings about intrinsic and reward-memory timescales to the single-cell level and, moreover, revealed two additional hierarchies of seasonal and choice-memory timescales.
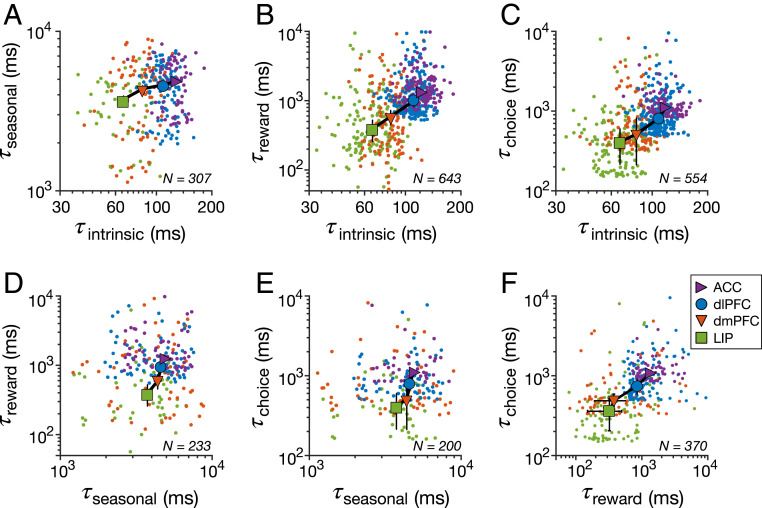
To examine the relationship among different timescales more closely, we computed the correlations between timescales within individual neurons across all cortical areas (cortexwise correlations) based on simultaneously estimated timescales for each neuron. As expected from the similar hierarchies of different timescales, we found significant correlations between most pairs of timescales except between seasonal and reward-memory timescales and between seasonal and choice-memory timescales (Fig. 3). Similar correlation between intrinsic and reward-memory timescales has been reported before but using only population-level estimates (15).
Fig. 3.
Relationship between different types of timescales across all cortical areas (cortexwise correlation). Plots show estimated timescales for individual neurons (color dots) and median timescales (symbols) against one another across four cortical areas as indicated in the legend: seasonal vs. intrinsic timescales (A), reward-memory vs. intrinsic timescales (B), choice-memory vs. intrinsic timescales (C), reward-memory vs. seasonal timescales (D), choice-memory vs. seasonal timescales (E), and choice-memory vs. reward-memory timescales (F). Error bars indicate SEM. The cortexwise correlation was significant between most pairs of timescales: intrinsic and seasonal (Spearman correlation, , ), intrinsic and reward-memory (Spearman correlation, , ), intrinsic and choice-memory (Spearman correlation, , ), and reward-memory and choice-memory (Spearman correlation, , ). There was no significant correlation between seasonal and reward-memory timescales (Spearman correlation, , ) and between seasonal and choice-memory timescales (Spearman correlation, , ).
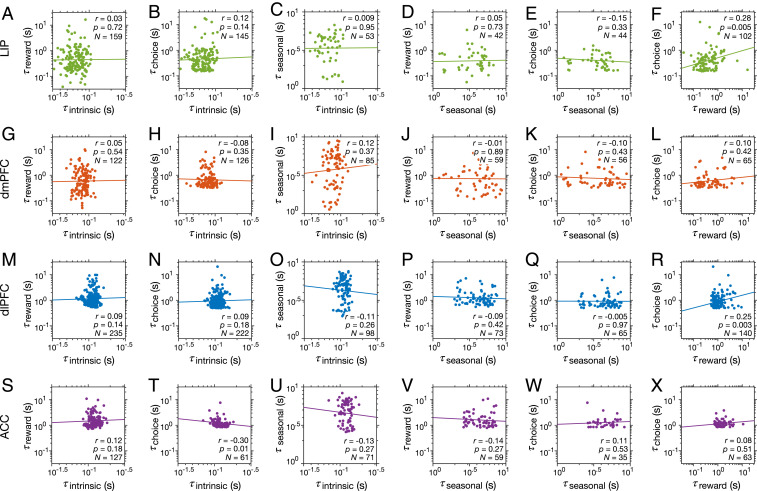
The observed cortexwise correlation between timescales, however, could be driven simply by the gradual increase in all timescales across the four cortical areas. Therefore, we tested whether these timescales are correlated across neurons within a given brain area. As mentioned earlier, the presence or lack of correlation between timescales within individual neurons would suggest similar or separate mechanisms for generations of these timescales, respectively. Indeed, we did not find any evidence for correlation between any pairs of timescales in any cortical areas (Fig. 4). The only evidence for such correlation, which did not survive the Bonferroni correction, was observed between choice- and reward-memory timescales in LIP and dlPFC. Results from additional control analysis demonstrated that this lack of significant correlation was not due to poor sensitivity of our method to detect such correlation (SI Appendix, Fig. S5).
Fig. 4.
Independence between different types of timescales within individual neurons within individual cortical areas. (A–X) Each row of panels shows the estimated timescales within individual neurons against one another for a given cortical area indicated on the left. Reported are the Spearman correlation coefficients and corresponding P values, and the number of neurons with significant values of a given pair of timescales. The solid lines represent the regression line that was fit to log timescales.
Overall, we found that although all four types of timescales consistently increased across cortex in tandem, there was no relationship between them across individual neurons in a given brain area. This indicates that the previously reported correlation between intrinsic and reward-memory timescales was mostly driven by between-region differences and suggests there are separate mechanisms underlying the generations of multiple timescales.
Behavioral Relevance of Estimated Timescales.
To estimate the four types of timescales, we fit neural response considering all task-relevant signals. This method guarantees that the estimated timescales capture unique variability in neural response and thus truly reflect multiple neural dynamics and integrations of task-relevant signals over time. However, it is still unclear whether these timescales are relevant and contribute to choice behavior. To examine whether any of the four neural timescales are relevant for choice behavior during the game of matching pennies, we estimated timescales at which monkeys’ choice behavior on the current trial is influenced by previous reward and choice for each session of the experiment (Estimation of Behavioral Timescales). The dependence on previous reward captures how reward feedback on preceding trials was integrated into reward value to influence choice. The dependence on previous choice captures how choice on preceding trials was integrated into a “choice” value to alter future choices. We then calculated the correlations between these two behavioral timescales and each of the four neural timescales.
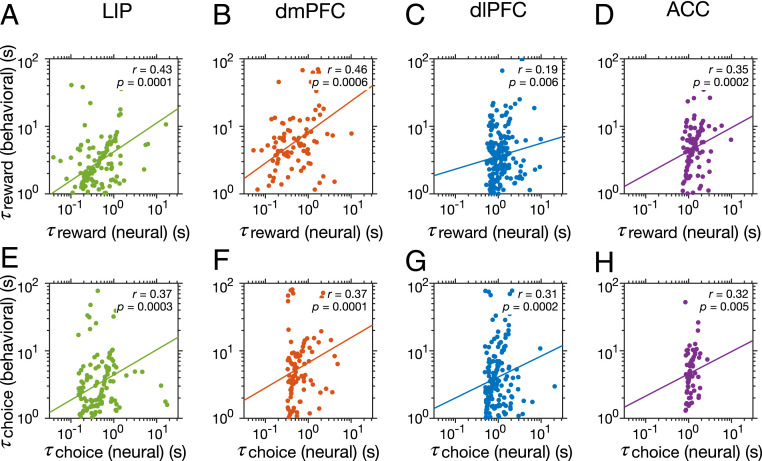
We found significant correlations between the behavioral reward timescales, which is directly related to the learning rate in the reinforcement learning model, and reward-memory timescales in all cortical areas (Fig. 5 A–D). A similar relationship has been reported previously but by considering behavioral and neural timescales from three of these cortical areas (LIP, dlPFC, and ACC) together and not individually (16). In addition, we also found significant correlations between behavioral choice timescales and choice-memory timescales of neurons in all cortical areas (Fig. 5 E–H). Importantly, there was no significant correlation between the behavioral reward timescales and choice-memory timescales (Spearman correlation; LIP: , ; dmPFC: , ; dlPFC: , ; ACC: , ) or between behavioral choice timescales and reward-memory timescales (Spearman correlation; LIP: , ; dmPFC: , ; dlPFC: , ; ACC: , ). These results illustrate that reward- and choice-memory timescales in all cortical areas were specifically predictive of behavior in terms of how previous reward and choice outcomes were integrated into reward and choice values to influence future choices.
Fig. 5.
Relationship between reward- and choice-memory timescales and behavioral timescales. (A–D) Plots show behavioral reward timescales vs. reward-memory timescales of individual neurons recorded during the same sessions, separately for different cortical areas as indicated on the top. Reported are the Spearman correlation coefficients and corresponding P values and the solid lines represent the regression line that was fit to log values. (E–H) The same as in A–D but for behavioral choice timescales. There were significant correlations between behavioral and neural timescales in all cortical areas .
In contrast to these links between behavioral timescales measuring the decays in the effect of previous reward and choice and corresponding neural timescales, there was no correlation between the behavioral timescales and intrinsic or seasonal timescales (SI Appendix, Fig. S6). Altogether, these results demonstrate that not only our estimated reward- and choice-memory timescales are linked to the integration of reward and choice outcomes over time (trials) but, more importantly, intrinsic timescales may not directly contribute to behavior as previously hypothesized (15, 16).
Dependence of Neural Timescales on Response Selectivity.
Our finding that four estimated timescales are independent of each other suggests that multiple mechanisms underlie the generation of these timescales. However, if all or some of the estimated timescales depend on response selectivity of individual neurons, inherent heterogeneity in response selectivity could render these timescales decorrelated across individual neurons even if they were generated via a single mechanism. Therefore, we performed additional analyses to examine whether the observed hierarchies of timescales and their relationships depend on the selectivity to task-relevant signals (reward outcome, choice, and their interaction). This was possible because in addition to ensuring that estimated timescales actually captured unique variability in neural response, our method also allowed us to measure the selectivity of individual neurons to task-relevant signals.
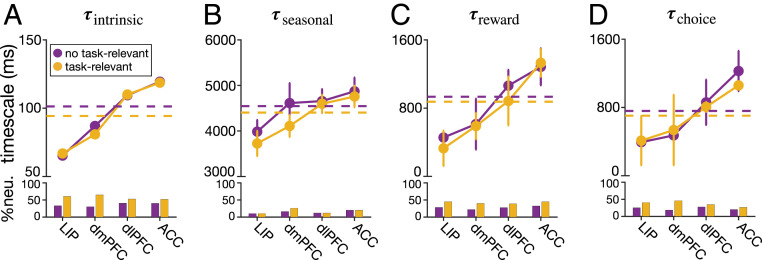
First, we found that a significant fraction of neurons in all cortical areas were selective to task-relevant signals, as reflected in the majority of best models to include the exogenous terms (LIP: 66%, ; dmPFC: 70%, ; dlPFC: 59%, ; ACC: 60%, ). Similar to previous findings based on fits of neural response with regression models (27, 28), we found significant fractions of neurons in all cortical areas to show selectivity to reward outcome right after reward feedback and selectivity to choice after target onset (SI Appendix, Fig. S7). Similar fractions of neurons encoded reward outcome across the four cortical areas , whereas the fraction of neurons selective to choice decreased from LIP to ACC .
Second, we did not find any significant difference between timescales of neurons with and without selectivity to task-relevant signals (Fig. 6 and SI Appendix, Table S2). We further examined whether estimated timescales depend on specific selectivity to reward outcome but did not find any evidence for this in any cortical area (SI Appendix, Fig. S8 and Table S3). Similarly, we did not find evidence for the dependence of timescales on specific selectivity to choice in any cortical areas. Nonetheless, the overall reward-memory timescales were significantly larger for neurons that were not selective to choice signal (SI Appendix, Fig. S9 and Table S4). This suggests a tendency for neurons with no choice selectivity to integrate reward feedback over longer timescales.
Fig. 6.
No evidence for the dependence of timescales on overall selectivity to task-relevant (reward outcome and choice) signals. Plots show the median of the estimated intrinsic (A), seasonal (B), reward-memory (C), and choice-memory timescales (D) in four cortical areas, separately for neurons with (gold) and without (purple) any type of selectivity to task-relevant signals. The dashed lines show the median across all four areas, and error bars indicate SEM. (Insets) The fractions of neurons with and without any task-relevant signals (for all neurons with a significant timescale) in different areas. Detailed statistics for comparing neurons with and without task-relevant selectivity are provided in SI Appendix, Table S2.
Recent studies have shown that the timescales for the decay of autocorrelation in the firing response of individual neurons during the fixation period, namely, intrinsic timescales, are predictive of encoding of task-relevant signals. Therefore, we also tested whether intrinsic timescales based on autocorrelation in activity during fixation depend on selectivity to task-relevant signals but did not find any difference between the intrinsic timescales of neuron with and without task-relevant selectivity (SI Appendix, Fig. S4C). This result indicates that the lack of a relationship between response selectivity and intrinsic timescales is not unique to our method.
Third, despite similar hierarchies of timescales for neurons with different types of selectivity, reward- and choice-memory timescales might still depend on the strength of modulation within each type. To test this possibility, we examined correlations between timescales of reward- and choice-memory integration and the magnitude of selectivity to reward, choice, and their interactions (quantified by standardized regression coefficients for the corresponding exogenous signals) but did not find any significant relationship (SI Appendix, Fig. S10). Furthermore, we did not find significant correlation between timescales and neural firing rates in any cortical area except for dlPFC where more active neurons showed shorter choice-memory timescales (SI Appendix, Fig. S11). These results illustrate that activity related to reward and choice memory were mostly independent of immediate response to these signals within individual neurons in a given brain area.
Together, results presented above illustrate the independence of estimated timescales and selectivity to task-relevant signals. These findings suggest that the four estimated timescales related to various dynamics of cortical neural response are not generated via a single mechanism and then modulated and sculpted by response properties of individual neurons. Instead, multiple mechanisms must underlie the generation of the four estimated timescales.
Discussion
We developed a comprehensive and robust method to estimate multiple timescales related to dynamics of neural response along with selectivity of individual neurons to important task-relevant signals. By applying this method to neuronal activity recorded from four cortical areas, we provide evidence for the presence of multiple, parallel hierarchies of timescales related to neural response modulations by previous reward and choice outcomes (reward- and choice-memory timescales), ongoing fluctuations in neural firing (intrinsic timescale), and response during similar task epochs in the preceding trials (seasonal timescale). Although evidence for hierarchies of intrinsic and reward- and choice-memory timescales have been provided before (15, 16), the relationship between these timescales within individual neurons and their dependence on response selectivity were unknown. Therefore, using our method, we addressed whether there is any relationship between intrinsic timescales and behaviorally relevant timescales within individual neurons, and whether these timescales depend on the selectivity of individual neurons to task-relevant signals and are relevant for behavioral flexibility.
We found four parallel hierarchies of timescales, from parietal to prefrontal to cingulate cortex, at the level of individual neurons. However, none of the four timescales depended on the selectivity of individual neurons to task-relevant signals, and there was no systematic relationship between these timescales across individual neurons in a given cortical area. These indicate that the previously reported correlation between intrinsic and reward-memory timescales (15) was mostly driven by between-region differences and was not a property of individual neural response. More importantly, the observed independence of the estimated timescales within any of four cortical areas is at odds with the idea that individual brain areas are specialized for the integration of task-relevant signals (e.g., reward feedback) at certain timescales. Compatible with our finding, a recent study has shown that a single brain area such as dorsal ACC can have a spectrum of value estimates based on different timescales of reward integration (29).
In addition, our findings contradict a few recent studies showing that intrinsic timescales based on the decay rate of autocorrelation in the firing response of individual neurons can predict encoding of task-relevant signals in some cortical areas (17–22). This could be due to differences in the methods used for estimations of intrinsic timescales or could simply reflect reporting bias considering the large number of studies that have examined the decay in autocorrelation of neural response. More specifically, intrinsic timescales using the decay in autocorrelation are usually obtained from a fixation period (presumably before strong task-relevant signals emerge in the cortical activity). Therefore, it is unclear whether the corresponding dynamics capture unique variability in neural response beyond task-relevant signals, which were obtained from other epochs of the task. This suggests that the relationship between such intrinsic timescales and encoding of task-relevant signals observed in previous studies might be spurious.
Our results suggest that the four estimated timescales and corresponding dynamics are not generated via a single mechanism and modulated by response properties of individual neurons and, instead, are produced by distinct mechanisms. More specifically, the independence of intrinsic timescales from neural selectivity and the gradual increase of these timescales across cortex confirm the previously postulated role of slower synaptic dynamics (perhaps due to short-term synaptic plasticity) in higher cortical areas (15, 30). Nonetheless, distinct hierarchies of timescales can be generated by mechanisms other than those underlying intrinsic timescales (23, 31). For example, seasonal timescales could be generated through circuit reverberations evoked by important task events and top-down signals and thus, could depend on the dynamics of interactions between neurons in the circuit. Therefore, independence of intrinsic and seasonal timescales within individual neurons challenges the idea that their cortical hierarchies occur due to successive processing of information (23, 24) and points to the importance of the heterogeneity of local circuits to which a neuron belongs (9). This suggests that multiple computations with distinct dynamics could be performed within a canonical microcircuit.
The lack of correlation between intrinsic (and seasonal) timescales and reward- or choice-memory timescales could undermine the proposal that intrinsic dynamics directly contribute to reward-based and goal-directed behavior (15). Instead, we speculate that the independence of different timescales within individual neurons could contribute to behavioral flexibility by allowing neurons to integrate different types of task-relevant information independently (32).
We found that reward- and choice-memory timescales selectively predict behavioral timescales related to behavioral integration of previous reward and choice outcomes, respectively, and thus are relevant to choice behavior. This indicates that these timescales are more likely to depend on long-term reward- and choice-dependent synaptic plasticity as presumed in different reinforcement learning models. Assuming Hebbian form of synaptic plasticity, one could predict that stronger response to reward feedback should result in stronger changes in synaptic plasticity and thus a shorter timescale for reward memory for a given neuron. However, we did not find any evidence for a relationship between these memory timescales and response selectivity to reward and choice. This result could indicate the presence of significant heterogeneity in synaptic plasticity rules. In addition, reward- and choice-memory timescales could be decorrelated because choice and reward are only weakly coupled during the game of matching pennies, but this might also reflect the fact that synaptic plasticity depends on both recent neural activity and reward history (33, 34). More specifically, because synaptic plasticity changes with preceding neural activity and reward history, heterogeneity in both of these factors could make choice and reward memory decorrelated. Interestingly, the observed independence of reward-memory timescales and behavioral choice timescales and independence of choice-memory timescales and behavioral reward timescales could allow the animals to integrate reward and choice outcomes independently of each other and thus results in more flexibility.
Our method also identified a separate timescale related to fluctuations of neural response to experimental epochs (events) across trials and the importance of these dynamics for capturing response variability even though only fewer than half of the recorded neurons exhibited seasonal timescales. The seasonal timescales were the longest timescales and could reflect internal neural dynamics controlled by top-down signals that could set the state of cortical dynamics that ultimately influence task performance (35). It is possible that seasonal timescales emerge and evolve as the task is being learned and that is why fewer neurons exhibit seasonal timescales.
Finally, although we only investigated response dynamics of individual neurons, there are recent studies showing that population activity exhibits similar dynamics and reflect task-relevant information (36–38). For example, Kobak et al. (36) showed that after proper demixing and dimensionality reduction, population response reflects task parameters such as reward and choice, similar to response of single neurons. In another study, Rossi-Pool et al. (38) found that during a temporal pattern discrimination task, population activity in the dorsal premotor cortex exhibits temporal dynamics similar to those of single neurons, but these dynamics diminish during a nondemanding task. Future studies are needed to compare the timescales underlying response of individual neurons to those of populations of neurons, which could be important for understanding how corresponding dynamics are generated.
In summary, our results show that timescales of neural dynamics across cortex can be used as an organizational principle to understand brain computations. However, changes in the real world happen on different timescales, each of which requires behavioral adjustments on a proper timescale. Therefore, the observed hierarchy and differences in timescales across the brain indicate that individual brain areas may contribute distinctly to behavioral adjustments on different timescales. Future experiments with distinct timescales of changes in the environment are needed to identify such unique contributions.
Methods
Experimental Paradigm and Neural Data.
All experimental procedures followed the guidelines by the National Institutes of Health and were approved by the University Committee on Animal Research at the University of Rochester and the Institutional Animal Care and Use Committee at Yale University. Experimental details for the datasets have been reported previously (27, 28, 39, 40). We used single-neuron spike train data that were recorded in macaque monkeys performing a competitive decision-making task of matching pennies against a computer opponent (28).
In this oculomotor free-choice task, monkeys were trained to choose between two identical targets by shifting their gaze (Fig. 1A). During a 0.5-s foreperiod, monkeys fixated on a small yellow square in the center of the computer screen. Next, two identical green disks were presented in opposite locations (5° away) around the center of the screen. When the central fixation square disappeared after a 0.5-s delay period, monkeys could select one of the two targets by moving their eyes and holding their gaze on a given target for 0.5 s. A red ring then appeared around the target selected by the computer and the monkeys were rewarded only if they selected the same target as the computer after holding fixation for another 0.2 s. The computer opponent made its choice by simulating a competitive opponent trying to predict the animal’s choice based on previous choices and reward outcomes by exploiting biases exhibited by the animal on the preceding trials (see ref. 28 for more details on the algorithm used by the computer opponent).
We used spike counts in 50-ms time bins starting with reward feedback (postfeedback) and spanning into the following trial (a maximum of 80 bins in a given trial). This choice of starting point was only for computational convenience. Data include recordings from 205 neurons in the LIP from one female and two male monkeys (39), 185 neurons in the dmPFC from two male monkeys (27), 322 neurons in the dlPFC from one female and four male monkeys (28), and 154 neurons in the dorsal ACC from two male monkeys (40). The recordings in ACC were obtained in the dorsal bank of the cingulate sulcus and correspond to area 24c and ventral to the dmPFC.
Method for Simultaneous Estimation of Multiple Timescales.
Our goal was to predict the spike counts as a nonstationary time series based on the preceding neural activity and task-relevant signals in order to simultaneously estimate various timescales in neural response and selectivity to task-relevant signals. A powerful method to capture nonstationarity of a time series due to factors with different timescales is the seasonal AR with exogenous inputs (ARX) model, which commonly has been used in various fields (40–44). The AR component of the ARX model aims to predict the output variable or response based on immediately preceding response, whereas the seasonal component allows the model to capture fluctuations or variations due to the periodic nature of the external factors. In our experiments, the seasonal component refers to the relationship between neural response across trials due to the specific structure of the task or task epochs (discussed below).
To predict neural response, we included two AR components, resulting in a seasonal two-dimensional (2D) ARX model that also includes two exponential memory traces for choice and reward. First, we assumed that neural response at any time point in a trial depends on earlier activity in the same trial (15). This dependence was captured by an AR component that predicts spikes in a given 50-ms time bin based on spikes in the preceding F time bins (AR model with order F). Therefore, this “intrinsic” AR component (referred to as ) uses a weighted average of firing rates in the preceding bins in order to predict the current firing rate. Our preliminary results showed that there is more than one significant autoregression coefficient for most neurons. We used different methods to assign a single intrinsic timescale for each neuron (discussed below).
Second, because of the structured nature of the task with specific time epochs, we hypothesized that neural response on a given epoch could be influenced by the activity in the same epoch in the preceding trials. In other words, task epochs could provide a “seasonal” source of variability in neural response. Therefore, we included a seasonal AR component (referred to as ) in our model in order to predict response in the current time bin based on responses in the same time bins in the preceding G trials (AR model with order G; Eq. 1). The corresponding autoregression coefficients were used to estimate a seasonal memory timescale for each neuron. Therefore, seasonal timescales capture how fluctuations of activity during a given epoch decay over trials (more precisely, between the same epoch over successive trials).
Third, we assumed that neural response at any time point in a trial depends on reward outcome (reward vs. no reward) and choice (left vs. right choice) in the preceding trials (16). These dependences relate spikes in a given time bin of the current trial to reward and choice outcomes in the preceding H trials. To capture these dependencies, we assumed two separate exponential memory-trace filters that are modulated by the average response in a given time bin and previous reward or choice signals (Eq. 1). The corresponding exponential memory-trace coefficients were used to estimate a reward-memory timescale and a choice-memory timescale for each neuron. Therefore, reward- and choice-memory timescales capture how the influence of reward and choice outcomes decays over time (time from the preceding reward feedback and choice, respectively).
Finally, we also included various exogenous terms to capture selectivity in response to current choice (C), current reward (R), and their interaction (C × R). We did not include terms for previous choice and reward because effects of previous choice and reward are captured by choice and reward memory, respectively. The selectivity to task-relevant signals was captured using four boxcars relative to relevant events in the task. More specifically, we considered 1) three terms (regressors) for choice, one for [0,500]-ms interval relative to the onset of choice targets (choice 1), one for [0,500]-ms interval relative to target fixation (choice 2), and one for [0,500]-msec interval relative to reward feedback (choice 3); 2) one term for reward for [0,500]-ms interval relative to reward feedback; and 3) one term for the interaction of choice and reward for [0,500]-ms interval relative to reward feedback.
As described above, the model for estimating timescales involves weighted average over 2D space of preceding time bins and trial firing rates (with order for time bins and for trials, F = G = 5), corresponding to and of order 5. In addition, the model involves two separate weighted averages over reward and choice outcomes on the preceding H trials (H = 5), corresponding to reward- and choice-memory traces over the preceding five trials, respectively. More formally, the spike counts in bin of trial , , is given by the following equation:
| [1] |
where is the average value of spike count in each bin over all trials, is the vector of coefficients for the task-relevant components, and is a row vector of five task-relevant inputs (three choice signals, reward, and interaction of choice and reward). AR coefficients for intrinsic and seasonal fluctuations are denoted by and , respectively (, ). Reward- and choice-memory timescales are indicated by and , whereas and are the amplitudes of reward- and choice-memory components, respectively. and indicate the time difference between current time and the time bin (with time resolution of 50 ms) at which reward or choice was occurred right before time bin on trial .
In order to estimate timescales associated with and components, for each component we solved a fifth-order difference equation (45). More specifically, an AR(5) model can be written as
| [2] |
By rewriting Eq. 2 in a vector format, a dynamic multiplier can be found by calculating the eigenvalues of the AR coefficient matrix :
| [3] |
The eigenvalues of this fifth-order polynomials in , , determine the dynamic behavior of the AR model. Considering that these eigenvalues can be real or complex numbers, we assigned a single timescale based on the absolute value of eigenvalues as follows:
| [4] |
where is the size of the time bin (time resolution). Therefore, intrinsic and seasonal timescales are equal to
| [5] |
where and are eigenvalues of the AR coefficient matrix associated with and components, respectively, and and are the size of time bins for these components ( and ). Note that for computing timescales we only considered AR coefficients that were statistically significant.
This is the most general model to predict spike counts from which we constructed more specific models by turning on and off the AR components, reward- and choice-memory traces, and task-relevant terms. These constructions resulted in 32 alternative models, consisting of all of the possible combinations of the general model components (the list of all possible combinations of the models can be found in SI Appendix, Table S1). To select the best model for each neuron, we ran all 32 models and used cross-validation (Model Selection and Parameters).
Two special cases of our method could mimic the autocorrelation model of Murray et al. (15) and the exponential memory-trace model of Bernacchia et al. (16) using only the and reward-memory components, respectively. To replicate the results of the two previous studies, we used their methods for profiling neural activity. More specifically, Murray et al. (15) used spike counts in a period starting from fixation point to 500 ms after that (postfixation) and then split spikes in this postfixation epoch into 10 time bins of 50 ms. Bernacchia et al. (16) used two time periods, each spanning 1,500 ms, that were further divided into six time bins of 250 ms each. The first period consisted of six successive, 250-ms bins starting from 1,000 ms before target onset to 500 ms after that. The second period consisted of six successive, 250-ms bins starting from 500 ms before feedback period to 1,000 ms after that.
Finally, each autoregression component involves five coefficients, and thus there could be multiple timescales associated with each AR component. Therefore, we tested a few alternative approaches for assigning a single timescale for each AR component of each neuron. This includes using only the real eigenvalues, the average of real and complex eigenvalues weighted according to their absolute values, and a third method based on transforming AR coefficients to a time constant via the time lag associated with a given coefficient. In the third approach, we used the longest timescale among all of the timescales estimated from statistically significant autoregression coefficients. More specifically, for an AR model of order 1, AR(1), that only has one single AR coefficient , a single timescale can be defined equal to , where is the size of the time bin (time resolution). By extending the same logic, we defined a set of intrinsic and seasonal timescales based on the AR components as follows:
| [6] |
where and are the size of time bins for the two components ( and ). To assign a single intrinsic and seasonal timescale to each neuron, we selected the longest timescales:
| [7] |
We did so because dynamics on smaller timescales would reach an asymptote faster and thus are less important for the overall time course of neural response. As we show in SI Appendix, Fig. S4, all these three methods provide comparable results to timescales based on autocorrelation. In this paper, we mainly report results based on the absolute values of eigenvalues of AR coefficient matrix (Eq. 4), but our main findings were consistent for all these models.
Model Selection and Parameters.
Model parameters for the AR components were determined by finding the best model for each neuron based on their performance (using R-squared measure). We performed a 10-fold cross-validation fitting process to calculate the overall performance for each model. Specifically, we generated each instance of training data by randomly sampling 90% of all data (time bins) for each neuron and then calculated fitting performance based on R-squared in the remaining 10% of data (test data). This process was repeated 30 times, and the performance was computed based on the median of performance across these 30 instances. To identify the best fit for each instance of the training data, we ran the model 50 times from different initial parameter values and minimized the residual sum of squares to obtain the best model parameters. The median of model parameters over the 30 instances was used to compute the best parameters for each model. In order to be able to compare parameters across different cross-validation instances, we z-scored all input and output vectors before fitting each instance.
To remove the outlier model parameters in a given cortical area, we used 1.5 × interquartile range method for each parameter (and not neuron). In order to determine the type of selectivity to task-relevant signals for each neuron, we first identified neurons for which the model with exogenous terms provided a better fit than the model with no exogenous terms. Neurons with a significant parameter value for a given task-relevant signal (e.g., reward signal) were determined as the neurons with that type of task-relevant selectivity (e.g., reward-selective neurons).
Model Recovery.
In order to test whether our method can identify the correct model for individual neurons, we measured the probability of finding the correct model in simulated data for which the ground truth of timescales was known. More specifically, we first randomly selected a set of 500 activity profiles (mean neural response of individual neurons divided into 50-ms time bins) from the 866 available neurons in the four cortical areas. To ensure that our model recovery is not specific to activity profile of neurons in our dataset, we permuted blocks of time bins (five bins in each block) for 200 among 500 activity profiles to generate synthetic activity profiles. For each activity profile, we used a specific model––for example, model 21 with the seasonal AR component and choice-memory trace––and 10 randomly selected sets of four timescale values to produce spike counts in each bin. The sets of timescales values were chosen from a larger set of 5,000 timescales values for the four types of timescales, each of which was generated by randomly selecting timescales from the range of estimated timescales across all areas. We then fit the simulated neural response with all 32 models and used the goodness-of-fit based on the Akaike information criterion to determine the best model for each simulated response. Finally, we computed the probability that each dataset generated with a given model was best fit by any of the 32 models. The results based on these simulations are presented in SI Appendix, Fig. S1.
Correlation Recovery Simulations.
We performed additional simulations to test whether our method is sensitive enough to detect correlations between timescales across individual neurons within a given cortical area if such correlations indeed exist. To this end, we used activity profiles of randomly selected neurons in our dataset to simulate neural response with significant correlations between certain pairs of timescales, and then used our method to estimate those timescales from the simulated data. That is, we first randomly selected 100 activity profiles (i.e., mean neural response from individual neurons) from neurons in our dataset. We then assigned a random set of four timescales to each profile and tested whether a certain pair of timescales (e.g., and ) are significantly correlated (with ) across the 100 profiles by chance. If so, we used our full ARMAX model to generate spike counts using the activity profiles and the chosen timescales. We repeated this procedure 60 times in order to generate 60 datasets of neural response for which there is a significant correlation between a given pair of timescales. We then used our full model to estimate timescales for neural response in each generated dataset and subsequently tested correlation between the estimated timescales. The results based on these simulations are presented in SI Appendix, Fig. S5.
Estimation of Behavioral Timescales.
In order to estimate behavioral timescales related to the influence of previous choice and reward outcomes, we used a reinforcement learning model with two sets of value functions, reward-dependent and choice-dependent values, that are updated according to reward outcomes and choice on every trial. More specifically, the reward-dependent value for choosing target (left or right option) on trial t,, is updated according to the following equation (46):
| [8] |
where (equal to 1 or 0) is the reward received by the animal on trial and is the learning rate. Therefore, reward-dependent values measure how reward feedback on preceding trials is integrated to influence choice. This update rule can be rearranged as
| [9] |
to show that can be used as the behavioral memory timescale of previous reward outcomes. We also considered a set of two choice-dependent value functions for capturing the effect of previous choices on the current choice:
| [10] |
where denotes the choice-dependent value function for target on trial , is the choice on trial (left or right), and is the decay rate. Therefore, choice-dependent values measure how monkeys’ choices on preceding trials are integrated to influence future choices. Similar to behavioral reward memory, can be used as the behavioral memory timescale of previous choice outcomes.
The overall value of selecting target x on trial t, , is a linear sum of the reward-dependent and choice-dependent value functions:
| [11] |
where determines the relative contribution of choice-dependent values. Finally, the probability that the animal chooses the rightward target on trial , , was determined using a softmax function of the overall values:
| [12] |
We used this model to fit choice data in each recording session of the experiment to estimate model parameters using a maximum likelihood procedure.
Supplementary Material
Acknowledgments
This work is supported by the National Institutes of Health (Grant R01DA047870 to A.S. and Grants R01DA029330 and R01MH 108629 to D.L.).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2005993117/-/DCSupplemental.
Data Availability.
All neural data and computer codes required for model fitting and data analyses presented in the paper are available in the following GitHub depository: https://github.com/DartmouthCCNL/NeuroARMAX_LeeLabData (47).
References
- 1.Felleman D. J., Van Essen D. C., Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1–47 (1991). [DOI] [PubMed] [Google Scholar]
- 2.Lennie P., Single units and visual cortical organization. Perception 27, 889–935 (1998). [DOI] [PubMed] [Google Scholar]
- 3.Shepherd G. M., Stepanyants A., Bureau I., Chklovskii D., Svoboda K., Geometric and functional organization of cortical circuits. Nat. Neurosci. 8, 782–790 (2005). [DOI] [PubMed] [Google Scholar]
- 4.Amunts K., Zilles K., Architectonic mapping of the human brain beyond Brodmann. Neuron 88, 1086–1107 (2015). [DOI] [PubMed] [Google Scholar]
- 5.Barbas H., General cortical and special prefrontal connections: Principles from structure to function. Annu. Rev. Neurosci. 38, 269–289 (2015). [DOI] [PubMed] [Google Scholar]
- 6.Siegle J. H., et al. , A survey of spiking activity reveals a functional hierarchy of mouse corticothalamic visual areas. bioRxiv:10.1101/805010 (16 October 2019).
- 7.Mountcastle V. B., The columnar organization of the neocortex. Brain 120, 701–722 (1997). [DOI] [PubMed] [Google Scholar]
- 8.Shamir M., Sompolinsky H., Implications of neuronal diversity on population coding. Neural Comput. 18, 1951–1986 (2006). [DOI] [PubMed] [Google Scholar]
- 9.Chaudhuri R., Knoblauch K., Gariel M. A., Kennedy H., Wang X. J., A large-scale circuit mechanism for hierarchical dynamical processing in the primate cortex. Neuron 88, 419–431 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Goris R. L., Simoncelli E. P., Movshon J. A., Origin and function of tuning diversity in macaque visual cortex. Neuron 88, 819–831 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wang X. J., Macroscopic gradients of synaptic excitation and inhibition in the neocortex. Nat. Rev. Neurosci. 21, 169–178 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hasson U., Yang E., Vallines I., Heeger D. J., Rubin N., A hierarchy of temporal receptive windows in human cortex. J. Neurosci. 28, 2539–2550 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Honey C. J. et al., Slow cortical dynamics and the accumulation of information over long timescales. Neuron 76, 423–434 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Goris R. L., Movshon J. A., Simoncelli E. P., Partitioning neuronal variability. Nat. Neurosci. 17, 858–865 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Murray J. D. et al., A hierarchy of intrinsic timescales across primate cortex. Nat. Neurosci. 17, 1661–1663 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bernacchia A., Seo H., Lee D., Wang X. J., A reservoir of time constants for memory traces in cortical neurons. Nat. Neurosci. 14, 366–372 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nishida S. et al., Discharge-rate persistence of baseline activity during fixation reflects maintenance of memory-period activity in the macaque posterior parietal cortex. Cereb. Cortex 24, 1671–1685 (2014). [DOI] [PubMed] [Google Scholar]
- 18.Cavanagh S. E., Wallis J. D., Kennerley S. W., Hunt L. T., Autocorrelation structure at rest predicts value correlates of single neurons during reward-guided choice. eLife 5, e18937 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cavanagh S. E., Towers J. P., Wallis J. D., Hunt L. T., Kennerley S. W., Reconciling persistent and dynamic hypotheses of working memory coding in prefrontal cortex. Nat. Commun. 9, 3498 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cirillo R., Fascianelli V., Ferrucci L., Genovesio A., Neural intrinsic timescales in the macaque dorsal premotor cortex predict the strength of spatial response coding. iScience 10, 203–210 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wasmuht D. F., Spaak E., Buschman T. J., Miller E. K., Stokes M. G., Intrinsic neuronal dynamics predict distinct functional roles during working memory. Nat. Commun. 9, 3499 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fascianelli V., Tsujimoto S., Marcos E., Genovesio A., Autocorrelation structure in the macaque dorsolateral, but not orbital or polar, prefrontal cortex predicts response-coding strength in a visually cued strategy task. Cereb. Cortex 29, 230–241 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hunt L. T., Hayden B. Y., A distributed, hierarchical and recurrent framework for reward-based choice. Nat. Rev. Neurosci. 18, 172–182 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yoo S. B. M., Hayden B. Y., Economic choice as an untangling of options into actions. Neuron 99, 434–447 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lee D., Seo H., Jung M. W., Neural basis of reinforcement learning and decision making. Annu. Rev. Neurosci. 35, 287–308 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Huk A. C., Katz L. N., Yates J. L., The role of the lateral intraparietal area in (the study of) decision making. Annu. Rev. Neurosci. 40, 349–372 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Donahue C. H., Seo H., Lee D., Cortical signals for rewarded actions and strategic exploration. Neuron 80, 223–234 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Barraclough D. J., Conroy M. L., Lee D., Prefrontal cortex and decision making in a mixed-strategy game. Nat. Neurosci. 7, 404–410 (2004). [DOI] [PubMed] [Google Scholar]
- 29.Meder D. et al., Simultaneous representation of a spectrum of dynamically changing value estimates during decision making. Nat. Commun. 8, 1942 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wang H., Stradtman G. G. 3rd, Wang X. J., Gao W. J., A specialized NMDA receptor function in layer 5 recurrent microcircuitry of the adult rat prefrontal cortex. Proc. Natl. Acad. Sci. U.S.A. 105, 16791–16796 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Miller K. D., Canonical computations of cerebral cortex. Curr. Opin. Neurobiol. 37, 75–84 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Farashahi S., Donahue C. H., Hayden B. Y., Lee D., Soltani A., Flexible combination of reward information across primates. Nat. Hum. Behav. 3, 1215–1224 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Abraham W. C., Metaplasticity: Tuning synapses and networks for plasticity. Nat. Rev. Neurosci. 9, 387 (2008). [DOI] [PubMed] [Google Scholar]
- 34.Farashahi S. et al., Metaplasticity as a neural substrate for adaptive learning and choice under uncertainty. Neuron 94, 401–414.e6 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Carnevale F., de Lafuente V., Romo R., Parga N., Internal signal correlates neural populations and biases perceptual decision reports. Proc. Natl. Acad. Sci. U.S.A. 109, 18938–18943 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kobak D. et al., Demixed principal component analysis of neural population data. eLife 5, e10989 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cueva C. J., et al. , Low dimensional dynamics for working memory and time encoding. bioRxiv:10.1101/504936 (31 January 2019). [Google Scholar]
- 38.Rossi-Pool R. et al., Temporal signals underlying a cognitive process in the dorsal premotor cortex. Proc. Natl. Acad. Sci. U.S.A. 116, 7523–7532 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Seo H., Barraclough D. J., Lee D., Lateral intraparietal cortex and reinforcement learning during a mixed-strategy game. J. Neurosci. 29, 7278–7289 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Seo H., Lee D., Temporal filtering of reward signals in the dorsal anterior cingulate cortex during a mixed-strategy game. J. Neurosci. 27, 8366–8377 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Seo H., Barraclough D. J., Lee D., Dynamic signals related to choices and outcomes in the dorsolateral prefrontal cortex. Cereb. Cortex 17, i110–i117 (2007). [DOI] [PubMed] [Google Scholar]
- 42.Hipel K. W., McLeod A. I., Time Series Modelling of Water Resources and Environmental Systems, (Elsevier, 1994). [Google Scholar]
- 43.Hamzaçebi C., Improving artificial neural networks’ performance in seasonal time series forecasting. Inf. Sci. 178, 4550–4559 (2008). [Google Scholar]
- 44.Box G. E., Jenkins G. M., Reinsel G. C., Ljung G. M., Time Series Analysis: Forecasting and Control, (John Wiley & Sons, 2015). [Google Scholar]
- 45.Hamilton J. D., Time Series Analysis, (Princeton University press, New Jersey, 1994). [Google Scholar]
- 46.Sutton R. S., Barto A. G., Reinforcement Learning: An Introduction, (MIT Press, Cambridge, MA, 1998). [Google Scholar]
- 47.Spitmaan M., et al. , Neural data and model scripts from “Multiple timescales of neural dynamics and integration of task-relevant signals across cortex.” Zenodo. 10.5281/zenodo.3978834. Deposited 11 August 2020. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All neural data and computer codes required for model fitting and data analyses presented in the paper are available in the following GitHub depository: https://github.com/DartmouthCCNL/NeuroARMAX_LeeLabData (47).