Physical mechanisms of platelet formation

Platelets are the second most abundant cell type in blood and play an essential role in the immune response by orchestrating blood coagulation during wound healing (1). Because of their short life span of under 10 d, it is critical for the body to be able to constantly replenish platelets in the blood stream, and low platelet counts are indeed associated with a slew of pathologies with major health and economic consequences. Understanding the process of platelet biogenesis is thus paramount for the development of efficient in vivo therapies, as well as for the design of bioreactors capable of producing platelets in vitro (2) for subsequent transfusion. In PNAS, Bächer et al. (3) cast light on the fundamental biophysics of this process using a computational model of platelet formation that recapitulates the salient features of in vitro experiments. Their model points to a primarily physical mechanism for platelet biogenesis based on an interfacial instability triggered by adenosine 5′-triphosphate (ATP)-driven membrane stresses and demonstrates a strong acceleration of the rate of platelet production in the presence of an external fluid flow.

The in vivo production of platelets takes place inside bone marrow, where large cells known as megakaryocytes develop long tubular membrane projections, or proplatelets, which continuously break up into small fragments destined to mature into functional platelets and enter the blood stream (1). The formation and growth of these tubular structures and their subsequent fragmentation are driven by ATP-powered processes involving biopolymers and molecular motors (4). The longitudinal extension of proplatelet tubes is attributed to arrays of microtubule bundles, stiff polymers whose continuous polymerization and sliding under the action of ATP-powered dynein motors drive elongation by exerting extensile stresses on the proplatelet membrane (5). On the other hand, breakup of the proplatelets into fragments stems from the actin cortex, a network of branched biopolymers, which, in concert with myosin motors, drives contractile stresses thought to be responsible for the pinching of the tubes (6). How these processes interact with the shape and mechanical properties of the bilayer membrane and with the local fluidic environment of the tube to produce viable platelets of controlled size remains, however, an active area of investigation.

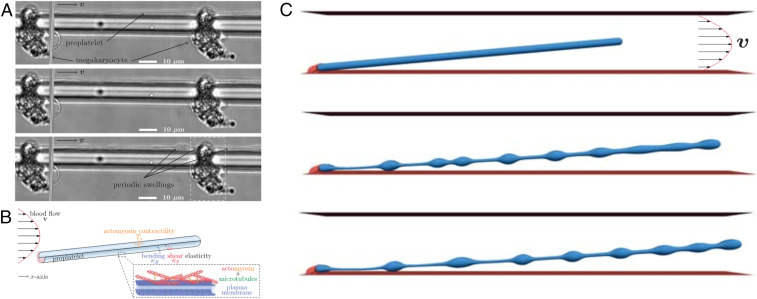
In their work, Bächer et al. (3) use a computational model along with experimental validation to elucidate the mechanics of proplatelet fragmentation under various flow conditions. Their focus is on the case of simple geometries and fluid flows, as arise in microfluidic bioreactors where megakaryocytes are cultured and form proplatelet projections in neighboring microchannels (Fig. 1A). Their simulations idealize the proplatelets as cylindrical membrane tubes (Fig. 1B), where the lipid bilayer is approximated classically as a thin elastic shell with an energetic penalty to bending (7). In addition to these passive elastic stresses, their model also incorporates an active stress contribution accounting for microscopic forces resulting from the extension of microtubule bundles and contraction of the actin–myosin cortex. In their description, both phenomena are captured by in-plane stresses akin to the surface tension acting at the interface between immiscible fluids. Unlike standard surface tension, however, these stresses are anisotropic: The effective tension is largest in the azimuthal direction due to the contractile stresses induced by actomyosin activity, but is reduced along the tube axis due to the preferential alignment and sliding of microtubules in that direction. This mechanical model for the membrane is coupled to a lattice-Boltzmann fluid flow solver (8), with an imposed flow mimicking experimental conditions in bioreactors.

Fig. 1.

In vitro experiments and numerical simulations of platelet biogenesis by Bächer et al. (3). (A) Experimental images of a megakaryocyte growing in vitro and forming a long tubular extension (proplatelet) inside a microchannel. Swellings are seen to form along the tube and will give rise to fragmentation into platelets. (B) Schematic of the computational model, where the proplatelet is represented as a cylindrical membrane tube anchored at a wall and subject to a pressure-driven parabolic flow. (C) Snapshots from a simulation, where swellings are seen to develop along the membrane tube by an active Rayleigh–Plateau instability and will ultimately break up into platelets. Adapted from ref. 3 with permission.

Under quiescent conditions, simulations of initially straight tubes develop axial radius variations in the form of quasiperiodic swellings. The necks between swellings progressively thin until pinching occurs as a prelude to breakup into individual platelets. As discussed by Bächer et al. (3), the dynamics of this process and resulting fragmentation is very similar to the breakup of a liquid jet into drops. In this classic fluid instability (9) named after Rayleigh and Plateau, surface tension forces at the interface between the two fluids cause long-wave axisymmetric radius fluctuations to become unstable as a result of curvature variations. In the present case, contractile active stresses exerted by the actin–myosin cortex play a role analogous to surface tension and drive the instability. As in the case of the liquid jet, the dominant wavelength of the emerging swellings is found to be largely independent of material parameters and only a function of the tube radius, and provides a reasonable estimate for the volume of platelets measured in experiments.

Bächer et al. (3) then address the role of fluid flow, which is found to have a profound effect on the rate of platelet formation. They first consider the effect of a pressure-driven flow, or Poiseuille flow, which approximates the flow experienced by the proplatelets in sinusoidal blood vessels in vivo, or in microfluidic channels inside bioreactors. They find, as seen in past studies, that the presence of flow has a strong impact on the fragmentation process. As illustrated in Fig. 1C, the applied flow first results in stretching of the proplatelets due to shear stresses acting along the tube, and also affects the spacing between developing swellings, which occasionally merge. This merging can result in the release of larger barbell-shaped fragments, known as preplatelets, which are also reported in experimental observations and eventually divide again into platelets of the desired size. Most remarkably, the authors find that the applied flow has a tremendous impact on the rate of platelet production, which is enhanced by an order of magnitude. Bächer et al. go on to study dynamics in a uniform flow, which approximates the flow through certain types of bioreactors where megakaryocytes are anchored at micropillars. Their findings are similar in that case, although the release of barbell-shaped preplatelets is suppressed, and the rate of fragmentation is further enhanced. These observations are all consistent with experiments, and altogether give strong credence to an active Rayleigh–Plateau instability for the mechanism of platelet biogenesis. In addition, the remarkable role of fluid flow uncovered by their model opens avenues for the design of microfluidic technologies for accelerated platelet production, where both device geometry and flow actuation could be optimized for enhanced fragmentation rates and control over polydispersity using computational modeling.

Beyond its direct relevance to platelet biogenesis, the work of Bächer et al. (3) highlights the strong promise of biomechanical modeling and simulations for uncovering the fundamental mechanisms of various cellular processes involving lipid membranes and their coupling with cytoskeletal mechanics and fluid flows. The theoretical modeling of biological membrane dynamics based on classic mechanics has a rich history in the biophysics and biomechanics literature (7, 10), yet its potential for explaining cellular dynamics in relevant biological systems remains to be fully unleashed. This is due, in part, to the high mathematical complexity of these models (11) and to technical challenges in the accurate numerical simulation of dynamically evolving surfaces. Much success has been achieved in the modeling of reconstituted in vitro systems, such as giant unilamellar vesicles whose dynamics in various microfluidic flows is now well understood (e.g., ref. 12). Living systems, however, are generally more complex and involve membrane interactions with the cytoskeletal networks, whose constant reorganization under ATP-driven processes drives nonconservative stresses.

The mathematical description of these couplings is still in its infancy. The model of active stresses employed by Bächer et al. (3), while adequate to capture the phenomenology of experiments, is highly idealized, as it lacks a detailed description of the underlying microscopic processes giving rise to these stresses. Efforts to develop continuum theories for the mechanics and thermodynamics of active biological membranes have been ongoing, and, in many cases, posit phenomenological constitutive relations for active stresses (e.g., ref. 13). A more rigorous approach should be based on the systematic coarse graining of ATP-driven microscopic dynamics inside the polymer networks, and should involve a model for the deformation and reconfiguration of the network microstructure under flow, for instance, in the form of evolution equations for configurational variables such as the polarity or nematic order parameter of the polymers. Several such models have been developed over the years to describe active particle suspensions (14), active nematics (15), and cross-linked active gels (16), and have been successful at elucidating ATP-driven dynamics in reconstituted polymer/motor protein systems (17). They have yet to be fully deployed, however, to the study of living cellular systems where their coupling with membrane deformations is a significant challenge. Another numerical approach naturally consists in explicitly modeling the polymer networks and provides exquisite information about microscopic dynamics (18, 19), albeit at a high computational cost. In addition to deformations resulting from couplings with the cytoskeleton, the cell membrane can also be subject to a variety of other complex dynamical effects arising from its viscous behavior and heterogeneous composition, and from various embedded proteins capable of driving active flows, undergoing phase separation, or inducing spontaneous curvature (20).

Despite these challenging physics, the field of membrane biomechanics has progressed tremendously over the last decade, and recent modeling efforts have significantly enhanced our understanding of various complex cellular processes. Examples include the mechanics of cytokinesis (21), endocytosis (22), and membrane tubule growth (23), among many others. The study of platelet biogenesis by Bächer et al. (3) is a valuable addition and makes a strong case for continued efforts in the areas of physics-based modeling and high-fidelity simulation of a wide-range of small-scale biological phenomena.