Target search and recognition mechanisms of glycosylase AlkD revealed by scanning FRET-FCS and Markov state models

Significance

DNA glycosylase repairs DNA damage to maintain the genome integrity, and thus it is essential for the survival of all organisms. However, it remains a long-standing puzzle how glycosylase diffuses along the genomic DNA to locate the sparse and aberrant lesion sites efficiently and accurately in the genome containing numerous base pairs. Previously, only the high-speed–low-accuracy search mode has been characterized experimentally, while the low-speed–high-accuracy mode is undetectable. Here, we observed the low-speed mode of glycosylase AlkD translocating, and further dissected its molecular mechanisms. To achieve this, we developed an integrated platform by combining scanning FRET-FCS with Markov state model. We expect that this platform can be widely applied to investigate other glycosylases and DNA-binding proteins.

Abstract

DNA glycosylase is responsible for repairing DNA damage to maintain the genome stability and integrity. However, how glycosylase can efficiently and accurately recognize DNA lesions across the enormous DNA genome remains elusive. It has been hypothesized that glycosylase translocates along the DNA by alternating between a fast but low-accuracy diffusion mode and a slow but high-accuracy mode when searching for DNA lesions. However, the slow mode has not been successfully characterized due to the limitation in the spatial and temporal resolutions of current experimental techniques. Using a newly developed scanning fluorescence resonance energy transfer (FRET)–fluorescence correlation spectroscopy (FCS) platform, we were able to observe both slow and fast modes of glycosylase AlkD translocating on double-stranded DNA (dsDNA), reaching the temporal resolution of microsecond and spatial resolution of subnanometer. The underlying molecular mechanism of the slow mode was further elucidated by Markov state model built from extensive all-atom molecular dynamics simulations. We found that in the slow mode, AlkD follows an asymmetric diffusion pathway, i.e., rotation followed by translation. Furthermore, the essential role of Y27 in AlkD diffusion dynamics was identified both experimentally and computationally. Our results provided mechanistic insights on how conformational dynamics of AlkD–dsDNA complex coordinate different diffusion modes to accomplish the search for DNA lesions with high efficiency and accuracy. We anticipate that the mechanism adopted by AlkD to search for DNA lesions could be a general one utilized by other glycosylases and DNA binding proteins.

Genome integrity is essential for the survival of all organisms and the inheritance of traits to offspring. However, due to the endogenous metabolites and environmental agents, DNA damage constantly happens and threatens the stability and integrity of the whole genome. To address this issue, various repair pathways have been evolved to guarantee the durability of accurate genetic information and to avoid faulty repair and unrepaired lesions from causing senescence, apoptosis, heritable disease, and carcinogenesis (1–4). DNA glycosylase is one kind of DNA-binding proteins responsible for repairing DNA damage, and its dysregulation could lead to tumorigenesis (5). One prerequisite for DNA glycosylase to accomplish this task is to locate the sparse and aberrant nucleobases among millions or billions of normal bases within the DNA genome (6). The efficiency and accuracy to inspect damaged bases on genomic DNA govern its ability to repair damage in chromatin (7). However, it remains a puzzle how glycosylase diffuses along genomic DNA to effectively search for damaged bases after initial nonspecific binding to DNA.

Crystal structures, NMR and molecular-dynamics (MD) simulations have revealed a loose-binding and a strong-binding conformation between DNA and proteins, including glycosylases, repressors, and zinc-finger proteins (8–13). The alternation between the two modes has been proposed as a common searching mechanism used by proteins to efficiently search for their target sites (11, 14). Using existing single-molecule imaging techniques with the limited temporal (10 to 100 ms) and spatial resolutions (20 to 50 nm) (15–21), one could only directly observe the fast mode, in which proteins travel over hundreds of base pairs within 10 ms. However, these techniques do not have sufficient resolutions to resolve the slow mode, as in this mode proteins travel over a shorter distance and time period than the resolutions of the techniques, so that the slow mode becomes indistinguishable from the stationary binding.

Single-molecule fluorescence resonance energy transfer (FRET) is more sensitive to the variations within small distance and has been successfully applied to monitor the 1-bp relative motions between DNA and nucleosome (22). However, according our estimation, to investigate the fast and slow diffusion modes of glycosylase for lesion sites search simultaneously, both nanometer spatial resolution and microsecond time resolution are required. Therefore, commonly used camera-based microscopy is not suitable to implement single-molecule FRET measurements due to its limitation in time resolution (∼10 ms). In this regard, we chose to combine FRET with our previously developed scanning fluorescence correlation spectroscopy (FCS) based on a confocal microscope (23) to design a scanning FRET-FCS method. This method can provide protein dynamics at subnanometer spatial resolution and microsecond temporal resolution, three orders of magnitude improvement from millisecond resolution provided by previous methods (16–19), serving as a useful platform to monitor the one-dimensional (1D) diffusion modes of glycosylase on double-stranded DNA (dsDNA).

In this study, we have utilized the high-resolution scanning FRET-FCS to successfully capture both the fast and slow modes within short-distance diffusion (21∼99 bp) of Bacillus cereus alkylpurine glycosylase D (AlkD), an alkylpurine DNA glycosylase targeting a range of diverse alkylpurine substrate (24, 25). We found that the fast mode has a similar diffusion timescale (∼0.12 μs per bp) as that found for other protein–DNA systems (19, 26–29). More interestingly, we directly captured a slow mode (∼15 μs per bp) of AlkD diffusion along the dsDNA, which has not been characterized before experimentally. To further dissect its underlying molecular mechanism, we constructed Markov state model (MSM) (30–49) based on extensive MD simulations with an accumulated time of ∼15 μs initiated from the crystal structure of AlkD–DNA complex (50). One 1-ms synthetic trajectory was generated according to the transition probability matrix of the MSM in order to visualize continuous cycles of AlkD diffusion over dsDNA, the timescale of which cannot be reached by conventional MD simulations. We further discovered that the slow mode is constituted by a rate-limiting rotational motion, followed by a sequential translational motion of AlkD on dsDNA. Moreover, the diffusion rate per base pair estimated by MSM is consistent with that of the slow mode measured by scanning FRET-FCS, suggesting the slow-diffusing AlkD adopts a conformation that closely resembles the crystal structure of AlkD in complex with the DNA lesion (50). Furthermore, we have pinpointed the essential role of residue Y27 in determining the AlkD’s dynamic diffusion on dsDNA. In summary, we have combined scanning FRET-FCS measurements and MSM to elucidate how diffusion modes are regulated by conformational dynamics of AlkD–DNA complexes to achieve efficient target search, paving the way to investigate the lesion recognition and excision in AlkD and other DNA-binding proteins.

Results

AlkD Displays 1D Diffusion on dsDNA via Two Different Modes.

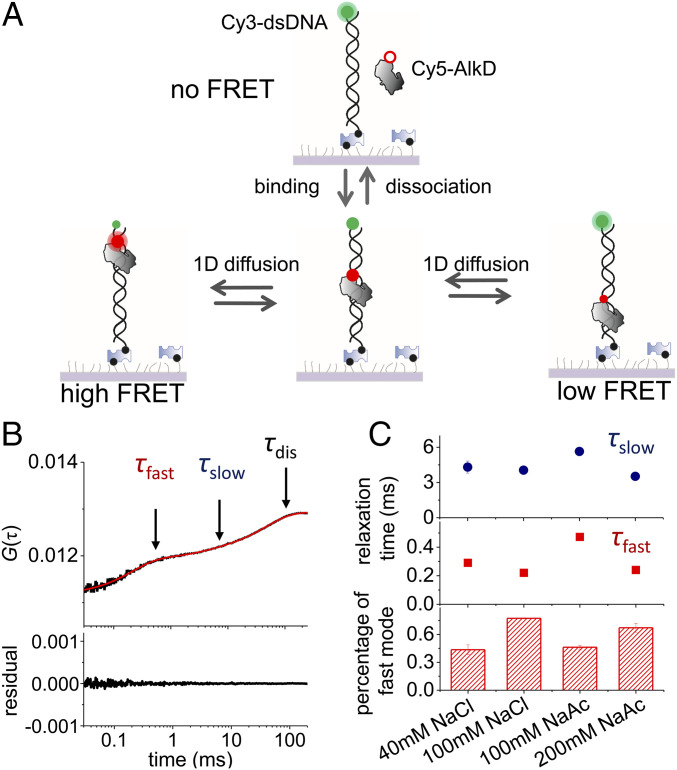
As shown in Fig. 1A, Cy5-labeled AlkD was present in the solution to transiently bind and diffuse laterally (1D) on immobilized Cy3-labeled dsDNA. A home-built inversed confocal fluorescence microscope equipped with a piezo stage was used to capture scanning FRET-FCS curves, which were calculated via cross-correlation between Cy3 and Cy5 signals.

Fig. 1.

Scanning FRET-FCS assay to capture 1D diffusion of AlkD on dsDNA. (A) Schematic of the scanning FRET-FCS assay. Cy3-labeled biotinylated dsDNA was immobilized on PEG passivated microscope glass slide via biotin−streptavidin interaction. Binding of Cy5-labeled AlkD on dsDNA and its 1D diffusion on dsDNA cause appearance and changes of Cy3/Cy5 FRET efficiency, respectively. (B) Representative scanning FRET-FCS curve of AlkD on 45-bp dsDNA calculated from correlation between Cy3 and Cy5 signals (black curve). Three relaxation times (τ_slow, τ_fast, and τ_dis) of negative correlation components, caused by biochemical processes leading to the changes of Cy3/Cy5 FRET efficiency, were extracted via exponential decay (red curve). (C) τ_slow, τ_fast, and percentage of the fast diffusion mode under different salt conditions, whose scanning FRET-FCS curves are shown in SI Appendix, Fig. S1G. Unless stated otherwise, 100 mM NaCl was used in other experiments.

From 0.03 to 100 ms, our scanning FRET-FCS curves displayed the rise of cross-correlation, which was caused by processes leading to changes of Cy3–Cy5 FRET signals at this timescale. Three anticorrelation components were extracted from the scanning FRET-FCS curves in this range (Fig. 1B). We assigned the slowest component as the process of binding and dissociation between AlkD and immobilized dsDNA, because its relaxation time (τ_dis = 44 ± 4 ms) agreed well with the relaxation time (66 ± 18 ms) estimated independently from the protein–dsDNA binding and dissociation rates (SI Appendix, Table S1) using our single-molecule total internal reflection fluorescence microscope (see SI Appendix for details). As expected, when the length of DNA duplex decreased to 8 bp to completely abolish 1D diffusion of AlkD, scanning FRET-FCS curve displayed only one anticorrelation component caused by binding and dissociation between AlkD and dsDNA (SI Appendix, Fig. S1A). Additional control experiments also showed that the two fast anticorrelation components in this range were not produced by breathing of dsDNA or motion of dyes and linkers (SI Appendix, Fig. S1B). Single-molecule FRET-FCS curves of each individual molecule all displayed two diffusion components (SI Appendix, Fig. S1 C and D), indicating that they were not caused by heterogeneity of immobilized molecules. Therefore, we anticipated that the remaining two components (τ_fast and τ_slow) were caused by 1D diffusion of AlkD on dsDNA.

Next, we aimed to dissect the origin of the two diffusion components. To achieve this, we performed Monte Carlo simulations (see SI Appendix for details) to model random diffusion trajectories of AlkD and to generate FRET-FCS curves by assuming that the FRET efficiency depends on both the relative distance and dipole orientation between Cy3 and Cy5 (SI Appendix, Fig. S1E). This enables us to examine whether diffusion-coupled rotational motions of AlkD around dsDNA are the cause for the two diffusion components in our measured FRET-FCS curves. The simulated FRET-FCS curves displayed two anticorrelation components, whose relaxation times were about 200-fold different from each other (SI Appendix, Fig. S1F). The simulated results did not agree with our measured relaxation times (τ_fast = 0.22 ± 0.01 ms and τ_slow = 4.1 ± 0.3 ms, which differ by about 20 times), disproving the assumed model and suggesting that two diffusion components were not caused by diffusion-coupled rotational motions of AlkD. This is understandable, as both dyes were linked to biomolecules by a single covalent bond, and thus the orientations of the dipoles of Cy3 and Cy5 are speculated to move most freely. As a result, their FRET efficiency only depended on their relative distance. Last, we discovered that the salt concentration affected two diffusion components differently (Fig. 1C and SI Appendix, Fig. S1G), further consolidating that the two diffusion components are caused by different modes. Specifically, high ionic strength, which weakens interactions between AlkD and dsDNA, reduced the relaxation times of both diffusion components and enhanced the contributions of the fast component. Therefore, the relaxation time of the fast component is more sensitive toward salt concentration than the slow component. Together, these results suggested that the two diffusion components, whose relaxation times are about 10- to 20-fold different from each other, were likely caused by two 1D diffusion modes of AlkD–dsDNA complexes possessing different interacting conformations and strengths.

Residence Times of AlkD per Base Pair Derived from Relaxation Times.

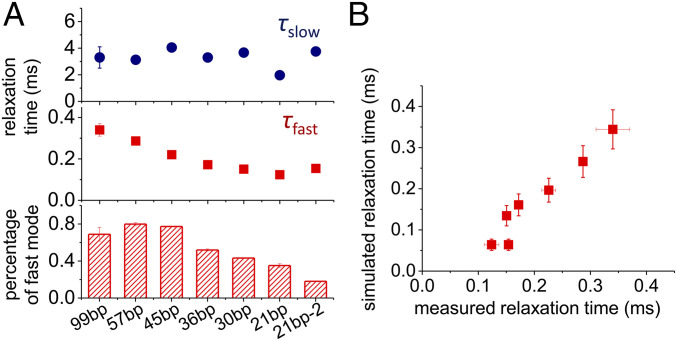
We first examined the influence of dsDNA length on the relaxation times τ_fast and τ_slow (Fig. 2A and SI Appendix, Fig. S2). When the length of dsDNA decreased from 99 to 21 bp, τ_fast deceased from ∼0.3 to ∼0.1 ms and the proportion of the fast component also decreased from ∼80% to ∼20%. On the contrary, τ_slow was less sensitive to the length of dsDNA and always remained at around 3 ms (Fig. 2A). In this regard, the residence time of AlkD on each base pair in the fast mode can be estimated by exploring the FRET-FCS curves of dsDNA with different lengths. In particular, we generated scanning FRET-FCS curves of AlkD on dsDNA of different lengths by Monte Carlo simulations (see SI Appendix for details). Two parameters, namely the residence times of AlkD on an internal base pair (τ_int) and on a terminal base pair (τ_ter), were introduced to perform the Monte Carlo simulations. When τ_int = 0.12 ± 0.08 μs and τ_ter = 11 ± 2 μs, the timescales estimated from Monte Carlo simulation yielded the best fit to the experimentally measured overall timescales for τ_fast at different lengths of dsDNA (Fig. 2B and SI Appendix, Fig. S3A). Based on this result, the residence time of AlkD is 0.12 ± 0.08 μs per bp in its fast 1D diffusion mode, and the corresponding diffusion coefficient D = (8 ± 5) × 10⁶ bp²/s is within the range of reported values for other glycosylase proteins (19).

Fig. 2.

Diffusion of AlkD on dsDNA with different lengths. (A) τ_slow, τ_fast, and percentage of the fast mode extracted from scanning FRET-FCS curves of AlkD on dsDNA of different lengths shown in SI Appendix, Fig. S2. (B) Correlation between measured τ_fast shown in A and simulated τ_fast with dsDNA of different lengths extracted from the Monte Carlo simulations shown in SI Appendix, Fig. S3A.

We found that τ_slow is highly sensitive to the DNA sequences by using two dsDNAs of the same length but with different sequences (21 bp vs. 21 bp-2, Fig. 2A). When the DNA sequence changed from 21 bp to 21 bp-2, τ_slow was extended from 2 to 4 ms and the proportion of the slow component also increased from ∼60% to ∼80%. By sharp contrast, the DNA sequence had marginal influence on τ_fast. Because τ_slow is not sensitive to the length of dsDNA (Fig. 2A), we cannot uniquely estimate τ_int and τ_ter of the slow component using the method described above (SI Appendix, Fig. S3A). To provide a rough estimation of the residence time of AlkD on each base pair in the slow mode, we fit the experimental FRET-FCS data of 45-bp dsDNA by setting τ_int:τ_ter = 1:1, 1:10, and 1:100, respectively, in the Monte Carlo simulations. Accordingly, simulation produced three respective sets of parameters τ_int = 17 ± 1 μs and τ_ter = 17 ± 1 μs for τ_int:τ_ter = 1:1, τ_int = 11 ± 1 μs and τ_ter = 110 ± 8 μs for τ_int:τ_ter = 1:10, and τ_int = 2.2 ± 0.2 μs and τ_ter = 220 ± 20 μs for τ_int:τ_ter = 1:100, all of which could match the experimental values of the slow mode (4.1 ± 0.3 ms) (SI Appendix, Fig. S3B). Although τ_int:τ_ter differs significantly in three sets of parameters, the residence times of AlkD on an internal base pair (τ_int) are similar and serve as a suitable metric for estimating the diffusion timescales. Therefore, we estimated that AlkD spends 2 to 17 μs per bp in the slow mode.

Diffusion Dynamics Characterized by Markov State Model.

A recent MD simulation study proposed that the AlkD–dsDNA complex can alternate between a loose-interacting conformation for general search along dsDNA and a tightly interacting conformation in the crystal-like structure when initiating excision (13). To establish the connection between the conformation of the AlkD–dsDNA complex and dynamics of 1D diffusion that we captured, we constructed MSM based on extensive all-atom MD simulations based on a published structure of AlkD (Protein Data Bank [PDB] ID: 5CL3) (50). MD simulations with aggregated simulation time of 15 μs were performed (see SI Appendix for details), and more than 700,000 MD conformations were utilized for the MSM construction.

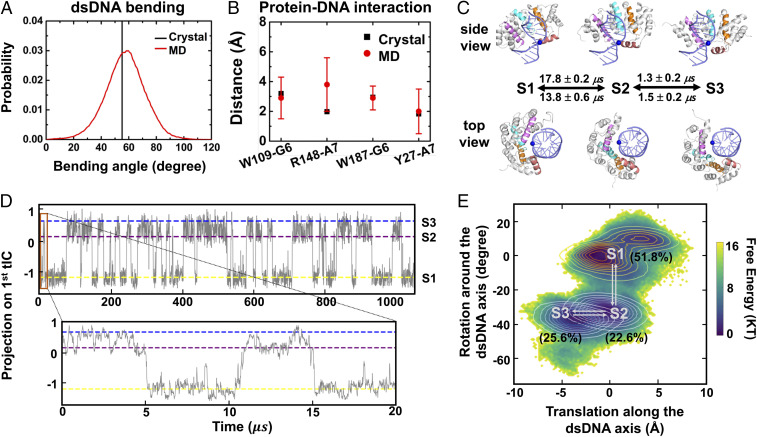
AlkD–dsDNA complex in our simulations adopted configurations closely resembling the crystal structure (PDB ID: 5CL3). First, dsDNA was bent in an extent quite similar to that of the crystal structure (Fig. 3A). The bend angle is a common metric to measure the bending of dsDNA (51) (see SI Appendix for details). We found that the bend angle of dsDNA in our simulations covered a wide range between 20$°$ and 100$°$, and the distribution centered at ∼59$°$. This matched well with the bend angle (∼55$°$) of the crystal structure. Second, most of the protein–DNA interactions observed in the crystal structure were well maintained in our MD simulations (Fig. 3B and see SI Appendix for details). For example, the hydroxyl group of Y27 was hydrogen bonded with the nitrogen atoms in the nucleobase of DNA. Also, nitrogen atoms in the side chain of R148 formed salt bridges with the phosphate group of the adjacent adenine. Furthermore, the hydrophobic ring of W109 and W187 formed CH–π interaction with the neighboring nucleosugar. Overall, dsDNA was bound to AlkD in a similar fashion as in the crystal structure.

Fig. 3.

Markov state modeling of AlkD–dsDNA complex. (A) Distribution of dsDNA bend angle sampled by MD simulations (red curve). For comparison, the bend angle calculated using the crystal structure (PDB ID: 5CL3) is shown in black line. (B) Comparison of protein–DNA distances between MD simulations (red circle with error bar) and the crystal structure (black square) (see SI Appendix for details). “G6” and “A7” represent G with residue ID 6 and A with residue ID 7 in our simulation model, respectively. (C) Representative conformations of three major metastable states from two different views. dsDNA and AlkD are shown in indigo and gray, respectively. The helixes close to the dsDNA are shown in individual colors, as well as one phosphate in blue sphere to demonstrate the conformational change of AlkD. The mean first passage times estimated from MSM are presented beside the arrows. (D) Projections of AlkD–dsDNA conformations onto the first tIC as a function of time for the 1-ms trajectory generated based on MSM. The state index is labeled at the right-hand side. The segment from 0 to 20 μs is expanded beneath. (E) Projection of MD conformations onto the angle describing the rotation of AlkD around the dsDNA (y axis) and the translating distance of AlkD along the dsDNA (x axis). Contour plots of each metastable state are also shown with the population in the parenthesis.

To fully elucidate the diffusion dynamics of AlkD along dsDNA, we used time-structure independent components analysis (tICA) (34, 52, 53) to determine the slowest relaxing degrees of freedom and constructed MSM using MSMbuilder (54) (see SI Appendix for details). The parameters for constructing MSM were validated by generalized matrix Rayleigh quotient (40, 41) (SI Appendix, Figs. S4 and S5). We identified three metastable states when AlkD diffuses over one base pair. Besides the pre- (S1) and post-translocation (S3) states, we identified a translocation intermediate state (S2, Fig. 3C). To further visualize the diffusion dynamics, we generated a 1-ms synthetic trajectory by sampling the transition probability matrix of our 1,000-state microstate MSM with a lag time of 15 ns (see SI Appendix for details). As shown in Fig. 3D, the AlkD–DNA complex oscillated between the pre- and post-translocation states through the intermediate state (S2) multiple times within 1 ms, and the averaged timescale to translocate over one base pair was 15∼20 μs (Fig. 3 C and D). These timescales estimated from the MSM matched well with our experimentally measured residence times, 2 to 17 μs per internal base pair in the slow mode.

Asymmetric Translocation Pathway Over One Base Pair.

Our MSM demonstrated that the translocation over one base pair followed an asymmetric pathway with a rotational motion followed by a sequential translational motion. As shown in Fig. 3 C and E, from S1 to S2, AlkD rotated ∼34$°$ around the dsDNA; from S2 to S3, AlkD slide ∼3.5 Å along the dsDNA, which corresponds to the length of one base pair (55). Furthermore, we found that the timescales of these two conformational transitions were drastically different (Fig. 3C). The transition from S1 to S2 caused by the rotation of AlkD around dsDNA was the rate-limiting step, which occurred at 13 to 17 μs, while transition from S2 to S3 caused by the sliding motion of AlkD only took 1.3 to 1.5 μs, 10 times faster than that from S1 to S2. This could be attributed to the extent of hydrogen bond network reconfiguration during the conformational change (SI Appendix, Fig. S6). From S1 to S2, ∼4.5 hydrogen bonds were broken while ∼7.0 hydrogen bonds were formed simultaneously; from S2 to S3, elimination of ∼3.1 hydrogen bonds was accompanied by the formation of ∼3.0 hydrogen bonds. In this regard, rotation of AlkD around dsDNA, identified as S1-to-S2 transition, involved more significantly reconfigurations of hydrogen bonds to complete its conformational change and therefore became the rate-limiting step in the asymmetric translocation pathway.

Effect of Residue Y27 on Diffusion Dynamics.

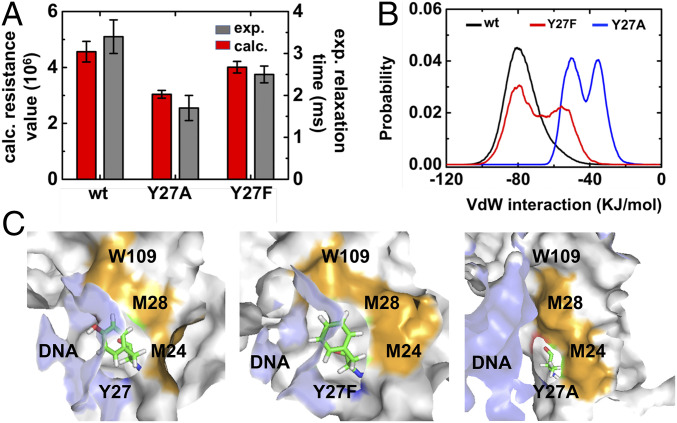
Previous studies have pinpointed several amino acid residues that are essential for recognizing and excising the damaged DNA (56–58). However, roles of any AlkD residues on protein diffusion dynamics have not been examined. Herein, we focused on residue Y27, which maintained its hydrogen bond with nucleotides during the whole cycle of diffusion (SI Appendix, Fig. S7). The hydroxyl group of hydrophilic residue Y27 inserts into the minor groove of DNA and contacts the nucleobase instead of the backbone (57). To separately examine the effects of hydrogen bonds and steric interactions, we designed Y27F and Y27A mutants, respectively. Both mutants eliminated hydrogen bond while Y27A mutation could further reduce the size of the side chain. The experimental scanning FRET-FCS curve indicated that Y27A accelerated the diffusion in both fast and slow modes, while Y27F mutation barely influenced the translocation rate (Fig. 4A and SI Appendix, Fig. S8), suggesting that it is the steric effect rather than the hydrogen bond that plays a key role in determining the diffusion dynamics. To further dissect the molecular mechanism of Y27 on the diffusion dynamics, mutant simulations were initiated from the conformational region corresponding to the rate-limiting rotation step in the translocation. It is worthy to note that our simulations were initiated from the crystal structure with DNA damage, and thereby can only examine how the mutants affect the rate of the slow mode. Specifically, we selected 10 conformations from the transition area between S1 state and S2 state. For each conformation, we generated the corresponding Y27 mutation to initiate two 50-ns MD simulations (see SI Appendix for details). As a comparison, these 10 conformations were also used to seed wild-type simulations. Consistent with the experimental observation, MD simulations also showed that the Y27A mutation promoted the rate (smaller resistance value; see SI Appendix for details) while Y27F mutation demonstrated a similar rate as wild type (Fig. 4A). As the steric effect of Y27 played a dominant role in determining the diffusion dynamics of AlkD along dsDNA, we examined the van der Waals interactions between Y27 and its neighboring protein residues, as well as nucleic acids (Fig. 4B and SI Appendix, Figs. S9 and S10). We found the wild-type Y27 experienced the strongest van der Waals interactions with its surroundings, which were slightly weakened in Y27F but greatly reduced in Y27A. This result supported the above assertion that the bulky side chain of Y27 or Y27F led to strong steric effect and thus hindered the 1D diffusion, while Y27A has smaller volume and accelerated diffusion. Further analysis pinpointed protein residues M24, M28, and W109 contributed significantly to the steric effect caused by Y27 or Y27F (Fig. 4C and SI Appendix, Fig. S9).

Fig. 4.

Effects of residue Y27 on the dynamics of diffusion. (A) Comparison between the resistance value computed from MD simulations (red bars) and the relaxation time derived from experiments (dark gray bars) for the wild-type AlkD, AlkD-Y27A, and AlkD-Y27F. Means and SDs of calculated resistance value were estimated by bootstrapping algorithm (see SI Appendix for details). (B) The distribution of van der Waals interactions between Y27 (wild type, black curve) and its surrounding residues (including residues 23 to 29, 109, and all nucleic acids), in comparison with that in Y27F (red curve) and Y27A (blue curve) mutants. (C) Representative conformations of Y27, Y27F, and Y27A in the AlkD–dsDNA complex. Residue 27 is shown in sticks, and nucleic acids are represented in light blue surface. W109, M28, and M24 are highlighted in orange and other protein residues are shown in silver surface.

Discussion

Glycosylase AlkD is an essential enzyme responsible for repairing DNA damage by utilizing a unique non–base-flipping recognition mechanism (50, 56, 58). However, it has been a long-lasting question how DNA glycosylases can locate the DNA lesions efficiently and accurately. It has been proposed that DNA glycosylases such as AlkD can alternative between a fast mode and a slow mode to search for DNA lesions. Unfortunately, existing single-molecule fluorescence imaging techniques do not have sufficient resolutions to capture the slow mode. In this study, our newly developed scanning FRET-FCS platform with improved spatial and temporal resolutions enabled us to examine the diffusion of AlkD along dsDNA at much higher resolutions, which captured the fast and slow 1D diffusions of AlkD simultaneously. In the fast mode, AlkD spends ∼0.12 μs on each base pair, which corresponds to 1D diffusion constant of ∼8 × 10⁶ bp²⋅s⁻¹. This is similar to the reported diffusion rates of other proteins, including hOgg1, MutY, and MutM glycosylases, along dsDNA (19). In the slow mode, AlkD spends 2 to 17 μs on each base pair with 100 mM NaCl, which corresponds to a 1D diffusion constant of 6 × 10⁴ to 5 × 10⁵ bp²⋅s⁻¹. On average, AlkD spends ∼70 ms on dsDNA during each binding event and diffuses across 70 to 190 bp in its slow mode before dissociation, which is beyond the detection limit of existing single-molecule imaging methods. This emphasizes the advantages of our FRET-FCS platform.

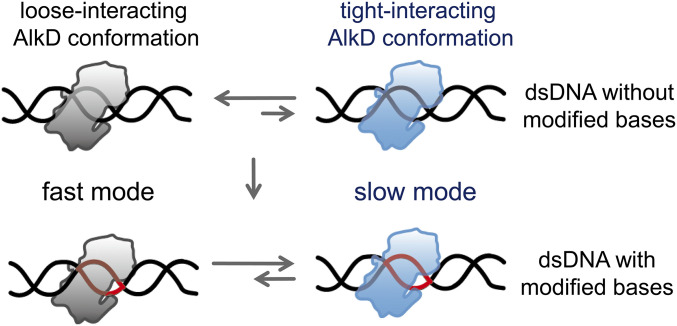
A recent MD simulation study identified two distinct AlkD–dsDNA conformations, a loose-binding state and a tight-binding state, which were hypothesized to cause different diffusion rates (13). Similarly, a DNA binding domain EngHD has been shown to switch between two different conformations to modulate its diffusion rates (11). Our MD simulations demonstrated that AlkD–dsDNA adopts a crystal-structure–like, tight-binding conformation and MSM estimated a diffusion timescale of 15 to 20 μs per bp, which agreed with the measured value of the slow mode. This confirmed our assertion that the slow mode corresponds to the tight-binding conformation as observed in the crystal structure and in our MD simulations, while the fast mode is likely caused by the loose-binding conformation identified by previous MD simulation (13). Collectively, evidence from experiments and computations support the model that AlkD–dsDNA switches between different conformations during target searching (Fig. 5).

Fig. 5.

Mechanistic scheme of diffusion and target search of AlkD. Modified bases are shown in red.

Combining our findings with previous studies, we proposed the following kinetic scheme to elucidate how conformational dynamics of AlkD and dsDNA interplay with each other to enable efficient target searching and recognition (Fig. 5). AlkD–dsDNA adopts the loose-binding conformation in the fast diffusion mode, which is a general search mode to screen through unmodified dsDNA with high efficiency. Although AlkD can occasionally transit into its slow mode on an unmodified dsDNA, distortions of dsDNA structure caused by modified or mismatched bases are likely to promote the slow diffusion mode by stabilizing the protein into its crystal-like conformation to form a tight-binding complex, which gives AlkD sufficient time to thoroughly search near the lesion (13). After locating the modified base, AlkD–dsDNA excision complex is formed to complete the target recognition and to initiate subsequent lesion excision. We hypothesized that similar search mechanisms are used by human glycosylase AAG, which also presents a loose-binding and a strong-binding structure with DNA (12).

Our MSM constructed from all-atom MD simulations provided additional insights into the diffusion mechanisms of AlkD. First, AlkD displays rotational motions around the helical structure of dsDNA during its 1D diffusion, a mechanism used by many DNA binding proteins (19). Our MSM further demonstrated that diffusion of AlkD over one base pair contained two sequential motions in the slow mode. The ∼34° rotation motion is the rate-limiting step, which is 10 times slower than the sliding motion over one base pair. Therefore, mutations affecting the rate-limiting rotational motion shall also impact the overall diffusion rate of the slow mode. Indeed, our mutant simulations indicate that Y27A can accelerate the rotational motion, and thus should also increase the overall rate of the slow diffusion mode. Our scanning FRET-FCS measurements of the Y27A mutant display a faster diffusion rate compared to wild type, and thus validated our theoretical prediction based on the asymmetric translocation model. This agreement between simulations and experiments on the mutant’s effect on AlkD’s diffusion rate indirectly supports our proposed mechanism of the asymmetric movement. In addition, the relaxation times of the fast and slow modes, which were 10 to 20 times different from each other, were affected by Y27A and Y27F mutations in a similar trend (SI Appendix, Fig. S8), suggesting that AlkD in the fast and slow modes may share similar interaction network surrounding residue Y27. We also note several previous studies have achieved direct comparisons between MSM predictions and experimental observations including FRET (59), and particularly the augmented Markov model framework has been developed to combine experimental and simulation data to improve the accuracy of the predicted biomolecular dynamics by MSMs (60). In this study, our MSMs only investigate the diffusion of AlkD over one base pair (with the slowest timescale of ∼15 μs), while the time resolution of our single-molecule FRET experiment is limited at 10 μs. Therefore, experimental measurements at significantly finer time resolutions or MSMs describing translocation over substantially longer DNA is needed to enable direct comparisons between dynamics of transitions among different metastable states in our MSMs and experimental observables.

Here, combining our newly developed scanning FRET-FCS method with MSM constructed from extensive MD simulations, we developed an integrative platform to elucidate atomistic diffusion dynamics of proteins on dsDNA. Our results suggested that AlkD utilizes a general fast diffusion mode to pass through unmodified bases with high efficiency and a slow diffusion mode to thoroughly search near the lesion site. Conformational dynamics of AlkD–dsDNA complex regulate transformation between two diffusion modes to ensure efficiency and accuracy of the target search processes. Similar mechanisms are likely being used by other glycosylases and DNA binding proteins.

Materials and Methods

Scanning FRET-FCS Measurements.

PEG-passivated slides were incubated with 0.05 mg/mL streptavidin for 3 min. Then biotinylated dsDNA was specifically attached to PEG-passivated slides via interactions between biotin and streptavidin. Free-diffusing Cy5-AlkD was added to microscope flow cells to examine interaction between Cy3-dsDNA and Cy5-AlkD. Unless stated otherwise, scanning FRET-FCS experiments were performed at 25 °C in buffer (50 mM Tris⋅HCl, pH 7.5, 100 mM NaCl, 0.1 mM EDTA, 1 mM DTT, and 1% BSA) with an oxygen scavenging system, containing 3 mg/mL glucose, 100 µg/mL glucose oxidase, 40 μg/mL catalase, 1 mM cyclooctatetraene, 1 mM 4-nitrobenzylalcohol, and 1.5 mM 6-hydroxy-2,5,7,8-tetramethyl-chromane-2-carboxylic acid (61, 62).

Scanning FRET-FCS measurements were performed on a home-built confocal microscope, based on a Zeiss AXIO Observer D1 fluorescence microscope with an oil-immersion objective (Zeiss; 100×; numerical aperture, 1.4), and solid-state 488-, 532-, and 640-nm excitation lasers (Coherent; OBIS Smart Lasers). The piezo nanopositioning stage (PI) was assembled on the stage of the microscope and controlled by a multifunction I/O card (National Instruments; PCI-6289) with a custom Labview script (National Instruments) to achieve accurate nanoscale scanning and positioning. For the scanning FRET-FCS experiments, the scan speed was 0.1 μm/s. Laser powers at the samples were ∼5 μW. Fluorescence signals from the sample passed through a pinhole (diameter, 50 μm) and were separated by a dichroic mirror (T635lpxr, Chroma), which were further filtered by bandpass filters ET585/65m (for Cy3, Chroma) and ET700/75m (for Cy5, Chroma) before detected by two avalanche photodiode (APD) detectors (Excelitas; SPCM-AQRH-14). The cross-correlation of fluorescence signals was calculated by a correlator (Correlator.com; Flex02-01D). For each experimental condition, three or more identical replicates were performed. Each replicates were collected for 5 min.

Scanning FRET-FCS curves between 30 μs and 250 ms were fitted by the following:

$$G\left(\tau \right)=A_{fast}\cdot e^{-\frac{\tau }{{\tau }_{\text{fast}}}}+A_{slow}\cdot e^{-\frac{\tau }{{\tau }_{\text{slow}}}}+A_{dis}\cdot e^{-\frac{\tau }{{\tau }_{\text{dis}}}},$$

to extract three relaxation times. Percentage of fast diffusion mode was calculated via $A_{fast}/\left(A_{fast}+A_{slow}\right)$.

MD Simulations.

The crystal structure of AlkD [PDB ID: 5CL3 (50)] was used as the structural basis for constructing the pre-translocation model and the post-translocation model for investigation the diffusion of AlkD over one base pair. Manual modifications were made to ensure the length and sequence of base pairs match between the pre- and post-translocation states. Preliminary pathways were generated using Climber algorithm (63, 64) and 30 representative conformations were selected from the preliminary pathways (SI Appendix, Fig. S11) to seed the first round of MD simulations. For each conformation, energy minimization and equilibration were performed, followed by one 50-ns NVT simulations at 298 K. The conformations in the first round of simulations were collected and used as the conformational basis to seed the extensive MD simulations for the MSM construction. Amber99sb-ildn force field (65) was utilized to simulate both the protein and nucleotides. All MD simulations were performed by Gromacs 5.0.4 package (11). See SI Appendix for the details about the model construction and MD simulations.

Markov State Model.

The conformational ensemble from the 300 × 50-ns MD simulations served as the structural basis to construct MSM using MSMbuilder (54). In particular, tICA (34, 52, 53) was used to determine the slowest relaxing degrees of freedom (see SI Appendix for details). Generalized matrix Rayleigh quotient (40, 41) was utilized to validate the parameters for constructing MSM, including the atom pairs, tIC number, tIC lag time, and the number of microstates (SI Appendix, Figs. S4 and S5). With the optimal parameters, the MD conformational ensemble was finally divided into 1,000 microstates by K-center algorithm (66, 67) (SI Appendix, Figs. S5A and S12) and a proper lag time of 15 ns was chosen to render the model Markovian (SI Appendix, Fig. S13). To gain the molecular insight, the 1,000 microstates were further grouped into macrostates based on their kinetic similarity. See SI Appendix for the details about MSM construction and validation.

For further experimental and computational details, see SI Appendix.

Data Availability.

Raw data used to plot all figures can be found in Dataset S1. All study data are included in the article and SI Appendix.