Demographic perspectives on the mortality of COVID-19 and other epidemics

Significance

What would a hypothetical 1 million US deaths in the COVID-19 epidemic mean for mortality of individuals at the population level? Life expectancy for 2020 would drop by 2.9 y. Those dying would lose an average of 11.7 y of expected remaining life, while for the general population the loss of remaining life would be 0.2 y for elders (at age 80) and much less at younger ages. Mortality per person would be less than that of the Spanish flu, but closer to that of the opioid and HIV/AIDS epidemics, while far more concentrated in time. The standard valuation of averting 1.75 million deaths would be many trillions of dollars.

Abstract

To put estimates of COVID-19 mortality into perspective, we estimate age-specific mortality for an epidemic claiming for illustrative purposes 1 million US lives, with results approximately scalable over a broad range of deaths. We calculate the impact on period life expectancy (down 2.94 y) and remaining life years (11.7 y per death). Avoiding 1.75 million deaths or 20.5 trillion person years of life lost would be valued at $10.2 to $17.5 trillion. The age patterns of COVID-19 mortality in other countries are quite similar and increase at rates close to each country’s rate for all-cause mortality. The scenario of 1 million COVID-19 deaths is similar in scale to that of the decades-long HIV/AIDS and opioid-overdose epidemics but considerably smaller than that of the Spanish flu of 1918. Unlike HIV/AIDS and opioid epidemics, the COVID-19 deaths are concentrated in a period of months rather than spread out over decades.

As we write, societies around the world are struggling to protect their populations from the COVID-19 pandemic. Both citizens and policymakers are trying to make sense of the magnitude of the crisis and the lives that it threatens.

In this paper, we provide several different ways to think about the mortality of the epidemic. It is possible to portray the death toll in a way that feels overwhelmingly large, but it is also possible to describe it in a way that makes the epidemic mortality seem almost negligible. Our view is that COVID-19 should be seen as an extremely large mortality threat. By most measures, the threat of the current epidemic is smaller in scale than that of the Spanish flu, but COVID-19 mortality could in a matter of months be equal in overall magnitude to the decades-long HIV and opioid epidemics.

Our intention here is not to provide new forecasts of COVID-19 mortality. Instead, we combine existing projections with observations to date about the age pattern of mortality, producing an estimated age profile of COVID-19 mortality. This age profile, which can be scaled up or down, enables estimation of the epidemic’s impact on period life expectancy and loss of person years of life at a population scale, as well as comparison with past epidemics.

A further contribution of this paper is to show that the age pattern of deaths, when appropriately adjusted, is quite similar across a wide range of countries and stages of the epidemic. Indeed, the increase in mortality by age from COVID-19 strongly resembles the age pattern of all-cause mortality. Whereas all-cause mortality tends to follow Gompertz’s law, increasing exponentially at a constant rate of about 10%/y of age, COVID-19 mortality increases at about 11%/y of age. There is some variation across populations, but this too seems to echo background mortality. The age profile of COVID-19 mortality may change over time, as treatment becomes more (or less) available. However, the age gradient we see to date suggests that the risk factors for COVID-19 are similar to those for all causes of death.

The Centers for Disease Control (CDC) ensemble forecast of total COVID-19 deaths, based on 33 forecasts by different groups as of August 3, is for 175,000 to 190,000 deaths by August 29 (1). The prospect of subsequent waves in the fall and afterward is uncertain. Earlier projections of epidemic mortality suggested that deaths could total more than 2 million if nothing were done to slow the spread of the novel coronavirus (2). For illustrative purposes we use an intermediate scenario of 1 million deaths in 2020 due directly to COVID-19 across all waves, at times comparing it to a lower scenario of 250,000 and a higher one of 2 million. The metrics we produce scale approximately proportionately with the number of deaths, so readers can translate our results under different mortality scenarios.

The age pattern we use in this paper does not include the indirect increase in deaths as healthcare systems are overwhelmed or the long-term effect of infection on the mortality of survivors. It also does not take into account any potential lowering of mortality, for example, from decreased air pollution, traffic accidents, and consumption of alcohol resulting from the economic slowdown. These effects may be important, but the age pattern of these changes might be quite different.

As we describe below, the most commonly used measure of mortality, life expectancy at birth, is not a good measure of transitory mortality shocks. Other measures, including the crude death rate, age-specific mortality, and the loss of remaining person years of life, together give a better summary of the magnitude of epidemic deaths. These perspectives allow us to compare mortality impacts over time and across populations. They also allow policymakers to make more informed judgments about the valuation of saved lives.

Mortality Measures

The most direct indicator of mortality is the number of deaths. This count is often given relative to population size. In the absence of the epidemic, recent levels of mortality suggest there would have been about 3 million deaths in the US population of 330 million, giving a crude death rate of about 9.1/1,000.

An additional 1 million deaths from COVID-19 would increase the total annual deaths to 4 million, raising the crude death rate to about 12.1/1,000 (or to 9.9/1,000 if there were 250,000 COVID-19 deaths). The increased risk to the average person is small in absolute size but large in relative terms, with a proportional increase of 1/3 for 1 million deaths and 1/12 for 250,000 deaths. Epidemic mortality in a given region may be compressed into a small portion of the year: If most of the deaths occurred within a 3-mo period, the daily risk of mortality implied by an additional 1 million deaths during this time would be more than double its normal level.

The epidemic is much more dangerous for the elderly than for the young. The most commonly reported age-specific measure is the “case fatality rate” (CFR), which is the ratio of COVID-19 deaths to diagnosed cases by age. There are challenges in the classification and reporting of COVID-19 deaths, in particular whether the coverage is restricted to hospitals or also includes deaths occurring at home or in nursing homes. But the bigger problem in relying on the CFR is the measurement of the denominator, the number of cases. Cases can be defined within hospital systems or within a testing regime, but neither approach is a reliable indicator of the actual number of infected individuals at the population level.

As an alternative, we estimate cause-specific mortality rates by age, using the counts in age groups of the entire population, focusing on the relative risk by age, rather than the overall level. We use compiled age-specific death data from the following countries: China (3), South Korea, Italy, Spain, France, Germany, England and Wales, and the United States (4).^† Our approach does not require that the counts of deaths have the same level of completeness across countries, which vary both in the definitions they use and in the stage of the epidemic for which we observe them. But we do assume that the age distributions of reported COVID-19 deaths are accurate.

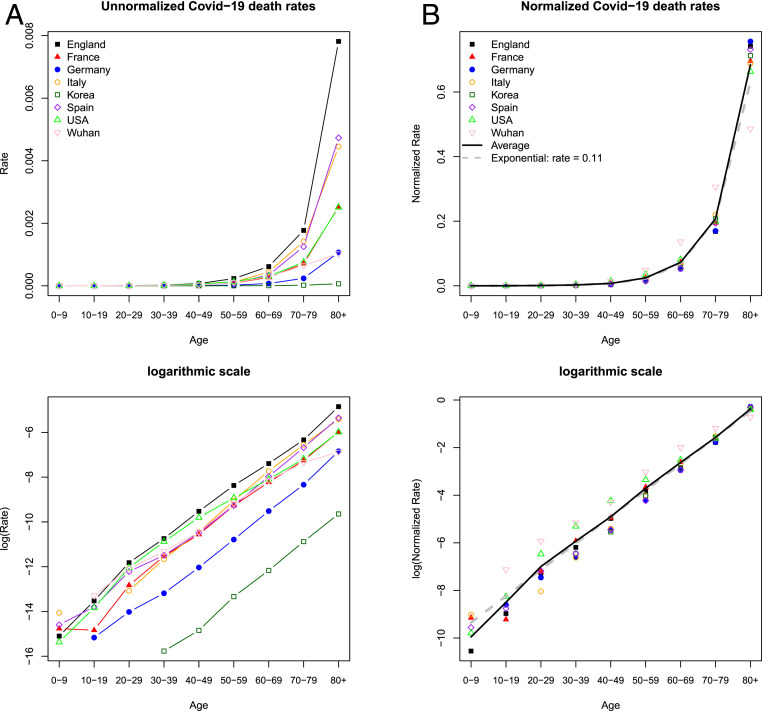
For each country, we calculate (unnormalized) age-specific death rates (ASDR) using reported COVID-19 deaths by age and the population by age, typically for the nation as a whole (Fig. 1A). We standardize mortality across countries for the open age interval (80+ y) to account for differences in the population age distribution of the elderly in different countries (Materials and Methods). Since the epidemic may be concentrated in one part of the country, and since some countries may be at earlier stages with fewer reported deaths, these ASDR may be extremely low in some countries and much higher in others, which does not necessarily signal a more or less severe epidemic and should not be so interpreted. Instead, we believe that the most reliable information is the shape or pattern by age of death rates, abstracting from the level. To make the age pattern comparable across populations, we normalize each country’s rates by dividing by the sum of the rates, so that the normalized rates sum to 1.0. We can see that the age patterns are quite similar across the eight countries (Fig. 1B).

Fig. 1.

Similar age pattern of COVID-19 mortality by region. (A) Unnormalized age-specific mortality, calculated as the ratio of deaths by age to population by age. The levels should not be interpreted as reflecting real differences in mortality because of unaccounted variation in time scale, stage of the epidemic, and the extent of spread within the region. (B) Normalized rates, dividing each region’s rates by the sum of these rates, allow comparison of the age pattern. The average is calculated across all regions. Exponential increase at a rate of 0.11 is plotted to intersect the average in the age group 70 to 79 y. A and B, Lower show the same data as A and B, Upper but in logarithmic scale. (For sources, see main text Epidemic Mortality Risk as Temporary Aging.)

It is evident from Fig. 1 that COVID-19 mortality risk is many times higher for the old than for the young, and indeed the vast majority of COVID-19 deaths are of older people. But the same is true for all-cause mortality—the vast majority of deaths are of the elderly. About 70% of all US COVID-19 deaths are to age 70 y or above, somewhat above the 64% for normal mortality. In fact, the age distribution of deaths attributed to COVID-19 is quite similar to that of all-cause mortality, which tends to increase by about 10% every year of age after age 30 y. Fig. 1B shows that in South Korea, Italy, France, Germany, England and Wales, and Spain, virus-attributed mortality rates rise by about 12%/y, while the United States and Wuhan, China show a slower rate of increase (about 9.5%/y of age).

At ages under 40 y, COVID-19 mortality risk is low, but so is mortality from other causes. It appears in Fig. 1B, Lower that average mortality below 20 or 30 y is less than would be predicted from the exponential pattern of mortality at older ages. However, the number of cases is so small that we are hesitant to draw a conclusion before more data become available.

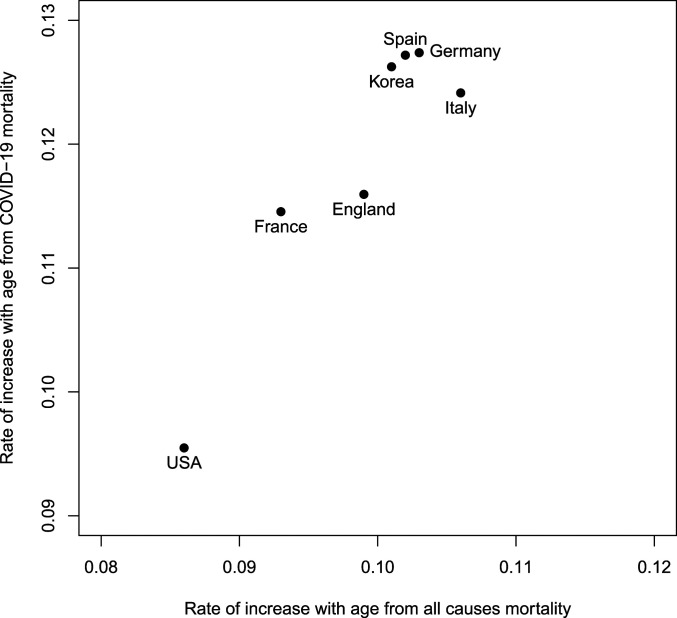
There also appears to be a relationship between the age distribution of COVID-19 mortality and that of all-cause mortality that holds across countries. Fig. 2 shows the exponential rate of increase in mortality by age for all causes and for COVID-19, for countries in the Human Mortality Database. The rate of increase of all-cause mortality varies from country to country around a central value of about 0.10, higher than the 0.086 for the United States. The smaller rate of increase in the United States is due to unusually high mortality at younger ages, not advantages at older ages, and has been used as an indirect indicator of the inequality of health status of the population (5, 6). From this small number of countries, at least, it appears that COVID-19 may be echoing the same factors as all-cause mortality, suggesting that there may be a relationship between the level of health inequality within populations and the age pattern of COVID-19 mortality.

Fig. 2.

The relationship between exponential rates of increase with age of all-cause mortality and COVID-19 mortality for countries in the Human Mortality Database. (Note that exponential rates are calculated from age groups 45 to 49 y to 85 to 89 y for all-cause mortality and ages 40 to 49 y to 80$+$ y for COVID-19 mortality, assuming 40-y ranges for both.)

All of the above results are for sexes-combined mortality, the approach we take throughout this study. As an aside, however, analysis of COVID-19 mortality by sex in the United States finds a steeper rate of increase for females above age 35 y (just above 0.10/y) than for males (just below 0.09), so the ratio of male to female COVID-19 death rates which is 1.44 from 35 to 54 y declines thereafter across 10-y age groups to 1.37, 1.34, 1.26, and finally 1.12 for 85+ y. Despite the widespread reporting of higher COVID-19 mortality for males, the relative risk of males to females is actually lower for COVID-19 than for all-cause mortality in the United States in 2017 (7).

Epidemic Mortality Risk as Temporary Aging

We can translate the elevated risk of mortality during an epidemic into a measure of “temporary aging.” This measure expresses the increased risk of an individual during the months of the epidemic in terms of the age of someone with equivalent mortality during normal, nonepidemic times. If $R$ is the ratio of mortality during the epidemic to normal mortality and $\beta$ is the exponential rate of increase of all-cause mortality with age, then the years of implied temporary aging will be $\log \left(R\right)/\beta$. For example, if there were 1 million COVID-19 deaths within a 3-mo period when only 750,000 deaths would normally occur, and if $\beta =0.10$, then the years of temporary aging would be $\log \left(1.75/0.75\right)/0.1=8.5$. This same effect applies across the range of ages when mortality is increasing at this rate, approximately from ages 30 to 85 y.

Table 1 shows such calculations for different epidemiological forecasts for the United States in terms of temporary aging, assuming a 3-mo window of epidemic mortality and $\beta =0.10$. We provide a range from as low as 125,000—the midrange of the CDC (2020) summarized projections to June 27—to a high of 2 million, a bit less than the estimate of an uncontrolled epidemic (2). The estimates in Table 1 tell us that a scenario of 1 million COVID-19 deaths over the course of 3 mo exposes a 30-y old to the risks of a 38.5-y old in normal times and exposes an 80-y old to the risks of an 88.5-y old in normal times. The same numbers of years of temporary aging, however, pose different absolute increases in risk. For the 30-y old, the absolute increase in mortality would be small, but for the 80-y old it would be large. Considering mortality risk in this manner allows, we believe, accurate communication of risk and understanding of the limited risk to the young and the much greater risk to the elderly. However, this approach has its limits, applying neither to children nor, probably, to the oldest old.

Table 1.

Years of temporary aging for hypothetical epidemics with mortality concentrated in a 3-mo period

Deaths	Temporary aging, y
2,000,000	13.0
1,000,000	8.5
500,000	5.1
250,000	2.9
125,000	1.5

For example, during a US epidemic with 1 million deaths, an 80-y old would be exposed to the normal mortality risk of an 88.5-y old. Note that estimates assume a 10% rate of mortality increase with each year of age.

Period Life Expectancy

Life expectancy decline overstates the impact of temporary epidemic mortality. The “period” life expectancy at birth is a familiar way to summarize the mortality in a year. In 2017—the most recent year reported in detail for the United States—life expectancy at birth was 78.86 y, a statistic which assumes people live their entire life, from birth to death, under the mortality conditions of 2017 (7). However, in the context of epidemic mortality, life expectancy at birth is a misleading indicator, because it implicitly assumes the epidemic is experienced each year over and over again as a person gets older.

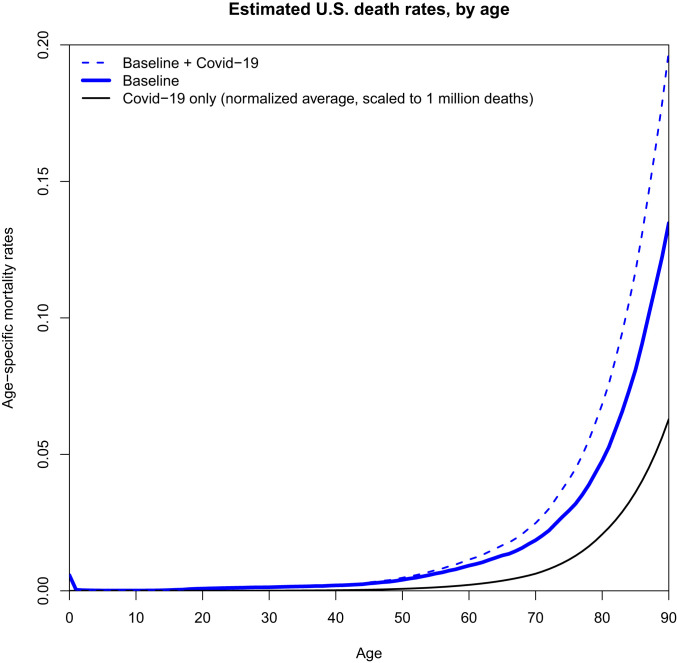
When we apply the observed average age pattern of COVID-19 mortality from Fig. 3, we find that 1 million COVID-19 deaths would produce a life expectancy decline of 2.94 y. Such a decline would temporarily take us back to the mortality conditions of 1995 when life expectancy was 75.88 y, 2.98 y less than 78.86 in 2017. The same calculation with 250,000 COVID-19 deaths would produce a decline of 0.84 y in life expectancy.

Fig. 3.

Estimated age-specific mortality in the United States in 2020 for the scenario of 1 million additional COVID-19 deaths. Baseline mortality in 2020 is assumed to equal that in 2017. COVID-19 mortality is estimated by averaging the normalized death rates in Fig. 1B and then multiplying these average rates to result in 1 million additional deaths using the US population age structure for 2020.

This decline in life expectancy is somewhat smaller than would be the case if epidemic mortality were exactly proportional to all-cause nonepidemic mortality at all ages—the slightly older ages of death of COVID-19 deaths reduce the impact on life expectancy. To estimate the effect of a proportional change in mortality, we can use an approximation due to Keyfitz (8), who showed that increasing mortality by $\mathrm{\Delta }$ at all ages causes life expectancy to drop by a factor approximately equal to $H\mathrm{\Delta }$, where $H$ is “life table entropy,” typically about 0.15 in low mortality settings (Materials and Methods). Under Keyfitz’s (8) model, 1 million epidemic deaths increasing mortality rates by about $1/3$ at all ages would lead to a drop in period life expectancy of $\left(1/3\right)\left(0.15\right)\left(78.86\right)=3.94$ y, about 1 y larger than our estimate based on our observed average COVID-19 mortality schedule.

Loss of Remaining Life

Whereas period life expectancy in an epidemic year tells us how long people would live if they were to experience an epidemic every year of their lives, what we really want to know is how a one-time epidemic affects the remaining life expectancy of the actual population.

Based on Social Security Administration projections of cohort mortality and remaining life expectancy (9), we calculate that the 2020 American population of 330 million people has on average 45.8 y of remaining life expectancy, totaling 14.9 billion person years. We calculate, using these same cohort life tables, that the average person dying of COVID-19 had 11.7 y of remaining life expectancy, so if the epidemic kills an additional 1 million people, it will result in a loss of 11.7 million y of remaining life expectancy. This represents a loss of less than 1/1,000th of the population’s remaining years to live. Older individuals ages 70 to 89 y, taking those who die and those who survive together, would on average lose about 0.2 y of remaining life, and younger individuals would lose far less.

How could such an enormous loss of lives produce such a seemingly small loss of remaining life expectancy? Two factors play a role. First, even with substantial additional COVID-19 mortality, death will still be a statistically rare event. Most people will survive and they will, if mortality returns to normal, have many years of life ahead of them. Second, those who die of COVID-19 are older and have on average fewer years of remaining life expectancy than the average person (11.7 y instead of 45.8 y).

Our above calculation is specific to the United States and to our estimated age pattern of COVID-19, but the small effect of a single year of epidemic mortality can be seen more generally by extending Keyfitz’s (8) model to a more general formulation of the loss of remaining life (Materials and Methods). This model, like Keyfitz’s, also shows that the effect of an epidemic on loss of remaining person years of life, like the effect on life expectancy, scales roughly proportionately with the magnitude of the epidemic. We consider a population that is not growing (“stationary”) experiencing an epidemic mortality proportional to the baseline age pattern. An epidemic that increases mortality by a factor $\mathrm{\Delta }$ at all ages results in a loss of remaining life expectancy equal to $\left(H/A\right)\mathrm{\Delta }$, where $H$ is Keyfitz’s life table entropy and $A$ is the mean remaining life expectancy of those people alive. For example, if $\mathrm{\Delta }=1/3$, $H=0.15$, and $A=40$—roughly the case of the United States—this model would predict the share of lost life would be about 1/800. Unlike our exact calculation above, this model does not include the older age of death of COVID-19 relative to all-cause mortality, improvements in mortality implied by using the cohort life expectancy forecast, or the particular features of the US age distribution. Nonetheless, such stylized calculations arrive at a result of the same order of magnitude.

Both of the above calculations may overstate the loss of remaining life in that they assign the remaining life expectancy based only on age, without taking into account that COVID-19 deaths are disproportionately occurring among those with compromised health status. Hanlon et al. (10) estimate that those dying from COVID-19 have only about 1 y less of remaining life on average than those at the same age in the general population, which would mean that the overstatement is not very large, around 8%. On the other hand, our calculations will be an understatement if the epidemic damages the health of survivors.

The loss of future life seems very small when compared to all of the years remaining. One way to put the years of remaining life lost from an epidemic into perspective is to consider them relative to the person years lost from mortality in a “normal” nonepidemic year. This calculation accounts for the number and age of deaths from the epidemic and weights them by the loss of remaining person years, comparing the result to the person years lost in a comparable nonepidemic year.

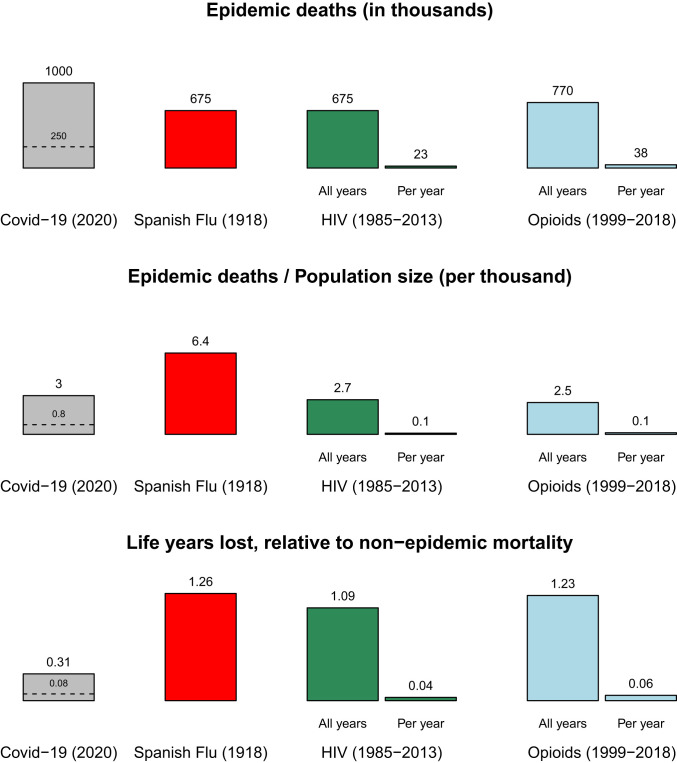
Using this metric, we estimated the average age of death and computed the comparative loss of life from COVID-19 relative to the Spanish flu, the HIV epidemic, and the recent opioid epidemic according to three different measurements. For COVID-19 we show scenarios for 1 million and 250,000 deaths. In Fig. 4, Top showing the counts of deaths, with 1 million deaths COVID-19 would be the largest threat we have faced. In Fig. 4, Middle, which takes population size into account, Spanish flu emerges as having produced the largest increase in per capita mortality rates. Taking the age of those who die into account and their remaining life expectancy, Fig. 4, Bottom shows that in terms of lost remaining life expectancy, our scenario for COVID-19 is much smaller than that for the Spanish flu. The dashed lines on the COVID-19 bars show the same calculations based on 250,000 deaths.

Fig. 4.

Mortality of COVID-19 scenario compared to past US epidemics according to different measures. In the scenario of 1 million COVID-19 deaths, the virus kills more Americans than past epidemics, but when population size is accounted for, Spanish flu is more deadly. Taking into account years of remaining life, we calculate that the Spanish flu resulted in even larger losses. The scales of the HIV and opioid epidemics were much smaller each year, but over decades became comparable to COVID-10 in terms of per-capita deaths and to Spanish flu in terms of life years lost. The scenario of 250,000 COVID-19 deaths is also shown with a dashed line. (Source: our calculations detailed in Materials and Methods.)

The HIV epidemic, which peaked in the 1990s, and opioid overdose deaths, which continue today, have each over the decades produced total mortality that is comparable, depending on the metric, to the 1 million deaths COVID-19 scenario we are considering and even to Spanish flu. However, on a deaths-per-year basis, they are an order of magnitude smaller. One million deaths from COVID-19 would confront society in 1 y, or possibly in just 3 or 4 mo, while the deaths we have experienced from HIV or opioid overdoses occur over the course of decades. This concentration of epidemic deaths in a short time creates a crisis which overwhelms the capacities of healthcare systems, morgues, and mortuaries, leading to triage in hospitals and makeshift storage of bodies such as in an ice rink in Madrid. The slower-moving epidemics bring other stresses and anguish, since afflicted individuals suffer for many years, and the prevalence of those afflicted at any moment is consequently much higher than for epidemics that kill quickly.

The Valuation of Life Saved

We can view these results from a different perspective, comparing the outcome of a hypothetical uncontrolled US epidemic in 2020 (2 million deaths, ref. 2) to the far smaller one we may perhaps achieve with social distancing, which we hypothetically set at 250,000. To ground this number, we note that current projections are pointing at close to 200,000 deaths by summer’s end, with mortality continuing at some unknown rate afterward (1). With 2 million deaths, period life expectancy at birth for 2020 would have dropped by 5.08 y, but with only 250,000 deaths it would drop by only 0.84 y. An 80-y old would lose 0.40 y of remaining life versus only 0.05 y. The population as a whole would lose about 1/650 of its remaining years versus only one 1 in 5,100.

In one of the most quoted lines of the Talmud, it is said that whoever destroys one life, destroys an entire world; and who ever saves one life is considered to have saved an entire world. Still, policymakers face the inescapable choice of how many lives to save at what cost. Federal policy decisions are guided by a substantial literature in this area. Current estimates for the United States by Viscusi (11, 12) give a single value of $10 million to each life regardless of age or alternatively $500,000 per year of life. Using Viscusi’s estimates, which are similar to those used by the federal government, we can attach a value to a hypothetical 1.75 million (= 2 million – 250,000) lives saved through public and private measures taken. Avoiding 1.75 million deaths would be valued at $17.5 trillion, and saving 20,475,000 person years of life would be valued at $10.2 trillion. Some other health economists use substantially lower values around $125,000/y of life (13), which would imply a value of $2.6 trillion for avoiding the loss of 20.5 million person years of life.

It is very difficult to evaluate the cost of measures taken to mitigate the epidemic. The various public transfer programs that have been enacted are redistributions rather than net social costs, although they will entail further redistributions as government debt is serviced in the future. The net societal economic cost of the public measures taken to mitigate the epidemic is the loss of gross domestic product (GDP) due to these measures. Estimating the net cost is an active area of work (14, 15). Early downward revisions of GDP forecasts for 2020 by the Congressional Budget Office (16) project about 8% less output than expected (−6% in 2020 rather than the +2% projected before the epidemic), a loss of about $1.6 trillion. Not all of this decline can be attributed to societal choices to slow the spread of the virus, because the economy would also suffer—perhaps even more—if the virus were uncontrolled. But even if we assign all of the drop in GDP to measures taken to save lives, the economic costs of the actions society has taken appear to be appropriate for the scale of the crisis.

Conclusion

With a hypothetical 1 million COVID-19 deaths, it is possible to portray the epidemic as unimaginably large—the biggest killer in American history—or small, reducing our remaining life by less than 1 part in 1,000. However, when the loss of life is put into comparative perspective, we see that the scale of an epidemic with 1 million deaths would be as large as that of the recent opioid and HIV crises but much smaller than that of the Spanish flu. The 1918 epidemic killed more people relative to population size, and it also caused a much greater loss of remaining life expectancy because those who died were so young.

As a society, we are and we should be making major and costly efforts to reduce mortality. The anticipated economic costs appear appropriate, or perhaps low, when compared to the statistical value of lives that may be saved.

The death toll of COVID-19 is a terrible thing, both for those who lose their lives and for their family, friends, colleagues, and all whom their lives touched. Those are real individuals, not the abstract statistics presented here. But the population perspective helps us to place this tragedy in a broader context. As we put our efforts into reducing the impact of the epidemic, it is important to know that we as a society have been through such mortality crises before.

Materials and Methods

Mathematical Models.

Keyfitz’s result for life table entropy.

Life expectancy at age 0 y is computed as the sum of expected person years of survival of a newborn:

$$e\left(0\right)={\int }_0^{\omega }\ell \left(x\right)\hspace{0.17em}dx.$$

Survival $\ell \left(x\right)$ is given in terms of the hazard of death $m\left(a\right)$ as

$$\ell \left(x\right)=e^{-{\int }_0^{x}m\left(a\right)\hspace{0.17em}da}.$$ [1]

A population subject to a new cause of mortality that increases death rates at all ages by $\mathrm{\Delta }$, such that $m\left(x|\mathrm{\Delta }\right)$ = $m\left(x\right)\left(1+\mathrm{\Delta }\right)$, will have life expectancy given by

$$e\left(0|\mathrm{\Delta }\right)=\int \ell {\left(x\right)}^{1+\mathrm{\Delta }}\hspace{0.17em}dx.$$

Differentiating the logarithm of life expectancy with respect to $\mathrm{\Delta }$,

$$\frac{d\log e\left(0|\mathrm{\Delta }\right)}{d\mathrm{\Delta }}=\frac{\int \log \ell \left(x\right)\ell {\left(x\right)}^{1+\mathrm{\Delta }}\hspace{0.17em}dx}{\int \log {\ell \left(x\right)}^{1+\mathrm{\Delta }}\hspace{0.17em}dx}.$$

At $\mathrm{\Delta }=0$, this simplifies to

$${\left.\frac{d\log e\left(0|\mathrm{\Delta }\right)}{d\mathrm{\Delta }}\right|}_{\mathrm{\Delta }=0}=\frac{\int \log \ell \left(x\right)\ell \left(x\right)\hspace{0.17em}dx}{e\left(0\right)}.$$

Keyfitz defines $H$ as $-\int \log \ell \left(x\right)\ell \left(x\right)\hspace{0.17em}dx/e\left(0\right)$. Some further manipulation gives us the form for $H$ in terms of remaining life expectancy:

$$H=\frac{\int d\left(x\right)e\left(x\right)\hspace{0.17em}dx}{e\left(0\right)}.$$ [2]

A new result for person years lost.

Assume the population is stationary with age structure $c\left(x\right)=\ell \left(x\right)/e\left(0\right)$ and that an epidemic raises mortality at all ages by the same factor $\left(1+\mathrm{\Delta }\right)$.

If mortality increases suddenly by a factor of $1+\mathrm{\Delta }$ at all ages, then deaths will also increase by the same factor, since in the immediate term the population exposed to risk will be the same. If mortality recovers back to its original level after the epidemic, then life expectancy of the survivors will remain unchanged, but there will be fewer survivors. This means that the total person years of life left in the population $\theta$ will be

$$\theta \left(\mathrm{\Delta }\right)=B\int \left[\ell \left(x\right)-\mathrm{\Delta }d\left(x\right)\right]e\left(x\right)\hspace{0.17em}dx,$$

where $B\left[\ell \left(x\right)-\mathrm{\Delta }d\left(x\right)\right]$ is the count of individuals aged $x$ after the epidemic.

The approximate proportional change in $\theta$ from an epidemic is then

$$-{\left.\frac{d\log {\theta }_0\left(\mathrm{\Delta }\right)}{d\mathrm{\Delta }}\right|}_{\mathrm{\Delta }=0}=\frac{\int d\left(x\right)e\left(x\right)\hspace{0.17em}dx}{\int \ell \left(x\right)e\left(x\right)\hspace{0.17em}dx}=\frac{H}{A}.$$

In this result, $H$ is Keyfitz’s entropy, defined in ref. 2, and $A$ is the mean age of the stationary population

$$A=\frac{\int x\ell \left(x\right)\hspace{0.17em}dx}{e\left(0\right)}.$$

In the United States, $H$ is about 0.15 and $A$ is about 40. If an epidemic produced an increase of 1/3 in mortality at all ages, ($\mathrm{\Delta }=1/3$), this would cause a loss of life equal to $\left(1/3\right)\left(0.15\right)/40=1/800$ of the remaining person years of life of the population.

Additional Methods and Data Sources.

Epidemic mortality rate estimation.

COVID-19 mortality age shares for Fig. 1 were calculated using both the age distribution of COVID-19–attributed deaths and the age structure of the population. Normalization enables comparison of the age structure of mortality from populations with different levels of the epidemic. Normalized rates were calculated by dividing the unnormalized rates by their sum over all ages, for each country separately. Prior to normalization, we adjust for the population age structure in the open interval aged $80+$ y, using indirect standardization.

Indirect standardization of open age interval.

For indirect standardization, we used the 2017 period both-sex mortality from the United States as the standard mortality schedule $M_x^s$ by single years of age $x=0,\dots ,99$ y. We then defined the share of each population $k$ at each age 80 to 99 y, $c_{x,k}$ such that $1={\sum }_{x=80}^{99}{c}_{x,k}$, letting the shares for the United States age structure be the reference age structure, $c_{x,R}$. The adjustment factor for population $k$ was defined as

$$\frac{\sum _x{c}_{x,R}{M}_x^s}{\sum _x{c}_{x,k}{M}_x^s}.$$

The adjustment factors (Table 2) were multiplied by the observed age-specific mortality rate from COVID-19 for the open interval age $80+$ y.

Table 2.

Adjustment factors used for open age interval

France	United States	England	Spain	Italy	Germany	Korea	Wuhan
0.997	1.000	1.036	1.051	1.067	1.098	1.160	1.162

Additional information for Fig. 1.

The average normalized rate is calculated as the arithmetic mean across countries of the normalized age-specific mortality rates. The exponential curve shown in Fig. 1B is a Gompertz hazard curve with exponential rate $b=0.11$, with the level set so that it will intersect the average normalized rate at age group 70 to 79 y.

Additional information for Fig. 4.

We define annual mortality equivalents of the loss of remaining life expectancy as

$$AME=\frac{\int D*\left(x\right)e\left(x\right)\hspace{0.17em}dx}{\int D\left(x\right)e\left(x\right)\hspace{0.17em}dx},$$ [3]

where $D*\left(x\right)$ is the number of deaths at age $x$ from a singular mortality event like an epidemic and $D\left(x\right)$ is the number of deaths that would have been expected in a normal year. This definition assumes that there is no difference in the functions of remaining life expectancy by age but allows for the case when an epidemic has a different age pattern of deaths.

We can approximate the denominator by expanding $e\left(x\right)$ around $x=A_D=\int xD\left(x\right)\hspace{0.17em}dx/\int D\left(x\right)\hspace{0.17em}dx$, such that $e\left(x\right)\approx e\left(A_D\right)+\left(A_D-x\right)e^{\prime }\left(A_d\right)$. The second term sums to zero when integrated against $D\left(x\right)$, giving us the approximation

$$\int D\left(x\right)e\left(x\right)\hspace{0.17em}dx\approx e\left(A_D\right)\cdot \int D\left(x\right)\hspace{0.17em}dx.$$ [4]

Applying the same method to the numerator around $x=A_D*$ gives

$$AME=\frac{\int D*\left(x\right)\hspace{0.17em}dx}{\int D\left(x\right)\hspace{0.17em}dx}\cdot \frac{e\left(A_D*\right)}{e\left(A_D\right)}.$$ [5]

This approximation was used for Fig. 4 for all of the epidemics considered, to enhance comparability by use of a single method (Table 3).

Table 3.

Parameters used to calculate Fig. 4

	Epidemic			All cause
	Deaths	${\overline{x}}_e$	$e\left({\overline{x}}_e\right)$	Reference year	Deaths, millions	$e\left(\overline{x}\right)$
Spanish flu	675,000	30	38.8	1920 (1933)	1.4	15.1
HIV	675,000	40	38.0	1990	2.1	11.0
Opioid	770,000	42	38.8	2010	2.5	9.8
COVID-19	1,000,000 (250,000)	80	9.6	2017	3.0	10.2

COVID-19 deaths are given for two scenarios. ${\overline{x}}_e$ is the mean age of death from each epidemic. $e\left({\overline{x}}_e\right)$ is the years of remaining life for those dying from each epidemic. Reference year for Spanish flu uses number of deaths from 1920 combined with life table from 1933, the first year national life tables are available to us. Remaining “all cause” life expectancy $e\left(\overline{x}\right)$ is calculated as life expectancy at average age of death in period life table of reference year. Reference years 1990 and 2010 include low-level epidemic mortality. The remaining life expectancy at average age of COVID-19 death differs from the value reported in the main text in order to use the same method for different epidemics.

Data sources for Fig. 4.

HIV/AIDS.

Count of deaths is from ref. 17. The mean age of HIV-caused death was estimated by tabulating all HIV deaths from 1979 to 1998 in 5-y age groups and computing the mean age assuming average deaths in midinterval. Our calculation is from CDC WONDER.

Opioid overdoses.

Total deaths were calculated by us from data available in ref. 18. The mean age of death for opioid overdoses was computed from CDC WONDER data tabulated by ref. 19.

Spanish influenza.

“The number of deaths was estimated to be at least 50 million worldwide with about 675,000 occurring in the United States” (CDC, ref. 20). The mean age of death was estimated from distributions graphed in Gagnon et al. (21).

Data Availability.

Data and computer code for replication are available at GitHub, https://github.com/josh-goldstein-git/dempersp_covid_mortality. All study data are included in the main text.