Significance
The yielding transition in soft materials manifests macroscopically as a reversible transition from solid-like deformation to liquid-like flow under sufficiently large loading or deformation. Despite the ubiquity of materials that exhibit yielding, an understanding of the transition has remained elusive due to experimental limitations of the simple rheological tests typically used to study it. We present here a more thorough understanding of yielding, obtained via an iterative test protocol and analysis that allow for the separation of solid-like and liquid-like behaviors in the response of these materials. We show that yielding is a gradual transition, occurring to an increased extent as the deformation increases.
Keywords: elastoviscoplastic materials, yield stress, recoverable strain, Payne effect, oscillatory shearing
Abstract
Materials that exhibit yielding behavior are used in many applications, from spreadable foods and cosmetics to direct write three-dimensional printing inks and filled rubbers. Their key design feature is the ability to transition behaviorally from solid to fluid under sufficient load or deformation. Despite its widespread applications, little is known about the dynamics of yielding in real processes, as the nonequilibrium nature of the transition impedes understanding. We demonstrate an iteratively punctuated rheological protocol that combines strain-controlled oscillatory shear with stress-controlled recovery tests. This technique provides an experimental decomposition of recoverable and unrecoverable strains, allowing for solid-like and fluid-like contributions to a yield stress material’s behavior to be separated in a time-resolved manner. Using this protocol, we investigate the overshoot in loss modulus seen in materials that yield. We show that this phenomenon is caused by the transition from primarily solid-like, viscoelastic dissipation in the linear regime to primarily fluid-like, plastic flow at larger amplitudes. We compare and contrast this with a viscoelastic liquid with no yielding behavior, where the contribution to energy dissipation from viscous flow dominates over the entire range of amplitudes tested.
Many materials blur the line between solids and fluids. These are typically referred to as either complex fluids or soft materials and exhibit a range of interesting behaviors. These behaviors include viscoelasticity (1–3), where solid-like and fluid-like behaviors coexist on different timescales, and plasticity or yielding (4–9), where a material transitions from solid-like to fluid-like behavior under increased loading.
Viscoelasticity is typical in polymer solutions and melts, surfactant systems, foams, emulsions, and concentrated colloidal suspensions, as well as many other soft materials. These systems have been studied extensively, as viscoelasticity is an equilibrium behavior that can be probed at small-enough deformations where a material’s microstructure remains intact (2). Plasticity, by contrast, is inherently an out-of-equilibrium behavior that is exhibited by a slew of industrial, biological, and environmental materials, including filled rubbers, spreadable foods, personal care products, muds, and mucous. The ability to yield is desirable for their particular processes such as spreadibility, squeezability, and moldability, and gives yielding materials relevance in many novel systems (10, 11), including additive manufacturing, and suspension of density-mismatched particles. Additionally, recent studies (12, 13) have demonstrated that yield stress fluids can store memories of oscillatory shearing at some long-applied “training” amplitude, which can be read via oscillatory shearing at the same amplitude at some later time. The strength of these memories is maximal at their yield point. Further, systems exhibiting significant intrinsic or hydrodynamic noise have the ability to store multiple memories from different training amplitudes, while noise-free systems will only store memories from the largest amplitude used to train the system.
The nonequilibrium nature of the yielding phenomenon has rendered it difficult to study, as it requires large nonlinear deformations to observe. Plasticity in soft materials was first categorized by Schwedoff at the turn of the 20th century (14) and later brought to prominence by Bingham in the 1910s (15). These works described the long-time, steady-state properties of soft plastic materials, such as aqueous clay suspensions, as requiring a nonzero minimum amount of stress to induce flow. This description resulted in what is now known as the Bingham model: an undeformable solid below a critical stress threshold, called the yield stress, with Newtonian fluid-like flow above it. This has led to the predominant description of yielding as being a binary phenomenon, as evidenced by the ubiquity of models in existence with a single yield stress (5, 16–20). There have been challenges to the existence of a yield stress in the past (5, 21), and a number of recent studies (22–24) have explicitly shown that attempts to define a single yield threshold are ambiguous, at best. Furthermore, the fact that Bingham chose to only investigate the steady-state properties of plastic materials, and did not consider any time dependence, led to the furtherance of the idea that yielding is an instantaneous phenomenon. It is now known that the transition requires a finite amount of time to complete (23). As a result, it has been difficult to develop an understanding of the processes and mechanisms (both rheological and microstructural) that occur during yielding (5, 7, 21–33). This has, in turn, reduced the availability or development of structure–property relations for the yielding transition, which has rendered the tailored design of novel plastic soft materials difficult (10, 11).
To study viscoelasticity and plasticity rheologically, a range of techniques has been implemented (1, 8, 9). One of the most widely employed is strain-controlled oscillatory shear rheology (1–3, 34, 35). This involves applying a sinusoidal signal in strain,
| [1] |
and measuring the corresponding stress response. Application of sinusoidal strains provides researchers with the ability to investigate the impact on the material properties of both the timescale and extent of deformation through the frequency, , and strain amplitude, , respectively (1, 2). Oscillatory shear rheology has the additional benefit that, at small amplitudes, the viscoelasticity of the response can be determined from the in-phase and out-of-phase components of the response (1, 2). The phase-shifted stress response, , allows for the definition of the frequency-dependent dynamic moduli, and , in the linear regime,
| [2] |
which probe the equilibrium structure of a material. The dynamic moduli are the components of the stress in phase with the strain and the strain rate and are referred to as the storage and loss moduli, due to the fact that in the linear regime they are related to the energy stored per unit volume (either potentially or inertially) and the rate at which energy is dissipated per unit volume, averaged over the entire oscillation in both cases (3):
| [3] |
| [4] |
Generic expressions exist that relate the storage modulus directly to the sum of all energy storage modes and the loss modulus to all dissipative modes (3).
These time-averaged energetic definitions give the dynamic moduli their physical meaning. Although often referred to as the “elastic” (in phase with strain) and “viscous” (in phase with strain rate) moduli, care needs to be applied to such use. Kelvin–Voigt viscoelastic solids, for example, dissipate energy and therefore, have nonzero values of , due to the presence of viscous processes that hinder the instantaneous acquisition of strain, yet cannot be said to experience viscous flow (1). Additionally, energy can be stored both elastically and inertially in nonlinear deformations (3). Choosing to refer to and as elastic and viscous thus results in potential sources of confusion, as there are two possible distinct contributions to each of the moduli: elastic storage and viscoelastic solid dissipation occur in solids, while inertial storage and viscoplastic flow correspond to fluids. The fact that there are two different possible dissipative contributions to the loss modulus precludes its use in clearly identifying a transition between solid-like and fluid-like responses.
For many complex fluid materials, the linear characterization by oscillatory rheology is insightful yet insufficient for a complete understanding of rheological behavior (34, 35) and may not exist for some thixotropic materials (36). In plastic materials with a yielding transition, for example, flow is typically only observed as the amplitude of the deformation is increased. To characterize the nonlinear behavior of materials, large-amplitude oscillatory shear (LAOS) is typically used (34, 35). While a range of specialized analytical techniques has been developed for analyzing these nonlinear responses (29, 37–42), the vast majority of plasticity studies using rheology opt instead to simply extend the linear regime measures to nonlinear responses, relying on the amplitude dependence of the dynamic moduli (34, 35). A detailed understanding of the specific sequence of processes undergone during yielding is therefore sacrificed in favor of a simpler visualization of the complex response. As the strain amplitude increases, the energetic definitions in Eqs. 3 and 4 hold in a time-averaged sense, meaning that the use of the dynamic moduli in the nonlinear regime still allows for the extraction of the average energetic contributions, even if solid–fluid distinctions are difficult.
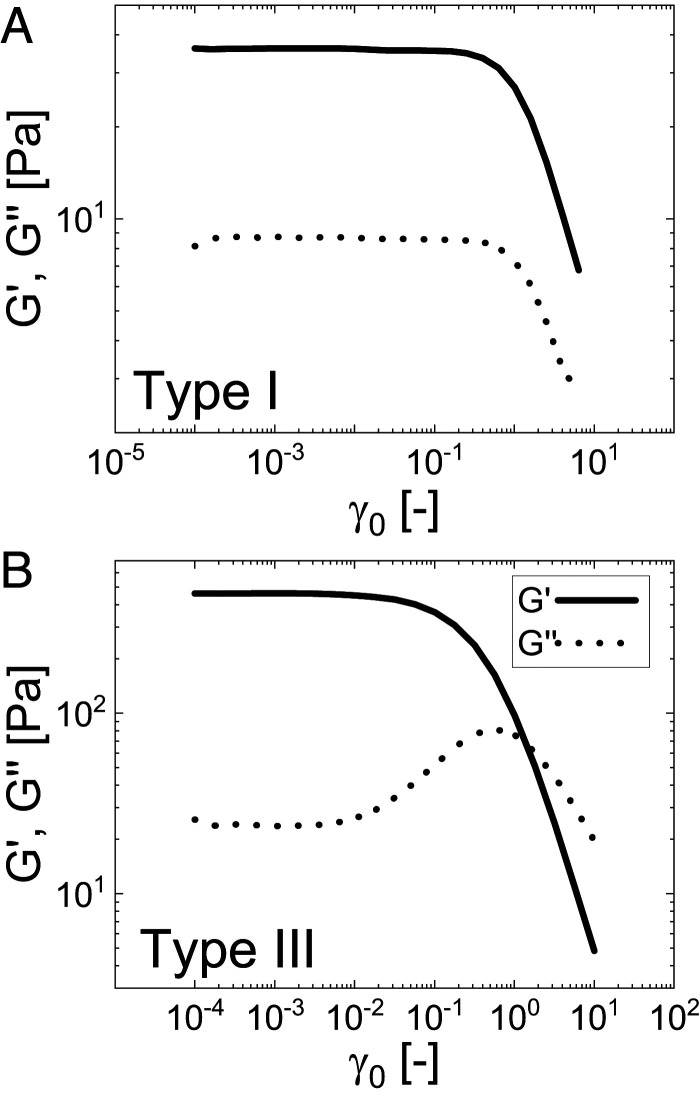
The results from so-called amplitude sweep tests, where the dynamic moduli are displayed as functions of the strain amplitude, typically take one of four distinct forms, as described by Hyun et al. (34). Many simple viscoelastic materials fall under the category of strain thinning (type I) (Fig. 1A), while most plastic materials fall into the category of weak strain overshoot (type III) (Fig. 1B). Both responses show a reduction in the dynamic moduli at very large strain amplitudes, but the type III response, shown in Fig. 1B, also shows an overshoot in the loss modulus at intermediate amplitudes.
Fig. 1.
Typical strain-controlled amplitude sweeps, with type designations from Hyun et al. (34): (A) type I (strain thinning) and (B) type III (weak strain overshoot).
The peak in the loss modulus at intermediate strain amplitudes was first observed in filled rubbers by Payne in the early 1960s (43) and has been associated with his name since. Within the filled polymer community, the overshoot in the loss modulus is known as the Payne effect (44–46). Since Payne’s original observations, an overshoot in the loss modulus has been observed in the response to oscillatory shearing of a wide range of other plastic soft materials, including glasses (47–51), gels (34, 52–55), suspensions (56–60), emulsions (22, 61–63), foams (22, 64, 65), microgels (22–24), associative polymers (39, 66–68), filled networks (69, 70), and electrorheological systems (71, 72). The overshoot in the loss modulus is now intimately related to plasticity and the yielding transition. Despite its ubiquity, a single rheological explanation of the overshoot in the loss modulus remains elusive. Clearly, for the same behavior to be observed in materials with widely varying microstructures, any universal description must be structurally agnostic. Possible explanations of the overshoot, some of which are specific to a certain material type, have been suggested (35). The suggestions include amplitude-dependent buildup/breakdown of structure (34, 35, 43, 44, 46, 60), transitions between intra- and interparticle interactions (34, 35, 56, 66–68, 71, 72), length scale-dependent rearrangements (34, 35, 55, 61, 62), and forced strain relaxation (58).
Much of the motivation for these explanations comes from the interpretation of the dynamic moduli as measures of the “deformation” and “flow,” respectively, instead of the more accurate average energetic descriptions. Only very recently (73) have studies begun to investigate the distinct solid-like and fluid-like contributions to the total energy dissipation.
To accurately investigate plasticity and the yielding transition and to differentiate between the two modes of dissipation, there needs to be a way of clearly distinguishing between solid-like and liquid-like responses. Clearly, looking at the total energy dissipation alone is insufficient. A clear and measurable difference between viscoelastic solids and fluids is in their ability to recover deformation when stress is removed. The use of zero-stress recovery tests (1, 73–76) allows materials to recover to their instantaneous “ground state” (76), thus enabling calculation of the relative amounts of elastic and viscous dissipation. The recoverable and unrecoverable components of the strain are additive:
| [5] |
as are their derivatives:
| [6] |
By iteratively performing a series of recovery tests at successive time instants during an oscillation (73), the recoverable and unrecoverable portions of the strain can be mapped. The decomposed strain measurements can then be used to define more detailed representations of the dynamic moduli that reflect energy storage and dissipation due to the viscoelastic solid-like and liquid-like deformation of the material:
| [7] |
| [8] |
| [9] |
It is mathematically possible to define a fourth component, , which would theoretically correspond to inertial energy storage in the viscoplastic fluid state. There are experimental complications that could interfere with the detection of inertial energy storage in these tests, and as our primary focus is on describing the overshoot in the loss modulus, the definition of and corresponding data are shown in SI Appendix.
To visualize the function of each of these component moduli, it is helpful to visualize the Jeffreys model, which has recently been studied extensively by de Souza Mendes and Thompson (77). The Jeffreys model exhibits both a relaxation and a retardation time. In this representation, is related to the recoverable storage of energy, is defined by the energy dissipated by the rate at which recoverable strain is acquired, and is related to the dissipation of energy associated with unrecoverable flow. The Jeffreys model contains a range of simpler viscoelastic models as simplifications. For example, a Kelvin–Voigt viscoelastic solid, which acquires all strain recoverably and exhibits retardation, will display no , while a Maxwell material, which exhibits relaxation but not retardation, will have When comparing with the linear regime moduli for a general viscoelastic material, , and .
We use recovery rheology to decompose the energetic contributions from the two dissipation modes throughout the amplitude sweeps of several plastic materials to elucidate the emergence of the overshoot in the loss modulus, as well as its absence in purely viscoelastic materials. In the process, we identify the underlying rheological cause of the overshoot in the loss modulus of plastic materials and develop a more nuanced understanding of the yielding transition.
Results
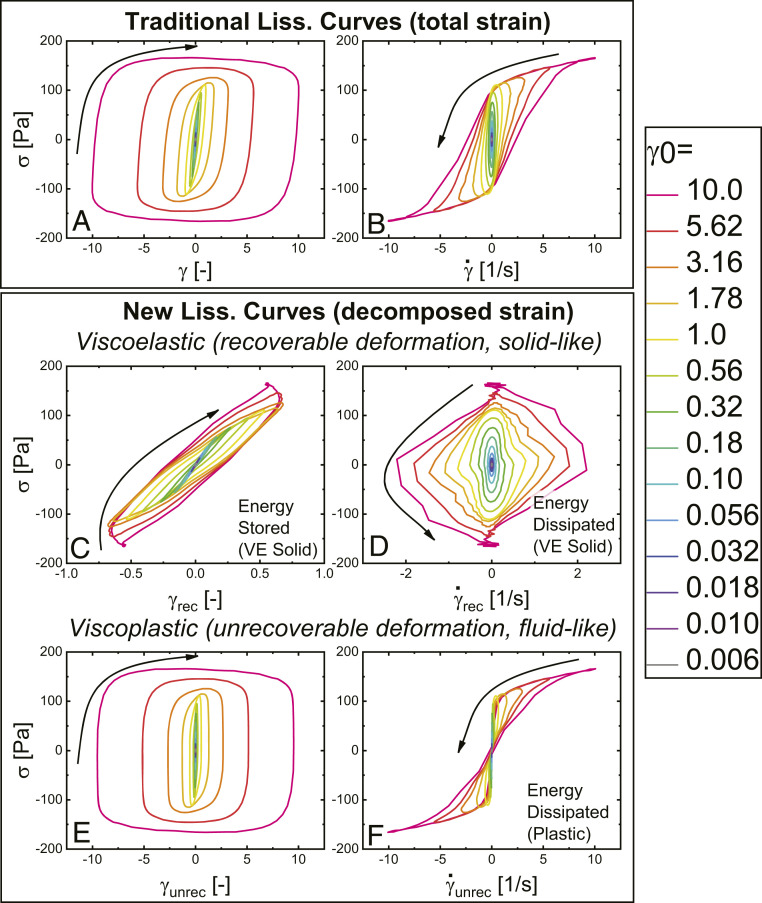
The traditional raw rheological signals, displayed as Lissajous–Bowditch curves in which the stress is plotted against the total strain and total strain rate, are shown in Fig. 2 A and B for a Carbopol 980 microgel. These are constructed using the total strain, , and the total strain rate, , as is iterated over a half cycle, with the results being reflected to a full cycle by symmetry. The shapes observed are typical of plastic materials (22–24).
Fig. 2.
Lissajous figures containing decomposed strain and strain rate for Carbopol: stress vs. (A) total strain, (B) total rate, (C) recoverable strain, (D) recoverable rate, (E) unrecoverable strain, and (F) unrecoverable rate. VE, viscoelastic.
The decomposed recoverable (viscoelastic solid) and unrecoverable (plastic) strains allow us to create four important Lissajous curves by plotting the stress against the recoverable (solid-like) strain (Fig. 2C) and strain rate (Fig. 2D) and the unrecoverable (plastic) strain (Fig. 2E) and strain rate (Fig. 2F). Detailed views of the smaller amplitudes are shown in SI Appendix.
By using Eqs. 7–9, we can define three moduli components, , , and , that carry more information between them than the traditional measures based on the total deformation. These represent the elastic potential energy storage, viscoelastic solid dissipation, and unrecoverable dissipation due to plastic flow.
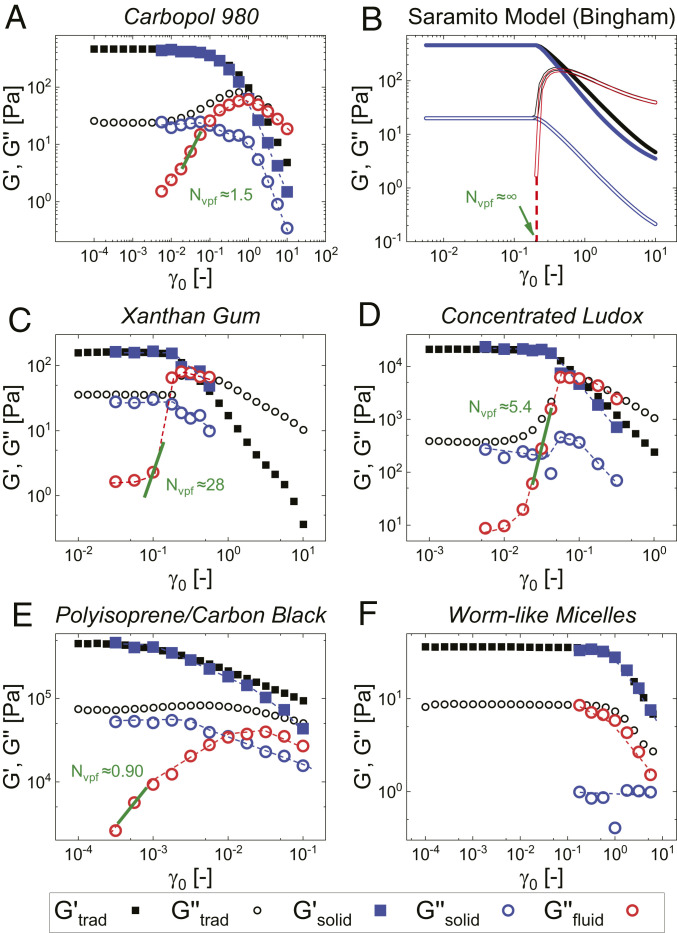
We show in Fig. 3 how these moduli compare with the traditionally defined versions across the amplitude sweep range for each material, as well as Saramito’s model with a Bingham flow viscosity (19). At small amplitudes, , which clearly reflects elastic (recoverable) deformation as being the primary energy storage mechanism at small amplitudes. Under large deformation amplitudes, the Carbopol and filled polymer solution show small deviations between the total and component moduli, which could be the result of at least two possible explanations. First, the fact that the storage modulus from the measured recoverable strain is lower than the traditionally defined modulus suggests the possibility of increased inertial effects at large amplitudes for some of the materials tested. This is supported by the fact that no deviations are seen at small amplitudes, as inertial energy storage is anticipated to be negligible in the linear regime (3) and only relevant at large amplitudes. Alternatively, deviations can be attributed to time-dependent evolution of the microstructure [e.g., microgel breakdown (78) for the Carbopol] over the long (∼4- to 6-h) timescales it takes to collect data from a single strain amplitude. This is supported by evidence from tests performed on foams, shown in SI Appendix, which show the softening effects of coarsening over the duration of the experiment (79).
Fig. 3.
Decomposed amplitude sweeps for the samples and model used in this study: (A) Carbopol, (B) Saramito model (Bingham version), (C) xanthan gum, (D) concentrated Ludox, (E) filled polymer, and (F) worm-like micelles. Green lines denote the slopes that lead to the dimensionless viscoplastic fragility number, as well the specific values for each material. The Saramito model parameters used here are , , , and . (Model details can be found in SI Appendix.)
While the storage modulus definitions are equivalent, our knowledge of the recoverable and unrecoverable components allows us to define two distinct contributions to the total energy dissipation, enhancing our understanding of the functional dependence of the loss modulus. In all cases, the total energy dissipated is a sum of viscoelastic solid-like and plastic terms.
In all of the plastic materials that display the Payne effect, or a type III response with an overshoot in the loss modulus (Fig. 3 A and C–E), the majority of the energy dissipation at small amplitudes is due to the viscoelastic solid component. In the case of the Saramito model (Fig. 3B), this component accounts for 100% of the energy dissipation at these small amplitudes. As the amplitude is increased, each of the type III materials gradually acquires more strain unrecoverably, leading to an increase in the energy dissipation via the plastic flow component. The slope of this increase varies from sample to sample, being steepest for the xanthan gum and shallowest for the filled polymer. The plastic flow component of the loss modulus remains at zero for the Saramito model below a well-defined yield condition and increases abruptly after the yield stress is exceeded. While the Saramito model has been constructed to ensure the stresses pre- and postyielding are continuous, the digital yielding element does not allow for the continuity of the moduli components as the amplitude is swept.
The maximum value of the derivative of the plastic component of the loss modulus as a function of the strain amplitude can be taken as a measure of viscoplastic fragility. The larger the derivative, the more rapidly the material acquires large amounts of strain unrecoverably. A dimensionless form of this metric would be the maximum value of a spatial equivalent to the mutation number of Mours and Winter (80):
| [10] |
As we only have data for at discrete amplitudes, we can simplify Eq. 10 by equating the derivative to a simple difference:
| [11] |
The value and location of this measure are shown for each model and material in Fig. 3 A–E. The values of throughout the amplitude sweep are shown in SI Appendix. This metric serves a similar function to the flow transition index (FTI) (81, 82), which is defined as the ratio between the stress at which the dynamic moduli cross (called the “flow stress”) and stress at which the first nonlinearity is observed (called the “yield stress”). The FTI is used in the grease industry to measure the breakage behavior of the microstructure of a material and has been applied as a quantification for the suitability of a material for three-dimensional printing (81). Our measure sheds additional light on this phenomenon, as it directly accounts for microstructural breakage in a way that merely looking at the total dissipation behavior cannot because such breakage can only reasonably come from the unrecoverable acquisition of strain.
As the plastic flow component of the loss modulus increases, the storage modulus begins to drop. This decrease can be explained by the fact that the introduction of a significant unrecoverable strain component results in a reduced percentage of the total strain amplitude being from the recoverable strain, necessarily reducing the normalized elastic potential energy storage.
As the loss modulus overshoots, the viscoelastic solid-like component decreases, while the plastic component begins to slow its increase, peaking slightly after the (total) loss modulus does. At large amplitudes, both components decrease, although the dissipation is still primarily due to unrecoverable plastic flow. In the case of the filled polymer (Fig. 3E), we still observe yielding despite there being no cross-over point in the traditional moduli, as significant acquisition of unrecoverable strain is observed. For the Saramito model, the choice of flow profile (Bingham, Herschel–Bulkley, etc.) will impact the rate at which this component decreases with increasing strain amplitude but will not affect the yielding or preyielding behavior. For a Herschel–Bulkley Saramito model, would decrease more rapidly with strain amplitude, as the stress amplitude would be lowered by the shear thinning.
The results for type III yielding materials contrast to those of a purely viscoelastic worm-like micellar sample without an overshoot in the loss modulus (Fig. 3F) (i.e., a type I response). The micelles display significant acquisition of unrecoverable strain even at the smallest amplitudes, with the recoverable component remaining small and essentially (negligibly) constant. The micellar solution is therefore a viscoelastic liquid at all strain amplitudes, despite the storage modulus being larger than the loss at the smallest deformations. It therefore displays no yielding. All of the plastic materials are viscoelastic solids at small amplitudes and yield to become fluids at larger amplitudes.
Discussion
We have shown that the overshoot in the loss modulus, which is typically associated with plasticity and yielding in soft materials and which has been referred to as a type III response or the Payne effect, is due to a continuous transition from recoverable to unrecoverable acquisition of strain from small to large strain amplitudes.
With the distinct viscoelastic solid and plastic contributions to the loss modulus, as shown in Fig. 3, we present a much more detailed and nuanced rheological view of plasticity and yielding than has previously been accessible (4, 5, 7, 22–24). Crucially, there is no single yield point identified by our experimental data but rather, a continuum of behaviors between the unyielded and the yielded. The importance of the solid-like and plastic dissipation contributions shows that common interpretations of the dynamic moduli as “elasticity” and “viscosity” are oversimplifications and that their energetic definitions are paramount. The loss modulus is a composite parameter, made of two distinct parts that reflect energy dissipation via viscoelastic solid and fluid mechanisms.
Our observation that nonnegligible contributions to the loss modulus from recoverable and unrecoverable processes are seen across the entire range of amplitudes strongly suggests that binary yielding models, such as that of Bingham (5, 18) or Herschel and Bulkley (17), or more recent models that account for yielding phenomena while assuring a continuous change from a solid to a fluid behavior (19, 20) can be no more than approximations of the steady-state behavior and need to be generalized to account for the transience of yielding. Specifically, the abrupt increase in for the Saramito model (Fig. 3B) at the yield point, leading to an infinite viscoplastic fragility number, is a much sharper increase than we observe in any of the measured material responses. The stated goal of the development of the Saramito model was to produce a model that “assures a continuous change from a solid to a fluid behavior of the material” (19). While that goal was indeed achieved in terms of the stress, we can now see from the decomposition of strains that the contribution to the loss modulus from the acquisition of unrecoverable strain is discontinuous in the model. The behavior of the range of materials we have probed is not. This suggests that models containing digital yielding elements that yield at a well-defined stress, such as the friction element of the Saramito model, are problematic.
Our results, in which significant recoverable strain is observed even when materials are flowing, are consistent with an interpretation of yielding as a spatially heterogeneous transition that becomes more widespread throughout the material as the amplitude of deformation increases. This study therefore provides rheological understanding and support of experimental results that suggest both the gradual propagation of yielding and persistence of some equilibrium structure above yielding in structurally resolved techniques such as diffusing-wave spectroscopy (83), rheo-microscopy (84), ultrasonic speckle velocimetry (32, 85–87), and rheo-scattering (88–90). It also correlates well with theoretical studies of soft glassy rheology (91, 92), shear transformation zone theory (93), and colloidal glass avalanche dynamics (94), in which evidence of intact structure is observed at amplitudes where our approach would likely identify significant recoverable and unrecoverable strains. Such results indicate the need for new constitutive models to model yielding that contain both solid-like and plastic behaviors at all amplitudes and gradual, spatially heterogenous transitions between them.
The experimental decomposition of strain in this work is unique among techniques designed to understand nonlinear oscillatory rheology (29, 37–42) for multiple reasons: 1) it has been shown to correlate the rheology and microstructure of soft materials in prior work (73); 2) it makes no mathematical assumptions about the material’s constitutive behavior beyond the additivity of recoverable and unrecoverable strains; 3) it is innately time resolved and can be defined with resolution well below the duration of a full period; and 4) the addition of the iterative recovery step provides more transient experimental information than measurements using the total strain and strain rates alone. With the addition of the separate contributions to the loss modulus, the experimental strain decomposition enables us to gain a deeper understanding of the complicated behaviors occurring during rheological measurements on plastic materials, specifically allowing us to see the transition from solid-like to fluid-like dissipation in these materials.
Our results also provide insight into the phenomenon of mechanical memory observed in colloidal glasses, emulsions, and foams (12, 13). In these systems, a memory is written mechanically into the material by oscillating at a small amplitude for an extended interval before reading the memory by sweeping from small to large amplitudes. Maximal memory effects are observed when the training step is performed near the maximum in the loss modulus, which we have shown occurs close to the point where the viscoelastic solid and liquid contributions to energy dissipation are equal, . Memory encoding in concentrated systems may therefore be seen as an interplay between elastic and plastic acquisition of strain. Memory is kept by the recoverable strain but requires the acquisition of unrecoverable strain to allow sufficient rearrangements to form the memory. The acquisition of unrecoverable strain distributed evenly throughout the material at larger amplitudes will destroy any structures capable of remembering prior deformations, while too little acquisition of unrecoverable strain will not allow sufficient rearrangements to create the memory. In this sense, the acquisition of unrecoverable strain acts like an increase in temperature, allowing the system to more freely explore its potential energy landscape, while the memory represents a local minimum in that landscape. Too much unrecoverable strain erases the deep potential energy minima, leaving the system in a fluid state with no ability to remember past states.
We note that while we have chosen to primarily focus on amplitude sweeps of plastic materials, the transient deformation/recovery technique can, in principle, be applied to any protocol of interest for any material that is stable for sufficiently long periods of time. These recovery tests provide detailed time-resolved tests of the assumptions inherent in other LAOS analyses (29, 37–42). Finally, while the tests here were carried out at steady alternance to mirror previous studies into the Payne effect and the overshoot in the loss modulus, similar tests could, in principle, be performed to study either start-up or steady-state yielding dynamics under any rheological protocol.
Materials and Methods
We study four representative soft materials from different classes of microstructure that exhibit plasticity as determined by a type III behavior in an amplitude sweep: a polymer microgel (Carbopol 980, 1 wt %) (23–27), a biopolymer suspension (xanthan gum, 4 wt %) (34), a dense (glassy) colloidal suspension (concentrated Ludox TM-50, 55 vol %) (95), and a filled polymer solution (2:1:1 polyisoprene/squalene/carbon black; similar to ref. 44 but with squalene added to facilitate measurement at “low” [∼50 °C] temperatures). A typical amplitude sweep for these materials resembles the one in Fig. 1B, where the overshoot in the loss modulus is apparent at intermediate amplitudes. Additionally, a self-assembled viscoelastic surfactant solution (cetylpyridinium chloride worm-like micelles) (73), which exhibits no overshoot in the loss modulus, was also tested. Specific preparation instructions for these materials can be found in SI Appendix.
All measurements were made with an Anton Paar Modular Compact Rheometer (MCR) 702 operating in single-drive mode. Using an electronically commutated synchronous motor allows one to do measurements under both stress-controlled and strain-controlled modes on one device. This instrument allowed for rapid switching on the order of milliseconds between strain-controlled oscillation and stress-controlled recovery steps. All data were collected at an angular frequency of rad s−1. The geometries used were chosen to replicate existing works in the literature for each system tested (23, 34, 44, 73, 95). Geometry details can be found in SI Appendix.
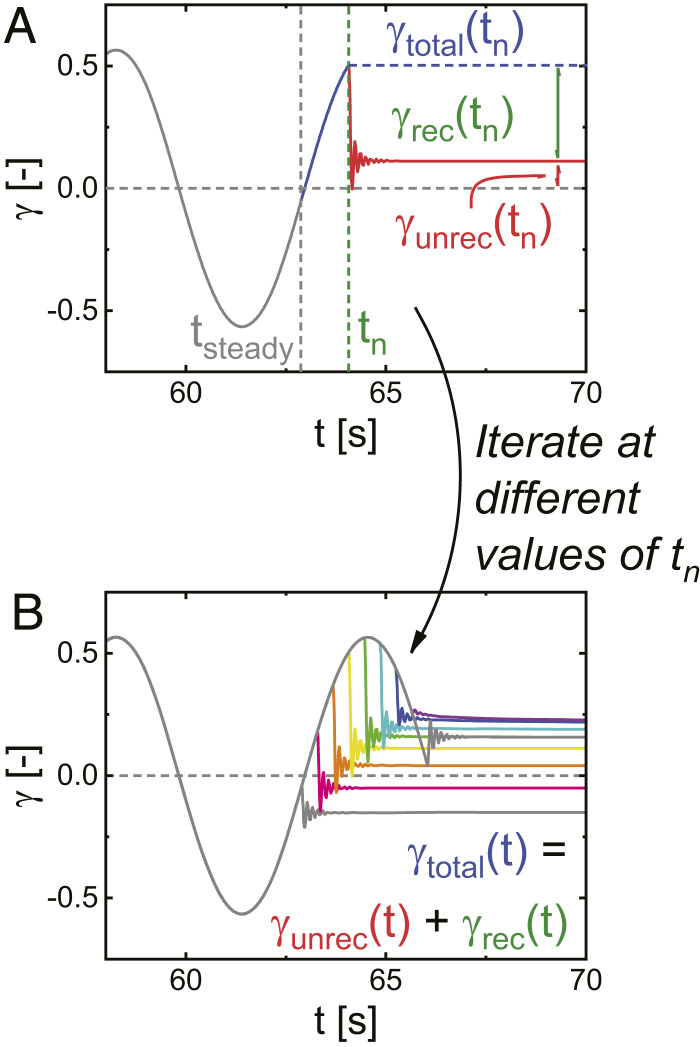
The protocol for the oscillatory shear/recovery tests used in this study contains multiple distinct steps that are iterated to form a complete set: 1) application of a sinusoidal strain for a time sufficient to achieve steady alternance; 2) continuation of the oscillatory strain for an additional fraction of a period; and 3) the application of zero stress to allow the material to recover to its ground state. This procedure was carried out in the forward and reverse directions, with the average result used to eliminate potential directional artifacts. A schematic of a single iteration of this protocol is displayed in Fig. 4A. This test provides three measured values: the strain at the end of step 2 is the total strain at time (the point at which the oscillation was ceased), and the strain at the end of step 3 is the unrecoverable strain at the same time point . Eq. 5 additionally allows for the determination of the recoverable strain at the given time .
Fig. 4.
(A) Schematic of single oscillatory shear/recovery protocol described in the text. (B) Demonstration of protocol iteration for Carbopol 980.
To obtain results throughout each amplitude, the protocol was iterated 40 times per amplitude (with forward and reverse at each ), varying the length of the second step such that each pair was spaced evenly in time with 32 points per half period (examples of several iterations are shown in Fig. 4B). Use of numerical differentiation and Eqs. 5 and 6 allowed for the determination of the recoverable and unrecoverable strains and rates throughout the period.
The data presented in this work were collected via Anton Paar’s commercially available RheoCompass software. To compare our experimental results with existing models, we have numerically calculated the LAOS response of Saramito’s model with a Bingham flow viscosity (19) in MATLAB. The equations used, as well as the simulated LAOS waveforms, can be found in SI Appendix. The full set of data shown in the manuscript, as well as the MATLAB code used for analysis and simulation, can be accessed via Mendeley Data (96).
Supplementary Material
Acknowledgments
We thank Anton Paar for the use of the TwinDrive MCR 702 through their academic program. We also thank Lubrizol and the Zhao laboratory at the University of Illinois at Urbana–Champaign (UIUC) for materials and assistance with sample preparation. Useful discussions with Johnny Ching-Wei Lee of UIUC and Prof. Gareth McKinley of Massachusetts Institute of Technology are acknowledged. This material is based upon work supported by NSF Grant 1847389 and the Laboratory Directed Research and Development program at Sandia National Laboratories. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia LLC, a wholly owned subsidiary of Honeywell International Inc. for the US Department of Energy’s National Nuclear Security Administration Contract DE-NA0003525.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2003869117/-/DCSupplemental.
Data Availability.
The full set of data shown in the manuscript, as well as the MATLAB code used for analysis and simulation, can be accessed via Mendeley Data (96).
References
- 1.Ferry J. D., Viscoelastic Properties of Polymers, (John Wiley & Sons, Incorporated, 1980). [Google Scholar]
- 2.Gemant A., A method of analyzing experimental results obtained from elasto-viscous bodies. J. Appl. Phys. 7, 311–317 (1936). [Google Scholar]
- 3.Tschoegl N. W., The Phenomenological Theory of Linear Viscoelastic Behavior, (Springer, Berlin, Germany, 1989). [Google Scholar]
- 4.Balmforth N. J., Frigaard I. A., Ovarlez G., Yielding to stress: Recent developments in viscoplastic fluid mechanics. Annu. Rev. Fluid Mech. 46, 121–146 (2014). [Google Scholar]
- 5.Barnes H. A., The yield stress—a review or “παντα ρει”—everything flows? J. Nonnewton. Fluid Mech. 81, 133–178 (1999). [Google Scholar]
- 6.Bonn D., Denn M. M., Materials science. Yield stress fluids slowly yield to analysis. Science 324, 1401–1402 (2009). [DOI] [PubMed] [Google Scholar]
- 7.Bonn D., Denn M. M., Berthier L., Divoux T., Manneville S., Yield stress materials in soft condensed matter. Rev. Mod. Phys. 89, 035005 (2017). [Google Scholar]
- 8.Nguyen Q. D., Boger D. V., Measuring the flow properties of yield stress fluids. Annu. Rev. Fluid Mech. 24, 47–48 (1992). [Google Scholar]
- 9.Coussot P., Yield stress fluid flows: A review of experimental data. J. Nonnewton. Fluid Mech. 211, 31–49 (2014). [Google Scholar]
- 10.Donley G. J., Hyde W. W., Rogers S. A., Nettesheim F., Yielding and recovery of conductive pastes for screen printing. Rheol. Acta 58, 361–382 (2019). [Google Scholar]
- 11.Nelson A. Z. et al., Designing and transforming yield-stress fluids. Curr. Opin. Solid State Mater. Sci. 23, 100758 (2019). [Google Scholar]
- 12.Keim N. C., Paulsen J. D., Zeravcic Z., Sastry S., Nagel S. R., Memory formation in matter. Rev. Mod. Phys. 91, 035002 (2019). [Google Scholar]
- 13.Mukherji S., Kandula N., Sood A. K., Ganapathy R., Strength of mechanical memories is maximal at the yield point of a soft glass. Phys. Rev. Lett. 122, 158001 (2019). [DOI] [PubMed] [Google Scholar]
- 14.Schwedoff T., “La rigidite des fluides” in Rapports Du Congres Intern de Physique, Guillaume C. E., Poincaré L., Eds. (Gauthier-Villars, Paris, France, 1900), Vol. 1, pp. 478–486. [Google Scholar]
- 15.Bingham E. C., An investigation of the laws of plastic flow. Bull. Bur. Stand. 13, 309–353 (1916). [Google Scholar]
- 16.Coussot P., Bingham’s heritage. Rheol. Acta 56, 163–176 (2017). [Google Scholar]
- 17.Herschel W. H., Bulkley R., Konsistenzmessungen von Gummi-benzollösungen. Kolloid-Zeitschrift 39, 291–300 (1926). [Google Scholar]
- 18.Yoshimura A. S., Prud’homme R. K., Response of an elastic Bingham fluid to oscillatory shear. Rheol. Acta 26, 428–436 (1987). [Google Scholar]
- 19.Saramito P., A new constitutive equation for elastoviscoplastic fluid flows. J. Nonnewton. Fluid Mech. 145, 1–14 (2007). [Google Scholar]
- 20.Saramito P., A new elastoviscoplastic model based on the Herschel-Bulkley viscoplastic model. J. Nonnewton. Fluid Mech. 158, 154–161 (2009). [Google Scholar]
- 21.Barnes H. A., Walters K., The yield stress myth? Rheol. Acta 24, 323–326 (1985). [Google Scholar]
- 22.Dinkgreve M., Paredes J., Denn M. M., Bonn D., On different ways of measuring “the” yield stress. J. Nonnewton. Fluid Mech. 238, 233–241 (2016). [Google Scholar]
- 23.Donley G. J., de Bruyn J. R., McKinley G. H., Rogers S. A., Time-resolved dynamics of the yielding transition in soft materials. J. Nonnewton. Fluid Mech. 264, 117–134 (2019). [Google Scholar]
- 24.Fernandes R. R., Andrade D. E. V., Franco A. T., Negrão C. O. R., The yielding and the linear-to-nonlinear viscoelastic transition of an elastoviscoplastic material. J. Rheol. 61, 893–903 (2017). [Google Scholar]
- 25.Divoux T., Tamarii D., Barentin C., Manneville S., Transient shear banding in a simple yield stress fluid. Phys. Rev. Lett. 104, 208301 (2010). [DOI] [PubMed] [Google Scholar]
- 26.Divoux T., Barentin C., Manneville S., From stress-induced fluidization processes to Herschel-Bulkley behaviour in simple yield stress fluids. Soft Matter 7, 8409–8418 (2011). [Google Scholar]
- 27.Ovarlez G., Cohen-Addad S., Krishan K., Goyon J., Coussot P., On the existence of a simple yield stress fluid behavior. J. Nonnewton. Fluid Mech. 193, 68–79 (2013). [Google Scholar]
- 28.Coussot P., Slow flows of yield stress fluids: Yielding liquids or flowing solids? Rheol. Acta 57, 1–14 (2018). [Google Scholar]
- 29.Dimitriou C. J., Ewoldt R. H., McKinley G. H., Describing and prescribing the constitutive response of yield stress fluids using large amplitude oscillatory shear stress (LAOStress). J. Rheol. 57, 27–70 (2013). [Google Scholar]
- 30.Møller P. C. F., Fall A., Bonn D., Origin of apparent viscosity in yield stress fluids below yielding. EPL 87, 38004 (2009). [Google Scholar]
- 31.Dinkgreve M., Denn M. M., Bonn D., “Everything flows?”: Elastic effects on startup flows of yield-stress fluids. Rheol. Acta 56, 189–194 (2017). [Google Scholar]
- 32.Bécu L., Manneville S., Colin A., Yielding and flow in adhesive and nonadhesive concentrated emulsions. Phys. Rev. Lett. 96, 138302 (2006). [DOI] [PubMed] [Google Scholar]
- 33.Coussot P., Nguyen Q. D., Huynh H. T., Bonn D., Avalanche behavior in yield stress fluids. Phys. Rev. Lett. 88, 175501 (2002). [DOI] [PubMed] [Google Scholar]
- 34.Hyun K., Kim S. H., Ahn K. H., Lee S. J., Large amplitude oscillatory shear as a way to classify the complex fluids. J. Nonnewton. Fluid Mech. 107, 51–65 (2002). [Google Scholar]
- 35.Hyun K. et al., A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Polym. Sci. 36, 1697–1753 (2011). [Google Scholar]
- 36.Mujumdar A., Beris A. N., Metzner A. B., Transient phenomena in thixotropic systems. J. Nonnewton. Fluid Mech. 102, 157–178 (2002). [Google Scholar]
- 37.Cho K. S., Hyun K., Ahn K. H., Lee S. J., A geometrical interpretation of large amplitude oscillatory shear response. J. Rheol. 49, 747–758 (2005). [Google Scholar]
- 38.Ewoldt R. H., Hosoi A. E., McKinley G. H., New measures for characterizing nonlinear viscoelasticity in large amplitude oscillatory shear. J. Rheol. 52, 1427–1458 (2008). [Google Scholar]
- 39.Klein C. O., Spiess H. W., Calin A., Balan C., Wilhelm M., Separation of the nonlinear oscillatory response into a superposition of linear, strain hardening, strain softening, and wall slip response. Macromolecules 40, 4250–4259 (2007). [Google Scholar]
- 40.Rogers S. A., A sequence of physical processes determined and quantified in LAOS: An instantaneous local 2D/3D approach. J. Rheol. 56, 1129–1151 (2012). [Google Scholar]
- 41.Singh P. K., Soulages J. M., Ewoldt R. H., Frequency-sweep medium-amplitude oscillatory shear (MAOS). J. Rheol. 62, 277–293 (2018). [Google Scholar]
- 42.Wilhelm M., Fourier-transform rheology. Macromol. Mater. Eng. 287, 83–105 (2002). [Google Scholar]
- 43.Payne A. R., The dynamic properties of carbon black loaded natural rubber vulcanizates. Part I. J. Appl. Polym. Sci. 6, 57–63 (1962). [Google Scholar]
- 44.Fan X. et al., Insight into the weak strain overshoot of carbon black filled natural rubber. Polymer 167, 109–117 (2019). [Google Scholar]
- 45.Hentschke R., The Payne effect revisited. Express Polym. Lett. 11, 278–292 (2017). [Google Scholar]
- 46.Roland C. M., Dynamic mechanical behavior of filled rubber at small strains. J. Rheol. 34, 25–34 (1990). [Google Scholar]
- 47.Christopoulou C., Petekidis G., Erwin B., Cloitre M., Vlassopoulos D., Ageing and yield behaviour in model soft colloidal glasses. Philos. Trans. A Math. Phys. Eng. Sci. 367, 5051–5071 (2009). [DOI] [PubMed] [Google Scholar]
- 48.Erwin B. M., Cloitre M., Gauthier M., Vlassopoulos D., Dynamics and rheology of colloidal star polymers. Soft Matter 6, 2825–2833 (2010). [Google Scholar]
- 49.le Grand A., Petekidis G., Effects of particle softness on the rheology and yielding of colloidal glasses. Rheol. Acta 47, 579–590 (2008). [Google Scholar]
- 50.Mason T. G., Weitz D. A., Linear viscoelasticity of colloidal hard sphere suspensions near the glass transition. Phys. Rev. Lett. 75, 2770–2773 (1995). [DOI] [PubMed] [Google Scholar]
- 51.Renou F., Stellbrink J., Petekidis G., Yielding processes in a colloidal glass of soft star-like micelles under large amplitude oscillatory shear (LAOS). J. Rheol. 54, 1219–1242 (2010). [Google Scholar]
- 52.Asai H., Masuda A., Kawaguchi M., Rheological properties of colloidal gels formed from fumed silica suspensions in the presence of cationic surfactants. J. Colloid Interface Sci. 328, 180–185 (2008). [DOI] [PubMed] [Google Scholar]
- 53.Daniel C., Hamley I. W., Wilhelm M., Mingvanish W., Non-linear rheology of a face-centred cubic phase in a diblock copolymer gel. Rheol. Acta 40, 39–48 (2001). [Google Scholar]
- 54.Hyun K., Nam J. G., Wilhelm M., Ahn K. H., Lee S. J., Nonlinear response of complex fluids under LAOS (large amplitude oscillatory shear) flow. Korea-Australia Rheol. J. 15, 97–105 (2003). [Google Scholar]
- 55.Hyun K., Nam J. G., Wilhelm M., Ahn K. H., Lee S. J., Large amplitude oscillatory shear behavior of PEO-PPO-PEO triblock copolymer solutions. Rheol. Acta 45, 239–249 (2006). [Google Scholar]
- 56.Bossard F., Moan M., Aubry T., Linear and nonlinear viscoelastic behavior of very concentrated plate-like kaolin suspensions. J. Rheol. 51, 1253–1270 (2007). [Google Scholar]
- 57.Raghavan S. R., Khan S. A., Shear‐induced microstructural changes in flocculated suspensions of fumed silica. J. Rheol. 39, 1311–1325 (1995). [Google Scholar]
- 58.Wyss H. M. et al., Strain-rate frequency superposition: A rheological probe of structural relaxation in soft materials. Phys. Rev. Lett. 98, 238303 (2007). [DOI] [PubMed] [Google Scholar]
- 59.Yziquel F., Carreau P. J., Moan M., Tanguy P. A., Rheological modeling of concentrated colloidal suspensions. J. Nonnewton. Fluid Mech. 86, 133–155 (1999). [Google Scholar]
- 60.Yziquel F., Carreau P. J., Tanguy P. A., Non-linear viscoelastic behavior of fumed silica suspensions. Rheol. Acta 38, 14–25 (1999). [Google Scholar]
- 61.Bower C., Gallegos C., Mackley M. R., Madiedo J. M., The rheological and microstructural characterisation of the non-linear flow behaviour of concentrated oil-in-water emulsions. Rheol. Acta 38, 145–159 (1999). [Google Scholar]
- 62.Mason T. G., Bibette J., Weitz D. A., Elasticity of compressed emulsions. Phys. Rev. Lett. 75, 2051–2054 (1995). [DOI] [PubMed] [Google Scholar]
- 63.Mason T. G. et al., Osmotic pressure and viscoelastic shear moduli of concentrated emulsions. Phys. Rev. E 56, 3150 (1997). [Google Scholar]
- 64.Rouyer F., Cohen-Addad S., Höhler R., Is the yield stress of aqueous foam a well-defined quantity? Colloids Surf. A Physicochem. Eng. Asp. 263, 111–116 (2005). [Google Scholar]
- 65.Saint-Jalmes A., Durian D. J., Vanishing elasticity for wet foams: Equivalence with emulsions and role of polydispersity. J. Rheol. 43, 1411–1422 (1999). [Google Scholar]
- 66.Tam K. C., Guo L., Jenkins R. D., Bassett D. R., Viscoelastic properties of hydrophobically modified alkali-soluble emulsion in salt solutions. Polymer 40, 6369–6379 (1999). [Google Scholar]
- 67.Tirtaatmadja V., Tam K. C., Jenkins R. D., Superposition of oscillations on steady shear flow as a technique for investigating the structure of associative polymers. Macromolecules 30, 1426–1433 (1997). [Google Scholar]
- 68.Tirtaatmadja V., Tam K. C., Jenkins R. D., Rheological properties of model alkali-soluble associative (HASE) polymers: Effect of varying hydrophobe chain length. Macromolecules 30, 3271–3282 (1997). [Google Scholar]
- 69.Phan-Thien N., Safari-Ardi M., Morales-Patiño A., Oscillatory and simple shear flows of a flour-water dough: A constitutive model. Rheol. Acta 36, 38–48 (1997). [Google Scholar]
- 70.Phan-Thien N., Safari-Ardi M., Linear viscoelastic properties of flour-water doughs at different water concentrations. J. Nonnewton. Fluid Mech. 74, 137–150 (1998). [Google Scholar]
- 71.Parthasarathy M., Klingenberg D. J., Large amplitude oscillatory shear of ER suspensions. J. Nonnewton. Fluid Mech. 81, 83–104 (1999). [Google Scholar]
- 72.Sim H. G., Ahn K. H., Lee S. J., Large amplitude oscillatory shear behavior of complex fluids investigated by a network model: A guideline for classification. J. Nonnewton. Fluid Mech. 112, 237–250 (2003). [Google Scholar]
- 73.Lee J. C.-W., Weigandt K. M., Kelley E. G., Rogers S. A., Structure-property relationships via recovery rheology in viscoelastic materials. Phys. Rev. Lett. 122, 248003 (2019). [DOI] [PubMed] [Google Scholar]
- 74.Laun H. M., Prediction of elastic strains of polymer melts in shear and elongation. J. Rheol. 30, 459–501 (1986). [Google Scholar]
- 75.Reiner M., “Rheology” in Elasticity and Plasticity, Flügge S., Ed. (Springer, Berlin, Germany, 1958), pp. 434–550. [Google Scholar]
- 76.Weissenberg K., A continuum theory of rheological phenomena. Nature 159, 310 (1947). [DOI] [PubMed] [Google Scholar]
- 77.de Souza Mendes P. R., Thompson R. L., A unified approach to model elasto-viscoplastic thixotropic yield-stress materials and apparent yield-stress fluids. Rheol. Acta 52, 673–694 (2013). [Google Scholar]
- 78.Dinkgreve M., Fazilati M., Denn M. M., Bonn D., Carbopol: From a simple to a thixotropic yield stress fluid. J. Rheol. 62, 773–780 (2018). [Google Scholar]
- 79.Cohen-Addad S., Hoballah H., Höhler R., Viscoelastic response of a coarsening foam. Phys. Rev. E 57, 6897 (1998). [Google Scholar]
- 80.Mours M., Winter H. H., Time-resolved rheometry. Rheol. Acta 33, 385–397 (1994). [Google Scholar]
- 81.Corker A., Ng H. C. H., Poole R. J., García-Tuñón E., 3D printing with 2D colloids: Designing rheology protocols to predict “printability” of soft-materials. Soft Matter 15, 1444–1456 (2019). [DOI] [PubMed] [Google Scholar]
- 82.Mezger T. G., The Rheology Handbook, (Vincentz Network, 2012). [Google Scholar]
- 83.Hébraud P., Lequeux F., Munch J. P., Pine D. J., Yielding and rearrangements in disordered emulsions. Phys. Rev. Lett. 78, 4657–4660 (1997). [Google Scholar]
- 84.Knowlton E. D., Pine D. J., Cipelletti L., A microscopic view of the yielding transition in concentrated emulsions. Soft Matter 10, 6931–6940 (2014). [DOI] [PubMed] [Google Scholar]
- 85.Gibaud T., Frelat D., Manneville S., Heterogeneous yielding dynamics in a colloidal gel. Soft Matter 6, 3482–3488 (2010). [Google Scholar]
- 86.Divoux T., Tamarii D., Barentin C., Teitel S., Manneville S., Yielding dynamics of a herschel-bulkley fluid: A critical-like fluidization behaviour. Soft Matter 8, 4151–4164 (2012). [Google Scholar]
- 87.Gibaud T., Barentin C., Manneville S., Influence of boundary conditions on yielding in a soft glassy material. Phys. Rev. Lett. 101, 258302 (2008). [DOI] [PubMed] [Google Scholar]
- 88.Leheny R. L., Rogers M. C., Chen K., Narayanan S., Harden J. L., Rheo-XPCS. Curr. Opin. Colloid Interface Sci. 20, 261–271 (2015). [Google Scholar]
- 89.Rogers M. C. et al., Echoes in x-ray speckles track nanometer-scale plastic events in colloidal gels under shear. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 90, 062310 (2014). [DOI] [PubMed] [Google Scholar]
- 90.Rogers M. C. et al., Microscopic signatures of yielding in concentrated nanoemulsions under large-amplitude oscillatory shear. Phys. Rev. Mater. 2, 095601 (2018). [Google Scholar]
- 91.Fielding S. M., Sollich P., Cates M. E., Aging and rheology in soft materials. J. Rheol. 44, 323–369 (2000). [Google Scholar]
- 92.Sollich P., Lequeux F., Hébraud P., Cates M. E., Rheology of soft glassy materials. Phys. Rev. Lett. 78, 2020–2023 (1997). [Google Scholar]
- 93.Falk M. L., Langer J. S., Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 57, 7192–7205 (1998). [Google Scholar]
- 94.Leishangthem P., Parmar A. D. S., Sastry S., The yielding transition in amorphous solids under oscillatory shear deformation. Nat. Commun. 8, 14653 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Rogers S. A., Park J. D., Lee C. W. J., Instantaneous dimensionless numbers for transient nonlinear rheology. Rheol. Acta 58, 539–556 (2019). [Google Scholar]
- 96.Donley G., Singh P., Shetty A., Rogers S., Dataset for Elucidating the G′’ overshoot in soft materials with a yield transition via a time-resolved experimental strain decomposition. Mendeley Data. 10.17632/y9m8ptydgw.1. Deposited 30 July 2020. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The full set of data shown in the manuscript, as well as the MATLAB code used for analysis and simulation, can be accessed via Mendeley Data (96).