The Impact of Covariance Priors on Arm-Based Bayesian Network Meta-Analyses with Binary Outcomes

Abstract

Bayesian analyses with the arm-based (AB) network meta-analysis (NMA) model require researchers to specify a prior distribution for the covariance matrix of the treatment-specific event rates in a transformed scale, e.g. the treatment-specific log-odds when a logit transformation is used. The commonly-used conjugate prior for the covariance matrix, the inverse-Wishart (IW) distribution, has several limitations. For example, although the IW distribution is often described as non- or weakly-informative, it may in fact provide strong information when some variance components are small (e.g., when the standard deviation of study-specific log-odds of a treatment is smaller than 1/2), as is common in NMAs with binary outcomes. In addition, the IW prior generally leads to underestimation of correlations between treatment-specific log-odds, which are critical for borrowing strength across treatment arms to estimate treatment effects efficiently and to reduce potential bias. Alternatively, several separation strategies (i.e., separate priors on variances and correlations) can be considered. To study the IW prior’s impact on NMA results and compare it with separation strategies, we did simulation studies under different missing-treatment mechanisms. A separation strategy with appropriate priors for the correlation matrix and variances performs better than the IW prior, and should be recommended as the default vague prior in the AB NMA approach. Finally, we re-analyzed three case studies and illustrated the importance, when performing AB-NMA, of sensitivity analyses with different prior specifications on variances.

1. INTRODUCTION

In recent decades, many systematic reviews and meta-analyses have summarized existing evidence on a given scientific question from multiple independent studies. Traditionally, a meta-analysis of randomized controlled trials compares only two treatments, typically an intervention and a control. With new treatments emerging, network meta-analysis (NMA) has been developed and is increasingly used to synthesize direct and indirect evidence comparing multiple treatments^1,2. For instance, if three treatments A, B, and C are available for a certain disease then in NMA, comparing treatments A and C provides direct evidence about A versus C while comparing A versus B plus B versus C offers indirect evidence. Both Bayesian hierarchical approaches^3,4,5 and frequentist methods^6,7 have been proposed for NMA; this article focuses on Bayesian methods because they have been widely applied.

Broadly, there are two Bayesian approaches for NMA: the arm-based (AB) approach^5,8, which models absolute effects, and the contrast-based (CB) approach^3,4,9, which models relative effects. Dias and Ades¹¹ and Hong et al.¹² thoroughly discussed the differences between these two approaches. The arm-based model has been shown to have several important advantages, e.g., the results produced by the AB-NMA are generally more robust to the choice of treatments to include in the NMA¹⁰. Both approaches involve estimating a covariance matrix of random effects and choosing a prior distribution for it, which are generally difficult in Bayesian analysis: the number of parameters in a covariance matrix increases rapidly with the dimension of the matrix, and these parameters are constrained because the matrix must be non-negative definite¹⁴. Also, the parameters of the two models are distinct. In the CB approach, if the total number of treatments in the NMA is T, then T − 1 variance parameters need to be estimated for contrasts and (T − 1)(T − 2)/2 parameters for correlations between contrasts but the T − 1 variances are constrained by triangle inequalities⁴, which complicate prior specification for heterogeneous variances. The AB approach estimates more parameters (i.e., a T-dimensional covariance matrix for variances of absolute effects and correlations between them), but does so without constraints other than positive definiteness. Finally, each study generally includes only a small portion of the NMA’s treatments, generally based on results of previous trials. This selection of treatments produces missing data (treatments excluded from a trial), which affects the AB and CB approaches differently because they use different exchangeability assumptions: CB models require contrasts to be missing at random (MAR)¹⁵ while AB models require treatments to be MAR⁸. Such differences could have distinct effects on estimates of the covariance matrix.

To model the variance structure of contrasts in the CB approach, Lu and Ades⁴ used an ancillary representation to circumvent the triangle inequalities and compared different prior specifications using case studies. However, in the AB approach little attention has been paid to the choice of priors for covariance matrices and their influence on the results. The obvious choice is the conjugate inverse-Wishart prior, which was used by Zhang et al.⁵ and Hong et al.⁸ However, this prior has some problems: the marginal distribution of the variances has low density in the region near zero¹⁶ and the prior imposes a dependency between the variances and the correlations¹⁷, which may cause the correlations to be underestimated in certain situations. Alternatives have been proposed, such as the scaled inverse Wishart¹⁸, a separation strategy¹⁴, the Cholesky decomposition¹⁹, and the LKJ prior for a correlation matrix²⁰. This article compares, for binary outcomes, the influence of selected priors for the AB model on the estimation of the log odds ratios of treatment comparisons and the correlations between treatment-specific log-odds, under different missing-treatment mechanisms. Based on these comparisons, we aim to recommend appropriate vague priors for the AB model’s covariance matrix.

The rest of this article is organized as follows. Section 2 describes AB approaches for NMA, followed by Section 3 on Bayesian analysis, focusing on priors for the covariance matrix. Section 4 presents simulation studies and results, followed by three case studies in Section 5. Section 6 presents our main conclusions with a brief discussion.

2. THE ARM-BASED NETWORK META-ANALYSIS

2.1. Notation

Suppose we have collected K studies comparing a total of T treatments and each study contains only a subset of the T treatments. Let A_k (k = 1, … , K) be the subset of treatments investigated in the k^th study. If the number of elements in the set A_k (denoted by |A_k|) is larger than 2, then study k is called multi-armed. Most randomized clinical trials are two-arm studies with |A_k| = 2. Let D_k = {(r_kt, n_kt), t ∊ A_k} be the data collected in the k^th study, where r_kt and n_kt are the numbers of events and total subjects in the t^th treatment group in the k^th study. Finally, let p_kt be the true probability of an event (i.e., absolute risk) for the t^th treatment in the k^th study.

2.2. The arm-based approach

Zhang et al.⁵ proposed the following arm-based NMA model:

$$\begin{gathered} r_{kt}~\text{Binomial}\left(n_{kt},p_{kt}\right),t\in A_k,k=1,\dots ,K; \\ \mathrm{\text{logit}}\left(p_{kt}\right)={\mu }_t+v_{kt}; \\ {\left(v_{k1},\dots ,v_{kT}\right)}^{\prime }~MVN(0,\Sigma ), \end{gathered}$$ (1)

where μ_t represents the overall fixed effect of treatment t and the vector (v_k1, … , v_kT)′ is a random effect specific to study k, following the multivariate normal distribution with mean 0 and covariance matrix Σ having dimension T. Here, a′ denotes the transpose of the vector a. We used logit instead of probit transformation to estimate both marginal and conditional log odds between treatments. Let δ_t be the between-study standard deviation of log-odds for treatment t, i.e., the square root of the t^th diagonal element in the covariance matrix Σ Here, Σ can also be written as ΔPΔ with Δ a diagonal matrix having standard deviation δ_t as its t^th diagonal element, and correlation matrix P with entries ρ_ij.

The marginal event rate of treatment t is p_t = E[p_kt|μ_t, δ_t]; for the logit link as in Equation (1), p_t can be approximated as in Zeger et al.,²¹

$$p_t\approx {\left[1+\text{exp}\left(-{\mu }_t/\sqrt{1+\frac{256}{75{\pi }^2}{\delta }_t^2}\right)\right]}^{-1}.$$

Using these marginal absolute risks of the T treatments, the risk ratio (RR) and risk difference (RD) for each pair of treatments can be estimated accordingly as RR_ij = p_i/p_j and RD_ij = p_i − p_j. We can also compute two log odds ratio estimands: 1) the marginal log odds ratio between treatments i and j ${\text{mLOR}}_{ij}=\text{log}\frac{p_i\left(1-p_j\right)}{p_i\left(1-p_i\right)}$, and 2) the conditional log odds ratio cLOR_ij = μ_i – μ_j, which is more commonly used in the meta-analyses literature. Agresti²² (pp. 496–497) provided further details differences between these two LORs. Other link functions could also be used in Equation (1). For example, using the probit link Φ⁻¹(p_kt) = μ_t + v_kt as in Zhang et al.⁵, the marginal absolute risk has an exact from, $p_t=\Phi \left({\mu }_t/\sqrt{1+{\delta }_t^2}\right)$, where Φ(·) and Φ⁻¹(·) denote the cumulative distribution function of the standard normal distribution and its inverse, respectively. When the logit link is used, both cLOR and mLOR can be estimated; using the probit link, only mLOR can be directly estimated.

3. PRIOR SPECIFICATIONS FOR THE COVARIANCE MATRIX

This section describes specifications of prior distributions for the AB-NMA in Bayesian analysis. Specifically, we place vague N(0, 100²) priors on μ_t (t = 1, … , T), and discuss prior distributions for the covariance matrix Σ. Two common ways to specify the prior distribution for the covariance matrix Σ are the natural conjugate prior for the multivariate normal likelihood, which treats the covariance matrix as a whole, and the separation strategy proposed by Barnard et al.¹⁴, which decomposes the covariance matrix into separate parts as Σ = ΔPΔ and assigns priors to the components Δ and P separately. As above, Δ is a diagonal matrix with standard deviation δ_i as its i^th diagonal element, and P is a correlation matrix with diagonal elements 1 and off-diagonal elements ρ_ij. The following subsections give more details about these two methods and their variations.

3.1. The Inverse-Wishart prior

The inverse-Wishart (IW) distribution for the covariance Σ is a conjugate prior for the multivariate normal likelihood, which can speed up computation compared to other priors. The density function of the IW distribution with degrees of freedom m (> T − 1) and positive definite scale matrix ψ is:

$$\pi (\Sigma ;\Psi ,m)\propto |\Psi {|}^{-m/2}|\Sigma {|}^{-(m+T+1)/2}\text{exp}\left(-\frac{1}{2}\text{tr}\left({\Sigma }^{-1}\Psi \right)\right),$$ (2)

Where | · | and tr(·) denote the determinant and trace of a matrix, respectively. The scale matrix ψ is often selected to be the T × T identity matrix I.

We now give some remarks about the IW prior’s properties and problems. The marginal distribution of each ${\delta }_i^2$ (the i^th diagonal element of Σ) is the inverse-gamma distribution $IG\left(\frac{m-T+1}{2},\frac{{\psi }_{ii}}{2}\right)$ for i = 1, … , T, where $\frac{m-T+1}{2}$ is the shape parameter and $\frac{{\psi }_{ii}}{2}$ is the scale parameter. Here, ψ_ii is the i^th diagonal element of ψ.

The IW prior has limitations. For example, simulation studies by Alvarez et al.¹⁷ showed that although the estimated covariances (posterior means) Σ_ij (i ≠ j) are unbiased, the estimated correlations (posterior means) ρ_ij are biased towards zero and the estimated variance (posterior mean) Σ_ii is biased upward when the true variance Σ_ii is small. These biases are caused by the lack of prior density near zero in the marginal prior for the variance and the dependence induced by the IW prior between the correlation matrix P and the variances. Section 4’s simulation studies also illustrate this problem.

Finally, the IW prior does not allow a user to specify different amounts of prior knowledge about different variance components; the single parameter m controls this uncertainty for all diagonal elements. To add more flexibility, the scaled IW prior¹⁸ and the hierarchical half-t prior²³ have been proposed; however, such flexibility may be limited compared to the separation strategy¹⁷.

3.2. The separation strategy

As mentioned, the separation strategy allows more flexibility by decomposing the covariance matrix Σ as ΔPΔ and placing independent prior distributions on the standard deviations δ_i and the correlation matrix P. Popular priors for δ_i include the inverse-gamma prior for the variance $\left({\delta }_i^2\right)$, the uniform prior between 0 and a certain upper bound, the half-Cauchy¹⁶ and the log-normal.¹⁴ There is less consensus about choice of a prior for the correlation matrix P, given the difficulty of constraining p to be positive definite. The following subsections elaborate this by discussing four possible choices.

3.2.1. The restricted inverse-Wishart prior and restricted Wishart Prior

We start with the restricted inverse-Wishart (RIW) prior mentioned by Barnard et al.¹⁴, where the correlation matrix P follows an IW distribution with the restriction that its diagonal elements are fixed as 1. Specifically, let Q ~ IW_T(I, m), then P = ΔQΔ follows a RIW_T(m) distribution, where Δ is a diagonal matrix with i^th diagonal element $Q_{ii}^{-1/2}$ and Q_ii is the i^th diagonal element of Q. In the RIW prior, the ρ_ij have the same marginal distributions for all i ≠ j:

$$\pi \left({\rho }_{ij}\right)\propto {\left(1-{\rho }_{ij}^2\right)}^{\frac{m-T-1}{2}},-1<{\rho }_{ij}<1,$$ (3)

a beta distribution, $\mathit{\text{Beta}}\left(\frac{m-T+1}{2},\frac{m-T+1}{2}\right)$ on the interval [−1, 1], which is uniform if m = T + 1. Hence, the RIW_T(T + 1) prior implies marginally uniform-distributed correlation coefficients. This prior is distinguished from the jointly uniform prior π(P) ∝ 1, which is a special case of the LKJ prior²⁰. Actually the LKJ prior is equivalent, in a specific sense, to the restricted Wishart (RW) prior, which we now discuss. (Appendix A gives the proof.)

To define the RW prior, as for the RIW prior let Q* follow a Wishart distribution W_T(I, m*), then P = ΔQ*Δ follows a restricted Wishart distribution RW_T(m*) with degrees of freedom m*(> T − 1); again, Δ is a diagonal matrix with i^th diagonal element $1/\sqrt{Q_{ii}^{*}}$. The RW prior has density π(P) ∝ |P|^{(m*−T−1)/2}; if m* = T + 1, this is uniform on a compact subspace of the T(T − 1)/2 dimensional hypercube (−1, 1)^T(^T−1)/2. Also, the ρ_ij for all i ≠ j follow the same beta distribution $\mathit{\text{Beta}}\left(\frac{m^{*}-1}{2},\frac{m^{*}-1}{2}\right)$ on [−1, 1], which is $\mathit{\text{Beta}}\left(\frac{T}{2},\frac{T}{2}\right)$ if m* = T + 1. Based on this, the marginal distributions of the correlation coefficients ρ_ij in the jointly uniform prior tend to place density close to zero as the dimension T increases, which is the key difference from the marginally uniform prior. Furthermore, the conditional distribution of the correlation coefficient ρ_ij given ρ_rs with (i, j) ≠ (r, s) in the RW prior also differs from that in the RIW prior.

Although the closed form for the conditional distribution of ρ_ij given ρ_rs only exists for special cases, we can visualize these conditional distributions as in Figure 1, which compares the RIW and RW distributions when the dimension T is 3 or 10. As shown in Figure 1, the RIW distribution puts a marginally uniform prior on each p_ij while the marginal prior on the individual correlation p₁₂ under the RW distribution (which is jointly uniform) concentrates around zero, more so as the dimension T increases. Figure 1 also shows that compared to the RW distribution, the RIW distribution puts more density close to 1 for ρ₁₂ when both ρ₂₃ and ρ₁₃ are larger than 0.6. Interestingly, of 1,000,000 random draws from the RW distribution with T = 10, only two satisfied the condition that both ρ₂₃ and ρ₁₃ are larger than 0.8. By contrast, randomly drawing correlation matrices from the RIW distribution, 26,174 out of 1,000,000 satisfied this condition. The above findings may have implications for prior choice in applications. For example, in NMA, we might prefer the RIW prior to the RW prior because the RW prior places less density on all correlation elements ρ_ij being large.

FIGURE 1.

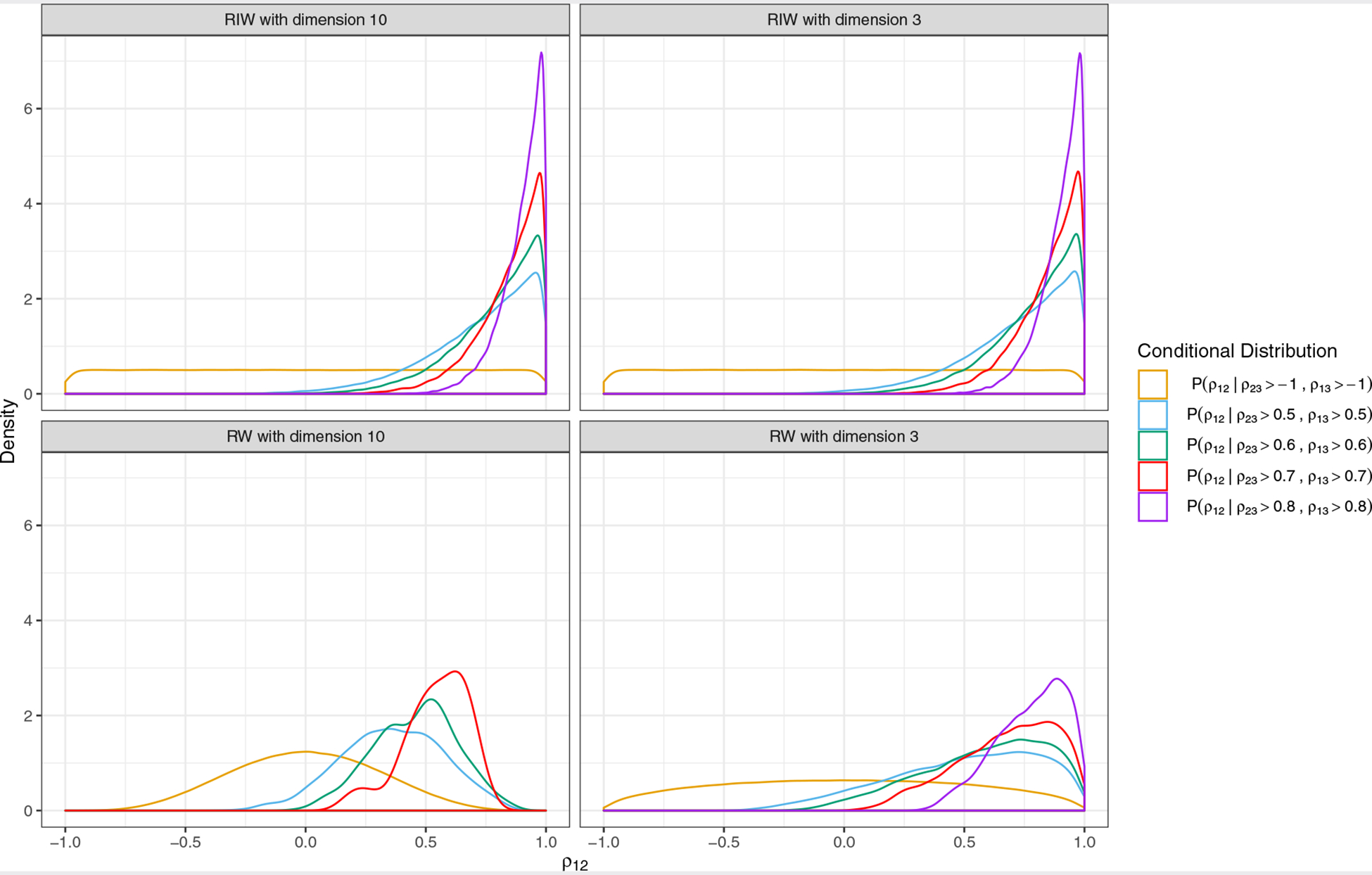
Conditional prior densities for ρ₁₂ with dimension T = 3 (right panels) and dimension T = 10 (left panels). Each distribution is estimated from 1,000,000 random draws from the respective distribution (restricted inverse-Wishart in the first row and restricted Wishart in the second row), using the R function geom_density() with default settings to compute and draw kernel density estimates. Different colors denote different conditioning criteria; e.g., the purple line is the conditional distribution of ρ₁₂ given ρ₂₃ and ρ₁₃ both larger than 0.8. We did not draw the purple density for the restricted Wishart with dimension 10 because only 2 out of 1,000,000 random draws had ρ₂₃ and ρ₁₃ both greater than 0.8.

3.2.2. Exchangeable correlation structure

To reduce model complexity, Lin et al.²⁴ proposed an exchangeable structure (EQ prior) for P, where all off-diagonal elements ρ_ij are assumed equal to a common value ρ. To keep P positive definite, ρ must be larger than $-\frac{1}{T-1}$, so we may specify a vague uniform prior for ρ on $\left(-\frac{1}{T-1},1\right)$.

4. SIMULATION STUDIES

We conducted simulation studies to compare the performance of AB-NMA using different priors (IW, RW, RIW and EQ) in terms of bias and coverage probability, under different mechanisms for selecting treatment arms to be included in each study of the AB-NMA.

4.1. Simulation settings

We describe the simulation studies using three main steps: first, how we generated a complete data set; second, how we applied the missing data mechanisms to omit some arms from studies; and third, which estimands and priors we chose. In the simulation, we fit the AB-NMA with different priors to each simulated dataset, saved estimates of the estimands, and described the performance measures.

Each simulated NMA dataset {D₁, … , D_K} had binary outcome data D_k = {(r_kt, n_kt),t = 1, 2, 3} from 18 studies (K = 18) comparing three treatments (T = 3), denoted 1, 2, and 3. The number of patients n_kt in each arm was fixed at 500. The number of simulated datasets in each setting was 1000. First, we generated complete datasets under the AB model specification in Equation (1) using the logit link and setting (μ₁, μ₂, μ₃) = (μ₂ + 0.5, μ₂, μ₂ − 0.5), (v_k1, v_k2, v_k3)′ ~ MV N(0, Σ) where Σ = ΔPΔ with standard deviations (δ₁, δ₂, δ₃) and correlation matrix P with entries (ρ₁₂, ρ₁₃, ρ₂₃). In Scenario I, we chose (δ₁, δ₂, δ₃) = (0.7, 0.4, 0.1), (μ₁, μ₂, μ₃) = (−1.0, −1.5, −2.0) and $\left({\rho }_{12},{\rho }_{13},{\rho }_{23}\right)=(\frac{2}{3},\frac{4}{8},\frac{2}{3})$. We also conducted additional simulations and analyses to confirm our findings under different correlation structures and μ’s. For these, we set (δ₁, δ₂, δ₃) = (0.7, 0.4, 0.1) and considered three different values of μ₂ ∈ {−0.5, −1.5, −2.5} with μ₁ = μ₂ + 0.5 and μ₃ = μ₂ − 0.5. We also considered three choices for P: high correlation scenario with a common between-treatment correlation ρ = 0.7, low correlation scenario with ρ = 0.2, and mixed between-treatment correlation scenario with (ρ₁₂, ρ₁₃, ρ₂₃) = (0.7, 0.1, 0.4).

After generating the complete dataset, we omitted treatment arms to create partially missing data under MAR and MNAR with respect to absolute effects. For each missingness setting, we obtained two different sets of nine two-arm studies: one set compared treatments 1 and 2, and another compared treatments 2 and 3. To generate partially missing data under the MAR assumption, we first kept all treatment 2 data observed and ranked the studies in ascending order by r_k2/n_k2. Then, we made treatment 1 missing in the first nine studies in this ordering and treatment 3 missing in the last nine studies. This created datasets in which the results for the control arm (treatment 2) had improved over time (r_k2/n_k2 increased with k), while only studies with treatment 1 (more advanced regimen) versus 2 were available in the more recent period and studies with treatment 3 (less advanced regimen) versus 2 were available in the earlier period. Next, we used the following strategy to create missing data under MNAR with respect to absolute effects. We used m_kt (k = 1, … , K and t = 1, … , T) to indicate missingness of the t^th treatment in the k^th study; m_kt = 1 indicated missing and m_kt = 0 indicated not missing. First, we assumed all treatment 2 data were observed, so m_k2 = 0, k = 1, … , K. Then we determined the missingness of treatment 1 based on the data for all 3 treatments. After determining m_k1, the missingness of treatment 3 followed automatically: m_k3 = 1 − m_k1. The model to generate the missingness indicators was:

$$\begin{gathered} m_{k1}~\text{Bernoulli}\left({\pi }_{k1}\right),k=1,\dots ,K; \\ \text{logit}\left({\pi }_{k1}\right)={\beta }_0+{\beta }_1\times \left[\text{logit}\left(r_{k1}/n_{k1}\right)+\text{logit}\left(r_{k2}/n_{k2}\right)+\text{logit}\left(r_{k3}/n_{k3}\right)\right], \end{gathered}$$ (4)

where π_k1 is the probability of treatment 1 being missing in study k. The parameters β₀ and β₁ were pre-defined to control the average number of studies without treatment 1 to be 9 in each scenario: β₁ = 1 and β₀ = −μ₁ – μ₂ – μ₃. A continuity correction of 0.5 was applied to both r and n when r_ki was zero.

We focus on these estimands: the two kinds of log odds ratio comparing treatments i and j, ${\text{mLOR}}_{ij}=\text{log}(\frac{p_i\left(1-p_j\right)}{p_j\left(1-p_i\right)})$ and cLOR_ij = μ_i – μ_j, the absolute risk of an event for treatment t (p_t), the standard deviation of log-odds for treatment t (δ_t), and the correlation between treatment-specific (treatments i and j) log-odds (ρ_ij). When applying the AB-IW model, we set the prior for the covariance matrix Σ to be IW_T(I, T + 1). For models using the RW, RIW and EQ priors, we imposed independent uniform priors U(0, 5) on standard deviations δ_i, i = 1, … , T, then set the RW_T(T + 1), RIW_T(T + 1) prior for the correlation matrix P and the uniform prior $U(-\frac{1}{T-1},1)$ for the correlation coefficient ρ, respectively. Clearly, the true standard deviations (δ₁, δ₂, δ₃) = (0.7, 0.4, 0.1) were not close to the center of the prior U(0,5), nor were the true correlations $\left({\rho }_{12},{\rho }_{13},{\rho }_{23}\right)=(\frac{2}{3},\frac{4}{9},\frac{2}{3})$ close to the center of the RW, RIW, and EQ priors.

We implemented the models using Stan²⁵ in conjunction with R²⁶. We chose posterior mean and 95% equal tailed credible interval as point and interval estimates respectively. To measure the performance of different methods, we used bias and coverage probability of 95% credible interval.

4.2. Simulation results

Table 1 summarizes bias of the estimates and coverage probability (CP) of the 95% credible intervals given by four AB models (AB-IW, AB-RW, AB-RIW and AB-EQ) under different missingness settings (no missing, MAR, and MNAR). The table includes the log odds ratio comparing treatments i and j, mLOR_ij and cLOR_ij, the absolute risk of an event for treatment t (p_t), the standard deviation of log-odds for treatment t (δ_t), and the correlation between treatment-specific (treatments i and j) log-odds (ρ_ij).

TABLE 1.

Simulation results comparing data generated under Scenario I with (δ₁, δ₂, δ₃) = (0.7, 0.4, 0.1), (μ₁, μ₂, μ₃) = (−1.0, −1.5, −2.0) and $\left({\rho }_{12},{\rho }_{13},{\rho }_{23}\right)=(\frac{2}{3},\frac{4}{9},\frac{2}{3})$ Performance of AB models (IW, RW, RIW, and EQ) under different missingness mechanisms (No missing, MAR, MNAR) is shown: the bias of estimates (posterior mean) of cLOR_ij, mLOR_ij, p_t, δ_t, and ρ_ij and coverage probability of 95% credible intervals. MCMC errors are at the 0.01 level.

		Bias (Coverage Probability)
Parameter	Truth	AB-IW	AB-RW	AB-RIW	AB-EQ	AB-IW	AB-RW	AB-RIW	AB-EQ	AB-IW	AB-RW	AB-RIW	AB-EQ
Scenario I
Missing Setting		No missing				MAR				MNAR
cLOR12	0.50	−0.001(0.976)	−0.003(0.970)	−0.003(0.962)	−0.003(0.964)	0.243(0.900)	0.136(0.954)	0.087(0.964)	0.032(0.962)	−0.226(0.884)	−0.186(0.921)	−0.172(0.918)	−0.151(0.916)
cLOR13	1.00	0.010(0.957)	0.001(0.950)	0.000(0.946)	0.001(0.937)	0.293(0.904)	0.174(0.946)	0.120(0.959)	0.034(0.970)	−0.240(0.927)	−0.205(0.921)	−0.188(0.927)	−0.155(0.937)
cLOR23	0.50	0.011(0.990)	0.004(0.965)	0.004(0.961)	0.004(0.960)	0.050(1.000)	0.039(0.977)	0.033(0.980)	0.003(0.978)	−0.014(0.999)	−0.019(0.970)	−0.017(0.976)	−0.004(0.965)
mLOR12	0.54	−0.010(0.979)	0.002(0.969)	0.002(0.965)	0.003(0.966)	0.208(0.913)	0.145(0.956)	0.112(0.966)	0.066(0.967)	−0.230(0.871)	−0.164(0.923)	−0.150(0.921)	−0.133(0.922)
mLOR13	1.07	−0.012(0.962)	0.012(0.957)	0.014(0.958)	0.015(0.945)	0.221(0.950)	0.187(0.944)	0.148(0.961)	0.072(0.971)	−0.280(0.898)	−0.181(0.927)	−0.162(0.933)	−0.133(0.936)
mLOR23	0.54	−0.002(0.994)	0.011(0.965)	0.012(0.964)	0.012(0.964)	0.013(1.000)	0.041(0.980)	0.036(0.980)	0.006(0.979)	−0.050(0.998)	−0.016(0.973)	−0.012(0.978)	−0.001(0.966)
p1	0.28	0.003(0.940)	0.005(0.945)	0.005(0.951)	0.005(0.947)	0.051(0.855)	0.038(0.948)	0.032(0.959)	0.021(0.965)	−0.037(0.864)	−0.025(0.926)	−0.022(0.930)	−0.019(0.928)
p2	0.19	0.003(0.977)	0.002(0.959)	0.003(0.962)	0.003(0.958)	0.003(0.974)	0.003(0.962)	0.003(0.962)	0.003(0.960)	0.003(0.975)	0.003(0.964)	0.003(0.964)	0.003(0.966)
p3	0.12	0.002(1.000)	0.000(0.965)	0.000(0.965)	0.000(0.963)	0.002(1.000)	−0.003(0.976)	−0.002(0.974)	0.001(0.981)	0.008(1.000)	0.003(0.956)	0.003(0.960)	0.002(0.962)
δ1	0.70	0.023(0.964)	0.052(0.948)	0.064(0.936)	0.067(0.934)	−0.044(0.980)	0.086(0.969)	0.131(0.957)	0.132(0.950)	−0.038(0.975)	0.063(0.957)	0.077(0.956)	0.079(0.958)
δ2	0.40	0.068(0.932)	0.029(0.961)	0.037(0.957)	0.038(0.954)	0.066(0.938)	0.034(0.958)	0.039(0.953)	0.039(0.957)	0.067(0.934)	0.034(0.955)	0.040(0.950)	0.039(0.955)
δ3	0.10	0.202(0.000)	0.004(0.980)	0.005(0.981)	0.005(0.979)	0.296(0.000)	0.035(0.977)	0.041(0.975)	0.041(0.977)	0.295(0.000)	0.031(0.988)	0.032(0.986)	0.032(0.982)
ρ12	0.67	−0.170(0.927)	−0.100(0.961)	−0.067(0.960)	−0.060(0.955)	−0.454(0.754)	−0.330(0.955)	−0.270(0.971)	−0.180(0.982)	−0.359(0.786)	−0.247(0.939)	−0.200(0.948)	−0.146(0.959)
ρ13	0.44	−0.316(0.914)	−0.196(0.986)	−0.091(0.989)	0.162(0.820)	−0.430(1.000)	−0.406(1.000)	−0.351(0.999)	0.042(0.970)	−0.411(1.000)	−0.363(1.000)	−0.280(1.000)	0.076(0.956)
ρ23	0.67	−0.511(0.098)	−0.293(0.974)	−0.228(0.983)	−0.060(0.955)	−0.623(0.293)	−0.546(0.983)	−0.508(0.989)	−0.180(0.982)	−0.593(0.211)	−0.471(0.973)	−0.423(0.984)	−0.146(0.959)

All four AB models gave unbiased estimates and good coverage probabilities for the log odds ratios mLOR_ij and cLOR_ij and the absolute risks p_t for complete datasets (“no missing”, i.e., no omitted arms). However, the AB-IW model produced biased estimates of the standard deviations δ_t and correlations ρ_ij and intervals with low coverage probabilities. In particular, the AB-IW method had bias 0.202 for δ₃, which was large relative to the true value δ₃ = 0.1, while all AB-RW, AB-RIW and AB-EQ had almost no bias (0.005). Also, for the IW prior the bias of ρ₂₃ (−0.511) was so large that this method estimated little posterior association between treatments 2 and 3, although the true correlation was 0.667. In summary, the IW prior gave upwardly biased estimates for small variances and correlation estimates biased towards zero, especially when the variance was small. In contrast, the AB-RW, AB-RIW and AB-EQ priors gave estimates of standard deviations and correlations with much smaller biases (albeit not exactly zero) with good coverage probability.

For complete datasets, mis-estimating correlations between treatment-specific log-odds did not bias estimates of log odds ratios and absolute risks. However, in datasets with missing entries (arms omitted under MAR/MNAR), underestimation of correlations, especially for the star-shaped network structure used here, gave estimated relative effects with larger bias and worse coverage probability. Underestimation of correlations increased under MAR/MNAR compared to complete data for all priors considered; e.g., for AB-IW, the estimated bias for (ρ₁₂, ρ₁₃, ρ₂₃) was (−0.17, −0.32, −0.51), (−0.45, −0.43, −0.62) and (−0.36, −0.41, −0.59) in the no missing, MAR, and MNAR scenarios, respectively. Also, while the AB-RIW and AB-EQ priors gave similar results under MNAR for mLOR_ij and cLOR_ij, the extra but reasonable assumption of equal correlations between treatment-specific log-odds reduced the bias of estimated correlations and log odds ratios under MAR. The performance of AB-RW prior is slightly worse than AB-RIW prior in terms of estimated relative effects and correlations because RW prior places less density on all correlation elements being large, as was mentioned regarding Figure 1.

We verified our findings using additional simulations, shown in Table 2, under various μ’s and correlation structures. The AB-RW prior gave smaller bias and higher coverage probability than the AB-IW prior for mLOR₁₃ (cLOR₁₃), the AB-RIW prior gave smaller bias and higher coverage probability than the AB-RW prior for mLOR₁₃ (cLOR₁₃), and the AB-EQ prior gave much smaller bias than the AB-RIW prior for mLOR₁₃ (cLOR₁₃) under MAR/MNAR. Also, AB-RIW and AB-EQ generally provided more reliable estimates of absolute risks (p₁) than AB-IW. These results were in line with our findings in Table 1.

TABLE 2.

Additional simulations comparing performance (bias and coverage probability of 95% credible intervals) of AB-IW, AB-RIW and AB-EQ with respect to posterior mean of cLOR₁₃, mLOR₁₃ and p₁ under MAR and MNAR using data generated with (μ₁, μ₂, μ₃) = (μ₂ + 0.5, μ₂, μ₂ − 0.5), (δ₁, δ₂, δ₃) = (0.7, 0.4, 0.1), μ₂ ∈ {−0.5, −1.5, −2.5} and correlation matrix Pchosen from low, high and mixed correlation scenarios. MCMC errors are at the 0.01 level.

			cLOR13: Bias (Coverage Probability)					mLOR13: Bias (Coverage Probability)					p1: Bias (Coverage Probability)
Scenario	μ2	Correlation structure	Truth	AB-IW	AB-RW	AB-RIW	AB-EQ	Truth	AB-IW	AB-RW	AB-RIW	AB-EQ	Truth	AB-IW	AB-RW	AB-RIW	AB-EQ
MAR
1	−0.50	High	1.00	0.302(0.883)	0.175(0.945)	0.117(0.957)	0.036(0.967)	1.00	0.263(0.913)	0.170(0.948)	0.119(0.959)	0.048(0.968)	0.50	0.059(0.847)	0.033(0.948)	0.023(0.954)	0.011(0.967)
2	−0.50	Low	1.00	0.090(0.979)	0.058(0.981)	0.045(0.978)	−0.063(0.978)	1.00	0.061(0.983)	0.053(0.980)	0.042(0.977)	−0.045(0.977)	0.50	0.017(0.961)	0.011(0.976)	0.009(0.971)	−0.009(0.976)
3	−0.50	Mixed	1.00	0.280(0.896)	0.152(0.946)	0.103(0.962)	0.042(0.961)	1.00	0.241(0.920)	0.147(0.945)	0.105(0.958)	0.049(0.961)	0.50	0.057(0.852)	0.031(0.949)	0.022(0.955)	0.016(0.953)
4	−1.50	High	1.00	0.291(0.895)	0.159(0.953)	0.099(0.965)	0.017(0.971)	1.07	0.218(0.939)	0.170(0.954)	0.126(0.962)	0.053(0.972)	0.28	0.051(0.858)	0.034(0.951)	0.027(0.962)	0.018(0.966)
5	−1.50	Low	1.00	0.093(0.982)	0.051(0.979)	0.035(0.977)	−0.069(0.977)	1.07	0.043(0.990)	0.087(0.980)	0.081(0.977)	−0.011(0.976)	0.28	0.020(0.965)	0.024(0.977)	0.024(0.977)	0.007(0.979)
6	−1.50	Mixed	1.00	0.280(0.903)	0.151(0.947)	0.097(0.961)	0.026(0.968)	1.07	0.207(0.946)	0.160(0.950)	0.121(0.960)	0.055(0.966)	0.28	0.052(0.856)	0.036(0.946)	0.029(0.955)	0.023(0.959)
7	−2.50	High	1.00	0.304(0.913)	0.181(0.946)	0.124(0.965)	0.031(0.973)	1.14	0.186(0.963)	0.195(0.949)	0.160(0.962)	0.074(0.981)	0.14	0.031(0.860)	0.027(0.933)	0.024(0.944)	0.018(0.955)
8	−2.50	Low	1.00	0.108(0.985)	0.059(0.983)	0.043(0.980)	−0.075(0.978)	1.14	0.026(0.995)	0.124(0.981)	0.123(0.975)	0.017(0.980)	0.14	0.015(0.969)	0.024(0.971)	0.025(0.968)	0.012(0.980)
9	−2.50	Mixed	1.00	0.289(0.919)	0.168(0.956)	0.115(0.966)	0.027(0.971)	1.14	0.172(0.977)	0.183(0.954)	0.151(0.966)	0.066(0.981)	0.14	0.031(0.870)	0.027(0.935)	0.024(0.948)	0.020(0.951)
MNAR
1	−0.50	High	1.00	−0.252(0.914)	−0.208(0.905)	−0.189(0.913)	−0.153(0.926)	1.00	−0.261(0.897)	−0.197(0.903)	−0.179(0.909)	−0.148(0.922)	0.50	−0.052(0.853)	−0.041(0.907)	−0.038(0.914)	−0.033(0.920)
2	−0.50	Low	1.00	−0.250(0.897)	−0.250(0.884)	−0.248(0.889)	−0.227(0.895)	1.00	−0.256(0.880)	−0.228(0.880)	−0.226(0.885)	−0.209(0.891)	0.50	−0.054(0.836)	−0.051(0.876)	−0.051(0.879)	−0.047(0.890)
3	−0.50	Mixed	1.00	−0.222(0.942)	−0.178(0.923)	−0.164(0.930)	−0.141(0.933)	1.00	−0.231(0.927)	−0.168(0.922)	−0.155(0.928)	−0.136(0.932)	0.50	−0.049(0.862)	−0.038(0.915)	−0.036(0.917)	−0.034(0.920)
4	−1.50	High	1.00	−0.244(0.917)	−0.207(0.905)	−0.188(0.906)	−0.155(0.925)	1.07	−0.285(0.870)	−0.185(0.910)	−0.165(0.913)	−0.137(0.925)	0.28	−0.037(0.860)	−0.025(0.916)	−0.022(0.916)	−0.019(0.921)
5	−1.50	Low	1.00	−0.239(0.904)	−0.243(0.896)	−0.241(0.894)	−0.223(0.902)	1.07	−0.274(0.871)	−0.198(0.906)	−0.195(0.897)	−0.182(0.912)	0.28	−0.037(0.846)	−0.029(0.912)	−0.028(0.914)	−0.027(0.923)
6	−1.50	Mixed	1.00	−0.204(0.937)	−0.170(0.923)	−0.154(0.932)	−0.130(0.937)	1.07	−0.247(0.903)	−0.148(0.921)	−0.132(0.934)	−0.111(0.936)	0.28	−0.033(0.885)	−0.021(0.928)	−0.018(0.934)	−0.017(0.930)
7	−2.50	High	1.00	−0.253(0.926)	−0.234(0.916)	−0.214(0.923)	−0.177(0.929)	1.14	−0.336(0.860)	−0.205(0.925)	−0.183(0.924)	−0.152(0.941)	0.14	−0.021(0.875)	−0.012(0.932)	−0.009(0.938)	−0.008(0.940)
8	−2.50	Low	1.00	−0.236(0.910)	−0.252(0.907)	−0.252(0.901)	−0.233(0.908)	1.14	−0.311(0.855)	−0.193(0.932)	−0.189(0.933)	−0.178(0.938)	0.14	−0.020(0.855)	−0.011(0.936)	−0.011(0.929)	−0.010(0.939)
9	−2.50	Mixed	1.00	−0.229(0.936)	−0.210(0.930)	−0.193(0.936)	−0.162(0.943)	1.14	−0.310(0.882)	−0.179(0.933)	−0.160(0.943)	−0.135(0.950)	0.14	−0.020(0.873)	−0.010(0.937)	−0.008(0.935)	−0.008(0.941)

5. CASE STUDIES

One pitfall of AB-NMA is that the data may not provide enough information about the variances of log-odds for some treatments or about correlations between treatment-specific log-odds. In a Bayesian analysis, such a lack of information may cause the posterior to be dominated by prior information. This section uses three examples with different levels of information to examine the performance of different AB methods. Here, we focus more on posterior distributions of standard deviations than on correlations for two reasons. First, Figure 1 shows, for the RIW prior, that the positive definiteness property already imposes strong prior information on relationships among individual correlations and the IW and EQ priors make more strict assumptions than the RIW prior, as shown in Sections 3.1 and 3.2.2, respectively. Second, NMAs commonly provide little information about correlations and no practical remedy is available to avoid the influence of the prior on the posterior. We considered seven models in these case studies: AB-IW, AB-RW, AB-RIW, AB-EQ, AB-RW-EV, AB-RIW-EV and AB-EQ-EV. The latter three new models were based on AB-RW, AB-RIW and AB-EQ with the further assumption that all δ_i(i = 1, … , T) were equal to δ, with a uniform prior U(0, 5).

5.1. Example 1: smoking abstinence data

Mills et al.²⁷ summarized results of 101 trials with 31,321 individuals comparing 4 interventions for the primary outcome of abstinence from smoking at least 4 weeks post-target quit date. Figure 2a shows the network plot of the data with treatments 1–4 being control, nicotine replacement therapy (NRT), bupropion, and varenicline, respectively. We used the AB-IW, AB-RW, AB-RIW, and AB-EQ models to analyze this dataset.

FIGURE 2.

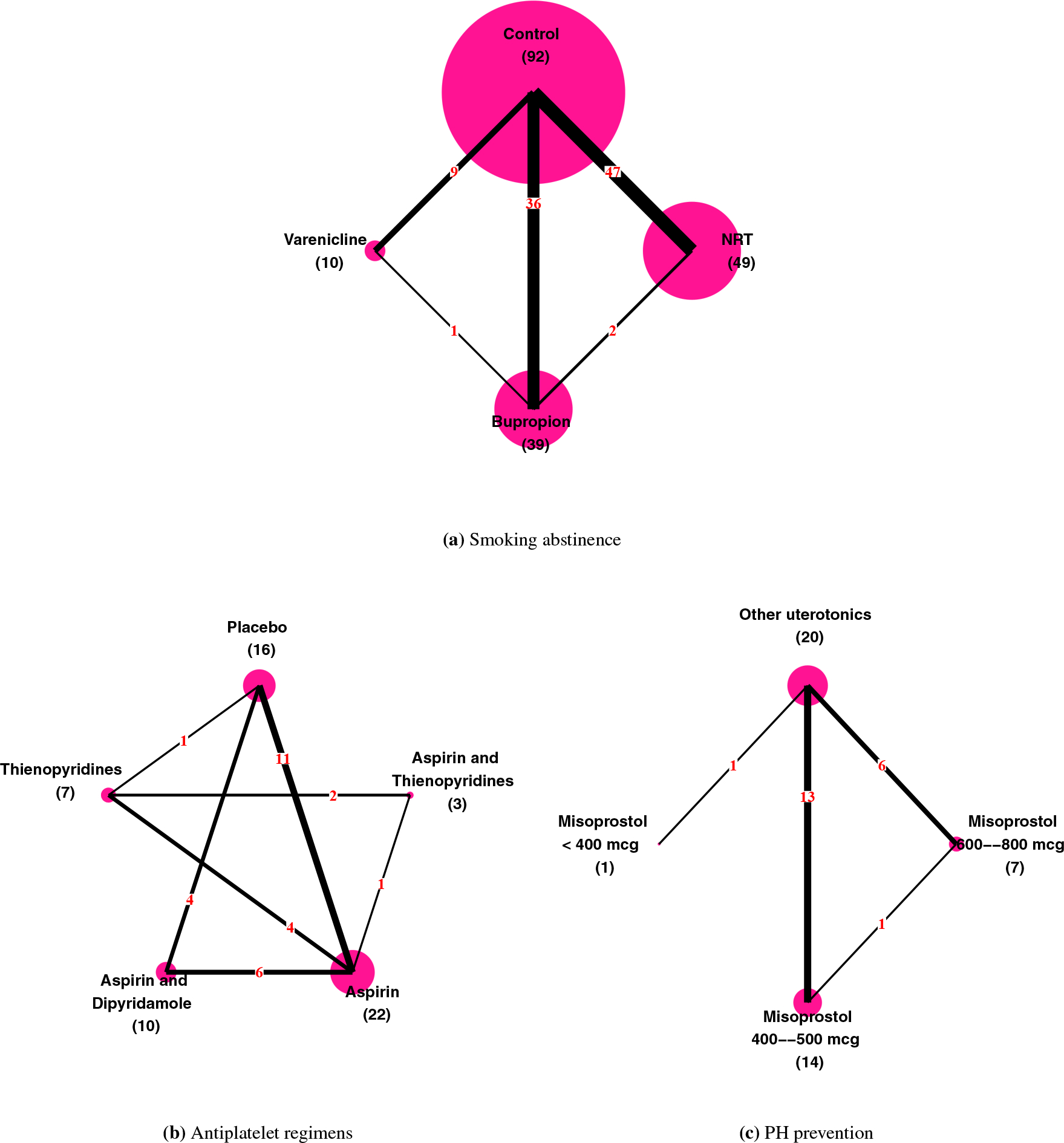
Network plots of the three example datasets. Each node in a plot stands for a treatment and each edge represents a direct comparison between two treatments. Vertex size is proportional to the number (in parenthesis) of direct comparisons containing that treatment; edge thickness is proportional to the number (in red) of direct comparisons.

Table 3 summarizes results for marginal log odds ratios, mLOR_ij, comparing treatments i and j, the absolute risk of treatment t (p_t), the standard deviation of log-odds for treatment t (δ_t), the correlation between treatment-specific (treatments i and j) log-odds (ρ_ij), the probability that treatment t ranks i^th (Rank_ti; a higher rank means a larger proportion with events), and the deviance information criterion (DIC)²⁸ using the different models. The four AB methods (AB-IW, AB-RW, AB-RIW, and AB-EQ) gave similar results except for the log odds ratio of bupropion versus varenicline (mLOR₃₄) and NRT versus varenicline (mLOR₂₄). Although the AB-RIW and AB-EQ models gave slightly different posterior means of the log odds ratios, they led to the same conclusions: all active therapies (NRT, bupropion, and varenicline) increased smoking abstinence compared to control in the short term, and varenicline was more effective than NRT or bupropion. The rank probabilities also indicated that varenicline had the best results (Rank₄₁ > 0.9) and control had the worst (Rank₁₄ = 1). Because this dataset was large and provided enough information — 101 trials comparing four treatments, each included in at least 9 trials (varenicline was in 9 trials) — it is not surprising that these AB methods gave similar conclusions.

TABLE 3.

Smoking abstinence data: comparison of posterior means and 95% credible intervals under 4 models, specifically mLOR_ij comparing the i^th and j^th treatment, absolute risk of events for the t^th treatment (p_t), standard deviation of log-odds for the t^th treatment (δ_t), correlation between treatment-specific (treatments i and j) log-odds (ρ_ij), and the i^th rank probability of the t^th treatment (Rank_ti). Regimen labels: (1) control, (2) nicotine replacement therapy, (3) bupropion, (4) varenicline.

	Point Estimate (95% Credible Interval)
Parameter	AB-IW	AB-RW	AB-RIW	AB-EQ
mLOR12	−0.58 (−0.74, −0.43)	−0.59 (−0.75, −0.42)	−0.58 (−0.73, −0.43)	−0.57 (−0.71,−0.43)
mLOR13	−0.67 (−0.83,−0.51)	−0.68 (−0.83, −0.53)	−0.67 (−0.80, −0.53)	−0.66 (−0.81,−0.51)
mLOR14	−0.90 (−1.22,−0.57)	−0.89 (−1.15,−0.59)	−0.94 (−1.16,−0.71)	−0.93 (−1.16,−0.73)
mLOR23	−0.09 (−0.30, 0.12)	−0.09 (−0.30,0.11)	−0.09 (−0.28, 0.11)	−0.09 (−0.28, 0.10)
mLOR24	−0.32 (−0.66, 0.02)	−0.30 (−0.59, 0.01)	−0.36 (−0.61,−0.11)	−0.36 (−0.61,−0.13)
mLOR34	−0.23 (−0.57,0.11)	−0.20 (−0.49, 0.10)	−0.27 (−0.51,−0.03)	−0.27 (−0.52, −0.04)
Rank11	0.00	0.00	0.00	0.00
Rank21	0.01	0.01	0.00	0.00
Rank31	0.08	0.08	0.01	0.01
Rank41	0.90	0.91	0.98	0.99
p1	0.28 (0.24, 0.32)	0.28(0.24,0.31)	0.28(0.24,0.31)	0.28 (0.24, 0.31)
p2	0.41 (0.36, 0.45)	0.41 (0.36,0.45)	0.41 (0.36,0.45)	0.41 (0.36,0.45)
p3	0.43 (0.38, 0.48)	0.43 (0.39,0.48)	0.43 (0.38, 0.47)	0.43 (0.38, 0.47)
p4	0.49(0.41,0.56)	0.48 (0.42, 0.55)	0.50 (0.44, 0.55)	0.50 (0.45, 0.55)
δ	·	·	·	·
δ1	0.89(0.76, 1.06)	0.88(0.74, 1.04)	0.91 (0.77, 1.08)	0.91 (0.77, 1.08)
δ2	0.83(0.66, 1.03)	0.82(0.66, 1.02)	0.85(0.68, 1.06)	0.87 (0.69, 1.08)
δ3	0.79 (0.64, 0.97)	0.76 (0.62, 0.94)	0.78 (0.63,0.96)	0.78 (0.63, 0.97)
δ4	0.54 (0.32, 0.90)	0.42 (0.23, 0.75)	0.49 (0.27, 0.82)	0.48 (0.28, 0.81)
ρ	·	·	·	0.87 (0.78, 0.93)
ρ12	0.80 (0.65, 0.89)	0.78(0.62,0.89)	0.83(0.69,0.92)	·
ρ13	0.85 (0.73, 0.93)	0.89 (0.74, 0.97)	0.92(0.81,0.98)	·
ρ14	0.57 (−0.15, 0.89)	0.60 (−0.14,0.94)	0.86 (0.48, 0.98)	·
ρ23	0.76(0.51,0.90)	0.68 (0.32, 0.94)	0.83 (0.57, 0.98)	·
ρ24	0.51 (−0.21,0.86)	0.47 (−0.31, 0.92)	0.79 (0.33, 0.98)	·
ρ34	0.53 (−0.18,0.87)	0.53 (−0.25, 0.95)	0.86 (0.42, 0.99)	·
DIC	331.38	332.70	332.40	330.30
$\overline{D}$	185.18	188.61	191.57	188.71
pD	146.20	146.09	146.83	141.59

5.2. Example 2: serious vascular events prevention data

This dataset, reported by Thijs et al.²⁹, consisted of 24 antiplatelet trials involving 42,688 patients after transient ischaemic attack (TIA) or stroke and compared 5 regimens: 1) placebo, 2) aspirin (ASA) plus thienopyridines (THIENO), 3) aspirin, 4) aspirin plus dipyridamole (DP), and 5) thienopyridines. The outcome was occurrence of a serious vascular event, including myocardial infarction and vascular death after TIA or stroke. Figure 2b shows the network plot; ASA plus thienopyridines was included in only 3 trials. As we had limited information about the variance of the effect of ASA plus THIENO, one may wonder how its posterior distribution was influenced by its prior. Hence, we added three models: 1) the AB-RW model assuming equal variances $\left({\delta }_t^2\right)$ (AB-RW-EV), 2) the AB-RIW model assuming equal variances (AB-RIW-EV), and 3) the AB-EQ model assuming equal variances (AB-EQ-EV).

Table 4 summarizes the results. For the absolute proportion of serious vascular events for ASA plus THIENO (p₂), which had limited information, both the AB-RIW and AB-EQ methods gave an unrealistically high upper bound for the 95% credible interval of δ₂ (RIW: 0.19 to 3.67; EQ: 0.23 to 2.73). This resulted in wide credible intervals for the absolute risk p₂ (RIW: 0.06 to 0.53; EQ: 0.11 to 0.48) and potentially biased estimates. Such wide intervals meant that we could not find any significant relative effects involving ASA plus THIENO; for example, using AB-RIW, mLOR₁₂ = 0.24 with 95% CI (−1.52, 1.35). However, assuming equal variances (the AB-RIW-EV and AB-EQ-EV methods) narrowed the credible intervals of p₂ and δ₂. Using the AB-IW model, standard deviations δ₁ and δ₄ were potentially overestimated when comparing with the other two separation strategy priors (RIW and EQ), which caused disruptions in estimating absolute risks and relative risks related to the placebo and aspirin plus DP arms. Moreover, correlations ρ₁₂, ρ₂₃, ρ₂₄, and ρ₂₅ were potentially underestimated by both AB-IW and AB-RW-EV models because of the lack of comparisons between these treatments. Although the AB-IW and AB-RW-EV models could also control the credible intervals of δ_t and p_t, DIC indicated that we may prefer AB-RIW-EV/AB-EQ-EV to AB-IW/AB-RW-EV (DIC: 74.91/74.55 vs. 89.97/87.08) and the DIC differences here were large enough to be of practical importance (larger than 5 units).

TABLE 4.

Serious vascular events prevention data: comparison of posterior mean and 95% credible interval under 7 different models, specifically marginal log odds ratio mLOR_ij comparing the i^th and j^th treatments, absolute risk of events for the t^th treatment (p_t), standard deviation of log-odds for t^th treatment (δ_t), and correlation between treatment-specific (treatments i and j) log-odds (ρ_ij). Regimen labels: (1) placebo, (2) aspirin plus thienopyridines, (3) aspirin, (4) aspirin plus dipyridamole, (5) thienopyridines.

	Point Estimate (95% Credible Interval)
Parameter	AB-IW	AB-RW	AB-RIW	AB-EQ	AB-RW-EV	AB-RIW-EV	AB-EQ-EV
mLOR12	0.82(0.03, 1.51)	0.66 (−0.90, 1.49)	0.24 (−1.52, 1.35)	0.14 (−1.32, 0.75)	0.80(0.28, 1.34)	0.39(0.16,0.89)	0.35 (0.16, 0.56)
mLOR13	0.28 (0.00, 0.57)	0.27 (0.06, 0.50)	0.22 (0.08, 0.38)	0.22 (0.08, 0.38)	0.23 (0.04, 0.46)	0.17(0.07,0.28)	0.17(0.07,0.28)
mLOR14	0.48 (0.06, 0.90)	0.48(0.16,0.77)	0.44 (0.26, 0.61)	0.44 (0.27, 0.60)	0.45(0.15,0.76)	0.41 (0.27, 0.55)	0.41 (0.28,0.54)
mLOR15	0.40 (−0.06, 0.85)	0.38 (−0.13, 0.81)	0.30 (0.06, 0.57)	0.30 (0.09, 0.53)	0.36 (0.06, 0.69)	0.25(0.10,0.41)	0.25(0.11,0.40)
mLOR23	−0.54 (−1.23, 0.23)	−0.39 (−1.24, 1.18)	−0.02 (−1.13, 1.74)	0.08 (−0.50, 1.53)	−0.57 (−1.10,−0.07)	−0.21 (−0.70,−0.01)	−0.18 (−0.36,−0.01)
mLOR24	−0.34 (−1.09,0.49)	−0.18 (−1.05, 1.39)	0.20 (−0.91, 1.96)	0.30 (−0.31, 1.75)	−0.35 (−0.92, 0.20)	0.02 (−0.48, 0.27)	0.06 (−0.17, 0.26)
mLOR25	−0.42 (−1.20,0.40)	−0.28 (−1.26, 1.30)	0.06 (−1.09, 1.80)	0.15 (−0.42, 1.57)	−0.43 (−1.03,0.09)	−0.13 (−0.63,0.07)	−0.10 (−0.28, 0.06)
mLOR34	0.21 (−0.20,0.60)	0.21 (−0.11, 0.51)	0.22 (0.03, 0.38)	0.22 (0.05, 0.38)	0.22 (−0.05, 0.50)	0.24(0.10,0.37)	0.24 (0.10, 0.36)
mLOR35	0.13 (−0.32, 0.56)	0.11 (−0.40,0.55)	0.08 (−0.13, 0.31)	0.07 (−0.09, 0.25)	0.13 (−0.15,0.43)	0.08 (−0.04, 0.21)	0.08 (−0.03, 0.19)
mLOR45	−0.08 (−0.62, 0.46)	−0.10 (−0.64, 0.40)	−0.14 (−0.40, 0.15)	−0.15 (−0.37,0.10)	−0.09 (−0.45, 0.28)	−0.16 (−0.33, 0.03)	−0.16 (−0.32, 0.02)
p1	0.21 (0.17,0.25)	0.21 (0.18,0.24)	0.20(0.17,0.23)	0.20(0.17,0.23)	0.20(0.17,0.24)	0.19(0.16,0.22)	0.19(0.16,0.22)
p2	0.11 (0.06,0.20)	0.13(0.06,0.39)	0.18 (0.06, 0.53)	0.19(0.11,0.48)	0.10(0.06,0.15)	0.14(0.09,0.17)	0.14(0.12,0.18)
p3	0.17(0.14,0.20)	0.17(0.14,0.20)	0.17(0.14,0.20)	0.17(0.14,0.20)	0.17(0.14,0.19)	0.17(0.14,0.19)	0.17(0.14,0.19)
p4	0.14(0.10,0.19)	0.14(0.11,0.18)	0.14(0.11,0.17)	0.14(0.11,0.17)	0.14(0.11,0.17)	0.14(0.11,0.16)	0.14(0.11,0.16)
p5	0.15(0.11,0.21)	0.15(0.11,0.23)	0.16(0.12,0.20)	0.16(0.12,0.19)	0.15(0.12,0.18)	0.15(0.13,0.18)	0.16(0.13,0.18)
δ	·	·	·	·	0.37 (0.27, 0.49)	0.42 (0.30, 0.59)	0.42 (0.30, 0.59)
δ1	0.42 (0.28, 0.65)	0.28(0.13,0.49)	0.36(0.19,0.61)	0.36(0.19,0.62)	·	·	·
δ2	0.55 (0.30, 1.05)	0.86(0.14,3.63)	0.93(0.19,3.67)	0.82 (0.23, 2.73)	·	·	·
δ3	0.52 (0.36, 0.75)	0.46 (0.30, 0.68)	0.51 (0.34,0.77)	0.52 (0.35, 0.77)	·	·	·
δ4	0.48 (0.29, 0.79)	0.34(0.12,0.74)	0.40(0.18,0.73)	0.41(0.19,0.73)	·	·	·
δ5	0.57 (0.35, 0.94)	0.60(0.29, 1.27)	0.55 (0.31, 1.00)	0.54 (0.32, 0.92)	·	·	·
ρ	·	·	·	0.97(0.85, 1.00)	·	·	0.98 (0.90, 1.00)
ρ12	0.05 (−0.62, 0.66)	0.07 (−0.71, 0.79)	0.73 (−0.95, 1.00)	·	0.10 (−0.68, 0.80)	0.90 (−0.24, 1.00)	·
ρ13	0.43 (−0.12,0.79)	0.68(0.11,0.96)	0.96(0.81, 1.00)	·	0.70(0.17,0.96)	0.98 (0.88, 1.00)	·
ρ14	0.25 (−0.37, 0.72)	0.42 (−0.33, 0.91)	0.95 (0.68, 1.00)	·	0.48 (−0.28, 0.93)	0.97 (0.83, 1.00)	·
ρ15	0.23 (−0.43, 0.73)	0.33 (−0.43, 0.87)	0.92 (0.54, 1.00)	·	0.40 (−0.31, 0.89)	0.96(0.78, 1.00)	·
ρ23	0.07 (−0.67, 0.73)	0.10 (−0.68, 0.80)	0.73 (−0.94, 1.00)	·	0.14 (−0.63, 0.81)	0.90 (−0.23, 1.00)	·
ρ24	0.04 (−0.65, 0.68)	0.04 (−0.73, 0.77)	0.72 (−0.94, 1.00)	·	0.08 (−0.70, 0.79)	0.90 (−0.23, 1.00)	·
ρ25	0.07 (−0.67, 0.76)	0.07 (−0.70, 0.80)	0.71 (−0.90, 1.00)	·	0.09 (−0.69, 0.81)	0.90 (−0.22, 1.00)	·
ρ34	0.35 (−0.27, 0.78)	0.50 (−0.18, 0.92)	0.95 (0.69, 1.00)	·	0.56 (−0.10, 0.94)	0.97 (0.83, 1.00)	·
ρ35	0.32 (−0.38, 0.79)	0.39 (−0.34, 0.88)	0.92 (0.56, 1.00)	·	0.48 (−0.15, 0.90)	0.97 (0.79, 1.00)	·
ρ45	0.18 (−0.54, 0.74)	0.21 (−0.59, 0.83)	0.91 (0.44, 1.00)	·	0.28 (−0.49, 0.86)	0.96(0.73, 1.00)	·
DIC	89.97	88.56	79.99	79.11	87.08	74.91	74.55
$\overline{D}$	48.23	49.77	46.60	46.48	49.71	46.27	46.19
pD	41.74	38.78	33.40	32.62	37.38	28.64	28.37

5.3. Example 3: postpartum haemorrhage prevention data

Hofmeyr et al.³⁰ reviewed 25 studies on prevention of postpartum haemorrhage (blood loss ≥ 1000 ml). This NMA compared four regimens: 1) other uterotonics, 2) misoprostol 600–800 mcg, 3) misoprostol 400–500 mcg, and 4) misoprostol <400 mcg as in Figure 2c. Table 5 summarizes the results; we focus on δ₄. As Figure 2c shows, only one trial directly compared treatment 4 with other treatments; therefore, for the AB-EQ method, δ₄’s posterior (mean 2.48; 95% CI, 0.19, 4.85) was dominated by the U(0,5) prior. However, this did not imply that AB-EQ was inferior to AB-EQ-EV. When confronted with a low-information situation, both the AB-EQ and AB-EQ-EV (or the AB-RIW and AB-RIW-EV) methods were useful: AB-EQ alerted us to a lack of information, while AB-EQ-EV showed the consequences of an extra assumption.

TABLE 5.

Postpartum haemorrhage prevention data: comparison of posterior mean and 95% credible interval under 7 different models, specifically marginal log odds ratio mLOR_ij comparing the i^th and j^th treatments, absolute risk of events for the t^th treatment (p_t), standard deviation of log-odds for t^th treatment (δ_t). Regimen labels: (1) other uterotonics, (2) misoprostol 600–800 mcg, (3) misoprostol 400–500 mcg, (4) misoprostol < 400 mcg.

	Point Estimate (95% Credible Interval)
	AB-IW	AB-RW	AB-RIW	AB-EQ	AB-RW-EV	AB-RIW-EV	AB-EQ-EV
mLOR12	−0.10 (−0.78, 0.57)	−0.21 (−1.38,0.69)	−0.16 (−0.83, 0.42)	−0.16 (−0.80, 0.38)	−0.13 (−0.81, 0.56)	−0.17 (−0.53, 0.25)	−0.17 (−0.49, 0.21)
mLOR13	−0.21 (−0.73, 0.29)	−0.21 (−0.83, 0.35)	−0.25 (−0.73, 0.20)	−0.26 (−0.76, 0.20)	−0.14 (−0.51, 0.25)	−0.18 (−0.45, 0.11)	−0.18 (−0.45, 0.10)
mLORl4	0.14 (−3.08,3.39)	−0.70 (−4.44, 2.76)	−0.59 (−4.40, 2.75)	0.73 (−1.27, 3.19)	0.08 (−2.61, 3.26)	0.05 (−2.76, 3.31)	1.13 (−0.74,3.78)
mLOR23	−0.11 (−0.87,0.68)	0.00 (−1.01, 1.24)	−0.09 (−0.78, 0.67)	−0.10 (−0.77, 0.64)	−0.01 (−0.75, 0.73)	−0.01 (−0.47, 0.43)	−0.02 (−0.44, 0.39)
mLOR24	0.23 (−3.00, 3.52)	−0.48 (−4.25,3.15)	−0.44 (−4.24, 2.96)	0.89 (−1.17, 3.42)	0.22 (−2.53, 3.46)	0.21 (−2.60, 3.50)	1.30 (−0.62, 3.98)
1T1LOR34	0.35 (−2.87, 3.62)	−0.49 (−4.20, 3.02)	−0.34 (−4.18, 3.05)	0.99 (−1.07, 3.47)	0.22 (−2.48, 3.41)	0.23 (−2.58, 3.49)	1.32 (−0.57, 3.96)
p1	0.05 (0.03, 0.09)	0.05 (0.03, 0.09)	0.06(0.03,0.10)	0.06(0.03,0.10)	0.05 (0.03, 0.08)	0.05 (0.03, 0.09)	0.05 (0.03, 0.09)
p2	0.06(0.03,0.12)	0.07(0.03,0.17)	0.07(0.03,0.14)	0.07(0.03,0.14)	0.06(0.03,0.11)	0.06(0.03,0.11)	0.06(0.03,0.11)
p3	0.06(0.03,0.12)	0.06(0.03,0.12)	0.07(0.04,0.14)	0.07(0.04,0.14)	0.06 (0.03, 0.09)	0.06(0.04,0.11)	0.06(0.04,0.11)
p4	0.09 (0.00, 0.52)	0.18(0.00,0.80)	0.19(0.00,0.79)	0.04(0.00,0.18)	0.09 (0.00, 0.39)	0.10(0.00,0.43)	0.03(0.00,0.10)
δ	·	·	·	·	1.15(0.82, 1.61)	1.25(0.86,1.81)	1.25(0.86,1.82)
δ1	1.23(0.82,1.81)	1.20(0.80,1.79)	1.32 (0.86, 2.01)	1.32 (0.86, 2.00)	·	·	·
δ2	1.17(0.64,2.00)	1.33(0.64,2.84)	1.32(0.71,2.38)	1.33(0.71,2.40)	·	·	·
δ3	1.32(0.82,2.08)	1.34(0.81,2.18)	1.46 (0.88, 2.34)	1.48 (0.89, 2.37)	·	·	·
δ4	1.14(0.38,3.19)	2.48(0.16,4.86)	2.50(0.13,4.88)	2.48(0.19,4.85)	·	·	·
D1C	68.83	70.62	68.03	67.86	69.25	65.09	64.68
$\overline{D}$	39.42	40.10	40.66	40.30	39.97	39.82	39.70
pD	29.41	30.52	27.37	27.55	29.28	25.28	24.98

6. SUMMARY AND DISCUSSION

This paper evaluated different prior distributions for the covariance matrix in an AB-NMA, including the IW prior and a separation strategy with uniform priors on standard deviations and the RW, RIW or EQ prior on correlations. We compared their performance using extensive simulation studies with data generated under different mechanisms for selecting each study’s treatments. Separation strategies with a RIW or EQ prior on correlations performed much better than the IW prior in all situations in terms of bias and coverage probability of log odds ratios, absolute risks, variances and correlations. The commonly used IW prior often overestimated variances and underestimated correlations, which can lead to substantial bias for log odds ratios and absolute effects, especially under MNAR. The separation strategy with the EQ prior gave relatively small biases for log odds ratios under all conditions considered. These findings suggest that the separation strategy with the equal correlation prior is a much better choice of default vague prior in AB-NMA than the widely-used IW prior.

We conducted three case studies and compared separation strategies to the IW prior in terms of DIC. In the meta-analysis of serious vascular event prevention, the RIW and EQ priors had noticeably improved DIC compared to the IW and RW priors. However, estimating treatment-specific variances of log-odds in AB-NMA can be encumbered due to lack of information (i.e., most treatments are included in only a few trials). Here we proposed a straightforward but perhaps overly simple solution of assuming the treatment-specific variances are equal. This equal-variances assumption gave narrower credible intervals for treatment effects in the NMAs of serious vascular event prevention and postpartum haemorrhage prevention, and improved model fits. Thus, we suggest that NMA users consider sensitivity analyses with different assumptions on variance (homogeneous and heterogeneous variance assumptions) when using the separation strategy with the equal correlation prior.

Due to space limitation, we compared only four covariance priors. Other potential choices include the Cholesky decomposition¹⁹ and the spherical decomposition³¹. These methods further decompose the correlation matrix P as L′L, where L is a T × T upper-triangular matrix. Then we can place a weakly informative prior on L through a spherical parameterization. Technical details and applications to multivariate meta-analyses are in Lu and Ades⁴, Wei and Higgins³², and Lin et al.³³. However, using this approach, the marginal distributions of the ρ_ij depend strongly on the indexes i and j; see, e.g., Figure 3 in Wei and Higgins³². The different marginal distributions lack statistical or clinical interpretations and meta-analysts may reasonably be concerned about the potential impact of using different marginal priors for different correlations.

We evaluated the performance of a Bayesian analysis with different prior specifications with simulations from a frequentist perspective (e.g., bias and coverage probability); one may argue that this may be philosophically inappropriate³⁴. Nevertheless, this does not affect the goal of this article, i.e., providing some practical recommendations of prior specifications for the Bayesian AB-NMA with less bias and better coverage probability.

In the continuing debate^11,12 between proponents of the AB and CB approaches, White et al.¹³ recently compared both approaches and concluded that ‘both AB and CB models are suitable for the analysis of NMA data, but using random study intercepts requires a strong rationale such as relating treatment effects to study intercepts’. Perhaps such a rationale exists: Houwelingen et al.^36,35 pointed out that the assumption of exchangeable absolute treatment risks is reasonable in most meta-analyses, while Béliveau et al.³⁷ also mentioned that disconnected networks could benefit from being analyzed using random study intercepts. But perhaps this assumption appeared to be important only by accident, because of the choice of prior distributions: in our simulation study (Table 1), the separation strategy approach (AB-EV), compared with AB-IW, substantially reduced bias and potentially reduced the risk of using random study intercepts by improving estimation of the correlations between different treatments’ random effects of log-odds.

While the most important variance parameter in a CB-NMA is the heterogeneity of the treatment contrasts¹³, in the AB approach the variances of log-odds and correlations between treatment-specific log-odds are crucial, because: 1) variances of log-odds are needed to derive absolute risks and a much wider range of estimands, which is a key advantage of the AB approach; 2) correlations are critical to keep contrasts (relationships) between treatments stable, which can reduce the risk of assuming random study intercepts. Also, the AB-EQ-EV prior discussed in Section 5, with homogeneous variance of treatment specific log-odds and homogeneous correlations, is equivalent to assuming homogeneous variance of treatment contrasts in the CB approach⁹, in terms of the covariance structure.

Several other issues deserve further exploration and discussion. First, the uniform prior on standard deviations δ_i, i = 1, … , T in the AB model may cause upward bias when the true standard deviation is low. Second, if certain treatments are included in only a few trials in a NMA, the posteriors of their standard deviations may be dominated by their priors, which could lead to wide credible intervals for both the standard deviations and absolute risks, and thus bias the estimated absolute risks. In some NMAs, the assumption of equal variances might be too strong. Alternatively, one may model the standard deviations of study-specific log-odds of different treatments as random draws from a common distribution and thus allow borrowing strength in the estimation to shrink them in a data-dependent manner. The idea of extrapolation^38,39 could also be applied to incorporate external evidence about standard deviations. Third, as mentioned in Sections 1, the T×T covariance matrix in the AB model is closely related to the CB model’s (T − 1)×(T − 1) covariance matrix, so we can probably apply corresponding RIW and EQ priors in the CB approach. Fourth, since the posterior distributions of some parameters (e.g., correlation coefficients ρ_ij and marginal absolute risks p_i) could be skewed, posterior medians might be better summaries than posterior means. Finally, it seems that all priors considered here may systematically underestimate the correlations. Further research on alternative priors may be fruitful.