Generalized Mean Residual Life Models for Case-Cohort and Nested Case-Control Studies

Abstract

Mean residual life (MRL) is the remaining life expectancy of a subject who has survived to a certain time point and can be used as an alternative to hazard function for characterizing the distribution of a time-to-event variable. Inference and application of MRL models have primarily focused on full-cohort studies. In practice, case-cohort and nested case-control designs have been commonly used within large cohorts that have long follow-up and study rare diseases, particularly when studying costly molecular biomarkers. They enable prospective inference as the full-cohort design with significant cost-saving benefits. In this paper, we study the modeling and inference of a family of generalized MRL models under case-cohort and nested case-control designs. Built upon the idea of inverse selection probability, the weighted estimating equations are constructed to estimate regression parameters and baseline MRL function. Asymptotic properties of the proposed estimators are established and finite-sample performance is evaluated by extensive numerical simulations. An application to the New York University Women’s Health Study is presented to illustrate the proposed models and demonstrate a model diagnostic method to guide practical implementation.

1. Introduction

The mean residual life (MRL) is the remaining life expectancy given that a subject has survived to a certain time point. For a non-negative survival time T with finite expectation, the MRL at time t is m(t) = E(T − t|T > t). As alternatives to models based on the hazard function, those based on the MRL have a more intuitive explanation often leading to easier communication with patients. For instance, providing patients who have been on a treatment for a year with their remaining life expectancy is likely to be more informative than providing them with instantaneous hazards.

Various statistical models have been proposed to characterize the MRL function given covariates. Specifically, the proportional MRL model (Oakes and Dasu, 1990; Maguluri and Zhang, 1994) is,

$$m(t\mid \mathit{Z})=m_0(t)\text{exp}\left({\beta }^{\prime }\mathit{Z}\right),$$ (1)

where β is a vector of regression parameters characterizing the multiplicative effects of covariates on the MRL function, and m₀(t) is an unknown baseline MRL function. The estimation and inference for model (1) have been developed to accommodate right censoring based on the counting process theory (Chen et al., 2005; Chen and Cheng, 2005). The additive MRL model (Chen and Cheng, 2006; Chen, 2007) is,

$$m(t\mid \mathit{Z})=m_0(t)+{\beta }^{\prime }\mathit{Z},$$ (2)

where the coefficients β characterize the additive change in remaining life expectancy per unit change in Z, and m₀(t) is an unknown baseline MRL function. A quasi-partial score (QPS) estimation procedure has been proposed for the estimation of models (1) and (2) (Chen and Cheng, 2005, 2006; Chen, 2007).

More recently, Sun and Zhang (2009) proposed a class of generalized MRL models,

$$m(t\mid \mathit{Z})=g\left\{m_0(t)+{\beta }^{\prime }\mathit{Z}\right\},$$ (3)

in which g(·) is a pre-specified link function to allow flexible model settings. Sun and Zhang (2009) proposed using the inverse probability of censoring weighting (IPCW) technique to develop estimating equations based on a zero-mean stochastic process. Model (3) can include the proportional MRL model and the additive MRL model as special cases. Moreover, model (3) has been extended to handle time-varying coefficients (Sun et al., 2012; Yang and Zhou, 2014). Note that the choice of g(·) link function can be flexible, but it needs to ensure that the MRL function is properly defined and satisfies the following conditions: (a) g(·) is twice continuously differentiable, (b) g(·) is strictly increasing, and (c) g{m₀(t) + β′ 0Z} is a proper MRL function for all possible values of random covariates Z.

The MRL models described above have primarily been studied and applied in prospective cohort studies, where large sample size and long follow-up duration enable investigations on rare diseases and their complex mechanisms. Many large cohort studies store biological samples for future research. However, when studying costly molecular biomarkers, assembling detailed covariate information for the entire cohort often becomes time-consuming, expensive, and particularly cost-prohibitive for studying rare diseases.

Case-cohort (CC) design (Prentice, 1986) and nested case-control (NCC) design (Thomas, 1977) are widely considered as alternatives to the full-cohort design. In the CC design, a random sample of the full cohort is selected and named the subcohort. All incident cases (i.e. participants who developed the event of interest during follow-up regardless of being included in the subcohort or not) and the selected controls (i.e. participants who did not develop the event of interest) in the subcohort will be included in the CC analysis. The NCC design randomly samples a fixed number of controls for each case from the case’s risk set (i.e. the set of cohort participants free of event at the time of the case), and then assembles covariate information for all the cases and the selected controls. Compared with the NCC design, the CC design is deemed to be more efficient since the selected subcohort can be used for multiple different case groups (Kupper et al., 1975; Prentice, 1986). However the NCC design has the advantage of matching cases and controls on follow-up duration and can be extended to match on other confounders as well. Both designs are efficient and cost-effective in studying the relationship between exposures and diseases. However, for analysis of the CC and NCC studies, estimation and inference have been mostly dependent on the Cox proportional hazards model (Chen and Lo, 1999; Liu et al., 2010a,b; Scheike and Juul, 2004) and MRL modeling remains understudied. Recently, Ma et al. (2017) studied the proportional MRL model for CC studies using the QPS approach based on mean-zero process; however, the adoption of the proportional MRL models in NCC studies is yet to be developed due to its complex sampling mechanism.

Here we study modeling and inference for the generalized MRL model (3) under the CC and NCC designs. We propose a unified estimation procedure for both the CC and NCC designs and establish asymptotic properties for our proposed estimators. Statistical inference procedure based on bootstrap method (Efron, 1979) is adopted for the CC design, and perturbation resampling method (Cai and Zheng, 2013) is needed for the NCC design. A practical contribution also includes an R package to implement the proposed approaches.

In Section 2, we present the proposed estimating equations and inference procedures for model (3) under the CC and NCC designs. Section 3 reports the results from extensive simulation studies. In Section 4, we apply our approach to a real dataset from the New York University Women’s Health Study (NYUWHS), and present a model diagnostic method that can be readily used for model selection. Discussion and concluding remarks are given in Section 5. Additional simulations, regularity conditions, and technical proofs are provided in Appendix.

2. Estimation and Inference

Consider a full cohort with size n. Let T_i be the failure time and C_i be the censoring time for subject i = 1, 2, …, n. We assume T_i and C_i are conditionally independent given covariate Z_i. The complete cohort data consist of n independently identically distributed random triplets $\left\{\left({\tilde{T}}_i,{\delta }_i,{\mathit{Z}}_i\right);i=1,2,\dots ,n\right\}$, where ${\tilde{T}}_i=\text{min}\left(T_i,C_i\right)$ and δ_i = I(T_i ≤ C_t). Let I(·) denote the indicator function throughout. In addition, denote $N_i(t)={\delta }_{i}I\left({\tilde{T}}_i\le t\right)$ and $Y_i(t)=I\left({\tilde{T}}_i\ge t\right)$ as the usual counting process and the at-risk process, respectively. We define filtration $\mathcal{G}=\left\{{\mathcal{G}}_t:t\in [0,\tau ]\right\}$, where ${\mathcal{G}}_t=\sigma \left\{N_i(u),Y_i(u),{\mathit{Z}}_i:0\le u\le t,i=1,\dots ,n\right\}$ and $\tau =\text{inf}\{t:\mathit{\text{Pr}}(T>t)=0\}<\infty$.

Under the CC design, a subcohort with a fixed size $\tilde{n}$ is drawn randomly from the entire full cohort. Let γ_i = 1 indicate that subject i is included in the subcohort; 0 otherwise. All cases in the cohort and controls in the selected subcohort constitute the CC sample, which can be summarized as $\left\{\left({\tilde{T}}_i,{\delta }_i,{\gamma }_i,\left[{\delta }_i+\left(1-{\delta }_i\right){\gamma }_i\right]{\mathit{Z}}_i\right),i=1,2,\dots ,n\right\}$. Based upon the idea of inverse selection probabilities, the weight w_i for each subject is defined as w_i = δ_i + (1−δ_i)γ_i/p₀, where $p_0=\tilde{n}/n$ is the proportion of subcohort to the full cohort.

Under the NCC design, for each case, m controls are randomly selected without replacement from the risk set excluding the case itself. The risk set at any time t is defined as $R(t)=\left\{i:{\tilde{T}}_i\ge t\right\}$. Following the notation of Samuelsen (1997), we define the “skeleton” filtration of the full-cohort as $\mathcal{F}=\left\{{\mathcal{F}}_t:t\in [0,\tau ]\right\}$, where ${\mathcal{F}}_t=\sigma \left\{N_i(u),Y_i(u):0\le u\le t,i=1,\dots ,n\right\}$. Note that $\mathcal{F}$ has all the information relevant to the NCC sampling and is contained in $\mathcal{G}$. Thus, the conditional probability that subject i is ever selected as a control given the skeleton filtration $\mathcal{F}$ can be calculated as (Samuelsen, 1997),

$$p_{0i}=1-\prod _{{\tilde{T}}_j<{\tilde{T}}_i}\left(1-\frac{m{\delta }_j}{R\left({\tilde{T}}_j\right)-1}\right).$$ (4)

Then, we define the weight for subject i under NCC studies as w_i = δ_i + (1 − δ_i)γ_i/p_0i, where γ_i is the indicator of whether subject i is ever selected as a control into the NCC study.

2.1. Estimation equations

Note that

$$M_i\left(t;{\beta }_{*},m_{*}\right)=N_i(t)-{\int }_0^t{Y}_i(u)d{\Lambda }_i\left(u;{\beta }_{*},m_{*}\right),$$ (5)

is a martingale with respect to ${\mathcal{G}}_t$ by the counting process and martingale theory (Fleming and Harrington 1991), where Λ_i(·) is the cumulative hazard function for subject i, β_* and m_*(·) are the true values of β and m₀(·), respectively. Under the generalized MRL model (3), the relationship between the MRL function and the survival function can be easily derived as,

$$S\left(t\mid \mathit{Z};\beta ,m_0\right)=\frac{g\left\{m_0(0)+{\beta }^{\prime }\mathit{Z}\right\}}{g\left\{m_0(t)+{\beta }^{\prime }\mathit{Z}\right\}}\text{exp}\left\{-{\int }_0^t\frac{du}{g\left\{m_0(u)+{\beta }^{\prime }\mathit{Z}\right\}}\right\},$$ (6)

and the hazard function as

$$d{\Lambda }_i\left(t\mid {\mathit{Z}}_i;\beta ,m_0\right)=\frac{d\left[g\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}+t\right]}{g\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}}.$$ (7)

Motivated by the inverse probability weighting technique (Samuelsen, 1997) and the QPS estimation approach (Chen and Cheng, 2005, 2006), we propose the following unified estimation equations for model (3) under the CC and NCC designs. For 0 ≤ t ≤ τ,

$$\frac{1}{n}\sum _{i=1}^n{w}_i\left[g\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-Y_i(t)d\left[g\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}+t\right]\right]=0,$$ (8)

$$\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }{w}_i{\mathit{Z}}_i\left[g\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-Y_i(t)d\left[g\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}+t\right]\right]=0,$$ (9)

where w_i is the design-specific weight for subject i as defined above. Although equations (8) and (9) do not have martingale interpretation because w_i’s are not predictable processes with respect to ${\mathcal{G}}_t$, they are mean-zero processes. Specifically, we have that $\text{E}\left\{w_i\left[d{N}_i(t)-Y_i(t)d{\Lambda }_i\left(t;{\beta }_{*},m_{*}\right)\right]\right\}=\text{E}\{[d{N}_i(t)-Y_i(t)d{\Lambda }_i\left(t;{\beta }_{*},m_{*}\right)]\text{E}\left(w_i\mid \mathcal{G}\right)\}=0$ because E[dM_i(t; β_*, m_*)] = 0 and $\text{E}\left(w_i\mid \mathcal{G}\right)=\text{E}\left(w_i\mid \mathcal{F}\right)=1$.

Given a fixed β and pre-specified g(·), equation (8) can be rewritten as a first-order linear ordinary differential equation about m₀(t), which leads to a closed form solution. Let ${\widehat{m}}_0(t;\beta )$ denote the solution of equation (8) with respect to m₀(t), and then it can be plugged back into equation (9). It is evident that equation (9) can be re-arranged and written as,

$$U(\beta )=\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }{w}_i\left[{\mathit{Z}}_i-\frac{{\sum }_{i=1}^n{w}_i{\mathit{Z}}_i{Y}_i(t)}{{\sum }_{i=1}^n{w}_i{Y}_i(t)}\right][g\left\{{\widehat{m}}_0(t;\beta )+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-Y_i(t)dg\left\{{\widehat{m}}_0(t;\beta )+{\beta }^{\prime }{\mathit{Z}}_i\right\}]=0.$$ (10)

To solve equation (10) for β, the Newton-Raphson algorithm can be applied after calculating the Jacobian matrix for multidimensional case. We denote $\widehat{\beta }$ as the resulting estimator of β.

Remark 1: We conducted numerical simulations to compare the IPCW method (Sun and Zhang, 2009) and the QPS estimator (Chen and Cheng, 2005, 2006) under the full-cohort design with various censoring proportions (results in Appendix) and observed that the QPS estimator outperformed the IPCW estimator in terms of estimation stability and 95% confidence interval coverage probability, especially under the high censoring scenarios. Based on these observations, we developed our estimating procedure based on the QPS approach for the generalized MRL modeling in the CC and NCC designs.

2.2. Asymptotic properties

In this section, we summarize the asymptotic properties of our proposed estimators and defer the details of assumptions and proofs toAppendix. We first introduce some notations. Let

$$\overline{\mathit{Z}}(t;\beta )=\frac{{\sum }_{i=1}^n{w}_i{\mathit{Z}}_i{Y}_i(t)\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}}{{\sum }_{i=1}^n{w}_i{Y}_i(t)\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}},$$

$$\breve{\mathit{Z}}(t;\beta )=\frac{1}{K(t;\beta )}{\int }_t^{\tau }K(u;\beta )Q(u;\beta ),$$

$$\tilde{\mathit{Z}}(t;\beta )=\frac{K(t;\beta )}{C(t;\beta )}{\int }_0^t\left[\frac{n^{-1}{\sum }_{j=1}^n{w}_j\left[{\mathit{Z}}_j-\overline{\mathit{Z}}(u;\beta )\right]\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)}{K(u;\beta )}-\frac{n^{-1}{\sum }_{j=1}^n{w}_j\left[{\mathit{Z}}_j-\overline{\mathit{Z}}(u;\beta )\right]Y_i(t)d\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}}{K(u;\beta )}\right],$$

$$C(t;\beta )=\frac{1}{n}\sum _{i=1}^n{w}_i{Y}_i(t)\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}$$

$$K(t;\beta )=\text{exp}\left\{-{\int }_0^t\left[\frac{{\sum }_{i=1}^n{w}_i\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)}{{\sum }_{i=1}^n{w}_i{Y}_i(t)\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}}-\frac{{\sum }_{i=1}^n{w}_i{Y}_i(t)d\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}}{{\sum }_{i=1}^n{w}_i{Y}_i(t)\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}}\right]\right\}.$$

$$Q(t;\beta )=\frac{{\sum }_{i=1}^n{w}_i{\mathit{Z}}_i\left[\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-Y_i(t)d\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}\right]}{{\sum }_{i=1}^n{w}_i{Y}_i(t)\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}}$$

Theorem 1 Under the regularity conditions (C1) to (C4) stated in Appendix, we have:

1. The estimators $\widehat{\beta }$ and ${\widehat{m}}_0(t)$ exist and are consistent.

2. $\sqrt{n}\left(\widehat{\beta }-{\beta }_{*}\right)\to N\left\{0,A^{-1}\Sigma {\left(A^{-1}\right)}^{\prime }\right\}$ in distribution. Moreover, variance matrix components A and Σ can be consistently estimated by $\widehat{A}$ and $\widehat{\Sigma }$ Specifically, for the CC design,

   $$\widehat{A}=\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }{w}_i\left[Z_i-\overline{Z}(t;\widehat{\beta })\right]{\left[Z_i-\breve{Z}(t;\widehat{\beta })\right]}^{\prime }\left[\dot{g}\left\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{Z}_i\right\}d{N}_i(t)-Y_i(t)d\dot{g}\left\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{Z}_i\right\}\right],$$

   $$\widehat{\Sigma }={\widehat{\Sigma }}_1+{\widehat{\Sigma }}_2,$$

   $${\widehat{\Sigma }}_1=\frac{1}{n}\sum _{i=1}^n{w}_i{\int }_0^{\tau }\left[{\left\{{\mathit{Z}}_i-\overline{\mathit{Z}}(t;\widehat{\beta })-\tilde{\mathit{Z}}(t;\widehat{\beta })\right\}}^{\otimes 2}{Y}_i(t)g\left\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{\mathit{Z}}_i\right\}\left[dg\left\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{\mathit{Z}}_i\right\}+dt\right]\right],$$

   $${\widehat{\Sigma }}_2=\frac{1}{n}\sum _{i=1}^n\frac{1-{\widehat{p}}_{0i}}{{\widehat{p}}_{0i}}{\left[{\int }_0^{\tau }\left(w_i-{\delta }_i\right)\left\{{\mathit{Z}}_i-\overline{\mathit{Z}}(t;\widehat{\beta })-\tilde{\mathit{Z}}(t;\widehat{\beta })\right\}g\left\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{\mathit{Z}}_i\right\}d{\widehat{M}}_i(t)\right]}^{\otimes 2}-{\left(\frac{1}{n}\sum _{i=1}^n\frac{1-{\widehat{p}}_{0i}}{{\widehat{p}}_{0i}}\left[{\int }_0^{\tau }\left(w_i-{\delta }_i\right)\left\{{\mathit{Z}}_i-\overline{\mathit{Z}}(t;\widehat{\beta })-\tilde{\mathit{Z}}(t;\widehat{\beta })\right\}g\left\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{\mathit{Z}}_i\right\}d{\widehat{M}}_i(t)\right]\right)}^{\otimes 2},$$

   where α^⨂2 denotes αα^T for a vector α. For the NCC design, ${\widehat{\Sigma }}_2$ is estimated differently as,

   $${\widehat{\Sigma }}_2=\frac{1}{n}\sum _{i=1}^n\left(w_i^2-w_i\right){\left[{\int }_0^{\tau }\left\{{\mathit{Z}}_i-\overline{\mathit{Z}}(t;\widehat{\beta })-\tilde{\mathit{Z}}(t;\widehat{\beta })\right\}g\left\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{\mathit{Z}}_i\right\}d{\widehat{M}}_i(t)\right]}^{\otimes 2}-m{\int }_0^{\tau }{\left(\frac{1}{n}\sum _{i=1}^n\left(w_i^2-w_i\right)Y_i(t)\left[{\int }_0^{\tau }\left\{{\mathit{Z}}_i-\mathit{Z}(t;\widehat{\beta })-\tilde{\mathit{Z}}(t;\widehat{\beta })\right\}g\left\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{\mathit{Z}}_i\right\}d{\widehat{M}}_i(t)\right]\right)}^{\otimes 2}\left(\frac{{\overline{g}}_1(t)}{\overline{y}(t)}d{\widehat{m}}_0(t)+\frac{{\overline{g}}_2(t)}{\overline{y}(t)}dt\right),$$

   where ${\overline{g}}_1(t)={\sum }_{j=1}^n{Y}_j(t)\dot{g}\left\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{\mathit{Z}}_j\right\}/g\left\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{\mathit{Z}}_j\},{\overline{g}}_2(t)={\sum }_{j=1}^n{Y}_j(t)/g\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{\mathit{Z}}_j\right\}$, and $\overline{y}(t)={\sum }_{j=1}^n{Y}_j(t)$.

Remark 2: The NCC sampling is a dynamic process and the probability of being selected as a control is neither a constant nor independent, even in the asymptotic sense. The asymptotic variance estimate derived under the NCC design explicitly contains the cross-product term between subject i and j as shown in the ${\widehat{\Sigma }}_2$ in Theorem 1.

2.3. Numerical variance estimation

The asymptotic variance formula and the plug-in estimators that are described above can be difficult to implement analytically. In practice, bootstrap method (Efron, 1979) is often adopted to compute the standard errors (SE) of estimators. Under the full-cohort design, estimating the SEs via the standard bootstrap method is straightforward. For the CC design, since the weight of each selected control is pre-specified, one can obtain the estimated SEs by implementing the bootstrapping within the selected subcohort.

Under the NCC design, however, the standard bootstrap approach cannot fully capture the complex correlation structure induced by repeated finite risk set sampling nor applicable for the proposed estimators. We thus employ the perturbation resampling method (Cai and Zheng, 2013) to estimate the SEs under the NCC design. Instead of resampling the selected subsample, the perturbation method approximates the variance of the IPW estimators by perturbing the weight of each subject. Specifically, the procedures are described below:

1. Generate n² random realizations of I_il from a given distribution with E(I_il) = 1 and let I = {I_il, i = 1, …, n; l = 1, …, n}.

2. Calculate the perturbed weights as ${\widehat{w}}_j=V_j/{\widehat{p}}_j$, where

   $$V_j={\delta }_j{I}_{jj}+\left(1-{\delta }_j\right)\left(1-\prod _{i:j\in R_i}\left(1-{\delta }_i{V}_{0ij}{I}_{ij}\right)\right),$$

   $${\widehat{p}}_j={\delta }_j+\left(1-{\delta }_j\right)\left(1-\text{exp}\left\{-\sum _{i:T_i\le t,{\delta }_i=1}\frac{{\sum }_{l\in R_1}{V}_{0il}{I}_{il}}{\Vert R_i\Vert }\right\}\right),$$

   and V_0ij = 1 denotes the jth subject is selected as a control for the ith subject.

3. Replace the w_i in (10) using the perturbed weights from step 2 and obtain the estimator ${\widehat{\beta }}_{\mathit{\text{perturb}}}$.

4. Repeat steps 1–3 for M times and use the standard deviation of these ${\widehat{\beta }}_{\mathit{\text{perturb}}}$ to approximate the SE of $\widehat{\beta }$.

3. Simulation Studies

We conducted simulations to evaluate the finite-sample performance of the proposed inference procedures and to compare their efficiency under the CC and NCC designs to the full-cohort analysis. We considered two models with g(t) = exp(t) and g(t) = t, which corresponded to the proportional MRL model and additive MRL model, respectively. To generate the data, the baseline function m₀(t) was taken from the Hall-Wellner family, which was m₀(t) = g⁻¹ {(D₁t + D₂)⁺}, where D₁ > −1, D₂ > 0 and d⁺ denoted dI(d ≥ 0) for any quantity d. In our setting, we considered D₁ = −0.5 and D₂ = 0.5. Let Z₁ be a Bernoulli random variable with success probability 0.5 and Z₂ be a uniform random variable on (0, 1). The true parameters (β₁, β₂)′ were set to be (0, 0)′ for null effects and (0.2, 0.2)′ for moderate effects. Censoring time C was generated from the exponential distribution with parameter λ, which was chosen to yield different censoring proportions. We conducted 500 simulations under each setting.

The first set of simulations evaluated our proposed methods for the proportional MRL model under the full-cohort, CC, and NCC designs. To mimic a practical setting, we considered a cohort size of 1000 and 5000, and high censoring rates of 70%, 80% and 90%. In addition, a long follow-up duration was assumed as in many large epidemiology cohort studies and for stable estimation of the MRL models. We selected 1 control for each case in the NCC design and 30% random subcohort for the CC design. The SEs of estimators were computed based on the standard bootstrap method for the full-cohort and CC designs. The perturbation-based method was applied to estimate SEs under the NCC design, where the weights were generated from a Gamma distribution with shape and scale parameters of 1.

Table 1 and Table 2 summarize the results for the proportional MRL model over 1000 simulations for cohort size of 1000 and 5000. The biases of the estimators were small, SDs and SEs matched well, and coverage probability (CP) of 95% Wald-type confidence interval was close to the nominal level. The SDs and SEs decreased as sample size increased. The estimates from the CC and NCC designs lost some efficiency when compared to those obtained in the full-cohort analysis, but noted that these within-cohort sampling designs also would save cost by only using the partially sampled subcohort.

Table 1.

Simulation results under proportional MRL models

N	β	censoring rate		Full†		CC (30%)‡		NCC (1-to-1)§
				β1	β2	β1	β2	β1	β2
1000	(0,0)	0.7	Bias	−0.002	−0.002	0.001	0.002	−0.002	−0.001
			SD	0.060	0.105	0.079	0.129	0.072	0.122
			SE	0.061	0.106	0.078	0.136	0.065	0.112
			CP	95.0	94.7	93.9	96.2	92.0	93.2
1000	(0,0)	0.8	Bias	−0.000	−0.001	−0.002	−0.012	−0.001	0.000
			SD	0.071	0.129	0.097	0.156	0.092	0.155
			SE	0.073	0.127	0.091	0.157	0.082	0.143
			CP	95.5	94.2	93.5	94.6	92.7	92.5
1000	(0,0)	0.9	Bias	0.001	−0.009	0.002	0.005	−0.007	−0.001
			SD	0.086	0.153	0.092	0.164	0.114	0.202
			SE	0.086	0.150	0.093	0.162	0.109	0.190
			CP	95.0	94.5	95.8	95.3	93.2	94.4
1000	(0.2,0.2)	0.7	Bias	0.000	−0.001	−0.002	0.002	−0.002	−0.006
			SD	0.048	0.087	0.063	0.104	0.057	0.093
			SE	0.050	0.087	0.060	0.105	0.051	0.088
			CP	95.1	95.3	94.2	95.9	91.7	93.4
1000	(0.2,0.2)	0.8	Bias	0.001	−0.002	0.008	0.002	−0.005	−0.006
			SD	0.057	0.105	0.073	0.125	0.069	0.123
			SE	0.059	0.103	0.073	0.127	0.067	0.116
			CP	95.3	95.4	95.3	95.4	94.2	94.1
1000	(0.2,0.2)	0.9	Bias	−0.004	−0.012	−0.011	−0.013	−0.018	−0.006
			SD	0.079	0.136	0.092	0.154	0.103	0.182
			SE	0.077	0.134	0.088	0.153	0.099	0.174
			CP	94.6	94.8	94.3	94.5	94.2	95.2

SD: sample standard deviation; SE: mean of estimated standard error;

CP: empirical coverage probability of 95% confidence interval;

^†Full-cohort population

^‡Case-Cohort design with 30% random sample from full-cohort population

^§Nested Case-Control design with 1 control for each case

Table 2.

Simulation results under proportional MRL models

N	β	censoring rate		Full†		CC (30%)‡		NCC (1-to-l)§
				β1	β2	β1	β1	β2	β1
5000	(0,0)	0.7	Bias	0.000	0.001	0.000	−0.003	0.000	−0.001
			SD	0.027	0.048	0.034	0.060	0.033	0.054
			SE	0.027	0.047	0.035	0.060	0.029	0.051
			CP	94.6	94.0	95.3	94.4	92.0	93.6
5000	(0,0)	0.8	Bias	0.000	0.002	−0.002	−0.001	−0.001	0.002
			SD	0.033	0.058	0.040	0.072	0.040	0.072
			SE	0.032	0.056	0.041	0.070	0.037	0.064
			CP	94.9	94.4	95.4	95.0	92.4	92.1
5000	(0,0)	0.9	Bias	−0.001	0.003	0.002	0.000	0.001	0.003
			SD	0.043	0.076	0.050	0.083	0.056	0.098
			SE	0.042	0.074	0.048	0.083	0.052	0.091
			CP	94.8	94.7	94.5	95.1	93.6	92.6
5000	(0.2,0.2)	0.7	Bias	0.000	0.001	−0.001	−0.001	−0.003	−0.004
			SD	0.023	0.040	0.027	0.047	0.023	0.042
			SE	0.022	0.038	0.027	0.047	0.023	0.039
			CP	94.6	94.2	95.0	94.9	93.9	93.6
5000	(0.2,0.2)	0.8	Bias	0.000	0.002	−0.001	−0.001	−0.002	0.002
			SD	0.026	0.046	0.031	0.054	0.032	0.056
			SE	0.026	0.045	0.032	0.056	0.030	0.052
			CP	95.1	94.8	95.4	96.1	93.8	93.4
5000	(0.2,0.2)	0.9	Bias	0.001	0.004	−0.003	0.000	−0.006	−0.009
			SD	0.036	0.063	0.043	0.071	0.050	0.088
			SE	0.036	0.062	0.042	0.072	0.047	0.082
			CP	95.6	95.2	94.0	95.3	93.4	93.2

SD: sample standard deviation; SE: mean of estimated standard error;

CP: empirical coverage probability of 95% confidence interval;

^†Full-cohort population

^‡Case-Cohort design with 30% random sample from full-cohort population

^§Nested Case-Control design with 1 control for each case

In Table 3 and Table 4, we summarized the simulation results for the additive MRL models under full cohort size of 1000 and 5000 with high censoring rates of 70%, 80%, and 90%. Note that the additive MRL model does not ensure positive baseline MRL functions at any time, which could make the estimating procedure unstable when the sample size is small. In order to have meaningful estimates from the estimating equations, by the convention of Reid (1981) and James (1986), the longest observation was always assumed to be a true event. We found that this single data-point change at the tail had minimal impact on the estimation. In general, the biases were small and the SDs of the estimates were close to the average of SEs. The 95% confidence interval coverage probabilities were around the nominal level, indicating that the bootstrapping and perturbation resampling methods worked well for the CC and NCC designs, respectively. The overall performance improved with increasing sample size. Figures 1 and 2 visually demonstrate the performance of the full-cohort, CC, and NCC designs, specifically on efficiency.

Table 3.

Simulation results under additive MRL models

N	β	censoring rate		Full†		CC (30%)‡		NCC (1-to-l)§
				β1	β2	β1	β1	β2	β1
1000	(0,0)	0.7	Bias	−0.001	−0.001	0.001	0.003	−0.002	0.000
			SD	0.045	0.070	0.057	0.096	0.054	0.095
			SE	0.045	0.079	0.057	0.099	0.051	0.089
			CP	94.9	94.4	94.2	95.9	93.5	92.8
1000	(0,0)	0.8	Bias	0.000	−0.001	0.002	−0.004	−0.002	−0.002
			SD	0.059	0.106	0.078	0.126	0.053	0.096
			SE	0.060	0.105	0.073	0.127	0.054	0.094
			CP	95.4	94.8	94.1	95.3	92.7	94.0
1000	(0,0)	0.9	Bias	0.004	0.000	0.009	0.017	0.000	0.012
			SD	0.080	0.143	0.088	0.168	0.103	0.187
			SE	0.079	0.139	0.088	0.154	0.106	0.193
			CP	95.8	94.8	95.6	93.9	94.0	93.0
1000	(0.2,0.2)	0.7	Bias	0.010	0.008	0.007	0.017	0.010	0.014
			SD	0.066	0.114	0.087	0.147	0.080	0.135
			SE	0.067	0.114	0.085	0.145	0.078	0.135
			CP	96.0	94.8	95.5	95.3	94.6	95.0
1000	(0.2,0.2)	0.8	Bias	0.010	0.007	0.014	0.013	0.007	0.012
			SD	0.088	0.158	0.117	0.204	0.114	0.192
			SE	0.091	0.155	0.115	0.194	0.112	0.194
			CP	95.7	95.1	95.5	95.8	94.7	95.3
1000	(0.2,0.2)	0.9	Bias	−0.006	−0.010	−0.007	0.010	−0.012	0.005
			SD	0.138	0.229	0.161	0.282	0.167	0.305
			SE	0.123	0.212	0.138	0.240	0.196	0.359
			CP	92.9	94.8	91.5	92.2	95.6	93.6

SD: sample standard deviation; SE: mean of estimated standard error;

CP: empirical coverage probability of 95% confidence interval;

^†Full-cohort population

^‡Case-Cohort design with 30% random sample from full-cohort population

^§Nested Case-Control design with 1 control for each case

Table 4.

Simulation results under additive MRL models

N	β	censoring rate		Full†		CC (30%)‡		NCC (1-to-l)§
				β1	β2	β1	β1	β2	β1
5000	(0,0)	0.7	Bias	0.000	0.000	0.000	−0.002	0.001	−0.001
			SD	0.020	0.035	0.025	0.044	0.025	0.042
			SE	0.020	0.034	0.025	0.044	0.024	0.041
			CP	94.6	94.2	95.9	94.9	93.4	94.2
5000	(0,0)	0.8	Bias	0.000	0.001	−0.001	0.000	−0.001	0.002
			SD	0.026	0.047	0.032	0.059	0.032	0.060
			SE	0.026	0.045	0.033	0.057	0.033	0.057
			CP	94.8	94.5	95.3	94.5	95.2	93.5
5000	(0,0)	0.9	Bias	0.000	0.004	0.002	0.001	0.001	0.005
			SD	0.039	0.068	0.045	0.074	0.052	0.091
			SE	0.038	0.066	0.044	0.076	0.050	0.088
			CP	94.8	94.7	94.4	95.7	94.6	94.2
5000	(0.2,0.2)	0.7	Bias	0.004	0.005	0.005	0.004	0.005	0.006
			SD	0.029	0.050	0.038	0.066	0.035	0.059
			SE	0.029	0.049	0.037	0.063	0.033	0.058
			CP	95.0	93.7	95.0	94.4	93.9	94.7
5000	(0.2,0.2)	0.8	Bias	0.004	0.006	0.009	0.001	0.005	0.008
			SD	0.039	0.067	0.051	0.083	0.048	0.084
			SE	0.039	0.065	0.049	0.082	0.048	0.082
			CP	94.7	94.1	95.0	94.8	94.8	94.2
5000	(0.2,0.2)	0.9	Bias	0.000	0.006	−0.001	0.000	−0.003	0.002
			SD	0.063	0.105	0.074	0.121	0.082	0.135
			SE	0.058	0.098	0.067	0.114	0.079	0.136
			CP	94.1	94.0	93.0	93.7	94.1	95.4

SD: sample standard deviation; SE: mean of estimated standard error;

CP: empirical coverage probability of 95% confidence interval;

^†Full-cohort population

^‡Case-Cohort design with 30% random sample from full-cohort population

^§Nested Case-Control design with 1 control for each case

Fig. 1.

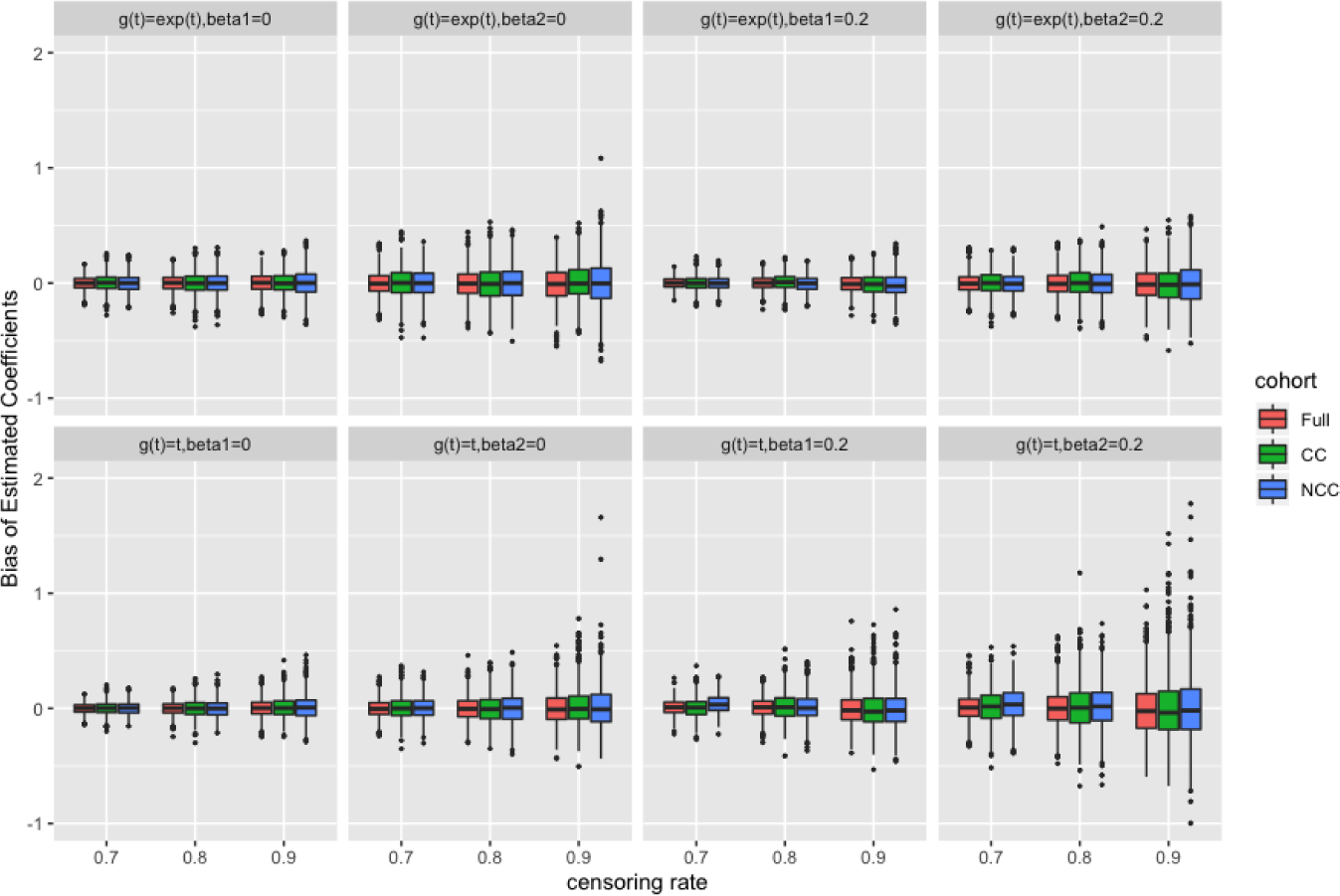
Bias of estimated coefficients with sample size of 1000

Fig. 2.

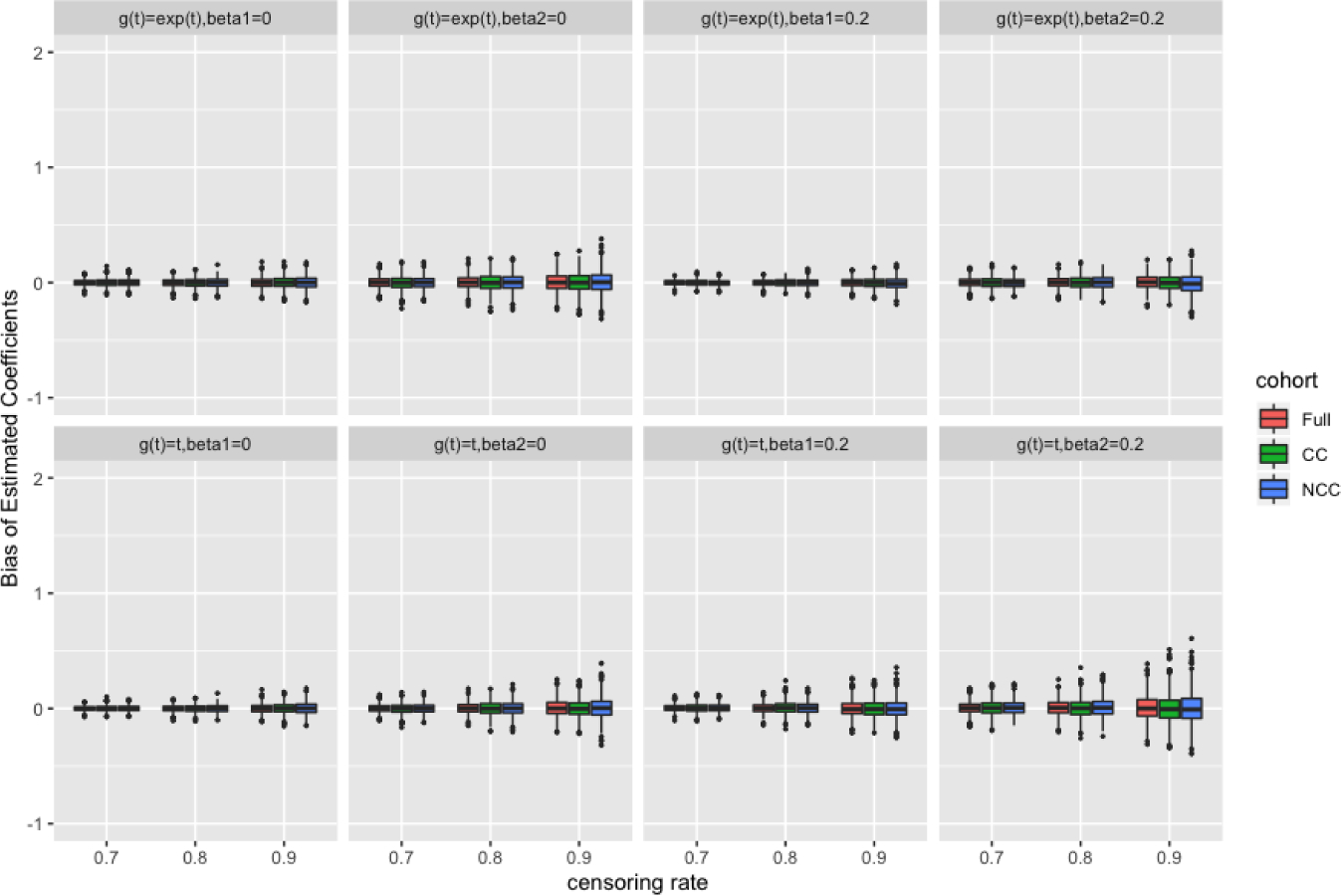
Bias of estimated coefficients with sample size of 5000

4. Application

4.1. Data analysis

The proposed models and estimation methods were demonstrated through a study conducted in the NYUWHS, a prospective cohort study that enrolled 14,274 healthy women aged 35–65 between 1985 and 1991 at a breast cancer screening center in New York City. One primary interest of the study was to investigate the association between endogenous sex hormones and breast cancer risk. At enrollment, participants completed a questionnaire on lifestyle and reproductive history. Blood samples were collected and stored for all participants. Every two to four years, study participants were asked to update information on their health conditions by completing a questionnaire. Within the NYUWHS, multiple nested case-control studies on breast cancer have been conducted (Scarmo et al., 2013; Clendenen et al., 2015).

The cohort dataset we considered here was from the NYUWHS including 6,610 women who were less than 50 years of age at enrollment and used in a recent study for breast cancer risk prediction in younger women (Ge et al., 2018). In this cohort, approximately 12% of the study participants developed breast cancer during the follow-up period (Mean = 21.3 years, SD = 4.8 years). We considered risk factors that are included in the Gail model (Breast Cancer Risk Assessment Tool) (Gail et al., 1989): age, race, age at menarche, number of breast biopsies, age at first live birth, and number of first-degree relatives with breast cancer. The proportional MRL model and the additive MRL model were applied to evaluate the multiplicative and the additive effects of these risk factors on the MRL function of time to breast cancer occurrence. Within this cohort, we conducted NCC sampling with one matched control, and CC sampling with 20% of the full-cohort size. In order to obtain empirical results, we ran 200 times for both the CC and NCC sampling, and reported the mean of point estimates, as well as the mean of estimated standard error of $\widehat{\beta }$. The SEs were computed using the same approach as in the simulation studies.

The results are summarized in Table 5. Under both the proportional and additive MRL models, the estimates from the CC and NCC designs were similar to the ones from full cohort. Specifically, age at first live birth, number of breast biopsies, and number of first-degree relatives with breast cancer had significant effects on shortening the expected residual disease-free time, which were consistent with the effects observed in the Gail model. As expected, we observed that SEs of the estimators in the CC and NCC designs were larger than that in the full-cohort design.

Table 5.

Analysis of NYUWHS data

	Full‡		CC (20%)§		NCC (1-to-1)¶
Covariate	Estimate	SE	Estimate	SE	Estimate	SE
g(t) = exp(t)
race	−0.0084*	0.0025	−0.0083*	0.0030	−0.0085*	0.0032
age at menarche	−0.0027	0.0018	−0.0027	0.0022	−0.0027	0.0024
age at 1st live birth	−0.0070*	0.0015	−0.0071*	0.0018	−0.0068*	0.0020
# of breast biopsies	−0.0116*	0.0032	−0.0116*	0.0038	−0.0116*	0.0040
# of relatives†	−0.0188*	0.0041	−0.0191*	0.0051	−0.0182*	0.0053
g(t) = t
race	−2.8210*	1.0297	−2.7862*	1.1421	−3.5018*	1.4782
age at menarche	−0.8995	0.6284	−0.8603	0.6994	−1.0138	0.9348
age at 1st live birth	−2.7701*	0.6331	−2.8038*	0.6993	−3.1273*	0.8129
# of breast biopsies	−2.3625*	0.5487	−2.3372*	0.6191	−2.8184*	0.9047
# of relatives†	−3.8616*	0.6153	−3.8675*	0.6984	−4.4870*	1.1350

SE: Average of estimated standard error

^*The coefficient is statistically significant at 0.05 significant level

^†Number of first-degree relatives diagnosed with breast cancer

^‡Full-cohort population

^§Case-Cohort design with 20% random sample from full-cohort population

^¶Nested Case-Control design with 1 control for each case

The interpretation of the additive MRL model is straightforward. For example, in the full-cohort, keeping all other covariates fixed, each additional breast biopsy decreased the expected remaining disease-free time by approximately 2.363 years. The average reduction of MRL estimated from the CC and NCC designs were 2.337 years and 2.818 years, respectively. For the proportional MRL model under the full-cohort design, keeping all other covariates fixed, each additional breast biopsy shortened the expected residual disease-free time by around 1.15%. The estimated percentage under the CC and NCC designs were both 1.15%.

4.2. Model diagnosis

The generalized MRL framework provides flexible model options to study the association between covariates and MRL time under the full-cohort, CC, and NCC designs. For its practical use, some model diagnostic methods would be useful for model selection. Several graphical and numerical model diagnostic approaches have been proposed based on martingale residuals (Lin et al., 1993), but mainly focused on full-cohort data. We adopt the approaches from Lin et al. (1993) and propose weighted test statistics and processes for model selection in the generalize MRL models for CC and NCC studies.

In the NYUWHS application, we used the standardized empirical score process $U(\widehat{\beta },t)$ to conduct model selection graphically. Figure 3 and Figure 4 show the results for the proportional and additive MRL models in full cohort, respectively. The standardized score process in the proportional MRL was smaller than that in the additive MRL model. Another method is to use the value $S={\text{sup}}_t\Vert U(\widehat{\beta },t)\Vert$ as a numerical measure to assess the overall fit of the model. The larger value of ${\text{sup}}_t\Vert U(\widehat{\beta },t)\Vert$ means the higher chance of violation of the specified model assumption. For the full-cohort data from the NYUWHS application, the measures were 0.0656 vs. 0.4402 for the proportional and additive MRL models, respectively, and thus we concluded the proportional MRL model fitted the data better in this application. For the CC and NCC designs with 200 times sampling, we observed the same conclusion, as the measure was 0.033 vs. 0.401 (CC) and 0.032 vs. 0.445 (NCC) for the proportional and additive MRL models.

Fig. 3.

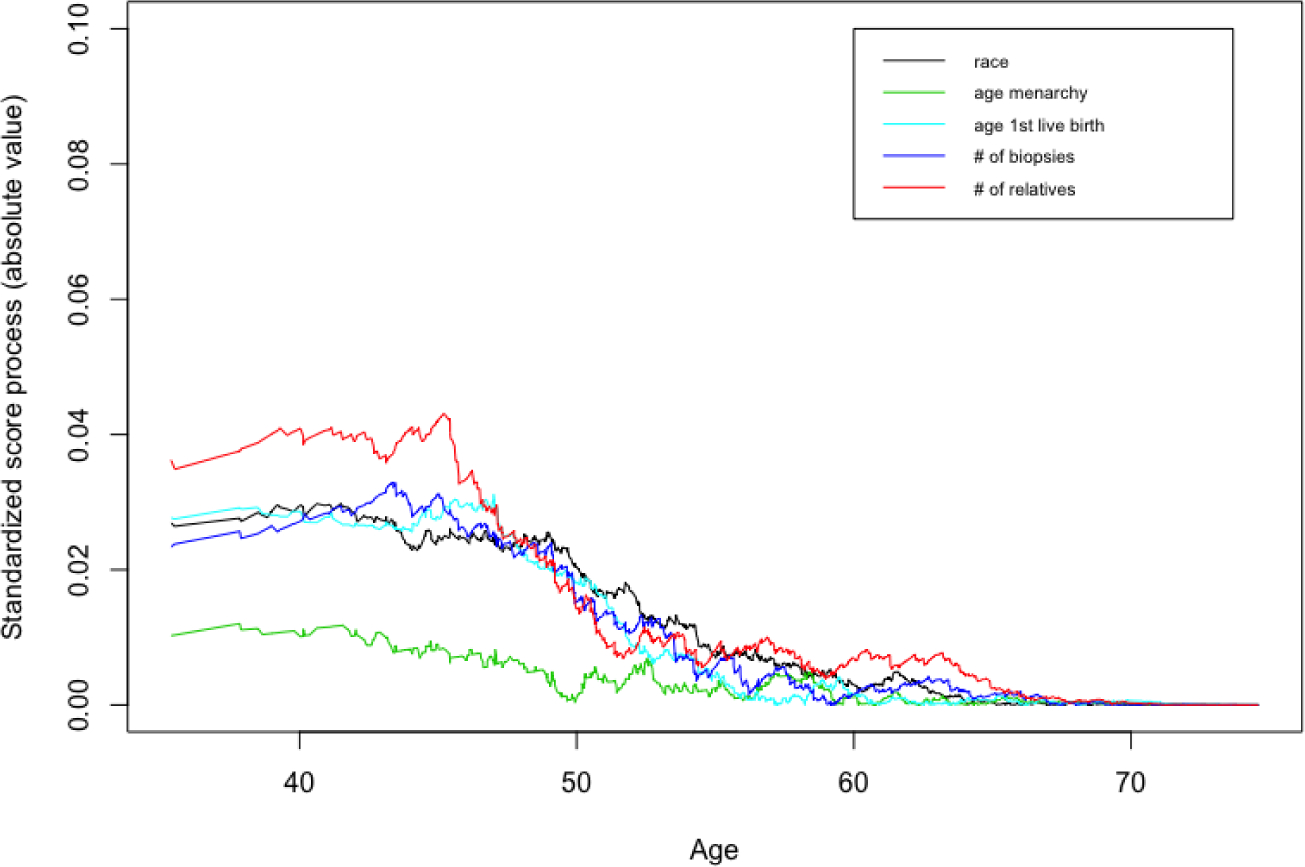
Model checking: proportional MRL model

Fig. 4.

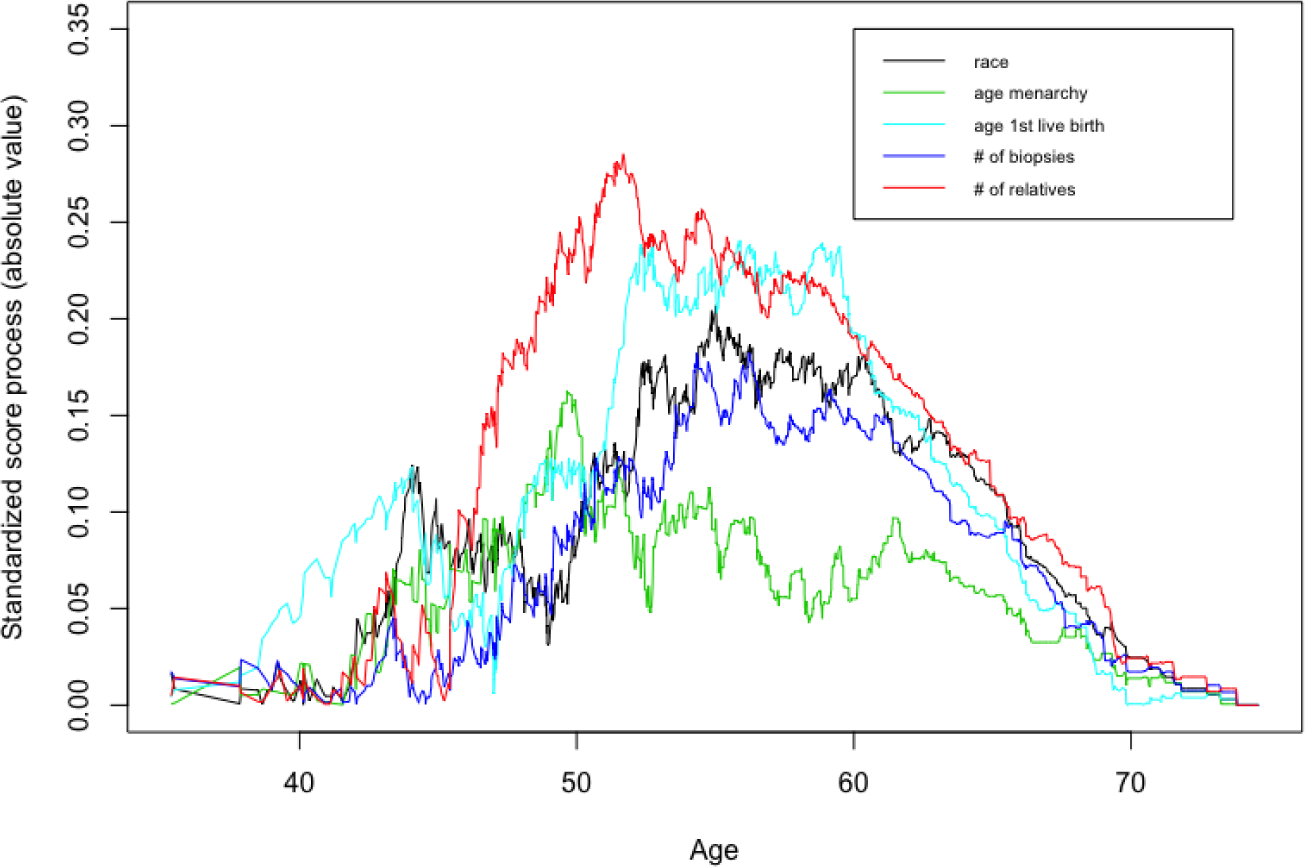
Model checking: additive MRL model

Although we do not study asymptotic properties of these model diagnostic measures for the generalized MRL models in this paper, we evaluated their empirical performance using simulations. Specifically, when the true model was proportional MRL model with sample size of 5000, β value of (0.2,0.2), and 80% censoring proportion, the proportions of numerical measure $S={\text{sup}}_t\Vert U(\widehat{\beta },t)\Vert$ indicating the correct model were 97.4%, 93.0%, and 97.8% under the full-cohort, CC, and NCC designs, respectively. When the true model was additive MRL model with the same sample size, effect size, and censoring proportion, the proportions of numerical measure $S={\text{sup}}_t\Vert U(\widehat{\beta },t)\Vert$ indicating the additive MRL model were 52.6%, 46.0%, and 63.6% under the full-cohort, CC, and NCC designs, respectively. We observed that the performance of the numerical measure was dependent on sample size, censoring rate, and effect size.

5. Discussion

In this manuscript, we developed unified inference procedures for the generalized MRL models under CC and NCC designs. The proposed models and inference procedures expand the analytical toolbox for these commonly used within-cohort sampling designs. In addition, we presented some model diagnostic and selection tools for the MRL models in full-cohort, CC, and NCC studies. Our numerical results support the use of the procedures, but the theoretical properties of which warrant further investigation.

The SEs of the proposed estimators were estimated using the bootstrapping method for CC data and the perturbation resampling approach for NCC data. Note that the perturbation approach requires the generation of n² random realization matrix and subsequent matrix calculations, and it does tend to be computationally heavier comparing to the bootstrap method.

Both CC and NCC designs have cost-saving benefits as compared to the full-cohort design. In simulation studies and the real data example, we found estimators performed consistently across the three study designs when the data structure supported the application of MRL modeling. Based on the inverse probability weighting approach, other cohort sampling designs including counter-matching design and quota-matching design can be considered as well. Moreover, the generalized MRL models with time-varying coefficients under full cohort can also be extended to CC and NCC designs in future research.

In practice, left truncation may occur in epidemiological cohort studies. To incorporate the left truncation, controls need to be drawn from an adjusted risk set defined as $R(t)=\left\{i:L_i<t\le {\tilde{T}}_i\right\}$, where L_i denotes the left-truncation time for subject i. Besides, it is not rare to see that some patients may have relative longer survival time comparing to others in a cohort. If only few subjects have long survival time, the results may be biased and the restricted MRL should be considered.

Remark: An R package gmrl is available at https://github.com/pengjin0105/gmrl

Appendix

Simulation study

We conducted numerical simulations to compare the IPCW method and the QPS estimator under the full cohort of 1000 subjects when censoring rates were approximately 10%, 30% and 80%. A total of 500 simulations were conducted for both the proportional and additive MRL models. We reported the bias, the standard deviation (SD) of the estimates, the average of estimated standard error (SE) and the coverage rate (CP) of 95% Wald-type confidence intervals (see results in Table 6). The SEs of the estimates were calculated through standard bootstrap method. Based on the simulation results, the two estimators had similar performance when censoring probability was low. The biases were all small and the means of estimated SEs were close to the empirical SDs of the parameter estimators. The 95% Wald-type confidence intervals had proper coverage rate. However, when the censoring rate was 80%, the IPCW performance dropped and underestimated SEs, which led to low coverage probabilities.

Table 6.

Comparison between IPCW estimator and QPS estimator

censoring rate		IPCW estimator†				QPS estimator‡
		β = (0, 0)		β = (0.2, 0.2)		β = (0, 0)		β = (0.2, 0.2)
g(t) =exp(t)
0.1	Bias	0.000	−0.006	0.000	−0.004	0.000	0.003	0.000	0.002
	SI)	0.038	0.065	0.032	0.049	0.039	0.065	0.033	0.056
	SE	0.037	0.065	0.030	0.051	0.038	0.066	0.032	0.056
	CP	94.0	94.6	92.7	94.8	94.2	96.2	94.2	95.5
0.3	Bias	−0.003	−0.004	−0.001	−0.002	0.001	−0.004	0.001	−0.003
	SD	0.047	0.078	0.037	0.059	0.043	0.075	0.036	0.063
	SE	0.046	0.080	0.035	0.060	0.042	0.073	0.036	0.062
	CP	94.4	94.6	93.7	93.9	94.2	94.1	95.1	94.6
0.8	Bias	0.001	0.004	0.006	0.005	−0.001	−0.001	0.001	−0.002
	SD	0.273	0.459	0.139	0.237	0.071	0.129	0.057	0.105
	SE	0.245	0.373	0.138	0.225	0.073	0.127	0.059	0.103
	CP	86.2	86.0	92.6	93.4	95.5	94.2	95.3	95.4
g(t) = t
0.1	Bias	0.000	−0.002	−0.001	−0.004	0.000	0.002	0.004	0.007
	SD	0.013	0.022	0.024	0.044	0.020	0.034	0.030	0.050
	SE	0.013	0.022	0.023	0.043	0.020	0.034	0.029	0.051
	CP	94.0	94.8	94.6	93.0	93.9	96.1	94.0	95.6
0.3	Bias	−0.001	−0.001	−0.004	−0.006	0.001	−0.002	0.001	−0.002
	SI)	0.016	0.028	0.030	0.057	0.024	0.042	0.034	0.060
	SE	0.016	0.028	0.029	0.057	0.024	0.042	0.034	0.058
	CP	94.6	94.6	93.6	93.8	94.4	94.3	94.3	94.1
0.8	Bias	0.000	0.001	−0.098	−0.091	0.001	−0.002	0.010	0.006
	SD	0.106	0.184	0.139	0.222	0.059	0.102	0.094	0.158
	SE	0.091	0.142	0.116	0.179	0.058	0.101	0.084	0.146
	CP	84.8	84.8	78.8	85.4	94.3	94.9	92.8	93.8

SD: sample standard deviation; SE: mean of estimated standard error;

CP: empirical coverage probability of 95% confidence interval;

^†Inverse probability censoring weighted estimator

^‡Quasi-partial score estimator

Regularity conditions

Let $u_{\tilde{\mathit{Z}}}(t;\beta )$, $u_{\breve{\mathit{Z}}}(t;\beta )$ and $u_{\overline{\mathit{Z}}}(t)$ be the limits of $\tilde{\mathit{Z}}(t;\beta )$, $\breve{\mathit{Z}}(t;\beta )$ and $\overline{\mathit{Z}}(t;\beta )$, respectively. We assume the following regularity conditions:

• (C1) sup supp(F) ≤ sup supp(G), where F(·) and G(·) are the distribution functions of T and C, respectively;

• (C2) Z is bounded;

• (C3) m_*(t) is continuously differentiable on [0,τ];

• (C4) $A={\int }_0^{\tau }E\left[\left(\mathit{Z}-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right){\left(\mathit{Z}-u_{\breve{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right)}^{\prime }(\dot{g}\left\{m_{*}(t)+{\beta }_{*}^{\prime }\mathit{Z}\right\}dN(t)-Y(t)d\dot{g}\left\{m_{*}(t)+{\beta }_{*}^{\prime }\mathit{Z}\right\})\right]$ is nonsingular;

Proof of Theorem 1(i)

First, we want to establish the consistency of the estimators ${\widehat{m}}_0(t)$ and $\widehat{\beta }$. Condition (C3) implies that m₀(t) is of bounded variation on [0, τ]. Define $\mathcal{B}=\left\{\beta :\Vert \beta -{\beta }_{*}\Vert \le ϵ\right\}$ for any ϵ > 0 and we have $E\left(w_i\mid \mathcal{F}\right)=1$. By the strong law of large numbers and the fact that E{w_idM_i(t)} = 0, for large n, t ∈ [0, τ], $\beta \in \mathcal{B}$, and sufficiently large θ,

$$\frac{1}{n}\sum _{i=1}^n{w}_i\left[d{N}_i(t)-Y_i(t)\frac{dg\left\{m_0(t)+\theta +{\beta }^{\prime }{\mathit{Z}}_i\right\}+dt}{g\left\{m_0(t)+\theta +{\beta }^{\prime }{\mathit{Z}}_i\right\}}\right]<0,$$ (11)

$$\frac{1}{n}\sum _{i=1}^n{w}_i\left[d{N}_i(t)-Y_i(t)\frac{dg\left\{m_0(t)-\theta +{\beta }^{\prime }{\mathit{Z}}_i\right\}+dt}{g\left\{m_0(t)-\theta +{\beta }^{\prime }{\mathit{Z}}_i\right\}}\right]>0.$$ (12)

By (11), (12), and the monotonicity and continuity of g function, for any t ∈ [0, τ] and $\beta \in \mathcal{B}$, there exists a unique ${\widehat{m}}_0(t;\beta )$ that satisfies

$$\frac{1}{n}\sum _{i=1}^n{w}_i\left[d{N}_i(t)-Y_i(t)\frac{dg\left\{{\widehat{m}}_0(t;\beta )+{\beta }^{\prime }{\mathit{Z}}_i\right\}+dt}{g\left\{{\widehat{m}}_0(t;\beta )+{\beta }^{\prime }{\mathit{Z}}_i\right\}}\right]=0.$$ (13)

Note that (11) and (12) hold for any θ > 0 when and only when β = β_*. Then we have that ${\widehat{m}}_0(t;\beta )$ converges to m₀(t; β) uniformly in t ∈ [0, τ] and β in a compact set which contains the true parameter β_*, and m₀(t; β_*) = m_*(t). Thus, to prove the existence and uniqueness of $\widehat{\beta }$ and ${\widehat{m}}_0(t)$, it suffices to show that there exists a unique solution to U(β) = 0. Take derivative of (13) with respect to β, we have

$$\frac{d{\widehat{m}}_0(t)}{d\beta }\frac{{\sum }_{i=1}^n{w}_i\left[\dot{g}\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-Y_i(t)d\dot{g}\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}\right]}{{\sum }_{i=1}^n{w}_i{Y}_i(t)\dot{g}\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}}-d\left(\frac{d{\widehat{m}}_0(t)}{d\beta }\right)=-\frac{{\sum }_{i=1}^n{w}_i{\mathit{Z}}_i\left[\dot{g}\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-Y_i(t)d\dot{g}\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}\right]}{{\sum }_{i=1}^n{w}_i{Y}_i(t)\dot{g}\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}},$$

which is a first-order linear ordinary differential equation about $d{\widehat{m}}_0(t)/d\beta$. The solution is

$$\frac{d{\widehat{m}}_0(t)}{d\beta }=\frac{d{\widehat{m}}_0(t;\beta )}{d\beta }=-\frac{1}{K(t;\beta )}{\int }_t^{\tau }K(u;\beta )Q(u;\beta )\equiv -\breve{\mathit{Z}}(t;\beta ),$$

where

$$K(t;\beta )=\text{exp}\left\{-{\int }_0^t\frac{{\sum }_{i=1}^n{w}_i\left[\dot{g}\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-Y_i(t)d\dot{g}\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}\right]}{{\sum }_{i=1}^n{w}_i{Y}_i(t)\dot{g}\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}}\right\},$$

$$Q(t;\beta )=\frac{{\sum }_{i=1}^n{w}_i{\mathit{Z}}_i\left[\dot{g}\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-Y_i(t)d\dot{g}\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}\right]}{{\sum }_{i=1}^n{w}_i{Y}_i(t)\dot{g}\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}}.$$

Let $\widehat{A}\left({\beta }_{*}\right)\doteq dU(\beta )/{d\beta |}_{\beta =\beta }$. We have

$$\begin{gathered} \widehat{A}\left({\beta }_{*}\right)\doteq \frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }{w}_i\left[\left.{\mathit{Z}}_i-\overline{\mathit{Z}}\left(t;{\beta }_{*}\right)\right]{\left[{\mathit{Z}}_i-\breve{\mathit{Z}}\left(t;{\beta }_{*}\right)\right]}^{\prime }\left[\dot{g}\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)\right.-Y_i(t)d\dot{g}\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}\right] \\ =\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }{w}_i\left[\left.{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]{\left[{\mathit{Z}}_i-u_{\breve{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]}^{\prime }\left[\dot{g}\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)\right.-Y_i(t)d\dot{g}\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}\right]\text{+}{o}_p\text{(1)} \\ =A+o_p\text{(1)} \end{gathered}$$

Thus, $\widehat{A}\left({\beta }_{*}\right)$ converges in probability to a nonrandom A. It is easy to check that U(β_*) → 0 almost surely, and A is nonsingular by (C4). The convergence of $\widehat{A}\left({\beta }_{*}\right)$ and the continuity of A(β) imply that we can find a small neighborhood of β_* in which $\widehat{A}\left({\beta }_{*}\right)$ is nonsingular when n is large enough. Therefore, it follows from the inverse function theorem that within a small neighborhood of β_*, there exists a unique solution $\widehat{\beta }$ to U(β) = 0 for sufficiently large n. Thus, there exists unique estimators $\widehat{\beta }$ and $\widehat{m}(t)$. Since $\widehat{\beta }$ is strongly consistent to β_*, then it follows the uniform convergence of ${\widehat{m}}_0(t;\beta )$ to m₀(t; β) that ${\widehat{m}}_0(t)\doteq {\widehat{m}}_0(t;\widehat{\beta })\to m_0\left(t;{\beta }_{*}\right)=m_{*}(t)$ almost surely in [0, τ].

Proof of Theorem 1(ii)

In this section, we first prove the theorem 1(ii) under the CC design, then prove the theorem under the NCC design following the proof from Lu and Liu (2012). We know from equation (8) that

$$\frac{1}{n}\sum _{i=1}^n{w}_i\left[g\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-Y_i(t)d\left[g\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}+t\right]\right]=\frac{1}{n}\sum _{i=1}^n{w}_{i}g\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_{i}d{M}_i(t)\right\}$$

$$\frac{1}{n}\sum _{i=1}^n{w}_i\left[g\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-Y_i(t)d\left[g\left\{{\widehat{m}}_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}+t\right]\right]=0$$

Subtract the above two equations and use Taylor expansion, we have,

$$\frac{1}{n}\sum _{i=1}^n{w}_i\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}\left[{\widehat{m}}_0(t)-m_0(t)\right]d{N}_i(t)-\frac{1}{n}\sum _{i=1}^n{w}_i{Y}_i(t)d\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}\left[{\widehat{m}}_0(t)-m_0(t)\right]-\frac{1}{n}\sum _{i=1}^n{w}_i{Y}_i(t)d\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}\left[d{\widehat{m}}_0(t)-d{m}_0(t)\right]=-\frac{1}{n}\sum _{i=1}^n{w}_{i}g\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{M}_i(t)$$

Hence, following the first-order ordinary differential equation,

$$\left[{\widehat{m}}_0(t)-m_0(t)\right]\frac{{\sum }_{i=1}^n{w}_i\left[\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-Y_i(t)d\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}\right]}{{\sum }_{i=1}^n{w}_i{Y}_i(t)\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}}-\left[d{\widehat{m}}_0(t)-d{m}_0(t)\right]=-\frac{{\sum }_{i=1}^n{w}_{i}g\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{M}_i(t)}{{\sum }_{i=1}^n{w}_i{Y}_i(t)\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}},$$

$${\widehat{m}}_0(t)-m_0(t)=-\frac{1}{K(t;\beta )}{\int }_t^{\tau }K(u;\beta )\frac{{\sum }_{i=1}^n{w}_{i}g\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}d{M}_i(t)}{{\sum }_{i=1}^n{w}_i{Y}_i(t)\dot{g}\left\{m_0(t)+{\beta }^{\prime }{\mathit{Z}}_i\right\}}.$$

Let $U\left({\beta }_{*}\right)\doteq U\left({\beta }_{*},{\widehat{m}}_0\left(t;{\beta }_{*}\right)\right)$ and we have

$$U\left({\beta }_{*},m_{*}(t)\right)=\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }{w}_i{\mathit{Z}}_i[g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-Y_i(t)dg\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}-Y_i(t)dt].$$

By using Taylor expansion again in $U\left({\beta }_{*},{\widehat{m}}_0\left(t;{\beta }_{*}\right)\right)-U\left({\beta }_{*},m_{*}(\cdot )\right)$, we have

$$\begin{gathered} U\left({\beta }_{*},{\widehat{m}}_0\left(t;{\beta }_{*}\right)\right)-U\left({\beta }_{*},m_{*}(\cdot )\right) \\ =\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }{w}_i{\mathit{Z}}_i\left[{\widehat{m}}_0(t)-m_0(t)\right]\dot{g}\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-w_i{\mathit{Z}}_i{Y}_i(t)\left[{\widehat{m}}_0(t)-m_0(t)\right]d\dot{g}\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}-w_i{\mathit{Z}}_i{Y}_i(t)\left[d{\widehat{m}}_0(t)-d{m}_0(t)\right]\dot{g}\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\} \\ =\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }{w}_i\left[{\mathit{Z}}_i-\mathit{Z}\left(t;{\beta }_{*}\right)\right]\left[{\widehat{m}}_0(t)-m_0(t)\right][\dot{g}\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{N}_i(t)-Y_i(t)d\dot{g}\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}]-w_i\overline{\mathit{Z}}\left(t;{\beta }_{*}\right)g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i(t) \\ =-\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }{w}_i\left[\tilde{\mathit{Z}}\left(t;{\beta }_{*}\right)+\mathit{Z}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i(t). \end{gathered}$$

Thus,

$$\begin{gathered} \sqrt{n}U\left({\beta }_{*}\right)=\sqrt{n}U\left({\beta }_{*},{\widehat{m}}_0\left(t;{\beta }_{*}\right)\right) \\ =\sqrt{n}U\left({\beta }_{*},m_{*}\right)+\sqrt{n}\left[U\left({\beta }_{*},{\widehat{m}}_0\left(t;{\beta }_{*}\right)\right)-U\left({\beta }_{*},m_{*}\right)\right] \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{\tau }{w}_i\left[{\mathit{Z}}_i-\overline{\mathit{Z}}\left(t;{\beta }_{*}\right)-\tilde{\mathit{Z}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i\left(t;{\beta }_{*},m_{*}\right) \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{\tau }{w}_i\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i\left(t;{\beta }_{*},m_{*}\right)+o_p\left(1\right) \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{\tau }\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i\left(t;{\beta }_{*},m_{*}\right)+\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{\tau }\left(w_i-1\right)\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i\left(t;{\beta }_{*},m_{*}\right)+o_p(1) \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{\tau }\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i\left(t;{\beta }_{*},m_{*}\right)-\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{\tau }\left(1-{\delta }_i\right)\left(1-{\gamma }_i/p_{0i}\right)\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i\left(t;{\beta }_{*},m_{*}\right)+o_p(1). \end{gathered}$$

As we defined in our manuscript, let ${\mathcal{G}}_i$ be the σ-field generated by $\left\{{\tilde{T}}_i,{\delta }_i,{\mathit{Z}}_i,i=1,\dots ,n\right\}$ and ${\mathcal{F}}_i$ be the σ-field generated by $\left\{{\tilde{T}}_i,{\delta }_i,i=1,\dots ,n\right\}$. We denote

$${\eta }_i=\left(1-{\delta }_i\right){\int }_0^{\tau }\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i\left(t;{\beta }_{*},m_{*}\right).$$

It is evident that $E\left(1-{\gamma }_i/p_{0i}\mid {\mathcal{F}}_i\right)=0$ and $E\left\{{\eta }_i\left(1-{\gamma }_i/p_{0i}\mid {\mathcal{F}}_i\right)\right\}=E\left\{{\eta }_{i}E(1-{\gamma }_i/p_{0i}\mid {\mathcal{F}}_i)\right\}=0$. Following the proof in Lu and Tsiatis (2006), $\mathit{\text{var}}\left\{{\eta }_i\left(1-{\gamma }_i/p_{0i}\right)\right\}=E\left\{{\eta }_i^{\otimes 2}\left(1-p_{0i}\right)/p_{0i}\right\}-E{\left[{\eta }_i\left(1-p_{0i}\right)/p_{0i}\right]}^{\otimes 2}={\Sigma }_2$. Condition on ${\mathcal{F}}_i,\left\{{\eta }_i\left(1-{\gamma }_i/p_{0i}\right),i=1,\dots ,n\right\}$, {η_i(1 – γ_i/p_0i), i = 1, …, n} and the first term of $\sqrt{n}U\left({\beta }_{*}\right)$ are uncorrelated. Therefore, $\sqrt{n}U\left({\beta }_{*}\right)$ is asymptotically normal with mean zero and variance-covariance Σ = Σ₁ + Σ₂. By Taylor expansion and consistency of $\widehat{\beta }$, it follows

$$\begin{array}{l}\sqrt{n}\left(\widehat{\beta }-{\beta }_{*}\right)\\ =-A^{-1}\sqrt{n}U\left({\beta }_{*}\right)+o_p(1)\\ =-A^{-1}\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{\tau }{w}_i\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i\left(t;{\beta }_{*},m_{*}\right)+o_p(1),\end{array}$$

thus $\sqrt{n}\left(\widehat{\beta }-{\beta }_{*}\right)\to N\left\{A^{-1}\Sigma {\left(A^{-1}\right)}^{\prime }\right\}$.

Under the nested case-control design, the asymptotic distribution of $\widehat{\beta }$ is more difficult to derive because the NCC sampling scheme is a dynamic process. The probability of being selected as a control is neither a constant not independent. Thus, we consider the idea of central limit theory for asymptotically negatively dependent random variables (Zhang, 2000), which has been used in the proof of Lu and Liu (2012). Based on the following asymptotical representation, we have

$$U\left({\beta }_{*}\right)=\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }{w}_i\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i\left(t;{\beta }_{*},m_{*}\right)+o_p(1)\equiv U_1\left({\beta }_{*}\right)+U_2\left({\beta }_{*}\right)+o_p\left(\frac{1}{\sqrt{n}}\right).$$

By martingale central limit theorem, $\sqrt{n}{U}_1\left({\beta }_{*}\right)=\frac{1}{\sqrt{n}}{\sum }_{i=1}^n{\int }_0^{\tau }{w}_i\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-\left.u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i\left(t;{\beta }_{*},m_{*}\right)\to N\left(0,{\Sigma }_1\right)\right.$ as n → ∞. Since $E\left(w_i-1\mid {\mathcal{F}}_i\right)=0$, it is evident that U₁(β_*) and U₂(β_*) are uncorrelated. However because of the NCC sampling scheme, w_i and w_j (i ≠ j) are correlated even after conditioning on $\mathcal{F}$. Since ${\left(w_i-1\right)}^2=\left(1-{\delta }_i\right)\left({\gamma }_i-p_{0i}^2\right)/p_{0i}^2$, then $E\left\{{\left(w_i-1\right)}^2\mid \mathcal{F}\right\}=\left(1-{\delta }_i\right)\left(1-p_{0i}\right)/p_{0i}$. Thus, the conditional variance of $\sqrt{n}{U}_2\left({\beta }_{*}\right)$ can be written as

$$\frac{1}{n}\sum _{i=1}^n\frac{1-p_{0i}}{p_{0i}}\left(1-{\delta }_i\right){\left[{\int }_0^{\tau }\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i(t)\right]}^{\otimes 2}+\frac{1}{n}\sum _{i\ne j}E\left\{\left(\frac{{\gamma }_i}{p_{0i}}-1\right)\left(\frac{{\gamma }_j}{p_{0j}}-1\right)\mid \mathcal{F}\right\}*\left(1-{\delta }_i\right)\left(1-{\delta }_j\right){\int }_0^{\tau }\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i(t){\left[{\int }_0^{\tau }\left[{\mathit{Z}}_j-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_j\right\}d{M}_j(t)\right]}^{\prime }.$$

According to Samuelsen (1997), for $i\ne j,\mathit{\text{Cov}}\left({\gamma }_i,{\gamma }_j\mid \mathcal{F}\right)={\rho }_{ij}\left(1-p_{0i}\right)\left(1-p_{0j}\right)$, where ${\rho }_{ij}=-\frac{m}{n}{\int }_0^{\mathit{\text{min}}\left({\tilde{T}}_i,{\tilde{T}}_j\right)}\frac{{\overline{g}}_1(t)}{\overline{y}(t)}d{m}_{*}(t)+\frac{{\overline{g}}_2(t)}{\overline{y}(t)}dt+O_p\left(n^{-2}\right)$. Thus, with some algebra, the $\text{Var}\left\{\sqrt{n}{U}_2\left({\beta }_{*}\right)\mid \mathcal{F}\right\}$ can be written as

$$\frac{1}{n}\sum _{i=1}^n\left(1-{\delta }_i\right)\frac{1-p_{0i}}{p_{0i}}{\left[{\int }_0^{\tau }\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i(t)\right]}^{\otimes 2}-m{\int }_0^{\tau }[\frac{1}{n}\sum _{i=1}^n{Y}_i(t)\frac{1-p_{0i}}{p_{0i}}\left(1-{\delta }_i\right){\int }_0^{\tau }\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]{g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i(t)]}^{\otimes 2}\left(\frac{{\overline{g}}_1(t)}{\overline{y}(t)}d{m}_{*}(t)+\frac{{\overline{g}}_2(t)}{\overline{y}(t)}dt\right)+o_p(1),$$

where ${\overline{g}}_1(t)={\sum }_{j=1}^n\frac{Y_j(t)\dot{g}\left\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{\mathit{Z}}_j\right\}}{g\left\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{\mathit{Z}}_j\right\}}$, ${\overline{g}}_2(t)={\sum }_{j=1}^n\frac{Y_j(t)}{g\left\{{\widehat{m}}_0(t)+{\widehat{\beta }}^{\prime }{\mathit{Z}}_j\right\}},\overline{y}(t)$. According to strong law of large numbers, we have where

$$\begin{gathered} {\Sigma }_2\equiv {\mathit{\text{lim}}}_{n\to \infty }\mathit{\text{Var}}\left\{\sqrt{n}{U}_2\left({\beta }_{*}\right)\mid \mathcal{F}\right\} \\ =E\left[\frac{1-s_0}{s_0}(1-\delta ){\left[\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}d{M}_i(t)\right]}^{\otimes 2}\right]-m{\int }_0^{\tau }(E[Y(t)(1-\delta )\frac{1-s_0}{s_0}{{\int }_0^{\tau }\left[{\mathit{Z}}_i-u_{\overline{\mathit{Z}}}\left(t;{\beta }_{*}\right)-u_{\tilde{\mathit{Z}}}\left(t;{\beta }_{*}\right)\right]g\left\{m_{*}(t)+{\beta }_{*}^{\prime }{\mathit{Z}}_i\right\}dM(t)])}^{\otimes 2}\left(\frac{{\overline{g}}_1(t)}{\overline{y}(t)}d{m}_{*}(t)+\frac{{\overline{g}}_2(t)}{\overline{y}(t)}dt\right), \end{gathered}$$

where

$$s_{0i}=li{m}_{n\to \infty }{p}_{0i}=1-\text{exp}\left\{-m{\int }_0^{{\tilde{T}}_i}\frac{{\overline{g}}_1(t)}{\overline{y}(t)}d{m}_0(t)+\frac{{\overline{g}}_2(t)}{\overline{y}(t)}dt\right\}$$

Thus, by the central limit theory for asymptotically negatively dependent random variables (Zhang, 2000), we have $\sqrt{n}{U}_2\left({\beta }_{*}\right)\to N\left(0,{\Sigma }_2\right)$ as n → ∞, and

$$\sqrt{n}U\left({\beta }_{*}\right)\to N\left(0,{\Sigma }_1+{\Sigma }_2\right),$$

in distribution as n → ∞. It is easy to see that Σ₁ + Σ₂ = Σ. Follow by Taylor expansion and consistency of $\widehat{\beta }$, we have $\sqrt{n}\left(\widehat{\beta }-{\beta }_{*}\right)\to N\left\{A^{-1}\Sigma {\left(A^{-1}\right)}^{\prime }\right\}$.