A Systems Biology Approach to Discovering Pathway Signaling Dysregulation in Metastasis

Abstract

Total metastatic burden is the primary cause of death for many cancer patients. While the process of metastasis has been studied widely, much remains to be understood. Moreover, few agents have been developed that specifically target the major steps of the metastatic cascade. Many individual genes and pathways have been implicated in metastasis but a holistic view of how these interact and cooperate to regulate and execute the process remains somewhat rudimentary. It is unclear whether all of the signaling features that regulate and execute metastasis are yet fully understood. Novel features of a complex system such as metastasis can often be discovered by taking a systems-based approach. We introduce the concepts of systems modeling and define some of the central challenges facing the application of a multidisciplinary systems-based approach to understanding metastasis and finding actionable targets therein. These challenges include appreciating the unique properties of the high dimensional omics data often used for modeling, limitations in knowledge of the system (metastasis), tumor heterogeneity and sampling bias, and some of the issues key to understanding critical features of molecular signaling in the context of metastasis. We also provide a brief introduction to integrative modeling that focuses on both the nodes and edges of molecular signaling networks. Finally, we offer some observations on future directions as they relate to developing a systems-based model of the metastatic cascade.

Introduction

A key goal for many research programs is to identify a gene, pathway, or signaling feature that regulates a critical biological function in a manner that is actionable either as a predictive and/or prognostic biomarker, and/or as a therapeutic target. Increasingly, these signaling features are extracted from high dimensional omic datasets (genome, transcriptome, proteome, metabolome and their respective subomes including the epigenome and kinome). These high dimensional omic data sets have unique properties that often differ from other high dimensional data spaces such as those in many large epidemiologic studies [1]. Moreover, most omic studies produce massively parallel data that represent only a snap-shot of the ome as it is represented at the time of sample collection, yet signaling pathways have critical dynamical sequencing features. The ability to detect this temporal sequencing may depend both on whether the key steps must be activated sequentially or if these can be acquired stochastically but retained (perhaps epigenetically), and/or if all steps are concurrently represented (and so can be detected) in the various cells present in heterogeneous tissue samples (Figure 1). Omic datasets are often obtained from heterogeneous bulk tissues, where cellular, molecular, and genetic heterogeneity, often compounded by sampling bias, can complicate the ability to identify correctly the molecular signaling associated with a complex biological phenotype of interest.

Figure 1:

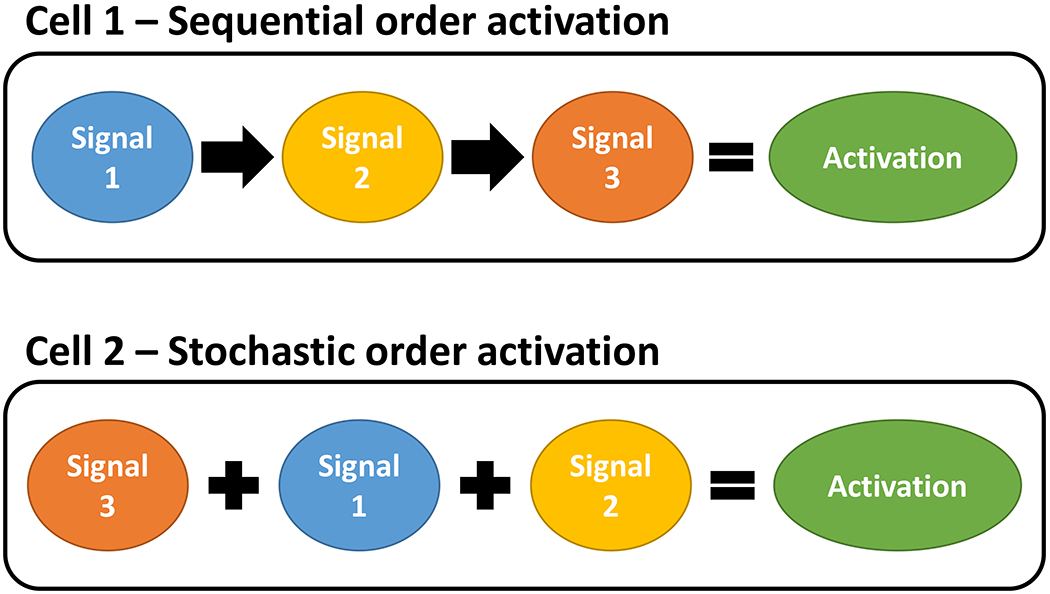
Sequential versus stochastic acquisition of the features necessary for a function to be executed successfully. Features could represent signaling events necessary to regulate and execute a function, such as a specific node or edge in a signaling network. Alternatively, features could represent a series of independent functions needed to execute the entire system, for example, invasion or extravasation.

Since metastatic dissemination and overall tumor burden are major contributors to cancer morbidity and death, the ability to metastasize is one such complex biological phenotype that continues to be studied extensively. Many genes and pathways have been implicated in affecting key features of the metastatic cascade (see [2–4] for reviews). Much is understood about the general process of metastasis, which can be described as comprising the steps of invasion, extravasation, intravasation, and colonization. However, each of these steps is a complex process, affected by activities or signals arising both within the cancer cell (intrinsic) and within the microenvironment (extrinsic). Successful metastatic dissemination requires coordination of the molecular actions underlying each of these steps in a manner that has the appearance of exhibiting some temporal sequencing. Despite what is known currently, knowledge of the precise mechanisms that enable cells to seed distant sites remains incomplete [5].

From a molecular signaling perspective, complex biological processes like metastasis are among the more difficult to study. The search space for the most functionally relevant genes can be large. In different cellular contexts some key genes may be more or less important for controlling the same outcome, or affected by different regulatory or control actions. For example, the relative importance of the receptors for estrogens (ESR1; ER) and androgens (AR) as drivers of metastasis is different in breast compared with prostate cancers. ER activation dominates the regulation of cell proliferation and key features of metastasis in ER-positive (ER+) breast cancers but is less important in AR-positive prostate cancers that are driven by AR activation. The reverse is true for many prostate cancers. Nonetheless, the basic concepts of the primary steps and key features of metastasis are the same in breast and prostate cancer and both cancers may share key endocrine-regulated features that are regulated by ER and AR, respectively.

In this review we will explore, at a relatively high level, some of the central aspects of molecular signaling from a systems perspective and the challenges to identifying actionable targets, with a focus on the metastatic cascade. We use the term molecular signaling to represent the molecular interactions in a cell that affect its behavior/phenotype. Such interactions are multiscale in nature and include protein-protein (PPI; proteome), protein-DNA (PDI; crosses the genome and proteome scales), and substrate-enzyme-product interactions (SEP; crosses the metabolome and proteome scales) in a chain of individual reactions that comprise a complex multiscale network. For metastasis, this network almost certainly includes PPIs, PDIs, and SEP interactions, crossing the scales of genome (and epigenome), transcriptome, proteome, and metabolome [6].

Below, we introduce systems and a view of metastasis from the perspective of a system and key challenges to understanding the complexities of the metastatic process. We first describe some of the challenges and opportunities in therapeutic targeting of metastasis and then introduce the modular structure of systems models. Since understanding the critical molecular features that explain module function mechanistically is key to understanding system function, we then introduce some of the properties of the omic datasets often used to discover these key features. Omic data are often obtained from heterogeneous tissues in animal and human subjects. Sampling bias and heterogeneity are often associated with these samples independent of the goals of the study, these are discussed briefly prior to giving a more detailed discussion of some of the key challenges associated with specifically modeling metastasis. We then follow by discussing some of the properties of molecular signaling that drive these essential components, the intrinsic and extrinsic nature of the signaling control and execution features, and the properties and utility of canonical pathways as guides to discovering cell context specific features. Finally, we introduce the emerging concept of modeling where the focus is less on discovering the nodes (such as individual genes, proteins, metabolites) of the network and more on discovering the edges that link these nodes.

Since it is not possible to cover all approaches, tools and workflows, the focus here is to introduce some of the more difficult challenges. The primary goal is to raise awareness of these challenges and their associated limitations, rather than to provide an exhaustive overview with detailed insights and potential solutions. Our approach here is multidisciplinary. Since some readers may not be experts in all of the fields, in several areas we have chosen to include a relative high proportion of citations to reviews, rather than providing an extensive listing of the primary papers that are cited within these reviews. Consequently, this review has its own limitations.

Targeting metastasis

Identifying molecular targets and developing drugs that can block the process of metastasis has been an active area of research for decades. Nonetheless, few, if any, true antimetastasis drugs have made it into routine clinical practice [3,4]. Cytotoxic and cytostatic drugs can eliminate or slow the results of the metastatic process and improve disease-free, progression-free, and overall survival in some patients with advanced cancer. However, these outcomes are less likely to reflect any specific effect on a step in the metastatic cascade than reflecting directly cytotoxic or cytostatic effects on cancer cells, whether in a primary tumor and/or its metastases. This observation is often overlooked in research where agents are claimed to specifically inhibit the process of metastasis in animal models while concurrently inhibiting the growth of the primary tumors. Such claims may be unwarranted, since drugs that kill or arrest cancer cells independent of their location will directly affect such endpoints as the number of metastases arising over time but can do so without any effect on the specifics of the metastatic cascade such as migration, invasion, or extravasation. While inhibiting growth at metastatic sites can be considered one step in the process, it is shared with the general feature of tumor growth that also occurs independent of the process of dissemination. While perhaps controversial, from a mechanistic perspective killing established metastases is often not considered as reflecting a purely antimetastasis activity. In contrast, blocking or reversing production of the premetastatic niche, and thereby preventing early cell survival at a distant site, would represent an antimetastasis action. Hence, a more easily interpreted outcome in such experiments would be a reduction in either the number of metastases, or the time to detection of metastases, by an agent that had no effect on tumor cell growth rate in the primary tumor or in any of its metastatic deposits. Such an intervention would be more likely to be considered as being truly antimetastatic than a generally cytotoxic antineoplastic drug. Of course, any drug that eliminated established metastatic deposits, even if it did not specifically target features of the metastatic cascade, could still produce major clinical benefit and be of great value.

Other challenges include the limitations inherent in both in vitro and in vivo models. In vitro models are widely used despite major limitations [7,8], particularly when 2D culture models are used as the primary or sole experimental models. 3D models [9] and those that can capture the physical forces related to early events in the metastatic cascade [10] generally offer more physiologically relevant tools but these remain less widely used. In vivo models often provide effective tools [3] but some experiments cannot be done in vivo because of technical and/or appropriate ethical constraints.

Perhaps not surprisingly, effectively and specifically targeting the process of metastasis has remained difficult, as clearly delineated in an excellent review by Steeg [4]. Indeed, skepticism that the process is at all targetable is evident among some academic and commercial investigators [4]. In addition to the limitations of in vitro and in vivo experimental models, the challenges of targeting metastasis specifically require an understanding of the processes that constitute the overall process, how these are integrated and regulated at the cellular and molecular levels, and how this knowledge can be leveraged to identify actionable and process-specific molecular targets and drugs. Obtaining this level of understanding likely requires a more systems-based [3] than reductionist approach. Clearly, both approaches can produce important insights. The critical mechanistic studies needed to validate or determine the functions of individual genes and their role(s) in the overall system require a largely reductionist approach. However, to identify these individual genes and to predict their relationships within the overall system generally requires a systems approach. Systems approaches also create an opportunity to identify key, actionable control points in a process, as has been proposed for studies of other complex problems in cancer research [6].

System structure

A key goal of systems modeling is to identify the critical control mechanisms that regulate system function. Often, these mechanisms represent candidates to target as a means to block system function. Models can be either mathematical (based primarily on stochastic differential equations and algorithms) using mostly low dimensional data, or computational (based primarily on machine learning approaches) using mostly high dimensional data [6]. Integrative modeling adaptively uses both approaches, as is most appropriate for the specific hypothesis and data available. Since the data modeled are often acquired from many different sources including molecular (multiple omic forms), tissue level (such as biopsies), and clinical (including patient characteristics; treatment and response outcomes measures), each of which represents a different scale, integrative systems models are multiscale.

Systems models of complex, dynamic, adaptive, and open systems are often modular in structure [6]. While some investigators define modules as either known or discovered signaling features, we define the modules by the physiological processes known to contribute to system function. For estrogen regulated signaling in breast cancer, we defined the initial structural modules as autophagy, cell death, metabolism, proliferation, and unfolded protein response (UPR) [11]. Each of these modules has underlying molecular signaling that both regulates and executes each module. Since regulation of the modular functions can be coordinated, integrated signaling is envisioned where some nodes, and perhaps also edges, are common to more than one module [11]. An example is BCL2, where free BCL2 can act in mitochondrial membranes to inhibit apoptosis (a node in the cell death module) but it is also available to sequester BECN1 and so affect the ability of BECN1 to regulate autophagy (a node in the autophagy module) [6].

Metastasis is an example of the complex, dynamic, adaptive and open nature of biological systems [6]. For example, the open nature of metastasis is evident from interactions with the external microenvironment, as occurs between the disseminated cancer cells and the metastatic niche, rather than metastasizing cells representing a closed system and so acting independent of extrinsic factors. Complexity, dynamism and adaptation are each evident at every step in the metastatic cascade. Unlike some biological systems, metastasis – and perhaps also the continuing accumulation of mutations in genetically unstable cancer cells – does not appear to be self-limiting. Whether the rate of dissemination increases or decreases over time is unclear and may vary among different patients with the same disease. Nonetheless, the general process of metastasis appears to continue until the ever increasing total body tumor burden can no longer be sustained and death of the host follows.

Functionally, metastasis can be reduced to the steps of local invasion, extravasation, intravasation, and distant colonization (cell survival at a distant but permissive site often referred to as the pre-metastatic niche) [12]. Thus, an initial model framework of the overall system (metastasis) could be constructed around these steps. Each step is treated as a general feature that can first be understood individually, and then pieced together to begin rebuilding the overall system. In this approach, there are two integrated levels of the system that are to be understood. Firstly, what are the properties (physiological processes) required to execute fully each step. Secondly, what are the multiscale molecular interactions that determine when these processes are regulated and integrated (control functions) and the overlapping multiscale interactions that then execute these processes (execution functions). Figure 2 provides a simplistic representation of how regulation and execution functions may be structured within a module. An ER-positive breast cancer cell is used as an example to illustrate how extrinsic (endocrine therapy) actions can affect intrinsic activities. Upstream regulatory activities (mostly reversible) control the execution of downstream activities (generally irreversible until the activity is completed). Downstream activities can appear to oscillate; for example, contractility likely oscillates in cycles of contraction and relaxation. The regulation (control) and extent of cell-cell adhesion, cell-matrix adhesion and matrix degradation, and cell contractility likely differ depending on the pattern of cancer cell invasion being performed such as collective cell migration, multicellular streaming, or single-cell migration [8]. A hierarchy of signaling events is implicit in this representation, where sensing and regulatory control activities (generally reversible) precede those actions that execute the modular function (generally irreversible). Since it is unlikely that each physiological process (module) and its control and execution signaling will be fully understood at the outset, the process of discovering components of each individual process, and how these may be integrated or cooperate within the overall system, will be iterative.

Figure 2:

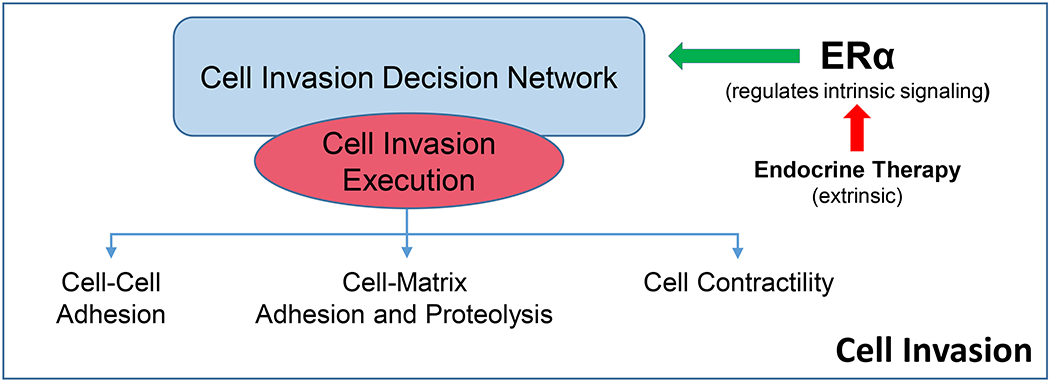
Simple representation of the relationship between the regulatory and executory activities of a process. Some level of hierarchical relationships is implied where most regulatory activities are upstream of most executory activities. The representation is not intended to exclude the potential for feedforward and feedback activities that may limit the process and/or induce oscillations in process execution.

Learning from mathematical models

In molecular systems biology, mathematical models are often developed to connect molecular regulatory networks to the cellular physiology that they regulate and execute. These models have been proven particularly helpful for revealing the basic principles of complex signalprocessing by molecular regulatory networks that would be difficult to discover heuristically. Understanding these principles allows us, for example, to predict a type of dynamic behavior or signal-response curve based on the topology of a reaction network. Reaction networks can exhibit complex internal regulatory activities such as positive or negative feedback loops for multiple stable steady states or oscillations [13,14]. Generally, mathematical models can accurately describe how the concentrations of chemical species (like intermediate metabolites) and/or the activities of genes and proteins (the enzymes that metabolize these intermediates) change in time and space within the cell or tissue. These changes are linked with corresponding qualitative and quantitative observations about the dynamic behavior of cells or populations in a variety of perturbed and unperturbed conditions. Mathematical models have been successfully developed to study cell cycle regulation [15–17], signaling in cancer cell lines [18–20], programmed cell death [21–23], stem cell differentiation [24,25], circadian rhythms [26–28], dynamic behavior of metabolic pathways [29,30], epithelial-to-mesenchymal plasticity [31], and even the entire molecular regulatory network of a bacterium [32,33].

Mathematical modeling can also help researchers to gain a deeper understanding of the metastatic process. One challenge to the accurate mathematical modeling of metastasis is that different aspects of the metastatic cascade and its molecular control are characterized in widely divergent details and many are yet to be experimentally characterized or discovered. Under these circumstances, mathematical modeling can be a particularly useful tool for testing incomplete hypotheses about the underlying molecular controls of the metastatic process. The limitations in data availability and quality, and uncertainties in mechanistic details, can be countered and managed by using hybrid mathematical approaches [16,18,19,34,35] that incorporate robustness and sensitivity analyses [20,23,36,37].

Overall, qualitative and quantitative insights into molecular regulation of the metastatic process derived from mathematical modeling can help us to design the next set of experiments to be pursued. Then, based on the new experimental data, the mathematical model can be further refined and improved. Iteratively, a detailed and accurate mathematical model of metastasis can be developed. A reliable model can be then used to predict features of the system, for example, the effect of novel and existing treatments on the metastatic process.

Mathematical models use relatively low dimensional or dimension-reduced data, largely because there are realistic limits on the number of parameters that can be included effectively in the models. However, there is often a good understanding of the properties and variability inherent in these data that can often be accounted for during model building. Computational modeling can learn or discover new features from within high dimensional data spaces. However, as we discuss next, the properties of high dimensional data spaces are different from those of low dimensional spaces and pose their own unique challenges to data analysis and modeling.

The properties and challenges of high dimensional omic data spaces

Many studies attempt to discover meaningful signaling and phenotype relationships from within high dimensional omic data sets. These data sets are defined by the presence of 100s-10,000s of measured experimental variables, with the structure of the data being critical for how these variables can be linked, successfully and correctly, to the outcome(s) of interest. Omic data are massively parallel, representing a snapshot of the state of the system at the time the samples were collected [1]. Hence, the dynamic nature of biological signaling can be difficult to capture adequately. Time series collections represent categorical sampling of a continuous process (like metastasis) and, depending on the sample collection intervals, may miss some dynamical features. The relative importance of what may (or may not) be missed is usually hypothesis specific and so is not considered further here.

In omic studies, most tools and workflows tend to focus on differential expression of the nodes (genes, proteins, metabolites) in a molecular signaling network, correlating these expression changes with specific outcome(s), such as disease-free survival, progression-free survival, or overall survival in samples from patients, or with experimental endpoints in cell culture or animal models including changes in cell proliferation rate, cell death rate, or colony formation. While experimental design is critical to understanding what may or may not be learned from the resulting data, the possible designs are too varied to be considered here in any detail. Hence, we use specific examples to illustrate key points.

Epidemiologic studies can produce high dimensional data but the data structure can usually be approached using established biostatistical methods, mostly because of the relationship between the dependent variables and predictors. For example, consider a validated questionnaire with 40 questions (each question is a data dimension) that is completed by 2,000 subjects and where the outcome measure is binary. An example of a binary outcome is a study comparing a quantitative exposure to an environmental agent (predictor variable) with a specific disease state (present or absent; dependent variable) that is more or less evenly distributed in the dataset (approximately similar numbers of affected and unaffected subjects). Here, the ratio of dependent:predictor variables is 1:50 (40:2000). A ratio of 1:10 is often considered appropriate as a general rule-of-thumb and so the statistical power to detect a meaningful association between the dependent and predictor variables is high using well-established biostatistical methods. Compare this data structure with that of a transcriptome study using a genechip or RNAseq method that can detect 20,000 genes (predictor variable where each gene is a dimension represented by its expression value) applied to tissue samples from 50 subjects with the same binary outcome (dependent variable). Here, the ratio of dependent:predictor variables is 400:1 (20,000:50) and the properties of the data are very different, as are the tools needed to extract meaningful associations. We have discussed these unique properties in detail elsewhere [1,6,38] and focus here only on a few properties and primarily from the perspective of a non-quantitatively trained investigator interested in molecular signaling.

Inflation of the type 1 error (false positive estimates) from multiple comparisons is problematic. Established approaches using the False Discovery Rate to control this rate are certainly useful and are used widely. Nonetheless, all such approaches will also tend to inflate the type 2 error (false negative estimates), which may or may not be problematic depending on the study design and goals of the investigator. For example, a high false negative rate could exclude mRNAs critical to obtaining a meaningful and correct answer to a mechanistic hypothesis tested in a high dimensional transcriptome study. Another major challenge in high dimensional spaces is that, unless directed otherwise, most search tools search the entire dataspace. However, the most informative data (for addressing the goals of the study) may be in one or a small number of subspaces that can be missed when the ratio of dependent:predictor variables is very high (for example, 400:1). With complex models, high dimensionality and variability in the outcomes measure, potentially further compounded by a large dependent: predictor variable ratio, the curse of dimensionality may cause the search algorithm to fail to converge to a true solution(s) [1]. For example, convergence to locally correct but globally incorrect solutions can arise and reflect a local overfit but global underfit. A common reflection of the curse of dimensionality is the need for large computational resources, causing the algorithm either to fail to converge or to take an unacceptable time to reach convergence when these resources are inadequate [1]. Conversely, overly simple analytical models may need few computational resources and converge quickly. However, these approaches can generate an underfit of the model to the data, with the model outcomes not being adequately representative of the truth and thereby also potentially misleading [1].

The biological source of the data contributes several additional challenges to the structure of the data. Noise (random fluctuation in the variables) can be large and arise from multiple sources. Given the many advances in the technologies used to collect omics data, the noise contributed by the technology may be relatively small for some datasets. For example, data from established omics tools such as commercial genechip or RNAseq facilities are often high quality in the sense that the technical noise associated with the measurements obtained is small. However, assignment of each signal to the correct molecular species can vary across technologies. Commercial genechips are often reasonably accurate. For some RNAseq, proteomic, and metabolomic technologies the accuracy of this assignment can vary and coverage of the ome being sampled can be limited. For example, current unbiased single cell RNAseq technologies may correctly detect and assign only 10-40% of the 50,000 or more RNA species potentially present [39], leaving the majority of transcripts undetected. A further challenge is that the accuracy of protein expression predictions from genome or transcriptome data is limited for molecular signaling studies. Approximately 50% of changes detected in the transcriptome are not detected in the proteome [40]; extrapolating from the genome (such as mutations, single nucleotide polymorphisms) to the proteome may be even less accurate.

A further challenge is the confound of multimodality, a consequence of cells executing multiple functions concurrently and where a single gene or protein may be implicated in affecting one or more of these concurrent activities [1]. This effect is compounded further when the data are obtained from heterogeneous tissue samples, such that the differential expression of the gene reflects an aggregate across different cell types concurrently performing different functions (heterogeneity is discussed below in greater detail). It can then become difficult to attribute correctly the differential expression of a gene to the varying proportion of these several activities or subtypes, or to the phenotype or outcome of interest to the investigator. This challenge is not unusual for some gene set enrichment or pathway analysis tools. The onus is often then on the investigator to determine whether (or not) the analytical solution to their dataset is acceptable [6]. Unfortunately, this challenge opens up the trap of self-fulfilling prophecy, where investigators may unwittingly find in the data precisely what they expected to find even if it is not the underlying truth [1].

These challenges are certainly not insurmountable and new tools and workflows continue to emerge [41–49]. Also, investigators may be able to use data on other genes in implied pathways, or other metadata in the dataset, as a means to constrain the search space during data analysis or to guide data interpretation after data analysis. Currently, the use of independent validation of model outcomes and objective approaches to data interpretation remain essential to finding truth in data [1,6].

Sampling bias, noise and heterogeneity

Cellular, molecular, and genetic heterogeneity are features of the metastatic process that contribute substantially to the difficulty observed in eliminating metastatic disease. These features reflect the heterogeneity inherent in the primary tumor, the different selection pressures applied at each step in the metastatic cascade [2], and the temporal variability in when these pressures and the responses that they induce occur relative to the timing of sampling, and how well the sample reflects the inherent heterogeneity of the tissue. Thus, a related source of noise in high dimensional omics and other data is the contribution of sampling bias and how this may also affect assessments of cellular, molecular, or genetic heterogeneity or confound studies associating data features with a cellular mechanism or phenotype. For example, a fine needle aspirate with 5x10⁶ cells taken from a palpable primary breast tumor of 10⁹ cells may be less representative of the heterogeneity present than a similar image-guided aspirate taken from a non-palpable metastasis of 5×10⁷ cells. For identifying driver mutations, this may not be problematic, since Reiter et al. [50] have estimated that the likelihood of missing a single driver mutation present in all metastases is below 3%. However, mechanistic studies often aim to find more than a single putative driver mutation. As discussed below, the assumption that any complex feature of cancer biology is solely the result of a single driver mutation may often be an oversimplification. The nature of sampling bias also is more complex than the relationship between the sample size and the population size.

Cancer progression and metastasis are dynamic processes (time is a variable) in which treatment interventions may be applied prior to or between sampling. When comparing samples from a time-dependent process across different patients there may be bias or noise introduced by both interpatient and intertumor variables. Interpatient variables, such as genetic (germline), age, gender, or differences in the drug combination, and/or time since treatment can each introduce variability in the omics data collected and in the outcomes measured if they are linked to samples collected from a study with human subjects. Intertumor variables include sample timing relative to the biological age of the tumor, different perfusion gradients for drugs and nutrients in tumors (often reflecting tumor vascularity), tumor growth rates, genetic instability, and differences in both the nature and degree of immune effector cell infiltration. The extent to which any of these variables affect the ability to address an investigator’s hypothesis is often study specific.

Spatial heterogeneity can arise from sampling different metastatic sites within a patient or among all patients within a study population. The sampling method may introduce additional variability if the same method is not used to collect all samples. In breast cancer, for example, samples taken from a primary tumor may be obtained by either a core needle biopsy or fine needle aspirate of the primary tumor taken prior to excision, or a tissue slice taken from what remains after a portion of an excised tumor is sent for pathologic examination.

In contrast, there is usually limited variability in the linked clinical outcomes measures of survival. For overall survival, the date of death measure is likely to be have little noise relative to the time scale of the clinical study. There may be more variability in the measures of progression-free or disease-free survival, depending on the intervals between clinical evaluations of the subjects.

The ability of an investigative team to account for and or all of the variables noted above will depend partly on the meta data available. For many public datasets, these metadata may not be available or adequate and so cannot easily be used. Both supervised and unsupervised tools are becoming available to address the cellular heterogeneity present in data collected from complex samples [51–55]. While the variables described here may require careful consideration in data analysis for some systems modeling studies, their detailed consideration is beyond the scope of this article.

Challenges to modeling metastasis as a system

We have described here some of the more important general challenges related to the types, properties, advantages, and limitations of data and the implications of these challenges for arriving at reasonable and likely correct interpretations. However, these are general issues and are not specific to studying metastasis, which has other challenges to building a systems-based model. The process of metastasis and how this is currently understood both add their own challenges to modeling metastasis as a system.

Several key issues arise from the general lack of consensus regarding whether metastasis occurs early or late in the biological age of the primary tumor (see [2] for an excellent and detailed review). Biological age of the tumor is often conceived as beginning with the initial transforming event in the single cell from which the tumor was ultimately derived. However, this can only be estimated and is often based on the apparent growth rate of the tumor. Commonly measured events that are often used to help separate early from late events in the metastatic process include the patterns of gene mutations in the primary and its metastases. Figure 3 shows a simple representation of this concept based on the assumption of a single clone of origin for metastases.

Figure 3:

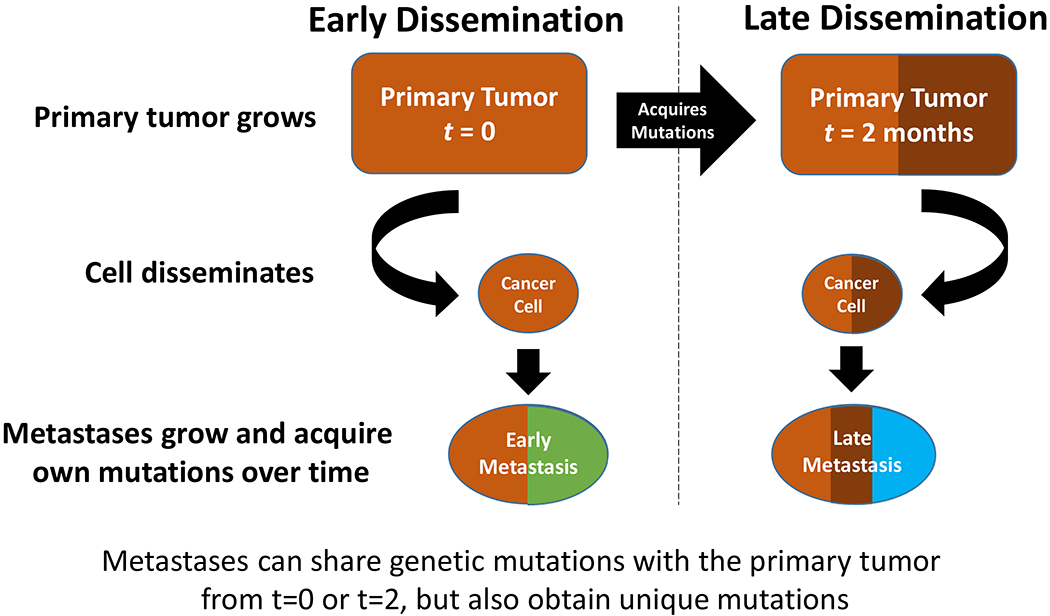
Mutation patterns in early compared with late dissemination. Simple representation based on the concept of a single clone of origin for the metastasis.

Early dissemination implies that the primary tumor and its metastases share a few common features but that other mutations unique to the primary tumor or its metastases will have been acquired independently over time. Thus, some level of genetic divergence will arise between a primary and its metastases – a process of parallel evolution [2]. If metastasis reflects continual seeding over time, some metastases will appear more divergent (early disseminated) than others (late disseminated) from the primary tumor. In each case, the metastases would share mutations with the primary tumor that reflected those present at the time they separated but not those acquired subsequently (and independently) by the primary tumor or its metastases [2].

Late dissemination is often conceived as representing the emergence of a single clone through a linear process whereby mutations are acquired until all of the necessary functions of metastasis become active and metastasis can be executed successfully. While this process would appear as serial evolution, the functions needed to execute metastasis fully do not need to be acquired in a specific sequence. Moreover, these functions could accumulate stochastically among several clones until one clone acquires all of the necessary functions.

The concept of a single clone of origin creates its own challenge. For example, cells that appear to have a high metastatic potential but lack one or two key properties may be present with those that have acquired all the properties needed to metastasize successfully. This is a realistic possibility, since the cells that have most but not all of the necessary properties are likely to be the population from which the fully metastasis-competent clone(s) arises. Without knowing in advance all of the properties and/or their drivers, it may be difficult to determine what is ‘necessary but not sufficient’ (all but one or two features are present in some cells) from what is ‘necessary and sufficient’ (all essential features are present in other cells) using data obtained from heterogeneous samples. The challenge may be further complicated if the proportion of cells that have the ‘necessary and sufficient’ features is low relative to cells that have a ‘necessary but not sufficient’ collection of features, if the number of different features between them is small and difficult to detect above the noise in the data, and/or if different subclones exhibit different but overlapping ‘necessary but not sufficient’ patterns. If some key features are not the result of gene mutations, which are relatively easy to find, then these non-mutation features may be difficult to discover.

From the perspective of patterns of mutations, late metastases from a single clone would exhibit a pattern similar to that of the primary tumor and to each other. However, the underlying assumption of all metastases being seeded by a single initiating clone may not always hold. For example, several clones could arise, perhaps present in different relative frequencies within the primary tumor and acquiring the full panel of the necessary metastasis properties at different times. In this case, there could be variability in mutation patterns among metastases that would still contain similarities to the primary tumor and to each other. Differences among metastases would partly reflect how recently (relative to each other) each clone had left the primary tumor, partly reflect clone-specific mutations present while each clone was still evolving within the primary tumor, and partly reflect those mutations acquired while growing at its distant site. The different models of this time-dependent feature of metastasis are not necessarily mutually exclusive, since different cells or subclones in a tumor may exhibit different properties at different times. Furthermore, there is not necessarily only one ‘correct’ model even for a specific cancer type.

None of these models account for the possibility that some metastases could seed other metastases; thus, all metastases may not arise only from the primary tumor [2]. Metastases arising from other metastases would likely appear to be very similar to the originating metastasis and so also appear to have arisen from the primary tumor at the same time as the seeding metastasis (early or late).

Over time, each individual metastatic deposit may acquire additional mutations. Mutation and growth rates of the primary tumor and each metastasis further affect their respective mutation patterns; both rates can vary significantly. For example, triple negative breast cancers (TNBC; lacking estrogen and progesterone receptors and HER2 amplification or overexpression) are notable for the rapid appearance of metastases. Many TNBC patients do not survive 5 years past their initial diagnosis [56]. In marked contrast, estrogen receptor positive (ER+) breast cancers are frequently characterized by late recurrences. Hence, breast cancer patients with ER+ tumors can experience distant recurrence a decade or more after their initial diagnosis, often referred to as dormancy [57,58]. The mutation landscape of these two breast cancer subtypes also vary notably, with greater mutational diversity generally seen in triple negative tumors compared with early ER+ tumors [59–61]. Tumor mutational burden increases significantly and correlates with poor clinical outcome in metastatic ER+ breast cancers [59,62].

The ability to use mutation patterns to separate early from late events is also affected by other considerations. For example, the assumption that metastasis is clonal in origin may not always apply. Metastasis may not only arise from a single cell but instead from a small community of cells. Evidence suggests that single circulating tumor cells (CTCs) are much less effective in creating viable metastatic deposits than clumps of CTCs [63]. Only if those clumps arise from cells of the same subclone would the metastasis be truly clonal in origin. Depending on how rapidly each metastatic clone grows, one that arose late could become clinically detectable before one that arose early in the growth of the primary tumor. Moreover, a metastasis with a high proportion of cycling cells could acquire more mutations in a shorter period of time, perhaps reflecting greater genetic instability and a higher rate of acquiring new persistent replication errors, than a slowly growing metastasis or one that entered dormancy for a prolonged period. Thus, a late disseminated but rapidly proliferating clone could look more like an early disseminated clone (more divergent from the primary tumor) than one that disseminated early but became dormant for a time or that grew very slowly (low pattern of mutational divergence from the primary tumor).

From the systems perspective, mutation patterns also may be used to inform an understanding of mechanism. A central assumption here is that the function of interest – metastasis or some individual feature of this process – is driven directly by the mutated gene(s) detected. However, the requirements for recognizing a mechanistically relevant pattern are difficult to establish. For example, should the mutations of greatest interest be present only in the metastases, should these also be present in the primary tumor, and/or must these mutations be present in all or most cells? Requiring the presence of a small number of common mutations may imply that these control all of the complex functions of the metastatic cascade, or at least control some of the most important functions. Moreover, particularly when relying exclusively on mutations as the primary drivers of mechanism(s), non-mutational events such as cell-communication or adaptable and/or reversible signaling or epigenetic changes within cells may be overlooked.

A common solution to these challenges is to use whatever is known about the mechanistic functions of the mutations present and select those that appear related to a feature of the overall process; examples for the process of metastasis could include an ability to increase cell invasion. While reasonable, this approach also is open to the trap of self-fulfilling prophecy [1], which can be exacerbated by the presence of many mutations that are acquired and maintained through neutral evolution. Indeed, by the time of diagnosis it is predicted that there is no DNA locus that remains wild type in every malignant cell [64].

Molecular signaling and the control and execution of complex biological functions

Complex, multistep biological processes are rarely controlled or executed by the actions of a single gene product, whether present in its wild-type or mutant form. Nonetheless, a hierarchy may exist where, in some specific circumstances, a single gene, mutation, or pathway may dominate or appear to dominate. Such examples would be the activation of ER or HER2 in some breast cancers. Functional dominance associated with ER− or HER2-driven signaling is evinced by the ability of specifically targeting ER (antiestrogen or aromatase inhibitors) or HER2 (Herceptin, Lapatinib) to kill enough cancer cells that some patients, but not all, are cured.

Why targeting these two drivers does not cure all patients with tumors that overexpress the respective molecular target is unclear. In principle, ER or HER2 signaling may not always dominate (a form of de novo resistance) or a sufficient number of cells in these tumors may adapt over time to any blockade in ER− or HER2-regulated signaling (a form of acquired resistance). A third possibility is that these tumors contain a sufficient number of cells that do not express the appropriate molecular target and come to dominate the tumor as the sensitive cells are killed off, a form of Darwinian clonal selection (one means for tumor heterogeneity to confer resistance). A fourth possibility has been demonstrated where sensitive and resistant cells communicate with each other to alter the overall responsiveness of the tumor [65], an ecological rather than evolutionary means to acquire resistance. Indeed, all of these mechanisms could coexist among different cell populations within a single tumor. Decomposing the features of each mechanism from data obtained from heterogeneous tissues remains a major challenge in systems-based research.

When viewed as a system, there are features of the metastatic cascade that are reflective of the complexity of the example of drug resistance phenotypes and their generation (above). For example, the properties of motility, invasiveness, and an ability to survive exposure to the physical and immunological pressures in the circulation, may not be present in all cells that metastasize, or may be lost by cells once they reach their final destination and the stresses are removed. Indeed, metastasis may be a property of small communities of cells that work together, rather than being solely a clonal phenomenon where all cells that metastasize exhibit all of the properties necessary to do so [66]. Indeed, collective invasion is the predominant process by which group of cancer cells with different properties can migrate [8,67]. For example, an epigenetically distinct breast cancer cell in a population can become the ‘trailblazer cells’ that enable local invasion and are followed by ‘opportunistic cells’ [68]. The challenge then becomes one of trying to understand the basic principles of how the system (metastasis or drug resistance) operates and the critical control or integration points that enable the individual components of the system to work together. Hopefully, but not necessarily, a few control and integration points will offer actionable targets to intervene and break the system, ideally where the opportunities to rewire and maintain the phenotype or system function (acquire resistance) are more limited.

Some properties (processes) can be common to more than one feature of a system. For example, the property of motility may be required to execute some components of the invasion, extravasation, and intravasation steps in metastasis. Execution (not necessarily regulation) of the property of motility may be performed by similar multiscale molecular interactions in many motile cells, and consequently be somewhat independent of cell context. When present, this commonality is a reflection of evolutionary parsimony, where the simplest means to execute a critical function has evolved and this mechanism is then largely conserved across divergent cell types and species. While some degeneracy in the execution signals may arise across evolutionary time [6], the basic topology of the execution machinery remains. Hence, we can gain critical insights into function execution in mammalian cells by studying how this is achieved in much simpler organisms like yeast, fly, or worm, as has been the case for metastasis [66]. There are many such examples. For example, much of what we have learned about how cells go through the cell cycle has been gleaned from modeling this process in yeast [15,69,70].

Where there is often much greater diversity is in the control functions of any given process among different tissues and species. The decision (output of a control function) to execute a turn of the cell cycle can often exhibit significant diversity in its upstream control functions. The example previously discussed of ER and AR in breast and prostate cancers can also be applied here to the control of proliferation. Indeed, dysregulation of the control of the cell cycle or key features of the metastatic cascade, relative to what occurs in normal cells that execute these functions as part of their normal physiological activities, are often considered among the hallmarks of cancer [71,72].

Similar to the notion that one property of the system may be shared among several steps, a protein may act in more than one signaling pathway. Glycolysis is sufficiently well known to easily exemplify several key points related to the importance of individual interactions within a pathway and how the activity of a single gene product may coordinate or integrate activities in more than one pathway or cellular function.

Within a pathway, some gene products can exert a greater level of influence over the output of a process than others. For example, only a few enzymes are rate-limiting for the process of glycolysis; hexokinase (converts glucose to glucose-6-phosphate), phosphofructokinase (converts fructose 6-phosphate to fructose 1,6-bisphosphate), and pyruvate kinase (converts phosphoenolpyruvate to pyruvate). While the level of expression or activity of a rate-limiting feature determines the rate of flux through a pathway, non-rate-limiting features may fluctuate in their levels of expression or activity with relatively limited consequences for flux. Thus, using a measure of the differential expression of a gene or protein as the primary determinant of its relative importance in an altered phenotype or pathway can sometimes be misleading. The scale of change, relative to output, also can vary. For example, a small (perhaps experimentally undetectable) change in the expression of a transcription factor may lead to a much larger, nonlinear change in the regulation of one of its target genes (more easily detected) that may or may not be the most relevant or functionally important among all of its concurrently regulated targets.

Molecules in one pathway may also participate in key events in another, as described above for the roles of BCL2 in autophagy and apoptosis. Following the example of glycolysis, the metabolic intermediate glucose-6-phosphate can be metabolized further to fructose-6-phosphate (the next step in the glycolysis pathway) or to 6-phosphogluconolactone and 6-phosphogluconate (6-PG; the next step in the pentose phosphate pathway; PPP). The rate-limiting step in PPP is catalyzed by glucose-6-phosphate dehydrogenase (G6PD), which oxidizes glucose-6-phosphate into 6-PG. Flux through the glycolytic pathway can affect both activity of the pentose phosphate pathway and the rate of proliferation. The ability to do so is entirely logical, since cells cannot complete a turn of the cell cycle if they do not have the energy needed from the ATP produced by glycolysis or the nucleic acids synthesized from the products of pentose phosphate metabolism. It is likely that similar types of relationships between genes and roles in multiple pathways also exist in the control of various components of the metastatic cascade.

Intrinsic versus extrinsic factors in the regulation of molecular signaling

For simplicity, the integrated signaling underlying each module can be conceived initially as exhibiting regulatory activities (for example, reversible; ‘on/off; ‘up/down’) that determine the level of activity of the execution activities (for example, irreversible; ‘on’ at the level(s) determined by regulatory activities until completed). These types of relationships are well known for apoptosis, where early (regulatory) events are reversible but later (execution) events are irreversible [25,73]. Other relationships also occur in signaling networks [74] that may or may not be known at the start of the modeling process. The signaling that determines when, where, and how these activities are regulated and performed can be either intrinsic or extrinsic to the cell.

Intrinsic and extrinsic activities are generally defined from the perspective of a specific cell type, with the focus here being on cancer cells (Figure 4). Thus, intrinsic factors or functions are those that occur within the cancer cells. Many of the key outcomes of interest to cancer researchers are sensed and executed by intrinsic factors (genes, proteins) or functions (a series of integrated signaling features that execute a specific cellular function such as the process of apoptosis). For example, cancer cell proliferation and programmed cell death outcomes are executed by actions that are almost exclusively intrinsic. Following the example of cell death, apoptosis (whether in the form of ‘intrinsic’ or ‘extrinsic’ apoptosis [75]) is ultimately executed by the activation of caspases that originate and act within the cancer cells (an intrinsic action).

Figure 4:

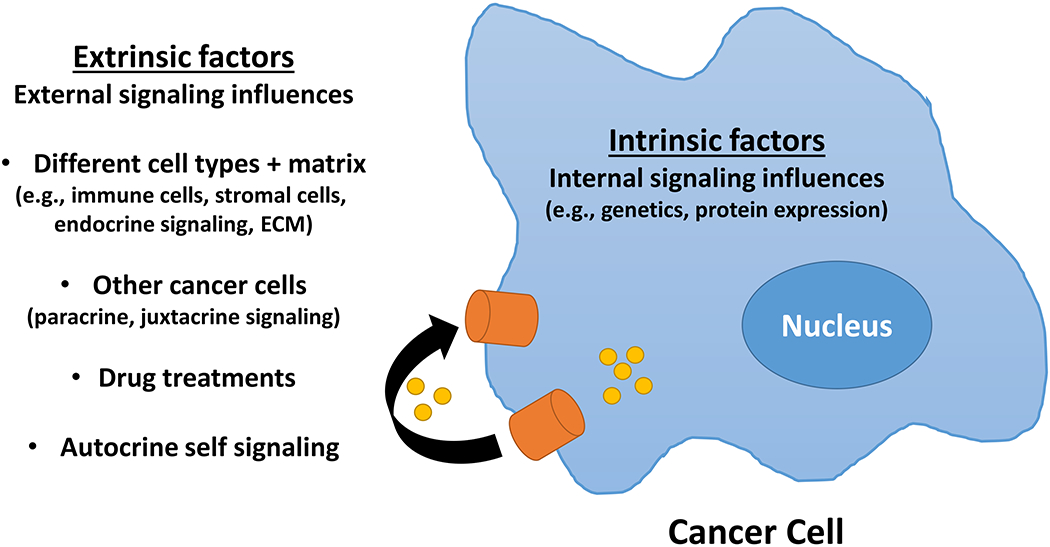
Intrinsic and extrinsic factors in molecular signaling. Within the tumor microenvironment, intrinsic signaling occurs within the cancer cell whereas extrinsic activities are external to the cancer cell but can regulate the activity of intrinsic signals, for example, by interacting with receptors exposed on the plasma membrane or by uptake into the cancer cell and interacting internally with other factors present in the cancer cell. ECM = extracellular matrix

Extrinsic factors are present in the tumor microenvironment in which the cancer cells live and die. These factors can originate locally including from stromal cells, infiltrating immune cells, or even from the cancer cells via autocrine, juxtacrine, or paracrine activities. Other extrinsic factors within the tumor microenvironment are produced distally by the host (endocrine) or may originate from outside the host as occurs with drug treatment. Thus, extrinsic factors can often regulate the activity of intrinsic factors or functions. Secretion of granzyme B into the tumor microenvironment by T cells is an example of an extrinsic action that can initiate an intrinsic activity (apoptosis) in sensitive cells. The consequences of granzyme B uptake by exocytosis into sensitive cancer cells, which include the activation of caspases in the presence of perforin and the activation of apoptosis leading to an apoptotic cell death [76], are intrinsic activities.

Distinguishing between an intrinsic and an extrinsic origin for a protein or gene can be difficult depending on the data being explored. Many genes are produced in cells that are very different in form and function. For example, TGFβ is a multifunctional cytokine that is produced by many different cell types and that has activities that are often highly cell context specific [77–79]. When TGFβ is detected in heterogeneous (cellular) tumor samples, is its origin primarily intrinsic or extrinsic to the cancer cell (acting as an autocrine, juxtacrine, or paracrine factor), and is its expression reflecting activation of only one, several, or all of the pathways associated with its activation of its cognate receptors? If more than one pathway is regulated concurrently (or appears to be), which is the most relevant and/or active, or does one pathway share features with another and so is being differentially regulated independent of TGFβ? Is TGFβ inhibiting some cells and stimulating others [77] within a heterogeneous (cellular) tumor microenvironment? Answering these questions is often not trivial. Even with exhaustive single cell mRNA sequencing, current methods can miss the majority of transcripts [39]. Moreover, many of these mRNAs will not be translated [40] and the rates of translation of those that are translated, and the activity or secretion of any translated proteins, may vary in different cell types at different times and with different treatments.

Canonical and non-canonical signaling

Canonical pathways are generally constructed from the literature, with their graphical representations rarely annotated with cell context specific interactions. Moreover, the more frequently a signaling feature is associated with a specific pathway, the more likely it is to be included in a canonical representation of that pathway [6]. Such a feature is two or more nodes, such as mRNAs, proteins, metabolites where the connecting edge(s) may include PPIs, PDIs, and/or SEP reactions. While an inherently intuitive approach, the potential that a different route(s) may exist (degeneracy) within a pathway to control the same function, or that the relative importance of any feature may vary with time or cell context, is rarely considered. Essentially, canonical pathways are idealized and mostly relatively simple linear graphs. These linear representations can be visually appealing and easily understood, as exemplified by those provided by the Kyoto Encyclopedia of Genes and Genomes (https://www.genome.jp/kegg/). While these are static representations, some directionality is captured and known feedback interactions may be included.

Current canonical representations rarely account easily for the ability of a molecule to participate in multiple different pathways. Hence, when databases with canonical pathway metadata are used by gene set enrichment and pathway analysis tools, it is not unusual to find that the same input gene list (for example, a list of previously identified differentially expressed mRNAs) implicates several different pathways in a single analysis. However, the direction of change in the genes that drive selection of that pathway may have been ignored. Hence, a pathway may be selected with an apparently high probability estimate when several of the genes that drive this selection are either regulated in directions that are inconsistent with how signaling is known to flow through the pathway, and/or are also features in other pathways that are identified by the algorithm but with larger p-values (less significance). The trap-of-self-fulfilling prophesy could then lead an investigator to select erroneously a specific pathway with a smaller (more significant) p-value as explaining a biological response or phenotype.

An underlying assumption is that canonical pathways are enriched in features that are truly conserved across different cell contexts and even species, again reflecting evolutionary parsimony. Thus, if features (some nodes and/or edges) of the pathways likely to be driving the system are known, or can be implied from canonical representations of signaling, these can be used to constrain the initial search space, as can the elimination of genes definitively known not to participate. Using only known genes could over constrain the search space and result in latent variables being missed. However, where the goal is to find topological features to initiate modeling, this approach can provide a useful starting point to reduce dimensionality and still allow for the discovery of new edges that can later be ‘built-out’ as the modeling progresses. Canonical representations can also be used to find latent variables or features of the signaling that are not differentially expressed in the primary data and yet are absolutely required for the system to function. For example, only one member of a protein complex may be differentially regulated but all members are required for the complex to function, perhaps where the level of complex activity is a direct reflection of the amount of the regulated partner available. Measuring only the regulated component may be sufficient for predictive model building but all members of the complex could be targets for drug discovery, where some may prove more actionable than others.

Focusing on edges and not just nodes

Figure 5 shows a simple representation of a signaling network. A common approach in modeling such networks is to measure the expression of other genes that are known targets and imply the activation or suppression of pathways from canonical pathway representations. This approach focuses primarily on the nodes in a co-expression network. However, there are limitations to this approach that reflect both the tools used and the collation of genes into canonical representations of signaling pathways [6]. Moreover, each node may have the opportunity to form an edge with more than one other node, often in a cell context-dependent manner, which creates complexity and the opportunity to rewire signaling that may not be evident from analyses that are focused mostly on the differential expression of nodes.

Figure 5:

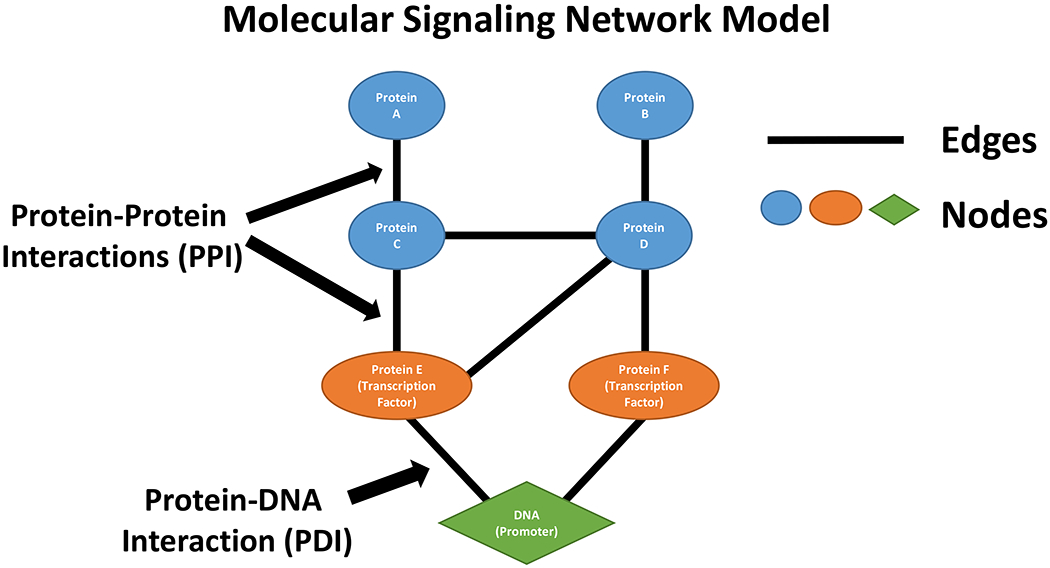
Simple representation of a feature within a molecular signaling network comprised of nodes (for example, genes, protein, metabolites, DNA) and their interconnecting edges.

Edges are the connections that link nodes and create network topology, often conferring the plastic nature of signal flow. Examples of edges include PPIs (the edge(s) represents the linkage(s) between the proteins in the complex), PDIs (the edge(s) represent the linkage(s) between the transcription factor and any other proteins in the complex and the DNA to which it binds), and SEP interactions (the edge(s) represent the links between substrate, enzyme and product). SEP interactions include the reactions involved in intermediate metabolism (like glycolysis or the TCA cycle) but also the reactions catalyzed by enzymes such as ATPases, kinases, phosphatases, methyl and acetyl transferases and many others.

Data-driven differential network analysis identifies a network of differentially connected molecular entities from within a complex and often unknown overall molecular regulatory circuitry. These entities comprise pairwise selective coupling or uncoupling that reflect the specific phenotypes or experimental conditions that are under investigation including the associated regulatory elements. Such differential regulatory networks are typically used to assist in the inference of potential key pathways and targets in tumor biology [80]. The regulatory networks discovered can serve as useful frameworks for the construction and verification of mechanistic cancer models, which in turn help to provide a plausible interpretation of data, new insights into cancer biology, and hypotheses for further validation and investigations [80,81].

Unique yet subtle advantages of focusing on edges rather than nodes are multifold when compared with classic differential expression analysis [53,82]. First, the low expression values for many transcription factors or other regulators make their detection challenging in classic differential analysis, while edge analysis can uncover the regulators’ role in functional activation or deactivation. For example, the edge between a transcription factor (low expression) and a primary molecular target gene(s) (higher expression) may be found from the differential co-expression of the transcription factor’s target gene(s). Second, advanced network analysis can identify more relevant pathways that functionally control phenotypes, where the ‘networked’ gene subset can improve the specificity of enrichment analysis. Lastly, while sectional random snapshot(s) of a dynamic system is a significant source of uncertainty in classic differential analysis, the dependency among genes exploited by edge modeling is concurrently ‘retained’ within and across samples, yet independent of sampling order or bias.

Concluding comments and future directions

Systems models allow for high-throughput simulations that can predict outcomes for testing in experimental in vitro or in vivo models [83]. We have identified some of the challenges for consideration in building systems-based models of the process of metastasis. We have chosen not to offer many specific solutions because these are diverse, emerging, and frequently hypothesis and data specific. However, by raising these issues investigative teams can best decide which problems they need to, and can, address. New and improved approaches continue to evolve rapidly. The challenges and limitations of current approaches, tools, and representations that have been noted above do not necessarily mislead. Rather, the use of these approaches requires some knowledge of the system being studied, the nature of the tools applied and their limitations, and an ability of the investigator(s) to approach the data objectively, rather than looking only for what they hope or expect to find. The challenge of maintaining objectivity during analysis reflects the ‘trap of self-fulfilling prophecy’ and it can be difficult to avoid [1]. Knowledge of the tools and workflows used, the properties of the data and meta data available, and applying an objective interpretation can help investigators to avoid the trap. Such knowledge is particularly important when approaching the published literature and the data and analyses of others.

While cell context is rarely captured fully in most gene ontology databases, cell context is present in the primary data being explored. If the primary data are from treated and untreated breast tumors then the differential expression of the genes, proteins, or metabolites reflect that cellular context. Investigators can then use prior knowledge of the system and cell context to try to determine which of a series of implied pathways are most likely to be relevant to their primary hypothesis. Hence, some of the limitations in using canonical pathways can be addressed by applying careful judgment and meta data from other sources to determine whether to retain or reject those canonical features that do not apply or are inconsistent with the cell context specific data. It is hoped that newer generations of pathway analysis tools will make good use of directional changes in nodes and the likely presence or absence of edges to help provide greater clarity and accuracy on which pathways are most likely to be biologically relevant when differentially expressed nodes implicate several pathways with high statistical significance. Perhaps these tools also will begin to incorporate prior cell context-specific knowledge.

To date, most of the omics data used for signaling has been from genome and transcriptome analyses. The limitations in these data are clearly noted above. Some of these limitations will be overcome by better analytical tools and work flows. However, as the sensitivity and specificity of other omic platforms improve, greater insights may be gained from multiscale modeling that incorporates high quality and high resolution data from the proteome and metabolome. From a signaling and systems perspective, many of the most important interactions are metabolic in nature, whether they represent the transfer of a phosphate group to another protein by a kinase or a methyl group to DNA. Consequently, some of the greatest insights may be gained when technologies with high depth, sensitivity, and specificity are available to fully sample the proteome and metabolome of single cells.