Forecast analysis of the epidemics trend of COVID-19 in the USA by a generalized fractional-order SEIR model

Abstract

In this paper, a generalized fractional-order SEIR model is proposed, denoted by SEIQRP model, which divided the population into susceptible, exposed, infectious, quarantined, recovered and insusceptible individuals and has a basic guiding significance for the prediction of the possible outbreak of infectious diseases like the coronavirus disease in 2019 (COVID-19) and other insect diseases in the future. Firstly, some qualitative properties of the model are analyzed. The basic reproduction number $R_0$ is derived. When $R_0<1$, the disease-free equilibrium point is unique and locally asymptotically stable. When $R_0>1$, the endemic equilibrium point is also unique. Furthermore, some conditions are established to ensure the local asymptotic stability of disease-free and endemic equilibrium points. The trend of COVID-19 spread in the USA is predicted. Considering the influence of the individual behavior and government mitigation measurement, a modified SEIQRP model is proposed, defined as SEIQRPD model, which is divided the population into susceptible, exposed, infectious, quarantined, recovered, insusceptible and dead individuals. According to the real data of the USA, it is found that our improved model has a better prediction ability for the epidemic trend in the next two weeks. Hence, the epidemic trend of the USA in the next two weeks is investigated, and the peak of isolated cases is predicted. The modified SEIQRP model successfully capture the development process of COVID-19, which provides an important reference for understanding the trend of the outbreak.

Introduction

The outbreak of the coronavirus disease (COVID-19) in 2019 occurred in Wuhan, China, at the end of 2019. This is a severe respiratory syndrome caused by the novel coronavirus of zoonotic origin [1]. The Chinese government has implemented many measures, including the establishment of specialized hospitals and restrictions on travel, to reduce the spread. By April 20, 2020, the outbreak in China has been basically controlled. However, the outbreak is still rampant all over the world. At present, the USA, Italy, Spain and other countries are still in the rising stage of the outbreak. It has posed a great threat to the public health and safety of the world.

At present, many countries have adopted mitigation measures to restrict travel and public gatherings, which have a serious impact on the economy. Therefore, it is very important to predict the development trend of this epidemic and estimate the peak of the isolated cases. The epidemic model is a basic tool to research the dynamic behaviors of disease and predict the spreading trend of disease. Establishing a reasonable epidemic model can effectively characterize the development process of the disease. Ricardo [2] researched a fractional SEIR model with treatment and given some sufficient conditions to ensure the local stability of equilibrium points. Yang and Xu [3] considered a fractional-order SEIR model with general incidence rate and established the local and uniform asymptotic stability of equilibria. However, these studies remain at the theoretical stage and do not use real data to analyze the trend of specific epidemics. In the outbreak of COVID-19, three types of data are usually available: isolated cases, recovered cases and death cases. The traditional fractional SEIR model cannot describe the trend of isolated individuals and dead individuals caused by diseases. Hence, it difficult for the traditional SEIR model to use the information contained in isolated cases and death cases. Therefore, a generalized SEIR epidemic model is proposed in this paper and is defined as SEIQRP model. Some qualitative properties of this model are first analyzed, including the existence and uniqueness of the disease-free and the endemic equilibrium points. Then, conditions are also established to ensure the local asymptotic stability of both disease-free and endemic equilibrium points.

So far, many scholars have researched COVID-19 from different perspectives [1, 4–8]. In [9], the epidemics trend of COVID-19 in China was predicted under public health interventions. In [10], the basic reproduction number of COVID-19 in China was estimated and the data-driven analysis was performed in the early phase of the outbreak. Peng [11] proposed a generalized SEIR model to analyze the spread of COVID-19 in China. The model can describe the trends of isolated individuals, recovered individuals and dead individuals, and make full use of the information contained in the real data. However, the model does not take into account the infectivity of patients in the incubation period. As we all know, one of the important reasons that COVID-19 can cause a global outbreak is that the epidemic has a long incubation period. Hence, considering the infectivity of the patients in the incubation period is in line with the actual situation. In order to predict the cumulative number of confirmed cases and combine the actual measures taken by the government on the outbreak of COVID-19, we further put forward an improved SEIQRP model, denoted by SEIQRPD model. At present, we can obtain the epidemic data of COVID-19 outbreak in the USA before April 20, 2020. We use these data and the improved model to predict the epidemic trend of the USA in the next two weeks, and estimate the peak of isolated cases. Firstly, the data before April 5 were selected to identify the model parameters, and the prediction ability of the improved model with the epidemiological data from April 6 to April 20 is verified. Then, the cumulative number of confirmed cases and isolated cases are predicted in the next two weeks. The peak of isolated cases is thus predicted.

In recent years, with the continuous development of fractional calculus theory, fractional-order system modeling approaches have been applied in various engineering and non-engineering fields [12–14]. Compared with the short memory of the integer derivative, the fractional derivative has the information of the whole time interval or long memory. It is more accurate to describe the biological behavior of population by using fractional differential equation.

The rest of this manuscript is structured as below. In Sect. 2.1, the fractional SEIQRP model and the modified SEIQRP model is proposed. Some qualitative properties of the SEIQRP model are discussed in Sect. 2.2. In Sect. 2.3, the prediction ability of the modified SEIQRP model is verified by using real data. The disease development in the USA in the next two weeks after April 21, 2020, is predicted. Finally, conclusion and some future works are discussed in Sect. 3.

Preliminaries and model derivation

Preliminaries

In this section, some useful lemmas and definitions will be given to analyze some results of this paper.

Definition 1

[15] The Caputo fractional-order derivative is given below

$$\begin{array}{c}\hfill {}_0^C{D}_t^{\alpha }f(t)=\left\{\begin{array}{ccc}& \frac{1}{\Gamma (n-\alpha )}{\int }_0^t\frac{f^{(n)}(\xi )}{{(t-\xi )}^{1+\alpha -n}}\mathrm{d}\xi ,& n-1<\alpha <n,\hfill \\ \hfill & \frac{{\mathrm{d}}^n}{\mathrm{d}{t}^n}f(t),& \alpha =n,\hfill \end{array}\right)\end{array}$$

where n is the smallest positive integer not less than $\alpha$.

Definition 2

[15, 16] The Mittag–Leffler function is given below

$$\begin{array}{c}\hfill E_{\alpha }(z)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (k\alpha +1)},\end{array}$$

where $n-1\le \alpha \le n$.

Consider the following n-dimensional fractional-order differential equation system

$$\begin{array}{c}\hfill {}_0^C{D}_t^{\alpha }X(t)=AX(t),x(0)=x_0,\end{array}$$ 1

where $\alpha \in (0,1)$, $X(t)={(x_1(t),x_2(t),\dots ,x_n(t))}^T$ is an n-dimensional state vector and A is an $n\times n$ constant matrix.

Lemma 1

[17] For the corresponding linear time-invariant system (1), the following results are true:

(i) The zero solution is asymptotically stable, if and only if all eigenvalues $s_j$ $(j=1,2,\dots ,n)$ of A satisfy $|arg(s_j)|>\frac{\alpha \pi }{2}$.

(ii) The zero solution is stable, if and only if all eigenvalues $s_j$ of A satisfy $|arg(s_j)|\ge \frac{\alpha \pi }{2}$ and eigenvalues with $|arg(s_j)|=\frac{\alpha \pi }{2}$ have the same algebraic multiplicity and geometric multiplicity.

SEIQRP model

The outbreak of COVID-19 has had a great impact on the economic growth of any country and daily life of any human. In order to control and prevent the possible outbreak of infectious diseases like the COVID-19 or other insect diseases in the future, it is very important to establish an appropriate model. The transmission diagram of the generalized SEIR model proposed in this paper is shown in Fig. 1. We divide the total population into six distinct epidemic classes: susceptible, exposed, infectious, quarantined, recovered and insusceptible. We will represent the number of individuals at time t in the above classes by S(t), E(t), I(t), Q(t), R(t) and P(t), respectively. The specific explanations of the above six categories are as follows:

• Susceptible S(t): the number of uninfected individuals at the time t.

• Exposed E(t): the number of infected individuals at the time t, but still in incubation period (without clinical symptoms and low infectivity).

• Infectious I(t): the number of infected individuals at the time t (with obvious clinical symptoms).

• Quarantined Q(t): the number of individuals who have been diagnosed and isolated at the time t.

• Recovered R(t): the number of recovered individuals at the time t.

• Insusceptible P(t): the number of susceptible individuals who are not exposed to the external environment at the time t.

The incidence rate plays a very important role in the epidemic, which can describe the evolution of infectious disease. According to the spread of different diseases in different regions, there are many forms of incidence rate [18–20]. We expect to establish a generalized incidence rate, which can contain most of these specific forms. Further, in order to match the dimensions of fractional-order model with respect to time t, Diethelm[21] pointed out that both the left-hand and the right-hand sides of fractional-order epidemic model must have the same dimensions. Inspired by the work of[3, 21, 22], the fractional-order SEIQRP model with general incidence rate is given by

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {}_0^C{D}_t^{\alpha }S(t)& =\Lambda -{\beta }_1^{\alpha }{f}_1(S(t))g_1(I(t))\hfill \\ \hfill & -{\beta }_2^{\alpha }{f}_2(S(t))g_2(E(t))-{\mu }^{\alpha }S(t)-{\rho }^{\alpha }S(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }E(t)& ={\beta }_1^{\alpha }{f}_1(S(t))g_1(I(t))+{\beta }_2^{\alpha }{f}_2(S(t))g_2(E(t))\hfill \\ \hfill & -{\epsilon }^{\alpha }E(t)-{\mu }^{\alpha }E(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }I(t)& ={\epsilon }^{\alpha }E(t)-({\delta }^{\alpha }+{\mu }^{\alpha })I(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }Q(t)& ={\delta }^{\alpha }I(t)-({\lambda }^{\alpha }+{\kappa }^{\alpha }+{\mu }^{\alpha })Q(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }R(t)& ={\lambda }^{\alpha }Q(t)-{\mu }^{\alpha }R(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }P(t)& ={\rho }^{\alpha }S(t)-{\mu }^{\alpha }P(t),\hfill \end{array}\right)\end{array}$$ 2

where $\alpha \in (0,1)$, $\Lambda$ is the inflow number of susceptible individuals, ${\beta }_1$ and ${\beta }_2$ denote the infection rates of the infected individuals and the exposed individuals, respectively, $\rho$ is the protection rate and $\epsilon$ represents the incubation rate. $\delta$ is the rate at which symptomatic infections are diagnosed and quarantined. $\lambda$ and $\kappa$ represent the cure rate of isolated individuals and the death rate caused by the disease, respectively, $\mu$ is the natural mortality, and the incidence rates ${\beta }_1{f}_1(S)g_1(I)$ and ${\beta }_2{f}_2(S)g_2(E)$ are used to describe the transmission of diseases, which satisfy the following conditions [23]:

Fig. 1.

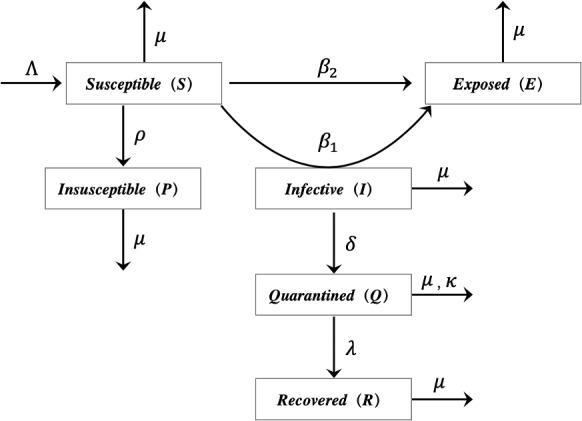
Transmission diagram for the model involving six population classes

(i) $f_1(0)=f_2(0)=g_1(0)=g_2(0)=0$,

(ii) $f_1(S)>0$, $f_2(S)>0$, $g_1(I)>0$, $g_2(E)>0$, for any S, E, $I>0$,

(iii) $f_1^{\prime }(S)>0$, $f_2^{\prime }(S)>0$, $g_1^{\prime }(I)>0$, $g_2^{\prime }(E)>0$, for any S, E, $I>0$,

(iv) $g_1^{\prime }(I)-\frac{g_1(I)}{I}\le 0$, $g_2^{\prime }(E)-\frac{g_2(E)}{E}\le 0$, for any E, $I>0$.

Modified SEIQRP model

In the following, we will combine the actual situation and government mitigation policy to improve the SEIQRP model (2). Firstly, during the outbreak of COVID-19, we need to make reasonable assumptions according to the actual mitigation policies and circumstances.

• During the COVID-19 outbreak, population mobility is strictly controlled by many countries. In particular, the policy of city closure was implemented in Hubei Province, China. Therefore, the impact of migration will not be considered in the improved model.

• For the prediction of this short-term virus transmission, the impact of natural mortality will not be considered. It is assumed that novel coronavirus is the only cause of death during the outbreak.

• In order to predict the trend of cumulative confirmed cases, it is necessary to simulate the number of death cases. Therefore, a new class D(t) to the SEIQRP model will be added in the modified model, which denotes the number of death cases at time t.

• The time-varying cure rate, mortality rate and infection rate will be applied to the improved model. This can better simulate the impact of the improvement of medical conditions and government control on individuals in reality.

Based on the above assumptions and analysis, the following improved model for COVID-19 is proposed.

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {}_0^C{D}_t^{\alpha }S(t)& =-{\beta }_1^{\alpha }(t)f_1(S(t))g_1(I(t))\hfill \\ \hfill & -{\beta }_2^{\alpha }{f}_2(S(t))g_2(E(t))-{\rho }^{\alpha }S(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }E(t)& ={\beta }_1^{\alpha }(t)f_1(S(t))g_1(I(t))\hfill \\ \hfill & +{\beta }_2^{\alpha }{f}_2(S(t))g_2(E(t))-{\epsilon }^{\alpha }E(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }I(t)& ={\epsilon }^{\alpha }E(t)-{\delta }^{\alpha }I(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }Q(t)& ={\delta }^{\alpha }I(t)-({\lambda }^{\alpha }(t)+{\kappa }^{\alpha }(t))Q(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }R(t)& ={\lambda }^{\alpha }(t)Q(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }P(t)& ={\rho }^{\alpha }S(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }D(t)& ={\kappa }^{\alpha }(t)Q(t),\hfill \end{array}\right)\end{array}$$ 3

where ${\beta }_1(t)={\sigma }_{1}exp(-{\sigma }_{2}t)$, $\lambda (t)={\lambda }_1(1-exp({\lambda }_{2}t))$ and $\kappa (t)={\kappa }_{1}exp(-{\kappa }_{2}t)$. The parameters ${\sigma }_1$, ${\sigma }_2$, ${\lambda }_1$, ${\lambda }_2$, ${\kappa }_1$ and ${\kappa }_2$ are all positive, where $\sigma$ is used to simulate the intensity of government control. It should be emphasized that the protection rate $\rho$ for susceptible individuals also reflects the intensity of government control.

Qualitative analysis of the SEIQRP model

The existence and uniqueness of equilibrium point

Obviously, the right-hand side of system (2) satisfies the local Lipschitz condition; then, there exists a unique solution of system (2) [15, 24].

Theorem 1

The solutions of system (2) are nonnegative, and the closed set $\mathrm{\Omega }=\{(S,E,I,Q,R,P)\in {\mathbb{R}}_{+}^6:0\le S+E+I+Q+R+D\le \frac{\Lambda }{{\mu }^{\alpha }}\}$ is a positive invariant set of system (2).

Proof

In order to investigate the non-negativity of solutions of system (2), we consider the following system

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {}_0^C{D}_t^{\alpha }{S}_1(t)& =-{\beta }_1^{\alpha }{f}_1(S(t))g_1(I(t))-{\beta }_2^{\alpha }{f}_2(S(t))g_2(E(t))\hfill \\ \hfill & -{\mu }^{\alpha }S(t)-{\rho }^{\alpha }S(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }{E}_1(t)& ={\beta }_1^{\alpha }{f}_1(S(t))g_1(I(t))+{\beta }_2^{\alpha }{f}_2(S(t))g_2(E(t))\hfill \\ \hfill & -{\epsilon }^{\alpha }E(t)-{\mu }^{\alpha }E(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }{I}_1(t)& ={\epsilon }^{\alpha }E(t)-({\delta }^{\alpha }+{\mu }^{\alpha })I(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }{Q}_1(t)& ={\delta }^{\alpha }I(t)-({\lambda }^{\alpha }+{\kappa }^{\alpha }+{\mu }^{\alpha })Q(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }{R}_1(t)& ={\lambda }^{\alpha }Q(t)-{\mu }^{\alpha }R(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }{P}_1(t)& ={\rho }^{\alpha }S(t)-{\mu }^{\alpha }P(t),\hfill \end{array}\right)\end{array}$$ 4

where the initial conditions are $S_{10}=0$, $E_{10}=0$, $I_{10}=0$, $Q_{10}=0$, $R_{10}=0$ and $P_{10}=0$. (0, 0, 0, 0, 0, 0) is the unique solution of the above system. According to the fractional-order comparison theorem [25], one can deduce that the solutions of system (2) satisfy $S(t)\ge 0$, $E(t)\ge 0$, $I(t)\ge 0$, $Q(t)\ge 0$, $R(t)\ge 0$ and $P(t)\ge 0$. By adding six equations of system (2), one can deduce

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}_0^C{D}_t^{\alpha }N(t)& =\Lambda -{\mu }^{\alpha }N(t)-{\kappa }^{\alpha }Q(t)\hfill \\ \hfill & \le \Lambda -{\mu }^{\alpha }N(t).\hfill \end{array}\end{array}$$

By applying the fractional-order comparison theorem, one has

$$\begin{array}{c}\hfill N(t)\le (-\frac{\Lambda }{{\mu }^{\alpha }}+N(0))E_{\alpha }(-{\mu }^{\alpha }{t}^{\alpha })+\frac{\Lambda }{{\mu }^{\alpha }}.\end{array}$$

When $N(0)\le \frac{\Lambda }{{\mu }^{\alpha }}$, since $E_{\alpha }(-{\mu }^{\alpha }{t}^{\alpha })\ge 0$, we have

$$\begin{array}{c}\hfill S(t)+E(t)+I(t)+Q(t)+R(t)+P(t)\le \frac{\Lambda }{{\mu }^{\alpha }}.\end{array}$$

Thus, we can draw the result of Theorem 1.

System (2) has an obvious disease-free equilibrium point $M_0=(S_0,0,0,0,0,P_0)$, where

$$\begin{array}{c}\hfill S_0=\frac{\Lambda }{{\mu }^{\alpha }+{\rho }^{\alpha }},P_0=\frac{{\rho }^{\alpha }\Lambda }{{\mu }^{\alpha }({\mu }^{\alpha }+{\rho }^{\alpha })}.\end{array}$$

In order to obtain the endemic equilibrium point of system (2), we set:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& \Lambda -{\beta }_1^{\alpha }{f}_1(S(t))g_1(I(t))-{\beta }_2^{\alpha }{f}_2(S(t))g_2(E(t))\hfill \\ \hfill & -{\mu }^{\alpha }S(t)-{\rho }^{\alpha }S(t)=0,\hfill \\ \hfill & {\beta }_1^{\alpha }{f}_1(S(t))g_1(I(t))+{\beta }_2^{\alpha }{f}_2(S(t))g_2(E(t))\hfill \\ \hfill & -{\epsilon }^{\alpha }E(t)-{\mu }^{\alpha }E(t)=0,\hfill \\ \hfill & {\epsilon }^{\alpha }E(t)-({\delta }^{\alpha }+{\mu }^{\alpha })I(t)=0,\hfill \\ \hfill & {\delta }^{\alpha }I(t)-({\lambda }^{\alpha }+{\kappa }^{\alpha }+{\mu }^{\alpha })Q(t)=0,\hfill \\ \hfill & {\lambda }^{\alpha }Q(t)-{\mu }^{\alpha }R(t)=0,\hfill \\ \hfill & {\rho }^{\alpha }S(t)-{\mu }^{\alpha }P(t)=0,\hfill \end{array}\right)\end{array}$$ 5

which implies

$$\begin{array}{c}\hfill S=\frac{\Lambda -({\epsilon }^{\alpha }+{\mu }^{\alpha })E}{{\mu }^{\alpha }+{\rho }^{\alpha }},I=\frac{{\epsilon }^{\alpha }E}{{\sigma }^{\alpha }+{\mu }^{\alpha }}.\end{array}$$

Combining the above equations and the second equation of (5), one has

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill ({\mu }^{\alpha }+{\epsilon }^{\alpha })E& ={\beta }_1^{\alpha }{f}_1\left(\frac{\Lambda -({\mu }^{\alpha }+{\epsilon }^{\alpha })E}{{\mu }^{\alpha }+{\rho }^{\alpha }}\right)g_1\left(\frac{{\epsilon }^{\alpha }E}{{\mu }^{\alpha }+{\delta }^{\alpha }}\right)\hfill \\ \hfill & +{\beta }_2^{\alpha }{f}_2\left(\frac{\Lambda -({\mu }^{\alpha }+{\epsilon }^{\alpha })E}{{\mu }^{\alpha }+{\rho }^{\alpha }}\right)g_2(E).\hfill \end{array}\end{array}$$ 6

Define

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \phi (E)& ={\beta }_1^{\alpha }{f}_1\left(\frac{\Lambda -({\mu }^{\alpha }+{\epsilon }^{\alpha })E}{{\mu }^{\alpha }+{\rho }^{\alpha }}\right)g_1\left(\frac{{\epsilon }^{\alpha }E}{{\mu }^{\alpha }+{\delta }^{\alpha }}\right)\hfill \\ \hfill & +{\beta }_2^{\alpha }{f}_2\left(\frac{\Lambda -({\mu }^{\alpha }+{\epsilon }^{\alpha })E}{{\mu }^{\alpha }+{\rho }^{\alpha }}\right)g_2(E)-({\mu }^{\alpha }+{\epsilon }^{\alpha })E.\hfill \end{array}\end{array}$$ 7

Note that $\phi (0)=0$ and $\phi (\frac{\Lambda }{{\mu }^{\alpha }+{\epsilon }^{\alpha }})=-\Lambda <0$. In order to show that $\phi (E)=0$ has at least one positive root in the interval $(0,\frac{\Lambda }{{\mu }^{\alpha }+{\epsilon }^{\alpha }}]$, we need to prove that ${\phi }^{\prime }(0)>0$. Hence,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\phi }^{\prime }(E)& =-\frac{({\mu }^{\alpha }+{\epsilon }^{\alpha }){\beta }_1^{\alpha }}{{\mu }^{\alpha }+{\rho }^{\alpha }}{f}_1^{\prime }\left(\frac{\Lambda -({\mu }^{\alpha }+{\epsilon }^{\alpha })E}{{\mu }^{\alpha }+{\rho }^{\alpha }}\right)g_1\left(\frac{{\epsilon }^{\alpha }E}{{\mu }^{\alpha }+{\delta }^{\alpha }}\right)\hfill \\ \hfill & +\frac{{\epsilon }^{\alpha }{\beta }_1^{\alpha }}{{\mu }^{\alpha }+{\delta }^{\alpha }}{f}_1\left(\frac{\Lambda -({\mu }^{\alpha }+{\epsilon }^{\alpha })E}{{\mu }^{\alpha }+{\rho }^{\alpha }}\right)g_1^{\prime }\left(\frac{{\epsilon }^{\alpha }E}{{\mu }^{\alpha }+{\delta }^{\alpha }}\right)\hfill \\ \hfill & -\frac{({\mu }^{\alpha }+{\epsilon }^{\alpha }){\beta }_2^{\alpha }}{{\mu }^{\alpha }+{\rho }^{\alpha }}{f}_2^{\prime }\left(\frac{\Lambda -({\mu }^{\alpha }+{\epsilon }^{\alpha })E}{{\mu }^{\alpha }+{\rho }^{\alpha }}\right)g_2(E)\hfill \\ \hfill & +{\beta }_2^{\alpha }{f}_2\left(\frac{\Lambda -({\mu }^{\alpha }+{\epsilon }^{\alpha })E}{{\mu }^{\alpha }+{\rho }^{\alpha }}\right)g_2^{\prime }(E)-({\mu }^{\alpha }+{\epsilon }^{\alpha }).\hfill \end{array}\end{array}$$ 8

Therefore, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\phi }^{\prime }(0)& =\frac{{\epsilon }^{\alpha }{\beta }_1^{\alpha }}{{\mu }^{\alpha }+{\delta }^{\alpha }}{f}_1(S_0)g_1^{\prime }(0)+{\beta }_2^{\alpha }{f}_2(S_0)g_2^{\prime }(0)-({\mu }^{\alpha }+{\epsilon }^{\alpha })\hfill \\ \hfill & =({\mu }^{\alpha }+{\epsilon }^{\alpha })(R_0-1),\hfill \end{array}\end{array}$$

where the basic reproduction number is given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill R_0& =\frac{{\epsilon }^{\alpha }{\beta }_1^{\alpha }}{({\mu }^{\alpha }+{\epsilon }^{\alpha })({\mu }^{\alpha }+{\delta }^{\alpha })}{f}_1(S_0)g_1^{\prime }(0)\hfill \\ \hfill & +\frac{{\beta }_2^{\alpha }}{{\mu }^{\alpha }+{\epsilon }^{\alpha }}{f}_2(S_0)g_2^{\prime }(0).\hfill \end{array}\end{array}$$ 9

If $R_0>1$, system (2) has at least one endemic equilibrium point $M_{\ast }=(S_{\ast },E_{\ast },I_{\ast },Q_{\ast },R_{\ast },P_{\ast })$, where

$$\begin{array}{c}\hfill S_{\ast }=\frac{\Lambda -({\mu }^{\alpha }+{\epsilon }^{\alpha })E_{\ast }}{{\mu }^{\alpha }+{\rho }^{\alpha }},I_{\ast }=\frac{{\epsilon }^{\alpha }{E}_{\ast }}{{\mu }^{\alpha }+{\delta }^{\alpha }},\\ \hfill Q_{\ast }=\frac{{\delta }^{\alpha }{I}_{\ast }}{{\mu }^{\alpha }+{\lambda }^{\alpha }+{\kappa }^{\alpha }},R_{\ast }=\frac{{\lambda }^{\alpha }{Q}_{\ast }}{{\mu }^{\alpha }},P_{\ast }=\frac{{\rho }^{\alpha }{S}_{\ast }}{{\mu }^{\alpha }}.\end{array}$$

In the following section, we show that endemic equilibrium point $M_{\ast }$ is unique. According to the above analysis and hypothesis (i)–(iii), one has

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\phi }^{\prime }(E_{\ast })& =-\frac{({\mu }^{\alpha }+{\epsilon }^{\alpha }){\beta }_1^{\alpha }}{{\mu }^{\alpha }+{\rho }^{\alpha }}{f}_1^{\prime }(S_{\ast })g_1(I_{\ast })+\frac{{\epsilon }^{\alpha }{\beta }_1^{\alpha }}{{\mu }^{\alpha }+{\delta }^{\alpha }}{f}_1(S_{\ast })g_1^{\prime }(I_{\ast })\hfill \\ \hfill & -\frac{({\mu }^{\alpha }+{\epsilon }^{\alpha }){\beta }_2^{\alpha }}{{\mu }^{\alpha }+{\rho }^{\alpha }}{f}_2^{\prime }(S_{\ast })g_2(E_{\ast })+{\beta }_2^{\alpha }{f}_2(S_{\ast })g_2^{\prime }(E_{\ast })\hfill \\ \hfill & -({\mu }^{\alpha }+{\epsilon }^{\alpha })\hfill \\ \hfill & =-\frac{({\mu }^{\alpha }+{\epsilon }^{\alpha }){\beta }_1^{\alpha }}{{\mu }^{\alpha }+{\rho }^{\alpha }}{f}_1^{\prime }(S_{\ast })g_1(I_{\ast })\hfill \\ \hfill & -\frac{({\mu }^{\alpha }+{\epsilon }^{\alpha }){\beta }_2^{\alpha }}{{\mu }^{\alpha }+{\rho }^{\alpha }}{f}_2^{\prime }(S_{\ast })g_2(E_{\ast })\hfill \\ \hfill & +\frac{{\epsilon }^{\alpha }{\beta }_1^{\alpha }}{{\mu }^{\alpha }+{\delta }^{\alpha }}{f}_1(S_{\ast })g_1^{\prime }(I_{\ast })-\frac{{\epsilon }^{\alpha }{\beta }_1^{\alpha }{f}_1(S_{\ast })g_1(I_{\ast })}{({\mu }^{\alpha }+{\delta }^{\alpha })I_{\ast }}\hfill \\ \hfill & +{\beta }_2^{\alpha }{f}_2(S_{\ast })g_2^{\prime }(E_{\ast })-\frac{{\beta }_2^{\alpha }{f}_2(S_{\ast })g_2(E_{\ast })}{E_{\ast }}\hfill \\ \hfill & =-\frac{({\mu }^{\alpha }+{\epsilon }^{\alpha }){\beta }_1^{\alpha }}{{\mu }^{\alpha }+{\rho }^{\alpha }}{f}_1^{\prime }(S_{\ast })g_1(I_{\ast })\hfill \\ \hfill & -\frac{({\mu }^{\alpha }+{\epsilon }^{\alpha }){\beta }_2^{\alpha }}{{\mu }^{\alpha }+{\rho }^{\alpha }}{f}_2^{\prime }(S_{\ast })g_2(E_{\ast })\hfill \\ \hfill & +\frac{{\epsilon }^{\alpha }{\beta }_1^{\alpha }}{{\mu }^{\alpha }+{\delta }^{\alpha }}{f}_1(S_{\ast })[g_1^{\prime }(I_{\ast })-\frac{g_1(I_{\ast })}{I_{\ast }}]\hfill \\ \hfill & +{\beta }_2^{\alpha }{f}_2(S_{\ast })[g_2^{\prime }(E_{\ast })-\frac{g_2(E_{\ast })}{E_{\ast }}].\hfill \end{array}\end{array}$$ 10

By hypothesis (iv), this implies ${\phi }^{\prime }(E_{\ast })<0$. If there is another endemic equilibrium point $M_{\ast \ast }$, then ${\phi }^{\prime }(E_{\ast \ast })\ge 0$ holds, which contradicts the previous discussion. Hence, system (2) has a unique endemic equilibrium point $M_{\ast }$ when $R_0>1$. Based on the above analysis, the following results can be obtained.

Theorem 2

System (2) has a unique disease-free equilibrium point $M_0$, if $R_0<1$. System (2) has a unique endemic equilibrium point $M_{\ast }$, if $R_0>1$.

Stability analysis

In this section, the local asymptotic stability of disease-free equilibrium point $M_0$ and endemic equilibrium point $M_{\ast }$ for system (2) is discussed.

Theorem 3

With regard to system (2), the disease-free equilibrium point $M_0$ is locally asymptotic stability, if $R_0<1$; the disease-free equilibrium point $M_0$ is unstable, if $R_0>1$.

Proof

The Jacobian matrix of system (2) at the disease-free equilibrium point $M_0$ is

$$\begin{array}{c}\hfill J_{M_0}=\left[\begin{array}{cc}{J}_{11}& J_{12}\\ J_{21}& J_{22}\end{array}\right],\end{array}$$

where

$$\begin{array}{c}\hfill J_{11}=\left[\begin{array}{ccc}-{\mu }^{\alpha }-{\rho }^{\alpha }& -h_2& -h_1\\ 0& h_2-{\mu }^{\alpha }-{\epsilon }^{\alpha }& h_1\\ 0& {\epsilon }^{\alpha }& -{\mu }^{\alpha }-{\delta }^{\alpha }\end{array}\right],\end{array}$$

$$\begin{array}{c}\hfill J_{12}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right],J_{21}=\left[\begin{array}{ccc}0& 0& {\delta }^{\alpha }\\ 0& 0& 0\\ {\rho }^{\alpha }& 0& 0\end{array}\right],\end{array}$$

$$\begin{array}{c}\hfill J_{22}=\left[\begin{array}{ccc}-{\mu }^{\alpha }-{\kappa }^{\alpha }-{\lambda }^{\alpha }& 0& 0\\ {\lambda }^{\alpha }& -{\mu }^{\alpha }& 0\\ 0& 0& -{\mu }^{\alpha }\end{array}\right],\end{array}$$

where $h_1={\beta }_1^{\alpha }{f}_1(S_0)g_1^{\prime }(0)$ and $h_1={\beta }_2^{\alpha }{f}_2(S_0)g_2^{\prime }(0)$. The corresponding characteristic equation is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill H(s)& =|sE-J_{M_0}|\hfill \\ \hfill & ={(s+{\mu }^{\alpha })}^2(s+{\mu }^{\alpha }+{\rho }^{\alpha })(s+{\mu }^{\alpha }+{\lambda }^{\alpha }+{\kappa }^{\alpha })H_1(s),\hfill \end{array}\end{array}$$ 11

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill H_1(s)& =s^2+({\delta }^{\alpha }+2{\mu }^{\alpha }+{\epsilon }^{\alpha }-{\beta }_2^{\alpha }{f}_2(S_0)g_2^{\prime }(0))s\hfill \\ \hfill & +({\mu }^{\alpha }+{\delta }^{\alpha })({\mu }^{\alpha }+{\epsilon }^{\alpha })\hfill \\ \hfill & -{\beta }_2^{\alpha }({\mu }^{\alpha }+{\delta }^{\alpha })f_2(S_0)g_2^{\prime }(0)-{\epsilon }^{\alpha }{\beta }_1^{\alpha }{f}_1(S_0)g_1^{\prime }(0).\hfill \end{array}\end{array}$$ 12

The characteristic equation $H(s)=0$ has four obvious negative characteristic roots, which are denoted by $s_1=s_2=-{\mu }^{\alpha }$, $s_3=-{\mu }^{\alpha }-{\rho }^{\alpha }$ and $s_4=-{\mu }^{\alpha }-{\lambda }^{\alpha }-{\kappa }^{\alpha }$, respectively. The discriminant of $H_1(s)$ in quadratic form is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{\Delta }& ={[{\delta }^{\alpha }+2{\mu }^{\alpha }+{\epsilon }^{\alpha }-{\beta }_2^{\alpha }{f}_2(S_0)g_2^{\prime }(0)]}^2\hfill \\ \hfill & -4[({\mu }^{\alpha }+{\delta }^{\alpha })({\mu }^{\alpha }+{\epsilon }^{\alpha })\hfill \\ \hfill & -{\beta }_2^{\alpha }({\mu }^{\alpha }+{\delta }^{\alpha })f_2(S_0)g_2^{\prime }(0)-{\epsilon }^{\alpha }{\beta }_1^{\alpha }{f}_1(S_0)g_1^{\prime }(0)]\hfill \\ \hfill & ={({\delta }^{\alpha }-{\epsilon }^{\alpha }+{\beta }_2^{\alpha }{f}_2(S_0)g_2^{\prime }(0))}^2+4{\epsilon }^{\alpha }{\beta }_1^{\alpha }{f}_1(S_0)g_1^{\prime }(0)\hfill \\ \hfill & >0.\hfill \end{array}\end{array}$$

This implies that the other two eigenvalues $s_5$ and $s_6$ of characteristic equation $H(s)=0$ are real roots. Hence,

$$\begin{array}{c}\hfill s_5+s_6=-({\delta }^{\alpha }+2{\mu }^{\alpha }+{\epsilon }^{\alpha }-{\beta }_2^{\alpha }{f}_2(S_0)g_2^{\prime }(0)),\\ \hfill s_5{s}_6=({\mu }^{\alpha }+{\delta }^{\alpha })({\mu }^{\alpha }+{\epsilon }^{\alpha })(1-R_0).\end{array}$$

If $R_0<1$, then one can obtain $s_5+s_6<0$ and $s_5{s}_6>0$, which imply $s_5<0$ and $s_6<0$. If $R_0>1$, one has $s_5{s}_6<0$, which imply $s_5>0$ or $s_6>0$. It follows from Lemma 1 that the proof is completed.

Further, we will show the locally asymptotic stability of the endemic equilibrium point $M_{\ast }$ of system (2). Similarly, the corresponding Jacobian matrix of system (2) at $M_{\ast }$ is

$$\begin{array}{c}\hfill J_{M_{\ast }}=\left[\begin{array}{cc}{J}_1& J_2\\ J_3& J_4\end{array}\right],\end{array}$$

where

$$\begin{array}{c}\hfill J_1=\left[\begin{array}{ccc}-l_3-l_4-{\mu }^{\alpha }-{\rho }^{\alpha }& -l_2& -l_1\\ l_3+l_4& l_2-{\epsilon }^{\alpha }-{\mu }^{\alpha }& l_1\\ 0& {\epsilon }^{\alpha }& -{\delta }^{\alpha }-{\mu }^{\alpha }\end{array}\right],\end{array}$$

$$\begin{array}{c}\hfill J_2=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ \end{array}\right],J_3=\left[\begin{array}{ccc}0& 0& {\delta }^{\alpha }\\ 0& 0& 0\\ {\rho }^{\alpha }& 0& 0\\ \end{array}\right],\end{array}$$

$$\begin{array}{c}\hfill J_4=\left[\begin{array}{ccc}-{\mu }^{\alpha }-{\lambda }^{\alpha }-{\kappa }^{\alpha }& 0& 0\\ {\lambda }^{\alpha }& -{\mu }^{\alpha }& 0\\ 0& 0& -{\mu }^{\alpha }\\ \end{array}\right],\end{array}$$

with

$$\begin{array}{cc}\hfill l_1=& {\beta }_1^{\alpha }{f}_1(S_{\ast })g_1^{\prime }(I_{\ast }),l_2={\beta }_2^{\alpha }{f}_2(S_{\ast })g_2^{\prime }(E_{\ast }),\hfill \\ \hfill l_3=& {\beta }_1^{\alpha }{f}_1^{\prime }(S_{\ast })g_1(I_{\ast }),l_4={\beta }_2^{\alpha }{f}_2^{\prime }(S_{\ast })g_2(E_{\ast }).\hfill \end{array}$$

Hence, the corresponding characteristic equation is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill L(s)& =|sE-J_{M_{\ast }}|\hfill \\ \hfill & ={(s+{\mu }^{\alpha })}^2(s+{\mu }^{\alpha }+{\lambda }^{\alpha }+{\kappa }^{\alpha })L_1(s),\hfill \end{array}\end{array}$$ 13

where

$$\begin{array}{c}\hfill L_1(s)=s^3+a_1{s}^2+a_{2}s+a_3,\end{array}$$

with

$$\begin{array}{cc}\hfill a_1=& {\epsilon }^{\alpha }+3{\mu }^{\alpha }+{\delta }^{\alpha }+{\rho }^{\alpha }-l_2+l_3+l_4,\hfill \\ \hfill a_2=& ({\mu }^{\alpha }+{\epsilon }^{\alpha }-l_2)(2{\mu }^{\alpha }+{\delta }^{\alpha }+{\rho }^{\alpha })+({\mu }^{\alpha }+{\delta }^{\alpha })({\mu }^{\alpha }+{\rho }^{\alpha })\hfill \\ \hfill & +(2{\mu }^{\alpha }+{\delta }^{\alpha }+{\epsilon }^{\alpha })(l_3+l_4)-{\epsilon }^{\alpha }{l}_1,\hfill \\ \hfill a_3=& ({\mu }^{\alpha }+{\delta }^{\alpha })({\mu }^{\alpha }+{\rho }^{\alpha })({\mu }^{\alpha }+{\epsilon }^{\alpha }-l_2)\hfill \\ \hfill & +({\mu }^{\alpha }+{\delta }^{\alpha })({\mu }^{\alpha }+{\epsilon }^{\alpha })(l_3+l_4)-{\epsilon }^{\alpha }({\mu }^{\alpha }+{\rho }^{\alpha })l_1.\hfill \end{array}$$

By the corresponding results in [26, 27], let

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill D_1(L_1(s))& =\left|\begin{array}{ccccc}1& a_1& a_2& a_3& 0\\ 0& 1& a_1& a_2& a_3\\ 3& 2l{a}_1& a_2& 0& 0\\ 0& 3& 2a_1& a_2& 0\\ 0& 0& 3& 2a_1& a_2\end{array}\right|\hfill \\ \hfill & =18a_1{a}_2{a}_3+a_1^2{a}_2^2-4a_1^3{a}_3-4a_2^3-27a_3^2.\hfill \end{array}\end{array}$$ 14

Then, the following result can be obtained.

Theorem 4

With regard to system (2), assume that $R_0>1$,

• (i)If $D_1(L_1(s))>0$, $a_1>0$, $a_3>0$ and $a_1{a}_2>a_3$, then the endemic equilibrium point $M_{\ast }$ is locally asymptotically stable.
• (ii)If $D_1(L_1(s))<0$, $a_1>0$, $a_2>0$ and $a_3>0$, then the endemic equilibrium point $M_{\ast }$ is locally asymptotically stable for $\alpha \in (0,\frac{2}{3})$.
• (iii)If $D_1(L_1(s))<0$, $a_1<0$ and $a_2<0$, then the endemic equilibrium point $M_{\ast }$ is unstable for $\alpha \in (\frac{2}{3},1)$.
• (iv)If $D_1(L_1(s))<0$, $a_1>0$, $a_2>0$ and $a_1{a}_2=a_3$, then for $\alpha \in (0,1)$, the endemic equilibrium point $M_{\ast }$ is locally asymptotically stable.

Proof

Based on the previous discussion, the characteristic equation $L(s)=0$ has three obvious negative roots $s_1=s_2=-{\mu }^{\alpha }$ and $s_3=-{\mu }^{\alpha }-{\lambda }^{\alpha }-{\kappa }^{\alpha }$. In order to investigate the stability of equilibrium point $M_{\ast }$, we only need to discuss the range of the root of $L_1(s)=0$, denoted by $s_4$, $s_5$ and $s_6$.

(i) By the results in [27], if $D_1(L_1(s))>0$, then $s_4$, $s_5$ and $s_6$ are real roots. Further, by Routh–Hurwitz criterion, the necessary and sufficient conditions for $s_i(i=4,5,6)$ to lie in the left half plane are

$$\begin{array}{c}\hfill a_1>0,a_3>0,a_1{a}_2>a_3.\end{array}$$

That is to say, under the above conditions, the roots of $L_1(s)=0$ satisfy

$$\begin{array}{c}\hfill |arg(s_i)|>\frac{\pi }{2}>\frac{\alpha \pi }{2}(i=4,5,6).\end{array}$$

Therefore, $M_{\ast }$ is locally asymptotically stable and (i) holds

(ii) By the results in [27], if $D_1(L_1(s))<0$, then $L_1(s)=0$ has a real root and a pair of conjugate complex roots, denoted by $s_4$, $m+ni$ and $m-ni$, respectively. Thus, one has

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill L_1(s)& =s^3+a_1{s}^2+a_{2}s+a_3\hfill \\ \hfill & =(s-s_4)(s-m-ni)(s-m+ni).\hfill \end{array}\end{array}$$

By calculation,

$$\begin{array}{c}\hfill a_1=-s_4-2m,a_2=2s_{4}m+m^2+n^2,a_3=-s_4(m^2+n^2).\end{array}$$

The conditions $a_1>0$, $a_2>0$ and $a_3>0$ imply that

$$\begin{array}{c}\hfill -s_1>2m,m^2+n^2>-2s_{4}m,s_4<0.\end{array}$$

Further, one has

$$\begin{array}{c}\hfill m^2+m^2{tan}^2\theta >-2s_{4}m>4m^2.\end{array}$$

That is to say ${tan}^2\theta >3$, which implies

$$\begin{array}{c}\hfill \theta =|arg(s)|>\frac{\pi }{3}.\end{array}$$

Therefore, in order to ensure the establishment of $|arg(s)|>\frac{\alpha \pi }{2}$, we must have $\alpha <\frac{2}{3}$. Thus, (ii) holds.

The proof of conclusions (iii) and (iv) is similar to that of conclusion (ii); hence, we omit it.

Numerical simulations

Data sources

The data used in this paper are from the Johns Hopkins University Center for Systems Science and Engineering (https://github.com/CSSEGISandData/COVID-19). the Johns Hopkins University publishes data of accumulated and newly confirmed cases, recovered cases and death cases of COVID-19 from January 22, 2020.

Analysis of the SEIQRP model

In the following discussion, the standard incidence rate [28] is used to describe the transmission of COVID-19 and is given by

$$\begin{array}{c}\hfill {\beta }_1^{\alpha }{f}_1(S)g_1(I)=\frac{{\beta }_1^{\alpha }SI}{N},{\beta }_2^{\alpha }{f}_2(S)g_2(E)=\frac{{\beta }_2^{\alpha }SE}{N},\end{array}$$

where N represents the total population of the region at the initial time. Hence,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {}_0^C{D}_t^{\alpha }S(t)& =\Lambda -\frac{{\beta }_1^{\alpha }S(t)I(t)}{N}-\frac{{\beta }_2^{\alpha }S(t)E(t)}{N}\hfill \\ \hfill & -{\mu }^{\alpha }S(t)-{\rho }^{\alpha }S(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }E(t)& =\frac{{\beta }_1^{\alpha }S(t)I(t)}{N}+\frac{{\beta }_2^{\alpha }S(t)E(t)}{N}\hfill \\ \hfill & -{\epsilon }^{\alpha }E(t)-{\mu }^{\alpha }E(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }I(t)& ={\epsilon }^{\alpha }E(t)-({\delta }^{\alpha }+{\mu }^{\alpha })I(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }Q(t)& ={\delta }^{\alpha }I(t)-({\lambda }^{\alpha }+{\kappa }^{\alpha }+{\mu }^{\alpha })Q(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }R(t)& ={\lambda }^{\alpha }Q(t)-{\mu }^{\alpha }R(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }P(t)& ={\rho }^{\alpha }S(t)-{\mu }^{\alpha }P(t).\hfill \end{array}\right)\end{array}$$ 15

The effectiveness of model (15) in describing the spread of COVID-19 is illustrated by selecting the confirmed, cured and death cases in the USA. According to the real data provided by the Johns Hopkins University, the outbreak in the USA has not been brought under full control. The data of confirmed cases, recovered cases and death cases are selected from January 22, 2020, to April 20, 2020. Assuming that the confirmed individuals will be isolated, then

$$\begin{array}{c}\hfill Isolated=Confirmed-Recovered-Death.\\ \hfill \end{array}$$ 16

This hypothesis is in line with the actual situation. Hence, we can obtain the real data of isolated cases. Let $e_Q=Q_r-Q_m$, $e_R=R_r-R_m$ and $e_D=D_r-D_m$, where $Q_r$, $R_r$ and $D_r$ denote the real data of isolated cases, recovered cases and death cases, respectively, $Q_m$, $R_m$ and $D_m$ represent the measured value of isolated cases, recovered cases and death cases, respectively. Here, we consider a minimization objective function as:

$$\begin{array}{c}\hfill J_{\mathit{min}}=\sum _{i=1}^T(e_Q^2(i)+e_R^2(i)+e_D^2(i)),\end{array}$$

where T is the number of real data of isolated cases available. The internal function lsqcurvefit of MATLAB is used to minimize the above objective function value. Similar methods are adopted for subsequent parameter identification. Through the fractional predictor–corrector method [29, 30] and the least squares fitting [31], we can identify the parameters of the model (15) through the real data, which is given in Table 1. For more detail with respect to fractional predictor–corrector algorithm, one can refer to [29, 30].

Table 1.

Summary table of the parameter identification for model (15) after using least squares fitting to real data from January 22, 2020, to April 20, 2020

Notation	Parameter identification
$\alpha$	0.7937
$\Lambda$	433994
${\beta }_1$	0.2209
${\beta }_2$	0.7392
$\mu$	$5.2129\times {10}^{-7}$
$\rho$	0.1224
$\epsilon$	0.2467
$\delta$	0.1031
$\lambda$	0.0024
$\kappa$	$1.2932\times {10}^{-5}$

Based on the parameters in Table 1, we can make a simple prediction of isolated cases and recovered cases in the USA, which is shown in Fig. 2. We need to emphasize that the peak here represents the number of isolated cases rather than the cumulative number of confirmed cases.

Fig. 2.

Number of isolated cases predicted and recovered cases predicted by the model (15) for the USA

Using the parameters in Table 1, it can be calculated by using (9) that $R_0=0.0289<1$. By the conclusion in Theorem 3, the disease-free equilibrium point is local asymptotic stable. The SEIQRP model has a basic guiding significance for predicting and fitting spreading dynamics of COVID-19. However, the prediction of this model for COVID-19 is relatively rough; we still need to improve model (15) according to actual mitigation policies and research objectives. According to the analysis in Sect. 2.1, we choose the SEIQRPD model to predict the trend of the epidemic in the USA under reasonable assumptions.

The SEIQRPD model for the prediction of COVID-19

Similarly, the standard incidence rate is used to describe the transmission of COVID-19, and the fractional SEIQRPD model can be expressed as

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {}_0^C{D}_t^{\alpha }S(t)& =-\frac{{\beta }_1^{\alpha }(t)S(t)I(t)}{N}-\frac{{\beta }_2^{\alpha }S(t)E(t)}{N}-{\rho }^{\alpha }S(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }E(t)& =\frac{{\beta }_1^{\alpha }(t)S(t)I(t)}{N}+\frac{{\beta }_2^{\alpha }S(t)E(t)}{N}-{\epsilon }^{\alpha }E(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }I(t)& ={\epsilon }^{\alpha }E(t)-{\delta }^{\alpha }I(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }Q(t)& ={\delta }^{\alpha }I(t)-({\lambda }^{\alpha }(t)+{\kappa }^{\alpha }(t))Q(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }R(t)& ={\lambda }^{\alpha }(t)Q(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }P(t)& ={\rho }^{\alpha }S(t),\hfill \\ \hfill {}_0^C{D}_t^{\alpha }D(t)& ={\kappa }^{\alpha }(t)Q(t).\hfill \end{array}\right)\end{array}$$ 17

It should be emphasized that the numerical properties of model (17) are mainly studied. Different from the analysis of model (2) and model (15), the fractional-order $\alpha$ of model (3) and model (17) is not required to be within (0, 1). Therefore, in the parameter identification of model (17), the search range of parameter $\alpha$ is considered as (0, 2). When $\alpha =1$, the fractional-order SEIQRPD model is similar to the integer-order model used in [24]. According to the data provided by Johns Hopkins University, by April 20, 2020, the outbreak in China has been basically controlled. In many provinces of China, the number of new cases per day is increasing in single digits. This means that the data in China contain more information about the spreading dynamics of COVID-19. Therefore, the data in Hubei, Guangdong, Hunan and Zhejiang are selected to research the fitting effect of the model (17). According to the real data of these four regions in China, the parameters of the model (17) are identified, and the results are shown in Table 2. The model (17) successfully capture the trend of the outbreak, which is shown in Fig. 3.

Table 2.

Summary of parameter identification of model (17) (data used from January 22, 2020, to April 20, 2020)

Notation	Hubei	Guangdong	Hunan	Zhejiang
$\alpha$	1.0771	1.0315	1.0133	1.0688
${\sigma }_1$	0.6295	1.2773	0.7255	1.9997
${\sigma }_2$	$5.59\times {10}^{-4}$	0.4525	0.1139	1.2108
${\beta }_2$	0.2863	0.2675	0.3352	0.3226
$\rho$	0.1494	0.0581	0.0464	0.0052
$\epsilon$	0.2781	0.3558	0.4649	0.4986
$\delta$	0.2598	0.3838	0.6756	0.4097
${\lambda }_1$	0.5118	0.7336	0.987	0.9997
${\lambda }_2$	0.0033	0.0036	0.0038	0.0032
${\kappa }_1$	0.0031	0.0013	$2.94\times {10}^{-4}$	$1.51\times {10}^{-4}$
${\kappa }_2$	$4.18\times {10}^{-4}$	0.0911	$4.09\times {10}^{-14}$	$4.12\times {10}^{-14}$

Fig. 3.

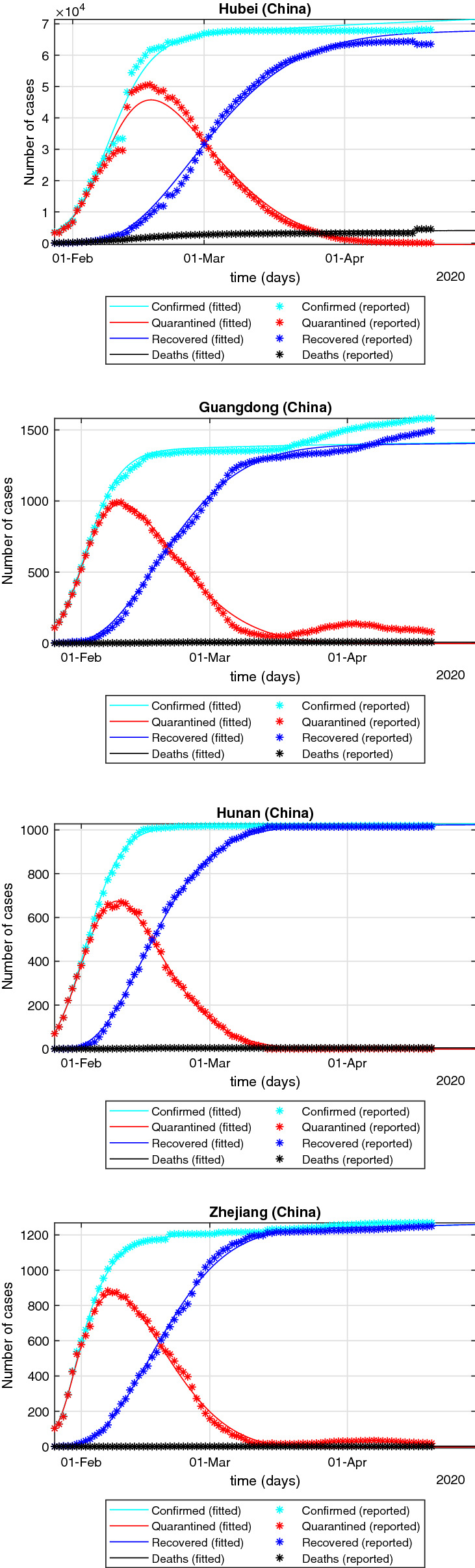
Fitting effect of the improved model (17) on the outbreak in Hubei, Guangdong, Hunan and Zhejiang

According to Definition 1, when $\alpha =1$, the fractional-order system (17) becomes integer-order system. Tables 5 and 6, respectively, show the prediction results of cumulative confirmed cases and isolated cases by the integer-order system corresponding to model (17). By comparing Table 3 with Tables 5 and 4 with Table 6, we can find that the fractional system (17) has better prediction effect than its corresponding integer system.

Table 5.

Summary of real and predicted data for the cumulative confirmed cases in the USA from April 6, 2020, to April 20, 2020, when $\alpha =1$

Data	Cumulative confirmed cases		Relative error (%)
	Reported	Predicted
6, April	366,667	372,660	1.63
7, April	397,505	408,046	2.65
8, April	429,052	444,475	3.59
9, April	462,780	481,813	4.11
10, April	496,535	519,923	4.71
11, April	526,396	558,665	6.13
12, April	555,313	597,901	7.67
13, April	580,619	637,494	9.8
14, April	607,670	677,308	11.46
15, April	636,350	717,213	12.71
16, April	667,592	757,082	13.4
17, April	699,706	796793	13.88
18, April	732,197	836,231	14.21
19, April	759,086	875,287	15.31
20, April	784,326	913,861	16.52
Average			9.19

Table 6.

Summary of real and predicted data for the isolated cases in the USA from April 6, 2020, to April 20, 2020, when $\alpha =1$

Data	Isolated cases		Relative error (%)
	Reported	Predicted
6, April	336,303	341,929	1.67
7, April	362,948	372,162	2.54
8, April	390,798	402,864	3.09
9, April	420,826	433,871	3.1
10, April	449,159	465,022	3.53
11, April	474,664	496,156	4.53
12, April	500,306	527,114	5.36
13, April	513,609	557,741	8.59
14, April	534,076	587,888	10.08
15, April	555,929	617,412	11.06
16, April	579,973	646,178	11.42
17, April	604,388	674,059	11.53
18, April	628,693	700,937	11.49
19, April	648,088	726,706	12.13
20, April	669,903	751,268	12.15
Average			7.48

Table 3.

Summary of real and predicted data for the cumulative confirmed cases in the USA from April 6, 2020, to April 20, 2020

Data	Cumulative confirmed cases		Relative error (%)
	Reported	Predicted
6, April	366,667	370,997	1.18
7, April	397,505	404,778	1.83
8, April	429,052	438,986	2.32
9, April	462,780	473,397	2.29
10, April	496,535	507,790	2.27
11, April	526,396	541,952	2.96
12, April	555,313	575,680	3.67
13, April	580,619	608,786	4.85
14, April	607,670	641,099	5.5
15, April	636,350	672,464	5.68
16, April	667,592	702,748	5.27
17, April	699,706	731,837	4.59
18, April	732,197	759,637	3.75
19, April	759,086	786,076	3.56
20, April	784,326	811,103	3.41
Average			3.54

Table 4.

Summary of real and predicted data for the isolated cases in the USA from April 6, 2020, to April 20, 2020

Data	Isolated cases		Relative error (%)
	Reported	Predicted
6, April	336,303	340,153	1.14
7, April	362,948	368,742	1.6
8, April	390,798	397,193	1.64
9, April	420,826	425,264	1.05
10, April	449,159	452,719	0.79
11, April	474,664	479,335	0.98
12, April	500,306	504,905	0.92
13, April	513,609	529,239	3.04
14, April	534,076	552,168	3.39
15, April	555,929	573,547	3.17
16, April	579,973	593,252	2.29
17, April	604,388	611,186	1.12
18, April	628,693	627,274	0.23
19, April	648,088	641,467	1.02
20, April	669,903	653,736	2.41
Average			1.65

At present, we can obtain the epidemic data of the USA from January 22, 2020, to April 20, 2020. We need to preprocess the data to remove the data smaller than 0.5% of the current highest number of confirmed cases. In order to test the prediction ability of the SEIQRPD model (17) for the development process of the epidemic in the USA, we select the data before April 5 to identify the parameters of the SEIQRPD model (17). Furthermore, in order to illustrate the ability of the SEIQRPD model (17) in predicting the outbreak, we compared the real data and fitted data after April 5, which is given in Tables 3, 4 and Fig. 4. According to the results in Tables 3 and 4, it can be found that the real values of current isolated cases and cumulative confirmed cases fall within the range of 94–106% of the predicted values. This shows that the SEIQRPD model (17) can effectively predict the data in the next two weeks.

Fig. 4.

Based on the data of the USA from January 22 to April 5, 2020, to verify the accuracy of the forecast for the next 15 days

The data before April 20, 2020, are selected to identify the parameters of the improved model (17), and the results are shown in Table 7. The cumulative number of confirmed cases and the number of isolated cases after two weeks are predicted, which is given in Table 8.

Table 7.

Summary table of the parameter identification for model (17) (data used from January 22, 2020, to April 20, 2020)

Notation	Parameter identification
$\alpha$	0.9806
${\sigma }_1$	0.9339
${\sigma }_2$	0.1958
${\beta }_2$	0.2654
$\rho$	$4.8484\times {10}^{-6}$
$\epsilon$	0.2881
$\delta$	0.4115
${\lambda }_1$	0.0076
${\lambda }_2$	0.2096
${\kappa }_1$	0.0079
${\kappa }_2$	0.0345

Table 8.

Summary of predicted data for the USA from April 21, 2020, to May 5, 2020

Data	Cumulative confirmed cases	Isolated cases
	Predicted	Predicted
21, April	804,417	684,573
22, April	829,428	702,336
23, April	853,882	719,428
24, April	877,785	735,862
25, April	901,144	751,654
26, April	923,967	766,819
27, April	946,265	781,374
28, April	968,047	795,334
29, April	989,322	808,715
30, April	1,010,102	821,533
1, May	1,030,397	833,805
2, May	1,050,217	845,546
3, May	1,069,574	856,771
4, May	1,088,477	867,495
5, May	1,106,937	877,733

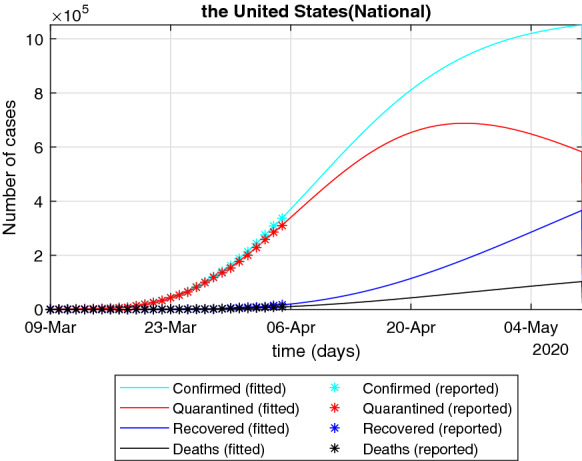
The isolated cases in the USA will peak on June 18, 2020, with the peak of $1.0431\times {10}^6$, which is shown in Fig. 5. We must point out that the peak forecast here is only based on the data before April 20, 2020. It is only a rough estimate from the point of view of numerical simulation. The peak value will be greatly influenced by the policy and environment. The change of policy and environment makes the prediction of peak value very difficult. For the peak prediction, we will do further research in the future work.

Fig. 5.

Based on the data of the USA from January 22 to April 20, 2020, to verify the accuracy of the forecast for the next 15 days

Conclusion

We first propose the fractional SEIQRP model with generalized incidence rates. Some qualitative properties of the SEIQRP model are discussed. In order to predict COVID-19 effectively, we propose an improved SEIQRPD model according to the actual mitigation situation. According to the data of the USA before April 5, 2020, the trend of the outbreak in the USA from April 6 to April 20 is successfully predicted as compared to the real records. Then, using the data before April 20, 2020, we forecast the trend of the outbreak in the USA in the next two weeks and estimate the peak of isolated cases and the date of the peak.

The improved SEIQRP model proposed in this paper successfully captures the trend of COVID-19. The long-term prediction needs to adjust the model appropriately according to the change of policy and medical level. We will discuss in the future work.

Compliance with ethical standards

Conflict of interest

We declare that we have no conflict of interest.